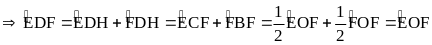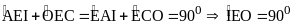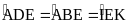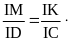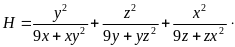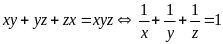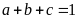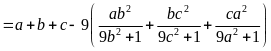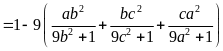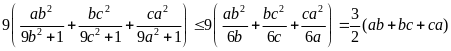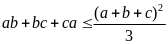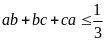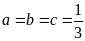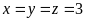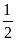Đề Thi Chuyên Toán Vào Lớp 10 Chuyên Sở GD Quảng Nam 2021-2022
>>> Mọi người cũng quan tâm:
Đề Thi Chuyên Toán Vào Lớp 10 Chuyên Sở GD Quảng Nam 2021-2022 Có Đáp Án – Toán 9 là tài liệu học tập được Trang Tài Liệu biên soạn và sưu tầm từ những nguồn dữ liệu mới nhất hiện nay. Tài liệu này sẽ giúp các em luyện tập, củng cố kiến thức từ đó nâng cao điểm số cho môn học. Ngoài ra, cũng giúp các thầy cô giáo có nguồn tài nguyên phong phú để giảng dạy.
Dưới đây là bản đọc trực tuyến giúp thầy cô và các em học sinh có thể nghiên cứu Online hoặc bạn có thể tải miễn phí với phiên bản word để dễ dàng in ấn cũng như học tập Offline.
SỞ GIÁO DỤC VÀ ĐÀO TẠO
|
KỲ THI TUYỂN SINH LỚP 10 THPT CHUYÊN
|
|
(Đề thi có 01 trang) |
Môn thi: TOÁN (Chuyên Toán) Thời gian: 150 phút (không kể thời gian giao đề) Khóa thi ngày: 03-05/6/2021
|
Câu 1. (2,0 điểm)
Rút gọn biểu thức
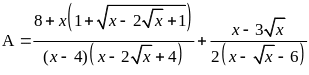
(với
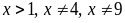 )
)
b)
Tìm tất cả
bộ ba số nguyên tố p,
q,
r
thỏa mãn
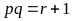 và
và
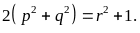
Câu 2. (1,0 điểm)
Cho
parabol
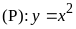 và đường thẳng
và đường thẳng
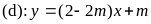 (m
là tham số).
Chứng minh rằng
(m
là tham số).
Chứng minh rằng
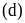 luôn cắt
luôn cắt
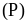 tại hai điểm phân biệt với mọi giá trị của m.
Khi đường thẳng
tại hai điểm phân biệt với mọi giá trị của m.
Khi đường thẳng
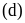 cắt
(P) tại hai điểm A,
B
sao
cho
cắt
(P) tại hai điểm A,
B
sao
cho
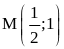 là trung điểm của đoạn thẳng AB, hai điểm
K, H
lần
lượt là hình chiếu vuông góc của A, B trên trục hoành.
Tính độ dài đoạn thẳng KH.
là trung điểm của đoạn thẳng AB, hai điểm
K, H
lần
lượt là hình chiếu vuông góc của A, B trên trục hoành.
Tính độ dài đoạn thẳng KH.
Câu 3. (2,0 điểm)
a)
Giải phương trình
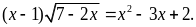
Câu 4. (2,0 điểm)
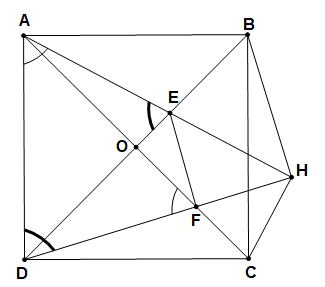
Cho hình vuông ABCD tâm O, điểm E nằm trên đoạn thẳng OB (E khác O, B), H là hình chiếu vuông góc của C trên đường thẳng AE. Gọi F là giao điểm của AC và DH.
a)
Chứng minh HD là tia phân giác của góc .
.
b) Chứng minh diện tích hình vuông ABCD bằng hai lần diện tích tứ giác AEFD.
Câu 5. (2,0 điểm)
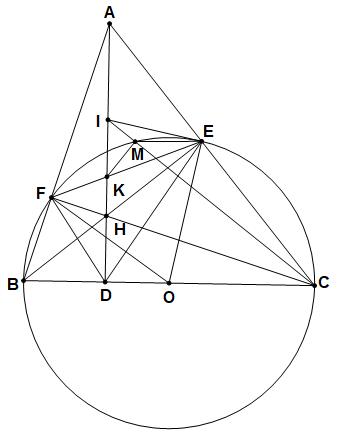
Cho tam giác nhọn ABC (AB < AC). Đường tròn (O) đường kính BC cắt AB, AC lần lượt tại F, E. Gọi H là giao điểm của BE và CF, đường thẳng AH cắt BC tại D.
a) Chứng minh tứ giác ODFE nội tiếp đường tròn.
b) Gọi K là giao điểm của AH và EF, I là trung điểm của AH. Đường thẳng CI cắt đường tròn (O) tại điểm M (M khác C). Chứng minh CI vuông góc với KM.
Câu 6. (1,0 điểm)
Cho
ba số thực dương
 thỏa mãn
thỏa mãn
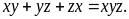 Tìm
giá trị nhỏ nhất của biểu thức
Tìm
giá trị nhỏ nhất của biểu thức
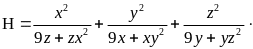
--------------- HẾT ---------------
Họ và tên thí sinh:................................................................Số báo danh: .........................
SỞ GIÁO DỤC VÀ ĐÀO TẠO
|
KỲ THI TUYỂN SINH LỚP 10 THPT CHUYÊN
|
|
|
HƯỚNG DẪN CHẤM MÔN: TOÁN (CHUYÊN TOÁN) |
(Bản hướng dẫn này gồm 06 trang)
Câu |
Nội dung |
Điểm |
Câu 1 (2,0) |
a) Rút gọn biểu thức
|
1,0 |
|
0,5 |
|
|
0,25 |
|
|
0,25 |
|
b) Tìm tất cả bộ
ba số nguyên tố p, q, r thỏa mãn
|
1,0 |
|
+ Nếu p, q cùng là số lẻ
Mà p, q lẻ nên
|
0,5 |
|
+ p, q khác tính chẵn lẻ, giả sử
Khi đó, ta có
|
0,25 |
|
Vậy có hai bộ số thỏa yêu cầu là:
|
0,25 |
|
Cách khác: Từ
|
0.25 |
|
Suy ra
|
0.25 |
|
Khi đó, ta có
|
0.25 |
|
Vai trò p,q như nhau nên có hai bộ
số thỏa yêu cầu là:
|
0.25 |
Câu 2 (1,0) |
Cho parabol
|
1,0 |
|
|
|
- Phương trình hoành
độ giao điểm của
|
0,25 |
|
Suy ra pt (*) luôn có hai nghiệm phân biệt, hay (d) luôn cắt (P) tại hai điểm phân biệt. |
0,25 |
|
+ Gọi
N là hình chiếu vuông góc của M lên trục hoành. +
M là trung điểm của AB, khi đó N là trung điểm của
|
0,25 |
|
Khi đó pt(*) trở
thành
Suy ra
|
0,25 |
|
Cách khác: Gọi
M trung điểm AB nên
|
0.25
|
|
Ta có
Theo
định lý Viet ta có
Do đó
|
0.25 |
Câu |
Nội dung |
Điểm |
Câu 3 (2,0) |
a) Giải phương trình
|
1,0 |
Điều kiện:
|
0,25 |
|
|
0,25 |
|
|
0,25 |
|
Vậy phương trình đã cho có hai nghiệm
|
0,25 |
|
b) Giải
hệ phương trình
|
1,0 |
|
* Cách 1:
|
0,25 |
|
+ Với
|
0,5 |
|
+ Với
Vậy hệ phương
trình đã cho có 4 nghiệm:
* Lưu ý: Nếu học sinh làm đúng 1 trong 2 trường hợp trên (với x = 2, với y = 1) thì cho 0,5đ |
0,25 |
|
* Cách 2:
|
0,25 |
|
|
0,25 |
|
- Với
Suy ra
|
0,25 |
|
- Với
Suy ra
Vậy hệ phương trình đã cho có 4
nghiệm:
|
0,25 |
|
* Cách 3
|
0,25 |
+ Đặt
+ Giải hệ (**) tìm được:
|
0,25 |
|
+ Với
|
0,25 |
|
+ Với
Vậy hệ phương trình đã cho có 4
nghiệm:
|
0,25 |
Câu |
Nội dung |
Điểm |
Câu 4 (2,0) |
Cho hình vuông ABCD tâm O, điểm E nằm trên đoạn thẳng OB (E khác O, B), H là hình chiếu vuông góc của C trên đường thẳng AE. Gọi F là giao điểm của AC và DH. |
|
(Hình vẽ phục vụ câu a: 0,25 điểm) |
0,25 |
|
a) Chứng minh HD là tia phân giác của
|
0,75 |
|
Các điểm B, H, D cùng nhìn đoạn AC dưới 1 góc vuông nên 5 điểm A, B, H, C, D cùng nằm trên đường tròn đường kính AC. |
0,25 |
|
Suy ra
|
0,25 |
|
|
0,25 |
|
b) Chứng minh diện tích hình vuông ABCD bằng hai lần diện tích tứ giác AEFD |
1,0 |
|
Ta có
Tứ giác AEFD có hai đường chéo vuông góc nhau nên
|
0,25 |
|
Xét hai tam giác AFD và DAE có: +
+
Suy ra hai tam giác AFD và DAE đồng dạng. |
0,5 |
|
Từ đó có tỉ lệ
Từ (1), (2), (3) ta có
|
0,25 |
Câu |
Nội dung |
Điểm |
Câu 5 (2,0) |
Cho tam giác nhọn ABC (AB < AC). Đường tròn (O) đường kính BC cắt AB, AC lần lượt tại F, E. Gọi H là giao điểm của BE và CF, đường thẳng AH cắt BC tại D. |
|
(Hình vẽ phục vụ câu a: 0,25 điểm) |
|
|
a) Chứng minh tứ giác ODFE nội tiếp đường tròn. |
0,75 |
|
+ Tứ giác CDHE nội tiếp đường tròn nên
|
0,25 |
|
+ Tứ giác BDHF nội tiếp đường tròn nên
|
0,25 |
|
Vậy tứ giác ODFE nội tiếp đường tròn. |
0,25 |
|
b) Gọi K là giao điểm của AH và EF, I là trung điểm của AH. Đường thẳng CI cắt đường tròn (O) tại điểm M (M khác C). Chứng minh CI vuông góc với KM. |
1,0 |
|
Suy ra IE là tiếp tuyến của đường tròn (O). |
0,25 |
|
+ Chứng minh được hai tam giác IEM và ICE đồng dạng. Suy ra IE2 = IM.IC (1) |
0,25 |
|
+ Tứ giác ABDE nội tiếp đường tròn nên
Suy ra được hai tam giác IEK và IDE đồng dạng. Suy ra IE2 = IK.ID (2) |
0,25 |
|
+ Từ (1) và (2) suy ra IM.IC = IK.ID hay
Suy ra được hai tam giác IMK và IDC đồng dạng. Hơn nữa tam giác IDC vuông tại D nên tam giác IMK vuông tại M. |
0,25 |
Câu |
Nội dung |
Điểm |
Câu 6 (1,0) |
Cho ba số thực dương
|
1,0 |
Từ giả thiết, suy ra :
Đặt
|
0,25 |
|
Suy ra
|
0,25 |
|
Chứng minh được
Thật
vậy:
Suy ra
|
0,25 |
|
Dấu bằng xảy ra
khi
|
0,25 |
* Lưu ý:
Nếu thí sinh làm bài không theo cách nêu trong đáp án nhưng đúng thì vẫn cho đủ số điểm từng phần như hướng dẫn quy định.
Ngoài Đề Thi Chuyên Toán Vào Lớp 10 Chuyên Sở GD Quảng Nam 2021-2022 Có Đáp Án – Toán 9 thì các tài liệu học tập trong chương trình 9 sẽ được cập nhật liên tục và nhanh nhất có thể sau khi kỳ thi diễn ra trên Danh mục Tài Liệu Học Tập nhằm giúp các bạn đọc thuận tiện trong việc nghiên cứu tài liệu. Quý thày cô và các bạn đọc có thể chia sẻ thêm những tài liệu học tập hữu ích đến địa chỉ email của chúng tôi, nhằm xây dựng nên kho đề thi phong phú, đa dạng cho các em học sinh tham khảo và rèn luyện.
Bộ đề thi này là một tài liệu ôn tập toán học chất lượng và đáng tin cậy, được thiết kế đặc biệt cho các bạn học sinh có mong muốn vào học lớp 10 tại trường chuyên. Đề thi không chỉ bám sát chương trình học lớp 9, mà còn đưa ra những bài toán thú vị, phong phú và đòi hỏi khả năng tư duy logic, vận dụng kiến thức và kỹ năng giải toán một cách linh hoạt.
Với “Bộ Đề Thi Chuyên Toán Vào Lớp 10 Chuyên Sở GD Quảng Nam 2021-2022”, các bạn sẽ có cơ hội ôn tập kiến thức toán học một cách toàn diện, nắm vững các dạng bài tập thường gặp và rèn luyện kỹ năng giải bài toán một cách tinh tế. Đặc biệt, đáp án chi tiết và lời giải logic sẽ giúp các bạn hiểu rõ từng bước giải quyết và cải thiện kỹ năng toán học một cách hiệu quả.
Hy vọng rằng “Bộ Đề Thi Chuyên Toán Vào Lớp 10 Chuyên Sở GD Quảng Nam 2021-2022” sẽ trở thành người bạn đồng hành đáng tin cậy, giúp các bạn nắm vững kiến thức và tự tin vượt qua kỳ thi chọn lớp 10 thành công. Chúc các bạn học tập hiệu quả và đạt được kết quả cao trong kỳ thi sắp tới!
>>> Bài viết có liên quan:







 QUẢNG
NAM
QUẢNG
NAM NĂM
HỌC
2021-2022
NĂM
HỌC
2021-2022
 QUẢNG
NAM
QUẢNG
NAM NĂM
HỌC 2021-2022
NĂM
HỌC 2021-2022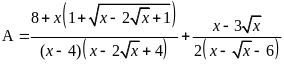 (
(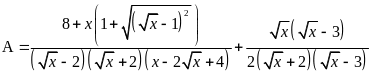
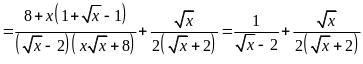
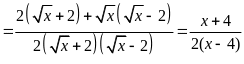
 và
và

 pq là số lẻ
pq là số lẻ
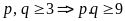 .
Khi đó
.
Khi đó
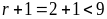 (không thỏa)
(không thỏa) ,
q là số nguyên tố lẻ.
,
q là số nguyên tố lẻ.
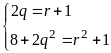
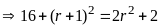

 .
.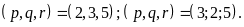
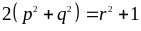 suy
ra r là
số lẻ.
suy
ra r là
số lẻ. là số chẵn, nên pq chẵn,
giả sử p
chẵn, p
nguyên tố nên
là số chẵn, nên pq chẵn,
giả sử p
chẵn, p
nguyên tố nên
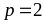
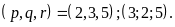

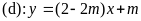


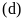
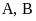

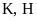
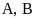
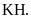

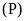

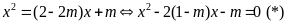
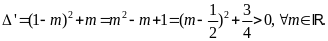
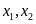
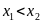
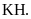
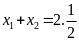
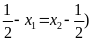
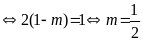
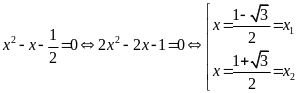
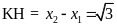
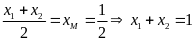
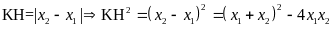
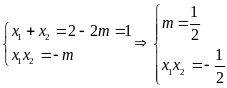
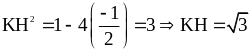
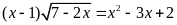
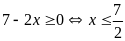
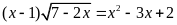
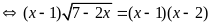

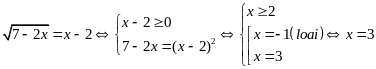

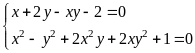
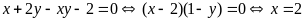

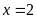
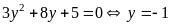
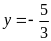
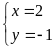
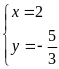
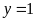
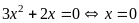
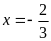
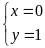
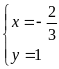
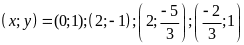
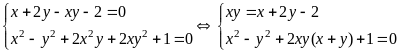
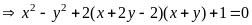
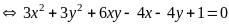
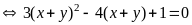
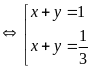
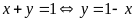
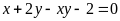

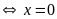
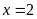

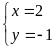

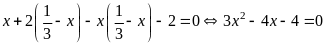

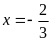
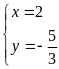
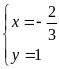
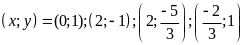
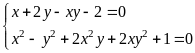
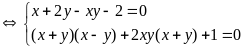





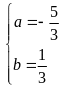
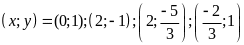
 .
.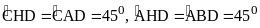 .
. Vậy HD là phân giác
Vậy HD là phân giác
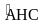 .
.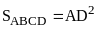 (1)
(1)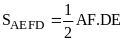 (2)
(2)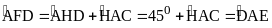
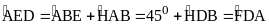
 hay
hay
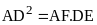 (3)
(3)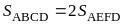 (đpcm)
(đpcm)