Phương Pháp Giải Toán 9 Phương Trình Bậc Nhất Hai Ẩn – Toán 9
>>> Mọi người cũng quan tâm:
Phương Pháp Giải Toán 9 Phương Trình Bậc Nhất Hai Ẩn – Toán 9 là tài liệu học tập được Trang Tài Liệu biên soạn và sưu tầm từ những nguồn dữ liệu mới nhất hiện nay. Tài liệu này sẽ giúp các em luyện tập, củng cố kiến thức từ đó nâng cao điểm số cho môn học. Ngoài ra, cũng giúp các thầy cô giáo có nguồn tài nguyên phong phú để giảng dạy.
Dưới đây là bản đọc trực tuyến giúp thầy cô và các em học sinh có thể nghiên cứu Online hoặc bạn có thể tải miễn phí với phiên bản word để dễ dàng in ấn cũng như học tập Offline.

Bài 1. PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
A. KIẾN THỨC TRỌNG TÂM
1. Khái niệm phương trình bậc nhất hai ẩn
Phương trình bậc nhất hai ẩn
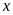 và
và
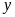 là hệ thức có dạng
là hệ thức có dạng
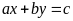 ,
trong đó
,
trong đó
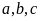 là các số thực (
là các số thực (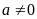 hoặc
hoặc
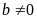 ).
).
2. Tập nghiệm và biểu diễn tập nghiệm của phương trình bậc nhất hai ẩn
Tập nghiệm của phương trình bậc nhất hai ẩn
Cặp
số
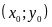 gọi là nghiệm của phương trình
gọi là nghiệm của phương trình
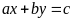 nếu có đẳng thức
nếu có đẳng thức
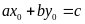 .
.
Ta
cũng viết: nghiệm của phương trình
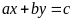 là
là
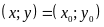 .
Với cách viết này, cần hiểu rằng
.
Với cách viết này, cần hiểu rằng
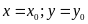 .
.
Lưu ý: + Đối với phương trình bậc nhất hai ẩn, khái niệm tập nghiệm và khái niệm nghiệm của phương trình tương đương cũng tương tự như đối với phương trình một ẩn.
+ Các quy tắc chuyển vế và quy tắc để biến đổi phương trình bậc nhất hai ẩn.
Tổng quát: Một phương trình bậc nhất hai ẩn
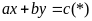 có vô số nghiệm.
có vô số nghiệm.
Điều kiện |
Dạng
phương trình
|
Tập nghiệm |
|
|
|
|
|
|
|
|
|
Biểu diễn tập nghiệm của phương trình bậc nhất hai ẩn trong hệ trục tọa độ
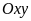 :
Tập nghiệm S của phương trình (*) được biểu diễn
bởi đường thẳng
:
Tập nghiệm S của phương trình (*) được biểu diễn
bởi đường thẳng
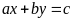 và kí hiệu là
và kí hiệu là
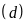 .
Biểu diễn tập nghiệm S trong hệ trục tọa độ
.
Biểu diễn tập nghiệm S trong hệ trục tọa độ
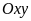 ,
tức là vẽ đường thẳng
,
tức là vẽ đường thẳng
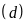 trong hệ trục tọa độ
trong hệ trục tọa độ
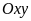 .
.
Điều kiện |
Dạng
phương trình đường thẳng |
Tính
chất của đường thẳng
|
|
|
Song song hoặc trùng với trục hoành, vuông góc với trục tung. |
|
|
Song song hoặc trùng với trục tung, vuông góc với trục hoành. |
|
|
Đồ
thị của
|
B. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
Dạng
1: Nhận
biết hàm số bậc nhất
|
|
Ví
dụ 1.
Trong
các phương trình sau, phương trình nào xác định một hàm
số bậc nhất dạng
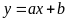 ?
?
a)
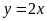 ;
ĐS:
Có. b)
;
ĐS:
Có. b)
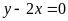 ;
ĐS:
Có.
;
ĐS:
Có.
c)
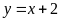 ;
ĐS:
Có. d)
;
ĐS:
Có. d)
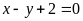 ;
ĐS:
Có.
;
ĐS:
Có.
e)
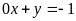 ;
ĐS:
Không. f)
;
ĐS:
Không. f)
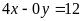 .
ĐS:
Không.
.
ĐS:
Không.
Dạng 2: Kiểm tra các cặp số cho trước có là nghiệm của phương trình bậc nhất hai ẩn không? |
|
Ví
dụ 2.
Cho các cặp số
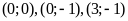 ,
cặp số nào là nghiệm của phương trình:
,
cặp số nào là nghiệm của phương trình:
a)
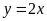 ;
ĐS:
;
ĐS:
 . b)
. b)
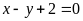 ;
ĐS:
Không
có điểm nào.
;
ĐS:
Không
có điểm nào.
c)
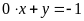 ; ĐS:
; ĐS:
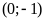 . d)
. d)
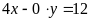 . ĐS:
. ĐS:
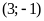 .
.
Dạng 3: Tìm một nghiệm của phương trình bậc nhất hai ẩn |
|
Ví dụ 3. Tìm một nghiệm của phương trình bậc nhất hai ẩn trong các trường hợp sau:
a)
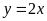 ;
ĐS:
;
ĐS:
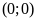 . b)
. b)
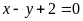 ;
ĐS:
;
ĐS:
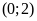 .
.
c)
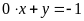 ;
ĐS:
;
ĐS:
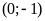 . d)
. d)
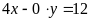 .
ĐS:
.
ĐS:
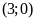 .
.
Dạng 4: Viết nghiệm tổng quát và vẽ đường thẳng biểu diễn tập nghiệm của phương trình |
|
Ví dụ 4. Viết nghiệm tổng quát và vẽ đường thẳng biểu diễn tập nghiệm của mỗi phương trình sau:
a)
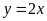 ;
ĐS:
;
ĐS:
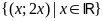 . b)
. b)
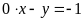 ;
ĐS:
;
ĐS:
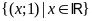 .
.
c)
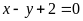 ;
ĐS:
;
ĐS:
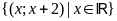 . d)
. d)
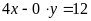 .
ĐS:
.
ĐS:
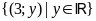 .
.
Dạng 5: Tìm điều kiện của tham số để đường thẳng đi qua một điểm cho trước |
|
Ví
dụ 5.
Trong mỗi trường hợp sau hãy tìm giá trị của
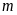 để:
để:
a)
Điểm
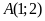 thuộc đường thẳng
thuộc đường thẳng
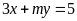 ;
ĐS:
;
ĐS:
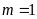 .
.
b)
Điểm
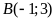 thuộc đường thẳng
thuộc đường thẳng
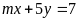 ;
ĐS:
;
ĐS:
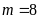 .
.
c)
Điểm
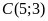 thuộc đường thẳng
thuộc đường thẳng
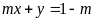 ;
ĐS:
;
ĐS:
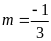 .
.
d)
Điểm
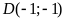 thuộc đường thẳng
thuộc đường thẳng
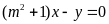 .
ĐS:
.
ĐS:
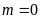 .
.
Dạng 6: Vẽ cặp đường thẳng và tìm giao điểm của chúng |
|
Ví dụ 6. Vẽ mỗi cặp đường thẳng sau trong cùng một mặt phẳng tọa độ và tìm tọa độ giao điểm của hai đường thẳng đó:
a)
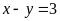 và
và
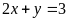 ;
ĐS:
;
ĐS:
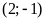 .
.
b)
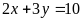 và
và
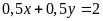 ;
ĐS:
;
ĐS:
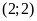 .
.
c)
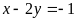 và
và
 ;
ĐS:
;
ĐS:
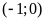 .
.
d)
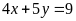 và
và
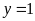 .
ĐS:
.
ĐS:
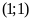 .
.
Ví
dụ 7.
Cho hai phương trình
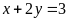 và
và
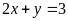 .
.
a) Vẽ hai đường thẳng biểu diễn tập nghiệm của hai phương trình đó trên cùng một hệ trục tọa độ. Xác định tọa độ giao điểm của hai đường thẳng đó và cho biết tọa độ giao điểm đó là nghiệm của các phương trình nào?
b)
Gọi
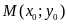 là giao điểm của hai đường thẳng
là giao điểm của hai đường thẳng
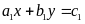 và
và
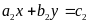 .
Chứng minh rằng
.
Chứng minh rằng
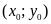 là nghiệm chung của hai phương trình đó.
là nghiệm chung của hai phương trình đó.
C. BÀI TẬP VẬN DỤNG
Bài
1.
Trong các phương trình sau, phương trình nào xác định một
hàm số dạng
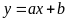 ?
?
a)
 ;
ĐS:
Có. b)
;
ĐS:
Có. b)
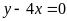 ;
ĐS:
Có.
;
ĐS:
Có.
c)
 ;
ĐS:
Có. d)
;
ĐS:
Có. d)
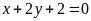 ;
ĐS:
Có.
;
ĐS:
Có.
e)
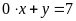 ;
ĐS:
Không. f)
;
ĐS:
Không. f)
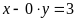 .
ĐS:
Không.
.
ĐS:
Không.
Bài
2.
Cho các cặp số
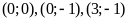 ,
cặp số nào là nghiệm của phương trình:
,
cặp số nào là nghiệm của phương trình:
a)
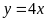 ;
ĐS:
;
ĐS:
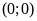 . b)
. b)
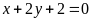 ;
ĐS:
;
ĐS:
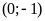 .
.
c)
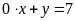 ;
ĐS:
Không
cặp nào. d)
;
ĐS:
Không
cặp nào. d)
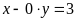 . ĐS:
. ĐS:
 .
.
Bài 3. Tìm một nghiệm của phương trình bậc nhất hai ẩn trong các trường hợp sau:
a)
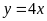 ;
ĐS:
;
ĐS:
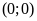 . b)
. b)
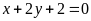 ;
ĐS:
;
ĐS:
 .
.
c)
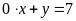 ;
ĐS:
;
ĐS:
 . d)
. d)
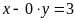 .
ĐS:
.
ĐS:
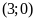 .
.
Bài 4. Viết nghiệm tổng quát và vẽ đường thẳng biểu diễn tập nghiệm của mỗi phương trình sau:
a)
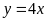 ;
ĐS:
;
ĐS:
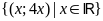 . b)
. b)
 ; ĐS:
; ĐS:
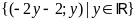 .
.
c)
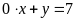 ;
ĐS:
;
ĐS:
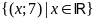 . d)
. d)
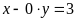 . ĐS:
. ĐS:
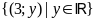 .
.
Bài
5.
Trong mỗi trường hợp sau hãy tìm giá trị của
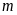 để:
để:
a)
Điểm
 thuộc đường thẳng
thuộc đường thẳng
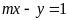 ;
ĐS:
;
ĐS:
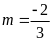 .
.
b)
Điểm
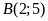 thuộc đường thẳng
thuộc đường thẳng
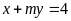 ;
ĐS:
;
ĐS:
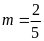 .
.
c)
Điểm
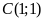 thuộc đường thẳng
thuộc đường thẳng
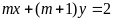 ;
ĐS:
;
ĐS:
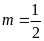 .
.
d)
Điểm
 thuộc đường thẳng
thuộc đường thẳng
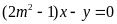 .
ĐS:
.
ĐS:
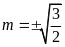 .
.
Bài 6. Vẽ mỗi cặp đường thẳng sau trong cùng một mặt phẳng tọa độ và tìm tọa độ giao điểm của hai đường thẳng đó:
a)
 và
và
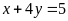 ;
ĐS:
;
ĐS:
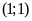 .
.
b)
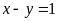 và
và
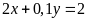 ;
ĐS:
;
ĐS:
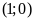 .
.
c)
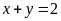 và
và
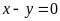 ;
ĐS:
;
ĐS:
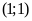 .
.
d)
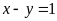 và
và
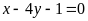 .
ĐS:
.
ĐS:
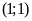 .
.
Bài
7.
Cho hai phương trình
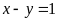 và
và
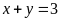 .
Vẽ hai đường thẳng biểu diễn tập nghiệm của hai
phương trình đó trên cùng một hệ trục tọa độ. Xác
định tọa độ giao điểm của hai đường thẳng đó và
cho biết tọa độ giao điểm đó là nghiệm của các
phương trình nào?
.
Vẽ hai đường thẳng biểu diễn tập nghiệm của hai
phương trình đó trên cùng một hệ trục tọa độ. Xác
định tọa độ giao điểm của hai đường thẳng đó và
cho biết tọa độ giao điểm đó là nghiệm của các
phương trình nào?
D. BÀI TẬP VỀ NHÀ
Bài
8.
Trong các phương trình sau, phương trình nào xác định một
hàm số bậc nhất dạng
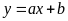 ?
?
a)
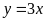 ; ĐS:
Có. b)
; ĐS:
Có. b)
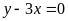 ; ĐS:
Có.
; ĐS:
Có.
c)
 ; ĐS:
Có. d)
; ĐS:
Có. d)
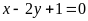 ; ĐS:
Có.
; ĐS:
Có.
e)
 ;
ĐS:
Không. f)
;
ĐS:
Không. f)
 .
ĐS:
Không.
.
ĐS:
Không.
Bài
9.
Cho các cặp số
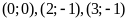 ,
cặp số nào là nghiệm của phương trình:
,
cặp số nào là nghiệm của phương trình:
a)
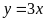 ;
ĐS:
;
ĐS:
 . b)
. b)
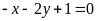 ;
ĐS:
;
ĐS:
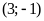 .
.
c)
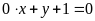 ;
ĐS:
Không
có điểm nào. d)
;
ĐS:
Không
có điểm nào. d)
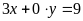 .
ĐS:
.
ĐS:
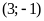 .
.
Bài 10. Tìm một nghiệm của phương trình bậc nhất hai ẩn trong các trường hợp sau:
a)
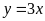 ;
ĐS:
;
ĐS:
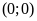 . b)
. b)
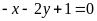 ;
ĐS:
;
ĐS:
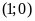 .
.
c)
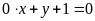 ;
ĐS:
;
ĐS:
 . d)
. d)
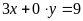 .
ĐS:
.
ĐS:
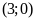 .
.
Bài 11. Viết nghiệm tổng quát và vẽ đường thẳng biểu diễn tập nghiệm của mỗi phương trình sau:
a)
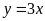 ;
ĐS:
;
ĐS:
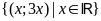 . b)
. b)
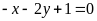 ; ĐS:
; ĐS:
 .
.
c)
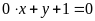 ;
ĐS:
;
ĐS:
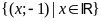 . d)
. d)
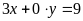 .
ĐS:
.
ĐS:
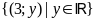 .
.
Bài
12.
Trong mỗi trường hợp sau hãy tìm giá trị của
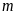 để:
để:
a)
Điểm
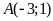 thuộc đường thẳng
thuộc đường thẳng
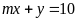 ;
ĐS:
;
ĐS:
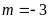 .
.
b)
Điểm
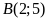 thuộc đường thẳng
thuộc đường thẳng
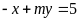 ;
ĐS:
;
ĐS:
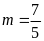 .
.
c)
Điểm
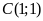 thuộc đường thẳng
thuộc đường thẳng
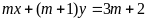 ;
ĐS:
;
ĐS:
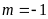 .
.
d)
Điểm
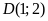 thuộc đường thẳng
thuộc đường thẳng
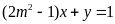 .
ĐS:
.
ĐS:
 .
.
Bài 13. Vẽ mỗi cặp đường thẳng sau trong cùng một mặt phẳng tọa độ và tìm tọa độ giao điểm của hai đường thẳng đó:
a)
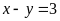 và
và
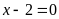 ;
ĐS:
;
ĐS:
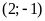 .
.
b)
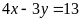 và
và
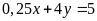 ;
ĐS:
;
ĐS:
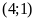 .
.
c)
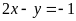 và
và
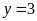 ;
ĐS:
;
ĐS:
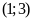 .
.
d)
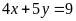 và
và
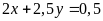 .
ĐS:
Không
có giao điểm.
.
ĐS:
Không
có giao điểm.
Bài
14.
Cho hai phương trình
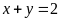 và
và
 .
Vẽ hai đường thẳng biểu diễn tập nghiệm của hai
phương trình đó trên cùng một hệ trục tọa độ. Xác
định tọa độ giao điểm của hai đường thẳng đó và
cho biết tọa độ giao điểm đó là nghiệm của các
phương trình nào?
.
Vẽ hai đường thẳng biểu diễn tập nghiệm của hai
phương trình đó trên cùng một hệ trục tọa độ. Xác
định tọa độ giao điểm của hai đường thẳng đó và
cho biết tọa độ giao điểm đó là nghiệm của các
phương trình nào?
--- HẾT ---
Ngoài Phương Pháp Giải Toán 9 Phương Trình Bậc Nhất Hai Ẩn – Toán 9 thì các tài liệu học tập trong chương trình 9 sẽ được cập nhật liên tục và nhanh nhất có thể sau khi kỳ thi diễn ra trên Danh mục Tài Liệu Học Tập nhằm giúp các bạn đọc thuận tiện trong việc nghiên cứu tài liệu. Quý thày cô và các bạn đọc có thể chia sẻ thêm những tài liệu học tập hữu ích đến địa chỉ email của chúng tôi, nhằm xây dựng nên kho đề thi phong phú, đa dạng cho các em học sinh tham khảo và rèn luyện.
Bài viết này sẽ đưa bạn qua từng bước cụ thể để giải quyết phương trình bậc nhất hai ẩn. Chúng ta sẽ cùng nhau xác định các hệ số, áp dụng các phương pháp biến đổi để tìm ra nghiệm chính xác của phương trình.
Bằng cách áp dụng phương pháp giải toán 9 phương trình bậc nhất hai ẩn, bạn sẽ trang bị cho mình một công cụ mạnh mẽ để giải quyết các bài toán phức tạp và thách thức. Điều này không chỉ giúp bạn nắm vững kiến thức toán mà còn phát triển khả năng tư duy logic, phân tích và giải quyết vấn đề.
Hãy cùng tham gia và thực hành với “Phương Pháp Giải Toán 9 Phương Trình Bậc Nhất Hai Ẩn”. Bằng sự nỗ lực và cố gắng trong việc giải quyết bài toán, bạn sẽ tự tin hơn trong việc áp dụng kiến thức toán vào thực tế và phát triển kỹ năng giải quyết vấn đề. Chúc các bạn thành công và vui vẻ trong hành trình toán học!
>>> Bài viết có liên quan:







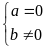
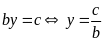
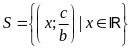
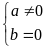
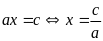

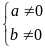
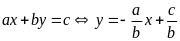

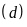
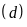 là đồ thị hàm số bậc nhất
là đồ thị hàm số bậc nhất
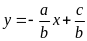
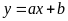
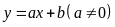 .
.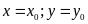 vào phương trình đã cho.
vào phương trình đã cho. làm cho đẳng thức
làm cho đẳng thức
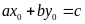 đúng thì
đúng thì
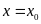 (hoặc
(hoặc
 )
để từ đó tìm
)
để từ đó tìm
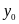 (hoặc
(hoặc
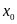 ),
trong đó
),
trong đó
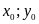 là một hằng số cụ thể.
là một hằng số cụ thể.