Phương Pháp Giải Toán Hàm Số Bậc 2 Lớp 9 Số $y = a{x^2}$ Có Giải
>>> Mọi người cũng quan tâm:
Phương Pháp Giải Toán Hàm Số Bậc 2 Lớp 9 Số $y = a{x^2}$ Có Giải – Toán 9 là tài liệu học tập được Trang Tài Liệu biên soạn và sưu tầm từ những nguồn dữ liệu mới nhất hiện nay. Tài liệu này sẽ giúp các em luyện tập, củng cố kiến thức từ đó nâng cao điểm số cho môn học. Ngoài ra, cũng giúp các thầy cô giáo có nguồn tài nguyên phong phú để giảng dạy.
Dưới đây là bản đọc trực tuyến giúp thầy cô và các em học sinh có thể nghiên cứu Online hoặc bạn có thể tải miễn phí với phiên bản word để dễ dàng in ấn cũng như học tập Offline.
ÔN TẬP CHƯƠNG IV
A. KIẾN THỨC TRỌNG TÂM
Xem lại phần kiến thức trọng tâm của các bài đã học.
B. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
Bài
1.
Vẽ đồ thị hàm số
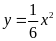 và
và
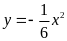 trên cùng một hệ trục tọa độ.
trên cùng một hệ trục tọa độ.
a)
Qua điểm
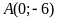 kẻ đường thẳng song song với trục
kẻ đường thẳng song song với trục
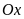 .
Nó cắt đồ thị hàm số
.
Nó cắt đồ thị hàm số
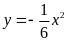 tại hai điểm
tại hai điểm
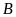 và
và
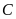 .
Tìm hoành độ của
.
Tìm hoành độ của
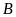 và
và
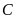 . ĐS:
. ĐS:
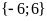 .
.
b)
Tìm trên đồ thị hàm số
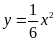 điểm
điểm
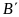 có cùng hoành độ với
có cùng hoành độ với
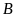 ,
điểm
,
điểm
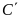 có cùng hoành độ với
có cùng hoành độ với
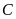 .
Đường thẳng
.
Đường thẳng
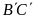 có song song với
có song song với
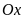 không? Vì sao? Tìm tung độ của
không? Vì sao? Tìm tung độ của
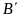 và
và
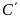 .
.
ĐS:
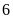 .
.
Bài
2.
Cho hàm số
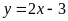 và
và
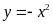 .
.
a) Vẽ đồ thị của hai hàm số này trong cùng một mặt phẳng tọa độ.
b)
Tìm tọa độ các giao điểm của hai đồ thị. ĐS:
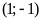 ;
;
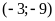 .
.
Bài 3. Giải các phương trình sau
a)
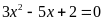 ; ĐS:
; ĐS:
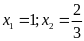 .
.
b)
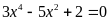 ; ĐS:
; ĐS:
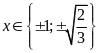 .
.
c)
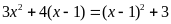 ; ĐS:
; ĐS:
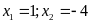 .
.
d)
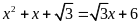 ; ĐS:
; ĐS:
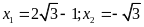 .
.
e)
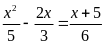 ; ĐS:
; ĐS:
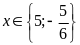 .
.
f)
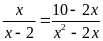 . ĐS:
. ĐS:
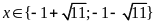 .
.
Bài 4. Giải các phương trình sau
a)
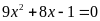 ; ĐS:
; ĐS:
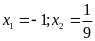 .
.
b)
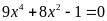 ; ĐS:
; ĐS:
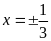 .
.
c)
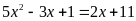 ; ĐS:
; ĐS:
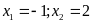 .
.
d)
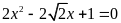 ; ĐS:
; ĐS:
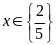 .
.
e)
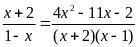 ; ĐS:
; ĐS:
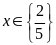 .
.
f)
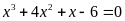 . ĐS:
. ĐS:
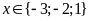 .
.
Bài 5. Giải các phương trình sau bằng phương pháp đặt ẩn phụ.
a)
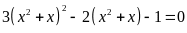 ; ĐS:
; ĐS:
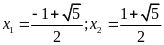 .
.
b)
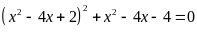 ; ĐS:
; ĐS:
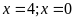 .
.
c)
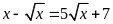 ; ĐS:
; ĐS:
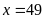 .
.
d)
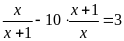 . ĐS:
. ĐS:
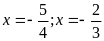 .
.
Bài 6. Giải các phương trình sau bằng phương pháp đặt ẩn phụ.
a)
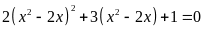 ; ĐS:
; ĐS:
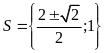 .
.
b)
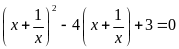 ; ĐS:
; ĐS:
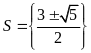 .
.
c)
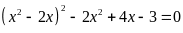 ; ĐS:
; ĐS:
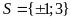 .
.
d)
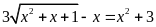 . ĐS:
. ĐS:
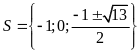 .
.
Bài
7.
Cho phương trình
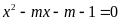 (
(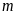 là tham số) Tìm
là tham số) Tìm
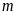 để phương trình:
để phương trình:
a)
Có một nghiệm bằng
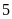 .
Tìm nghiệm còn lại; ĐS:
.
Tìm nghiệm còn lại; ĐS:
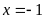 .
.
b)
Có hai nghiệm phân biệt cùng dương; ĐS:
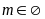 .
.
c) Có hai nghiệm trái dấu, trong đó nghiệm âm có giá trị tuyệt đối lớn hơn nghiệm dương;
ĐS:
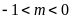 .
.
d)
Có hai nghiệm cùng dấu; ĐS:
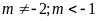 .
.
e)
Có hai nghiệm
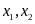 thỏa mãn
thỏa mãn
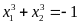 . ĐS:
. ĐS:
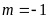 .
.
Bài
8.
Cho phương trình
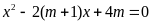 (
(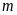 là tham số)
là tham số)
a)
Tìm
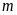 để phương trình có nghiệm kép. Tìm nghiệm kép đó. ĐS:
để phương trình có nghiệm kép. Tìm nghiệm kép đó. ĐS:
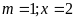 .
.
b)
Tìm
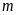 để phương trình có một nghiệm bằng
để phương trình có một nghiệm bằng
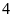 và tìm nghiệm còn lại khi đó. ĐS:
và tìm nghiệm còn lại khi đó. ĐS:
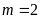 .
.
c)
Tìm
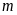 để phương trình:
để phương trình:
i)
Có hai nghiệm trái dấu; ĐS:
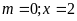 .
.
ii)
Có hai nghiệm cùng dấu; ĐS:
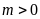 .
.
iii)
Có hai nghiệm dương; ĐS:
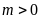 .
.
iv)
Có hai nghiệm âm; ĐS:
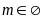 ..
..
v)
Có hai nghiệm
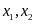 thỏa mãn
thỏa mãn
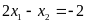 . ĐS:
. ĐS:
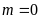 hoặc
hoặc
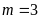 .
.
Bài
9.
Cho parabol
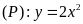 và đường thẳng
và đường thẳng
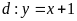 .
.
a)
Vẽ đồ thị của
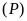 và
và
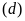 trên cùng một hệ trục tọa độ.
trên cùng một hệ trục tọa độ.
b)
Bằng phép tính, xác định tọa độ giao điểm
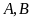 của
của
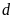 và
và
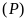 .
Tính độ dài đoạn thẳng
.
Tính độ dài đoạn thẳng
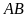 .
.
ĐS:
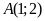 ;
;
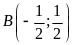 ;
;
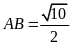 .
.
Bài
10.
Tìm tọa độ giao điểm
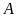 và
và
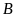 của đồ thị hàm số
của đồ thị hàm số
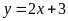 và
và
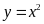 .
Gọi
.
Gọi
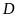 và
và
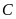 lần lượt là hình chiếu vuông góc của
lần lượt là hình chiếu vuông góc của
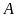 và
và
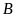 lên trục hoành. Tính diện tích tứ giác
lên trục hoành. Tính diện tích tứ giác
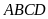 .
.
ĐS:
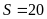 .
.
Bài
11.
Một đội thợ mỏ phải khai thác
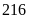 tấn than trong một thời gian nhất định. Ba ngày đầu,
mỗi ngày đội khai thác theo đúng định mức. Sau đó,
mỗi ngày họ đều khai thác vượt định mức
tấn than trong một thời gian nhất định. Ba ngày đầu,
mỗi ngày đội khai thác theo đúng định mức. Sau đó,
mỗi ngày họ đều khai thác vượt định mức
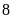 tấn. Do đó họ khai thác được
tấn. Do đó họ khai thác được
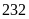 tấn và xong trước thời hạn
tấn và xong trước thời hạn
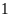 ngày. Hỏi theo kế hoạch mỗi ngày đội thợ phải khai
thác bao nhiêu tấn than? ĐS:
ngày. Hỏi theo kế hoạch mỗi ngày đội thợ phải khai
thác bao nhiêu tấn than? ĐS:
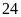 tấn.
tấn.
Bài
12.
Khoảng cách giữa hai bến sông
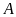 và
và
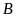 là
là
 km. Một ca-nô đi từ
km. Một ca-nô đi từ
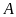 đến
đến
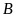 ,
nghỉ
,
nghỉ
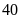 phút ở
phút ở
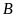 ,
rồi lại trở về bến
,
rồi lại trở về bến
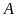 .
Thời gian kể từ lúc đi đến lúc trở về đến
.
Thời gian kể từ lúc đi đến lúc trở về đến
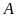 là
là
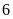 giờ. Tính vận tốc của ca-nô khi nước yên lặng, biết
rằng vận tốc của dòng nước là
giờ. Tính vận tốc của ca-nô khi nước yên lặng, biết
rằng vận tốc của dòng nước là
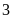 km/h. ĐS:
km/h. ĐS:
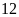 km/h.
km/h.
C. BÀI TẬP VẬN DỤNG
Bài
13.
Cho phương trình
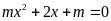 với
với
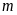 là tham số.
là tham số.
a)
Tìm
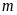 để phương trình có hai nghiệm dương. ĐS:
để phương trình có hai nghiệm dương. ĐS:
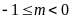 .
.
b)
Tìm
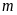 để phương trình có hai nghiệm âm. ĐS:
để phương trình có hai nghiệm âm. ĐS:
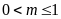 .
.
Bài
14.
Cho phương trình
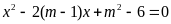 (
(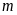 là tham số)
là tham số)
a)
Giải phương trình khi
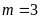 . ĐS:
. ĐS:
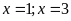 .
.
b)
Tìm
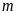 để phương trình có hai nghiệm
để phương trình có hai nghiệm
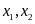 thỏa mãn
thỏa mãn
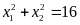 . ĐS:
. ĐS:
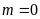 .
.
Bài
15.
Trên mặt phẳng tọa độ
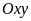 cho parabol
cho parabol
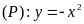 và đường thẳng
và đường thẳng
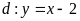 cắt nhau tại hai điểm
cắt nhau tại hai điểm
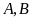 .
Tìm tọa độ các điểm
.
Tìm tọa độ các điểm
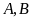 và tính diện tích
và tính diện tích
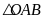 (trong đó
(trong đó
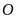 là gốc tọa độ, hoành độ giao điểm
là gốc tọa độ, hoành độ giao điểm
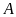 lớn hơn hoành độ giao điểm
lớn hơn hoành độ giao điểm
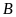 ) ĐS:
) ĐS:
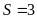 .
.
Bài
16.
Cho parapol
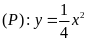 và đường thẳng
và đường thẳng
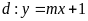 .
.
a)
Chứng minh với mọi giá trị của
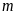 đường thẳng
đường thẳng
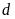 và
và
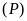 luôn cắt nhau tại hai điểm phân biệt.
luôn cắt nhau tại hai điểm phân biệt.
b)
Gọi
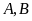 là giao điểm của
là giao điểm của
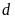 và
và
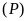 .
Tính diện tích tam giác
.
Tính diện tích tam giác
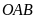 theo
theo
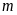 (
(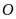 là gốc tọa độ) .
là gốc tọa độ) .
ĐS:
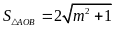 .
.
Bài
17.
Một xe lửa đi từ Hà Nội vào Bình sơn (Quảng Ngãi) Sau
đó
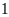 giờ, một xe lửa khác đi từ Bình Sơn ra Hà Nội với
vận tốc lớn hơn vận tốc của xe lửa thứ nhất là
giờ, một xe lửa khác đi từ Bình Sơn ra Hà Nội với
vận tốc lớn hơn vận tốc của xe lửa thứ nhất là
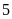 km/h. Hai xe gặp nhau tại một ga ở chính giữa quãng
đường. Tìm vận tốc của mỗi xe, giả thiết rằng
quãng đường từ Hà Nội - Bình Sơn dài
km/h. Hai xe gặp nhau tại một ga ở chính giữa quãng
đường. Tìm vận tốc của mỗi xe, giả thiết rằng
quãng đường từ Hà Nội - Bình Sơn dài
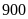 km. ĐS:
km. ĐS:
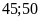 km/h.
km/h.
Bài
18.
Một đội xe theo kế hoạch chở hết
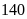 tấn hàng trong một số ngày quy định. Do mỗi ngày đội
đó vượt mức
tấn hàng trong một số ngày quy định. Do mỗi ngày đội
đó vượt mức
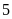 tấn nên đội đã hoàn thành sớm hơn thời gian quy định
tấn nên đội đã hoàn thành sớm hơn thời gian quy định
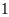 ngày và chở thêm được
ngày và chở thêm được
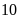 tấn hàng. Hỏi theo kế hoạch đội xe chở hết hàng
trong bao nhiêu ngày? ĐS:
tấn hàng. Hỏi theo kế hoạch đội xe chở hết hàng
trong bao nhiêu ngày? ĐS:
 ngày.
ngày.
ĐỀ KIỂM TRA CHƯƠNG IV – ĐỀ SỐ 1
A. PHẦN TRẮC NGHIỆM
Câu
1.
Phương trình
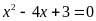 có tập nghiệm là
có tập nghiệm là
A.
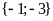 . B.
. B.
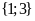 . C.
. C.
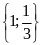 . D.
. D.
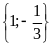 .
.
Câu 2. Phương trình nào sau đây có hai nghiệm phân biệt?
A.
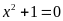 . B.
. B.
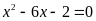 . C.
. C.
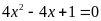 . D.
. D.
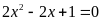 .
.
Câu
3.
Cho đường thẳng
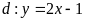 và parabol
và parabol
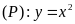 .
Khi đó đường thẳng
.
Khi đó đường thẳng
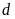 cắt
cắt
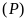 tại số giao điểm là
tại số giao điểm là
A.
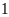 . B.
. B.
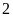 . C.
. C.
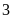 . D.
. D.
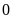 .
.
Câu
4.
Cho phương trình
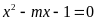 .
Khẳng định nào sau đây đúng?
.
Khẳng định nào sau đây đúng?
A. Phương trình có vô số nghiệm. B. Có hai nghiệm cùng dấu.
C.
Phương trình có một nghiệm
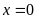 . D.
Phương trình có hai nghiệm trái dấu.
. D.
Phương trình có hai nghiệm trái dấu.
B. PHẦN TỰ LUẬN
Bài 1. Giải các phương trình sau
a)
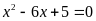 ; b)
; b)
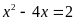 .
.
Bài
2.
Cho đường thẳng
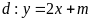 và parabol
và parabol
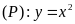 .
.
a)
Vẽ
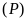 và
và
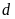 trên cùng một trục tọa độ khi
trên cùng một trục tọa độ khi
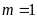 .
.
b)
Tìm
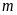 để
để
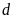 cắt
cắt
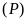 tại hai điểm phân biệt có hoành độ dương.
tại hai điểm phân biệt có hoành độ dương.
Bài
3.
Cho phương trình
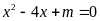 .
Tìm
.
Tìm
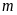 để phương trình:
để phương trình:
a) Có hai nghiệm phân biệt.
b) Có hai nghiệm trái dấu.
c)
Có hai nghiệm phân biệt
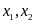 sao cho
sao cho
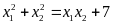 .
.
ĐỀ KIỂM TRA CHƯƠNG IV – ĐỀ SỐ 2
A. PHẦN TRẮC NGHIỆM
Câu
1.
Cho hàm số
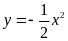 kết luận nào sau đây đúng?
kết luận nào sau đây đúng?
A. Hàm số luôn nghịch biến. B. Hàm số luôn đồng biến.
C. Giá trị của hàm số luôn âm.
D.
Hàm số nghịch biến khi
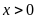 ,
đồng biến khi
,
đồng biến khi
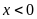 .
.
Câu
2.
Điểm
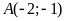 thuộc đồ thị hàm số nào?
thuộc đồ thị hàm số nào?
A.
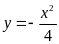 . B.
. B.
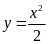 . C.
. C.
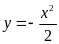 . D.
. D.
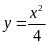 .
.
Câu
3.
Phương trình
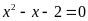 có nghiệm là
có nghiệm là
A.
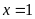 và
và
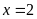 . B.
. B.
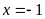 và
và
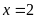 .
.
C.
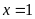 và
và
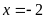 . D.
Vô nghiệm.
. D.
Vô nghiệm.
Câu
4.
Gọi
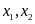 là nghiệm của phương trình
là nghiệm của phương trình
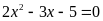 .
Kết quả đúng là
.
Kết quả đúng là
A.
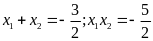 . B.
. B.
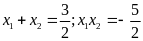 .
.
C.
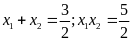 . D.
. D.
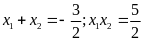 .
.
B. PHẦN TỰ LUẬN
Bài 1. Giải các phương trình sau
a)
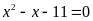 ; b)
; b)
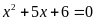 .
.
Bài
2.
Một tàu tuần tra chạy ngược dòng
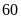 km, sau đó chạy xuôi dòng
km, sau đó chạy xuôi dòng
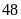 km trên cùng một dòng sông có vận tốc dòng nước là
km trên cùng một dòng sông có vận tốc dòng nước là
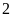 km/h. Tính vận tốc của tàu tuần tra khi nước yên lặng,
biết thời gian xuôi dòng ít hơn ngược dòng
km/h. Tính vận tốc của tàu tuần tra khi nước yên lặng,
biết thời gian xuôi dòng ít hơn ngược dòng
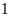 giờ.
giờ.
Bài
3.
Cho parabol
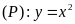 và đường thẳng
và đường thẳng
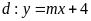 .
.
a)
Cho
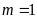 vẽ
vẽ
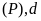 trên cùng hệ trục tọa độ.
trên cùng hệ trục tọa độ.
b)
Chứng minh rằng
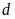 cắt
cắt
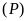 tại hai điểm phân biệt với mọi giá trị của
tại hai điểm phân biệt với mọi giá trị của
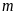 .
.
c)
Gọi
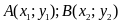 là hai giao điểm của
là hai giao điểm của
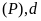 .
Tìm giá trị của
.
Tìm giá trị của
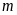 sao cho
sao cho
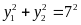 .
.
HƯỚNG DẪN GIẢI
Vẽ đồ thị hàm số
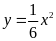 và
và
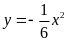 trên cùng một hệ trục tọa độ.
trên cùng một hệ trục tọa độ.
a)
Qua điểm
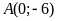 kẻ đường thẳng song song với trục
kẻ đường thẳng song song với trục
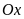 .
Nó cắt đồ thị hàm số
.
Nó cắt đồ thị hàm số
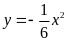 tại hai điểm
tại hai điểm
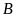 và
và
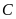 .
Tìm hoành độ của
.
Tìm hoành độ của
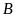 và
và
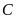 .
.
b)
Tìm trên đồ thị hàm số
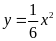 điểm
điểm
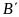 có cùng hoành độ với
có cùng hoành độ với
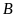 ,
điểm
,
điểm
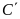 có cùng hoành độ với
có cùng hoành độ với
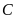 .
Đường thẳng
.
Đường thẳng
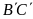 có song song với
có song song với
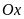 không? Vì sao? Tìm tung độ của
không? Vì sao? Tìm tung độ của
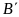 và
và
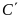 .
.
Lời giải.
Bảng giá trị
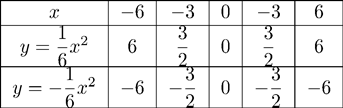
Đồ thị
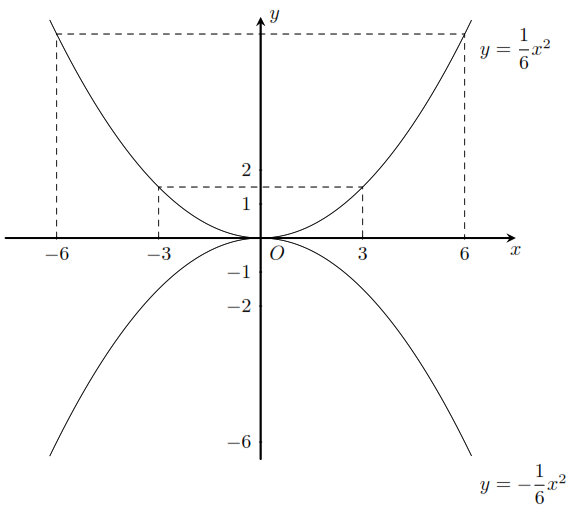
a)
Đường thẳng song song với trục
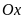 và đi qua điểm
và đi qua điểm
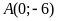 là
là
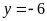 .
.
Phương
trình hoành độ giao điểm của đường thẳng
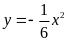 và
và
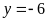 là
là
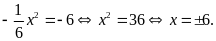
Vậy
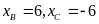 hoặc
hoặc
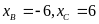 .
.
b)
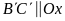 vì
vì
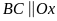 .
Tung độ của
.
Tung độ của
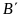 và
và
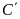 là
là
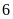 .
.
Cho hàm số
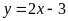 và
và
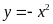 .
.
a) Vẽ đồ thị của hai hàm số này trong cùng một mặt phẳng tọa độ.
b) Tìm tọa độ các giao điểm của hai đồ thị.
Lời giải.
a) Bảng giá trị
![]()
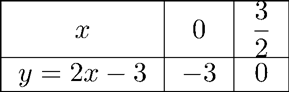
Đồ thị
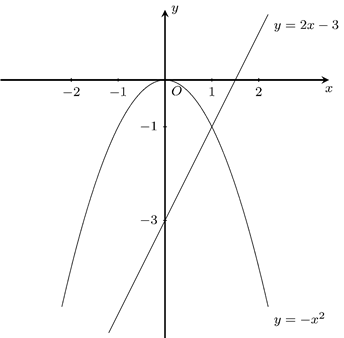
b)
Phương
trình hoành độ giao điểm của
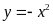 và
và
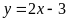 là
là
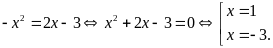
Vậy
giao điểm của hai đồ thị là điểm có tọa độ
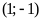 và
và
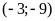 .
.
Giải các phương trình sau.
a)
 ; b)
; b)
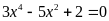 ;
;
c)
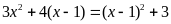 ; d)
; d)
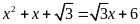 ;
;
e)
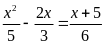 ; f)
; f)
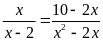 .
.
Lời giải.
a)
Phương trình có
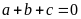 nên có hai nghiệm
nên có hai nghiệm
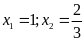 .
.
b)
Đặt
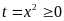 .
.
Ta
có phương trình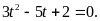
Phương
trình có
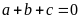 nên có hai nghiệm
nên có hai nghiệm
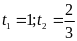 (đều thỏa mãn)
(đều thỏa mãn)
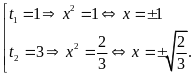
Vậy
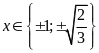 .
.
c)
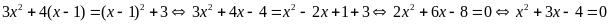 .Phương
trình có
.Phương
trình có
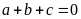 nên có hai nghiệm
nên có hai nghiệm
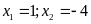 .
.
d)
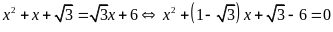 .
.
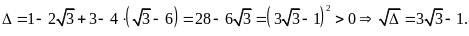
Phương
trình có hai nghiệm phân biệt
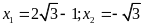 .
.
e)
Ta có
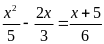
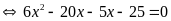
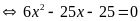
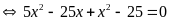
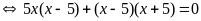
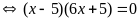
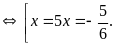
Vậy
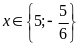 .
.
f)
Với
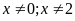 ,
ta có
,
ta có
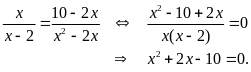
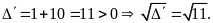
Phương
trình có hai nghiệm phân biệt
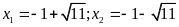 (thỏa điều kiện)
(thỏa điều kiện)
Vậy
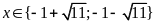 .
.
Giải các phương trình sau.
a)
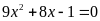 ; b)
; b)
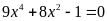 ;
;
c)
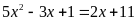 ; d)
; d)
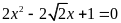 ;
;
e)
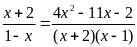 ; f)
; f)
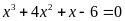 .
.
Lời giải.
a)
Phương trình có
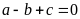 nên có hai nghiệm
nên có hai nghiệm
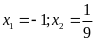 .
.
b)
Đặt
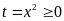 ,
ta có phương trình
,
ta có phương trình
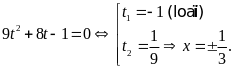
c)
Ta có
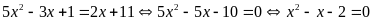 .
.
Phương
trình có
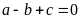 nên có hai nghiệm
nên có hai nghiệm
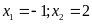 .
.
d)
Ta có
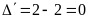 .
Phương trình có nghiệm
.
Phương trình có nghiệm
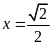 .
.
e)
Với
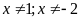 ,
ta có
,
ta có
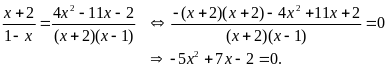
Phương
trình có
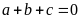 nên có hai nghiệm
nên có hai nghiệm
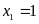 (không thỏa điều kiện);
(không thỏa điều kiện);
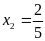 .
.
Vậy
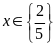 .
.
f) Ta có
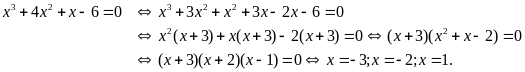
Vậy
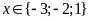 .
.
Giải các phương trình sau bằng phương pháp đặt ẩn phụ.
a)
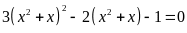 ; b)
; b)
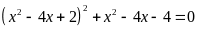 ;
;
c)
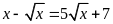 ; d)
; d)
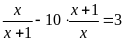 .
.
Lời giải.
a)
Đặt
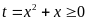 .
.
Phương
trình đã cho trở
thành
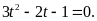
Phương
trình có
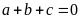 nên có hai nghiệm
nên có hai nghiệm
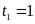 ;
;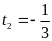 (loại)
(loại)
Với
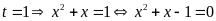 .
.
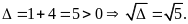 Phương
trình có nghiệm
Phương
trình có nghiệm
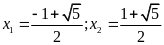 .
.
b)
Đặt
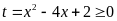 .
.
Phương trình đã cho trở thành
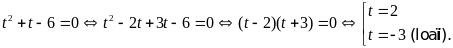
Với
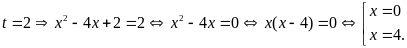
c)
Đặt
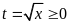 .
Phương trình đã cho trở thành
.
Phương trình đã cho trở thành
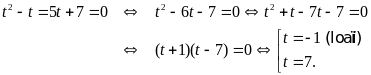
Với
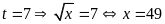 .
.
d)
Điều kiện:
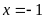 .
.
Đặt
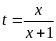 .
Phương trình đã cho trở thành
.
Phương trình đã cho trở thành
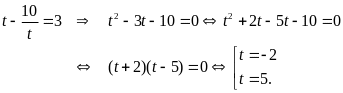
Với
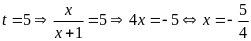 .
.
Với
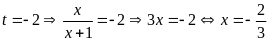 .
.
Giải các phương trình sau bằng phương pháp đặt ẩn phụ.
a)
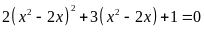 ; b)
; b)
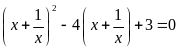 ;
;
c)
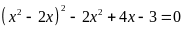 ; d)
; d)
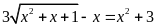 .
.
Lời giải.
a)
Đặt
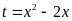 .
Phương trình đã cho trở thành
.
Phương trình đã cho trở thành
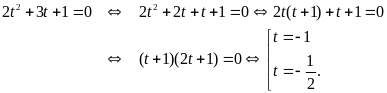
Với
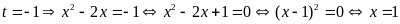 .
.
Với
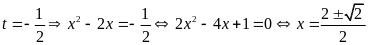 .
.
Vậy
tập nghiệm của phương trình là
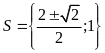 .
.
b)
Điều kiện:
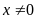 .
Đặt
.
Đặt
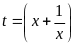 .
Phương trình đã cho trở thành
.
Phương trình đã cho trở thành
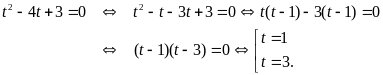
Với
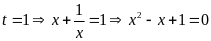 (vô nghiệm)
(vô nghiệm)
Với
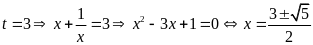 .
.
Vậy
tập nghiệm của phương trình là
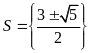 .
.
c)
Đặt
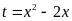 .
Phương trình đã cho trở thành
.
Phương trình đã cho trở thành
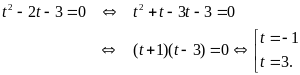
Với
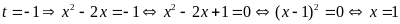 .
.
Với
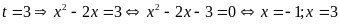 .
.
Vậy
tập nghiệm của phương trình là
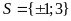 .
.
d)
Đặt
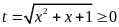 .
Phương trình đã cho trở thành
.
Phương trình đã cho trở thành
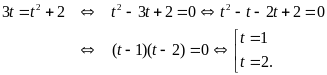
Với

Với
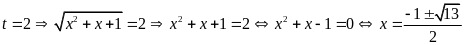 .
.
Vậy
tập nghiệm của phương trình là
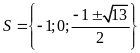 .
.
Cho phương trình
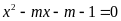 (
(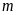 là tham số) Tìm
là tham số) Tìm
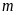 để phương trình:
để phương trình:
a)
Có một nghiệm bằng
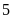 .
Tìm nghiệm còn lại;
.
Tìm nghiệm còn lại;
b) Có hai nghiệm phân biệt cùng dương;
c) Có hai nghiệm trái dấu, trong đó nghiệm âm có giá trị tuyệt đối lớn hơn nghiệm dương;
d) Có hai nghiệm cùng dấu;
e)
Có hai nghiệm
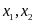 thỏa mãn
thỏa mãn
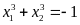 .
.
Lời giải.
a)
Thay
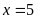 vào phương trình, ta tìm được
vào phương trình, ta tìm được
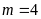 .
.
Do
đó ta có phương trình
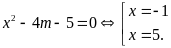
b)
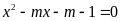 (
(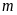 là tham số)
là tham số)
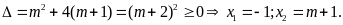
Phương trình có hai nghiệm phân biệt cùng dương
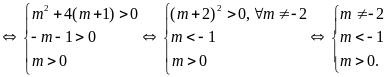
Không
có
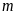 nào thỏa mãn yêu cầu bài toán.
nào thỏa mãn yêu cầu bài toán.
c) Phương trình có hai nghiệm trái dấu, trong đó nghiệm âm có giá trị tuyệt đối lớn hơn nghiệm dương
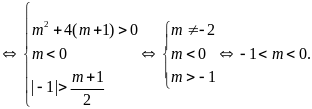
d) Phương trình có hai nghiệm cùng dấu
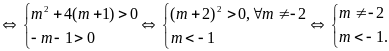
e)
Phương trình có hai nghiệm
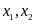 thỏa mãn
thỏa mãn
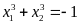
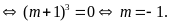
Cho phương trình
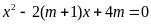 (
(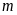 là tham số)
là tham số)
a)
Tìm
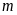 để phương trình có nghiệm kép. Tìm nghiệm kép đó.
để phương trình có nghiệm kép. Tìm nghiệm kép đó.
b)
Tìm
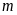 để phương trình có một nghiệm bằng
để phương trình có một nghiệm bằng
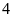 và tìm nghiệm còn lại khi đó.
và tìm nghiệm còn lại khi đó.
c)
Tìm
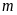 để phương trình:
để phương trình:
i) Có hai nghiệm trái dấu;
ii) Có hai nghiệm cùng dấu;
iii) Có hai nghiệm dương;
iv) Có hai nghiệm âm;
v)
Có hai nghiệm
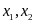 thỏa mãn
thỏa mãn
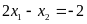 .
.
Lời giải.
a)
Phương trình có nghiệm kép
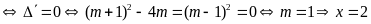 .
.
b)
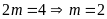 .
.
c)
Phương trình
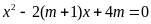 (
(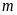 là tham số)
là tham số)
i)
Có hai nghiệm trái dấu
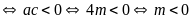 .
.
ii)
Có hai nghiệm cùng dấu
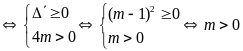 .
.
iii)
Có hai nghiệm dương
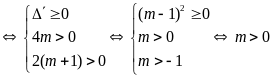 .
.
iv)
Có hai nghiệm âm
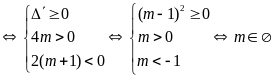 .
.
v)
Vì
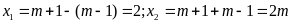 nên
nên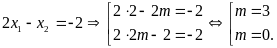
Cho parabol
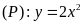 và đường thẳng
và đường thẳng
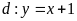 .
.
a)
Vẽ đồ thị của
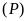 và
và
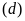 trên cùng một hệ trục tọa độ.
trên cùng một hệ trục tọa độ.
b)
Bằng phép tính, xác định tọa độ giao điểm A,B của
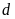 và
và
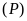 .
Tính độ dài đoạn thẳng
.
Tính độ dài đoạn thẳng
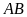 .
.
Lời giải.
a) Bảng giá trị
![]()
![]()
Đồ thị
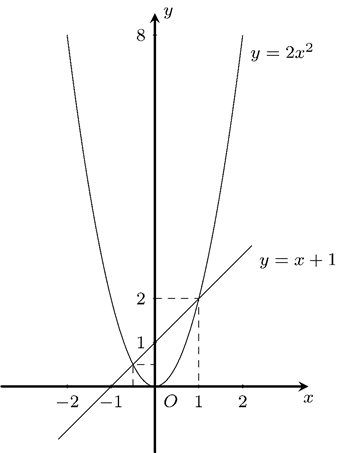
b)
Phương
trình hoành độ giao điểm của
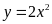 và
và
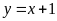 là
là
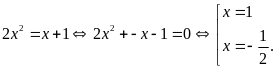
Suy
ra điểm
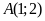 và
và
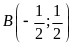 .
.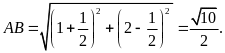
Tìm tọa độ giao điểm
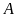 và
và
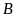 của đồ thị hàm số
của đồ thị hàm số
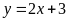 và
và
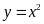 .
Gọi
.
Gọi
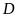 và
và
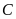 lần lượt là hình chiếu vuông góc của
lần lượt là hình chiếu vuông góc của
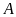 và
và
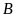 lên trục hoành. Tính diện tích tứ giác
lên trục hoành. Tính diện tích tứ giác
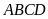 .
.
Lời giải.
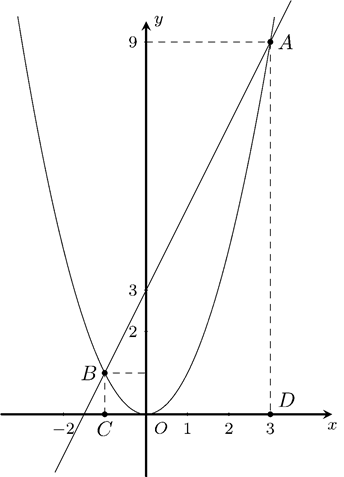
Phương
trình hoành độ giao điểm của
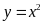 và
và
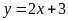 là
là
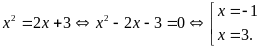
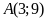 và
và
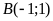 .
Suy ra
.
Suy ra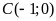 ;
;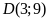 .
Do đó
.
Do đó
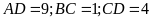 .
.
Diện
tích hình thang vuông
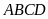 là
là
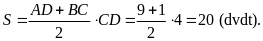
Một đội thợ mỏ phải khai thác
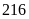 tấn than trong một thời gian nhất định. Ba ngày đầu,
mỗi ngày đội khai thác theo đúng định mức. Sau đó,
mỗi ngày họ đều khai thác vượt định mức
tấn than trong một thời gian nhất định. Ba ngày đầu,
mỗi ngày đội khai thác theo đúng định mức. Sau đó,
mỗi ngày họ đều khai thác vượt định mức
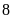 tấn. Do đó họ khai thác được
tấn. Do đó họ khai thác được
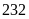 tấn và xong trước thời hạn
tấn và xong trước thời hạn
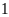 ngày. Hỏi theo kế hoạch mỗi ngày đội thợ phải khai
thác bao nhiêu tấn than?
ngày. Hỏi theo kế hoạch mỗi ngày đội thợ phải khai
thác bao nhiêu tấn than?
Lời giải.
Gọi
lượng than mà đội phải khai thác trong
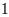 ngày theo kế hoạch là
ngày theo kế hoạch là
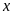 (tấn),
(tấn),
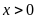 .
.
Thời
hạn quy định để khai thác
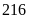 tấn là
tấn là
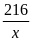 (ngày)
(ngày)
Lượng
than khai thác được trong
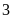 ngày đầu là
ngày đầu là
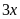 (tấn)
(tấn)
Do
đó lượng than khai thác được trong những ngày còn lại
là
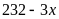 (tấn)
(tấn)
Thời
gian để khai thác
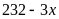 tấn là
tấn là
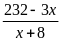 (ngày)
(ngày)
Theo
đề
bài ta có phương trình
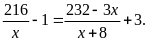
Giải
phương trình ta được
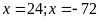 (loại)
(loại)
Vậy
theo kế hoạch mỗi ngày đội thợ phải khai thác
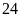 tấn than.
tấn than.
Khoảng cách giữa hai bến sông
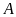 và
và
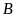 là
là
 km. Một ca-nô đi từ
km. Một ca-nô đi từ
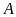 đến
đến
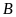 ,
nghỉ
,
nghỉ
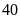 phút ở
phút ở
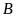 ,
rồi lại trở về bến
,
rồi lại trở về bến
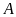 .
Thời gian kể từ lúc đi đến lúc trở về đến
.
Thời gian kể từ lúc đi đến lúc trở về đến
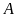 là
là
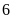 giờ. Tính vận tốc của ca-nô khi nước yên lặng, biết
rằng vận tốc của dòng nước là
giờ. Tính vận tốc của ca-nô khi nước yên lặng, biết
rằng vận tốc của dòng nước là
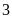 km/h.
km/h.
Lời giải.
Gọi
vận tốc của ca-nô khi nước yên lặng là
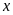 (km/h),
(km/h),
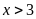 .
.
Vận
tốc khi ca-nô đi xuôi dòng là
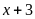 (km/h)
(km/h)
Vận
tốc khi ca-nô đi ngược dòng là
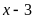 (km/h)
(km/h)
Thời
gian ca-nô đi xuôi dòng là
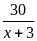 (giờ)
(giờ)
Thời
gian ca-nô đi ngược dòng là
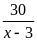 (giờ)
(giờ)
Theo
đề
bài ta có phương trình
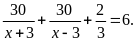
Giải
phương trình ta được
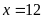 (thỏa mãn)
(thỏa mãn)
Vậy
vận tốc của ca-nô khi nước yên lặng là
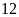 (km/h)
(km/h)
Cho phương trình
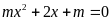 với
với
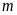 là tham số.
là tham số.
a)
Tìm
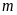 để phương trình có hai nghiệm dương.
để phương trình có hai nghiệm dương.
b)
Tìm
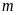 để phương trình có hai nghiệm âm.
để phương trình có hai nghiệm âm.
Lời giải.
a) Phương trình có hai nghiệm dương
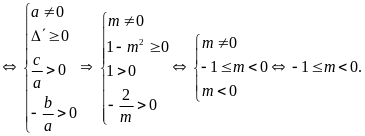
b)
Phương trình có hai nghiệm âm
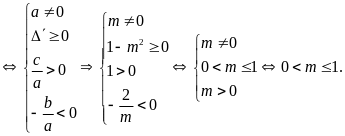
Cho phương trình
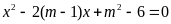 (
(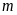 là tham số)
là tham số)
a)
Giải phương trình khi
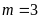 .
.
b)
Tìm
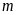 để phương trình có hai nghiệm
để phương trình có hai nghiệm
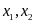 thỏa mãn
thỏa mãn
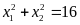 .
.
Lời giải.
a)
Khi
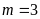 ,
phương trình trở thành
,
phương trình trở thành
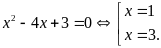
b)
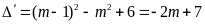 .
.
Để
phương trình có hai nghiệm phân biệt
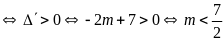 .
.
Với
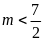 ,
theo định lý Vi-ét, ta có
,
theo định lý Vi-ét, ta có 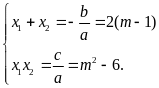
Ta
có
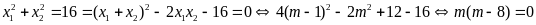 .
.
Giải
phương trình ta tìm được
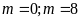 (loại)
(loại)
Vậy
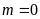 thỏa mãn yêu cầu bài toán.
thỏa mãn yêu cầu bài toán.
Trên mặt phẳng tọa độ
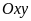 cho parabol
cho parabol
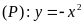 và đường thẳng
và đường thẳng
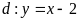 cắt nhau tại hai điểm A,B. Tìm tọa độ các điểm A,B
và tính diện tích
cắt nhau tại hai điểm A,B. Tìm tọa độ các điểm A,B
và tính diện tích
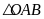 (trong đó
(trong đó
 là gốc tọa độ, hoành độ giao điểm
là gốc tọa độ, hoành độ giao điểm
 lớn hơn hoành độ giao điểm
lớn hơn hoành độ giao điểm
 ).
).
Lời giải.
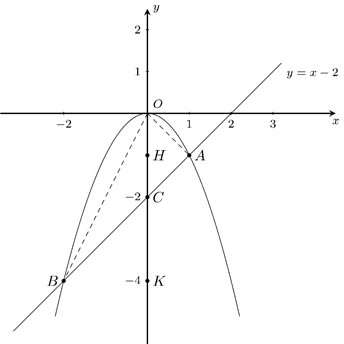
Phương
trình hoành độ giao điểm
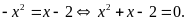
Giải
phương trình ta nhận được
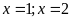 .
Suy ra
.
Suy ra
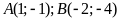 .
.
Diện
tích tam giác
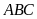 là
là
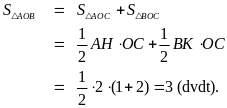
Cho parapol
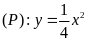 và đường thẳng
và đường thẳng
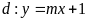 .
.
a)
Chứng minh với mọi giá trị của
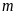 đường thẳng
đường thẳng
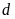 và
và
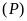 luôn cắt nhau tại hai điểm phân biệt.
luôn cắt nhau tại hai điểm phân biệt.
b)
Gọi A,B là giao điểm của
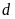 và
và
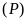 .
Tính diện tích tam giác
.
Tính diện tích tam giác
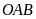 theo
theo
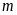 (
(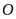 là gốc tọa độ) .
là gốc tọa độ) .
Lời giải.
a)
Phương trình hoành độ giao điểm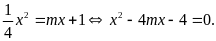
Ta
có
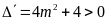 với mọi
với mọi
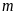 .
.
Do
đó phương trình (*) luôn có hai nghiệm phân biệt với
mọi
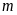 .
.
Vậy
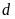 và
và
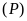 luôn cắt nhau tại hai điểm phân biệt với mọi
luôn cắt nhau tại hai điểm phân biệt với mọi
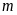 .
.
b)
Giải phương trình (*) ta được
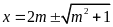 .
.
Suy
ra
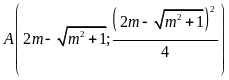 ;
;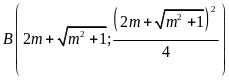 .
.
Vậy
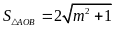 (đvdt).
(đvdt).
Một xe lửa đi từ Hà Nội vào Bình sơn (Quảng Ngãi) Sau đó
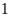 giờ, một xe lửa khác đi từ Bình Sơn ra Hà Nội với
vận tốc lớn hơn vận tốc của xe lửa thứ nhất là
giờ, một xe lửa khác đi từ Bình Sơn ra Hà Nội với
vận tốc lớn hơn vận tốc của xe lửa thứ nhất là
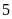 km/h. Hai xe gặp nhau tại một ga ở chính giữa quãng
đường. Tìm vận tốc của mỗi xe, giả thiết rằng
quãng đường từ Hà Nội - Bình Sơn dài
km/h. Hai xe gặp nhau tại một ga ở chính giữa quãng
đường. Tìm vận tốc của mỗi xe, giả thiết rằng
quãng đường từ Hà Nội - Bình Sơn dài
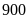 km.
km.
Khi
đó vận tốc của xe lửa thứ hai là
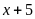 (km/h)
(km/h)
Thời
gian xe lửa thứ nhất đi từ Hà Nội đến chỗ găp nhau
là 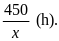
Thời
gian xe lửa thứ hai đi từ Bình Sơn đến chỗ gặp
nhau là
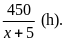
Theo
đề, ta có phương trình 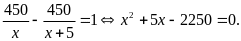
Giải
phương trình ta được
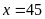 (nhận);
(nhận);
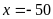 (loại)
(loại)
Vậy
vận tốc xe lửa thứ nhất là
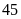 km/h, xe thứ hai là
km/h, xe thứ hai là
 km/h.
km/h.
Một đội xe theo kế hoạch chở hết
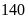 tấn hàng trong một số ngày quy định. Do mỗi ngày đội
đó vượt mức
tấn hàng trong một số ngày quy định. Do mỗi ngày đội
đó vượt mức
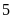 tấn nên đội đã hoàn thành sớm hơn thời gian quy định
tấn nên đội đã hoàn thành sớm hơn thời gian quy định
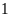 ngày và chở thêm được
ngày và chở thêm được
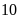 tấn hàng. Hỏi theo kế hoạch đội xe chở hết hàng
trong bao nhiêu ngày?
tấn hàng. Hỏi theo kế hoạch đội xe chở hết hàng
trong bao nhiêu ngày?
Lời giải.
Gọi
khối lượng hàng chở theo định mức trong
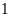 ngày là
ngày là
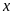 (tấn) Điều kiện
(tấn) Điều kiện
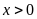 .
.
Khi
đó, số ngày quy định là
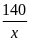 (ngày)
(ngày)
Do
chở vượt mức nên số ngày đội đã chở là
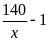 (ngày)
(ngày)
Khối
lượng hàng đội đã chở được là
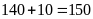 (tấn)
(tấn)
Theo
đề,
ta có phương trình:
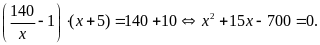
Giải
phương trình ta được
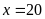 (nhận);
(nhận);
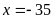 (loại)
(loại)
Vậy
số ngày đội phải chở theo kế hoạch là
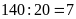 (ngày).
(ngày).
LỜI GIẢI ĐỀ KIỂM TRA CHƯƠNG IV – ĐỀ SỐ 1
A. PHẦN TRẮC NGHIỆM
Câu 1 |
Câu 2 |
Câu 3 |
Câu 4 |
B |
B |
A |
D |
B. PHẦN TỰ LUẬN
Giải các phương trình sau.
a)
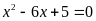 ; b)
; b)
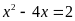 .
.
Lời giải.
a)
Phương trình có
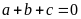 nên có nghiệm
nên có nghiệm
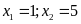 .
.
b)
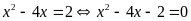 .
.
Ta
có
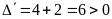 nên phương trình có nghiệm
nên phương trình có nghiệm
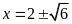 .
.
Cho đường thẳng
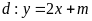 và parabol
và parabol
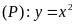 .
.
a)
Vẽ
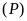 và
và
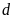 trên cùng một trục tọa độ khi
trên cùng một trục tọa độ khi
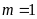 .
.
b)
Tìm
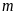 để
để
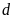 cắt
cắt
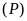 tại hai điểm phân biệt có hoành độ dương.
tại hai điểm phân biệt có hoành độ dương.
Lời giải.
a)
Khi
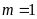 thì
thì
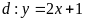 và
và
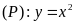 .
.
Bảng giá trị
![]()
![]()
Đồ thị
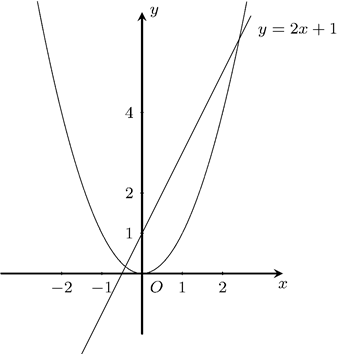
b)
Phương trình hoành độ giao điểm của
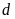 và
và
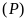
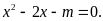 Đường
thẳng
Đường
thẳng
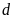 cắt
cắt
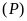 tại hai điểm phân biệt có hoành độ cùng dương khi
tại hai điểm phân biệt có hoành độ cùng dương khi 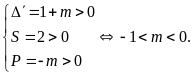
Cho phương trình
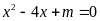 .
Tìm
.
Tìm
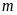 để phương trình:
để phương trình:
a) Có hai nghiệm phân biệt. b) Có hai nghiệm trái dấu.
c)
Có hai nghiệm phân biệt
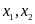 saocho
saocho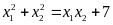 .
.
Lời giải.
Ta
có
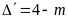 .
.
a)
PT có hai nghiệm phân biệt
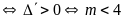 .
.
b)
PT có hai nghiệm trái dấu
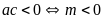 .
.
c)
Để phương trình có hai nghiệm phân biệt
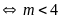 .
.
Theo
định lí Vi-ét ta có 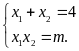
Ta
có
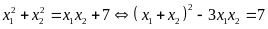 .
.
Từ
đó tìm được
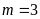 (thỏa mãn).
(thỏa mãn).
LỜI GIẢI ĐỀ KIỂM TRA CHƯƠNG IV – ĐỀ SỐ 2
A. PHẦN TRẮC NGHIỆM
Câu 1 |
Câu 2 |
Câu 3 |
Câu 4 |
D |
A |
B |
B |
B. PHẦN TỰ LUẬN
Giải các phương trình sau.
a)
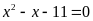 ; b)
; b)
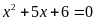 .
.
Lời giải.
a)
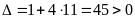 nên phương trình có hai nghiệm
nên phương trình có hai nghiệm
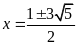 .
.
b)
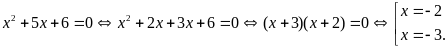
Một tàu tuần tra chạy ngược dòng
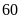 km, sau đó chạy xuôi dòng
km, sau đó chạy xuôi dòng
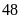 km trên cùng một dòng sông có vận tốc dòng nước là
km trên cùng một dòng sông có vận tốc dòng nước là
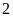 km/h. Tính vận tốc của tàu tuần tra khi nước yên lặng,
biết thời gian xuôi dòng ít hơn ngược dòng
km/h. Tính vận tốc của tàu tuần tra khi nước yên lặng,
biết thời gian xuôi dòng ít hơn ngược dòng
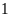 giờ.
giờ.
Lời giải.
Gọi
vận tốc của tàu khi nước yên lặng là
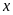 (km/h) Điều kiện
(km/h) Điều kiện
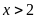 .
.
Theo
đề, ta có phương trình 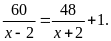
Giải
phương trình, ta được
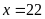 (thỏa mãn)
(thỏa mãn)
Vậy
vận tốc của tàu khi nước yên lặng là
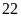 (km/h)
(km/h)
Cho parabol
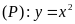 và đường thẳng
và đường thẳng
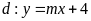 .
.
a)
Cho
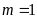 vẽ
vẽ
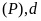 trên cùng hệ trục tọa độ.
trên cùng hệ trục tọa độ.
b)
Chứng minh rằng
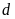 cắt
cắt
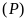 tại hai điểm phân biệt với mọi giá trị của
tại hai điểm phân biệt với mọi giá trị của
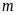 .
.
c)
Gọi
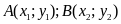 là hai giao điểm của
là hai giao điểm của
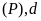 .
Tìm giá trị của
.
Tìm giá trị của
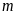 sao cho
sao cho
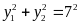 .
.
Lời giải.
a)
Cho
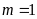 thì
thì
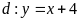 .
.
Bảng giá trị
![]()
![]()
Đồ thị
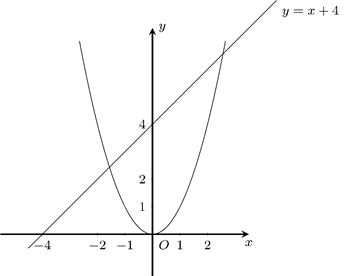
b)
Phương trình hoành độ giao điểm của
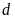 và
và
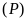 là
là
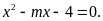
Vì
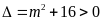 với mọi
với mọi
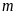 nên ta có đpcm.
nên ta có đpcm.
c)
Từ giả thiết và theo hệ thức Vi-ét ta có 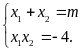
Ta
có
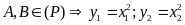 .
.
Nên
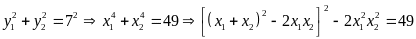 .
.
Ta
tìm được
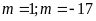 .
.
--- HẾT ---
Ngoài Phương Pháp Giải Toán Hàm Số Bậc 2 Lớp 9 Số $y = a{x^2}$ Có Giải – Toán 9 thì các tài liệu học tập trong chương trình 9 sẽ được cập nhật liên tục và nhanh nhất có thể sau khi kỳ thi diễn ra trên Danh mục Tài Liệu Học Tập nhằm giúp các bạn đọc thuận tiện trong việc nghiên cứu tài liệu. Quý thày cô và các bạn đọc có thể chia sẻ thêm những tài liệu học tập hữu ích đến địa chỉ email của chúng tôi, nhằm xây dựng nên kho đề thi phong phú, đa dạng cho các em học sinh tham khảo và rèn luyện.
Phương pháp giải toán hàm số bậc 2 sẽ giúp bạn nắm vững cách giải các bài toán liên quan đến hàm số bậc hai, được biểu diễn bởi phương trình $y = ax^2$. Điều này làm nền tảng quan trọng cho việc giải các bài toán tính toán, phân tích đồ thị và các bài toán ứng dụng thực tế trong hình học và vật lý.
Phương pháp giải toán hàm số bậc 2:
- Bước 1: Xác định các thông tin có sẵn trong bài toán và viết phương trình hàm số bậc hai dưới dạng $y = ax^2$.
- Bước 2: Tìm hiểu các tính chất của hàm số bậc hai, như đồ thị parabol, đỉnh của đồ thị, điểm cắt trục hoành và trục tung, hướng mở của đồ thị và vị trí tương đối giữa đồ thị và trục hoành.
- Bước 3: Áp dụng các tính chất trên vào việc giải quyết bài toán. Điều này bao gồm việc tìm giá trị của $a$ và các thông số liên quan khác, vẽ đồ thị và sử dụng đồ thị để giải quyết các bài toán liên quan đến hàm số bậc hai.
- Bước 4: Kiểm tra kết quả và đảm bảo rằng các bước giải quyết bài toán đã được thực hiện chính xác.
Lời giải:
Trong bài học này, chúng tôi sẽ cung cấp các ví dụ và bài tập minh họa, giúp bạn hiểu rõ hơn về cách giải các bài toán hàm số bậc hai. Lời giải sẽ đi kèm với các bước chi tiết, giúp bạn tự kiểm tra và tự đánh giá năng lực của mình sau mỗi bài tập.
>>> Bài viết có liên quan:






