Cách Chúng Minh Tứ Giác Nội Tiếp Năm 2023 Có Lời Giải
>>> Mọi người cũng quan tâm:
Cách Chúng Minh Tứ Giác Nội Tiếp Năm 2023 Có Lời Giải – Toán 9 là tài liệu học tập được Trang Tài Liệu biên soạn và sưu tầm từ những nguồn dữ liệu mới nhất hiện nay. Tài liệu này sẽ giúp các em luyện tập, củng cố kiến thức từ đó nâng cao điểm số cho môn học. Ngoài ra, cũng giúp các thầy cô giáo có nguồn tài nguyên phong phú để giảng dạy.
Dưới đây là bản đọc trực tuyến giúp thầy cô và các em học sinh có thể nghiên cứu Online hoặc bạn có thể tải miễn phí với phiên bản word để dễ dàng in ấn cũng như học tập Offline.
A. KIẾN THỨC TRỌNG TÂM
1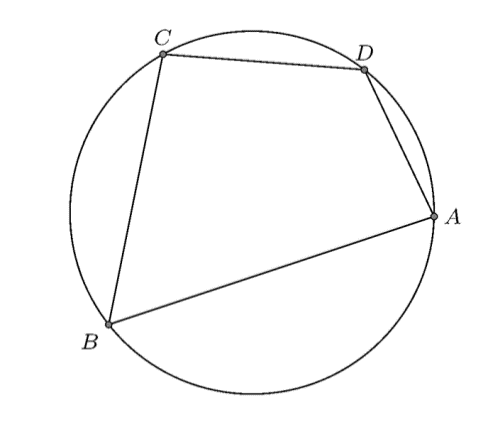 .
Định
nghĩa
.
Định
nghĩa
Tứ giác nội tiếp là tứ giác có bốn đỉnh nằm trên đường tròn đó. Trong hình 1, tứ giác
 nội tiếp đường tròn
nội tiếp đường tròn
 và đường tròn
và đường tròn
 gọi là ngoại tiếp tứ giác.
gọi là ngoại tiếp tứ giác.
2.
Định lí:
Tứ
giác nội tiếp đường tròn khi và chỉ khi tổng số đo
của hai góc đối bằng
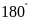 .
.
Một số dấu hiệu nhận biết tứ giác nội tiếp.
Tổng của hai góc đối bằng
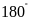 .
.Tứ giác có góc ngoài tại một đỉnh bằng góc trong của đỉnh không kề với nó.
Tứ giác có bốn đỉnh cách đều một điểm
 cố định.
cố định.Tứ giác có hai đỉnh kề nhau cùng nhìn cạnh nối hai đỉnh còn lại với góc bằng nhau.
Chú ý Trong các hình tứ giác đã học thì hình vuông, hình chữ nhật, hình thang cân là các tứ giác nội tiếp được trong đường tròn.
B. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
Dạng 1: Tính số đo các góc và chứng minh tứ giác nội tiếp |
|
V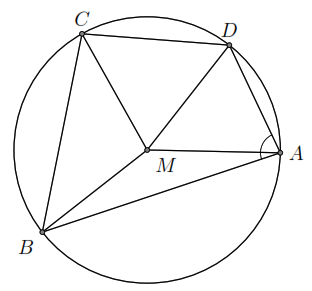 í
dụ 1.
Cho
tứ giác
í
dụ 1.
Cho
tứ giác
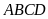 nội tiếp đường tròn tâm
nội tiếp đường tròn tâm
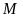 .
Biết
.
Biết
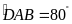 ,
,
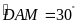 và
và
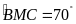 .
Tính số đo các góc
.
Tính số đo các góc
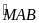 ,
,
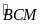 và
và
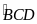 .
.
Lời giải
Ta
có
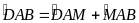
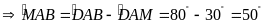 .
.
Do
tam giác
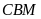 cân tại
cân tại
 nên
nên
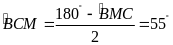 .
.
Do
tứ giác
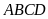 nội tiếp nên
nội tiếp nên
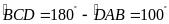 .
.
Ví
dụ 2.
Cho tứ giác
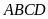 nội tiếp đường tròn tâm
nội tiếp đường tròn tâm
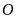 ,
,
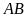 và
và
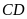 cắt nhau tại
cắt nhau tại
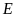 ,
,
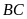 và
và
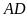 cắt nhau tại
cắt nhau tại
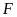 .
Cho biết
.
Cho biết
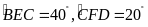 .
Tính số đo các góc của tứ giác.
.
Tính số đo các góc của tứ giác.
L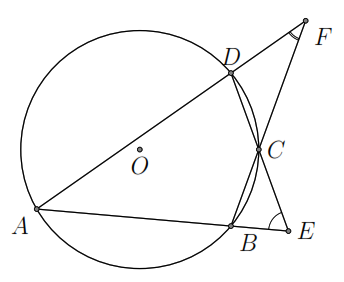 ời
giải
ời
giải
Ta
có
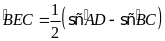 ,
,
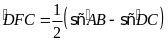 .
.
Suy
ra
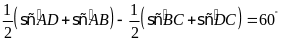 .
.
Hay
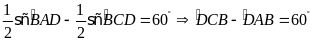 .
.
Mà
tứ giác
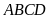 nội tiếp nên
nội tiếp nên
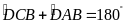 .
Do đó
.
Do đó
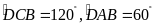 .
.
Tương
tự như trên ta suy ra
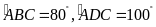 .
.
Ví
dụ 3.
Trên đường tròn
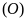 có một cung
có một cung
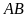 ,
,
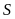 là điểm chính giữa của cung đó. Trên dây
là điểm chính giữa của cung đó. Trên dây
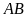 lấy hai điểm
lấy hai điểm
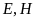 .
Các đường thẳng
.
Các đường thẳng
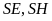 cắt đường tròn theo thứ tự tại
cắt đường tròn theo thứ tự tại
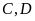 .
Chứng minh rằng:
.
Chứng minh rằng:
a)
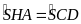 . b)
Tứ giác
. b)
Tứ giác
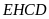 nội tiếp.
nội tiếp.
L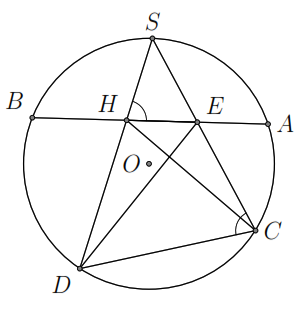 ời
giải
ời
giải
a)
Ta có
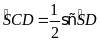
và
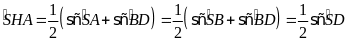 do
do
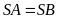 .
Do đó
.
Do đó
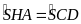 .
.
Theo
câu trên ta có
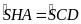 mà
mà
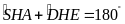 nên
nên
 .
Suy ra tứ giác
.
Suy ra tứ giác
 nội tiếp.
nội tiếp.
V í
dụ 4.
Cho tam giác
í
dụ 4.
Cho tam giác
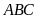 nội tiếp đường tròn
nội tiếp đường tròn
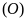 .
Gọi
.
Gọi
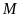 là điểm chính giữa cung nhỏ
là điểm chính giữa cung nhỏ
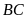 và
và
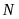 là một điểm thuộc cung nhỏ
là một điểm thuộc cung nhỏ
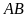 .
.
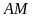 ,
,
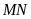 cắt
cắt
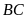 lần lượt tại
lần lượt tại
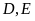 .
Chứng minh rằng tứ giác
.
Chứng minh rằng tứ giác
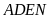 nội tiếp.
nội tiếp.
Lời giải
Ta
có
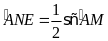
và
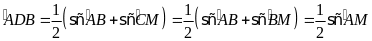 do
do
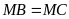 .
Do đó
.
Do đó
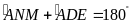 ,
suy ra tứ giác
,
suy ra tứ giác
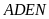 nội tiếp.
nội tiếp.
Dạng 2: Khai thác tính chất của tứ giác nội tiếp |
|
Ví
dụ 5.
Cho
đường tròn tâm
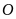 đường kính
đường kính
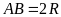 và điểm
và điểm
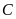 thuộc đường tròn đó (
thuộc đường tròn đó (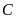 khác
khác
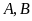 ).
Lấy điểm
).
Lấy điểm
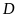 thuộc dây
thuộc dây
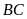 (
(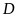 khác
khác
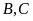 ).
Tia
).
Tia
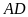 cắt cung nhỏ
cắt cung nhỏ
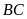 tại điểm
tại điểm
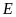 ,
tia
,
tia
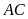 cắt
cắt
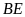 tại
tại
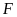 .
Chứng minh
.
Chứng minh
a)
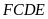 nội tiếp. b)
nội tiếp. b)
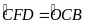 . c)
. c)
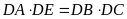 .
.
L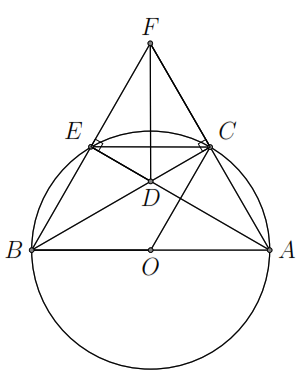 ời
giải
ời
giải
a)
Ta có
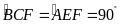 suy ra tứ giác
suy ra tứ giác
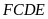 nội tiếp.
nội tiếp.
Do
tứ giác
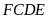 nội tiếp nên
nội tiếp nên
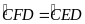 .
Mà
.
Mà
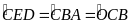 ,
do đó
,
do đó
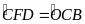 .
.
Ta
có
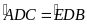 và
và
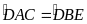 (cùng chắn cung
(cùng chắn cung
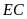 ).
).
Suy
ra, hai tam giác
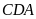 và
và
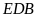 đồng dạng (g-g), nên
đồng dạng (g-g), nên
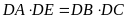 .
.
Ví
dụ 6.
Cho tam giác
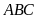 nhọn nội tiếp đường tròn
nhọn nội tiếp đường tròn
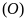 .
Các đường cao
.
Các đường cao
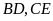 cắt nhau tại
cắt nhau tại
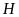 .
Chứng minh
.
Chứng minh
a)
Các tứ giác
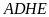 và
và
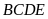 nội tiếp.
nội tiếp.
b)
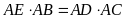 . c)
. c)
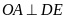 .
.
L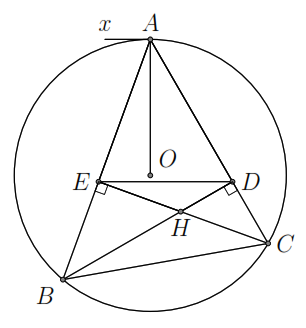 ời
giải
ời
giải
a)
Ta có
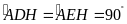 hay
hay
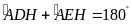 .
Suy ra tứ giác
.
Suy ra tứ giác
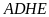 nội tiếp.
nội tiếp.
Và
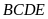 có hai góc kề nhìn cạnh còn lại góc bằng nhau nên nội
tiếp.
có hai góc kề nhìn cạnh còn lại góc bằng nhau nên nội
tiếp.
Xét
hai tam giác vuông
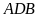 và
và
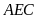 có
có
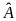 là góc chung, do đó chúng đồng dạng. Suy ra
là góc chung, do đó chúng đồng dạng. Suy ra
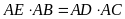 .
.
Vẽ
tiếp tuyến
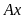 với đường tròn
với đường tròn
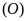 khi đó ta có
khi đó ta có
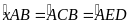 .
Suy ra
.
Suy ra
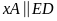 ,
mà
,
mà
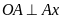 hay
hay
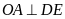 .
.
Ví
dụ 7.
Cho tam giác
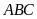 nhọn nội tiếp đường tròn
nhọn nội tiếp đường tròn
 .
Các đường cao
.
Các đường cao
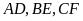 cắt nhau tại
cắt nhau tại
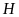 và cắt đường tròn
và cắt đường tròn
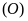 lần lượt tại
lần lượt tại
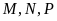 .
Chứng minh rằng
.
Chứng minh rằng
a)
Tứ giác
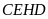 nội tiếp.
nội tiếp.
b )
Bốn điểm
)
Bốn điểm
 cùng thuộc một đường tròn.
cùng thuộc một đường tròn.
c)
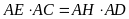 và
và
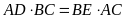 .
.
d)
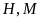 đối xứng nhau qua
đối xứng nhau qua
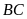 .
.
Lời giải
a)
Ta có
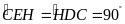 suy ra tứ giác
suy ra tứ giác
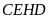 có tổng hai góc đối bằng
có tổng hai góc đối bằng
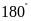 nên nội tiếp.
nên nội tiếp.
Ta
có
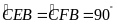 suy ra tứ giác
suy ra tứ giác
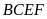 nội tiếp.
nội tiếp.
Do
hai tam giác vuông
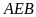 và
và
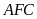 đồng dạng (g-g) nên
đồng dạng (g-g) nên
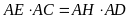 .
.
Ta
có
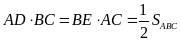 .
.
Ta
có
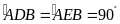 nên tứ giác
nên tứ giác
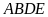 nội tiếp.Do đó
nội tiếp.Do đó
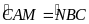 (cùng chắn cung
(cùng chắn cung
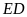 )
nên
)
nên
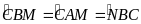 . Suy ra tam giác
. Suy ra tam giác
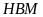 cân tại
cân tại
 hay
hay
 đối xứng nhau qua
đối xứng nhau qua
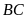 .
.
Ví
dụ 8.
Cho tam giác
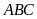 cân tại
cân tại
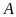 các đường cao
các đường cao
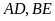 cắt nhau tại
cắt nhau tại
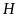 .
Gọi
.
Gọi
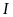 là tâm đường tròn ngoại tiếp tam giác
là tâm đường tròn ngoại tiếp tam giác
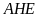 .
Chứng minh rằng
.
Chứng minh rằng
a)
Tứ giác
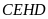 nội tiếp.
nội tiếp.
b)
Bốn điểm
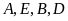 cùng thuộc một đường tròn.
cùng thuộc một đường tròn.
c)
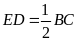 .
.
d)
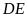 là tiếp tuyến của đường tròn
là tiếp tuyến của đường tròn
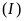 .
.
L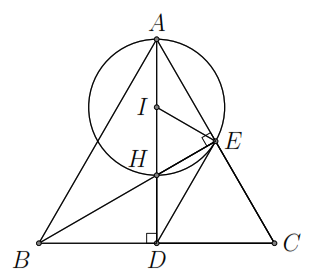 ời
giải
ời
giải
a)
Ta có
 suy ra tứ giác
suy ra tứ giác
 có
có
 nên nội tiếp.
nên nội tiếp.
Ta
có
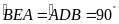 suy ra tứ giác
suy ra tứ giác
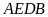 nội tiếp.
nội tiếp.
Ta
có tam giác
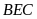 vuông tại
vuông tại
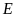 và
và
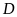 là trung điểm
là trung điểm
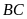 suy ra
suy ra
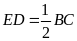 .
.
Ta
có
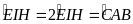 .
Do tứ giác
.
Do tứ giác
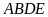 nội tiếp suy ra
nội tiếp suy ra
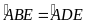 .
Mà
.
Mà
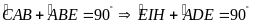 .
Suy ra
.
Suy ra
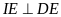 hay
hay
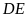 là tiếp tuyến của đường tròn
là tiếp tuyến của đường tròn
 .
.
C. BÀI TẬP VẬN DỤNG
B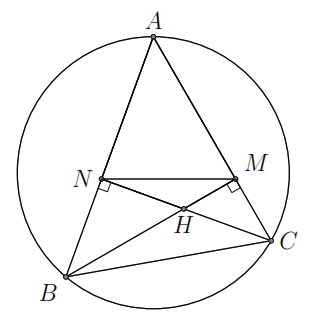 ài
1.
Cho tam giác
ài
1.
Cho tam giác
 nhọn các đường cao
nhọn các đường cao
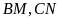 cắt nhau tại
cắt nhau tại
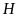 .
Chứng minh rằng
.
Chứng minh rằng
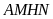 và
và
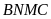 là các tứ giác nội tiếp.
là các tứ giác nội tiếp.
Lời giải
Ta
có
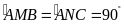 suy ra
suy ra
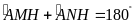 hay tứ giác
hay tứ giác
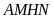 nội tiếp.
nội tiếp.
Và
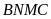 có
có
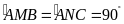 nên nội tiếp.
nên nội tiếp.
Bài
2.
Cho đường tròn
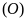 và điểm
và điểm
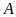 nằm ngoài đường tròn. Từ
nằm ngoài đường tròn. Từ
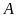 vẽ hai tiếp tuyến
vẽ hai tiếp tuyến
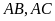 và cát tuyến
và cát tuyến
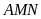 với đường tròn (
với đường tròn (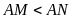 ).
Gọi
).
Gọi
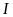 là giao điểm thứ hai của đường thẳng
là giao điểm thứ hai của đường thẳng
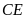 với đường tròn (
với đường tròn (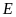 là trung điểm của
là trung điểm của
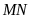 ).
Chứng minh
).
Chứng minh
a)
Bốn điểm
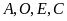 cùng thuộc một đường tròn.
cùng thuộc một đường tròn.
b)
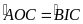 .
.
c)
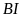 song song với
song song với
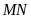 .
.
L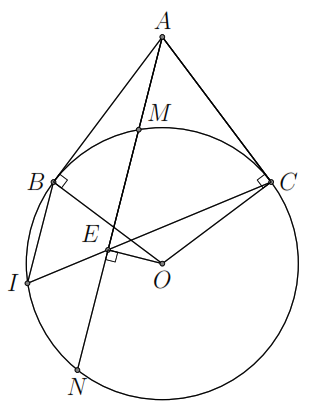 ời
giải
ời
giải
a)
Ta có
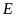 là trung điểm của đoạn
là trung điểm của đoạn
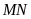 nên
nên
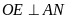 ,
,
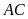 là tiếp tuyến của
là tiếp tuyến của
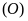 nên
nên
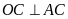 .
Do đó
.
Do đó
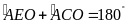 hay tứ giác
hay tứ giác
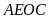 nội tiếp.
nội tiếp.
Vì
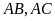 là các tiếp tuyến của
là các tiếp tuyến của
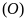 nên
nên
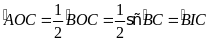 hay
hay
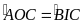 .
.
Do
tứ giác
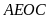 nội tiếp nên
nội tiếp nên
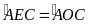 ,
mà theo câu trên lại có
,
mà theo câu trên lại có
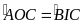 suy ra
suy ra
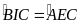 .
Do đó
.
Do đó
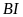 song song với
song song với
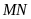 .
.
Bài
3.
Cho đường tròn
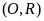 và điểm
và điểm
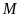 nằm ngoài đường tròn. Từ
nằm ngoài đường tròn. Từ
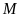 vẽ hai tiếp tuyến
vẽ hai tiếp tuyến
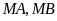 và cát tuyến
và cát tuyến
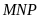 với đường tròn. Gọi
với đường tròn. Gọi
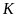 là trung điểm
là trung điểm
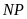 ,
kẻ
,
kẻ
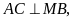
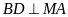 .
Gọi
.
Gọi
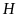 là giao điểm của
là giao điểm của
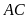 và
và
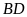 ,
,
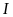 là giao điểm của
là giao điểm của
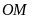 và
và
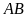 .
Chứng minh
.
Chứng minh
a)
Bốn điểm
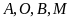 cùng thuộc một đường tròn.
cùng thuộc một đường tròn.
b)
Năm điểm
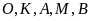 cùng thuộc một đường tròn.
cùng thuộc một đường tròn.
c)
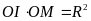 .
.
d)
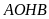 là hình thoi.
là hình thoi.
e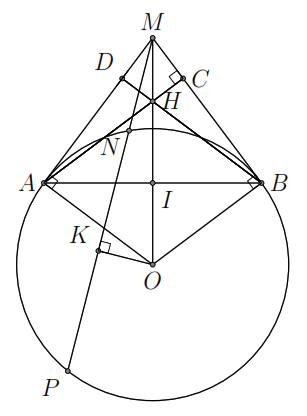 )
)
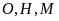 thẳng hàng.
thẳng hàng.
Lời giải
a)
Ta có
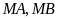 là các tiếp tuyến của
là các tiếp tuyến của
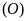 nên
nên
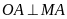 ,
,
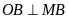 .
Suy ra
.
Suy ra
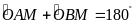 hay
hay
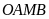 nội tiếp.
nội tiếp.
Ta
có các điểm
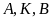 cùng nhìn
cùng nhìn
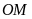 một góc vuông nên năm điểm
một góc vuông nên năm điểm
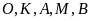 cùng thuộc một đường tròn.
cùng thuộc một đường tròn.
Tam
giác
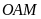 vuông tại
vuông tại
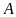 và
và
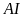 là đường cao nên
là đường cao nên
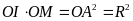 .
.
Ta
có
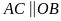 vì cùng vuông góc với
vì cùng vuông góc với
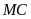 .
Tương tự
.
Tương tự
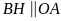 nên tứ giác
nên tứ giác
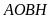 là hình bình hành. Hơn nữa,
là hình bình hành. Hơn nữa,
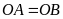 nên
nên
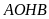 là hình thoi.
là hình thoi.
Ta
có
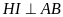 do
do
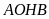 là hình thoi và
là hình thoi và
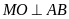 nên
nên
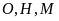 thẳng hàng.
thẳng hàng.
Bài
4.
Cho đường tròn
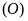 và điểm
và điểm
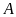 nằm ngoài đường tròn. Từ
nằm ngoài đường tròn. Từ
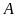 vẽ hai tiếp tuyến
vẽ hai tiếp tuyến
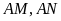 .
Một đường thẳng
.
Một đường thẳng
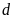 đi qua
đi qua
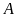 cắt
cắt
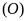 tại hai điểm
tại hai điểm
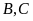 (
(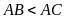 ,
,
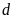 không đi qua
không đi qua
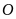 ).
Chứng
minh
).
Chứng
minh
a)
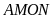 nội tiếp đường tròn.
nội tiếp đường tròn.
b)
Chứng minh
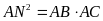 .
Tính độ dài
.
Tính độ dài
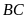 khi
khi
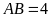 cm,
cm,
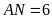 cm.
cm.
c)
Gọi
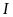 là trung điểm
là trung điểm
 .
Đường thẳng
.
Đường thẳng
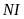 cắt đường tròn
cắt đường tròn
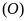 tại điểm thứ hai
tại điểm thứ hai
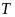 .
Chứng minh
.
Chứng minh
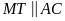 .
.
Lời giải
a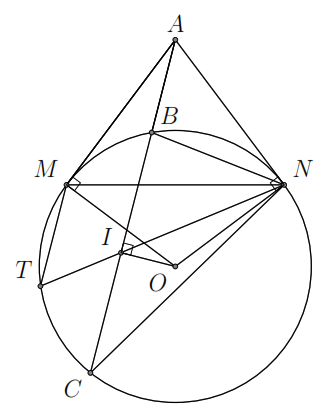 )
Ta có
)
Ta có
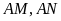 là các tiếp tuyến của
là các tiếp tuyến của
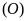 nên
nên
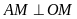 ,
,
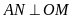 .
Do đó
.
Do đó
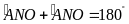 hay tứ giác
hay tứ giác
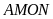 nội tiếp đường tròn.
nội tiếp đường tròn.
Xét
hai tam giác
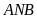 và
và
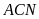 có
có
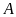 là góc chung,
là góc chung,
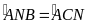 (do cùng chắn cung
(do cùng chắn cung
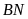 ).
Do đó hai tam giác
).
Do đó hai tam giác
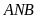 và
và
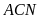 đồng dạng nhau. Suy ra
đồng dạng nhau. Suy ra
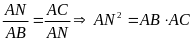 .
.
Do
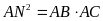 suy ra
suy ra
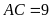 .
Do đó
.
Do đó
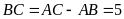
Ta
có các điểm
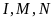 cùng nhìn
cùng nhìn
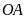 một góc
một góc
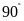 nên năm điểm
nên năm điểm
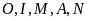 cùng nằm trên một đường tròn suy ra
cùng nằm trên một đường tròn suy ra
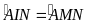 .
Lại có
.
Lại có
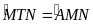 hay
hay
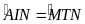 suy ra
suy ra
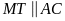 .
.
--- HẾT ---
Ngoài Cách Chúng Minh Tứ Giác Nội Tiếp Năm 2023 Có Lời Giải – Toán 9 thì các tài liệu học tập trong chương trình 9 sẽ được cập nhật liên tục và nhanh nhất có thể sau khi kỳ thi diễn ra trên Danh mục Tài Liệu Học Tập nhằm giúp các bạn đọc thuận tiện trong việc nghiên cứu tài liệu. Quý thày cô và các bạn đọc có thể chia sẻ thêm những tài liệu học tập hữu ích đến địa chỉ email của chúng tôi, nhằm xây dựng nên kho đề thi phong phú, đa dạng cho các em học sinh tham khảo và rèn luyện.
Công nghệ trí tuệ nhân tạo (Artificial Intelligence – AI) là một trong những xu hướng công nghệ đang định hình tương lai của thế giới. AI đã và đang tiếp tục thay đổi cách chúng ta sống, làm việc và tương tác với nhau. Được phát triển với mục tiêu giúp máy móc có khả năng suy luận, học tập và thực hiện các nhiệm vụ thông minh mà trước đây chỉ có con người mới làm được, công nghệ trí tuệ nhân tạo đã mang đến những ứng dụng đáng kinh ngạc trong nhiều lĩnh vực cuộc sống.
Trong đoạn giới thiệu trên, chúng ta đã đề cập đến chủ đề là công nghệ trí tuệ nhân tạo (AI), cung cấp một cái nhìn tổng quan về ý nghĩa và tầm quan trọng của AI trong thế giới hiện đại. Đoạn giới thiệu này có thể tiếp tục mở rộng để giới thiệu thêm các ứng dụng và tiềm năng của AI trong các lĩnh vực như y tế, giao thông, kỹ thuật, hay giáo dục.
>>> Bài viết có liên quan:






