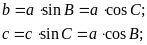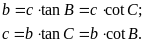Giải Toán 9 Bài 4 Hình Học Hệ Thức Về Cạnh Và Góc Trong Tam Giác Vuông
>>> Mọi người cũng quan tâm:
Giải Toán 9 Bài 4 Hình Học Hệ Thức Về Cạnh Và Góc Trong Tam Giác Vuông – Toán 9 là tài liệu học tập được Trang Tài Liệu biên soạn và sưu tầm từ những nguồn dữ liệu mới nhất hiện nay. Tài liệu này sẽ giúp các em luyện tập, củng cố kiến thức từ đó nâng cao điểm số cho môn học. Ngoài ra, cũng giúp các thầy cô giáo có nguồn tài nguyên phong phú để giảng dạy.
Dưới đây là bản đọc trực tuyến giúp thầy cô và các em học sinh có thể nghiên cứu Online hoặc bạn có thể tải miễn phí với phiên bản word để dễ dàng in ấn cũng như học tập Offline.
Bài 4-5. MỘT SỐ HỆ THỨC VỀ CẠNH VÀ GÓC TRONG TAM GIÁC VUÔNG
ỨNG DỤNG THỰC TẾ CÁC TỈ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN
A. KIẾN THỨC TRỌNG TÂM
1 .
Liên hệ giữa cạnh và góc trong tam giác vuông
.
Liên hệ giữa cạnh và góc trong tam giác vuông
Trong một tam giác vuông, mỗi cạnh góc vuông bằng
Tích của cạnh huyền với sin của góc đối hoặc cô-sin của góc kề.
Tích của cạnh góc vuông kia với tang góc đối hoặc cô-tang góc kề.
Trong hình bên, ta có
2. Giải tam giác vuông
Giải tam giác vuông là tìm tất cả các cạnh và các góc còn lại của tam giác vuông đó khi biết trước hai cạnh hoặc một cạnh và một góc nhọn.
B. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
Dạng 1: Giải tam giác vuông |
Lưu ý:
|
Ví
dụ 1.
Giải tam giác
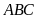 vuông tại
vuông tại
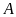 ,
biết
,
biết
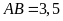 và
và
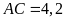 .
.
Lời giải
T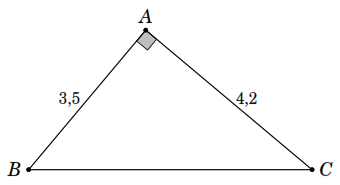 a
có
a
có
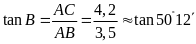 .
.
Suy
ra
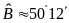 mà
mà
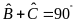
nên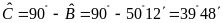 .
.
Mặt khác, theo định lí Py-ta-go ta có
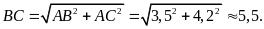
Ví
dụ 2.
Giải tam giác
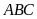 vuông tại
vuông tại
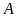 ,
biết
,
biết
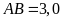 và
và
 .
.
Lời giải
D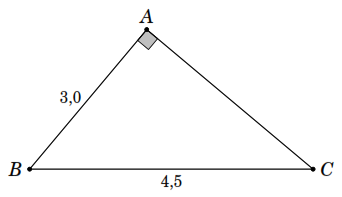 o
giả thiết ta có
o
giả thiết ta có
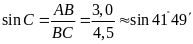 suy ra
suy ra
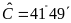 .
.
Mà
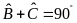 nên
nên
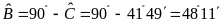 .
.
Mặt khác theo định lí Py-ta-go
 .
.
suy
ra
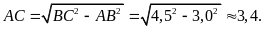
Ví
dụ 3.
Giải tam giác
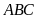 vuông tại
vuông tại
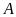 ,
biết
,
biết
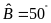 và
và
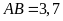 .
.
L ời
giải
ời
giải
Ta
có
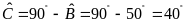 .
.
Mặt
khác
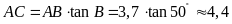 .
.
Tương
tự
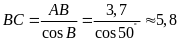 .
.
Ví
dụ 4.
Giải tam giác
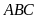 vuông tại
vuông tại
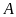 ,
biết
,
biết
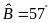 và
và
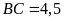 .
.
L ời
giải
ời
giải
Ta
có
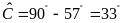 .
.
Mặt
khác
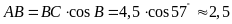
và
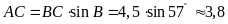 .
.
Ví
dụ 5.
Cho tam giác
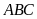 vuông tại
vuông tại
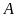 ,
đường cao
,
đường cao
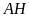 .
Biết
.
Biết
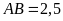 ,
,
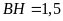 .
Tính
.
Tính
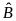 ,
,
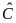 và
và
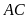 .
.
L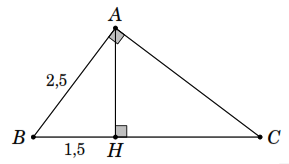 ời
giải
ời
giải
Xét
tam giác
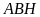 vuông tại
vuông tại
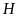 ,
ta có
,
ta có
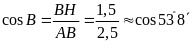 suy
ra
suy
ra
 .
.
Mà
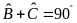 nên
nên
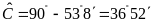 .
.
Xét
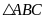 vuông tại
vuông tại
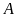 ,
ta có
,
ta có
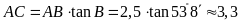 .
.
Dạng 2: Giải tam giác nhọn |
Lưu ý: Dùng đường cao làm trung gian để tính các độ dài cạnh hoặc số đo góc.
|
Ví
dụ 6.
Cho tam giác
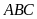 có
có
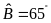 ,
,
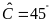 và
và
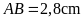 .
Tính các góc và cạnh còn lại của tam giác đó (gọi là
giải tam giác
.
Tính các góc và cạnh còn lại của tam giác đó (gọi là
giải tam giác
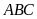 ).
).
L ời
giải
ời
giải
Ta
có
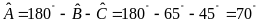 .
.
Kẻ
đường cao
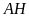 .
Xét
.
Xét
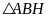 vuông tại
vuông tại
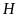 ,
ta có
,
ta có
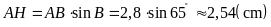 .
.
Tương
tự
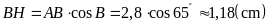 .
.
Mặt
khác, do giả thiết suy ra tam giác
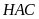 vuông cân tại
vuông cân tại
 nên
nên
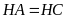 .
Do đó
.
Do đó
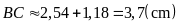 .
.
Xét
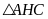 vuông tại
vuông tại
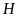 ,
ta có
,
ta có
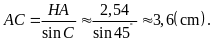
Ví
dụ 7.
Giải tam giác
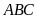 biết
biết
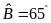 ,
,
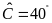 và
và
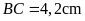 .
.
L ời
giải
ời
giải
Ta
có
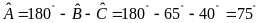 .
.
Kẻ
đường cao
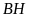 .
Xét
.
Xét
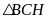 vuông tại
vuông tại
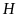 ,
ta có
,
ta có
 .
.
Tương
tự, xét
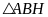 vuông tại
vuông tại
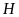 ,
ta có
,
ta có
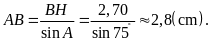
Mặt khác, ta có
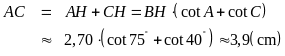
Ví
dụ 8.
Giải tam giác nhọn
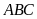 biết
biết
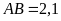 ,
,
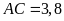 và
và
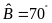 .
.
L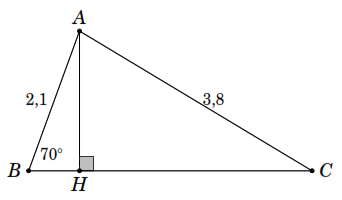 ời
giải
ời
giải
Vẽ
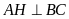 .
Xét
.
Xét
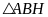 vuông tại
vuông tại
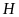 ,
ta có
,
ta có
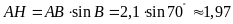 .
.
Tương
tự, xét
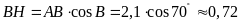 .
.
Mặt
khác, xét
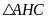 vuông tại
vuông tại
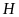 ,
ta có
,
ta có
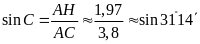 do đó
do đó
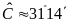 .
.
Mà
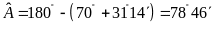 .
.
Ta
có
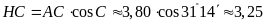 .
.
Mà
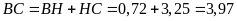 .
.
Dạng 3: Tính diện tích tam giác, tứ giác |
|
Ví
dụ 9.
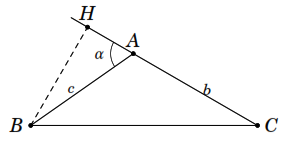
Cho tam giác
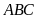 như hình vẽ bên. Chứng minh rằng diện tích tam giác
như hình vẽ bên. Chứng minh rằng diện tích tam giác
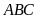 có diện tích là
có diện tích là
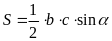 .
.
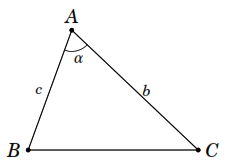
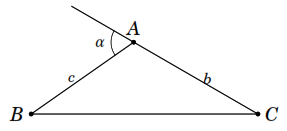
Lời giải
Vẽ
đường cao
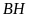 của tam giác
của tam giác
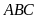 .
.
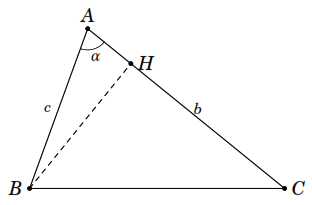
Xét
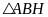 vuông tại
vuông tại
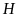 ,
ta có
,
ta có
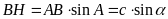 .
.
Do
đó diện tích
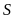 của tam giác
của tam giác
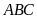 là
là
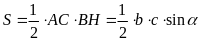 .
.
Nhận xét: Qua ví dụ này ta có thêm một cách tính diện tích tam giác. Diện tích tam giác bằng nửa tích hai cạnh nhân với sin của góc nhọn xen giữa hai đường thẳng chứa hai cạnh đó.
V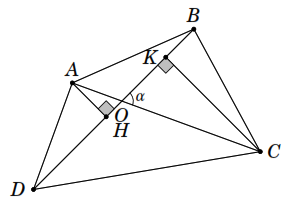 í
dụ 10.
Tứ giác
í
dụ 10.
Tứ giác
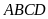 như hình vẽ phía dưới. Biết
như hình vẽ phía dưới. Biết
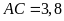 ,
,
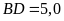 và
và
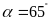 .
Tính diện tích của tứ giác đó.
.
Tính diện tích của tứ giác đó.
Lời giải
Vẽ
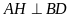 và
và
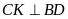 .
Xét
.
Xét
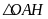 ta có
ta có
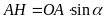 .
.
Tương
tự, xét
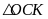 ta có
ta có
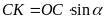 .
.
Mà
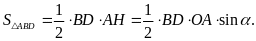
Tương
tự
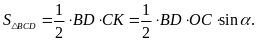
Gọi
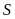 là diện tích tứ giác
là diện tích tứ giác
 ta có
ta có
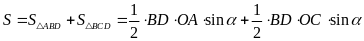
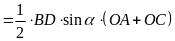
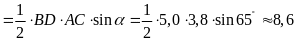 .
.
Ví
dụ 11.
Tam giác
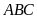 có
có
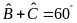 ,
,
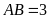 ,
,
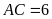 .
Tính độ dài đường phân giác
.
Tính độ dài đường phân giác
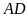 .
.
Lời giải
D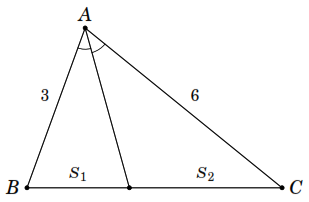 o
giả thiết
o
giả thiết
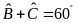 nên
nên
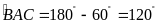 .
.
Mà
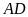 là đường phân giác nên
là đường phân giác nên
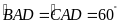 .
.
Mà
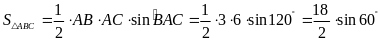 .
.
Mặt khác
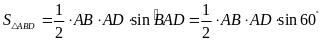
và
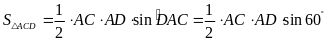
V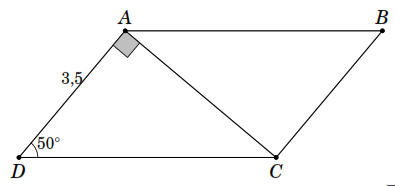 í
dụ 12.
Hình bình hành
í
dụ 12.
Hình bình hành
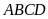 có
có
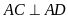 và
và
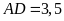 ,
,
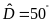 .
Tính diện tích của hình bình hành.
.
Tính diện tích của hình bình hành.
Lời giải
Xét
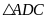 vuông tại
vuông tại
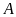 ,
ta có
,
ta có
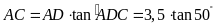 .
.
Khi
đó gọi
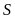 là diện tích hình bình hành
là diện tích hình bình hành
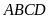 ,
ta có
,
ta có
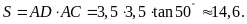
Dạng 4: Ứng dụng thực tế của hệ thức lượng trong tam giác vuông |
|
Ví
dụ 13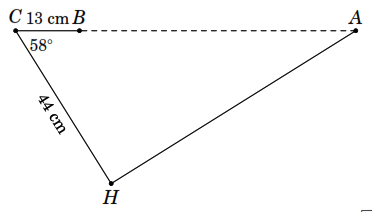 .
Tính khoảng cách giữa hai điểm
.
Tính khoảng cách giữa hai điểm
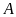 và
và
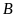 trên một bờ hồ nước sâu, biết
trên một bờ hồ nước sâu, biết
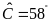 ,
,
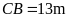 ,
,
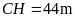 như hình bên.
như hình bên.
Lời giải
Xét
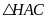 vuông tại
vuông tại
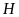 ,
ta có
,
ta có
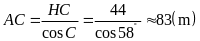 .
.
Mà
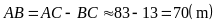 .
.
Ví
dụ 14.
Trong hình vẽ bên dưới, tính chiều rộng
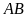 của con sông, biết
của con sông, biết
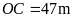 ,
,
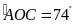 ,
,
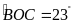 .
.
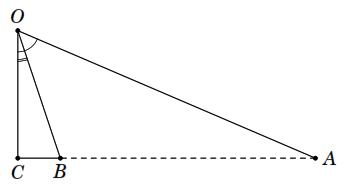
Lời giải
Xét
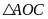 vuông ở
vuông ở
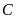 ,
ta có
,
ta có
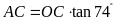 và
và
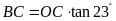 .
.
Do đó
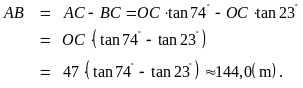
Vậy
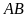 bằng
bằng
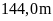 .
.
Ví
dụ 15.
Khoảng cách giữa hai chân tháp
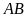 và
và
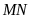 là
là
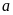 như hình vẽ bên dưới. Từ đỉnh
như hình vẽ bên dưới. Từ đỉnh
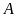 của tháp
của tháp
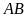 nhìn lên đỉnh
nhìn lên đỉnh
 của tháp
của tháp
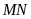 ta được góc
ta được góc
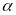 .
Từ đỉnh
.
Từ đỉnh
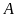 nhìn xuống chân
nhìn xuống chân
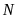 của tháp
của tháp
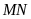 ta được góc
ta được góc
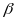 (so với phương nằm ngang
(so với phương nằm ngang
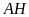 ).
Hãy tìm chiều cao
).
Hãy tìm chiều cao
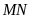 nếu
nếu
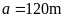 ,
,
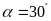 ,
,
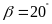 .
.
Lời giải
X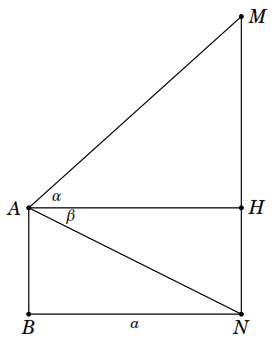 ét
ét
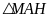 vuông tại
vuông tại
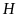 ,
ta có
,
ta có
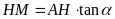 .
.
Tương
tự, xét
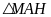 vuông tại
vuông tại
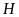 ,
ta có
,
ta có
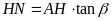 .
.
Mà
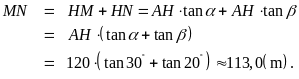
Vậy
chiều cao
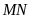 là
là
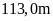 .
.
C. BÀI TẬP VẬN DỤNG
Bài
1.
Giải tam giác
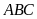 vuông tại
vuông tại
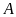 ,
biết
,
biết
a)
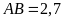 và
và
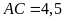 ; b)
; b)
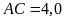 và
và
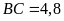 .
.
Lời giải
a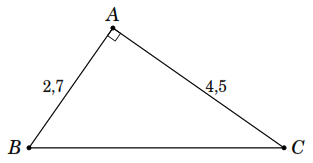 )
Xét
)
Xét
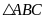 vuông ở
vuông ở
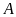 ,
ta có
,
ta có
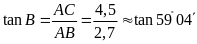
Suy
ra
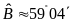 mà
mà
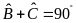 nên
nên
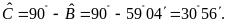
Mặt khác, theo định lí Py-ta-go ta có
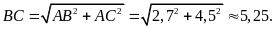
b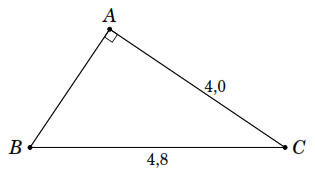 )
Xét
)
Xét
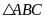 vuông ở
vuông ở
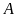 ,
ta có
,
ta có
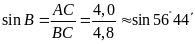
Suy
ra
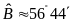 mà
mà
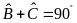 nên
nên
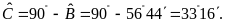
Mặt khác, theo định lí Py-ta-go ta có
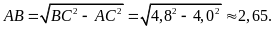
Bài
2.
Giải tam giác
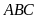 vuông tại
vuông tại
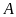 ,
biết
,
biết
a)
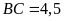 và
và
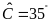 ; b)
; b)
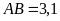 và
và
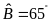 .
.
Lời giải
a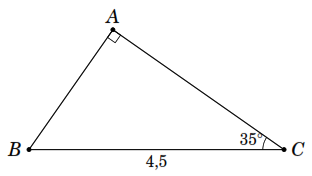 )
Xét
)
Xét
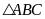 vuông ở
vuông ở
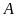 ,
,
ta
có
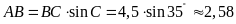 .
.
Tương
tự,
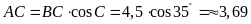 .
.
Do
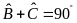 nên
nên
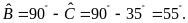
b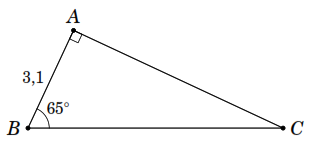 )
Xét
)
Xét
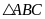 vuông ở
vuông ở
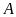 ,
ta có
,
ta có
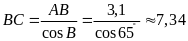 .
.
Tương
tự,
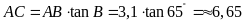 .
.
Do
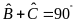 nên
nên
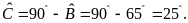
Bài
3.
Cho tam giác
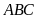 cân tại
cân tại
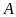 ,
đường cao
,
đường cao
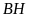 .
Biết
.
Biết
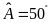 ,
,
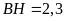 .
Tính chu vi của
.
Tính chu vi của
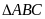 .
.
Lời giải
Do
giả thiết suy ra
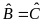 nên
nên
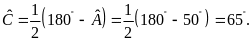 X
X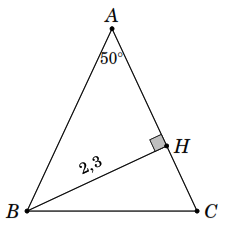 ét
ét
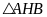 vuông tại
vuông tại
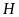 ,
ta có
,
ta có
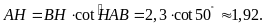
Tương
tự, xét
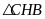 vuông tại
vuông tại
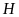 ,
ta có
,
ta có
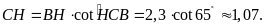
và
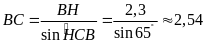 .
.
Mà
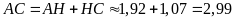 .
Do đó chu vi tam giác
.
Do đó chu vi tam giác
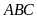 bằng
bằng
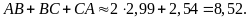
Bài
4.
Hình thang
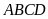 có
có
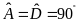 .
Biết
.
Biết
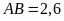 ,
,
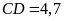 và
và
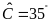 .
Tính diện tích hình thang.
.
Tính diện tích hình thang.
Lời giải
Vẽ
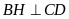 ,
do giả thiết suy ra
,
do giả thiết suy ra
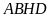 là hình chữ nhật nên
là hình chữ nhật nên
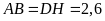 .
.
M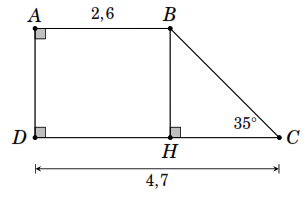 à
à
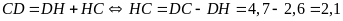 .
.
Xét
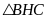 vuông tại
vuông tại
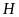 ,
ta có
,
ta có
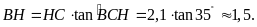
Gọi
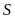 là diện tích hình thang
là diện tích hình thang
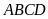 .
.
Ta
có
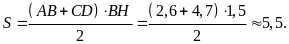
Bài
5.
Cho tam giác nhọn
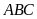 ,
,
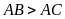 ,
đường cao
,
đường cao
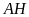 và đường trung tuyến
và đường trung tuyến
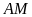 .
Gọi
.
Gọi
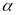 là số đo góc
là số đo góc
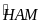 .
.
a)
Chứng minh rằng
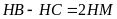 ;
;
b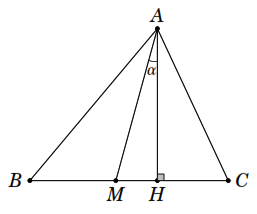 )
Chứng minh rằng
)
Chứng minh rằng
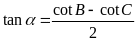 .
.
Lời giải
a)
Do giả thiết
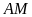 là trung tuyến nên
là trung tuyến nên
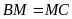 .
.
Mà
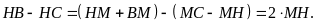
b)
Đặt
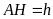 ,
xét
,
xét
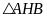 ,
ta có
,
ta có
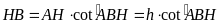 .
.
Tương
tự, xét
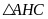 ,
ta có
,
ta có
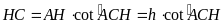 .
.
Suy
ra
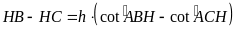 hay
hay
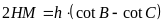 . (1)
. (1)
Mặt
khác, xét
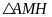 vuông tại
vuông tại
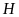 ,
ta có
,
ta có
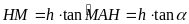
hay
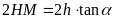 . (2)
. (2)
Từ
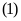 và
và
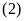 suy ra
suy ra
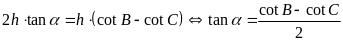 .
.
Bài
6.
Giải tam giác nhọn
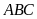 biết
biết
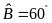 ,
,
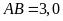 và
và
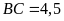 .
.
L ời
giải
ời
giải
Kẻ
đường cao
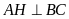 .
Xét
.
Xét
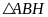 vuông tại
vuông tại
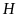 ,
ta có
,
ta có
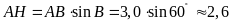 .
.
Tương
tự, xét
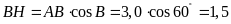 .
.
Mà
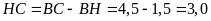 .
.
Theo
định lí Py-ta-go ta có
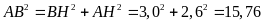 suy ra
suy ra
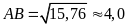 .
.
Xét
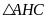 vuông tại
vuông tại
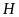 ta có
ta có
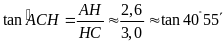 .
.
Do
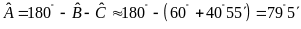 .
.
Bài
7.
Hình thang
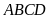 (
(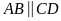 )
có
)
có
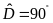 ,
,
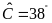 ,
,
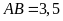 ,
,
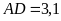 .
Tính diện tích hình thang đó.
.
Tính diện tích hình thang đó.
L ời
giải
ời
giải
Vẽ
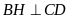 ,
do giả thiết suy ra
,
do giả thiết suy ra
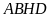 là hình chữ nhật. Do đó
là hình chữ nhật. Do đó
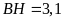 ,
,
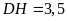 .
.
Xét
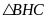 vuông tại
vuông tại
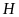 ,
ta có
,
ta có
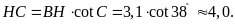
Mà
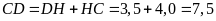 .
.
Gọi
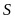 là diện tích hình thang
là diện tích hình thang
 khi đó
khi đó
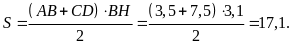
D. BÀI TẬP TỰ LUYỆN
Bài 8. Các cạnh của một tam giác vuông có độ dài 4cm; 6cm và 6cm. Hãy tính góc nhỏ nhất của tam giác đó.
Bài
9.
Tam giác
 vuông tại
vuông tại
 có
có
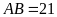 cm,
cm,
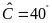 .
Hãy tính các độ dài
.
Hãy tính các độ dài
a)
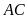 ; b)
; b)
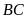 ; c)
Phân giác
; c)
Phân giác
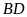 .
.
B ài
10.
Cho hình bên, biết:
ài
10.
Cho hình bên, biết:
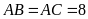 cm,
cm,
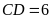 cm,
cm,
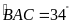 và
và
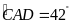 .
Hãy tính
.
Hãy tính
a)
Độ dài cạnh
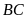 ;
;
b)
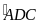 ;
;
c)
Khoảng cách từ điểm
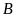 đến cạnh
đến cạnh
 .
.
Bài
11.
Trong một tam giác
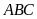 có
có
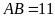 cm,
cm,
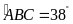 ,
,
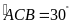 ,
,
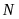 là chân đường vuông góc kẻ từ
là chân đường vuông góc kẻ từ
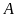 đến
đến
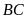 .
Hãy tính
.
Hãy tính
 ,
,
 .
.
Bài
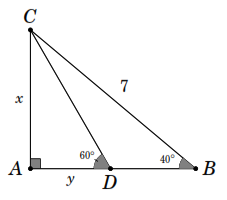
12.
Tìm
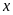 và
và
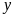 trong các hình sau
trong các hình sau
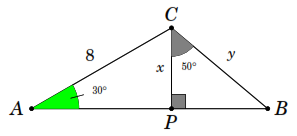
Bài
13.
Cho tam giác
 đều cạnh
đều cạnh
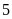 cm
và
cm
và
 .
Hãy tính
.
Hãy tính
a)
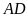 ; b)
; b)
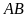 .
.

--- HẾT ---
Ngoài Giải Toán 9 Bài 4 Hình Học Hệ Thức Về Cạnh Và Góc Trong Tam Giác Vuông – Toán 9 thì các tài liệu học tập trong chương trình 9 sẽ được cập nhật liên tục và nhanh nhất có thể sau khi kỳ thi diễn ra trên Danh mục Tài Liệu Học Tập nhằm giúp các bạn đọc thuận tiện trong việc nghiên cứu tài liệu. Quý thày cô và các bạn đọc có thể chia sẻ thêm những tài liệu học tập hữu ích đến địa chỉ email của chúng tôi, nhằm xây dựng nên kho đề thi phong phú, đa dạng cho các em học sinh tham khảo và rèn luyện.
Bài tập liên quan đến hệ thức về cạnh và góc trong tam giác vuông thường bao gồm việc sử dụng các hệ thức trigonometri như sin, cos, tan và các quy tắc liên quan đến các cạnh và góc. Bộ tài liệu này sẽ hướng dẫn bạn qua từng bước cụ thể để áp dụng các hệ thức này vào việc giải quyết các bài toán thực tế.
Mỗi phần trong bộ tài liệu được giải thích chi tiết và kèm theo ví dụ minh họa giúp bạn hiểu rõ hơn về cách áp dụng kiến thức vào giải quyết các bài tập. Điều này giúp bạn nắm vững kỹ năng và tự tin hơn khi giải quyết các bài toán liên quan đến hệ thức về cạnh và góc trong tam giác vuông.
Hãy cùng tham gia và khám phá với “Giải Toán 9 Bài 4 Hình Học Hệ Thức Về Cạnh Và Góc Trong Tam Giác Vuông”. Bằng sự nỗ lực và cố gắng trong việc học tập, bạn sẽ nắm vững kiến thức hình học và có khả năng giải quyết các bài toán phức tạp liên quan đến hệ thức về cạnh và góc trong tam giác vuông. Chúc các bạn thành công và vui vẻ trong hành trình học tập toán học!
>>> Bài viết có liên quan: