Phương Pháp Giải Toán 9 Đồ Thị Hàm Số y = ax2 Kèm Lời Giải
>>> Mọi người cũng quan tâm:
Phương Pháp Giải Toán 9 Đồ Thị Hàm Số y = ax2 Kèm Lời Giải – Toán 9 là tài liệu học tập được Trang Tài Liệu biên soạn và sưu tầm từ những nguồn dữ liệu mới nhất hiện nay. Tài liệu này sẽ giúp các em luyện tập, củng cố kiến thức từ đó nâng cao điểm số cho môn học. Ngoài ra, cũng giúp các thầy cô giáo có nguồn tài nguyên phong phú để giảng dạy.
Dưới đây là bản đọc trực tuyến giúp thầy cô và các em học sinh có thể nghiên cứu Online hoặc bạn có thể tải miễn phí với phiên bản word để dễ dàng in ấn cũng như học tập Offline.
A. KIẾN THỨC TRỌNG TÂM
Đồ
thị của hàm số
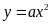
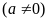 là một parabol
đi qua gốc tọa độ
là một parabol
đi qua gốc tọa độ
 ,
nhận
,
nhận
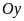 làm trục đối xứng (
làm trục đối xứng ( là đỉnh của parabol).
là đỉnh của parabol).
Nếu
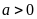 thì đồ thị nằm phía trên trục hoành,
thì đồ thị nằm phía trên trục hoành,
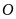 là điểm thấp nhất của đồ thị.
là điểm thấp nhất của đồ thị.Nếu
 thì đồ thị nằm phía dưới trục hoành,
thì đồ thị nằm phía dưới trục hoành,
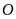 là điểm cao nhất của đồ thị.
là điểm cao nhất của đồ thị.
B. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
Dạng 1: Vẽ đồ thị hàm số |
|
Ví
dụ 1.
Cho
hàm số
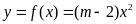 (
(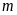 là tham số). Tìm
là tham số). Tìm
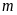 để:
để:
a)
Đồ thị hàm số đi qua điểm
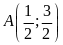 .
ĐS:
.
ĐS:
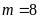 .
.
b)
Đồ thị hàm số đi qua điểm
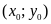 với
với
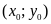 là nghiệm của hệ phương trình
là nghiệm của hệ phương trình
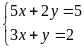 .
.
ĐS:
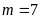 .
.
c)
Vẽ đồ thị hàm số với các giá trị
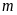 tìm được trên cùng một mặt phẳng tọa độ.
tìm được trên cùng một mặt phẳng tọa độ.
Ví
dụ 2.
Cho hàm số
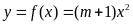 (
(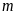 là tham số). Tìm
là tham số). Tìm
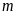 để:
để:
a)
Đồ thị hàm số đi qua điểm
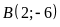 .
ĐS:
.
ĐS:
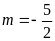 .
.
b)
Đồ thị hàm số đi qua điểm
 với
với
 là nghiệm của hệ phương trình
là nghiệm của hệ phương trình
 .
.
ĐS:
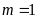 .
.
c)
Vẽ đồ thị hàm số với các giá trị
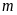 tìm được trên cùng một mặt phẳng tọa độ.
tìm được trên cùng một mặt phẳng tọa độ.
Ví
dụ 3.
Cho hàm số
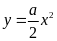
 có đồ thị là parabol
có đồ thị là parabol
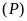 .
.
a)
Xác định
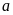 để
để
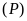 đi qua điểm
đi qua điểm
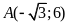 .
ĐS:
.
ĐS:
 .
.
b)
Với giá trị
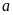 vừa tìm được ở trên, hãy:
vừa tìm được ở trên, hãy:
i)
Vẽ
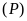 trên mặt phẳng tọa độ.
trên mặt phẳng tọa độ.
ii)
Tìm các điểm trên
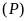 có hoành độ bằng
có hoành độ bằng
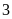 .
.
iii)
Tìm các điểm trên
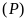 cách đều hai trục tọa độ. ĐS:
cách đều hai trục tọa độ. ĐS:
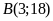 ;
;
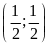 ;
;
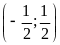 .
.
Ví
dụ 4.
Cho hàm số
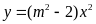
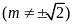 có đồ thị là parabol
có đồ thị là parabol
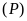 .
.
a)
Xác định
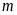 để
để
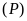 đi qua điểm
đi qua điểm
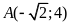 .
ĐS:
.
ĐS:
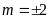 .
.
b)
Với giá trị
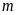 vừa tìm được ở trên, hãy:
vừa tìm được ở trên, hãy:
i)
Vẽ
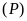 trên mặt phẳng tọa độ.
trên mặt phẳng tọa độ.
ii)
Tìm các điểm trên
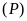 có hoành độ bằng
có hoành độ bằng
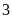 .
.
iii)
Tìm các điểm trên
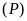 cách đều hai trục tọa độ. ĐS:
cách đều hai trục tọa độ. ĐS:
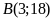 ;
;
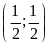 ;
;
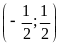 .
.
Ví
dụ 5.
Cho hàm số
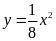 có đồ thị là parabol
có đồ thị là parabol
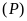 .
.
a)
Vẽ
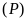 trên mặt phẳng tọa độ.
trên mặt phẳng tọa độ.
b)
Trong các điểm
 ;
;
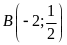 ;
;
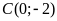 ,
điểm nào thuộc
,
điểm nào thuộc
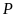 ,
điểm nào không thuộc
,
điểm nào không thuộc
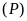 ?
?
Ví
dụ 6.
Cho hàm số
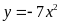 có đồ thị là parabol
có đồ thị là parabol
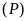 .
.
a)
Vẽ
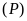 trên mặt phẳng tọa độ.
trên mặt phẳng tọa độ.
b)
Trong các điểm
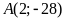 ;
;
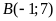 ;
;
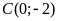 ,
điểm nào thuộc
,
điểm nào thuộc
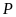 ,
điểm nào không thuộc
,
điểm nào không thuộc
 ?
?
Dạng 2: Tọa độ giao điểm của Parabol và đường thẳng |
Chú ý: Số nghiệm của phương trình (*) đúng bằng số giao điểm của (P) và d, cụ thể
|
Ví
dụ 7.
Cho parabol
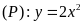 và đường thẳng
và đường thẳng
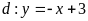 .
.
a)
Vẽ
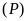 và
và
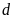 trên cùng một mặt phẳng tọa độ.
trên cùng một mặt phẳng tọa độ.
b)
Xác định tọa độ giao điểm của
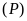 và
và
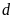 .
ĐS:
.
ĐS:
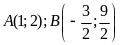 .
.
c)
Dựa vào đồ thị, hãy giải bất phương trình
 .
ĐS:
.
ĐS:
 .
.
Ví
dụ 8.
Cho parabol
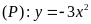 và đường thẳng
và đường thẳng
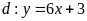 .
.
a)
Vẽ
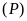 và
và
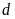 trên cùng một mặt phẳng tọa độ.
trên cùng một mặt phẳng tọa độ.
b)
Xác định tọa độ giao điểm của
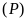 và
và
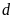 .
ĐS:
.
ĐS:
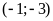 .
.
c)
Dựa vào đồ thị, hãy giải bất phương trình
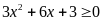 .
ĐS:
.
ĐS:
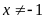 .
.
Ví
dụ 9.
Cho hàm số
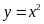 có đồ thị là parabol
có đồ thị là parabol
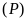 .
.
a)
Vẽ
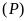 trên mặt phẳng tọa độ.
trên mặt phẳng tọa độ.
b)
Dựa vào đồ thị, hãy biện luận số nghiệm của phương
trình
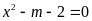 theo
theo
 .
.
Ví
dụ 10.
Cho hàm số
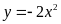 có đồ thị là parabol
có đồ thị là parabol
 .
.
a)
Vẽ
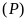 trên mặt phẳng tọa độ.
trên mặt phẳng tọa độ.
b)
Dựa vào đồ thị, hãy biện luận số nghiệm của phương
trình
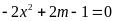 theo
theo
 .
.
Ví
dụ 11.
Cho parabol
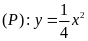 và đường thẳng
và đường thẳng
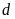 có phương trình
có phương trình
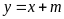 .
Tìm
.
Tìm
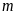 để:
để:
a)
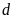 và
và
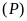 có điểm chung duy nhất. ĐS:
có điểm chung duy nhất. ĐS:
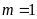 .
.
b)
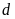 và
và
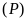 cắt nhau tại hai điểm phân biệt. ĐS:
cắt nhau tại hai điểm phân biệt. ĐS:
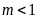 .
.
c)
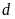 và
và
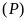 không có điểm chung. ĐS:
không có điểm chung. ĐS:
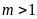 .
.
Ví
dụ 12.
Cho parabol
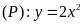 và đường thẳng
và đường thẳng
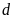 có phương trình
có phương trình
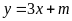 .
Tìm
.
Tìm
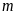 để:
để:
a)
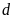 và
và
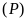 có điểm chung duy nhất. ĐS:
có điểm chung duy nhất. ĐS:
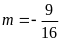 .
.
b)
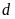 và
và
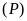 cắt nhau tại hai điểm phân biệt. ĐS:
cắt nhau tại hai điểm phân biệt. ĐS:
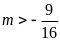 .
.
c)
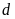 và
và
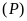 không có điểm chung. ĐS:
không có điểm chung. ĐS:
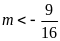 .
.
C. BÀI TẬP VẬN DỤNG
Bài
1.
Cho hàm số
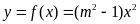 (
(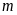 là tham số). Tìm
là tham số). Tìm
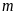 để:
để:
a)
Đồ thị hàm số đi qua điểm
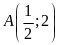 .
ĐS:
.
ĐS:
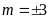 .
.
b)
Đồ thị hàm số đi qua điểm
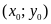 với
với
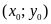 là nghiệm của hệ phương trình
là nghiệm của hệ phương trình
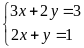 .
.
ĐS:
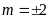 .
.
c)
Vẽ đồ thị hàm số với các giá trị
 tìm được trên cùng một mặt phẳng tọa độ.
tìm được trên cùng một mặt phẳng tọa độ.
Bài
2.
Cho hàm số
 có đồ thị là parabol
có đồ thị là parabol
 .
.
a)
Xác định
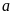 để
để
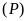 đi qua điểm
đi qua điểm
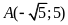 .
ĐS:
.
ĐS:
 .
.
b) Với giá trị vừa tìm được ở trên, hãy:
i)
Vẽ
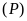 trên mặt phẳng tọa độ.
trên mặt phẳng tọa độ.
ii)
Tìm các điểm trên
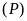 có hoành độ bằng
có hoành độ bằng
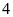 .
.
iii)
Tìm các điểm trên
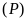 cách đều hai trục tọa độ. ĐS:
cách đều hai trục tọa độ. ĐS:
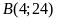 ;
;
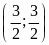 ;
;
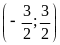 .
.
Bài
3.
Cho hàm số
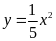 có đồ thị là parabol
có đồ thị là parabol
 .
.
a)
Vẽ
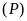 trên mặt phẳng tọa độ.
trên mặt phẳng tọa độ.
b)
Trong các điểm
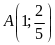 ;
;
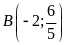 ;
;
 ,
điểm nào thuộc
,
điểm nào thuộc
 ,
điểm nào không thuộc
,
điểm nào không thuộc
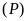 ?
?
Bài
4.
Cho parabol
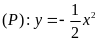 và đường thẳng
và đường thẳng
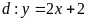 .
.
a)
Vẽ
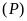 và
và
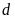 trên cùng một mặt phẳng tọa độ.
trên cùng một mặt phẳng tọa độ.
b)
Xác định tọa độ giao điểm của
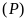 và
và
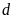 .
ĐS:
.
ĐS:
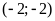 .
.
Bài
5.
Cho hàm số
 có đồ thị là parabol
có đồ thị là parabol
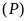 .
.
a)
Vẽ
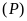 lên mặt phẳng tọa độ.
lên mặt phẳng tọa độ.
b)
Dựa vào đồ thị, hãy biện luận số nghiệm của phương
trình
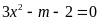 theo
theo
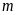 .
.
Bài
6.
Cho parabol
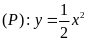 và đường thẳng
và đường thẳng
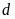 có phương trình
có phương trình
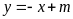 .
Tìm
.
Tìm
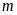 để:
để:
a)
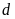 và
và
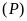 có điểm chung duy nhất. ĐS:
có điểm chung duy nhất. ĐS:
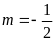 .
.
b)
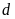 và
và
 cắt nhau tại hai điểm phân biệt. ĐS:
cắt nhau tại hai điểm phân biệt. ĐS:
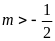 .
.
c)
 và
và
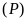 không có điểm chung. ĐS:
không có điểm chung. ĐS:
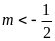 .
.
HƯỚNG DẪN GIẢI
Cho hàm số
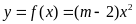 (
(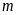 là tham số). Tìm
là tham số). Tìm
 để:
để:
a).
Đồ thị hàm số đi qua điểm
 .
.
b).
Đồ thị hàm số đi qua điểm
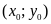 với
với
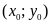 là nghiệm của hệ phương trình
là nghiệm của hệ phương trình
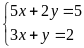 .
.
c).
Vẽ đồ thị hàm số với các giá trị
 tìm được trên cùng một mặt phẳng tọa độ.
tìm được trên cùng một mặt phẳng tọa độ.
Lời giải.

a).
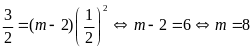 .
.
b).
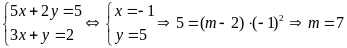 .
.
c).
Với
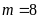 và
và
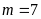 thì
thì
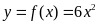 và
và
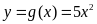 .
.
Cho hàm số
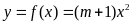 (
(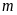 là tham số). Tìm
là tham số). Tìm
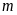 để:
để:
a).
Đồ thị hàm số đi qua điểm
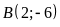 .
.
b).
Đồ thị hàm số đi qua điểm
 với
với
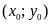 là nghiệm của hệ phương trình
là nghiệm của hệ phương trình
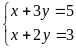 .
.
c).
Vẽ đồ thị hàm số với các giá trị
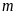 tìm được trên cùng một mặt phẳng tọa độ.
tìm được trên cùng một mặt phẳng tọa độ.
Lời giải.
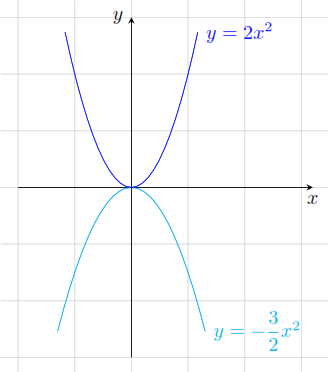
a).
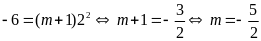 .
.
b).
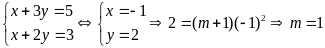 .
.
c).
Với
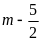 và
và
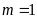 thì
thì
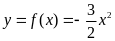 và
và
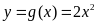 .
.
Cho hàm số

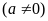 có đồ thị là parabol
có đồ thị là parabol
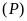 .
.
a).
Xác định
 để
để
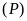 đi qua điểm
đi qua điểm
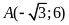 .
.
b).
Với giá trị
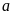 vừa tìm được ở trên, hãy:
vừa tìm được ở trên, hãy:
i)
Vẽ
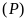 trên mặt phẳng tọa độ.
trên mặt phẳng tọa độ.
ii)
Tìm các điểm trên
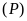 có hoành độ bằng
có hoành độ bằng
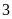 .
.
iii)
Tìm các điểm trên
 cách đều hai trục tọa độ.
cách đều hai trục tọa độ.
Lời giải.
a).
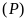 đi qua điểm
đi qua điểm
 nên
nên
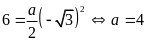 .
.
b).
i)
Với
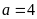 ta có hàm số
ta có hàm số
 .
.
ii)
Ta có
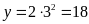 suyra
suyra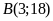 .
.
iii)
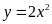 ;
;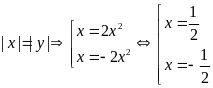 ;
; .
.
Cho hàm số
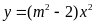
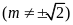 có đồ thị là parabol
có đồ thị là parabol
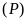 .
.
a).
Xác định
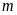 để
để
 đi qua điểm
đi qua điểm
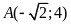 .
.
b).
Với giá trị
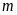 vừa tìm được ở trên, hãy:
vừa tìm được ở trên, hãy:
i)
Vẽ
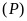 trên mặt phẳng tọa độ.
trên mặt phẳng tọa độ.
ii)
Tìm các điểm trên
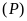 có hoành độ bằng
có hoành độ bằng
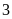 .
.
iii)
Tìm các điểm trên
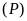 cách đều hai trục tọa độ.
cách đều hai trục tọa độ.
Lời giải.
a).
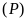 đi qua điểm
đi qua điểm
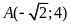 nên
nên
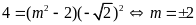 .
.
b).
i) Với
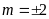 ta có hàm số
ta có hàm số
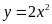 .
.
ii)
Ta có
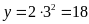 suyra
suyra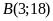 .
.
iii)
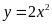 ;
; ;
;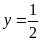 .
.
Cho hàm số
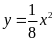 có đồ thị là parabol
có đồ thị là parabol
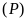 .
.
a).
Vẽ
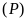 trên mặt phẳng tọa độ.
trên mặt phẳng tọa độ.
b).
Trong các điểm
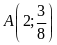 ;
;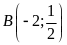 ;
;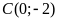 ,
điểm nào thuộc
,
điểm nào thuộc
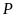 ,
điểm nào không thuộc
,
điểm nào không thuộc
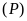 ?
?
Lời giải.
a).
b).
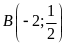 thuộc
thuộc
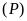 ,
,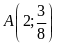 ;
;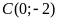 không thuộc
không thuộc
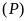 .
.
Cho hàm số
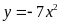 có đồ thị là parabol
có đồ thị là parabol
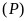 .
.
a).
Vẽ
 trên mặt phẳng tọa độ.
trên mặt phẳng tọa độ.
b).
Trong các điểm
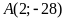 ;
;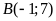 ;
;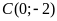 ,
điểm nào thuộc
,
điểm nào thuộc
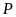 ,
điểm nào không thuộc
,
điểm nào không thuộc
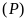 ?
?
Lời giải.

a).
b).
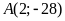 thuộc
thuộc
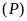 ,
,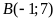 ;
;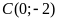 không thuộc
không thuộc
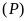 .
.
Cho parabol
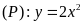 và đường thẳng
và đường thẳng
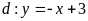 .
.
a).
Vẽ
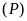 và
và
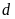 trên cùng một mặt phẳng tọa độ.
trên cùng một mặt phẳng tọa độ.
b).
Xác định tọa độ giao điểm của
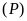 và
và
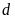 .
.
c).
Dựa vào đồ thị, hãy giải bất phương trình
 .
.
Lời giải.
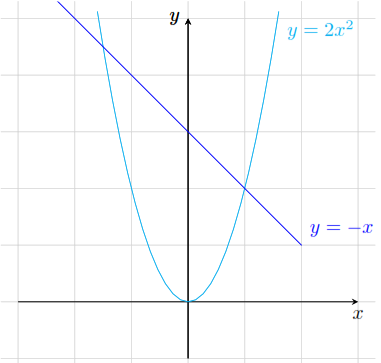
a).
b).
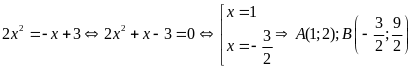 .
.
c).
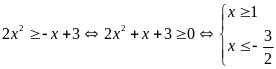 .
.
Cho parabol
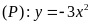 và đường thẳng
và đường thẳng
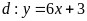 .
.
a).
Vẽ
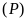 và
và
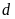 trên cùng một mặt phẳng tọa độ.
trên cùng một mặt phẳng tọa độ.
b).
Xác định tọa độ giao điểm của
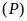 và
và
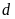 .
.
c).
Dựa vào đồ thị, hãy giải bất phương trình
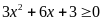 .
.
Lời giải.
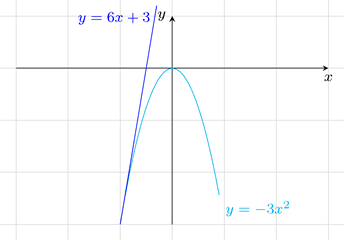
a).
b).
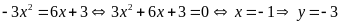 .
.
c).
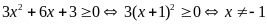 .
.
Cho hàm số
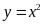 có đồ thị là parabol
có đồ thị là parabol
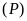 .
.
a).
Vẽ
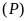 trên mặt phẳng tọa độ.
trên mặt phẳng tọa độ.
b).
Dựa vào đồ thị, hãy biện luận số nghiệm của phương
trình
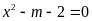 theo
theo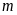 .
.
Lời giải.
a).
b).
Xét đường thẳng
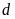 có phương trình
có phương trình
 .
Số nghiệm của phương trình
.
Số nghiệm của phương trình
 (1) là số giao điểm của đường thẳng
(1) là số giao điểm của đường thẳng
 và
và
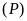 .
Từ đồ thị ta thấy:
.
Từ đồ thị ta thấy:
+
Với
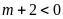 hay
hay ,
,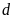 không cắt
không cắt
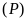 .
Do đó phương trình
.
Do đó phương trình
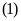 vô nghiệm.
vô nghiệm.
+
Với
 hay
hay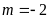 ,
,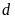 tiếp xúc
tiếp xúc
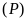 .
Do đó phương trình
.
Do đó phương trình
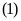 có nghiệm kép.
có nghiệm kép.
+
Với
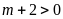 hay
hay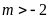 ,
, cắt
cắt
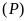 tại hai điểm phân biệt. Do đó phương trình
tại hai điểm phân biệt. Do đó phương trình
 có hai nghiệm phân biệt.
có hai nghiệm phân biệt.
Vậy:
+
Với
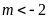 phương trình
phương trình
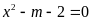 vô nghiệm.
vô nghiệm.
+
Với
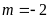 phương trình
phương trình
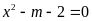 có nghiệm kép.
có nghiệm kép.
+
Với
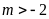 phương trình
phương trình
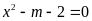 có hai nghiệm phân biệt.
có hai nghiệm phân biệt.
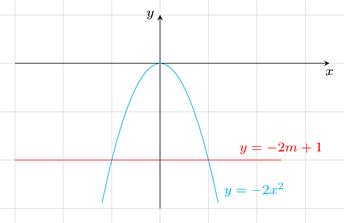
Cho hàm số
 có đồ thị là parabol
có đồ thị là parabol
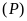 .
.
a).
Vẽ
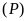 trên mặt phẳng tọa độ.
trên mặt phẳng tọa độ.
b).
Dựa vào đồ thị, hãy biện luận số nghiệm của phương
trình
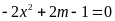 theo
theo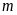 .
.
Lời giải.
a).
b).
Xét đường thẳng
 có phương trình
có phương trình
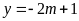 .
Số nghiệm của phương trình
.
Số nghiệm của phương trình
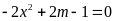 (1) là số giao điểm của đường thẳng
(1) là số giao điểm của đường thẳng
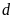 và
và
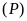 .
Từ đồ thị ta thấy:
.
Từ đồ thị ta thấy:
+
Với
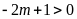 hay
hay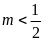 ,
, không cắt
không cắt
 .
Do đó phương trình
.
Do đó phương trình
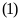 vô nghiệm.
vô nghiệm.
+
Với
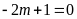 hay
hay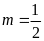 ,
, tiếp xúc
tiếp xúc
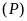 .
Do đó phương trình
.
Do đó phương trình
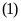 có nghiệm kép.
có nghiệm kép.
+
Với
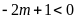 hay
hay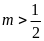 ,
,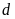 cắt
cắt
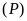 tại hai điểm phân biệt. Do đó phương trình
tại hai điểm phân biệt. Do đó phương trình
 có hai nghiệm phân biệt.
có hai nghiệm phân biệt.
Vậy:
+
Với
 phương trình
phương trình
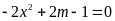 vô nghiệm.
vô nghiệm.
+
Với
 phương trình
phương trình
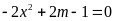 có nghiệm kép.
có nghiệm kép.
+
Với
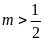 phương trình
phương trình
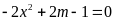 có hai nghiệm phân biệt.
có hai nghiệm phân biệt.
Cho parabol
 và đường thẳng
và đường thẳng
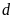 có phương trình
có phương trình
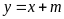 .
Tìm
.
Tìm
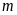 để:
để:
a).
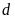 và
và
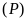 có điểm chung duy nhất.
có điểm chung duy nhất.
b).
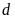 và
và
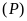 cắt nhau tại hai điểm phân biệt.
cắt nhau tại hai điểm phân biệt.
c).
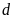 và
và
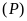 không có điểm chung.
không có điểm chung.
Lời giải.
Cách
1:
Vẽ đồ thị
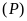 và
và
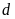 trên cùng một mặt phẳng tọa độ. Chú ý hình dạng của
trên cùng một mặt phẳng tọa độ. Chú ý hình dạng của
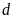 là một đường thẳng song song với đường thẳng với
trục
là một đường thẳng song song với đường thẳng với
trục
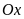 .
Sử dụng thước di chuyển
.
Sử dụng thước di chuyển
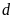 trên đồ thị và nhận xét.
trên đồ thị và nhận xét.
Cách 2: Xét phương trình hoành độ giao điểm
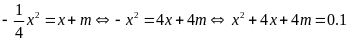
a).
Đường thẳng
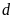 và parabol
và parabol
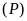 có điểm chung duy nhất khi và chỉ khi phương trình
có điểm chung duy nhất khi và chỉ khi phương trình
 có nghiệm kép
có nghiệm kép
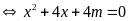 có dạng hằng đẳng thức
có dạng hằng đẳng thức
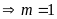 .
.
b).
Đường thẳng
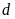 và parabol
và parabol
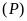 cắt nhau tại hai điểm phân biệt khi và chỉ khi phương
trình
cắt nhau tại hai điểm phân biệt khi và chỉ khi phương
trình
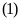 có hai nghiệm phân biệt.
có hai nghiệm phân biệt.
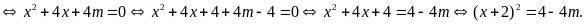
Phương
trình có hai nghiệm phân biệt khi
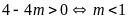 .
.
c).
Đường thẳng
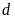 và parabol
và parabol
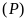 không có điểm chung khi và chỉ khi phương trình
không có điểm chung khi và chỉ khi phương trình
 vô nghiệm.
vô nghiệm.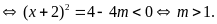
Cho parabol
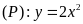 và đường thẳng
và đường thẳng
 có phương trình
có phương trình
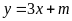 .
Tìm
.
Tìm
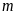 để:
để:
a).
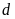 và
và
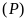 có điểm chung duy nhất.
có điểm chung duy nhất.
b).
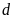 và
và
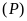 cắt nhau tại hai điểm phân biệt.
cắt nhau tại hai điểm phân biệt.
c).
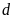 và
và
 không có điểm chung.
không có điểm chung.
Lời giải.
Xét
phương trình hoành độ giao điểm
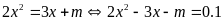
a).
Đường thẳng
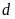 và parabol
và parabol
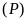 có điểm chung duy nhất khi và chỉ khi phương trình
có điểm chung duy nhất khi và chỉ khi phương trình
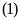 có nghiệm kép
có nghiệm kép
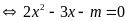 có dạng hằng đẳng thức
có dạng hằng đẳng thức
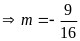 .
.
b).
Đường thẳng
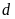 và parabol
và parabol
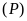 cắt nhau tại hai điểm phân biệt khi và chỉ khi phương
trình
cắt nhau tại hai điểm phân biệt khi và chỉ khi phương
trình
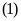 có hai nghiệm phân biệt.
có hai nghiệm phân biệt.
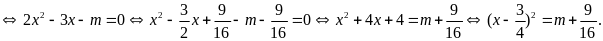
Phương
trình có hai nghiệm phân biệt khi
 .
.
c).
Đường thẳng
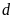 và parabol
và parabol
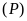 không có điểm chung khi và chỉ khi phương trình
không có điểm chung khi và chỉ khi phương trình
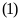 vô nghiệm.
vô nghiệm.
Cho hàm số
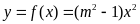 (
(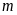 là tham số). Tìm
là tham số). Tìm
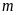 để:
để:
a).
Đồ thị hàm số đi qua điểm
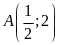 .
.
b).
Đồ thị hàm số đi qua điểm
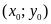 với
với
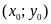 là nghiệm của hệ phương trình
là nghiệm của hệ phương trình
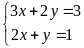 .
.
c).
Vẽ đồ thị hàm số với các giá trị
 tìm được trên cùng một mặt phẳng tọa độ.
tìm được trên cùng một mặt phẳng tọa độ.
Lời giải.
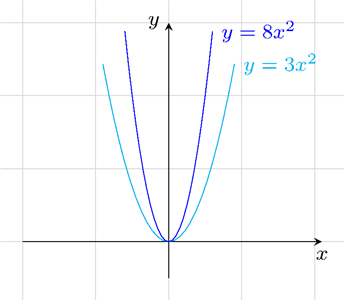
a).
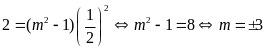 .
.
b).
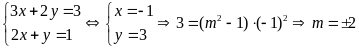 .
.
c).
Với
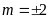 và
và
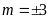 thì
thì
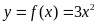 và
và
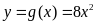 .
.
Cho hàm số
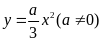 có đồ thị là parabol
có đồ thị là parabol
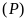 .
.
a).
Xác định
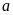 để
để
 đi qua điểm
đi qua điểm
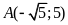 .
.
b). Với giá trị vừa tìm được ở trên, hãy:
i)
Vẽ
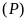 trên mặt phẳng tọa độ.
trên mặt phẳng tọa độ.
ii)
Tìm các điểm trên
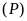 có hoành độ bằng
có hoành độ bằng
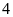 .
.
iii)
Tìm các điểm trên
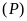 cách đều hai trục tọa độ.
cách đều hai trục tọa độ.
Lời giải.
a).
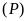 đi qua điểm
đi qua điểm
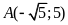 nên
nên
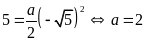 .
.
b).
i)
Với
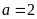 ta có đồ thị hàm số
ta có đồ thị hàm số
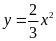 .
.
ii)
Ta có
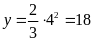 suyra
suyra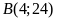 .
.
iii)
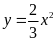 ;
;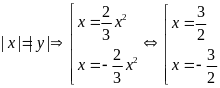 ;
;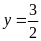 .
.
Cho hàm số
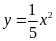 có đồ thị là parabol
có đồ thị là parabol
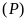 .
.
a).
Vẽ
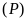 trên mặt phẳng tọa độ.
trên mặt phẳng tọa độ.
b).
Trong các điểm
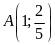 ;
;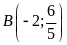 ;
;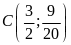 ,
điểm nào thuộc
,
điểm nào thuộc
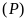 ,
điểm nào không thuộc
,
điểm nào không thuộc
 ?
?
Lời giải.
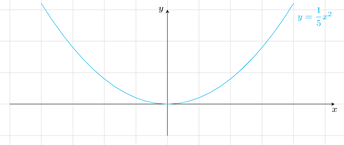
a).
b).
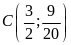 thuộc
thuộc
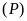 ,
,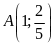 ;
;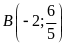 không thuộc
không thuộc
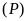 .
.
Cho parabol
 và đường thẳng
và đường thẳng
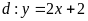 .
.
a).
Vẽ
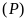 và
và
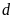 trên cùng một mặt phẳng tọa độ.
trên cùng một mặt phẳng tọa độ.
b).
Xác định tọa độ giao điểm của
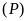 và
và
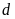 .
.
Lời giải.
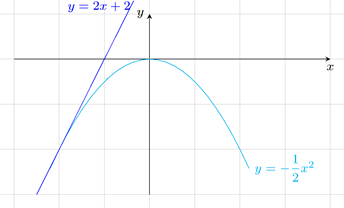
a).
b).
Phương trình hoành độ giao điểm của
 và
và
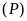
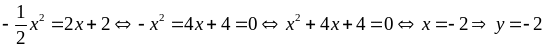 .
.
Cho hàm số
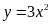 có đồ thị là parabol
có đồ thị là parabol
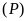 .
.
a).
Vẽ
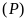 lên mặt phẳng tọa độ.
lên mặt phẳng tọa độ.
b).
Dựa vào đồ thị, hãy biện luận số nghiệm của phương
trình
 theo
theo .
.
Lời giải.
a).
b).
Xét đường thẳng
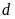 có phương trình
có phương trình
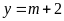 .
Số nghiệm của phương trình
.
Số nghiệm của phương trình
 (1) là số giao điểm của đường thẳng
(1) là số giao điểm của đường thẳng
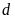 và
và
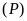 .
Từ đồ thị ta thấy:
.
Từ đồ thị ta thấy:
+
Với
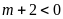 hay
hay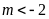 ,
,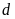 không cắt
không cắt
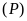 .
Do đó phương trình
.
Do đó phương trình
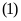 vô nghiệm.
vô nghiệm.
+
Với
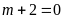 hay
hay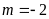 ,
,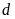 tiếp xúc
tiếp xúc
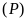 .
Do đó phương trình
.
Do đó phương trình
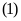 có nghiệm kép.
có nghiệm kép.
+
Với
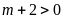 hay
hay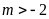 ,
,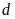 cắt
cắt
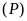 tại hai điểm phân biệt. Do đó phương trình
tại hai điểm phân biệt. Do đó phương trình
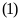 có hai nghiệm phân biệt.
có hai nghiệm phân biệt.
Vậy:
+
Với
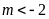 phương trình
phương trình
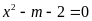 vô nghiệm.
vô nghiệm.
+
Với
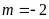 phương trình
phương trình
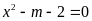 có nghiệm kép.
có nghiệm kép.
+
Với
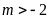 phương trình
phương trình
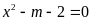 có hai nghiệm phân biệt.
có hai nghiệm phân biệt.
Cho parabol
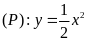 và đường thẳng
và đường thẳng
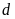 có phương trình
có phương trình
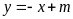 .
Tìm
.
Tìm
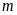 để:
để:
a).
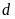 và
và
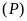 có điểm chung duy nhất.
có điểm chung duy nhất.
b).
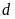 và
và
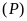 cắt nhau tại hai điểm phân biệt.
cắt nhau tại hai điểm phân biệt.
c).
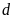 và
và
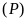 không có điểm chung.
không có điểm chung.
Lời giải.
Cách
1:
Vẽ đồ thị
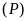 và
và
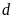 trên cùng một mặt phẳng tọa độ. Chú ý hình dạng của
trên cùng một mặt phẳng tọa độ. Chú ý hình dạng của
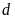 là một đường thẳng song song với đường thẳng với
trục
là một đường thẳng song song với đường thẳng với
trục
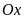 .
Sử dụng thước di chuyển
.
Sử dụng thước di chuyển
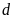 trên đồ thị và nhận xét.
trên đồ thị và nhận xét.
Cách 2: Xét phương trình hoành độ giao điểm
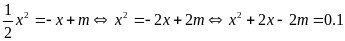
a).
Đường thẳng
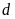 và parabol
và parabol
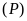 có điểm chung duy nhất khi và chỉ khi phương trình
có điểm chung duy nhất khi và chỉ khi phương trình
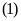 có nghiệm kép
có nghiệm kép
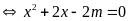 có dạng hằng đẳng thức
có dạng hằng đẳng thức
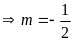 .
.
b).
Đường thẳng
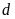 và parabol
và parabol
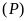 cắt nhau tại hai điểm phân biệt khi và chỉ khi phương
trình
cắt nhau tại hai điểm phân biệt khi và chỉ khi phương
trình
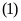 có hai nghiệm phân biệt.
có hai nghiệm phân biệt.
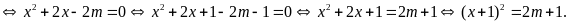
Phương
trình có hai nghiệm phân biệt khi
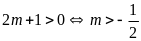 .
.
c).
Đường thẳng
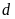 và parabol
và parabol
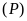 không có điểm chung khi và chỉ khi phương trình
không có điểm chung khi và chỉ khi phương trình
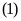 vô nghiệm.
vô nghiệm.
--- HẾT ---
Ngoài Phương Pháp Giải Toán 9 Đồ Thị Hàm Số y = ax2 Kèm Lời Giải – Toán 9 thì các tài liệu học tập trong chương trình 9 sẽ được cập nhật liên tục và nhanh nhất có thể sau khi kỳ thi diễn ra trên Danh mục Tài Liệu Học Tập nhằm giúp các bạn đọc thuận tiện trong việc nghiên cứu tài liệu. Quý thày cô và các bạn đọc có thể chia sẻ thêm những tài liệu học tập hữu ích đến địa chỉ email của chúng tôi, nhằm xây dựng nên kho đề thi phong phú, đa dạng cho các em học sinh tham khảo và rèn luyện.
Phương Pháp Giải Toán 9 Đồ Thị Hàm Số y = ax^2 Kèm Lời Giải là một bộ tài liệu ôn tập dành cho học sinh lớp 9, tập trung vào chủ đề “Đồ thị hàm số y = ax^2”. Bộ tài liệu này giúp học sinh nắm vững kiến thức về hàm số bậc hai và cách vẽ đồ thị của nó.
Bộ tài liệu cung cấp các phương pháp giải toán về đồ thị hàm số y = ax^2, từ cách tính giá trị của hàm số, tìm điểm cực trị, vẽ đồ thị cơ bản đến các bài toán liên quan. Nội dung được biên soạn rõ ràng, dễ hiểu và đi kèm với ví dụ minh họa, giúp học sinh dễ dàng nắm bắt và ứng dụng vào việc giải các bài tập thực tế.
Đặc biệt, bộ tài liệu đi kèm với lời giải chi tiết, giải thích từng bước giải một, giúp học sinh hiểu rõ cách thức giải toán một cách logic và chính xác. Điều này giúp học sinh tự tin và thành thạo hơn khi đối diện với các bài toán về hàm số y = ax^2 trong kỳ thi và bài kiểm tra.
>>> Bài viết có liên quan:







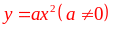
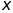 và
và
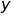 của hàm số
của hàm số
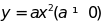 .
.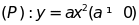 và đường thẳng
và đường thẳng
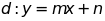 .
Để tìm tọa độ giao điểm (nếu có) của (P) và d,
ta làm như sau
.
Để tìm tọa độ giao điểm (nếu có) của (P) và d,
ta làm như sau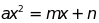 . (*)
. (*)