Hướng Dẫn Áp Dụng Công Thức Giải Tỉ Số Lượng Giác Lớp 9 Để Giải Toán

CHỦ ĐỀ 2: TỈ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN

TRONG TAM GIÁC VUÔNG.

Xét góc nhọn α trong tam giác vuông ABC

Cạnh AB kề với góc α

Cạnh AC đối diện góc α

Cạnh huyền BC.

1/ Tỉ số lượng giác của góc nhọn trong tam giác vuông.

* Có bốn tỉ số lượng giác của góc nhọn trong tam giác vuông:

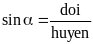
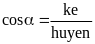
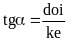
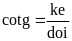
* Chú ý:

- Tỉ số lượng giác của góc nhọn luôn dương.

- Muốn có tỉ số lượng giác của góc nhọn α phải tạo ra tam giác vuông chứa góc nhọn α

- Nếu biết một góc nhọn và một cạnh của tam giác vuông sẽ tính được góc nhọn và cạnh còn lại theo tỉ số lượng giác.

2 / Hệ thức liên hệ giữa các tỉ số lượng giác góc nhọn.

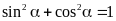
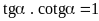
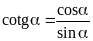
3/ Tỉ số lượng giác của hai góc phụ nhau.

* Gọi α và β là hai góc phụ nhau trong tam giác vuông. Ta có: α + β = 90^o

sinα = cosβ cosα = sinβ

tgα = cotgβ cotgα = tgβ

* Chú ý

1^o = 60’ 90^o = 89^o60’

CÁC DẠNG TOÁN

DẠNG 1: Tính cạnh và góc nhọn chưa biết trong tam giác vuông.

I/ Phương pháp.

- Nếu biết góc và cần tính cạnh: Xác định cạnh cần tìm là cạnh đối hay cạnh kề của góc nhọn hay cạnh huyền từ đó lựa chọn dùng tỉ số lượng giác nào của góc nhọn để tính.

- Nếu biết cạnh và cần tính góc: Dùng tỉ số lượng giác của góc nhọn liên quan tới cạnh đã biết (kề hoặc đối hoặc huyền) và góc nhọn cần tính.

- Có thể vận dụng kết hợp hệ thức liên hệ “cạnh góc vuông, cạnh huyền và đường cao” trong tam giác vuông để tính cạnh.

II/ Bài tập vận dụng.

Bài 1: Cho tam giác ABC vuông tại A. Góc B bằng 30^o , BC = 10cm. Hãy tính cạnh AB?

Bài 2: Cho tam giác ABC vuông tại A. Góc B bằng α, biết tgα = 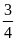, AB = 8cm. Hãy tính cạnh AC và BC?

Bài 3: Tính giá trị x ; y trong hình. Biết tg47^o = 1,072 và cos38^o = 0,788.

a) b)

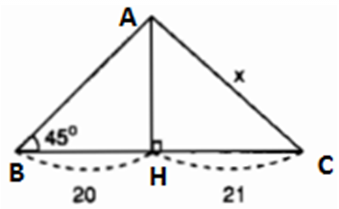c) d)

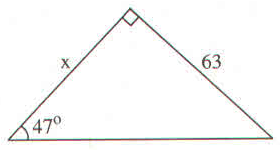
Bài 4: (SBT toán 9 – trang 107) Cho tam giác ABC vuông tại A. Đường cao AH. Tính sinB và sinC trong mỗi trường hợp sau:

a) AB = 13 ; BH = 5.

b) BH = 3 ; CH = 4.

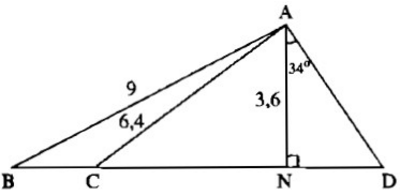
Bài 5: (SBT toán 9 – trang 111) Cho hình vẽ. Biết AB = 9cm; AC = 6,4cm ; AN = 36cm ; góc AND bằng 90^o ; góc DAN bằng 34^o. Hãy tính: CN ; góc ABN ; góc CAN và AD?

B ài 6: (SBT toán 9 – trang 111) Cho hình vẽ bên. Biết AB = BC = CD = DE = 2cm. Hãy tính:

a) AD ; BE

b) góc DAC

c) góc BXD

Bài 7: (SBT toán 9 – trang 114) Tìm x ; y trong các hình sau:

DẠNG 2: Tính cạnh và góc nhọn chưa biết trong tam giác thường.

I/ Phương pháp.

- Nếu tam giác đã cho là tam giác thường, ta phải dựng thêm đường cao của tam giác để có được tam giác vuông.

- Đường cao dựng sao cho tam giác vuông tạo ra phải chứa yếu tố góc nhọn và một cạnh đã biết.

- Áp dụng tỉ số lượng giác góc nhọn tương ứng trong tam giác vuông vừa tạo.

II/ Bài tập vận dụng.

Bài 1: (SBT toán 9 – trang 108) Tính sinL trong Hình 1 ở dưới. Biết sin30^o = 0,5.

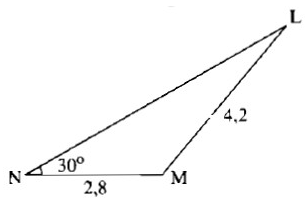
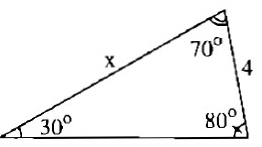
Hình 1 Hình 2

B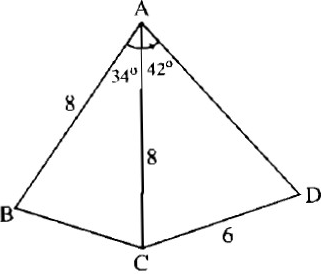 ài 2: (SBT toán 9 – trang 108). Tính x trong Hình 2 ở trên.

Bài 3: (SBT toán 9 – trang 115) Cho Hình 3. Hãy tính

a) Độ dài cạnh BC

b) góc ADC

c) Khoảng cách từ điểm B đến cạnh AD

Bài 4: (SBT toán 9 – trang 113) Cho Hình 4. Hãy tính

a) Độ dài cạnh PT

b) Diện tích tam giác PQR Hình 3

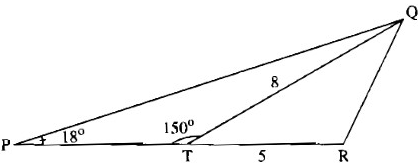
Hình 4 Hình 5

Bài 5: (SBT toán 9 – trang 115). Cho Hình 5, tam giác BCD là tam giác đều cạnh 5cm và góc DAB bằng 40^o. Hãy tính AD và AB.

Bài 6: (SBT toán 9 – trang 115) Cho tam giác ABC có BC = 12cm, góc B bằng 60^o; góc C bằng 40^o. Tính:

a) Đường cao CH và cạnh AC.

b) Diện tích tam giác ABC.

Bài 7: Hình bình hành ABCD có AB = 20cm và BD = 15cm, góc tạo bởi hai cạnh AB và BD là 110^o. Tính diện tích hình bình hành ABCD.

Bài 8: Hình thang cân ABCD (AB // DC). Biết AB = 15cm và DC = 20cm. Góc ở đáy bằng 75^o. Tính diện tích hình thang cân ABCD.

DẠNG 3: Tỉ số lượng giác của hai góc phụ nhau.

I/ Phương pháp.

* Nếu α và β là hai góc phụ nhau (α + β = 90^o):

sinα = cosβ cosα = sinβ

tgα = cotgβ cotgα = tgβ

* Chú ý: 1^o = 60’ 90^o = 89^o60’

Ví dụ: Góc 20^o35’ phụ với góc 69^o25’ vì 20^o35’ + 69^o25’ = 89^o60’

* Vận dụng:

- Xác định tỉ số lượng giác của góc nhọn nhỏ hơn 45^o khi biết tỉ số lượng giác của góc lớn hơn 45^o (hoặc ngược lại).

- Rút gọn (hoặc tính) các biểu thức liên quan tới góc phụ nhau.

II/ Bài tập vận dụng.

Bài 1: Đổi tỉ số lượng giác của các góc nhọn sau đây thành tỉ số lượng giác của góc nhỏ hơn 45^o.

sin82^o ; cos47^o ; sin48^o ; cos55^o ; sin47^o20’ ; tg62^o ; cotg82^o45’

Bài 2: Cho tam giác ABC. Biết AB = 21cm, AC = 28cm, BC = 35cm.

a) Chứng minh tam giác ABC vuông;

b) Tính sinB, sinC.

Bài 4: Đơn giản biểu thức: A = sin(90^o – x)sin(180^o – x)

B = cos(90^o – x)cos(180^o – x)

Bài 5: Tính kết quả của biểu thức

a) A = sin²10^o + sin²20^o + sin²30^o + sin²80^o + sin²70^o + sin²60^o.

b) B = cos² 12^o + cos² 78^o + cos² 1^o + cos² 89^o

c) C = sin² 3^o + sin² 15^o + sin² 75^o + sin² 87^o .

d) D = cos45^o.cos²23^o + sin45^o.cos²67^o.

e) E =

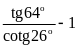
DẠNG 4: Chứng minh đẳng thức. Rút gọn biểu thức theo góc 𝛂.

I/ Phương pháp.

Vận dụng các hệ thức liên hệ sau để biến đổi một vế đẳng thức cho bằng vế còn lại (rút gọn biểu thức)

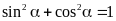
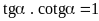
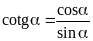
HỆ THỨC MỞ RỘNG:

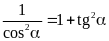
II/ Bài tập vận dụng.

Bài 1: Chứng minh các hằng đẳng thức:

a) (sinx + cosx)² = 1 + 2sinx.cosx

b) (sinx – cosx)² = 1 – 2sinx.cosx

c) sin⁴x + cos⁴x = 1 – 2sin²x cos²x

d) sinxcosx(1 + tgx)(1 + cotgx) = 1 + 2sinx . cosx .

Bài 2: Chứng minh các đẳng thức sau:

a)

b) sin⁴x – cos⁴x = 2sin²x – 1

c) 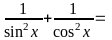tg²x + cotg²x + 2

d)

f) Cho α, b là hai góc nhọn. Chứng minh rằng:

cos²α – cos²b = sin²b - sin²α = -

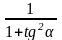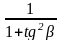
Bài 3: Rút gọn biểu thức:

a) A = sin⁶x + 3sin⁴x.cos²x + 3sin²x.cos⁴x + cos⁶x

b) B = (1 + cosα)(1 – cosα) – sin²α

Bài 4: Đơn giản các biểu thức:

A = cosy + siny . tgy B = .

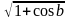C =

Bài 5: (Nâng cao) Cho các góc α, b nhọn, α < b. Chứng minh rằng:

a) cos(b -α) = cosbcosα + sinbsinα

1. sin(b - α) = sinbcosα - sinbsinα.

Bài 6: (Nâng cao) Cho tam giác ABC nhọn. Chứng minh rằng:

a) 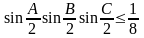b) .

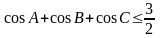Bài 7: (Nâng cao) Cho tam giác ABC nhọn có ba cạnh là a, b, c. Chứng minh rằng:

c² = a² + b² – 2ab.cosC (AB = c, BC = a, CA = b).

DẠNG 5: Biết một tỉ số lượng giác của góc α tính các tỉ số lượng giác còn lại.

I/ Phương pháp.

Vận dụng các hệ thức liên hệ sau để biến đổi một vế đẳng thức cho bằng vế còn lại (rút gọn biểu thức)

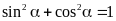
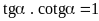
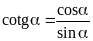
HỆ THỨC MỞ RỘNG:

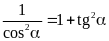
Chú ý: Các tỉ số lượng giác góc nhọn luôn dương.

II/ Bài tập vận dụng.

Bài 1: Biết rằng sinα = 0,6. Tính cosα và tgα.

Bài 2: Biết rằng cosα = 0,7. Tính sinα và tgα.

Bài 3: Biết rằng tgα = 0,8. Tính sinα và cosα.

Bài 4: Biết cosx = 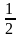, tính P = 3sin²x + 4cos²x.

Bài 5:

a) Cho góc nhọn b mà sinb = 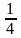. Tính cosb và tgb.

b) Cho góc α mà cosα = - . Tính sinα, tgα và cotgα .

c) Cho tgx = 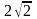. Tính sinx và cosx.

Bài 6: Hãy tính sinα, tgα nếu:

a)

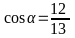
b)

Bài 7: Biết rằng sin15^o = 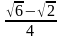. Tính tỉ số lượng giác của góc 15^o .

Dạng 6: Tính khoảng cách - Tính chiều cao - Tính diện tích tam giác - Tính độ dài đoạn thẳng - C /m các hệ thức trong tam giác: Bằng cách áp dụng tỉ số LG góc nhọn.

Bài 1: Cho tam giác ABC có AB = 26cm, AC = 25cm, đường cao AH = 24cm. Tính cạnh BC.

Bài 2: Cho tam giác ABC cân (AB = AC) và đường tròn tâm O tiếp xúc với hai cạnh AB và AC lần lượt ở B và C. Từ điểm M trên cung nhỏ BC (M khác B và C) kẻ MD, ME, MF lần lượt vuông góc với các đường thẳng BC, CA, AB.

a) Chứng minh các tứ giác MDBF, MBCE nội tiếp.

b) Chứng minh các tam giác DBM và ECM đồng dạng.

c) Cho góc BAC = 60^o và AB = 2, tính bán kính đường tròn tâm O.

Bài 3:

a) Cho tam giác ABC có A nhọn. Chứng minh rằng: S_ABC =

Gợi ý : Vẽ BH là đường cao của tam giác ABC.

BH = ABsinBAH; S_ABC = 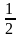BH.AC.

b) Cho tứ giác ABCD có AC cắt BD tại O và AOB nhọn. Chứng minh rằng:

S_ABCD = 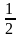AC.BD.sin AOB.

Bài 4: Cho tam giác ABC vuông tại A, đường phân giác AD. Chứng minh rằng:

a)

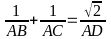
b) .

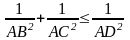Bài 5: Cho hình thang ABCD có hai cạnh bên là AD và BC bằng nhau, đường chéo AC vuông góc với cạnh bên BC. Biết AD = 5a, AC = 12a.

a) Tính

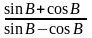
b) Tính chiều cao của hình thang ABCD.

Bài 6: Cho hình thang ABCD. Biết đáy AB = a và CD = 2a ; cạnh bên AD = a, góc A = 90^o

a) Chứng minh tgC = 1 ;

b) Tính tỉ số diện tích tam giác DBC và diện tích hình thang ABCD ;

c) Tính tỉ số diện tích tam giác ABC và diện tích tam giác DBC.

Bài 7: Gọi AM, BN, CL là ba đường cao của tam giác ABC.

a) Chứng minh: D ANL ~ D ABC ;

b) Chứng minh: AN.BL.CM = AB.BC.CA.cosAcosBcosC.