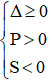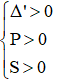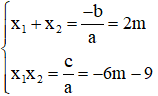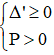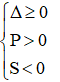Bài toán tìm m để phương trình có 2 nghiệm trái dấu
Tìm m để phương trình có 2 nghiệm trái dấu là một dạng bài tập mà chúng ta hay bắt gặp trong Toán 9 và đề thi tuyển sinh vào lớp 10. Để giúp các em học tốt phần này, Trang Tài Liệu gửi tới các bạn lý thuyết cơ bản và một số dạng bài tập để các em biết cách làm các bài toán Tìm m để phương trình có hai nghiệm trái dấu. Nội dung bài sẽ giúp các em học tốt môn Toán lớp 9 hiệu quả hơn, chuẩn bị cho các bài thi học kì và ôn thi vào lớp 10 hiệu quả nhất. Dưới đây là nội dung chi tiết, các em cùng tham khảo nhé.
Mục lục
Kiến thức cần nhớ khi làm dạng bài tìm m để phương trình có hai nghiệm trái dấu
Định lý Vi-ét
Nếu phương trình có hai nghiệm
phân biệt thì
+ Lưu ý: Trước khi áp dụng định lý Vi ét, ta cần tìm điều kiện để phương trình có 2 nghiệm phân biệt.
Xác định dấu các nghiệm của phương trình bậc hai
Điều kiện để phương trình có hai nghiệm trái dấu, cùng dấu, cùng dương, cùng âm,…
+ Để phương trình có hai nghiệm phân biệt trái dấu
+ Để phương trình có hai nghiệm phân biệt cùng dấu
Bài tập tự luận về bài toán tìm m để phương trình có hai nghiệm
Bài 1: Tìm m để phương trình có 2 nghiệm trái dấu
Hướng dẫn:
Để phương trình có hai nghiệm phân biệt trái dấu .
Lời giải:
Để phương trình có hai nghiệm phân biệt trái dấu
Xảy ra hai trường hợp:
Trường hợp 1:
Trường hợp 2: có hai nghiệm phân biệt cùng dấu.
Hướng dẫn:
Để phương trình có hai nghiệm phân biệt cùng dấu
Để phương trình có hai nghiệm phân biệt
Với mọi m ≠ 3, phương trình có hai nghiệm phân biệt thỏa mãn hệ thức Vi-ét:
Để phương trình có hai nghiệm phân biệt cùng dấu khi và chỉ khi:
Xảy ra hai trường hợp:
Trường hợp 1:
Vậy với m < -1 hoặc m < 3 nên phương trình có hai nghiệm phân biệt cùng dấu
Bài 3: Tìm m để phương trình có hai nghiệm phân biệt cùng dấu âm
Hướng dẫn:
Để phương trình có hai nghiệm cùng dấu âm
Lời giải:
Để phương trình có hai nghiệm cùng dấu âm
Với
Với kết hợp với m > 0
Vậy không tồn tại m để phương trình có hai nghiệm phân biệt cùng dấu âm
Bài 4: Tìm m để phương trình có hai nghiệm phân biệt cùng dấu dương.
Hướng dẫn:
Để phương trình có hai nghiệm cùng dấu dương
Với (m là tham số). Chứng minh phương trình luôn có hai nghiệm trái dấu.
Hướng dẫn giải
Ta có a.c = 1.(-1) < 0 với mọi m nên phương trình (*) luôn có hai nghiệm trái dấu với mọi m.
Vậy phương trình có hai nghiệm trái dấu với mọi giá trị của tham số m.
Một số bài tập trắc nghiệm về tìm m để phương trình có hai nghiệm
Câu 1: Cho phương trình x2 – 2x – 1 = 0 (m là tham số). Tìm khẳng định đúng
A. Phương trình luôn có hai nghiệm trái dấu.
B. Phương trình vô nghiệm < /p>
C. Phương trình có hai nghiệm cùng dấu
D. Phương trình có nghiệm kép
Giải
Vì ac = 1.(-1) = -1 < 0 nên phương trình có 2 nghiệm trái dấu
Đáp án đúng là A
Câu 2: Cho phương trình x2 – (2m + 1)x + m2 + m – 6 = 0. Tìm m để phương trình có 2 nghiệm âm.
A. m > 2
B. m < -4
C. m > 6
D. m < -3
Giải
Phương trình có 2 nghiệm cùng dấu âm khi
Δ = (2m + 1)2 – 4(m2 + m – 6) = 4m2 + 4m + 1 – 4m2 – 4m + 24 = 25 > 0 với mọi giá trị của m(1)
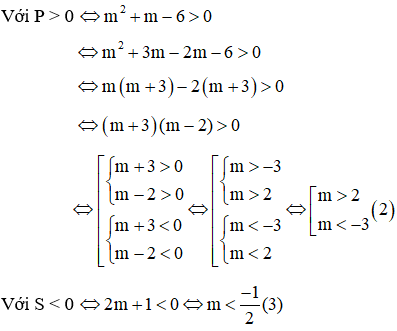
Suy ra m < -3 đồng thời thỏa mãn (1), (2) và (3)
Vậy m < -3 thỏa mãn đề bài.
Đáp án đúng là D
Câu 3: Cho phương trình: x2 – 2mx + 2m – 4 = 0. Có bao nhiêu giá trị nguyên của m nhỏ hơn 2020 để phương trình có 2 nghiệm dương phân biệt.
A. 2016
B. 2017
C. 2018
D. 2019
Giải
Phương trình có 2 nghiệm phân biệt cùng dấu dương khi
Với Δ’ > 0 ⇔ m2 – (2m – 4) > 0 ⇔ (m2 – 2m + 1) + 3 > 0 ⇔ (m – 1)2 + 3 > 0 ∀ m(1)
Với P > 0 ⇔ 2m – 4 > 0 ⇔ m > 2(2)
Với S > 0 ⇔ 2m > 0 ⇔ m > 0(3)
Từ (1), (2), (3) ta có các giá trị m cần tìm là m > 2
Suy ra số các giá trị nguyên của m thỏa mãn: 2 < m < 2020 có 2017 số
Đáp án đúng là B
Câu 4: Cho phương trình: x2 – 2mx – 6m – 9 = 0. Tìm m để phương trình có 2 nghiệm trái dấu thỏa mãn x12+x22=13
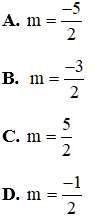
Giải
Phương trình có 2 nghiệm trái dấu khi:
Theo Vi-et ta có:
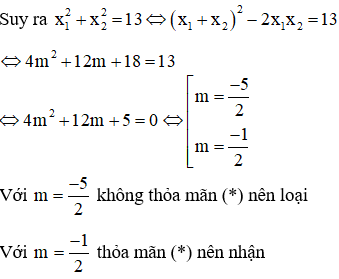
Đáp án đúng là D
Câu 5: Cho phương trình: x2 – 8x + m + 5 = 0. Gọi S là tập hợp chứa tất cả các giá trị nguyên của m để phương trình có 2 nghiệm cùng dấu. Tính tổng tất cả các phần tử của S
A. 30
B. 56
C. 18
D. 29
Giải
Phương trình có 2 nghiệm cùng dấu khi
Với Δ’ ≥ 0 ⇔ 16 – m – 5 ≥ 0 ⇔ 11-m ≥ 0 ⇔ m ≤ 11 (1)
Với P > 0 ⇔ m + 5 > 0 ⇔ m > -5(2)
Từ (1), (2) ta có các giá trị m cần tìm là -5 < m ≤ 11
Suy ra S = {-4,-3,-2,-1,0,1,2,3,4,5,6,7,8,9,10,11}
Vậy tổng tất cả các phần tử của S là 56
Đáp án đúng là B
Câu 6: Cho phương trình: 2x2 + (2m – 1)x + m – 1 = 0. Tìm m để phương trình có 2 nghiệm âm.
A. m > 3
B. m < -1
C. m > 1
D. m < -3
Giải
Phương trình có 2 nghiệm cùng dấu âm khi
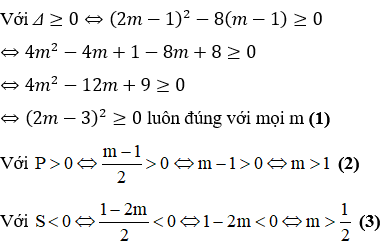
Từ (1), (2), (3) ta có các giá trị của m cần tìm là: m > 1
Đáp án đúng là C
Câu 7: Cho phương trình mx2 + 2(m – 2)x + m – 3 = 0. Xác định m để phương trình có hai nghiệm trái dấu.
A. m > 0
B. 1 < m < -1
C. 0 <m < 3
D. m < 3
Giải
Để phương trình có hai nghiệm trái dấu thì m ≠ 0 và a.c < 0
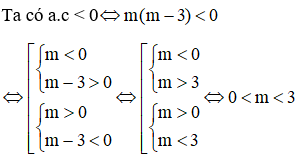
Suy ra các giá trị m cần tìm là 0 < m < 3
Đáp án đúng là C
Câu 8: Tìm m để phương trình mx2 – (5m – 2)x + 6m – 5 = 0 có hai nghiệm đối nhau.
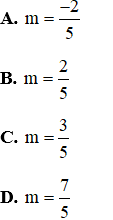
Giải
Xét phương trình: mx2 – (5m – 2)x + 6m – 5 = 0
Để để phương trình có hai nghiệm đối nhau thì:
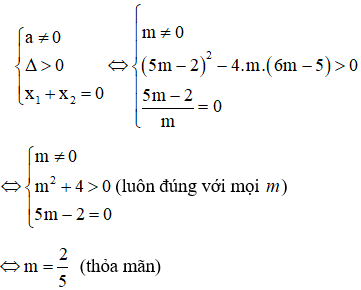
Vậy 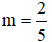
Đáp án đúng là B
Câu 9: Tìm giá trị m để phương trình 2x2 + mx + m – 3 = 0 có 2 nghiệm trái dấu và nghiệm âm có giá trị tuyệt đối lớn hơn nghiệm dương.
A. 0 < m < 3
B. -1 < m < 3
C. m < 2
D. m > -3
Giải
Để phương trình có hai nghiệm trái dấu thì: a.c < 0 ⇔ 2.(m-3) < 0 ⇔ m < 3 (1)
Giả sử phương trình có hai nghiệm trái dấu: x1 < 0 < x2
Với m < 3 , áp dụng hệ thức Vi- ét ta có:
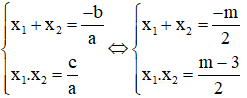
Vì nghiệm âm có giá trị tuyệt đối lớn hơn nghiệm dương nên:
|x1| > |x2| trong đó x1 < 0; x2 > 0 nên 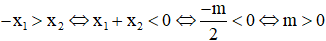
Từ (1) và (2) suy ra 0 < m < 3
Vậy 0 < m < 3 thì phương trình có hai nghiệm trái dấu và nghiệm âm có giá trị tuyệt đối lớn hơn nghiệm dương.
Đáp án đúng là A
Câu 10: Tìm giá trị m để phương trình x2 – 2(m – 1)x + m – 3 = 0 có 2 nghiệm trái dấu và bằng nhau về giá trị tuyệt đối.
A. m = 1
B. m = 4
C. m = 2
D. m = -3
Giải
Xét phương trình: x2 – 2(m – 1)x + m – 3 = 0 có: a = 1, b = -2(m – 1), c = m – 3
Phương trình có 2 nghiệm trái dấu và bằng nhau về giá trị tuyệt đối
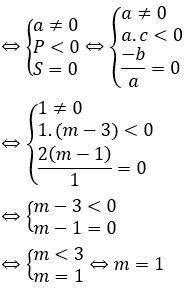
Vậy với m = 1 thì phương trình đã cho có hai nghiệm trái dấu và bằng nhau về giá trị tuyệt đối.
Đáp án đúng là A
Bài tập tự luyện về bài toán tìm m để phương trình có hai nghiệm
Bài 1: Tìm m để phương trình có hai nghiệm phân biệt:
| a) Trái dấu. | b) Cùng dấu. |
| c) Cùng dấu âm. | d) Cùng dấu dương. |
Bài 2: Tìm m để phương trình có hai nghiệm phân biệt trái dấu thỏa mãn
Bài 3: Tìm m để phương trình có hai nghiệm phân biệt:
| a) Trái dấu. | b) Cùng dấu. |
| c) Cùng dấu âm. | d) Cùng dấu dương. |
Bài 4: Tìm m để phương trình có hai nghiệm phân biệt:
Bài 5: Tìm m để phương trình có hai nghiệm phân biệt:
Bài 6: Tìm m để phương trình có hai nghiệm phân biệt cùng dấu âm
Bài 7: Tìm m để phương trình có hai nghiệm phân biệt cùng dấu âm
Bài 8: Tìm m để phương trình có hai nghiệm phân biệt cùng dấu dương
Bài 9: Tìm m để phương trình có hai nghiệm phân biệt cùng dấu dương
Bài 10: Cho phương trình . Tìm m để phương trình có hai nghiệm phân biệt cùng dấu. Khi đó hai nghiệm mang dấu gì?
Trang Tài Liệu xin giới thiệu tới các em bài Tính m để phương trình bậc hai có hai nghiệm trái dấu. Hy vọng với tài liệu học tập này các em sẽ nắm chắc kiến thức cũng như nâng cao kỹ năng giải bài toán lớp 9. Qua đó chuẩn bị tốt cho các bài thi học kì và thi vào lớp 10 sắp tới. Chúc các em học tốt.