Luyện Thi HSG Toán 6 – Bài Tập & Định Nghĩa Hình Bình Hành Có Lời Giải
>>> Mọi người cũng quan tâm:
Luyện Thi HSG Toán 6 – Bài Tập & Định Nghĩa Hình Bình Hành Có Lời Giải – Tài Liệu Toán là tài liệu học tập được Trang Tài Liệu biên soạn và sưu tầm từ những nguồn dữ liệu mới nhất hiện nay. Tài liệu này sẽ giúp các em luyện tập, củng cố kiến thức từ đó nâng cao điểm số cho môn học. Ngoài ra, cũng giúp các thầy cô giáo có nguồn tài nguyên phong phú để giảng dạy.
Dưới đây là bản đọc trực tuyến giúp thầy cô và các em học sinh có thể nghiên cứu Online hoặc bạn có thể tải miễn phí với phiên bản word để dễ dàng in ấn cũng như học tập Offline.
HH6.CHUYÊN ĐỀ 1 – MỘT SỐ HÌNH PHẲNG TRONG THỰC TIỄN
PHẦN I. TÓM TẮT LÝ THUYẾT
A. NHẬN BIẾT CÁC YẾU TỐ CỦA HÌNH BÌNH HÀNH:
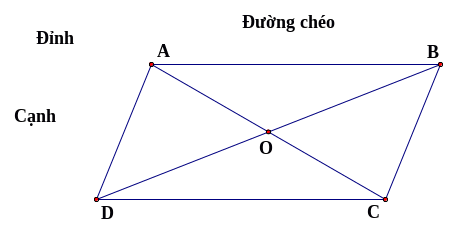
*Hình hình hành
 có:
có:
Các điểm
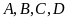 gọi là các đỉnh của hình bình hành
gọi là các đỉnh của hình bình hành
 .
.
Các đoạn thẳng
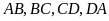 gọi là các cạnh của hình bình hành
gọi là các cạnh của hình bình hành
 .
.
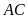 và
và
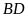 gọi là hai đường chéo của hình bình hành
gọi là hai đường chéo của hình bình hành
 .
.
I. Định nghĩa:
Hình bình hành là tứ giác có các cạnh đối song song.

Ta có:
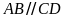 và
và
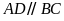 nên
tứ giác
nên
tứ giác
 là hình bình hành.
là hình bình hành.
*Chú ý: Hình bình hành là hình thang có hai cạnh bên song song.

Ta có:
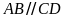 nên tứ giác
nên tứ giác
 là hình thang
là hình thang
Mà
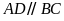 .
Vậy tứ giác
.
Vậy tứ giác
 là hình bình hành.
là hình bình hành.
II. Tính chất:
Trong hình bình hành:
+ Các cạnh đối bằng nhau
+ Các góc đối bằng nhau
+ Hai đường chéo cắt nhau tại trung điểm mỗi đường.
Nhận xét: Hình bình hành
 có:
có:
-
Hai cạnh đối
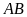 và
và
 ,
,
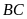 và
và
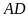 song song với nhau;
song song với nhau;
-
Hai cạnh đối bằng nhau:

- Hai góc ờ các đinh
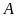 và
và
 bằng nhau; hai góc ở các đỉnh
bằng nhau; hai góc ở các đỉnh
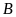 và
và
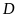 bằng nhau.
bằng nhau.
B. CÔNG THỨC TÍNH CHU VI VÀ DIỆN TÍCH CỦA HÌNH BÌNH HÀNH:
I. Công thức tính chu vi hình bình hành:
Muốn tính chu vi hình bình hành ta lấy tổng hai cạnh kề bất kỳ của hình bình hành rối nhân 2.
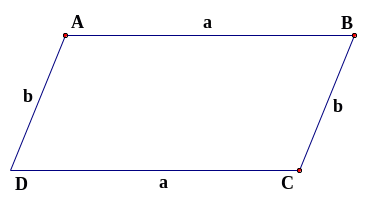
Chu vi hình bình hành:
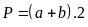
Với
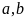 là các cạnh của hình bình hành.
là các cạnh của hình bình hành.
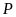 là chu vi của hình bình hành.
là chu vi của hình bình hành.
II. Công thức tính diện tích hình bình hành:
Muốn tính diện tích hình bình hành ta lấy cạnh đáy nhân chiều cao.
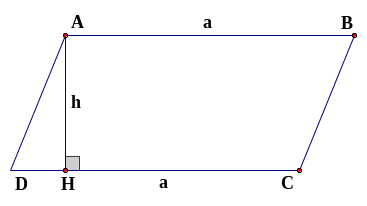
Diện tích hình bình hành:
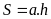
Với độ dài cạnh là
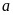 ;
độ dài đường cao ứng với cạnh
;
độ dài đường cao ứng với cạnh
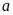 là
là
 ;
;
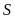 là diện tích của hình bình hành.
là diện tích của hình bình hành.
PHẦN II. CÁC DẠNG BÀI
Dạng 1: Nhận dạng hình bình hành. Vẽ hình bình hành.. Dạng 2: Nhận biết các độ dài bằng nhau trên hình bình hành.. Dạng 3: Tính chu vi, diện tích hình thoi. |
Dạng 1: Nhận dạng hình bình hành. Vẽ hình bình hành.
I.Phương pháp giải
Hình
bình hành
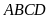 có:
có:

-
Hai cạnh đối
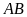 và
và
 ,
,
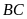 và
và
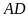 song song với nhau;
song song với nhau;
-
Hai cạnh đối bằng nhau:

-
Hai góc ở các đỉnh
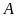 và
và
 bằng nhau; hai góc ở các đỉnh
bằng nhau; hai góc ở các đỉnh
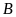 và
và
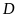 bằng nhau.
bằng nhau.
- Để nhận dạng hay vẽ hình bình hành, ta thường dùng các nhận xét: Các cạnh đối bằng nhau, hai cạnh đối song song và bằng nhau, hai đường chéo cắt nhau tại trung điểm của mỗi đường.
II.Bài toán
Bài 1: Cho ba
điểm
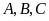 trên giấy kẻ ô vuông. Vẽ ba điểm
trên giấy kẻ ô vuông. Vẽ ba điểm
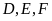 sao cho mỗi điểm đó cùng với ba điểm
sao cho mỗi điểm đó cùng với ba điểm
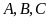 là bốn đỉnh của một hình bình hành.
là bốn đỉnh của một hình bình hành.
Lời giải:
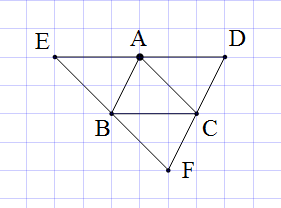
Qua điểm
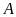 ,
,
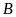 ,
,
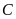 lần lượt vẽ các đường thẳng song song với
lần lượt vẽ các đường thẳng song song với
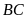 ,
,
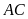 ,
,
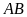 ,
chúng cắt nhau tại
,
chúng cắt nhau tại
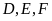 .
.
Có ba hình bình hành:
Hình bình hành
 (với
(với
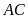 là một đường chéo)
là một đường chéo)
Hình bình hành
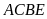 (với
(với
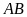 là một đường chéo)
là một đường chéo)
Hình bình hành
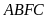 (với
(với
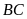 là một đường chéo)
là một đường chéo)
Bài 2: Hình vẽ dưới đây có bao nhiêu hình bình hành?

Lời giải:
Có ba hình bình hành là:
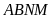 ,
,
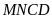 và
và
 .
.
Bài 3: Hình vẽ dưới đây có bao nhiêu hình bình hành?
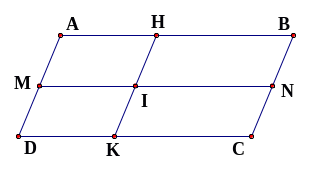
Lời giải:
Có chín hình bình hành là:
 và
và
 .
.
Bài 4: Hình vẽ dưới đây có bao nhiêu hình bình hành?
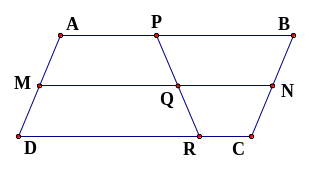
Lời giải:
Có ba hình bình hành là:
 và
và
 .
.
Bài
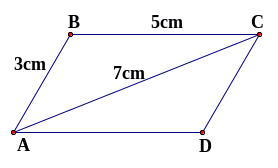
5: Vẽ hình bình hành
 biết
biết
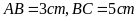 và đường chéo
và đường chéo
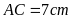 .
.
a/ Dùng compa để kiểm tra xem các cạnh đối diện của hình bình hành có bằng nhau không?
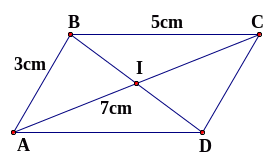
b/
Vẽ đường chéo
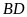 cắt đường chéo
cắt đường chéo
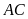 tại
tại
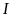 .
So sánh
.
So sánh
 và
và
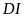 .
.
Lời giải:
-
Vẽ đoạn thẳng
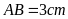 .
.
-
Vẽ đường tròn tâm
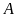 bán kính 7 cm; vẽ đường tròn tâm
bán kính 7 cm; vẽ đường tròn tâm
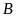 bán kính 5 cm; hai đường tròn cắt nhau tại
bán kính 5 cm; hai đường tròn cắt nhau tại
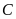 .
Nối
.
Nối
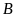 với
với
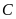 .
.
-
Từ
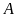 kẻ đường thẳng song song với
kẻ đường thẳng song song với
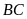 ;
từ
;
từ
 kẻ đường thẳng song song với
kẻ đường thẳng song song với
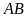 ;
hai đường thẳng này cắt nhau tại
;
hai đường thẳng này cắt nhau tại
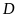 .
.
-
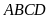 là hình bình hành cần vẽ.
là hình bình hành cần vẽ.
a/
Kết quả đo:
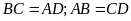 .
.
b/
Kết quả đo:
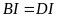 .
.
Bài
6: Vẽ hình bình hành
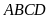 bất kỳ trên giấy.
bất kỳ trên giấy.
Lời giải:
*Cách 1: Vẽ trên giấy kẻ ô vuông
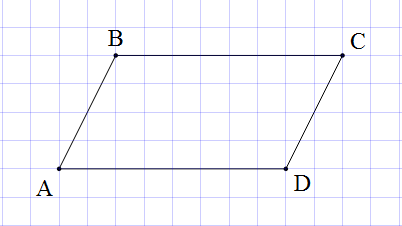
Chú
ý: Khi vẽ các cặp đoạn thẳng
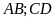 phải
song song và
phải
song song và
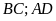 phải song song nhờ vào các ô trên giấy vẽ.
phải song song nhờ vào các ô trên giấy vẽ.
*Cách 2: Vẽ trên giấy có hai đường thẳng song song
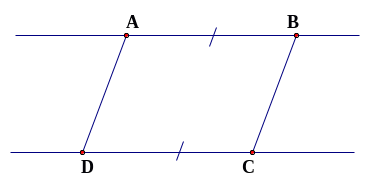
Chú
ý: Phải vẽ được
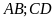 song song và
song song và
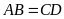 .
.
Dạng 2: Nhận biết các độ dài bằng nhau trên hình bình hành.
I.Phương pháp giải
-
Hình bình hành
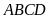 có
có
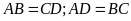 .
.
-
Nếu
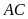 cắt
cắt
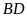 ở
ở
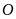 thì
thì
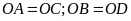 .
.
II.Bài toán
Bài
1: Cho hình vẽ với
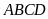 là hình bình hành,
là hình bình hành,
 cắt
cắt
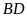 ở
ở
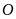 và
và
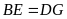 .
.
Hãy kể tên các đoạn thẳng bằng nhau trên hình.
Lời giải:

Ta
có:
 là hình bình hành
là hình bình hành
Nên
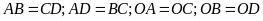 .
.
Ta
có:
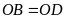 mà
mà
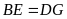 nên
nên
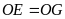 .
.
Bài
2: Cho hình bình hành
 .
.
a/ Tìm các đoạn thẳng bằng nhau.
b/
Dùng ê ke vẽ các đường cao
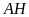 và
và
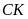 .
Đo và so sánh độ dài
.
Đo và so sánh độ dài
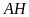 và
và
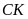 .
.
Lời giải:

a/
Vì
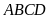 là hình bình hành.
là hình bình hành.
Nên
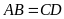 và
và
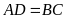 .
.
b/
Kết quả đo:
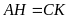 .
.
Bài
3: Cho ba điểm
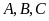 trên giấy kẻ ô vuông. Vẽ điểm
trên giấy kẻ ô vuông. Vẽ điểm
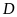 sao cho
sao cho
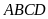 là một hình bình hành.
là một hình bình hành.
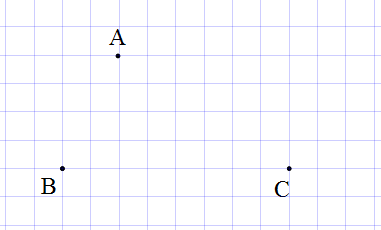
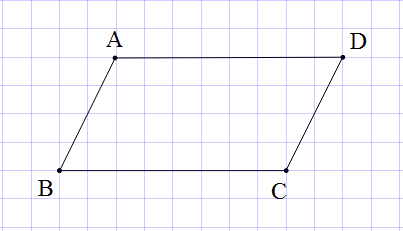
Lời giải:
Để
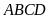 là một hình bình hành thì các cạnh đối phải song song.
là một hình bình hành thì các cạnh đối phải song song.
Nên
điểm
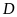 nằm trên đường thẳng song song với
nằm trên đường thẳng song song với
 và
và
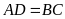 .
.
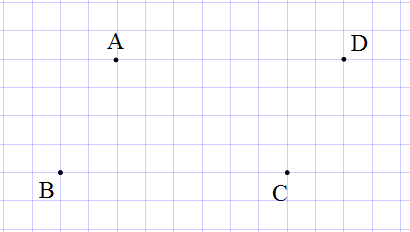
Nối
các đoạn thẳng
 ta được hình bình hành
ta được hình bình hành
 .
.
Bài
4: Vẽ hình bình hành
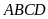 .
Dùng ê ke vẽ các đường cao kẻ từ
.
Dùng ê ke vẽ các đường cao kẻ từ
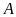 đến
đến
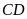 và từ
và từ
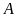 đến
đến
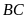 .
Nêu tên các đường cao đó.
.
Nêu tên các đường cao đó.
Lời giải:

Ta
có:
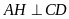 nên
nên
 là đường cao của hình bình hành
là đường cao của hình bình hành
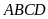 .
.
Ta
có:
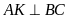 nên
nên
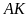 là đường cao của hình bình hành
là đường cao của hình bình hành
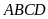 .
.
Bài 5: Xem các hình sau:

a/ Hãy cho biết hình 1, hình 2, hình 3 có bao nhiêu hình bình hành ?
b/ Tìm số hình bình hành của hình thứ 24?
Lời giải:
a/ Ta có:
Hình
1 có 3 hình bình hành (vì
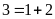 )
)
Hình
2 có 6 hình bình hành (vì
 )
)
Hình
3 có 10 hình bình hành (vì
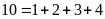 )
)
b/ Số hình bình hành của hình số 24 là :
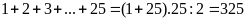 (hình bình hành)
(hình bình hành)
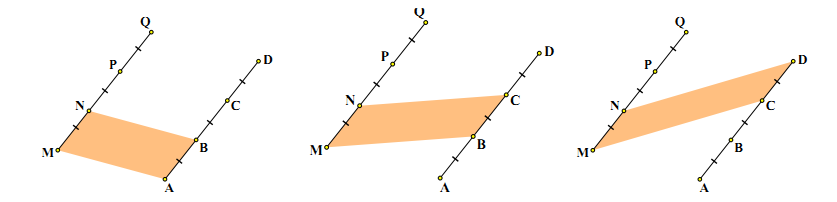
Bài
4: Cho hình vẽ biết
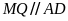 .
Chỉ ra các hình bình hành tạo thành từ các điểm
.
Chỉ ra các hình bình hành tạo thành từ các điểm
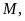
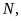
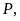
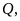
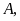
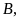
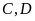 .
.
Lời giải:

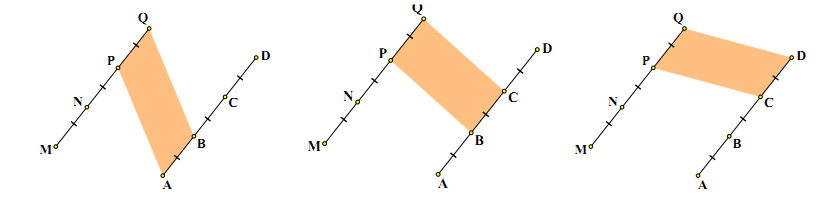
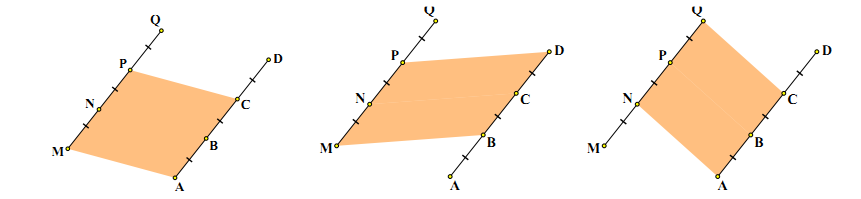
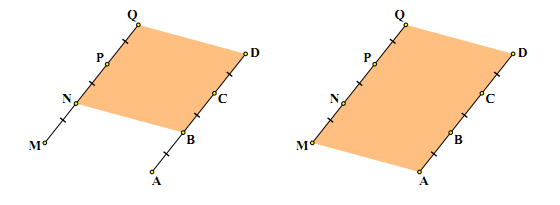
Dạng 3: Tính chu vi và diện tích của hình bình hành.
I.Phương pháp giải
- Dựa vào các công thức chu vi và diện tích của hình bình hành để tìm kết quả bài toán.
II.Bài toán
Bài 1: Một
hình bình hành có độ dài hai cạnh
đáy là
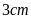 và
và
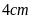 .
Tính chu vi hình bình hành.
.
Tính chu vi hình bình hành.
Lời giải:
Chu vi hình bình hành là :
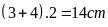 .
.
Bài 2: Một
hình bình hành có đáy là
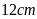 và chiều cao là
và chiều cao là
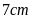 .
Tính diện tích hình bình hành.
.
Tính diện tích hình bình hành.
Lời giải:
Diện
tích hình bình hành là:
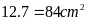 .
.
Bài 3: Một khu
rừng có dạng hình bình hành có chiều cao là
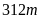 ,
độ dài đáy gấp đôi chiều cao. Hỏi diện tích của
khu rừng đó là bao nhiêu?
,
độ dài đáy gấp đôi chiều cao. Hỏi diện tích của
khu rừng đó là bao nhiêu?
Lời giải:
Độ dài đáy của khu rừng là:
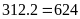 (m)
(m)
Diện tích của khu rừng là:
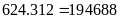 m2.
m2.
Bài 4:
Một miếng đất hình bình hành
có cạnh đáy dài
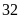 m;
chiều cao bằng cạnh đáy. Trên
miếng đất người ta trồng rau, mỗi mét vuông đất thu
hoạch được
m;
chiều cao bằng cạnh đáy. Trên
miếng đất người ta trồng rau, mỗi mét vuông đất thu
hoạch được
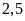 kg
rau. Hỏi trên miếng đất đó thu hoạch được tất cả
là bao nhiêu kg rau?
kg
rau. Hỏi trên miếng đất đó thu hoạch được tất cả
là bao nhiêu kg rau?
Lời giải:
Theo đề bài ta có:
Chiều
cao của miếng đất bằng:
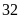 m.
m.![]()
Diện
tích miếng đất là:
 m2
m2![]()
Số
rau thu hoạch trên miếng đất là:
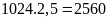 kg.
kg.
![]()
Bài 5:
Hình bình hành
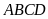 có chu vi là 94cm, cạnh
có chu vi là 94cm, cạnh
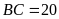 cm.
Chiều cao
cm.
Chiều cao
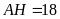 cm.
Khi đó, diện tích hình bình hành
cm.
Khi đó, diện tích hình bình hành
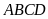 bằng bao nhiêu cm2?
bằng bao nhiêu cm2?
Lời giải:

Cạnh đáy
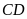 dài:
dài:
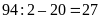 cm
cm
Diện tích hình bình hành
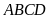 là:
là:
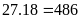 cm2.
cm2.
Bài 6: Cho một
hình bình hành có diện tích bằng
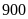 cm2 biết
nếu giảm chiều cao đi 6cm thì diện tích hình bình hành
giảm đi
cm2 biết
nếu giảm chiều cao đi 6cm thì diện tích hình bình hành
giảm đi
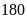 cm2.
Tìm độ dài đáy, chiều cao của hình bình hành đó ?
cm2.
Tìm độ dài đáy, chiều cao của hình bình hành đó ?
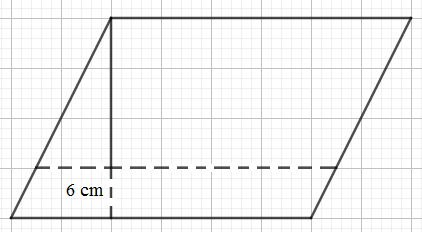
Phân tích: Khi giảm chiều cao của hình bình hành đi 6cm thì khi đó phần giảm đi là 1 hình bình hành mới có chiều cao bằng 6cm và cạnh đáy tương ứng chính bằng cạnh đáy của hình bình hành ban đầu.
Vậy
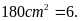 cạnh
đáy. Từ đó tính được độ dài đáy của hình bình
hành ban đầu.
cạnh
đáy. Từ đó tính được độ dài đáy của hình bình
hành ban đầu.
Lời giải:
Độ dài đáy của hình bình hành ban đầu là:
 (cm)
(cm)
Độ dài chiều cao của hình bình hành ban đầu là:
 (cm)
(cm)
Bài 7: Tính diện tích hình bình hành, biết tổng số đo độ dài đáy và và chiều cao là 24cm, độ dài đáy hơn chiều cao 4cm.
Lời giải:
Ta có: Chiều cao + độ dài đáy = 24cm (1)
Mà, độ dài đáy - chiều cao = 4cm (2)
Từ (1) và (2), ta suy ra:
Chiều cao

Chiều cao = 10cm
Do đó, độ dài đáy là
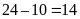 cm
cm
Diện tích hình bình hành là
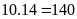 cm2.
cm2.
Bài 8: Một hình bình hành có diện tích bằng diện tích hình vuông cạnh 6cm, chiều cao bằng 4cm. Tính độ dài đáy của hình đó.
Lời giải:
Diện tích hình vuông là
 cm2.
cm2.
Diện tích hình bình hành bằng diện tích hình vuông = 36cm2.
Độ dài đáy của hình bình hành là
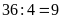 cm.
cm.
Bài
9: Có một
miếng đất hình bình hành cạnh đáy bằng 32m, người ta
mở rộng miếng đất bằng cách tăng độ dài cạnh đáy
thêm 4m được miếng đất hình bình hành mới. Có diện
tích hơn diện tích miếng đất ban đầu là
 .
Hỏi diện tích của miếng đất ban đầu là bao nhiêu?
.
Hỏi diện tích của miếng đất ban đầu là bao nhiêu?
Lời giải:
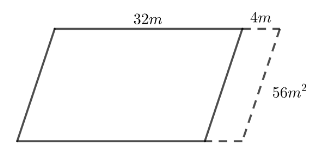
Miếng đất sau khi mở rộng có diện tích hơn diện tích ban đầu là 56m2. Phần tăng thêm là diện tích một hình bình hành có cạnh đáy là 4m và có chiều cao bằng chiều cao của miếng đất ban đầu.
Chiều cao của miếng đất ban đầu bằng:
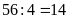 (m)
(m)
Diện tích của miếng đất ban đầu:
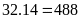 (m2)
(m2)
Bài
10: Tìm
diện tích của hình
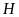 gồm hình bình hành
gồm hình bình hành
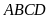 và hình chữ nhật
và hình chữ nhật
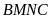 ,
biết hình chữ nhật
,
biết hình chữ nhật
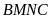 có chu vi bằng 18cm và chiều dài
có chu vi bằng 18cm và chiều dài
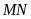 gấp hai lần chiều rộng
gấp hai lần chiều rộng
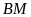 .
.

Lời giải:
Nửa
chu vi hình chữ nhật
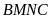 bằng:
bằng:
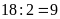 (cm)
(cm)
Coi
chiều dài hình chữ nhật
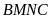 gồm 2 phần bằng nhau thì chiều rộng của nó gồm 1 phần
như thế.
gồm 2 phần bằng nhau thì chiều rộng của nó gồm 1 phần
như thế.
Tổng số phần bằng nhau là:
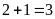 (phần)
(phần)
Chiều
rộng của hình chữ nhật
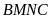 :
:
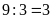 (cm)
(cm)
Chiều
dài của hình chữ nhật
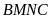 :
:
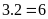 (cm)
(cm)
Diện
tích của hình chữ nhật
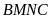 :
:
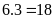 (cm2)
(cm2)
Diện
tích hình bình hành
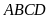 :
:
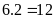 (cm2)
(cm2)
Diện
tích hình
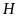 là:
là:
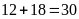 (cm2)
(cm2)
Bài 11:
Hình
bình hành
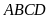 có cạnh đáy
có cạnh đáy
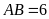 cm,
cạnh bên
cm,
cạnh bên
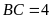 cm
với
cm
với
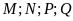 lần
lượt là trung điểm của các cạnh
lần
lượt là trung điểm của các cạnh
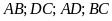 .
Hỏi:
.
Hỏi:
a) Hình trên có tất cả bao nhiêu hình bình hành?
b) Tổng chu vi của tất cả các hình bình hành trên bằng bao nhiêu?
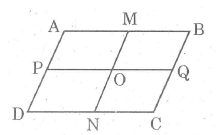
Lời giải:
a) Có tất cả 9 hình bình hành là:
 .
.
b) Các
hình bình hành 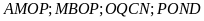 có chu vi bằng nhau, mỗi hình có cạnh đáy bằng:
có chu vi bằng nhau, mỗi hình có cạnh đáy bằng:
 (cm)
(cm)
Cạnh bên bằng:
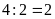 (cm)
(cm)
Chu vi của mỗi hình là:
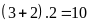 (cm)
(cm)
Các
hình bình hành
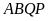 và
và
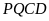 có chu vi bằng nhau, mỗi hình có cạnh đáy bằng 6 cm và
cạnh bên bằng:
có chu vi bằng nhau, mỗi hình có cạnh đáy bằng 6 cm và
cạnh bên bằng:
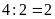 (cm)
(cm)
Chu vi của mỗi hình bằng:
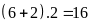 (cm)
(cm)
Các
hình
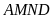 và
và
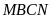 có chu vi bằng nhau mỗi hình có cạnh bên bằng 4 cm và
cạnh đáy bằng:
có chu vi bằng nhau mỗi hình có cạnh bên bằng 4 cm và
cạnh đáy bằng:
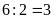 (cm)
(cm)
Chu vi của mỗi hình là:
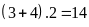 (cm)
(cm)
Hình bình hành ABCD có chu vi bằng:
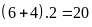 (cm)
(cm)
Tổng chu vi các hình bình hành là:
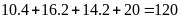 (cm)
(cm)
Bài 12:
Tính
diện tích hình chữ nhật
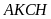 biết hình bình hành
biết hình bình hành
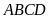 có diện tích bằng
có diện tích bằng
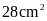 .
.
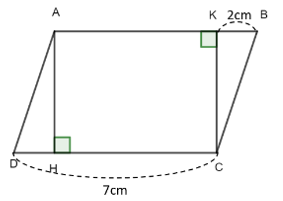
Lời giải:
Chiều
cao
 của hình bình hành
của hình bình hành
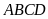 là:
là:
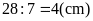
Độ
dài cạnh
 hình chữ nhật AKCH là:
hình chữ nhật AKCH là:
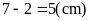
Diện
tích của hình chữ nhật AKCH là:
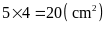
HẾT
Ngoài Luyện Thi HSG Toán 6 – Bài Tập & Định Nghĩa Hình Bình Hành Có Lời Giải – Tài Liệu Toán thì các tài liệu học tập trong chương trình 6 sẽ được cập nhật liên tục và nhanh nhất có thể sau khi kỳ thi diễn ra trên Danh mục Tài Liệu Học Tập nhằm giúp các bạn đọc thuận tiện trong việc nghiên cứu tài liệu. Quý thày cô và các bạn đọc có thể chia sẻ thêm những tài liệu học tập hữu ích đến địa chỉ email của chúng tôi, nhằm xây dựng nên kho đề thi phong phú, đa dạng cho các em học sinh tham khảo và rèn luyện.
Tài liệu này tập trung vào một chủ đề quan trọng trong toán học là hình bình hành. Hình bình hành là một khái niệm cơ bản và cũng là một trong những kiến thức cốt lõi của môn Toán. Qua tài liệu này, các bạn sẽ được hướng dẫn chi tiết về định nghĩa, tính chất và công thức tính diện tích, chu vi của các loại hình bình hành như hình chữ nhật, hình vuông, hình thang, và hình bình hành tổng quát.
Tài liệu được thiết kế với mục tiêu giúp các bạn rèn kỹ năng giải bài tập, nắm vững lý thuyết và áp dụng hiệu quả vào thực tế. Mỗi bài tập trong tài liệu đi kèm với lời giải chi tiết, giúp các bạn hiểu rõ cách giải quyết từng bài tập một cách logic và khoa học.
Ngoài ra, tài liệu còn cung cấp các định nghĩa và công thức cơ bản, giúp các bạn làm quen với các khái niệm và công thức quan trọng trong hình học. Điều này giúp các bạn xây dựng nền tảng vững chắc và tự tin hơn khi tiếp cận các bài tập khó hơn.
>>> Bài viết có liên quan






