Giáo Án Bồi Dưỡng Học Sinh Giỏi Toán 6: Dãy Số Tự Nhiên Theo Quy Luật
>>> Mọi người cũng quan tâm:
Giáo Án Bồi Dưỡng Học Sinh Giỏi Toán 6: Dãy Số Tự Nhiên Theo Quy Luật – Toán 6 là tài liệu học tập được Trang Tài Liệu biên soạn và sưu tầm từ những nguồn dữ liệu mới nhất hiện nay. Tài liệu này sẽ giúp các em luyện tập, củng cố kiến thức từ đó nâng cao điểm số cho môn học. Ngoài ra, cũng giúp các thầy cô giáo có nguồn tài nguyên phong phú để giảng dạy.
Dưới đây là bản đọc trực tuyến giúp thầy cô và các em học sinh có thể nghiên cứu Online hoặc bạn có thể tải miễn phí với phiên bản word để dễ dàng in ấn cũng như học tập Offline.
CHUYÊN ĐỀ 4: DÃY SỐ TỰ NHIÊN THEO QUY LUẬT
A = 1+2+3+…+(n-1)+n =
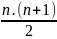
A = 1.2 + 2.3 + 3.4 +.…+ (n – 1) n =
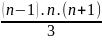
A = 1.3+2.4+3.5+...+(n-1)(n+1) =
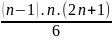
A = 1.2.3+2.3.4+3.4.5+...+(n-2)(n-1)n =
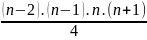
A = 12 +22 +32+...+(n-1)2 +n2 =
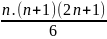
A = 13 +23 +33+...+(n-1)3 +n3 =
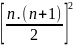
A = 15 + 25 + .... + n5 =
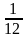 .n2
(n + 1) 2 ( 2n2 + 2n – 1 )
.n2
(n + 1) 2 ( 2n2 + 2n – 1 )
A = 1+ p + p 2 + p3 + ..... + pn =
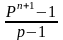 ( p
( p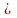 1)
1)
A = 1+ 2p +3p 2 + .... + ( n+1 ) pn =
 ( p
( p
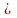 1)
1)
A =1.2+2.5+3.8+.......+n(3n-1) = n2.(n + 1)
A = 13+ +33 +53 +... + (2n +1 )3 = (n +1)2.(2n2 +4n +1)
A =
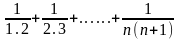 =
=
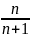 , ( n > 1 )
, ( n > 1 )
A = =
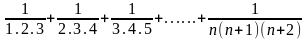 =
=
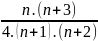
A =
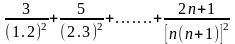 =
=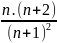
Bài 1: Tính giá trị của các biểu thức sau:
A = 1 + 2 + 3 + …+ 2015
B = 1 + 3 + 5 + …+ 1017
C = 2 + 4 + 6 +… + 2014
D = 1 + 4 + 7 + …+ 2008
E = 1.2 + 2.3 + 3.4 + … + 1001.1002
F = 1.3 + 2.4 + 3.5 + …+ 2013.2015
G = 1.2.3 + 2.3.4 + 3.4.5 +…+ 2013.2014.2015
H = 12 +22 +32+...+ 992 + 1002
I = 12 +22 +32+...+10012 +10022
J = 6+16+30+48+...+19600+19998
K = 2+5+9+14+...+4949+5049
L = 22 +42 +62 +...+982 +1002
M = 13+23+33+...+993+1003
N = 1 + 52 + 53 + … + 5100
O = 1 + 31 + 32 + …+ 3100
Bài 2: Tìm giá trị của x để thỏa mãn điều kiện:
Cho A= 3 + 32 + 33 + 34 +.....3100
Tìm số tự nhiên n biết rằng 2A + 3 = 3n
Cho M = 3 + 32 + 33 + 34 +.....3100
Hỏi :
a. M có chia hết cho 4, cho 12 không ? vì sao?
b.Tìm số tự nhiên n biết rằng 2M+3 = 3n
Cho biểu thức: M = 1 +3 + 32+ 33+…+ 3118+ 3119
a) Thu gọn biểu thức M.
b) Biểu thức M có chia hết cho 5, cho 13 không? Vì sao?
Cho A = 1 – 2 + 3 – 4 +....... 99 – 100
a) Tính A.
b) A có chia hết cho 2, cho 3, cho 5 không ?
c) A có bao nhiêu ước tự nhiên. Bao nhiêu ước nguyên ?
Cho A= 1– 7 + 13 – 19 + 25 – 31 +....
a) Biết A = 181. Hỏi A có bao nhiêu số hạng ?
b) Biết A có n số hạng. Tính giá trị của A theo n ?
Cho A= 1– 7 + 13 – 19 + 25 – 31 +....
a) Biết A có 40 số hạng. Tính giá trị của A.
b) Tìm số hạng thứ 2004 của A.
Tìm giá trị của x trong dãy tính sau:
(x+2)+(x+12)+(x+42)+(x+47) = 655
Tìm x biết :
x + (x+1) + (x+2) + (x+3) + …+ (x+2009) = 2009.2010
Bạn Lâm đánh số trang một cuốn sách dày 284 trang bằng dãy số chẵn 2, 4, 6, 8, … Biết mỗi chữ số viết mất 1 giây. Hỏi bạn Lâm cần bao nhiêu phút để đánh số trang cuốn sách?
Tích A = 1.2.3…500 tận cùng bằng bao nhiêu chữ số 0?
Tính giá trị của biểu thức sau:
A = 9 + 99 + 999
+ …+
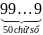
Cho A = 1 + 4 + 42 + … + 499, B = 4100. Chứng minh rằng: A < B/3
HƯỚNG DẪN - LỜI GIẢI – ĐÁP SỐ
Bài 1: Tính giá trị của các biểu thức sau:
A = 1 + 2 + 3 + …+ 2015
A =
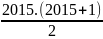 =
=
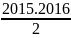 = 2015.1008 = 2031120
= 2015.1008 = 2031120
B = 1 + 3 + 5 + …+ 1017
B = (1017 + 1).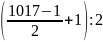 = 1018.509:2 = 259081
= 1018.509:2 = 259081
C = 2 + 4 + 6 +… + 2014
C= (2014 + 2).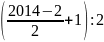 = 2016.1007:2= 1015056
= 2016.1007:2= 1015056
D = 1 + 4 + 7 + …+ 2008
D = (2008 +1).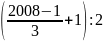 = 2009.670:2= 673015
= 2009.670:2= 673015
E = 1.2 + 2.3 + 3.4 + … + 1001.1002
E =
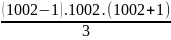 =
=
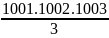 = 335337002
= 335337002
F = 1.3 + 2.4 + 3.5 + …+ 2013.2015
F =
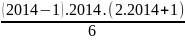 =
=
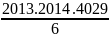 = 2722383213
= 2722383213
G = 1.2.3 + 2.3.4 + 3.4.5 +…+ 2013.2014.2015
G =
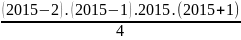 =
=
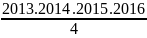
G = 4117265071920
H = 12 +22 +32+...+ 992 + 1002
H =
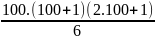 =
=
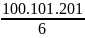 = 338350
= 338350
I = 12 +22 +32+...+10012 +10022
I =
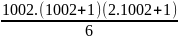 =
=
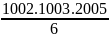 = 335839505
= 335839505
J = 6+16+30+48+...+19600+19998
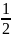 .J
= 1.3 + 2.4 + 3.5 + 4.6 + …. + 98.100 + 99.101
.J
= 1.3 + 2.4 + 3.5 + 4.6 + …. + 98.100 + 99.101
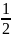 .J
=
.J
=
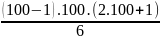 =
=
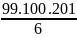 = 331650
= 331650
J = 331650 . 2 = 663300
K = 2+5+9+14+...+4949+5049
2K = 1.4 + 2.5 + 3.6 + 4.7 + … + 99.102
2K = 1.(2 + 2) + 2.(2 + 3) + 3.(2 + 4) + …+ 99.(2 + 100)
2K = 1.2 + 1.2 + 2.2 + 2. 3 + 3.2 + 3.4 + …+ 2.99 + 99.100
2K = (1.2 + 2.3 + 3.4 +… + 99.100) + 2.(1 + 2 + 3 + 4 + …+ 99)
2K =
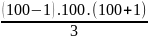 + 2.
+ 2.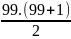
2K = 333300 + 9900
2K = 343200
K = 343200 : 2 = 171600
L = 22 +42 +62 +...+982 +1002
L = 22.(12 + 22 + 32 +… + 502)
L = 4.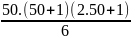 = 4.
= 4.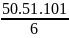 = 171700
= 171700
M = 13+23+33+...+993+1003
M =
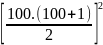 =
=
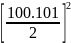 = 50502 = 25502500
= 50502 = 25502500
N = 1 + 52 + 53 + … + 5100
N = 1+5.(1+5+52 +....... + 599 )
N = 1+5.( 1 + 5 +52+ ...... + 599 + 5 100 - 5100 )
=> N= 1+5.( N - 5100 )
=> N = 1+ 5.N - 5101
4N = 5101-1
N =
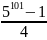
O = 1 + 31 + 32 + …+ 3100
O =
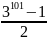
Bài 2: Tìm giá trị của x để thỏa mãn điều kiện:
Cho A= 3 + 32 + 33 + 34 +.....+ 3100
Tìm số tự nhiên n biết rằng 2A + 3 = 3n
Ta có A = 3.(1+ 3 + 32 + 33 + 34 +.....+ 399)
A = 3.(1 + 3 + 32 + 33 + 34 +.....+ 399 + 3100 – 3100)
A = 3.(1 + A – 3100)
A = 3 + 3.A - 3101
2A = 3101 – 3
A =
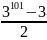
2A + 3 = 3n
2.
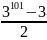 + 3 = 3n
+ 3 = 3n
3101 – 3 + 3 = 3n
3101 = 3n
n = 101
Cho M = 3 + 32 + 33 + 34 +.....3100
Hỏi :
M có chia hết cho 4, cho 12 không ? vì sao?
Ta có: M chia hết cho 4 vì
M = 3.(1 + 3) + 32.(1 + 3) + …+ 399.(1 + 3)
M = 3.4 + 32.4+ …+ 399.4
M = 4.(3 + 32
+ …+ 399)
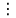 4
4
Ta có:
M
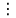 12 vì M = 4.(3 + 32 + …+ 399)
12 vì M = 4.(3 + 32 + …+ 399)
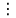 4; 3 mà (4;3)=1
4; 3 mà (4;3)=1
b.Tìm số tự nhiên n biết rằng 2M+3 = 3n
M = 3.(1+ 3 + 32 + 33 + 34 +.....+ 399)
M = 3.(1 + 3 + 32 + 33 + 34 +.....+ 399 + 3100 – 3100)
M = 3.(1 + M – 3100)
M = 3 + 3.M - 3101
2M = 3101 – 3
M =
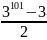
2M + 3 = 3n
2.
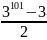 + 3 = 3n
+ 3 = 3n
3101 – 3 + 3 = 3n
3101 = 3n
n = 101
Cho biểu thức: M = 1 +3 + 32+ 33+…+ 3118+ 3119
Thu gọn biểu thức M.
M =
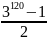
Biểu thức M có chia hết cho 5, cho 13 không? Vì sao?
Xét M =
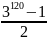
Một số có tận cùng là 3 khi nâng lên lũy thừa bậc 4n (n thuộc N) thì chữ số tận cùng là 1. Do đó, 3120 =34.30 có tận cùng là 1 => M có tận cùng là 0 => M chia hết cho 5
M = 1 +3 + 32+ 33+…+ 3118+ 3119
M =(1 +3 + 32) + 33.(1 +3 + 32) + …+ 3117.(1 +3 + 32)
M = 13 + 33 .13 + …+ 3117 .13
M = 13.(1 + 33
+…+ 3117)
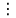 13
13
Vậy M chia hết cho 5, chia hết cho 13.
Cho A = 1 – 2 + 3 – 4 +....... 99 – 100
Tính A.
A = ( 1 + 3 + … + 99) – (2 + 4 +…+ 100)
A = (99 + 1).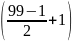 :
2 – (100+2).
:
2 – (100+2).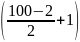 :
2
:
2
A = 100.50:2 – 102.51:2
A = 2500 – 2601 = -101
A có chia hết cho 2, cho 3, cho 5 không ?
A không chia hết cho 2, 3 và 5
A có bao nhiêu ước tự nhiên. Bao nhiêu ước nguyên ?
Ư(A) ={-101; -1; 1; 101} và 4 ước nguyên.
vậy A có 2 ước tự nhiên
Cho A= 1– 7 + 13 – 19 + 25 – 31 +....
Biết A = 181. Hỏi A có bao nhiêu số hạng ?
A = 1 + 6 + 6 + ….
Nếu n lẻ : A = 1 + 6.
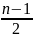 = 181 => 6.
= 181 => 6.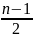 = 180 =>
= 180 =>
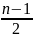 = 30 => n = 61 ( TM )
= 30 => n = 61 ( TM )Nếu n chẵn: A = - 6 – 6 - 6 - …. = (-6).
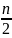 = -3n = 181 (loại)
= -3n = 181 (loại)
Vậy A có 61 số hạng.
Biết A có n số hạng. Tính giá trị của A theo n ?
Nếu n chẵn:
A = - 6 – 6 - 6 - …. = (-6).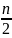 = -3n
= -3n
Nếu n lẻ: A
= 1 + 6 + 6 + …. = 1 + 6.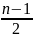 = 3n - 2
= 3n - 2
Cho A= 1– 7 + 13 – 19 + 25 – 31 +....
Biết A có 40 số hạng. Tính giá trị của A.
Theo câu 5 n chẵn => A = -3n = -3.40 = -120
Tìm số hạng thứ 2004 của A.
Ta có số hạng thứ nhất: A1 = 1
Số hạng thứ 2: A2 = (-1)2-1.(1 + 6)
Số hạng thứ 3: A3 = (-1)3-1.(1 + 6.2)
Số hạng thứ 4: A4 = (-1)4-1.(1 + 6.3)
….
Số hạng thứ n: An = (-1)n-1.[1+6.(n-1)]
n = 2004 => A2004 = (-1)2003-1.[1+6(2004-1)] = - (1+6.2003)
A2004 = -12019
Tìm giá trị của x trong dãy tính sau:
(x+2)+(x+12)+(x+42)+(x+47) = 655
4.x + 2 + 12 + 42 + 47 = 655
4.x + 103 = 655
4.x = 655 – 103 = 552
x = 552 : 4 = 138
Tìm x biết :
x + (x+1) + (x+2) + (x+3) + …+ (x+2009) = 2009.2010
2010x + (1 + 2 + 3 +…+ 2009) = 2009.2010
2010x +
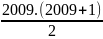 = 2009.2010
= 2009.2010
2010x = 2009.2010 – 2009.2010:2
x = 2009 – 2009: 2 = 1004,5
Bạn Lâm đánh số trang một cuốn sách dày 284 trang bằng dãy số chẵn 2, 4, 6, 8, … Biết mỗi chữ số viết mất 1 giây. Hỏi bạn Lâm cần bao nhiêu phút để đánh số trang cuốn sách?
Từ
trang 2 đến trang 8 gồm: (8 - 2) : 2 +1 = 4 trang ứng với 4
chữ số
Từ trang
10 - 98 gồm ( 98 - 10) : 2 + 1 = 45 trang ứng với 90 chữ
số
Từ trang 100 -
284 gồm (284 - 100) : 2 + 1 = 93 trang ứng với 93.3 = 279 chữ
số
Vậy bạn Lâm
phải viết tất cả : 4 + 90 + 279 = 373 chữ số tương ứng
với 373
giây
hay 6 phút 13 giây .
Tích A = 1.2.3…500 tận cùng bằng bao nhiêu chữ số 0?
Số mũ của 5 trong 500! là
[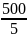 ]+[
]+[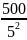 ]+[
]+[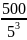 ]=124
]=124
Vậy
tích 500! có
tận cùng 124 chữ
số 0.
Tính giá trị của biểu thức sau:
A = 9 + 99 + 999 +
…+
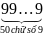
A = 10 – 1 + 102 – 1 + 103 – 1 +…+ 1050 – 1
A = 10 + 102
+ 103 +…+ 1050 –
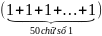
A =
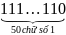 – 50 =
– 50 =
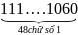
Cho A = 1 + 4 + 42 + … + 499, B = 4100. Chứng minh rằng: A < B/3
Ta có A =
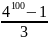 <
<
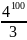 = B (đpcm)
= B (đpcm)
Ngoài Giáo Án Bồi Dưỡng Học Sinh Giỏi Toán 6: Dãy Số Tự Nhiên Theo Quy Luật – Toán 6 thì các tài liệu học tập trong chương trình 6 sẽ được cập nhật liên tục và nhanh nhất có thể sau khi kỳ thi diễn ra trên Danh mục Tài Liệu Học Tập nhằm giúp các bạn đọc thuận tiện trong việc nghiên cứu tài liệu. Quý thày cô và các bạn đọc có thể chia sẻ thêm những tài liệu học tập hữu ích đến địa chỉ email của chúng tôi, nhằm xây dựng nên kho đề thi phong phú, đa dạng cho các em học sinh tham khảo và rèn luyện.
Chương trình bồi dưỡng học sinh giỏi toán lớp 6 với chuyên đề “Dãy số tự nhiên theo quy luật” nhằm giúp học sinh nắm vững kiến thức về dãy số tự nhiên và hiểu rõ các quy luật và tính chất của chúng. Đây là một chủ đề quan trọng trong toán học, giúp phát triển tư duy logic, khả năng phân tích và quy tắc suy luận.
Giáo án này được xây dựng dựa trên nền tảng của chương trình giảng dạy chính thức, nhưng với phần nâng cao và bổ sung cho học sinh giỏi. Nội dung giáo án được cấu trúc rõ ràng và chi tiết, giúp giáo viên dễ dàng triển khai bài học một cách logic và có hệ thống.
Qua giáo án này, học sinh sẽ có cơ hội nắm vững kiến thức về dãy số tự nhiên và phát triển khả năng suy luận, phân tích và giải quyết vấn đề. Giáo án được thiết kế một cách cụ thể và chi tiết, giúp giáo viên có thể dễ dàng triển khai và hỗ trợ học sinh đạt được những thành tựu cao trong môn toán.
>>> Bài viết có liên quan






