Giáo Án Bồi Dưỡng Học Sinh Giỏi Toán 6 Một Số Phương Pháp Giải Toán
Giáo Án Bồi Dưỡng Học Sinh Giỏi Toán 6 Một Số Phương Pháp Giải Toán – Toán 6 là tài liệu học tập được Trang Tài Liệu biên soạn và sưu tầm từ những nguồn dữ liệu mới nhất hiện nay. Tài liệu này sẽ giúp các em luyện tập, củng cố kiến thức từ đó nâng cao điểm số cho môn học. Ngoài ra, cũng giúp các thầy cô giáo có nguồn tài nguyên phong phú để giảng dạy. Dưới đây là bản đọc trực tuyến giúp thầy cô và các em học sinh có thể nghiên cứu Online hoặc bạn có thể tải miễn phí với phiên bản word để dễ dàng in ấn cũng như học tập Offline. PHƯƠNG
PHÁP 1: DÙNG SƠ ĐỒ ĐOẠN THẲNG Bài tập minh họa: Bài 1: Hiện
nay, tuổi mẹ gấp 4 lần tuổi con. Bốn năm trước đây,
tuổi mẹ gấp 6 lần tuổi con. Tính tuổi mẹ, tuổi con
hiện nay.
Bài
giải Hiện
nay , tuổi mẹ gấp bốn lần tuổi con nên hiệu số tuổi
của mẹ và con hiện nay số lần là: 4- 1 = 3 (lần) Bốn
năm trước đây, tuổi mẹ gấp 6 lần tuổi con nên hiệu
số tuổi của mẹ và con bốn năm trước đây gấp tuổi
con trước đây là 6 – 1 = 5 (lần) Vì
hiệu số tuổi của hai mẹ con không đổi nên 3 lần tuổi
còn hiện nay bằng 5 lần tuổi con bốn năm trước, hay
tuổi mẹ hiện nay bằng 5/3 tuổi con bốn năm trước. Tuổi
con hiện nay hơn tuổi con 4 năm trước là 4 tuổi. Ta
có sơ đồ:
4 tuổi Tuổi
con 4 năm trước: |-----|-----|-----| Hiệu
số phần bằng nhau là: 5 - 3 = 2 (phần) Tuổi
con hiện nay là: 4 : 2 x 5 = 10 (tuổi) Tuổi
mẹ hiện nay là: 10 x 4 = 40 (tuổi) Đáp
số: con 10 tuổi; mẹ 40 tuổi. Bài 2: Tuổi
bà gấp đôi tuổi mẹ, tuổi con bằng
Bài
giải Theo
bài ra ta có sơ đồ:
36 tuổi Tuổi
mẹ: |-----|-----|-----|-----|-----| Tuổi
con là: 36 : (1 + 5) = 6 (tuổi) Tuổi
mẹ là: 36 – 6 = 30 (tuổi) Tuổi
bà là: 30 x 2 = 60 (tuổi) Đáp
số: Tuổi con: 6 tuổi Tuổi
mẹ: 30 tuổi Tuổi
bà: 60 tuổi Bài 3: Tuổi
bố gấp 3 lần tuổi anh, tuổi anh gấp 2 lần tuổi em.
Tuổi bố cộng với tuổi em bằng 42 tuổi. Tính tuổi của
mỗi người.
Bài
giải Tuổi bố gấp
ba lần tuổi anh, tuổi anh gấp 2 lần tuổi em nên tuổi
bố gấp tuổi em số lần là: 3 x 2 = 6 (lần).
42 tuổi Tuổi bố:
|------|------|------|------|------|------| Theo sơ đồ,
tuổi của em là: 42 : (1 + 6) = 6 (tuổi) Tuổi của anh
là: 6 x 2 = 12 (tuổi) Tuổi của bố
là: 12 x 3 = 36 (tuổi). Đáp
số: Em 6 tuổi, Anh 12 tuổi, Bố 36 tuổi. Bài 4: Năm
nay tuổi cô gấp 6 lần tuổi cháu. Đến khi tuổi cháu
bằng tuổi cô hiện nay thì tuổi của hai cô cháu cộng
lại bằng 68. Hỏi hiện nay mỗi người bao nhiêu tuổi?
Bài
giải Năm nay, nếu coi
tuổi cháu là 1 phần thì tuổi cô là 6 phần như thế.
Hiệu số phán tuổi của hai cô cháu là: 6 – 1 = 5 (phần). Vì hiệu số
tuổi của hai cô cháu không thay đổi theo thời gian nên
khi tuổi cháu bằng tuổi cô hiện nay thì cháu vẫn kém
cô 5 phần tuổi cháu hiện nay.
Khi đó ta có sơ
đồ:
68 tuổi Tuổi
cô:
|------|------|------|------|------|------|------|------|------|------|------| Theo
sơ đồ, tổng số phần bằng nhau là: 6 + 11 = 17 (phần) Khi
đó tuổi cháu là: 68 : 17 x 6 = 24 (tuổi) Khi
đó tuổi cháu bằng tuổi cô hiện nay nên tuổi cô hiện
nay là 24 tuổi. Tuổi
cháu hiện nay là: 24 : 6 = 4 (tuổi).
Đáp số: Cháu: 4 tuổi; Cô: 24 tuổi. Bài 5: Tổng
số tuổi chị và tuổi em hiện nay bằng 32. Khi tuổi chị
bằng tuổi em hiện nay thì tuổi chị gấp 3 lần tuổi
em. Hỏi hiện nay mỗi người bao nhiêu tuổi?
Bài
giải Khi tuổi chị
bằng tuổi em hiện nay thì tuổi chị gấp ba lần tuổi
em, vậy nếu coi tuổi em hiện nay là 3 phần bằng nhau thì
tuổi em trước đây là 1 phần. Số phần tuổi
chị nhiều hơn tuổi em trước đây là : 3 – 1 = 2
(phần). Vì hiệu số
tuổi của hai chị em không thay đổi theo thời gian nên
hiện nay chị vẫn hơn em hai phần tuổi em trước đây.
Do đó nếu coi tuổi em hiện nay là 3 phần tuổi em trước
đây thì tuổi chị hiện nay là 5 phần như thế (2 + 3 =
5) ta có sơ đồ:
32 tuổi Tuổi chị hiện
nay: |------|------|------|------|------| Tổng số phần
bằng nhau là: 3 + 5 = 8 (phần) Tuổi em hiện
nay là: 32 : 8 x 3 = 12 (tuổi) Tuổi chị hiện
nay là: 32 – 12 = 20 (tuổi) Đáp
số: Em: 12 tuổi; Chị: 20 tuổi. Bài 6: Tuổi
của hai anh em năm nay cộng lại bằng 16. Đến khi tuổi
em bằng tuổi anh hiện nay thì tuổi anh bằng
Bài
giải
Khi
tuổi em bằng tuổi anh hiện nay thì tuổi anh bằng
5 –
3 = 2 (phần) Vì hiệu số
tuổi của hai anh em không đổi theo thời gian nên hiện
nay anh vẫn hơn em 2 phần tuổi em lúc đó. Do vậy nếu
coi tuổi anh hiện nay bằng 3 phần tuổi em lúc đó thì
tuổi em hiện nay là một phần như thế (3 – 2 = 1). Ta có
sơ đồ:
16 tuổi Tuổi anh hiện
nay: |------|------|------| Theo sơ đồ,
tổng số phần bằng nhau là: 3 + 1 = 4 (phần) Tuổi của em
hiện nay là: 16 : 4 = 4 (tuổi) Tuổi của anh
hiện nay là: 16 – 4 = 12 (tuổi) Đáp
số: Em: 4 tuổi; Anh: 12 tuổi. Bài 7: Hiệu
của hai số là 1773. Tìm hai số đó biết rằng nếu viết
thêm chữ số 0 vòa tận cùng bên phải số bế thì được
số lớn.
Bài
giải
1773 Số lơn:
|------|------|------|------|------|------|------|------|------|------| Theo sơ đồ,
hiệu số phần bằng nhau là: 10 – 1 = 9 (phần) Số bé
là: 1773 : 9 x 1 = 197 Số lớn là:
197 + 1773 = 1970 Đáp
số: Số bé: 197; Số lớn: 1970. Bài 8: Hiện
nay mẹ 35 tuổi, con 8 tuổi. Hỏi: Mấy năm nữa tuổi mẹ
gấp 4 lần tuổi con? Có khi nào tuổi mẹ gấp
5 nần tuổi con không?
Bài
giải Hiệu số tuổi của hai mẹ
con là: 35 – 8 = 27 (tuổi)
27 tuổi Hiệu số
tuổi của hai mẹ con sẽ không thay đổi theo thời gian
nên khi tuổi mẹ gấp 4 lần tuổi con thì mẹ vẫn hơn
con 27 tuổi. Ta có sơ đồ: Tuổi con:
|------| Tuổi mẹ:
|------|------|------|------| Khi đó tuổi
con là: 27 : (4 – 1 ) = 9 (tuổi) Vì 9 – 8 =
1 nên sau một năm nữa thì tuổi mẹ gấp 4 lần tuổi
con. Khi tuổi mẹ gấp 5 lần
tuổi con thì mẹ vẫn hơn con 27 tuổi. Ta có sơ đồ khi
đó:
27 tuổi Tuổi con:
|------| Tuổi mẹ:
|------|------|------|------|------| Tuổi con khi
đó là: 27 : (5 – 1) = 27 : 4 Vì 27 không
chia hết cho 4 nên không có khi nào tuổi mẹ gấp 5 lần
tuổi con. Bài 9: Cho
phân số
Bài
giải Hiệu của mẫu
số và tử số của phân số
Nếu cùng bớt m
ở cả tử số và mẫu số thì hiệu mẫu số và tử số
không đổi (vẫn bằng 5) mà khi đó được phân số mới
có giá trị bằng
5 Tử số mới là:
5 : (3 – 2) x 2 = 10 Số tự nhiên m
là:23 – 10 = 13. Đáp
số: số tự nhiên m là 13. Bài 10: Năm
năm trước cha hơn con 36 tuổi. Hỏi năm cha bao nhiêu tuổi
thì 3 lần tuổi cha bằng 7 lần tuổi con?
Bài
giải Vì hiệu số
tuổi của hai cha con không thay đổi theo thời gian nên
cha luôn hơn con 36 tuổi. Đến năm mà 3
lần tuổi cha bằng 7 lần tuổi con nghĩa là năm tuổi con
bằng
36 tuổi Theo sơ đồ,
hiệu số phần bằng nhau là: 7 – 3 = 4 (phần) Khi đó tuổi của
cha là: 36 : 4 x 7 = 63 (tuổi) Đáp
số: tuổi cha: 63 tuổi. Bài 11: Năm
nay mẹ 73 tuổi. Khi tuổi mẹ bằng tuổi con hiện nay thì
tuổi mẹ hơn 7 lần tuổi con lúc đó là 4 tuổi. Tính
tuổi con hiện nay?
Bài
giải Coi tuổi con là
1 phần (khi tuổi mẹ bằng tuổi con hiện nay) thì tuổi
mẹ lúc đó là 7 phần như thế là cộng thêm 4 tuổi. Ta
có hiệu số tuổi của hai mẹ con là:
7 phần tuổi con
+ 4 tuổi – 1 phần tuổi con = 6 phần tuổi con + 4 tuổi. Vì hiệu số
tuổi của hai mẹ con không đổi theo thời gian nên hiện
nay mẹ vẫn hơn con 6 phần tuổi con khi đó công thêm 4
tuổi. Ta có sơ đồ:
4 tuổi
4 tuổi
4 tuổi
73 tuổi Theo sơ đồ ta
có: 7 phần tuổi con
+ 4 tuổi + 6 phần tuổi con + 4 tuổi = 73 tuổi Hay 13 phần tuổi
con + 8 tuổi = 73 (tuổi) 13 phần tuổi
con = 65 (tuổi) Vậy một phần
tuổi con khi đó là: 65 : 13 = 5 (tuổi) Tuổi con hiện
nay là : 5 x 7 + 4 = 39 (tuổi).
Đáp số: 39 tuổi.
Bài 12: Bố
nói với con: “10 năm trước đây tuổi bố gấp 10 lần
tuổi con”, 22 năm sau nữa thì tuổi bố sẽ gấp đôi
tuổi con. Hãy tính tuổi bố và tuổi con hiện nay.
Bài
giải Mười năm trước
đây, nếu coi tuổi con là 1 phần thì tuổi bố là 10 phần
như thế. Thời gian từ cách đây 10 năm đến sau đây 22
năm nữa có số năm là:
10 +
22 = 32 (năm) Theo bài ra ta có
sơ đồ: Tuổi con 10 năm
trước: |----|
32 tuổi
32 tuổi Nhìn sơ đồ ta
thấy: 1 phần tuổi con
+ 32 tuổi = (10 phần tuổi con + 32 tuổi) : 2 Hay 1 phần tuổi
con + 32 tuổi = 5 phần tuổi con + 16 tuổi 16 tuổi = 4
phần tuổi con Vậy tuổi con
cách đây 10 năm là: 16 : 4 = 4 (tuổi). Tuổi bố cách
đây 10 năm là: 4 x 10 = 40 (tuổi) Tuổi con hiện
nay là: 4+ 10 = 14 (tuổi) Tuổi bố hiện
nay là: 40 + 10 = 50 (tuổi) Đáp
số: Con: 14 tuổi; Bố: 50 tuổi. Bài 13: Lớp
5A có số học sinh nữ bằng
Bài
giải
?
4 h/s
? Theo sơ đồ số
học sinh nữ lúc đầu là: 4 : (3 – 2) x 2 = 8 (học sinh) Số học sinh nam
là: 8 :
Đáp
số: 8 học sinh nữ 20 học
sinh nam
Bài 14: Có 3 bình nước đựng nước chưa đầy. Sau
khi đổ
Bài giải
Sau khi đổ
Vậy trước đó bình ba có số lít nước là: 9: (1 -
Trước khi nhận
9 – 10x
Vậy lúc đầu bình 1 có số lít nước là: 8 : (1 -
Sau khi đổ
Vậy trước khi nhận
12 – 12x
Bình 2 đổ sang bình 3 số lít nước là: 12 x
Theo lời giải đầu thì trước khi đổ
Đáp số: Bình 1: 12l; Bình 2: 8l; Bình 3: 7l. Bài 15: Tìm
bốn số tự nhiên chẵn liên tiếp có tổng bằng 5420
Bài
giải Gọi
bốn số tự nhiên chẵn có dạng: 2k; 2k + 2; 2k + 4; 2k +6.
(k
Theo bài ra ta có:
2k + 2k +2 + 2k + 4 +2k + 6 = 5420 Hay 8k + 12 =
5420 8k = 5408 k = 676 ( TM ) Vậy 4 số tự
nhiên cần tìm là: 1352; 1354; 1356; 1358. Bài 16: Tìm
ba số tự nhiên lẻ liên tiếp biết rằng tổng của số
lớn nhất và số nhỏ nhất bằng 114. Bài
giải Gọi ba số tự
nhiên lẻ liên tiếp là: 2k + 1; 2k + 3; 2k + 5 (k
Theo bài ra ta có:
2k + 1 + 2k + 5 = 114 Hay 4k + 6 =
114 k = 27 ( TM )
Vậy 3 số tự
nhiên lẻ cần tìm là: 55; 57; 59 Bài 17: Hiệu
của hai số bằng 1217. Nếu tăng số trừ gấp bốn lần
thì được số lớn hơn số bị trừ là 376. Tìm số bị
trừ và số trừ.
Bài
giải Theo bài ra ta có
sơ đồ: Số bị trừ:
|------------------------|
376
1217 Số trừ x 4:
|--------|--------|--------|--------| Ba lần số trừ:
1217 + 376 = 1593 Số trừ: 1953 :
3 = 531 Số bị trừ: 531
+ 1217 = 1748 Đáp
số: Số trừ: 531; Số bị trừ: 1748 Bài 18: Năm
2000, bố 40 tuổi, Mai 11 tuổi, em Nam 5 tuổi. Đến năm
nào, tuổi bố bằng tổng số tuổi của hai chị em?
Bài
giải Năm 2000, chênh
lệch giữa tuổi bố và tổng số tuổi của hai chị em
là: 40 –
(11 + 5) = 24 (tuổi) Cứ mỗi năm mỗi
người tăng thêm một tuổi nên chênh lệch giữa tuổi bố
là tuổi 2 chị em sẽ giảm đi: (1 + 1) – 1 = 1 (tuổi) Số năm để số
tuổi bố bằng tổng số tuổi hai chị em là: 24 :
1 = 24 (năm) Lúc đó là năm
: 2000 + 24 = 2024. Đáp
số: Năm 2024 Bài tập tự luyện: Bài 1: Năm
nay tuổi cha hơn 7 lần tuổi con là 3 tuổi. Đến khi tuổi
con bằng tuổi cha hiện nay thì tuổi hai cha con cộng lại
bằng 109. Tìm tuổi của mỗi người hiện nay.
Bài
giải Nếu coi tuổi
con là 1 phần thì tuổi cha là 7 phần như thế cộng thêm
3 tuổi. Vậy hiệu số tuổi của hai cha con là 6 phần
tuổi con cộng thêm 3 tuổi. Vì hiệu số
tuổi của hai cha con không thay đổi theo thời gian nên khi
tuổi con bằng tuổi cha hiện nay thì con vẫn kém cha 6
phần tuổi con hiện nay cộng thêm 3 tuổi, ta có sơ đồ
khi đó:
3t
7 phần
3t
6 phần
7 phần
109 tuổi Tuổi cha:
|---|---|---|---|---|---|---|--|---|---|---|---|---|---|--| Theo sơ đồ ta
có: 7 phần + 7 phần
+ 6 phần + 3 tuổi + 3 tuổi + 3 tuổi = 109 tuổi 20 phần + 9 tuổi
= 109 tuổi 20
phần = 100 tuổi Vậy tuổi con
hiện nay là: 100 : 20 = 5 (tuổi) Tuổi cha hiện
nay là: 5 x 7 + 3 = 38 (tuổi). Đáp
số: Con: 5 tuổi; Cha: 38 tuổi. Bài 2: Hiệu
của hai số là 2345. Tìm hai số đó, biết rằng nếu viết
thê chữ số 5 vào tận cùng bên phải số bé thì được
số lớn.
Bài
giải Nếu viết thêm
chữ số 5 vào tận cùng bên phải số bé thì được số
lớn hơn, như vậy số lớn gấp 10 lần số bé và cộng
thêm 5 đơn vị. Theo bài ra ta có
sơ đồ:
2345
5 Theo
sơ đồ ta có 9 lần số bé là: 2345 – 5 = 2340 Số bé là :
2340 : 9 = 260 Số lớn là:
260 + 2345 = 2605 Đáp
số: Số bé: 260 ; Số lớn: 2605. Bài 3: Mẹ
hơn con 24 tuổi. Cách đây 4 năm tuổi con bằng
Bài
giải Hiệu số tuổi
của hai mẹ con không thay đổi theo thời gian nên cách đây
4 năm mẹ vẫn hơn con 24 tuổi. Ta có sơ đồ khi đó:
24 tuổi
5 Theo
sơ đồ tuổi mẹ cách đây 4 năm là: 24 : (4 – 1) x 4 = 32
(tuổi) Vì
mỗi năm mỗi người tăng lên 1 tuổi nên hiện nay tuổi
mẹ là:
32 + 4 x 1 = 36 (tuổi) Tuổi
con hiện nay là: 36 – 24 = 12 (tuổi) Đáp
số: Mẹ: 36 tuổi ; Con: 12 tuổi. Bài 4: Cho
phân số
Bài
giải Hiệu
của tử số và mẫu số của phân số
Nếu
cùng bớt cả tử số và mẫu số đi cùng một số tự
nhiên thì hiệu mẫu số và tử số vẫn không đổi (vẫn
bằng 80) mà khi đó thì được phân số mới có giá trị
bằng
80
Mẫu số mới:
|-----|-----|-----|-----|-----|-----|-----|-----|-----| Tử
số mới là: 80 : (9 – 5) x 5 = 100 Số
tự nhiên cần tìm là: 107 -100 = 7 Đáp
số: số tự nhiên là 7. Bài
5: Hiệu của hai số bằng 0,8. Thương của hai số cùng
bằng 0,8. Hãy tìm hai số đó.
Bài
giải 0,8 =
Ta
có sơ đồ:
0,8
Số lớn là: |-----|-----|-----|-----|-----| Theo
sơ đồ hiệu số phần bằng nhau là: 5 – 4 = 1 (phần) Số
bé là: 0,8 : 1 x 4 = 3,2 Số
lớn là: 3,2 + 0,8 = 4 Đáp
số: 3,2 và 4. Bài 6: Hiệu
của hai số bằng 20. Thương của hai số bằng 2,25. Tìm
hai số đó.
Bài
giải Theo
bài ta có sơ đồ:
20
Số lớn :
|-----|-----|-----|-----|-----|-----|-----|-----|-----| Theo
sơ đồ hiệu số phần bằng nhau là: 9 – 4 = 5 (phần) Số
lớn là: 20 : 5 x 9 = 36 Số
bé là: 36 – 20 = 16 Đáp
số: 36 và 16. Bài 7: Tìm
hai số có hiệu bằng 252, biết số bé bằng
Bài
giải Số
bé bằng
4 –
1 = 3 (phần) Vậy số bé bằng
252
Số lớn : |-----|-----|-----| Theo
sơ đồ hiệu số phần bằng nhau là: 3 – 1 = 2 (phần) Số
bé là: 252 : 2 x 1 = 126 Số
lớn là: 126 + 252 = 378 Đáp
số: số bé: 126; số lớn:378. Bài 8: Ba
năm trước em 6 tuổi và kém chị 6 tuổi. Hỏi mấy năm
sau nữa thì 3 lần tuổi chị bằng 4 lần tuổi em?
Bài
giải Vì
hiệu số tuổi của hai chị em không thay đổi theo thời
gian nên em luôn kém chị 6 tuổi. Khi
3 lần tuổi chị bằng 4 lần tuổi em nghĩa là khi tuổi
em bằng
Ta
có sơ đồ khi đó:
6t
Tuổi chị : |-----|-----|-----|-----| Theo
sơ đồ hiệu số phần bằng nhau là: 4 – 3 = 1 (phần) Khi
đó tuổi của em là: 6 : 1 x 3 = 18 (tuổi) Từ
khi em 6 tuổi đến lúc em 18 tuổi có số năm là: 18 – 6
= 12 (năm) Vậy
sau 12 năm từ lúc em 6 tuổi thì 3 lần tuổi chị bằng 4
lần tuổi em Đáp
số: 12 năm. Bài 9: Một
quầy bán vải, lần thứ nhất bán 2m vải, lần thứ hai
bán
Bài
giải
2m
Sô vải sau khi
bán lần thứ nhất:
|---------------------|--|-------------------|
Số vải sau khi
bán lần thứ ba:
|---|---|
Theo sơ đồ số
vải còn lại sau khi bán lần thứ 3 là:
Số vải còn lại
sau khi bán lần thứ hai là: (1 +
Số vải còn lại
sau khi bán lần thứ nhất là: (3 +
Số vải cửa
hàng đó bán được tất cả là: 7 + 2 = 9 (m) Đáp
số: 9 m vải.
Bài 10: Bình đọc một quyển truyện trong 3 ngày.
Ngày đầu Bình đọc được
Bài giải
16
trang
20
trang
Số trang còn lại sau khi đọc ngày đầu:
|----|----|----|---|- |----|----|----|----|----|----|
37
trang
Theo sơ đồ, số trang còn lại sau khi Bình đọc ngày thứ
hai là:
37 x 4 = 148 (trang)
Số trang còn lại sau khi Bình đọc ngày đầu là:
(148 + 20) : 7 x 10 = 240 (trang)
Số trang của quyển truyện đó là: (240 + 16) : 4 x 5 = 320
(trang)
Đáp số: 320 trang Bài 11: Hai
ngăn sách lúc đầu có tổng cộng 118 cuốn. Sau khi lấy
đi 8 cuốn sách ở nhân I, thêm 10 cuốn sách vào ngăn II
thì số sách ở ngăn II gấp đôi số sách ở ngăn I. Tính
số sách ở mỗi ngăn lúc đầu. Bài
giải Ta
vẽ sơ đồ lúc cuốn sách ngăn II gấp đôi số sách ngăn
I (tức là số sách ở hai ngăn lúc sau):
Tổng
số sách ở hai ngăn lúc sau:
118 – 8 + 10 = 120 (cuốn) Số
sách ở ngăn I lúc sau: 120 : 3 = 40 (cuốn) Số
sách ở ngăn I lúc đầu là: 40 + 8 = 48 (cuốn) Số
sách ở ngăn II lúc đầu: 118 – 48 = 70 (cuốn) Bài 12: Tìm
số tự nhiên tận cùng bằng 7 biết rằng sau khi xóa chữ
số 7 đó thì số ấy giảm đi 484 đơn vị. Bài
Giải Xóa
đi chữ số 7 tận cùng của một số là trừ số đó đi
7 đơn vị rồi chia cho 10. Ta có sơ đồ:
484 Số
ban đầu: |----|----|----|----|----|----|----|----|----|----|--| Số
còn lại: (484 – 7) : 9 = 53. Số
ban đầu: 484 + 53 = 537. Bài 13: Tìm
số tự nhiên biết rằng nếu viết thêm chữ số 2 vào
sau chữ số hàng đơn vị thì số ấy tăng thêm 2000 đơn
vị. Bài
Giải Theo
bài ra ta có: 2000 – 2 = 1998 gấp 9 lần số phải tìm Số
phải tìm là: 1998 : 9 = 222. Đáp
số: 222 Bài 14: Tìm
ba số có tổng bằng 210, biết rằng
Bài
Giải Số
thứ nhất bằng:
Số
thứ ba bằng:
Tổng
của ba số bằng
Đáp
số: 63, 66, 81. Bài 15: Mẹ
hơn con 28 tuổi. Sau 5 năm nữa, tuổi mẹ gấp ba tuổi
con. Tính tuổi mẹ và con hiện nay. Bài
Giải Vì
hiệu số tuổi của mẹ và con không đổi theo thời gian
nên sau 5 năm nữa tuổi mẹ vẫn hơn con 28 tuổi. Ta
có sơ đồ:
28tuổi Tuổi
mẹ sau 5 năm: |--------|--------|--------| Dựa
vào sơ đồ ta thấy: Tuổi
con sau 5 năm là: 28 : 2 = 14 (tuổi) Tuổi con hiện
nay là: 14 – 5 = 9 (tuổi) Tuổi mẹ hiện
nay là: 9 + 28 = 37 (tuổi) Đáp
số: Con: 9 tuổi; Mẹ: 37 tuổi. Bài 16: Năm
2000, mẹ 36 tuổi, hai con 7 tuổi và 12 tuổi. Bắt đầu từ
năm nào, tuổi mẹ ít hơn tổng số tuổi của hai con? HD: Trước
hết ta tính xem đến năm nào thì tuổi mẹ bằng tổng số
tuổi của hai con. Đó là năm 2017. Vậy từ năm 2018 trở
đi thì tuổi mẹ ít hơn tổng số tuổi của hai con. Bài
giải Số
năm để tuổi mẹ bằng tổng tuổi hai con là:
36 –
( 7 + 12) = 17 (năm) Sô
năm để tuổi mẹ bắt đầu nhỏ hơn tổng số tuổi là
con là: 17 +
1 = 18 (năm) Vậy
năm đầu tiên là tuổi mẹ ít hơn tổng số tuổi 2 con
là: 2000
+ 18 = 2018 Đáp
số:năm 2018 Bài 17: Anh
hơn em 3 tuổi. Tuổi anh hiện nay gấp rưỡi tuổi em, lúc
anh bằng tuổi em hiện nay. Tính tuổi hiện nay của mỗi
người. Bài
giải Vì
hiệu số tuổi của anh và em không thay đổi theo thời
gian nên coi tuổi em trước
đây là 1 phần thì tuổi anh trước đây là: 1
phần cộng thêm 3 tuổi Bài 18: Tuổi
mẹ hiện nay gấp 2,3 lần tuổi con. 16 năm trước, tuổi
mẹ gấp 7,5 lần tuổi con. Hỏi mấy năm sau thì tuổi mẹ
gấp đôi tuổi con? Bài
giải Hiện nay mẹ hơn
con: 2,3 – 1 = 1,3 lần tuổi con hiện nay. Còn 16 năm trước
mẹ hơn con: 7,5 – 1 = 6,5 lần tuổi con trước kia. Vì mẹ luôn hơn
con một số tuổi không đổi nên 6,5 lần tuổi con trước
kia bằng 1,3 lần tuổi con hiện nay, tức là tuổi con hiện
nay gấp: 6,5 : 1,3 = 5 lần tuổi con trước kia. Do đó 4 lần
tuổi con trước kia là: 16 năm, tuổi con trước kia là 4
tuổi, tuổi con hiện nay là: 4 + 16 = 20 tuổi, tuổi mẹ
hiện nay là: 20 x 2,3 = 46 tuổi. Mẹ hơn con : 46
– 20 = 26 tuổi. Lúc mẹ gấp đôi tuổi con thì con 26
tuổi, tức là 26 – 20 = 6 năm sau thì tuổi mẹ gấp đôi
tuổi con. Đáp
số: 6 năm PHƯƠNG
PHÁP 2: GIẢ THIẾT TẠM BÀI
TẬP MINH HỌA: Bài 1: Ba ô
tô chở tổng cộng 50 chuyến, gồm 118 tấn hàng. Mỗi
chuyến, xe thứ nhất chở 2 tấn, xe thứ hai chỏ 2,5 tấn,
xe thứ ba chở 3 tấn. Hỏi mỗi xe chở bao nhiêu chuyến
biết rằng số chuyến xe thứ nhất gấp rưỡi số chuyến
xe thứ hai? Bài
Giải Giả thiết rằng
tất cả 50 chuyến đều do xe thứ ba chở thì khối lượng
hàng chở được là: 3.50 = 150 (tấn). Dôi ra: 150 –
118 = 32 (tấn) Để không dôi
ra, phải thay một số chuyến của xe thứ ba bằng các
chuyến của hai xe kia theo quy luật sau: cứ 5 chuyến của
xe thứ ba thay bởi 2 chuyến của xe thứ nhất và 2 chuyến
của xe thứ hai. Mỗi lần thay bởi như vậy thì số
chuyến không thay đổi, số chuyến của xe thứ nhất luôn
gấp rưỡi số chuyến của xe thứ hai, còn khối lượng
hàng giảm đi: 3.5 –
(2.3 + 2,5.2) = 15 – 11 = 4 (tấn) Số lần thay:
32 : 4 = 8 (tấn) Xe thứ nhất
chở: 3.8 = 24 (chuyến) Xe thứ hai chở:
2 .8 = 16 (chuyến) Xe thứ ba chở :
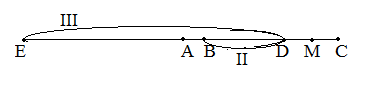
50 – (24 + 16) = 10 (chuyến) Bài 2: Trên
quãng đường AC dài 200 km có một điểm B cách A là 10
km. Lúc 7 giờ, một ô tô đi từ A, một ô tô khác đi từ
B, cả hai cùng đi tới C với vận tốc thứ tự bằng
50km/h và 40km/h. Hỏi lúc mấy giờ thì khoảng cách đến
C của xe thứ hai gấp đôi khoảng cách đến C của xe thứ
nhất?
Bài
Giải
I
M
C
A
B
D
II Lúc xe thứ hai
đến D là thời điểm phải tìm. (DM = DC). Giả thiết rằng
có một xe thứ ba phải đi quan quãng đường EC dài gấp
đôi quãng đường AC của xe thứ nhất phải đi (EC =
200.2 = 400 km), với vận tốc gấp đôi vận tốc của xe
thứ nhất (như vậy vận tốc xe thứ ba bằng : 50.2 = 100
km/h) thì cũng trong thời gian như xe thứ nhất, quãng đường
còn lại đến C của xe thứ nhất và như vậy xe thứ ba
này sẽ gặp xe thứ hại tại D. (Minh họa bằng hình dưới
đây) Quãng
đường ED dài hơn quãng đường BD: 400 –
190 = 210 (km). Vận
tốc xe thứ ba lớn hơn vận tốc xe thứ hai: 100 –
40 = 60 (km/h). Thời
gian để xe thứ ba gặp xe thứ hai tại D: 210 :
60 = 3,5 (h). Vậy
thời điểm phải tìm là: 7 + 3,5 = 10h 30ph. Đáp
số: 10 giờ 30 phút Bài 3: Người
ta bơm nước vào một bể: dùng máy I trong 30 phút, dùng
máy II trong 20 phút. Tính xem trong mỗi phút mỗi máy bơm
được bao nhiêu lít nước, biết rằng mỗi phút máy II
bơm được nhiều hơn máy I là 50 lít và tổng cộng hai
máy bơm được 21000 lít nước?
Bài
Giải Giả sử trong
mỗi phút, máy II bơm số nước bằng máy I thì trong 50
phút cả hai máy bơm được: 21000
– 50.20 = 20000 (lít) Trong
mỗi phút, máy I bơm được: 20000
: 50 = 400 (lít) Trong
mỗi phút, máy II bơm được: 400 +
50 = 450 (lít) Bài 4: Khối
6 của một trường có 366 học sinh, gồm 8 lớp. Mỗi lớp
gồm một số tổ, mỗi tổ có 9 người hoặc 10 người.
Biết rằng số tổ của các lớp đều bằng nhau, tính số
tổ có 9 người, số tổ có 10 người cả khối?
HD
Giải
366 : 10 = 36
còn dư
Do đó số
tổ của các lớp nằm trong khoảng từ 37 đến 40
40 .10 = 400
(HS)
So với bài
ra thừa ra 400 – 366 = 34 (HS) là do còn có tổ 9 người.
10 – 9 =1
Vậy số tổ
có 9 người là 34 : 1 = 34 ( tổ) Bài 5: Một
câu lạc bộ có 22 chiếc ghế gồm ba loại: ghế ba chân,
ghế bốn chân, ghế sáu chân. Tính số ghế mỗi loại,
biết rằng tổng số chân ghế bằng 100 và số ghế sáu
chân gấp đôi số ghế ba chân?
Bài
Giải Giả sử 22 chiếc
ghế đều là 4 chân. Khi đó số chân ghế là: 4 .
22 = 88 (Chân) So với bài ra bị
hụt mất 100 – 88 = 12 (chân) => là do còn có ghê 3
chân, 6 chân. Để không bị hụt đi ta thay các ghế 4 chân
bằng hai loại ghế kia theo quy luật: một ghế 3 chân, 2
ghế 6 chân cho 3 ghế 4 chân, khi đó số ghế không thay
đổi, quan hệ giữa ghế 3 chân và ghế 6 chân được đảm
bảo. Mỗi lần thay,
số chân ghế tăng thêm: 2.6 + 1.3 – 3.4 = 3 (chân) Vậy số lần
thay là: 12 : 3 = 4 (lần) Số ghế 3 chân
là: 4.1 = 4 (ghế) Số ghế 6 chân
là: 4.2 = 8 (ghế) Số ghế 4 chân
là: 22 – (4 + 8) = 10 (ghế) BÀI
TẬP TỰ LUYỆN: Bài 1: Một
số học sinh xếp hàng 12 thì thừa 5 học sinh, còn xếp
hàng 15 cũng thừa 5 học sinh và ít hơn trước là 4 hàng.
Tính số học sinh?
HD giải:
Giả thiết
tạm rằng số HS đó khi xếp hang 15 thì cũng được số
hàng như khi
15. 4 = 60
(HS) Trong
hai trường hợp số HS ở mỗi hàng chênh lệch nhau :
15 – 12 = 3
(HS) Số
hàng khi xếp hàng 12 là : 60 : 3 = 20 ( hàng) Bài 2: Anh
vào cửa hàng mua 12 vở và 4 bút chì hết 36000 đồng.
Bích mua 8 vở và 5 bút chì cùng loại hết 27500 đồng.
Tính giá trị một quyển vở, giá trị một bút chì.
HD giải
36 000. 2 =
72 000 đ Bích
mua gấp ba số hàng đã mua là 24 quyển vở và 15 bút chì
hết
27 500 . 3 =
82 500 đ Như
vậy Bích mua nhiều hơn An 15 – 8 = 7 ( bút chì) Bài 3: Một
tổ may phải may 1800 chiếc cả quần và áo trong 13 giờ.
Trong 8 giờ đầu tổ may áo và trong thời gian còn lại tổ
may quần. Biết rằng trong 1 giờ, tổ may được số áo
nhiều hơn số quần là 30 chiếc. Tính số áo và số quần
tổ đã may.
HD giải Bài 4: Một
lớp học có 6 tổ, số người của mỗi tổ bằng nhau.
Trong một bài kiểm tra, tất cả học sinh đều được
điểm 7 hoặc 8. Tổng số điểm của cả lớp là 350. Hãy
tính số học sinh của lớp, số học sinh đạt tửng loại
điểm?
HD
giải Trước hết tính
số học sinh của lớp ta thấy: 350 chia cho 8 ,
được 43, còn dư;
350 : 7 = 50 Do
đó số học sinh từ 44 đến 50. Do số học sinh chia hết
cho 6 nên số học sinh là 48 người. Giải
tiếp bài toán bằng phương pháp tạm, ta tìm được: 4
học sinh được điểm 8; 34 học sinh được điểm 7. Bài 5: Một
đội bóng thi đấu 25 trận, chỉ có thắng và hòa, mỗi
trận thẳng được 3 điểm, mỗi trận hòa được 1 điểm,
kết quả đội đó được 59 điểm. Tính số trận thắng,
số trận hòa của đội bóng.
HD
giải 25
. 3 = 75 (điểm) So
với bài ra thừa ra 75 – 59 = 16 ( điểm) => là do còn
có trận hòa Bài 6: Có
25 gói đường gồm ba loại: gói 5 lạng, gói 2 lạng, gói
1 lạng, có tổng khối lượng tổng cộng là 56 lạng.
Biết số gói 1 lạng gấp đôi số gói 5 lạng. Tính số
gói mỗi loại.
HD
giải: Giả sử
cả 25 gói đường là gói 2 lạng. khi đó khối lượng
tổng cộng là: 25 .
2 = 50 (lạng) So với bài hụt
đi: 56 – 50 = 6 (lạng) Để không bị
hụt đi ta thay các gói 2 lạng bằng các gói 5 lạng và
gói 1 lạng theo quy luật 1 gói 5 lạng, 2 gói 1 lạng cho 3
gói 2 lạng khi đó số gói không thay đổi, quan hệ giữa
gói 5 lạng và gói 1 lạng được đảm bảo. Mỗi lần
thay tăng thêm được: 1.5 + 2.1 – 3.2 = 1 (lạng). Số lần thay: 6
: 1 = 6 (lần) Vậy số gói
đường 5 lạng là: 6.1 = 6 (gói) Số gói đường
1 lạng là: 6.2 = 12 (gói) Số gói đường
2 lạng là: 25 – (6 + 12) = 7 (gói) Bài 7: Một
hộp có thể chứa được vừa vặn 25 gói bánh hoặc 30
gói kẹo. Người ta xếp 28 gói cả bánh và kẹo thì vừa
đầy hộp đó. Biết rằng giá tiền bánh và kẹo đều
bằng nhau và bằng 36000 đồng. Tính giá một gói bánh,
một gói kẹo.
HD
giải Một hộp có thể
chứa được vừa vặn 25 gói bánh hoặc 30 gói kẹo Thể tích của 25 gói bánh
bằng thể tích của 30 gói kẹo thể tích
của 5 gói bánh = thể tích của 6 gói kẹo Giả sử trong
hộp đựng cả 30 gói kẹo. So với bài ra thì thừa: 30 –
28 = 2 (gói) Để kẹo không
bị thừa ra ta thay các gói kẹo bằng các gói bánh theo
quy luật 6 gói kẹo bằng 5 gói bánh. Mỗi lần thay như
thế tổng thể tích không thay đổi, số gói bớt đi: 6 –
5 = 1 (gói). Số lần thay: 2
: 1 = 2 (lần) Vậy số gói
bánh trong hộp là: 2 . 5 = 10 (gói) Số gói kẹo
trong hộp là: 28 – 10 = 18 (gói) Giá tiền một
gói bánh là: 36000 : 10 = 3600 (đ) Giá tiền một
gói kẹo là: 36000 : 18 = 2000 (đ) PHƯƠNG
PHÁP 3: PHƯƠNG PHÁP DÙNG ĐƠN VỊ QUY ƯỚC BÀI
TẬP MINH HỌA: Bài 1: Hai
xe ô tô khởi hành cùng một lúc: xe thứ nhất đi từ A
đến B, xe thứ hai đi từ B đến A. Sau 1 giờ 30 phút,
chúng còn cách nhau 108 km. Tính quãng đường AB biết rằng
xe thứ nhất đi cả quãng đường AB hết 6 giờ, xe thứ
hai đi cả quãng đường BA hết 5 giờ. Bài
giải Lấy quãng
đường AB làm đơn vị quy ước Trong một giờ
xe thứ nhất đi được
Trong một giờ
xe thứ nhất đi được
Trong một giờ
cả hai xe đi được:
Trong
một giờ 30 phút cả hai xe đi được:
Quãng
đường còn lại: 1 -
Vậy
quãng đường AB dài: 108 :
Bài 2: Một
công nhân làm một mình xong một công việc trong 10 ngày,
người thứ hai làm xong công việc đó trong 15 ngày, còn
người thứ ba muốn hoàn thành công việc nói trên cần
một số ngày gấp 5 lần số ngày hai người trên cùng
làm để hoàn thành công việc. Hỏi nếu cả ba người
cùng làm công việc đó thì mấy ngày xong? Bài
giải Chọn khối lượng
công việc làm đơn vị quy ước Trong 1 ngày người
thứ nhất làm được
Trong 1 ngày người
thứ hai làm được
Trong
1 ngày cả hai người làm được
Nếu
cả hai người cùng làm thì công việc hoàn thành trong
thời gian:
1 :
Từ
đó suy ra người thứ ba hoàn thành công việc trong thời
gian:
5. 6 = 30 (ngày) Trong
một ngày người thứ ba làm được
Trong
1 ngày cả ba người làm được
Nếu
cả ba người cùng làm thì hoàn thành công việc trên
trong thời gian là:
1 :
BÀI
TẬP TỰ LUYỆN: Bài 1: Một
người cần 15 ngày để làm xong một công việc, trong khi
đó người thứ hai làm xong công việc ấy cần 18 ngày.
Cả hai cùng làm 3 ngày, sau đó chỉ còn người thứ nhất
làm thêm 3 ngày nữa thì có người thứ ba đến giúp và
tất cả làm 4 ngày thì xong. Hỏi người thứ ba làm một
bình bao nhiêu lâu thì xong công việc nói trên? Bài
giải Chọn
khối lượng công việc làm đơn vị quy ước Trong 1 ngày người
thứ nhất làm được
Trong 1 ngày người
thứ hai làm được
Trong
3 ngày cả hai người làm được ( Trong
3 ngày người thứ nhất làm được
Trong
4 ngày thì người thứ nhất và người thứ ba làm được
số phần công việc là: 1 -
Trong
4 ngày thì người thứ ba làm được
Trong
1 ngày thì người thứ ba làm được
Vậy
người thứ ba làm một mình thì hoàn thành công việc
trên trong thời gian là:
1 :
Bài 2: Ba
máy cày cùng cày một cánh đồng. Lúc đầu chỉ có hai
máy thứ nhất và thứ hai cày trong 3 giờ, sau đó máy thứ
hai nghỉ, máy thứ ba vào làm thay với năng suất gấp đôi
máy thứ hai và trong 5 giờ thì hai máy này cày xong cánh
đồng. Hỏi mỗi máy cày một mình xong cánh đồng đó
trong bao lâu, biết rằng nếu máy thứ nhất và máy thứ
hai cùng làm thì sau 12 giờ xong công việc? Bài
giải Một
giờ máy thứ nhất và máy thứ hai là được
Vậy
3 giờ máy thứ nhất và máy thứ hai là được 3.
Trong
5 giờ máy thứ nhất và máy thứ ba cày được: 1 -
Một
giờ máy thứ nhất và máy thứ ba cày được:
Gọi
một giờ máy thứ nhất làm được x công việc Một giờ máy thứ hai làm
được:
Một giờ máy thứ ba làm
được:
Do năng suất
của máy thứ 3 gấp đôi năng suất của máy thứ 2 nên
ta có: Vậy máy thứ
nhất cày một mình mất: 1 :
Máy thứ hai cày
một mình mất: 1 :
Máy thứ ba cày
một mình mất: 1 :
PHƯƠNG
PHÁP 4: PHƯƠNG PHÁP TÍNH NGƯỢC TỪ CUỐI BÀI
TẬP MINH HỌA: Bài 1: Một
nông dân ra chợ bán hết số cam của mình cho năm người
: Bài
giải Gọi
số cam ban đầu là x Vậy
còn lại:
Bài 2:
Có 100 viên bi. Hai người
lần lượt lấy số bi bất kỳ từ 1 đến 4 viên, người
nào lấy được viên bi cuối cùng là người thắng cuộc. Hỏi người đi
trước hay người đi sau sẽ thắng và cách lấy số bi để
đảm bảo phần thắng thuộc về mình? Cũng hỏi như câu a nếu
mỗi người được lấy từ 5 đến 10 viên bi. Cũng câu hỏi như câu a
nếu mỗi người lấy được 5 đến 10 viên bi và người
lấy viên bi cuối cùng là người thua cuộc? Bài
giải Người thắng cuộc cần
để lại 5 viên bi cho đối thủ của mình. Bao giờ người
đó cũng có cách để số bi lúc sau ít hơn số bi lúc
trước là: 1 + 4 = 5, do đó người đó cần để lại cho
đối thủ của mình: 5, 10, 15, 20, …bi, tức là số bi để
lại là bội của 5. Người đi
sau sẽ thắng cuộc nếu nắm được quy luật chơi: khi
người đi trước lấy k viên bi ( 1≤ k ≤ 4 ) thì người
đi sau lấy 5 – k viên bi. Người thắng cuộc cần
để lại 11 viên bi cho đối thủ của mình. Bao giờ
người đó cũng có cách để số bi lúc sau ít hơn số
bi lúc trước là: 5 + 10 = 15, do đó người đó cần để
lại cho đối thủ của mình: 11, 26, 41, 56, 71, 86 bi. Người đi
sau sẽ thắng cuộc bằng cách: khi người đi trước lấy
k viên bi ( 5 ≤ k ≤ 10 ) thì người đi sau lấy 14 – k
viên bi. Khi đó có 86 viên bi. Tiếp theo nếu người đi
trước lấy m viên bi thì người đi sau lấy 15 – m viên,
và số bi còn lại lần lượt là 71, 56, 41, 26, 11. Lúc này
người đi trước lấy số bi bất kì thì người đi sau
lấy nốt số còn lại. Người đi trước thắng
bằng cách: lấy 5 bi, khi đối thủ lấy tiếp k bi thì
người đi trước lấy 15 – k bi, lần lượt để lại
cho người kia 80, 65, 50, 35, 20, 5 viên bi. BÀI
TẬP TỰ LUYỆN: Bài 1: Một
người ra chợ bán trứng. Người khách thứ nhất mua
Bài
giải Gọi
số trứng người bán hàng bán được là x Vậy
còn lại:
Vậy
còn lại
Người
thứ 4 mua:
Vậy
còn lại:
Bài 2: Trong
dịp Tết trồng cây, khối 6 phân chia số cây cho các lớp
đem trồng như sau: Lớp 6A trồng 10 cây và
Cứ chia như vậy
cho đến lớp cuối cùng thì vừa hết số cây và số cây
các lớp được chia đem trồng đều bằng nhau. Hỏi có
mấy lớp 6, mỗi lớp được chia bao nhiêu cây đem trồng? Bài
giải Xét
2 lớp cuối cùng là lớp thứ n-1 và lớp thứ n. Giả
sử lớp thứ n-1 được chia x cây +
Theo
quy luật của bài toán lớp thứ n được chia x + 5 (cây)
( Vì không còn số còn lại). Vì
số cây đem trồng đều bằng nhau nên ta có:
x +
suy ra
=> y = 40 Tìm
ra lớp thứ n được chia 35 cây Suy
ra mỗi lớp được chia 35 cây Vì
lớp 6A trồng 10 cây và
Tổng
số cây là 10 + 25.8 = 210(cây) Số
lớp 6 là 210 : 35 = 6(lớp) PHƯƠNG
PHÁP 5: GIẢI TOÁN BẰNG PHƯƠNG PHÁP LỰA CHỌN BÀI
TẬP MINH HỌA: Bài 1: Tìm
số tự nhiên có ba chữ số biết rằng số đó chia hết
cho 18 và các chữ số của nó đều sắp xếp từ nhỏ
đến lớp thì tỉ lệ với 1: 2: 3. Bài
giải Căn cứ vào điều
kiện các chữ số tỉ lệ với: 1 : 2 : 3, các chữ số
của số phải tìm có thể là 1, 2, 3 hoặc 2, 4, 6 hoặc 3,
6, 9. Chú ý rằng số
phải tìm chia hết cho 18 nên chia hết cho 9, do đó tổng
các chữ số của nó chia hết cho 9. Trong các trường hợp
trên ta thấy chỉ có bộ ba 3, 6, 9 là thỏa mãn. Số phải tìm
chia hết cho 2 nên chữ số tận cùng phải bằng 6. Các số
396, 936 đều thỏa mãn bài toán. Bài 2: Anh
Văn nói với bạn: Năm 1990, tuổi
mình đúng bằng tổng các chữ số của năm sinh. Hãy tính
xem anh Văn sinh năm nào? Bài
giải Gọi năm sinh của
anh Văn là
Do đó: 90 –
(10x + y) = 10 + x + y 80 = 11x + 2y Do 11x ≤ 80 nên
x ≤ 7. Do 2y ≤ 18 nên 11x ≥ 80 – 18 = 62, do đó x ≥
6. Như vậy chỉ cần xét x = 6 hoặc x = 7. Với x = 6 thì 2y
= 80 – 11.6 = 17 => y = 7 Với x = 7 thì 2y
= 80 – 11.7 = 3, loại. Vậy anh Văn sinh
vào năm 1967. Ta có: 1990 –
1967 = 1 + 9 + 6 + 7 Bài 3: Tìm
số tự nhiên có ba chữ số, biết rằng tổng sáu số tự
nhiên có hai chữ số lập bởi hai trong ba chữ số ấy
gấp đôi số phải tìm. Bài
giải Gọi
số tự nhiên cần tìm là:
Theo
bài ra ta có:
10a
+ b + 10b + c +10c + a + 10a + c +10 c +b +10b + a = 2(100a + 10b +
c) 22a
+ 22b + 22c = 200a + 20b + 2c
178a = 2b + 20c Ta có: 178a =
2b + 20c ≤ 2.9 + 20.9 = 198 và 178a ≥ 178.1 = 178. => a = 1. 2b + 20c = 178 b + 10c = 89 Ta tìm được
duy nhất cặp số: b = 9, c = 8 thỏa mãn. Vậy số cần
tìm là: 198 BÀI
TẬP TỰ LUYỆN: Bài 1: Tìm
số tự nhiên có hai chữ số, biết rằng nếu chia số ấy
cho tích các chữ số của nó thì được
Bài
giải Gọi chữ
số cần tìm là:
Theo bài ra ta có:
Do
Trong các số
trên chỉ có 64 chia hết cho 8. Thử lại : 64 –
16 = 18, 64 : (6.4) =
Bài 2: Tìm
số tự nhiên x, biết rằng tổng các chữ số của x bằng
y, tổng các chữ số của y bằng z và x + y + z = 60. Bài
giải
Từ đầu bài ta có x là số có 2 chữ số. Đặt
x =
x = 10a + b => y = a + b, z có 2 trường
hợp :
* Nếu y = a + b
( 10a + b) + ( a + b ) + ( a + b ) = 60 => 4a + b = 20
b
* Nếu y = a + b
Ta có : ( 10a + b ) + ( a + b ) + ( a + b – 9 ) = 60
=> 4a + b = 23 => a = 4 , b = 7
=>
Kết luận: có 3 số 44, 47, 50 đều thỏa mãn đề bài. Bài 3: Tìm
ba chữ số khác nhau và khác 0, biết rằng tổng các số
tự nhiên có ba chữ số gồm cả ba chữ số ấy bằng
1554. Bài
giải Gọi
ba số phải tìm là a,b,c.
Theo bài ra ta có: a ≠
b ≠
c ≠
0 và Ngoài Giáo Án Bồi Dưỡng Học Sinh Giỏi Toán 6 Một Số Phương Pháp Giải Toán – Toán 6 thì các tài liệu học tập trong chương trình 6 sẽ được cập nhật liên tục và nhanh nhất có thể sau khi kỳ thi diễn ra trên Danh mục Tài Liệu Học Tập nhằm giúp các bạn đọc thuận tiện trong việc nghiên cứu tài liệu. Quý thày cô và các bạn đọc có thể chia sẻ thêm những tài liệu học tập hữu ích đến địa chỉ email của chúng tôi, nhằm xây dựng nên kho đề thi phong phú, đa dạng cho các em học sinh tham khảo và rèn luyện. Giáo Án Bồi Dưỡng Học Sinh Giỏi Toán 6: Một Số Phương Pháp Giải Toán là một tài liệu dạy và bồi dưỡng cho học sinh lớp 6 với mục tiêu nâng cao kỹ năng giải toán và phát triển tư duy toán học. Giáo án này tập trung vào một số phương pháp giải toán hiệu quả và mang tính sáng tạo, giúp học sinh tiếp cận và giải quyết các bài toán phức tạp một cách tự tin và hiệu quả. Giáo án được xây dựng dựa trên các chủ đề toán học cơ bản trong chương trình lớp 6 và bao gồm các phương pháp giải toán như: Giáo án cung cấp các bài tập và ví dụ minh họa cho từng phương pháp giải toán, giúp học sinh nắm vững và áp dụng kiến thức vào thực tế. Ngoài ra, giáo án còn đưa ra những bài toán thực tế, bài toán khó và phần thưởng cho các học sinh giải quyết tốt nhằm tạo động lực và đam mê trong học tập.
Toán Lớp 6 Chương Trình Mới Sách Chân Trời Sáng Tạo Kèm Hướng Dẫn
Đề Cương Giáo Dục Công Dân Lớp 6 Kì 2 Năm 2022-2023 Kèm Hướng Dẫn
Giáo Án Dạy Thêm Toán 6 Ôn Tập Chương Những Hình Hình Học Cơ Bản
Phân Phối Chương Trình Toán 6 Sách Cánh Diều Năm Học 2021-2022
Đề Thi Giáo Dục Công Dân 6 Học Kì 1 Kết Nối Tri Thức 2022-2023 (Đề 2) Có Đáp Án
CHUYÊN ĐỀ 10: MỘT
SỐ PHƯƠNG PHÁP GIẢI TOÁN


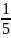 tuổi mẹ. Tính tuổi của mỗi người, biết tổng
số tuổi của mẹ và con là 36.
tuổi mẹ. Tính tuổi của mỗi người, biết tổng
số tuổi của mẹ và con là 36.



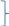

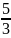 tuổi em. Tính tuổi anh và tuổi em hiện nay.
tuổi em. Tính tuổi anh và tuổi em hiện nay.
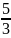 tuổi em, vậy nếu coi tuổi em lúc đó là 5 phần như thế.
Hiệu số phần tuổi của hai anh em lúc đó là:
tuổi em, vậy nếu coi tuổi em lúc đó là 5 phần như thế.
Hiệu số phần tuổi của hai anh em lúc đó là: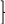


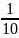 số lớn. Theo bài ra ta có sơ đồ:
số lớn. Theo bài ra ta có sơ đồ: Số
bé: |------|
Số
bé: |------|




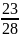 .
Hãy tìm số tự nhiên m sao cho khi cùng bớt cả tử số
và mẫu số của phân số đã cho đi m thì ta được phân
số mới có giá trị bằng
.
Hãy tìm số tự nhiên m sao cho khi cùng bớt cả tử số
và mẫu số của phân số đã cho đi m thì ta được phân
số mới có giá trị bằng
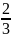 .
.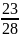 là 28 – 23 = 5
là 28 – 23 = 5
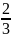 nên ta có sơ đồ:
nên ta có sơ đồ:
 Mẫu
số mới: |------|------|------|
Mẫu
số mới: |------|------|------|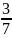 tuổi cha. Ta có sơ đồ khi đó:
tuổi cha. Ta có sơ đồ khi đó:

 Tuổi
cha: |------|------|------|------|------|------|------|
Tuổi
cha: |------|------|------|------|------|------|------|






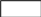




 Tuổi
con 22 năm sau: |----|--------------------------------|
Tuổi
con 22 năm sau: |----|--------------------------------|
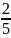 số học sinh nam. Sang đầu học kỳ II có 4 bạn nữ
từ lớp khác chuyển đến nên số học sinh nữa bằng
số học sinh nam. Sang đầu học kỳ II có 4 bạn nữ
từ lớp khác chuyển đến nên số học sinh nữa bằng
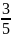 số học sinh nam. Hỏi đầu năm học lớp 5A có bao nhiêu
học sinh nữ, bao nhiêu học sinh nam?
số học sinh nam. Hỏi đầu năm học lớp 5A có bao nhiêu
học sinh nữ, bao nhiêu học sinh nam?





 Số
học sinh nam: |----|----|----|----|----|
Số
học sinh nam: |----|----|----|----|----|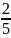 = 20 (học sinh).
= 20 (học sinh).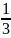 số nước ở bình 1 sang bình 2, rồi đổ
số nước ở bình 1 sang bình 2, rồi đổ
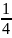 số nước hiện có ở bình 2 sang bình 3, cuối cùng đổ
số nước hiện có ở bình 2 sang bình 3, cuối cùng đổ
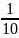 số nước hiện có ở bình 3 sang bình 1 thì mỗi bình đều
có 9 lít nước. Hỏi lúc đầu mỗi bình có bao nhiêu lít
nước?
số nước hiện có ở bình 3 sang bình 1 thì mỗi bình đều
có 9 lít nước. Hỏi lúc đầu mỗi bình có bao nhiêu lít
nước?
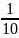 số lít nước ở bình 3 sang bình 1 thì bình 3 còn 9 lít
nước.
số lít nước ở bình 3 sang bình 1 thì bình 3 còn 9 lít
nước.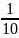 )
= 10 (l)
)
= 10 (l)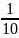 số lít nước của bình 3 thì bình 1 có số lít nước
là:
số lít nước của bình 3 thì bình 1 có số lít nước
là: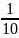 = 8(l)
= 8(l)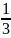 )
= 12 (l)
)
= 12 (l)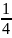 số nước ở bình 2 sang bình 3 thì bình 2 còn 9 lít (theo
bài ra), vậy trước khi đó bình 2 có số lít nước là:
9 : (1 -
số nước ở bình 2 sang bình 3 thì bình 2 còn 9 lít (theo
bài ra), vậy trước khi đó bình 2 có số lít nước là:
9 : (1 -
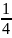 )
= 12 (l).
)
= 12 (l).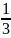 số nước của bình 1 hay lúc đầu bình 2 có số lít nước
là:
số nước của bình 1 hay lúc đầu bình 2 có số lít nước
là: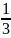 = 8 (l).
= 8 (l).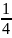 = 3 (l)
= 3 (l)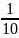 số nước sang bình 1 thì bình 3 có 10 lít nước, vậy
trước khi nhận 3 lít nước ở bình 2 đổ sang hay lúc
đầu bình 3 có số lít nước là: 10 – 3 = 7 (l).
số nước sang bình 1 thì bình 3 có 10 lít nước, vậy
trước khi nhận 3 lít nước ở bình 2 đổ sang hay lúc
đầu bình 3 có số lít nước là: 10 – 3 = 7 (l).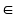 N)
N)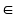 N)
N)





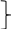










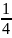 tuổi mẹ. Hỏi hiện nay mỗi người bao nhiêu tuổi?
tuổi mẹ. Hỏi hiện nay mỗi người bao nhiêu tuổi?


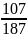 .
Hãy tìm số tự nhiên, biết rằng nếu cùng bớt cả tử
số và mẫu số đi số tự nhiên đó thì ta được phân
số mới có giá trị bằng
.
Hãy tìm số tự nhiên, biết rằng nếu cùng bớt cả tử
số và mẫu số đi số tự nhiên đó thì ta được phân
số mới có giá trị bằng
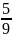 .
.
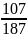 là : 187 – 107 = 80
là : 187 – 107 = 80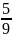 nên
ta có sơ đồ:
nên
ta có sơ đồ:

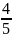




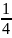 tổng của hai số.
tổng của hai số.
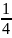 tổng
hai số, nếu coi số bé là 1 phần thì tổng của hai số
là 4 phần như vậy. Do đó số lớn có số phần bằng
nhau là:
tổng
hai số, nếu coi số bé là 1 phần thì tổng của hai số
là 4 phần như vậy. Do đó số lớn có số phần bằng
nhau là: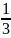 số
lớn. Ta có sơ đồ:
số
lớn. Ta có sơ đồ:

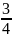 tuổi chị.
tuổi chị.
 số vải còn lại và
số vải còn lại và
 m.
Lần thứ ba bán
m.
Lần thứ ba bán
 số vải còn lại và
số vải còn lại và
 m,
lần thứ tư bán
m,
lần thứ tư bán
 số vải còn lại và
số vải còn lại và
 m thì vừa hết. Hỏi quầy vải đó bán được tất cả
bao nhiêu mét vải?
m thì vừa hết. Hỏi quầy vải đó bán được tất cả
bao nhiêu mét vải?



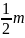

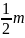

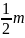
 x 2 = 1 (m)
x 2 = 1 (m) ) x 2 = 3 (m)
) x 2 = 3 (m) ) x 2 = 7 (m)
) x 2 = 7 (m)
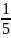 số trang và 16 trang. Ngày thứ hai Bình đọc được
số trang và 16 trang. Ngày thứ hai Bình đọc được
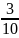 số trang còn lại và 20 trang. Ngày thứ ba Bình đọc
được
số trang còn lại và 20 trang. Ngày thứ ba Bình đọc
được
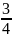 số trang còn lại và 37 trang cuối cùng. Hỏi quyển truyện
đó có bao nhiêu trang?
số trang còn lại và 37 trang cuối cùng. Hỏi quyển truyện
đó có bao nhiêu trang?



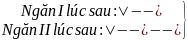 120
120

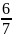 số thứ nhất bằng
số thứ nhất bằng
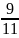 số thứ hai và bằng
số thứ hai và bằng
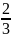 số thứ ba.
số thứ ba.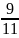 :
:
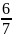 =
=
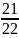 (số thứ hai).
(số thứ hai).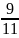 :
:
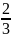 =
=
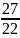 (số thứ hai).
(số thứ hai).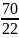 số thứ hai hay 210.
số thứ hai hay 210.

Vậy
tuổi em hiện nay cũng là 1 phần cộng thêm 3 tuổi .
Tuổi
anh hiện nay là:
1
phần + 3tuổi + 3tuổi = 1 phần + 6 tuổi
Vì
( 1 phần + 6 tuổi ) này cũng chính là 1,5 phần. Vậy 0,5
phần là 6 tuổi.
1
phần là: 6
: 0,5 = 12 ( tuổi )
Tuổi
em hiện nay là: 12
+ 3 = 15 ( tuổi )
Tuổi
anh hiện nay là: 15
+ 3 = 18 ( tuổi )
Đáp
số: Anh:
18 tuổi ; Em:
15 tuổi









Mỗi lớp gồm một số tổ mỗi tổ 9 người hoặc 10
người, Trước hết ta nhận thấy :
366
: 9 = 40 còn dư
Mặt
khác số tổ chia hết cho 8 => Số tổ của khối lớp 6
đó là 40 tổ
Giả
sử cả 40 tổ đều là tổ 10 người. Khi đó số HS của
khối là:
Nếu
thay mỗi tổ 10 người bằng một tổ 9 người thì mỗi
lần thay bớt được :
Số
tổ có 10 người là 40 – 34 = 6 (tổ)
xếp
hàng 12, nghĩa là ta phải có thêm 4 hàng nữa. Khi đó có
thêm:
Số
HS là: 20 . 12 + 5 = 245 ( HS)
Giả
sử An mua gấp đôi số hàng đã mua là 24 quyển vở và 8
bút chì hết
Số
tiền chênh lệch là: 82 500 - 72 000 = 10 500 đ,
Vậy
giá tiền một bút chì là: 10 500 : 7 = 1 500 đ,
Giá
tiền một quyển vở là 🙁 36 000 – 4. 1 500) : 12 = 2 500 đ
Giả
sử trong thời gian còn lại tổ vẫn may áo . Khi đó số
áo may thêm được là:
(13
– 8). 30 = 150 ( chiếc)
Số
áo tổ đó may được trong 13 giờ là :1800 + 150 = 1950 (
chiếc)
Số
áo tổ đó may được là:
(1950
: 13) . 8 = 1 200 ( chiếc)
Số
quần tổ đó may được là:
1800
– 1200 = 600 ( chiếc)
Giả
sử cả 25 trận đều thắng. Khi dó số diểm đội đó
có được là :
Chênh
lệch điểm số của trận thắng và trận hòa là : 3-1 =
2
Như
vậy nếu thay mỗi trận thắng bằng một trận hòa thì
mỗi lần thay giảm được 2 điểm
=> Số trận hòa là 16 : 2 = 8 ( trận)
Số
trận thắng là : 25 – 8 = 17 ( trận)
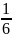 quãng đường AB
quãng đường AB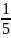 quãng đường AB
quãng đường AB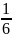 +
+
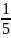 =
=
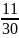 quãng đường AB
quãng đường AB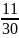 .
.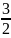 =
=
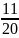 quãng đường AB
quãng đường AB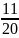 =
=
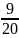 quãng đường AB tương ứng với 108 km
quãng đường AB tương ứng với 108 km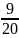 = 240 (km)
= 240 (km)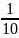 công việc
công việc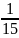 công việc
công việc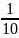 +
+
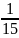 =
=
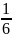 công việc
công việc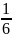 = 6 (ngày)
= 6 (ngày)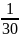 công việc
công việc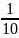 +
+
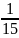 +
+
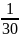 =
=
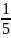 công việc
công việc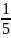 = 5 (ngày)
= 5 (ngày)
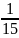 công việc
công việc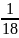 công việc
công việc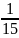 +
+
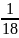 ).3
=
).3
=
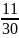 công việc
công việc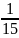 . 3 =
. 3 =
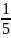 công
việc
công
việc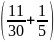 =
=
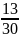 công việc
công việc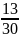 – 4.
– 4.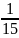 =
=
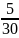 =
=
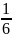 công việc
công việc
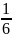 : 4 =
: 4 =
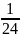 công việc
công việc
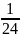 = 24 (ngày)
= 24 (ngày)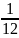 công
việc
công
việc
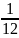 =
=
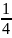 công
việc
công
việc
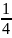 =
=
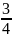 công việc
công việc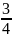 : 5 =
: 5 =
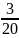 công việc
công việc
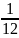 –
x công việc
–
x công việc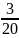 – x công việc
– x công việc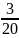 – x = 2.
– x = 2.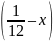 => x =
=> x =
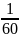
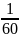 = 60 giờ
= 60 giờ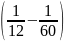 = 15 giờ
= 15 giờ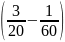 = 7,5 giờ
= 7,5 giờ
Người thứ nhất
mua
 số cam rồi mua thêm
số cam rồi mua thêm
 quả, người thứ hai mua
quả, người thứ hai mua
 số
còn lại rồi mua thêm
số
còn lại rồi mua thêm
 quả
, người thứ ba mua
quả
, người thứ ba mua
 số
quả còn lại rồi mua thêm
số
quả còn lại rồi mua thêm
 quả,
người thứ tư mua 1
quả,
người thứ tư mua 1 số
còn lai rổi mua
số
còn lai rổi mua
 quả,
người thứ năm mua
quả,
người thứ năm mua
 số còn lại rồi mua thêm
số còn lại rồi mua thêm
 quả
thì vừa hết.
quả
thì vừa hết.
Tính
số cam người nông dân đem đi bán và số cam những người
khác đã mua.
Người
thứ nhất mua (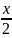 +
+ )
vậy còn lại x - (
)
vậy còn lại x - (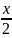 +
+ )
=
)
=
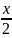 -
-

Người
thứ 2 mua
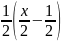 +
+
 =
=
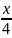 -
-
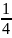 +
+
 =
=
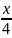 +
+
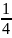
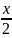 -
-
 -
-
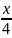 -
-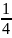 =
=
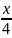 -
-
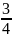
Người
thứ 3 mua: 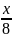 -
-
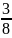 +
+ =
=
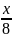 +
+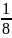 vậy còn lại
vậy còn lại
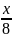 -
-
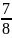
Người
thứ 4 mua:
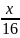 -
-
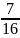 +
+
 =
=
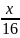 +
+
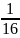 vậy còn lại
vậy còn lại
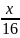 -
-
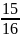
Người
thứ 5 mua:
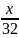 -
-
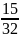 +
+
 =
=
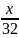 +
+
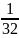 vậy còn lại
vậy còn lại
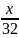 +
+
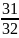 = 0
= 0
Vậy
x = 31 => ban đầu có
31 quả cam đem đi bán
Người
1 mua : 31 – 15 = 16 quả
Người
2 mua : 15 – 7 = 8 quả
Người
3 mua : 7 – 3 = 4 quả
Người
4 mua : 3 – 1 = 2 quả
Người
5 mua : 1 quả
 số trứng rồi mua thêm 2 quả, người thứ hai mua
số trứng rồi mua thêm 2 quả, người thứ hai mua
 số còn lại rồi mua thêm 2 quả, người thứ ba mua
số còn lại rồi mua thêm 2 quả, người thứ ba mua
 số còn lại rồi mua thêm 2 quả, người thứ tư mua
số còn lại rồi mua thêm 2 quả, người thứ tư mua
 số còn lại rồi mua thêm 2 quả thì hết. Hỏi người
bán hàng bán được bao nhiêu quả trứng?
số còn lại rồi mua thêm 2 quả thì hết. Hỏi người
bán hàng bán được bao nhiêu quả trứng?
Người
thứ nhất mua (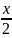 +
+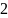 )
vậy còn lại x - (
)
vậy còn lại x - (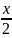 +
+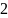 )
=
)
=
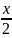 -
-
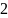
Người
thứ 2 mua
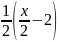 + 2 =
+ 2 =
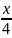 -
1 + 2
=
-
1 + 2
=
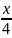 +
1
+
1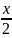 – 2 -
– 2 -
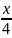 -
-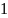 =
=
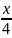 - 3
- 3
Người
thứ 3 mua: 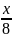 -
-
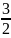 +
+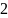 =
=
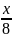 +
+

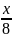 -
-
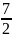
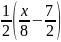 + 2 =
+ 2 =
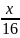 +
+
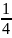
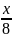 -
-
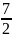 -
-
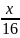 -
-
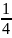 =
=
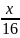 -
-
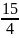 = 0
= 0
Vậy
x = 60 => Người bán
hàng bán được 60 quả trứng.
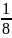 số còn lại, lớp 6B trồng 15 cây và
số còn lại, lớp 6B trồng 15 cây và
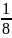 số còn lại, lớp 6C trồng 20 cây và
số còn lại, lớp 6C trồng 20 cây và
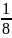 số còn lại …
số còn lại …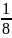 số cây còn lại hay x +
số cây còn lại hay x +
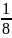 .y
(cây). Lớp thứ n được chia nốt
.y
(cây). Lớp thứ n được chia nốt
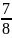 .y
(cây).
.y
(cây).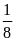 .y
= x + 5
.y
= x + 5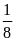 .y
= 5
.y
= 5
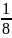 số cây còn lại nên
số cây còn lại nên
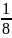 số cây còn lại là 25 cây
số cây còn lại là 25 cây
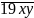 thì 1990 -
thì 1990 -
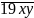 = 1 + 9+ x + y.
= 1 + 9+ x + y.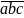 (1≤ a, b, c ≤ 9)
(1≤ a, b, c ≤ 9)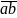 +
+
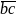 +
+
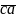 +
+
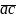 +
+
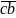 +
+
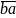 = 2
= 2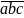
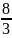 và hiệu giữa số phải tìm với số gồm các chữ số
của số ấy viết theo thứ tự ngược lại bằng 18.
và hiệu giữa số phải tìm với số gồm các chữ số
của số ấy viết theo thứ tự ngược lại bằng 18.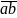 (a ≠ 0)
(a ≠ 0)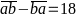 ,
ta được a – b = 2, các số thỏa mãn điều kiện này
là: 20, 31, 42, 53, 64, 75, 86, 97.
,
ta được a – b = 2, các số thỏa mãn điều kiện này
là: 20, 31, 42, 53, 64, 75, 86, 97.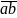 =
=
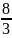 ab => 3
ab => 3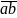
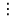 8.
8.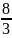 .
.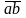
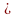 9 => z = a + b ta có :
9 => z = a + b ta có :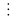 4 => b = 0; 4; 8 => a = 5, 4, 3 loại a = 3, b = 8 ( do a +
b > 9)
4 => b = 0; 4; 8 => a = 5, 4, 3 loại a = 3, b = 8 ( do a +
b > 9)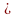 10 => z = a + b – 9
10 => z = a + b – 9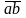 = 44, 47, 50.
= 44, 47, 50.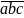 +
+
 +
+ 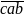 +
+ 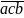 +
+ 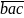 +
+ 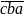 =
1554
=
1554
=> 222a + 222b
+ 222 c = 1554
=> a
+ b + c = 7 ;
Vì
a ≠ b ≠ c ≠ 0. Không làm mất tính tổng quát giả sử
a > b > c ta có c=1; b=2; a=4
Vậy
ba chữ số khác nhau đó là 1; 2; 4
Giáo Án Dạy Thêm Toán 6 Góc Số Đo Góc Các Góc Đặc Biệt Chi Tiết
Các Công Thức Toán 6 Học Kì 1 Sách Kết Nối Tri Thức Môn Số Học 6 (Bộ 2)
Đề Cương Giáo Dục Công Dân Lớp 6 Kì 1 Năm 2022-2023 Kèm Lời Giải
Giáo Án Dạy Thêm Toán 6 Đoạn Thẳng Trung Điểm Của Đoạn Thẳng Hay Nhất
Phân Phối Chương Trình Toán 6 Sách Kết Nối Tri Thức Với Cuộc Sống
Đề Kiểm Tra 45 Phút Giáo Dục Công Dân 6 (Đề 7) Năm 2022-2023 Có Đáp Án
Giáo Án Dạy Thêm Toán 6 Ôn Tập Chung Về Tỉ Số Phần Trăm Đầy Đủ & Chi Tiết
Phân Phối Chương Trình Toán 6 Mới Nhất Sách Kết Nối Tri Thức Chi Tiết
Đề Thi Giáo Dục Công Dân 6 1 Tiết Tự Luận (Đề 6) Năm 2022-2023 Có Đáp Án
Giáo Án Dạy Thêm Toán 6 Tỉ Số Và Tỉ Số Phần Trăm Đầy Đủ Nhất






