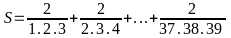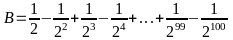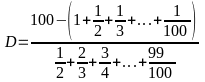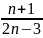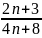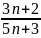Giáo Án Bồi Dưỡng Học Sinh Giỏi Toán 6: Dãy Phân Số Theo Quy Luật
>>> Mọi người cũng quan tâm:
Giáo Án Bồi Dưỡng Học Sinh Giỏi Toán 6: Dãy Phân Số Theo Quy Luật – Toán 6 là tài liệu học tập được Trang Tài Liệu biên soạn và sưu tầm từ những nguồn dữ liệu mới nhất hiện nay. Tài liệu này sẽ giúp các em luyện tập, củng cố kiến thức từ đó nâng cao điểm số cho môn học. Ngoài ra, cũng giúp các thầy cô giáo có nguồn tài nguyên phong phú để giảng dạy.
Mục lục
Dưới đây là bản đọc trực tuyến giúp thầy cô và các em học sinh có thể nghiên cứu Online hoặc bạn có thể tải miễn phí với phiên bản word để dễ dàng in ấn cũng như học tập Offline.
CHUYÊN ĐỀ 9: DÃY PHÂN SỐ THEO QUY LUẬT
DẠNG 1: MỘT SỐ BÀI TOÁN CƠ BẢN VỀ PHÂN SỐ
Bài tập minh họa:
Bài 1: Tìm
số tự nhiên n để phân số A =
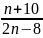 có giá trị là một số nguyên.
có giá trị là một số nguyên.
Bài 2: Tìm
số tự nhiên n để phân số A =
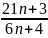
Bài 3: Cho
phân số: A =
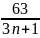 với n thuộc số tự nhiên.
với n thuộc số tự nhiên.
Với giá trị nào của n thì A rút gọn được.
Với giá trị nào của n thì A là số tự nhiên?
Bài tập tự luyện:
Bài 4: Tìm
số tự nhiên n để phân số A =
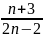 có giá trị là số nguyên.
có giá trị là số nguyên.
Bài 5: Tìm
số tự nhiên n để phân số A =
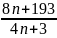 sao cho:
sao cho:
Có giá trị là số tự nhiên.
Là phân số tối giản
Với giá trị nào của n trong khoảng 150 đến 170 thì phân số A rút gọn được?
Bài 6: Tìm các giá trị nguyên của n để các phân số sau có giá trị là số nguyên:
A =
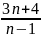
B =
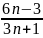
Bài tập minh họa:
Bài 1: Rút gọn biểu thức sau:
S =
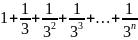
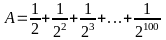
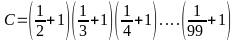
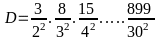 .
.
Bài 2: Tính các tổng sau:
A =
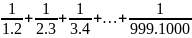
B =
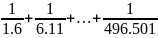
C =
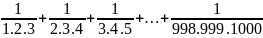
D =
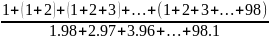
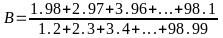
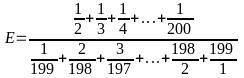
Bài tập tự luyện:
A =

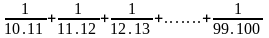
B = 1! +2.2 ! + 3.3 ! + ...... + n .n!
C =
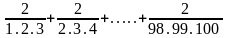
D = 9 + 99 + 999 +...... + 99..... .....9
(50 chữ số 9)
Bài tập minh họa:
Bài 1: Chứng minh rằng các phân số sau tối giản:
Bài 2: Chứng
minh rằng:
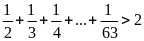
Bài 3: Cho A
=1 +
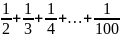
Chứng minh rằng tổng A không phải là số tự nhiên.
Bài 4 : Chứng minh rằng với mọi số tự nhiên n khác 0 ta đều có:
a)
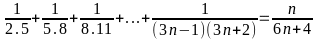
b)
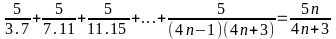
Bài 5: Chứng minh rằng với mọi
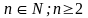 ta có:
ta có:
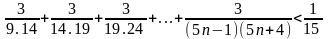
Bài 6: Cho
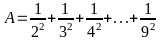 .
Chứng minh
.
Chứng minh
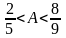
Bài 7: Tổng
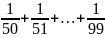 bằng phân số
bằng phân số
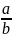 .
Chứng minh rằng a chia hết cho 149.
.
Chứng minh rằng a chia hết cho 149.
Bài tập tự luyện:
Bài
8: Cho
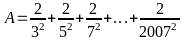 .
Chứng minh:
.
Chứng minh:
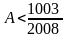
Bài
9: Cho
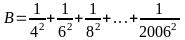 .
Chứng minh:
.
Chứng minh:
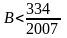
Bài
10: Cho
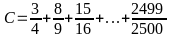 .
Chứng minh C > 48
.
Chứng minh C > 48
Bài
11: Cho
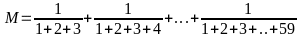 .
Chứng minh
.
Chứng minh
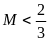
Bài
12: Cho
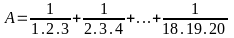 .
Chứng minh
.
Chứng minh
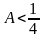
Bài
13: Chứng minh với mọi n
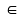 N;
n > 1 ta có:
N;
n > 1 ta có:
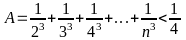
Bài 14: Cho
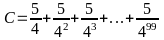 .
Chứng minh:
.
Chứng minh:
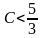
Bài 15: Cho
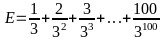 .
Chứng minh:
.
Chứng minh:
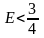
Bài
16: Cho
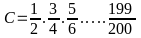 .
Chứng minh:
.
Chứng minh:
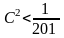
Bài
17: Cho
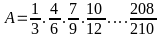 .
Chứng minh:
.
Chứng minh:
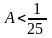
DẠNG 4: TÌM X
Bài tập minh họa:
Bài 1: Tìm
x, biết rằng:
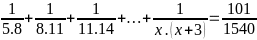
Bài 2: Tìm
x, biết rằng:
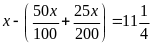
Bài 3: Tìm
x, biết rằng:
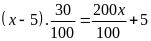
Bài 4: 1 + 2 + 3 + 4 +.............+ x = 820
Bài tập tự luyện:
Bài 5: 1 +
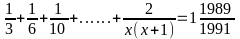
Bài 6:
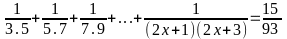
Bài
7:
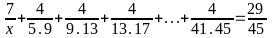
DẠNG 5: SO SÁNH PHÂN SỐ
Bài tập minh họa:
Bài 1: Cho
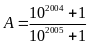 và
và
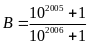
So sánh A và B?
Bài 2: Cho A = 1 + 2 + 3 + … + 1000 và B = 1.2.3…11
So sánh A và B?
Bài 3: So
sánh
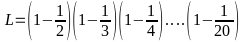 với
với
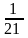
Bài
4: So sánh
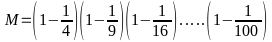 với
với
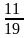
Bài tập tự luyện:
Bài 1: Cho
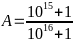 và
và
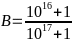
So sánh A và B?
Bài 2: Cho
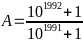 và
và
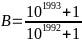
So sánh A và B?
Bài 3: So
sánh
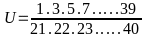 và
và
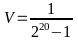
Bài 4: So sánh:
637 và 1612
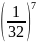 và
và
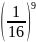
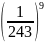 và
và
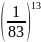
5299 và 3501
323 và 515
12723 và 51318
199010 + 19909 và 199110
3500 và 7300
9920 và 999910
202303 và 303202
Bài 1: Tìm các số tự nhiên x và y sao cho:
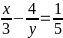
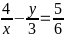
Bài 2: Tìm các số nguyên x và y sao cho:
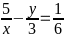
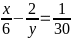
HƯỚNG DẪN – LỜI GIẢI – ĐÁP SỐ
Bài tập minh họa:
Bài 1: Tìm
số tự nhiên n để phân số A =
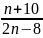 có giá trị là một số nguyên.
có giá trị là một số nguyên.
A =
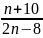 => 2A =
=> 2A =
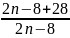 = 1 +
= 1 +
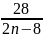 Để 2A nguyên thì 2n – 8 phải là ước của 28
Để 2A nguyên thì 2n – 8 phải là ước của 28
Ta có bảng đáp số:
2n - 8 |
n |
2A |
A |
Kết luận |
-28 |
-10 |
-1 |
-1/2 |
L |
-14 |
-3 |
-2 |
-1 |
TM |
-7 |
½ |
-4 |
-2 |
L |
-4 |
2 |
-7 |
-7/2 |
L |
-2 |
3 |
-14 |
-7 |
TM |
-1 |
7/2 |
-28 |
-14 |
L |
1 |
9/2 |
28 |
14 |
L |
2 |
5 |
14 |
7 |
TM |
4 |
6 |
7 |
7/2 |
L |
7 |
15/2 |
4 |
2 |
L |
14 |
11 |
2 |
1 |
TM |
28 |
18 |
1 |
1/2 |
L |
Bài 3: Cho
phân số: A =
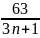 với n thuộc số tự nhiên.
với n thuộc số tự nhiên.
Với giá trị nào của n thì A rút gọn được.
Với giá trị nào của n thì A là số tự nhiên?
Hướng dẫn:
Ta có: A =
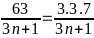
Để A rút gọn
được <=> 3n + 1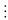 3 hoặc 3n + 1
3 hoặc 3n + 1
 7.
7.
TH1: 3n +
1
 3 (Vô lý)
3 (Vô lý)
TH2: 3n +
1
 7. Với n = 7k + 2 (k N) thì
3n + 1
7. Với n = 7k + 2 (k N) thì
3n + 1
 7.
7.
Kết luận: n
= 7k + 2 (k N) thì phân số
A =
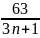 rút gọn được.
rút gọn được.
Để A là số tự nhiên <=> 63
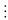 (3n + 1) <=> 3n + 1 là ước của 63.
(3n + 1) <=> 3n + 1 là ước của 63.
Ư(63) = {1; 3; 7; 9; 21; 63}
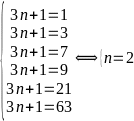
Bài tập minh họa:
Bài 1: Rút gọn biểu thức sau:
S =
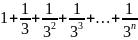
3S = 3 + (1
+
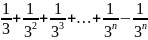 )
)
3S = 3 + S -
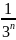
2S = 3 -
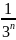
S =
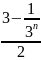
2A = 1 +
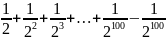
2A = 1 +A -
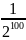
A = 1 -
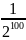
C =
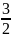 .
.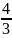 .
.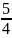 …..
…..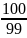 =
=
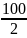 = 50
= 50
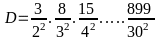 .
.
Bài 2: Tính các tổng sau:
A =
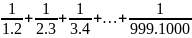
A = 1 -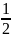 +
+
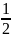 -
-
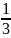 +
+
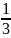 -
-
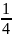 + ..+
+ ..+
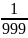 -
-
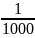
A = 1 -
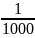 =
=
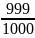
B =
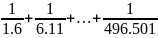
B =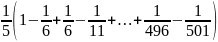 =
=
B =
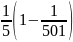 =
=
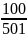
C =
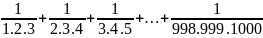
Áp dụng phương pháp khử liên tiếp ta viết mỗi số hạng thành hiệu của hai số sao cho số trừ ở nhóm trước bằng số bị trừ ở nhóm sau:
Ta xét:
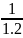 -
-
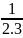 =
=
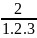 ;
;
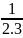 -
-
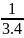 =
=
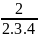 ;
…;
;
…;
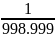 -
-
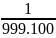 =
=
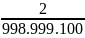
Tổng quát:
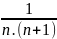 -
-
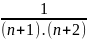 =
=
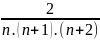
2C =
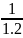 -
-
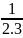 +
+
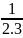 -
-
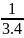 + …+
+ …+
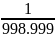 -
-
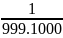 =
=
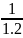 -
-
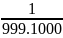
2C =
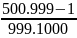 =
=
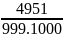
C =
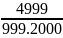
D =
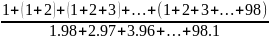
D =
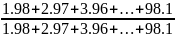 = 1
= 1
Bài tập tự luyện:
A =

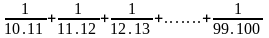
A =
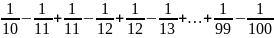
A =
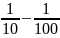 =
=
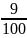
B = 1! +2.2 ! + 3.3 ! + ...... + n .n!
Ta
có : 1! = 2! -1!
2.2!
= 3 ! -2!
3.3!
= 4! -3!
.....
..... .....
n.n!
= (n + 1) –n!
Vậy
B = 2! - 1! +3! – 2 ! + 4! - 3! +...... + ( n+1) ! – n! = ( n+1) ! - 1! = ( n+ 1) ! - 1
C =
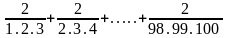
Áp dụng phương pháp khử liên tiếp ta viết mỗi số hạng thành hiệu của hai số sao cho số trừ ở nhóm trước bằng số bị trừ ở nhóm sau:
Ta xét:
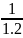 -
-
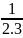 =
=
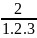 ;
;
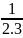 -
-
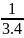 =
=
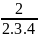 ;
…;
;
…;
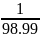 -
-
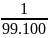 =
=
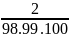
Tổng quát:
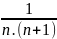 -
-
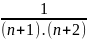 =
=
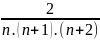
C =
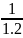 -
-
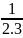 +
+
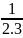 -
-
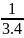 + …+
+ …+
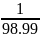 -
-
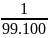 =
=
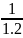 -
-
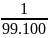
C=
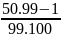 =
=
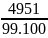
D = 9 + 99 + 999 +...... + 99..... .....9
(50 chữ số 9)
D = 10 – 1 +
100 -1 + 1000 – 1 + ….+
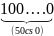 - 1
- 1
D =
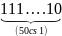 – 50.1 =
– 50.1 =
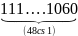
S = Áp dụng phương pháp khử liên tiếp ta viết mỗi số hạng thành hiệu của hai số sao cho số trừ ở nhóm trước bằng số bị trừ ở nhóm sau:
Ta xét:
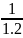 -
-
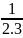 =
=
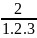 ;
;
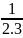 -
-
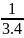 =
=
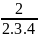 ;
…;
;
…;
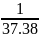 -
-
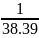 =
=
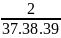
Tổng quát:
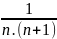 -
-
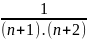 =
=
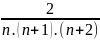
C =
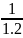 -
-
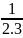 +
+
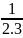 -
-
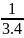 + …+
+ …+
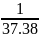 -
-
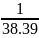 =
=
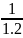 -
-
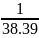
C =
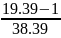 =
=
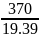
Bài tập minh họa:
Bài 1: Chứng minh rằng các phân số sau tối giản:
Bài 2: Chứng
minh rằng:
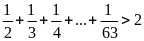
Bài 3: Cho A
=1 +
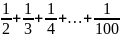
Chứng minh rằng tổng A không phải là số tự nhiên.
Bài 4 : Chứng minh rằng với mọi số tự nhiên n khác 0 ta đều có:
a)
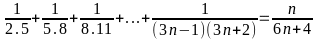
VT
=
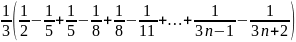
=
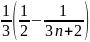 =
=
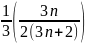 =
=
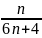 = VP (đpcm)
= VP (đpcm)
b)
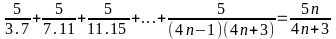
VT =
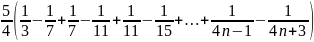
=
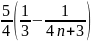 =
=
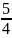 .
.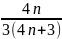 =
=
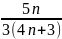
Bài 5: Chứng minh rằng với mọi
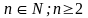 ta có:
ta có:
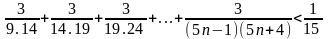
Ta có VT =
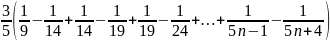
=
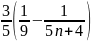 <
<
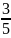 .
.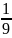 =
=
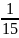 => đpcm
=> đpcm
Bài 6: Cho
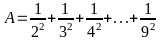 .
Chứng minh
.
Chứng minh
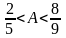
A >
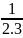 +
+
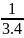 +
+
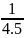 +…+
+…+
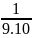 =
=
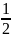 -
-
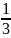 +
+
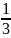 -
-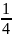 +…+
+…+
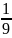 -
-
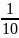
=
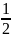 -
-
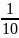 =
=
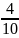 =
=
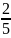 (1)
(1)
A <
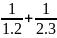 +
+
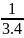 +…+
+…+
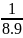 = 1 -
= 1 -
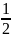 +
+
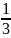 -
-
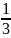 +…+
+…+
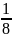 -
-
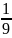 = 1 -
= 1 -
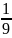 =
=
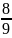 (2)
(2)
Từ (1) và (2) => đpcm
Bài 7: Tổng
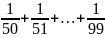 bằng phân số
bằng phân số
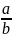 .
Chứng minh rằng a chia hết cho 149.
.
Chứng minh rằng a chia hết cho 149.
Bài tập tự luyện:
Bài
8: Cho
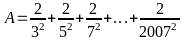 .
Chứng minh:
.
Chứng minh:
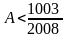
Ta
có:
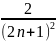 <
<
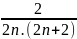 =
=
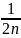 -
-
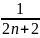
Thay n = 1, 2, 3, …, 1003
Ta
có: A <
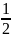 -
-
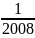 =
=
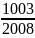 (đpcm)
(đpcm)
Bài
9: Cho
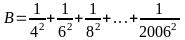 .
Chứng minh:
.
Chứng minh:
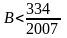
Ta
có:
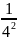 <
<
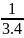 ;
;
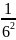 <
<
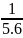 ; … ;
; … ;
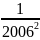 <
<
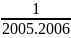
B =
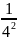 +
+
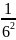 + …+
+ …+
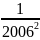 <
<
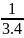 +
+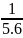 + …+
+ …+
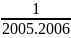
Bài
10: Cho
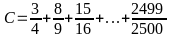 .
Chứng minh C > 48
.
Chứng minh C > 48
C có 49 số hạng
Ta
có: C – 49 = -(1 -
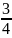 + 1 -
+ 1 -
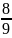 + 1 -
+ 1 -
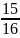 + …+ 1 -
+ …+ 1 -
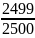 )
)
C – 49 = -
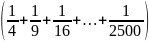
C = 49 -
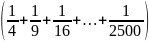 = 49 – D
= 49 – D
Xét D =
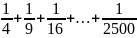 =
=
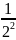 +
+
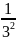 + …+
+ …+
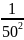
D
<
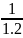 +
+
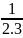 + … +
+ … +
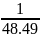 = 1 -
= 1 -
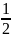 +
+
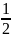 -
-
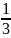 + …+
+ …+
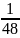 -
-
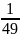 = 1 -
= 1 -
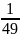 < 1
< 1
D < 1 => 49 – D > 49 – 1 = 48
C > 48 (đpcm)
Bài
11: Cho
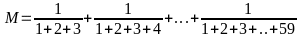 .
Chứng minh
.
Chứng minh
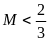
Áp
dụng công thức: 1 +2+ 3 + …+ n =
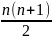
M
=
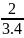 +
+
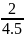 + …+
+ …+
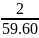 = 2
= 2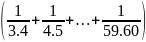
=
2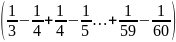 = 2
= 2
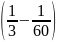 = 2.
= 2.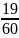 =
=
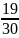 <
<
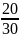 =
=
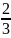
M <
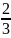 (đpcm).
(đpcm).
Bài
12: Cho
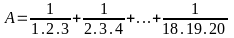 .
Chứng minh
.
Chứng minh
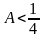
Áp dụng phương pháp khử liên tiếp ta viết mỗi số hạng thành hiệu của hai số sao cho số trừ ở nhóm trước bằng số bị trừ ở nhóm sau:
Ta xét:
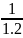 -
-
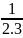 =
=
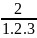 ;
;
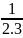 -
-
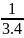 =
=
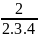 ;
…;
;
…;
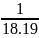 -
-
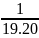 =
=
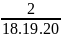
Tổng
quát:
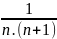 -
-
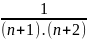 =
=
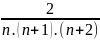
Do
đó: 2A =
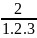 +
+
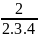 + …+
+ …+
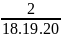
=
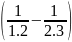 +
+
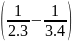 +…+
+…+
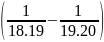
=
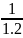 -
-
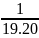 =
=
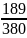
A =
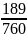 <
<
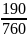 =
=
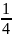 (đpcm)
(đpcm)
Bài
13: Chứng minh với mọi n
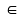 N;
n > 1 ta có:
N;
n > 1 ta có:
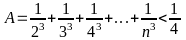
A <
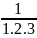 +
+
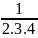 +
+
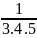 + …+
+ …+
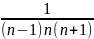
Nhận xét: mỗi số hạng tổng có dạng:
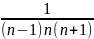 =
=
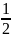 .
.
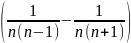
Từ đó suy ra:
A <
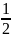 .
.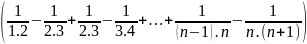
=
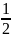 .
.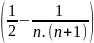 <
<
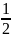 .
.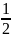 =
=
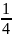 (đpcm)
(đpcm)
Bài 14:
Cho
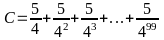 .
Chứng minh:
.
Chứng minh:
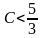
Hướng dẫn giải:

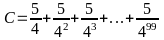
 4
4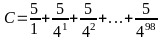
 3C = 5 -
3C = 5 -
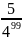
 C <
C <
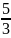
Bài 15:
Cho
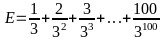 .
Chứng minh:
.
Chứng minh:
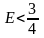
Hướng dẫn giải:
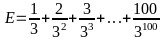

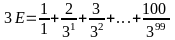

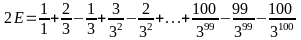

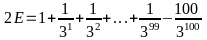 (1)
(1)

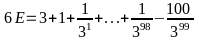 (2)
(2)
Từ (1), (2) suy ra:
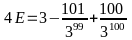

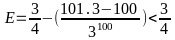
Bài
16: Cho
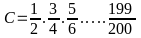 .
(1) Chứng minh:
.
(1) Chứng minh:
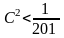
Biểu thức C là tích của 100 phân số nhỏ hơn 1, trong đó các tử đều lẻ, các mẫu đều chẵn. Ta đưa ra biểu thức trung gian là một tích các phân số mà các tử đều chẵn, các mẫu đều lẻ. Thêm 1 vào tử và mẫu của mỗi phân số của A, giá trị mỗi phân số tăng thêm, do đó:
C
<
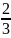 .
.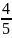 .
.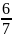 …..
…..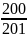 (2)
(2)
Nhân (1) với (2) theo từng vế ta được:
C2
< (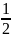 .
.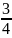 .
.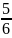 …..
…..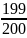 ).(
).(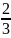 .
.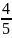 .
.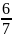 …..
…..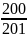 )
)
Vế
phải của bất đẳng thức trên bằng
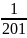
Vậy
C2 <
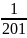 (đpcm)
(đpcm)
Bài tập minh họa:
Bài 1: Tìm
x, biết rằng:
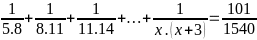
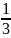 .(
.(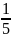 -
-
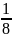 +
+
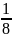 -
-
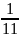 +
+
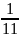 -
-
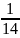 + … +
+ … +
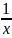 -
-
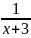 ) =
) =
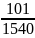
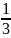 .(
.(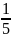 -
-
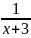 )
=
)
=
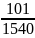
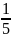 -
-
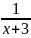 =
=
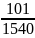 .3
=
.3
=
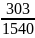
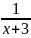 =
=
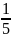 -
-
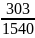 =
=
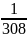
x + 3 = 308
x = 305
Bài 2:
Tìm x, biết rằng:
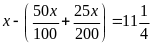
<=> x -
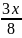 =
=
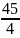
5x = 90
x = 18
Bài 3:
Tìm x, biết rằng:
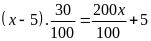
(x – 5).30 = 200x + 500
(x – 5).3 = 20x + 50
3x – 15 = 20x + 50
17x = -65
x = -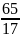
Bài 4: 1 + 2 + 3 + 4 +.............+ x = 820
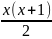 = 820
= 820
x(x+1) = 1640 = 40.41
Vậy x = 40
Bài tập minh họa:
Bài 1: Cho
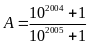 và
và
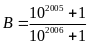
So sánh A và B?
Ta có:
10A
=
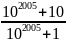 = 1 +
= 1 +
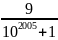
10B
=
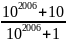 = 1 +
= 1 +
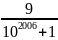
Vì
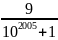 >
>
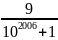 nên 10A > 10B, do đó A > B.
nên 10A > 10B, do đó A > B.
Bài 2: Cho A = 1 + 2 + 3 + … + 1000 và B = 1.2.3…11
So sánh A và B?
Ta
có: A =
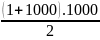 < 103.103 = 106
< 103.103 = 106
B = (2.5).(3.4).(6.7).(8.9).10.11 > 106
Vậy A < B
Bài 3:
So sánh
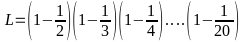 với
với
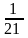
Ta có : L =
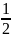 .
.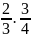 .
… .
.
… .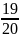 =
=
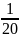 >
>
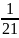
Vậy L >
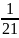
Bài
4: So sánh
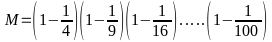 với
với
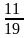
Ta có:
M
=
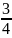 .
.
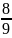 .
.
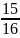 …..
…..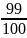 =
=
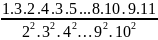 =
=
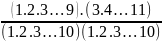 =
=
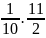 =
=
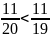
Bài tập tự luyện:
Bài 1: Cho
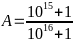 và
và
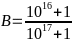
So sánh A và B?
Ta có:
10A
=
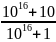 = 1 +
= 1 +
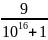
10B
=
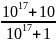 = 1 +
= 1 +
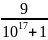
Vì
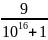 >
>
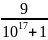 nên 10A > 10B, do đó A > B.
nên 10A > 10B, do đó A > B.
Bài 2: Cho
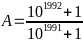 và
và
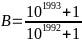
So sánh A và B?
Áp
dụng tính chất: nếu
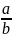 > 1 thì
> 1 thì
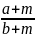 <
<
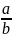 (m > 0)
(m > 0)
Vì B > 1 nên
B
=
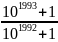 >
>
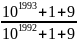 =
=
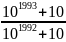 =
=
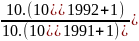 =
=
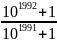 = A
= A
Vậy A < B
Bài 3: So
sánh
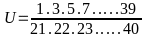 và
và
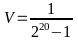
Ta có: U =
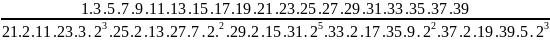
U =
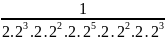 =
=
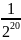
Vì
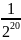 <
<
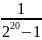 => U < V
=> U < V
Bài 4: So sánh:
637 và 1612
637 < 647 = (82)7 = 814
1612 = (24)12 = 248 = 23.16 = (23)16 = 816
814 < 816 nên 637 < 1612
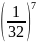 và
và
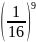
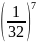 =
=
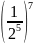 =
=
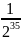
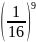 =
=
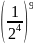 =
=
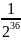
Ta có : 235
< 236 nên
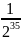 >
>
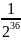 =>
=>
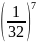 >
>
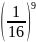
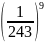 và
và
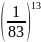
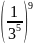 =
=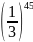 và
và
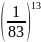 <
<
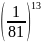 =
=
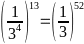
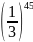 >
>
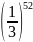 =>
=>
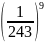 >
>
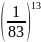
5299 và 3501
5299 < 5300 = (53)100 < (35)100 = 3500 < 3501
Vậy 5299 < 3501
323 và 515
323 = 9.(33)7 > 5.(52)7 = 515
12723 và 51318
12723
< 12823
= (27)23
= 2161
51318
> 51218
= (29)18
= 2162
Vì 2162 > 2161 nên 51318 > 12723
199010 + 19909 và 199110
19909.(1990+1) = 1991.19909
199110 = 1991.19919
Vì 19919 > 19909 nên 1991.19919 > 1991.19909 => 199110 > 199010 + 19909
3500 và 7300
3500
= 35.100
=
(35)100
= 243100
7300
= 73.100
.
(73
)100
= (343)100
Vì
243100
< 343100
=> 3500
< 7300
9920 và 999910
9920
= (992)10
= (99.99)10
= 9910.
9910
999910
=( 101.99)10
= 10110
. 9910
Vì
101> 99 nên 10110
> 9910
=>
10110
. 9910
> 9910.
9910
Vậy
999910
> 9920
202303 và 303202
Vì 202303 = (2.101)3.101 = (23.1013)101 = (8.101.1012)101 = (808.1012)101
Và 303202 = (3.101)2.101 = (32.1012)101 = (9.1012)101
Mà (808.1012)101 > (9.1012)101 nên 202303 > 303202
Bài 1: Tìm các số tự nhiên x và y sao cho:
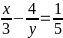
Đkxđ : y ≠ 0
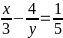
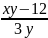 =
=
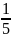
5xy – 60 = 3y
y(5x – 3) = 60
y =
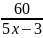
Vì y là số tự nhiên nên 5x – 3 phải là ước của 60
Vì x cũng là số tự nhiên nên giá trị của x thỏa mãn là x = 1; x = 3
Vậy x = 3, y = 5; x = 1, y = 30
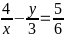
Đkxđ: x ≠ 0
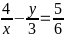
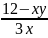 =
=
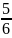
24 – 2xy= 5x
x(5 + 2y) = 24
x =
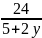
Vì x là số tự nhiên nên 5 +2y là ước của 24 , vì y cũng là số tự nhiên nên không có giá trị nào của x, y thỏa mãn.
Bài 2: Tìm các số nguyên x và y sao cho:
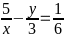
Đkxđ:
x≠0
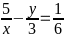 <=>
<=>
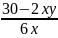 =
=
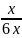
<=>
x+2xy=3
<=> x =
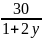
x
nguyên nên 2y + 1 là ước lẻ của 30. Ta có:
2y+ 1 |
1 |
-1 |
3 |
-3 |
5 |
-5 |
15 |
-15 |
2y |
0 |
-2 |
2 |
-4 |
4 |
-6 |
14 |
-16 |
y |
0 |
-1 |
1 |
-2 |
2 |
-3 |
7 |
-8 |
x |
30 |
-30 |
10 |
-10 |
6 |
-6 |
2 |
-2 |
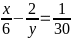
Đkxđ : y ≠ 0
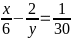
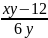 =
=
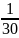
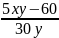 =
=
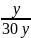
5xy – 60 = y
5xy – y = 60
y (5x – 1) = 60
y =
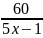
Vì y là số nguyên nên 5x – 1 phải là ước của 60 và chia cho 5 thiếu 1. Ta có:
-
5x – 1
-1
4
-6
5x
0
5
-5
x
0
1
-1
y
-60
15
-10
Ngoài Giáo Án Bồi Dưỡng Học Sinh Giỏi Toán 6: Dãy Phân Số Theo Quy Luật – Toán 6 thì các tài liệu học tập trong chương trình 6 sẽ được cập nhật liên tục và nhanh nhất có thể sau khi kỳ thi diễn ra trên Danh mục Tài Liệu Học Tập nhằm giúp các bạn đọc thuận tiện trong việc nghiên cứu tài liệu. Quý thày cô và các bạn đọc có thể chia sẻ thêm những tài liệu học tập hữu ích đến địa chỉ email của chúng tôi, nhằm xây dựng nên kho đề thi phong phú, đa dạng cho các em học sinh tham khảo và rèn luyện.
Giáo Án Bồi Dưỡng Học Sinh Giỏi Toán 6 với chủ đề “Dãy phân số theo quy luật” là một tài liệu giáo dục đặc biệt dành cho học sinh lớp 6 có năng khiếu và khát khao phát triển trong môn toán. Giáo án này tập trung vào việc khám phá và hiểu quy luật của dãy phân số, từ đó rèn luyện khả năng tư duy logic, phân tích và vận dụng kiến thức vào việc giải quyết các bài toán liên quan đến dãy phân số.
Giáo án được thiết kế một cách cụ thể và chi tiết, bao gồm các hoạt động thực hành, bài tập và ví dụ minh họa, giúp học sinh nắm vững quy luật của dãy phân số. Học sinh sẽ được khám phá các tính chất và quy tắc cộng, trừ, nhân, chia trong dãy phân số, đồng thời họ cũng sẽ được rèn luyện khả năng áp dụng kiến thức để giải quyết các bài toán về dãy phân số.
Giáo Án Bồi Dưỡng Học Sinh Giỏi Toán 6 với chủ đề “Dãy phân số theo quy luật” sẽ giúp học sinh khám phá thú vị và phát triển khả năng toán học của mình. Qua việc hiểu và áp dụng quy luật vào giải quyết các bài toán, học sinh sẽ rèn luyện được tư duy logic, sáng tạo và khả năng xử lý vấn đề. Đồng thời, giáo án cũng giúp học sinh phát triển lòng tự tin, sự kiên nhẫn và sự chính xác trong việc giải quyết các bài toán dãy phân số.
>>> Bài viết có liên quan