Các Chuyên Đề Luyện Thi Học Sinh Giỏi Toán 9 Có Lời Giải Chi Tiết
>>> Mọi người cũng quan tâm:
Các Chuyên Đề Luyện Thi Học Sinh Giỏi Toán 9 Có Lời Giải Chi Tiết – Toán 9 là tài liệu học tập được Trang Tài Liệu biên soạn và sưu tầm từ những nguồn dữ liệu mới nhất hiện nay. Tài liệu này sẽ giúp các em luyện tập, củng cố kiến thức từ đó nâng cao điểm số cho môn học. Ngoài ra, cũng giúp các thầy cô giáo có nguồn tài nguyên phong phú để giảng dạy.
Dưới đây là bản đọc trực tuyến giúp thầy cô và các em học sinh có thể nghiên cứu Online hoặc bạn có thể tải miễn phí với phiên bản word để dễ dàng in ấn cũng như học tập Offline.
CÁC CHUYÊN ĐỀ BỒI DƯỠNG HSG TOÁN THCS
I- ĐỊNH NGHĨA: Số chính phương là số bằng bình phương đúng của một số nguyên.
II- TÍNH CHẤT:
1- Số chính phương chỉ có thể có chữ số tận cùng bằng 0, 1, 4, 5, 6, 9; không thể có chữ tận cùng bằng 2, 3, 7, 8.
2- Khi phân tích ra thừa số nguyên tố, số chính phương chỉ chứa các thừa số nguyên tố với số mũ chẵn.
3-
Số chính phương chỉ có thể có một trong hai dạng 4n
hoặc 4n+1. Không có số chính phương nào có dạng 4n + 2
hoặc 4n + 3 (n
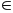 N).
N).
4-
Số chính phương chỉ có thể có một trong hai dạng 3n
hoặc 3n +1. Không có số chính phương nào có dạng 3n + 2
( n
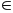 N ).
N ).
5- Số chính phương tận cùng bằng 1, 4 hoặc 9 thì chữ số hàng chục là chữ số chẵn.
Số chính phương tận cùng bằng 5 thì chữ số hàng chục là 2.
Số chính phương tận cùng bằng 6 thì chữ số hàng chục là chữ số lẻ.
6- Số chính phương chia hết cho 2 thì chia hết cho 4.
Số chính phương chia hết cho 3 thì chia hết cho 9
Số chính phương chia hết cho 5 thì chia hết cho 25
Số chính phương chia hết cho 8 thì chia hết cho 16.
III- MỘT SỐ DẠNG BÀI TẬP VỀ SỐ CHÍNH PHƯƠNG.
A- Dạng 1: CHỨNG MINH MỘT SỐ LÀ SỐ CHÍNH PHƯƠNG.
Bài 1: Chứng minh rằng mọi số nguyên x, y thì:
A= (x + y)(x
+ 2y)(x + 3y)(x + 4y) +
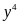 là số chính phương.
là số chính phương.
Giải :
Ta có A = (x + y)(x + 2y)(x + 3y)(x +
4y) +
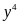
= (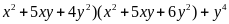
Đặt
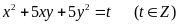 thì
thì
A = (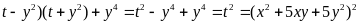
Vì x, y, z
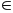 Z nên
Z nên
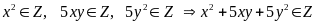
Vậy A là số chính phương.
Bài 2: Chứng minh tích của 4 số tự nhiên liên tiếp cộng 1 luôn là số chính phương.
Giải :
Gọi 4 số tự nhiên, liên tiếp đó là n, n+1, n+2, n+3 (n
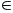 Z). Ta có:
Z). Ta có:
n(n + 1)(n + 2)(n + 3) + 1 = n . ( n + 3)(n + 1)(n + 2) + 1
= (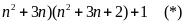
Đặt
 thì (*) = t(t + 2) + 1 = t2
+ 2t + 1 = (t + 1)2
thì (*) = t(t + 2) + 1 = t2
+ 2t + 1 = (t + 1)2
= (n2 + 3n + 1)2
Vì
n
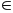 N nên n2
+ 3n + 1
N nên n2
+ 3n + 1
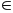 N. Vậy n(n + 1)(n + 2)(+ 3) + 1 là số chính phương.
N. Vậy n(n + 1)(n + 2)(+ 3) + 1 là số chính phương.
Bài 3: Cho S = 1.2.3 + 2.3.4 + 3.4.5 + ...+ k(k + 1)(k + 2)
Chứng minh rằng 4S + 1 là số chính phương.
Giải :
Ta có: k(k + 1)(k + 2) =
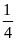 k
(k + 1)(k + 2). 4=
k
(k + 1)(k + 2). 4=
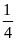 k(k
+ 1)(k + 2).
k(k
+ 1)(k + 2).
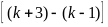
=
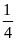 k(k
+ 1)(k + 2)(k + 3) -
k(k
+ 1)(k + 2)(k + 3) -
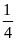 k(k + 1)(k + 2)(k - 1)
k(k + 1)(k + 2)(k - 1)
=> 4S =1.2.3.4 - 0.1.2.3 + 2.3.4.5 - 1.2.3.4 + . . . + k(k + 1)(k + 2)(k + 3)
- k(k + 1)(k + 2)(k - 1) = k(k + 1)(k + 2)(k + 3)
=> 4S + 1 = k(k + 1)(k + 2)(k + 3) + 1
Theo kết quả bài 2 => k(k + 1)(k + 2)(k + 3) + 1 là số chính phương.
Bài 4: Cho dãy số 49; 4489; 444889; 44448889; . . .
- Dãy số trên được xây dựng bằng cách thêm số 48 vào giữa các chữ số đứng trước và đứng sau nó. Chứng minh rằng tất cả các số của dãy trên đều là số chính phương.
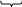 Ta
có 44 ...488...89 = 44...488...8 + 1 = 44...4 . 10n
+ 8 . 11 ... 1 + 1
Ta
có 44 ...488...89 = 44...488...8 + 1 = 44...4 . 10n
+ 8 . 11 ... 1 + 1
n chữ số 4 n - 1 chữ số 8 n chữ số 4 n chữ số 8 n chữ số 4 n chữ số 1
=
4.
=
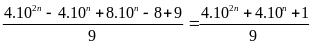
=
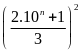
 Ta
thấy 2.10n
+ 1 = 200...01 có tổng các chữ số chia hết cho 3 nên nó
chia hết cho 3
Ta
thấy 2.10n
+ 1 = 200...01 có tổng các chữ số chia hết cho 3 nên nó
chia hết cho 3
n - 1 chữ số 0
=>
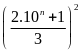
 Z hay các số có dạng 44 ... 488 ... 89 là số chính phương.
Z hay các số có dạng 44 ... 488 ... 89 là số chính phương.
Các bài tương tự:
Chứng minh rằng số sau đây là số chính phương.

 A
= 11 ... 1 + 44 ... 4 + 1
A
= 11 ... 1 + 44 ... 4 + 1
2n chữ số 1 n chữ số 4


 B
= 11 ... 1 + 11 . . .1 + 66 . . . 6 + 8
B
= 11 ... 1 + 11 . . .1 + 66 . . . 6 + 8
2n chữ số 1 n+1 chữ số 1 n chữ số 6


 C=
44 . . . 4 + 22 . . . 2 + 88 . . . 8 + 7
C=
44 . . . 4 + 22 . . . 2 + 88 . . . 8 + 7
2n chữ số 4 n+1 chữ số 2 n chữ số 8
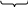
 D
= 22499 . . .9100 . . . 09
D
= 22499 . . .9100 . . . 09
n-2 chữ số 9 n chữ số 0

 E
= 11 . . .155 . . . 56
E
= 11 . . .155 . . . 56
n chữ số 1 n-1 chữ số 5
Kết
quả: A=

D
= (15.10n
- 3)2 E
=
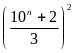
Bài 5: Chứng minh rằng tổng các bình phương của 5 số tự nhiên liên tiếp không thể là một số chính phương.
Gọi
5 số tự nhiên liên tiếp đó là n - 2, n - 1, n +1, n + 2 (
n
 N, n >2).
N, n >2).
Ta có (n - 2)2 + ( n - 1)2 + n2 + (n + 1)2 + (n + 2)2 = 5 . (n2 + 2)
Vì n2 không thể tận cùng bởi 3 hoặc 8 do đó n2 + 2 không thể chia hết cho 5
=> 5. (n2 + 2) không là số chính phương hay A không là số chính phương.
Bài
6: Chứng minh rằng số có
dạng n6
- n4 +
2n3 +
2n2
trong đó n
 N và n >1
N và n >1
không phải là số chính phương.
n6 - n 4 + 2n3 + 2n2 = n2. (n4 - n2 + 2n +2) = n2. [n2(n-1)(n+1) +2(n+1)]
= n2[(n+1)(n3 - n2 + 2)] = n2(n + 1) . [(n3 + 1) - (n2 - 1)]
= n2(n + 1)2 . (n2 - 2n + 2)
Với
n N,
n > 1 thì n2
- 2n + 2 = ( n -1)2
+ 1 > ( n - 1)2
N,
n > 1 thì n2
- 2n + 2 = ( n -1)2
+ 1 > ( n - 1)2
Và n2 - 2n + 2 = n2 - 2(n - 1) < n2
Vậy (n - 1)2 < n2 - 2n + 2 < n2 => n2 - 2n + 2 không phải là một số chính phương.
Bài 7: Cho 5 số chính phương bất kỳ có chữ số hàng chục khác nhau còn chữ số hàng đơn vị đều là 6. Chứng minh rằng tổng các chữ số hàng chục của 5 số chính phương đó là một số chính phương.
Ta biết một số chính phương có chữ số hàng đơn vị là 6 thì chữ số hàng chục của nó là số lẻ. Vì vậy chữ số hàng chục của 5 số chính phương đó là 1,3,5,7,9 khi đó tổng của chúng bằng 1 + 3 + 5 + 7 + 9 = 25 = 52 là số chính phương.
Bài 8: Chứng minh rằng tổng bình phương của 2 số lẻ bất kỳ không phải là số chính phương.
a
và b lẻ nên a = 2k + 1, b= 2m + 1 (Với k, m
 N).
N).
=> a2 + b2 = (2k + 1)2 + ( 2m + 1)2 = 4k2 + 4k + 1 + 4m2 + 4m + 1
= 4 (k2 + k + m2 + m) + 2
=> a2 + b2 không thể là số chính phương.
Bài 9: Chứng minh rằng nếu p là tích của n (với n > 1) số nguyên tố đầu tiên
thì p - 1 và p + 1 không thể là các số chính phương.
Vì
p là tích của n số nguyên tố đầu tiên nên p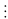 2
và p không thể chia hết cho 4 (1)
2
và p không thể chia hết cho 4 (1)
a-
Giả sử p + 1 là số chính phương. Đặt p + 1 = m2
( m
 N).
N).
Vì p chẵn nên p + 1 lẻ => m2 lẻ => m lẻ.
Đặt
m = 2k + 1 (k
 N). Ta có m2
= 4k2
+ 4k + 1 => p + 1 = 4k2
+ 4k + 1
N). Ta có m2
= 4k2
+ 4k + 1 => p + 1 = 4k2
+ 4k + 1
=>
p = 4k2
+ 4k = 4k (k + 1)
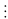 4 mâu thuẫn với (1).
4 mâu thuẫn với (1).
=> p + 1 không phải là số chính phương.
b- p = 2.3.5... là số chia hết cho 3 => p - 1 có dạng 3k + 2.
=> p - 1 không là số chính phương.
Vậy nếu p là tích n (n >1) số nguyên tố đầu tiên thì p - 1 và p + 1 không là số chính phương.
Bài 10: Giả sử N = 1.3.5.7 . . . 2007. 2011
Chứng minh rằng trong 3 số nguyên liên tiếp 2N - 1, 2N và 2N + 1 không có số nào là số chính phương.
a- 2N - 1 = 2.1.3.5.7 . . . 2011 - 1
Có
2N
 3 => 2N - 1 = 3k + 2 (k
3 => 2N - 1 = 3k + 2 (k
 N)
N)
=> 2N - 1 không là số chính phương.
b- 2N = 2.1.3.5.7 . . . 2011 => 2N chẵn.
=>
N lẻ => N không chia hết cho 2 và 2N
 2 nhưng 2N không chia hết cho 4.
2 nhưng 2N không chia hết cho 4.
2N chẵn nên 2N không chia cho 4 dư 1 hoặc dư 3 => 2N không là số chính phương.
c- 2N + 1 = 2.1.3.5.7 . . . 2011 + 1
2N + 1 lẻ nên 2N + 1 không chia hết cho 4
2N không chia hết cho 4 nên 2N + 1 không chia cho 4 dư 1.
=> 2N + 1 không là số chính phương.

 Bài
11: Cho a = 11 . . . 1 ; b
= 100 . . . 05
Bài
11: Cho a = 11 . . . 1 ; b
= 100 . . . 05
2010 chữ số 1 2009 chữ số 0
Chứng minh
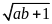 là số tự nhiên.
là số tự nhiên.


Giải: b = 100 . . . 05 = 100 . . . 0 - 1 + 6 = 99 . . . 9 + 6 = 9a + 6
2009 chữ số 0 2010 chữ số 0 2010 chữ số 9
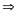 ab + 1 = a(9a + 6) + 1 = 9a2
+ 6a + 1 = (3a + 1)2
ab + 1 = a(9a + 6) + 1 = 9a2
+ 6a + 1 = (3a + 1)2
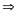
B. DẠNG 2: TÌM GIÁ TRỊ CỦA BIẾN ĐỂ BIỂU THỨC LÀ SỐ CHÍNH PHƯƠNG
Bài 1: Tìm số tự nhiên n sao cho các số sau là số chính phương
a) n2 + 2n + 12 b) n(n + 3)
c) 13n + 3 d) n2 + n + 1589
Giải:
a) Vì n2
+ 2n + 12 là số chính phương nên đặt n2
+ 2n + 12 = k2
(k
 N)
N)
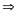 (n2
+ 2n + 1) + 11 = k2
(n2
+ 2n + 1) + 11 = k2
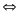 k2
– (n + 1)2
= 11
k2
– (n + 1)2
= 11
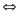 (k + n + 1)(k – n - 1) = 11
(k + n + 1)(k – n - 1) = 11
Nhận xét thấy k + n + 1 > k - n - 1 và
chúng là những số nguyên dương, nên ta có thể viết (k
+ n + 1) (k - n - 1) = 11.1
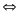 k
+ n + 1 = 11
k
+ n + 1 = 11 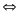 k
= 6
k
= 6
k - n – 1 = 1 n = 4
b) đặt n(n + 3) = a2
(n
 N)
N)
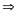 n2 +
3n = a2
n2 +
3n = a2
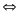 4n2 +
12n = 4a2
4n2 +
12n = 4a2
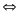 (4n2
+ 12n + 9) – 9 = 4a2
(4n2
+ 12n + 9) – 9 = 4a2
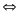 (2n + 3)2
– 4a2
= 9
(2n + 3)2
– 4a2
= 9
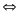 (2n
+ 3 + 2a)(2n + 3 – 2a) = 9
(2n
+ 3 + 2a)(2n + 3 – 2a) = 9
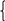
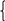
Nhận xét thấy 2n + 3 + 2a > 2n + 3 – 2a
và chúng là những số nguyên dương, nên ta có thể viết
(2n + 3 + 2a)(2n + 3 – 2a) = 9.1 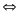 2n
+ 3 + 2a = 9
2n
+ 3 + 2a = 9 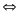 n = 1
n = 1
2n + 3 – 2a = 1 a = 2
c) Đặt 13n + 3 = y2
(y
 N)
N) 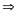 13(n - 1) = y2
– 16
13(n - 1) = y2
– 16
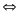 13(n
- 1) = (y + 4)(y – 4)
13(n
- 1) = (y + 4)(y – 4)
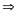 (y
+ 4)(y – 4)
(y
+ 4)(y – 4)
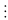 13 mà 13 là số nguyên tố nên y + 4
13 mà 13 là số nguyên tố nên y + 4
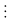 13 hoặc y – 4
13 hoặc y – 4
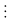 13
13
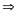 y = 13k
y = 13k
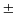 4 (với k
4 (với k
 N)
N)
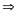 13(n - 1) = (13k
13(n - 1) = (13k
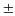 4)2 –
16 = 13k.(13k
4)2 –
16 = 13k.(13k
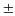 8)
8)
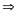 13k2
13k2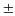 8k + 1
8k + 1
Vậy n = 13k2
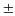 8k + 1 (với k
8k + 1 (với k
 N) thì 13n + 3 là số chính phương
N) thì 13n + 3 là số chính phương
d) Đặt n2
+ n + 1589 = m2
(m
 N)
N) 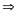 (4n2 +
1)2 +
6355 = 4m2
(4n2 +
1)2 +
6355 = 4m2
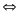 (2m
+ 2n + 1) (2m – 2n – 1) = 6355
(2m
+ 2n + 1) (2m – 2n – 1) = 6355
Nhận xét thấy 2m + 2n + 1 > 2m – 2n – 1 > 0 và chúng là những số lẻ, nên ta có thể viết (2m + 2n + 1) (2m – 2n – 1) = 6355.1 = 1271.5 = 205.31 = 155.41
Suy ra n có thể có các giá trị sau : 1588 ; 316 ; 43 ; 28
Bài tương tự :
Tìm a để các số sau là những số chính phương
a) a2 + a + 43
b) a2 + 81
c) a2 + 31a + 1984
Kết quả: a) 2; 42; 13
b) 0; 12; 40
c) 12 ; 33 ; 48 ; 97 ; 176 ; 332 ; 565 ; 1728
Bài
2 :
Tìm số tự nhiên n
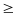 1 sao cho tổng 1! + 2! + 3! + … + n! là một số chính
phương.
1 sao cho tổng 1! + 2! + 3! + … + n! là một số chính
phương.
Với n = 1 thì 1! = 1 = 12 là số chính phương
Với n = 2 thì 1! + 2! = 3 không là số chính phương
Với n = 3 thì 1! + 2! + 3! = 1 + 1.2 + 1.2.3 = 9 = 33 là số chính phương
Với
n
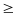 4 ta có 1! + 2! + 3! + 4! = 1 + 1.2 + 1.2.3 + 1.2.3.4 = 33 còn 5!;
6!; …; n! đều tận cùng bởi
0 do đó 1! + 2! + 3! + … n! có tận cùng bởi chữ số 3
nên nó không phải là số chính phương.
4 ta có 1! + 2! + 3! + 4! = 1 + 1.2 + 1.2.3 + 1.2.3.4 = 33 còn 5!;
6!; …; n! đều tận cùng bởi
0 do đó 1! + 2! + 3! + … n! có tận cùng bởi chữ số 3
nên nó không phải là số chính phương.
Vậy có 2 số tự nhiên n thoả mãn đề bài là n = 1; n = 3
Bài 3: Có hay không số tự nhiên n để 2010 + n2 là số chính phương.
Giả
sử 2010 + n2
là số chính phương thì 2010 + n2
= m2
(m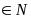 )
)
Từ
đó suy ra m2
- n2 =
2010
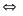 (m
+ n) (m – n) = 2010
(m
+ n) (m – n) = 2010
Như vậy trong 2 số m và n phải có ít nhất 1 số chẵn (1)
Mặt
khác m + n + m – n = 2m
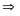 2 số m + n và m – n cùng tính chẵn lẻ (2)
2 số m + n và m – n cùng tính chẵn lẻ (2)
Từ
(1) và (2)
 m + n và m – n là 2 số chẵn.
m + n và m – n là 2 số chẵn.
 (m + n) (m – n)
(m + n) (m – n)
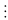 4 nhưng 2006 không chia hết cho 4
4 nhưng 2006 không chia hết cho 4
 Điều giả sử sai.
Điều giả sử sai.
Vậy không tồn tại số tự nhiên n để 2006 + n2 là số chính phương.
Bài
4: Biết x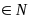 và x > 2. Tìm x sao cho
và x > 2. Tìm x sao cho

Đẳng
thức đã cho được viết lại như sau:
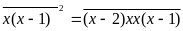
Do vế trái là một số chính phương nên vế phải cũng là một số chính phương.
Một số chính phương chỉ có thể tận cùng bởi một trong các chữ số 0; 1; 4; 5; 6; 9 nên x chỉ có thể tận cùng bởi một trong các chữ số 1; 2; 5; 6; 7; 0 (1)
Do
x là chữ số nên x
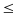 9, kết hợp với điều kiện đề bài ta có x
9, kết hợp với điều kiện đề bài ta có x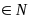 và 2 < x
và 2 < x
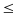 9 (2)
9 (2)
Từ
(1) và (2)
 x chỉ có thể nhận một trong các giá trị 5; 6; 7
x chỉ có thể nhận một trong các giá trị 5; 6; 7
Bằng phép thử ta thấy chỉ có x = 7 thoả mãn đề bài, khi đó 762 = 5776
Bài 5: Tìm số tự nhiên n có 2 chữ số biết rằng 2n + 1 và 3n + 1 đều là các số chính phương.
Ta
có 10
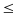 n
n
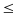 99 nên 21
99 nên 21
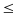 2n + 1
2n + 1
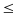 199. Tìm số chính phương lẻ trong khoảng trên ta được
2n + 1 bằng 25; 49; 81; 121; 169 tương ứng với số n bằng
12; 24; 40; 60; 84
199. Tìm số chính phương lẻ trong khoảng trên ta được
2n + 1 bằng 25; 49; 81; 121; 169 tương ứng với số n bằng
12; 24; 40; 60; 84
Số 3n + 1 bằng 37; 73; 121; 181; 253. Chỉ có 121 là số chính phương.
Vậy n = 40
Bài 6: Chứng minh rằng nếu n là số tự nhiên sao cho n + 1 và 2n + 1 đều là các số chính phương thì n là bội số của 24
Vì
n + 1 và 2n + 1 là các số chính phương nên đặt n + 1 =
k2,
2n + 1 = m2
(k, m
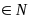 )
)
Ta
có m là số lẻ
 m = 2a + 1
m = 2a + 1
 m2 =
4a(a + 1) + 1
m2 =
4a(a + 1) + 1
Mà

 n chẵn
n chẵn
 n + 1 lẻ
n + 1 lẻ
 k lẻ
k lẻ
 đặt k = 2b + 1 (với b
đặt k = 2b + 1 (với b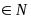 )
)
 k2 =
4b(b+1) + 1
k2 =
4b(b+1) + 1
 n = 4b(b+1)
n = 4b(b+1)
 n
n
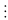 8 (1)
8 (1)
Ta
có: k2
+ m2 =
3n + 2
 2 (mod3)
2 (mod3)
Mặt khác k2 chia cho 3 dư 0 hoặc 1, m2 chia cho 3 dư 0 hoặc 1
Nên
để k2
+ m2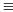 2 (mod3) thì k2
2 (mod3) thì k2
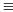 1 (mod3)
1 (mod3)
m2
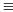 1 (mod3)
1 (mod3)
 m2
– k2
m2
– k2
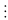 3 hay (2n + 1) – (n + 1)
3 hay (2n + 1) – (n + 1)
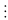 3
3
 n
n
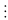 3 (2)
3 (2)
Mà (8; 3) = 1 (3)
Từ
(1), (2), (3)
 n
n
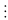 24
24
Bài 7: Tìm tất cả các số tự nhiên n sao cho số 28 + 211 + 2n là số chính phương
Giả
sử 28
+ 211
+ 2n =
a2 (a
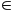 N) thì
N) thì
2n = a2 – 482 = (a + 48) (a – 48)
2p.
2q =
(a + 48) (a – 48) với p, q
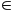 N ;
p + q = n và p > q
N ;
p + q = n và p > q
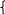
 a + 48 = 2p
a + 48 = 2p
 2p 2q
= 96
2p 2q
= 96
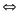 2q
(2p-q
– 1) = 25.3
2q
(2p-q
– 1) = 25.3
a – 48 = 2q
 q = 5 và p – q = 2
q = 5 và p – q = 2
 p = 7
p = 7
 n = 5 + 7 = 12
n = 5 + 7 = 12
Thử lại ta có: 28 + 211 + 2n = 802
C.DẠNG 3 : TÌM SỐ CHÍNH PHƯƠNG
Bài 1 : Cho A là số chính phương gồm 4 chữ số. Nếu ta thêm vào mỗi chữ số của A một đơn vị thì ta được số chính phương B. Hãy tìm các số A và B.
Gọi
A =
 .
Nếu thêm vào mỗi chữ số của A một đơn vị thì ta có
số
.
Nếu thêm vào mỗi chữ số của A một đơn vị thì ta có
số
B
=
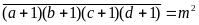 với k, m
với k, m
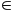 N và 32 < k < m < 100
N và 32 < k < m < 100
a, b, c, d =

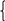
 Ta có: A =
Ta có: A =

B =
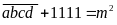 .
Đúng khi cộng không có nhớ
.
Đúng khi cộng không có nhớ
 m2
– k2
= 1111
m2
– k2
= 1111
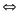 (m - k)(m + k) = 1111 (*)
(m - k)(m + k) = 1111 (*)
Nhận xét thấy tích (m – k)(m + k) > 0 nên m – k và m + k là 2 số nguyên dương.
Và m – k < m + k < 200 nên (*) có thể viết (m – k) (m + k) = 11.101
 Do
đó: m – k = 11
Do
đó: m – k = 11 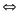 m = 56
m = 56 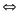 A
= 2025
A
= 2025
m + k = 101 n = 45 B = 3136
Bài 2: Tìm một số chính phương gồm 4 chữ số biết rằng số gồm 2 chữ số đầu lớn hơn số gồm 2 chữ số sau một đơn vị.
Đặt
 ta có
ta có
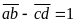 và k
và k
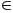 N, 32
N, 32
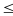 k < 100
k < 100
Suy
ra :
101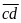 = k2 –
100 = (k – 10)(k + 10)
= k2 –
100 = (k – 10)(k + 10)
 k + 10
k + 10
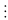 101 hoặc k – 10
101 hoặc k – 10
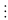 101
101
Mà
(k – 10; 101) = 1
 k + 10
k + 10
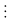 101
101
Vì
32
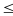 k < 100 nên 42
k < 100 nên 42
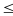 k + 10 < 110
k + 10 < 110
 k + 10 = 101
k + 10 = 101
 k = 91
k = 91

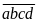 = 912
= 8281
= 912
= 8281
Bài 3: Tìm số chính phương có 4 chữ số biết rằng 2 chữ số đầu giống nhau, 2 chữ số cuối giống nhau.
Gọi
số chính phương phải tìm là:
 = n2
với a, b
= n2
với a, b
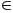 N, 1
N, 1
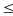 a
a
 9; 0
9; 0
 b
b
 9
9
Ta
có: n2
=
 = 11.
= 11.
 = 11.(100a + b) = 11.(99a + a + b) (1)
= 11.(100a + b) = 11.(99a + a + b) (1)
Nhận
xét thấy

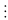 11
11
 a + b
a + b
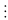 11
11
Mà
1
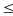 a
a
 9; 0
9; 0
 b
b
 9 nên 1
9 nên 1
 a + b
a + b
 18
18
 a + b = 11
a + b = 11
Thay a + b = 11 vào (1) được n2 = 112(9a + 1) do đó 9a + 1 là số chính phương
Bằng
phép thử với a = 1; 2;…; 9 ta thấy chỉ có a = 7 thoả
mãn
 b = 4
b = 4
Số cần tìm là: 7744
Bài 4: Tìm một số có 4 chữ số vừa là số chính phương vừa là một lập phương.
Gọi
số chính phương đó là
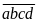 .
Vì abcd vừa là số chính phương vừa là một lập phương
nên đặt
.
Vì abcd vừa là số chính phương vừa là một lập phương
nên đặt
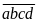 = x2 =
y3 với
x, y
= x2 =
y3 với
x, y
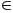 N
N
Vì y3 = x2 nên y cũng là một số chính phương.
Ta
có :
1000

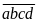
 9999
9999
 10
10
 y
y
 21 và y chính phương
21 và y chính phương
 y = 16
y = 16

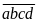 = 4096
= 4096
Bài 5 : Tìm một số chính phương gồm 4 chữ số sao cho chữ số cuối là số nguyên tố, căn bậc hai của số đó có tổng các chữ số là một số chính phương.
Gọi
số phải tìm là
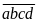 với a, b, c, d nguyên và 1
với a, b, c, d nguyên và 1
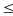 a
a
 9; 0
9; 0
 b, c, d
b, c, d
 9
9
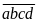 chính phương
chính phương
 d
d
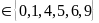
d
nguyên tố
 d = 5
d = 5
Đặt
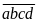 = k2 <
10000
= k2 <
10000
 32
32
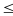 k < 100
k < 100
k
là một số có hai chữ số mà k2
có tận cùng bằng 5
 k tận cùng bằng 5
k tận cùng bằng 5
Tổng
các chữ số của k là một số chính phương
 k = 45
k = 45

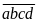 = 2025
= 2025
Vậy số phải tìm là: 2025
Bài 6: Tìm số tự nhiên có hai chữ số biết rằng hiệu các bình phương của số đó và viết số bở hai chữ số của số đó nhưng theo thứ tự ngược lại là một số chính phương
Gọi
số tự nhiên có hai chữ sốphải tìm là
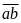 (a, b
(a, b
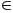 N, 1
N, 1
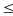 a, b
a, b
 9)
9)
Số
viết theo thứ tự ngược lại
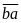
Ta
có
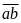 2
-
2
-
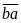 2
= (10a + b)2
– (10b + a)2
= 99 (a2
– b2)
2
= (10a + b)2
– (10b + a)2
= 99 (a2
– b2)
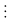 11
11
 a2 –
b2
a2 –
b2
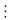 11
11
Hay
(a - b) (a + b)
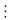 11
11
Vì
0 < a – b
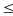 8, 2
8, 2
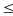 a + b
a + b
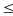 18 nên a + b
18 nên a + b
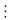 11
11
 a + b = 11
a + b = 11
Khi
đó:
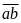 2
-
2
-
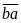 2=
32 .
112 .
(a – b)
2=
32 .
112 .
(a – b)
Để
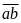 2
-
2
-
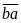 2
là số chính phương thì a – b phải là số chính phương
do đó a – b = 1 hoặc a – b = 4
2
là số chính phương thì a – b phải là số chính phương
do đó a – b = 1 hoặc a – b = 4
Nếu
a – b = 1 kết hợp với a + b = 11
 a = 6, b = 5 ,
a = 6, b = 5 ,
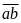 =
65
=
65
Khi đó 652 – 562 = 1089 = 332
Nếu
a – b = 4 kết hợp với a + b = 11
 a = 7,5 loại
a = 7,5 loại
Vậy số phải tìm là 65
Bài 7: Cho một số chính phương có 4 chữ số. Nếu thêm 3 vào mỗi chữ số đó ta cũng được một số chính phương. Tìm số chính phương ban đầu.
(Kết quả: 1156)
Bài 8: Tìm số có 2 chữ số mà bình phương của số ấy bằng lập phương của tổng các chữ số của nó.
Gọi
số phải tìm là
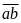 với a, b
với a, b
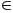 N, 1
N, 1
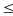 a
a
 9; 0
9; 0
 b
b
 9
9
Theo giả thiết
ta có:
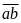 = (a + b)3
= (a + b)3
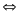 (10a
+b)2 = (a + b)3
(10a
+b)2 = (a + b)3

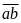 là một lập phương và a + b là một số chính phương
là một lập phương và a + b là một số chính phương
Đặt
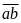 = t3
(t
= t3
(t
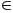 N), a + b = 12
(1
N), a + b = 12
(1
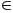 N)
N)
Vì
10
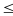 ab
ab
 99
99

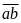 = 27 hoặc
= 27 hoặc
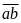 = 64
= 64
Nếu
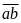 = 27
= 27
 a + b = 9 là số chính phương
a + b = 9 là số chính phương
Nếu
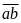 = 64
= 64
 a + b = 10 không là số chính phương
a + b = 10 không là số chính phương
 loại
loại
Vậy số cần tìm là ab = 27
Bài 9 : Tìm 3 số lẻ liên tiếp mà tổng bình phương là một số có 4 chữ số giống nhau.
Gọi
3 số lẻ liên tiếp đó là 2n - 1 ; 2n + 1 ;
2n + 3 (n
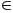 N)
N)
Ta có : A = (2n – 1)2 + (2n + 1)2 + (2n +3)2 = 12n2 + 12n + 11
Theo
đề bài ta đặt 12n2
+ 12n + 11 =
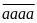 = 1111 . a với a lẻ và 1
= 1111 . a với a lẻ và 1
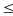 a
a
 9
9
 12n(n + 1) = 11(101a – 1)
12n(n + 1) = 11(101a – 1)
 101a – 1
101a – 1
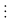 3
3 2a – 1
2a – 1
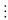 3
3
Vì
1
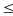 a
a
 9 nên 1
9 nên 1
 2a – 1
2a – 1
 17
và 2a – 1 lẻ nên 2a – 1
17
và 2a – 1 lẻ nên 2a – 1
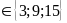
 a
a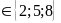
Vì
a lẻ
 a = 5
a = 5
 n = 21
n = 21
3 số cần tìm là: 41; 43; 45
Bài 10 : Tìm số có 2 chữ số sao cho tích của số đó với tổng các chữ số của nó bằng tổng lập phương các chữ số của số đó.
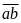 (a + b) = a3
+ b3
(a + b) = a3
+ b3
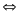 10a + b = a2
– ab + b2
= (a + b)2
– 3ab
10a + b = a2
– ab + b2
= (a + b)2
– 3ab
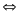 3a (3 + b) = (a + b) (a + b – 1)
3a (3 + b) = (a + b) (a + b – 1)
a + b và a + b – 1 nguyên tố cùng nhau do đó
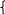
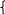
a + b = 3a hoặc a + b – 1 = 3a
a + b – 1 = 3 + b a + b = 3 + b
 a = 4, b = 8 hoặc a = 3, b = 7
a = 4, b = 8 hoặc a = 3, b = 7
Vậy
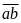 = 48 hoặc
= 48 hoặc
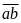 = 37
= 37
Chuyên đề 2: PHƯƠNG TRÌNH NGHIỆM NGUYÊN
1. Tìm nghiệm nguyên của Phương trình và hệ phương trình bậc nhất hai ẩn
Tuỳ từng bài cụ thể mà làm các cách khác nhau.
VD1: Tìm nghiệm nguyên của phương trình: 2x + 3y = 11 (1)
Cách 1: Phương pháp tổng quát:
Ta có: 2x + 3y = 11
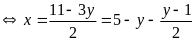
Để
phương trình có nghiệm nguyên
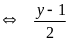 nguyên
nguyên
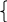 Đặt
Đặt
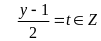
 y = 2t + 1
y = 2t + 1
x = -3t + 4
Cách 2 : Dùng tính chất chia hết
Vì
11 lẻ
 2x + 3y
luôn là số lẻ mà 2x luôn là số chẵn
2x + 3y
luôn là số lẻ mà 2x luôn là số chẵn
 3y lẻ
3y lẻ
 y lẻ
y lẻ
 Do
đó : y
= 2t + 1 với
Do
đó : y
= 2t + 1 với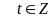
x = -3t + 4
Cách 3 : Ta nhân thấy phương trình có một cặp nghiệm nguyên đặc biệt là
x0 = 4 ; y0 = 1
Thật vậy : 2 . 4 + 3.1 = 11 (2)
Trừ (1) cho (2) vế theo vế ta có :
2(x - 4) + 3(y - 1) = 0
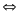 2(x
-4) = -3(y -1) (3)
2(x
-4) = -3(y -1) (3)
Từ
(3)
 3(y - 1)
3(y - 1)
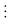 2 mà (2 ;
3) = 1
2 mà (2 ;
3) = 1
 y - 1
y - 1
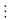 2
2
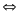 y = 2t + 1 với
y = 2t + 1 với
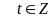
Thay y = 2t + 1 vào (3) ta có : x = -3t + 4
Nhận xét : Với cách giải này ta phải mò ra một cặp nghiệm nguyên (x0, y0) của phương trình ax + by = c ; cách này sẽ gặp khó khăn nếu hệ số a, b, c quá lớn.
Các bài tập tương tự : Tìm nghiệm nguyên của phương trình.
a) 3x + 5y = 10
b) 4x + 5y = 65
c) 5x + 7y = 112
VD2 : Hệ phương trình.
Tìm nghiệm nguyên dương của hệ phương trình sau :

3x + y + z = 14 (1)
5x + 3y + z = 28 (2)
Giải : Từ hệ đã cho ta có : 2(x + y) = 14 vậy x = 7 - y (*)
Thay (*) vào (1) ta được z = 14 - y - 3x = 2y -7
Vì
x > 0 nên 7 - y > 0
 y < 7 mà z >
0 nên 2y - 7 > 0
y < 7 mà z >
0 nên 2y - 7 > 0
 y >
y >
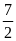
Vậy
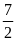 < y < 7 và
< y < 7 và
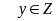
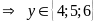
Giải tiếp hệ đã cho có 3 nghiệm (3; 4; 1); (2; 5; 3); (1; 6; 5)
Bài tập tương tự:
a) Tìm nghiệm nguyên của hệ

2x -5y = 5
2y - 3z = 1
b) Trăm trâu ăn trăm bó cỏ – trâu đứng ăn năm, trâu nằm ăn ba, trâu già 3 con 1 bó. Tìm số trâu mỗi loại.
c) Tìm số nguyên dương nhỏ nhất chia cho 1000 dư 1 và chia cho 761 dư 8.
2. Tìm nghiệm nguyên của phương trình, hệ phương trình bậc cao.
Phương pháp 1 : Dùng dấu hiệu chia hết để giải phương trình.
VD1: a) Tìm cặp số nguyên (x ; y) thoả mãn phương trình
6x2 + 5y2 = 74 (1)
Cách 1 : Ta có : 6 (x2 - 4) = 5 (10 - y2) (2)
Từ
(2)
 6(x2
- 4)
6(x2
- 4)
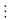 5 và (6 ;
5) = 1
5 và (6 ;
5) = 1
 x2
- 4
x2
- 4
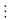 5
5
 x2
= 5t + 4 với
x2
= 5t + 4 với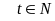
Thay x2 - 4 = 5t vào (2) ta có : y2 = 10 – 6t
 Vì
x2
> 0 và y2
> 0
Vì
x2
> 0 và y2
> 0
 5t + 4 >
0
5t + 4 >
0
10 - 6t > 0

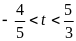 với
với

 t = 0 hoặc t = 1
t = 0 hoặc t = 1
Với
t = 0
 y2 =
10 (loại)
y2 =
10 (loại)

 Với
t = 1
Với
t = 1
 x2
= 9
x2
= 9 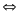 x
=
x
=
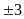
y2
= 4 y =
Vậy các cặp nghiệm nguyên là :........................
 Cách
2 :
Từ (1) ta có x2
+ 1
Cách
2 :
Từ (1) ta có x2
+ 1
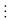 5
5
0
< x2
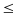 12
12  x2 =
4 hoặc x2
= 9
x2 =
4 hoặc x2
= 9
Với
x2
= 4
 y2
= 10 (loại)
y2
= 10 (loại)
Với
x2 = 9
 y2 = 4
(thoả mãn)
y2 = 4
(thoả mãn)
Vậy.....................
 Cách
3 :
Ta có :(1)
Cách
3 :
Ta có :(1)
 y2
chẵn
y2
chẵn
0 < y2
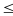 14
14  y2
= 4
y2
= 4
 x2
= 9
x2
= 9
Vậy...............
VD2 : Chứng minh rằng phương trình sau không có nghiệm nguyên
a) x5 + 29x = 10(3y + 1)
b) 7x = 2y - 3z - 1
Giải : x5 - x + 30x = 10(3y+1)
 VP
VP
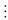 30 còn VT
30 còn VT
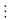 30
30
 phương trình vô nghiệm
phương trình vô nghiệm
Phương pháp 2: Phân tích một vế thành tích, một vế thành hằng số nguyên
VD1: Tìm nghiệm nguyên của phương trình:
a) xy + 3x - 5y = -3
b) 2x2 - 2xy + x - y + 15 = 0
c) x2 + x = y2 - 19
Giải : a) Cách 1: x(y + 3) – 5(y + 3) = -18
 (x
– 5) (y + 3) = -18...
(x
– 5) (y + 3) = -18...
Cách
2 :
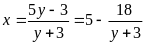
b) Tương tự.
c) 4x2 + 4x = 4y2 - 76
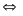 (2x + 1)2
- (2y)2
= -75...
(2x + 1)2
- (2y)2
= -75...
Phương pháp 3 : Sử dụng tính chẵn lẻ (đặc biệt của chia hết)
VD2 : Tìm nghiệm nguyên.
x3 - 2y3 - 4z3 = 0
Giải :
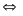 x3
= 2(y3
+ 2z3)
x3
= 2(y3
+ 2z3)
VP
 2
2
 x3
x3
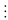 2
2
 x
x
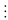 2 đặt x = 2k
2 đặt x = 2k
8k3
= 2(y3
+ 2z3)
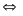 4k3
= y3
+ 2z3
4k3
= y3
+ 2z3
 y3
= 4k3
- 2z3
= 2(2k3
- z3)
y3
= 4k3
- 2z3
= 2(2k3
- z3)
 y chẵn. Đặt y = 2t ta có :
y chẵn. Đặt y = 2t ta có :
8t3
= 2(2k3
- z3)
 4t3 =
2k3
- z3
4t3 =
2k3
- z3
 z3
= 2k3
- 4t3
z3
= 2k3
- 4t3
 z chẵn
z chẵn
 z = 2m
z = 2m
 8m3
= 2(k3
- 2t3)
8m3
= 2(k3
- 2t3)
 ......k chẵn.......
......k chẵn.......
Phương pháp 4 : Phương pháp sử dụng tính chất của số chính phương
VD1 : Tìm nghiệm nguyên của.
a) x2 - 4xy + 5y2 = 169
b) x2 - 6xy + 13y2 = 100
Giải :
a) (x - 2y)2 + y2 = 169 = 0 + 169 = 25 + 144...
b) (x – 3y)2 + (2y)2 = 100 = 0 + 100 = 36 + 64 = ...
Phương pháp 5 : Phương pháp công thức nghiệm phương trình bậc 2
VD1 : Tìm nghiệm nguyên của phương trình.
a) 2x2 -2xy + x + y + 15 = 0
b) 5(x2 + xy + y2) = 7(x+2y) (đề thi học sinh giỏi tỉnh 2009 – 2010)
c) x(x + 1) = y (y + 1) (y2 + 2)
Phương pháp 6 : Phương pháp đặt ẩn phụ
VD:
Tìm nghiệm nguyên của phương trình:
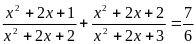 (1)
(1)
Đặt
y = x2
+ 2x + 2 (y
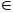 Z)
Z)
(1)
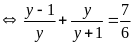
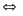 5y2
– 7y – 6 = 0
5y2
– 7y – 6 = 0
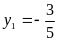 (loại) ; y2
= 2 (thoả mãn)
(loại) ; y2
= 2 (thoả mãn) 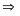 x1
= 0; x2
= -2
x1
= 0; x2
= -2
Các bài tập tương tự:
a) x3 + (x + 1)3 + (x + 2)3 = (x + 3)3
b)
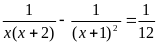
* Một số phương pháp khác.
VD1 : Tìm nghiệm nguyên của phương trình :
2x2 + 4x = 19 -3y2
Giải :
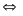 4x2
+ 8x + 4 = 42 - 6y2
4x2
+ 8x + 4 = 42 - 6y2
(2x + 2)2 = 6 (7 - y2)
Vì
(2x + 2)2
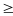 0
0
 7 - y2
7 - y2
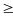 0
0

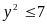
Mà
y
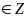
 y = 0 ;
y = 0 ;
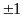 ;
;
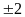 Từ đây ta tìm được giá trị tương ứng của x
Từ đây ta tìm được giá trị tương ứng của x
3. Một số bài toán liên quan tới hình học.
a) Cho tam giác có độ dài của 3 đường cao là những số nguyên dương và đường tròn nội tiếp tam giác đó có bán kính bằng 1(đ.v.đ.d). Chứng minh tam giác đó là tam giác đều
Giải: Gọi độ dài các cạnh và các đường cao tương ứng theo thứ tự là a; b; c và x; y; z. R là bán kính đường tròn nội tiếp.
Ta
có R = 1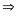 x; y; z > 2 và giả sử x
x; y; z > 2 và giả sử x
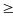 y
y
 z > 2
z > 2
Ta có : ax = by = cz = (a + b+ c).1 (=2S)
Suy
ra:
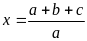 ;
;
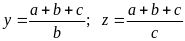
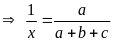 ;
;
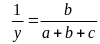 ;
;
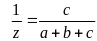
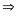
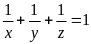 mà x
mà x
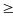 y
y
 z > 2
z > 2
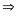
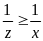 và
và
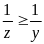 nên
nên
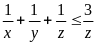
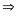
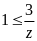
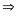

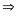 z = 3 Tương
tự ta có: x = 3; y = 3
z = 3 Tương
tự ta có: x = 3; y = 3
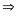 tam giác đó là tam giác đều
tam giác đó là tam giác đều
b) Tìm tất cả các hình chữ nhật với độ dài các cạnh là các số nguyên dương có thể cắt thành 13 hình vuông bằng nhau sao cho mỗi cạnh của hình vuông là số nguyên dương không lớn hơn 4 (đ.v.đ.d)
Giải : Gọi các cạnh hình chữ nhật cần tìm là a và b, cạnh hình vuông là c. Từ giả thiết hình chữ nhật cắt thành 13 hình vuông nên phải có:
ab = 13c2
(1) với 0 < c
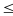 4 (2)
4 (2)
Từ (1) suy ra a hoặc b chia hết cho 13. Vì vai trò a, b như nhau ta có thể giả giả sử a chia hết cho 13, tức là a = 13d
Thay vào (1) ta được : 13db = 13c2
Hay db = c2
Ta hãy xét các trường hợp có thể có của c.
Với c = 1, chỉ có thể: d = 1, b = 1, suy ra a = 13
Với c = 2, chỉ có thể: d = 1, b = 4, suy ra a = 13
d = 2, b = 2, suy ra a = 26
d = 4, b = 1, suy ra a = 52
Với c = 3, chỉ có thể: d = 1, b = 9, suy ra a = 13
d = 3, b = 3, suy ra a = 39
d = 9, b = 1, suy ra a = 117
Với c = 4, chỉ có thể: d = 1, b = 16, suy ra a = 13
d = 2, b = 8, suy ra a = 26
d = 4, b = 4, suy ra a = 52
d = 8, b = 2, suy ra a = 104
d = 16, b = 1, suy ra a = 208
Với 12 nghiệm của phương trình (1) chỉ có 4 trường hợp thoả mãn bài toán. Bài toán có 4 nghiệm. Ta tìm được 4 hình chữ nhật thoả mãn đề bài:
(a = 13, b = 1); (a = 26, b = 2); (a = 39, b = 3); (a = 52, b = 4)
Chuyên đề 3: GIẢI PHƯƠNG TRÌNH VÔ TỶ VÀ HỆ PHƯƠNG TRÌNH
(Dành cho bồi dưỡng học sinh giỏi tỉnh)
I. GIẢI PHƯƠNG TRÌNH VÔ TỶ
* Các phương pháp
1. Luỹ thừa khử căn
2. Đặt ẩn phụ
3. Dùng bất đẳng thức
4. Xét khoảng
II. ÁP DỤNG CÁC PHƯƠNG PHÁP
A. Phương pháp luỹ thừa khử căn
1. Giải các phương trình
a)

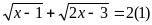
Điều
kiện:
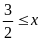
Với
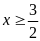 PT (1)
PT (1)

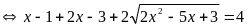

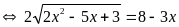
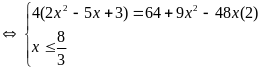
PT
(2)
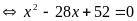

Vậy PT đã cho có nghiệm x=2
b)
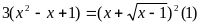
ĐK: 
Với
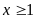 PT (1)
PT (1)
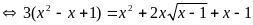

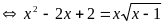
Do
 nên 2 vế của PT này không âm vì vậy PT này
nên 2 vế của PT này không âm vì vậy PT này
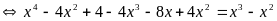
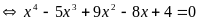
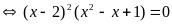
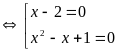
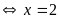 ™
™
c)
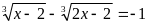 (1)
(1)
Giải:
Pt (1)
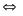
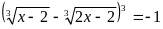
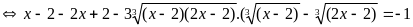

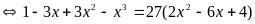
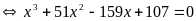

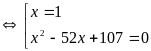
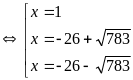
B. Phương pháp đặt ẩn phụ
(2) Giải các phương trình:
a)
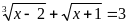
Giải:
ĐK:
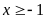
Đặt
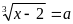 ;
; 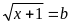 (
( )
)
Ta có hệ PT
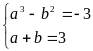
Suy ra
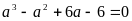
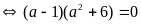
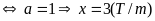
Vậy phương trình nghiệm

b.
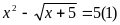
ĐK:
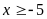
Đặt :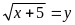 (
(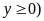 ta có hệ phương trình
ta có hệ phương trình
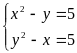
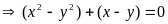
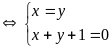
+)
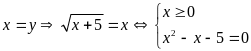

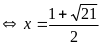 (Ko
T/m)
(Ko
T/m)
+)
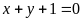
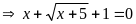
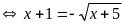
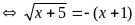
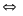
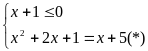
PT (*)
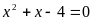
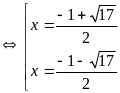 (ko
t/m)
(ko
t/m)
Vậy PT vô nghiệm
c)
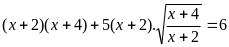 ; ĐK:
; ĐK:
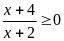
Đặt
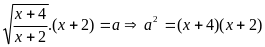 ; Ta có PT:
; Ta có PT:
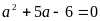 ;
;
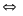

+)
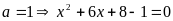
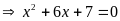
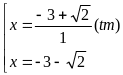
+)


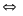
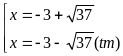
Vậy
pt có 2 nghiệm 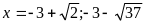
C. áp dụng bất đẳng thức
(3) Giải các phương trình
a)
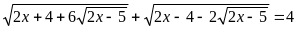 (1)
ĐK:
(1)
ĐK:

Với
Đk:
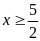 PT (1)
PT (1) 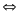

Ta
có: 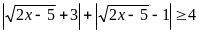
Đẳng
thức xẩy ra

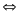
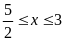
Vậy nghiệm của PT đã cho là
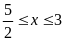
b)
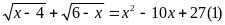
Giải
ĐK
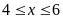
Trên TXĐ
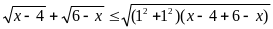
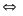
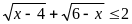
Lại có
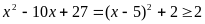
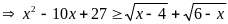
Đẳng thức xẩy ra
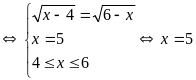
Vậy PT (1) có nghiệm là x=5
c) Giải phương trình
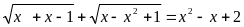
Giải
ĐK: 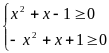
áp dụng BĐT cô si cho các số không âm ta có


Ta có
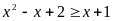 (Vì
(Vì
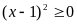 )
)
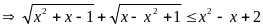
Đẳng thức xẩy ra
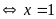 ; Vậy pt có nghiệm là x=1
; Vậy pt có nghiệm là x=1
D. Xét khoảng
(4) Giải các PT
a)
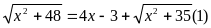
Giải
TXĐ:
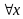
PT(1)
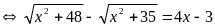
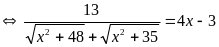
Thấy
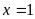 là nghiệm của PT (1)
là nghiệm của PT (1)
+)
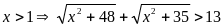
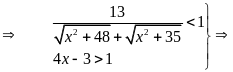 PT
vô nghiệm
PT
vô nghiệm
+)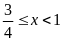
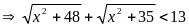
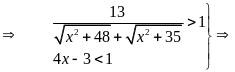 PT vô nghiệm
PT vô nghiệm
Vậy phương trình có nghiệm duy nhất là x=1
b)
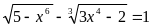 (1)
(1)
Giải
Ta có:
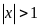 thì
thì
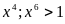
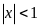 thì
thì
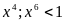
+)
Xét
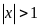
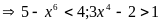
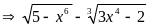
PT (1) vô nghiệm
Xet

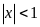 týừng tự ta suy ra phýừng trỡnh vụ nghiệm
týừng tự ta suy ra phýừng trỡnh vụ nghiệm
Thấy x= 1 hoặc x= -1 là nghiệm của PT (1)
Bài tập:
Giải các PT
(1)
a)
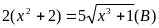
(b)
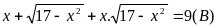
(2)
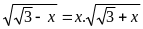 (A)
(A)
(3)
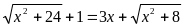 (D)
(D)
(4)
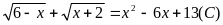
(5)
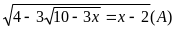
(6)
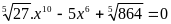 (C)
(C)
III. Giải hệ phương trình
* Các phương pháp:
1. Phương pháp thế
2. Công thức trừ, nhân, chia các vế
3. Đặt ẩn phụ
4. Dùng bất đẳng thức.
IV. áp dụng các phương pháp.
A. Phương pháp thế.
1. Giải các hệ pgương trình
a)
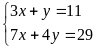
Giải
Hệ đã cho tương đương với
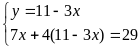

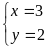
Vậy hệ đã cho có nghiệm là: (x;y) = (3;2)
b)
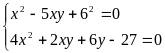
Giải
Hệ đã cho tương đương với
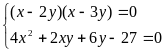
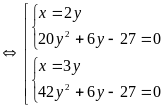
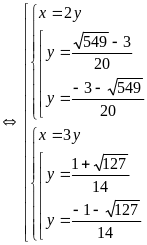
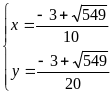 Hoặc
Hoặc
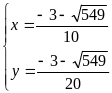
 Hoặc
Hoặc
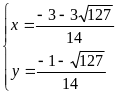
c)



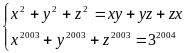
Giải:

Ta có:
PT
(1) 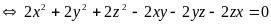
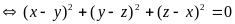
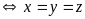
Thế
vào (2) ta có:
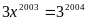
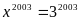
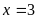
Do đó x= y=z = 3
Vậy nghiệm của hệ đã cho là:
(x;y;z) = (3;3;3)
B. Phương pháp cộng, trừ, nhân, chia các vế
(2) Giải các hệ phương trình
a)
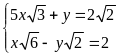
Giải:
Hệ đã cho tương đương với:
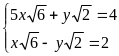
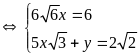
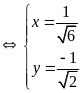
b)
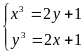
Giải:
Hệ đã cho tương đương với

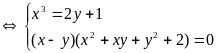
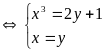 (do
(do
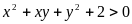 )
)
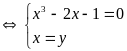
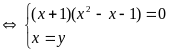
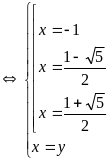
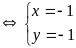 hoặc
hoặc
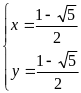 hoặc
hoặc
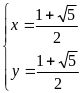
c)
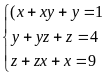 trong đó
trong đó
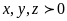
Giải
Hệ đã cho tương đương với
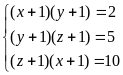
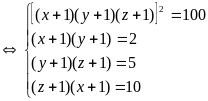
(Do x,y,z>0)
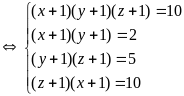
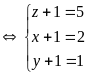

Vậy hệ đã cho có nghiệm là
(x;y;z)=(1;0;4)
C. Phương pháp đặt ẩn phụ
(3). Giải các hệ phương trình
a)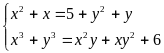
Đặt: x-y=a; x+y =b
Hệ
đã cho trở thành 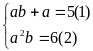
Từ
PT (2) ta suy ra

Do
đó:
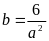
Thế
vào (1) ta được: 
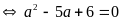 (Vì
(Vì
 )
)
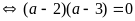
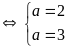
+)
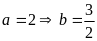 Hay
Hay
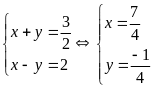
+)
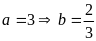 Hay
Hay
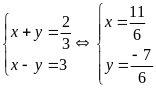
Tóm lại hệ phương trình đã cho có nghiệm là:
(x;y) =
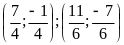
b)
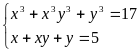
Giải: Đặt x+y = a; xy=b
Hệ đã cho trở thành
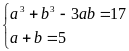
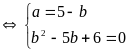
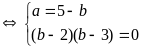
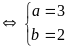 Hoặc
Hoặc
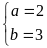
+)
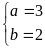 Ta
có hệ phương trình
Ta
có hệ phương trình
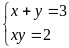
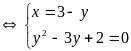
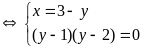
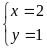 Hoặc
Hoặc 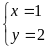
+)
 Ta
có hệ phương trình
Ta
có hệ phương trình
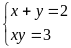
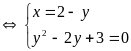 (Vô
nghiệm)
(Vô
nghiệm)
Hệ này vô nghiệm
Vậy nghiệm của hệ đã cho là:
(x;y) = (1;2); (2;1)
c)
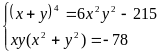
Giải
Hệ đã cho tương đương với
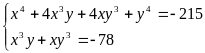
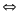
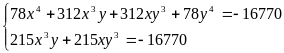
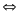
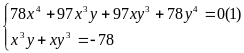
Đặt
 PT (1) trở thành
PT (1) trở thành 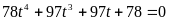
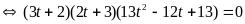
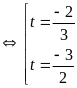
+)

Thế
vào (2) ta được
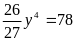
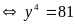
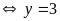 Hoặc
Hoặc
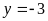
Suy
ra:
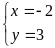 Hoặc
Hoặc 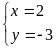
+)
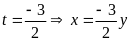
Thế
vào (2) ta được

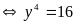
 Hoặc
Hoặc
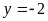
Suy
ra:
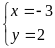 Hoặc
Hoặc 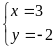
Tóm lại hệ đã cho có nghiệm là:
(x;y) = (-2;3); (2;-3); (-3;2) ; (3;-2)
D. áp dụng bất đẳng thức
(4) Giải các hệ phương trình
a)
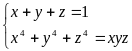
Giải:
Nhận
xét: Từ BĐT

Ta
suy ra:
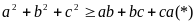
áp dụng liên tiếp BĐT (*) ta được

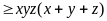
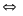
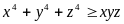
Đẳng
thức xẩy ra khi:
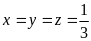
Vậy
hệ đã cho có nghiệm là: 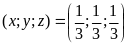
b)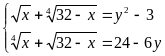
Giải:
ĐK:
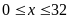
Hệ đã cho tương đương với
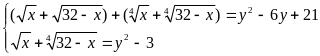
Theo bất đẳng thức BunhiaCốp xki ta có
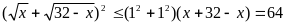
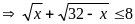
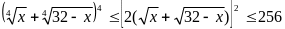

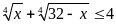
Suy
ra

Mặt
khác

Đẳng thức xẩy ra khi x= 16 và y=3 (t/m)
Vậy hệ đã có nghiệm là (x;y) = (16;3)
Chuyªn ®Ò 4:
BẤT ĐẲNG THỨC VÀ GIÁ TRỊ LỚN NHẤT, GIÁ TRỊ NHỎ NHẤT
A - CÁC PHƯƠNG PHÁP CHỨNG MINH BẤT ĐẲNG THỨC
Phương pháp đổi tương đương
Để chứng minh:
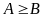
Ta biến đổi
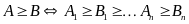 (đây
là bất đẳng thức đúng)
(đây
là bất đẳng thức đúng)
Hoặc từ bất đẳng thức đứng
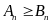 ,
ta biến đổi
,
ta biến đổi
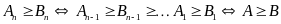
Ví dụ 1.1
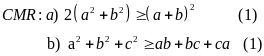
Giải

Do bất đẳng thức (2) đúng nên bất đẳng thức (1) được chứng minh.
b)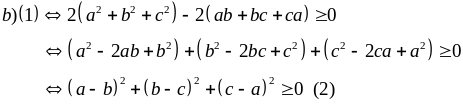
Bất đẳng thức (2) đúng suy ra điều phải chứng minh.
Ví dụ 1.2 CMR
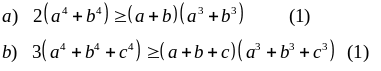
Giải
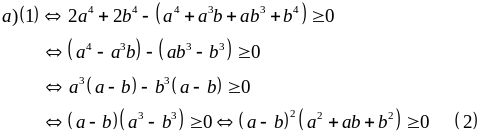
Do bất đẳng thức (2) đúng suy ra điều phải chứng minh.
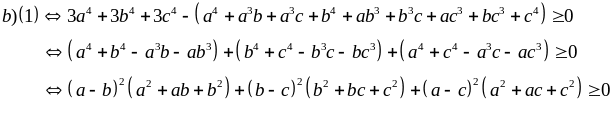
Ví dụ 1.3
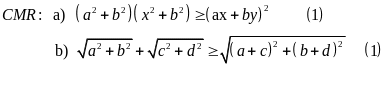
Giải
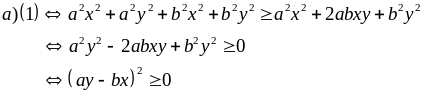
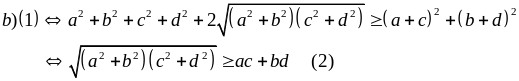
Nếu ac + bd < 0 thì (2) đúng
Nếu
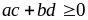 thì
thì

Ví dụ 1.4
Cho a, b, c > 0, chứng minh rằng:
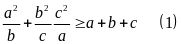
Giải
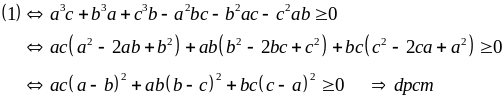
Ví dụ 1.5
Cho a, b, c > 0. CMR:
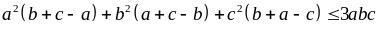 (1)
(1)
Giải

Suy ra ĐPCM.
Phương pháp biến đổi đồng nhất
Để chứng minh
BĐT: A
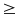 B. Ta biến đổi biểu thức A – B thành tổng các biểu
thức có giá trị không âm.
B. Ta biến đổi biểu thức A – B thành tổng các biểu
thức có giá trị không âm.
Ví dụ 2.1
Chứng minh rằng:

Giải
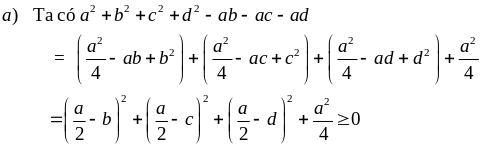
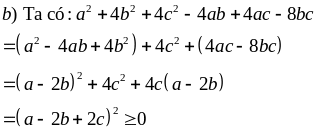
Ví dụ 2.2
Chứng minh rằng:
a)
 với a, b > 0
với a, b > 0
b)
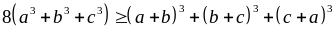 với a, b, c > 0
với a, b, c > 0
c)
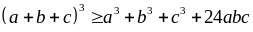 với a, b, c
với a, b, c
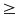 0
0
Giải
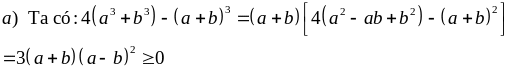
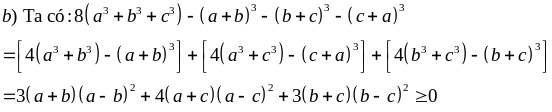

Ví dụ 2.3
Với a, b, c > 0. Chứng minh rằng:

Giải
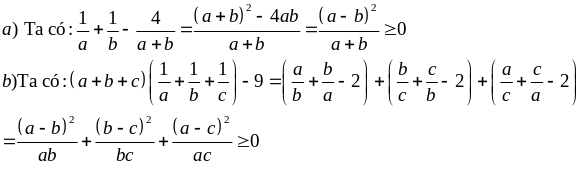
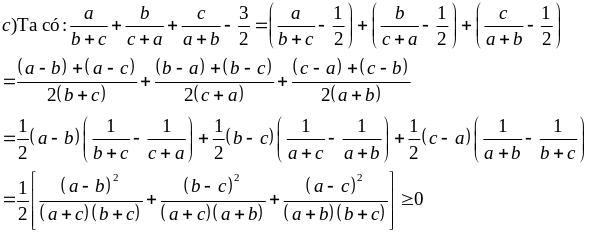
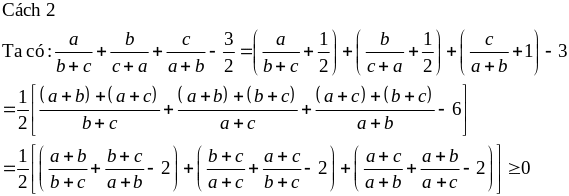
Ví dụ 2.4
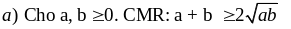 (Bất đẳng thức Cô – si)
(Bất đẳng thức Cô – si)
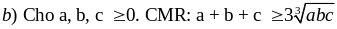 (Bất đẳng thức Cô – si)
(Bất đẳng thức Cô – si)
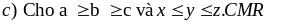
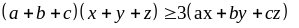 (Bất đẳng thức Trê bư sếp)
(Bất đẳng thức Trê bư sếp)
Giải
Ta có:

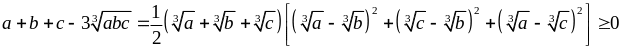
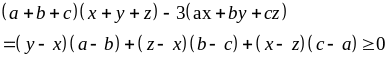
Ví dụ 2.5
Cho a, b, c > 0. Chứng minh:
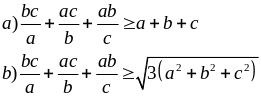
Giải

Ví dụ 2.6
Chứng minh rằng
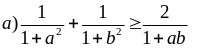 nếu
ab
nếu
ab
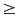 0
0
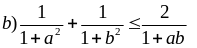 nếu
a2 +
b2 <
2
nếu
a2 +
b2 <
2
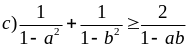 nếu -1 < a, b < 1
nếu -1 < a, b < 1
 nếu
a, b > 0
nếu
a, b > 0
Giải
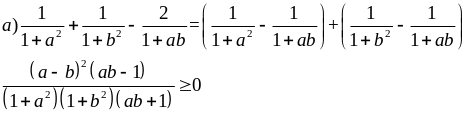
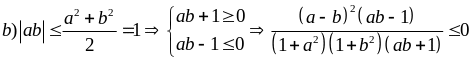
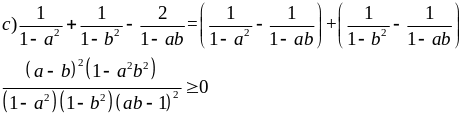

Phương pháp sử dung tính chất của bất đẳng thức
Cơ sở của phương pháp này là các tính chất của bất đẳng thức và một số bất đẳng thức cơ bản như:
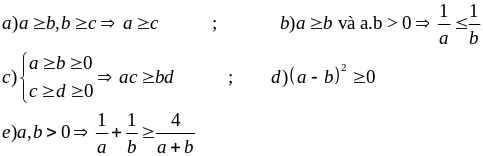
Ví dụ 3.1
Cho a + b > 1 . Chứng minh:
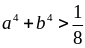
Giải
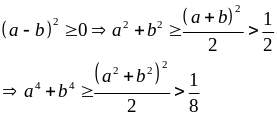
Ví dụ 3.2
Với a, b, c > 0. CMR
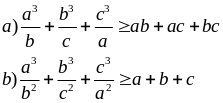
Giải

Ví dụ 3.3
Cho a, b, c > 0. CMR:
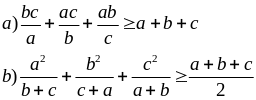
Giải
dễ dàng chứng minh

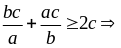 đpcm
đpcmdễ dàng chứng minh
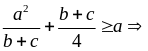 đpcm
đpcm
Ví dụ 3.4
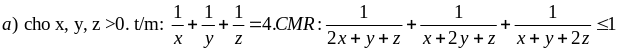
b) Cho a, b, c là độ dài ba cạnh của một tam giác. Chứng minh
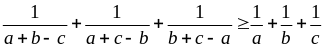
c) Cho a, b, c > 0 thỏa mãn: abc = ab + bc + ca. Chứng minh:
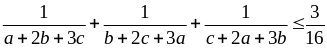
Giải
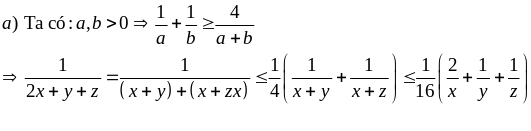
Tương tự:
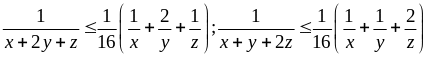
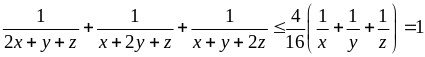
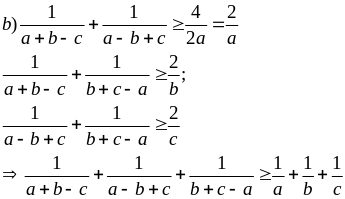

Ví dụ 3.5
Cho a, b, c > 0. Chứng minh rằng:
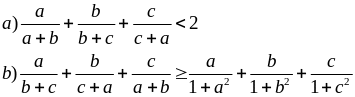
Giải
áp dụng BĐT:
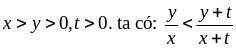
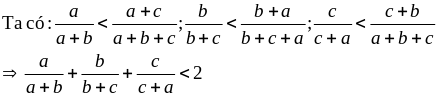
b)

suy ra điều phải chứng minh.
4)Phương pháp sử dung bất đẳng thức Co-si
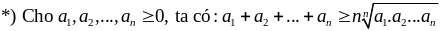
Dấu “=” xảy ra khi
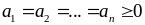
Ví dụ 4.1
Cho a, b > 0 thỏa
mãn ab = 1. CMR:
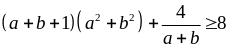
Giải
Áp dụng BĐT Cosi ta có
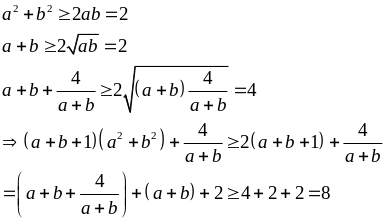
Ví dụ 4.2
Chứng minh rằng:
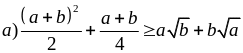 với a, b
với a, b
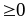
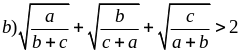 với
a,b,c > 0
với
a,b,c > 0
Giải
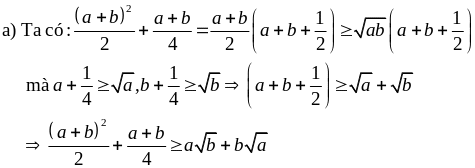
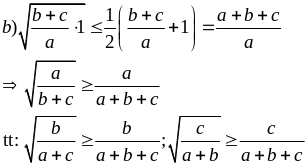
Cộng vế với vế
ta được:
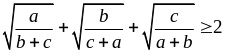
Dấu “=” xảy
ra khi
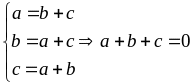 vô lí.
vô lí.
Vậy dấu “=” không xảy ra.
Ví dụ 4.3
Cho a, b, c > 0. Chứng minh rằng:
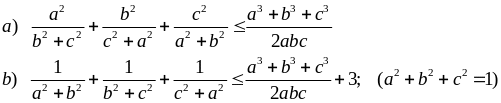
Giải
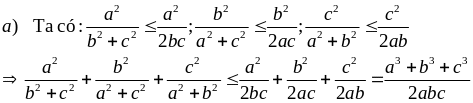
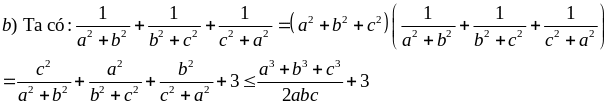
Ví dụ 4.4
Cho a, b, c > 0. Chứng minh rằng
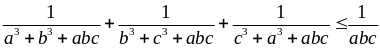
Giải
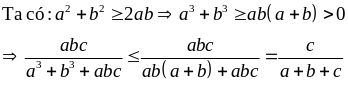
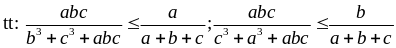
Cộng vế với vế suy ra điều phải chứng minh
Ví dụ 4.5
Cho a, b, c > 0 thỏa mãn a2 +b2 + c2 = 3. Chứng minh rằng

Gải

Suy ra điều phải chứng minh.
Ví dụ 4.6
Cho x, y, z > 0 thỏa mãn xyz = 1. Chứng minh
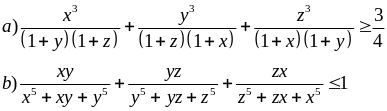
Giải
a) Áp dụng bất đẳng thức cô si ta có:
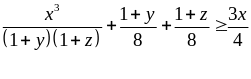
Tương tự suy ra
VT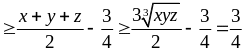
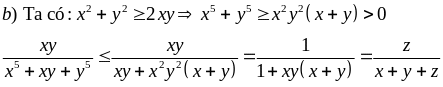
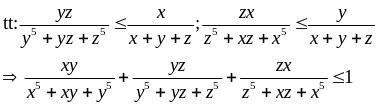
Ví dụ 4.7
Cho x, y, z > 0. Chứng minh

Giải
Áp dụng bất đẳng thức Cosi ta có:
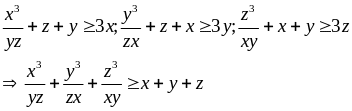
5)Phương pháp sử dung bất đẳng thức Bunhiacopski
*)
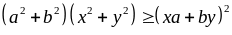 dấu “=” xảy ra khi
dấu “=” xảy ra khi
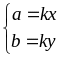
*)
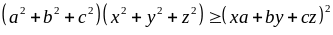 dấu “=” xảy ra khi
dấu “=” xảy ra khi
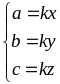
Tổng quát:
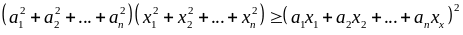 dấu “=” xảy ra khi ai = kxi
dấu “=” xảy ra khi ai = kxi
Ví dụ 5.1
Cho a, b > 0. Chứng minh
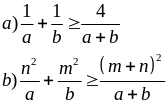
Giải
a) Áp dụng bất đẳng thức Bunhiacopski ta có:

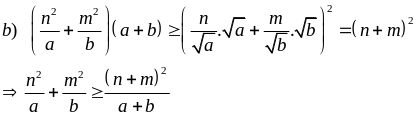
Tổng quát:
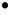 Cho
Cho
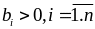 thì
thì
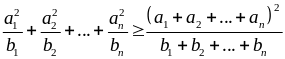 (1)
(1)
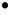 Với
Với
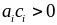 với
với
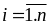 thì
thì
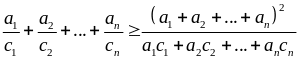 (2)
(2)
Thật vậy:
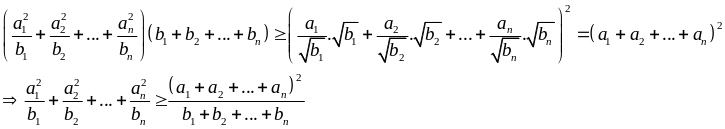 đặt
aici = bi > 0 thay vào (1) được
(2)
đặt
aici = bi > 0 thay vào (1) được
(2)
Ví dụ 5.2
Cho a,b,c là các số thực dương. Chứng minh
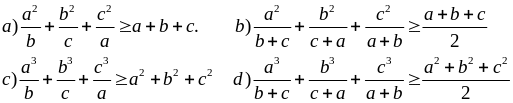
Giải
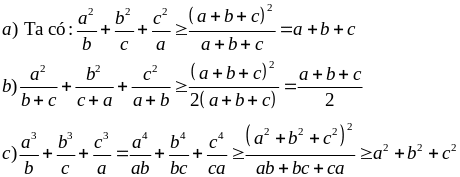
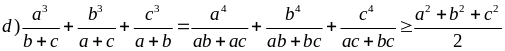
Ví dụ 5.3
Cho
a, b, c > 0. Chứng minh:
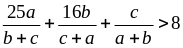
Giải
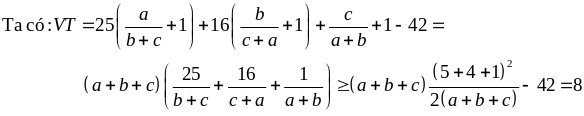
Dấu “=” xảy
ra khi
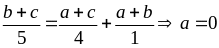 vô lí suy ra điều phải chứng minh.
vô lí suy ra điều phải chứng minh.
Ví dụ 5.4
Cho
x, y, z > 0. Chứng minh:
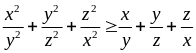
Giải
Áp dụng bất đẳng thức Bunhiacopki ta có

B – CÁC PHƯƠNG PHÁP TÌM GIÁ TRỊ LỚN NHẤT, GIÁ TRỊ NHỎ NHẤT
Cho biểu thức f(x,y…)
Ta nói M là giá trị lớn nhất của f(x,y…) kí hiệu maxf(x,y…) = M, nếu hai điều kiện sau được thỏa mãn:
Với mọi x,y… để f(x,y…) xá định thì f(x,y…)
 M
MTồn tại x0, y0… sao cho f(x0,y0…) = M
Ta nói m là giá trị nhỏ nhất của f(x,y…) kí hiệu minf(x,y…) = m, nếu hai điều kiện sau được thỏa mãn:
Với mọi x,y… để f(x,y…) xá định thì f(x,y…)
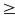 m
mTồn tại x0, y0… sao cho f(x0,y0…) = m
I) TÌM GTLN, GTNN CỦA ĐA THỨC BẬC HAI
1) Đa thức bậc hai một biến
Ví dụ 1.1
Tìm GTNN của A = 3x2 – 4x + 1
Tìm GTLN của B = - 5x2 + 6x – 2
Tìm GTNN của C = (x – 2)2 + (x – 3)2
Cho tam thức bậc hai P = ax2 + bx + c
Tìm GTNN của P nếu a > 0
Tìm GTNN của P nếu a > 0
Giải
A =
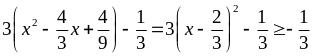 .
Vậy minA=
.
Vậy minA=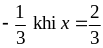
B =
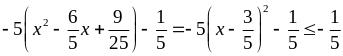 .
Vậy maxB =
.
Vậy maxB =

C =
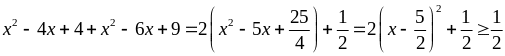 .
.
Vậy maxC =
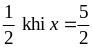
Ta có: P =
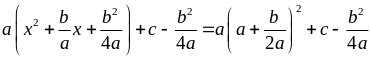
Nếu a > 0 thì P
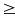
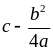 . Vậy minP =
. Vậy minP =
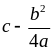 khi
khi
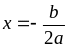
Nếu a < 0 thì P
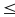
 .
Vậy maxP =
.
Vậy maxP =
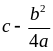 khi
khi
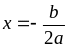
Ví dụ 1.2
a) Tìm GTNN của M = x2 – 3x + 1 với
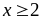
b) Tìm GTLN của N = x2
– 5x + 1 với
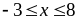
Giải
a) M =
 .
Vậy minM = -1 khi x = 2
.
Vậy minM = -1 khi x = 2
b) N =
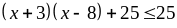 .
Vậy maxN = 25 khi x = -3, x = 8
.
Vậy maxN = 25 khi x = -3, x = 8
2. Đa thức bậc hai hai biến
a) Đa thức bậc hai hai biến có điều kiện
Ví dụ 2a.1
Cho x + y = 1. Tìm GTLN của P = 3xy – 4
Cho x – 2y = 2. Tìm GTNN của Q = x2 + 2y2 – x + 3y
Giải
a)
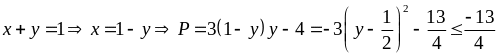
Vậy maxP =
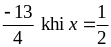
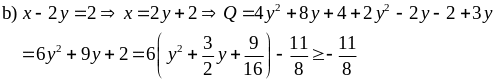
Vậy minQ =
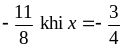
Ví dụ 2a.2
Tìm GTLN của của P = xy vói x, y thỏa mãn
a)
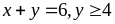
b)
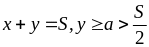
a)
 .
Vậy maxP = 8 khi x = 2, y = 4
.
Vậy maxP = 8 khi x = 2, y = 4
b)
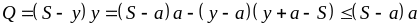 .
.
Vậy maxQ = (S – a)a khi x = S – a, y = a
b) Đa thức bậc hai hai biến
Cho đa thức: P(x,y) = ax2 + bxy + cy2
+ dx + ey + h (1), với a,b,c
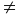 0
0
Ta thường đưa P(x, y) về dạng
P(x, y) = mF2(x, y) + nG2(y) + k (2)
P(x, y) = mH2(x, y) + nG2(x) + k (3)
Trong đó G(y), H(x) là hai biểu thức bậc nhất một ẩn, H(x, y) là biểu thức bậc nhất hai ẩn.
Chẳng hạn nếu ta biến đổi (1) về (2)
với a, (4ac – b2)
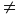 0
0
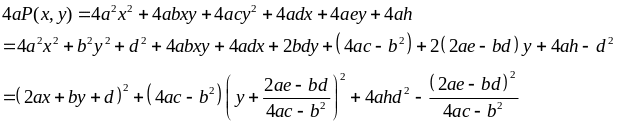
(Tương tự nhân hai vế của (1) với 4c để chuyển về (3))
Ví dụ 3.1
Tìm GTNN của P = x2 + y2 + xy + x + y
Tìm GTLN của Q = -5x2 – 2xy – 2y2 + 14x + 10y – 1
Giải
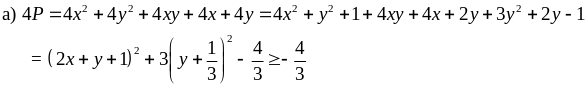
Vậy minP =
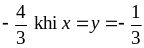
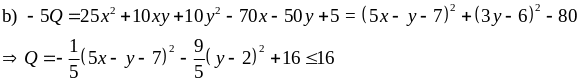
Vậy maxQ = 16 khi x = 1, y = 2
Ví dụ 3.2
Tìm cặp số (x, y) với y nhỏ nhất thỏa mãn: x2 + 5y2 + 2y – 4xy – 3 = 0 (*)
Giải
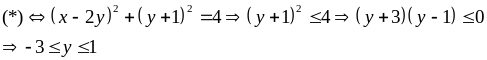
Vậy miny = -3 khi x = -6. Vậy ccawpj số (x, y) = (-6; -3)
Ví dụ 3.3
Cho x, y liên hệ với nhau bởi hệ thức x2 + 2xy + 7(x + y) + 7y2 + 10 = 0 (**).
Hãy tìm GTLN, GTNN của S = x + y + 1.
Giải
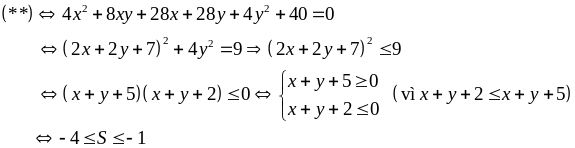
Vậy minS = -4 khi x = -5, y = 0. maxS = -1 khi x = -2, y = 0.
II. PHƯƠNG PHÁP MIỀN GIÁ TRỊ
Ví dụ 1
Tìm GTLN, GTNN của A =

Giải
Biểu thức A nhận giá trị a khi phương trình sau đây có a nghiệm
a =

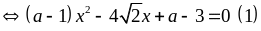
Nếu a = 1 thì phương trình (1) có nghiệm x =
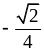
Nếu a
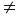 1 thì phương trình (1) có nghiệm khi –a2 + 4a +5
1 thì phương trình (1) có nghiệm khi –a2 + 4a +5
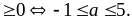
Vậy minA = -1 khi

maxA = 5 khi
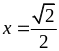
Ví dụ 2
Tìm GTLN, GTNN của biểu thức B =
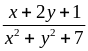
Giải
Biểu thức B nhận giá trị b khi phương trình sau có nghiệm
b =
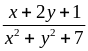
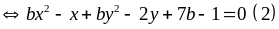
Trong đó x là ẩn, y là tham số và b là tham số có điều kiện
Nếu b = 0
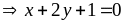
Nếu b
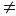 để (2) có nghiệm x khi 1 – 4b(by2 – 2y + 7b -1)
để (2) có nghiệm x khi 1 – 4b(by2 – 2y + 7b -1)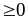 (3)
(3)
Coi (3) là bất phương trình ẩn y. BPT này xảy ra với mọi giá trị của y khi
16b2 + 4b2(-28b2 + 4b + 1)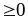
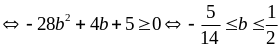
Vậy minB =
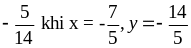
maxB =
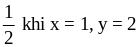
III. PHƯƠNG PHÁP SỬ DỤNG BẤT ĐẲNG THỨC
Sử dụng bất đẳng thức Cô-si
Ví dụ 1.1
Tìm GTLN, GTNN của A =
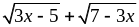 với
với
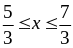
Giải
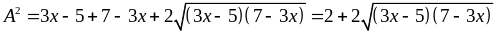
Vậy A2
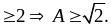 Vậy minA =
Vậy minA =

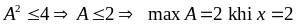
(Biểu thức được cho dưới dạng tổng hai căn thức. Hai biểu thức lấy căn có tổng là hằng số)
Ví dụ 1.2
Cho x, y > 0 thỏa mãn x + y
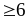 .
Hãy tìm GTNN của P =
.
Hãy tìm GTNN của P =
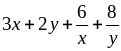
Giải
Ta có:
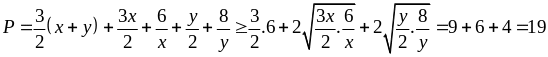
Vậy minP = 19 khi x = 2, y = 4.
Ví dụ 1.3
Tìm GTLN của biểu thức M =
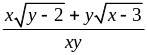 với
với
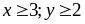
Giải
To có:

Theo bất đẳng thức Cô – si ta có:
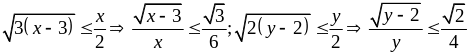

Ví dụ 1.4
Cho x, y, z > 0 thỏa mãn:
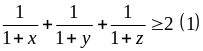 .
Tìm TGLN của P = xyz
.
Tìm TGLN của P = xyz
Giải
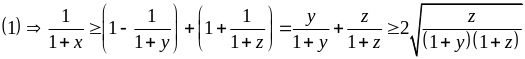
Tương tự:
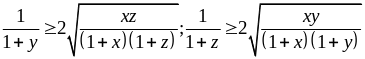
Nhân vế với vế của ba BĐT trên
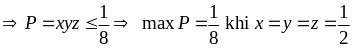
Ví dụ 1.5
Cho 0 < x < 1, Tìm GTNN của Q =
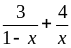
Giải
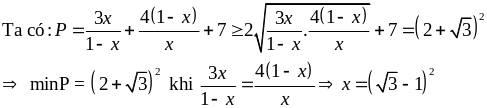
(Đặt P =
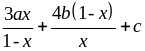 đồng nhất hệ số suy ra a = b = 1; c = 7)
đồng nhất hệ số suy ra a = b = 1; c = 7)
Ví dụ 1.6
Cho x, y, z, t > 0. Tìm GTNN của biểu thức.
M
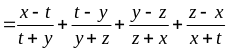
Giải
Áp dụng bất đẳng thức Cô-si ta có:
 với a, b > 0.
với a, b > 0.
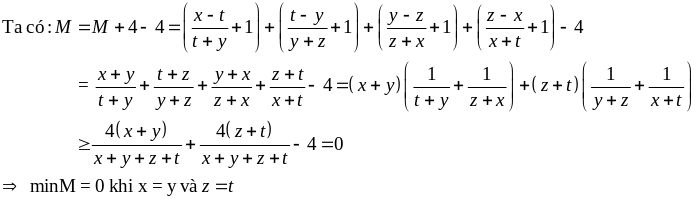 2.
Sử dụng BĐT Bunhiacopski (BCS)
2.
Sử dụng BĐT Bunhiacopski (BCS)
Ví dụ 2.1
Cho x, y, z thỏa mãn: xy + yz + zx =1. Tìm GTNN của biểu thức
A = x4 + y4 + z4
Giải
Áp dụng BĐT BCS ta có
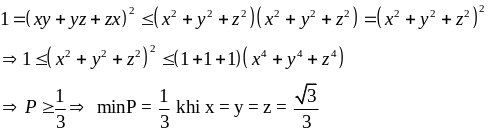
Ví dụ 2.2
Tìm GTNN của P =
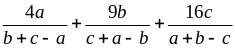 trong đó a, b, c là độ dài ba cạnh của một tam giác.
trong đó a, b, c là độ dài ba cạnh của một tam giác.
Giải
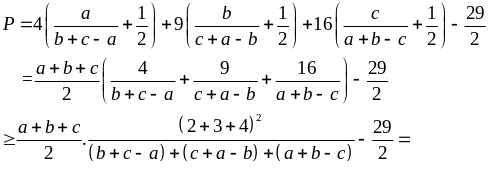
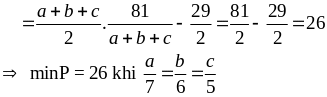
Ví dụ 2.3
Tìm giá trị nhỏ nhất của Q = \f(a,1+b-a + \f(b,1+c-b + \f(c,1+a-c
trong đó a, b, c > 0 thỏa mãn a + b + c = 1
Giải
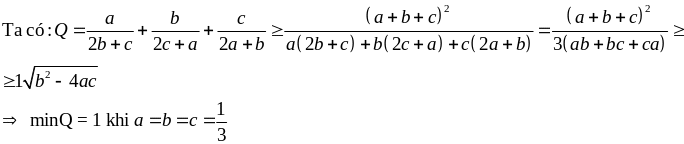
Ví dụ 2.4
Cho a, b, c > 0 thỏa mãn a + b + c = 1. Tìm GTNN của
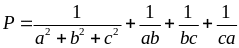
Giải
Chuyên đề 5: TỨ GIÁC NỘI TIẾP
I -CÁC DẤU HIỆU NHẬN BIẾT TỨ GIÁC NỘI TIẾP
1- Tổng hai góc đối bằng 1800
2- Hai góc liên tiếp cùng nhìn một cạnh dưới hai góc bằng nhau.
3- Nếu hai cạnh đối diện cuả giác ABCD cắt nhau tại M thỏa mãn:
MA.MB =MC.MD ; hoặc hai đường chéo cắt nhau tại O thỏa mãn
OA.OC = OB.OD thì ABCD là tứ giác nội tiếp
4- Sử dụng định lý Ptôlêmê
II- CÁC VÍ DỤ
Ví dụ1: Cho đường tròn tâm O và một điểm C ở ngoài đường tròn đó. Từ C kẻ hai tiếp tuyến CE ; CF ( E và F là các tiếp điểm) và cát tuyến CMN ( N nằm giữa C và M ) tới đường tròn.Đường thẳng CO cắt đường tròn tại hai điểm A và B. Gọi I là giao điểm của AB với EF. Chứng minh rằng:
a, Bốn điểm O, I, M, N cùng thuộc một đường tròn
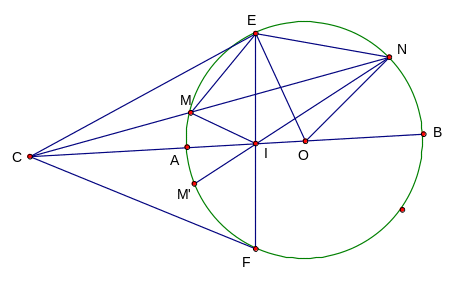 b,
=
b,
=
Giải
a, Do CE là tiếp tuyến của (O) nên:
= (Cùng chắn )
CEM ~ CNE .
\f(CE,CM = \f(CN,CE
CM.CN =CE2
Mặt Khác , do CE; CF là các tiếp tuyến của (O) nên
AB EF tại I vì vậy trong tam giác vuông CEO đường cao EI ta có:
CE2 = CI.CO
Từ (1) và (2) suy ra CM.CN = CI.CO => \f(CM,CI = \f(CO,CN
CMI ~ CON
=
Tứ giác OIMN nội tiếp
b Kéo dài NI cắt đường tròn tại M’.
Do tứ giác IONM nội tiếp nên :
= = \f(1,2 sđ
=> = . Do đó:
= =
Ví Dụ 2
Cho tam giác ABC có = 450 ; BC =a nội tiếp trong đường tròn tâm O; các đường cao BB’ và CC’. Gọi O’ là điểm đối xứng của O qua đường thẳng B’C’.
Chứng minh rằng A; B’; C’; O’ cùng thuộc một đường tròn
Tính B’C’ theo a.
L ời
giải
ời
giải
Do O là tâm đường tròn ngoại tiếp tam giác ABC nên
= 2 =900
Từ đó suy ra các điểm O; B’; C’
Cùng thuộc đường tròn đường kính BC.Xét tứ giác nội tiếp CC’OB’ có :
= 1800 -
= 1800 - ( 900 - ) =1350.
Mà O’ đối xứng với O qua B’C’ nên:
= = 1350 =1800 -
Hay tứ giác AC’O’B’ nội tiếp.
Do = 450 nên BB’A vuông cân tại B’
Vì vậy B’ nằm trên đường trung trực của đoạn AB hay B’O AB
C’OB’C là hình thang cân nên B’C’ =OC
Mặt khác BOC
vuông cân nên: B’C’ =OC =

III bµi tËp ¸p dông
Bài tập 1:
Cho tứ giác ABCD nội tiế đường tròn đường kính AD. Hai đường chéo AC và BD cắt nhau tại E. Vẽ EF vuông góc với AD. Chứng minh:
a/ Tứ giác EBEF, tứ giác DCEF nội tiếp.
b/ CA là phân giác của
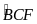
c/ Gọi M là trung điểm của DE. Chứng minh tứ giác BCMF nội tiếp.
Bài tập 2:
Tứ giác ABCD nội tiếp đường tròn đường kính AD. Hai đường chéo AC, BD cắt nhau tại E. Hình chiếu vuông góc của E trên AD là F. Đường thẳng CF cắt đường tròn tại điểm thứ hai là M. Giao điểm của BD và CF là N. Chứng minh:
a/ CEFD là tứ giác nội tiếp
b/ Tia FA là phân giác của góc BFM
c/ BE.DN = EN.BD.
Bài tập 3:
Cho tam giác ABC vuông ở A và một điểm D nằm giữa A và B. Đường tròn đường kính BD cắt BC tại E. Các đường thẳng CD, AE lần lượt cắt đường tròn tại các điểm thứ hai F, G. Chứng minh:
a/ Tam giác ABC đồng dạng với tam giác EBD
b/ Tứ giác ADEC và AFBC nội tiếp được một đường tròn
c/ AC song song với FG
d/ Các đường thẳng AC, DE, BF đồng quy.
Bài tập 4:
Cho tam giác ABC có
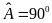 ;
AB > AC, và một điểm M nằm trên đoạn AC ( M không
trùng với A và C ). Gọi N và D lần lượt là giao điểm
thứ hai của BC và MB với đường tròn đường kính MC;
gọi S là giao điểm thứ hai giữa AD với đường tròn
đường kính MC; T là giao điểm của MN và AB. Chứng minh:
;
AB > AC, và một điểm M nằm trên đoạn AC ( M không
trùng với A và C ). Gọi N và D lần lượt là giao điểm
thứ hai của BC và MB với đường tròn đường kính MC;
gọi S là giao điểm thứ hai giữa AD với đường tròn
đường kính MC; T là giao điểm của MN và AB. Chứng minh:
a/ Bốn điểm A, M, N, B cùng thuộc một đường tròn
b/ CM là phân giác của góc BCS.
c/
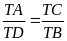
Bài tập 5:
Cho đường tròn (O) và điểm A nằm ngoài đường tròn. Qua A dựng hai tiếp tuyến AM và AN với đường tròn ( M, N là các tiếp điểm ) và một cact tuyến bất kỳ cắt đường tròn tại P, Q. Gọi L là trung điểm của PQ.
a/ Chứng minh 5 điểm: O, L, M, A, N cùng thuộc một đường tròn
b/ Chứng minh LA là phân giác của góc MLN
c/ Gọi I là giao điểm của MN và LA.
Chứng minh: MA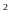 =
AI. AL
=
AI. AL
d/ Gọi K là giao điểm của ML với (O). Chứng minh rằng: KN // AQ
e/ Chứng minh tam giác KLN cân.
Bài tập 6:
Cho đường tròn (O;R) tiếp xúc với đường thẳng d tại A. Trên d lấy điểm H không trùng với điểm A và AH < R. Qua H kẻ đường thẳng vuông góc với d, đường thẳng này cắt đường tròn tại hai điểm E và B ( E nằm giữa B và H )
a/ Chứng minh: góc ABE bằng góc EAH và tam giác AHB đồng dạng với tam giác EAH.
b/ Lấy điểm C trên d sao cho H lá trung điểm của đoạn AC, đường thẳng CE cắt AB tại K. Chứng minh: AHEK là tứ giác nội tiếp
c/ Xác định vị trí của
điểm H để AB = R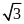
Bài tập 7:
Từ điểm P nằm ngoài đường tròn (O), kẻ hai tiếp tuyến PM và PN với đường tròn (O) ( M, N là tiếp điểm ). Đường thẳng đi qua điểm P cắt đường tròn (O) tại hai điểm E và F. Đường thẳng qua O song song với MP cắt PN tại Q. Gọi H là trung điểm của đoạn EF. Chứng minh:
a/ Tứ giác PMON nội tiếp đường tròn
b/ Các điểm P, N, O, H cùng nằm trên một đường tròn
c/ Tam giác PQO cân
d/ MP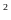 =
PE. PF
=
PE. PF
e/ =
Bài tập 8:
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O). Các đường cao AD, BE, CF cắt nhau tại H và cắt đường tròn (O) lần lượt tại M, N, P.
Chứng minh rằng:
a/ Các tứ giác AEHF, BFHD nội tiếp.
b/ Bốn điểm B, C, E, F cùng nằm trên một đường tròn.
c/ AE. AC = AH. AD và AD. BC = BE. AC
d/ H và M đối xứng nhau qua BC
e/ Xác định tâm đường tròn nội tiếp tam giác DEF.
Bài tập 9:
Cho tam giác ABC không cân, đường cao AH, nội tiếp trong đường tròn tâm O. Gọi E, F thứ tự là hình chiếu của B, C lên đường kính AD của đường tròn (O) và M, N thứ tự là trung điểm của BC, AB. Chứng minh:
a/ Bốn điểm A, B, H, E cùng nằm trên một đường tròn tâm N và HE // CD.
b/ M là tâm đường tròn ngoại tiếp tam giác HEF.
Bài tập 10:
Cho đường tròn (O) và điểm A ở bên ngoài đường tròn. Vẽ các tiếp tuyến AB, AC và cát tuyến ADE với đường tròn ( B và C là các tiếp điểm ). Gọi H là trung điểm của DE.
a/ CMR: A, B,H, O, C cùng thuộc một đường tròn. Xác định tâm của đường tròn này.
b/ Chứng minh: HA là tia phân giác .
c/ Gọi I là giao điểm của BC và DE. Chứng
minh: AB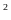 =
AI.AH
=
AI.AH
d/ BH cắt (O) tại K. Chứng minh: AE // CK.
Bài tập 11:
Từ một điểm S ở ngoài đường tròn (O) vẽ hai tiếp tuyến SA, SB và cát tuyến SCD của đường tròn đó.
a/ Gọi E là trung điểm của dây CD. Chứng minh 5 điểm S, A, E, O, B cùng thuộc một đường tròn.
b/ Nếu SA = AO thì SAOB là hình gì? Tại sao?.
c/ CMR: AC.BD = BC.DA =

Bài tập 12:
Trên đường thẳng d lấy 3 điểm A, B, C theo thứ tự đó. Trên nửa mặt phẳng bờ d kẻ hai tia Ax, By cùng vuông góc với d. Trên tia Ax lấy I. Tia vuông góc với CI tại C cắt By tại K. Đường tròn đường kính IC cắt IK tại P.
a/ Chứng minh tứ giác CBPK nội tiếp được đường tròn
b/ Chứng minh: AI. BK = AC. CB
c/ Giả sử A, B, I cố định hãy xác định vị trí điểm C sao cho diện tích hình thang vuông ABKI lớn nhất.
Bài tập 13:
Cho tam giác đều ABC nội tiếp đường tròn (O). M là điểm di động trên cung nhỏ BC. Trên đoạn thẳng MA lấy điểm D sao cho MD = MC.
a/ Chứng minh:

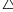 DMC
đều
DMC
đều
b/ Chứng minh: MB + MC = MA
c/ Chứng minh tứ giác ADOC nội tiếp được.
d/ Khi M di động trên cung nhỏ BC thì D di động trên đường cố định nào?.
Bài tập 14:
Cho đường tròn (O;R), từ một điểm A trên O kẻ tiếp
tuyến d với O. Trên đường thẳng d lấy điểm M bất kỳ
( M khác A ) kẻ cát tuyến MNP và gọi K là trung điểm của
NP, kẻ tiếp tuyến MB ( B là tiếp điểm ). Kẻ AC
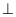 MB, BD
MB, BD
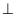 MA, gọi H là giao điểm của AC và BD, I là giao điểm của
OM và AB.
MA, gọi H là giao điểm của AC và BD, I là giao điểm của
OM và AB.
a/ Chứng minh tứ giác AMBO nội tiếp
b/ Chứng minh năm điểm O, K, A, M, B cùng nằm trên một đường tròn.
c/ Chứng minh OI. OM = R ;
OI. IM = IA
;
OI. IM = IA
d/ Chứng minh OAHB là hình thoi
e/ chứng minh ba điểm O, H, M thẳng hàng
f/ Tìm quỹ tích của điểm H khi M di chuyển trên đường thẳng d.
Bài tập 15:
Cho hình thang cân ABCD ( AB > CD; AB // CD ) nội tiếp trong đường tròn (O). Tiếp tuyến với đường tròn (O) tại A và D cắt nhau tại E. Gọi I là giao điểm của hai đường chéo AC và BD.
a/ Chứng minh tứ giác AEDI nội tiếp.
b/ Chứng minh AB // EI
c/ Đường thẳng EI cắt cạnh bên AD và BC của hình thang tương ứng ở R và S. Chứng minh: * I là trung điểm của RS
*
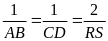
Bài tập 16:
Cho ba điểm M, N, P thẳng hàng theo thứ tự đó. Một đường tròn (O) thay đổi đi qua hai điểm M, N. Từ P kẻ các tiếp tuyến PT, PQ với đường tròn (O).
a/ Chứng minh: PT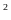 = PM. PN. Từ đó suy ra khi (O) thay đổi vẫn qua M, N thì T,
Q thuộc một đường tròn cố định.
= PM. PN. Từ đó suy ra khi (O) thay đổi vẫn qua M, N thì T,
Q thuộc một đường tròn cố định.
b/ Gọi giao điểm của TQ với PO, PM là I và J. K là trung điểm của MN. Chứng minh các tứ giác OKTP, OKIJ nội tiếp.
c/ CMR: Khi đường tròn (O) thay đổi vẫn đi qua M, N thì TQ luôn đi qua điểm cố định.
d/ Cho MN = NP = a. Tìm vị trí của tâm O để =600
Bài tập 17:
Cho tam giác ABC vuông ở A. Trên AC lấy điểm M (M
 A
và C). Vẽ đường tròn đường kính MC. Gọi T là giao
điểm thứ hai của cạnh BC với đường tròn. Nối BM kéo
dài cắt đường tròn tại điểm thứ hai là D. Đường
thẳng AD cắt đường tròn (O) tại điểm thứ hai S. Chứng
minh:
A
và C). Vẽ đường tròn đường kính MC. Gọi T là giao
điểm thứ hai của cạnh BC với đường tròn. Nối BM kéo
dài cắt đường tròn tại điểm thứ hai là D. Đường
thẳng AD cắt đường tròn (O) tại điểm thứ hai S. Chứng
minh:
a/ Tứ giác ABTM nội tiếp.
b/ Khi M chuyển động trên AC thì có số đo không đổi
c/ AB // ST.
Bài tập 18:
Cho đường tròn (O), đường kính AB cố định, điểm I nằm giữa A và O sao cho AI = 2/3AO. Kẻ dây MN vuông góc với AB tại I, gọi C là điểm tùy ý thuộc cung lớn MN sao cho C không trùng với M, N và B. Nối AC cắt MN tại E.
a/ Chứng minh tứ giác IECB nội tiếp.
b/ Chứng minh: AME ~ ACM
c/ Chứng minh AM = AE. AC
= AE. AC
d/ chứng minh AE. AC – AI. IB = AI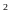
e/ Hãy xác định vị trí của C sao cho khoảng cách từ N đến tâm đường tròn ngoại tiếp tam giác CME là nhỏ nhất.
Bài tập 19:
Cho điểm A bên ngoài đường tròn (O; R). Từ A vẽ tiếp tuyến AB, AC và cát tuyến ADE đến đường tròn (O). Gọi H là trung điểm của DE.
a/ Chứng minh năm điểm: A, B, H, O, C cùng nằm trên một đường tròn.
b/ Chứng minh AH là tia phân giác của
c/ DE cắt BC tại I. Chứng minh: AB = AI. AH
= AI. AH
d/ Cho AB = R và OH =
và OH =
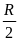 .
Tính HI theo R.
.
Tính HI theo R.
Bài tập 20:
Cho đường tròn (O) đường kính AB = 2R.
Đường thẳng (d) tiếp xúc với đường tròn (O) tại A.
M và Q là hai điểm trên (d) sao cho M
 A,
M
A,
M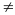 Q,
Q
Q,
Q
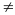 A.
Các đường thẳng BM và BQ lần lượt cắt đường tròn
(O) tại các điểm thứ hai là N và P. Chứng minh:
A.
Các đường thẳng BM và BQ lần lượt cắt đường tròn
(O) tại các điểm thứ hai là N và P. Chứng minh:
a/ Tích BN. BM không đổi
b/ Tứ giác MNPQ nội tiếp
c/ Bất đẳng thức: BN + BP + BM + BQ > 8R.
Chuyên đề 6: ĐƯỜNG ĐI QUA ĐIỂM CỐ ĐỊNH
Trong các đề thi học sinh giỏi, thi vào trường chuyên, lớp chọn thường có những bài toán liên quan đến tìm điểm cố định, chứng minh đường đi qua điểm cố định. Thực tế cho thấy đây là bài toán khó, học sinh thường khó khăn khi gặp phải bài toán dạng này.
Bài toán “Đường đi qua điểm cố định” đòi hỏi HS phải có kĩ năng nhất định cộng với sự đầu tư suy nghĩ, tìm tòi nhưng đặc biệt phải có phương pháp làm bài.
Tìm hiểu nội dung bài toán
Dự đoán điểm cố định
Tìm tòi hướng giải
Trình bày lời giải
Tìm hiểu bài toán:
Yếu tố cố định.( điểm, đường … )
Yếu tố chuyển động.( điểm, đường … )
Yếu tố không đổi.( độ dài đoạn, độ lớn góc … )
Quan hệ không đổi ( Song song, vuông góc, thẳng hàng … )
Khâu tìm hiểu nội dung bài toán là rất quan trọng. Nó định hướng cho các thao tác tiếp theo. Trong khâu này đòi hỏi học sinh phải có trình độ phân tích bài toán, khả năng phán đoán tốt. Tuỳ thuộc vào khả năng của từng đối tượng học sinh mà giáo viên có thể đưa ra hệ thống câu hỏi dẫn dắt thích hợp nhằm giúp học sinh tìm hiểu tốt nội dung bài toán. Cần xác định rõ yếu tố cố định, không đổi, các quan hệ không đổi và các yếu tố thay đổi, tìm mối quan hệ giữa các yếu tố đó.
Dự đoán điểm cố định:
Dựa vào những vị trí đặc biệt của yếu tố chuyển động để dự đoán điểm cố định. Thông thường ta tìm một hoặc hai vị trí đặc biệt cộng thêm với các đặc điểm bất biến khác như tính chất đối xứng, song song, thẳng hàng … để dự đoán điểm cố định
Tìm tòi hướng giải
T ừ
việc dự đoán điểm cố định tìm mối quan hệ giữa
điểm đó với các yếu tố chuyển động, yếu tố cố
định và yếu tố không đổi. Thông thường để
chứng tỏ một điểm là cố định ta chỉ ra điểm đó
thuộc hai đường cố định, thuộc một đường cố
định và thoả mãn một điều kiện (thuộc một tia và
cách gốc một đoạn không đổi, thuộc một đường
tròn và là mút của một cung không đổi ...) thông thường
lời giải của một bài toán thường được cắt
bỏ những suy nghĩ bên trong nó chính vì vậy ta thường
có cảm giác lời giải có cái gì đó thiếu tự nhiên,
không có tính thuyết phục chính vì vậy khi trình bày ta
cố gắng làm cho lời giải mang tính tự nhiên hơn, có
giá trị về việc rèn luyện tư duy cho học sinh.
ừ
việc dự đoán điểm cố định tìm mối quan hệ giữa
điểm đó với các yếu tố chuyển động, yếu tố cố
định và yếu tố không đổi. Thông thường để
chứng tỏ một điểm là cố định ta chỉ ra điểm đó
thuộc hai đường cố định, thuộc một đường cố
định và thoả mãn một điều kiện (thuộc một tia và
cách gốc một đoạn không đổi, thuộc một đường
tròn và là mút của một cung không đổi ...) thông thường
lời giải của một bài toán thường được cắt
bỏ những suy nghĩ bên trong nó chính vì vậy ta thường
có cảm giác lời giải có cái gì đó thiếu tự nhiên,
không có tính thuyết phục chính vì vậy khi trình bày ta
cố gắng làm cho lời giải mang tính tự nhiên hơn, có
giá trị về việc rèn luyện tư duy cho học sinh.
MỘT VÀI VÍ DỤ:
Bài
1: Cho ba điểm A, C, B thẳng
hành theo thứ tự đó. Vẽ tia Cx vuông góc với AB.Trên
tia Cx lấy hai điểm D, E sao cho
 .
Đường tròn ngoại tiếp tam giác ADC cắt đường tròn
ngoại tiếp tam giác BEC tại H khác C. Chứng minh rằng:
Đường thẳng HC luôn đi qua một điểm cố định khi C
di chuyển trên đoạn thẳng AB.
.
Đường tròn ngoại tiếp tam giác ADC cắt đường tròn
ngoại tiếp tam giác BEC tại H khác C. Chứng minh rằng:
Đường thẳng HC luôn đi qua một điểm cố định khi C
di chuyển trên đoạn thẳng AB.
Tìm hiểu đề bài:
* Yếu tố cố định: Đoạn AB
* Yếu tố không đổi:
+ Góc BEC = 300, Góc ADB = 600 do đó sđ cung BC, cung CA không đổi
+ B, D, H thẳng hàng; E, H, A thẳng hàng
Dự đoán điểm cố định:
khi C trùng B thì (d) tạo với BA một góc 600 => điểm cố định thuộc tia By tạo với tia BA một góc 600
khi C trùng A thì (d) tạo với AB một góc 300 => điểm cố định thuộc tia Az tạo với tia AB một góc 300
By và Az cắt nhau tại M thì M là điểm cố định? Nhận thấy M nhìn AB cố định dưới 900 => M thuộc đường tròn đường kính AB.
Tìm hướng chứng minh:
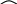 M
thuộc đường tròn đường kính AB cố định do đó cần
chứng minh sđ cung AM không đổi thật vậy:
M
thuộc đường tròn đường kính AB cố định do đó cần
chứng minh sđ cung AM không đổi thật vậy:
sđ cung AM = 2sđGóc MCA=2sđGóc CHA =2sđGóc CDA = 1200
Lời giải:

 Ta
có
Ta
có
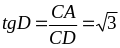 => Góc D=600
=> Góc D=600
có Góc CHA = Góc CDA = 600
 G/s
đường tròn đường kính AB cắt CH tại M
G/s
đường tròn đường kính AB cắt CH tại M
ta có Góc MHA= 600 => sđ cung MA không đổi
lại có đường tròn đường kính AB cố định vậy:
M cố định do đó CH luôn qua M cố định.
Bài 2: Cho đường tròn (O) và đường thẳng (d) nằm ngoài đường tròn. I là điểm di động trên (d). Đường tròn đường kính OI cắt (O) tại M, N. Chứng minh đường tròn đường kính OI luôn đi qua một điểm cố định khác O và đường thẳng MN luôn đi qua một điểm cố định.
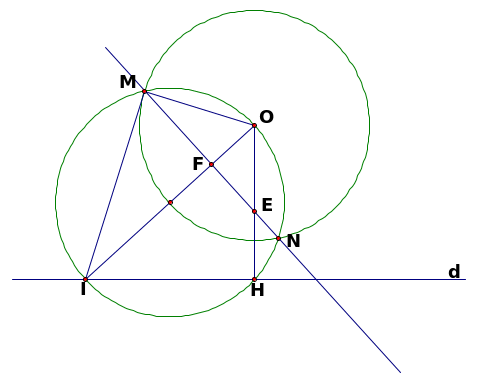
Hướng dẫn:
do tính chất đối xứng nên điểm cố định nằm trên trục đối xứng hay đường thẳng qua O và vuông góc với (d)
Giải:
Kẻ OH vuông góc với (d) cắt MN tại E.
ta có H cố định và H thuộc đường tròn đường kính OI vậy đường tròn đường kính OI luôn đi qua K cố định.
Xét tam giác OEF và tam giác OIH có góc O chung, góc OFE = góc OHI = 900
Nên tam giác OEF đồng dạng với tam giác OIH do đó: OF/ OE = OH/ OI => OE. OH = OF. OI
Lại có góc IMO = 900 ( nội tiếp chắn nửa đường tròn đường kính OI )
Xét tam giác vuông OMI có đường cao ứng với cạnh huyền MF nên:
OF. OI = OM2
D o
đó:
o
đó:
 =
hằng số vây E cố định do đó MN đi qua E cố định.
=
hằng số vây E cố định do đó MN đi qua E cố định.
Bài 3: Cho đường tròn (O; R) và dây AB cố định. C là một điểm chuyển động trên đường tròn và M là trung điểm của AC. Chứng minh rằng đường thẳng kẻ từ M vuông góc với BC luôn đi qua một điểm cố định.
Giải:
Vẽ đường kính BD => D cố định.
Giả sử đường thẳng qua M và vuông góc với BC cắt BC cắt AD tại I.
Dễ thấy góc BCD = 900 hay MI // CD.
Xét tam giác ACD có MC = MA; MI // CD => I là trung điểm của DA cố định hay đường thẳng qua M vuông góc với BC đi qua I cố định.
Bài 4: Cho tam giác ABC và hai điểm M, N thứ tự chuyển động trên hai tia BA, CA sao cho BM= CN. Chứng minh rằng đường trung trực của MN luôn đi qua một điểm cố định.
Hướng dẫn:
Khi
M
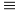 B
thì N
B
thì N
 C
khi đó đường trung trực của MN là trung trực của BC.
Vậy điểm cố định nằm trên đường trung trực của
BC
C
khi đó đường trung trực của MN là trung trực của BC.
Vậy điểm cố định nằm trên đường trung trực của
BC
Giải: Giả sử trung trực của BC cắt trung trực của MN tại I
D ễ
thấy tam giác IMB = tam giác INC (c-c-c) vậy góc MBI = góc
NCI
ễ
thấy tam giác IMB = tam giác INC (c-c-c) vậy góc MBI = góc
NCI
Xét tứ giác ABCI có góc MBI = góc NCI vậy tứ giác ABCI nội tiếp hay I thuộc đường tròn Ngoại tiếp tam giác ABC cố định, mà Trung trực của BC cố định Vậy I cố định hay trung trực của MN đi qua I cố định.
Bài
5: Cho đường tròn (O; R) và
dây cung AB = R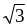 .
Điểm P khác A và B. Gọi (C; R1)
là đường tròn đi qua P tiếp xúc với đường tròn (O;
R) tại A.Gọi (D; R2)
là đường tròn đi qua P tiếp xúc với đường tròn (O;
R) tại B. Các đường tròn (C; R1)
và (D; R2)
cắt nhau tại M khác P. Chứng minh rằng khi P di động trên
AB thì đường thẳng PM luôn đi qua một điểm cố định.
.
Điểm P khác A và B. Gọi (C; R1)
là đường tròn đi qua P tiếp xúc với đường tròn (O;
R) tại A.Gọi (D; R2)
là đường tròn đi qua P tiếp xúc với đường tròn (O;
R) tại B. Các đường tròn (C; R1)
và (D; R2)
cắt nhau tại M khác P. Chứng minh rằng khi P di động trên
AB thì đường thẳng PM luôn đi qua một điểm cố định.
Tìm hiểu đề bài:
* Yếu tố cố định: (O; R), dây AB
* Yếu tố không đổi: DPCO là hình bình hành. Sđ cung BP của (D), sđ cung AP của (C), Góc BMA không đổi
Dự đoán
Khi
P
 A thì PM là tiếp tuyến của (O; R) => điểm cố định
nằm trên tiếp tuyến của (O; R) tại A
A thì PM là tiếp tuyến của (O; R) => điểm cố định
nằm trên tiếp tuyến của (O; R) tại A
Khi
P
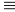 B thì PM là tiếp tuyến của (O; R)=> điểm cố định
nằm trên tiếp tuyến của (O; R) tại B
B thì PM là tiếp tuyến của (O; R)=> điểm cố định
nằm trên tiếp tuyến của (O; R) tại B
Do tính chất đối xứng của hình => Điểm cố định nằm trên đường thẳng qua O và vuông góc với AB
=> Điểm cố định nằm trên đường tròn ngoại tiếp tam giác OAB
Lời giải:
Vẽ đường tròn ngoại tiếp tam giác OAB cắt PM tại I .
v ì
AB = R
ì
AB = R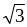 => sđ cung AB của (O) bằng 1200
=> sđ cung AB của (O) bằng 1200
tam giác BDP cân do đó góc OBA = góc DPB
tam giác OAB cân do đó góc OBA = góc OAB => góc BDP = góc BOA => sđcung BP của (D) = sđ cung BA của (O) = 1200 .
tương tự sđ cung PA của (C) = 1200 .
ta
có góc BMP =
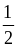 sđ
cung BP của (D) = 600
sđ
cung BP của (D) = 600
ta
có góc AMP =
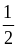 sđ
cung AP của (C) = 600
sđ
cung AP của (C) = 600
Vậy
góc BMA = góc BMP + góc AMP = 1200 =
góc BOA
=
góc BOA
xét
tứ giác BMOA có góc BMA = góc BOA do đó tứ giác BMOA nội
tiếp hay M thuộc đường tròn ngoại tiếp tam giác BOA.

Vậy
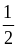 sđ
cung IA = góc IMA = góc PMA =
sđ
cung IA = góc IMA = góc PMA =
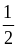 sđ
cung PA của (C) = 1200
.Vậy I thuộc đường tròn ngoại tiếp tam giác AOB và sđ
cung IA = 1200
=> I cố định hay MP đi qua I cố định.
sđ
cung PA của (C) = 1200
.Vậy I thuộc đường tròn ngoại tiếp tam giác AOB và sđ
cung IA = 1200
=> I cố định hay MP đi qua I cố định.
Bài 6: Cho đoạn AB cố định, M di động trên AB. Trên cùng một nửa mặt phẳng bờ AB vẽ hai hình vuông MADE và MBHG. Hai đường tròn ngoại tiếp hai hình vuông cắt nhau tại N. Chứng minh đường thẳng MN luôn đi qua một điểm cố định khi M di chuyển trên AB.
H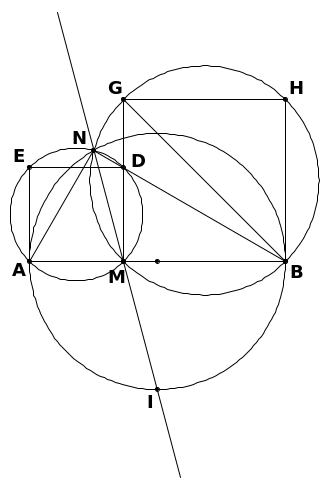 ướng
dẫn:
ướng
dẫn:
Tương tự bài 1
Giải:
Giả sử MN cắt đường tròn đường kính AB tại I
Ta có Góc ANM = Góc ADM = 450( góc nội tiếp cùng chắn cung AM của đường tròn ngoại tiếp hình vuông AMDE)
Ta có Góc BNM = Góc BGM = 450( góc nội tiếp cùng chắn cung BM của đường tròn ngoại tiếp hình vuông MBGH)
=> gócANB = Góc ANM + Góc BNM = 900 => N thuộc đường tròn đường đường kính AB vậy sđ cung AI = 2sđGóc ANI
=2sđGóc ANM = 900
Vậy I thuộc đường tròn đường kính AB và số đo cung AI bằng 900
=> I cố định hay MN đi qua I cố định
Vµi ®Þnh híng khai th¸c bµi to¸n h×nh häc
Để có được một giờ luyện tập tốt cần lưu ý một số vấn đề sau
- Chọn hệ thống bài tập như thế nào cho một giờ luyện tập;
- Phải sắp xếp hệ thống các câu hỏi từ dễ đến khó (có gợi mở);
- Phải tổ chức tốt và thể hiện vai trò chủ đạo của người thày;
- Sau mỗi bài cần tập dượt cho học sinh nghiên cứu sâu lời giải (nếu có).
Nội dung chính của bài viết tôi bắt đầu từ một số bài toán đơn giản trong chương trình lớp 9 bậc THCS rồi phát triển nó rộng ra ở mức độ tương đương, phức tạp hơn rồi cao hơn nhưng vẫn phù hợp với tư duy lôgíc của các em để tạo cho các em niềm say mê học tập môn toán đặc biệt là môn hình học.
Từ bài tập số 7 trang 134 (SGK hình học lớp 9-NXB Giáo dục 2005), sau khi học sinh được làm, tôi đã thay đổi thành bài toán có nội dung như sau:
Bài toán 1: Cho ∆ABC đều cạnh a, gọi O là trung điểm của BC. Trên cạnh AB, AC theo thứ tự lấy M, N sao cho góc MON = 600.
a)
Chứng minh
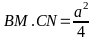 ;
;
b) Gọi I là giao điểm của BN và OM. Chứng minh BM.IN = BI.MN;
c) Chứng minh MN luôn tiếp xúc với một đường tròn cố định.
Phân tích bài toán:
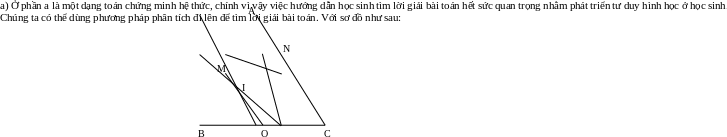
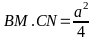
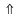
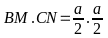
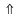

Căn cứ vào sơ đồ ta có lời giải sau:
Ta có ∆BMO:
gócB+gócM+gócO = 1800 gócBMO+gócMON+gócNOC
= 1800 (gócBOC = 1800)
hay

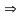 gócBMO
= gócCON; lại có
gócBMO
= gócCON; lại có
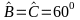 (vì∆ABCđều)
(vì∆ABCđều)
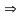 ∆BMO
đồng dạng ∆CON (g.g), từ đó suy ra
∆BMO
đồng dạng ∆CON (g.g), từ đó suy ra

 ;
mà
;
mà
 do đó
do đó
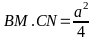 (đpcm)
(đpcm)

∆BMO đồng dạng ∆CON
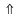
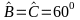
gócBMO = gócCON
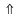
gócB+gócBMO+gócBOM = gócBMO+gócMON+gócNOC (= 1800).
b) Cũng tương tự như vậy ở phần b) thày giáo cũng giúp học sinh phát triển tư duy lôgic, thao tác tư duy phân tích, tổng hợp, đặc biệt là tư duy phân tích đi lên- một thao tác tư duy đặc trưng của môn hình học. Với sự phân tích như vậy học sinh sẽ thấy đó chính là sử dụng tính chất đường phân giác của tam giác BMN. Nghĩa là học sinh cần chỉ ra MI là tia phân giác của gócBMN. Từ đó ta có lời giải sau:
Theo
phần a) ∆BMO đồng dạng ∆CON suy ra
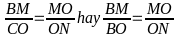 lại có gócB = gócMON (=600)
lại có gócB = gócMON (=600)
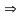 ∆BMO
đồng dạng ∆OMN (c.g.c). Từ đó suy ra gócBMO = gócOMN do
đó MO là tia phân giác của góc BMN hay MI là tia phân giác
gócBMN.
∆BMO
đồng dạng ∆OMN (c.g.c). Từ đó suy ra gócBMO = gócOMN do
đó MO là tia phân giác của góc BMN hay MI là tia phân giác
gócBMN.
Xét
∆BMN có MI là tia phân giác của gócBMN, áp dụng tính
chất đường phân giác trong tam giác ta có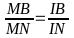 hay
hay
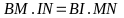 (đpcm).
(đpcm).
c) Đây là một dạng toán liên quan giữa tính bất biến (cố định) và tính thay đổi: Ứng với mỗi điểm M, N thì ta có vị trí của đoạn thẳng MN thay đổi theo (chuyển động) nhưng lại luôn tiếp xúc với một đường tròn cố định (bất biến). Vậy trước khi tìm lời giải của bài toán giáo viên cần cho học sinh chỉ ra yếu tố cố định, yếu tố nào thay đổi.
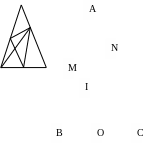
Ta có lời giải sau: Từ O kẻ OH, OK theo tứ tự vuông góc với AB và MN. Do O, AB cố định nên OH cố định Vậy đường tròn (O;OH) là đường tròn cố định.
Vì MO là tia phân giác của góc BMN nên OK = OH (t/c đường phân giác)
→
K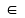 (O;OH)
(1) lại có OK
(O;OH)
(1) lại có OK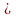 MN
( cách dựng) (2)
MN
( cách dựng) (2)
từ (1) và (2) suy ra MN là tiếp tuyến của đường tròn (O;OH). Vậy MN luôn tiếp xúc với một đường tròn (O;OH) cố định.
Khai thác bài toán:
Ở phần a) của bài toán ta thấy tích BM.CN không đổi, nếu sử dụng BĐT Côsi ta có thêm câu hỏi sau:
1.1: Tìm vị trí của M, N trên AB, AC để BM + CN đạt giá trị nhỏ nhất.
Lời
giải: Áp dụng BĐT Côsi cho hai số không âm là BM,
CN ta có
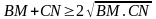 dấu "=" xảy ra
dấu "=" xảy ra
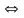 BM = CN. Theo phần a)
BM = CN. Theo phần a)
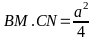
do
đó
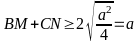 (không đổi).
(không đổi).
Vậy
GTNN của BM+CN = a
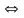 BM = CN =
BM = CN =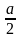
 M,
N theo thứ tự là trung điểm của AB và AC.
M,
N theo thứ tự là trung điểm của AB và AC.
1.2: Ta thử suy nghĩ nếu tam giác ABC là tam giác cân thì bài toán còn đúng không? và giả thiết như thế nào? từ đó ta có bài toán sau:
 Bài
toán 1.2: Cho tam giác ABC cân ở A, O là trung điểm
BC. Trên cạnh AB, AC theo thứ tự lấy các điểm M, N sao
cho gócBMO = gócCON.
Bài
toán 1.2: Cho tam giác ABC cân ở A, O là trung điểm
BC. Trên cạnh AB, AC theo thứ tự lấy các điểm M, N sao
cho gócBMO = gócCON.
Chứng minh rằng:
a)
b)
BN
BI.MN = IN.BM; c)
Khi M, N thay đổi trên AB, AC thì MN luôn tiếp xúc với
một đường tròn cố định.
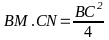 ;
; MO
=
MO
=
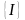 ,
Chứng minh
,
Chứng minh
Bài toán 1.3: Cho tam giác ABC cân ở A, O thuộc cạnh BC đường tròn tâm O tiếp xúc với các cạnh AB, AC của tam giác. Trên AB, AC theo thứ tự lấy hai điểm M, N.
Chứng
minh rằng MN là tiếp tuyến của đ ường tròn (O)
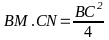
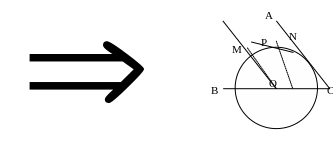

góc
MON = gócB; gócBOM = gócONC; gócNOC = gócBMO; từ đó suy ra
∆BMO đồng dạng ∆CON (g.g)
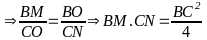 (đpcm).
(đpcm).
( )
Giả sử có
)
Giả sử có
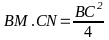 cần phải chứng minh MN là tiếp tuyến của (O).
cần phải chứng minh MN là tiếp tuyến của (O).
Cách 1: Chứng minh tương tự bài toán 1;
Cách 2: Từ M dựng tiếp tuyến với (O) cắt
AC ở N'. Ta chứng minh N' N.
N.
Theo
phần thuận ta có
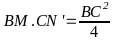 kết hợp với giả thiết ta suy ra BM.CN' = BM.CN
kết hợp với giả thiết ta suy ra BM.CN' = BM.CN
 CN' = CN. Mà N', N cùng thuộc cạnh AC do đó N'
CN' = CN. Mà N', N cùng thuộc cạnh AC do đó N'
 N (đpcm).
N (đpcm).
Chú ý: - Nếu M nằm trong đoạn AB thì N nằm trong đoạn AC.
- Nếu M nằm ngoài đoạn AB thì N cũng nằm ngoài đoạn AC.
Bài toán 1.4: Cho tam giác ABC cân ở B có gócB = 400, O là trung điểm cạch AC, K là chân đường vuông góc kẻ từ O xuống AB, (O) là đường tròn tâm O bán kính OK.
1) Chứng minh (O) tiếp xúc với BC;
2) Giả sử E là một điểm thay đổi trên cạnh AC sao cho
góc
AOE =
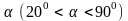 ,
kẻ tiếp tuyến EF với đường tròn (O) tiếp súc với
(O) tại P. a) Tính theo
,
kẻ tiếp tuyến EF với đường tròn (O) tiếp súc với
(O) tại P. a) Tính theo
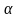 các
góc của tứ giác AEFC;
các
góc của tứ giác AEFC;
b)
 AEO
đồng dạng với
AEO
đồng dạng với
 COF;
COF;
HD Giải:
1)
Kẻ OH vuông góc với BC. do tam giác ABC cân ở B nên OH =
OK do đó H nằm trên (O), lại có OH
2)
a) Ta có
góc
CFE = 2
b)
c) Tương tự lời giải bài ý 1.1 ta suy ra E, F là trung
điểm của BA, BC

 BC
tại H nên BC là tiếp tuyến của (O).
BC
tại H nên BC là tiếp tuyến của (O).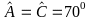 ,
tương tự bài toán trên ta suy ra góc AEF = 2(1100-
,
tương tự bài toán trên ta suy ra góc AEF = 2(1100-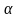 ),
),
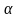 .
. AEO
đồng dạng với
AEO
đồng dạng với
 COF
(c.g.c)
COF
(c.g.c)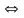

 để AE + CF nhỏ nhất. (Đề thi
chuyên toán ĐHSP H N năm 2005)
để AE + CF nhỏ nhất. (Đề thi
chuyên toán ĐHSP H N năm 2005)
O
A
E
B
F
C
P












Bài toán 1.5: Cho đường tròn (I) tiếp xúc với hai cạnh của góc xOy tại A và B. Từ C trên cung nhỏ AB kẻ tiếp tuyến với đường tròn (I) cắt Ox, Oy theo thứ tự tại M, N. Xác định vị trí của C trên cung nhỏ AB để MN có độ dài nhỏ nhất.


Ta có MN = AM + BN = MP + NQ - AP - BQ = MP + NQ - 2AP.
Do
đó MN nhỏ nhất
 MP + NQ nhỏ nhất (Áp dụng kết quả bài toán 1.1) ta có
được C là điểm chính giữa cung nhỏ AB.
MP + NQ nhỏ nhất (Áp dụng kết quả bài toán 1.1) ta có
được C là điểm chính giữa cung nhỏ AB.
Nếu vẫn tiếp tục khai thác bài toán ban đầu ta có thể đưa ra một số bài toán cho học sinh tự làm, coi như bài tập về nhà để học sinh tự giải quyết.
Bài
toán 1.6: Cho
 ABC
cân ở A. Lấy M, N trên cạnh AB, AC sao cho
ABC
cân ở A. Lấy M, N trên cạnh AB, AC sao cho
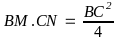 .
Tìm vị trí của M, N sao cho
.
Tìm vị trí của M, N sao cho
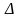 AMN
có diện tích lớn nhất.
AMN
có diện tích lớn nhất.
Bài toán 1.7: Cho M, M' trên tia AB và tia đối của tia BA; N, N' thuộc tia CA và tia đối của tia CA. Chứng minh rằng:
1) Nếu MB.NC = M'B.N'C =
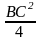 thì tứ giác MM'N'N ngoại tiếp được một đường tròn;
thì tứ giác MM'N'N ngoại tiếp được một đường tròn;
2)Phân giác tạo bởi MN và MM' đi qua một điểm cố định.
Bài toán 1.8:
1) Cho
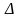 ABC.
Dựng hai điểm P, Q thứ tự trên AB và AC sao cho AP = AQ và
BP.CQ =
ABC.
Dựng hai điểm P, Q thứ tự trên AB và AC sao cho AP = AQ và
BP.CQ =
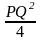 ;
;
2) Cho hình vuông ABCD, lấy điểm F thuộc CD, G thuộc BC sao cho EG//AF (với E là trung điểm của AB). Chứng minh rằng FG là tiếp tuyến của đường tròn nội tiếp hình vuông.
Bài toán 1.9: Cho tam giác ABC cân ở A. Đường tròn có tâm O là trung điểm của BC tiếp xúc với AB, AC thứ tự ở H và K. Lấy P thuộc đoạn AB, Q thuộc đoạn AC sao cho PQ là tiếp tuyến của (O). Tìm quĩ tích tâm O' của đường tròn ngoại tiếp tam giác OPQ.
Với cách làm tương tự trên, bằng phương pháp đặc biệt hoá, khái quát hoá, tương tự và thao tác tư duy thuận đảo ta cũng hình thành cho học sinh tư duy lôgíc, tư duy sáng tạo, tính độc đáo trong toán học. Chẳng hạn ta có bài toán sau:
Bài toán 2: Cho đường tròn (O) đường kính CD. Từ C và D kẻ hai tiếp tuyến Cx, Dy với đường tròn. Từ một điểm E nằm trên đường tròn, kẻ tiếp tuyến với đường tròn đó cắt Cx tại A và Dy tại B. Chứng minh góc AOB = 900.
Phân tích bài toán:

Để chứng minh góc AOB = 900, ta có thể làm bằng nhiều cách khác nhau. Chẳng hạn:
- Ta chứng minh OA, OB là hai tia phân giác của cặp góc kề bù;
- Ta chứng minh góc AOB = góc CED, mà góc CED = 900
nên gócAOB = 900.
Do +)
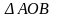 đồng
dạng với
đồng
dạng với
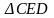 (g.g) nên góc AOB = góc CED,
(g.g) nên góc AOB = góc CED,
mà góc CED = 900 vậy góc AOB = 900.
+) Tứ giác OKEJ là hình chữ nhật ( có ba góc vuông) nên góc AOB = 900.
Tiếp tục tư duy chúng ta còn tìm được thêm một vài cách giải khác nữa. Sau đây ta xét một trong các cách giải đó:
Ta có góc ACO = gócAEO = 900 (tính chất hai tiếp tuyến cắt nhau)
suy ra gócACO + góc AEO = 1800 suy ra tứ giác ACOE nội tiếp
Do đó ta có gócEAO = gócECO (hai góc cùng chắn một cung OE)
Tương tự ta cũng có gócEBO = gócEDO, mà gócECO + gócEDO = 900 (vì gócCEO = 900-góc nội tiếp chắn nửa đường tròn). Nên gócEAO + gócEBO = 900. Từ đó suy ra gócAOB = 900. (Đpcm).
Khai thác bài toán:
- Nếu ta thay đổi một vài điều kiện của bài toán, chẳng hạn vị trí của điểm O thay bằng điểm M bất kì trên CD. Khi đó đường thẳng vuông góc với ME tại E không còn là tiếp tuyến nữa mà trở thành cát tuyến với (O). Thế thì yêu cầu của bài toán chứng minh gócAMB = 900 còn đúng nữa hay không?. Điều này vẫn còn đúng, từ đó ta có bài toán khác như sau:
Bài toán 2.1: Cho đường tròn (O) đường kính CD. Từ C, D kẻ hai tiếp tuyến Cx, Dy. Một điểm E bất kỳ nằm trên đường tròn, điểm M bất kỳ nằm trên CD (M không trùng với C, D, O). Qua E kẻ đường thẳng vuông góc với ME cắt Cx, Dy theo thứ tự tại A và B. Chứng minh rằng gócAMB = 900.
-)Tại sao ta lại đặt vấn đề M khác C, D, O. - Vì nếu M
- Còn nếu M
Nếu M
|
x
y
A
E
D
O
M
|
Ta trở lại bài toán: Như vậy tương tự bài toán trên ta cũng có:
gócMAB = gócECM (do tứ giác ACME nội tiếp)
gócEBM = gócEDM (do tứ giác BDME nội tiếp)
mà gócECM + góc EDM = 900 (do gócCED = 900). Nên gócAMB = 900.
-) Ta tiếp tục khai thác và mở rộng bài toán, chẳng hạn điểm M không nằm trong đoạn CD mà nằm trên đường thẳng CD và giữ nguyên các điều kiện của bài toán 2.1 thì sao? từ đó ta có bài toán sau:
 Bài
toán 2.2: Cho đường tròn
(O) đường kính CD. Từ C, D kẻ hai tiếp tuyến Cx, Dy. Một
điểm E bất kỳ nằm trên đường tròn, điểm M bất kỳ
nằm trên đường thẳng CD (M không trùng với C, D, O). Qua
E kẻ đường thẳng vuông góc với ME cắt Cx, Dy theo thứ
tự tại A và B. Chứng minh rằng gócAMB = 900.
Bài
toán 2.2: Cho đường tròn
(O) đường kính CD. Từ C, D kẻ hai tiếp tuyến Cx, Dy. Một
điểm E bất kỳ nằm trên đường tròn, điểm M bất kỳ
nằm trên đường thẳng CD (M không trùng với C, D, O). Qua
E kẻ đường thẳng vuông góc với ME cắt Cx, Dy theo thứ
tự tại A và B. Chứng minh rằng gócAMB = 900.
- Muốn chứng minh góc AMB = 900 ta dựa vào cách chứng minh bài toán trên. Ta chứng minh gócMAB + gócMBA = 900.
Muống chứng minh gócMAB + góc MBA = 900 ta chứng minh
gócMAB + gócMBA = gócCDE + gócDCE = 900
Để chứng minh điều này ta cần chứng minh gócMAB = gócECD,
gócMBA = gócMDE. Như vậy ta cần phải chứng minh các tứ giác AMCE, MEDB nội tiếp.
Từ đó ta có lời giải sau:
Chứng minh: Ta có gócACM = gócAEM = 900, do đó tứ giác AMCE nội tiếp
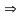 gócMAB = góc ECD (cùng bù gócMCE)
gócMAB = góc ECD (cùng bù gócMCE)
Tương
tự tứ giác MEDB nội tiếp
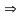 gócMAB = gócMDE (cùng chắn một cung).
gócMAB = gócMDE (cùng chắn một cung).
Mà gócECD + gócEDC = 900. Do đó gócMBA + gócMAB = 900.
Suy ra gócAMB = 900.
Như vậy nhìn lại bài toán trên ta có thể đưa thành bài toán tổng quát hơn như sau:
Bài toán 2.3: (Bài toán tổng quát)
Cho đường tròn (O) đường kính CD. Một điểm E thuộc đường tròn (O). M là điểm bất kì thuộc đường thẳng CD. Kẻ đường thẳng vuông góc với ME tại E cắt các tiếp tuyến Cx, Dy của đường tròn tại A và B. Chứng minh góc AMB = 900.
Vẫn tiếp tục bài toán 2 ta khai thác theo khía cạnh khác, ta có bài toán sau:
Bài
toán 2.4: Cho đường tròn
(O;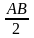 ),
qua A và B kẻ hai tiếp tuyến Ax, By của đường tròn. Một
điểm M thuộc đường tròn, qua M kẻ tiếp tuyến cắt
Ax, By theo thứ tự ở C và D.
),
qua A và B kẻ hai tiếp tuyến Ax, By của đường tròn. Một
điểm M thuộc đường tròn, qua M kẻ tiếp tuyến cắt
Ax, By theo thứ tự ở C và D.
1) Chứng minh CD = AC + BD;
2) Đường tròn ngoại tiếp tam giác COD luôn tiếp xúc với một đường thẳng cố định khi M thay đổi trên đường tròn.
 3)
AD cắt BC ở H chứng minh MH // AC.
3)
AD cắt BC ở H chứng minh MH // AC.
Phân tích bài toán:
1) Với phần này rất phù hợp với học sinh trung bình khi học xong bài tính chất hai tiếp tuyến cắt nhau, Ta thấy ngay CM = CA; DM = DB
từ đó suy ra CM + DM = CA + DB mà M nằm giữa C và D nên CD = CA + DB.
2)
Cũng tương tự bài toán trên ta có
 COD
vuông ở O. Mặt khác gọi I là trung điểm của CD thì O
COD
vuông ở O. Mặt khác gọi I là trung điểm của CD thì O
 (1).
(1).
Lại có tứ giác ABDC là hình thang, OI là đường trung
bình nên OI // CA, mà CA
 AB do đó IO
AB do đó IO
 AB (2)
AB (2)
Từ (1) và (2) suy ra AB là tiếp tuyến của đường tròn ngoại tiếp tam giác COD. Mà AB là đường thẳng cố định nên đường tròn ngoại tiếp tam giác COD luôn tiếp xúc với đường thẳng AB cố định khi M thay đổi trên đường tròn.
3) Với phần này là một bài toán rất hay vì nó đòi hỏi học sinh phải dùng phương pháp phân tích đi lên để tìm lời giải của bài toán. Hơn nữa để tìm ra lời giải học sinh còn phải huy động kiến thức về định lí Talét đảo.
Giáo viên hướng dẫn học sinh tìm lời giải của bài toán bằng sơ đồ phân tích đi lên, như sau:
MH //AC
AC // DB (
|
Từ đó yêu cầu học sinh lên bảng căn cứ vào sơ đồ trình bày lời giải của bài toán: Ta có AC, BD là
hai tiếp tuyến của (O) đường kính AB nên AC Xét
|
Khai thác bài toán:
-) Giáo viên đặt vấn đề cho học sinh suy nghĩ. Gọi giao điểm của MH và AB là K, có nhận xét gì về vị trí của H đối với MK? Từ đó ta có bài toán:
Bài toán 2..5: Với giả thiết của bài toán trên. Chứng minh H là trung điểm của MK.
-) Nếu gọi P là giao điểm của BM và Ax. Thì ta cũng có kết quả C là trung điểm của AP.
-)
Nếu giáo viên cho thêm điều kiện AC = R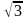 (AB = 2R) thì chúng ta lại có bài toán liên quan đến tính
toán. Từ đó ta có bài toán sau:
(AB = 2R) thì chúng ta lại có bài toán liên quan đến tính
toán. Từ đó ta có bài toán sau:
Bài
toán 2.6: Cho
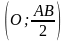 ,
từ A, B kẻ các tiếp tuyến Ax, By của đường tròn. Một
điểm C trên tia Ax sao cho AC = R
,
từ A, B kẻ các tiếp tuyến Ax, By của đường tròn. Một
điểm C trên tia Ax sao cho AC = R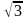 .
Từ C kẻ tiếp tuyến CM tới đường tròn cắt By ở D.
AD cắt BC ở H.
.
Từ C kẻ tiếp tuyến CM tới đường tròn cắt By ở D.
AD cắt BC ở H.
1) Tính số đo gócAOM;
2) Chứng minh trực tâm của tam giác ACM nằm trên (O);
3) Tính MH theo R.
-)
Bây chúng ta lại xét bài toán không tĩnh như trên nữa,
mà cho điểm C thay đổi trên tia Ax sao cho AC
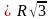 thì khi đó trực tâm của
thì khi đó trực tâm của
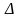 ACM
cũng thay đổi theo. Từ đó ta có bài toán sau:
ACM
cũng thay đổi theo. Từ đó ta có bài toán sau:
Bài
toán 2.7: Cho
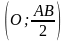 ,
từ A, B kẻ các tiếp tuyến Ax, By của đường tròn. Một
điểm C trên tia Ax sao cho AC
,
từ A, B kẻ các tiếp tuyến Ax, By của đường tròn. Một
điểm C trên tia Ax sao cho AC
 R
R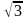 .
Từ C kẻ tiếp tuyến CM tới đường tròn cắt By ở
D.Gọi H là trực tâm của tam giác ACM. Tìm quĩ tích điểm
H.
.
Từ C kẻ tiếp tuyến CM tới đường tròn cắt By ở
D.Gọi H là trực tâm của tam giác ACM. Tìm quĩ tích điểm
H.
-) Lại nhìn bài toán dưới góc độ bài toán cực trị hình học, ta có bài toán sau:
Bài
toán 2.8: Cho
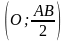 từ A, B kẻ các tiếp tuyến Ax, By của đường tròn. Một
điểm M trên đường tròn, từ M kẻ tiếp tuyến của (O)
cắt Ax, By thứ tự ở C và D. Tìm vị trí của điểm M
để:
từ A, B kẻ các tiếp tuyến Ax, By của đường tròn. Một
điểm M trên đường tròn, từ M kẻ tiếp tuyến của (O)
cắt Ax, By thứ tự ở C và D. Tìm vị trí của điểm M
để:
1) CD có độ dài nhỏ nhất;
2) Diện tích tam giác COD nhỏ nhất.
Như vậy xuất phát từ bài toán trong SGK, bằng những thao tác tư duy lật ngược vấn đề, tương tự, khái quát hoá, tương tự hoá,… chúng ta đã sáng tạo ra được rất nhiều bài toán xuất phát từ bài toán gốc trong quá trình tìm lời giải, nghiên cứu sâu lời giải: như bài toán tính toán, bài toán quĩ tích, bài toán cực trị,…. Việc làm như thế ở người thày được lặp đi, lặp lại và thường xuyên trong quá trình lên lớp sẽ dần dần hình thành cho học sinh có phương pháp, thói quen đào sâu suy nghĩ, khai thác bài toán ở nhiều góc độ khác nhau. Đặc biệt là rèn cho học sinh có phương pháp tìm lời giải bài toán bằng phương pháp phân tích đi lên-một phương pháp tư duy rất đặc trưng và cực kì hiệu quả khi học môn hình học. Thông qua đó học sinh được phát triển năng lực sáng tạo toán học, nhất là những học sinh khá giỏi. Qua mỗi giờ dạy người thày cần giúp học sinh làm quen và sau đó tạo cơ hội cho học sinh luyện tập, thể hiện một cách thường xuyên thông qua hệ thống câu hỏi gợi mở, hệ thống bài tập từ dễ đến khó.
Trên đây là một vài ý tưởng của tôi đã đưa ra trong quá trình lên lớp trong giờ luyện tập hình học. Theo tôi nó có tác dụng:
- Giúp các em củng cố kiến thức đã học;
- Giúp các em biết vận dụng kiến thức đã học vào bài tập;
- Rèn kĩ năng trình bày cho học sinh;
- Phát triển tư duy toán học thông qua các thao tác tư duy khái quát hoá, đặc biệt hoá, tương tự hoá, tư duy thuận đảo,…
- Dần dần hình thành phương pháp tìm lời giải bài toán hình học, tư duy linh hoạt, phương pháp học toán, học sáng tạo toán học.
Ngoài Các Chuyên Đề Luyện Thi Học Sinh Giỏi Toán 9 Có Lời Giải Chi Tiết – Toán 9 thì các tài liệu học tập trong chương trình 9 sẽ được cập nhật liên tục và nhanh nhất có thể sau khi kỳ thi diễn ra trên Danh mục Tài Liệu Học Tập nhằm giúp các bạn đọc thuận tiện trong việc nghiên cứu tài liệu. Quý thày cô và các bạn đọc có thể chia sẻ thêm những tài liệu học tập hữu ích đến địa chỉ email của chúng tôi, nhằm xây dựng nên kho đề thi phong phú, đa dạng cho các em học sinh tham khảo và rèn luyện.
Bộ tài liệu gồm những chuyên đề luyện tập với nhiều dạng bài toán đa dạng, từ cơ bản đến phức tạp, giúp bạn làm quen với những dạng bài thường gặp trong kỳ thi. Mỗi bài toán đi kèm với lời giải chi tiết, rõ ràng và dễ hiểu, giúp bạn nắm vững cách giải từng bước một.
Bộ tài liệu này không chỉ giúp bạn rèn luyện kiến thức mà còn phát triển khả năng suy luận, tư duy và sáng tạo trong việc giải quyết các bài toán khó. Ngoài ra, bạn còn được ôn tập và củng cố kiến thức từ các chương trình học, từ cơ bản đến nâng cao.
Với sự hỗ trợ của “Các Chuyên Đề Luyện Thi Học Sinh Giỏi Toán 9 Có Lời Giải Chi Tiết”, bạn sẽ tự tin hơn trong kỳ thi và có cơ hội nắm bắt những điểm số cao. Đồng thời, tài liệu này cũng là nguồn kiến thức bổ ích cho những ai muốn tìm hiểu và thử thách bản thân trong môn Toán.
>>> Bài viết có liên quan: