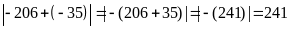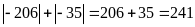Chuyên Đề Tập Hợp Các Số Nguyên Toán 6 Có Lời Giải Chi Tiết Nhất
>>> Mọi người cũng quan tâm:
Chuyên Đề Tập Hợp Các Số Nguyên Toán 6 Có Lời Giải Chi Tiết Nhất – Toán 6 là tài liệu học tập được Trang Tài Liệu biên soạn và sưu tầm từ những nguồn dữ liệu mới nhất hiện nay. Tài liệu này sẽ giúp các em luyện tập, củng cố kiến thức từ đó nâng cao điểm số cho môn học. Ngoài ra, cũng giúp các thầy cô giáo có nguồn tài nguyên phong phú để giảng dạy.
Dưới đây là bản đọc trực tuyến giúp thầy cô và các em học sinh có thể nghiên cứu Online hoặc bạn có thể tải miễn phí với phiên bản word để dễ dàng in ấn cũng như học tập Offline.
CHUYÊN ĐỀ 9: TẬP HỢP CÁC SỐ NGUYÊN
PHẦN I. TÓM TẮT LÝ THUYẾT
1. Định nghĩa:
+ Số nguyên là tập hợp bao gồm các số: Số không, số tự nhiên dương và các số đối của chúng còn gọi là số tự nhiên âm.
+ Số nguyên được chia làm hai loại là số nguyên dương và số nguyên âm.
*
Số nguyên dương là tập hợp các số nguyên lớn hơn
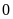 (ví
dụ:
(ví
dụ:
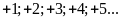 đôi
khi còn viết
đôi
khi còn viết
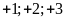
 nhưng
dấu
nhưng
dấu
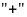 thường được bỏ đi).
thường được bỏ đi).
*
Số nguyên âm là tập hợp các số nguyên nhỏ hơn
 (
ví dụ:
(
ví dụ: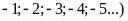
Tập
hợp các số nguyên được kí hiệu là 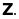
Lưu
ý: Số
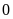 không phải là số nguyên dương cũng không phải là số
nguyên âm.
không phải là số nguyên dương cũng không phải là số
nguyên âm.
2. Biểu diễn số nguyên trên trục số:
Số
nguyên âm có thể được biểu diễn trên tia đối của
tia số đó, gọi là trục số. Điểm
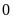 được
gọi là điểm gốc của trục số. Trục số có thể được
vẽ theo hướng ngang (nằm) hoặc hướng dọc (đứng).
được
gọi là điểm gốc của trục số. Trục số có thể được
vẽ theo hướng ngang (nằm) hoặc hướng dọc (đứng).
Khi vẽ trục số ngang, chiều từ trái sang phải gọi là chiều dương (thường được đánh dấu bằng mũi tên), chiều từ phải sang trái gọi là chiều âm.
Tương tự như vậy, khi vẽ trục số dọc, chiều từ dưới lên trên gọi là chiều dương (cũng được đánh dấu bằng mũi tên), chiều từ trên xuống dưới gọi là chiều âm.
Điểm
biểu diễn số nguyên
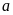 trên
trục số được gọi là điểm
trên
trục số được gọi là điểm
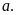
Như
vậy một trục số là một đường thẳng trên đó đã
chọn điểm
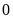 gọi
là điểm gốc, thường chọn chiều từ trái sang phải
làm chiều dương và một đơn vị độ dài , mỗi số tự
nhiên (hay số nguyên dương) được biểu diễn bởi một
điểm ở bên phải điểm
gọi
là điểm gốc, thường chọn chiều từ trái sang phải
làm chiều dương và một đơn vị độ dài , mỗi số tự
nhiên (hay số nguyên dương) được biểu diễn bởi một
điểm ở bên phải điểm ,
mỗi số nguyên âm được biểu diễn bởi một điểm ở
bên trái điểm
,
mỗi số nguyên âm được biểu diễn bởi một điểm ở
bên trái điểm


3. Số đối:
Hai
số đối nhau khi chúng cách đều điểm
 và nằm ở hai phía của điểm
và nằm ở hai phía của điểm
 trên
trục số. Để viết số đối của một số nguyên dương,
chỉ cần viết dấu
trên
trục số. Để viết số đối của một số nguyên dương,
chỉ cần viết dấu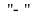 trước số đó; và ngược lại với số nguyên âm.
trước số đó; và ngược lại với số nguyên âm.
*Lưu
ý:
Số đối của số
 là
là
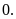
4. So sánh hai số nguyên:
Khi
biểu diễn trên trục số (nằm ngang), điểm
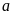 nằm bên trái điểm
nằm bên trái điểm
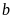 thì
số nguyên
thì
số nguyên
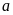 bé hơn số nguyên
bé hơn số nguyên
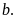 Như vậy:
Như vậy:
– Mọi
số dương đều lớn hơn số
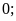
– Mọi
số âm đều bé hơn số
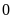 và mọi số nguyên bé hơn
và mọi số nguyên bé hơn
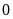 đều là số âm;
đều là số âm;
– Mỗi số âm đều bé hơn mọi số dương.
Lưu
ý:
Số nguyên
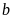 được gọi là số liền sau số nguyên
được gọi là số liền sau số nguyên
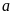 nếu
nếu
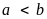 và
không có số nguyên nào nằm giữa
và
không có số nguyên nào nằm giữa
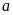 và
và
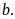 Khi đó ta cũng nói số nguyên
Khi đó ta cũng nói số nguyên
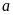 là số liền trước của
là số liền trước của
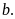
Khi
nói
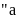 lớn hơn hoặc bằng
lớn hơn hoặc bằng
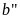 xảy
ra hai trường hợp hoặc
xảy
ra hai trường hợp hoặc
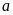 lớn hơn
lớn hơn
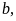 hoặc
hoặc
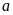 bằng
bằng
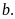
PHẦN II. CÁC DẠNG BÀI
Dạng 1. Điền kí hiệu thích hợp vào chỗ trống:
I. Phương pháp giải:
-Dạng
điền kí hiệu
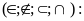
-Tập
hợp số tự nhiên 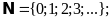
-Tập
hợp số nguyên gồm các số nguyên âm, số 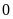 và
số nguyên dương
và
số nguyên dương 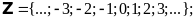
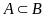 nếu
mọi phần tử của A đều
thuộc B
nếu
mọi phần tử của A đều
thuộc B
-Dạng điền Đ (đúng) hoặc chữ S (sai); đánh dấu "x" vào ô đúng hoặc sai.
II. Bài toán:
Bài
1:
Điền kí hiệu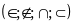 vào
chỗ trống:
vào
chỗ trống:
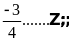
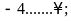
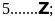
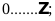
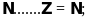
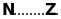
Lời giải:
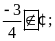
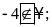

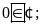
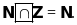
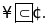
Bài 2: Điền chữ Đ (đúng) hoặc chữ S (sai) vào chỗ trống :
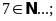
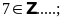
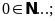
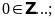
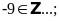
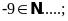
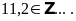
Lời giải:
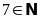 (Đ);
(Đ);
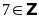 (Đ);
(Đ);
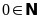 (Đ);
(Đ);
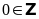 (Đ);
(Đ);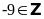 (Đ);
(Đ);
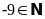 (S);
(S);
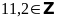 (S).
(S).
Bài 3: Đánh dấu “x” vào ô thích hợp
Câu |
Đúng |
Sai |
a)
Nếu
|
|
|
b)
Nếu
|
|
|
c)
Nếu
|
|
|
d)
Nếu
|
|
|
Lời giải:
Câu |
Đúng |
Sai |
a)
Nếu
|
x |
|
b)
Nếu
|
|
x |
c)
Nếu
|
|
x |
d)
Nếu
|
x |
|
Câu
a đúng vì
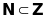
Câu
b sai vì
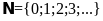 Vậy
nên Nếu
Vậy
nên Nếu
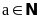 thì
thì
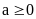
Câu
c sai, giả sử
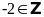 nhưng
nhưng
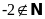
Câu
d đúng vì
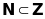
Bài 4. Đánh dấu “X” vào ô thích hợp :
Khẳng định |
Đúng |
Sai |
a) Tích của hai số nguyên âm là một số nguyên dương |
|
|
b) Tổng của hai số nguyên âm là một số nguyên dương |
|
|
c) Tích của hai số nguyên dương là một số nguyên dương |
|
|
d)
Số |
|
|
Lời giải:
Khẳng định |
Đúng |
Sai |
a) Tích của hai số nguyên âm là một số nguyên dương |
x |
|
b) Tổng của hai số nguyên âm là một số nguyên dương |
|
x |
c) Tích của hai số nguyên dương là một số nguyên dương |
x |
|
d)
Số |
|
x |
Dạng 2. Biểu diễn số nguyên trên trục số
I.Phương pháp giải.
|
|
|
II.Bài toán.
Bài
1.Trên
trục số, mỗi điểm sau cách gốc
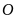 bao
nhiêu đơn vị?
bao
nhiêu đơn vị?
a)
Điểm
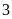 b)
Điểm
b)
Điểm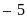 c)
Điểm
c)
Điểm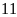 d)
Điểm
d)
Điểm
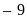
Lời giải
Trên trục số
a)
Điểm
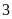 cách
gốc
cách
gốc
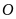 là
là
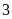 đơn vị b) Điểm
đơn vị b) Điểm
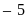 cách
gốc
cách
gốc
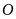 là
là
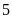 đơn vị
đơn vị
c)
Điểm
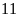 cách
gốc
cách
gốc
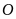 là
là
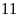 đơn vị d) Điểm
đơn vị d) Điểm
 cách
gốc
cách
gốc
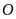 là
là
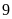 đơn vị
đơn vị
Bài
2.Trên
trục số, xuất phát từ gốc
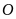 ta sẽ đi đến điểm nào nếu:
ta sẽ đi đến điểm nào nếu:
a)
Di chuyển
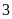 đơn vị theo chiều dương. b)
Di
chuyển
đơn vị theo chiều dương. b)
Di
chuyển
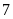 đơn vị theo chiều âm.
đơn vị theo chiều âm.
c)
Di chuyển
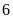 đơn vị theo chiều dương. d)
Di
chuyển
đơn vị theo chiều dương. d)
Di
chuyển
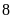 đơn vị theo chiều âm.
đơn vị theo chiều âm.
Lời giải
Trên
trục số, xuất phát từ gốc
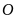
Di chuyển
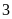 đơn vị theo chiều dương ta sẽ đi đến điểm
đơn vị theo chiều dương ta sẽ đi đến điểm
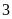 .
.Di chuyển
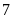 đơn vị theo chiều âm ta sẽ đi đến điểm
đơn vị theo chiều âm ta sẽ đi đến điểm
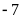 .
.Di chuyển
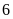 đơn vị theo chiều dương ta sẽ đi đến điểm
đơn vị theo chiều dương ta sẽ đi đến điểm
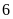 .
.Di chuyển
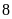 đơn vị theo chiều âm ta sẽ đi đến điểm
đơn vị theo chiều âm ta sẽ đi đến điểm
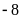 .
.
Bài
3.
Vẽ trục số và biểu diễn các số nguyên sau trên trục
số:
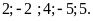
Lời giải
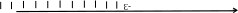
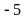
Bài 4. Điền số nguyên thích hợp vào trong các ô trống.
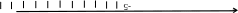





Lời giải
4
0
-3
-5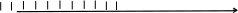





Bài
5.
Các điểm
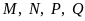 trong
hình vẽ sau đây biểu diễn những số nào?
trong
hình vẽ sau đây biểu diễn những số nào?
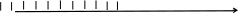
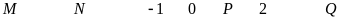
Lời giải
Điểm
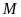 biểu diễn số
biểu diễn số
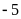 Điểm
Điểm
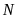 biểu diễn số
biểu diễn số
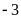
Điểm
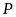 biểu diễn số
biểu diễn số
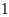 Điểm
Điểm
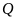 biểu diễn số
biểu diễn số
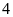
Bài 6.Vẽ một trục số nằm ngang
Tìm trên trục số những điểm cách gốc
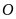 một khoảng bằng
một khoảng bằng
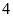 đơn vị.
đơn vị.Chỉ ra hai số nguyên có điểm biểu diễn cách điểm
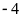 một khoảng là
một khoảng là
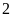 đơn vị.
đơn vị.
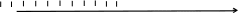 Lời
giải
Lời
giải

Trên trục số những điểm cách gốc
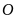 một khoảng bằng
một khoảng bằng
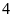 đơn vị là điểm
đơn vị là điểm
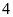 và
điểm
và
điểm
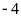
Hai số nguyên có điểm biểu diễn cách điểm
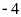 một khoảng là
một khoảng là
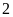 đơn vị là
đơn vị là
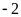 và
và
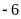
Bài
7.Trên
trục số điểm
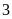 cách điểm
cách điểm
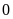 ba đơn vị theo chiều dương, điểm
ba đơn vị theo chiều dương, điểm
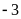 cách điểm
cách điểm
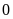 ba đơn vị theo chiều âm.Điền
vào chỗ trống các câu sau đây:
ba đơn vị theo chiều âm.Điền
vào chỗ trống các câu sau đây:
a) Điểm
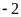 cách điểm
cách điểm
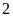 là …. đơn vị và theo chiều ….
là …. đơn vị và theo chiều ….
b) Điểm
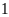 cách điểm
cách điểm
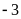 là …. đơn vị và theo chiều ….
là …. đơn vị và theo chiều ….
Lời giải
a) Điểm
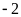 cách điểm
cách điểm
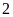 là
là 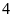 đơn
vị và theo chiều âm.
đơn
vị và theo chiều âm.
b) Điểm
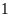 cách điểm
cách điểm
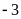 là
là 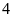 đơn
vị và theo chiều dương.
đơn
vị và theo chiều dương.
Bài 8.Trắc nghiệm
Câu 8.1: Điểm gốc trong trục số là điểm nào?
A. Điểm
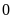 B. Điểm
B. Điểm
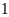 C. Điểm
C. Điểm
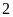 D. Điểm
D. Điểm
Lời giải
Trong
trục số: Điểm
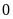 được gọi là điểm gốc của trục số.Chọn
đáp án A.
được gọi là điểm gốc của trục số.Chọn
đáp án A.
Câu
8.2: Điểm
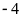 cách điểm
cách điểm
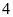 bao nhiêu đơn vị?
bao nhiêu đơn vị?

Lời giải
+
Điểm
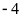 cách điểm
cách điểm
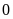 là
là
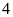 đơn vị.
đơn vị.
+
Điểm
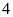 cách điểm
cách điểm
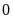 là
là
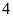 đơn vị.
đơn vị.
Vậy
điểm
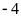 cách điểm
cách điểm
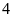 là
là
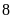 đơn vị.Chọn
đáp án B.
đơn vị.Chọn
đáp án B.
Câu
8.3: Những
điểm cách điểm
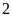 ba đơn vị là?
ba đơn vị là?

Lời giải
+
Điểm
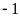 cách điểm
cách điểm
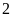 là
là
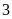 đơn vị.
đơn vị.
+
Điểm
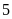 cách điểm
cách điểm
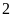 là
là
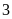 đơn vị.
đơn vị.
Vậy
điểm
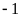 và
và
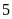 cách điểm
cách điểm
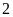 là
là
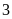 đơn vị.Chọn
đáp án C.
đơn vị.Chọn
đáp án C.
Câu 8.4: Chiều từ trái sang phải trong trục số được gọi là?
A. Chiều âm B. Chiều dương C. Chiều thuận D. Chiều nghịch
Lời giải
Trong trục số: Chiều từ trái sang phải trong trục số được gọi là chiều dương (thường được đánh dấu bằng mũi tên). Chọn đáp án B.
Dạng 3: So sánh hai hay nhiều số nguyên
I. Phương pháp giải
Cách 1:
Biểu diễn các số nguyên cần so sánh trên trục số;
Giá trị các số nguyên tăng dần từ trái sang phải(điểm a nằm bên trái điểm b thì số nguyên a bé hơn số nguyên b)
Cách 2: Căn cứ vào các nhận xét sau:
Số
nguyên dương lớn hơn
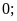
Số
nguyên âm nhỏ hơn
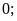
Số nguyên dương lớn hơn số nguyên âm;
Trong hai số nguyên dương, số nào có giá trị tuyệt đối lớn hơn thì số ấy lớn hơn;
Trong hai số nguyên âm, số nào có giá trị tuyệt đối nhỏ hơn thì số ấy lớn hơn.
Kiến thức về giá trị tuyệt đối
- Giá trị tuyệt đối của một số tự nhiên là chính nó;
- Giá trị tuyệt đối của một số nguyên âm là số đối của nó;
- Giá trị tuyệt đối của một số nguyên là một số tự nhiên;
- Hai số nguyên đối nhau có cùng một giá trị tuyệt đối.
II. Bài toán:
Bài
1:Điền
dấu
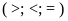 thích
hợp vào chỗ trống:
thích
hợp vào chỗ trống:
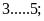
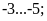
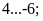
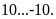
Lời giải:
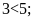
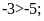
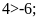
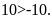
Bài
2: Điền
dấu
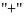 hoặc vào chỗ trống để được kết quả đúng:
hoặc vào chỗ trống để được kết quả đúng:
a)
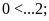 b)
b)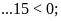
c)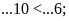 d)
d)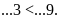
(Chú ý : có thể có nhiều đáp số).
Lời giải:
a)
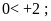 b)
b)
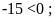

c)
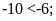
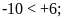 d)
d)
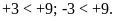
Bài
3:
Điền dấu
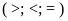 thích
hợp vào chỗ trống:
thích
hợp vào chỗ trống:
a)
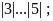 b)
b)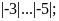 c)
c)
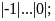 d)
d)
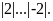
Lời giải:
a)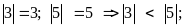 b)
b)
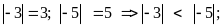
c)
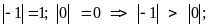 d)
d)
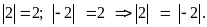
Bài 4. So sánh các số nguyên sau:
a)
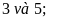 b)
b)
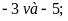 c)
c)
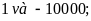
d)
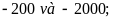 e)
e)
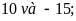 f)
f)
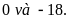
Lời giải:
a)
vì điểm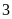 nằm
ở bên trái của điểm
nằm
ở bên trái của điểm
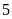 nên
nên
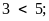
b)
vì giá trị tuyệt đối của
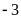 nhỏ hơn giá trị tuyệt đối của
nhỏ hơn giá trị tuyệt đối của
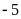 nên
nên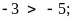
c)
vì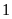 là
số nguyên dương,
là
số nguyên dương,
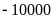 là số nguyên âm nên
là số nguyên âm nên
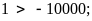
d)
vì giá trị tuyệt đối của
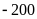 nhỏ hơn giá trị tuyệt đối của
nhỏ hơn giá trị tuyệt đối của
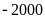 nên
nên
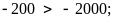
e)
vì
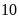 là
số nguyên dương,
là
số nguyên dương,
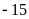 là
số nguyên âm nên nên
là
số nguyên âm nên nên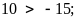
f)
vì số
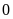 lớn hơn số nguyên âm nên
lớn hơn số nguyên âm nên
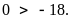
Bài
5:
Điền dấu
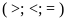 vào chỗ trống:
vào chỗ trống:
a.
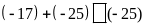 b.
b.
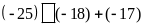
c.


Lời giải:
a.
Ta
có:
|
b.
Ta
có:
|
c.
Ta
có:
|
|
Bài 6: So sánh và rút ra nhận xét:
a.
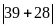 với
với
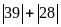 b.
b.
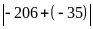 với
với
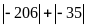
Lời giải:
a.
Có:
|
b.
Có:
|
Bài
7:
So sánh
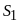 và
và
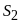
a.
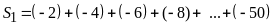
b.
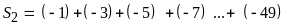
Lời giải:
a)
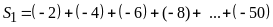
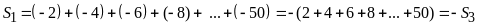
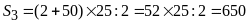
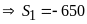
b)
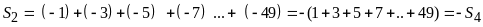
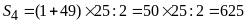
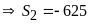
Có
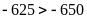
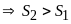
Dạng 4: Viết tập hợp số.
I.Phương pháp giải.
Tên tập hợp được viết bằng chữ cái in hoa như: A, B, C,…
Hai cách viết tập hợp số
Cách 1: Liệt kê các phần tử
Ví
dụ: 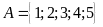
Cách 2: Chỉ ra các tính chất đặc trưng.
Ví
dụ: 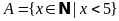
Chú ý:
Các phần tử của một tập hợp được viết trong hai dấu ngoặc nhọn { }, ngăn cách nhau bởi dấu “;” (nếu có phần tử số) hoặc dấu “,” nếu không có phần tử số.
Mỗi phần tử được liệt kê một lần, thứ tự liệt kê tùy ý.
II.Bài toán.
Bài 1. Liệt kê các phần tử của mỗi tập hợp sau.

Lời giải

Bài 2.Viết các tập hợp sau bằng cách chỉ ra tính chất đặc trưng.

Lời giải

Bài
3:
Cho các tập hợp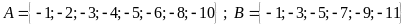
a)
Viết tập hợp
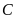 các phần tử thuộc
các phần tử thuộc
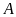 và không thuộc
và không thuộc
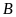 .
.
b)
Viết tập hợp
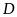 các phần tử thuộc
các phần tử thuộc
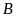 và không thuộc
và không thuộc
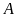 .
.
c)
Viết tập hợp
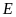 các phần tử vừa thuộc
các phần tử vừa thuộc
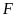 vừa thuộc
vừa thuộc
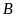 .
.
d)
Viết tập hợp
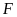 các phần tử hoặc thuộc
các phần tử hoặc thuộc
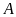 hoặc thuộc
hoặc thuộc
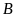 .
.
Lời giải:
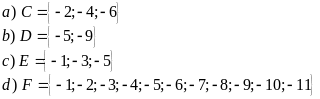
Bài
4:
Cho tập hợp
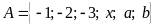
a)
Hãy chỉ rõ các tập hợp con của
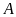 có
có
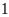 phần tử.
phần tử.
b)
Hãy chỉ rõ các tập hợp con của
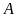 có
có
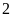 phần tử.
phần tử.
c)
Tập hợp
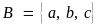 có
phải là tập hợp con của
có
phải là tập hợp con của
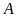 không?
không?
Lời giải:
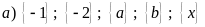
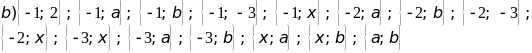
c)
Tập hợp B không phải là tập hợp con của tập hợp
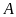 bởi
vì
bởi
vì
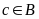 nhưng
nhưng
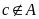
Bài
5:
Cho tập hợp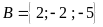 .
Hỏi tập hợp
.
Hỏi tập hợp
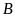 có tất cả bao nhiêu tập hợp con?
có tất cả bao nhiêu tập hợp con?
Lời giải:
+
Tập hợp con của
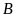 không có phần từ nào là
không có phần từ nào là
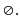
+
Các tập hợp con của
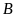 có một phần tử là:
có một phần tử là:
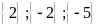
+
Các tập hợp con của
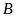 có hai phần tử là:
có hai phần tử là:
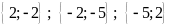
+
Tập hợp con của
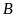 có
có
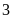 phần tử chính là
phần tử chính là
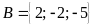
Vậy
tập hợp
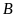 có tất cả
có tất cả
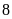 tập hợp con.
tập hợp con.
Bài
6:
Gọi
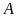 là tập hợp các số nguyên âm có
là tập hợp các số nguyên âm có
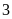 chữ số. Hỏi tập hợp
chữ số. Hỏi tập hợp
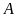 có bao nhiêu phần tử?
có bao nhiêu phần tử?
Lời giải:
Ta
có:
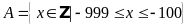
Tập
hợp
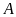 có
có
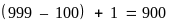 phần
tử.
phần
tử.
Bài 7: Hãy tính số phần tử của các tập hợp sau:
a)
Tập hợp
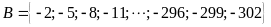
b)
Tập hợp
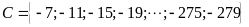
Lời giải:
a)
Tập hợp
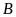 có
có
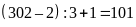 phần
tử.
phần
tử.
b)
Tập hợp
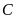 có
có
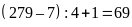 phần
tử.
phần
tử.
Bài
8: Cho
hai tập hợp
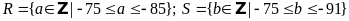
a) Viết các tập hợp trên bằng cách liệt kê các phần tử;
b) Mỗi tập hợp có bao nhiêu phần tử;
c)
Dùng kí hiệu
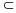 để thực hiên mối quan hệ giữa hai tập hợp đó.
để thực hiên mối quan hệ giữa hai tập hợp đó.
Lời giải:
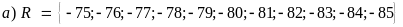
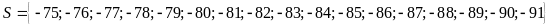
b)
Tập hợp
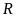 có
có
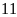 phần tử. Tập hợp
phần tử. Tập hợp
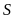 có
có
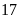 phần tử
phần tử
c)
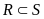
Dạng 5: Sử dụng số nguyên âm trong thực tế.
I.Phương pháp giải.
Số dương và số âm được dùng để biểu thị các đại lượng đối lập nhau hoặc có hướng ngược nhau.
Số âm thường dùng để chỉ:
Nhiệt độ dưới
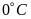
Độ cao dưới mực nước biển
Số tiền còn nợ
Số tiền lỗ
Độ cận thị
Thời gian trước Công Nguyên.
......
II.Bài toán.
Bài 1. Sử dụng số nguyên âm để diễn tả lại ý nghĩa các câu sau
Độ sâu của vịnh Cam Ranh từ
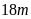 đến
đến
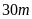 dưới mức nước biển.
dưới mức nước biển.Nhiệt độ trung bình vào mùa đông ở Hàn Quốc là
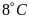 đến
đến
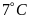 dưới
dưới
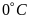 .
.Với bình dưỡng khí, thợ lặn có thể lặn sâu đến
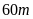 dưới
mực nước biển.
dưới
mực nước biển.Độ sâu của đáy vực Ma-ri-an thuộc vùng biển Phi-lip-pin là
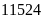 mét (sâu nhất thế giới) dưới mực nước biển.
mét (sâu nhất thế giới) dưới mực nước biển.Trong năm nay, doanh thu của công ty thua lỗ
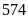 tỉ
đồng.
tỉ
đồng.Nhà toán học Archimedes sinh năm
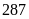 trước
công nguyên.
trước
công nguyên.Ông A nợ ngân hàng
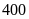 triệu
đồng.
triệu
đồng.Thế vận hội đầu tiên diễn ra năm
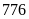 trước
Công nguyên.
trước
Công nguyên.
Lời giải
Độ sâu của vịnh Cam Ranh từ
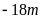 đến
đến
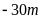
Nhiệt độ trung bình vào mùa đông ở Hàn Quốc là
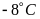 đến
đến
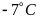
Với bình dưỡng khí, thợ lặn có thể lặn sâu đến
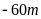
Độ sâu của đáy vực Ma-ri-an thuộc vùng biển Phi-lip-pin là
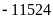 mét (sâu nhất thế giới)
mét (sâu nhất thế giới)
Trong năm nay, doanh thu của công ty
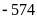 tỉ
đồng.
tỉ
đồng.Nhà toán học Archimedes sinh năm
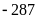
Ông A bị
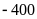 triệu
đồng ở ngân hàng.
triệu
đồng ở ngân hàng.Năm tổ chức Thế vận hội đầu tiên là năm
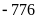 .
.
Bài
2.Hình 35
minh họa một phần các nhiệt kế (tính theo độ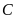 ):
):
a) Viết và đọc nhiệt độ ở các nhiệt kế.
b) Trong hai nhiệt kế a và b, nhiệt độ nào cao hơn?
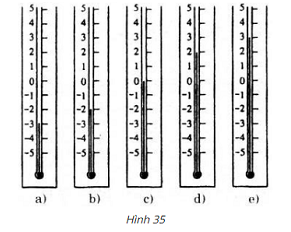
Lời giải
a)
Nhiệt kế a chỉ
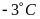 đọc
là âm ba độ
đọc
là âm ba độ
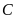 hoặc trừ ba độ
hoặc trừ ba độ
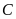 .
.
Nhiệt
kế b chỉ 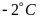 đọc là âm hai độ
đọc là âm hai độ
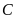 hoặc trừ hai độ
hoặc trừ hai độ
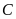 .
.
Nhiệt
kế c chỉ 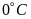 đọc
là không độ
đọc
là không độ
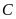 .
.
Nhiệt
kế d chỉ 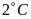 đọc
là hai độ
đọc
là hai độ
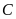 .
.
Nhiệt
kế e chỉ 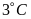 đọc
là ba độ
đọc
là ba độ
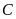 .
.
b) Trong
hai nhiệt kế a và b thì nhiệt độ của nhiệt kế b cao
hơn nhiệt độ của nhiệt kế a ( vì 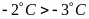 ).
).
Bài 2. Nêu ý nghĩa của mỗi câu sau:
Cá voi xanh có thể lặn được
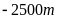
Tàu ngầm có thể lặn được
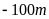
Công ty năm nay bị
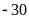 tỉ
đồng
tỉ
đồngNhiệt độ mùa đông ở Miền bắc Việt Nam có năm tới
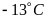
Lời giải
Cá voi xanh có thể lặn sâu
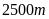 so với mực nước biển.
so với mực nước biển.Tàu ngầm có thể lặn sâu
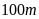 so với mực nước biển.
so với mực nước biển.Công ty năm nay bị thua lỗ
 tỉ
đồng
tỉ
đồngNhiệt độ mùa đông ở Miền bắc Việt Nam có năm xuống tới
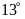 dưới
dưới
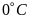
HẾT
Ngoài Chuyên Đề Tập Hợp Các Số Nguyên Toán 6 Có Lời Giải Chi Tiết Nhất – Toán 6 thì các tài liệu học tập trong chương trình 6 sẽ được cập nhật liên tục và nhanh nhất có thể sau khi kỳ thi diễn ra trên Danh mục Tài Liệu Học Tập nhằm giúp các bạn đọc thuận tiện trong việc nghiên cứu tài liệu. Quý thày cô và các bạn đọc có thể chia sẻ thêm những tài liệu học tập hữu ích đến địa chỉ email của chúng tôi, nhằm xây dựng nên kho đề thi phong phú, đa dạng cho các em học sinh tham khảo và rèn luyện.
Chuyên đề “Tập hợp các số nguyên” trong môn Toán lớp 6 là một tài liệu quan trọng giúp học sinh hiểu về khái niệm và tính chất của các tập hợp số nguyên. Tài liệu này cung cấp lời giải chi tiết cho các bài tập liên quan đến tập hợp các số nguyên, giúp học sinh rèn luyện kỹ năng và nắm vững kiến thức về chủ đề này.
Chuyên đề bao gồm một loạt các bài tập từ cơ bản đến nâng cao, được phân loại theo độ khó và nội dung. Các bài tập tập trung vào các khái niệm như tập hợp số nguyên dương, tập hợp số nguyên âm, tập hợp số nguyên không âm, tập hợp số nguyên chẵn, tập hợp số nguyên lẻ, và quy tắc phép toán trên các tập hợp này.
Mỗi bài tập trong tài liệu đi kèm với lời giải chi tiết, giúp học sinh hiểu rõ từng bước giải quyết vấn đề. Lời giải giải thích cách áp dụng các quy tắc và tính chất của các tập hợp số nguyên để đưa ra kết quả chính xác. Điều này giúp học sinh phát triển tư duy logic, khả năng suy luận và ứng dụng kiến thức vào các bài toán thực tế.
Chuyên đề “Tập hợp các số nguyên” cung cấp một tài liệu tổng quan và chi tiết nhất về các khái niệm và tính chất của các tập hợp số nguyên trong môn Toán lớp 6. Nó giúp học sinh nắm vững kiến thức, rèn luyện kỹ năng và tự tin trong việc giải quyết các bài toán liên quan đến tập hợp số nguyên.
>>> Bài viết có liên quan







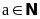 thì
thì
 thì
thì
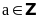 thì
thì
 thì
thì
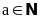 thì
thì
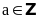
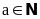 thì
thì
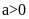
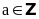 thì
thì
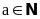
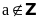 thì
thì
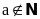
 là
số nguyên dương nhỏ nhất.
là
số nguyên dương nhỏ nhất. là
số nguyên dương nhỏ nhất.
là
số nguyên dương nhỏ nhất.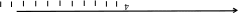

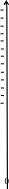
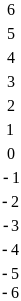
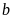
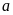
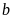
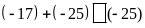
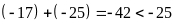
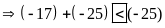
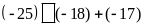
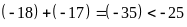
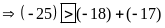

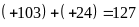
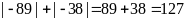
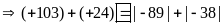
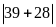 với
với
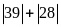
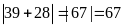
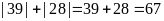
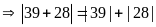
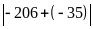 với
với