Phương Pháp Giải Bài 5 Toán 9 Tập 2 Giải Bài Toán Bằng Cách Lập Hệ (Tiếp Theo)
>>> Mọi người cũng quan tâm:
Phương Pháp Giải Bài 5 Toán 9 Tập 2 Giải Bài Toán Bằng Cách Lập Hệ (Tiếp Theo) – Toán 9 là tài liệu học tập được Trang Tài Liệu biên soạn và sưu tầm từ những nguồn dữ liệu mới nhất hiện nay. Tài liệu này sẽ giúp các em luyện tập, củng cố kiến thức từ đó nâng cao điểm số cho môn học. Ngoài ra, cũng giúp các thầy cô giáo có nguồn tài nguyên phong phú để giảng dạy.
Dưới đây là bản đọc trực tuyến giúp thầy cô và các em học sinh có thể nghiên cứu Online hoặc bạn có thể tải miễn phí với phiên bản word để dễ dàng in ấn cũng như học tập Offline.
Bài 6. GIẢI BÀI TOÁN BẰNG CÁCH LẬP HỆ PHƯƠNG TRÌNH (TT)
A. KIẾN THỨC TRỌNG TÂM
B. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
Dạng 1: Bài toán về công việc làm chung và làm riêng |
Lưu ý sử dụng các kết quả sau: |
Ví
dụ 1.
Hai
đội công nhân cùng làm 1 đoạn đường trong
 ngày thì xong. Mỗi ngày, phần việc đội A làm được
gấp hai lần đội B. Hỏi nếu làm một mình thì mỗi đội
làm xong đoạn đường đó trong bao lâu. ĐS:
ngày thì xong. Mỗi ngày, phần việc đội A làm được
gấp hai lần đội B. Hỏi nếu làm một mình thì mỗi đội
làm xong đoạn đường đó trong bao lâu. ĐS:
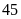 ngày và
ngày và
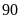 ngày.
ngày.
Ví
dụ 2.
Hai đội công nhân cùng làm một công việc. Nếu hai đội
làm chung thì hoàn thành sau
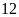 ngày. Nếu mỗi đội làm riêng thì đội I sẽ hoàn thành
công việc chậm hơn đội II là
ngày. Nếu mỗi đội làm riêng thì đội I sẽ hoàn thành
công việc chậm hơn đội II là
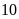 ngày. Hỏi nếu làm riêng thì mỗi đội phải làm trong
bao nhiêu ngày để hoàn thành công việc đó?
ngày. Hỏi nếu làm riêng thì mỗi đội phải làm trong
bao nhiêu ngày để hoàn thành công việc đó?
ĐS:
 ngày và
ngày và
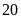 ngày.
ngày.
Ví
dụ 3.
Để hoàn thành một công việc, hai tổ làm chung và dự
kiến hoàn thành sau
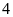 giờ. Trên thực tế sau
giờ. Trên thực tế sau
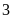 giờ hai tổ làm chung thì tổ I bị điều đi làm việc
khác, tổ II hoàn thành nốt công việc còn lại trong
giờ hai tổ làm chung thì tổ I bị điều đi làm việc
khác, tổ II hoàn thành nốt công việc còn lại trong
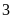 giờ. Hỏi nếu mỗi tổ làm riêng thì sau bao lâu sẽ hoàn
thành công việc?
giờ. Hỏi nếu mỗi tổ làm riêng thì sau bao lâu sẽ hoàn
thành công việc?
ĐS:
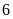 giờ và
giờ và
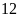 giờ.
giờ.
Ví
dụ 4.
Hai người thợ quét sơn một tòa nhà. Nếu họ cùng làm
trong
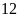 ngày thì xong công trình. Tuy nhiên thực tế hai người làm
cùng nhau trong
ngày thì xong công trình. Tuy nhiên thực tế hai người làm
cùng nhau trong
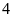 ngày thì người thứ nhất được chuyển đi làm công
việc khác, người thứ hai làm một mình trong
ngày thì người thứ nhất được chuyển đi làm công
việc khác, người thứ hai làm một mình trong
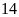 ngày nữa mới xong. Hỏi nếu làm riêng thì mỗi người
hoàn thành công việc đó trong bao lâu. ĐS:
ngày nữa mới xong. Hỏi nếu làm riêng thì mỗi người
hoàn thành công việc đó trong bao lâu. ĐS:
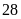 ngày và
ngày và
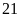 ngày.
ngày.
Ví
dụ 5.
Hai vòi nước cùng chảy vào một bể không có nước thì
sau
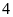 giờ đầy bể. Nếu lúc đầu chỉ vòi I chảy một mình
trong
giờ đầy bể. Nếu lúc đầu chỉ vòi I chảy một mình
trong
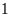 giờ, sau đó mở thêm vòi II cùng chảy trong
giờ, sau đó mở thêm vòi II cùng chảy trong
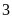 giờ nữa thì được
giờ nữa thì được
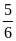 bể. Tính thời gian mỗi vòi chảy một mình đầy bể.
ĐS:
bể. Tính thời gian mỗi vòi chảy một mình đầy bể.
ĐS:
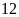 giờ và
giờ và
 giờ.
giờ.
Ví
dụ 6.
Hai vòi nước cùng chảy vào bể trống trong
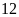 giờ thì đầy bể. Nếu vòi I chảy trong
giờ thì đầy bể. Nếu vòi I chảy trong
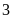 giờ rồi khóa lại, vòi II chảy tiếp trong
giờ rồi khóa lại, vòi II chảy tiếp trong
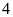 giờ thì được
giờ thì được
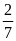 bể. Hỏi mỗi vòi chảy riêng trong bao lâu thì đầy
bể? ĐS:
bể. Hỏi mỗi vòi chảy riêng trong bao lâu thì đầy
bể? ĐS:
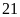 giờ và
giờ và
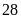 giờ.
giờ.
Dạng 2: Bài toán về năng suất lao động |
Chú
ý công thức
|
Ví
dụ 7.
Một
phân xưởng theo kế hoạch cần phải sản xuất
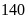 sản phẩm trong một số ngày quy định. Do mỗi ngày phân
xưởng đó sản xuất vượt mức
sản phẩm trong một số ngày quy định. Do mỗi ngày phân
xưởng đó sản xuất vượt mức
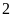 sản phẩm nên đã hoàn thành sớm hơn dự định
sản phẩm nên đã hoàn thành sớm hơn dự định
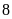 ngày. Hỏi mỗi ngày phân xưởng phải sản xuất bao nhiêu
sản phẩm? ĐS:
ngày. Hỏi mỗi ngày phân xưởng phải sản xuất bao nhiêu
sản phẩm? ĐS:
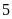 sản phẩm.
sản phẩm.
Ví
dụ 8.
Một xưởng may lập kế hoạch may một lô hàng, theo dự
định mỗi ngày may xong
 áo. Nhưng nhờ cải tiến kỹ thuật, xưởng đã may được
áo. Nhưng nhờ cải tiến kỹ thuật, xưởng đã may được
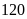 áo mỗi ngày. Do đó xưởng không những hoàn thành trước
thời hạn
áo mỗi ngày. Do đó xưởng không những hoàn thành trước
thời hạn
 ngày mà còn may thêm
ngày mà còn may thêm
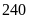 áo. Hỏi theo kế hoạch phân xưởng phải may bao nhiêu áo?
ĐS:
áo. Hỏi theo kế hoạch phân xưởng phải may bao nhiêu áo?
ĐS:
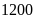 .
.
Dạng 3: Bài toán về tỉ lệ phần trăm |
|
Ví
dụ 9.
Theo kế hoạch hai tổ sản xuất
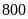 sản phẩm trong thời gian nhất định. Do cải tiến kỹ
thuật tổ I đã vượt mức
sản phẩm trong thời gian nhất định. Do cải tiến kỹ
thuật tổ I đã vượt mức
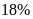 ,
tổ II vượt mức
,
tổ II vượt mức
 .
Do vậy trong thời gian quy định hai tổ vượt mức
.
Do vậy trong thời gian quy định hai tổ vượt mức
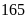 sản phẩm. Hỏi số sản phẩm được giao theo kế hoạch
của mỗi tổ là bao nhiêu?
sản phẩm. Hỏi số sản phẩm được giao theo kế hoạch
của mỗi tổ là bao nhiêu?
ĐS:
 sản phẩm và
sản phẩm và
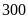 sản phẩm.
sản phẩm.
Ví
dụ 10.
Trong tháng đầu hai tổ công nhân sản xuất được
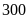 chi tiết máy. Sang tháng thứ hai tổ I sản xuất vượt
mức
chi tiết máy. Sang tháng thứ hai tổ I sản xuất vượt
mức
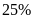 ,
tổ II vượt mức
,
tổ II vượt mức
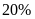 .
Do đó cuối tháng cả hai tổ sản xuất được
.
Do đó cuối tháng cả hai tổ sản xuất được
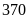 chi tiết máy. Hỏi rằng trong tháng đầu mỗi tổ sản
xuất được bao nhiêu chi tiết máy.
chi tiết máy. Hỏi rằng trong tháng đầu mỗi tổ sản
xuất được bao nhiêu chi tiết máy.
ĐS:
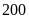 chi tiết máy và
chi tiết máy và
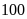 chi tiết máy.
chi tiết máy.
Dạng 4: Bài toán về nội dung hình học |
|
Ví
dụ 11.
Cho
một hình chữ nhật. Nếu tăng độ dài mỗi cạnh của
nó lên
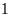 cm thì diện tích của hình chữ nhật tăng thêm
cm thì diện tích của hình chữ nhật tăng thêm
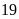 cm
cm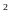 .
Nếu chiều rộng tăng thêm
.
Nếu chiều rộng tăng thêm
 cm, chiều dài giảm đi
cm, chiều dài giảm đi
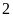 cm thì diện tích hình chữ nhật giảm đi
cm thì diện tích hình chữ nhật giảm đi
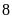 cm
cm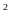 .
Tính chiều dài và chiều rộng ban đầu của hình chữ
nhật.
.
Tính chiều dài và chiều rộng ban đầu của hình chữ
nhật.
ĐS:
 m và
m và
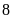 m.
m.
Ví
dụ 12.
Một miếng đất hình chữ nhật có chu vi
 m. Nếu tăng chiều rộng thêm
m. Nếu tăng chiều rộng thêm
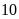 m và giảm chiều dài đi
m và giảm chiều dài đi
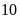 m thì diện tích miếng đất tăng thêm
m thì diện tích miếng đất tăng thêm
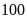 m
m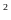 .
Tính chiều dài và chiều rộng ban đầu của mảnh đất.
ĐS:
.
Tính chiều dài và chiều rộng ban đầu của mảnh đất.
ĐS:
 m và
m và
 m.
m.
Ví
dụ 13.
Một mảnh vườn hình chữ nhật có độ dài đường chéo
là
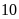 m, chiều dài lớn hơn chiều rộng là
m, chiều dài lớn hơn chiều rộng là
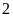 m. Tính chiều dài và chiều rộng mảnh vườn đó. ĐS:
m. Tính chiều dài và chiều rộng mảnh vườn đó. ĐS:
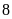 m và
m và
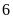 m.
m.
Ví
dụ 14.
Một khu đất hình chữ nhật có độ dài đường chéo là
 m, chiều dài lớn hơn chiều rộng là
m, chiều dài lớn hơn chiều rộng là
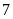 m. Tính chiều dài và chiều rộng của khu đất đó. ĐS:
m. Tính chiều dài và chiều rộng của khu đất đó. ĐS:
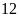 m và
m và
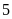 m.
m.
Dạng 5: Bài toán về nội dung sắp xếp chia đều |
|
Ví
dụ 15.
Trong
một buổi tọa đàm, một lớp có
 khách mời đến giao lưu. Vì lớp đã có
khách mời đến giao lưu. Vì lớp đã có
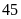 học sinh nên phải kê thêm một dãy ghế nữa và mỗi dãy
ghế xếp thêm hai chỗ ngồi. Biết mỗi dãy đều có số
người ngồi như nhau và ngồi không quá năm người. Hỏi
lớp học lúc đầu có bao nhiêu dãy ghế?
học sinh nên phải kê thêm một dãy ghế nữa và mỗi dãy
ghế xếp thêm hai chỗ ngồi. Biết mỗi dãy đều có số
người ngồi như nhau và ngồi không quá năm người. Hỏi
lớp học lúc đầu có bao nhiêu dãy ghế?
ĐS:
 dãy ghế.
dãy ghế.
Ví
dụ 16.
Người ta cần chở một số lượng hàng. Nếu xếp vào
mỗi xe
 tấn thì còn thừa lại
tấn thì còn thừa lại
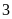 tấn, nếu xếp vào mỗi xe
tấn, nếu xếp vào mỗi xe
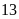 tấn thì còn có thể chở thêm
tấn thì còn có thể chở thêm
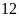 tấn nữa. Hỏi có bao nhiêu xe tham gia chở hàng? ĐS:
tấn nữa. Hỏi có bao nhiêu xe tham gia chở hàng? ĐS:
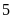 xe.
xe.
C. BÀI TẬP VẬN DỤNG
Bài
1.
Để hoàn thành công việc hai tổ làm chung trong
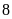 giờ. Tuy nhiên sau
giờ. Tuy nhiên sau
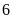 giờ làm chung tổ hai được điều đi làm việc khác, tổ
một hoàn thành nốt công việc còn lại trong
giờ làm chung tổ hai được điều đi làm việc khác, tổ
một hoàn thành nốt công việc còn lại trong
 giờ. Hỏi hai tổ làm riêng sau bao lâu hoàn thành xong công
việc. ĐS:
giờ. Hỏi hai tổ làm riêng sau bao lâu hoàn thành xong công
việc. ĐS:
 giờ và
giờ và
 giờ.
giờ.
Bài
2.
Nếu hai vòi nước cùng chảy vào bể sau
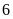 giờ thì đầy. Nếu mở vòi thứ nhất
giờ thì đầy. Nếu mở vòi thứ nhất
 giờ đóng lại, sau đó mở vòi thứ hai
giờ đóng lại, sau đó mở vòi thứ hai
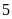 giờ thì
giờ thì
được
 bể. Hỏi mỗi vòi chảy một mình thì sau bao lâu bể
đầy. ĐS:
bể. Hỏi mỗi vòi chảy một mình thì sau bao lâu bể
đầy. ĐS:
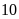 giờ và
giờ và
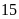 giờ.
giờ.
Bài
3.
Nếu hai vòi nước cùng chảy vào bể sau
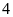 giờ thì đươc
giờ thì đươc
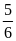 bể. Nếu lúc đầu chỉ mở vòi thứ nhất chảy một
mình trong
bể. Nếu lúc đầu chỉ mở vòi thứ nhất chảy một
mình trong
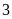 giờ, sau đó mở thêm vòi thứ hai chảy trong
giờ, sau đó mở thêm vòi thứ hai chảy trong
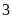 giờ thì đầy bể. Hỏi mỗi vòi chảy một mình thì sau
bao lâu bể đầy. ĐS:
giờ thì đầy bể. Hỏi mỗi vòi chảy một mình thì sau
bao lâu bể đầy. ĐS:
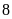 giờ và
giờ và
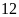 giờ.
giờ.
Bài
4.
Một đội máy cày dự định mỗi ngày cày
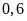 ha. Khi thực hiện mỗi ngày cày được
ha. Khi thực hiện mỗi ngày cày được
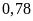 ha. Vì vậy đội không những đã cày xong trước thời
hạn
ha. Vì vậy đội không những đã cày xong trước thời
hạn
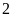 ngày mà còn cày thêm
ngày mà còn cày thêm
 ha nữa. Tính diện tích đội phải cày theo dự định. ĐS:
ha nữa. Tính diện tích đội phải cày theo dự định. ĐS:
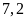 ha.
ha.
Bài
5.
Một xưởng may theo kế hoạch cần phải sản xuất
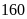 cái áo trong một số ngày quy định. Do mỗi ngày phân
xưởng đó sản xuất vượt mức
cái áo trong một số ngày quy định. Do mỗi ngày phân
xưởng đó sản xuất vượt mức
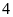 cái áo nên phân xưởng đã hoàn thành sớm hơn dự định
cái áo nên phân xưởng đã hoàn thành sớm hơn dự định
 ngày. Hỏi mỗi ngày phân xưởng phải sản xuất bao nhiêu
sản phẩm theo dự định? ĐS:
ngày. Hỏi mỗi ngày phân xưởng phải sản xuất bao nhiêu
sản phẩm theo dự định? ĐS:
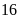 .
.
Bài
6.
Năm ngoái, hai đơn vị sản xuất nông nghiệp thu hoạch
được
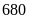 tấn thóc. Năm nay đơn vị thứ nhất vượt mức
tấn thóc. Năm nay đơn vị thứ nhất vượt mức
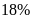 ,
đơn vị thứ hai làm vượt mức
,
đơn vị thứ hai làm vượt mức
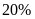 so với năm ngoái. Do đó cả hai đơn vị thu hoạch vượt
mức
so với năm ngoái. Do đó cả hai đơn vị thu hoạch vượt
mức
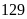 tấn thóc. Hỏi năm ngoái mỗi đơn vị thu hoạch được
bao nhiêu tấn thóc.
tấn thóc. Hỏi năm ngoái mỗi đơn vị thu hoạch được
bao nhiêu tấn thóc.
ĐS:
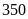 sản phẩm và
sản phẩm và
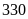 sản phẩm.
sản phẩm.
Bài
7.
Tháng thứ nhất hai tổ sản xuất được
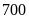 sản phẩm. Sang tháng thứ hai tổ I vượt
sản phẩm. Sang tháng thứ hai tổ I vượt
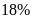 ,
tổ II vượt
,
tổ II vượt
 .
Do đó cuối tháng cả hai tổ sản xuất được
.
Do đó cuối tháng cả hai tổ sản xuất được
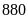 sản phẩm. Tính xem trong tháng thứ nhất mỗi tổ sản
xuất được bao nhiêu sản phẩm. ĐS:
sản phẩm. Tính xem trong tháng thứ nhất mỗi tổ sản
xuất được bao nhiêu sản phẩm. ĐS:
 và
và
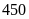 .
.
Bài
8.
Một miếng đất hình chữ nhật có chu vi
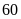 m. Nếu tăng chiều rộng thêm
m. Nếu tăng chiều rộng thêm
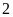 m và giảm chiều dài đi
m và giảm chiều dài đi
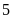 m thì diện tích miếng đất giảm đi
m thì diện tích miếng đất giảm đi
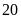 m
m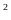 .
Tính chiều dài và chiều rộng ban đầu của mảnh
đất. ĐS:
.
Tính chiều dài và chiều rộng ban đầu của mảnh
đất. ĐS:
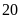 m và
m và
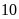 m.
m.
Bài
9.
Cho một miếng đất hình chữ nhật. Nếu tăng chiều rộng
thêm
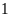 m và tăng chiều dài thêm
m và tăng chiều dài thêm
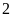 m thì diện tích miếng đất tăng lên
m thì diện tích miếng đất tăng lên
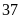 m
m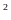 .
Nếu giảm chiều rộng thêm
.
Nếu giảm chiều rộng thêm
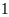 m và tăng chiều dài thêm
m và tăng chiều dài thêm
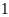 m thì diện tích miếng đất giảm đi
m thì diện tích miếng đất giảm đi
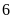 m
m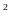 .
Tính chiều dài và chiều rộng ban đầu của mảnh đất.
.
Tính chiều dài và chiều rộng ban đầu của mảnh đất.
ĐS:
 m và
m và
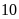 m.
m.
Bài
10.
Một mảnh vườn hình chữ nhật có độ dài đường chéo
là
 m, chiều dài lớn hơn chiều rộng là
m, chiều dài lớn hơn chiều rộng là
 m. Tính chiều dài và chiều rộng mảnh vườn đó. ĐS:
m. Tính chiều dài và chiều rộng mảnh vườn đó. ĐS:
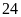 m và
m và
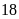 m.
m.
Bài
11.
Một đoàn xe vận tải dự định điều một số xe cùng
loại đi vận chuyển
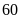 tấn hàng. Lúc sắp khởi hành, đoàn xe được giao chở
thêm
tấn hàng. Lúc sắp khởi hành, đoàn xe được giao chở
thêm
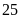 tấn nữa, do đó phải điều thêm
tấn nữa, do đó phải điều thêm
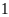 xe cùng loại và mỗi xe phải chở thêm
xe cùng loại và mỗi xe phải chở thêm
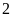 tấn. Tính số xe phải điều theo dự định. Biết mỗi
xe chở số hàng như nhau và số xe nhỏ hơn
tấn. Tính số xe phải điều theo dự định. Biết mỗi
xe chở số hàng như nhau và số xe nhỏ hơn
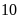 . ĐS:
. ĐS:
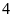 xe.
xe.
--- HẾT ---
HƯỚNG DẪN GIẢI
Hai đội công nhân cùng làm 1 đoạn đường trong
 ngày thì xong. Mỗi ngày, phần việc đội A làm được
gấp hai lần đội B. Hỏi nếu làm một mình thì mỗi
đội làm xong đoạn đường đó trong bao lâu.
ngày thì xong. Mỗi ngày, phần việc đội A làm được
gấp hai lần đội B. Hỏi nếu làm một mình thì mỗi
đội làm xong đoạn đường đó trong bao lâu.
Lời giải
Gọi
số ngày đội
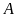 ,
,
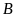 làm một mình xong đoạn đường lần lượt là
làm một mình xong đoạn đường lần lượt là
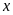 và
và
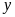 (ngày,
(ngày,
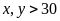 ).
).
Suy
ra trong 1 ngày đội
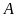 ,
,
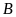 làm được
làm được
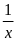 và
và
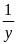 công việc.
công việc.
Ta
có HPT:
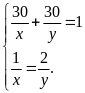
Giải
ra ta được
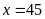 và
và
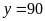 (TMĐK).
(TMĐK).
Vậy
đội A làm một mình trong
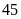 ngày, đội B làm một mình trong
ngày, đội B làm một mình trong
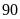 ngày thì xong đoạn đường.
ngày thì xong đoạn đường.
Hai đội công nhân cùng làm một công việc. Nếu hai đội làm chung thì hoàn thành sau
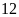 ngày. Nếu mỗi đội làm riêng thì đội I sẽ hoàn thành
công việc chậm hơn đội II là
ngày. Nếu mỗi đội làm riêng thì đội I sẽ hoàn thành
công việc chậm hơn đội II là
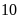 ngày. Hỏi nếu làm riêng thì mỗi đội phải làm trong
bao nhiêu ngày để hoàn thành công việc đó?
ngày. Hỏi nếu làm riêng thì mỗi đội phải làm trong
bao nhiêu ngày để hoàn thành công việc đó?
Lời giải
Gọi
số ngày đội I, II làm một mình xong công việc lần lượt
là
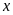 và
và
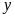 (ngày,
(ngày,
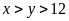 ).
).
Ta
có HPT:

Giải
ra ta được
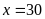 và
và
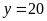 (TMĐK).
(TMĐK).
Vậy
nếu làm một mình đội I làm trong
 ngày, đội II làm trong
ngày, đội II làm trong
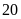 ngày thì hoàn thành công việc.
ngày thì hoàn thành công việc.
Để hoàn thành một công việc, hai tổ làm chung và dự kiến hoàn thành sau
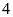 giờ. Trên thực tế sau
giờ. Trên thực tế sau
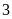 giờ hai tổ làm chung thì tổ I bị điều đi làm việc
khác, tổ II hoàn thành nốt công việc còn lại trong
giờ hai tổ làm chung thì tổ I bị điều đi làm việc
khác, tổ II hoàn thành nốt công việc còn lại trong
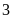 giờ. Hỏi nếu mỗi tổ làm riêng thì sau bao lâu sẽ
hoàn thành công việc?
giờ. Hỏi nếu mỗi tổ làm riêng thì sau bao lâu sẽ
hoàn thành công việc?
Lời giải
Gọi
số giờ đội I, II làm một mình xong công việc lần lượt
là
 và
và
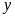 (giờ;
(giờ;
 ).
).
Ta
có HPT:
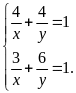
Giải
ra ta được
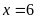 và
và
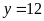 (TMĐK).
(TMĐK).
Vậy
nếu làm một mình đội I làm trong
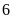 giờ, đội II làm trong
giờ, đội II làm trong
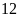 giờ thì xong việc.
giờ thì xong việc.
Hai người thợ quét sơn một tòa nhà. Nếu họ cùng làm trong
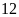 ngày thì xong công trình. Tuy nhiên thực tế hai người
làm cùng nhau trong
ngày thì xong công trình. Tuy nhiên thực tế hai người
làm cùng nhau trong
 ngày thì người thứ nhất được chuyển đi làm công
việc khác, người thứ hai làm một mình trong
ngày thì người thứ nhất được chuyển đi làm công
việc khác, người thứ hai làm một mình trong
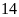 ngày nữa mới xong. Hỏi nếu làm riêng thì mỗi người
hoàn thành công việc đó trong bao lâu.
ngày nữa mới xong. Hỏi nếu làm riêng thì mỗi người
hoàn thành công việc đó trong bao lâu.
Lời giải
Gọi
số ngày người thứ nhất, người thứ hai làm một mình
xong công việc lần lượt là
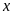 và
và
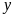 (ngày;
(ngày;
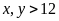 ).
).
Ta
có HPT:

Giải
ra ta được
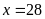 và
và
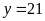 (TMĐK).
(TMĐK).
Vậy
nếu làm một mình người thứ nhất làm trong
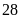 ngày, người thứ hai làm trong
ngày, người thứ hai làm trong
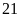 ngày thì xong việc.
ngày thì xong việc.
Hai vòi nước cùng chảy vào một bể không có nước thì sau
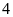 giờ đầy bể. Nếu lúc đầu chỉ vòi I chảy một mình
trong
giờ đầy bể. Nếu lúc đầu chỉ vòi I chảy một mình
trong
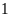 giờ, sau đó mở thêm vòi II cùng chảy trong
giờ, sau đó mở thêm vòi II cùng chảy trong
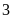 giờ nữa thì được
giờ nữa thì được
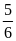 bể. Tính thời gian mỗi vòi chảy một mình đầy bể.
bể. Tính thời gian mỗi vòi chảy một mình đầy bể.
Lời giải
Gọi
thời gian vòi I, II chảy một mình đầy bể lần lượt
là
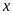 và
và
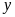 (giờ;
(giờ;
 ).
).
Theo
đề bài, ta có hệ phương trình:
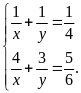
Giải
HPT ta được
 (TMĐK).
(TMĐK).
Vậy
thời gian vòi I và vòi II chảy một mình đầy bể lần
lượt là
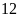 giờ và
giờ và
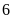 giờ.
giờ.
Hai vòi nước cùng chảy vào bể trống trong
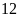 giờ thì đầy bể. Nếu vòi I chảy trong
giờ thì đầy bể. Nếu vòi I chảy trong
 giờ rồi khóa lại, vòi II chảy tiếp trong
giờ rồi khóa lại, vòi II chảy tiếp trong
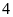 giờ thì được
giờ thì được
 bể. Hỏi mỗi vòi chảy riêng trong bao lâu thì đầy bể?
bể. Hỏi mỗi vòi chảy riêng trong bao lâu thì đầy bể?
Lời giải
Gọi
thời gian vòi I, II chảy một mình đầy bể lần lượt
là
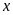 và
và
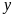 (giờ;
(giờ;
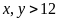 ).
).
Theo
đề bài, ta có hệ phương trình:
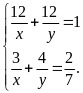
Giải
HPT ta được
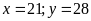 (TMĐK).
(TMĐK).
Vậy
thời gian vòi I và vòi II chảy một mình đầy bể lần
lượt là
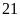 giờ và
giờ và
 giờ.
giờ.
Một phân xưởng theo kế hoạch cần phải sản xuất
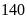 sản phẩm trong một số ngày quy định. Do mỗi ngày phân
xưởng đó sản xuất vượt mức
sản phẩm trong một số ngày quy định. Do mỗi ngày phân
xưởng đó sản xuất vượt mức
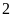 sản phẩm nên đã hoàn thành sớm hơn dự định
sản phẩm nên đã hoàn thành sớm hơn dự định
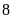 ngày. Hỏi mỗi ngày phân xưởng phải sản xuất bao
nhiêu sản phẩm?
ngày. Hỏi mỗi ngày phân xưởng phải sản xuất bao
nhiêu sản phẩm?
Lời giải
Gọi
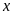 là số sản phẩm mỗi ngày phân xưởng làm và
là số sản phẩm mỗi ngày phân xưởng làm và
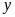 là số ngày làm theo kế hoạch. ĐK:
là số ngày làm theo kế hoạch. ĐK:
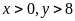 .
.
Theo
đề bài, ta có HPT
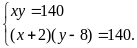
Giải
HPT ta được
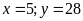 (TMĐK).
(TMĐK).
Vậy
mỗi ngày theo kế hoạch phân xưởng phải sản xuất
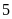 sản phẩm.
sản phẩm.
Một xưởng may lập kế hoạch may một lô hàng, theo dự định mỗi ngày may xong
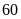 áo. Nhưng nhờ cải tiến kỹ thuật, xưởng đã may được
áo. Nhưng nhờ cải tiến kỹ thuật, xưởng đã may được
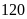 áo mỗi ngày. Do đó xưởng không những hoàn thành trước
thời hạn
áo mỗi ngày. Do đó xưởng không những hoàn thành trước
thời hạn
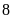 ngày mà còn may thêm
ngày mà còn may thêm
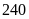 áo. Hỏi theo kế hoạch phân xưởng phải may bao nhiêu
áo?
áo. Hỏi theo kế hoạch phân xưởng phải may bao nhiêu
áo?
Lời giải
Gọi
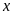 là số áo và
là số áo và
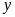 là số ngày phân xưởng cần làm theo kế hoạch. ĐK:
là số ngày phân xưởng cần làm theo kế hoạch. ĐK:
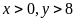 .
.
Từ
đề bài, ta có HPT
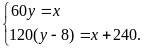
Giải
HPT ta được
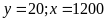 (TMĐK).
(TMĐK).
Vậy
theo kế hoạch phân xưởng phải may
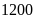 áo.
áo.
Theo kế hoạch hai tổ sản xuất
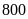 sản phẩm trong thời gian nhất định. Do cải tiến kỹ
thuật tổ I đã vượt mức
sản phẩm trong thời gian nhất định. Do cải tiến kỹ
thuật tổ I đã vượt mức
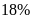 ,
tổ II vượt mức
,
tổ II vượt mức
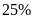 .
Do vậy trong thời gian quy định hai tổ vượt mức
.
Do vậy trong thời gian quy định hai tổ vượt mức
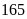 sản phẩm. Hỏi số sản phẩm được giao theo kế hoạch
của mỗi tổ là bao nhiêu?
sản phẩm. Hỏi số sản phẩm được giao theo kế hoạch
của mỗi tổ là bao nhiêu?
Lời giải
Gọi
số sản phẩm theo kế hoạch của tổ I là
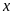 (sản phẩm), tổ II là
(sản phẩm), tổ II là
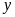 (sản phẩm). (ĐK:
(sản phẩm). (ĐK:
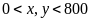 ).
).
Ta
có HPT:
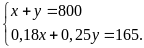
Giải
hệ phương trình ta được
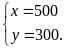
Vậy
theo kế hoạch tổ I được giao
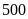 sản phẩm, tổ II được giao
sản phẩm, tổ II được giao
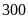 sản phẩm.
sản phẩm.
Trong tháng đầu hai tổ công nhân sản xuất được
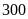 chi tiết máy. Sang tháng thứ hai tổ I sản xuất vượt
mức
chi tiết máy. Sang tháng thứ hai tổ I sản xuất vượt
mức
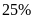 ,
tổ II vượt mức
,
tổ II vượt mức
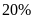 .
Do đó cuối tháng cả hai tổ sản xuất được
.
Do đó cuối tháng cả hai tổ sản xuất được
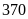 chi tiết máy. Hỏi rằng trong tháng đầu mỗi tổ sản
xuất được bao nhiêu chi tiết máy.
chi tiết máy. Hỏi rằng trong tháng đầu mỗi tổ sản
xuất được bao nhiêu chi tiết máy.
Lời giải
Gọi
số chi tiết máy sản xuất trong tháng đầu của tổ I là
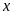 (chi tiết máy), của tổ II là
(chi tiết máy), của tổ II là
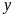 (chi tiết máy). (ĐK:
(chi tiết máy). (ĐK:
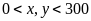 ).
).
Ta
có HPT:
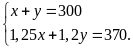
Giải
HPT ta được
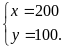
Vậy
trong tháng đầu tổ I sản xuất được
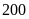 chi tiết máy, tổ II sản xuất được
chi tiết máy, tổ II sản xuất được
 chi tiết máy.
chi tiết máy.
Cho một hình chữ nhật. Nếu tăng độ dài mỗi cạnh của nó lên
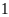 cm thì diện tích của hình chữ nhật tăng thêm
cm thì diện tích của hình chữ nhật tăng thêm
 cm
cm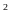 .
Nếu chiều rộng tăng thêm
.
Nếu chiều rộng tăng thêm
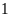 cm, chiều dài giảm đi
cm, chiều dài giảm đi
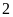 cm thì diện tích hình chữ nhật giảm đi
cm thì diện tích hình chữ nhật giảm đi
 cm
cm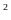 .
Tính chiều dài và chiều rộng ban đầu của hình chữ
nhật.
.
Tính chiều dài và chiều rộng ban đầu của hình chữ
nhật.
Lời giải
Gọi
chiều dài, chiều rộng ban đầu của hình chữ nhật lần
lượt là
 ,
,
 (m) (
(m) (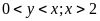 ).
).
Theo
đề bài, ta có HPT
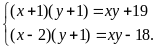
Giải
HPT ta được
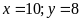 (TMĐK).
(TMĐK).
Vậy
chiều dài, chiều rộng ban đầu của hình chữ nhật là
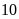 m và
m và
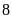 m.
m.
Một miếng đất hình chữ nhật có chu vi
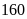 m. Nếu tăng chiều rộng thêm
m. Nếu tăng chiều rộng thêm
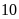 m và giảm chiều dài đi
m và giảm chiều dài đi
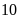 m thì diện tích miếng đất tăng thêm
m thì diện tích miếng đất tăng thêm
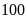 m
m .
Tính chiều dài và chiều rộng ban đầu của mảnh đất.
.
Tính chiều dài và chiều rộng ban đầu của mảnh đất.
Lời giải
Gọi
chiều rộng, chiều dài ban đầu của hình chữ nhật lần
lượt là
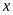 ,
,
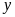 (m) (
(m) (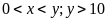 ).
).
Theo
đề bài, ta có HPT
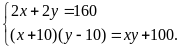
Giải
HPT ta được
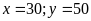 (TMĐK).
(TMĐK).
Vậy
chiều dài và chiều rộng ban đầu của mảnh đất là
 m và
m và
 m.
m.
Một mảnh vườn hình chữ nhật có độ dài đường chéo là
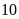 m, chiều dài lớn hơn chiều rộng là
m, chiều dài lớn hơn chiều rộng là
 m. Tính chiều dài và chiều rộng mảnh vườn đó.
m. Tính chiều dài và chiều rộng mảnh vườn đó.
Lời giải
Gọi
chiều rộng, chiều dài của mảnh vườn lần lượt là
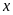 ,
,
 (m) (
(m) (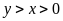 ).
).
Theo
đề bài, ta có HPT:
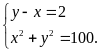
Giải
HPT ta được
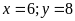 (TMĐK).
(TMĐK).
Vậy,
chiều dài và chiều rộng mảnh vườn là
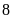 m và
m và
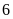 m.
m.
Một khu đất hình chữ nhật có độ dài đường chéo là
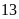 m, chiều dài lớn hơn chiều rộng là
m, chiều dài lớn hơn chiều rộng là
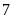 m. Tính chiều dài và chiều rộng của khu đất đó.
m. Tính chiều dài và chiều rộng của khu đất đó.
Lời giải
Gọi
chiều rộng, chiều dài của mảnh vườn lần lượt là
 ,
,
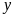 (m) (
(m) (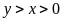 ).
).
Theo
đề bài, ta có HPT:
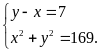
Giải
HPT ta được
 (TMĐK).
(TMĐK).
Vậy,
chiều dài và chiều rộng mảnh vườn là
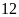 m và
m và
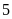 m.
m.
Trong một buổi tọa đàm, một lớp có
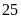 khách mời đến giao lưu. Vì lớp đã có
khách mời đến giao lưu. Vì lớp đã có
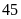 học sinh nên phải kê thêm một dãy ghế nữa và mỗi
dãy ghế xếp thêm hai chỗ ngồi. Biết mỗi dãy đều có
số người ngồi như nhau và ngồi không quá năm người.
Hỏi lớp học lúc đầu có bao nhiêu dãy ghế?
học sinh nên phải kê thêm một dãy ghế nữa và mỗi
dãy ghế xếp thêm hai chỗ ngồi. Biết mỗi dãy đều có
số người ngồi như nhau và ngồi không quá năm người.
Hỏi lớp học lúc đầu có bao nhiêu dãy ghế?
Lời giải
Gọi
số dãy ghế trong lớp và số người ngồi ở mỗi dãy
là
 ,
,
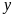 (
(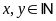 ).
).
Theo
đề bài, ta có HPT:
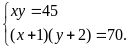
Giải
HPT ta được
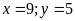 (TMĐK).
(TMĐK).
Vậy,
lớp học lúc đầu có
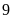 dãy ghế.
dãy ghế.
Người ta cần chở một số lượng hàng. Nếu xếp vào mỗi xe
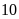 tấn thì còn thừa lại
tấn thì còn thừa lại
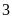 tấn, nếu xếp vào mỗi xe
tấn, nếu xếp vào mỗi xe
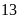 tấn thì còn có thể chở thêm
tấn thì còn có thể chở thêm
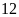 tấn nữa. Hỏi
có bao nhiêu xe tham gia chở hàng?
tấn nữa. Hỏi
có bao nhiêu xe tham gia chở hàng?
Lời giải
Gọi
số hàng cần vận chuyển là
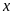 (tấn,
(tấn,
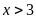 );
Số xe tham gia chở hàng là
);
Số xe tham gia chở hàng là
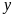 (xe,
(xe,
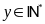 ).
).
Theo
đầu bài, ta có HPT:
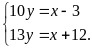
Giải
HPT được
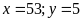 (TMĐK).
(TMĐK).
Vậy,
có
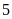 xe tham gia chở hàng.
xe tham gia chở hàng.
Để hoàn thành công việc hai tổ làm chung trong
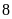 giờ. Tuy nhiên sau
giờ. Tuy nhiên sau
 giờ làm chung tổ hai được điều đi làm việc khác, tổ
một hoàn thành nốt công việc còn lại trong
giờ làm chung tổ hai được điều đi làm việc khác, tổ
một hoàn thành nốt công việc còn lại trong
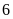 giờ. Hỏi hai tổ làm riêng sau bao lâu hoàn thành xong
công việc.
giờ. Hỏi hai tổ làm riêng sau bao lâu hoàn thành xong
công việc.
Lời giải
Gọi
số giờ đội I, II làm một mình xong công việc lần lượt
là
 và
và
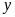 (giờ;
(giờ;
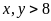 ).
).
Ta
có HPT:
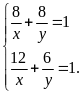
Giải
ra ta được
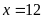 và
và
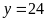 (TMĐK).
(TMĐK).
Vậy
nếu làm một mình đội I làm trong
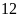 giờ, đội II làm trong
giờ, đội II làm trong
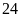 giờ thì xong việc.
giờ thì xong việc.
Nếu hai vòi nước cùng chảy vào bể sau
 giờ thì đầy. Nếu mở vòi thứ nhất
giờ thì đầy. Nếu mở vòi thứ nhất
 giờ đóng lại, sau đó mở vòi thứ hai
giờ đóng lại, sau đó mở vòi thứ hai
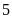 giờ thìđược
giờ thìđược
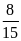 bể. Hỏi mỗi vòi chảy một mình thì sau bao lâu bể
đầy.
bể. Hỏi mỗi vòi chảy một mình thì sau bao lâu bể
đầy.
Lời giải
Gọi
số giờ vòi thứ nhất, vòi thứ hai chảy một mình đầy
bể lần lượt là
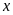 và
và
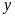 (giờ;
(giờ;
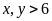 ).
).
Ta
có HPT:
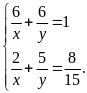
Giải
ra ta được
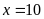 và
và
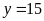 (TMĐK).
(TMĐK).
Vậy
vòi thứ nhất chảy một mình
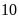 giờ, vòi thứ hai chảy một mình
giờ, vòi thứ hai chảy một mình
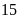 giờ thì đầy bể.
giờ thì đầy bể.
Nếu hai vòi nước cùng chảy vào bể sau
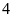 giờ thì đươc
giờ thì đươc
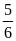 bể. Nếu lúc đầu chỉ mở vòi thứ nhất chảy một
mình trong
bể. Nếu lúc đầu chỉ mở vòi thứ nhất chảy một
mình trong
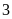 giờ, sau đó mở thêm vòi thứ hai chảy trong
giờ, sau đó mở thêm vòi thứ hai chảy trong
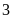 giờ thì đầy bể. Hỏi mỗi vòi chảy một mình thì sau
bao lâu bể đầy.
giờ thì đầy bể. Hỏi mỗi vòi chảy một mình thì sau
bao lâu bể đầy.
Lời giải
Gọi
số giờ vòi thứ nhất, vòi thứ hai chảy một mình đầy
bể lần lượt là
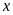 và
và
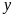 (giờ;
(giờ;
 ).
).
Ta
có HPT:
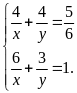
Giải
ra ta được
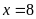 và
và
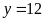 (TMĐK).
(TMĐK).
Vậy
vòi thứ nhất chảy một mình
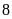 giờ, vòi thứ hai chảy một mình
giờ, vòi thứ hai chảy một mình
 giờ thì đầy bể.
giờ thì đầy bể.
Một đội máy cày dự định mỗi ngày cày
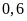 ha. Khi thực hiện mỗi ngày cày được
ha. Khi thực hiện mỗi ngày cày được
 ha. Vì vậy đội không những đã cày xong trước thời
hạn
ha. Vì vậy đội không những đã cày xong trước thời
hạn
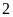 ngày mà còn cày thêm
ngày mà còn cày thêm
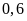 ha nữa. Tính
diện tích đội phải cày theo dự định.
ha nữa. Tính
diện tích đội phải cày theo dự định.
Lời giải
Gọi
 (ha;
(ha;
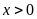 )
là diện tích và
)
là diện tích và
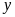 (ngày;
(ngày;
 )
là số ngày đội dự định cày.
)
là số ngày đội dự định cày.
Từ
đề bài, ta có HPT
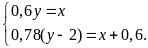
Giải
HPT ta được
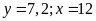 (TMĐK).
(TMĐK).
Vậy
theo dự định đội phải cày
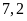 ha.
ha.
Một xưởng may theo kế hoạch cần phải sản xuất
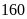 cái áo trong một số ngày quy định. Do mỗi ngày phân
xưởng đó sản xuất vượt mức
cái áo trong một số ngày quy định. Do mỗi ngày phân
xưởng đó sản xuất vượt mức
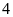 cái áo nên phân xưởng đã hoàn thành sớm hơn dự định
cái áo nên phân xưởng đã hoàn thành sớm hơn dự định
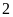 ngày. Hỏi mỗi ngày phân xưởng phải sản xuất bao
nhiêu sản phẩm theo dự định?
ngày. Hỏi mỗi ngày phân xưởng phải sản xuất bao
nhiêu sản phẩm theo dự định?
Lời giải
Gọi
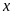 là số áo sản xuất mỗi ngày và
là số áo sản xuất mỗi ngày và
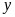 là số ngày xưởng cần làm theo kế hoạch. ĐK:
là số ngày xưởng cần làm theo kế hoạch. ĐK:
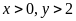 .
.
Từ
đề bài, ta có HPT
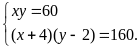
Giải
HPT ta được
 (TMĐK).
(TMĐK).
Vậy
theo kế hoạch xưởng phải may
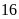 áo mỗi ngày.
áo mỗi ngày.
Năm ngoái, hai đơn vị sản xuất nông nghiệp thu hoạch được
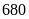 tấn thóc. Năm nay đơn vị thứ nhất vượt mức
tấn thóc. Năm nay đơn vị thứ nhất vượt mức
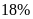 ,
đơn vị thứ hai làm vượt mức
,
đơn vị thứ hai làm vượt mức
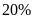 so với năm ngoái. Do đó cả hai đơn vị thu hoạch vượt
mức
so với năm ngoái. Do đó cả hai đơn vị thu hoạch vượt
mức
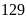 tấn thóc. Hỏi năm ngoái mỗi đơn vị thu hoạch được
bao nhiêu tấn thóc.
tấn thóc. Hỏi năm ngoái mỗi đơn vị thu hoạch được
bao nhiêu tấn thóc.
Lời giải
Gọi
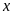 (tấn),
(tấn),
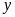 (tấn) lần lượt là khối lượng thóc đơn vị thứ nhất
và đơn vị thứ hai thu hoạch năm ngoái. (ĐK:
(tấn) lần lượt là khối lượng thóc đơn vị thứ nhất
và đơn vị thứ hai thu hoạch năm ngoái. (ĐK:
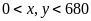 ).
).
Ta
có HPT:

Giải
hệ phương trình ta được
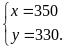
Vậy
năm ngoái đơn vị thứ nhất thu hoạch được
 tấn thóc, đơn vị thứ hai thu hoạch được
tấn thóc, đơn vị thứ hai thu hoạch được
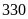 tấn thóc.
tấn thóc.
Tháng thứ nhất hai tổ sản xuất được
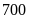 sản phẩm. Sang tháng thứ hai tổ I vượt
sản phẩm. Sang tháng thứ hai tổ I vượt
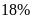 ,
tổ II vượt
,
tổ II vượt
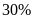 .
Do đó cuối tháng cả hai tổ sản xuất được
.
Do đó cuối tháng cả hai tổ sản xuất được
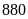 sản phẩm. Tính xem trong tháng thứ nhất mỗi tổ sản
xuất được bao nhiêu sản phẩm.
sản phẩm. Tính xem trong tháng thứ nhất mỗi tổ sản
xuất được bao nhiêu sản phẩm.
Lời giải
Gọi
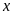 ,
,
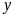 lần lượt là số sản phẩm tổ I, tổ II sản xuất
trong tháng thứ nhất. (ĐK:
lần lượt là số sản phẩm tổ I, tổ II sản xuất
trong tháng thứ nhất. (ĐK:
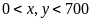 ).
).
Ta
có HPT:

Giải
HPT ta được
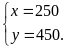
Vậy
trong tháng đầu tổ I sản xuất được
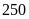 chi tiết máy, tổ II sản xuất được
chi tiết máy, tổ II sản xuất được
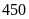 sản phẩm.
sản phẩm.
Một miếng đất hình chữ nhật có chu vi
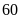 m. Nếu tăng chiều rộng thêm
m. Nếu tăng chiều rộng thêm
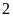 m và giảm chiều dài đi
m và giảm chiều dài đi
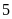 m thì diện tích miếng đất giảm đi
m thì diện tích miếng đất giảm đi
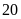 m
m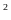 .
Tính chiều dài và chiều rộng ban đầu của mảnh đất.
.
Tính chiều dài và chiều rộng ban đầu của mảnh đất.
Lời giải
Gọi
chiều rộng, chiều dài ban đầu của hình chữ nhật lần
lượt là
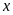 ,
,
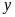 (m) (
(m) (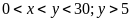 ).
).
Theo
đề bài, ta có HPT
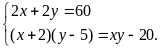
Giải
HPT ta được
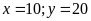 (TMĐK).
(TMĐK).
Vậy
chiều dài và chiều rộng ban đầu của mảnh đất là
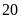 m và
m và
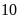 m.
m.
Cho một miếng đất hình chữ nhật. Nếu tăng chiều rộng thêm
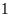 m và tăng chiều dài thêm
m và tăng chiều dài thêm
 m thì diện tích miếng đất tăng lên
m thì diện tích miếng đất tăng lên
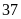 m
m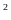 .
Nếu giảm chiều rộng thêm
.
Nếu giảm chiều rộng thêm
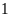 m và tăng chiều dài thêm
m và tăng chiều dài thêm
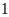 m thì diện tích miếng đất giảm đi
m thì diện tích miếng đất giảm đi
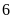 m
m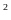 .
Tính chiều dài và chiều rộng ban đầu của mảnh đất.
.
Tính chiều dài và chiều rộng ban đầu của mảnh đất.
Lời giải
Gọi
chiều dài, chiều rộng ban đầu của hình chữ nhật lần
lượt là
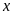 ,
,
 (m) (
(m) (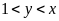 ).
).
Theo
đề bài, ta có HPT
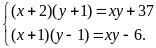
Giải
HPT ta được
 (TMĐK).
(TMĐK).
Vậy
chiều dài, chiều rộng ban đầu của hình chữ nhật là
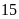 m và
m và
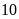 m.
m.
Một mảnh vườn hình chữ nhật có độ dài đường chéo là
 m, chiều dài lớn hơn chiều rộng là
m, chiều dài lớn hơn chiều rộng là
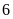 m. Tính chiều dài và chiều rộng mảnh vườn đó.
m. Tính chiều dài và chiều rộng mảnh vườn đó.
Lời giải
Gọi
chiều rộng, chiều dài của mảnh vườn lần lượt là
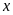 ,
,
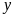 (m) (
(m) (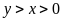 ).
).
Theo
đề bài, ta có HPT:
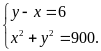
Giải
HPT ta được
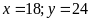 (TMĐK).
(TMĐK).
Vậy,
chiều dài và chiều rộng mảnh vườn là
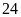 m và
m và
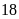 m.
m.
Một đoàn xe vận tải dự định điều một số xe cùng loại đi vận chuyển
 tấn hàng. Lúc sắp khởi hành, đoàn xe được giao chở
thêm
tấn hàng. Lúc sắp khởi hành, đoàn xe được giao chở
thêm
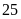 tấn nữa, do đó phải điều thêm
tấn nữa, do đó phải điều thêm
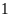 xe cùng loại và mỗi xe phải chở thêm
xe cùng loại và mỗi xe phải chở thêm
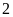 tấn. Tính số xe phải điều theo dự định. Biết mỗi
xe chở số hàng như nhau và số xe nhỏ hơn
tấn. Tính số xe phải điều theo dự định. Biết mỗi
xe chở số hàng như nhau và số xe nhỏ hơn
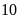 .
.
Lời giải
Gọi
số xe tham gia chở hàng là
 (xe,
(xe,
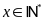 );
số hàng mỗi xe cần vận chuyển là
);
số hàng mỗi xe cần vận chuyển là
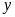 (tấn,
(tấn,
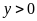 );
.
);
.
Theo
đầu bài, ta có HPT:
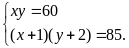
Giải
HPT được
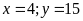 (TMĐK).
(TMĐK).
Vậy,
có
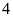 xe tham gia chở hàng.
xe tham gia chở hàng.
--- HẾT ---
Ngoài Phương Pháp Giải Bài 5 Toán 9 Tập 2 Giải Bài Toán Bằng Cách Lập Hệ (Tiếp Theo) – Toán 9 thì các tài liệu học tập trong chương trình 9 sẽ được cập nhật liên tục và nhanh nhất có thể sau khi kỳ thi diễn ra trên Danh mục Tài Liệu Học Tập nhằm giúp các bạn đọc thuận tiện trong việc nghiên cứu tài liệu. Quý thày cô và các bạn đọc có thể chia sẻ thêm những tài liệu học tập hữu ích đến địa chỉ email của chúng tôi, nhằm xây dựng nên kho đề thi phong phú, đa dạng cho các em học sinh tham khảo và rèn luyện.
Bài viết này sẽ dẫn bạn qua từng bước cụ thể trong việc lập hệ phương trình để giải quyết bài toán số 5 trong cuốn sách Toán 9 Tập 2. Chúng ta sẽ cùng nhau xác định các biến số, thiết lập hệ phương trình và thực hiện các phép biến đổi để đưa về dạng dễ dàng giải.
Bằng cách áp dụng phương pháp giải bài 5 toán 9 tập 2 – giải bài toán bằng cách lập hệ (tiếp theo), bạn sẽ trang bị cho mình một khả năng mạnh mẽ để giải quyết các bài toán phức tạp và thách thức. Điều này không chỉ giúp bạn nắm vững kiến thức toán mà còn phát triển khả năng phân tích, tổ chức và giải quyết vấn đề.
Hãy cùng tham gia và thực hành với “Phương Pháp Giải Bài 5 Toán 9 Tập 2 – Giải Bài Toán Bằng Cách Lập Hệ (Tiếp Theo)”. Bằng sự nỗ lực và cố gắng trong việc giải quyết bài toán, bạn sẽ tự tin hơn trong việc áp dụng kiến thức toán vào thực tế và phát triển tư duy logic. Chúc các bạn thành công và vui vẻ trong hành trình toán học!
>>> Bài viết có liên quan:







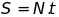 .
Trong đó
.
Trong đó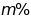 thì ta được một một lượng mới là
thì ta được một một lượng mới là
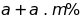 .
.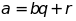 .
.