Giáo Án Bồi Dưỡng Học Sinh Giỏi Toán 6: Dấu Hiệu Chia Hết-Chia Có Dư
>>> Mọi người cũng quan tâm:
Giáo Án Bồi Dưỡng Học Sinh Giỏi Toán 6: Dấu Hiệu Chia Hết-Chia Có Dư – Toán 6 là tài liệu học tập được Trang Tài Liệu biên soạn và sưu tầm từ những nguồn dữ liệu mới nhất hiện nay. Tài liệu này sẽ giúp các em luyện tập, củng cố kiến thức từ đó nâng cao điểm số cho môn học. Ngoài ra, cũng giúp các thầy cô giáo có nguồn tài nguyên phong phú để giảng dạy.
Dưới đây là bản đọc trực tuyến giúp thầy cô và các em học sinh có thể nghiên cứu Online hoặc bạn có thể tải miễn phí với phiên bản word để dễ dàng in ấn cũng như học tập Offline.
CHUYÊN ĐỀ 2: DẤU HIỆU CHIA HẾT – CHIA CÓ DƯ
LÝ THUYẾT
Định nghĩa.
Với mọi a, bN (b0) ta luôn tìm được số tự nhiên r sao cho
a = bq + r (0 r < b)
a là số bị chia, b là số chia, q là thương, r là số dư
- Nếu r = 0 ta được phép chia hết, tanói rằng a chia hết
cho b (a:
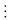 b),
hay a là bội của b, hay b chia hết a, hay b là ước của a
(b/a).
b),
hay a là bội của b, hay b chia hết a, hay b là ước của a
(b/a).
- Nếu r > 0,ta được phép chia có dư, ta nói rằng a
không chia hết cho b (a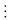 :b).
:b).
2. Các tính chất về phép chia hết. (10 tính chất)
Số 0 chia hết cho mọi số b0.
Số a chia hết cho mọi a0.
Nếu a
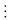 b,
b
b,
b
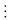 c
thì a
c
thì a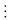 c.
c.Nếu a và b cùng chia hết cho m thì a+b và a-b đều chia hết cho m.
Nếu một trong hai số a và b chia hết cho m, số kia không chia hết cho m thì a+b và a-b đều không chia hết cho m.
Nếu tổng hoặc hiệu hai số chia hết cho m và một trong hai số ấy chia hết cho m thì số còn lại cũng chia hết cho m.
Nếu một thừa số của tích chia hết cho m thì tích chia hết cho m.
Suy ra a
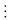 m thì an
m thì an
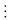 m
(nN*).
m
(nN*).Nếu a
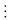 m, b
m, b
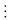 n thì ab
n thì ab
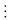 mn
mnSuy ra nếu a
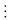 b thì an
b thì an
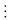 bn.
bn.Nếu một số chia hết cho hai số nguyên tố cùng nhau thì nó chia hết cho tích của hai số đó.
Nếu tích ab chia hết cho m, trong đó b và m là hai số nguyên tố cùng nhau thì a chia hết cho m.
Nếu một tích chia hết cho số nguyên tố p thì tồn tại một thừa số của tích chia hết cho p. Suy ra nếu an
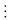 p, p là ngyên tố thì a
p, p là ngyên tố thì a
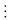 p.
p.
Dấu hiệu chia hết cơ bản:
Dấu hiệu chia hết cho 2: Các số có chữ số tận cùng là: 0,2,4,6,8
Dấu hiệu chia hết cho 5: Các số có chữ số tận cùng là: 0,5
Dấu hiệu chia hết cho 3: Tổng các chữ số của số đó phải chia hết cho 3
Dấu hiệu chia hết cho 9: Tổng các chữ số của số đó phải chia hết cho 9
Dấu hiệu chia hết cho các số khác:
Dấu hiệu chia hết cho 4(25): Hai chữ số tận cùng tạo thành một số chia hết cho 4(25)
Dấu hiệu chia hết cho 8(125): Ba chữ số tận cùng tạo thành một số chia hết cho 8(125)
Dấu hiệu chia hết cho 11: Tổng các chữ số hàng lẻ trừ đi tổng chữ số hàng chẵn chia hết cho 11 hoặc ngược lại.
CÁC BÀI TOÁN LIÊN QUAN
Bài 1: Chứng minh rằng:
A = 1 + 3 + 32 + …+ 311 chia hết cho 4
B = 165 + 215 chia hết cho 33
C = 5 + 52 + 53 + …+ 58 chia hết cho 30
D = 45 + 99 + 180 chia hết cho 9
E = 1 + 3 + 32 + 33 +…+ 3119 chia hết cho 13.
F = 1028 + 8 chia hết cho 72
G = 88 + 220 chia hết cho 17
H = 2 + 22 + 23 +…+ 260 chia hết cho 3, 7, 15
I = E = 1 + 3 + 32 + 33 +…+ 31991 chia cho 13 và 41.
J = 10n + 18n – 1 chia hết cho 27
K = 10n + 72n – 1 chia hết cho 81
Bài 2: Chứng minh rằng:
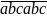 chia hết cho 7, 11 và 13
chia hết cho 7, 11 và 13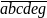 chia hết cho 23 và 29, biết
chia hết cho 23 và 29, biết
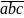 = 2.
= 2.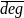
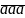 chia hết cho a
chia hết cho aChứng minh rằng số gồm 27 chữ số 1 thì chia hết cho 27
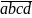 chia hết cho 29 <=> a + 3b + 9c + 27d chia hết cho 29
chia hết cho 29 <=> a + 3b + 9c + 27d chia hết cho 29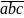 chia hết cho 21 <=> a - 2b + 4c chia hết cho 21
chia hết cho 21 <=> a - 2b + 4c chia hết cho 21
Bài 3: Chứng minh rằng:
Chứng minh rằng tổng ba số tự nhiên liên tiếp chia hết cho 3.
Chứng minh rằng
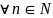 thì 60n + 45 chia hết cho 15 nhưng không chia hết cho 30.
thì 60n + 45 chia hết cho 15 nhưng không chia hết cho 30.Chứng minh rằng không có số tự nhiên nào mà chia cho 15 dư 6 và chia 9 dư 1.
Chứng minh rằng: (1005a + 2100b) chia hết cho 15,
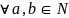 .
.Chứng minh rằng: A = n2 + n + 1 không chia hết cho 2 và 5,
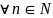 .
.Chứng minh rằng:
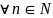 thì tích (n + 3)(n + 6) chia hết cho 2.
thì tích (n + 3)(n + 6) chia hết cho 2.
Tìm các chữ số a và b sao cho a – b = 4 và
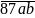 chia hết cho 9
chia hết cho 9Cho n =
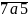 +
+
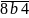 .
Biết a – b = 6 và n chia hết cho 9. Tìm a và b
.
Biết a – b = 6 và n chia hết cho 9. Tìm a và bTìm hai số tự nhiên chia hết cho 9, biết rằng: Tổng của chúng bằng
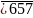 và hiệu của chúng bằng
và hiệu của chúng bằng
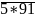 .
.Tìm chữ số a, biết rằng:
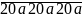 chia hết cho 7
chia hết cho 7Tìm số tự nhiên có hai chữ số, sao cho nếu viết nó tiếp sau số 1999 thì ta được một số chia hết cho 37.
Tìm các số tự nhiên chia cho 4 dư 1, còn chia cho 25 thì dư 3
Tìm số tự nhiên có 5 chữ số, biết rằng số đó bằng 45 lần tích các chữ số của nó.
Tìm số
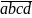 ,
biết rằng số đó chia hết cho tích các số
,
biết rằng số đó chia hết cho tích các số
 và
và
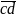 .
.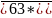 chia hết cho cả 2,3,5,9
chia hết cho cả 2,3,5,9Tìm tất cả các số có 5 chữ số dạng:
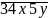 mà chia hết cho 36.
mà chia hết cho 36.
Từ 1 đến 100 có bao nhiêu số chia hết cho 2, bao nhiêu số chia hết cho 5?
Có bao nhiêu số tự nhiên nhỏ hơn 100 chia hết cho 5 và dư 3?
Có bao nhiêu số tự nhiên có ba chữ số và chia hết cho 3?
Trong các số tự nhiên nhỏ hơn 1000, có bao nhiêu số chia hết cho 2 nhưng không chia hết cho 5?
Bài 1: Chứng minh rằng:
A = 1 + 3 + 32 + …+ 311 chia hết cho 4
A = (1 + 3) + 32.(1 + 3) + … + 310(1 + 3)
A = 4 + 32.4 + … + 310.4
A = 4.(1 + 32
+ 310)
 4(đpcm)
4(đpcm)
B = 165 + 215 chia hết cho 33
B = (24)5 + 215
B = 220 + 215
B = 215.(1 + 25)
B = 215.33
 33 (đpcm)
33 (đpcm)
C = 5 + 52 + 53 + …+ 58 chia hết cho 30
C = (5 + 52) + 52.(5 + 52) + … + 56.(5 + 52)
C = 30 + 52.30 + … + 56.30
C = 30.(1 + 52
+…+ 56)
 30 (đpcm)
30 (đpcm)
D = 45 + 99 + 180 chia hết cho 9
Ta có: 45
 9; 99
9; 99
 9; 180
9; 180
 9 nên D = 45 + 99 + 180
9 nên D = 45 + 99 + 180
 9 (đpcm) (tính chất chia hết của một tổng)
9 (đpcm) (tính chất chia hết của một tổng)
E = 1 + 3 + 32 + 33 +…+ 3119 chia hết cho 13.
E = (1 + 3 + 32) + 33.(1 + 3 + 32) + … + 3117.(1 + 3 + 32)
E = 13 + 33.13 + … + 3117.13
E = 13.(1 + 33
+ … + 3117)
 13 (đpcm)
13 (đpcm)
F = 1028 + 8 chia hết cho 72
Ta thấy: 72 = 8.9
Ta có:
1028
+ 8
 9 vì tổng các chữ số bằng 9
9 vì tổng các chữ số bằng 9
1028
+ 8
 8 vì có tận cùng là 008
8 vì có tận cùng là 008
Mà (8;9) = 1
nên 1028 + 8
 8.9 = 72 (đpcm)
8.9 = 72 (đpcm)
G = 88 + 220 chia hết cho 17
G = (23)8 + 220
G = 224 + 220
G = 220.(24 + 1)
G = 220.17 17 (đpcm)
17 (đpcm)
H = 2 + 22 + 23 +…+ 260 chia hết cho 3, 7, 15
Ta có:
H = 2.(1 + 2) + 23.(1 + 2) + … + 259.(1+2)
H = 2.3 + 23.3 + … + 259.3
H = 3.(2 + 23
+ .. . + 259)
 3
3
Ta có:
H = 2.(1 + 2 + 22) + 24.(1 + 2 + 22) + … + 258.(1 + 2 + 22)
H = 2.7 + 24.7 + … + 258.7
H = 7.(2 + 24
+…+ 258)
 7
7
Ta có:
H = 2.(1 + 2 + 22 + 23) + 25.(1 + 2 + 22 + 23) +…+ 257.(1 + 2 + 22 + 23)
H = 2.15 + 25.15 + … + 257.15
H = 15.(2 + 25
+…+ 257)
 15
15
Vậy H chia hết cho 3, 7, 15.
I = 1 + 3 + 32 + 33 +…+ 31991 chia cho 13 và 41.
Ta có:
I = (1 + 3 + 32) + 33.(1 + 3 + 32) + … + 31989.(1 + 3 + 32)
I = 13 + 33.13 + … + 31989.13
I = 13.(1 + 33
+ … + 31989)
 13 (đpcm)
13 (đpcm)
Ta có:
I = (1 + 32 + 34 + 36) + (3 + 33 + 35 + 37) + … + (31984 + 31986 + 31988 + 31990 ) + (31985 + 31987 + 31989 + 31991 )
I = (1 + 32 + 34 + 36) + 3.(1 + 32 + 34 + 36) +…+ 31984.(1 + 32 + 34 + 36) + 31985.(1 + 32 + 34 + 36)
I = 820.(1 + 3+ …+ 31984 + 31985)
I = 41.20.(1 +
3+ …+ 31984 + 31985)
 41
41
Vậy I chia hết cho 13, 41.
J = 10n + 18n – 1 chia hết cho 27
Ta có:
J = 10n + 18n – 1 = (10n - 1) + 18n
J = 99...9 + 18n (số 99...9 có n chữ số
9)
j = 9(11...1 + 2n) (số 11...1 có n chữ số 1)
J = 9.L
Xét biểu thức trong
ngoặc
L = 11...1 + 2n = 11...1 - n + 3n (số 11...1
có n chữ số 1).
Ta đã biết một số tự nhiên
và tổng các chữ số của nó sẽ có cùng số dư trong
phép chia cho 3. Số 11...1 (n chữ số 1) có tổng các chữ
số là 1 + 1 + ... + 1 = n (vì có n chữ số 1).
=>
11...1 (n chữ số 1) và n có cùng số dư trong phép chia cho
3
=> 11...1 (n chữ số 1) - n chia hết cho 3
=> L chia hết cho 3
=> 9.L chia hết cho 27 hay J =10n + 18n – 1 chia hết cho 27 (đpcm)
K = 10n + 72n – 1 chia hết cho 81
Ta có:
K = 10n
+ 72n – 1
K
=10n
-
1 + 72n
K
=(10-1)[10n-1
+
10n-2+...+
10 + 1] + 72n
K
=9.[10n-1
+
10n-2+...+
10 + 1] - 9n + 81n
K
=9. [10n-1
+
10n-2+...+
10 + 1- n] + 81n
K
=9[(10n-1
- 1)+(10n-2
- 1)+...+(10-1) + (1 – 1)] + 81n
Ta
có:
10k - 1 = (10-1)[10k-1 + ... + 10 +1] chia hết cho 9
=>9[(10n-1 - 1)+(10n-2 - 1)+...+(10-1) + (1 – 1)] chia hết cho 81
=>9[10n-1 + 10n-2+...+ 10 + 1- n] + 81n chia hết cho 81
=>K
= 10n + 72n – 1
 81 (đpcm).
81 (đpcm).
Bài 2: Chứng minh rằng:
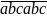 chia hết cho 7, 11 và 13
chia hết cho 7, 11 và 13
Ta có:
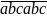 = 1000
= 1000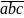 +
+
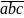 = 1001.
= 1001.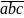 = 7.11.13.
= 7.11.13.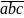
 7; 11; 13 (đpcm)
7; 11; 13 (đpcm)
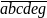 chia hết cho 23 và 29, biết
chia hết cho 23 và 29, biết
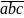 = 2.
= 2.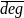
Ta có:
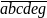 = 1000
= 1000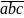 +
+
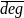 = 1000.2.
= 1000.2.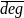 +
+
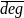
=
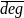 (2000
+ 1) =
(2000
+ 1) =
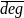 .2001
=
.2001
=
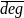 .23.29.3
.23.29.3
 23; 29 (đpcm)
23; 29 (đpcm)
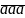 chia hết cho a
chia hết cho a
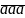 = 100.a + 10.a + a = 111.a
= 100.a + 10.a + a = 111.a
 a (đpcm)
a (đpcm)
Chứng minh rằng số gồm 27 chữ số 1 thì chia hết cho 27
Gọi A là số gồm 27 chữ số 1, B là số gồm 9 chữ số 1.
Lấy A chia cho B ta được thương là C=10..010..01.
Như vậy : A=B.C , trong đó B chia hết cho 9, C chia hết cho 3
Vậy A chia hết cho 27 (đpcm).
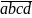 chia hết cho 29 <=> a + 3b + 9c + 27d chia hết cho 29
chia hết cho 29 <=> a + 3b + 9c + 27d chia hết cho 29
Ta có:
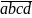
 29
29
1000.a +
100.b + 10.c + d
 29
29
2000.a +
200.b + 20.c +2d
 29
29
2001.a –
a + 203.b – 3.b + 29.c – 9.c + 29.d – 27.d
 29
29
(2001.a +
203.b + 29.c + 29.d) – (a + 3.b + 9.c + 27.d)
 29
29
(69.29.a +
7.29.b + 29.c + 29.d) - (a + 3.b + 9.c + 27.d)
 29
29
(a + 3.b +
9.c + 27.d)
 29 (đpcm)
29 (đpcm)
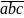 chia hết cho 21 <=> a - 2b + 4c chia hết cho 21
chia hết cho 21 <=> a - 2b + 4c chia hết cho 21
Ta có:
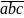 = 100a + 10b
+ c
= 100a + 10b
+ c
=
100a - 84a +10b - 42b + c + 63c +84a + 42b -63c
= 16a - 32b +
64c + 84a + 42b -63c
=
16( a-2b+4c) + 84a + 42b -63c
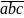 chia hết cho 21, 84a + 42b -63c chia hết
cho 21 => a-2b+4c (đpcm)
chia hết cho 21, 84a + 42b -63c chia hết
cho 21 => a-2b+4c (đpcm)
Bài 3: Chứng minh rằng:
Chứng minh rằng tổng ba số tự nhiên liên tiếp chia hết cho 3.
Gọi 3 số tự nhiên liên tiếp là: a; a + 1; a + 2
Tổng của ba
số là: a + a +1 + a +2 = 3.a + 3
 3(đpcm) (tính chất chia hết của một tổng)
3(đpcm) (tính chất chia hết của một tổng)
Chứng minh rằng
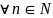 thì 60n + 45 chia hết cho 15 nhưng không chia hết cho 30.
thì 60n + 45 chia hết cho 15 nhưng không chia hết cho 30.
Ta có:
60
 15 => 60n
15 => 60n
 15 ; 45
15 ; 45
 15 => 60n + 45
15 => 60n + 45
 15 (theo tính chất chia hết của một tổng)
15 (theo tính chất chia hết của một tổng)
60
 30 => 60n
30 => 60n
 30; 45 không chia hết cho 30 => 60n + 45 không chia hết cho
30 ( theo tính chất chia hết của một tổng).
30; 45 không chia hết cho 30 => 60n + 45 không chia hết cho
30 ( theo tính chất chia hết của một tổng).
Chứng minh rằng không có số tự nhiên nào mà chia cho 15 dư 6 và chia 9 dư 1.
Giả sử có
số a
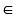 N thỏa mãn cả hai điều kiện trên thì:
N thỏa mãn cả hai điều kiện trên thì:
 => Mâu thuẫn
=> Mâu thuẫn
Vậy không có số tự nhiên nào thỏa mãn. (đpcm)
Chứng minh rằng: (1005a + 2100b) chia hết cho 15,
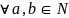 .
.
Vì 1005 chia hết cho 3 nên 1005.a chia hết cho 3 với mọi a
Vì 2100 chia hết cho 3 nên 2100.b chia hết cho 3 với mọi b
(1005a + 2100b) chia hết cho 3 với mọi a,b
Vì 1005 chia hết cho 5 nên 1005a chia hết cho 5 với mọi a
Vì 2100 chia hết cho 5 nên 2100b chia hết cho 5 với mọi b
(1005a + 2100b) chia hết cho 5 với mọi a, b
Mà (3;5) = 1 => (1005a + 2100b) chia hết cho 15 với mọi a,b
Chứng minh rằng: A = n2 + n + 1 không chia hết cho 2 và 5,
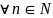 .
.
Vì n.(n+1) là tích hai số tự nhiên liên tiếp, trong 2 số liên tiếp luôn luôn có 1 số chẵn => n.(n+1) là số chẵn, cộng thêm 1 sẽ là số lẻ => n.(n+1) + 1 là số lẻ, không chia hết cho 2.
Để chứng minh n.(n+1) + 1 không chia hết cho 5 ta thấy hai số n và n+1 có thể có các chữ số tận cùng sau:
n tận cùng là 0, 1, 2, 3, 4, 5, 6, 7, 8, 9; tương ứng số tận cùng của n+ 1 như sau:
n+ 1 tận cùng là 1, 2, 3, 4, 5, 6, 7, 8, 9, 0
=> tích của n.(n+1) tận cùng là:
0, 2, 6, 2, 0, 0, 2, 6, 2, 0
Hay là n.(n+1) tận cùng là 0, 2, 6
=> n.(n+1) +1 tận cùng là: 1, 3, 7 không chia hết cho 5
Chứng minh rằng:
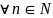 thì tích (n + 3)(n + 6) chia hết cho 2.
thì tích (n + 3)(n + 6) chia hết cho 2.
Ta xét các trường hợp:
(+) Nếu n là số lẻ thì n + 3 là số chẵn ; n + 6 là số lẻ. Mà số chẵn nhân với số lẻ có tận cùng là số chẵn => (n+3) (n+6) chia hết cho 2.
(+) Nếu n là số chẵn thì n+3 là số lẻ ; n+6 là số chẵn. Mà tích của 1 số lẻ với 1 số chẵn có tận cùng là số chẵn nên => (n+3)(n+6) chia hết cho 2.
Vậy
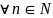 thì tích (n + 3)(n + 6) chia hết cho 2 (đpcm).
thì tích (n + 3)(n + 6) chia hết cho 2 (đpcm).
Tìm các chữ số a và b sao cho a – b = 4 và
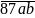 chia hết cho 9
chia hết cho 9
Vì a – b = 4
=> a = b + 4 mà
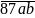 chia hết cho 9 => 15 + a + b chia hết cho 9 => 19 + 2b
chia hết cho 9 => b = 4; a = 8.
chia hết cho 9 => 15 + a + b chia hết cho 9 => 19 + 2b
chia hết cho 9 => b = 4; a = 8.
Cho n =
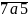 +
+
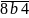 .
Biết a – b = 6 và n chia hết cho 9. Tìm a và b
.
Biết a – b = 6 và n chia hết cho 9. Tìm a và b
n
chia hết cho 9
![]()
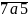 +
+
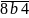 chia hết cho 9
chia hết cho 9
![]() 7
+ a + 5 + 8 + b + 4 chia hết cho 9
7
+ a + 5 + 8 + b + 4 chia hết cho 9
![]() 24
+ a + b chia hết cho 9.
24
+ a + b chia hết cho 9.
Mà
a, b ![]() 9
9 ![]() a
+ b
a
+ b ![]() 18
18
![]() a
+ b = 3 hoặc a + b = 12.
a
+ b = 3 hoặc a + b = 12.
-
a + b = 3
![]() a
= (3 + 6) : 2 = 9/2 không thuộc N (loại)
a
= (3 + 6) : 2 = 9/2 không thuộc N (loại)
-
a + b = 12
![]() a
= (12 + 6) : 2 = 9 ; b = 9 - 6 = 3 (chọn)
a
= (12 + 6) : 2 = 9 ; b = 9 - 6 = 3 (chọn)
Vậy
a = 9 và b = 3.
Tìm hai số tự nhiên chia hết cho 9, biết rằng: Tổng của chúng bằng
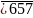 và hiệu của chúng bằng
và hiệu của chúng bằng
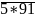 .
.
Vì hai số
chia hết cho 9 nên tổng của hai số là:
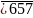
 9 * = 9; và hiệu của
chúng bằng
9 * = 9; và hiệu của
chúng bằng
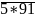
 9 * = 3.
9 * = 3.
Vậy tổng
của hai số là 9657 và hiệu của hai số là 5391.
Hai số cần tìm là: 7524 và 2133
Tìm chữ số a, biết rằng:
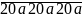 chia hết cho 7
chia hết cho 7
Ta có
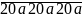 =
=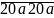 .1000 +
.1000 +
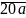
= (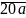 .1000
+
.1000
+
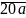 ).1000
+
).1000
+
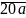
= 1001.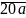 .1000
+
.1000
+
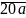
= 7.143.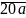 .1000
+
.1000
+
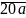
 7
7
Mà 7.143.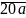 .1000
.1000
 7 =>
7 =>
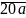
 7
7
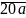 = 200 + a = 196 + 4 + a = 196 + (4 + a)
= 200 + a = 196 + 4 + a = 196 + (4 + a)
 7
7
Mà 196
 7 => 4 + a
7 => 4 + a
 7 => a = 3
7 => a = 3
Tìm số tự nhiên có hai chữ số, sao cho nếu viết nó tiếp sau số 1999 thì ta được một số chia hết cho 37.
Gọi số phải
tìm là
 . Ta có:
. Ta có:
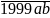
 37 => 199900 +
37 => 199900 +
 37
37
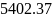 + 26 +
+ 26 +
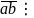 37
3726 +
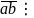 37
37
Vậy
 =
{11; 48; 85}
=
{11; 48; 85}
Tìm các số tự nhiên chia cho 4 dư 1, còn chia cho 25 thì dư 3
Gọi
thương của số tự nhiên x cần tìm tuần tự là a và
b
Theo
đề, ta có:
x
= 4a + 1
x
= 25b + 3
<=>
4a + 1 = 25b + 3
4a
= 25b + 2
a
= (25b + 2)/4
b
= 2 ; a = 13 <=> x = 53
b
= 6 ; a = 38 <=> x = 153
b
= 10 ; a = 63 <=> x = 253
b
= 14 ; a = 88 <=> x = 353
b
= 18 ; a = 113 <=> x = 453
...
Đáp
số:
Tất
cả các số tự nhiên, tận cùng là 53 đều thoả mãn
điều kiện.
Tìm số tự nhiên có 5 chữ số, biết rằng số đó bằng 45 lần tích các chữ số của nó.
Goi
số đó là
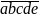 (a,
b, c,d, e là các chữ số và a khác 0). Theo đề bài ta
có:
(a,
b, c,d, e là các chữ số và a khác 0). Theo đề bài ta
có:
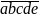 =
45*a*b*c*d*e
=
45*a*b*c*d*e
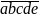 = 5*9*a*b*c*d*e
= 5*9*a*b*c*d*e
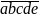 chia hết cho 5 nên e = 0 (loại) hoăc e = 5. Dễ thấy e = 5.
Số abcd5 là số lẻ nên a, b,c, d, e đầu là các chữ số
lẻ.
chia hết cho 5 nên e = 0 (loại) hoăc e = 5. Dễ thấy e = 5.
Số abcd5 là số lẻ nên a, b,c, d, e đầu là các chữ số
lẻ.
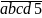 = 5*9*a*b*c*d*5
= 5*9*a*b*c*d*5
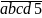 = 25*9*a*b*c*d
= 25*9*a*b*c*d
Do đó,
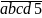 chia hết cho 25. Mà
chia hết cho 25. Mà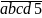 = abc*100 + d5. d5 chia hết cho 25 và d lẻ => d = 7.
= abc*100 + d5. d5 chia hết cho 25 và d lẻ => d = 7.
Ta
có
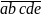 =
=
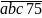 chia hết cho 9 nên a + b + c + 7 + 5 = a + b + c + 12 chia hết
cho 9. Mà 2 < a + b + c < 28.
chia hết cho 9 nên a + b + c + 7 + 5 = a + b + c + 12 chia hết
cho 9. Mà 2 < a + b + c < 28.
Do
đó: a + b + c = 6; 15 hoặc 24
Vì
a, b, c lẻ nên a + b + c lẻ = > a + b + c = 15
Mà
15 = 1 + 5 + 9 = 1 + 7 + 7 = 3 + 3 + 9 = 3 + 5 + 7 = 5 + 5 + 5
Vì
ta có 45*a*b*c*7*5 < 100000
nên
a*b*c < 64. Do đó ta chỉ còn xét hai trường hợp,
ba chữ số a, b, c có tổng là 1 + 5 + 9 và 1 + 7 + 7.
Thử
chọn thấy 77175 là thích hợp.
Đ/S:
77175.
Tìm số
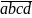 ,
biết rằng số đó chia hết cho tích các số
,
biết rằng số đó chia hết cho tích các số
 và
và
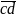 .
.
Ta
có:
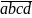 =
=
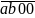 +
+
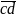 = 100.
= 100. +
+
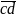 chia hết cho
chia hết cho
 .
.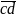
=>
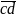 chia hết cho
chia hết cho
 .
Đặt
.
Đặt
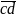 = k.
= k. (1 ≤ k ≤ 9)
(1 ≤ k ≤ 9)
có
 .100
+ k.
.100
+ k. chia hết cho
chia hết cho
 .
.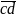 =
=
 .k.
.k.
=> 100 + k chia hết cho k. (1) => 100 chia hết cho k
(1) => 100 chia hết cho k
=> k = {1, 2, 4, 5}
+ k
= 1;
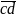 =
=
 ;
từ (1) => 101 chia hết cho
;
từ (1) => 101 chia hết cho
 vô lí vì 101 nguyên tố
vô lí vì 101 nguyên tố
+ k = 2;
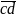 = 2.
= 2. ,
từ (1) => 102 chia hết cho 2.
,
từ (1) => 102 chia hết cho 2. => 51 chia hết cho
=> 51 chia hết cho

 không thể là 51 (vì nếu thế thì
không thể là 51 (vì nếu thế thì
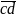 = 102 vô lí) =>
= 102 vô lí) =>
 = 17 =>
= 17 =>
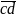 = 34
= 34
Số cần tìm là 1734 (dễ kiểm tra 1734 : (17.34) =
3)
+
k = 4;
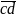 = 4.
= 4. => 104 chia hết cho 4.
=> 104 chia hết cho 4. => 26 chia hết cho
=> 26 chia hết cho
 =>
=>
 = 13,
= 13,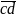 = 52 (nhận) hoặc
= 52 (nhận) hoặc
 = 26,
= 26,
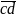 = 104 (loại)
= 104 (loại)
+ k = 5;
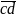 = 5.
= 5. ,
từ (1) => 105 chia hết cho 5.
,
từ (1) => 105 chia hết cho 5. => 21 chia hết cho
=> 21 chia hết cho

=>
 = 21 =>
= 21 =>
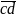 = 105 vô lí
= 105 vô lí
Vậy có hai cặp số thỏa mãn yêu cầu là: 1734 và 1352
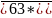 chia hết cho cả 2,3,5,9
chia hết cho cả 2,3,5,9
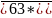 chia hết cho 2 và 5 =>
chia hết cho 2 và 5 =>
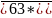 =
=
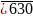 .
.
Vì
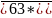 chia hết cho 9 nên tổng các số phải chia hết cho 9
chia hết cho 9 nên tổng các số phải chia hết cho 9
* + 6 + 3 + 0 = * + 9 chia hết cho 9
* = 0 (loại) hoặc * = 9.
Số chia hết cho 9 thì sẽ chia hết cho 3. Vậy số cần tìm là: 9630
Tìm tất cả các số có 5 chữ số dạng:
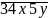 mà chia hết cho 36.
mà chia hết cho 36.
Ta có: 36 = 9.4 mà ƯC(4;9) = 1
Vậy để
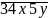 chia hết cho 36 thì
chia hết cho 36 thì
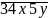 chia hết cho 4 và 9
chia hết cho 4 và 9
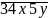 chia hết cho 9 3+4+x+5+y
chia hết cho 9 3+4+x+5+y
 9
12 + x + y
9
12 + x + y
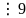 (1)
(1)
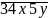 chia hết cho 4
chia hết cho 4
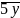 chia hết cho 4 => y = 2 hoặc y = 6
chia hết cho 4 => y = 2 hoặc y = 6
Với y = 2
thay vào (1) => 14 + x
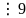 => x = 4
=> x = 4
Với y = 6
thay vào (1) => 18 + x
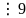 => x = 0 hoặc x = 9
=> x = 0 hoặc x = 9
Vậy các cặp (x, y) cần tìm là: (4; 2), (0; 6), (9; 6).
Từ 1 đến 100 có bao nhiêu số chia hết cho 2, bao nhiêu số chia hết cho 5?
Các số chia hết cho 2 từ 1 đến 100 là: 2; 4; 6; 8; …; 100
Số các số chia hết cho 2 từ 1 đến 100 là
(100 – 2) : 2 + 1= 50 (số)
Các số chia hết cho 5 từ 1 đến 100 là: 5; 10; 15; …; 100
Số các số chia hết cho 5 từ 1 đến 100 là
(100 – 5) : 5 + 1= 20 (số)
Có bao nhiêu số tự nhiên nhỏ hơn 100 chia cho 5 và dư 3?
Số chia cho 5 và dư 3 nhỏ hơn 100 là: 3; 8; 13; 18; …; 98
Vậy có:
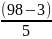 +1= 19 + 1 = 20 số tự nhiên nhỏ hơn 100 chia cho 5 và dư 3
+1= 19 + 1 = 20 số tự nhiên nhỏ hơn 100 chia cho 5 và dư 3
Có bao nhiêu số tự nhiên có ba chữ số và chia hết cho 3?
Các số tự nhiên chia hết cho 3 và có 3 chữ số là: 102; 105; 108; …; 999
Vậy có:
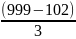 + 1 = 299+1 = 300 số tự nhiên chia hết cho 3 và có 3 chữ
số.
+ 1 = 299+1 = 300 số tự nhiên chia hết cho 3 và có 3 chữ
số.
Trong các số tự nhiên nhỏ hơn 1000, có bao nhiêu số chia hết cho 2 nhưng không chia hết cho 5?
Các số tự nhiên chia hết cho cả 2 và 5 là: 0; 2; 4 ; 6; 8; …; 998; 1000
Các số tự nhiên chẵn chia hết cho 5 là: 0; 10; 20;…;990;1000
Vậy có: [
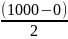 + 1] -[
+ 1] -[
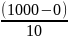 + 1 ] = 501 – 101 = 400 số tự nhiên nhỏ hơn 1000 chia hết
cho 2 nhưng không chia hết cho 5.
+ 1 ] = 501 – 101 = 400 số tự nhiên nhỏ hơn 1000 chia hết
cho 2 nhưng không chia hết cho 5.
Ngoài Giáo Án Bồi Dưỡng Học Sinh Giỏi Toán 6: Dấu Hiệu Chia Hết-Chia Có Dư – Toán 6 thì các tài liệu học tập trong chương trình 6 sẽ được cập nhật liên tục và nhanh nhất có thể sau khi kỳ thi diễn ra trên Danh mục Tài Liệu Học Tập nhằm giúp các bạn đọc thuận tiện trong việc nghiên cứu tài liệu. Quý thày cô và các bạn đọc có thể chia sẻ thêm những tài liệu học tập hữu ích đến địa chỉ email của chúng tôi, nhằm xây dựng nên kho đề thi phong phú, đa dạng cho các em học sinh tham khảo và rèn luyện.
Giáo án này tập trung vào hai khái niệm quan trọng trong toán học: “chia hết” và “chia có dư”. Học sinh sẽ được học cách nhận biết dấu hiệu chia hết và áp dụng chúng để giải quyết các bài toán có liên quan. Họ sẽ làm quen với các thuật ngữ và quy tắc cơ bản của chia hết, bao gồm bội số, ước số, và số nguyên tố. Ngoài ra, học sinh cũng sẽ được tìm hiểu về phép chia có dư và cách tính toán dư của phép chia.
Giáo án bồi dưỡng học sinh giỏi toán 6 với chuyên đề này sẽ cung cấp cho học sinh những kiến thức cơ bản và kỹ năng toán học cần thiết để giải quyết các bài toán liên quan đến dấu hiệu chia hết và chia có dư. Nó sẽ giúp học sinh hiểu rõ hơn về quy tắc và ứng dụng của chúng trong các bài toán thực tế.
Giáo án này sẽ bao gồm các hoạt động đa dạng như giảng dạy lý thuyết, thảo luận nhóm, bài tập rèn luyện và các bài toán ứng dụng. Ngoài ra, cũng có thể có các hoạt động tương tác và sử dụng công cụ học tập phù hợp để tăng cường hiệu quả giảng dạy.
>>> Bài viết có liên quan






