CHUYÊN ĐỀ 3: LŨY THỪA TRONG SỐ TỰ NHIÊN

CÁC DẠNG BÀI TẬP CƠ BẢN VÀ NÂNG CAO

• DẠNG 1: TÍNH GIÁ TRỊ CỦA BIỂU THỨC

1. 4¹⁰.8¹⁵

2. 4¹⁵.5³⁰

3. 

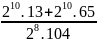
4. (1 + 2 + 3 + … + 100).(1² + 2² + 3² + … + 10²). (65.111 – 13.15.37)

5. 19991999.1998 – 19981998.1999

6. 

7. 

8. 

9. 

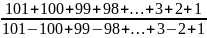
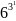
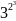
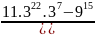
10. 9! – 8! – 7! . 8²

11. 27¹⁶ : 9¹⁰

• DẠNG 2: TÌM CHỮ SỐ TẬN CÙNG

Bài 1: Tìm chữ số tận cùng của các số sau:

1. 74³⁰

2. 49³¹

3. 87³²

4. 58³³

5. 23³⁵

6. 2¹⁰¹

7. 3¹⁹

8. 2 + 2² + 2³ + …+ 2²⁰.

Bài 2: Tìm hai chữ số tận cùng của các số sau:

1. 51⁵¹

2. 99⁹⁹

3. 6⁶⁶⁶

• DẠNG 3: SO SÁNH LŨY THỪA VỚI LŨY THỪA

1. 27¹¹ và 81⁸

2. 625⁵ và 125⁷

3. 5³⁶ và 11²⁴

4. 3²ⁿ và 2³ⁿ

5. 5²³ và 6.5²²

6. 199²⁰ và 2003¹⁵

7. 3⁹⁹ và 11²¹

• DẠNG 4: TÌM GIÁ TRỊ CỦA SỐ TỰ NHIÊN

Bài 1: Tìm x biết:

1. (x - 47) – 115 = 0

2. 2^x – 15 = 17

3. (7x - 11)³ = 2⁵.5² + 200

4. x¹⁰ = 1^x

5. x¹⁰ = x

6. (2x - 15)⁵ = (2x - 15)³

7. 2.3^x = 10.3¹² + 8.27⁴

HƯỚNG DẪN – ĐÁP ÁN

• DẠNG 1: TÍNH GIÁ TRỊ CỦA BIỂU THỨC

• 4¹⁰.8¹⁵ = (2²)¹⁰ . (2³)¹⁵ = 2²⁰.2⁴⁵ = 2⁶⁵

• 4¹⁵.5³⁰ = (2²)¹⁵.5³⁰ = 2³⁰.5³⁰ = (2.5)³⁰ = 10³⁰

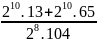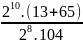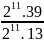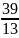• = = = =3

• (1 + 2 + 3 + … + 100).(1² + 2² + 3² + … + 10²). (65.111 – 13.15.37)

= (1 + 2 + 3 + … + 100).(1² + 2² + 3² + … + 10²). (13.5.3.37 - 13.15.37)

= (1 + 2 + 3 + … + 100).(1² + 2² + 3² + … + 10²). 0 = 0

• 19991999.1998 – 19981998.1999 = 1999.10001.1998-1998.10001.1999=0

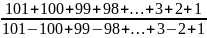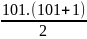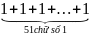
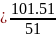• = : = 101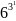

• = 6³ = 216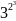

• =3⁸ = 6561

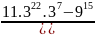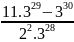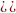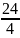• = = = = 6

• 9! – 8! – 7! . 8² = 8!.(9 – 1) - 7! . 8² = 8.8.7! - 7! . 8² = 8².7! - 7! . 8² = 0

• 27¹⁶ : 9¹⁰ = (3³)¹⁶ : (3²)¹⁰ = 3⁴⁸ : 3²⁰ = 3²⁸

1. DẠNG 2: TÌM CHỮ SỐ TẬN CÙNG

Bài 1: Tìm chữ số tận cùng của các số sau:

1. 74³⁰ Luỹ thừa của một số có tận cùng bằng 4 là một số có tận cùng bằng 6 nếu số mũ chẵn, tận cùng bằng 4 nếu số mũ lẻ. 30 là số chẵn nên 74³⁰ có tận cùng bằng 6 .

2. 49³¹ Luỹ thừa của một số có tận cùng bằng 9 là một số có tận cùng bằng 1 nếu số mũ chẵn, tận cùng bằng 9 nếu số mũ lẻ. 31 là số lẻ nên 49³¹ có tận cùng bằng 9

3. 87³² = (87⁴)⁸ Ta có các số có tận cùng 7 nâng lên luỹ thừa 4 thì được số có tận cùng bằng 1. Những số có tận cùng bằng 1 dù nâng lên luỹ thừa bao nhiêu thì tận cùng cũng bằng 1. Vậy 87³² có tận cùng bằng 1

4. 58³³ Ta có các số có tận cùng 8 nâng lên luỹ thừa 4 thì được số có tận cùng bằng 6. Do đó ta biến đổi như sau: 58³³ = (58⁴)⁸.58=(…6)⁸.58 = (…8). Vậy 58³³ có tận cùng bằng 8.

5. 23³⁵ Ta có các số có tận cùng 3 nâng lên luỹ thừa 4 thì được số có tận cùng bằng 1.Do đó ta biến đổi như sau: 23³⁵ = (23⁴)⁸.23³ = (…1)⁸.(…7). Vậy 23³⁵ có tận cùng bằng 7.

6. 2¹⁰¹ Ta có các số có tận cùng 2 nâng lên luỹ thừa 4 thì được số có tận cùng bằng 6.Do đó ta biến đổi như sau: 2¹⁰¹ = (2⁴)²⁵.2 = 16²⁵.2 = (…6).2 = (…2). Vậy 2¹⁰¹ có tận cùng bằng 2

7. 3¹⁹ Ta có các số có tận cùng 3 nâng lên luỹ thừa 4 thì được số có tận cùng bằng 1.Do đó ta biến đổi như sau: 3¹⁹ = (3⁴)⁴.3³ = (…1)⁴.27 = …7. Vậy 3¹⁹ có tận cùng bằng 7.

8. 2 + 2² + 2³ + …+ 2²⁰.

Bài 2: Tìm hai chữ số tận cùng của các số sau:

• 51⁵¹

51⁵¹ = (51²)²⁵ .51.Một chữ số có tận cùng bằng 01 dù nâng lên bất kì luỹ thừa tự nhiên nào cũng có tận cùng vẫn bằng 01 nên 51⁵¹ có tận cùng bằng 51.

• 99⁹⁹

(99²)⁴⁹ . 9 = 9801⁴⁹ . 9

Một chữ số có tận cùng bằng 01 dù nâng lên bất kì luỹ thừa tự nhiên nào cũng có tận cùng vẫn bằng 01 nên 9801⁴⁹ có tận cùng bằng 01. Do đó, 99⁹⁹ có tận cùng bằng 99.

• 6⁶⁶⁶

Ta có 6⁵ có tận cùng bằng 76. Một số tận cùng bằng 76 dù nâng lên bất kì một số tự nhiên nào khác 0 nào cũng vẫn tận cùng bằng 76. Do đó 6⁶⁶⁶ = (6⁵)¹³³.6 = (…76)¹³³.6 = (…76).6 = (…56) . Vậy 6⁶⁶⁶ có tận cùng là 56

2. DẠNG 3: SO SÁNH LŨY THỪA VỚI LŨY THỪA

1. 27¹¹ và 81⁸

Ta có: 27¹¹ = (3³)¹¹ = 3³³ và 81⁸ = (3⁴)⁸ = 3³²

3³³ > 3³² nên 27¹¹ > 81⁸

2. 625⁵ và 125⁷

Ta có: 625⁵ = (5⁴)⁵ = 5²⁰ và 125⁷ = (5³)⁷ = 5²¹

5²⁰ < 5²¹ nên 625⁵ < 125⁷

3. 5³⁶ và 11²⁴

Ta có 5³⁶ = (5³)¹² = 125¹²

11²⁴ = (11²)¹² = 121¹² < 125¹²

1. 5³⁶ > 11²⁴

4. 3²ⁿ và 2³ⁿ

Ta có : 3²ⁿ = 9ⁿ; 2³ⁿ = 8ⁿ

9ⁿ > 8ⁿ => 3²ⁿ > 2³ⁿ

5. 5²³ và 6.5²²

Ta có: 6.5²² = (5 + 1).5²² = 5.5²² + 5²² = 5²³ + 5²² > 5²³

vậy 5²³ < 6.5²²

6. 199²⁰ và 2003¹⁵

199²⁰ < 200²⁰ = (8.25)²⁰ = (2³.5²)²⁰ = 2⁶⁰.5⁴⁰

2003¹⁵ > 2000¹⁵ = (16.125)¹⁵ = (2⁴.5³)¹⁵ = 2⁶⁰.5⁴⁵

Vậy 2003¹⁵ > 199²⁰

7. 3⁹⁹ và 11²¹

11²¹ < 27²¹ = (3³)²¹ = 3⁶³ < 3⁹⁹

vậy 3⁹⁹ > 11²¹

3. DẠNG 4: TÌM GIÁ TRỊ CỦA SỐ TỰ NHIÊN

Bài 1: Tìm x 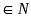biết:

1. (x - 47) – 115 = 0

 x – 47 = 115

 x = 115 + 47

 x = 162

2. 2^x – 15 = 17

 2^x = 32

 2^x = 2⁵

 x = 5

3. (7x - 11)³ = 2⁵.5² + 200

 (7x – 11)³ = 32.25 + 200

 (7x – 11)³ = 800 +200

(7x – 11)³ = 1000

 (7x – 11)³ = 10³

 7x – 11 = 10

 7x = 21

 x = 3

4. x¹⁰ = 1^x

 x¹⁰ = 1

 x = 1

5. x¹⁰ = x



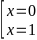
6. (2x - 15)⁵ = (2x - 15)³

 (2x – 15)³ .[(2x – 15)² – 1] = 0





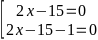
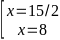
7. 2.3^x = 10.3¹² + 8.27⁴

 3^x = 5.3¹² + 4.3¹²

 3^x = 3¹².(5 + 4)

 3^x = 3¹².3² = 3¹⁴

 x = 14