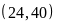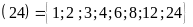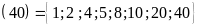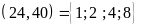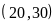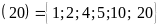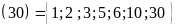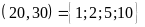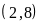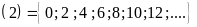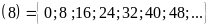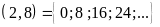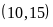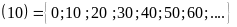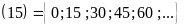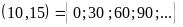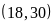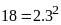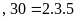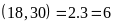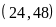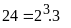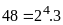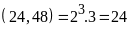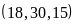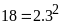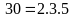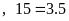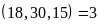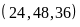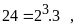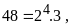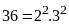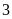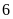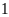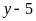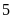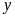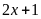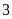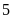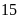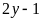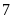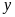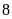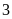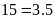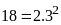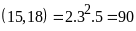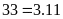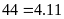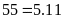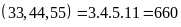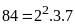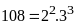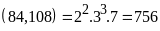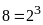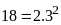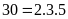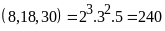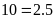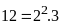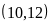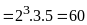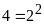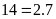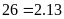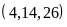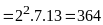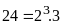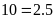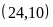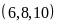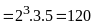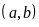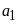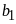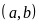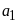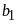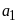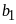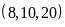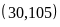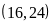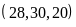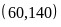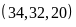Toán 6 Ước Và Bội Của Số Tự Nhiên Có Lời Giải Chi Tiết Nhất
>>> Mọi người cũng quan tâm:
Toán 6 Ước Và Bội Của Số Tự Nhiên Có Lời Giải Chi Tiết Nhất – Toán 6 là tài liệu học tập được Trang Tài Liệu biên soạn và sưu tầm từ những nguồn dữ liệu mới nhất hiện nay. Tài liệu này sẽ giúp các em luyện tập, củng cố kiến thức từ đó nâng cao điểm số cho môn học. Ngoài ra, cũng giúp các thầy cô giáo có nguồn tài nguyên phong phú để giảng dạy.
Dưới đây là bản đọc trực tuyến giúp thầy cô và các em học sinh có thể nghiên cứu Online hoặc bạn có thể tải miễn phí với phiên bản word để dễ dàng in ấn cũng như học tập Offline.
CHUYÊN ĐỀ 8:
ƯỚC VÀ BỘI CỦA SỐ TỰ NHIÊN
ƯỚC CHUNG LỚN NHẤT – BỘI CHUNG NHỎ NHẤT
PHẦN I.TÓM TẮT LÍ THUYẾT.
1. Ước và bội:
Nếu có số tự nhiên a chia hết cho b thì ta nói a là bội của b, còn b là ước của a.
Tập hợp ước của a là: Ư
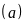 ,
tập hợp các bội của b kí
hiệu: B
,
tập hợp các bội của b kí
hiệu: B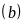 .
.
Ví
dụ:
Ư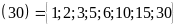
B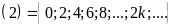 .
.
2. Ước chung và ước chung lớn nhất
Số tự nhiên n được gọi là ước chung của hai số a và b nếu n vừa là ước của a vừa là ước của b.
Số lớn nhất trong các ước chung của a và b được gọi là ước chung lớn nhất của a và b.
Ta kí hiệu: tập hợp các ước chung của a và b là: ƯC
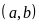 ,
,
tập
hợp các ước chung lớn nhất của a
và
b kí
hiệu: ƯC
LN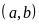 .
.
Ví
dụ:ƯC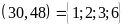 ,
ƯCLN
,
ƯCLN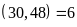 .
.
Chú ý: ước chung của hai số là ước của ước chung lớn nhất của chúng.
Hai số nguyên tố cùng nhau là hai số có ước chung lớn nhất bằng 1.
Phân số tối giản là phân số có tử và mẫu là hai số nguyên tố cùng nhau.
Cách tìm ƯCLN:
Bước 1: Phân tích các số ra thừa số nguyên tố
Bước 2: Chọn ra các thừa số chung
Bước 3: Lập tích các thừa số đã chọn. mỗi thừa số lấy với số mũ nhỏ nhất của nó. Tích đó là ƯCLN phải tìm.
3. Bội chung và bội chung nhỏ nhất
Số tự nhiên n được gọi là bội chung của hai số a và b nếu n vừa là bội của a vừa là bội của b.
Số nhỏ nhất khác 0 trong các bội chung của a và b được gọi là bội chung nhỏ nhất của a và b.
Ta kí hiệu: tập hợp các bội chung của a và b là: BC
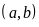 ,
,
tập
hợp các bội chung nhỏ nhất của a
và
b kí
hiệu: BCNN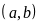 .
.
Ví
dụ:BC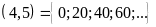 ,
,
BCNN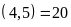 .
.
Chú ý: Bội chung của nhiều số là bội của bội chung nhỏ nhất của chúng.
Nếu các số đã cho từng đôi một nguyên tố cùng nhau thì BCNN của chúng là tích của các số đó.
Cách tìm BCNN:
Bước 1: Phân tích các số ra thừa số nguyên tố
Bước 2: Chọn ra các thừa số chung và riêng
Bước 3: Lập tích các thừa số đã chọn. mỗi thừa số lấy với số mũ lớn nhất của nó. Tích đó là BCNN phải tìm.
Nhận xét:
BCNN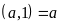
BCNN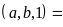 BCNN
BCNN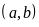
PHẦN II.CÁC DẠNG BÀI.
A. ƯỚC VÀ BỘI, ƯỚC CHUNG - BỘI CHUNG CỦA SỐ TỰ NHIÊN.
Dạng 1. Nhận biết một số là ước (bội) của một số cho trước.
I.Phương pháp giải.
+
Để xét
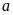 có
là ước của một số cho trước hay không, ta chia số đó
cho
có
là ước của một số cho trước hay không, ta chia số đó
cho
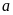 .
Nếu chia hết thì
.
Nếu chia hết thì
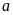 là ước của số đó.
là ước của số đó.
+
Để xét
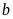 có
là bội của một số khác
có
là bội của một số khác
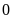 hay không, ta chia
hay không, ta chia
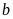 cho
số đó. Nếu chia hết thì
cho
số đó. Nếu chia hết thì
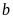 là
bội của số đó.
là
bội của số đó.
II.Bài toán.
Bài
1.
Cho các số sau
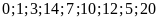 ,
tìm các số
,
tìm các số
a)
Là Ư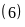 b)
Là Ư
b)
Là Ư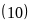
Lời giải
a)
Vì trong các số đã cho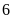 chia hết cho
chia hết cho
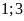 nên
nên
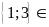 Ư
Ư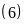
b)
Vì trong các số đã cho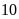 chia hết cho
chia hết cho
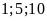 nên
nên
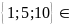 Ư
Ư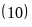
Bài
2.
Cho các số sau
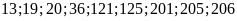 ,
chỉ ra các số thuộc tập hợp sau:
,
chỉ ra các số thuộc tập hợp sau:
a)
Là B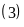 b)
Là B
b)
Là B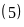
Lời giải
a)
Vì trong các số đã cho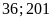 chia hết cho
chia hết cho
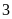 nên
nên
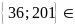 B
B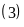
b)
Vì trong các số đã cho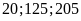 chia hết cho
chia hết cho
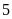 nên
nên
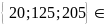 B
B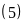
Dạng 2. Tìm tất cả các ước (bội) của một số.
I.Phương pháp giải.
+
Để tìm tất cả các ước của một số
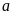 ta
làm như sau:
ta
làm như sau:
Bước
1: Chia
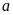 lần lượt cho các số
lần lượt cho các số
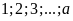
Bước
2: Liệt kê các số mà
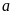 chia
hết. Đó là tất cả các ước của
chia
hết. Đó là tất cả các ước của
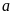
+
Để tìm bội của một số
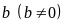 ta
làm như sau:
ta
làm như sau:
Bước
1: Nhân
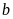 lần lượt cho các số
lần lượt cho các số
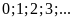
Bước
2: Liệt kê các số thu được. Đó là tất cả các bội
của
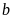
Lưu ý: Nếu bài toán tìm ước (bội) của một số thỏa mãn điều kiện cho trước ta làm như sau:
Bước 1: Liệt kê các ước (bội) của số đó
Bước 2: Chọn ra các số thỏa mãn điều kiện đề bài.
II.Bài toán.
Bài 1.
a)
Tìm tập hợp các ước của
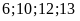
b)
Tìm tập hợp các bội của
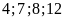
Lời giải
a)
Ư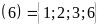 Ư
Ư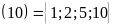
Ư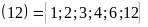 Ư
Ư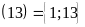
b)
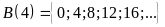
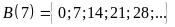
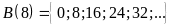
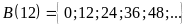
Bài
2.
Tìm các số tự nhiên
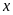 sao
cho
sao
cho
a)
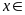 Ư
Ư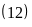 và
và
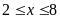 b)
b)
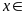
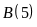 và
và
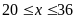
c)
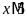 và
và
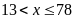 d)
d)
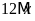 và
và
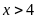
Lời giải
a)
Ta có Ư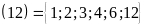 Vì
Vì
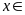 Ư
Ư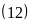 và
và
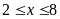 nên
nên
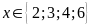
b)
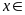
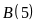 và
và
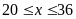 Vì
Vì
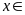
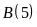 nên
nên
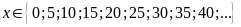
Mặt
khác
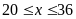
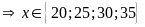
c)
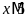 và
và
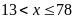 Vì
Vì
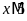 nên
nên
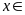
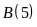 do
đó
do
đó
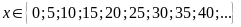
Mặt
khác
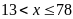
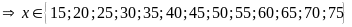
d)
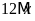 và
và
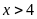 Vì
Vì
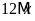 nên
nên
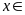 Ư
Ư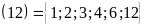 và
và
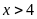 nên
nên
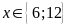
Bài
3. Tìm
tập hợp các số tự nhiên vừa là ước của
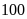 vừa
là bội của
vừa
là bội của
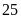 .
.
Lời giải
Gọi
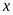 là
số tự nhiên cần tìm. Ta có Ư
là
số tự nhiên cần tìm. Ta có Ư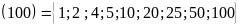
Vì
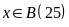 nên
nên
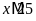
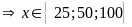
Dạng 3. Tìm số tự nhiên thỏa mãn điều kiện chia hết.
I.Phương pháp giải.
Áp dụng tính chất chia hết của một tổng (hiệu) và định nghĩa ước của một số tự nhiên.
II.Bài toán.
Bài
1.
Tìm số tự nhiên
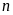 sao
cho:
sao
cho:
a)
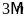 b)
b)
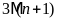
c)
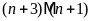 d)
d)
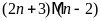
Lời giải
a)
 Ư
Ư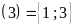
Vậy
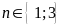
b)
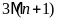
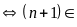 Ư
Ư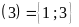
Vậy
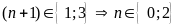
c)
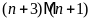
Ta
có
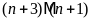 và
và
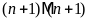 .
.
Áp
dụng tính chất chia hết của tổng (hiệu) ta có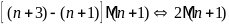
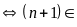 Ư
Ư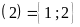
Vậy
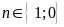
d)
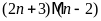
Ta
có
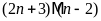 và
và
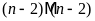 .
.
Áp
dụng tính chất chia hết của tổng (hiệu) ta có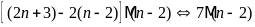
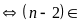 Ư
Ư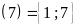
Vậy
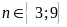
Dạng 4. Viết tập hợp các ước chung (bội chung) của hai hay nhiều số.
I.Phương pháp giải.
Bước 1. Viết tập hợp các ước (bội) của các số đã cho.
Bước 2. Tìm giao của các tập hợp đó.
II.Bài toán.
Bài 1. Viết các tập hợp sau:
a)
ƯC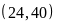 b)
ƯC
b)
ƯC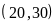
c)
BC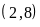 d)
BC
d)
BC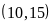
Lời giải
a)
ƯC Ta
có Ư
Ư ƯC |
b)
ƯC Ta
có Ư
Ư ƯC |
c)
BC Ta
có B
B BC |
d)
BC Ta
có B
B BC |
Dạng 5: Bài toán có lời văn.
I.Phương pháp giải.
Bước 1: Phân tích đề bài, chuyển bài toán về tìm ước (bội), ước chung, (bội chung) của các số cho trước.
Bước 2: Áp dụng cách tìm ước (bội), ước chung, (bội chung) của các số cho trước.
II.Bài toán.
Bài
1.Có
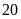 viên bi. Bạn Minh muốn chia đều số viên bi vào các hộp.
Tìm số hộp và số viên bi trong mỗi hộp? Biết không có
hộp nào chứa
viên bi. Bạn Minh muốn chia đều số viên bi vào các hộp.
Tìm số hộp và số viên bi trong mỗi hộp? Biết không có
hộp nào chứa
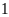 hay
hay
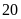 viên
bi.
viên
bi.
Lời giải
Số
hộp và số viên bi trong mỗi hộp phải là ước số của
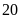 .
.
Ta
có Ư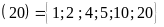 .
.
Vì
không có hộp nào chứa
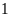 hay
hay
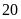 viên bi, nên số viên bi trong mỗi hộp chỉ có thể là
viên bi, nên số viên bi trong mỗi hộp chỉ có thể là
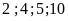 tương ứng với số hộp là
tương ứng với số hộp là
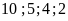
Bài
2.
Năm nay Bình
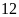 tuổi. Tuổi của mẹ Bình là bội số của tuổi Bình.
Tìm tuổi của mẹ Bình biết tuổi của mẹ lớn hơn
tuổi. Tuổi của mẹ Bình là bội số của tuổi Bình.
Tìm tuổi của mẹ Bình biết tuổi của mẹ lớn hơn
 và
nhỏ hơn
và
nhỏ hơn
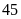 .
.
Lời giải
Gọi
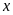 là
số tuổi của mẹ Bình
là
số tuổi của mẹ Bình
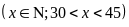
Tuổi
của mẹ Bình là bội số của tuổi Bình nên
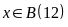
Mà
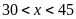 nên
nên
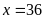 thỏa
mãn đk. Vậy mẹ Bình
thỏa
mãn đk. Vậy mẹ Bình
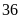 tuổi.
tuổi.
Bài
3. Học
sinh lớp 6A nhận được phần thưởng của nhà trường
và mỗi em nhận được phần thưởng như nhau. Cô hiệu
trưởng đã chia hết
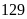 quyển
vở và
quyển
vở và
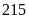 bút
chì màu. Hỏi số học sinh lớp 6A là bao nhiêu?
bút
chì màu. Hỏi số học sinh lớp 6A là bao nhiêu?
Lời giải
Ta
thấy số phần thưởng phải là ƯC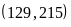
Có
ƯC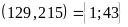
Vì
số học sinh lớp 6A không thể bằng
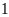 nên số học sinh lớp 6A bằng
nên số học sinh lớp 6A bằng
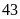
Bài
4. Tính
số học sinh của một trường biết rằng mỗi lần xếp
hàng
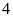 ,
hàng
,
hàng
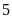 ,
hàng
,
hàng
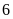 ,
hàng
,
hàng
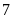 đều
vừa đủ hàng và số học sinh của trường trong khoàng
từ
đều
vừa đủ hàng và số học sinh của trường trong khoàng
từ
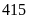 đến
đến
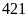 .
.
Lời giải
Gọi
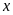 là số học sinh của trường.
là số học sinh của trường.
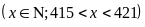
Vì
mỗi lần xếp hàng
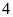 ,
hàng
,
hàng
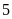 ,
hàng
,
hàng
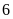 ,
hàng
,
hàng
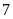 đều
vừa đủ hàng nên
đều
vừa đủ hàng nên
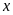 chia
hết cho
chia
hết cho
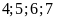 .
.
Tức
là
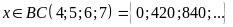 Mà
Mà
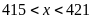 nên
nên
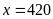
Vậy
số học sinh của trường là
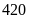 học sinh.
học sinh.
B. ƯỚC CHUNG LỚN NHẤT
Dạng 1. Tìm ước chung lớn nhất của các số cho trước.
I.Phương pháp giải.
Cách 1. Để tìm ƯCLN của các số cho trước ta thực hiện quy tắc 3 bước phía trên.
Chú
ý
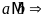 ƯCLN
ƯCLN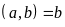
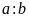 dư
dư
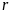 thì
ƯCLN
thì
ƯCLN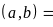 ƯCLN
ƯCLN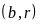
Cách 2. Sử dụng thuật toán Ơclit
Bước
1. Lấy số lớn chia số nhỏ. Giả sử
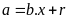
+
Nếu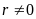 ta thực hiện bước 2
ta thực hiện bước 2
+
Nếu
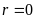 thì
ƯCLN
thì
ƯCLN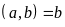
Bước 2. Lấy số chia, chia cho số dư,
+
Nếu
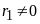 ta
thực hiện bước 3
ta
thực hiện bước 3
+
Nếu
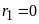 thì
ƯCLN
thì
ƯCLN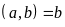
Bước 3. Quá trình này được tiếp tục cho đến khi được một phép chia hết.
II.Bài toán.
Bài 1. Tìm ƯCLN của các số
a)
ƯCLN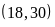 b)
ƯCLN
b)
ƯCLN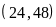
c)
ƯCLN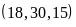 d)
ƯCLN
d)
ƯCLN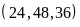
Lời giải
a)
ƯCLN Phân tích các số ra thừa số nguyên tố
Từ
đó ƯCLN |
b)
ƯCLN Phân tích các số ra thừa số nguyên tố
Từ
đó ƯCLN |
c)
ƯCLN Phân tích các số ra thừa số nguyên tố.
Từ
đó ƯCLN |
d)
ƯCLN Phân tích các số ra thừa số nguyên tố. Từ
đó ƯCLN |
Bài 2. Sử dụng thuật toán Ơclit để tìm
a)
ƯCLN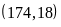 b)
ƯCLN
b)
ƯCLN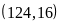
Lời giải
a) Ta thực hiện theo các bước:
Lấy
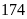 chia cho
chia cho
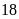 ta được
ta được
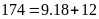
Lấy
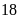 chia cho
chia cho
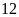 ta được
ta được
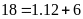
Lấy
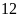 chia cho
chia cho
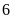 ta được
ta được
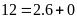
Vậy
ta được ƯCLN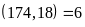
b) Ta thực hiện theo các bước:
Lấy
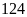 chia cho
chia cho
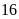 ta được
ta được
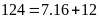
Lấy
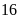 chia cho
chia cho
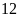 ta được
ta được
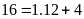
Lấy
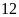 chia cho
chia cho
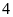 ta được
ta được
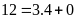
Vậy
ta được ƯCLN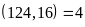
Dạng 2. Tìm các ước chung của hai hay nhiều số thỏa mãn điều kiện cho trước.
I.Phương pháp giải.
Bước 1. Tìm ƯCLN của hai hay nhiều số cho trước.
Bước 2. Tìm các ước của ƯCLN này.
Bước 3. Chọn trong số đó các ước thỏa mãn điều kiện đã cho.
Lưu ý: nếu không có điều kiện gì của bài toán thì ước chung của hai hay nhiều số là ƯCLN của các số đó.
Cách tìm ước chung thông qua ƯCLN
Bước 1. Tìm ƯCLN của hai hay nhiều số cho trước.
Bước 2. Tìm các ước của ƯCLN này.
II.Bài toán.
Bài
1. Tìm
các ước chung của
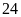 và
và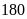 thông qua tìm ƯCLN
thông qua tìm ƯCLN
Lời giải
Phân tích các số ra thừa số nguyên tố.
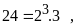
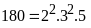
Từ
đó ƯCLN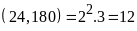
Mà
Ư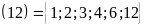 .
.
Vậy
ƯC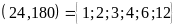
Bài
2. Tìm
số tự nhiên
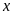 thõa
mãn
thõa
mãn
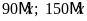 và
và
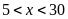 .
.
Lời giải
Số
tự nhiên
![]() thõa
mãn
thõa
mãn
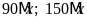 nên
nên
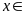 ƯCLN
ƯCLN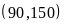
Phân tích các số ra thừa số nguyên tố.
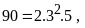
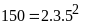
Từ
đó ƯCLN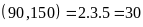
Mà
Ư![]() .
.
Vì
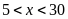 nên
nên
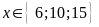
Bài
3. Tìm
số tự nhiên
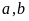 biết
ƯCLN
biết
ƯCLN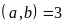 và
và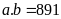
Lời giải
Ta
có
ƯCLN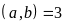 nên
nên
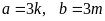 và ƯCLN
và ƯCLN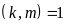
Giả
sử
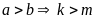 .
Ta có
.
Ta có
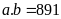
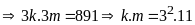
TH1:
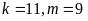
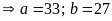
TH2:
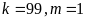
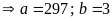
Bài
4.
Tìm số tự nhiên
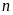 để
biểu thức
để
biểu thức
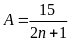 có
giá trị là một số tự nhiên.
có
giá trị là một số tự nhiên.
Lời giải
Để
A là một số tự nhiên thì
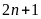 phải là ước của
phải là ước của
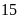
Ta
có Ư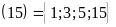 .
.
Do đó:
+
Với
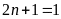
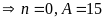
+
Với
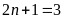
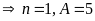
+
Với
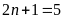
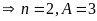
+
Với
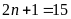
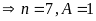
Bài
5. Tìm
số tự nhiên
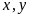
a)
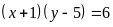 b)
b)
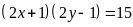
Lời giải
a)
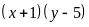
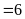
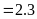
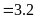
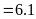
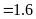
Ta có bảng sau:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Vậy
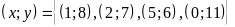
b)
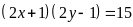
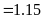
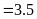
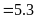
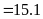
Ta có bảng sau:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Vậy
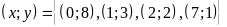
Dạng 3. Bài toán có lời văn đưa về tìm ƯCLN
I.Phương pháp giải.
Bước 1: Phân tích đề bài; suy luận để đưa về việc tìm ƯCLN của hai hay nhiều số;
Bước 2: Áp dụng quy tắc 3 bước để tìm ƯCLN đó.
II.Bài toán.
Bài
1. Cô
giáo chủ nhiệm muốn chia
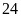 quyển
vở,
quyển
vở,
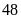 bút bi và
bút bi và
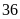 gói
bánh thành một số phần thưởng như nhau để trao trong
dịp sơ kết học kì. Hỏi có thể chia được nhiều nhất
bao nhiêu phần thưởng? Khi đó mỗi phần thưởng có bao
nhiêu quyển vở, bút bi và gói bánh.
gói
bánh thành một số phần thưởng như nhau để trao trong
dịp sơ kết học kì. Hỏi có thể chia được nhiều nhất
bao nhiêu phần thưởng? Khi đó mỗi phần thưởng có bao
nhiêu quyển vở, bút bi và gói bánh.
Lời giải
Gọi
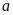 là
số phần thưởng để cô giáo chủ nhiệm trao trong dịp
sơ kết học kì
là
số phần thưởng để cô giáo chủ nhiệm trao trong dịp
sơ kết học kì
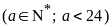
Để
số phần thưởng là nhiều nhất thì
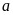 phải là số lớn nhất sao cho
phải là số lớn nhất sao cho
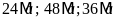 .
.
Tức
là
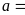 ƯCLN
ƯCLN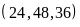 .
.
Ta
có
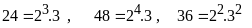 .
.
Từ
đó ƯCLN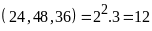
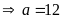
Vậy
có thể chia được nhiều nhất
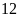 phần
thưởng.
phần
thưởng.
Trong
đó có
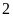 quyển
vở,
quyển
vở,
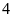 bút
bi,
bút
bi,
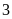 gói
bánh.
gói
bánh.
Bài
2. Một
hình chữ nhật có chiều dài
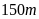 và
chiều rộng
và
chiều rộng
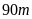 được
chia thành các hình vuông có diện tích bằng nhau. Tính độ
dài cạnh hình vuông lớn nhất trong cách chia trên ? (số
đo cạnh là số tự nhiên với đơn vị là
được
chia thành các hình vuông có diện tích bằng nhau. Tính độ
dài cạnh hình vuông lớn nhất trong cách chia trên ? (số
đo cạnh là số tự nhiên với đơn vị là
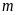 )
)
Lời giải
Để
chia hình chữ nhật thành các hình vuông có diện tích
bằng nhau thì độ dài mỗi cạnh hình vuông phải là ước
chung của
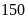 và
và
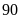
Do
đó độ dài cạnh hình vuông lớn nhất là
ƯCLN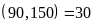 .
.
Vậy
độ dài cạnh hình vuông lớn nhất là
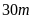
Dạng 4. Chứng minh hai hay nhiều số là các số nguyên tố cùng nhau.
I.Phương pháp giải.
Bước
1: Gọi
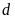 là ƯCLN của các số.
là ƯCLN của các số.
Bước
2: Dựa vào cách tìm ƯCLN và các tính chất chia hết của
tổng (hiệu) để chứng minh
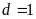
II.Bài toán.
Bài
1.
Chứng minh
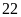 và
và
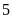 là
hai số nguyên tố cùng nhau.
là
hai số nguyên tố cùng nhau.
Lời giải
Phân tích các số ra thừa số nguyên tố.
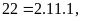
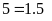 .Từ
đó ƯCLN
.Từ
đó ƯCLN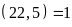
Vậy
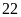 và
và
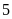 là
hai số nguyên tố cùng nhau.
là
hai số nguyên tố cùng nhau.
Bài
2.
Chứng minh rằng với mọi số tự nhiên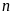 ,
các số sau là các số nguyên tố cùng nhau.
,
các số sau là các số nguyên tố cùng nhau.
a)
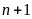 và
và
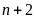 b)
b)
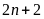 và
và
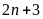
c)
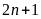 và
và
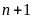 d)
d)
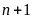 và
và
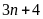
Lời giải
a)
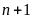 và
và
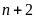
Gọi
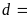 ƯCLN
ƯCLN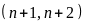
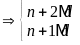
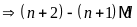
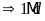
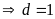
Từ
đó ƯCLN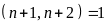
Vậy
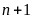 và
và
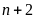 là các số nguyên tố cùng nhau với mọi
là các số nguyên tố cùng nhau với mọi
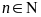 .
.
b)
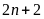 và
và
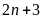
Gọi
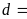 ƯCLN
ƯCLN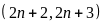
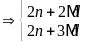
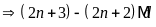
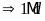
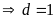
Từ
đó ƯCLN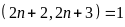
Vậy
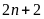 và
và
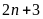 là các số nguyên tố cùng nhau với mọi
là các số nguyên tố cùng nhau với mọi
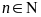 .
.
c)
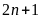 và
và
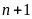
Gọi
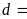 ƯCLN
ƯCLN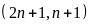
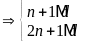
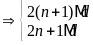
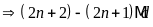
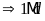
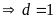
Từ
đó ƯCLN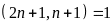
d)
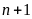 và
và
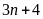
Gọi
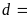 ƯCLN
ƯCLN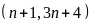
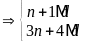
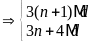
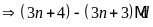
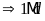
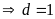
Từ
đó ƯCLN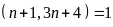
C. BỘI CHUNG NHỎ NHẤT
Dạng 1. Tìm bội chung nhỏ nhất của các số cho trước
I.Phương pháp giải.
Bước 1. Phân tích mỗi số ra thừa số nguyên tố
Bước 2. Chọn ra các thừa số nguyên tố chung và các thừa số nguyên tố riêng
Bước 3. Với mỗi thừa số nguyên tố chung và riêng, ta chọn lũy thừa với số mũ lớn nhất.
Bước 4. Lấy tích của các lũy thừa đã chọn, ta nhận được BCNN cần tìm
II.Bài toán.
Bài 1. Tìm:
a)
BCNN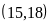 c)
BCNN
c)
BCNN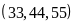
b)
BCNN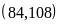 d)
BCNN
d)
BCNN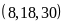
Lời giải
a)
Ta có:
BCNN |
c)
Ta có:
BCNN |
b)
Ta
có:
BCNN |
d)
Ta có:
BCNN |
Bài 2. Tìm:
a)
BCNN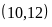 c)
BCNN
c)
BCNN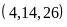
b)
BCNN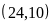 d)
BCNN
d)
BCNN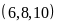
Lời giải
a)
Ta có:
BCNN |
c)
Ta có:
BCNN |
b)
Ta
có:
BCNN |
d)
Ta có:
BCNN |
Dạng 2. Tìm bội chung của hai hay nhiều số thỏa mãn điều kiện cho trước
I.Phương pháp giải.
Bước 1. Tìm BCNN của các số đó
Bước 2. Tìm các bội của BCNN này
Bước 3. Chọn trong các số đó các bội thỏa mãn điều kiện đã cho
II.Bài toán.
Bài 1. Tìm các bội chung của 8 và 10 thông qua BCNN
Lời giải
Ta
có BCNN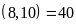 .
.
Vậy
BC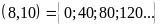
Bài 2. Tìm các bội chung của 8; 12 và 15 thông qua BCNN
Lời giải
Ta
có BCNN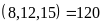 .
.
Vậy
BC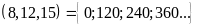
Bài
3.
Tìm số tự nhiên x
thỏa mãn
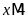 ;
;
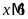 và
và
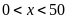 .
.
Lời giải
Vì
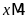 ;
;
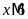 nên
nên
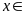 BC
BC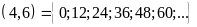
Mà
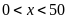 nên
nên
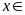
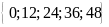
Bài
4.
Tìm số tự nhiên x
thỏa mãn
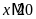 ;
;
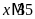 và
và
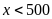 .
.
Lời giải
Vì
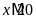 ;
;
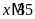 nên
nên
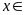 BC
BC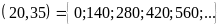
Mà
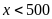 nên
nên
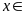
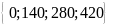
Bài 5. Tìm các bội chung của 7; 9 và 6 thông qua BCNN
Lời giải
Ta
có BCNN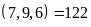 .
.
Vậy
BC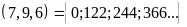
Dạng 3. Tim các số tự nhiên thỏa mãn điều kiện cho trước
I.Phương pháp giải.
Sử dụng định nghĩa về BCNN.
Khi tìm hai số biết ƯCLN và BCNN thì tích của hai số là tích của BCNN và ƯCLN.
II.Bài toán.
Bài 1. Tìm số tự nhiên a,b biết rằng
a)
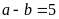 và BCNN
và BCNN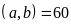 . b)
ƯCLN
. b)
ƯCLN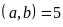 và BCNN
và BCNN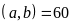 .
.
Lời giải
a)
BCNN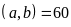
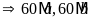 .
Hay a,
b
là ước tự nhiên của 60.
.
Hay a,
b
là ước tự nhiên của 60.
Các ước tự nhiên của 60: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60.
Vì
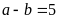 nên
nên
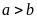 .
.
Ta xét bảng sau
a |
6 |
10 |
15 |
20 |
b |
1 |
5 |
10 |
15 |
BCNN |
6 |
5 |
30 |
60 |
|
Loại |
Loại |
Loại |
Nhận |
Vậy cặp số tự nhiên cần tìm là 20 và 15.
b)
ƯCLN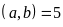
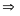
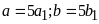 và
và
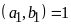 .
.
Ta
có
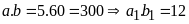 .
.
Ta có bảng sau:
|
1 |
12 |
3 |
4 |
a |
5 |
60 |
15 |
20 |
|
12 |
1 |
4 |
3 |
b |
60 |
5 |
20 |
15 |
Vậy
các cặp số tự nhiên
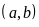 cần tìm là:
cần tìm là:
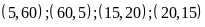 .
.
Bài 2. Tìm số tự nhiên a, b biết rằng
a)
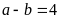 và BCNN
và BCNN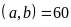 . b)
ƯCLN
. b)
ƯCLN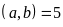 và BCNN
và BCNN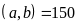 .
.
Lời giải
a)
BCNN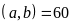
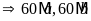 .
Hay a,
b
là ước tự nhiên của 60.
.
Hay a,
b
là ước tự nhiên của 60.
Các ước tự nhiên của 60: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60.
Vì
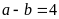 nên
nên
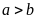 .
.
Ta xét bảng sau
a |
5 |
6 |
10 |
b |
1 |
2 |
6 |
BCNN |
5 |
6 |
30 |
|
Loại |
Loại |
Loại |
Vậy không tìm được cặp số tự nhiên thỏa mãn đề bài.
b)
ƯCLN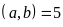
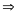
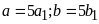 và
và
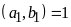 .
.
Ta
có
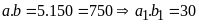 .
.
Ta có bảng sau:
|
1 |
2 |
3 |
5 |
a |
5 |
10 |
15 |
25 |
|
30 |
15 |
10 |
6 |
b |
150 |
75 |
50 |
30 |
Vì
vai trò của a, b như nhau nên ta có các cặ đảo ngược
vị trí. Vậy các cặp số tự nhiên
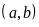 cần tìm là:
cần tìm là:
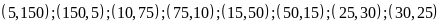 .
.
Bài 3. Tìm số tự nhiên a, b biết rằng
a)
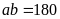 và BCNN
và BCNN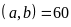 . b)
. b)
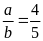 và BCNN
và BCNN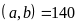 .
.
Lời giải
a)
Gọi ƯCLN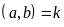
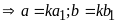 với
với
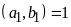
Ta
có:
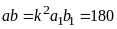 .
Mà BCNN
.
Mà BCNN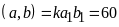 .
.
Suy
ra
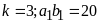 .
.
Ta có bảng sau:
|
1 |
20 |
4 |
5 |
a |
3 |
60 |
12 |
15 |
|
20 |
1 |
5 |
4 |
b |
60 |
3 |
15 |
12 |
Vậy
các cặp số tự nhiên
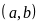 cần tìm là:
cần tìm là:
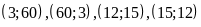 .
.
b)
Gọi ƯCLN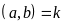 .
Vì
.
Vì
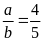 mà
mà
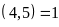 nên
nên
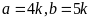 .
.
BCNN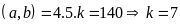 .
.
Vậy
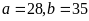 .
.
Bài
4.
Tìm số tự nhiên a, b biết rằng
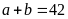 và BCNN
và BCNN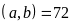 .
.
Lời giải
Gọi
ƯCLN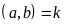 .
Nên
.
Nên
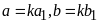 .
.
Ta
có
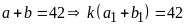 (1)
(1)
BCNN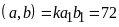 (2)
(2)
Từ
(1) và (2) suy ra
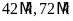 hay
hay
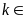 ƯC
ƯC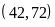
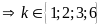 .
.
Thay k lần lượt các trường hợp trên ta thấy k = 3 hoăc k = 6
Khi
đó: tìm được các cặp
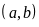 là
là
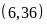 ,
,
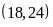 .
.
Dạng 4: Bài toán có lời văn
I.Phương pháp giải.
Bước 1. Gọi ẩn, đặt đơn vị, điều kiện cho ẩn
Bước 2. Dựa vào đề bài biểu diễn các dữ kiện theo ẩn.
Bước 3. Tìm ẩn, so sánh điều kiện
Bước 4. Trả lời và kết luận
II.Bài toán.
Bài 1. Một số sách khi xếp thành từng bó 10 cuốn, 12 cuốn, 18 cuốn đều vừa đủ. Tìm tổng số sách biết số sách trong khoảng 200 đến 500.
Lời giải
Gọi
số sách cần tìm là x
quyển, (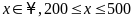 )
)
Vì
khi xếp thành từng bó 10 cuốn, 12 cuốn, 18 cuốn đều
vừa đủ nên
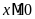 ,
,
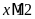 ,
,
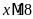 suy ra
suy ra
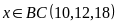 .
.
BCNN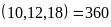 .
.
BC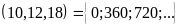 .
.
Suy
ra
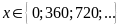 ,
mà
,
mà
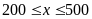 nên
nên
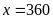 (thỏa mãn điều kiện)
(thỏa mãn điều kiện)
Vậy số quyển sách cần tìm là 360 quyển.
Bài 2. Hai bạn A và B cùng học chung một trường nhưng ở hai lớ khác nhau. A cứ 10 ngày lại trực nhật, B cứ 12 ngày lại trực nhật. Lần đầu tiên hai bạn trực nhật vào một ngày. Hỏi sau ít nhất bao nhiêu ngày hai bạn lại cùng trực nhật.
Lời giải
Do
cứ 10 ngày A trực nhật một lần nên ngày trực của A
là B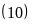 .
.
Do
cứ 12 ngày B trực nhật một lần nên ngày trực của B
là B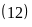 .
.
Lần
đầu tiên hai bạn trực cùng 1 ngày, để đến lần gần
nhất trực cùng nhau thì sẽ là BCNN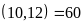
Vậy sau ít nhất 60 ngày hai bạn lại cùng trực nhật.
Bài 3. Số học sinh khối 6 của một trường trong khoảng từ 300 đến 400. Biết rằng nếu xếp hàng 5, 8, 12 thì thiếu 1 em. Tính số học sinh khối 6 của trường.
Lời giải
Gọi
số học sinh khối 6 của trường cần tìm là x
học sinh, (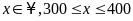 )
)
Vì
khi xếp thành 5, 8, 12 thì thiếu 1 em nên
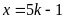 ,
,
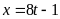 ,
,
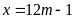 suy ra x là 1 bôi chung của 5, 8, 12 trừ 1.
suy ra x là 1 bôi chung của 5, 8, 12 trừ 1.
BCNN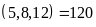 .
.
BC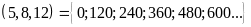 .
.
Suy
ra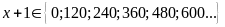 ,
mà
,
mà
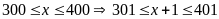 nên
nên
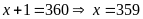 (thỏa mãn điều kiện)
(thỏa mãn điều kiện)
Vậy số học sinh khối 6 là 359 học sinh.
Bài 4. Tìm số tự nhiên nhỏ nhất sao cho khi chia cho 3 thì dư 2, khi chia cho 7 thì dư 6 khi chia cho 25 thì dư 24.
Lời giải
Gọi x là số cần tìm.
Vì
x
chia 3 dư 2, chia cho 7 thì dư 6, chia cho 25 thì dư 24. Nên
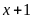 chia hết cho 2, 7, 25.
chia hết cho 2, 7, 25.
Do
đó
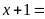 BCNN
BCNN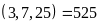 .
.
Vậy số cần tìm là 525 – 1 = 524.
Bài 5. Có ba chiếc hộp hình vuông: Hộp màu đỏ cao 8cm, hộp màu xanh cao 7cm, hộp màu vàng cao 12cm. Người ta xếp thành ba chồng bằng nhau, mỗi chồng một màu. Hỏi chiều cao nhỏ nhất của chồng hộp đó.
Lời giải
Gọi chiều cao nhỏ nhất của chồng hộp là x (cm).
Ta
có:
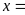 BCNN
BCNN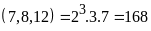 .
.
Vậy chiều cao nhỏ nhất của chồng hộp là 168 (cm)
Bài
6.
Tìm số tự nhiên x.
Biết số đó chia hết cho 7 và khi chia cho 2, cho 3, cho 4,
cho 5, cho 6 đều dư 1 và
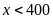 .
.
Lời giải
Ta
có:
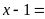 BC
BC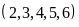 .
.
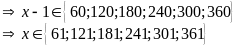
Do x chia hết cho 7 nên x = 301.
Bài 7. Một liênđội thiếu niên khi xếp hàng 2, hàng 3, hàng 4, hàng 5 đều thừa 1 người. Tính số đội viên của liên đội biết rằng số đó trong khoảng từ 100 đến 150.
Lời giải
Gọi số đội viên của liên đội là x (đội viên).
Vì
xếp thành hàng 2, hàng 3, hàng 4, hàng 5 đều thừa 1 ngươi
nên: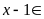 BC
BC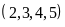 .
.
BCNN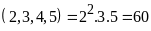
BC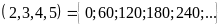 .
.
Mà số đội viên trong khoảng từ 100 đến 150.
Nên
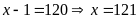 đội viên.
đội viên.
Bài 8. Một bộ phận của máy có hai bánh răng cửa khớp với nhau, bánh một có 18 răng cưa, bánh xe hai có 12 răng cưa. Người ta đánh dấu “x” vào hai răng cửa khớp với nhau. Hỏi mỗi bánh xe phải quay ít nhất bao nhiêu răng cưa để hai răng cưa đánh dấu ấy lại khớp với nhau ở vị trí giống lần trước? Khi đó mỗi bánh xe đã quay được bao nhiêu vòng.
Lời giải
Gọi số răng cưa phải tìm là x (răng).
Ta
có
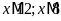 .
Vì x
nhỏ nhất nên x
là BCNN
.
Vì x
nhỏ nhất nên x
là BCNN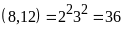 .
.
Vậy mỗi bánh xe phải quay ít nhất 36 răng cưa để hai răng cưa đánh dấu ấy lại khớp với nhau ở vị trí giống lần trước.
Khi đó:Bánh xe thứ nhất quay được 36 : 18 = 2 vòng
Bánh xe thứ hai quay được 36 : 12 = 3 vòng.
BÀI TẬP TƯƠNG TỰ TỰ GIẢI
A. ƯỚC VÀ BỘI, ƯỚC CHUNG - BỘI CHUNG CỦA SỐ TỰ NHIÊN.
Dạng 2. Tìm tất cả các ước (bội) của một số.
Bài
1.
Tìm các số tự nhiên
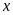 sao
cho
sao
cho
a)
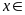 Ư
Ư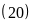 và
và
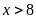 b)
b)
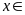
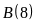 và
và
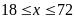
c)
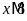 và
và
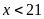 d)
d)
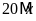 và
và
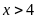
Bài
2. Tìm
tập hợp các số tự nhiên vừa là ước của
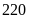 vừa là bội của
vừa là bội của
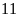 .
.
Dạng 3. Tìm số tự nhiên thỏa mãn điều kiện chia hết.
Bài
3. Tìm
số tự nhiên
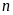 sao
cho:
sao
cho:
a)
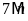 b)
b)
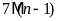
c)
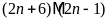 d)
d)
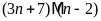
Dạng 4. Viết tập hợp các ước chung (bội chung) của hai hay nhiều số.
Bài 4. Viết các tập hợp sau:
a)
ƯC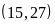 b)
ƯC
b)
ƯC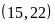
c)
BC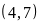 d)
BC
d)
BC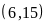
Bài 5. Viết các tập hợp sau:
a)
Ư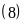 ,
Ư
,
Ư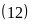 ,
ƯC
,
ƯC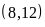 b)
B
b)
B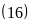 ,
B
,
B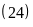 ,
BC
,
BC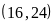
c)
B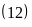 ;
B
;
B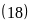 và BC
và BC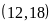 d)
Ư
d)
Ư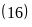 ,
Ư
,
Ư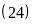 ,
ƯC
,
ƯC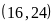
Dạng 5: Bài toán có lời văn.
Bài
6. Có
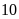 chiếc bánh trung thu. Bạn Ngọc muốn chia đều số bánh
vào các hộp. Tìm số hộp và số bánh trong mỗi hộp,
biết số bánh trong mỗi hộp phải nhiều hơn
chiếc bánh trung thu. Bạn Ngọc muốn chia đều số bánh
vào các hộp. Tìm số hộp và số bánh trong mỗi hộp,
biết số bánh trong mỗi hộp phải nhiều hơn
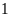 và ít hơn
và ít hơn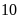 .
.
Bài
7. Bạn
Ngọc mua
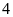 cốc trà sữa. Số cốc trà sữa ở cửa hàng là bội số
của số cốc bạn Ngọc mua. Tìm số cốc trà sữa ở cửa
hàng, biết số cốc trà sữa lớn hơn
cốc trà sữa. Số cốc trà sữa ở cửa hàng là bội số
của số cốc bạn Ngọc mua. Tìm số cốc trà sữa ở cửa
hàng, biết số cốc trà sữa lớn hơn
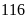 và nhỏ hơn
và nhỏ hơn
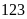 .
.
Bài
8. Tổ
I của lớp 6A nhận được phần thưởng của cô giáo
chủ nhiệm và mỗi em nhận được phần thưởng như
nhau. Cô giáo chủ nhiệm đã chia hết
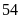 quyển
vở và
quyển
vở và
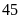 bút
bi. Hỏi số học sinh của tổ I của lớp 6A là bao nhiêu?
bút
bi. Hỏi số học sinh của tổ I của lớp 6A là bao nhiêu?
Bài
9. Tính
số đồng chí của một đội văn nghệ bội đội, biết
rằng mỗi lần xếp hàng
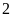 ,
hàng
,
hàng
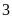 ,
hàng
,
hàng
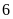 ,
hàng
,
hàng
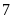 đều
vừa đủ hàng và số học sinh của trường trong khoàng
từ
đều
vừa đủ hàng và số học sinh của trường trong khoàng
từ
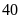 đến
đến
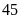 .
.
Bài
10. Một
số sách khi xếp thành từng bó
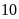 cuốn,
cuốn,
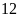 cuốn,
cuốn,
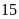 cuốn,
cuốn,
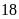 cuốn,
đều vừa đủ bó. Tính số sách đó, biết số sách
trong khoảng
cuốn,
đều vừa đủ bó. Tính số sách đó, biết số sách
trong khoảng
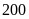 đến
đến
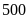 .
.
B. ƯỚC CHUNG LỚN NHẤT
Dạng 1. Tìm ước chung lớn nhất của các số cho trước.
Bài 1. Tìm ƯCLN của các số
a)
ƯCLN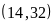 b)
ƯCLN
b)
ƯCLN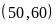
c)
ƯCLN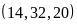 d)
ƯCLN
d)
ƯCLN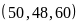
Dạng 2. Tìm các ước chung của hai hay nhiều số thỏa mãn điều kiện cho trước.
Bài
2. Tìm
các ước chung của
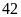 và
và thông qua tìm ƯCLN
thông qua tìm ƯCLN
Bài 3: Tìm ƯCLN rồi tìm ƯC của các số sau:
a)
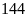 và
và
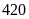 b)
b)
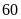 và
và
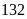
c)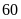 và
và
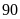 d)
d)
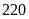 ;
;
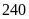 ;
;
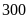
Bài
4.
Tìm
số tự nhiên
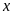 thõa
mãn
thõa
mãn
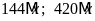 và
và
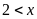
Bài
5.
Tìm
số tự nhiên
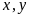 biết
ƯCLN
biết
ƯCLN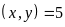 và
và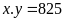
Bài
6:
Tìm số tự nhiên ,
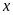 biết:
biết:
a)
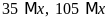 và
và
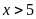
b)
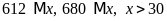
c)
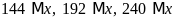 và
và
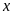 là số tự nhiên có hai chữ số
là số tự nhiên có hai chữ số
d)
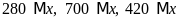 và
và
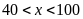
e)
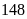 chia
chia
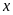 dư
dư
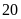 còn
còn
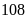 chia cho
chia cho
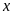 thì dư
thì dư
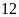 .
.
Bài
7:
Tìm các số tự nhiên
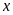 ,
,
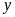 biết:
biết:
a)
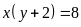 b)
b)
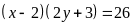
c)
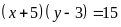 d)
d)
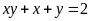
Bài
8.
Tìm số tự nhiên
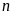 để
các biểu thức saucó giá trị là một số tự nhiên.
để
các biểu thức saucó giá trị là một số tự nhiên.
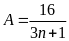
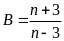
Dạng 3. Bài toán có lời văn đưa về tìm ƯCLN
Bài
9. Bạn
Hà có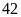 viên
bi màu đỏ và
viên
bi màu đỏ và
 viên bi màu vàng. Hà có thể chia nhiều nhất vào bao nhiêu
túi sao cho số bi đỏ và bi vàng được chia đều vào các
túi? Khi đó mỗi túi có bao nhiêu viên bi đỏ và viên bi
vàng?.
viên bi màu vàng. Hà có thể chia nhiều nhất vào bao nhiêu
túi sao cho số bi đỏ và bi vàng được chia đều vào các
túi? Khi đó mỗi túi có bao nhiêu viên bi đỏ và viên bi
vàng?.
Bài
10. Một
hình chữ nhật có chiều dài
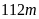 và
chiều rộng
và
chiều rộng
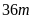 được
chia thành các hình vuông có diện tích bằng nhau. Tính độ
dài cạnh hình vuông lớn nhất trong cách chia trên ? (số
đo cạnh là số tự nhiên với đơn vị là
được
chia thành các hình vuông có diện tích bằng nhau. Tính độ
dài cạnh hình vuông lớn nhất trong cách chia trên ? (số
đo cạnh là số tự nhiên với đơn vị là
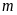 )
)
Bài
11:
Ba khối
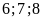 theo thứ tự có
theo thứ tự có
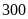 học sinh,
học sinh,
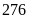 học sinh,
học sinh,
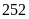 học sinh xếp thành hàng dọc để điều hành sao cho số
hàng dọc của mỗi khối như nhau. Có thể xếp nhiều
nhất thành mấy hàng dọc để mỗi khối đều không có
ai lẻ hàng? Khi đó ở mỗi khối có bao nhiêu hàng ngang?
học sinh xếp thành hàng dọc để điều hành sao cho số
hàng dọc của mỗi khối như nhau. Có thể xếp nhiều
nhất thành mấy hàng dọc để mỗi khối đều không có
ai lẻ hàng? Khi đó ở mỗi khối có bao nhiêu hàng ngang?
Bài
12:
Mỗi công nhân của hai đội 1 và 2 được giao nhiệm vụ
trồng một số cây như nhau (nhiều hơn 1 cây). Đội 1
phải trồng
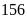 cây, đội 2 phải trồng
cây, đội 2 phải trồng
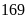 cây. Hỏi mỗi đội công nhân phải trồng bao nhiêu cây
và mỗi đội có bao nhiêu công nhân?
cây. Hỏi mỗi đội công nhân phải trồng bao nhiêu cây
và mỗi đội có bao nhiêu công nhân?
Dạng 4. Chứng minh hai hay nhiều số là các số nguyên tố cùng nhau.
Bài
13.
Chứng minh
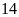 và
và
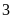 là
hai số nguyên tố cùng nhau.
là
hai số nguyên tố cùng nhau.
Bài
14.
Chứng minh rằng với mọi số tự nhiên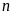 ,
các số sau là các số nguyên tố cùng nhau.
,
các số sau là các số nguyên tố cùng nhau.
a)
![]() và
và
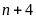 b)
b)
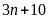 và
và
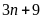
c)
![]() và
và
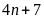 d)
d)
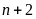 và
và
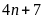
Bài 15: Chứng minh các số sau nguyên tố cùng nhau:
a)
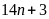 và
và
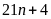 b)
b)
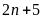 và
và
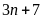
C. BỘI CHUNG NHỎ NHẤT
Dạng 1. Tìm bội chung nhỏ nhất của các số cho trước
Bài 1. Tìm
a)
BCNN |
|
f)
BCNN |
|
b)
BCNN |
|
g)
BCNN |
|
c)
BCNN |
|
h)
BCNN |
|
d)
BCNN |
|
k)
BCNN |
|
e)
BCNN |
|
l)
BCNN |
|
Dạng 2. Tìm bội chung của hai hay nhiều số thỏa mãn điều kiện cho trước
Bài 2. Tìm số tự nhiên x thỏa mãn:
a)
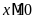 ;
;
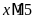 và
và
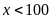 .
.
b)
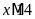 ;
;
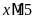 ,
,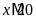 và
và
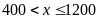 .
.
Dạng 3. Tim các số tự nhiên thỏa mãn điều kiện cho trước
Bài 3. Tìm số tự nhiên a, b biết rằng
a)
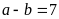 và BCNN
và BCNN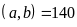 .
.
b)
ƯCLN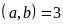 và BCNN
và BCNN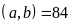 .
.
Dạng 4: Bài toán có lời văn
Bài 4. Một công ty dùng ba ca nô để trở hàng. Ca nô thứ nhất 4 ngày cập bến một lần, ca nô thứ hai 6 ngày cậ bến một lần, ca nô thứ ba 8 ngày cập bến một lần. Hỏi nếu lần đầu ba ca nô đều cập bến cùng lúc thì sau ít nhất bao nhiêu ngày ba ca nô lại cùng cập bến lần thứ hai?
Bài 5. Đội sao đỏ của một lớp 6 có ba bạn là An, Bình, Mai. Ngày đầu tháng cả đội trực cùng một ngày. Cứ sau 7 ngày An lại trực một lần, sau 4 ngày Bình lại trực một lần và sau 6 ngày Mai lại trực một lần. Hỏi sau bao nhiêu ngày thì cả đội lại cùng trực vào một ngày ở lần tiếp theo? Khi đó mỗi bạn đã trực bao nhiêu lần.
ĐÁP ÁN BÀI TẬP TƯƠNG TỰ TỰ GIẢI
A. ƯỚC VÀ BỘI, ƯỚC CHUNG - BỘI CHUNG CỦA SỐ TỰ NHIÊN.
Bài 1.
a)
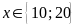 b)
b)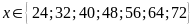
c)
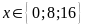 d)
d)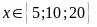
Bài
2.
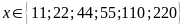
Bài 3.
a)
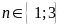 b)
b)
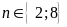
c)
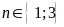 d)
d)
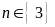
Bài 4.
a)
ƯC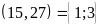 b)
ƯC
b)
ƯC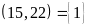
c)
BC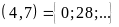 d)
BC
d)
BC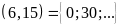
Bài 5.
a)
Ư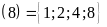 Ư
Ư
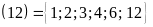 ƯC
ƯC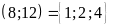
b)
B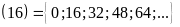 B
B
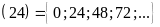 BC
BC
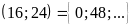
c)
B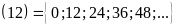 B
B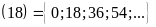 BC
BC
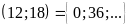
d)
Ư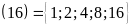 Ư
Ư
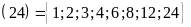 ƯC
ƯC
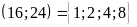
Bài
6. Số
bánh trong mỗi hộp là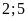 tương ứng số hộp là
tương ứng số hộp là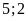
Bài
7. Số
cốc trà sữa ở cửa hàng bằng
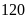
Bài
8. Số
học sinh của tổ I của lớp 6A là
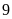 học sinh.
học sinh.
Bài
9. Số
đồng chí của một đội văn nghệ là
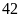 đồng chí.
đồng chí.
Bài
10. Số
sách là
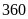 .
.
B. ƯỚC CHUNG LỚN NHẤT
Bài
1.
a)
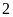 b)
b)
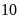 c)
c)
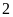 d)
d)
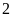
Bài
2. ƯCLN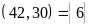
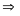 ƯC
ƯC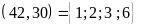
Bài
3. a)
ƯCLN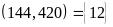
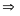 ƯC
ƯC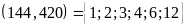
b)
ƯCLN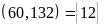
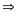 ƯC
ƯC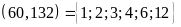
c)
ƯCLN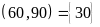
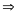 ƯC
ƯC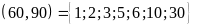
d)
ƯCLN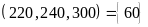
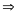 ƯC
ƯC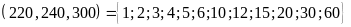
Bài
4. 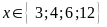
Bài 5.
TH1:
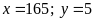 TH2:
TH2:
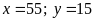
Bài
6. a)
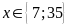 b)
b)
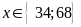
c)
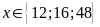 d)
d)
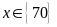 e)
e)
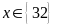
Bài
7.
a)
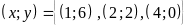 b)
b)
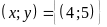
c)
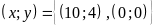 d)
d)
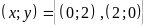
Bài 8.
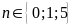
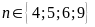
Bài
9.Có
thể chia được nhiều nhất
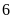 túi.
Trong đó có
túi.
Trong đó có
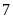 bi
đỏ,
bi
đỏ,
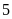 bi
vàng.
bi
vàng.
Bài
10.
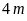
Bài
11.
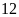 hàng, Mỗi hàng khối
hàng, Mỗi hàng khối
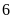 là
là
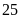 em. Mỗi hàng khối
em. Mỗi hàng khối
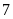 là
là
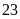 em. Mỗi hàng khối
em. Mỗi hàng khối
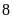 là
là
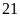 em.
em.
Bài
12.
Mỗi công nhân trồng được
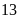 cây. Đội
cây. Đội
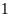 có
có
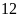 công nhân. Đội
công nhân. Đội
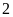 có
có
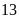 công
nhân.
công
nhân.
Bài 13.14,15 chứng minh tương tự.
C. BỘI CHUNG NHỎ NHẤT
Bài 1.
a) 40 |
b) 48 |
c) 420 |
d) 693 |
e) 3240 |
f) 210 |
g) 420 |
h) 2720 |
k) 5460 |
l) 990 |
Bài
2.a)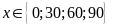 b)
b)
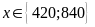
Bài
3.
a) a
= 35, b
=28. b)
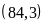 ;
;
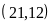 .
.
Bài 4. 24 ngày.
Bài 5. 8 lần và 4 ngày.
Ngoài Toán 6 Ước Và Bội Của Số Tự Nhiên Có Lời Giải Chi Tiết Nhất – Toán 6 thì các tài liệu học tập trong chương trình 6 sẽ được cập nhật liên tục và nhanh nhất có thể sau khi kỳ thi diễn ra trên Danh mục Tài Liệu Học Tập nhằm giúp các bạn đọc thuận tiện trong việc nghiên cứu tài liệu. Quý thày cô và các bạn đọc có thể chia sẻ thêm những tài liệu học tập hữu ích đến địa chỉ email của chúng tôi, nhằm xây dựng nên kho đề thi phong phú, đa dạng cho các em học sinh tham khảo và rèn luyện.
Tài liệu “Toán 6: Ước và bội của số tự nhiên có lời giải chi tiết nhất” là một nguồn tư liệu quan trọng giúp học sinh lớp 6 nắm vững kiến thức về ước và bội của số tự nhiên. Tài liệu này cung cấp lời giải chi tiết cho các bài tập liên quan đến chủ đề này, giúp học sinh hiểu rõ cách giải quyết và áp dụng công thức và quy tắc vào các bài toán thực tế.
Tài liệu bao gồm một loạt các bài tập với độ khó và nội dung đa dạng. Học sinh sẽ tìm hiểu về khái niệm của ước và bội, cách tìm ước chung lớn nhất và bội chung nhỏ nhất của hai hoặc nhiều số, cách áp dụng các quy tắc và thuật toán để tìm ước và bội của một số tự nhiên.
Mỗi bài tập trong tài liệu đi kèm với lời giải chi tiết, bước giải được trình bày rõ ràng và dễ hiểu. Lời giải giải thích cách áp dụng công thức và quy tắc tìm ước và bội để đạt được kết quả chính xác. Điều này giúp học sinh nắm vững kiến thức và phát triển kỹ năng giải toán số học một cách chính xác và tự tin.
“Tài liệu Toán 6: Ước và bội của số tự nhiên có lời giải chi tiết nhất” cung cấp một nguồn tư liệu toàn diện và chi tiết nhất về ước và bội của số tự nhiên. Nó giúp học sinh rèn luyện kỹ năng giải quyết bài toán liên quan đến chủ đề này, nắm vững kiến thức và phát triển tư duy logic trong môn Toán.
>>> Bài viết có liên quan