Định lý hàm số cos? Chứng minh định lý hàm số cosin – Kiến thức Toán

Định lí Côsin hay còn gọi là định lí Hàm Cos trong tam giác là một trong những phần kiến thức trọng tâm của chương trình Hình học 12. Bài viết hôm nay, Trang tài liệu sẽ giúp bạn hệ thống lại các kiến thức, khái niệm cần ghi nhớ về chuyên đề này và cách vận dụng định lý Côsin trong tam giác cực hay cùng nhiều dạng bài tập. Các bạn theo dõi để có thêm nguồn tư liệu hữu ích phục vụ quá trình dạy và học nhé!

Định lý hàm số Cos trong tam giác?

Định lý hàm Cos lần đầu tiên được phát minh bởi Al Kashi. Al Kashi ( 1380 – 22/06/1429), một nhà toán học nổi tiếng người Iran. Nhắc đến định lý Côsin của ông, người ta còn gọi là định lý Al Kashi.

Về mặt khái quát, định lý Cosin là mở rộng của định lý Pythagore. Cụ thể hơn, nếu công thức Pythagore cho chúng ta con đường để xác định một cạnh còn thiếu trong một tam giác vuông, thì hàm số Cosin sẽ giúp ta giác định được cạnh hay góc của một tam giác thường. Trong đó, ta có thể:

• Xác định cạnh của tam giác thường khi biết trước hai cạnh và góc xen giữa
• Xác định góc của một tam giác khi biết các cạnh của tam giác đó
• Xác định cạnh thứ ba của một tam giác nếu biết hai cạnh và góc đối của một trong hai cạnh đã biết.

Trong một tam giác, ta phát biểu định lý hàm số Cosin như sau: Trong một tam giác, bình phương một cạnh bằng tổng của hai cạnh kia trừ đi hai lần tích của chúng với cosin của góc xen giữa hai cạnh đó.

Trong tam giác ABC, với AB = c, BC = a, AC = b ta có:

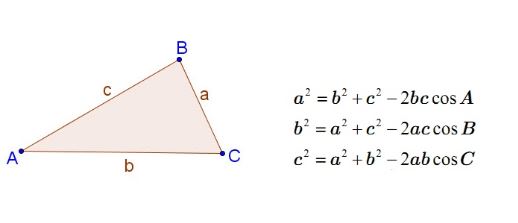
Như vậy, trong một tam giác nếu biết được hai cạnh và góc xen giữa ta sẽ tính được độ dài của cạnh còn lại.

Chứng minh định lý Cosin?

Có nhiều cách để chứng minh định lý có thể kể đến nhứ:

• Sử dụng công thức tính khoảng cách
• Sử dụng công thức lượng giác
• Sử dụng định lý Pytago
• Sử dụng định lý Ptolemy

Ở đây, để dễ dàng nhất ta nên sử dụng định lý Pytago, cách làm sẽ như sau:

Xét tam giác ABC là tam giác nhọn, có BC = a, AC = b, AB = c, kė AH vuông góc với BC tại H, AH = h, HC = d.

Xét tam giác vuông ABH, ta có:

h2 = c2-(a-d)2=c2–a2+2ad-d2 (1)

Xét tam giác vuông ACH, áp dụng Pytago ta có:

h2=b2–d2(2)

Từ (1) và (2) ta được:

c2–a2+2ad-d2=b2–d2(3)

c2=a2+b2-2ad

Với d = bcosC:

c2=a2+b2-2abcosC

Với d = bcosC thế vào (3) ta được điều phải chứng minh!

Hệ quả của định lý cos

CosA = b2 + c2 – a22bc

CosB = c2 + a2 – b22ca

CosC = a2 + b2 – c22ab

Hệ quả này có một ý nghĩa quan trọng: “Trong một tam giác, ta luôn tính được các góc nếu biết 3 cạnh.”

Vậy nếu định lý cosin cho phép tính các cạnh thì hệ quả của nó cho phép tính góc trong tam giác. Có thể áp dụng chúng vào một bài toán khá quen thuộc: “Lập công thức đường trung bình trong tam giác”.