Chuyên Đề bồi Dưỡng HSG Toán 6: Hình Có Trục Đối Xứng Tâm Đối Xứng
>>> Mọi người cũng quan tâm:
Chuyên Đề bồi Dưỡng HSG Toán 6: Hình Có Trục Đối Xứng Tâm Đối Xứng – Toán 6 là tài liệu học tập được Trang Tài Liệu biên soạn và sưu tầm từ những nguồn dữ liệu mới nhất hiện nay. Tài liệu này sẽ giúp các em luyện tập, củng cố kiến thức từ đó nâng cao điểm số cho môn học. Ngoài ra, cũng giúp các thầy cô giáo có nguồn tài nguyên phong phú để giảng dạy.
Dưới đây là bản đọc trực tuyến giúp thầy cô và các em học sinh có thể nghiên cứu Online hoặc bạn có thể tải miễn phí với phiên bản word để dễ dàng in ấn cũng như học tập Offline.
HH6. CHUYÊN ĐỀ 2 - HÌNH HỌC TRỰC QUAN
CHỦ ĐỀ 1: HÌNH CÓ TRỤC ĐỐI XỨNG – HÌNH CÓ TÂM ĐỐI XỨNG
PHẦN I. TÓM TẮT LÝ THUYẾT
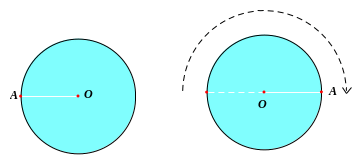
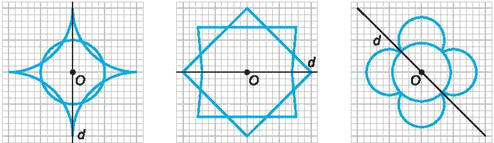
1. HÌNH CÓ TRỤC ĐỐI XỨNG
a) Khái niệm
-
Có đường thẳng
 chia hình thành hai phần,
mà nếu “gấp”
hình theo đường
thẳng
chia hình thành hai phần,
mà nếu “gấp”
hình theo đường
thẳng
 thì hai phần đó “chồng
khít” lên nhau. Những hình như thế gọi là hình có trục
đối xứng và đường
thẳng
thì hai phần đó “chồng
khít” lên nhau. Những hình như thế gọi là hình có trục
đối xứng và đường
thẳng
 được gọi là trục đối xứng của hình đó.
được gọi là trục đối xứng của hình đó.
Ví
dụ: Các
hình
 ,
,
 ,
,
 là các hình có trục đối xứng là đường thẳng
là các hình có trục đối xứng là đường thẳng
 .
.
b) Nhận xét
- Mỗi đường thẳng đi qua tâm là một trục đối xứng của hình tròn.
- Mỗi đường chéo là một trục đối xứng của hình thoi.
- Mỗi đường thẳng đi qua trung điểm hai cạnh đối diện là một trục đối xứng của hình chữ nhật.
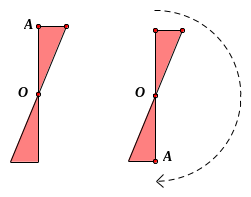
2. HÌNH CÓ TÂM ĐỐI XỨNG
a) Khái niệm
-
Mỗi hình có một điểm
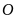 ,
mà khi quay hình đó xung quanh điểm
,
mà khi quay hình đó xung quanh điểm
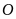 đúng một nửa vòng thì hình thu được “chồng khít”
với chính nó ở vị trí ban đầu (trước khi quay). Những
hình như thế gọi là hình có tâm đối xứng và điểm
đúng một nửa vòng thì hình thu được “chồng khít”
với chính nó ở vị trí ban đầu (trước khi quay). Những
hình như thế gọi là hình có tâm đối xứng và điểm
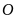 được gọi là tâm đối xứng của hình đó.
được gọi là tâm đối xứng của hình đó.
Ví
dụ:
Hình tròn tâm
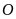 hay chong chóng hai cánh là các hình có tâm đối xứng
hay chong chóng hai cánh là các hình có tâm đối xứng
|
|
b) Nhận xét
- Tâm đối xứng của hình bình hành, hình thoi, hình vuông, hình chữ nhật là giao điểm hai đường chéo.
- Tâm đối xứng của hình lục giác đều là giao điểm của các đường chéo chính.
PHẦN II.CÁC DẠNG BÀI
Dạng 1: Xác định trục đối xứng, tâm đối xứng của hình
I. Phương pháp giải
-
Để xác định
trục đối xứng của một hình, ta xác định
một đường thẳng
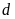 chia hình thành hai phần mà nếu “gấp” hình theo đường
thẳng
chia hình thành hai phần mà nếu “gấp” hình theo đường
thẳng
 thì hai phần đó “chồng
khít” lên nhau.
thì hai phần đó “chồng
khít” lên nhau.
-
Để xác định
tâm đối xứng của một hình, ta xác định
một điểm
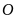 ,
mà khi quay hình đó xung quanh điểm
,
mà khi quay hình đó xung quanh điểm
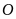 đúng một nửa vòng thì hình thu được “chồng khít”
với chính nó ở vị trí ban đầu (trước khi quay).
đúng một nửa vòng thì hình thu được “chồng khít”
với chính nó ở vị trí ban đầu (trước khi quay).
II. Bài toán
Bài 1: Mỗi hình sau: hình tam giác đều, hình vuông, hình lục giác đều, hình tròn, có bao nhiêu trục đối xứng?
Lời giải:
+)
Hình tam giác đều có
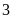 trục đối xứng:
trục đối xứng:

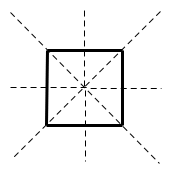
+)
Hình vuông có
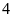 trục đối xứng:
trục đối xứng:
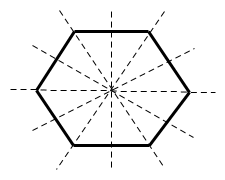
+)
Hình lục giác đều có
 trục đối xứng là:
trục đối xứng là:
+) Hình tròn có vô số trục đối xứng là: đường thẳng đi qua tâm

Bài 2: Trong các chữ cái và chữ số dưới đây, em hãy liệt kê:
a) Chữ cái và chữ số có đúng một trục đối xứng;
b) Chữ cái và chữ số có hai trục đối xứng.

Lời giải:
a)
Các chữ cái và chữ số có đúng một trục đối xứng
là:
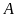 ,
,
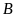 ,
,
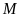 ,
,
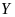 ,
,
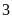 .
.

b)
Các chữ cái và chữ số có hai trục đối xứng là:
 ,
,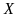 ,
,
 ,
,
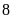
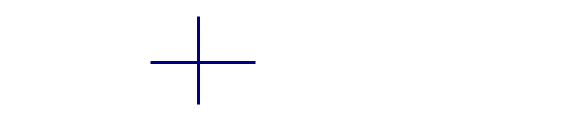
Bài 3: Trong các hình sau, hình nào có trục đối xứng?
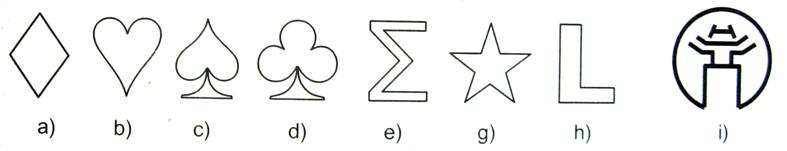
Lời giải:
Hình
có trục đối xứng là:
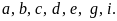
Bài 4: Quan sát các hình dưới đây:
|
|
|
|
|
|
a) Có bao nhiêu hình có tâm đối xứng?
b) Có bao nhiêu hình có đúng một trục đối xứng?
c) Có bao nhiêu hình có cả tâm đối xứng và trục đối xứng?
d) Có bao nhiêu hình không có cả tâm đối xứng lẫn trục đối xứng?
Lời giải:
a)
Có
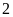 hình có tâm đối xứng là:
hình có tâm đối xứng là:
|
|
b)
Có
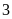 hình có đúng
hình có đúng
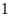 trục đối xứng là:
trục đối xứng là:
|
|
|
c)
Có
 hình có cả tâm đối xứng và trục đối xứng là:
hình có cả tâm đối xứng và trục đối xứng là:

d)
Có
 hình
không có tâm đối xứng và trục đối xứng là:
hình
không có tâm đối xứng và trục đối xứng là:
Bài 5: Trong các biển báo giao thông sau, biển báo nào có tâm đối xứng? Chỉ ra tâm đối xứng (nếu có) của các hình đó.
|
|
|
|
a) Đường cấm |
b) Cấm đi ngược chiểu |
c) Cấm đỗ xe |
d) Cấm dừng và đỗ xe |
Lời giải:
Biển
báo có tâm đối xứng là:
+) Tâm đối xứng của các hình đó là:
-

a) Đường cấm
b) Cấm đi ngược chiểu
d) Cấm dừng và đỗ xe
Bài 6: Trong các hình hoa văn sau, hình hoa văn nào có tâm đối xứng?
|
|
Lời giải:
Cả 3 hình hoa văn trên đều có tâm đối xứng.
+) Tâm đối xứng của các hình đó là:

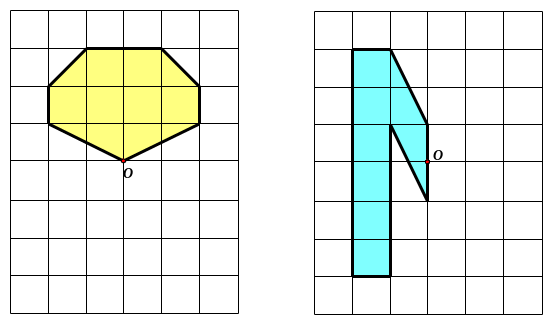
Bài 7: Trong các hình dưới đây, hình nào dưới đây có tâm đối xứng? Em hãy xác định tâm đối xứng (nếu có) của chúng.

Lời giải:
Các hình có tâm đối xứng là hình a, c.
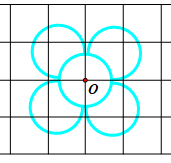
a) c)
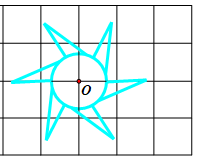
Bài 8: Hình nào sau đây có đường nét đứt là trục đối xứng?

Lời giải:
Các
hình
 có
đường nét đứt là trục đối xứng.
có
đường nét đứt là trục đối xứng.
Bài
9: Mỗi hình sau đây có bao
nhiêu trục đối xứng?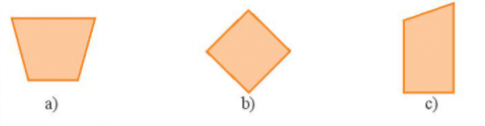
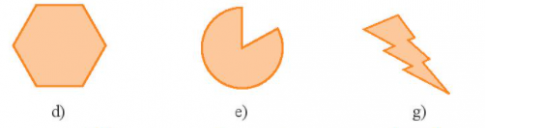
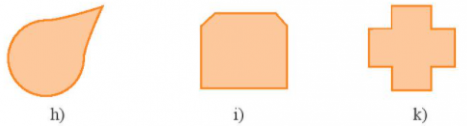
Lời giải:
Số trục đối xứng của mỗi hình được thể hiện trong bảng sau:

Bài 10: Hãy vẽ một trục đối xứng của mỗi hình sau (nếu có)
|
|
|
|
|
|
Lời giải:
Một trục đối xứng của mỗi hình được chỉ ra trong các hình vẽ dưới đây
|
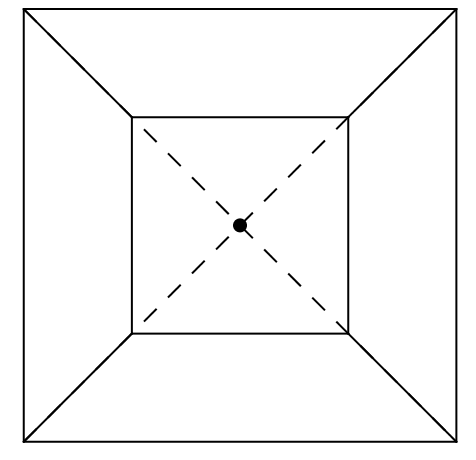
Bài 11: Tìm tâm đối xứng của mỗi hình sau (nếu có):

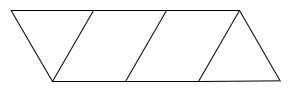

Lời giải:
Tâm đối xứng được chỉ ra như hình vẽ
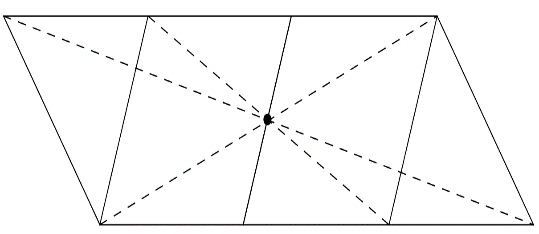
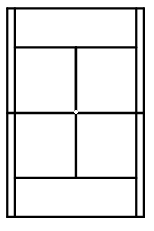
Bài 12: Dưới đây là hình ảnh một di tích ở Hà Nội. Em hãy tìm tính đối xứng và cho biết tên di tích này.

Lời giải:
Hình ảnh một di tích này có trục đối xứng. Đây là Khuê Văn Các, Hà Nội
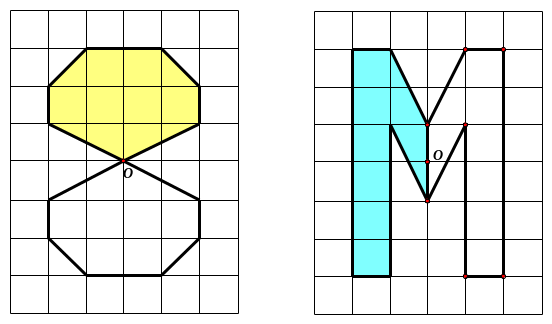
 Bài
13:
Trong
các hình sau hình nào có trục đối xứng, hình nào có
tâm đối xứng? Xác định các trục đối xứng và tâm
đối xứng (nếu có) của các hình đó.
Bài
13:
Trong
các hình sau hình nào có trục đối xứng, hình nào có
tâm đối xứng? Xác định các trục đối xứng và tâm
đối xứng (nếu có) của các hình đó.
Lời giải:
Hình
 có tâm đối xứng. Hình
có tâm đối xứng. Hình
 có trục đối xứng.
có trục đối xứng.
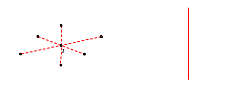
Bài 14. Vẽ trục đối xứng của các hình dưới dây


Lời giải


Bài 15. Vẽ trục đối xứng của hai biển báo sau dưới dây


Lời giải
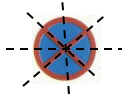
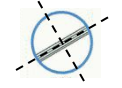
Bài
16: Bàn
cờ vua gồm
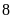 hàng
(đánh số từ
hàng
(đánh số từ
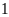 đến
đến
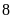 )
và
)
và
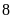 cột
(đánh các chữ cái từ
cột
(đánh các chữ cái từ
 đến
đến
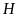 )
)
a) Tìm trục đối xứng và tâm đối xứng của bàn cờ vua.
b)
Mã trắng nằm ở
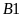 ,
hãy tìm quân cờ đối xứng với nó qua tâm đối xứng.
,
hãy tìm quân cờ đối xứng với nó qua tâm đối xứng.
c)
Vua trắng nằm ở ô
 ,
hãy tìm quân cờ đối xứng với nó qua trục đối xứng
ngang (đường thẳng giữa hàng
,
hãy tìm quân cờ đối xứng với nó qua trục đối xứng
ngang (đường thẳng giữa hàng
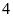 và hàng
và hàng
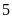 )
)

Lời giải:
a)
Bàn cờ vua có
 trục đối xứng gồm: hai đường chéo của bàn cờ, trục
ngang là đường thẳng giữa hàng
trục đối xứng gồm: hai đường chéo của bàn cờ, trục
ngang là đường thẳng giữa hàng
 và
và
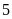 ,
trục dọc là đường thẳng giữa cột
,
trục dọc là đường thẳng giữa cột
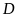 và cột
và cột
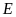 .
.
Tâm
đối xứng của bàn cờ là giao của
 trục đối xứng
trục đối xứng
b)
Mã trắng ở ô
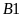 ,
có hình đối xứng qua tâm là mã đen ở ô
,
có hình đối xứng qua tâm là mã đen ở ô
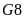
c)
Vua trắng ở ô
 ,
có hình đối xứng qua trục ngang (giữa hàng 4 và hàng 5)
là vua đen ở ô
,
có hình đối xứng qua trục ngang (giữa hàng 4 và hàng 5)
là vua đen ở ô


Dạng 2. Vẽ hình có tính đối xứng
I. Phương pháp giải
-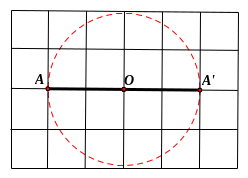 Để vẽ điểm
Để vẽ điểm
 đối xứng với điểm
đối xứng với điểm
 qua
qua
 ta thực hiện như sau: Dựng đường tròn tâm
ta thực hiện như sau: Dựng đường tròn tâm
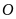 bán kính
bán kính
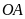 ,
đường tròn này cắt lại đường thẳng
,
đường tròn này cắt lại đường thẳng
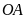 tại điểm
tại điểm
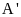 khác
khác
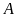 .
Khi đó điểm
.
Khi đó điểm
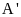 là điểm đối xứng với điểm
là điểm đối xứng với điểm
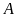 qua
qua
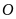 .
.
-
Để vẽ được 2 hình đối xứng với nhau qua 1 điểm
 ,
ta sẽ chọn một số điểm đặc biệt thuộc hình đó,
lấy đối xứng qua
,
ta sẽ chọn một số điểm đặc biệt thuộc hình đó,
lấy đối xứng qua
 rồi nối các điểm đó lại để được hình mới đối
xứng với hình đã cho qua tâm
rồi nối các điểm đó lại để được hình mới đối
xứng với hình đã cho qua tâm
 .
.
-
Để vẽ được hình đối xứng qua trục
 thì đường thẳng
thì đường thẳng
 cần
chia hình thành hai phần,
mà nếu “gấp”
hình theo đường
thẳng
cần
chia hình thành hai phần,
mà nếu “gấp”
hình theo đường
thẳng
 thì hai phần đó “chồng
khít” lên nhau.
thì hai phần đó “chồng
khít” lên nhau.
II. Bài toán
Bài
1. Em
hãy vẽ thêm vào mỗi hình dưới đây để được các
hình có
 là trục đối xứng.
là trục đối xứng.
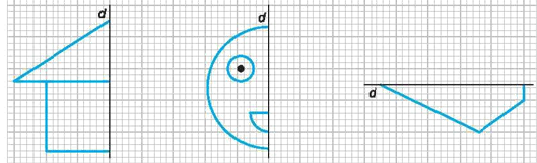
Lời giải
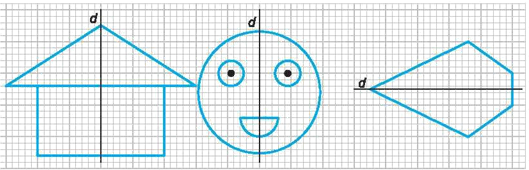
Bài
2. Em
hãy hoàn thiện các bức tranh dưới đây để được các
hình có trục đối xứng
 .
.
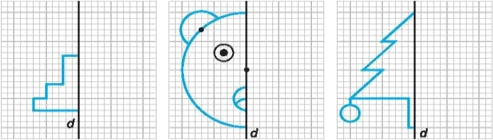
Lời giải
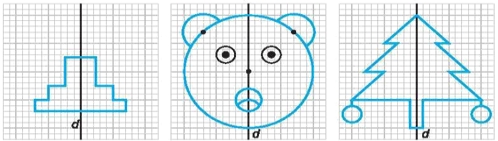
Bài
3. Em
hãy hoàn thiện các bức tranh dưới đây để được các
hình có tâm đối xứng
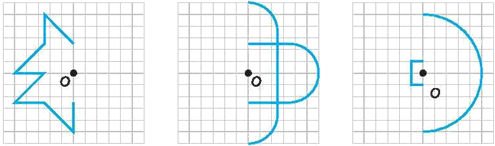
Lời giải
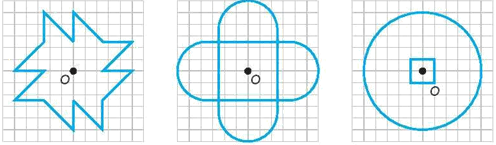
Bài
4. Em
hãy hoàn thiện các bức tranh dưới đây để được các
hình có tâm đối xứng
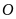 và
trục đối xứng
và
trục đối xứng

Lời giải
Bài
5. Vẽ
lại các hình bên vào giấy kẻ ô vuông rồi vẽ thêm để
được một hình nhận điểm
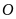 làm tâm đối xứng.
làm tâm đối xứng.
Lời giải
Bài
6. Vẽ
lại hình bên vào giấy kẻ ô vuông rồi vẽ thêm để
được một hình nhận điểm
 làm tâm đối xứng.
làm tâm đối xứng.
L ời
giải
ời
giải
Bài
7. Em
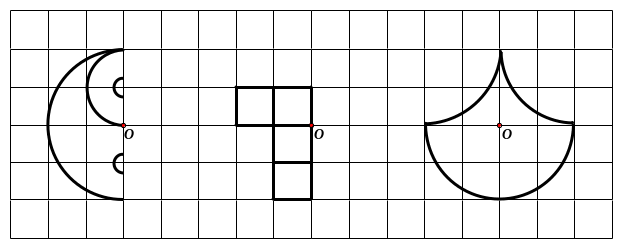
hãy vẽ thêm vào mỗi hình dưới đây để được các
hình có điểm
 là tâm đối xứng.
là tâm đối xứng.
Lời giải
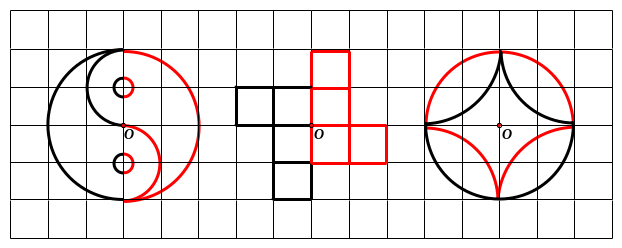
B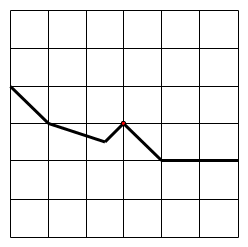 ài
8. Em
hãy hoàn thiện hình sau để được một hình nhận điểm
ài
8. Em
hãy hoàn thiện hình sau để được một hình nhận điểm
 làm tâm đối xứng đồng thời hình đó có trục đối
xứng.
làm tâm đối xứng đồng thời hình đó có trục đối
xứng.
Lời giải
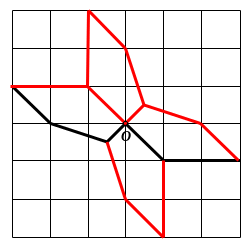
Bài
9. Hình
gấp khúc dưới đây có độ dài bằng
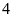 đơn vị. Em hãy vẽ thêm vào hình đó:
đơn vị. Em hãy vẽ thêm vào hình đó:
a)
Một đường gấp khúc có độ dài bằng
 đơn vị để được một hình có tâm đối xứng nhưng
không có trục đối xứng.
đơn vị để được một hình có tâm đối xứng nhưng
không có trục đối xứng.
b)
Một đường gấp khúc có độ dài bằng
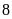 đơn
vị để được một hình có tâm đối xứng và có
đơn
vị để được một hình có tâm đối xứng và có
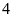 trục đối xứng.
trục đối xứng.
c )
Một đường gấp khúc có độ dài ngắn nhất để được
một hình có tâm đối xứng.
)
Một đường gấp khúc có độ dài ngắn nhất để được
một hình có tâm đối xứng.
d) Một đường gấp khúc có độ dài ngắn nhất để được một hình có tâm đối xứng và có trục đối xứng.
Lời giải
a) b)
c
 ) d)
) d)
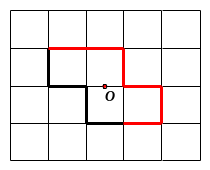
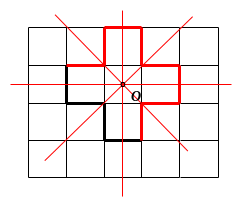
Bài
10. Hình
gấp khúc dưới đây gồm
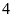 đoạn thẳng có độ dài bằng
đoạn thẳng có độ dài bằng
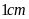 .
Em hãy vẽ thêm một đường gấp khúc có độ dài bằng
.
Em hãy vẽ thêm một đường gấp khúc có độ dài bằng
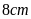 để được một hình có cả tâm đối xứng và trục đối
xứng.
để được một hình có cả tâm đối xứng và trục đối
xứng.

L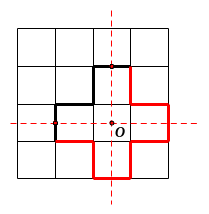 ời
giải
ời
giải
HẾT
Ngoài Chuyên Đề bồi Dưỡng HSG Toán 6: Hình Có Trục Đối Xứng Tâm Đối Xứng – Toán 6 thì các tài liệu học tập trong chương trình 6 sẽ được cập nhật liên tục và nhanh nhất có thể sau khi kỳ thi diễn ra trên Danh mục Tài Liệu Học Tập nhằm giúp các bạn đọc thuận tiện trong việc nghiên cứu tài liệu. Quý thày cô và các bạn đọc có thể chia sẻ thêm những tài liệu học tập hữu ích đến địa chỉ email của chúng tôi, nhằm xây dựng nên kho đề thi phong phú, đa dạng cho các em học sinh tham khảo và rèn luyện.
Chuyên Đề Bồi Dưỡng HSG Toán 6 với chủ đề “Hình Có Trục Đối Xứng – Tâm Đối Xứng” là một bài học dành cho học sinh lớp 6 có năng khiếu và đam mê trong môn Toán. Chuyên đề này tập trung vào khái niệm và tính chất của hình có trục đối xứng và tâm đối xứng.
Trong chuyên đề này, học sinh sẽ được giới thiệu về khái niệm trục đối xứng và tâm đối xứng trong hình học. Họ sẽ được làm quen với các ví dụ cụ thể về các hình có trục đối xứng và tâm đối xứng, cũng như hiểu rõ các tính chất và quy tắc áp dụng cho việc tìm trục đối xứng và tâm đối xứng của các hình.
Chuyên đề này cung cấp các bài tập và ví dụ minh họa, giúp học sinh nắm vững kiến thức và áp dụng chúng vào việc giải các bài toán liên quan. Ngoài ra, chuyên đề cũng tập trung vào việc phát triển kỹ năng tư duy logic, khả năng phân tích và quan sát của học sinh.
Các tài liệu tham khảo và lời giải chi tiết được cung cấp trong chuyên đề giúp học sinh tự học và tự rèn kỹ năng trong quá trình ôn tập và bồi dưỡng. Chuyên đề cũng khuyến khích học sinh tham gia vào các hoạt động thảo luận nhóm và giải bài tập thực hành để tăng cường khả năng làm việc nhóm và trau dồi kiến thức.
>>> Bài viết có liên quan