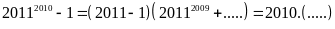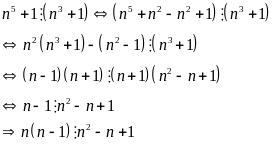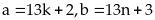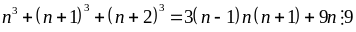Dạng Toán Chia Hết Ôn Thi HSG Đại Số 8 Có Lời Giải Chi Tiết
Có thể bạn quan tâm
Dạng Toán Chia Hết Ôn Thi HSG Đại Số 8 Có Lời Giải Chi Tiết là tài liệu học tập được Trang Tài Liệu biên soạn và sưu tầm từ những nguồn dữ liệu mới nhất hiện nay. Tài liệu này sẽ giúp các em luyện tập, củng cố kiến thức từ đó nâng cao điểm số cho môn học. Ngoài ra, cũng giúp các thầy cô giáo có nguồn tài nguyên phong phú để giảng dạy.
Dưới đây là bản đọc trực tuyến giúp thầy cô và các em học sinh có thể nghiên cứu Online hoặc bạn có thể tải miễn phí với phiên bản word để dễ dàng in ấn cũng như học tập Offline.
A.Bài toán
Chứng minh rằng:
 với
với
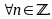
Chứng minh rằng:
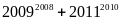 chia
hết cho
chia
hết cho
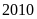
a) Chứng minh rằng nếu tổng của hai số nguyên chia hết cho
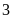 thì tổng các lập phương của chúng chia hết cho 9
thì tổng các lập phương của chúng chia hết cho 9
b)
Tìm các số nguyên n để
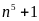 chia
hết cho
chia
hết cho
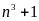
Chứng minh rằng nếu tổng của hai số nguyên chia hết cho 3 thì tổng các lập phương của chúng chia hết cho 9
Chứng minh
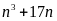 chia hết cho
chia hết cho
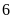 với
mọi
với
mọi
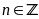
Chứng minh rằng:
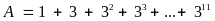 chia
hết cho
chia
hết cho
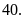
Chứng minh rằng tổng lập phương của ba số nguyên liên tiếp chia hết cho 9
b)
Chứng minh rằng với mọi số tự nhiên
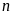 thì
thì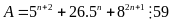
Chứng minh rằng
a)
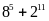 chia
hết cho 17
chia
hết cho 17
b)
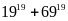 chia
hết cho 44
chia
hết cho 44
Chứng minh rằng
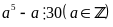
Cho
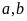 là hai số tự nhiên. Biết
rằng
là hai số tự nhiên. Biết
rằng
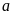 chia cho 5 dư 3 và
chia cho 5 dư 3 và
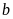 chia cho 5 dư 2. Hỏi
tích
chia cho 5 dư 2. Hỏi
tích
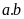 chia cho 5 dư bao nhiêu ?
chia cho 5 dư bao nhiêu ?
Cho các số nguyên
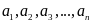 .
Đặt
.
Đặt
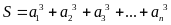 và
và
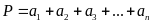 .
Chứng minh rằng: S chia hết cho 6 khi và chỉ khi P chia hết
cho 6.
.
Chứng minh rằng: S chia hết cho 6 khi và chỉ khi P chia hết
cho 6.
a) Chứng minh rằng:
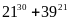 chia hết cho 45
chia hết cho 45
b)
Chứng minh rằng: Với mọi số tự nhiên n ta có:
![]() .
.
Chứng minh:
a)
![]() chia hết cho 7.
chia hết cho 7.
b)
![]() chia hết cho 2, với
chia hết cho 2, với
![]() .
.
c)
![]() chia hết cho 30, với
chia hết cho 30, với
![]() .
.
d)Nếu
![]() thì
thì
![]() chia hết cho
chia hết cho
![]() .
.
e)
![]() là bình phương của một số nguyên, với
là bình phương của một số nguyên, với
![]() .
.
f)
![]() chia hết cho
chia hết cho
![]() .
.
g)
![]() chia hết cho
chia hết cho
![]() ,
với
,
với
![]() .
.
Chứng minh rằng:
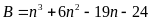 chia hết cho 6 (Câu 2b đề 10)
chia hết cho 6 (Câu 2b đề 10)Chứng minh: Với mọi n là số tự nhiên chẵn thì biểu thức:
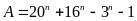
chia
hết cho
![]()
Chứng minh rằng
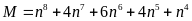 chia hết cho 16, với
chia hết cho 16, với
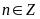
a) Chứng minh rằng tổng lập phương của ba số nguyên liên tiếp chia hết cho 9
b)Chứng
minh rằng với mọi số tự nhiên
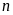 thì
thì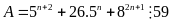
Cho
 là
các số tự nhiên có tổng chia hết cho 3
là
các số tự nhiên có tổng chia hết cho 3
Chứng
minh rằng:
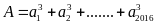 chia
hết cho 3.
chia
hết cho 3.
Cho hai số nguyên, số thứ nhất chia cho 5 dư 1, số thứ hai chia cho 5 dư 2. Hỏi tổng bình phương của chúng có chia hết cho 5 không ?
Chứng minh rằng
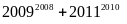 chia
hết cho
chia
hết cho
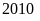
Chứng minh rằng:
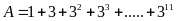 chia
hết cho 40
chia
hết cho 40
Chứng minh rằng
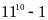 chia
hết cho
chia
hết cho
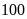
Chứng minh rằng
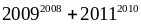 chia
hết cho
chia
hết cho
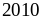
Chứng minh rằng:
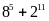 chia
hết cho 17
chia
hết cho 17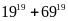 chia
hết cho 44
chia
hết cho 44
a)Chứng minh rằng:
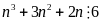 với
mọi số nguyên
với
mọi số nguyên
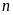
b)Tìm
số nguyên n sao cho:
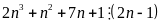
. Cho số tự nhiên
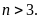 Chứng
minh rằng nếu
Chứng
minh rằng nếu
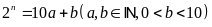 thì
tích
thì
tích
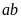 chia
hết cho 6
chia
hết cho 6Cho n là số nguyên dương, chứng minh rằng 16n – 15n – 1 chia hết cho 225.
Chứng minh rằng
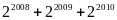 chia hết cho 7
chia hết cho 7Chứng minh rằng
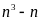 chia
hết cho 6 với mọi số tự nhiên n
chia
hết cho 6 với mọi số tự nhiên nChứng minh rằng
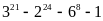 chia hết cho 1930
chia hết cho 1930
Chứng
minh rằng:
![]() chia hết cho 3 với mọi số tự nhiên
chia hết cho 3 với mọi số tự nhiên
![]() .
.
Tìm các số có 3 chữ số chia hết cho 7 và tổng các chữ số của nó cũng chia hết cho 7
Chứng minh rằng vơi mọi số tự nhiên
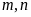
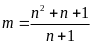
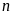 thì
phân số
thì
phân số
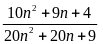 tối
giản
tối
giảnChứng minh rằng
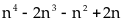 chia
hết cho
chia
hết cho
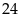 với
mọi
với
mọi
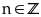
Chứng minh rằng
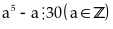
Đặt
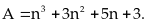 Chứng
minh rằng
Chứng
minh rằng
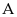 chia
hết cho 3 với mọi giá trị nguyên dương của
chia
hết cho 3 với mọi giá trị nguyên dương của
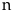
Nếu
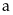 chia
chia
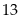 dư
dư
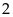 và
b chia
và
b chia
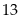 dư
3 thì
dư
3 thì
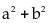 chia
hết cho 13
chia
hết cho 13
Tìm các số nguyên thỏa mãn
Chứng minh rằng:
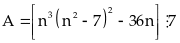 với
với
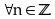
Hãy chứng minh :
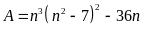 chia
hết cho 210 với mọi số tự nhiên n
chia
hết cho 210 với mọi số tự nhiên n
Chứng minh rằng tổng lập phương của ba số nguyên liên tiếp chia hết cho 9
Chứng minh rằng với mọi số tự nhiên
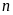 thì
thì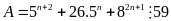
Cho
 là
các số tự nhiên có tổng chia hết cho 3
là
các số tự nhiên có tổng chia hết cho 3
Chứng
minh rằng:
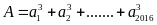 chia
hết cho 3
chia
hết cho 3
Cho hai số nguyên, số thứ nhất chia cho 5 dư 1, số thứ hai chia cho 5 dư 2. Hỏi tổng bình phương của chúng có chia hết cho 5 không ?
Chứng minh rằng nếu tổng của hai số nguyên chia hết cho 3 thì tổng các lập phương của chúng chia hết cho 9
Chứng minh rằng với mọi số nguyên
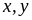 ta
có:
ta
có:
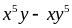 chia
hết cho 30.
chia
hết cho 30.Hãy viết thêm vào bên phải số 43 hai chữ số để nhận được một số có 4 chữ số chia hết cho 3 và 7.
Chứng minh rằng vơi mọi số tự nhiên
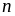 thì
phân số
thì
phân số
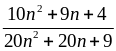 tối
giản.
tối
giản.
a)
Cho
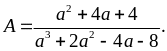 Tìm
Tìm
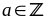 để
để
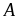 là
số nguyên.
là
số nguyên.
b)
Tìm số tự nhiên
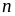 để
để
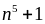 chia
hết cho
chia
hết cho
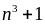 .
.
Chứng minh tổng lập phương của ba số tự nhiên liên tiếp chia hết cho 9.
Cho a, b, c
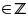 thỏa
mãn
thỏa
mãn
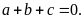 Chứng
minh:
Chứng
minh:
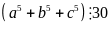
Chứng minh rằng với mọi số tự nhiên n thìA = 5n+2 + 26.5n + 82n+1
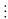 59
59a. Tìm số tự nhiên n để đa thức A chia hết cho đơn thức B
A = 3xn-1y6 - 5xn+1y4 và B = 2x3yn
b. Xác định các giá trị của a,b và c để đa thức P(x) = x4 + ax2 + bx + c chia hết cho (x – 3)3
Chứng minh rằng số có dạng
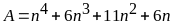 chia hết cho 24 với mọi số tự nhiên n.
chia hết cho 24 với mọi số tự nhiên n.
Chứng minh rằng
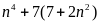 chia hết cho 64 với mọi n là số nguyên lẻ.
chia hết cho 64 với mọi n là số nguyên lẻ.Chứng minh rằng không tồn tại số nguyên
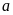 thỏa
mãn
thỏa
mãn
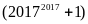 chia hết
chia hết
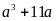
Cho số tự nhiên n 3. Chứng minh răng nếu 2n 10a b (a, b
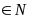 ,
0
b
10) thì tích ab chia hết cho 6.
,
0
b
10) thì tích ab chia hết cho 6.
Chứng
minh
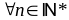 thì
thì
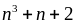 là hợp số
là hợp số
Chứng
minh rằng với mọi số tự nhiên
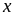 thì
biểu thức
thì
biểu thức
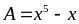 luôn
chia hết cho 30.
luôn
chia hết cho 30.
Chứng minh rằng:
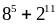 chia
hết cho 17
chia
hết cho 17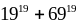 chia
hết cho 44
chia
hết cho 44
Cho n là số tự nhiên lẻ. Chứng minh
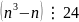
Chứng minh
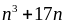 chia
hết cho
chia
hết cho
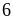 với
mọi
với
mọi
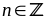
Cho
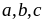 là
các số nguyên. Chứng
minh rằng
là
các số nguyên. Chứng
minh rằng
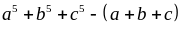 chia
hết cho 30.
chia
hết cho 30.Cho 3 số tự nhiên
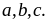 Chứng
minh rằng nếu
Chứng
minh rằng nếu
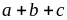 chia
hết cho 3 thì
chia
hết cho 3 thì
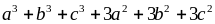 chia
hết cho 6
chia
hết cho 6
Chứng minh rằng nếu tổng của hai số nguyên chia hết cho 3 thì tổng các lập phương của chúng chia hết cho 9
Tìm các số nguyên n để
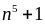 chia
hết cho
chia
hết cho
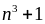
Chứng minh rằng với mọi số
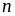 nguyên
dương thì:
nguyên
dương thì:
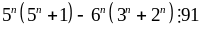
Chứng minh
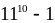 chia
hết cho 100
chia
hết cho 100Chứng minh rằng:
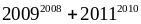 chia
hết cho
chia
hết cho
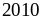
Cho
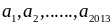 là
các số tự nhiên có tổng cộng bằng
là
các số tự nhiên có tổng cộng bằng
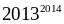
Chứng
minh rằng:
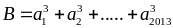 chia
hết cho 3.
chia
hết cho 3.
Tìm
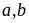 sao cho
sao cho
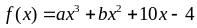 chia
hết cho đa thức
chia
hết cho đa thức
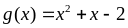
Chứng minh rằng với mọi số nguyên
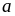 thì
thì
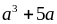 chia
hết cho 6
chia
hết cho 6Chứng minh rằng:
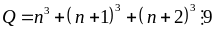 với
mọi
với
mọi
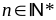
B. HƯỚNG DẪN
Chứng minh rằng: với
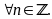
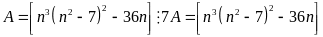
 Lời
giải
Lời
giải
Ta có:
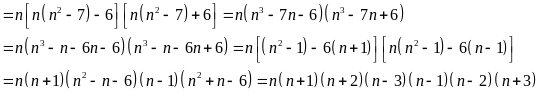 Do
đó
Do
đó
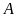 là
tích của
là
tích của
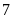 số
nguyên liên tiếp
số
nguyên liên tiếp
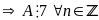
Chứng minh rằng:
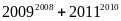 chia
hết cho
chia
hết cho
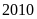
Lời giải
Ta
có:
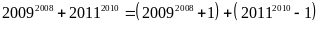
Vì
 chia hết cho 2010 (1)
chia hết cho 2010 (1)
Từ (1) và (2) ta có điều phải chứng minh.
a) Chứng minh rằng nếu tổng của hai số nguyên chia hết cho
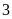 thì tổng các lập phương của chúng chia hết cho 9
thì tổng các lập phương của chúng chia hết cho 9
b)
Tìm các số nguyên n để
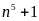 chia
hết cho
chia
hết cho
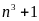
Lời giải
Gọi 2 số phải tìm là
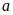 và
và
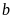 ,
ta có
,
ta có
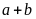 chia
hết cho 3
chia
hết cho 3
Ta
có:
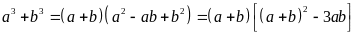
Vì
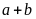 chia
hết cho 3 nên
chia
hết cho 3 nên
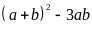 chia hết cho 3.
chia hết cho 3.
Do
vậy,
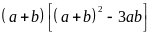 chia
hết cho 9
chia
hết cho 9
Hay
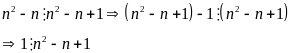
Xét hai trường hợp:
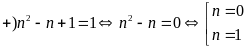
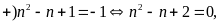 không
có giá trị của n thỏa mãn
không
có giá trị của n thỏa mãn
Chứng minh rằng nếu tổng của hai số nguyên chia hết cho 3 thì tổng các lập phương của chúng chia hết cho 9
Lời giải
Gọi
2 số phải tìm là
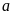 và b, ta có
và b, ta có
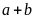 chia
hết cho 3.
chia
hết cho 3.
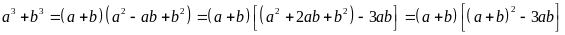
Vì
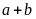 chia
hết cho
chia
hết cho
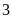 nên
nên
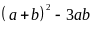 chia
hết cho 3
chia
hết cho 3
Do
vậy
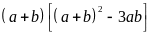 chia hết cho 9
chia hết cho 9
Chứng minh
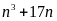 chia hết cho
chia hết cho
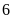 với
mọi
với
mọi
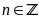
Lời giải
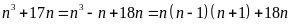
Vì
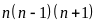 là tích ba số nguyên liên tiếp nên chia hết cho 2 và 3,
là tích ba số nguyên liên tiếp nên chia hết cho 2 và 3,
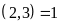 nên chia hết cho 6
nên chia hết cho 6
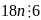 ,
suy ra điều phải chứng minh
,
suy ra điều phải chứng minh
Chứng minh rằng:
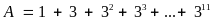 chia
hết cho
chia
hết cho
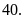
Lời giải
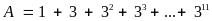
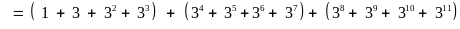
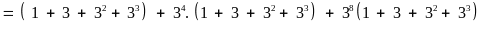
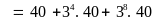
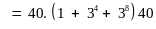
Vậy
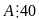
a) Chứng minh rằng tổng lập phương của ba số nguyên liên tiếp chia hết cho 9
b)
Chứng minh rằng với mọi số tự nhiên
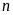 thì
thì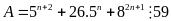
Lời giải
a)
Ta phải chứng minh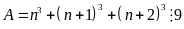 với
với
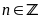
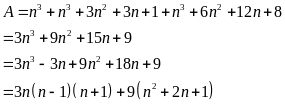
Nhận
thấy
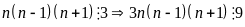 và
và
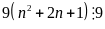 Vậy
Vậy
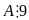
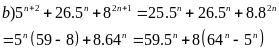
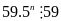 và
và
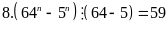
Vậy
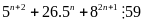
Chứng minh rằng
a)
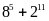 chia
hết cho 17
chia
hết cho 17
b)
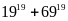 chia
hết cho 44
chia
hết cho 44
Lời giải
a)Ta
có:
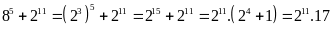 chia
hết cho 17
chia
hết cho 17
b)Ta có:
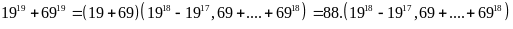 chia
hết cho 44
chia
hết cho 44
Chứng minh rằng
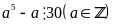
Lời giải
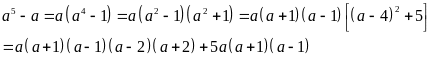
Do
tích của số nguyên liên tiếp thì chia hết cho 5 và
trong 5 số nguyên liên tiếp luôn có ba số nguyên liên
tiếp mà tích của chúng chia hết cho 6 và
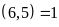
Suy
ra
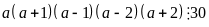 và
và
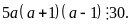
Vậy
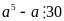
Cho
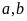 là hai số tự nhiên. Biết
rằng
là hai số tự nhiên. Biết
rằng
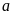 chia cho 5 dư 3 và
chia cho 5 dư 3 và
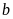 chia cho 5 dư 2. Hỏi
tích
chia cho 5 dư 2. Hỏi
tích
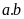 chia cho 5 dư bao nhiêu ?
chia cho 5 dư bao nhiêu ?
Lời giải
![]() chia
cho 5 dư 3 nên tồn tại số tự nhiên m sao cho
chia
cho 5 dư 3 nên tồn tại số tự nhiên m sao cho
![]() (1)
(1)
![]() chia
cho 5 dư 2 nên tồn tại số tự nhiên n sao cho
chia
cho 5 dư 2 nên tồn tại số tự nhiên n sao cho
![]() (2)
(2)
Từ
(1) và (2) suy ra
![]()
Suy
ra
![]() chia cho 5 dư
1.
chia cho 5 dư
1.
Cho các số nguyên
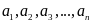 .
Đặt
.
Đặt
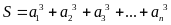 và
và
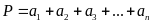 .
Chứng minh
rằng: S chia hết cho 6 khi và chỉ khi P chia hết cho 6.
.
Chứng minh
rằng: S chia hết cho 6 khi và chỉ khi P chia hết cho 6.
Lời giải
HD:
Xét hiệu:
![]()
Chứng
minh:
![]() với mọi số nguyên
với mọi số nguyên
![]() .
.
Sau đó sử dụng tính chât chia hết của một tổng suy ra đpcm.
a) Chứng minh rằng:
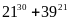 chia hết cho 45
chia hết cho 45
b)
Chứng minh rằng: Với mọi số tự nhiên n ta có:
![]() .
.
Lời giải
a)
Chứng minh rằng:
![]() chia hết cho 45.
chia hết cho 45.
HD:
Đặt
![]()
Nhận xét 45 = 5.9 mà 5 và 9 là hai số nguyên tố cùng nhau (1)
Vậy
để c/m
![]() ta cần c/m
ta cần c/m
![]() và
và
![]()
Thật
vậy,
![]() (2)
(2)
(Vì
![]() và
và
![]() )
)
Mặt
khác,
![]() và
và
![]() .
Do đó,
.
Do đó,
![]() (3)
(3)
Từ (1), (2) và (3) suy ra đpcm.
*
Chú ý:
![]()
b)
Chứng minh rằng: Với mọi số tự nhiên n ta có:
![]() .
.
Ta
có:
![]()
(
Vì
![]() ).
).
Suy ra đpcm.
Chứng minh:
a)
![]() chia hết cho 7.
chia hết cho 7.
b)
![]() chia hết cho 2, với
chia hết cho 2, với
![]() .
.
c)
![]() chia hết cho 30, với
chia hết cho 30, với
![]() .
.
d)
Nếu
![]() thì
thì
![]() chia hết cho
chia hết cho
![]() .
.
e)
![]() là bình phương của một số nguyên, với
là bình phương của một số nguyên, với
![]() .
.
f)
![]() chia hết cho
chia hết cho
![]() .
.
g)
![]() chia hết cho
chia hết cho
![]() ,
với
,
với
![]() .
.
Lời giải
Chứng minh:
a)
![]() chia hết cho 7
chia hết cho 7
Ta
có:
![]()
Vậy,
![]() chia hết cho 7 .
chia hết cho 7 .
b)
![]() chia hết cho 2, với
chia hết cho 2, với
![]() .
.
Ta
có:![]()
Vậy,
![]() chia hết cho 2, với
chia hết cho 2, với
![]()
c)
![]() chia hết cho 30, với
chia hết cho 30, với
![]() .
.
Ta
có:
![]()
Vì
![]() và
và
![]() mà
mà
![]() nên
nên
![]()
Vậy,
![]() chia hết cho 30, với
chia hết cho 30, với
![]() .
.
d)
Nếu
![]() thì
thì
![]() chia hết cho
chia hết cho
![]() .
.
Ta
có:
![]()
![]()
Vậy,
![]() chia hết cho
chia hết cho
![]()
e)
![]() là bình phương của một số nguyên, với
là bình phương của một số nguyên, với
![]() .
.
Ta
có:
![]()
![]()
![]()
Vậy,
![]() là bình phương của một số nguyên, với
là bình phương của một số nguyên, với
![]()
f)
![]() chia hết cho
chia hết cho
![]() .
.
Ta
có![]()
Xét
tại
![]() thì
thì
![]()
Vậy,
![]() chia hết cho
chia hết cho
![]() .
.
g)
![]() chia hết cho
chia hết cho
![]() ,
với
,
với
![]() .
.
Ta
có:
![]() (1)
(1)
Mặt
khác,
![]()
Từ
(1) và (2) suy ra
![]()
Vậy,
![]() chia hết cho
chia hết cho
![]() ,
với
,
với
![]() .
.
Chứng minh rằng:
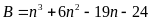 chia hết cho 6
chia hết cho 6
Lời giải
Chứng
minh rằng:
![]() chia hết cho 6
chia hết cho 6
Ta
có:
![]()
![]()
Vì
![]() và
và
![]() nên
nên
![]() (đpcm)
(đpcm)
Chứng minh: Với mọi n là số tự nhiên chẵn thì biểu thức:
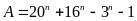
chia
hết cho
![]()
Lời giải
Chứng
minh: Với mọi n là số tự nhiên chẵn thì biểu thức:![]()
chia
hết cho
![]() .
.
Ta
có:
![]() và
và
![]() .
Ta
cần c/m:
.
Ta
cần c/m:
![]() và
và
![]() .
.
Ta
có![]()
Mà
![]() hay
hay
![]()
Và
![]() ( vì
( vì
![]() là số chẵn ) hay
là số chẵn ) hay
![]()
Từ
(1) và (2) suy ra
![]() .
.
Tương
tự,
![]()
Mà
![]() hay
hay
![]()
Và
![]() ( vì
( vì
![]() là số chẵn ) hay
là số chẵn ) hay
![]()
Từ
(3) và (4) suy ra
![]() .
.
Vì
![]() và
và
![]() mà
mà
![]() suy ra
suy ra
![]() (đpcm)
(đpcm)
Chứng minh rằng
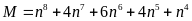 chia hết cho 16, với
chia hết cho 16, với
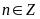
Lời giải
Chứng
minh rằng
![]() chia hết cho 16, với
chia hết cho 16, với
![]()
Ta
có:
![]()
![]()
![]()
![]()
Vì
![]() là
tích của hai số nguyên liên tiếp nên
là
tích của hai số nguyên liên tiếp nên![]()
Suy
ra
![]() mà
mà
![]()
Vậy,
![]() với
với
![]() .
.
a)Chứng minh rằng tổng lập phương của ba số nguyên liên tiếp chia hết cho 9
b)
Chứng minh rằng với mọi số tự nhiên
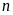 thì
thì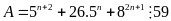
Lời giải
Ta phải chứng minh
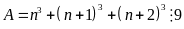 với
với
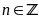
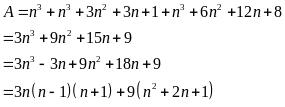
Nhận
thấy
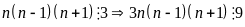 và
và
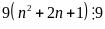
Vậy
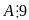
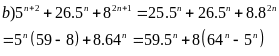
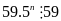 và
và
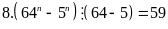
Vậy
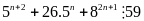
Cho
 là
các số tự nhiên có tổng chia hết cho 3
là
các số tự nhiên có tổng chia hết cho 3
Chứng
minh rằng:
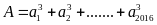 chia
hết cho 3.
chia
hết cho 3.
Lời
giải: Dễ thấy
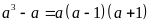 là
tích của 3 số tự nhiên liên tiếp nên chia hết cho 3
là
tích của 3 số tự nhiên liên tiếp nên chia hết cho 3
Xét hiệu:
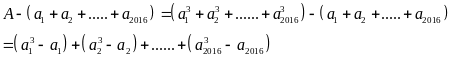
Các hiệu trên chia hết cho 3 , do vậy A chia hết cho 3
Cho hai số nguyên, số thứ nhất chia cho 5 dư 1, số thứ hai chia cho 5 dư 2. Hỏi tổng bình phương của chúng có chia hết cho 5 không ?
Lời giải
Vì
số thứ nhất chia cho 5 dư 1 nên có dạng
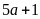 ,
số thứ hai chia cho 5 dư 2 nên có dạng
,
số thứ hai chia cho 5 dư 2 nên có dạng
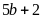 (
(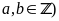
Ta có tổng bình phương hai số đó là:
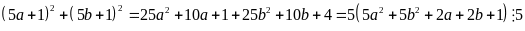
Vậy tổng bình phương của hai số chia hết cho 5
Chứng minh rằng
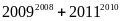 chia
hết cho
chia
hết cho
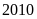
Lời giải
Ta
có:
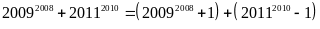
Vì
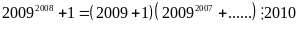 (1)
(1)
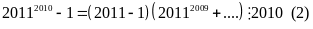
Từ (1) và (2) ta có dpcm.
Chứng minh rằng:
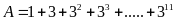 chia
hết cho 40
chia
hết cho 40
Lời giải
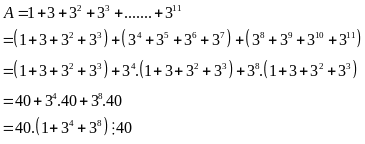
Vậy
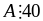
Chứng minh rằng
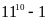 chia
hết cho
chia
hết cho
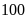
Lời giải
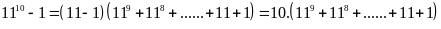
Vì
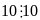
Và
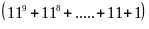 có
chữ số tận cùng bằng 0
có
chữ số tận cùng bằng 0
Nên
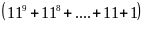 chia hết cho 10
chia hết cho 10
Vậy
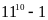 chia
hết cho
chia
hết cho
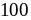
Chứng minh rằng
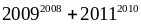 chia
hết cho
chia
hết cho
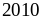
Lời giải
Ta
có:
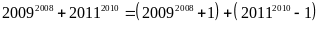
Vì
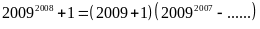
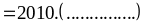 chia
hết cho 2010 (1)
chia
hết cho 2010 (1)
Vì
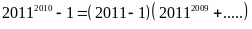
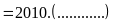 chia
hết cho
chia
hết cho
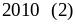
Từ (1) và (2) ta có đpcm.
Chứng minh rằng:
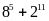 chia
hết cho 17
chia
hết cho 17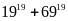 chia
hết cho 44
chia
hết cho 44
Lời giải
Ta có:
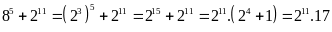
Rõ ràng kết quả trên chia hết cho 17
Áp dụng hằng đẳng thức
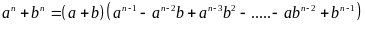 với
mọi n lẻ
với
mọi n lẻ
Ta
có:
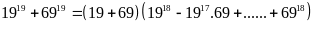
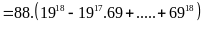 chia
hết cho 44
chia
hết cho 44
a) Chứng minh rằng:
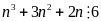 với
mọi số nguyên
với
mọi số nguyên
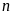
Lời giải
Ta có:
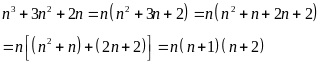
Vì
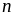 là
số nguyên nên:
là
số nguyên nên:
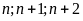 là ba số nguyên liên tiếp
là ba số nguyên liên tiếp
Do đó có ít nhất một số chia hết cho 2, 1 số chia hết cho 3
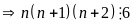 hay
hay
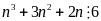 với
mọi số nguyên
với
mọi số nguyên
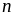
b)Tìm
số nguyên n sao cho:
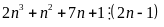
Lời giải
Để
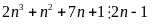 thì
thì
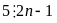 hay
hay
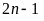 là
Ư
là
Ư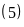
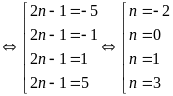
Vậy
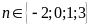 thì
thì
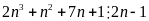
Cho số tự nhiên
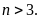 Chứng
minh rằng nếu
Chứng
minh rằng nếu
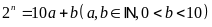 thì
tích
thì
tích
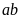 chia
hết cho 6
chia
hết cho 6
Lời giải
Ta
có:
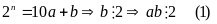
Ta
chứng minh
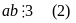
Thật
vậy , từ đẳng thức
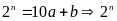 có
chữ số tận cùng là
có
chữ số tận cùng là
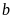
Đặt
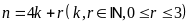 ta có:
ta có:
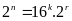
Nếu
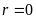 thì
thì
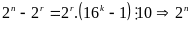 tận
cùng là
tận
cùng là
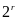
Suy
ra
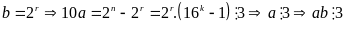
Từ
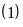 và
và
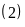 suy
ra
suy
ra
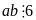
Cho n là số nguyên dương, chứng minh rằng 16n – 15n – 1 chia hết cho 225.
Lời giải
Với
n = 1 ta có: 16
– 15 – 1 = 0
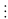 225
225
Giả sử bài toán đúng với n = k tức là ta có:
16k
– 15k – 1
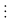 225
225
Ta chứng minh bài toán đúng với n = k + 1
Thật vậy: 16k+1 – 15(k+1) – 1 = 16.16k – 15k – 15 – 1
= 16k (15 + 1) – 15k – 15 – 1
= (16 k – 15k – 1) + 15(15k – 1)
=
(16
k
– 15k – 1) + 225. A(k)
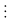 225
225
Vậy 16n – 15n – 1 chia hết cho 225 với mọi n là số nguyên dương.
Chứng minh rằng
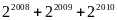 chia hết cho 7
chia hết cho 7
Lời giải
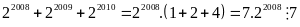
Chứng minh rằng
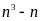 chia
hết cho 6 với mọi số tự nhiên n
chia
hết cho 6 với mọi số tự nhiên n
Lời giải
Ta
có:
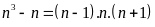 chia
hết cho 3 vì tích của 3 số nguyên liên tiếp
chia
hết cho 3 vì tích của 3 số nguyên liên tiếp
Ta
cũng có
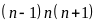 chia
hết cho 2 vì trong 3 số liên tiếp có 1 số chẵn
chia
hết cho 2 vì trong 3 số liên tiếp có 1 số chẵn
Mà
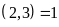 .
Vậy
.
Vậy
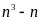 chia
hết cho 6
chia
hết cho 6
. Chứng minh rằng
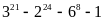 chia hết cho 1930
chia hết cho 1930
Lời giải
Đặt
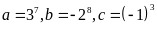 .
Ta có:
.
Ta có:
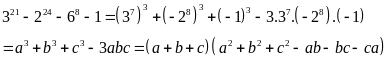
Mà
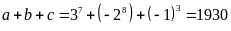 nên
suy ra đpcm.
nên
suy ra đpcm.
Chứng
minh rằng:
![]() chia hết cho 3 với mọi số tự nhiên
chia hết cho 3 với mọi số tự nhiên
![]() .
.
Lời giải
Chứng
minh rằng:
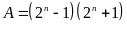 chia hết cho 3 với mọi số tự nhiên
chia hết cho 3 với mọi số tự nhiên
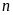 .
.
Theo
giả thiết
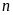 là một số tự nhiên nên
là một số tự nhiên nên
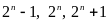 là ba số tự nhiên liên tiếp
là ba số tự nhiên liên tiếp
Vì
tích của ba số tự nhiên liên tiếp luôn chia hết cho 3
nên
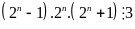
Mặt
khác,
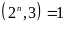 nên
nên
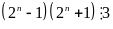 .
.
Vậy,
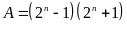 chia hết cho 3 với mọi số tự nhiên
chia hết cho 3 với mọi số tự nhiên
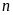 .
.
Tìm các số có 3 chữ số chia hết cho 7 và tổng các chữ số của nó cũng chia hết cho 7
Lời giải
Gọi
số có ba chữ số cần tìm là
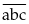
Ta
có:
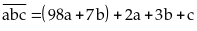
Vì
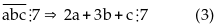
Mặt
khác, vì
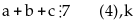 ết
hợp với (3) suy ra
ết
hợp với (3) suy ra
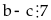
Do
đó
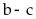 chỉ
có thể nhận các giá trị
chỉ
có thể nhận các giá trị
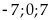
Với
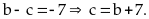 Kết
hợp với (4) ta chọn được các số
Kết
hợp với (4) ta chọn được các số
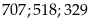 thỏa
mãn.
thỏa
mãn.
Với
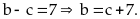 Đổi
vai trò
Đổi
vai trò
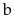 và
và
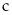 của
trường hợp trên ta được các cặp số
của
trường hợp trên ta được các cặp số
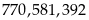 thỏa
mãn Câu toán.
thỏa
mãn Câu toán.
Với
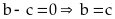 mà
do (4) nên
mà
do (4) nên
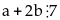
Do
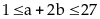 nên
nên
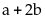 chỉ
có thể nhận các giá trị
chỉ
có thể nhận các giá trị
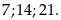
Từ
đó ta chọn được 12 số thỏa mãn là
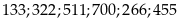
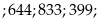
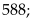
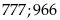
Vậy
có 18 số thỏa mãn Câu toán:
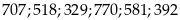
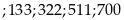
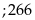
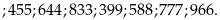
Chứng minh rằng vơi mọi số tự nhiên
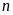 thì
phân số
thì
phân số
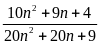 tối
giản
tối
giản
Lời giải
Gọi
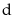 là
ƯCLN của
là
ƯCLN của
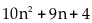 và
và
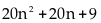
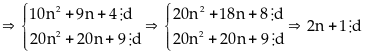
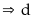 là
số tự nhiên lẻ
là
số tự nhiên lẻ
Mặt
khác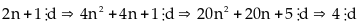 ,
mà
,
mà
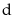 lẻ
nên
lẻ
nên
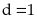
Vậy phân số trên tối giản
Chứng minh rằng
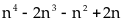 chia
hết cho
chia
hết cho
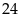 với
mọi
với
mọi
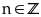
Lời giải
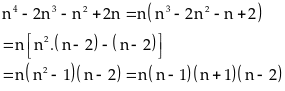
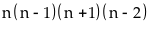 là
tích 4 số nguyên liên tiếp trong đó phải có 1 số chia
hết cho 2, một số chia hết cho 3 và một số chia hết
cho 4
là
tích 4 số nguyên liên tiếp trong đó phải có 1 số chia
hết cho 2, một số chia hết cho 3 và một số chia hết
cho 4
Nên
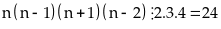
Vậy
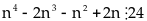
Chứng minh rằng
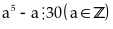
Lời giải
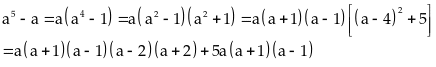
Do
tích của số nguyên liên tiếp thì chia hết cho 5 và
trong 5 số nguyên liên tiếp luôn có ba số nguyên liên
tiếp mà tích của chúng chia hết cho 6 và
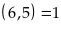
Suy
ra
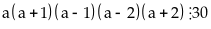 và
và
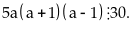
Vậy
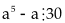
a) Đặt
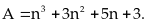 Chứng
minh rằng
Chứng
minh rằng
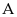 chia
hết cho 3 với mọi giá trị nguyên dương của
chia
hết cho 3 với mọi giá trị nguyên dương của
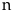
b)Nếu
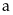 chia
chia
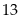 dư
dư
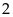 và
b chia
và
b chia
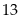 dư
3 thì
dư
3 thì
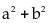 chia
hết cho 13
chia
hết cho 13
c)Tìm
các số nguyên
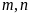 thỏa
mãn
thỏa
mãn
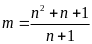
Lời giải
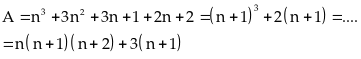
Khi
đó:
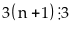 ;
;
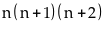 là
tích của 3 số nguyên dương liên tiếp nên chia hết cho 3
là
tích của 3 số nguyên dương liên tiếp nên chia hết cho 3
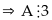
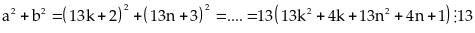
Thực hiện chia
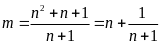
Để
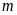 nguyên
với n nguyên khi
nguyên
với n nguyên khi
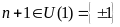
Khi
đó
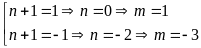
Chứng minh rằng:
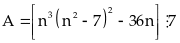 với
với
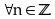
Lời giải
Ta
có:
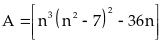
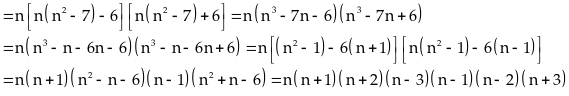 Do
đó
Do
đó
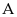 là
tích của
là
tích của
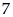 số
nguyên liên tiếp
số
nguyên liên tiếp
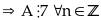
Hãy chứng minh :
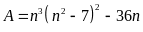 chia
hết cho 210 với mọi số tự nhiên n
chia
hết cho 210 với mọi số tự nhiên n
Lời giải
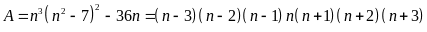
Đây là tích của 7 số nguyên liên tiếp nên có một bộ của 2, 1 bội của 3, 1 bội của 5, 1 bội của 7
Mà
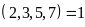 nên
nên
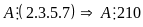
Chứng minh rằng tổng lập phương của ba số nguyên liên tiếp chia hết cho 9
Chứng minh rằng với mọi số tự nhiên
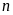 thì
thì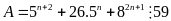
Lời giải
Ta phải chứng minh
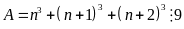 với
với
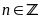
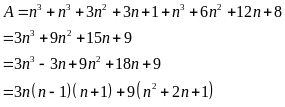
Nhận
thấy
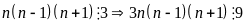 và
và
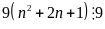
Vậy
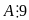
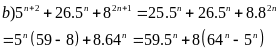
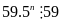 và
và
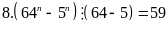
Vậy
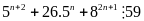
Cho
 là
các số tự nhiên có tổng chia hết cho 3
là
các số tự nhiên có tổng chia hết cho 3
Chứng
minh rằng:
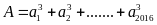 chia
hết cho 3.
chia
hết cho 3.
Lời giải
Dễ
thấy
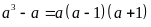 là
tích của 3 số tự nhiên liên tiếp nên chia hết cho 3
là
tích của 3 số tự nhiên liên tiếp nên chia hết cho 3
Xét hiệu:
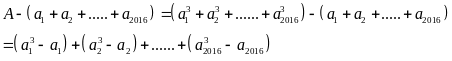
Các hiệu trên chia hết cho 3 , do vậy A chia hết cho 3
Cho hai số nguyên, số thứ nhất chia cho 5 dư 1, số thứ hai chia cho 5 dư 2. Hỏi tổng bình phương của chúng có chia hết cho 5 không ?
Lời giải
Cho hai số nguyên, số thứ nhất chia cho 5 dư 1, số thứ hai chia cho 5 dư 2. Hỏi tổng bình phương của chúng có chia hết cho 5 không ?
Chứng minh rằng nếu tổng của hai số nguyên chia hết cho 3 thì tổng các lập phương của chúng chia hết cho 9
Lời giải
Gọi
2 số phải tìm là
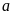 và
b, ta có
và
b, ta có
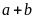 chia
hết cho 3.
chia
hết cho 3.
Ta
có:
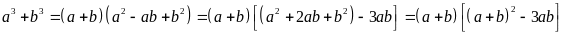 Vì
Vì
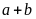 chia
hết cho
chia
hết cho
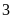 nên
nên
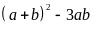 chia
hết cho 3
chia
hết cho 3
Do
vậy
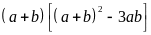 chia
hết cho 9
chia
hết cho 9
Chứng minh rằng với mọi số nguyên
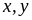 ta
có:
ta
có:
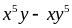 chia
hết cho 30.
chia
hết cho 30.
Lời giải
Ta có:
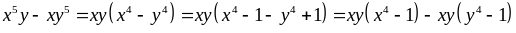
Ta
có:
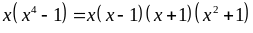 chia
hết cho 2, 3 và 5
chia
hết cho 2, 3 và 5
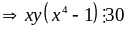
Tương
tự, ta có:
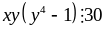
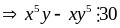
Hãy viết thêm vào bên phải số 43 hai chữ số để nhận được một số có 4 chữ số chia hết cho 3 và 7.
Lời giải
Vì
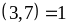 ,
theo bài toán ta có
,
theo bài toán ta có
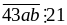
Vì
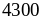 chia
21 dư 16 nên
chia
21 dư 16 nên
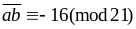 hay
hay
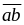 chia
21 dư 5.
chia
21 dư 5.
Vậy
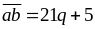
Cho
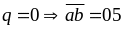 ,
số mới là 4305
,
số mới là 4305
Cho
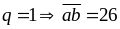 ,
số mới là 4326
,
số mới là 4326
Cho
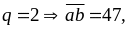 số
mới là 4347
số
mới là 4347
Cho
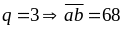 ,
số mới là
,
số mới là
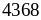
Cho
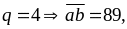 số
mới là 4389
số
mới là 4389
Chứng minh rằng vơi mọi số tự nhiên
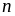 thì
phân số
thì
phân số
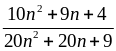 tối
giản.
tối
giản.
Lời giải
Gọi
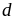 là
ƯCLN của
là
ƯCLN của
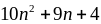 và
và
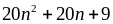
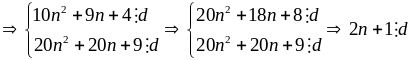
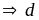 là
số tự nhiên lẻ
là
số tự nhiên lẻ
Mặt
khác:
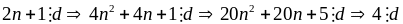 ,
mà
,
mà
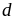 lẻ
nên
lẻ
nên
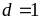
Vậy phân số trên tối giản
a) Cho
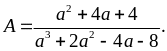 Tìm
Tìm
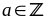 để
để
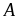 là
số nguyên.
là
số nguyên.
b)
Tìm số tự nhiên
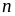 để
để
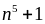 chia
hết cho
chia
hết cho
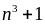
Lời giải
a)
Rút gọn
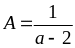
Để
A nguyên
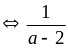 nguyên
nguyên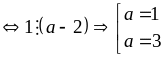
b)
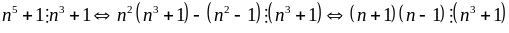
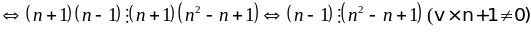
+)
Nếu
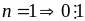
+)
Nếu
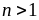 thì
thì
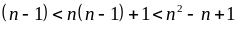 nên không thể xảy ra
nên không thể xảy ra
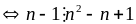
Vậy
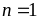
Chứng minh tổng lập phương của ba số tự nhiên liên tiếp chia hết cho 9.
Lời giải
Ta
có ba số tự nhiên liên tiếp là
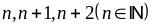
Cho
a, b, c
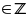 thỏa
mãn
thỏa
mãn
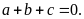 Chứng
minh:
Chứng
minh:
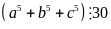
Lời giải
Ta có:
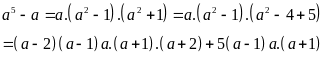
Do
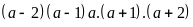 là tích 5 số nguyên liên tiếp nên chia hết cho 2, 3 và
5, do đó chia hết cho 30.
là tích 5 số nguyên liên tiếp nên chia hết cho 2, 3 và
5, do đó chia hết cho 30.
Lại
có
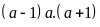 chia
hết cho 6 nên
chia
hết cho 6 nên
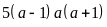 chia
hết cho 30.
chia
hết cho 30.
Từ
đó suy ra
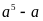 chia
hết cho 30
chia
hết cho 30
Tương
tự
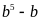 chia
hết cho 30 và
chia
hết cho 30 và
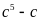 chia
hết cho 30
chia
hết cho 30
Từ
đó suy ra
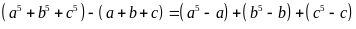 chia
hết cho 30
chia
hết cho 30
Mà
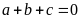 nên
nên
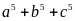 chia
hết cho 30
chia
hết cho 30
Chứng minh rằng với mọi số tự nhiên n thìA = 5n+2 + 26.5n + 82n+1
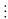 59
59
Lời giải
5n+2 + 26.5n + 82n+1 = 25.5n + 26.5n + 8.82n = 5n(59 – 8) + 8.64n = 59.5n + 8(64n – 5n)
59.5n
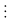 59 vaø 8(64n
– 5n)
59 vaø 8(64n
– 5n)
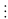 (64
– 5) = 59
(64
– 5) = 59
Vaäy
5n+2
+ 26.5n
+ 82n+1
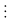 59
59
a. Tìm số tự nhiên n để đa thức A chia hết cho đơn thức B
A = 3xn-1y6 - 5xn+1y4 và B = 2x3yn
b. Xác định các giá trị của a,b và c để đa thức P(x) = x4 + ax2 + bx + c chia hết cho (x – 3)3
Lời giải a) Điểu kiện để A chia hết cho B là
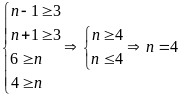
Vậy với n = 4 thì đa thức A chia hết cho đơn thức B
Khi
đó A:B = (3x3y6
– 5x5y4)(2x3y4)
=
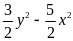
b) Chia P(x) cho (x – 3)3 ta được thương là x + 9 và dư là
R(x) = (a + 54)x2 + (b-216)x + 243 + c
P(x)
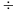 (x
- 3)3
(x
- 3)3
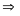 R (x)
R (x)
 0 cho ta
0 cho ta
a
+ 54 = 0
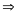 a = -54; b – 216 = 0
a = -54; b – 216 = 0
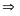 b = 216; c + 243 = 0
b = 216; c + 243 = 0
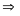 c = -243
c = -243
Chứng minh rằng số có dạng
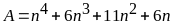 chia hết cho 24 với mọi số tự nhiên n.
chia hết cho 24 với mọi số tự nhiên n.
Lời giải
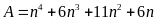 =
=
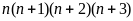
Vì
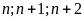 là ba số tự nhiên liên tiếp nên tồn tại 1 số chia hết
cho 3. Do đó
là ba số tự nhiên liên tiếp nên tồn tại 1 số chia hết
cho 3. Do đó
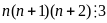
Vì
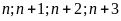 là bốn số tự nhiên liên tiếp nên có 2 số chẵn liên
tiếp, trong 2 số chẵn liên tiếp có 1 số chia hết cho 2,
số kia chia hết cho 4.
là bốn số tự nhiên liên tiếp nên có 2 số chẵn liên
tiếp, trong 2 số chẵn liên tiếp có 1 số chia hết cho 2,
số kia chia hết cho 4.
Vậy
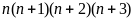
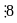
Vì
ƯCLN(3;8) =1 nên
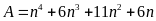 chia hết cho 24.
chia hết cho 24.
Chứng minh rằng
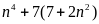 chia hết cho 64 với mọi n là số nguyên lẻ.
chia hết cho 64 với mọi n là số nguyên lẻ.
Lời giải
Ta
có
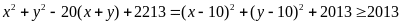 với mọi x, y.
với mọi x, y.
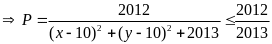
P
=
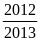 khi x = 10 và y = 10
khi x = 10 và y = 10
Vậy
Max P
=
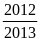 khi x = 10 và y = 10.
khi x = 10 và y = 10.
Chứng minh rằng không tồn tại số nguyên
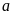 thỏa
mãn
thỏa
mãn
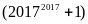 chia hết
chia hết
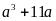
Lời giải
Giả
sử tồn tại số nguyên
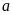 thỏa
mãn
thỏa
mãn
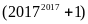 chia hết
chia hết
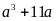
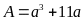 =
=
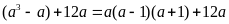
ta
có
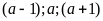 là 3 số nguyên liên tiếp nên tồn tại một số là bội
của 3 suy ra
là 3 số nguyên liên tiếp nên tồn tại một số là bội
của 3 suy ra
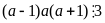
Vì
12a chia hết cho 3 nên
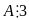 (1)
(1)
Mặt
khác
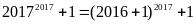 chia cho 3 dư 2 (2)
chia cho 3 dư 2 (2)
Từ (1) và (2) dẫn đến điều giả sử trên là sai, tức là không có số nguyên nào thỏa mãn điều kiện bài toán đã cho.
Cho số tự nhiên n 3. Chứng minh rằng nếu 2n 10a b (a, b
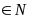 ,
0
b
10) thì tích ab chia hết cho 6.
,
0
b
10) thì tích ab chia hết cho 6.
Lời giải
Ta
có 2n
10a
b
b
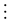 2
ab
2
ab
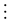 2 (1)
2 (1)
Ta
chứng minh ab
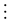 3 (2)
3 (2)
Thật vậy, từ đẳng thức 2n 10a b 2n có chữ số tận cùng là b.
Đặt n 4k r (k, r N, 0 r 3) ta có: 2n 16k2r.
Nếu
r 0 thì 2n
16k
tận cùng là 6 b 6 ab
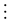 6.
6.
Nếu
1
r
3 thì 2n
2r
2r(16k
1)
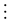 10 2n
tận cùng là 2r
10 2n
tận cùng là 2r
suy
ra b 2r
10a 2n
2r
2r(16k
1)
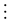 3 a
3 a
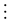 3 ab
3 ab
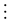 3.
3.
Từ
(1) và (2) suy ra ab
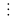 6.
6.
Chứng minh
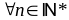 thì
thì
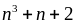 là hợp số
là hợp số
Lời giải
Ta có:
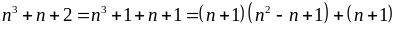
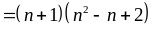
Do
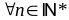 nên
nên
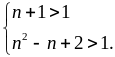 .Vậy
.Vậy
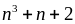 là
hợp số.
là
hợp số.
: Chứng minh rằng với mọi số tự nhiên
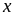 thì
biểu thức
thì
biểu thức
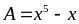 luôn
chia hết cho 30.
luôn
chia hết cho 30.
Lời giải
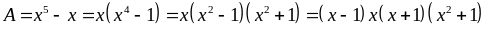
Vì
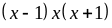 là tích ba số nguyên liên tiếp nên
là tích ba số nguyên liên tiếp nên
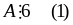
+)
Nếu
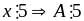
+)Nếu
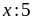 dư
1 thì
dư
1 thì
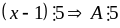
+)Nếu
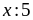 dư
4 thì
dư
4 thì
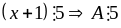
+)Nếu
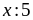 dư
2 hoặc 3 thì
dư
2 hoặc 3 thì
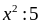 dư
4
dư
4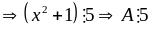
Vậy
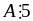 với
mọi x và
với
mọi x và
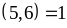 (2)
(2)
Từ
(1) và (2) suy ra
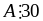
Chứng minh rằng:
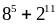 chia
hết cho 17
chia
hết cho 17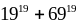 chia
hết cho 44
chia
hết cho 44
Lời giải
Ta có:
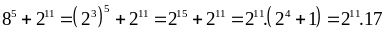
Rõ ràng kết quả trên chia hết cho 17
Áp dụng hằng đẳng thức
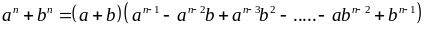 với
mọi n lẻ
với
mọi n lẻ
Ta
có:
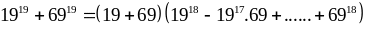
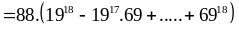 chia
hết cho 44
chia
hết cho 44
Lời giải
Ta
có:
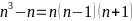
Vì
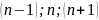 là
ba số tự nhiên liên tiếp nên có một trong ba số đó
chia hết cho 3 (1)
là
ba số tự nhiên liên tiếp nên có một trong ba số đó
chia hết cho 3 (1)
Do đó
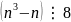 (2)
(2)
Vì 3 và 8 là hai số nguyên tố cùng nhau nên kết hợp với (1); (2) suy ra
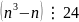
Vì
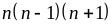 là
tích ba số nguyên liên tiếp nên chia hết cho 2 và 3,
là
tích ba số nguyên liên tiếp nên chia hết cho 2 và 3,
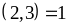 nên
chia hết cho 6
nên
chia hết cho 6
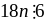 ,
suy ra điều phải chứng minh
,
suy ra điều phải chứng minh
Học sinh biến đổi được
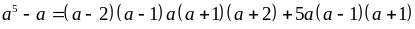
Lập
luận được
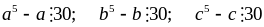 ,
kết luận
,
kết luận
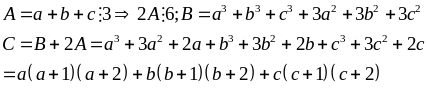
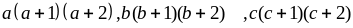 là
tích của 3 số nguyên liên tiếp nên chia hết cho 6
là
tích của 3 số nguyên liên tiếp nên chia hết cho 6
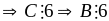
Gọi 2 số phải tìm là
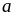 và
và
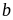 ,
ta có
,
ta có
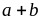 chia
hết cho 3
chia
hết cho 3
Ta
có:
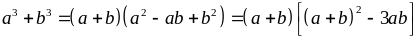
Vì
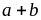 chia
hết cho 3 nên
chia
hết cho 3 nên
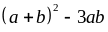 chia
hết cho 3.
chia
hết cho 3.
Do
vậy,
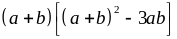 chia
hết cho 9
chia
hết cho 9
Hay
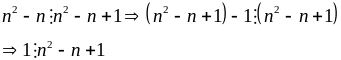
Xét hai trường hợp:
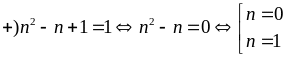
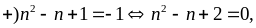 không
có giá trị của n thỏa mãn
không
có giá trị của n thỏa mãn
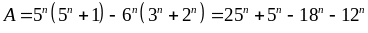
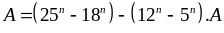 chia
hết cho 7
chia
hết cho 7
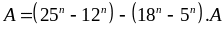 chia
hết cho 13
chia
hết cho 13
Do
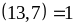 nên
nên
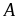 chia
hết cho 91
chia
hết cho 91
Vì
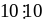
Và
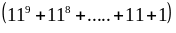 có
chữ số tận cùng (hàng đơn vị ) bằng 0
có
chữ số tận cùng (hàng đơn vị ) bằng 0
Nên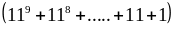 chia
hết cho 10
chia
hết cho 10
Vậy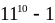 chia
hết cho 10.
chia
hết cho 10.
Ta có:
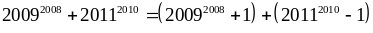
Vì
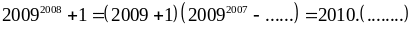 chia hết cho 2010 (1)
chia hết cho 2010 (1)
Vì
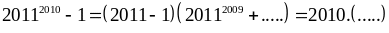 chia hết cho 2010 (2)
chia hết cho 2010 (2)
Từ (1) và (2) ta có điều phải chứng minh.
Dễ thấy
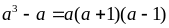 là
tích của 3 số tự nhiên liên tiếp nên chia hết cho 3
là
tích của 3 số tự nhiên liên tiếp nên chia hết cho 3
Xét
hiệu
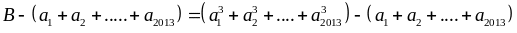
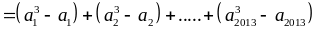 chia
hết cho 3
chia
hết cho 3
Mà
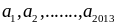 là
các số tự nhiên có tổng bằng
là
các số tự nhiên có tổng bằng
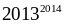
Do
vậy
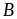 chia
hết cho 3.
chia
hết cho 3.
Tìm
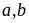 sao cho
sao cho
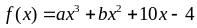 chia
hết cho đa thức
chia
hết cho đa thức
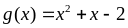
Lời giải
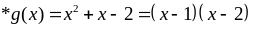
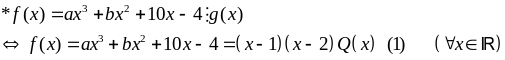
Thay
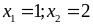 vào
vào
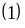 ta
có:
ta
có:
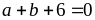 và
và
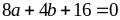
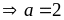 và
và
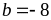
Vậy
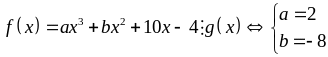
Chứng minh rằng với mọi số nguyên
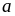 thì
thì
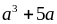 chia
hết cho 6
chia
hết cho 6
Lời giải
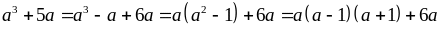
Vì
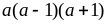 là
tích 3 số nguyên liên tiếp nên có 1 số chia hết cho 2,
một số chia hết cho 3 mà
là
tích 3 số nguyên liên tiếp nên có 1 số chia hết cho 2,
một số chia hết cho 3 mà
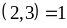 nên
nên
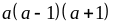 chia
hết cho 6
chia
hết cho 6
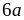 chia
hết cho 6 Nên
chia
hết cho 6 Nên
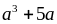 chia
hết cho 6
chia
hết cho 6
Chứng minh rằng:
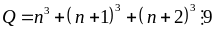 với
mọi
với
mọi
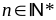
Lời
giải
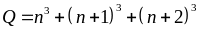
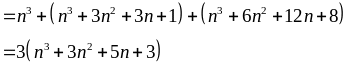
Đặt
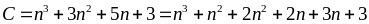
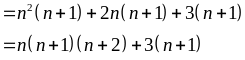
Ta
thấy
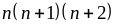 chia
hết cho 3( vì tích 3 số tự nhiên liên tiếp)
chia
hết cho 3( vì tích 3 số tự nhiên liên tiếp)
Và
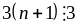
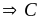 chia
hết cho 3
chia
hết cho 3
Nên
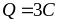 chia
hết cho 9
chia
hết cho 9
Ngoài Dạng Toán Chia Hết Ôn Thi HSG Đại Số 8 Có Lời Giải Chi Tiết thì các tài liệu học tập trong chương trình 8 sẽ được cập nhật liên tục và nhanh nhất có thể sau khi kỳ thi diễn ra trên Danh mục Tài Liệu Học Tập nhằm giúp các bạn đọc thuận tiện trong việc nghiên cứu tài liệu. Quý thày cô và các bạn đọc có thể chia sẻ thêm những tài liệu học tập hữu ích đến địa chỉ email của chúng tôi, nhằm xây dựng nên kho đề thi phong phú, đa dạng cho các em học sinh tham khảo và rèn luyện.
Xem thêm
| Đề Cương Ôn Tập Sinh Học 8 Học Kì 2 Có Lời Giải |