Top 10 Đề Thi Học Kì 1 Toán 11 Hay Nhất Năm 2023 Có Đáp Án
Top 10 Đề Thi Học Kì 1 Toán 11 Hay Nhất Năm 2023 Có Đáp Án – Tài Liệu Toán được Trang Tài Liệu sưu tầm với các thông tin mới nhất hiện nay. Đề thi này sẽ giúp các em học sinh ôn tập, củng cố kiến thức, rèn luyện kĩ năng làm bài. Cũng như hỗ trợ thầy cô trong quá trình giảng dạy. Hy vọng những tài liệu này sẽ giúp các em trong quá trình ôn luyện và đạt kết quả cao trong bài thi sắp tới.
>>> Mọi người cũng quan tâm:

Dưới đây là bản đọc trực tuyến giúp thầy cô và các em học sinh có thể nghiên cứu Online hoặc bạn có thể tải miễn phí với phiên bản word để dễ dàng in ấn cũng như học tập Offline
SỞ GD&ĐT VĨNH PHÚC
|
ĐỀ KIỂM TRA HỌC KÌ I NĂM HỌC 2016-2017 MÔN: TOÁN – LỚP 11 Thời gian làm bài: 90 phút, không kể thời gian giao đề. |
( Thí
sinh làm bài vào tờ giấy thi)
Thí
sinh làm bài vào tờ giấy thi)
I. PHẦN TRẮC NGHIỆM (2,0 điểm)
Câu 1. Trong mặt phẳng tọa độ
![]() ,
cho điểm
,
cho điểm
![]() .
Phép quay tâm
.
Phép quay tâm
![]() góc
góc
![]() biến điểm
biến điểm
![]() thành điểm
thành điểm
A.
![]() . B.
. B.
![]() . C.
. C.
![]() . D.
. D.
![]() .
.
Câu 2. Khẳng định nào sau đây là sai?
A. Hàm số
![]() là hàm số chẵn. B. Hàm số
là hàm số chẵn. B. Hàm số
![]() là hàm số lẻ.
là hàm số lẻ.
C. Hàm số
![]() là hàm số chẵn. D. Hàm số
là hàm số chẵn. D. Hàm số
![]() là hàm số lẻ.
là hàm số lẻ.
Câu 3. Tính giá trị biểu thức
![]() .
.
A.
![]() . B.
. B.
![]() . C.
. C.
![]() . D.
. D.
![]() .
.
Câu 4. Một câu lạc bộ cầu lông có 26 thành viên. Số cách chọn một ban đại diện gồm một trưởng ban, một phó ban và một thư ký là
A. 13800. B. 6900. C. 15600. D. 1560.
Câu 5. Trong
mặt phẳng tọa độ Oxy,
cho
![]()
![]() Phép
tịnh tiến biến điểm A
thành
điểm B
có vectơ tịnh tiến là
Phép
tịnh tiến biến điểm A
thành
điểm B
có vectơ tịnh tiến là
A.
![]() . B.
. B.
![]() . C.
. C.
![]() . D.
. D.
![]() .
.
Câu 6. Gieo một đồng tiền xu cân đối, đồng chất liên tiếp hai lần. Xác suất để cả hai lần xuất hiện mặt sấp là
A. 0,75. B.
![]() . C.
0,25. D.
. C.
0,25. D.
![]() .
.
Câu 7. Trong các mệnh đề sau đây, mệnh đề nào đúng?
A. Có duy nhất một mặt phẳng đi qua 3 điểm cho trước.
B. Có duy nhất một mặt phẳng đi qua ba điểm không thẳng hàng cho trước.
C. Có duy nhất một mặt phẳng đi qua một điểm và một đường thẳng.
D. Có duy nhất một mặt phẳng đi qua 4 điểm cho trước.
Câu 8. Trong các khẳng định sau, khẳng định nào đúng?
A. Hai đường thẳng cắt nhau thì chúng không đồng phẳng.
B. Tồn tại duy nhất một mặt phẳng đi qua một điểm và một đường thẳng cho trước.
C. Hai đường thẳng cắt nhau nếu chúng đồng phẳng và không song song.
D. Hai đường thẳng phân biệt cắt nhau nếu chúng đồng phẳng và không song song
II. PHẦN TỰ LUẬN (8,0 điểm)
Câu 9 (3,0 điểm). Giải các phương trình lượng giác sau:
a)
![]() b)
b)
![]() c)
c)
![]()
Câu 10 (2,0 điểm)
a) Có 9 viên bi xanh, 5 viên bi đỏ, 4 viên bi vàng có kích thước đôi một khác nhau. Hỏi có bao nhiêu cách chọn ra 6 viên bi, trong đó số bi xanh bằng số bi đỏ?
b) Tìm số hạng không chứa x trong khai
triển biểu thức
![]() (với
(với
![]() ).
).
Câu 11 (1,0 điểm).
Trong mặt phẳng tọa độ Oxy,
cho hai điểm
![]() ,
,
![]() .
Tìm tâm của phép vị tỉ số
.
Tìm tâm của phép vị tỉ số![]() biến điểm A
thành A’.
biến điểm A
thành A’.
Câu 12 ( 2,0 điểm). Cho
hình chóp S.ABCD
có đáy ABCD
là hình bình hành. Gọi M
là trung điểm của SC,
![]() là mặt phẳng qua AM và
song song với BD.
là mặt phẳng qua AM và
song song với BD.
a) Xác định thiết diện của hình chóp
khi cắt bởi mặt phẳng
![]() .
.
b) Gọi E,
F lần
lượt là giao điểm của
![]() với các cạnh SB
và SD.
Hãy tìm tỉ số giữa diện tích của tam giác SME
và tam giác SBC;
tỉ số giữa diện tích của tam giác SMF
và tam giác SCD.
với các cạnh SB
và SD.
Hãy tìm tỉ số giữa diện tích của tam giác SME
và tam giác SBC;
tỉ số giữa diện tích của tam giác SMF
và tam giác SCD.
------------- Hết ------------
(Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm)
Họ tên học sinh………………........................………..........Số báo danh…………….………….........................
SỞ GD&ĐT VĨNH PHÚC
|
HƯỚNG DẪN CHẤM KIỂM TRA HỌC KÌ I NĂM HỌC 2016-2017 MÔN: TOÁN 11
|
LƯU Ý CHUNG:
- Hướng dẫn chấm chỉ trình bày một cách giải với những ý cơ bản phải có. Khi chấm bài học sinh làm theo cách khác nếu đúng và đủ ý thì vẫn cho điểm tối đa.
- Với Câu 12 nếu thí sinh không vẽ hình phần nào thì không cho điểm tương ứng với phần đó.
- Điểm toàn bài tính đến 0,25 và không làm tròn.
I. PHẦN TRẮC NGHIỆM (2,0đ): 0,25đ/câu
1.B |
2.A |
3.B |
4.C |
5.B |
6.C |
7.B |
8.D |
II. PHẦN TỰ LUẬN
Câu |
Nội dung |
Điểm |
9a |
Giải phương trình
|
1,0 |
|
0,5 |
|
|
0,5 |
|
9b |
Giải phương trình
|
1,0 |
|
0,5 |
|
|
0,5 |
|
9c |
Giải phương trình
|
1,0 |
|
0,5 |
|
|
0,25 |
|
|
0,25 |
|
10a |
Có 9 viên bi xanh, 5 viên bi đỏ, 4 bi vàng có kích thước đôi một khác nhau. Hỏi có bao nhiêu cách chọn ra 6 viên bi, trong đó số bi xanh bằng số bi đỏ? |
1,0 |
Trường hợp 1: Chọn 3 xanh, 3 đỏ ta có:
|
0,25 |
|
Trường hợp 2: Chọn 2 xanh, 2 đỏ, 2 vàng, ta có:
|
0,25 |
|
Trường hợp 3: Chọn 1 xanh, 1 đỏ, 4 vàng, ta có:
|
0,25 |
|
Theo qui tắc cộng, ta có:
|
0,25 |
|
10b |
Tìm số hạng không chứa x trong khai triển biểu thức
|
1,0 |
Ta có:
|
0,5 |
|
Số hạng không chứ x thì k phải thỏa mãn điều kiện:
Vậy
số hạng không chứa x là:
|
0,5 |
|
11 |
Trong mặt phẳng tọa độ Oxy, cho hai điểm
|
1,0 |
Gọi
|
0,25 |
|
|
0,5 |
|
|
0,25 |
|
12a |
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là trung điểm của SC, (P) là mặt phẳng qua AM và song song với BD. Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng (P)
|
1,0 |
Gọi
Gọi
|
0,25 |
|
|
0,25 |
|
GỌi
Suy ra: E, F cũng là giao điểm của SB,SD với mặt phẳng (P) Vậy: Thiết diện cần tìm là tứ giác AEMF. |
0,5 |
|
12b |
Gọi E, F lần lượt là giao điểm của (P) với các cạnh SB và SD. Hãy tìm tỉ số diện tích của tam giác SME với tam giác SBC và tỉ số diện tích tam giác SMF và tam giác SCD. |
1,0 |
I là trọng tâm của tam giác SAC nên:
|
0,25 |
|
Xét tam giác SBD có EF song song với BD ta có:
|
0,25 |
|
|
0,5 |
-----------------------------------------------HẾT-----------------------------------------------
SỞ GIÁO DỤC VÀ ĐÀO TẠO TUYÊN QUANG TRƯỜNG THPT ĐÔNG THỌ
|
ĐỀ KIỂM TRA HỌC KÌ I NĂM HỌC 2016 - 2017 Môn: Toán – Lớp 11 Thời gian làm bài: 50 phút, không kể thời gian phát đề
|
Họ và tên:..................................................................... Lớp: 11B |
Mã đề: 135 |
PHẦN 1: ĐẠI SỐ VÀ GIẢI TÍCH
Câu
1. Tập xác định của hàm số
![]() là:
là:
A.
![]() .
B.
.
B.
![]() .
.
C.
![]() .
D.
.
D.
![]() .
.
Câu 2. Giá trị lớn
nhất và giá trị nhỏ nhất của hàm số
![]() lần lượt là
lần lượt là
A. 2 và – 3. B. – 1 và – 5. C. 0 và – 3. D. 2 và 0.
Câu
3. Giá trị
![]() là nghiệm phương trình nào sau đây?
là nghiệm phương trình nào sau đây?
A.
![]() B.
B.
![]()
C.
![]() D.
D.
![]()
Câu 4. Phương trình
![]() có tập nghiệm là
có tập nghiệm là
A.
![]() .
.
![]() B.
B.
![]() .
.
C.
![]() . D.
. D.
![]() .
.
Câu 5.Phương trình
![]() có tập nghiệm là.
có tập nghiệm là.
A.
![]() .
.![]() B.
B.
![]() .
.
C.
![]() . D.
. D.
![]() .
.
Câu 6. Phương trình
![]() có tập nghiệm là.
có tập nghiệm là.
A.
![]() .
.![]() B.
B.
![]() .
.
C.
![]() . D.
. D.
![]() .
.
Câu 7. Một cửa hàng có 7 chiếc áo màu hồng, 3 chiếc áo màu đỏ và 11 chiếc áo màu xanh. Hỏi có bao nhiêu cách chọn hai chiếc áo có màu khác nhau?
A. 131. B. 21 . C. 210 . D. 231.
Câu 8. Các thành phố A, B, C, D được nối với nhau bởi các con đường như hình vẽ. Hỏi có bao nhiêu cách đi từ A đến D mà qua B và C chỉ một lần?

A. 18. B. 9. C. 24. D. 10.
Câu 9. Từ các chữ số 0; 2; 3; 4; 5; 6; 7 lập được bao nhiêu số tự nhiên lẻ gồm 4 chữ số khác nhau ?
A. 490. B. 360. C. 240. D. 300.
Câu 10. Trong mặt phẳng, cho 6 điểm phân biệt A, B, C, D, E, F. Hỏi có thể tạo thành bao nhiêu đoạn thẳng mà hai đầu mút thuộc tập 6 điểm đã cho ?
A. 12. B. 6. C. 15. D. 30.
Câu 11. Trong mặt phẳng, cho 6 điểm phân biệt A, B, C, D, E, F. Hỏi có thể tạo thành bao nhiêu vectơ khác vectơ - không mà điểm đầu, điểm cuối thuộc tập 6 điểm đã cho ?
A. 6. B. 12. C. 30. D. 15.
Câu 12. Có 5 người đến nghe một buổi hòa nhạc. Số cách xếp 5 người này vào một hàng có 5 ghế là
A. 5. B. 210. C. 120. D. 25.
Câu 13. Giá trị
của biểu thức :
![]() bằng:
bằng:
A. 225 . B. 152. C. 252 . D. 522.
Câu 14. Nếu
![]() thì
thì
![]() bằng bao nhiêu ?
bằng bao nhiêu ?
A. 10. B. 40. C. 30. D. 20.
Câu 15. Cho
![]() .
Khi đó, S là khai triển của nhị thức nào dưới đây.
.
Khi đó, S là khai triển của nhị thức nào dưới đây.
A.
![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
Câu 16. Hệ số của số hạng
thứ 3 trong khai triển
![]() là ?
là ?
A.
![]() . B.
. B.
![]() .
C.
.
C.
![]() .
D.
.
D.
![]() .
.
Câu 17. Gieo ngẫu nhiên một đồng tiền cân đối và đồng chất ba lần. Xác suất để ba lần gieo giống nhau là.
A.
![]() .
B.
.
B.
![]() .
C.
.
C.
![]() .
D.
.
D.
![]() .
.
Câu 18. Gieo một con súc sắc hai lần. Xác suất để tổng số chấm xuất hiện trên hai mặt bằng 4 là
A.
![]() .
B.
.
B.
![]() .
C.
.
C.
![]() .
D.
.
D.
![]() .
.
Câu 19. Một người đi du lịch mang 3 hộp thịt, 2 hộp cá và 3 hộp sữa có kích cỡ, hình dáng giống nhau.Do trời mưa nên các hộp bị mất nhãn. Người đó chọn ngẫu nhiên ba hộp. Tính xác suất sao cho chọn được 1 hộp thịt, 1 hộp cá và 1 hộp sữa.
A.
![]() .
B.
.
B.
![]() .
C.
.
C.
![]() .
D.
.
D.
![]() .
.
Câu 20. Một công ty cần tuyển 3 nhân viên. Có 10 người nộp đơn trong đó có một người tên là Hoa. Khả năng được tuyển của mỗi người là như nhau. Chọn ngẫu nhiên 3 người. Tính xác suất để người tên Hoa được chọn
A.
![]() .
B.
.
B.
![]() .
C.
.
C.
![]() .
D.
.
D.
![]() .
.
Câu 21. Một khách sạn có 6 phòng đơn. Có 10 người khách đến thuê phòng, trong đó có 6 nam và 4 nữ. Chủ khách sạn chọn ngẫu nhiên 6 người khách. Tính xác suất để có ít nhất hai khách là nữ.
A.
![]() .
B.
.
B.
![]() .
C.
.
C.
![]() .
D.
.
D.
![]() .
.
Câu 22. Trong lễ kỉ niệm 20 năm thành lập trường THPT Đông Thọ, đội văn nghệ của trường đã hoàn thành xuất sắc nhiệm vụ được giao. Biết rằng thành phần đội văn nghệ gồm có 6 học sinh khối 10, 7 học sinh khối 11 và 9 học sinh khối 12. Chọn ngẫu nhiên 5 bạn để khen thưởng. Tính xác suất để trong 5 bạn được chọn thì khối nào cũng có ít nhất một đại diện.
A.
![]() .
B.
.
B.
![]() .
C.
.
C.
![]() .
D.
.
D.
![]() .
.
Câu 23. Trong một hộp có 20 tấm thẻ được đánh số từ 1 đến 20. Chọn ngẫu nhiên ra 5 tấm thẻ. Tính xác suất để trong 5 thẻ được chọn ra có 3 tấm thẻ mang số lẻ, 2 tấm thẻ mang số chẵn trong đó chỉ có đúng 1 tấm thẻ mang số chia hết cho 4.
A.
![]() .
B.
.
B.
![]() .
C.
.
C.
![]() .
D.
.
D.
![]() .
.
Câu 24. Biết dãy số
![]() là một cấp số cộng. Công sai của cấp số cộng đã
cho là
là một cấp số cộng. Công sai của cấp số cộng đã
cho là
A.
![]() . B.
. B.
![]() .
C.
.
C.
![]() .
D.
.
D.
![]() .
.
Câu 25. Tìm số hạng thứ năm của
cấp số cộng
![]() ,
biết số hạng đầu bằng 2 và công sai bằng 3.
,
biết số hạng đầu bằng 2 và công sai bằng 3.
A. 15. B. 5. C. 17. D. 11.
Câu 26. Cho cấp số
nhân
![]() có
có
![]() và
và
![]() .
Tổng năm số hạng đầu tiên của cấp số nhân đó
bằng?
.
Tổng năm số hạng đầu tiên của cấp số nhân đó
bằng?
A.
![]() . B.
. B.
![]() .
C.
.
C.
![]() .
D.
.
D.
![]() .
.
PHẦN 2: HÌNH HỌC
Câu
27. Trong mặt phẳng Oxy, hai điểm
![]() và
và
![]() .
Gọi C, D lần lượt là ảnh của A và B tịnh tiến
theo vectơ
.
Gọi C, D lần lượt là ảnh của A và B tịnh tiến
theo vectơ
![]() . Khẳng định nào sau đây là khẳng định đúng?
. Khẳng định nào sau đây là khẳng định đúng?
A. ABCD là hình thang. B. ABCD là hình bình hành.
C. ABDC là hình bình hành. D. Bốn điểm A, B, C, D thẳng hàng.
Câu 28. Cho: 3x – 2
y – 1 = 0. Ảnh của đường thẳng
![]() qua phép tịnh tiến theo vectơ
qua phép tịnh tiến theo vectơ
![]() là đường thẳng nào dưới đây.
là đường thẳng nào dưới đây.
A.
![]() .
B.
.
B.
![]() .
.
C.
![]() .
D.
.
D.
![]() .
.
Câu 29. Điểm nào
dưới đây là ảnh của
![]() qua
phép vị tự tâm O( 0, 0 ) tỉ số
qua
phép vị tự tâm O( 0, 0 ) tỉ số
![]()
A.![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
Câu 30. Điểm nào sau đây là ảnh của M ( 1, 2) qua phép quay tâm O(0,0) góc quay 900
A. A( 2, -1). B. B( 1, -2) . C. C(-2, 1) . D. D( -1, -1).
Câu 31. Trong các mệnh đề sau, mệnh đề nào sai:
A. Phép vị tự biến đường tròn thành đường tròn có cùng bán kính.
B. Phép tịnh tiến biến đường thẳng thành đường thẳng song song hoặc trùng với nó.
C. Phép dời hình biến ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự giữa các điểm.
D. Phép vị tự biến đường thẳng thành đường thẳng song song hoặc trùng với nó.
Câu 32. Nhận xét nào sau đây là đúng trong hình học không gian:
A. Hình biểu diễn của một góc phải là một góc bằng nó.
B. Qua ba điểm xác định duy nhất một mặt phẳng.
C. Qua ba điểm phân biệt không thẳng hàng xác định duy nhất một mặt phẳng.
D. Qua ba điểm phân biệt xác định duy nhất một mặt phẳng.
Câu 33. Tìm mệnh đề đúng trong các mệnh đề sau
A. Hai đường thẳng phân biệt cùng nằm trong một mặt phẳng thì không chéo nhau.
B. Hai đường thẳng phân biệt không cắt nhau thì chéo nhau.
C. Hai đường thẳng phân biệt không song song thì chéo nhau.
D. Hai đường thẳng phân biệt lần lượt thuộc hai mặt phẳng khác nhau thì chéo nhau.
Câu 34. Trong các phép biến hình dưới đây, phép nào không bảo toàn khoảng cách giữa hai điểm bất kì?
A. Phép tịnh tiến. B. Phép vị tự bất kì.
C. Phép dời hình. D. Phép quay.
Câu 35. Cho tam giác ABC. Gọi M, N lần lượt là trung điểm của AB và AC. Phép vị tự tâm A tỉ số k bằng bao nhiêu sẽ biến tam giác ABC thành tam giác AMN.
A.
![]() .
B.
.
B.
![]() . C.
. C.
![]() .
D.
.
D.
![]() .
.
Câu 36. Trong mặt phẳng Oxy, cho
đường tròn (C) có phương trình
![]() .
Phép đồng dạng có được bằng cách thực hiện liên
tiếp phép vị tự tâm O, tỉ số
.
Phép đồng dạng có được bằng cách thực hiện liên
tiếp phép vị tự tâm O, tỉ số
![]() và phép quay tâm O, góc quay
và phép quay tâm O, góc quay
![]() biến (C) thành đường tròn nào trong các đường tròn
sau:
biến (C) thành đường tròn nào trong các đường tròn
sau:
A.
![]() .
B.
.
B.
![]() .
.
C.
![]() . D.
. D.
![]() .
.
Câu 37. Cho hình
chóp
![]() có đáy
có đáy
![]() là hình vuông tâm
là hình vuông tâm
![]() Giao tuyến của hai mặt phẳng
Giao tuyến của hai mặt phẳng
![]() và
và
![]() là
là
A.
đường thẳng
![]() B.
đường thẳng
B.
đường thẳng
![]() C.
đường thẳng
C.
đường thẳng
![]() D.
đường thẳng
D.
đường thẳng
![]()
Câu 38. Cho tứ diện
![]()
![]() lần lượt lấy trên hai cạnh
lần lượt lấy trên hai cạnh
![]() sao cho đường thẳng
sao cho đường thẳng
![]() cắt đường thẳng
cắt đường thẳng
![]() tại
tại
![]() Giao tuyến của hai mặt phẳng
Giao tuyến của hai mặt phẳng
![]() và
và
![]() là
là
A.
đường thẳng
![]() B.
đường thẳng qua
B.
đường thẳng qua
![]() và song song với
và song song với
![]()
C.
đường thẳng
![]() D.
đường thẳng
D.
đường thẳng
![]()
Câu 39. Cho tứ diện
![]() Mặt phẳng
Mặt phẳng
![]() cắt các cạnh
cắt các cạnh
![]() lần lượt tại các trung điểm
lần lượt tại các trung điểm
![]() Thiết diện tạo bởi mặt phẳng
Thiết diện tạo bởi mặt phẳng
![]() và tứ diện
và tứ diện
![]() là
là
A. một hình bình hành. B. một hình thoi.
C. một hình chữ nhật. D. là một hình vuông.
Câu 40. Phương trình nào sau đây có nghiệm trên tập số thực?
A.
![]() .
B.
.
B.
![]() .
.
C.
![]() . D.
. D.
![]()
……………………Hết……………………..
TRƯỜNG THPT KỲ LÂM
|
ĐỀ KIỂM TRA HỌC KÌ I NĂM HỌC 2016-2017 MÔN: TOÁN – LỚP 11 Thời gian làm bài: 60 phút, không kể thời gian giao đề. |
I.PHẦN TRẮC NGHIỆM
Câu 1. Trong các hình sau hình nào không có tâm đối xứng
A.Hình tròn. B.Hình chữ nhật . C. Hình vuông D.Tam giác đều .
Câu 2. Tập xác định của hàm số y = sin3x là:
A.D = R
![]() .
B. D
= R \
.
B. D
= R \
![]()
C.D
=
![]() R
D. D
=
R
D. D
=
![]()
Câu 3:
Các nghiệm của phương trình
![]() là
là
A. x =
![]() B.
x =
B.
x =
![]()
C. x =
![]() D.x
=
D.x
=
![]() và
x =
và
x =
![]()
Câu 4 :Trong mặt phẳng Oxy cho điểm M ( 2 ; 3) ,điểm nào sau đây là ảnh của M qua phép đối xứng trục Ox
A. A(3 ;2) B. B(2; -3) C. C(3; -2) D.D(-2; 3)
Câu 5: Trong một đội văn nghệ có 8 bạn nam và 6 bạn nữ . Số cách chọn một đôi song ca nam nữ là:
A. 14 B. 48 C. 6 D. Đáp án khác
Câu 6:
Trong mặt phẳng tọa độ
![]() cho vectơ
cho vectơ
![]() điểm
điểm
![]() Ảnh của điểm
Ảnh của điểm
![]() qua
phép tịnh tiến theo vectơ
qua
phép tịnh tiến theo vectơ
![]() là điểm
là điểm
A.
![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
Câu 7: Cho
các giả thiết sau đây. Giả thiết nào kết luận đường
thẳng a song song với mặt phẳng
![]()
A. a
// b và b //
![]() B. a
B. a
![]() = Ø C. a // b và b
= Ø C. a // b và b
![]() D. a //
D. a //
![]() và
và
![]() //
//![]()
Câu 8: Cho hình chóp SABCD. Giao tuyến của 2 mặt phẳng (SAB) và (SCB) là
A. AC B. BC C. SB D. SA
Câu 9:
Các nghiệm của phương trình tan(x+![]() )
=
)
=
![]() là:
là:
A. x =
![]() ;
B. x =
;
B. x =
![]() ;
C. x =
;
C. x =
![]() D. x =
D. x =
![]()
Câu 10: Tìm
hệ số của x![]() trong khai triển thành đa thức của biểu thức : P = 2
trong khai triển thành đa thức của biểu thức : P = 2![]()
A. -11 B. 11 C. 22 D. -22
Câu 11: Số cách chọn 3 bạn từ 10 bạn của một tổ để làm trực nhật là:
A. 720 B.3 C. 13 D.120
Câu 12: Các nghiệm của phương trình
![]() cox
+ sinx = -2 là
cox
+ sinx = -2 là
A. x =
![]() B. x =
B. x =![]()
C. x =
![]() D. x =
D. x =
![]()
Câu 13: Số cách sắp xếp 5 bạn vào một ghế dài là :
A. 5 B. 120 C. 1 D.20
Câu 14: Một bình đựng 4 quả cầu xanh và 6 quả cầu trắng. Chọn ngẫu nhiên 4 quả cầu. Xác suất để được 2 quả cầu xanh và 2 quả cầu trắng là:
A.
![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
Câu 15: Trên giá sách có 4 quyển sách toán, 3 quyển sách lý, 2 quyển sách hóa. Lấy ngẫu nhiên 3 quyển sách. Tính xác suất để 3 quyển được lấy ra có ít nhất một quyển là toán.
A.
![]() B.
B.
![]() C .
C .
![]() D.
D.![]()
II.PHẦN TỰ LUẬN
Câu 1.Giải phương trình lượng giác sau:
2![]()
Câu 2:Cho hình chóp SABCD . ABCD là hình bình hành, hai đường chéo cắt nhau tại O. M là trung điểm SB.Chứng minh rằng OM // mp ( SDC)
Câu 3: Tìm n thỏa mãn :
![]()
TRƯỜNG THPT KỲ LÂM
|
ĐỀ KIỂM TRA HỌC KÌ I NĂM HỌC 2016-2017 MÔN: TOÁN – LỚP 11 Thời gian làm bài: 60 phút, không kể thời gian giao đề. |
PHẦN TRẮC NGHIỆM
Câu 1. Trong các hình sau hình nào có tâm đối xứng
A.Hình thang cân. B. Hình bình hành C. Hình vuông D.Tam giác đều .
Câu 2. Tập xác định của hàm số y = cos3x là:
A.D = R
![]() .
B. D
= R \
.
B. D
= R \
![]()
C.D
=
![]() R
D. D
=
R
D. D
=
![]()
Câu 3:
Các nghiệm của phương trình
![]() là
là
A. x =
![]() B.
x =
B.
x =
![]()
C. x =
![]() D.x
=
D.x
=
![]() và
x =
và
x =
![]()
Câu 4: Số cách sắp xếp 4 bạn vào một ghế dài là :
A. 4 B. 24 C. 1 D. 12
Câu 5 : Trong mặt phẳng Oxy cho điểm M ( 2 ; 3) , hỏi trong 4 điểm sau điểm nào ảnh của M qua phép đối xứng qua trục Oy là
A. A(3 ;2) B. (2; -3) C. C(3; -2) D.(-2; 3)
Câu 6: Trong một đội văn nghệ có 8 bạn nam và 6 bạn nữ . Số cách chọn một bạn bất kỳ hát đơn ca là:
A. 48 B. 14 C. 6 D. 8
Câu 7:
Trong mặt phẳng tọa độ
![]() cho vectơ
cho vectơ
![]() điểm
điểm
![]() Ảnh của điểm
Ảnh của điểm
![]() qua phép tịnh tiến theo vectơ
qua phép tịnh tiến theo vectơ
![]() là điểm
là điểm
A.
![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
Câu 8: Cho hình chóp SABCD. Giao tuyến của 2 mặt phẳng (SAD) và (SCD) là
A. AC B. SD C. SB D. SA
Câu 9:
Các nghiệm của phương trình tan(x-![]() )
=
)
=
![]() là:
là:
A. x =
![]() ;
B. x =
;
B. x =
![]() ;
C. x =
;
C. x =
![]() D. x =
D. x =
![]()
Câu 10: Tìm
hệ số của x![]() trong khai triển thành đa thức của biểu thức : P = 2
trong khai triển thành đa thức của biểu thức : P = 2![]()
A. 924 B. 925 C. 1848. D. -924
Câu 11: Cho
các giả thiết sau đây. Giả thiết nào kết luận đường
thẳng a song song với mặt phẳng
![]()
A. a // b và b
//
![]() B. a
B. a
![]() = Ø C. a // b và b
= Ø C. a // b và b
![]() D. a //
D. a //
![]() và
và
![]() //
//![]()
Câu 12: Số cách chọn 3 bạn từ 8 bạn để làm trực nhật là:
A.336 B.2 C. 11 D.56
Câu 13: Các
nghiệm của phương trình
![]() sinx
+ cosx = -2 là
sinx
+ cosx = -2 là
A. x =
![]() B. x =
B. x =![]()
C. x =
![]() D. x =
D. x =
![]()
Câu 14: Một bình đựng 4 quả cầu xanh và 6 quả cầu trắng. Chọn ngẫu nhiên 3 quả cầu. Xác suất để chọn được 2 quả cầu xanh và 1 quả cầu trắng là:
A.
![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
Câu 15: Trên giá sách có 4 quyển sách toán, 3 quyển sách lý, 2 quyển sách hóa. Lấy ngẫu nhiên 3 quyển sách. Xác suất để 3 quyển được lấy ra có ít nhất một quyển là lý là:
A.![]() B.
B.![]() C .
C .
![]() D.
D.![]()
PHẦN TỰ LUẬN
Câu 1.Giải phương trình lượng giác sau:
2![]()
Câu 2:Cho hình chóp SABCD, ABCD là hình bình hành, hai đường chéo cắt nhau tại O. M là trung điểm SC. Chứng minh rằng OM // mp ( SAB)
Câu 3: Tìm n thỏa mãn :
![]()
ĐÁP ÁN MÃ ĐỀ 1
I/ PHẦN TRẮC NGHIỆM
Câu 1 |
Câu2 |
Câu 3 |
Câu 4 |
Câu 5 |
Câu 6 |
Câu 7 |
Câu 8 |
Câu 9 |
Câu 100 |
Câu 11 |
Câu 12 |
Câu 13 |
Câu 14 |
Câu 15 |
C |
C |
B |
B |
D |
B |
B |
B |
B |
C |
B |
D |
D |
D |
B |
II/PHẦN TỰ LUẬN
Câu 1: Đặt sinx = t , t
![]()
Phương trình trở thành
2t![]() (0,5đ)
(0,5đ)
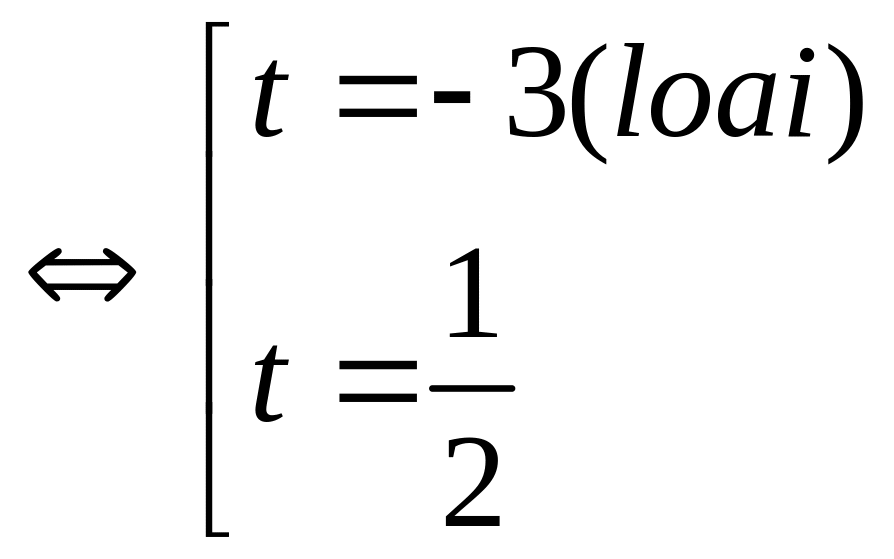 ((0,5đ)
((0,5đ)
Với t =
![]() sinx =
sinx =
![]()
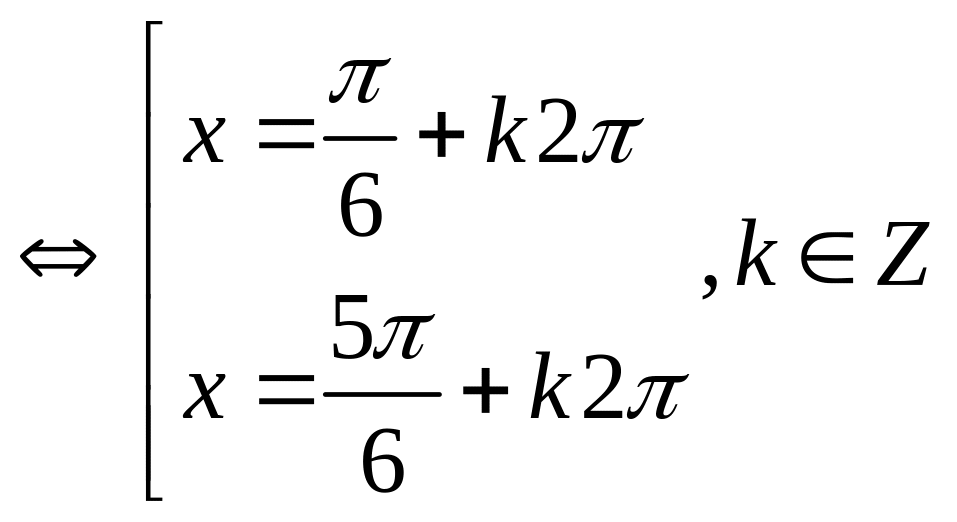 (0,5đ)
(0,5đ)
Vậy phương trình có 2 họ nghiệm
x =
![]() và x =
và x =
![]() , k
, k
![]()
Câu 2: Vì M là trung điểm SB, O là trung điểm BD (0,5đ)
nên OM // SD ( 0,5đ). Từ đó suy ra OM // mp( SDC) (0,5đ)
ĐÁP ÁN MÃ ĐỀ 2
I/ PHẦN TRẮC NGHIỆM
Câu 1 |
Câu2 |
Câu 3 |
Câu 4 |
Câu 5 |
Câu 6 |
Câu 7 |
Câu 8 |
Câu 9 |
Câu 100 |
Câu 11 |
Câu 12 |
Câu 13 |
Câu 14 |
Câu 15 |
D |
C |
D |
B |
B |
B |
B |
C |
D |
D |
D |
A |
B |
B |
A |
II/PHẦN TỰ LUẬN
Câu 1: Đặt cosx = t , t
![]()
Phương trình trở thành
2t![]() (0,5đ)
(0,5đ)
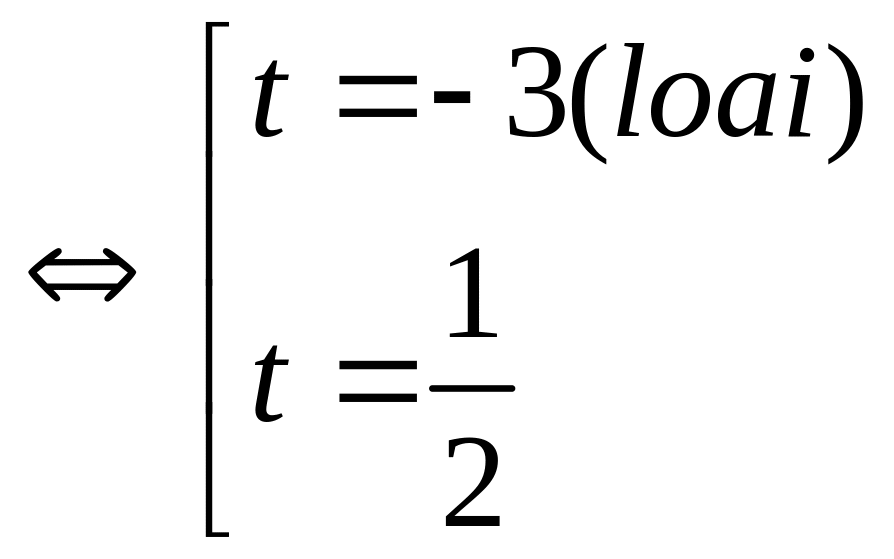 ((0,5đ)
((0,5đ)
Với t =
![]() cosx =
cosx =
![]()
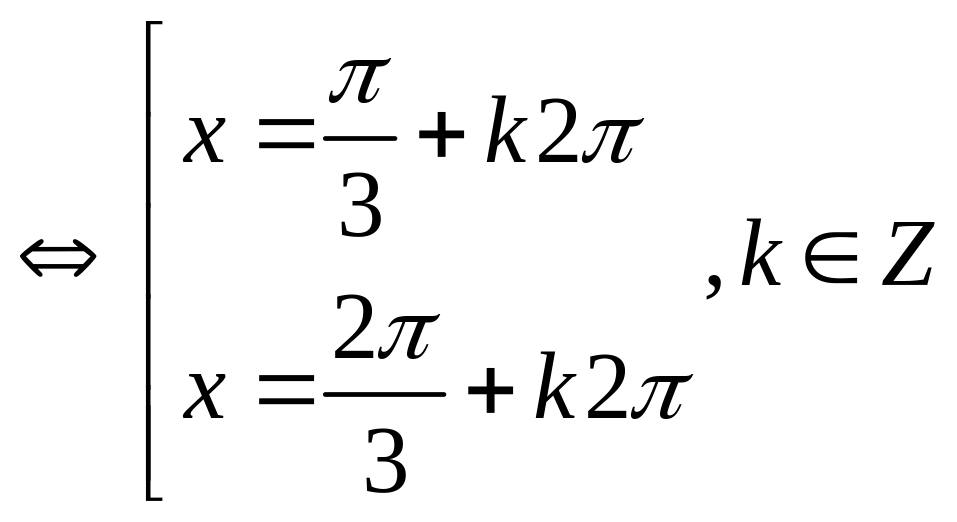 (0,5đ)
(0,5đ)
Vậy phương trình có 2 họ nghiệm
x =
![]() và x =
và x =
![]() , k
, k
![]()
Câu 2: Vì M là trung điểm SC, O là trung điểm AC (0,5đ)
nên OM // SA ( 0,5đ). Từ đó suy ra OM // mp( SAB) (0,5đ)
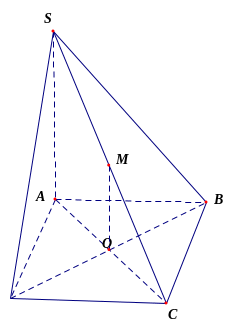
SỞ GIÁO DỤC VÀ ĐÀO TẠO THÀNH PHỐ ĐÀ NẴNG |
KIỂM TRA HỌC KỲ I |
TRƯỜNG TRUNG HỌC PHỔ THÔNG NGUYỄN HIỀN |
NĂM HỌC 2016-2017 |
Mã Đề: T11-
01
Chữ ký của Giám
thị: 1)…………...…..2)……………….………..
Thời gian: 90 phút (không kể thời gian giao đề)
Họ và tên học sinh:.........................................................................................................Lớp 11/.......Số báo danh: ............................
I. PHẦN TRẮC NGHIỆM(3,0 điểm) Thời gian 25 phút
Học sinh khoanh tròn ký tự tương
ứng phương án trả lời đúng ở mỗi câu hỏi (ví
dụ
 )
)
Câu 1 |
Câu 2 |
Câu 3 |
Câu 4 |
Câu 5 |
Câu 6 |
Câu 7 |
Câu 8 |
Câu 9 |
Câu 10 |
Câu 11 |
Câu 12 |
A |
A |
A |
A |
A |
A |
A |
A |
A |
A |
A |
A |
B |
B |
B |
B |
B |
B |
B |
B |
B |
B |
B |
B |
C |
C |
C |
C |
C |
C |
C |
C |
C |
C |
C |
C |
D |
D |
D |
D |
D |
D |
D |
D |
D |
D |
D |
D |
Câu
1. Trong mặt phẳng tọa độ Oxy, phép
tịnh tiến theo vectơ
![]() biến điểm
biến điểm
![]() thành điểm
thành điểm
![]() .
Tìm toạ độ của vectơ
.
Tìm toạ độ của vectơ
![]() A.
A.
![]() B.
B.
![]() C.
C.
![]() D.
D.
![]() .
.
Câu 2. Tìm tập xác định
![]() của hàm số
của hàm số![]()
A.
![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
Câu 3. Tìm tất cả các nghiệm của phương
trình
![]() .
.
A.![]() B.
B.![]() C.
C.
![]() D.
D.
![]()
Câu 4. Với giá trị nào của góc
![]() sau đây thì phép quay
sau đây thì phép quay
![]() biến hình vuông ABCD tâm O thành chính nó:
biến hình vuông ABCD tâm O thành chính nó:
A.
![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
Câu 5. Một tổ có 5 học sinh trong đó có bạn An. Có bao nhiêu cách xếp 5 bạn đó thành một hàng dọc sao cho bạn An luôn đứng đầu? A.120 cách xếp B. 5 cách xếp C. 24 cách xếp D. 25 cách xếp
Câu 6. Giải phương trình
![]() .
Kết luận đúng về các nghiệm của phương trình là:
.
Kết luận đúng về các nghiệm của phương trình là:
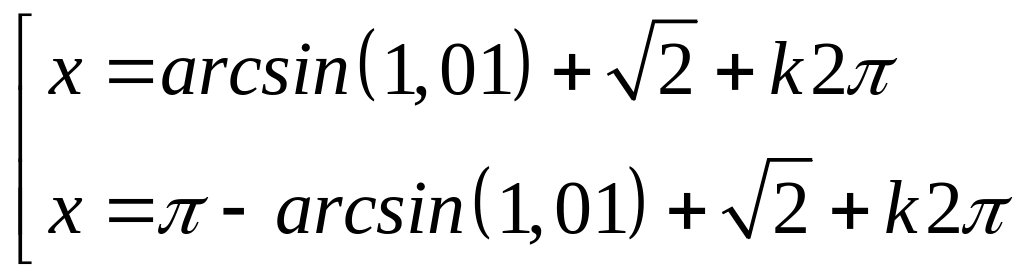 B.
B.
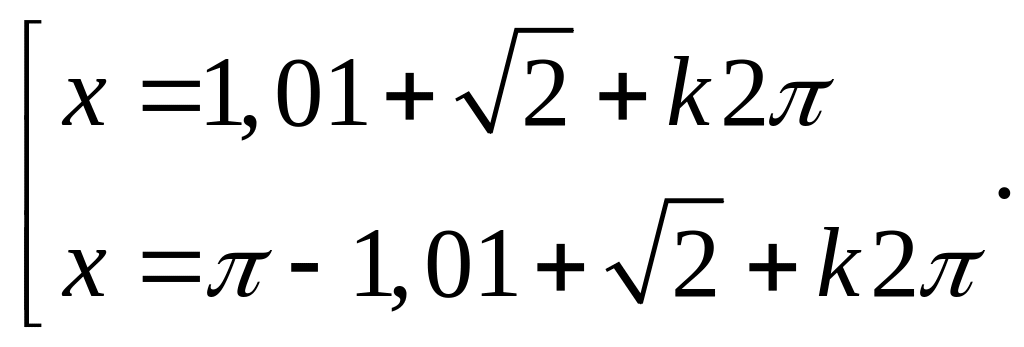
C.![]() D. Phương trình vô
nghiệm
D. Phương trình vô
nghiệm
Câu 7. Gọi S là số cách chọn 4 bạn từ một tổ gồm 10 bạn để trực thư viện. Tìm giá trị của S.
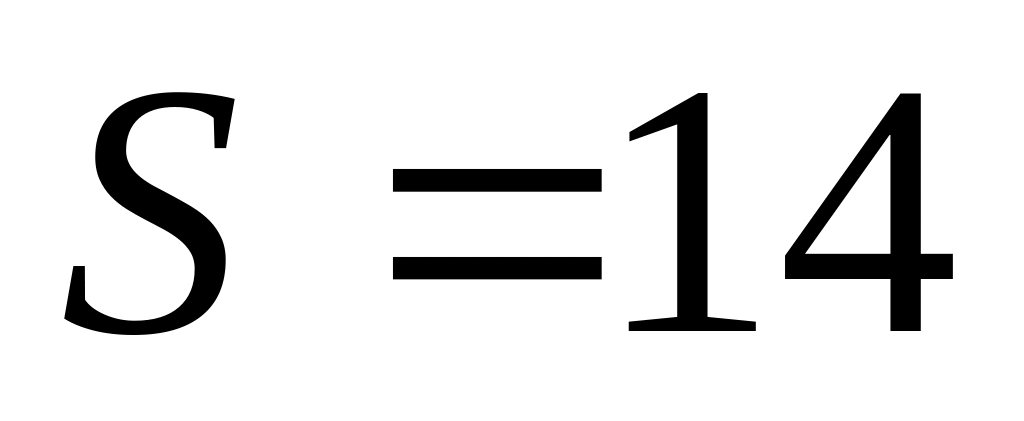 B.
B.
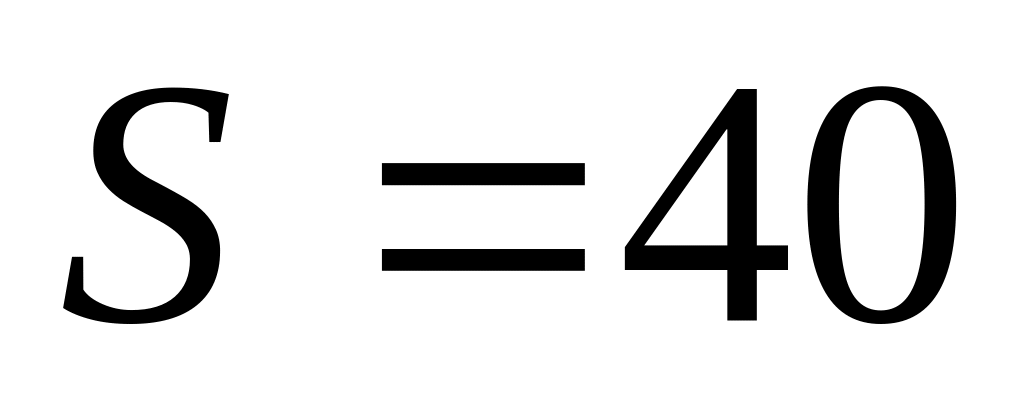 C.
C.
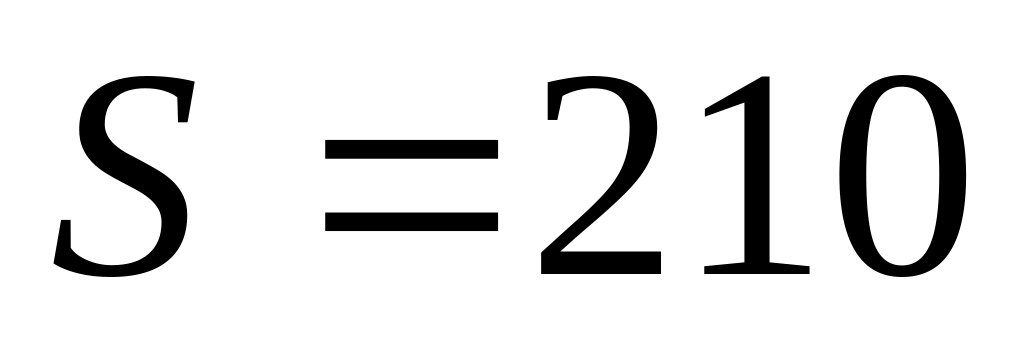 D.
D.
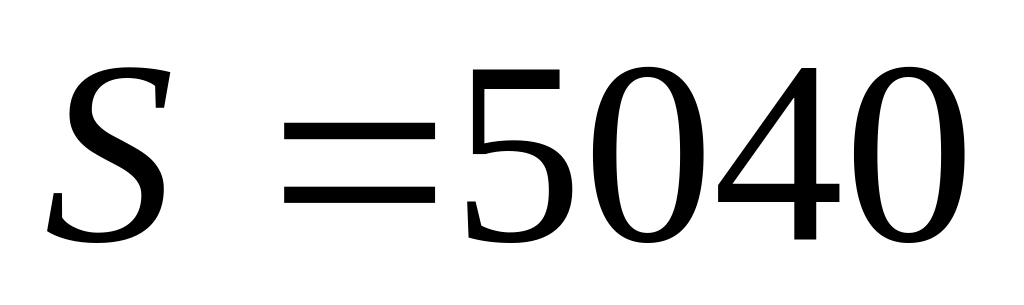
Câu 8. Hệ thức nào sau đây là điều kiện để
phép vị tự tâm A tỉ số
![]() biến điểm M thành điểm N?
biến điểm M thành điểm N?
A.
![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
Câu
9. Trong một hộp có 9 quả cầu đồng
chất và cùng kích thước được đánh số từ 1 đến 9.
Lấy ngẫu nhiên một quả cầu. Tính xác suất
![]() của
biến cố A:” Lấy được quả cầu được đánh số là
số chẵn”.
của
biến cố A:” Lấy được quả cầu được đánh số là
số chẵn”.
A.
![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
Câu 10. Cho ba số
![]() theo thứ tự đó lập thành một cấp số nhân. Tìm giá
trị của x.
theo thứ tự đó lập thành một cấp số nhân. Tìm giá
trị của x.
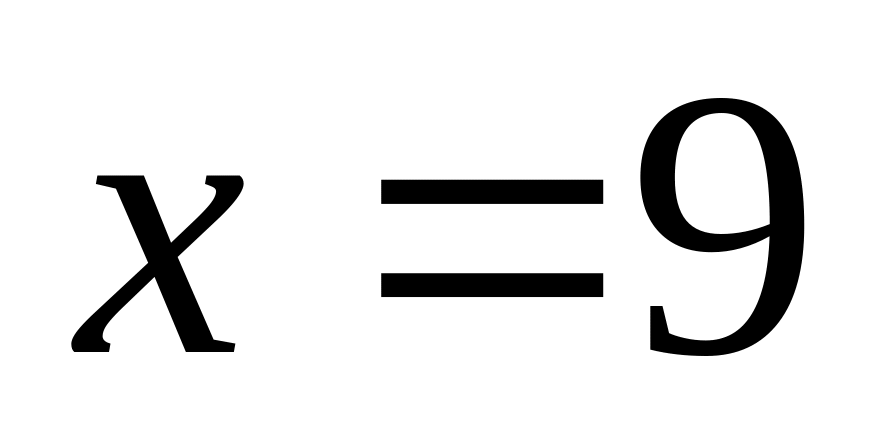 B.
B.
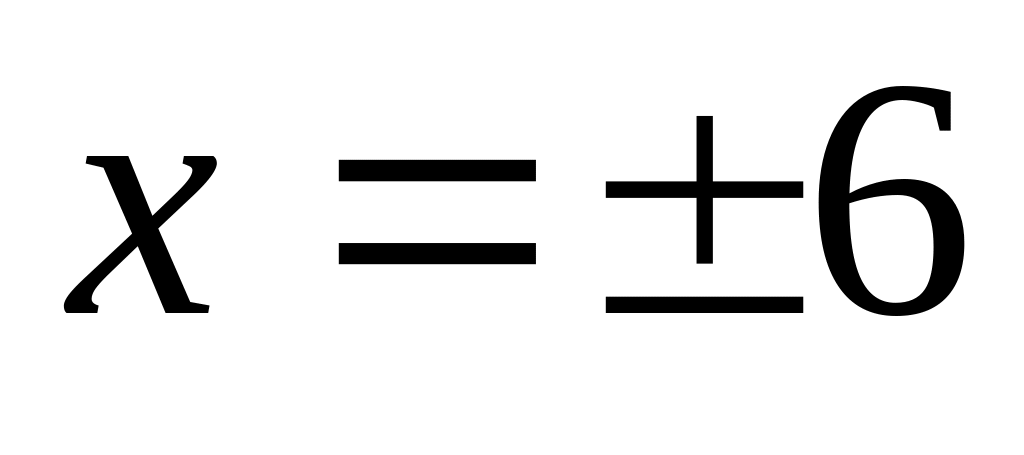 C.
C.
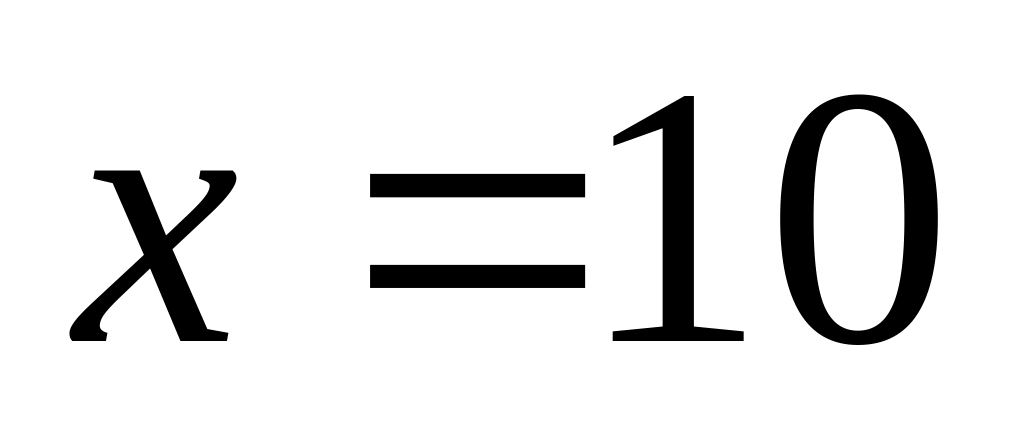 D.
D.
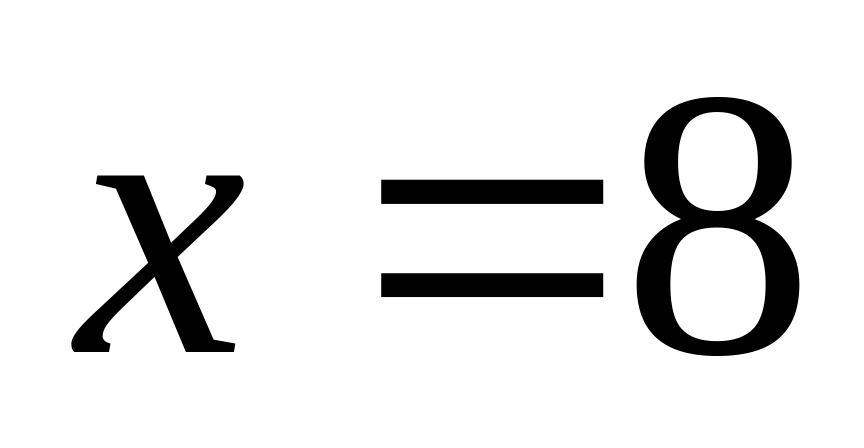
Câu 11. Tìm mệnh đề đúng trong các mệnh đề sau:
A. Hai đường thẳng không cùng thuộc một mặt phẳng thì chéo nhau.
B. Hai đường thẳng thuộc hai mặt phẳng khác nhau thì chéo nhau;
C. Hai đường thẳng không song song thì chéo nhau;
D. Hai đường thẳng không có điểm nào chung thì chéo nhau;
Câu 12. Cho cấp số cộng
![]() có số hạng đầu
có số hạng đầu
![]() và công sai
và công sai
![]() Tìm
công thức tính số hạng tổng quát
Tìm
công thức tính số hạng tổng quát
![]() của cấp số cộng đó theo n. A.
của cấp số cộng đó theo n. A.
![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
PHẦN TỰ LUẬN (7,0 điểm) Thời gian 65 phút
Bài I (4,50 điểm).
1) (2,25 điểm ). Giải các phương trình lượng giác sau:
a)
![]() b)
b)
![]()
2) (0,50 điểm). Câu lạc bộ toán học của Nhà trường có 15 học sinh nam trong đó có An và 10 học sinh nữ đều có khả năng học tốt môn toán như nhau. Chọn ngẫu nhiên từ đó 5 bạn để tham gia “Diễn đàn toán học Thành phố”. Tính xác suất của biến cố: “ trong 5 bạn được chọn phải có An và có ít nhất 3 bạn nữ”.
3) (1,00 điểm) . Cho cấp số
cộng
![]() ,
biết rằng:
,
biết rằng:
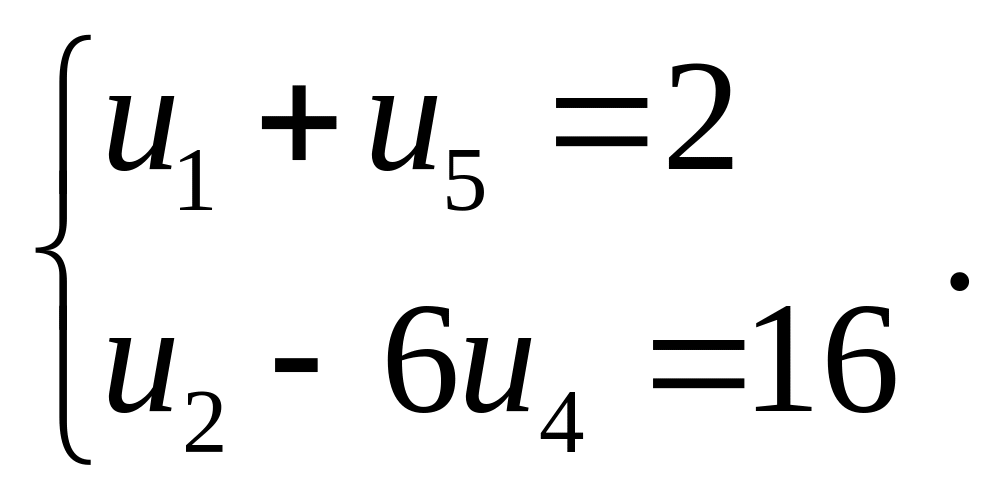 Tìm
Tìm
![]() và
tính
và
tính
![]() .
.
4) (0,75 điểm). Tìm hệ số của
![]() trong khai triển của biểu thức:
trong khai triển của biểu thức:
![]()
Bài II (2,50 điểm).
1) (0,75 điểm). Trong mặt phẳng tọa
độ Oxy cho vectơ
![]() và đường tròn
và đường tròn
![]() có phương trình
có phương trình
![]() Viết phương trình của đường tròn
Viết phương trình của đường tròn
![]() là ảnh của
là ảnh của
![]() qua phép tịnh tiến theo vectơ
qua phép tịnh tiến theo vectơ
![]()
2) (1,75 điểm). Cho hình chóp S.ABCD có đáy ABCD là hình thang với AB là đáy lớn (AB // CD).
a) Tìm giao tuyến của các cặp mặt phẳng:
![]() và
và
![]() ;
;
![]() và
và
![]() .
.
b) Gọi E, F lần lượt là hai điểm thuộc
các cạnh AB và CD sao cho EF // BC.
Gọi
![]() là mặt phẳng đi qua hai điểm E, F và song song với
SA. Tìm thiết diện của hình chóp S.ABCD bị
cắt bởi mặt phẳng
là mặt phẳng đi qua hai điểm E, F và song song với
SA. Tìm thiết diện của hình chóp S.ABCD bị
cắt bởi mặt phẳng
![]() .
.
-----------Hết-----------
( Học sinh làm bài tự luận trực tiếp trên tờ đề thi này )
Điểm trắc nghiệm: ……………………………
Điểm tự luận: …………………………… TỔNG ĐIỂM:
…………………………………………….…………… |
Lời nhận xét của Giám khảo:
……………………………………………………………………………….………………………...
……………………………………………………………………….………………………………..
Họ và tên, chữ ký của Giám khảo:
……………………………………………………………………….………………………………..
|
PHẦN LÀM BÀI TỰ LUẬN CỦA HỌC SINH
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
……………………………………………………………………………….…………………………………………………………………………………………
…………………………………………………………………………………………………………………………………………………………………………..
HƯỚNG DẪN CHẤM MÔN TOÁN LỚP 11 KT HỌC KỲ I - 2016-2017
PHẦN TRẮC NGHIỆM( 3 điểm. Mỗi câu đúng 0,25 điểm)
ĐÁP ÁN MÃ ĐỀ T11-01
Câu 1 |
Câu 2 |
Câu 3 |
Câu 4 |
Câu 5 |
Câu 6 |
Câu 7 |
Câu 8 |
Câu 9 |
Câu 10 |
Câu 11 |
Câu 12 |
C |
A |
D |
A |
C |
D |
C |
D |
B |
B |
A |
B |
|
|
|
|
|
|
|
|
|
|
|
|
ĐÁP ÁN MÃ ĐỀ T11-02
Câu 1 |
Câu 2 |
Câu 3 |
Câu 4 |
Câu 5 |
Câu 6 |
Câu 7 |
Câu 8 |
Câu 9 |
Câu 10 |
Câu 11 |
Câu 12 |
D |
B |
A |
C |
D |
A |
C |
B |
C |
D |
B |
C |
ĐÁP ÁN MÃ ĐỀ T11-03
Câu 1 |
Câu 2 |
Câu 3 |
Câu 4 |
Câu 5 |
Câu 6 |
Câu 7 |
Câu 8 |
Câu 9 |
Câu 10 |
Câu 11 |
Câu 12 |
B |
D |
A |
C |
A |
B |
D |
C |
B |
C |
D |
A |
ĐÁP ÁN MÃ ĐỀ T11-04
Câu 1 |
Câu 2 |
Câu 3 |
Câu 4 |
Câu 5 |
Câu 6 |
Câu 7 |
Câu 8 |
Câu 9 |
Câu 10 |
Câu 11 |
Câu 12 |
A |
C |
B |
D |
B |
A |
D |
C |
B |
A |
C |
D |
PHẦN TỰ LUẬN ( 7 điểm)
Câu |
Đáp án |
Điểm |
Câu I (4,50đ)
|
1a.
+
|
0, 75 0,5 |
1b.
|
0,25
0,5
0,25 |
|
2. Gọi A là biến cố: “trong 5 bạn được chọn phải có An và có ít nhất 3 bạn nữ”.
TH1: Số cách
chọn 3 bạn nữ và 2 bạn nam trong đó có An là:
TH2: Số cách
chọn 4 bạn nữ và 1 bạn nam là An là:
Suy ra
Vậy xác suất của biến cố A:
|
0,25
0,25
|
|
3. Có
Tính
được
|
0,25
0,5
0,25 |
|
4. (+) Nhị thức
(+) Số
hạng tổng quát
(+) Số hạng chứa
|
0,25
0,25
0,25 |
|
Câu II (2,50đ)
|
1. Đường tròn
Gọi I’ và R’ lần lượt là tâm và bán
kính của đường tròn
Ta có R’=R=3 và
Phương trình của
|
0,25
0,25
0,25 |
Cách khác: Đường tròn
Gọi
Thay
vào (*) ta được : |
(0,5)
(0,25) |
|
2. Vẽ đúng dạng hình chóp S.ABCD
|
0,25 |
|
và
I là
điểm chung thứ hai với
|
0.25 0,25 |
|
Có S
là điểm chung và AB//CD mà
Suy ra
|
0,25 0, 25 |
|
b) Vì
có
EF//BC ,
suy
ra
Vậy thiết
diện của của mặt phẳng
|
0,25
0,25 |
Chú thích:
Mọi cách giải khác nếu đúng vẫn cho điểm, tương ứng với phần đó trong đáp án
Sau khi chấm xong, điểm toàn bài được làm tròn đến 1 chữ số thập phân. Chẳng hạn :
5,00 5,0 5, 25 5,3 5,50 5,5 5, 75 5,8.
TRƯỜNG THPT BUÔN HỒ ĐỀ KIỂM TRA HỌC KỲ I - NĂM HỌC 2016-2017
TỔ TOÁN MÔN: TOÁN LỚP 11
ĐỀ CHÍNH THỨC

(Đề gồm 01 trang)
Bài 1. (2,0 điểm) Giải các phương trình sau :
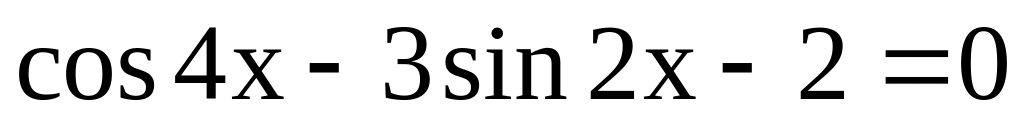 .
b)
.
b)
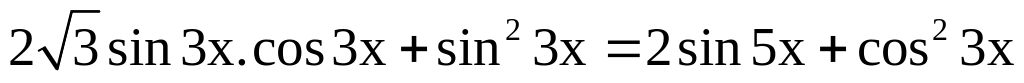 .
.
Bài 2. (2,0 điểm)
a)
Tìm
số hạng không chứa x trong khai triển
![]() .
.
b) Một hộp đựng 6 tấm thẻ màu đỏ, 4 tấm thẻ màu xanh và 9 tấm thẻ màu vàng ( các tấm
thẻ chỉ khác nhau về màu sắc). Rút ngẫu nhiên 3 tấm thẻ. Tính xác suất để rút được 3 tấm
thẻ cùng màu.
Bài 3.(2,0 điểm)
a) Cho cấp số cộng
hữu hạn có số hạng đầu
![]() và số hạng cuối
và số hạng cuối
![]() .Tìm
công sai d
.Tìm
công sai d
và tính tổng tất cả các số hạng của cấp số cộng đó.
b) Tìm hai số thực x và y . Biết rằng 3 số 4x-2y, 3x+y, x+6y theo thứ tự đó lập thành
một cấp số cộng
và 3 số
![]() ,
xy-1,
,
xy-1,
![]() theo
thứ tự đó lập thành một cấp số
theo
thứ tự đó lập thành một cấp số
nhân.
Bài 4. (1,0 điểm) Trong mặt phẳng tọa độ Oxy cho đường tròn (C) có phương trình
![]() .
Viết phương trình (C’) là ảnh của đường tròn (C)
qua phép vị
.
Viết phương trình (C’) là ảnh của đường tròn (C)
qua phép vị
tự tâm O tỉ số k= -2.
Bài 5. (2,0 điểm) Cho hình chóp S.ABCD có ABCD là hình thang với AB đáy lớn. Gọi I, J
lần lượt là trọng tâm của tam giác SAB và SAD.
a) Tìm giao tuyến của (SAB) và (SCD). Chứng minh: IJ//(ABCD)
b) Gọi K là trung điểm BC. Tìm thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (IJK).
Bài 6. (1,0 điểm). Một nhóm sinh viên tình nguyện có 8 nam và 5 nữ. Có bao nhiêu cách phân
công nhóm sinh viên này về 7 tỉnh khác nhau sao cho mỗi tỉnh có không quá hai nữ và có
ít nhất một nam ?
----------------------------------- HẾT ----------------------------------
Thí sinh không được sử dụng tài liệu. Giám thị không giải thích gì thêm.
Họ và tên thí sinh:........................................................... Số báo danh:..........................................
Chữ kí của giám thị :.......................................................................................................................
ĐÁP ÁN TOÁN 11
-
Bài 1a
1 điểm
PT
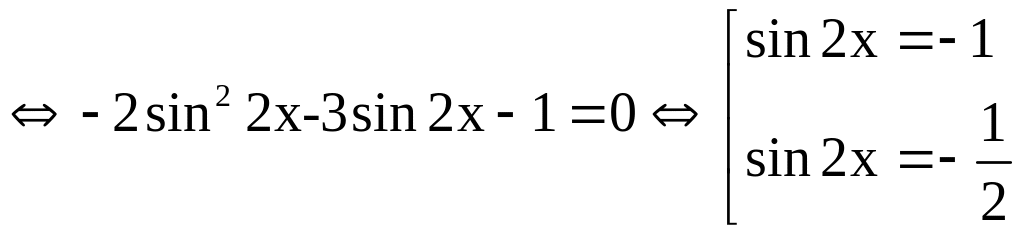
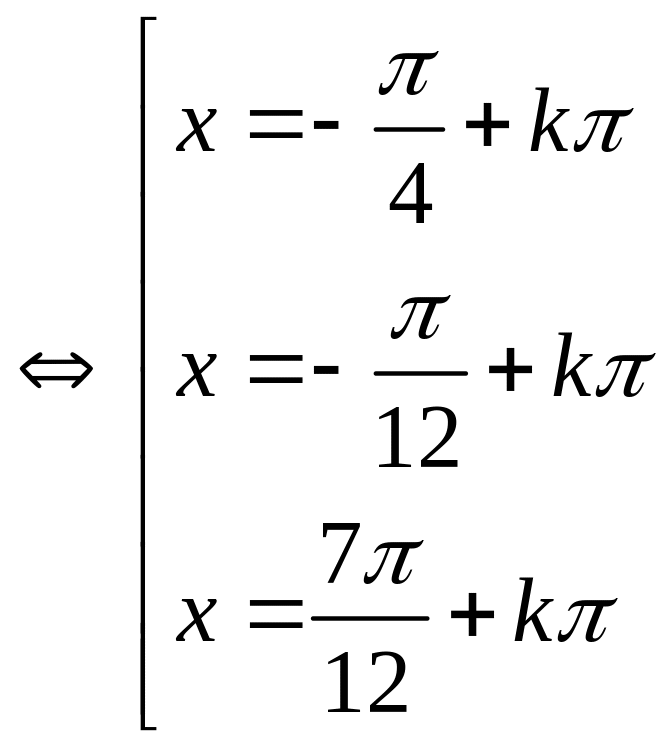
0.25x4
1b
1 điểm
PT
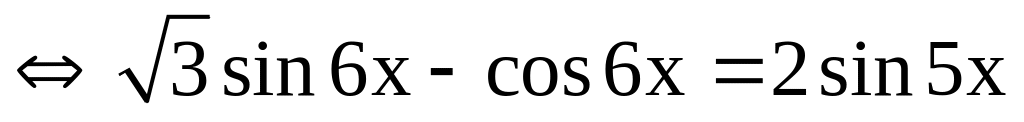
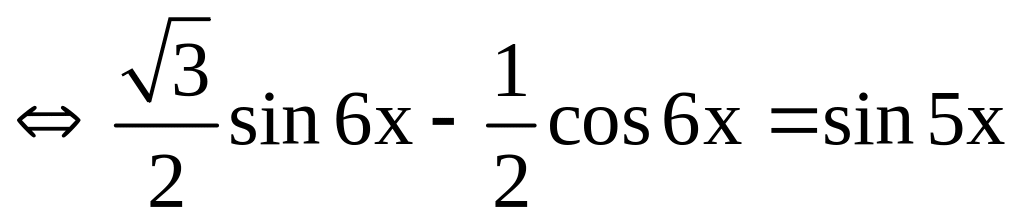
0,25x2
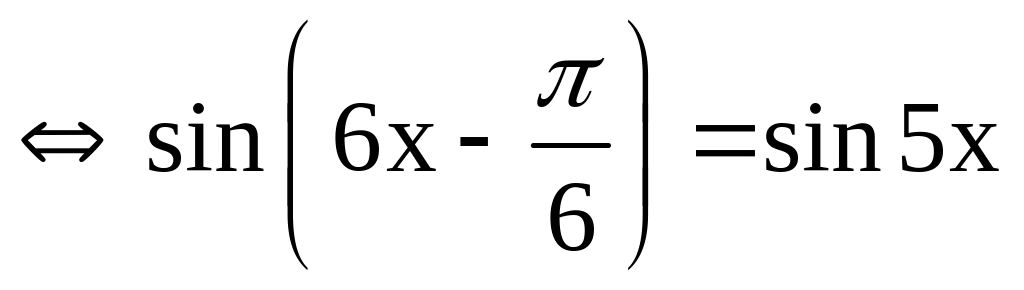
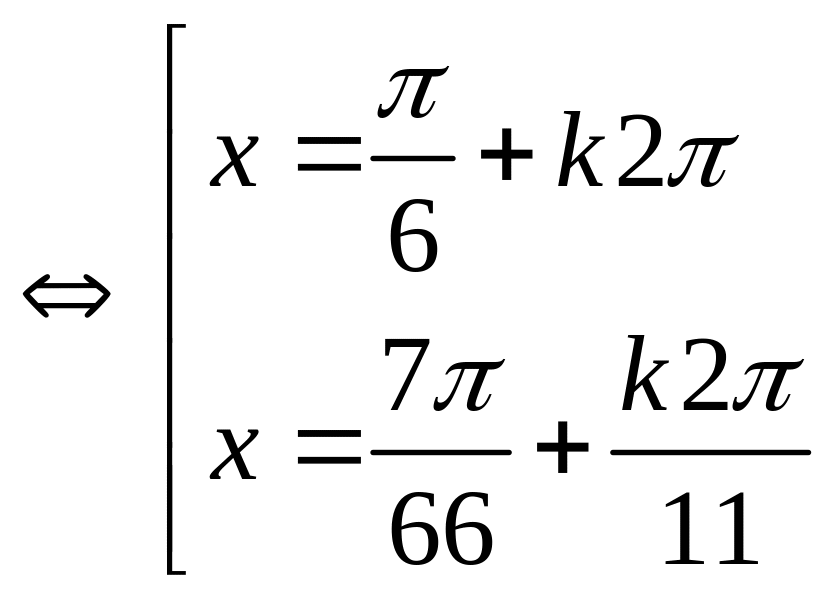
0,25x2
Bài 2a
1 điểm
Các số hạng trong khai triển nhị thức đã cho có dạng:
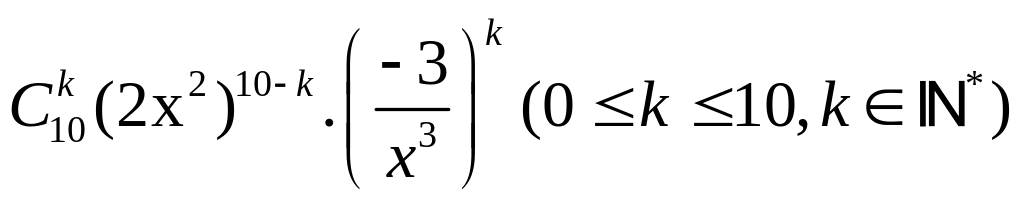
0,25
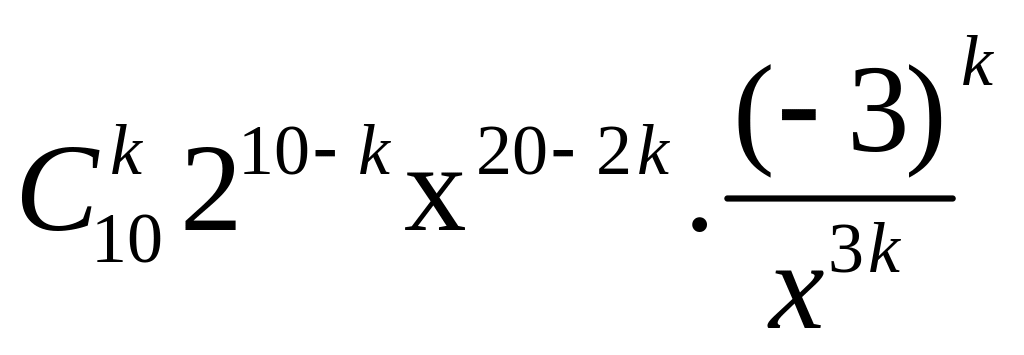 =
=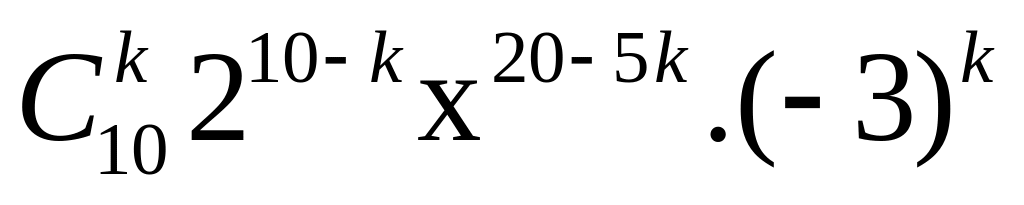
0,25
Số hạng không chứa x thì
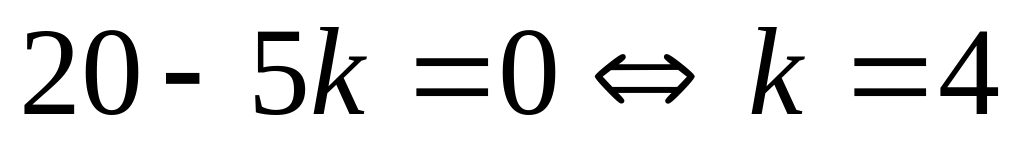
0,25
Vậy số hạng không chứa x trong khai triển là:
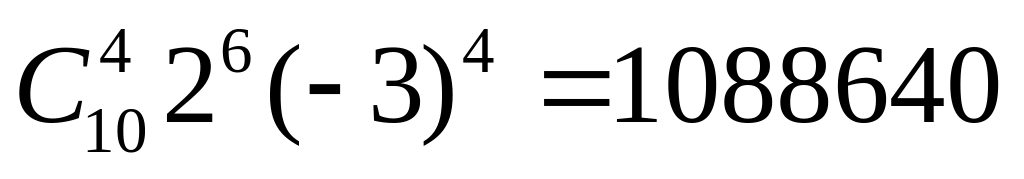
0,25
Bài 2b
1 điểm
Không gian mẫu có số phần tử là:
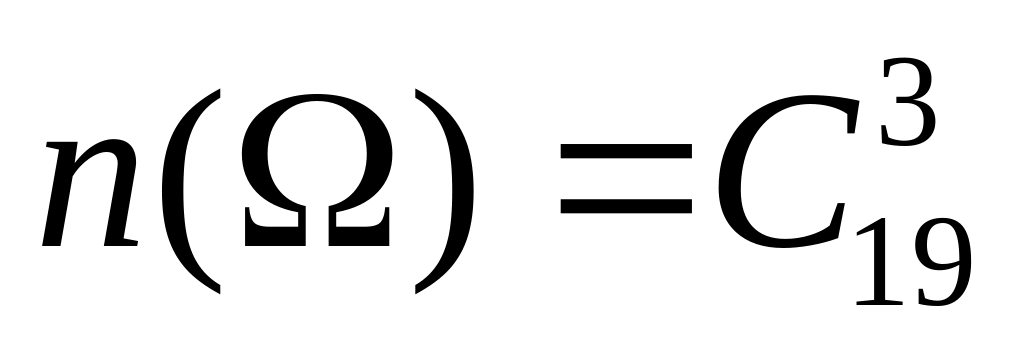
Gọi A là biến cố “ Rút được 3 tấm thẻ cùng màu”
+ Rút được 3 tấm thẻ đỏ:
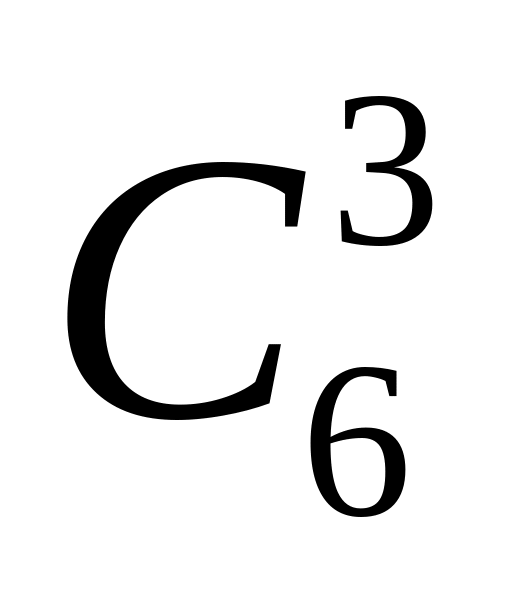
+ Rút được 3 tấm thẻ xanh:

+ Rút được 3 tấm thẻ vàng:
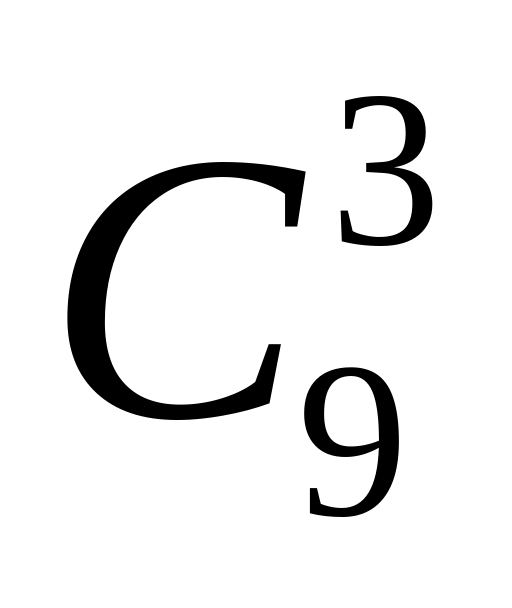
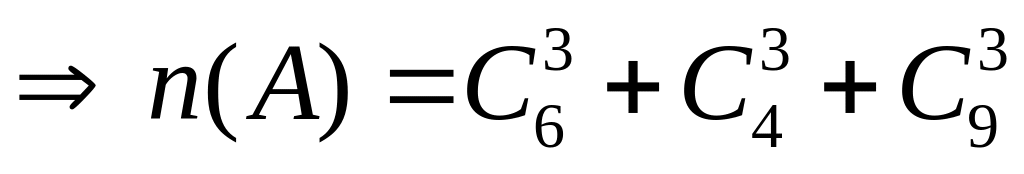
Xác suất của biến cố A là:
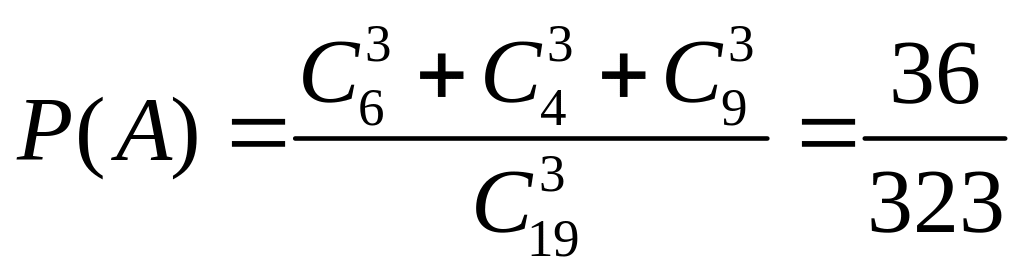
0,25
0,25
0,25
0,25
Bài 3a
1điểm
+
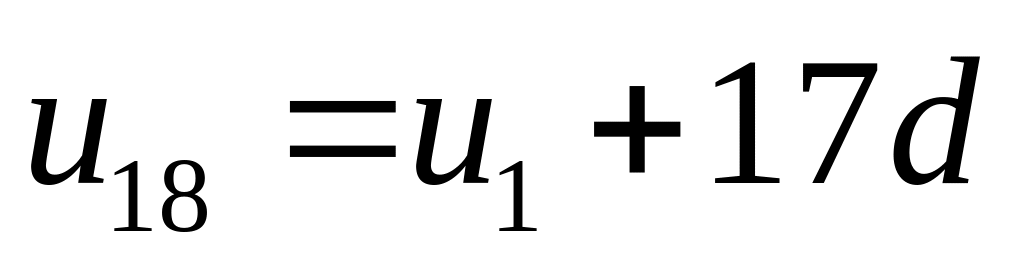
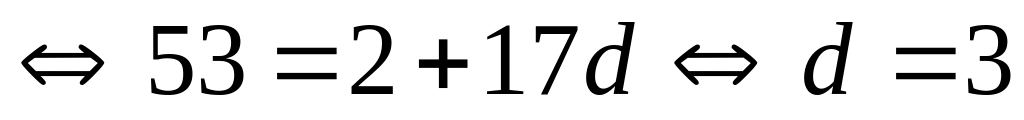
+
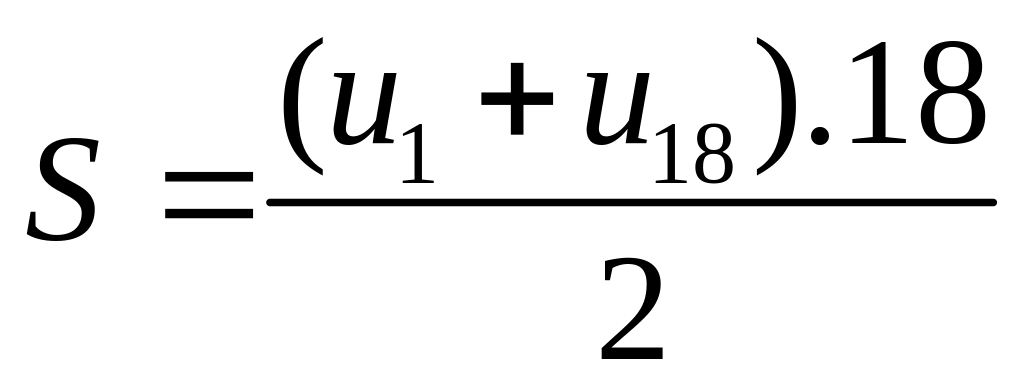
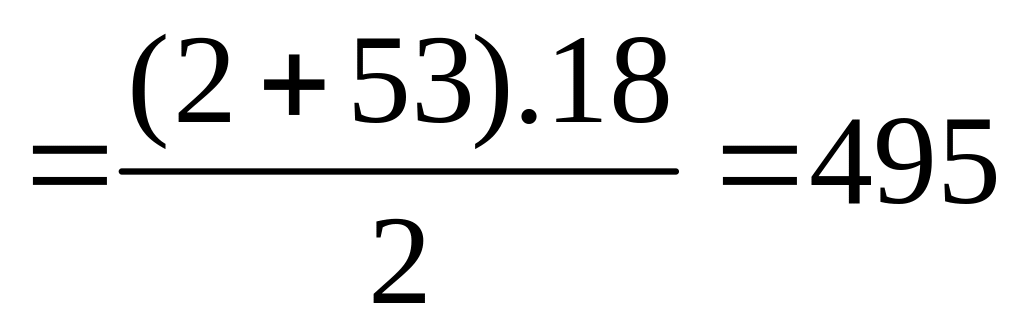
0,25x2
0,25x2
Bài 3b
1điểm
4x-2y, 3x+y, x+6y lập thành một cấp số cộng nên:
2(3x+y)=(4x-2y)+(x+6y)
 x=2y
(1)
x=2y
(1)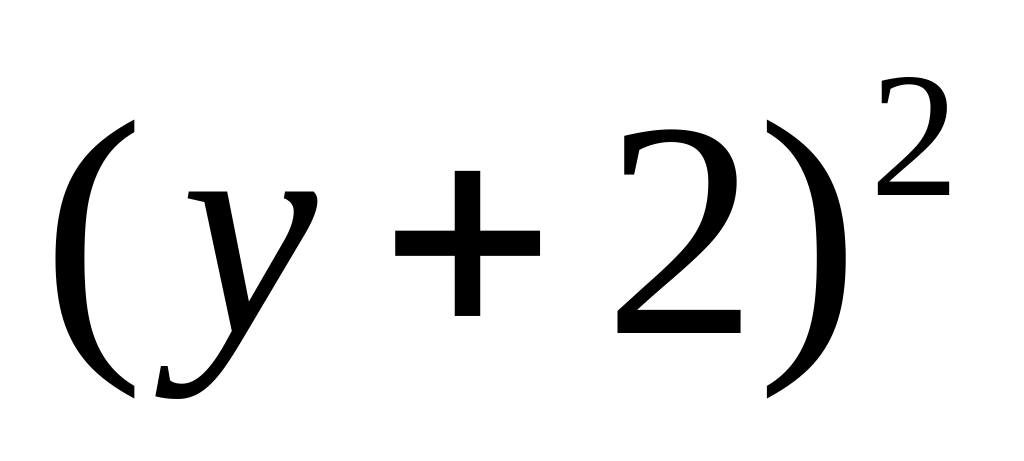 ,
xy-1,
,
xy-1,
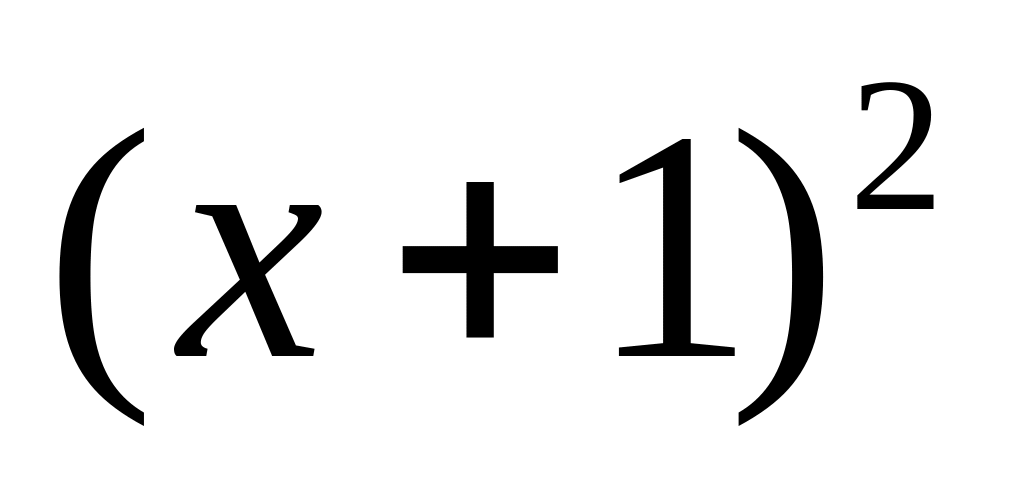 lập thành một cấp số nhân nên:
lập thành một cấp số nhân nên:
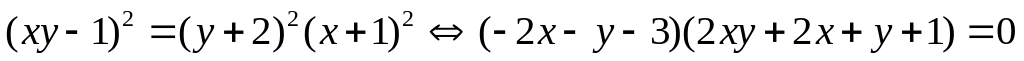 (2)
(2)
Thay (1) vào (2):
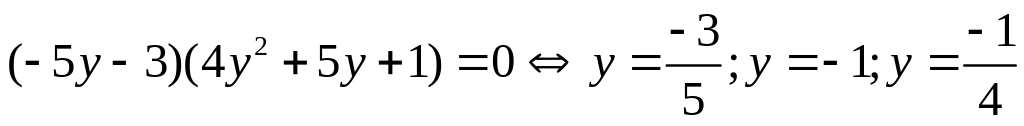
Suy ra có 3 cặp (x;y) là
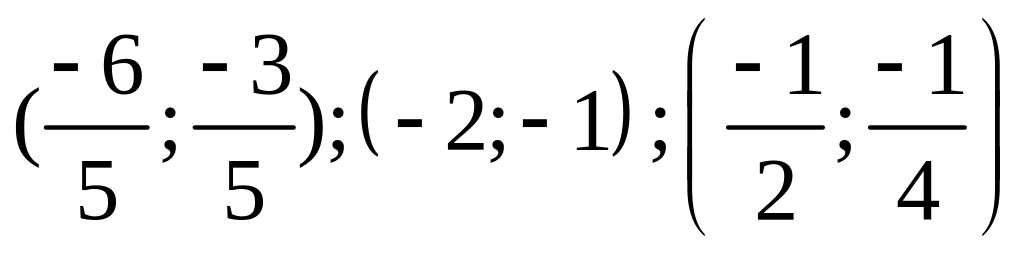
0,25
0,25
0,25
0,25
Bài 4
1 điểm
Đường tròn (C ) có tâm I(1;2), bán kính R=3
Gọi I’ (x;y) là ảnh của I qua phép vị tự tâm O tỉ số k=-2
Ta có:
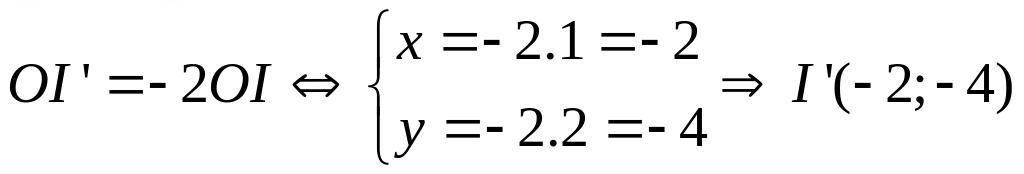
Đường tròn (C’) có tâm I’(-2;-4), bán kính
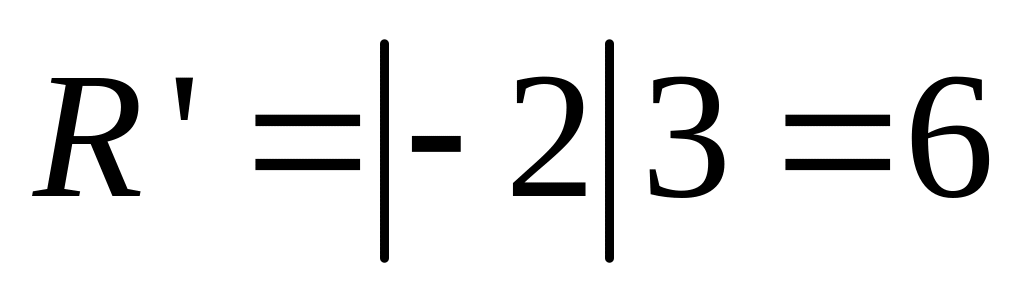
Phương trình (C’):
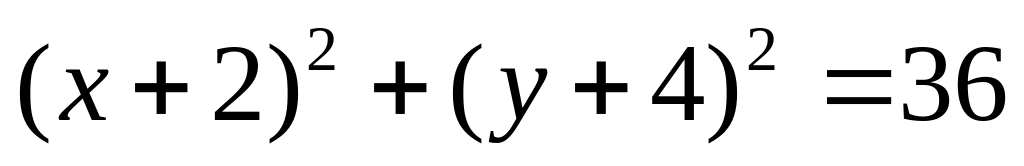
0,25
0,25x2
0,25
Bài 5
2 điểm
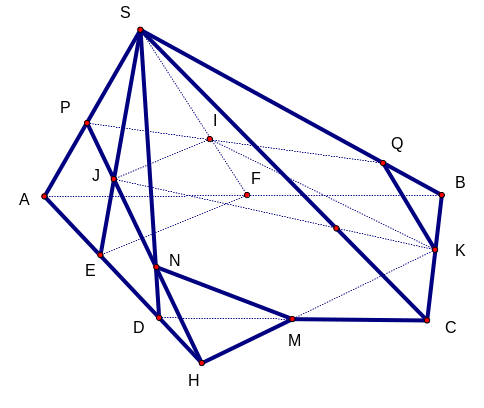
a) Hai mp(SAB), (SCD) có S chung; AB//CD nên giao tuyến cúa chúng là đường thẳng qua S và // AB.
Gọi E;F lần lượt là trung điểm của AB và AD
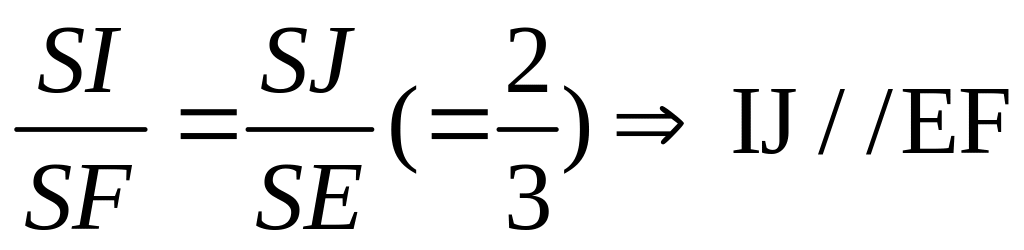 mà
mà
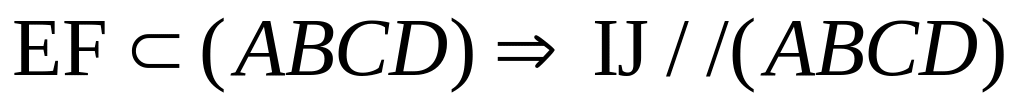
b)Xét 2 mp(IJK) và (ABCD) có K chung, IJ//EF nên giao tuyến của chúng là đt qua K song song với EF cắt CD tại M và AD tại H. HJ cắt SD tại N và SA tại P. PI cắt SB tại Q. Thiết diện là ngũ giác MNPQK.
Hình vẽ
0,25
0,25x2
0,25x2
0,25x3
Bài 6
1 điểm
Vì mỗi tỉnh có ít nhất một nam nên có đúng một tỉnh có đúng 2 nam còn lại mỗi tỉnh một nam.
Số cách phân công nam là
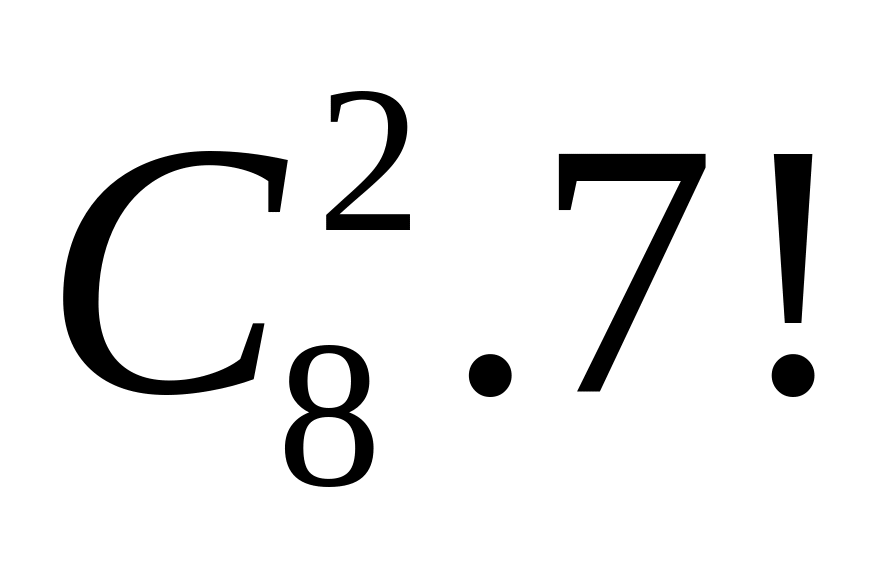 cách
cách
0,25
Cách phân công nữ:
Th1: Không có tỉnh nào có hai nữ có:
 cách
cáchTh2: Có đúng một tỉnh có hai nữ:
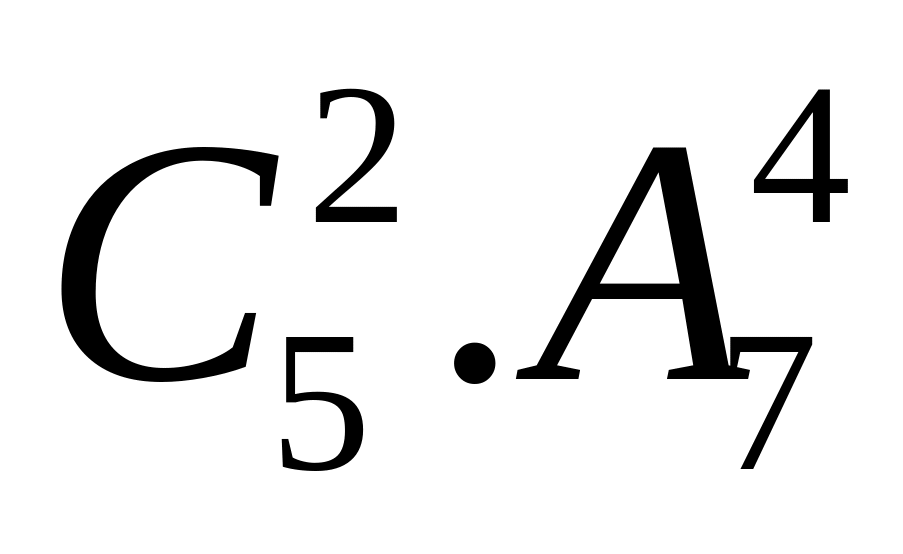 cách
cáchTh3: Có đúng 2 tỉnh mà mỗi tỉnh có 2 nữ:
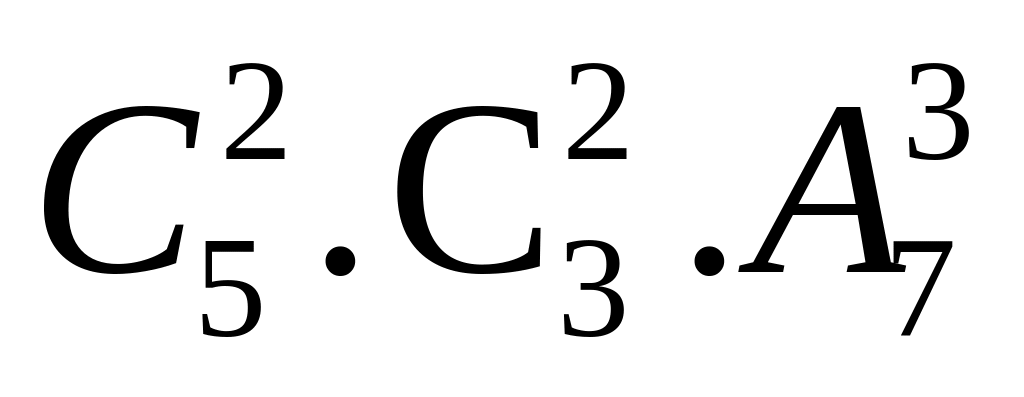 cách
cáchCó
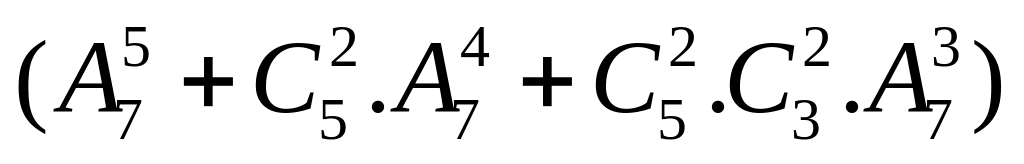 =
17220 cách
=
17220 cách
0,25
0,25
Vậy có 17220.
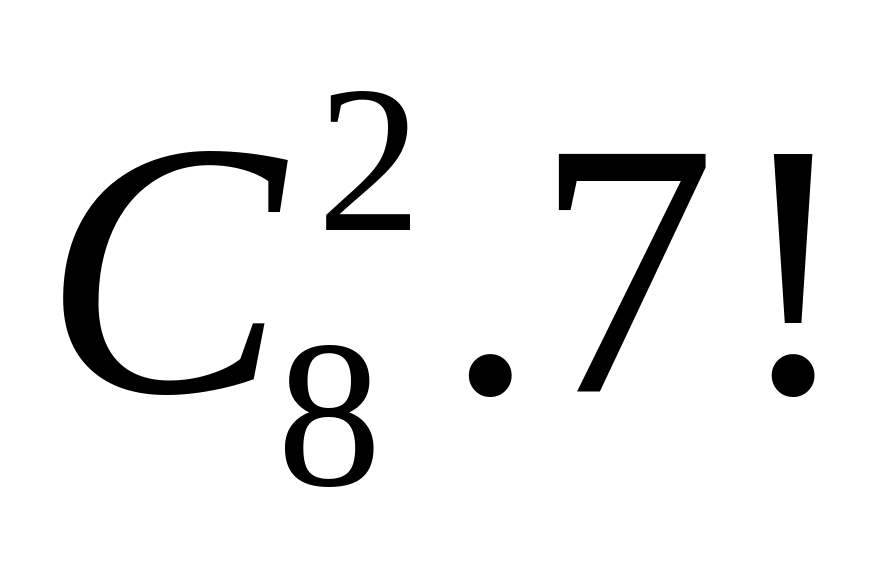 cách phân công nhóm sinh viên tình nguyện trên.
cách phân công nhóm sinh viên tình nguyện trên.0,25
Học sinh giải cách khác đúng phần nào cho điểm tối đa phần đó!
SỞ GIÁO DỤC VÀ ĐÀO TẠO ĐĂK NÔNG TRƯỜNG THPT HÙNG VƯƠNG ___________________ |
ĐỀ KIỂM TRA HỌC KỲ I, NĂM HỌC 2016 – 2017 Môn thi: TOÁN 11. Thời gian làm bài: 90 phút (không kể giao đề). |
|
|
Mã đề: |
|
Họ, tên thí sinh:
Số báo danh:
I. PHẦN TRẮC NGHIỆM (6.0 điểm):
Phương trình
![]() có các nghiệm (với mọi số nguyên k) là?
có các nghiệm (với mọi số nguyên k) là?
A. 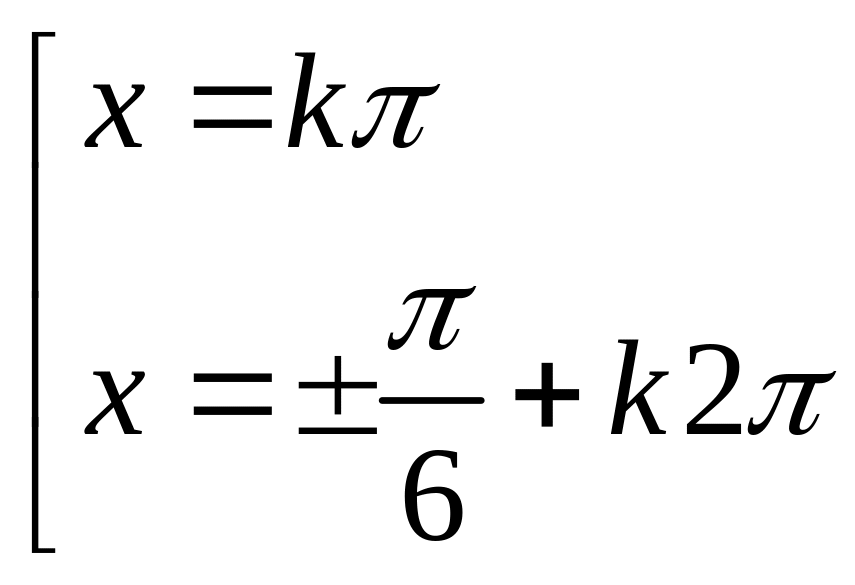
B. 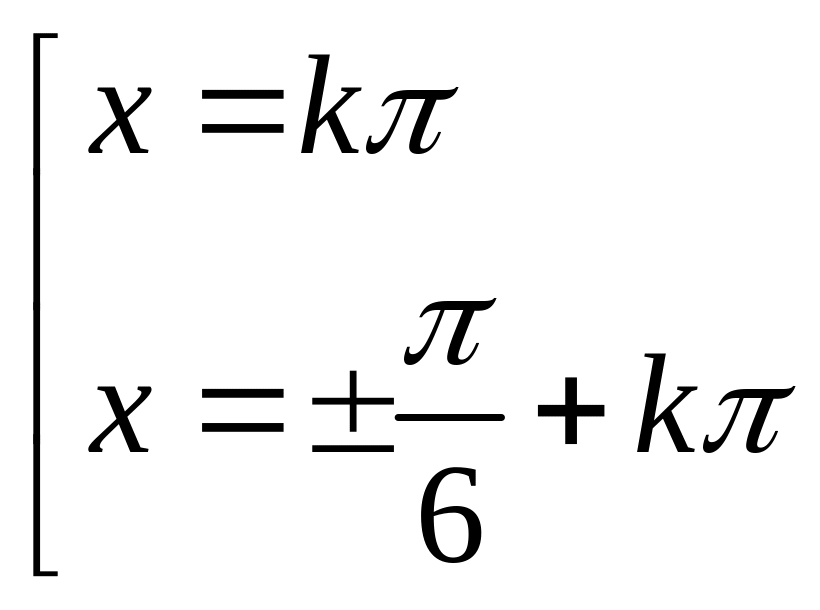
C. 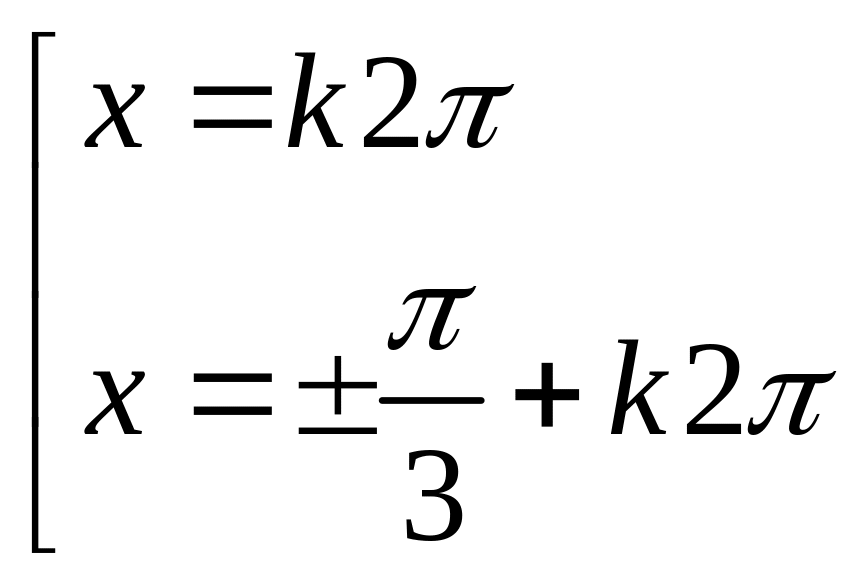
D. ![]()
Trong các hàm số sau, hàm số nào nhận trục
![]() làm trục đối xứng?
làm trục đối xứng?
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Trong các tập sau, tập nào là tập giá trị của hàm số:
![]() ?
?
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Điều kiện để phương trình:
![]() vô nghiệm là gì?
vô nghiệm là gì?
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Từ một chiếc hộp chứa ba quả cầu trắng và hai quả cầu đen, lấy ngẫu nhiên hai quả cầu. Trong các giá trị sau, giá trị nào là xác suất lấy được hai quả cầu trắng?
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Gieo một con súc sắc (cân đối và đồng chất) hai lần. Gọi A là biến cố: “Mặt 6 chấm xuất hiện ít nhất một lần”. Khi đó, xác suất của biến cố A là gì?
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Trong các giá trị sau, giá trị nào là số hạng không
chứa x của khai triển:
![]() ?
?
A. 70
B. 56
C. 28
D. 10
Số các số tự nhiên có ba chữ số khác nhau được lập
từ tập
![]() là gì?
là gì?
A. 20
B. 60
C. 720
D. 120
Cho tổng
![]() .
Khi đó, công thức của
.
Khi đó, công thức của
![]() là gì?
là gì?
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Cho dãy số
![]() với
với
![]() .
Số hạng
.
Số hạng
![]() là gì?
là gì?
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Trong các giá trị sau, giá trị nào của x để dãy
số gồm các số hạng:
![]() ,
theo thứ tự đó, là một cấp số nhân?
,
theo thứ tự đó, là một cấp số nhân?
A. 36
B. ![]()
C. 6
D. ![]()
Trong các giá trị sau, giá trị nào của x, y để
dãy số gồm các số hạng:
![]() ,
theo thứ tự đó, là một cấp số cộng?
,
theo thứ tự đó, là một cấp số cộng?
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Trong các phép biến hình sau, phép nào không phải là phép dời hình?
A. Phép chiếu vuông góc lên một đường thẳng
B. Phép đồng nhất
C. Phép vị tự tỉ số
![]()
D. Phép đối xứng trục
Mệnh đề nào sai?
A. Phép tịnh tiến biến đường thẳng thành đường thẳng song song hoặc trùng với nó
B. Phép đối xứng trục biến đường thẳng thành đường thẳng song song hoặc trùng với nó
C. Phép đối xứng tâm biến đường thẳng thành đường thẳng song song hoặc trùng với nó
D. Phép vị tự biến đường thẳng thành đường thẳng song song hoặc trùng với nó
Trong mặt phẳng
![]() ,
cho đường thẳng d có phương trình:
,
cho đường thẳng d có phương trình:
![]() .
Để phép tịnh tiến theo vectơ
.
Để phép tịnh tiến theo vectơ
![]() biến đường thẳng d thành chính nó thì
biến đường thẳng d thành chính nó thì
![]() phải là vectơ nào?
phải là vectơ nào?
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Trong mặt phẳng
![]() ,
cho điểm
,
cho điểm
![]() .
Qua phép vị tự
.
Qua phép vị tự
![]() ,
điểm A biến thành điểm nào?
,
điểm A biến thành điểm nào?
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Mệnh đề nào đúng?
A. Hai đường thẳng phân biệt cùng nằm trong một mặt phẳng thì không chéo nhau
B. Hai đường thẳng phân biệt không cắt nhau thì chéo nhau
C. Hai đường thẳng phân biệt không song song thì chéo nhau
D. Hai đường thẳng phân biệt lần lượt thuộc hai mặt phẳng khác nhau thì chéo nhau
Mệnh đề nào đúng?
A. Nếu hai mặt phẳng
![]() và
và
![]() song song với nhau thì mọi đường thẳng nằm trong
song song với nhau thì mọi đường thẳng nằm trong
![]() đều song song với mọi đường thẳng nằm trong
đều song song với mọi đường thẳng nằm trong
![]()
B. Nếu hai mặt phẳng
![]() và
và
![]() song song với nhau thì mọi đường thẳng nằm trong
song song với nhau thì mọi đường thẳng nằm trong
![]() đều song song với
đều song song với
![]()
C. Nếu hai đường thẳng song song với nhau lần lượt
thuộc hai mặt phẳng phân biệt
![]() và
và
![]() thì
thì
![]() và
và
![]() song song với nhau
song song với nhau
D. Qua một điểm nằm ngoài mặt phẳng cho trước, ta vẽ được một và chỉ một đường thẳng song song với mặt phẳng đã cho
Cho tứ diện ABCD. Gọi I, J và K lần lượt là trung điểm của AC, BC và BD. Giao tuyến của hai mặt phẳng (ABD) và (IJK) là?
A. KD
B. KI
C. Đường thẳng đi qua K và song song với AB
D. Không có
Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi I, J lần lượt là trọng tâm của các tam giác ABC và A’B’C’. Thiết diện tạo bởi mặt phẳng (AIJ) với hình lăng trụ là?
A. Tam giác cân
B. Tam giác vuông
C. Hình thang
D. Hình bình hành
II. PHẦN TỰ LUẬN (4.0 điểm):
Câu 1 (1.0 điểm):
Giải phương trình:
![]() .
.
Câu 2 (1.0 điểm):
Chứng minh rằng, với mọi số nguyên dương n ta
luôn có:
![]() chia hết cho 5.
chia hết cho 5.
Câu 3 (2.0 điểm):
Cho tứ diện
![]() .
Gọi
.
Gọi
![]() ,
,
![]() lần lượt là trọng tâm của hai tam giác
lần lượt là trọng tâm của hai tam giác
![]() và
và
![]() .
.
Xác định giao tuyến của hai mặt phẳng:
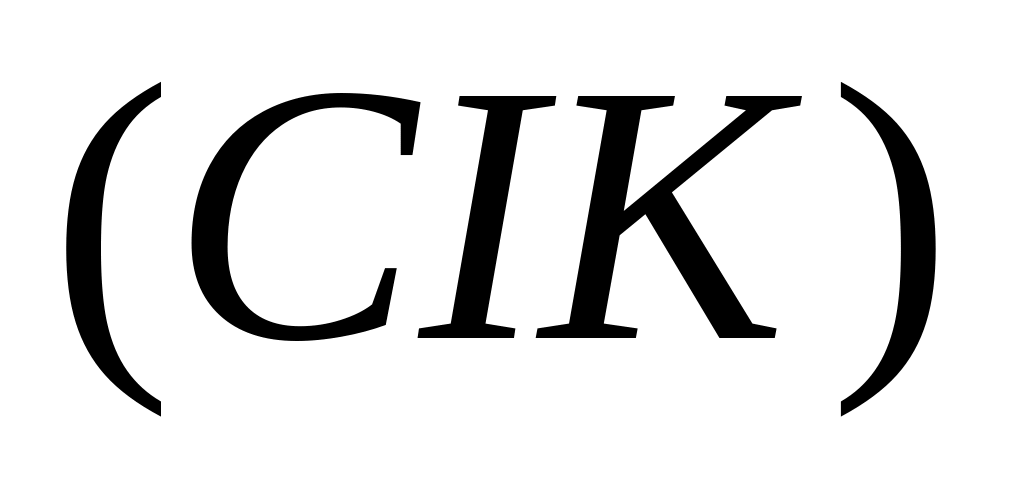 và
và
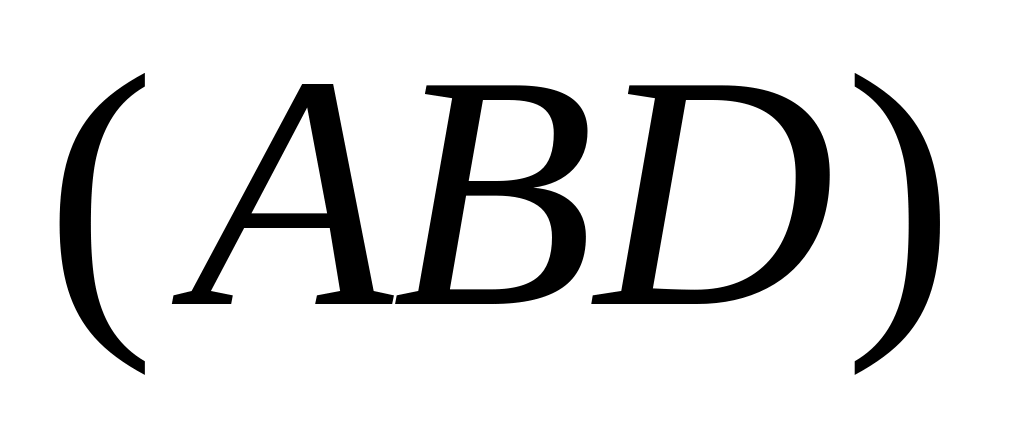 . (1.0
điểm)
. (1.0
điểm)Chứng minh rằng
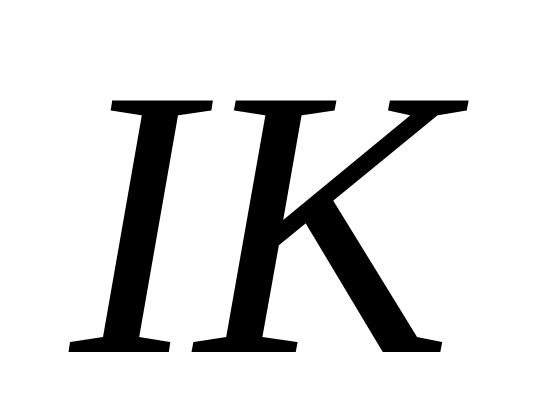 song song với
song song với
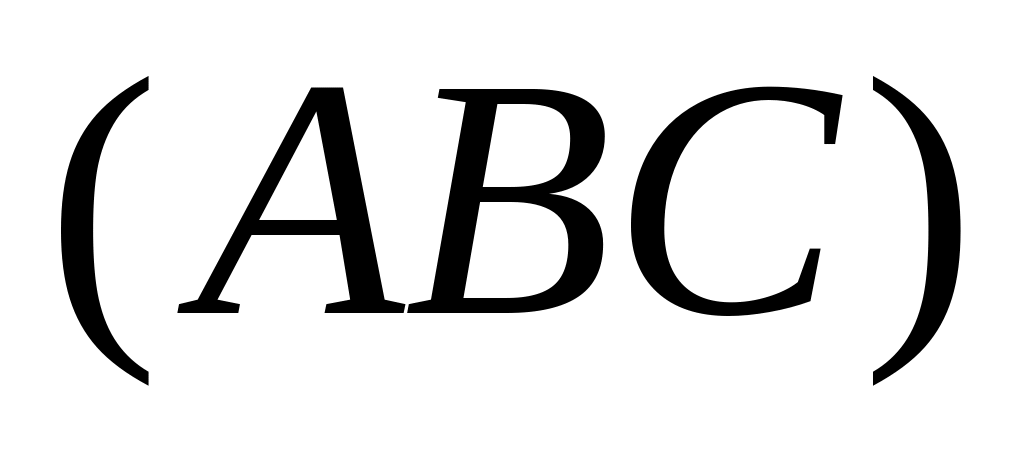 . (1.0
điểm)
. (1.0
điểm)
-----------------------------------------------
----------- HẾT -----------
MA TRẬN ĐỀ KIỂM TRA HỌC KÌ 1, NĂM HỌC 2016 – 2017
MÔN TOÁN KHỐI 11
(Thời gian: 90 phút, không kể giao đề)
Cấp độ
Tên Chủ đề (nội dung, chương…) |
Nhận biết |
Thông hiểu |
Vận dụng |
Cộng |
|||||
Cấp độ thấp |
Cấp độ cao |
||||||||
TNKQ |
TL |
TNKQ |
TL |
TNKQ |
TL |
TNKQ |
TL |
||
Chủ đề 1: Hàm số lượng giác – Phương trình lượng giác |
|||||||||
Số câu |
1 |
|
2 |
|
1 |
1 |
|
|
Số câu: 5 Số điểm: 2.2 Tỉ lệ %: 22% |
Số điểm |
0.3 |
|
0.6 |
|
0.3 |
1.0 |
|
|
|
Chủ đề 2: Tổ hợp – Xác suất |
|||||||||
Số câu |
1 |
|
1 |
|
1 |
|
1 |
|
Số câu: 4 Số điểm: 1.2 Tỉ lệ %: 12% |
Số điểm |
0.3 |
|
0.3 |
|
0.3 |
|
0.3 |
|
|
Chủ đề 3: Dãy số – Cấp số cộng – Cấp số nhân |
|||||||||
Số câu |
1 |
|
2 |
|
1 |
|
|
1 |
Số câu: 5 Số điểm: 2.2 Tỉ lệ %: 22% |
Số điểm |
0.3 |
|
0.6 |
|
0.3 |
|
|
1.0 |
|
Chủ đề 4: Phép biến hình |
|||||||||
Số câu |
2 |
|
2 |
|
|
|
|
|
Số câu: 4 Số điểm: 1.2 Tỉ lệ %: 12% |
Số điểm |
0.6 |
|
0.6 |
|
|
|
|
|
|
Chủ đề 5: Dường thẳng và mặt phẳng trong không gian – Quan hệ song song |
|||||||||
Số câu |
1 |
|
1 |
1 |
1 |
1 |
1 |
|
Số câu: 6 Số điểm: 3.2 Tỉ lệ %: 32% |
Số điểm |
0.3 |
|
0.3 |
1.0 |
0.3 |
1.0 |
0.3 |
|
|
Tổng số câu |
6 |
9 |
6 |
3 |
Số câu: 24 Số điểm: 10.0 |
||||
Tổng số điểm |
1.8 |
3.4 |
3.2 |
1.6 |
|||||
Tỉ lệ % |
18% |
34% |
32% |
16% |
|||||
HƯỚNG DẪN CHẤM PHẦN TỰ LUẬN
(Bản hướng dẫn này gồm 02 trang)
I. HƯỚNG DẪN CHUNG
1. Nếu thí sinh làm bài không theo cách nêu trong đáp án nhưng đúng thì vẫn cho đủ số điểm của từng phần như Hướng dẫn chấm thi.
2. Việc chi tiết hóa số điểm của từng câu (nếu có) trong Hướng dẫn chấm thi phải đảm bảo không làm sai lệch Hướng dẫn chấm thi và phải thống nhất thực hiện trong Hội đồng chấm thi.
3. Sau khi cộng điểm toàn bài, làm tròn đến 0,50 điểm (lẻ 0,25 làm tròn thành 0,50; lẻ 0,75 làm tròn thành 1,00).
II. ĐÁP ÁN VÀ THANG ĐIỂM
CÂU |
ĐÁP ÁN |
ĐIỂM |
Câu 1 (1.0 điểm) |
c.
|
0.25
|
|
0.25
|
|
|
0.25 |
|
|
0.25 |
|
Câu 2 (1.0 điểm) |
Đặt
Với
|
0.25
|
Giả sử, điều cần chứng minh đúng với
|
0.25 |
|
Ta cần chứng minh,
Thật vậy,
|
0.25 |
|
|
0.25 |
|
Câu 3 (2.0 điểm) |
a. Vẽ hình đúng
|
0.5
|
Gọi
|
0.25 |
|
Khi đó,
|
0.25 |
|
b. Gọi
|
0.25 |
|
Trong tam giác
|
0.25 |
|
Khi đó
|
0.25 |
|
Hơn nữa,
|
0.25 |
Trường: THPT Ba Chúc Đề: 132 |
ĐỀ KIỂM TRA HỌC KÌ 1_NĂM HỌC: 2016 – 2017 MÔN TOÁN_KHỐI 11 Thời gian: 90 phút (Không kể phát đề) |
Họ & Tên: _______________________________ Số báo danh: ______________ Lớp: 11a
Chọn 1 đáp án đúng và tô vào phiếu trả lời trắc nghiệm
-----------
Câu 1: Cô dâu và chú rể mời 6 người ra chụp hình kỉ niệm, người thợ chụp hình có bao nhiêu cách sắp xếp sao cho cô dâu và chú rể đứng cạnh nhau
A. 30240 B. 1440 C. 10080 D. 40320
Câu 2: Công thức nghiệm phương trình:
![]() là:
là:
A.
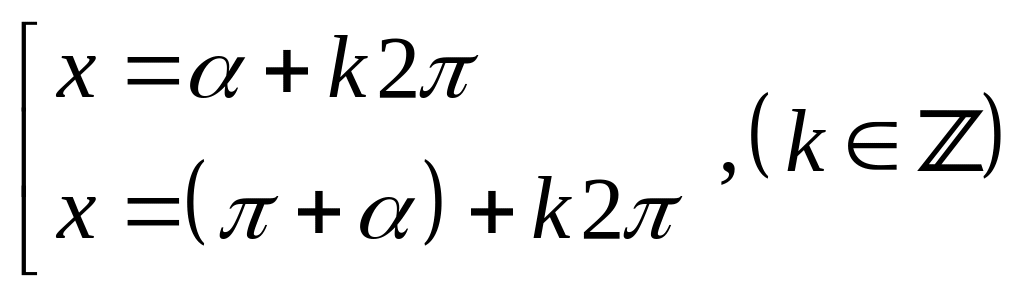 B.
B.
![]()
C.
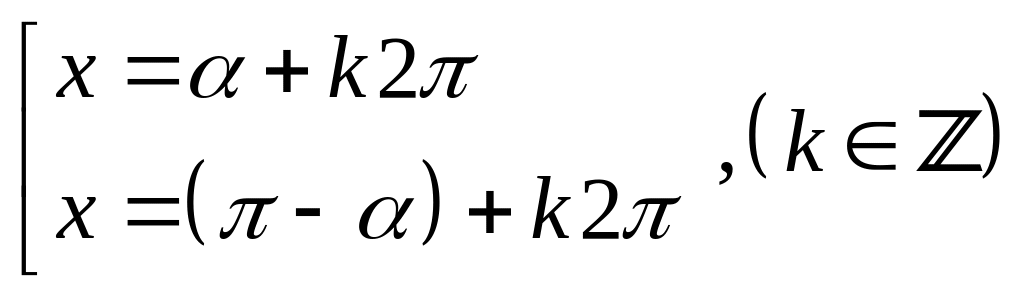 D.
D.
![]()
Câu 3: Nghiệm của phương trình :
![]() là :
là :
A.
![]() B.
B.
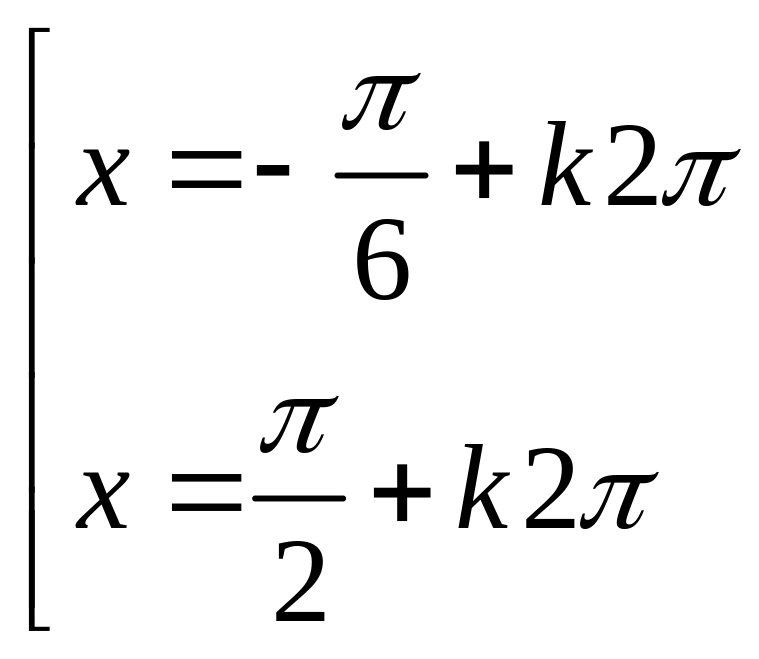 C.
C.
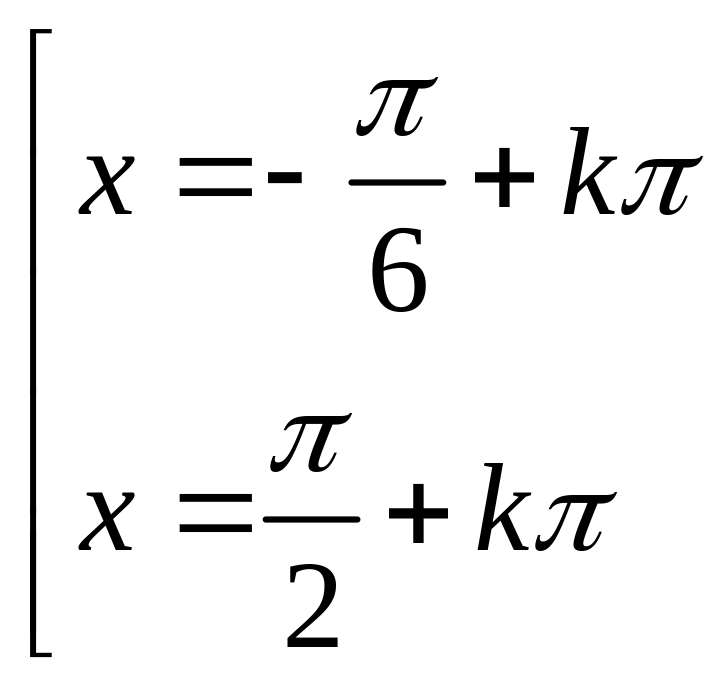 D.
D.
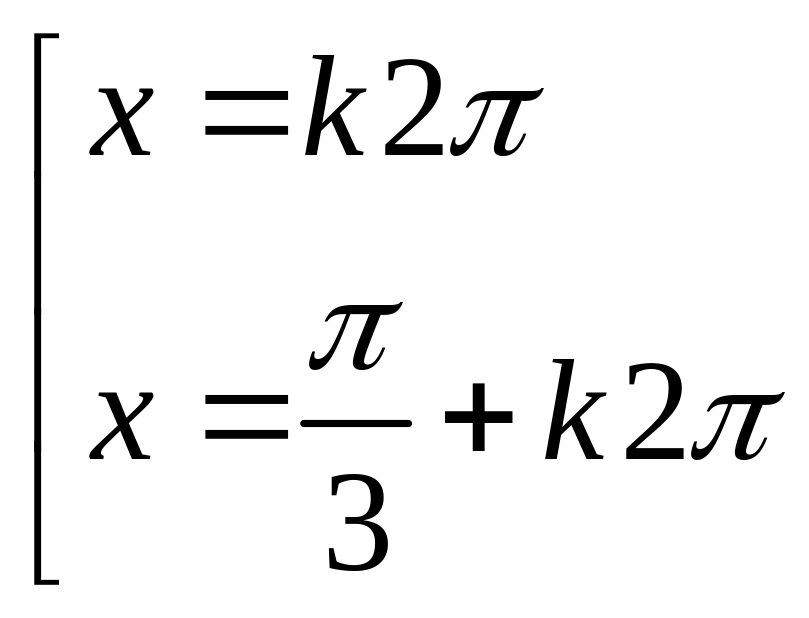
Câu 4:
Cho điểm
![]() .
Ảnh của điểm M qua phép tịnh tiến theo vecto
.
Ảnh của điểm M qua phép tịnh tiến theo vecto
![]() là:
là:
A.
![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
Câu 5: Nghiệm của phương trình : sin x + cos x = 1 là :
A.
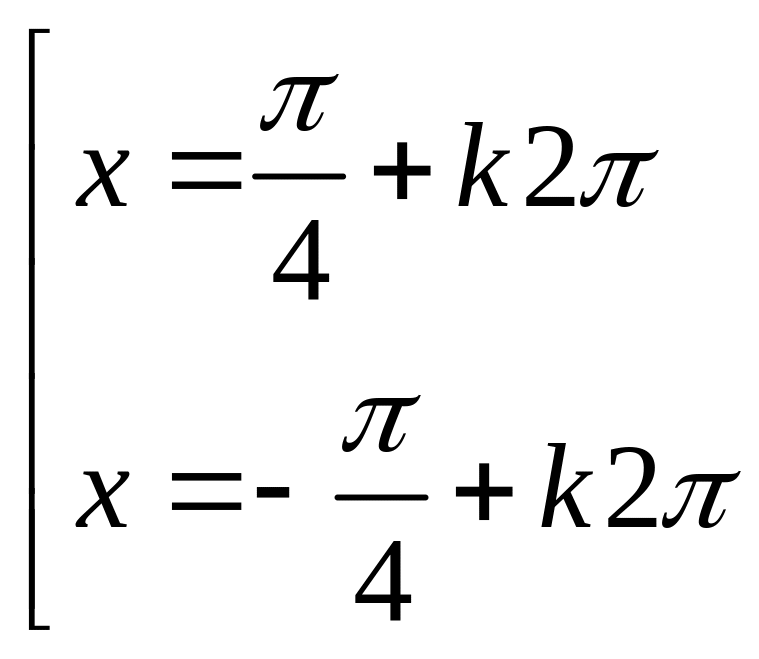 B.
B.
![]() C.
C.
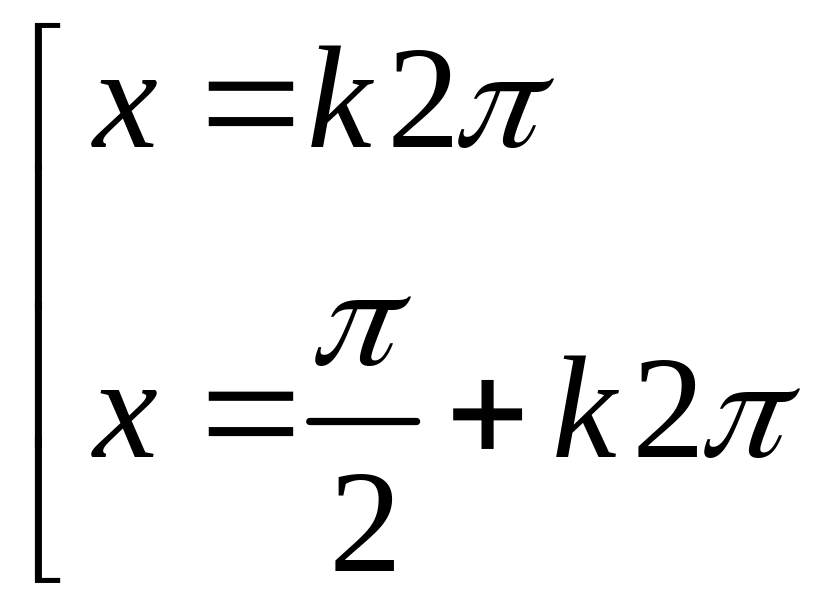 D.
D.
![]()
Câu 6: Cho hình chóp S.ABCD, đáy là hình thang, đáy lớn AB, Gọi M là trung điểm BC. Giao tuyến của mặt (SAB) và (SDM) là:
A. SI
, với
![]() B.
SI
, với
B.
SI
, với
![]()
C. Sx
, với
![]() D.
SI
, với
D.
SI
, với
![]()
Câu 7: Trong các phương trình sau, phương trình nào có nghiệm:
A.
![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
Câu 8: Nghiệm phương trình:
![]() là:
là:
A.
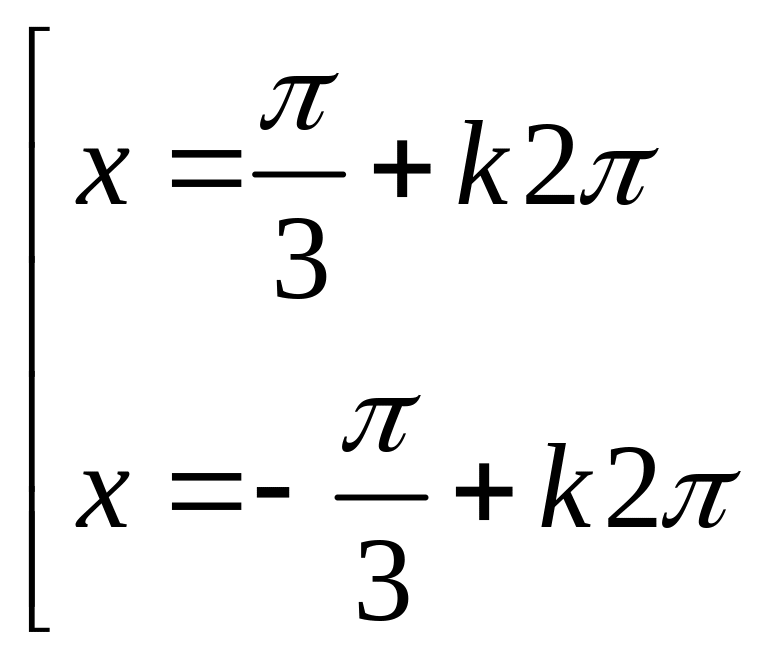 B.
B.
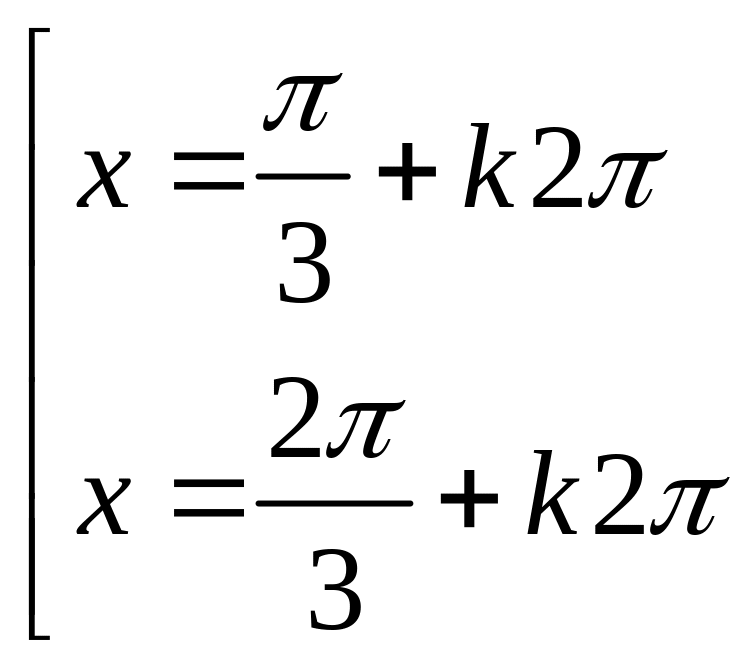 C.
C.
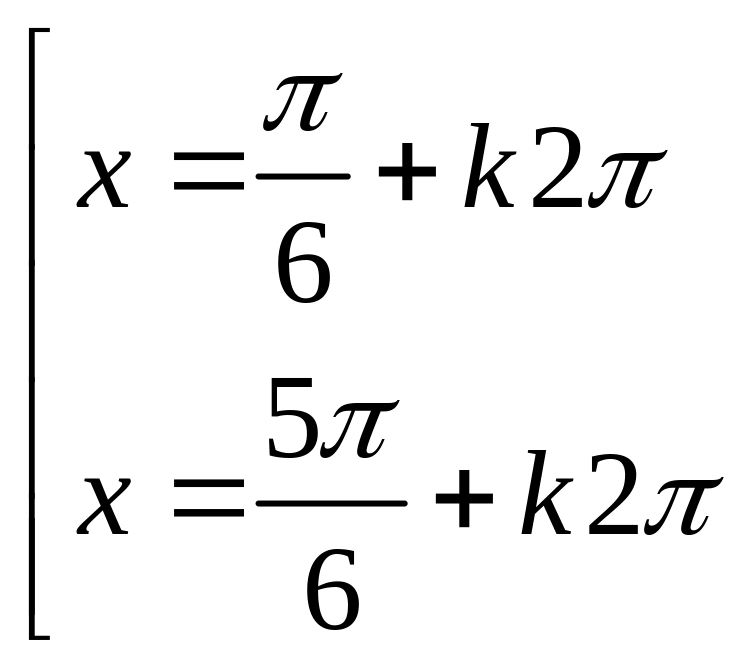 D.
D.
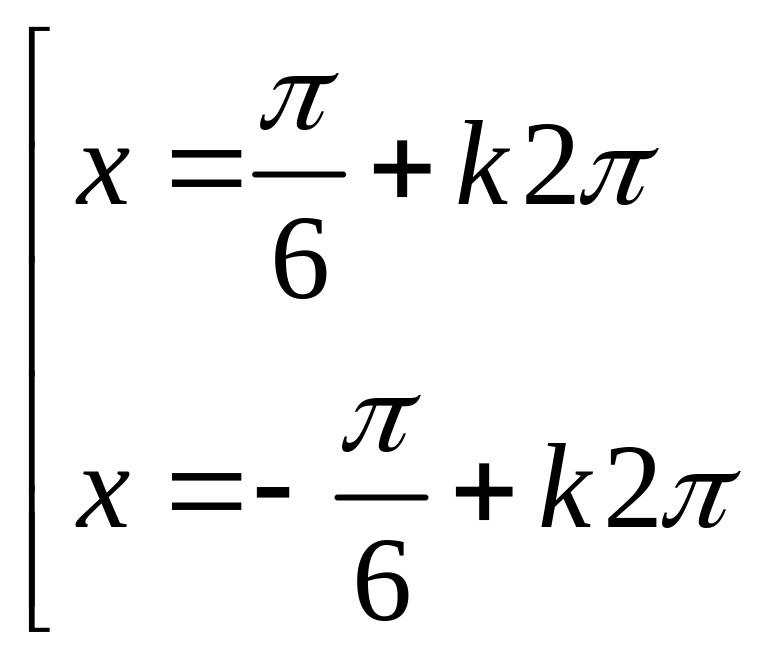
Câu 9: Từ A đến B có 3 cách, B đến C có 5 cách , C đến D có 2 cách. Hỏi có bao nhiêu cách đi từ A đến D rồi quay lại A?
A. 90 B. 900 C. 60 D. 30
Câu 10: Cho tập
![]() .
Từ tập
.
Từ tập
![]() có thể lập được bao nhiêu số tự nhiên có 3 chữ số
khác nhau. Tính xác suất biến cố sao cho tổng 3 chữ số
bằng 9
có thể lập được bao nhiêu số tự nhiên có 3 chữ số
khác nhau. Tính xác suất biến cố sao cho tổng 3 chữ số
bằng 9
A.
![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
Câu 11: Cho cấp số cộng
![]() có
có
![]() .
Vậy
.
Vậy
![]() là
là
A. 13 B. 15 C. 12 D. 11
Câu 12: Số hạng không chứa
![]() trong khai triển:
trong khai triển:
![]() là.
là.
A. 28 B. 70 C. 56 D. 10
Câu 13: Giá trị nhỏ nhất của hàm số
![]() bằng:
bằng:
A.
![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
Câu 14: Cho hình chóp S.ABC. G là trọng tâm của tam giác ABC. M, N,K lần lượt là trung điểm BC, AC,SA. Giao tuyến của (SAM) và (SBN) là
A. SG B. SN C. SM D. Sx//AM//BN
Câu 15: Với giá trị nào của m thì phương trình
![]() có nghiệm:
có nghiệm:
A.
![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
Câu 16: Cho tập
![]() .
Từ tập
.
Từ tập
![]() có thể lập được bao nhiêu số tự nhiên có bốn chữ
số khác nhau và chia hết cho
có thể lập được bao nhiêu số tự nhiên có bốn chữ
số khác nhau và chia hết cho
![]() :
:
A.
![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
Câu 17: Giá trị của
![]() thỏa mãn
thỏa mãn
![]() là:
là:
A.
![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
Câu 18: Cho tập
![]() .
Từ tập
.
Từ tập
![]() có thể lập được bao nhiêu số tự nhiên gồm bốn chữ
số đôi một khác nhau?
có thể lập được bao nhiêu số tự nhiên gồm bốn chữ
số đôi một khác nhau?
A.
![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
Câu 19: Phương trình:
![]() có nghiệm là:
có nghiệm là:
A.
![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
Câu 20: Số hạng thứ 3 trong khai triển:
![]() bằng:
bằng:
A.
![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
Câu 21:
Cho
![]() .
Ảnh của đường thẳng d qua phép tịnh tiến theo vecto
.
Ảnh của đường thẳng d qua phép tịnh tiến theo vecto
![]() là:
là:
A.
![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
Câu 22: Gieo 1 con súc sắc 2 lần. Xác suất của biến cố A sao cho tổng số chấm trong 2 lần bằng 8 là:
A.
![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
Câu 23: Cho cấp
số cộng
![]() có
có
![]() .
Vậy
.
Vậy
![]() là
là
A. -41 B. -42 C. -40 D. -43
Câu 24: Cho
![]() .
Giá trị biểu thức
.
Giá trị biểu thức
![]() bằng:
bằng:
A.
![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
Câu 25: Có 7 viên bi xanh và 3 viên bi đỏ. Chọn ngẫu nhiên 5 viên bi. Xác suất của biến cố A sao cho chọn đúng 3 viên bi xanh là.
A.
![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
Câu 26: Nghiệm
phương trình:
![]() là:
là:
A.
![]() B.
B.
![]() C.
C.
![]() D.
D.
![]() 0
0
Câu 27: Trong một mặt phẳng có 5 điểm trong đó không có 3 điểm nào thẳng hàng. Hỏi tổng số đọan thẳng và tam giác có thể lập được từ các điểm trên là:
A. 40 B. 80 C. 20 D. 10
Câu 28: Có 5 nam, 5 nữ xếp thành một hàng dọc. Tính xác suất để nam, nữ đứng xen kẻ nhau .
A.
![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
Câu 29: Điều
kiện m
để phương trình:
![]() có nghiệm là :
có nghiệm là :
A.
![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
Câu 30: Cho
![]() . với
. với
![]() . Giá trị
. Giá trị
![]()
A.
![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
Câu 31: Cho cấp
số cộng
![]() có
có
![]() .
Vậy
.
Vậy
![]() là
là
A. -68 B. 76 C. -71 D. -72
Câu 32: Có 6 học sinh nam và 4 học sinh nữ. Có bao nhiêu cách chọn 5 học sinh sao cho số học sinh nữ là số lẻ.
A. 3600 B. 60 C. 252 D. 120
Câu 33: Cho dãy
số
![]() có
công thức tổng quát
có
công thức tổng quát
![]() .
Hỏi số
.
Hỏi số
![]() là số hạng thứ mấy?
là số hạng thứ mấy?
A. 6 B. 8 C. 7 D. 9
Câu
34:
Cho đường tròn
![]() .
Ảnh của đường tròn (C) qua phép vị tự tâm O, tỉ số
.
Ảnh của đường tròn (C) qua phép vị tự tâm O, tỉ số
![]() có phương trình là:
có phương trình là:
A.
![]() B.
B.
![]()
C.
![]() D.
D.
![]()
Câu 35: Giá trị
lớn nhất của hàm số
![]() bằng:
bằng:
A.
![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
Câu 36: Trong
mặt phẳng Oxy, ảnh của điểm
![]() qua
phép quay
qua
phép quay
![]() là:
là:
A.
![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
Câu 37: Cho hình
chóp S.ABCD có đáy ABCD là tứ giác. Gọi M,N,P lần lượt
là trung điểm SA, AB, BC.
![]() ,
,
![]() .
Giao điểm cuả SD và (MNP) là K,
Với K là giao của:
.
Giao điểm cuả SD và (MNP) là K,
Với K là giao của:
A. SD và MF B. MN và SD C. SD và ME D. SD và NP
Câu
38:
Cho đường tròn
![]() .
Ảnh của đường tròn (C) qua phép quay tâm O, góc quay
.
Ảnh của đường tròn (C) qua phép quay tâm O, góc quay
![]() có phương trình là:
có phương trình là:
A.
![]() B.
B.
![]()
C.
![]() D.
D.
![]()
Câu 39: Cho hình chóp S.ABCD, đáy là hình bình hành tâm O, giao tuyến của mặt (SAC) và (SBD) là:
A. SC B. SA C. SB D. SO
Câu 40: Cho tứ diện ABCD. Có bao nhiêu cặp đường thẳng chéo nhau
A. 3 B. 4 C. 5 D. 2
Câu 41: Số nghiệm
của phương trình :
![]() thỏa điều kiện
thỏa điều kiện
![]() là :
là :
A. 1 B. 4 C. 3 D. 2
Câu 42: Cho hình chóp S.ABCD có đáy ABCD là hình thang, đáy lớn AB. O là giao của AC và BD. M,N,K lần lượt là trung điểm SA, SC, BC. Giao tuyến của (DMN) và (ABCD) là
A. By//MN//AC B. Dy//MN//AC C. Sx//MN//AC D. DM
Câu 43: Cho 15 học sinh (8nam – 7 nữ). Chọn ra 4 em. Tính xác suất sao cho các em được chọn có cả nam và nữ:
A.
![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
Câu 44: Cho hình chóp S.ABCD, đáy là hình bình hành tâm O, giao tuyến của mặt (SAB) và (SCD) là :
A. SK
, với
![]() B.
SO
B.
SO
C. Sx
, với
![]() D.
Sy
, với
D.
Sy
, với
![]()
Câu 45: Cho hình chóp S.ABCD có đáy ABCD là tứ giác.
Gọi M,N,P lần lượt là trung điểm SA, AB, BC.
![]() .
Giao tuyến của (SBD) và (SNP) là SI với I là giao của:
.
Giao tuyến của (SBD) và (SNP) là SI với I là giao của:
A. NP và BD B. SP và BD C. tất cả đều sai D. MN và BD
Câu 46: Cho tứ diện ABCD. Gọi
![]() sao
cho AM = 2MB. N và K lần lượt là trung điểm BC, CD. Giao
tuyến của (ABD) và (MNK) là
sao
cho AM = 2MB. N và K lần lượt là trung điểm BC, CD. Giao
tuyến của (ABD) và (MNK) là
A. MN B. MD C. MC D. Mx//BD//NK
Câu 47: Cho tứ diện ABCD. Gọi
![]() sao
cho AM = 2MB. N và K lần lượt là trung điểm BC, CD. Giao
tuyến của (ACD) và (MNK) là KP với P là giao điểm của
sao
cho AM = 2MB. N và K lần lượt là trung điểm BC, CD. Giao
tuyến của (ACD) và (MNK) là KP với P là giao điểm của
A. MN và CD B. MN và AD C. MN và AC D. tất cả đều sai
Câu 48: Có bao nhiêu cách xếp 5 học sinh A,B,C,D,E sao cho A,B ngồi cạnh nhau.
A. 48 B. 12 C. 24 D. 120
Câu 49: Trong các phương trình sau, phương trình nào là phương trình bậc 2 theo 1 hàm số lượng giác:
A.
![]() B.
B.
![]()
C.
![]() D.
D.
![]()
Câu 50: Cho dãy số
![]() có
có
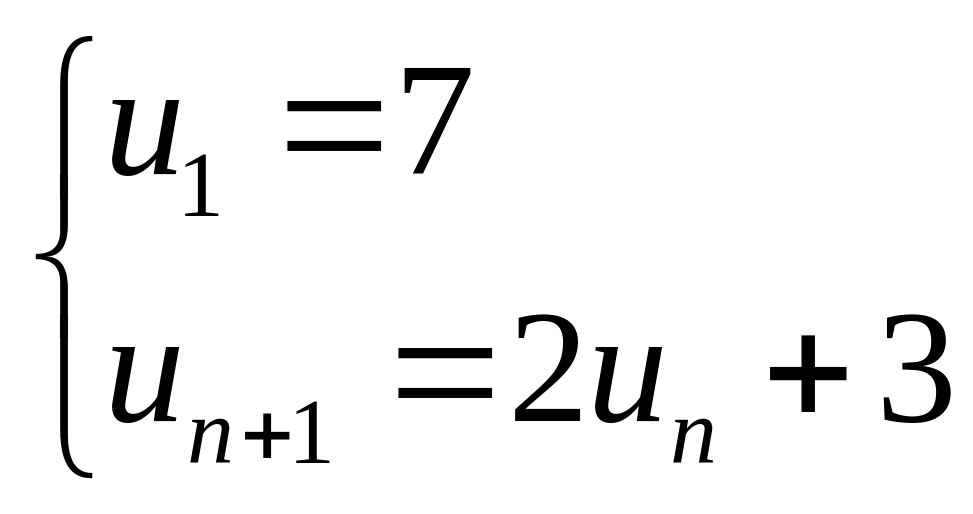 .
Khi đó
.
Khi đó
![]() là
là
A. 157 B. 317 C. 77 D. 112
-----------------------------------------------
----------- HẾT ----------
SỞ GD&ĐT VĨNH LONG TRƯỜNG THPT: HTH
|
ĐỀ KIỂM TRA HỌC KÌ I - NĂM HỌC 2016 - 2017 Môn: TOÁN LỚP 11 - CƠ BẢN Thời gian làm bài: 90 phút;
|
PHẦN TRẮC NGHIỆM:
Câu 1. Trong mặt phẳng tọa độ
![]() ,
cho điểm
,
cho điểm
![]() .
Phép quay tâm
.
Phép quay tâm
![]() góc
góc
![]() biến điểm
biến điểm
![]() thành điểm
thành điểm
A.
![]() . B.
. B.
![]() . C.
. C.
![]() . D.
. D.
![]() .
.
Câu 2. Khẳng định nào sau đây là sai?
A. Hàm số
![]() là hàm số chẵn. B. Hàm số
là hàm số chẵn. B. Hàm số
![]() là hàm số lẻ.
là hàm số lẻ.
C. Hàm số
![]() là hàm số chẵn. D. Hàm số
là hàm số chẵn. D. Hàm số
![]() là hàm số lẻ.
là hàm số lẻ.
Câu 3. Tính giá trị biểu thức
![]() .
.
A.
![]() . B.
. B.
![]() . C.
. C.
![]() . D.
. D.
![]() .
.
Câu 4. Một câu lạc bộ cầu lông có 26 thành viên. Số cách chọn một ban đại diện gồm một trưởng ban, một phó ban và một thư ký là
A. 13800. B. 6900. C. 15600. D. 1560.
Câu 5.
Trong
mặt phẳng tọa độ Oxy,
cho
![]()
![]() Phép
tịnh
tiến
biến điểm A
thành
điểm B
có
vectơ tịnh tiến là
Phép
tịnh
tiến
biến điểm A
thành
điểm B
có
vectơ tịnh tiến là
A.
![]() . B.
. B.
![]() . C.
. C.
![]() . D.
. D.
![]() .
.
Câu 6. Trong các mệnh đề sau đây, mệnh đề nào đúng?
A. Có duy nhất một mặt phẳng đi qua 3 điểm cho trước.
B. Có duy nhất một mặt phẳng đi qua ba điểm không thẳng hàng cho trước.
C. Có duy nhất một mặt phẳng đi qua một điểm và một đường thẳng.
D. Có duy nhất một mặt phẳng đi qua 4 điểm cho trước.
Câu 7. Trong các khẳng định sau, khẳng định nào đúng?
A. Hai đường thẳng cắt nhau thì chúng không đồng phẳng.
B. Tồn tại duy nhất một mặt phẳng đi qua một điểm và một đường thẳng cho trước.
C. Hai đường thẳng cắt nhau nếu chúng đồng phẳng và không song song.
D. Hai đường thẳng phân biệt cắt nhau nếu chúng đồng phẳng và không song song
Câu 8 Một nhóm học sinh gồm 7 nam và 3 nữ. Cần chọn ra 5 học sinh để tham gia đồng diễn thể dục, với yêu cầu có không quá 1 bạn nữ. Hỏi có bao nhiêu cách chọn?
A. 126 B. 105 C. 252 D. 63
Câu 9:Cho tứ diện
![]() với
với
![]() là 3 điểm lần lượt lấy trên 3 cạnh
là 3 điểm lần lượt lấy trên 3 cạnh
![]() sao cho
sao cho
![]() Giao điểm
Giao điểm
![]() của đường thẳng
của đường thẳng
![]() và mặt phẳng
và mặt phẳng
![]() nằm trên đường thẳng nào sau đây?
nằm trên đường thẳng nào sau đây?
A. Đường thẳng
![]()
B. Đường thẳng
![]() đi qua
đi qua
![]() và song song với
và song song với
![]()
C. Đường thẳng
![]()
D. Đường thẳng
![]() đi qua
đi qua
![]() và song song với
và song song với
![]()
Câu 10 Giá trị lớn
nhất của hàm số
![]() là:
là:
A.
![]() B.
0 C. 3 D. 1
B.
0 C. 3 D. 1
Câu 11:
Tổng
![]() bằng
bằng
A.
![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
Câu 12:Cho hình chóp
![]() có đáy
có đáy
![]() là hình vuông tâm
là hình vuông tâm
![]() Giao tuyến
của hai mặt phẳng
Giao tuyến
của hai mặt phẳng
![]() và
và
![]() là
là
A. đường thẳng
![]() B.
đường thẳng
B.
đường thẳng
![]() C.
đường thẳng
C.
đường thẳng
![]() D.
đường thẳng
D.
đường thẳng
![]()
Câu 13:
Số hạng
tổng quát trong khai
triển biểu thức
![]() là
là
A.
![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
Câu 14: Trên mặt phẳng cho 10 điểm, trong đó không có 3 điểm nào thẳng hàng. Có bao nhiêu
đoạn thẳng khác nhau được tạo bởi 2 trong 10 điểm nói trên?
A. 90 B. 20 C. 50 D. 45
Câu 15: Trong mặt phẳng tọa độ
![]() cho đường thẳng
cho đường thẳng
![]() có phương trình
có phương trình
![]() là ảnh của
đường thẳng
là ảnh của
đường thẳng
![]() qua phép quay tâm
qua phép quay tâm
![]() góc quay
góc quay
![]() Phương trình đường thẳng
Phương trình đường thẳng
![]() là
là
A.
![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
Câu 16: Trên bàn có bày 2 loại bánh khác nhau, 4 loại mứt khác nhau và 5 loại trái cây khác nhau để cho khách dùng tráng miệng. Hỏi mỗi người khách có thể có bao nhiêu cách chọn một loại bánh hoặc một loại mứt hoặc một loại trái cây?
A. 11 B. 20 C. 12 D. 40
Câu 17: Trong mặt phẳng tọa độ
![]() cho vectơ
cho vectơ
![]() điểm
điểm
![]() Ảnh của điểm
Ảnh của điểm
![]() qua phép tịnh tiến theo vectơ
qua phép tịnh tiến theo vectơ
![]() là điểm
là điểm
A.
![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
Câu 18:Tập xác định
của hàm số
![]() là:
là:
A.
![]() B.
B.
![]()
C.
![]() D.
D.
![]()
Câu 19:Tập giá trị
của hàm số
![]() là:
là:
A.
![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
Câu 20: Tập xác định
của hàm số
![]() là:
là:
A.
![]() B.
B.
![]()
C.
![]() D.
D.
![]()
Câu 21: Phương trình
![]() có nghiệm là:
có nghiệm là:
A.
![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
Câu 22: Trong mặt phẳng tọa độ
![]() cho vectơ
cho vectơ
![]() đường thẳng d’
có phương trình
đường thẳng d’
có phương trình
![]() là ảnh của
đường thẳng d
qua phép tịnh tiến theo vectơ
là ảnh của
đường thẳng d
qua phép tịnh tiến theo vectơ
![]() .
Đường thẳng d có phương trình
là
.
Đường thẳng d có phương trình
là
A.
![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
Câu 23: Trong mặt phẳng tọa độ
![]() cho
điểm
cho
điểm
![]() Ảnh của điểm
Ảnh của điểm
![]() qua phép quay tâm O góc quay
qua phép quay tâm O góc quay
![]() là
là
A.
![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
Câu 24: Phương trình
![]() có nghiệm là:
có nghiệm là:
A.
![]() B.
B.
![]()
C.
![]() D.
D.
![]()
Câu 25: Cho tứ diện
![]()
![]() lần lượt lấy trên hai cạnh
lần lượt lấy trên hai cạnh
![]() sao cho đường thẳng
sao cho đường thẳng
![]() cắt đường thẳng
cắt đường thẳng
![]() tại
tại
![]() Giao tuyến của
hai mặt phẳng
Giao tuyến của
hai mặt phẳng
![]() và
và
![]() là
là
A. đường thẳng
![]() B.
đường thẳng
B.
đường thẳng
![]()
C. đường thẳng
![]() D.
đường thẳng qua
D.
đường thẳng qua
![]() và song song với
và song song với
![]()
Câu
26: Cho hình chóp
![]() có đáy
có đáy
![]() là hình chữ nhật tâm
là hình chữ nhật tâm
![]() điểm
điểm![]() nằm trên cạnh
nằm trên cạnh
![]() sao
cho
sao
cho
![]() Giao điểm của
đường thẳng
Giao điểm của
đường thẳng
![]() và mặt phẳng
và mặt phẳng
![]() nằm trên đường thẳng nào sau đây?
nằm trên đường thẳng nào sau đây?
A. Đường thẳng
![]() B.
Đường thẳng
B.
Đường thẳng
![]() C.
Đường thẳng
C.
Đường thẳng
![]() D.
Đường thẳng
D.
Đường thẳng
![]()
Câu 27: Nếu
![]() thì
n có giá trị là:
thì
n có giá trị là:
A. 8 B. 7 C. 6 D. 5
II. PHẦN TỰ LUẬN:
Câu 1: Giải các phương trình lượng giác sau:
a)
![]() b)
b)
![]() c)
c)
![]()
Câu 2:
a) Có 9 viên bi xanh, 5 viên bi đỏ, 4 viên bi vàng có kích thước đôi một khác nhau. Hỏi có bao nhiêu cách chọn ra 6 viên bi, trong đó số bi xanh bằng số bi đỏ?
b) Tìm số hạng không chứa x trong khai
triển biểu thức
![]() (với
(với
![]() ).
).
Câu
3: Trong mp(α), cho tứ giác ABCD có AB và CD không
song song,
![]()
Xác định giao tuyến hai mặt phẳng
a) (SAC) và (SBD)
b) (SAB) và (SCD).
Câu 4:Cho hình chóp S.ABCD có đáy là hình thang AD // BC. M, N là 2 điểm bất kỳ trên SB, SD.
Tìm giao tuyến của (SAD) và (SBC). b)Tìm giao điểm của MN và (SAC).
SỞ GIÁO DỤC VÀ ĐÀO TẠO ĐĂKLAK TRƯỜNG THCS – THPT ĐÔNG DU
|
KIỂM TRA HỌC KÌ 1 NĂM HỌC 2016 – 2017 Môn Toán 11 Thời gian : 90 Phút |
ĐỀ 2
PHẦN I: TRẮC NGHIỆM (3 điểm)
C©u 1 : |
Trong
mặt phẳng tọa độ Oxy
,
cho đường thẳng
|
|||||||||
A. |
|
B. |
|
C. |
|
D. |
|
|
||
C©u 2 : |
Trong mặt phẳng Oxy , ảnh của hai điểm A1;2 và B2;3 qua phép vị tự tâm I 1;2 tỉ số vị tự k 2 là: |
|||||||||
A. |
|
B. |
|
|||||||
C. |
|
D. |
|
|||||||
C©u 3 : |
Trong
mặt phẳng tọa độ Oxy
,
cho phép tịnh tiến theo
|
|||||||||
A. |
|
B. |
|
|||||||
C. |
|
D. |
|
|||||||
C©u 4 : |
Dãy số nào sau đây là dãy số giảm ? |
|||||||||
A. |
|
B. |
|
C. |
|
D. |
Không có dãy nào giảm. |
|
||
C©u 5 : |
Giá trị nhỏ nhất của hàm số
|
|||||||||
A. |
1 |
B. |
|
C. |
|
D. |
|
|
||
C©u 6 : |
Một bình đựng 12 quả cầu được đánh số từ 1 đến 12. Chọn ngẫu nhiên bốn quả cầu. Xác suất để bốn quả được chọn có số đều không vượt quá 8. |
|||||||||
A. |
|
B. |
|
C. |
|
D. |
|
|
||
C©u 7 : |
Cho
hình bình hành ABCD
tâm
O
,
phép quay
|
|||||||||
A. |
AC |
B. |
CD |
C. |
BC |
D. |
BA |
|
||
C©u 8 : |
Tập xác định của hàm số
|
|||||||||
A. |
|
B. |
|
|||||||
C. |
|
D. |
|
|||||||
C©u 9 : |
Ban văn nghệ lớp có 10 em nữ, 3 em nam. Cần chọn ra 3 em để lập một tốp ca sao cho có ít nhất 1 em nữ. Hỏi có bao nhiêu cách chọn ? |
|||||||||
A. |
|
B. |
|
C. |
|
D. |
|
|
||
C©u 10 : |
Chọn ngẫu nhiên một số tự nhiên nhỏ hơn 30. Tính xác suất của biến cố A : ‘‘Số được chọn là số nguyên tố’’ ? |
|||||||||
A. |
|
B. |
|
C. |
|
D. |
|
|
||
C©u 11 : |
Dãy số
|
|||||||||
A. |
|
B. |
|
C. |
|
D. |
|
|
||
C©u 12 : |
Hàm số nào là hàm số chẵn ? |
|||||||||
A. |
|
B. |
|
C. |
|
D. |
|
|
||
C©u 13 : |
Có bao nhiêu số tự nhiên có 3 chữ số đôi một khác nhau ? |
|||||||||
A. |
900 số |
B. |
504 số |
C. |
648 số |
D. |
999 số |
|
||
C©u 14 : |
Trong các phép biến hình có được bằng cách thực hiện liên tiếp hai phép biến hình sau đây, phép nào không là phép dời hình? |
|||||||||
A. |
Phép quay và phép đối xứng tâm. |
B. |
Phép đối xứng tâm và phép vị tự tỉ số k –1. |
|||||||
C. |
Phép quay và phép tịnh tiến. |
D. |
Phép quay và phép chiếu vuông góc lên một đường thẳng. |
|||||||
C©u 15 : |
Dãy số
|
|||||||||
A. |
11 |
B. |
8 |
C. |
19 |
D. |
27 |
|
||
PHẦN II: TỰ LUẬN (7 điểm)
Câu 1: (2đ) Giải phương trình:
a.
![]() b.
b.
![]()
c.
![]() d.
d.![]()
Câu 2: (1đ)
a.
Khai triển nhị thức:
![]()
b.
Tìm hệ số của x3 trong khai triển biểu
thức sau. (![]() +
+
![]() )15
)15
Câu 3: (2đ)
a. Tìm số hạng đầu, công sai và tổng 50 số hạng đầu của cấp số cộng sau, biết:
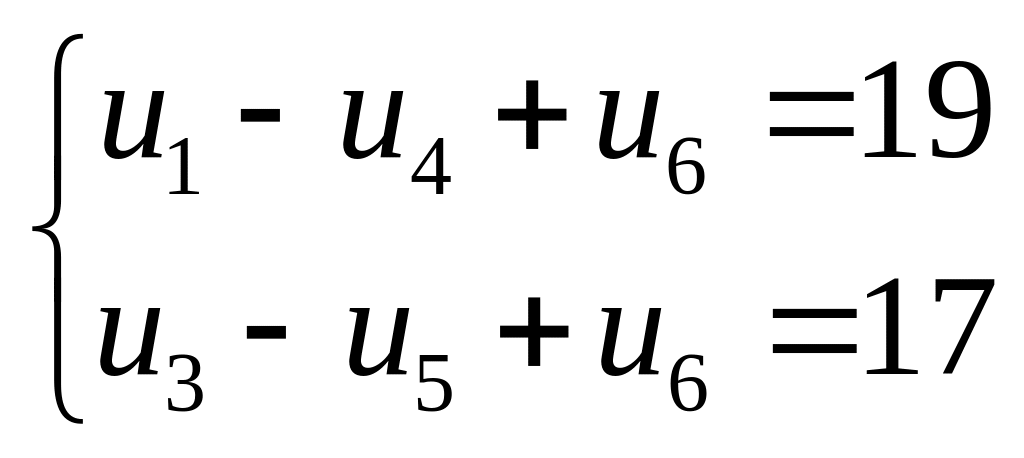
b. Tìm
số hạng đầu
![]() ,công bội q và
,công bội q và
![]() của cấp số nhân
của cấp số nhân
![]() , biết
, biết
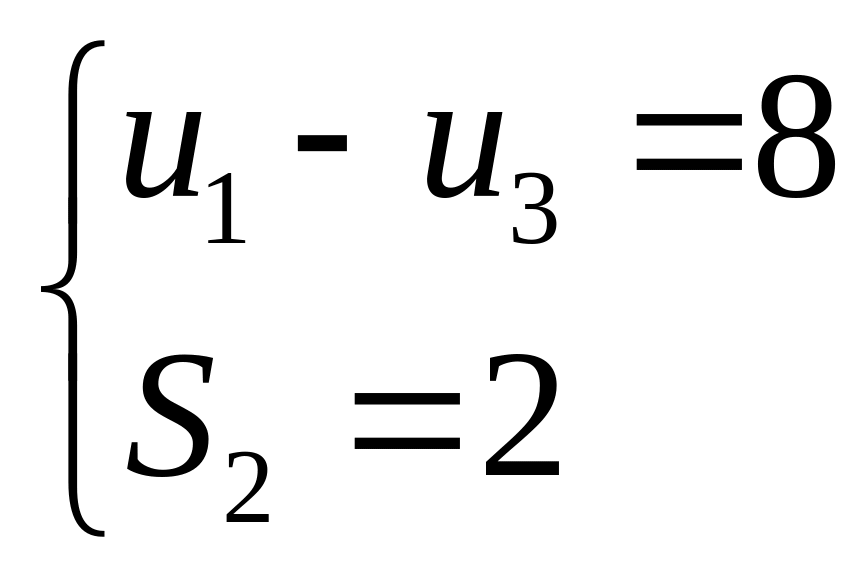 .
.
Câu 4: (2đ) Cho hình chóp S.ABCD. Đáy ABCD là hình thang có đáy lớn AB. Gọi M là trung điểm CD. () là mặt phẳng qua M song song với SA và BC.
a) Tìm giao tuyến của hai mặt phẳng (SAD) và (SBC) ; (SAB) và (SCD)
b) Xác định thiết diện tạo bởi mp() và hình chóp S.ABCD.
HẾT
ĐÁP ÁN ĐỀ 2
PHẦN I TRẮC NGHIỆM
01 |
) | } ~ |
06 |
{ | ) ~ |
11 |
{ | } ) |
02 |
{ | ) ~ |
07 |
{ | ) ~ |
12 |
) | } ~ |
03 |
{ ) } ~ |
08 |
) | } ~ |
13 |
{ | ) ~ |
04 |
{ ) } ~ |
09 |
{ | } ) |
14 |
{ | } ) |
05 |
) | } ~ |
10 |
{ ) } ~ |
15 |
{ ) } ~ |
|
|
|
|
|
|
PHẦN II TỰ LUẬN
Câu 1a 0.5đ |
|
0.25
0.25 |
Câu 1b 0.5đ |
|
0.25
0.25 |
Câu 1c 0.5đ |
Vậy nghiệm
|
0.25
0.25 |
Câu 1d 0.5đ |
Ta có :
|
0.25
0.25
|
Câu 2 1đ |
a.
b. Số
hạng tổng quát trong khai triển (
Để có x3
trong khai triển thì :
Vậy ta có hệ số trong khai triển là:
|
0.5
0.25
0.25 |
Câu 3a 1đ |
Hệ phương trình tương đương
u1 = 23; d = –2 S50 = 50*23 + 50.(50 – 1 )(–2)/2 = –1300 |
0.25 0.5 0.25 |
Câu 3b 1đ |
|
0.75
0.25
|
|
Tìm giao tuyến của hai mặt phẳng (SAD) và (SBC) |
1,00 |
Câu 4a 1đ
|
|
0,5
0.5 |
|
Xác định thiết diện tạo bởi () và hình chóp. Thiết diện là hình gì? |
|
Câu 4b 1đ |
|
0,50
0,50
|
SỞ GIÁO DỤC VÀ ĐÀO TẠO ĐĂKLAK TRƯỜNG THCS – THPT ĐÔNG DU
|
KIỂM TRA HỌC KÌ 1 NĂM HỌC 2016 – 2017 Môn Toán 11 Thời gian : 90 Phút |
PHẦN I: TRẮC NGHIỆM (3 điểm)
C©u 1 : |
Tập xác định của hàm số
|
||||||||||||
A. |
|
B. |
|
||||||||||
C. |
|
D. |
|
||||||||||
C©u 2 : |
Giá trị nhỏ nhất của hàm số
|
||||||||||||
A. |
1 |
B. |
|
C. |
|
D. |
|
|
|||||
C©u 3 : |
Trong
mặt phẳng tọa độ Oxy
,
cho đường thẳng
|
||||||||||||
A. |
|
B. |
|
C. |
|
D. |
|
|
|||||
C©u 4 : |
Hàm số nào là hàm số chẵn ? |
||||||||||||
A. |
|
B. |
|
C. |
|
D. |
|
|
|||||
C©u 5 : |
Chọn ngẫu nhiên một số tự nhiên nhỏ hơn 30. Tính xác suất của biến cố A : ‘‘Số được chọn là số nguyên tố’’ ? |
||||||||||||
A. |
|
B. |
|
C. |
|
D. |
|
|
|||||
C©u 6 : |
Trong
mặt phẳng tọa độ Oxy
,
cho phép tịnh tiến theo
|
||||||||||||
A. |
|
B. |
|
||||||||||
C. |
|
D. |
|
||||||||||
C©u 7 : |
Dãy số nào sau đây là dãy số giảm ? |
||||||||||||
A. |
|
B. |
|
C. |
|
D. |
Không có dãy nào giảm. |
|
|
||||
C©u 8 : |
Dãy số
|
||||||||||||
A. |
11 |
B. |
8 |
C. |
19 |
D. |
27 |
|
|||||
C©u 9 : |
Có bao nhiêu số tự nhiên có 3 chữ số đôi một khác nhau ? |
||||||||||||
A. |
648 số |
B. |
900 số |
C. |
504 số |
D. |
999 số |
|
|||||
C©u 10 : |
Cho
hình bình hành ABCD
tâm
O
,
phép quay
|
||||||||||||
A. |
CD |
B. |
AB |
C. |
BC |
D. |
AC |
|
|||||
C©u 11 : |
Trong mặt phẳng Oxy , ảnh của hai điểm A1;2 và B2;3 qua phép vị tự tâm I 1;2 tỉ số vị tự k 2 là: |
||||||||||||
A. |
|
B. |
|
||||||||||
C. |
|
D. |
|
||||||||||
C©u 12 : |
Một bình đựng 12 quả cầu được đánh số từ 1 đến 12. Chọn ngẫu nhiên bốn quả cầu. Xác suất để bốn quả được chọn có số đều không vượt quá 8. |
||||||||||||
A. |
|
B. |
|
C. |
|
D. |
|
|
|||||
C©u 13 : |
Ban văn nghệ lớp có 10 em nữ, 3 em nam. Cần chọn ra 3 em để lập một tốp ca sao cho có ít nhất 1 em nữ. Hỏi có bao nhiêu cách chọn ? |
||||||||||||
A. |
|
B. |
|
C. |
|
D. |
|
|
|||||
C©u 14 : |
Dãy số
|
||||||||||||
A. |
|
B. |
|
C. |
|
D. |
|
|
|||||
C©u 15 : |
Trong các phép biến hình có được bằng cách thực hiện liên tiếp hai phép biến hình sau đây, phép nào không là phép dời hình? |
||||||||||||
A. |
Phép quay và phép đối xứng tâm. |
B. |
Phép đối xứng tâm và phép vị tự tỉ số k –1. |
||||||||||
C. |
Phép quay và phép tịnh tiến. |
D. |
Phép quay và phép chiếu vuông góc lên một đường thẳng. |
||||||||||
PHẦN II : TỰ LUẬN (7 điểm)
Câu 1: (2đ) Giải phương trình:
a.
![]() c.
c.![]()
b.
![]() d.
d.
![]()
Câu 2: (1đ)
a.
Khai triển nhị thức:
![]()
b.
Tìm hệ số không chứa x trong khai triển nhị thức
![]()
Câu 3: (2đ)
a. Tính số hạng đầu, công sai và tổng 20 số hạng đầu tiên của một cấp số cộng (un ) biết: u3 = 25 và u8 = 15.
b.
Tìm
![]() ,công bội q và
,công bội q và
![]() của cấp số nhân
của cấp số nhân
![]() biết
biết
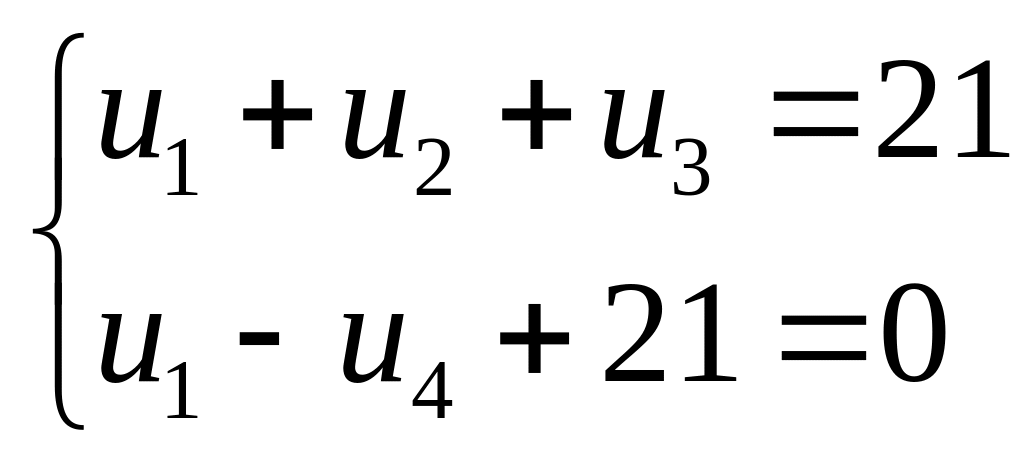
Câu 4: (2đ) Cho hình chóp S.ABCD. Đáy ABCD là hình bình hành có tâm O. Gọi M là trung điểm cạnh SC, N thuộc cạnh AB sao cho BN = 2NA.
a) Tìm giao tuyến của hai mặt phẳng (SAB) và (SCD) và chứng minh OM song song với mp(SAD).
b) Tìm giao điểm của AM và mặt phẳng (SND).
c) Xác định thiết diện của hình chóp S.ABCD khi cắt bởi mặt phẳng (P) chứa MN và song song AD.
HẾT
ĐÁP ÁN ĐỀ 1
Phần trắc nghiệm
01 |
) | } ~ |
06 |
{ | ) ~ |
11 |
{ | } ) |
02 |
) | } ~ |
07 |
{ | ) ~ |
12 |
{ ) } ~ |
03 |
{ | } ) |
08 |
{ ) } ~ |
13 |
{ ) } ~ |
04 |
) | } ~ |
09 |
) | } ~ |
14 |
{ | ) ~ |
05 |
{ ) } ~ |
10 |
{ | ) ~ |
15 |
{ | } ) |
|
|
|
|
|
|
Phần tự luận
1 |
a |
Vậy nghiệm của pt là:
|
0,25
0,25 |
b |
Vậy nghiệm của pt là:
|
0,25
0,25
|
|
c |
Vậy
nghiệm của pt là:
|
0,25
025 |
|
d |
|
0.25
0.25 |
|
2 (1.0đ) |
|
a.
b.Ta có số hạng tổng quát của khai triển nhị thức
Số hạng không chứa x tương ứng với 24–
3k = 0
Vậy số hạng
không chứa x là
|
0.5
0,25 0,25 |
3 2.0đ |
a |
Từ gt ta có hệ
Tìm được tổng S20 = 10(2u1 + 19d) = 200. |
0,5
0,5 |
b |
|
0.75đ
0.25 |
|
4 (2,0đ) |
|
|
|
a) |
* Xác định được điểm chung S * Xác định được giao tuyến d qua S, d // AB / /DC * Chứng minh được OM // SA OM // (SAD) |
0.5
0.5 |
|
b) |
Gọi I =
|
0,5 |
|
c) |
Do
PM // NQ//AD, QCD và PSB. Vậy thiết diện của hình chóp và mp(P) là hình thang NQMP. |
0.25
0.25 |
Ngoài Top 10 Đề Thi Học Kì 1 Toán 11 Hay Nhất Năm 2023 Có Đáp Án – Tài Liệu Toán thì các đề thi trong chương trình lớp 11 sẽ được cập nhật liên tục và nhanh nhất có thể sau khi kỳ thi diễn ra trên Danh mục Kho Đề Thi nhằm giúp các bạn đọc thuận tiện trong việc tra cứu và đối chiếu đáp án. Quý thầy cô và các bạn đọc có thể chia sẻ thêm những tài liệu học tập hữu ích đến địa chỉ email của chúng tôi, nhằm xây dựng nên kho đề thi phong phú, đa dạng cho các em học sinh tham khảo và rèn luyện.
Top 10 Đề Thi Học Kì 1 Toán 11 Hay Nhất Năm 2023 Có Đáp Án là tập hợp những đề thi xuất sắc và đầy thách thức dành cho học sinh lớp 11 để kiểm tra và đánh giá kiến thức Toán học của mình trong kỳ học đầu tiên. Tập sách này bao gồm những đề thi được tuyển chọn kỹ lưỡng từ nhiều nguồn tài liệu uy tín và các kỳ thi chọn đội tuyển Toán học hàng đầu.
Các đề thi trong tập sách được thiết kế để kiểm tra sự hiểu biết, tư duy logic, và khả năng giải quyết vấn đề của học sinh. Chúng đòi hỏi sự sáng tạo và linh hoạt trong việc áp dụng các kiến thức và phương pháp toán học để giải quyết các bài toán phức tạp.
Bên cạnh những câu hỏi và bài tập thú vị, tập sách còn cung cấp đáp án chi tiết và lời giải mẫu cho từng đề thi. Điều này giúp học sinh hiểu rõ cách suy nghĩ và giải quyết các bài toán một cách chi tiết và logic. Hơn nữa, việc tự kiểm tra và so sánh kết quả của mình với đáp án chuẩn sẽ giúp học sinh định hình lại khả năng và điểm mạnh yếu trong môn Toán học.
Top 10 Đề Thi Học Kì 1 Toán 11 Hay Nhất Năm 2023 Có Đáp Án là nguồn tài liệu hữu ích cho học sinh lớp 11 trong quá trình ôn tập và chuẩn bị cho các kỳ thi quan trọng. Đồng thời, nó cũng là công cụ hỗ trợ giáo viên trong việc đánh giá và giảng dạy Toán học một cách hiệu quả và phù hợp.
>>> Bài viết liên quan:







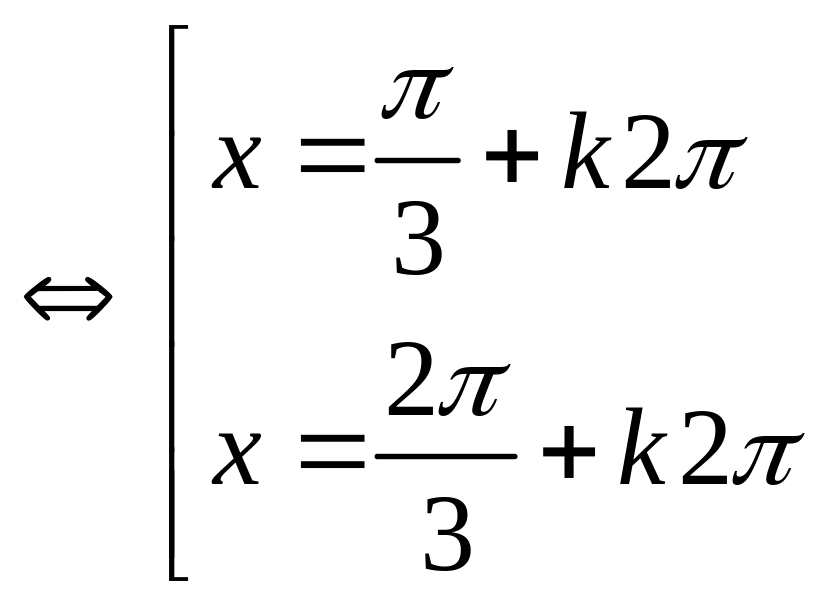
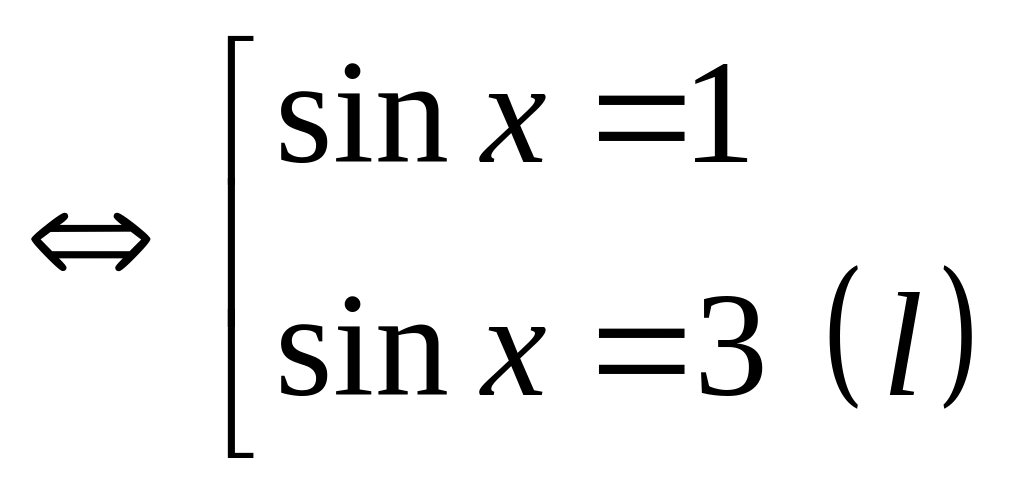
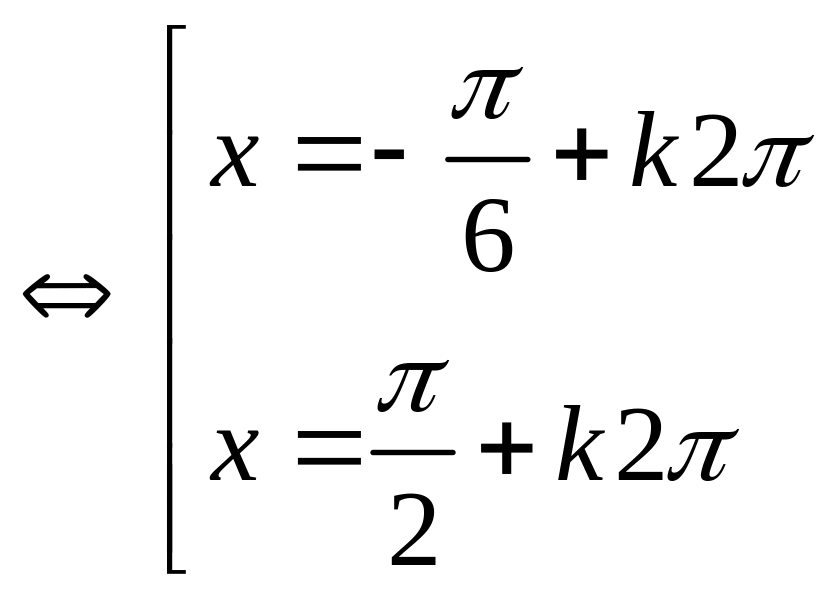
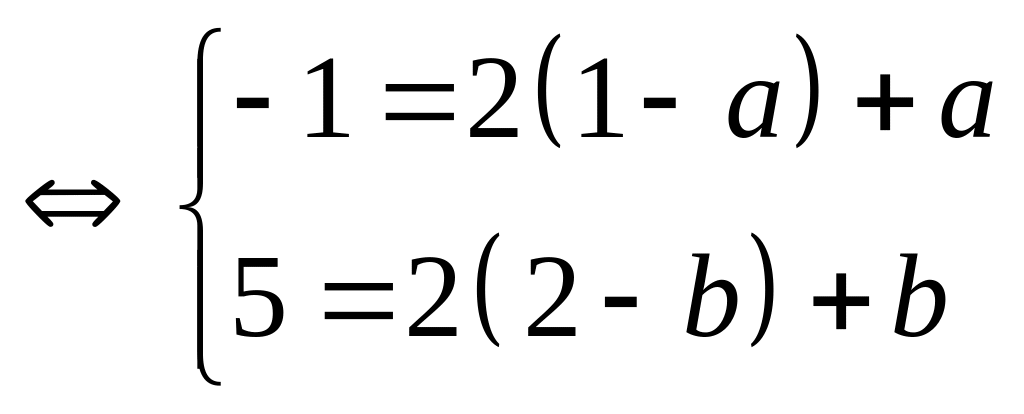
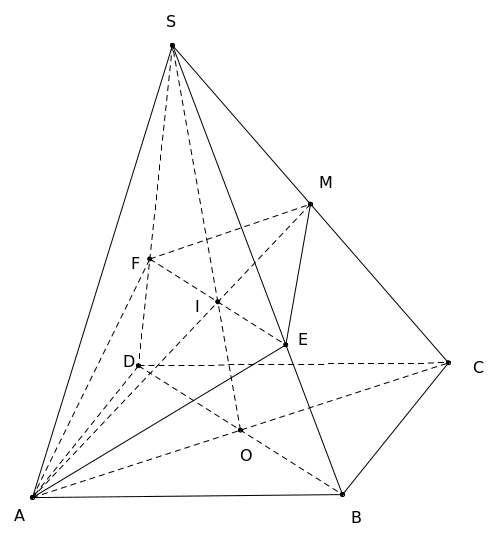
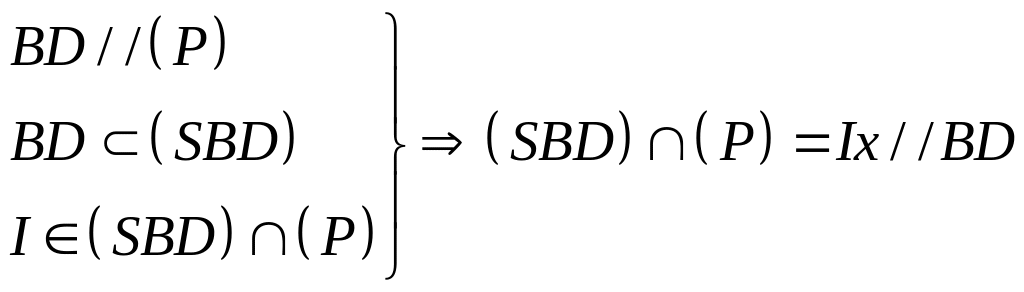
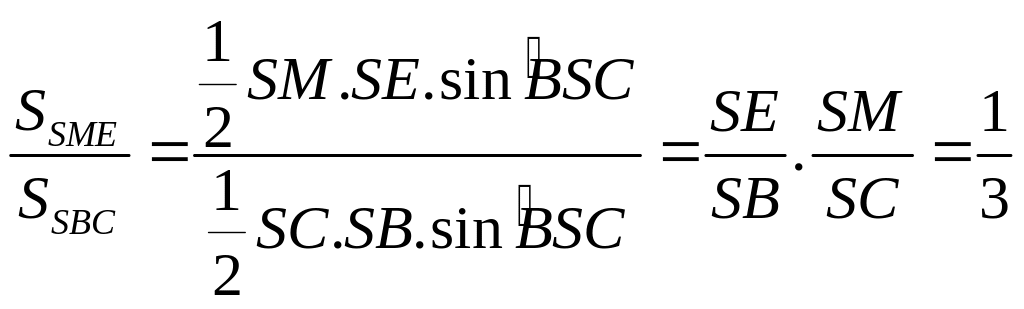
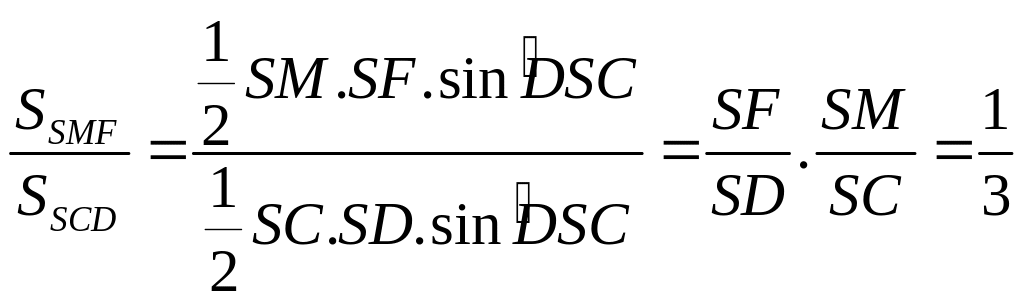

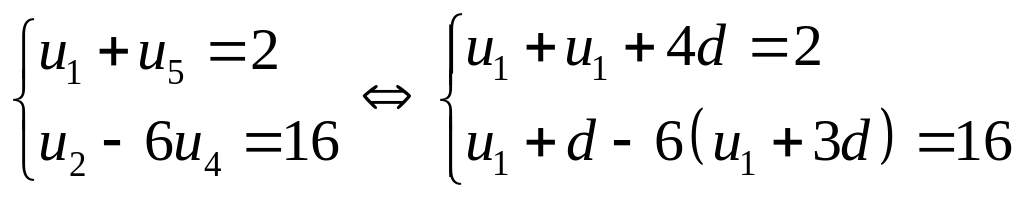
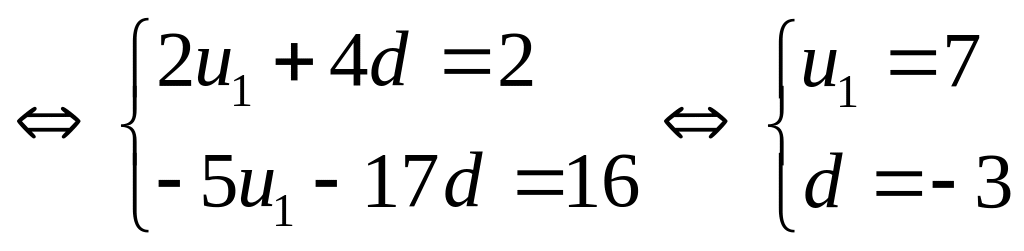
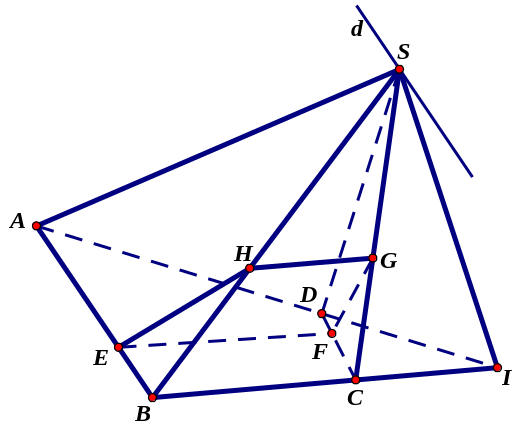
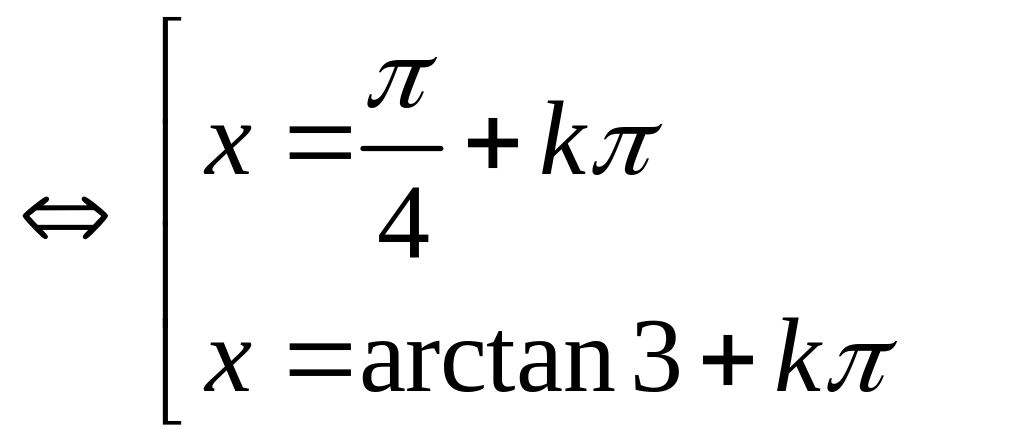 ,
(với mọi số nguyên k)
,
(với mọi số nguyên k)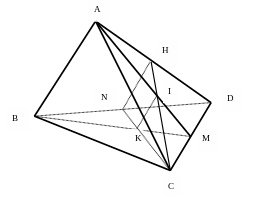
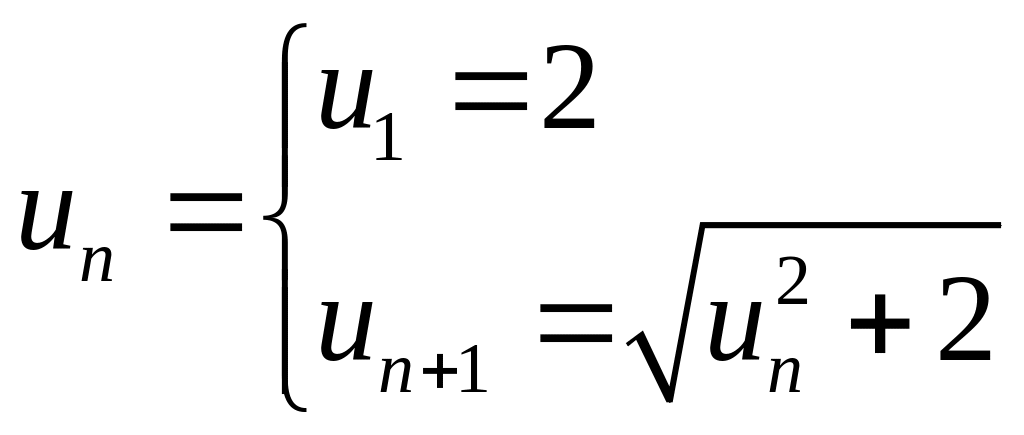
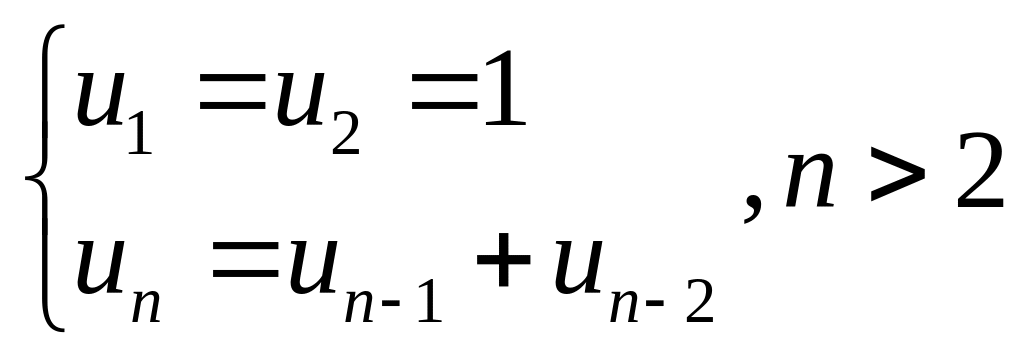 . Số hạng
. Số hạng
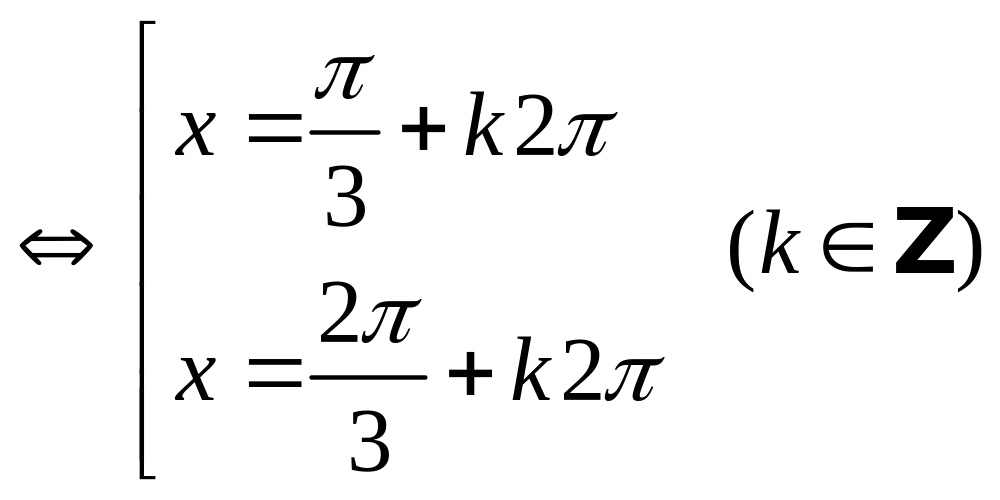
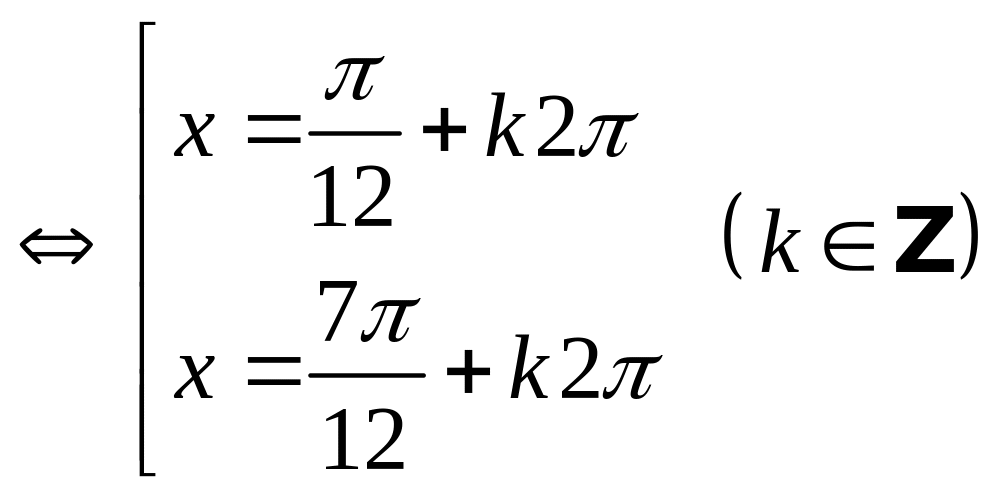
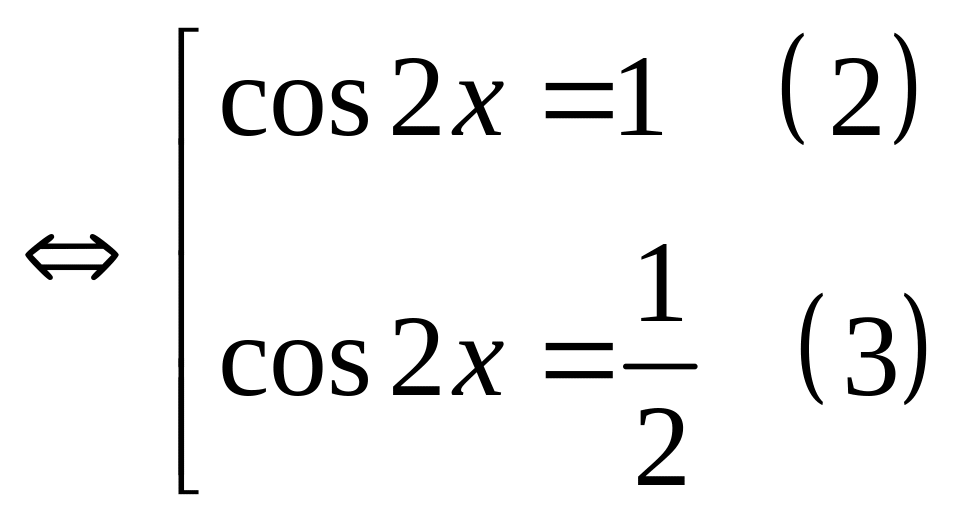
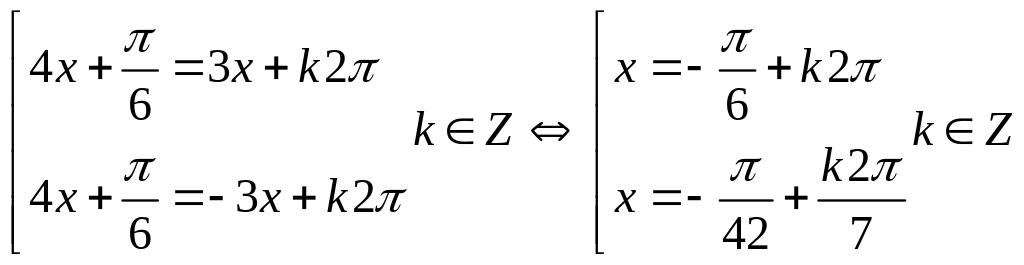
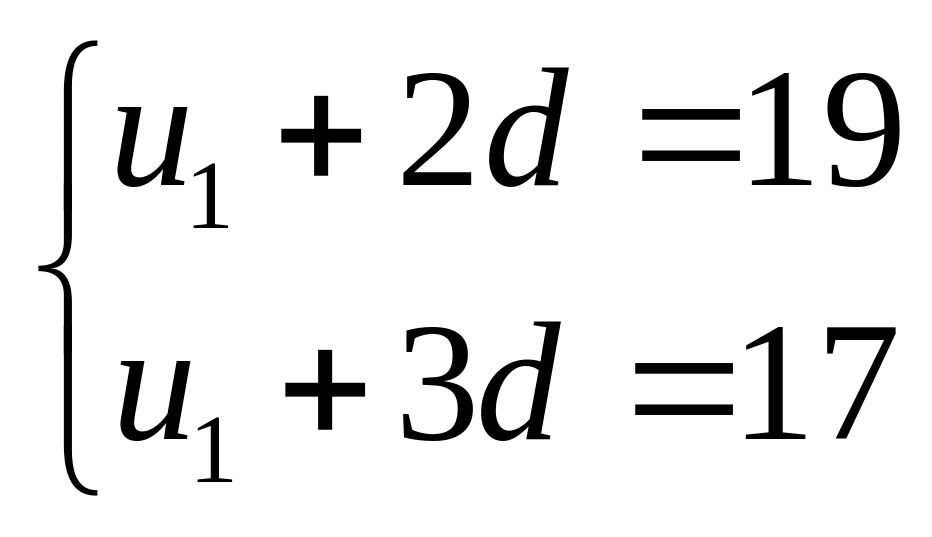
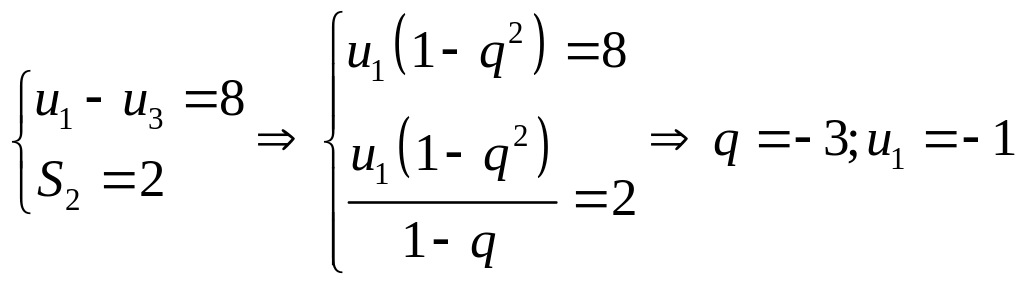
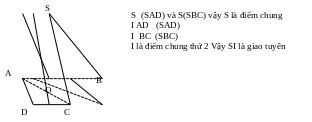

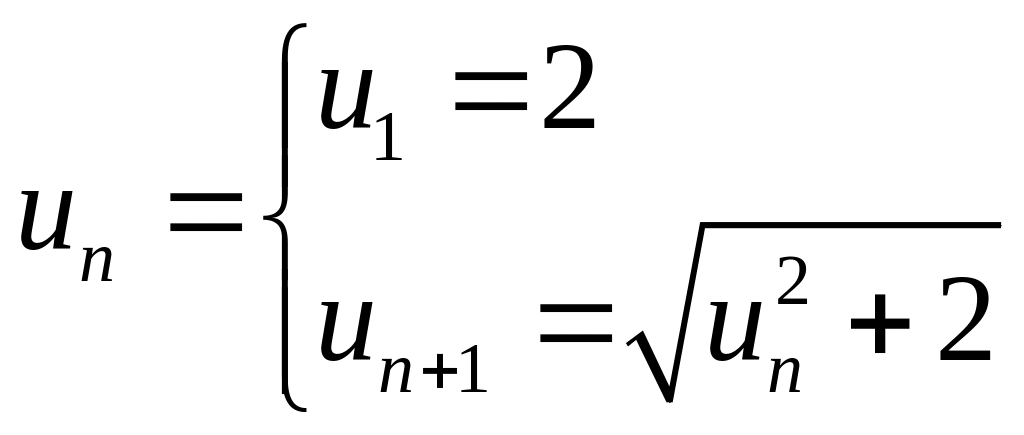
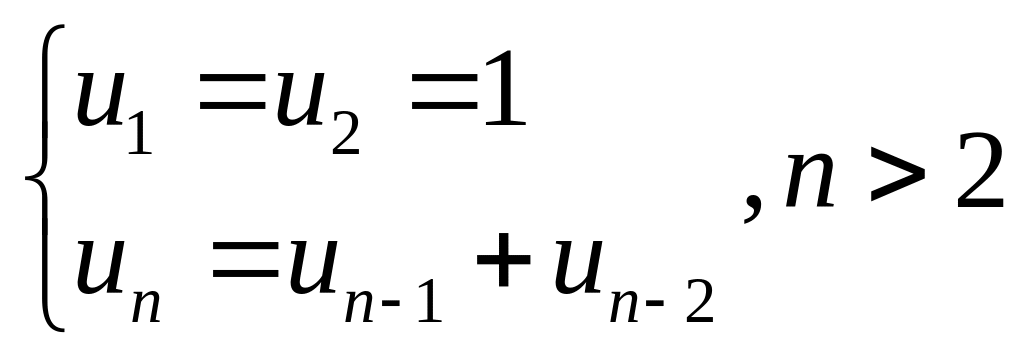 . Số hạng
. Số hạng
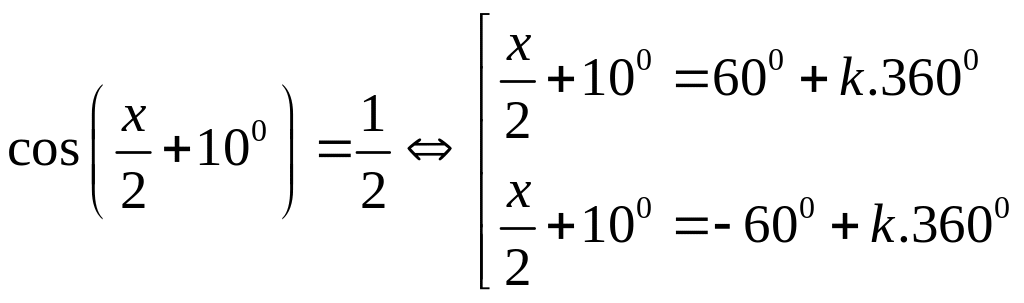
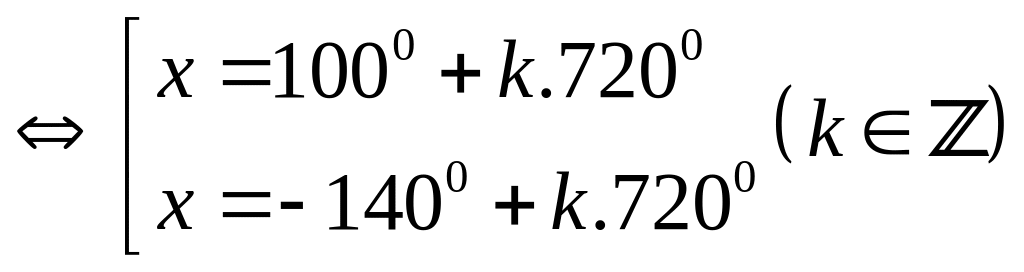
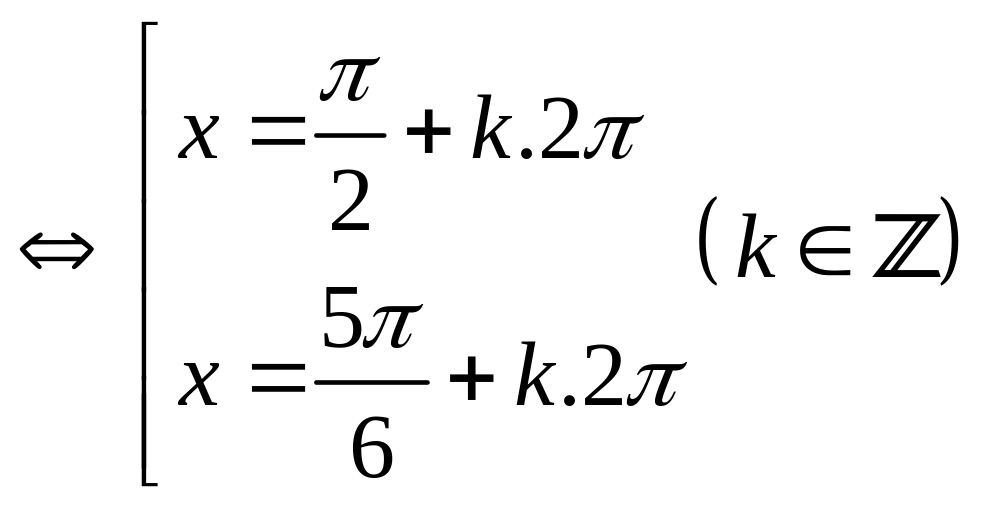
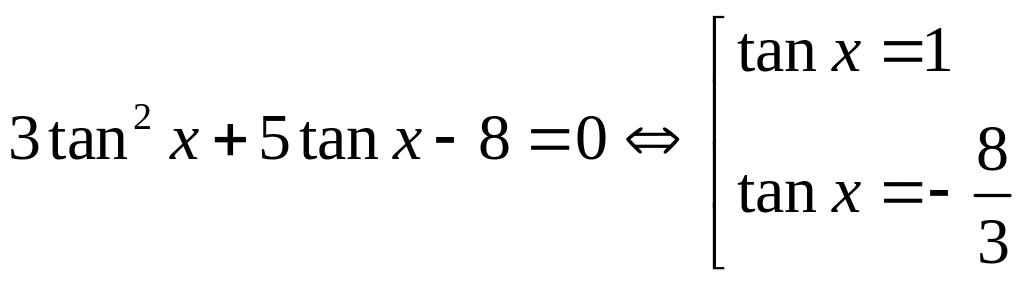
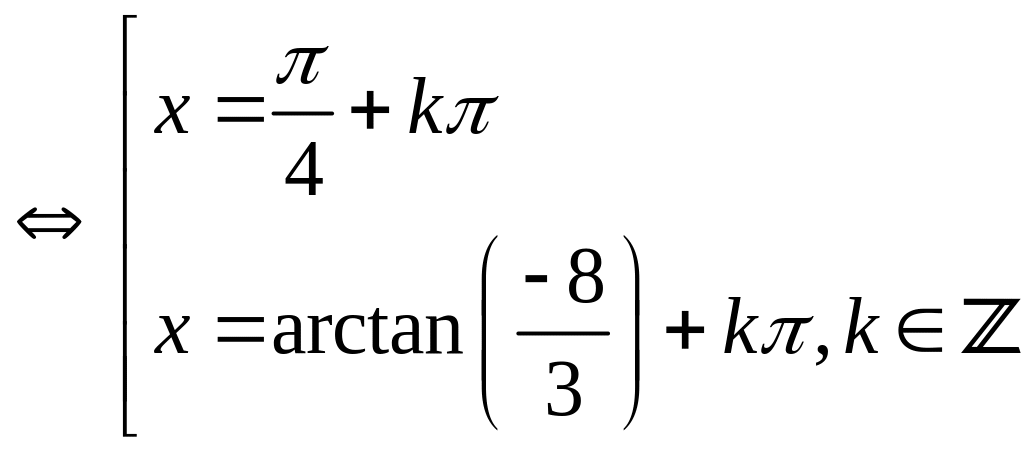
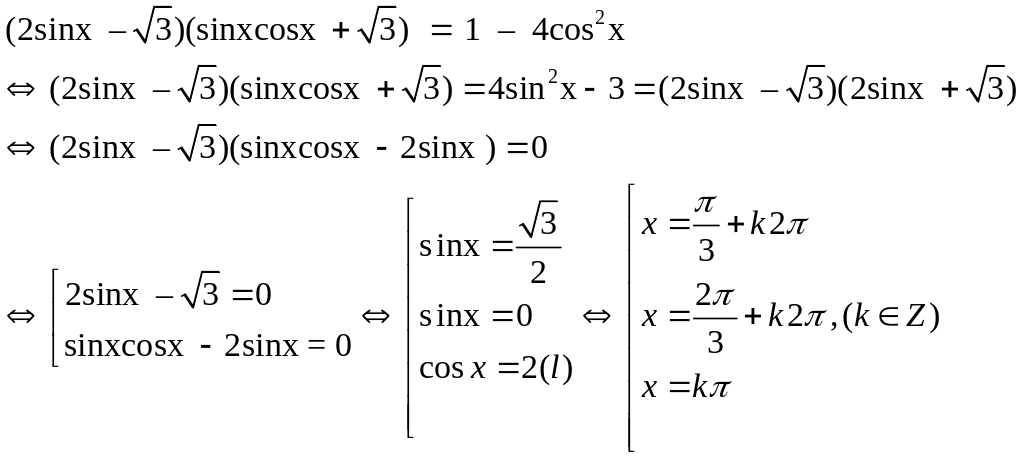
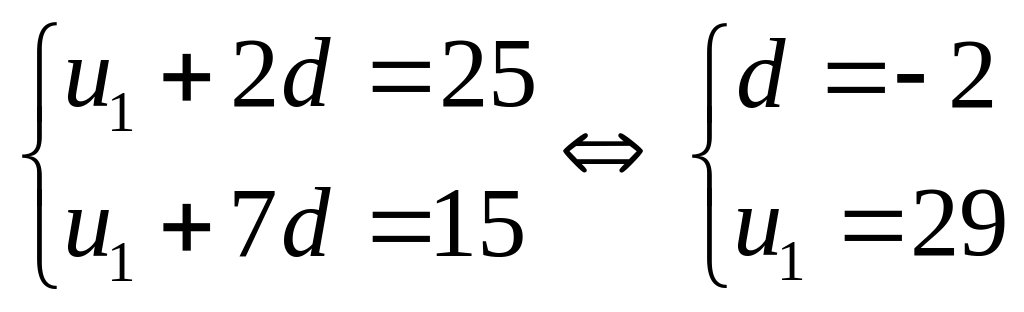 .
.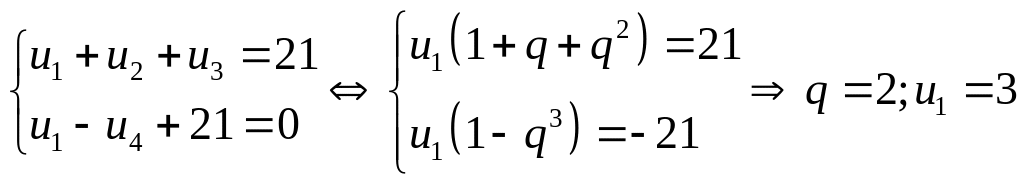
 *
*