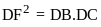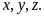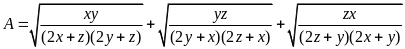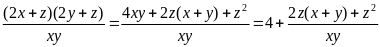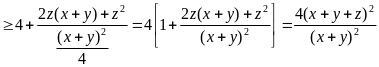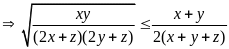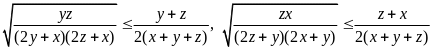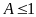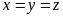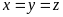Đề Thi Tuyển Sinh Lớp 10 Môn Toán Sở GD Quảng Nam 2019-2020 Có Đáp Án – Toán 9
Đề Thi Tuyển Sinh Lớp 10 Môn Toán Sở GD Quảng Nam 2019-2020 Có Đáp Án – Toán 9 được Trang Tài Liệu sưu tầm với các thông tin mới nhất hiện nay. Đề thi này sẽ giúp các em học sinh ôn tập, củng cố kiến thức, rèn luyện kĩ năng làm bài. Cũng như hỗ trợ thầy cô trong quá trình giảng dạy. Hy vọng những tài liệu này sẽ giúp các em trong quá trình ôn luyện và đạt kết quả cao trong bài thi sắp tới.
Trong hành trình tìm kiếm kiến thức và chuẩn bị cho kỳ thi tuyển sinh lớp 10, môn Toán luôn đóng vai trò quan trọng. Và hôm nay, chúng ta sẽ khám phá một tài liệu hữu ích – Đề Thi Tuyển Sinh Lớp 10 Môn Toán Sở GD Quảng Nam 2019-2020 Có Đáp Án. Đây là một nguồn tài liệu đáng giá để chúng ta rèn luyện và nắm vững kiến thức Toán học.
Đề thi này là một bài kiểm tra thực tế, được tổ chức bởi Sở Giáo dục Quảng Nam. Nó mang đến cho chúng ta một cái nhìn sâu sắc về cấu trúc đề thi, dạng bài và yêu cầu của kỳ thi tuyển sinh. Đáp án đi kèm giúp chúng ta tự đánh giá kỹ năng và hiểu rõ cách giải các bài tập. Chúng ta có cơ hội kiểm tra và sửa chữa những sai sót, củng cố kiến thức và chuẩn bị tốt hơn cho kỳ thi sắp tới.
Bộ Đề Thi Tuyển Sinh Lớp 10 Môn Toán Sở GD Quảng Nam 2019-2020 Có Đáp Án là một công cụ hữu ích để chúng ta nắm vững kiến thức và rèn luyện kỹ năng giải quyết các bài toán Toán học. Hãy cùng nhau tận dụng tài liệu này để chuẩn bị một cách tốt nhất cho kỳ thi tuyển sinh lớp 10 và chinh phục môn Toán một cách tự tin.
Bộ đề thi lớp 9 tham khảo
Dưới đây là bản đọc trực tuyến giúp thầy cô và các em học sinh có thể nghiên cứu Online hoặc bạn có thể tải miễn phí với phiên bản word để dễ dàng in ấn cũng như học tập Offline
SỞ GIÁO DỤC VÀ ĐÀO TẠO
|
KỲ THI TUYỂN SINH LỚP 10 THPT CHUYÊN
|
|
(Đề có 01 trang) |
Môn thi: TOÁN (chuyên Tin) Thời gian: 150 phút (không kể thời gian giao đề) Khóa thi ngày: 10 - 12/6/2019 |
Câu 1 (1,5 điểm).
Cho
biểu thức
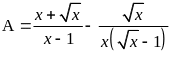 với
với
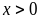 và
và
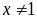 .
.
Rút
gọn biểu thức
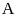 và tìm
và tìm
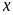 để
để
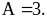
Câu 2 (1,0 điểm).
Tìm
tất cả các cặp số tự nhiên
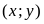 thỏa mãn
thỏa mãn
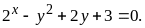
Câu 3 (2,0 điểm).
a)
Giải phương trình
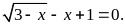
b)
Giải hệ phương trình
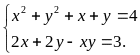
Câu 4 (1,0 điểm).
Cho
parabol
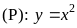 và đường thẳng
và đường thẳng
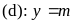 (
(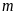 là
tham số). Tìm
là
tham số). Tìm
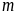 để
để
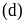 cắt
cắt
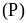 tại hai điểm phân biệt A, B
sao cho tam giác OAB đều (với O là gốc tọa độ).
tại hai điểm phân biệt A, B
sao cho tam giác OAB đều (với O là gốc tọa độ).
Câu 5 (3,5 điểm).
Cho
tam giác ABC (AB < AC) nội tiếp đường tròn (O) đường
kính BC, tiếp tuyến của đường tròn (O) tại A cắt
đường thẳng BC tại D. Vẽ dây cung AE của đường tròn
(O) vuông góc với BC. Gọi H là giao điểm của AE và BC, K
là hình chiếu vuông góc của A lên CE. Tia
phân giác của
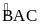 cắt BC tại F.
cắt BC tại F.
a) Chứng minh AB.HC = AC.HA.
b)
Chứng minh
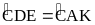 .
.
c)
Chứng minh
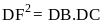 .
.
Câu 6 (1,0 điểm).
Cho
ba số thực dương
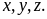 Tìm
giá trị lớn nhất của biểu thức
Tìm
giá trị lớn nhất của biểu thức
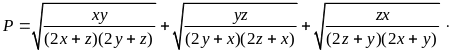
--------------- HẾT ---------------
Họ và tên thí sinh: .................................................................. Số báo danh: ...........................
SỞ GIÁO DỤC VÀ ĐÀO TẠO
|
KỲ THI TUYỂN SINH LỚP 10 THPT CHUYÊN
|
|
|
HƯỚNG DẪN CHẤM MÔN: TOÁN (Chuyên Tin) |
(Bản hướng dẫn này gồm 04 trang)
Câu |
Nội dung |
Điểm |
Câu 1 (1,5) |
Cho biểu thức
|
1,5 |
|
0,5 |
|
|
0,5 |
|
|
0,25 |
|
- Đối chiếu điều kiện suy ra
|
0,25 |
Câu |
Nội dung |
Điểm |
Câu 2 (1,0) |
Tìm tất cả các cặp số tự nhiên
|
1,0 |
|
0,25 |
|
*
|
0,25 |
|
Suy ra:
|
0,25 |
|
Khi đó
Vậy
|
0,25 |
Câu |
Nội dung |
Điểm |
Câu 3 (2,0) |
a) Giải phương trình
|
1,0 |
(Nếu học
sinh chỉ ghi được điều
|
0,25 |
|
|
0,25 |
|
|
0,25 |
|
Vậy phương trình đã cho có một
nghiệm
|
0,25 |
|
b) Giải hệ phương trình
|
1,0 |
|
|
0,25 |
|
Đặt
|
0,25 |
|
|
0,25 |
|
|
0,25 |
Câu |
Nội dung |
Điểm |
Câu 4 (1,0) |
Cho parabol
|
1,0 |
+ Phương trình
hoành độ giao điểm của (P) và (d) là: + Để (d) cắt (P) tại hai điểm phân
biệt thì
|
0,25 |
|
Với điều kiện trên, ta có: |
0,25 |
|
Gọi H là trung điểm của AB. Tam giác OAB cân tại O, do đó tam giác
OAB đều khi: |
0,25 |
|
Vậy
|
0,25 |
Câu |
Nội dung |
Điểm |
Câu 5 (3,5) |
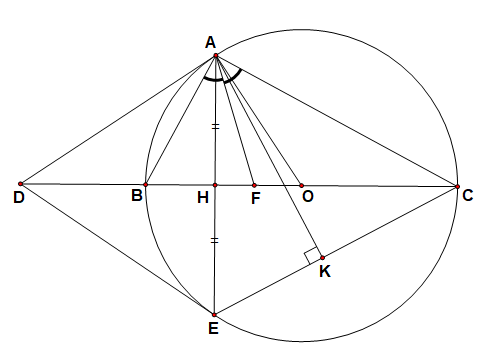
Cho tam giác ABC (AB < AC) nội tiếp
đường tròn (O) đường kính BC, tiếp tuyến của đường
tròn (O) tại A cắt đường thẳng BC tại D. Vẽ dây
cung AE của đường tròn (O) vuông góc với BC. Gọi H là
giao điểm của AE và BC, K là hình chiếu vuông góc của
A lên CE. Tia phân
giác của
a) Chứng minh AB.HC = AC.HA. b)
Chứng minh
c) Chứng minh
|
|
Hình vẽ phục câu b: 0,25 Hình vẽ phục cả hai câu b và c: 0,25 |
0,5 |
|
a) Chứng minh AB.HC = AC.HA. |
1,0 |
|
Xét hai tam giác
|
0,25 |
|
|
0,25 |
|
Do đó
|
0,25 |
|
|
0,25 |
|
b) Chứng minh
|
1,0 |
|
|
0,5 |
|
+ Lập luận được tam giác ADE cân tại D nên
|
0,25 |
|
Suy ra
|
0,25 |
|
c) Chứng minh
|
1,0 |
|
|
0,25 |
|
Suy ra:
|
0,25 |
|
+ Chứng minh được hai tam giác
|
0,25 |
|
Suy ra
|
0,25 |
Câu |
Nội dung |
Điểm |
Câu 6 (1,0) |
Cho ba số thực dương
|
1,0 |
|
0,25 |
|
|
0,25 |
|
|
0,25 |
|
Tương tự:
Suy
ra
Vậy giá trị lớn nhất
của A
bằng 1 khi
|
0,25 |
--------------- HẾT ---------------
* Lưu ý: Nếu thí sinh làm bài không theo cách nêu trong đáp án nhưng đúng thì vẫn cho đủ số điểm từng phần như hướng dẫn quy định.
Ngoài Đề Thi Tuyển Sinh Lớp 10 Môn Toán Sở GD Quảng Nam 2019-2020 Có Đáp Án – Toán 9 thì các đề thi trong chương trình lớp 9 sẽ được cập nhật liên tục và nhanh nhất có thể sau khi kỳ thi diễn ra trên Danh mục Kho Đề Thi nhằm giúp các bạn đọc thuận tiện trong việc tra cứu và đối chiếu đáp án. Quý thầy cô và các bạn đọc có thể chia sẻ thêm những tài liệu học tập hữu ích đến địa chỉ email của chúng tôi, nhằm xây dựng nên kho đề thi phong phú, đa dạng cho các em học sinh tham khảo và rèn luyện.
Cuối cùng, chúng ta đã khám phá Đề Thi Tuyển Sinh Lớp 10 Môn Toán Sở GD Quảng Nam 2019-2020 Có Đáp Án – một tài liệu vô cùng quý giá trong quá trình chuẩn bị cho kỳ thi tuyển sinh lớp 10. Đề thi này không chỉ giúp chúng ta làm quen với cấu trúc và yêu cầu của kỳ thi, mà còn là một cẩm nang hữu ích để nắm vững kiến thức và kỹ năng Toán học.
Việc có đáp án đi kèm là một lợi thế lớn. Chúng ta có thể tự đánh giá và kiểm tra lại kết quả của mình sau khi làm bài. Điều này giúp chúng ta nhận ra những lỗi sai và củng cố kiến thức một cách hiệu quả. Chúng ta có thể tìm hiểu cách giải các bài toán, áp dụng các phương pháp và quy tắc Toán học một cách chính xác và linh hoạt.
Bộ Đề Thi Tuyển Sinh Lớp 10 Môn Toán Sở GD Quảng Nam 2019-2020 Có Đáp Án giúp chúng ta tìm hiểu và nắm vững các dạng bài tập, củng cố kiến thức và rèn luyện kỹ năng làm bài trong kỳ thi tuyển sinh. Đồng thời, nó cũng là một công cụ hữu ích để đo đạc sự chuẩn bị và khả năng của chúng ta trước kỳ thi quan trọng này.
Hãy sử dụng tài liệu này một cách thông minh và cố gắng hết mình trong quá trình ôn tập. Với sự nỗ lực và sự tự tin, chúng ta sẽ vượt qua mọi thử thách và đạt được kết quả tốt trong kỳ thi tuyển sinh lớp 10. Hãy tin tưởng vào khả năng của bản thân và không ngừng rèn luyện để vươn tới thành công trong môn Toán học.
Xem thêm







 QUẢNG
NAM
QUẢNG
NAM NĂM
HỌC 2019
- 2020
NĂM
HỌC 2019
- 2020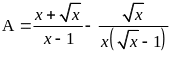 ,
với
,
với
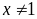 .
Rút gọn biểu thức
.
Rút gọn biểu thức
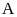 và tìm
và tìm
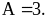
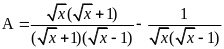
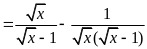
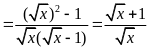
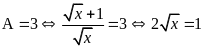 .
.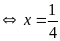
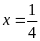 là giá trị cần tìm.
là giá trị cần tìm.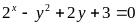
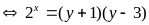 (1)
(1)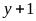 và
và
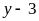 là hai số cùng chẵn, cùng lẻ và
là hai số cùng chẵn, cùng lẻ và
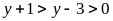 .
Do đó từ (1) ta có:
.
Do đó từ (1) ta có: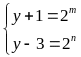 ( với
( với
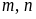 là hai số tự nhiên và
là hai số tự nhiên và
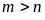 ).
).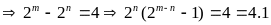 (2)
(2)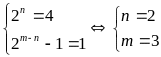 .
.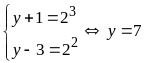
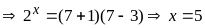
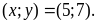
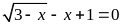
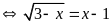
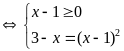
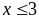
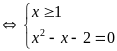
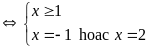
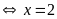
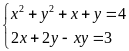
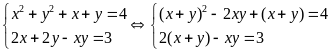
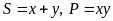
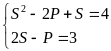
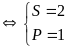
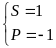
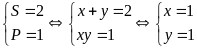
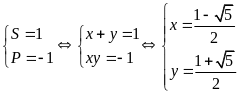
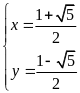
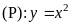
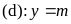
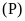
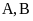 sao cho tam giác
sao cho tam giác
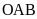 đều (với
đều (với
 là
gốc tọa độ).
là
gốc tọa độ).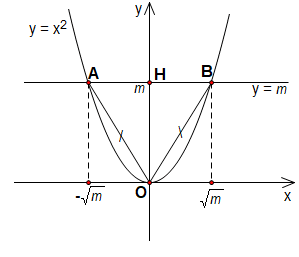
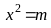
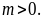
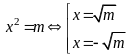
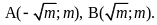
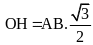
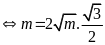
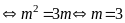
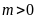
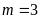
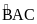 cắt BC tại F.
cắt BC tại F.
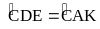 .
.
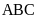 và
và
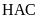 có:
có:
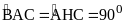 ,
,
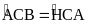 .
Suy ra hai tam giác
.
Suy ra hai tam giác
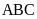 và
và
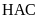 đồng
dạng.
đồng
dạng.
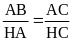
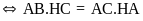 .
.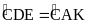
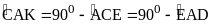 (đúng mỗi ý được 0,25)
(đúng mỗi ý được 0,25)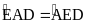
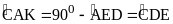
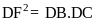 .
.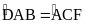 (cùng chắn cung
(cùng chắn cung
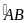 ),
),
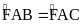 (vì
(vì
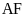 là phân giác của
là phân giác của
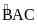 )
)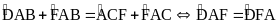 .
Suy ra tam giác ADF cân tại D.
.
Suy ra tam giác ADF cân tại D.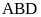 và
và
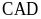 đồng
dạng.
đồng
dạng.
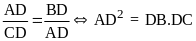 .
Hơn nữa
.
Hơn nữa
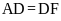 nên
nên