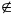Bộ đề ôn tập Toán 8 giữa HK1 Năm 2022-2023 có đáp án
Bộ Đề Ôn Tập Toán 8 Giữa HK1 Năm 2022-2023 Có Đáp Án Và Ma Trận Đặc Tả – Toán 8 được Trang Tài Liệu sưu tầm với các thông tin mới nhất hiện nay. Đề thi này sẽ giúp các em học sinh ôn tập, củng cố kiến thức, rèn luyện kĩ năng làm bài. Cũng như hỗ trợ thầy cô trong quá trình giảng dạy. Hy vọng những tài liệu này sẽ giúp các em trong quá trình ôn luyện và đạt kết quả cao trong bài thi sắp tới.
XEM THÊM
Bộ đề ôn tập Toán lớp 8 giữa học kỳ 1 năm 2022-2023 đã sẵn sàng để các bạn thử sức và củng cố kiến thức. Bộ đề này được thiết kế đặc biệt để giúp các bạn học sinh ôn tập và nắm vững các khái niệm và kỹ năng toán học đã học trong học kỳ.
Bộ đề bao gồm một loạt các câu hỏi và bài tập đa dạng, tương ứng với các chủ đề như phép tính, đại số, hình học và xác suất. Mỗi câu hỏi được lựa chọn kỹ càng để kiểm tra sự hiểu biết và ứng dụng của bạn trong từng lĩnh vực toán học.
Đáp án chi tiết được cung cấp kèm theo mỗi bài tập, giúp bạn tự kiểm tra và đánh giá kết quả của mình. Bằng cách xem lại quy trình giải quyết và hiểu rõ từng bước, bạn có thể nâng cao khả năng toán học của mình và tự tin hơn khi đối mặt với các bài tập tương tự trong tương lai.
Với bộ đề ôn tập Toán lớp 8 giữa học kỳ 1 năm 2022-2023, chúng ta sẽ có cơ hội rèn luyện kỹ năng toán học và chuẩn bị tốt cho kỳ thi sắp tới. Hãy bắt đầu và cùng nhau chinh phục thách thức toán học!
Dưới đây là bản đọc trực tuyến giúp thầy cô và các em học sinh có thể nghiên cứu Online hoặc bạn có thể tải miễn phí với phiên bản word để dễ dàng in ấn cũng như học tập Offline
ĐỀ ÔN TẬP GIỮA KỲ I NĂM HỌC 2022 – 2023 (ĐỀ 1)
MÔN: TOÁN-LỚP 8
I/ TRẮC NGHIỆM:(5 điểm) Chọn đáp án đúng trong mỗi câu sau rồi ghi vào bài làm.
Câu 1: Kết quả của phép nhân 2x( x2 – 1) là
A. x3 – 2x B. 2x3 – 1 C. 2x3 – 2x D. x3 – 2
Câu 2: Tích (x-2)(x-5) bằng
A. x2 + 7x + 10 B. x2 - 7x+10 C. x2 +10 D. x2 - 3x+10
Câu 3: Đa thức x2 + 4y2 – 4xy được phân tích thành
A. (x - 2y)(x+2y) B. - (x-2y)2 C. (x - 2y)2 D. (x+2y)2
Câu 4: Biểu thức rút gọn của (2x+y)(4x2-2xy+y2) là :
A. 8x3-y3 B. 8x3+y3 C. x3- 8y3 D. 2x3-y3
Câu 5: Kết quả được viết dưới dạng tích của đa thức 8x3 + 12x2y + 6xy2 + y3 là
A. 2x3 + y3 B. 2x + y3 C. (2x + y)3 D. (2x – y)3
Câu 6: Cho đẳng thức (3x + 2 )2 = 9x2 ...+ 4. Biểu thức thích hợp điền vào chỗ … là
A. -6x B. +6x C. +12x D. -12x
Câu 7: Đa thức: 4x(2y - z) +7y(2y - z) được phân tích thành nhân tử là
A. (2y-z)(4x-7y) B. (2y-z)(4x+7y)
C. (2y+z)(4x+7y) D. (2y+z)(4x-7y)
Câu 8: Giá trị của x thoả mãn 2x(x+3) +2(x+3) =0 là
A. -3 hoặc 1 B. 3 hoặc 1 C. 3 hoặc -1 D. -3 hoặc -1
Câu 9: Kết quả phân tích đa thức (x2 +2x)2 - 1 thành nhân tử là
A. (x2 + 2x - 1)2 . B. (x2 + 2x - 1)(x - 1)2. .
C. (x2 - 2x - 1)(x + 1)2 . D. (x2 + 2x - 1)(x + 1)2 .
Câu 10:
Cho tứ giác ABCD, có
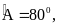
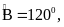
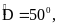 Số đo
Số đo
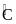 là:
là:
A.
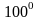 .
B.
.
B.
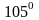 .
C.
.
C.
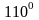 .
D.
.
D.
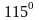 .
.
Câu 11: Hình bình hành BCDE là hình chữ nhật nếu
A. BE=CD. B. BC=EB. C. BE=BC. D. BD=CE.
Câu 12: Hình thang ABCD (AB // CD) là hình thang cân khi
A . AC=BD. B . AB=AD. C . AB=CD. D . AD=BC.
Câu 13: Hình không có tâm đối xứng là
A . hình chữ nhật. B . hình tròn.
C . hình bình hành. D . hình thang cân.
Câu 14: Một tam giác đều có chu vi bằng 37,8 cm. Độ dài đường trung bình của tam giác đó là
A . 37,5cm B . 6,3cm C . 6,25cm D . 12,5cm
Câu 15: Một hình thang có đáy thứ nhất dài 6cm, đường trung bình dài 8cm. Độ dài đáy thứ hai của hình thang đó là
A
. 10cm B . 5cm C .
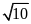 cm
D .
cm
D .
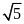 cm
cm
II/ TỰ LUẬN: (5 điểm)
Bài 1: a) (0.5 đ) Viết dưới dạng tích rồi tính giá trị biểu thức
25a2 + 4b2 + 20ab tại a =1, b = -2.
b) (0.75 đ) Rút gọn biểu thức A = (x – 2)(x2 + 2x + 4) – (x3 + 5).
Bài
2: (0.75
đ)
Phân
tích đa thức thành nhân tử
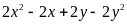
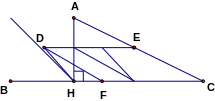
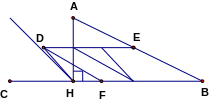
Bài 3: (2 đ) Cho tam giác ABC (AB > AC), đường cao AH. Gọi E, D, F lần lượt là trung điểm của các cạnh AB, AC, BC.
a) Chứng minh rằng tứ giác CDEF là hình bình hành.
b) Chứng minh tứ giác EFHD là hình thang cân.
Bài 4: (1 đ) Tìm giá trị nhỏ nhất của biểu thức A = x2 - 2xy + 2y2 - 4y + 5
-------------------------------HẾT-----------------------------
ĐÁP ÁN VÀ BIỂU ĐIỂM
I - TRẮC NGHIỆM : (5 điểm)
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
C |
B |
C |
B |
C |
C |
B |
D |
D |
C |
D |
A |
D |
B |
B |
( Mỗi câu trả lời đúng được 0,33 điểm ).
II – TỰ LUẬN: (5 điểm)
Bài |
ĐÁP ÁN |
Điểm |
1a (0.5 đ) |
25a2 + 4b2 + 20ab = (5a+2b)2 |
0,25 |
Thay a=1, b= -2 vào ta được giá trị bằng 1 |
0,25 |
|
1b (0.75 đ) |
A= (x – 2)(x2 + 2x + 4) – (x3 + 5) = x3 – 8 – x3 – 5 |
0,5 |
= -13 |
0,25 |
|
2 (0.75 đ) |
|
0,25 |
= 2[(x+y)(x – y) – (x – y)] |
0,25 |
|
= 2(x – y)(x + y – 1) |
0,25 |
|
3 (2 đ) |
|
|
Hình vẽ
|
Hình vẽ phục vụ cho giải ít nhất 2 câu a bà b
|
0,5 |
a/
|
a) Chứng minh rằng tứ giác CDEF là hình bình hành. Vì DE là đường trung bình của tam giác ABC nên DE // BC và DE = BC :2 (1) Lại có F là trung điểm của BC nên BF = BC:2 (2) Từ (1) và (2) suy ra DE // CF và DE = CF Do đó tứ giác CDEF là hình bình hành. |
0,25 0,25 0,25 0,25 |
b/ |
b) Chứng minh tứ giác EFHD là hình thang cân. Vì DE //BC (chứng minh trên), nên tứ giác EFHD là hình thang (3) Lại có HE = AB:2 (đường trung tuyến ứng với cạnh huyền trong tam giác vuông AHB) (4) Mặt khác, có DF = AB:2 (vì DF là đường trung bình của tam giác ABC) (5) Từ (4) và (5) suy ra HE = DF (6) Từ (3) và (6) suy ra EFHD là hình thang cân
|
0,25
0,25 |
4 (1 đ)
|
Ta có : A = x2 - 2xy + y2 +y2 - 4y +4 + 1 = (x-y)2 + (y - 2)2 + 1 Do
(x-y)2
Nên
A= (x-y)2
+ (y - 2)2
+ 1 Dấu
''='' xảy ra
Vậy
GTNN của A là 1 |
0,25 0,25
0,25 0,25 |
ĐỀ ÔN TẬP GIỮA KỲ I NĂM HỌC 2022 – 2023 (ĐỀ 2)
MÔN: TOÁN-LỚP 8
I/ TRẮC NGHIỆM:(5 điểm) Chọn đáp án đúng trong mỗi câu sau rồi ghi vào bài làm.
Câu 1: Kết quả của phép nhân 3x( x2 + 1) là
A. 3x3 + 1. B. 3x3 + 3; C. 3x2 + 3x; D. 3x3 + 3x
Câu 2: Tích (x-2)(x+5) bằng
A. x2 + 3x - 10 B. x2 - 7x+10 C. x2 +10 D. x2 - 3x+10
Câu 3: Đa thức x2 + 9y2 – 6xy được phân tích thành
A. (x - 3y)(x+3y) B. - (x-3y)2 C. (x+3y)2 D. (x-3y)2
Câu 4: Biểu thức rút gọn của (x+2y)(x2-2xy+4y2) là :
A. x3-8y3 B. x3+8y3 C. x3+ 6y3 D. x3-2y3
Câu 5: Kết quả được viết dưới dạng tích của đa thức 8x3 - 12x2y + 6xy2 - y3 là
A. (2x3 + y)3 B. (2x + y3)3 C. (2x + y)3 D. (2x – y)3
Câu 6: Cho đẳng thức (3x - 2 )2 = 9x2 ...+ 4. Biểu thức thích hợp điền vào chỗ dấu … là
A. -6x B. +6x C. +12x D. -12x
Câu 7: Đa thức: 4x(2y - z) +7y(2y - z) được phân tích thành nhân tử là
A. (2y-z)(4x-7y) B. (2y-z)(4x+7y)
C. (2y+z)(4x+7y) D. (2y+z)(4x-7y)
Câu 8: Giá trị của x thoả mãn 2x(x+3) +2(x+3) =0 là
A. -3 hoặc 1 B. 3 hoặc 1 C. 3 hoặc -1 D. -3 hoặc -1
Câu 9: Kết quả phân tích đa thức 1 - (x2 - 2x)2 thành nhân tử là
A. (x2 - 2x +1)2 B. (1- x2 - 2x )(x - 1)2.
C. (x2 - 2x - 1)(x - 1)2 D. (x2 + 2x - 1)(x - 1)2
Câu 10:
Cho tứ giác ABCD, có
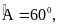
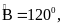
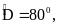 Số đo
Số đo
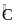 là:
là:
A.
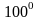 B.
B.
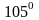 C.
C.
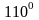 D.
D.
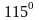
Câu 11: Hình bình hành ABCD là hình chữ nhật nếu
A. AB=CD B. AD=BC C. AC=BD D. AB=AD
Câu 12: Hình thang BCDE (BC // DE) là hình thang cân khi
A. BC=ED B. BD=CE C. BC=CD D . BE=CD
Câu 13: Hình có tâm đối xứng là
A. hình thang cân B. tam giác cân C. hình bình hành D. tam giác đều
Câu 14: Nếu một tam giác đều có độ dài đường trung bình bằng 6,25cm thì chu vi của tam giác đó bằng
A. 6,75cm B. 12,5cm C. 18,75cm D. 37,5cm
Câu 15: Một hình thang có đáy thứ nhất dài 8cm, đường trung bình dài 7cm. Độ dài đáy thứ hai của hình thang đó là
A.
6cm B. 12cm C.
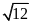 cm
D.
cm
D.
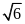 cm
cm
II/ TỰ LUẬN: (5 điểm)
Bài 1: a) (0.5 đ) Viết dưới dạng tích rồi tính giá trị biểu thức
9a2 + 16b2 + 24ab tại a = -1, b = 2.
b) (0.75 đ) Rút gọn biểu thức B = (x – 3)(x2 + 3x + 9) – (x3 – 5).
Bài
2: (0.75
đ)
Phân
tích đa thức thành nhân tử
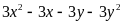
Bài 3: (2 đ) Cho tam giác ABC (AB < AC), đường cao AH. Gọi D, E, F lần lượt là trung điểm của các cạnh AB, AC, BC.
a) Chứng minh rằng tứ giác BDEF là hình bình hành.
b) Chứng minh tứ giác EFHD là hình thang cân.
Bài 4: (1 đ) Tìm giá trị nhỏ nhất của biểu thức A = y2 - 2xy + 2x2 – 4x + 7
-------------------------------HẾT-----------------------------
ĐÁP ÁN VÀ BIỂU ĐIỂM
I - TRẮC NGHIỆM : (5 điểm)
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
D |
A |
D |
B |
D |
D |
B |
D |
B |
A |
C |
B |
C |
D |
A |
( Mỗi câu trả lời đúng được 0,33 điểm ).
II – TỰ LUẬN: (5 điểm)
Bài |
ĐÁP ÁN |
Điểm |
1a (0.5 đ) |
9a2 + 16b2 + 24ab = (3a+4b)2 |
0,25 |
Thay a=-1, b= 2 vào ta được giá trị bằng 25 |
0,25 |
|
1b (0.75 đ) |
B = (x – 3)(x2 + 3x + 9) – (x3 – 5) = x3 – 27 – x3 + 5 |
0,5 |
= -22 |
0,25 |
|
2 (0.75 đ) |
|
0,25 |
= 3[(x+y)(x – y) – (x +y)] |
0,25 |
|
= 3(x + y)(x – y – 1) |
0,25 |
|
3 (2 đ) |
|
|
Hình vẽ
|
Hình vẽ phục vụ cho
giải ít nhất 2 câu a và b
|
0,5 |
a/ |
a) Chứng minh rằng tứ giác BDEF là hình bình hành. Vì D và E thứ tự là trung điểm của AB và AC nên DE // BC và DE = BC :2 (1) Lại có F là trung điểm của BC nên BF = BC:2 (2) Từ (1) và (2) suy ra DE // BF và DE = BF Do đó tứ giác BDEF là hình bình hành. |
0,25 0,25 0,25 0,25 |
b/
|
b) Chứng minh tứ giác EFHD là hình thang cân. Vì DE //BC (chứng minh trên), nên tứ giác EFHD là hình thang (3) Lại có HE = AC:2 (đường trung tuyến ứng với cạnh huyền trong tam giác vuông AHC) (4) Mặt khác, có DF = AC:2 (vì DF là đường trung bình của tam giác ABC) (5) Từ (4) và (5) suy ra HE = DF (6) Từ (3) và (6) suy ra EFHD là hình thang cân |
0,25
0,25
|
4 (1 đ) |
Ta có : A = y2 - 2xy + 2x2 – 4x + 7 = (y-x)2 + (x - 2)2 + 3 Do
(y-x)2
Nên
A= (y-x)2
+ (x - 2)2
+ 3 Dấu
''='' xãy ra
Vậy
GTNN của A là 3 |
0,25 0,25
0,25 0,25 |
ĐỀ ÔN TẬP GIỮA KỲ I NĂM HỌC 2022 – 2023 (ĐỀ 3)
MÔN: TOÁN-LỚP 8
I/ TRẮC NGHIỆM:(5 điểm) Chọn đáp án đúng trong mỗi câu sau rồi ghi vào bài làm.
Câu 1: Kết quả của phép nhân xy( x2 + x – 1) là
A. x3y + x2y + xy; B. x3y – x2y – xy; C. x3y – x2y + xy; D. x3y + x2y – xy
Câu 2: Tích (x-2)(x-5) bằng
A. x2 + 7x + 10 B. x2 - 7x+10 C. x2 +10 D. x2 - 3x+10
Câu 3: Đa thức x2 + 4y2 – 4xy được phân tích thành
A. (x - 2y)(x+2y) B. - (x-2y)2 C. (x - 2y)2 D. (x+2y)2
Câu 4: Biểu thức rút gọn của (2x+y)(4x2-2xy+y2) là :
A. 8x3-y3 B. 8x3+y3 C. x3- 8y3 D. 2x3-y3
Câu 5: Kết quả được viết dưới dạng tích của đa thức sau : 8x3 + 12x2y + 6xy2 + y3 là
A. (2x3 + y)3 B. (2x + y3)3 C. (2x + y)3 D. (2x – y)3
Câu 6: Biểu thức thích hợp điền vào chỗ dấu … để có đẳng thức
(3x + 2 )2 = 9x2 + ...+ 4 đúng là
A. -6x B. 6x C. 12x D. -12x
Câu 7: Đa thức: 4x(2y - z) +7y(2y - z) được phân tích thành nhân tử là
A. (2y-z)(4x-7y) B. (2y-z)(4x+7y) C. (2y+z)(4x+7y) D. (2y+z)(4x-7y)
Câu 8: Giá trị của x thoả mãn 2x(x+3) +2(x+3) =0 là
A. -3 hoặc 1 B. 3 hoặc 1 C. 3 hoặc -1 D. -3 hoặc -1
Câu 9: Đa thức 9x6 +24x3y2 +16y4 được phân tích thành nhân tử là
A. (3y3-2x2)2 B. (3x3-4y2)2 C. (3x3+4y2)2 D. -(3x3+4y2)2
Câu 10:
Cho tứ giác ABCD, có
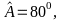
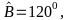
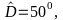 Số đo
Số đo
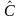 là:
là:
A.
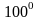 ,
B.
,
B.
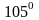 ,
C.
,
C.
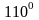 ,
D.
,
D.
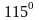
Câu 11: Hình bình hành BCDE là hình chữ nhật nếu
A. BE=CD B. BC=EB C. BE=BC D. BD=CE
Câu 12: Hình thang ABCD (AB // CD) là hình thang cân khi
A . AC=BD B . AB=AD C . AB=CD D . AD=BC
Câu 13: Trong các hình sau, hình không có tâm đối xứng là
A . Hình chữ nhật B . Hình tròn C . Hình bình hành D . Hình thang cân
Câu 14: Một tam giác đều có độ dài cạnh bằng 12,5 cm. Độ dài đường trung bình của tam giác đó là
A . 37,5cm B . 6,3cm C . 6,25cm D . 12,5cm
Câu 15: Một hình thang có đáy thứ nhất dài 6cm, đường trung bình dài 8cm. Độ dài đáy thứ hai của hình thang đó là
A
. 10cm B . 5cm C .
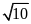 cm
D .
cm
D .
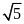 cm
cm
II/ TỰ LUẬN: (5 điểm)
Câu 16: (0.5 điểm) Rút gọn rồi tính giá trị biểu thức 25a2 + 4b2 + 20ab tại a =1, b = -2.
Câu 17: (0.75 điểm) Rút gọn biểu thức A = x(x - 2) + (3 - x)(3 + x) .
Câu 18: (0.75 điểm) Phân tích đa thức thành nhân tử x2 – 10x – 9y2 + 25 .
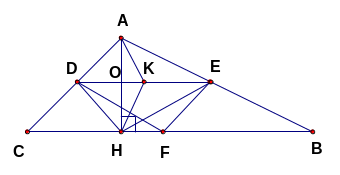
Câu 19: (3 điểm) Cho tam giác ABC (AB > AC), đường cao AH. Gọi E, D, F lần lượt là trung điểm của các cạnh AB, AC, BC.
a) Chứng minh rằng tứ giác CDEF là hình bình hành.
b) Chứng minh tứ giác EFHD là hình thang cân.
c) Gọi K là trung điểm của DE. Nêu cách xác định đỉnh A của tam giác ABC để tứ giác ADHK là hình thoi.
ĐÁP ÁN VÀ BIỂU ĐIỂM
I - TRẮC NGHIỆM : (5 điểm)
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
A |
B |
C |
B |
C |
C |
B |
D |
B |
C |
D |
A |
D |
C |
B |
( Mỗi câu trả lời đúng được 0,33 điểm ).
II – TỰ LUẬN: (5 điểm)
Câu |
ĐÁP ÁN |
Điểm |
16 (0.5 đ) |
25a2 + 4b2 + 20ab = (5a+2b)2 |
0,25 |
Thay a=1, b= -2 vào ta được giá trị bằng 1 |
0,25 |
|
17 (0.75 đ) |
A = x(x - 2) + (3 - x)(3 + x) = x2- 2x + 32 – x2 |
0,5 |
= -2x+ 9 |
0,25 |
|
18 (0.75 đ) |
x2 – 10x – 9y2 + 25 = x2 – 10x + 25 – 9y2 = (x-5)2 – (3y)2 |
0,5 |
=(x- 5- 3y)(x- 5+3y) |
0,25 |
|
19 (3 đ) |
|
|
|
|
|
Hình vẽ
|
Hình vẽ phục vụ cho giải ít nhất 2 câu a bà b
|
0,5 |
a/
|
a) Chứng minh rằng tứ giác CDEF là hình bình hành. Vì DE là đường trung bình của tam giác ABC nên DE // BC và DE = BC :2 (1) Lại có F là trung điểm của BC nên BF = BC:2 (2) Từ (1) và (2) suy ra DE // CF và DE = CF Do đó tứ giác CDEF là hình bình hành. |
0,25 0,25 0,25 0,25 |
b/ |
b) Chứng minh tứ giác EFHD là hình thang cân. Vì DE //BC (chứng minh trên), nên tứ giác EFHD là hình thang (3) Lại có HE = AB:2 (đường trung tuyến ứng với cạnh huyền trong tam giác vuông AHB) (4) Mặt khác, có DF = AB:2 (vì DF là đường trung bình của tam giác ABC) (5) Từ (4) và (5) suy ra HE = DF (6) Từ (3) và (6) suy ra EFHD là hình thang cân |
0,25
0,25 |
c/ |
c) Gọi O là giao điểm của AH và DK.
Tứ giác ADHK là hình thoi
|
0,25 0,25 0,25 0,25 |
ĐỀ ÔN TẬP GIỮA KỲ I NĂM HỌC 2022 – 2023 (ĐỀ 4)
MÔN: TOÁN-LỚP 8
I/ TRẮC NGHIỆM:(5 điểm) Chọn đáp án đúng trong mỗi câu sau rồi ghi vào bài làm.
Câu 1: Kết quả của phép nhân xy( x2 - x + 1) là
A. x3y + x2y + xy; B. x3y – x2y – xy; C. x3y – x2y + xy; D. x3y + x2y – xy
Câu 2: Tích (x-2)(x+5) bằng
A. x2 + 3x - 10 B. x2 - 7x+10 C. x2 +10 D. x2 - 3x+10
Câu 3: Đa thức x2 + 9y2 – 6xy được phân tích thành
A. (x - 3y)(x+3y) B. - (x-3y)2 C. (x+3y)2 D. (x-3y)2
Câu 4: Biểu thức rút gọn của (x+2y)(x2-2xy+4y2) là :
A. x3-8y3 B. x3+8y3 C. x3- 8y3 D. x3-2y3
Câu 5: Kết quả được viết dưới dạng tích của đa thức sau : 8x3 - 12x2y + 6xy2 - y3 là
A. (2x3 + y)3 B. (2x + y3)3 C. (2x + y)3 D. (2x – y)3
Câu 6: Biểu thức thích hợp điền vào chỗ dấu … để có đẳng thức
(3x - 2 )2 = 9x2 ……..+ 4 đúng là
A. -6x B. 6x C. 12x D. -12x
Câu 7: Đa thức: 4x(2y - z) +7y(2y - z) được phân tích thành nhân tử là
A. (2y-z)(4x-7y) B. (2y-z)(4x+7y) C. (2y+z)(4x+7y) D. (2y+z)(4x-7y)
Câu 8: Giá trị của x thoả mãn 2x(x+3) +2(x+3) =0 là
A. -3 hoặc 1 B. 3 hoặc 1 C. 3 hoặc -1 D. -3 hoặc -1
Câu 9: Đa thức 9x6 +24x3y2 +16y4 được phân tích thành nhân tử là
A. (3y3-2x2)2 B. (3x3-4y2)2 C. (3x3+4y2)2 D. -(3x3+4y2)2
Câu 10:
Cho tứ giác ABCD, có
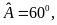
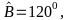
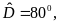 Số đo
Số đo
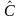 là:
là:
A.
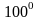 ,
B.
,
B.
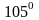 ,
C.
,
C.
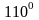 ,
D.
,
D.
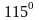
Câu 11: Hình bình hành ABCD là hình chữ nhật nếu
A. AB=CD B. AD=BC C. AC=BD D. AB=AD
Câu 12: Hình thang BCDE (BC // DE) là hình thang cân khi
A . BC=ED B . BD=CE C . BC=CD D . BE=CD
Câu 13: Trong các hình sau, hình có tâm đối xứng là:
A . Hình thang cân B . tam giác cân C . Hình bình hành D . tam giác đều
Câu 14: Một tam giác đều có độ dài cạnh bằng 13,5 cm. Độ dài đường trung bình của tam giác đó là:
A . 6,75cm B . 6,6cm C . 6,25cm D . 13,5cm
Câu 15: Một hình thang có đáy thứ nhất dài 8cm, đường trung bình dài 7cm. Độ dài đáy thứ hai của hình thang đó là
A
. 6cm B . 12cm C .
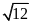 cm
D .
cm
D .
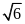 cm
cm
II/ TỰ LUẬN: (5 điểm)
Câu 16:(0.5 điểm) Rút gọn rồi tính giá trị biểu thức 9a2 + 16b2 + 24ab tại a = -1, b = 2.
Câu 17: (0.75 điểm) Rút gọn biểu thức B = x(x - 3) + (2 - x)(2 + x).
Câu 18:(0.75 điểm) Phân tích đa thức thành nhân tử x2 – 8x – 25y2 + 16 .
Câu 19: (3 điểm) Cho tam giác ABC (AB < AC), đường cao AH. Gọi D, E, F lần lượt là trung điểm của các cạnh AB, AC, BC.
a) Chứng minh rằng tứ giác BDEF là hình bình hành.
b) Chứng minh tứ giác EFHD là hình thang cân.
c) Gọi K là trung điểm của DE. Nêu cách xác định đỉnh A của tam giác ABC để tứ giác ADHK là hình thoi.
ĐÁP ÁN VÀ BIỂU ĐIỂM
I - TRẮC NGHIỆM : (5 điểm)
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
C |
A |
D |
B |
D |
D |
B |
D |
B |
A |
C |
B |
C |
A |
A |
( Mỗi câu trả lời đúng được 0,33 điểm ).
II – TỰ LUẬN: (5 điểm)
Câu |
ĐÁP ÁN |
Điểm |
16 (0.5 đ) |
9a2 + 16b2 + 24ab = (3a+4b)2 |
0,25 |
Thay a=-1, b= 2 vào ta được giá trị bằng 25 |
0,25 |
|
17 (0.75 đ) |
B = x(x - 3) + (2 - x)(2 + x) = x2- 3x + 22 – x2 |
0,5 |
= -3x+ 4 |
0,25 |
|
18 (0.75 đ) |
x2 – 8x – 25y2 + 16 = x2 – 8x + 16 – 25y2 = (x-4)2 – (5y)2 |
0,5 |
=(x- 4- 5y)(x- 4+5y) |
0,25 |
|
19 (3 đ) |
|
|
Hình vẽ
|
Hình vẽ phục vụ cho
giải ít nhất 2 câu a và b
|
0,5 |
|
a) Chứng minh rằng tứ giác BDEF là hình bình hành. Vì D và E thứ tự là trung điểm của AB và AC nên DE // BC và DE = BC :2 (1) Lại có F là trung điểm của BC nên BF = BC:2 (2) Từ (1) và (2) suy ra DE // BF và DE = BF Do đó tứ giác BDEF là hình bình hành. |
0,25 0,25 0,25 0,25 |
|
b) Chứng minh tứ giác EFHD là hình thang cân. Vì DE //BC (chứng minh trên), nên tứ giác EFHD là hình thang (3) Lại có HE = AC:2 (đường trung tuyến ứng với cạnh huyền trong tam giác vuông AHC) (4) Mặt khác, có DF = AC:2 (vì DF là đường trung bình của tam giác ABC) (5) Từ (4) và (5) suy ra HE = DF (6) Từ (3) và (6) suy ra EFHD là hình thang cân |
0,25 0,25 |
|
c) Gọi O là giao điểm của AH và DK.
Tứ giác ADHK là hình thoi
|
0,25 0,25
0,25 0,25 |
BẢNG MÔ TẢ KIỂM TRA GIỮA HKI MÔN TOÁN 8
Câu |
Mức độ |
Nội dung |
1–TN |
NB |
Biết phép nhân đơn thức với đa thức |
2–TN |
NB |
Biết phép nhân đa thức với đa thức |
3–TN |
NB |
Biết hằng đẳng thức bình phương của một hiệu |
4– TN |
NB |
Biết hằng đẳng thức tổng hai lập phương |
5– TN |
NB |
Biết hằng đẳng thức lập phương của một tổng |
6– TN |
TH |
Điền giá trị biểu thức đề hoàn chình hằng đẳng thức |
7– TN |
NB |
Biết phân tích thành nhân tử bằng pp đặt nhân tử chung |
8– TH |
TH |
Tìm giá trị biến x bằng cách phân tích thành nhân tử |
9–TN |
TH |
Phân tích đa thức thành nhân tử bằng pp dùng hằng đẳng thức |
10–TN |
NB |
Biết tổng số đo góc của một tứ giác |
11- TN |
NB |
Biết dấu hiệu nhận biết tứ giác là hình chữ nhật |
12- TN |
NB |
Biết dấu hiệu nhận biết hình thang cân |
13- TN |
NB |
Biết được hình có tâm đồi xứng |
14- TN |
NB |
Biết tính chất đường trung bình tam giác |
15- TN |
NB |
Biết tính chất đường trung bình hình thang |
Bài1a –TL |
TH |
Áp dụng hằng đẳng thức để tính giá trị biểu thức |
Bài1b –TL |
VDT |
Áp dụng phép tính và hằng đẳng thức để rút gọn biểu thức |
Bài2 – TL |
VDT |
Vận dụng các phương pháp dùng hằng đẳng thức, nhóm hạng tử vao việc phân tích đa thức thành nhân tử. |
Bài3a- TL |
TH |
Hiểu tính chất số đo góc của hình bình hành, tính chất của hình thang |
Bài3b-TL |
VDT |
Vận dụng các tính chất đường đường trung bình của tam giác, dấu hiệu nhận biết hình thang cân |
Bài4-TL |
VDC |
Vận dụng linh hoạt các phép tính và hằng đẳng thức để tìm giá trị nhỏ nhất của biểu thức. |
-
MA TRẬN ĐỀ KIỂM TRA GIỮA HỌC KÌ I- MÔN TOÁN - LỚP 8 (thời gian 60 phút)
Cấp độ
Chủ đề
Nhận biêt
Thông hiểu
Vận dụng
Cộng
Thấp
Cao
TNKQ
TL
TNKQ
TL
TNKQ
TL
TNKQ
TL
1. Phép nhân đa thức và những hằng đẳng thức đáng nhớ
Biết thực hiện phép nhân đơn thức với đa thức, nhân hai đa thức đơn giản. Biết khai triển các hằng đẳng thức đáng nhớ đơn giản
Hoàn chỉnh hằng đẳng thức.
Áp dụng hằng đẳng thức để tính giá trị biểu thức.
Vận dụng phép nhân đơn thức với đa thức, nhân hai đa thức và hằng đẳng thức đáng nhớ để rút gọn biểu thức.
Vận dụng hằng đẳng thức đề tìm giá trị nhỏ nhất của biểu thức
Số câu
5
1
1
1
1
9
Số điểm
1.(6)
0.(3)
0.5
0.75
1.0
4.25
2. Phân tích đa thức thành nhân tử.
Biết phân tích đa thức thành nhân tử đơn giản nhất
Áp dụng phương pháp đặt nhân tử chung hoặc dùng hằng đẳng thức vào việc phân tích đa thức thành nhân tử.
Áp dụng phân tích đa thức thành nhân tử để giải bài toán tìm x.
Vận dụng các phương pháp đặt nhân tử chung, dùng hằng đẳng thức, nhóm hạng tử vao việc phân tích đa thức thành nhân tử.
Số câu
1
2
1
4
Số điểm
0.(3)
0.(6)
0.75
1.75
3. Tứ giác (tứ giác, hình thang, hình thang cân, hình bình hành); Đường trung bình của tam giác, đường trung bình của hình thang; phép đối xứng trục.
Biết khái niệm, tính chất, dấu hiệu nhận biết của các tứ giác. Biết tính chất đường trung bình của tam giác, đường trung bình của hình thang. Biết trục đối xứng của một hình, hình có trục đối xứng.
Hiểu tính chất tứ giác (hình thang, hình thang cân, hình bình hành), tính chất đường trung bình của tam giác. Áp dụng được dấu hiệu nhận biết các tứ giác nói trên.Vẽ hình chính xác theo yêu cầu.
Vận dụng được định nghĩa, tính chất, dấu hiệu nhận biết của các tứ giác để giải toán.
Số câu
6
2
1
9
Số điểm
2.0
1. 5
0.5
4,0
TS câu
12
6
3
1
22
TS điểm
4.0
3.0
2.0
1.0
10
Tỉ lệ
40%
30%
20%
10%
100%
Ngoài Bộ Đề Ôn Tập Toán 8 Giữa HK1 Năm 2022-2023 Có Đáp Án Và Ma Trận Đặc Tả – Toán 8 thì các đề thi trong chương trình lớp 8 sẽ được cập nhật liên tục và nhanh nhất có thể sau khi kỳ thi diễn ra trên Danh mục Kho Đề Thi nhằm giúp các bạn đọc thuận tiện trong việc tra cứu và đối chiếu đáp án. Quý thầy cô và các bạn đọc có thể chia sẻ thêm những tài liệu học tập hữu ích đến địa chỉ email của chúng tôi, nhằm xây dựng nên kho đề thi phong phú, đa dạng cho các em học sinh tham khảo và rèn luyện.







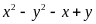 )
)
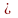
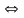
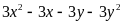 =
3 (
=
3 (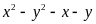 )
)