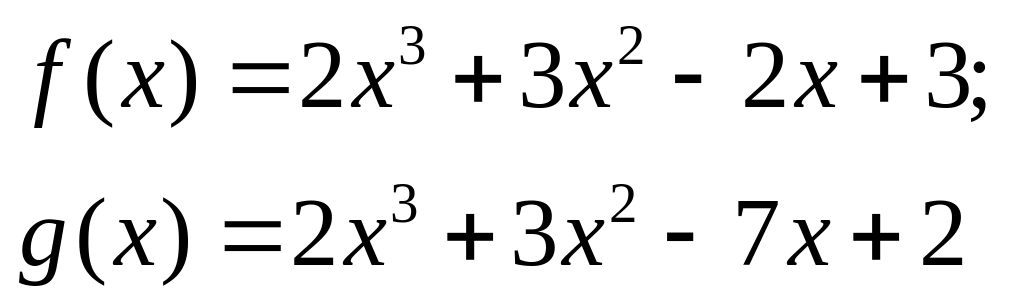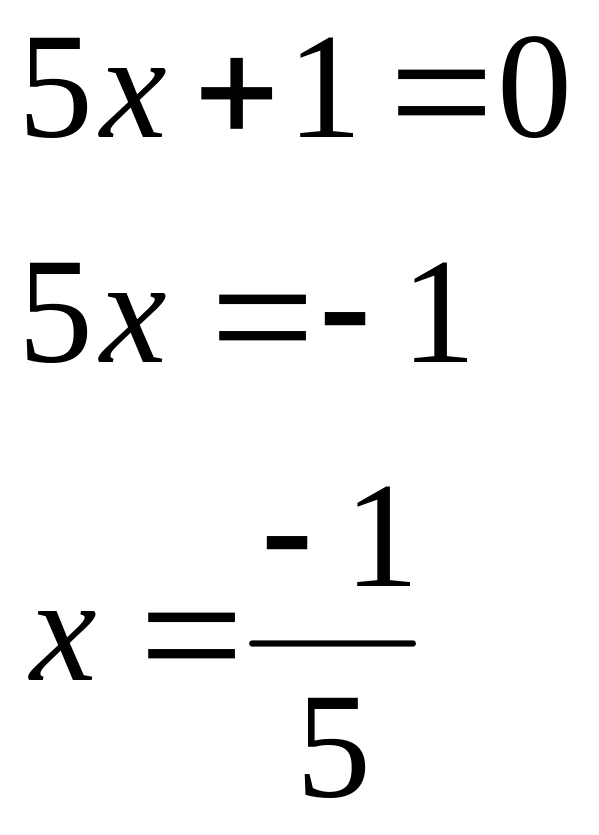15 Đề Thi kì 2 Toán 7 Có Đáp Án – Tài Liệu Toán
15 Đề Thi kì 2 Toán 7 Có Đáp Án – Tài Liệu Toán được Trang Tài Liệu sưu tầm với các thông tin mới nhất hiện nay. Đề thi này sẽ giúp các em học sinh ôn tập, củng cố kiến thức, rèn luyện kĩ năng làm bài. Cũng như hỗ trợ thầy cô trong quá trình giảng dạy. Hy vọng những tài liệu này sẽ giúp các em trong quá trình ôn luyện và đạt kết quả cao trong bài thi sắp tới.
Trong quá trình học tập môn Toán, tìm kiếm tài liệu ôn thi là một việc quan trọng để chuẩn bị tốt cho kỳ thi kì 2. Hôm nay, chúng ta sẽ khám phá một nguồn tài liệu đặc biệt – Bộ 15 đề thi kì 2 Toán lớp 7, đầy đủ đáp án đi kèm.
Bộ 15 đề thi kì 2 Toán lớp 7, với sự hỗ trợ của đáp án, là một kho tàng kiến thức và bài tập bổ ích để chúng ta ôn tập và rèn luyện kỹ năng giải quyết các bài toán. Qua việc làm và kiểm tra đáp án, chúng ta có thể đánh giá sự tiến bộ của mình và xác định những khía cạnh cần cải thiện.
Bộ 15 đề thi kì 2 Toán lớp 7 không chỉ giúp chúng ta ôn tập và củng cố kiến thức đã học mà còn giúp chúng ta khám phá các dạng bài toán mới và áp dụng kiến thức đã nắm vững vào thực tế. Qua việc làm các bài tập, chúng ta có cơ hội rèn luyện khả năng tư duy logic, phân tích và giải quyết vấn đề.
Bộ 15 đề thi kì 2 Toán lớp 7 cùng với đáp án là một nguồn tài liệu quý giá để chuẩn bị cho kỳ thi sắp tới. Qua việc làm và kiểm tra kết quả, chúng ta có thể tự tin hơn khi đối mặt với các câu hỏi và thử thách trong kỳ thi.
Hãy tận dụng tài liệu bổ ích này để ôn tập và nắm vững kiến thức Toán. Bộ 15 đề thi kì 2 Toán lớp 7, cùng với đáp án, sẽ giúp chúng ta nắm bắt kiến thức một cách toàn diện và tự tin đạt được thành tích tốt trong môn học quan trọng này.
Đề thi tham khảo
Dưới đây là bản đọc trực tuyến giúp thầy cô và các em học sinh có thể nghiên cứu Online hoặc bạn có thể tải miễn phí với phiên bản word để dễ dàng in ấn cũng như học tập Offline
ĐỀ 1 |
ĐỀ THI HỌC KỲ II TOÁN 7 Thời gian: 90 phút |
Câu 1: (1.0 điểm) Điểm kiểm tra một tiết môn Toán của học sinh một lớp 7 tại một trường THCS được cho trong bảng tần số sau:
Điểm số (x) |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Tần số (n) |
1 |
2 |
7 |
8 |
5 |
11 |
4 |
2 |
N = 40 |
Dấu hiệu điều tra ở đây là gì?
Dấu hiệu có bao nhiêu giá trị khác nhau? Tìm mốt.
Câu 2: (2.0 điểm)
Thu gọn đơn thức A. Xác định phần hệ số và tìm bậc của đơn thức thu gọn, biết:
![]()
Tính giá trị của biểu thức
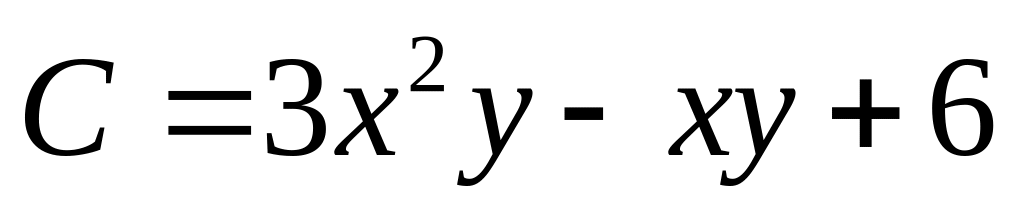 tại x
= 2, y
= 1.
tại x
= 2, y
= 1.
Câu
3: (2.0
điểm)
Cho hai đa thức:
![]()
![]()
Tính
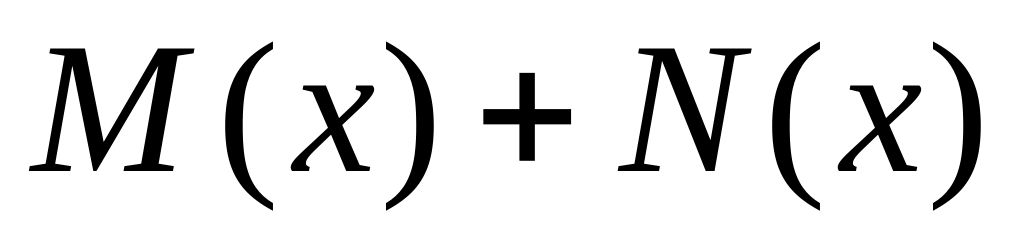 .
.
Tìm đa thức P(x) biết: P(x) + N(x) = M(x)
Câu 4: (1.0 điểm) Tìm nghiệm của các đa thức sau:
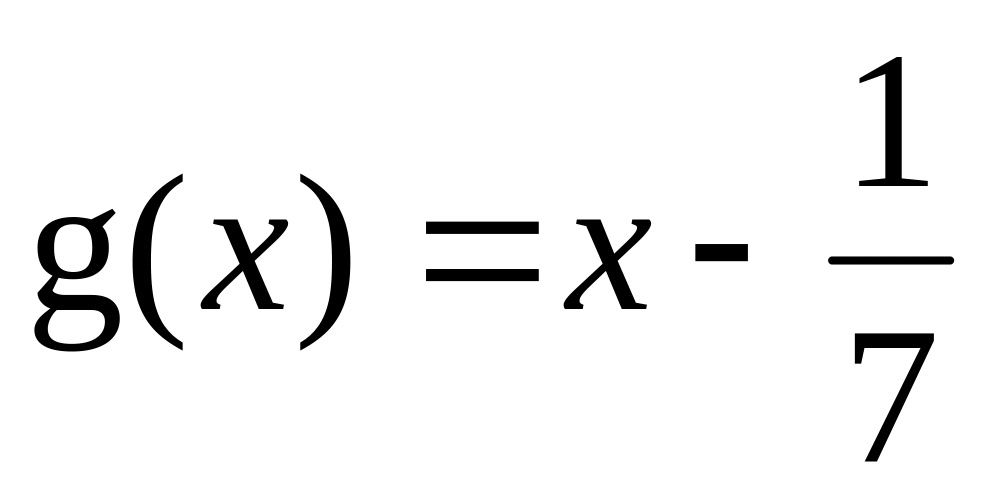 b)
b)
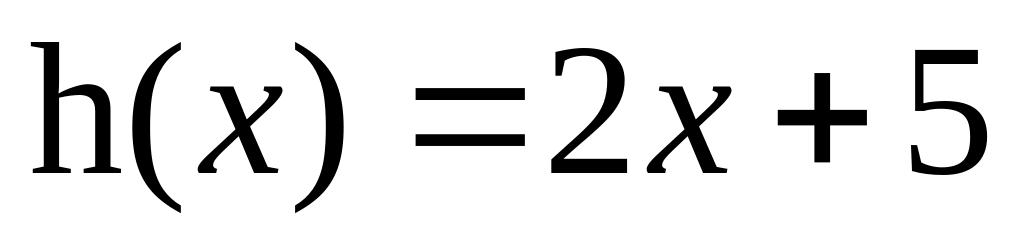
Câu
5: (1.0
điểm)
Tìm m để đa thức![]() có
một nghiệm
x
= 1.
có
một nghiệm
x
= 1.
Câu
6: (1.0
điểm)
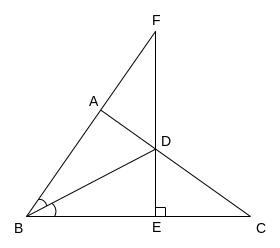
Cho
![]() vuông
tại A, biết AB = 6 cm, BC = 10cm. Tính độ dài cạnh AC và
chu vi tam giác ABC.
vuông
tại A, biết AB = 6 cm, BC = 10cm. Tính độ dài cạnh AC và
chu vi tam giác ABC.
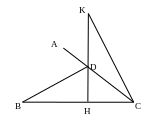
Câu
7: (2.0
điểm)
Cho
![]() vuông
tại A, đường phân giác của góc B cắt AC tại D.
vuông
tại A, đường phân giác của góc B cắt AC tại D.
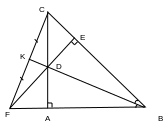
Vẽ
![]() .
.
Chứng minh:
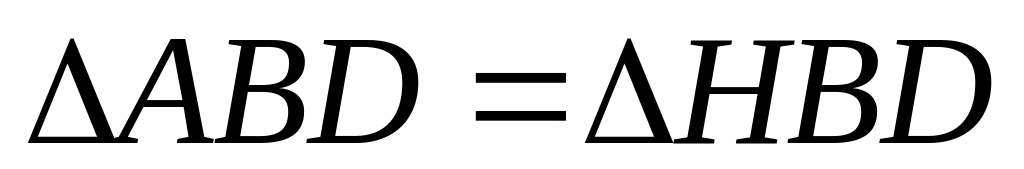
Trên tia đối của AB lấy điểm K sao cho AK = HC. Chứng minh ba điểm K, D, H thẳng hàng.
----------HẾT----------
(Học sinh không được sử dụng máy tính)
ĐÁP ÁN – THANG ĐIỂM
Câu |
Đáp án |
Thang điểm |
Câu 1 (1.0 điểm) |
|
0.5 |
|
0.5 |
|
Câu 2 (2.0 điểm) |
Hệ
số:
|
0.5
0.5 |
|
1.0 |
|
Câu 3 (2.0 điểm) |
|
0.5
0.5 |
|
|
1.0 |
|
Câu 4 (1.0 điểm) |
Vậy
|
0.5 |
|
Vậy
|
0.5
|
|
Câu 5 (1.0 điểm) |
Vậy
với
|
0.5
0.25
0.25
|
Câu 6 (1.0 điểm) |
Áp dụng định lý Py-ta-go vào tam giác vuông ABC ta có:
Chu
vi
|
0.25
0.25 0.5 |
Câu 7 (2 điểm) |
BD là cạnh chung DA = DH (D nằm trên tia phân giác của góc B)
|
0.25 0.25 0.25 0.25 |
Suy
ra,
Khi
đó, BD vừa là phân giác, vừa là đường cao xuất
phát từ đỉnh B
Mặt
khác,
Vậy ba điểm K, D, H thẳng hàng. |
0.25
0.25
0.25
0.25 |
ĐỀ 2 |
ĐỀ THI HỌC KỲ II TOÁN 7 Thời gian: 90 phút |
Bài 1 (2,0 điểm): Điểm kiểm tra 1 tiết đại số của học sinh lớp 7A được ghi lại như sau: 6 4 9 7 8 8 4 8 8 10
10 9 8 7 7 6 6 8 5 6
4 9 7 6 6 7 4 10 9 8
a) Lập bảng tần số.
b) Tính số trung bình cộng và tìm mốt của dấu hiệu.
Bài
2
(1,5
điểm)
Cho đơn thức
![]()
a) Thu gọn và xác định hệ số, phần biến, bậc của đa thức P.
b) Tính giá trị của P tại x = -1 và y = 2.
Bài 3 (1,5 điểm): Cho 2 đa thức sau:
A(x) = 4x3 – 7x2 + 3x – 12
B(x) = – 2x3 + 2x2 + 12 + 5x2 – 9x
a) Thu gọn và sắp xếp đa thức B(x) theo lũy thừa giảm dần của biến.
b) Tính A(x) + B(x) và B(x) – A(x)
Bài 4 (1,5 điểm): Tìm nghiệm của các đa thức sau:
a) M(x) = 2x – 6
b) N(x) = x2 + 2x + 2015
Bài
5
(3,5
điểm):
Cho
∆ABC vuông tại A, vẽ trung tuyến AM (M
BC). Từ M kẻ MH![]() AC,
trên tia đối của tia MH lấy điểm K sao cho MK = MH.
AC,
trên tia đối của tia MH lấy điểm K sao cho MK = MH.
Chứng minh ∆MHC = ∆MKB.
Chứng minh AB // MH.
Gọi G là giao điểm của BH và AM, I là trung điểm của AB. Chứng minh I, G, C thẳng hàng.
------------------------HẾT--------------------------
ĐÁP ÁN
Bài 1 2,0đ
|
a) Lập đúng bảng tần số :
|
1,0
|
||||||||||||||||||
b)
M0 = 8 |
0,5
0,5 |
|||||||||||||||||||
Bài 2 1,5 |
a)
Hệ số: 3 Phần biến: x3y2 Bậc của đa thức: 5 |
0,25 0,25 0,25 0,25
|
||||||||||||||||||
b) Tại x = -1 và y = 2. P = 3.(-1)3.22 = -12 |
0,5 |
|||||||||||||||||||
Bài 3 1,5 đ |
a) B(x) = – 2x3 + 2 x2 + 12 + 5x2 – 9x = – 2x3 + (2 x2 + 5x2)+12 – 9x = – 2x3 + 7x2 +12 – 9x Sắp xếp: B(x) = - 2x3 + 7x2– 9x +12 |
0,25 0,25 |
||||||||||||||||||
b
+ B(x) = - 2x3 + 7x2 - 9x + 12
A
- A(x) = 4x3 – 7x2 + 3x – 12
|
0,5
0,5 |
|||||||||||||||||||
Bài 4 1,5đ
|
a) M(x) = 2x – 6 Ta có M(x) = 0 hay 2x – 6 =0 2x = 6 x = 3 Vậy nghiệm của đa thức M(x) là x = 3 |
0,25
0,5 0,25 |
||||||||||||||||||
b) N(x) = x2 + 2x + 2015 Ta có: x2 + 2x + 2015 = x2 + x +x +1+ 2014 = x(x +1) + (x +1) +2014 = (x +1)(x+1) + 2014 = (x+1)2 + 2014 Vì (x+1)2≥ 0 =>(x+1)2 + 2014≥ 2014>0 Vậy đa thức N(x) không có nghiệm. |
0,25
0,25 |
|||||||||||||||||||
Bài 5 1,0 đ |
Vẽ
hình ghi đúng GT, KL
|
0,5 |
||||||||||||||||||
a) Xét ∆MHC và ∆MKB. MH = MK(gt)
MC = MB = > ∆MHC = ∆MKB(c.g.c) |
0,5 |
|||||||||||||||||||
AB => AB // MH. |
0,25 0,25 0,5 |
|||||||||||||||||||
=>BK=AH=HC => G là trọng tâm Mà CI là trung tuyến => I, G, C thẳng hàng |
0,25 0,25 0,25 0,25 |
Chú ý : HS làm theo cách khác nếu đúng vẫn cho điểm tối đa
ĐỀ 3 |
ĐỀ THI HỌC KỲ II TOÁN 7 Thời gian: 90 phút |
I. TRẮC NGHIỆM : (3 điểm)Chọn câu trả lời em cho là đúng nhất:
Câu
1: Đơn thức nào
sau đây đồng dạng với đơn thức
![]()
![]()
A.
![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
Câu
2: Đơn thức
![]() có bậc là :
có bậc là :
A. 6 B. 8 C. 10 D. 12
Câu
3: Bậc của đa
thức![]() là :
là :
A. 7 B. 6 C. 5 D. 4
Câu 4: Gía trị x = 2 là nghiệm của đa thức :
A.![]() B.
B.![]() C.
C.
![]() D.
D.![]()
Câu
5: Kết qủa phép
tính
![]()
![]()
A.
![]() B.
B.![]() C.
C.![]() D.
D.
![]()
Câu
6. Giá trị biểu
thức 3x2y
+ 3y2x
tại x
= -2
và y
= -1
là:![]()
A. 12 B. -9 C. 18 D. -18
Câu 7. Thu gọn đơn thức P = x3y – 5xy3 + 2 x3y + 5 xy3 bằng :
A. 3 x3y B. – x3y C. x3y + 10 xy3 D. 3 x3y - 10xy3
Câu
8. Số nào sau đây
là nghiệm của đa thức f(x) =
![]() x
+ 1 :
x
+ 1 :
A.
![]() B.
B.
![]() C. -
C. -
![]() D. -
D. -![]()
Câu 9: Đa thức g(x) = x2 + 1
A.Không có nghiệm B. Có nghiệm là -1 C.Có nghiệm là 1 D. Có 2 nghiệm
Câu 10: Độ dài hai cạnh góc vuông liên tiếp lần lượt là 3cm và 4cm thì độ dài cạnh huyền là :
A.5 B. 7 C. 6 D. 14
Câu 11: Tam giác có một góc 60º thì với điều kiện nào thì trở thành tam giác đều :
A. hai cạnh bằng nhau B. ba góc nhọn C.hai góc nhọn D. một cạnh đáy
Câu 12: Nếu AM là đường trung tuyến và G là trọng tâm của tam giác ABC thì :
A.![]()
![]()
![]() B.
B.
![]() C.
C.![]() D.
D.
![]()
II. TỰ LUẬN: (7,0 điểm)
Câu 1:( 1,5 ®iÓm). Điểm thi đua trong các tháng của 1 năm học của lớp 7A được liệt kê trong bảng sau:
-
Tháng
9
10
11
12
1
2
3
4
5
Điểm
80
90
70
80
80
90
80
70
80
a) Dấu hiệu là gì?b) Lập bảng tần số. Tìm mốt của dấu hiệu.
c) Tính điểm trung bình thi đua của lớp 7A.
Câu
2. (1,5 điểm) Cho
hai đa thức
![]() và
và![]()
Thu gọn hai đa thức P(x) và Q(x)
Tìm đa thức M(x) = P(x) + Q(x) và N(x) = P(x) – Q(x) c)Tìm nghiệm của đa thức M(x).
Câu 3: (3,0 điểm).Cho ABC có AB = 3 cm; AC = 4 cm; BC = 5 cm.
a) Chứng tỏ tam giác ABC vuông tại A.
b)Vẽ phân giác BD (D thuộc AC), từ D vẽ DE BC (E BC). Chứng minh DA = DE.
c) ED cắt AB tại F. Chứng minh ADF = EDC rồi suy ra DF > DE.
Câu
4 (1,0 điểm): Tìm
n
![]() Z sao cho 2n - 3
Z sao cho 2n - 3
![]() n + 1
n + 1
ĐÁP ÁN VÀ BIỂU ĐIỂM
I. TRẮC NGHIỆM ( 3 điểm):- Mỗi câu đúng được 0,25 điểm.
Câu |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
Đáp án |
B |
C |
D |
C |
A |
D |
A |
C |
A |
A |
A |
B |
II. TỰ LUẬN: (7 điểm).
Câu |
Nội dung |
Điểm |
|||||||||||
1
|
a) |
Dấu hiệu điều tra là: Điểm thi đua trong tháng của lớp 7A. |
0.25 |
||||||||||
b) |
Lập chính xác bảng “ tần số” dạng ngang hoặc dạng cột:
Mốt của dấu hiệu là: 80. |
0.75 |
|||||||||||
c) |
Tính số điểm trung bình thi đua của lớp 7A là: X |
0.5 |
|||||||||||
2 |
a) |
Thu gọn hai đơn thức P(x) và Q(x)
|
0.25
0.25 |
||||||||||
b) |
b) Tính tổng hai đa thức đúng được
M(x)
= P(x) + Q(x)
|
1,0
|
|||||||||||
c) |
c)
Đa
thức M(x) có hai nghiệm
|
|
|||||||||||
3 |
Hình vẽ |
|
0.5
|
||||||||||
a) |
Chứng
minh
Suy
ra
|
0.75 |
|||||||||||
b) |
Chứng
minh
Suy ra DA = DE. |
0.75 |
|||||||||||
c) |
Chứng minh ADF = EDC suy ra DF = DC Chứng minh DC > DE. Từ đó suy ra DF > DE. |
1 |
|||||||||||
4 |
|
Xét các giá trị của n + 1 là ước của 5:
|
0.5
0.5 |
||||||||||
ĐỀ 4 |
ĐỀ THI HỌC KỲ II TOÁN 7 Thời gian: 90 phút |
I. Trắc nghiệm: (3 điểm).
Hãy viết vào bài thi chỉ một chữ cái in hoa đứng trước đáp số đúng .
Câu 1: Điểm thuộc đồ thị hàm số y=2x-1 là:
A.
![]() B.
B.
![]() C. (0;1) D. (1;-1)
C. (0;1) D. (1;-1)
Câu 2: Giá trị của biểu thức 2x-3y tại x=-1; y=-2 là:
A. 4 B. -8 C. -4 D. -1
Câu
3:
Tích
![]() bằng:
bằng:
A.
![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
Câu
4:
Tìm x biết
![]() ta được các kết quả là:
ta được các kết quả là:
A. x=-5; x=1 B. x=-1 C. x=5; x=-1 D. x=5
II. Tự luận: (7 điểm).
Câu 5:
a) Vẽ đồ thị hàm số y=-2x.
b)
Tính giá trị của biểu thức
![]() tại
tại
![]()
Câu
6: Cho
tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm
M, trên tia đối của tia CB lấy điểm N sao cho BM=CN. Kẻ
![]() ,
,
![]() .
Chứng minh rằng:
.
Chứng minh rằng:
a) Tam giác AMN cân
b) MH=KN
c) HK// MN
------------------------------- Hết --------------------------------
(Cán bộ coi thi không giải thích gì thêm)
ĐÁP ÁN
I) Trắc nghiệm (3 điểm ): Mỗi câu đúng cho 0,75 điểm
Câu |
1 |
2 |
3 |
4 |
Đáp án đúng |
B |
A |
D |
C |
II) Tự luận (7điểm)
Câu |
Nội dung |
Điểm |
5
|
a
+ Vẽ đúng đồ thị y=-2x b)
Thay
|
0,5 điểm
1,5 điểm
0,5 điểm 0,5 điểm
0,5 điểm 0,5 điểm |
6
|
a)
b)
c) X |
h.vẽ 0,5 điểm 0,5 điểm
1,0 điểm
0,5 điểm
0,5 điểm |
ĐỀ 5 |
ĐỀ THI HỌC KỲ II TOÁN 7 Thời gian: 90 phút |
A. TRẮC NGHIỆM (2 điểm)
Em hãy chọn phương án trả lời đúng nhất.
Câu 1: Điểm kiểm tra môn Toán của một nhóm học sinh được cho bởi bảng sau:
8 |
9 |
7 |
10 |
5 |
7 |
8 |
7 |
9 |
8 |
5 |
7 |
4 |
9 |
4 |
7 |
5 |
7 |
7 |
3 |
a) Số các giá trị khác nhau của dấu hiệu là:
A. 20 |
B. 10 |
C. 8 |
D. 7 |
b) Mốt của dấu hiệu là:
A. 10 |
B. 7 |
C. 4 |
D. 3 |
c) Số trung bình cộng của dấu hiệu là:
A. 6,8 |
B. 6,6 |
C. 6,7 |
D. 6,5 |
Câu
2:
Đơn thức nào sau đây đồng dạng với đơn thức
![]() ?
?
A.
![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
Câu
3:
Tam giác ABC có
![]() ,
,
![]() .
Số đo góc C là:
.
Số đo góc C là:
A. 500 B. 700 C. 800 D. 900
Câu 4: Cho tam giác ABC vuông tại A, AB = 3cm và AC = 4cm thì độ dài cạnh BC là:
A. 5 cm B. 7 cm C. 6 cm D. 14 cm
Câu 5: Nếu AM là đường trung tuyến và G là trọng tâm của tam giác ABC thì:
A.
![]()
![]()
![]() B.
B.
![]() C.
C.![]() D.
D.
![]()
Câu 6: Cho tam giác ABC cân tại A, khi đó đường trung tuyến xuất phát từ đỉnh A cũng chính là:
A. Đường phân giác. |
B. Đường trung trực. |
C. Đường cao. |
D. Đường phân giác, đường cao, đường trung trực.
|
B. TỰ LUẬN (8 điểm)
Bài
1:
(1
điểm)
Tính giá trị của biểu thức:
![]() tại x = 1 và y = 1.
tại x = 1 và y = 1.
Bài
2:
(2
điểm)
Cho hai đa thức: ![]()
![]()
Tính A(x) + B(x); A(x) – B (x).
Bài 3: (2 điểm) Tìm nghiệm của các đa thức sau:
P(x) = 2x – 1
Q(x) =
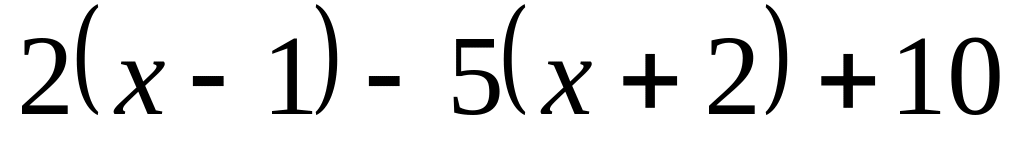
Bài 4: (3 điểm) Cho tam giác DEF cân tại D với đường trung tuyến DI.
a)
Chứng minh:
![]() DEI
=
DEI
=![]() DFI.
DFI.
b) Chứng minh DI EF.
c) Kẻ đường trung tuyến EN. Chứng minh rằng: IN song song với ED.
--------------------hết---------------------
ĐÁP ÁN VÀ THANG ĐIỂM
A. TRẮC NGHIỆM (2 điểm)
Mỗi câu trả lời đúng được 0,25 điểm.
Câu |
1 |
2 |
3 |
4 |
5 |
6 |
||
a) |
b) |
c) |
||||||
Đáp án |
D |
B |
A |
C |
B |
A |
B |
D |
B. TỰ LUẬN: (8 điểm)
BÀI |
ĐÁP ÁN |
ĐIỂM |
1 (1đ) |
Thay x = 1 và y = 1 vào biểu thức 2xy + y - 1 ta được: 2.1.1 + 1 - 1 = 2 ( 0,75đ) Vậy giá trị của biểu thức 2xy + y - 1 tại x = 1 và y = 1 là 2. |
0,25 0,5 0,25 |
2 (2đ) |
A(x) = -7x4 – 2x3 + 4x2 - 2 + B(x) = x4 + 4x3 - 2x2 + 3x - 5 A(x) + B(x) = - 6x4 + 2x3 + 2x2 + 3x - 7
A(x) = -7x4 – 2x3 + 4x2 - 2 - B(x) = x4 + 4x3 - 2x2 + 3x - 5 A(x) - B(x) = - 8x4 - 6x3 + 6x2 - 3x + 3
|
1
1 |
3 (2đ) |
a) 2x – 1 = 0 2x = 1 x = 1/2 Vậy x = ½ là nghiệm của đa thức 2x - 1
2x - 2 – 5x - 10 + 10 = 0 -3x = 2 x = -2/3 Vậy x = -2/3 là nghiệm của đa thức Q(x).
|
0,25 0,25 0,25 0,25
0,5 0,25
0,25 |
4 (3đ) |
Vẽ hình viết GT - KL đúng
D
N
E
F
I
GT IE = IF ND = NF KL
a)
Chứng minh:
b) Chứng minh DI EF. c) IN // ED.
a)
Xét
DE
= DF (vì
DI : cạnh chung IE = IF (vì DI là đường trung tuyến)
b)
Theo câu a ta có
mà
Từ
(1) và (2)
c)
DIF
vuông (vì
IN
= DN = FN =
DIN cân tại N
*Mặt
khác
Từ
(1), (2) suy ra:
|
0,5
0,25 0,25 0,25 0,25
0,5
0,5
0,25
0,25 |
Lưu
ý: Học sinh làm theo cách khác đúng vẫn được điểm
tối đa.
ĐỀ 6 |
ĐỀ THI HỌC KỲ II TOÁN 7 Thời gian: 90 phút |
Câu 1: (1.0 điểm) Điểm kiểm tra một tiết môn Toán của học sinh một lớp 7 tại một trường THCS được cho trong bảng tần số sau:
Điểm số (x) |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Tần số (n) |
1 |
2 |
7 |
8 |
5 |
11 |
4 |
2 |
N = 40 |
Dấu hiệu điều tra ở đây là gì?
Dấu hiệu có bao nhiêu giá trị khác nhau? Tìm mốt.
Câu 2: (2.0 điểm)
Thu gọn đơn thức A. Xác định phần hệ số và tìm bậc của đơn thức thu gọn, biết:
![]()
Tính giá trị của biểu thức
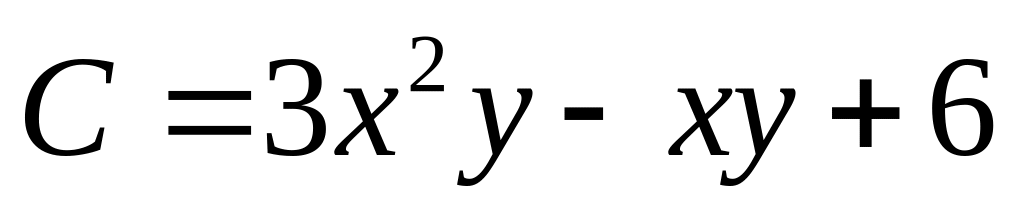 tại x
= 2, y
= 1.
tại x
= 2, y
= 1.
Câu
3: (2.0
điểm)
Cho hai đa thức:
![]()
![]()
Tính
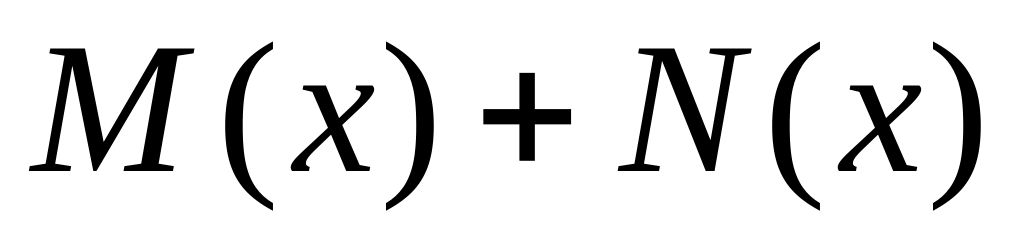 .
.
Tìm đa thức P(x) biết: P(x) + N(x) = M(x)
Câu 4: (1.0 điểm) Tìm nghiệm của các đa thức sau:
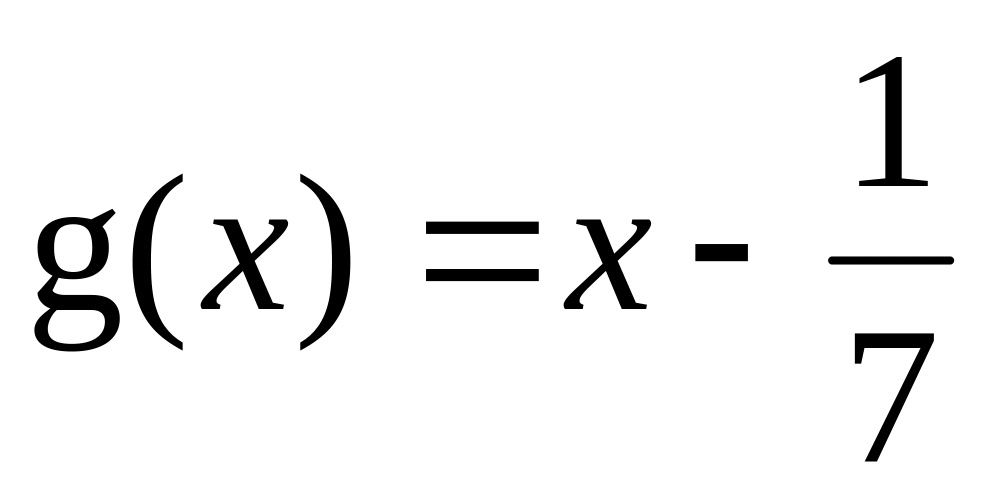 b)
b)
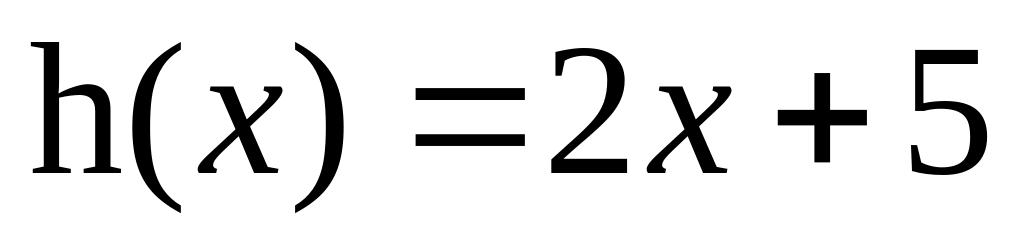
Câu
5: (1.0
điểm)
Tìm m để đa thức![]() có
một nghiệm
x
= 1.
có
một nghiệm
x
= 1.
Câu
6: (1.0
điểm)
Cho
![]() vuông
tại A, biết AB = 6 cm, BC = 10cm. Tính độ dài cạnh AC và
chu vi tam giác ABC.
vuông
tại A, biết AB = 6 cm, BC = 10cm. Tính độ dài cạnh AC và
chu vi tam giác ABC.
Câu
7: (2.0
điểm)
Cho
![]() vuông
tại A, đường phân giác của góc B cắt AC tại D.
vuông
tại A, đường phân giác của góc B cắt AC tại D.
Vẽ
![]() .
.
Chứng minh:
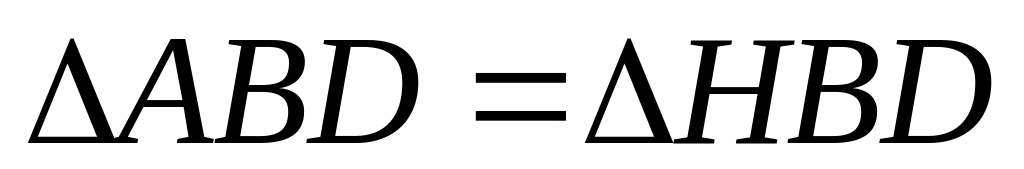
Trên tia đối của AB lấy điểm K sao cho AK = HC. Chứng minh ba điểm K, D, H thẳng hàng.
----------HẾT----------
(Học sinh không được sử dụng máy tính)
Câu |
Đáp án |
Thang điểm |
Câu 1 (1.0 điểm) |
|
0.5 |
|
0.5 |
|
Câu 2 (2.0 điểm) |
Hệ
số:
|
0.5
0.5 |
|
1.0 |
|
Câu 3 (2.0 điểm) |
|
0.5
0.5 |
|
|
1.0 |
|
Câu 4 (1.0 điểm) |
Vậy
|
0.5 |
|
Vậy
|
0.5
|
|
Câu 5 (1.0 điểm) |
Vậy
với
|
0.5
0.25
0.25
|
Câu 6 (1.0 điểm) |
Áp dụng định lý Py-ta-go vào tam giác vuông ABC ta có:
Chu
vi
|
0.25
0.25 0.5 |
Câu 7 (2 điểm) |
BD là cạnh chung DA = DH (D nằm trên tia phân giác của góc B)
|
0.25 0.25 0.25 0.25 |
Suy
ra,
Khi
đó, BD vừa là phân giác, vừa là đường cao xuất
phát từ đỉnh B
Mặt
khác,
Vậy ba điểm K, D, H thẳng hàng. |
0.25
0.25
0.25
0.25 |
ĐỀ 7 |
ĐỀ THI HỌC KỲ II TOÁN 7 Thời gian: 90 phút |
Bài 1: (2 điểm) Điều tra về điểm kiểm tra học kỳ II môn toán của học sinh lớp 7A, người điều tra có kết quả sau:
-
6
9
8
7
7
10
5
8
10
6
7
8
6
5
9
8
5
7
7
7
4
6
7
6
9
3
6
10
8
7
7
8
10
8
6
Lập bảng tần số, tính số trung bình cộng
Tìm mốt của dấu hiệu
Bài
2: (1,5
điểm)
Cho đơn thức
![]() (a là hằng số khác 0)
(a là hằng số khác 0)
Thu gọn rồi cho biết phần hệ số và phần biến của A
Tìm bậc của đơn thức A
Bài 3: (2,5 điểm) Cho hai đa thức:
![]() và
và
![]()
Tính
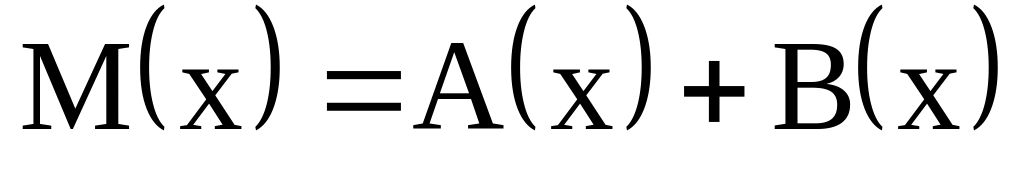 rồi
tìm nghiệm của đa thức
rồi
tìm nghiệm của đa thức
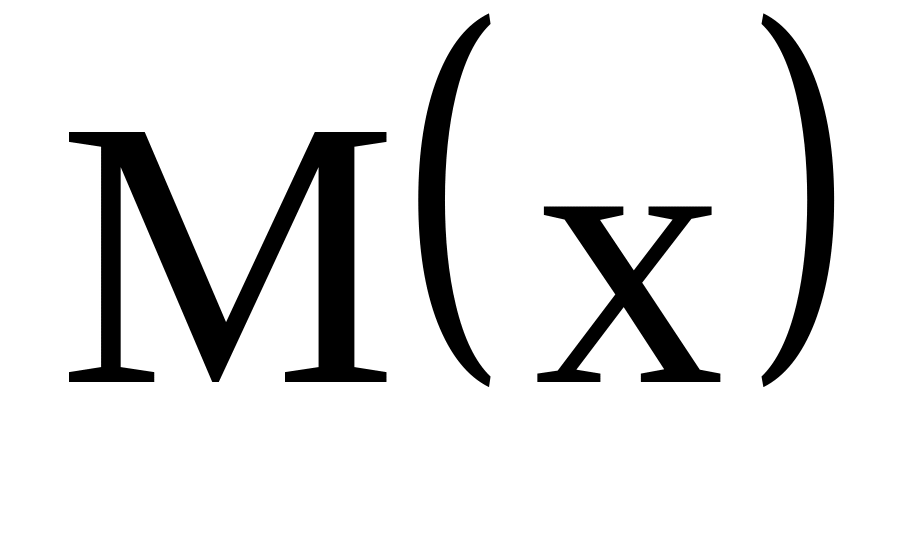
Tìm đa thức
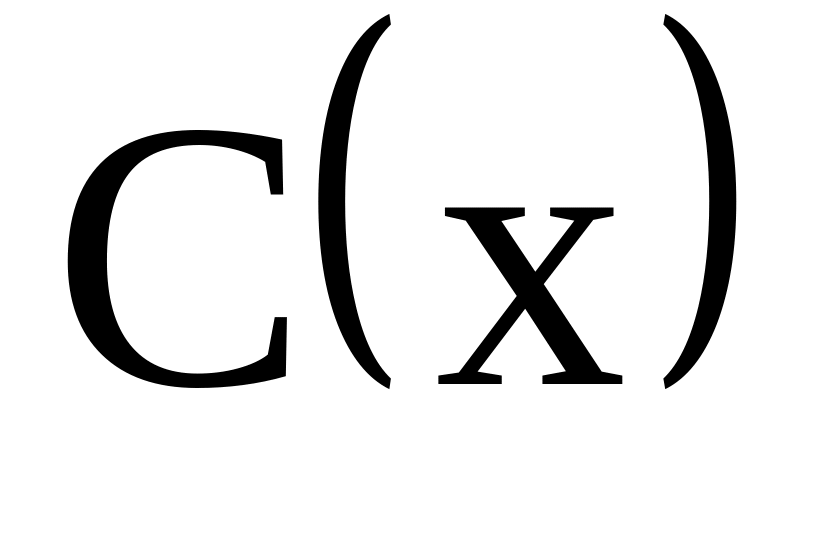 sao cho
sao cho
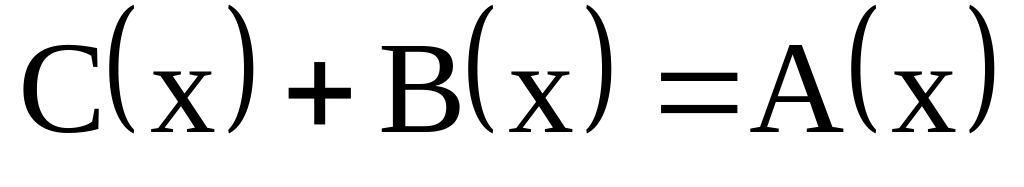
Bài
4: (0,5
điểm)
Cho
![]() .
Hỏi a có phải là nghiệm của đa thức
.
Hỏi a có phải là nghiệm của đa thức
![]() không? Vì sao?
không? Vì sao?
Bài 5: (3,5 điểm) Cho ΔABC vuông tại A, đường trung tuyến CM
Cho biết BC = 10cm, AC = 6cm. Tính độ dài đoạn thẳng AB, BM
Trên tia đối của tia MC lấy điểm D sao cho MD = MC
Chứng minh rằng ΔMAC = ΔMBD và AC = BD
Chứng minh rằng AC + BC > 2CM
Gọi K là điểm trên đoạn thẳng AM sao cho
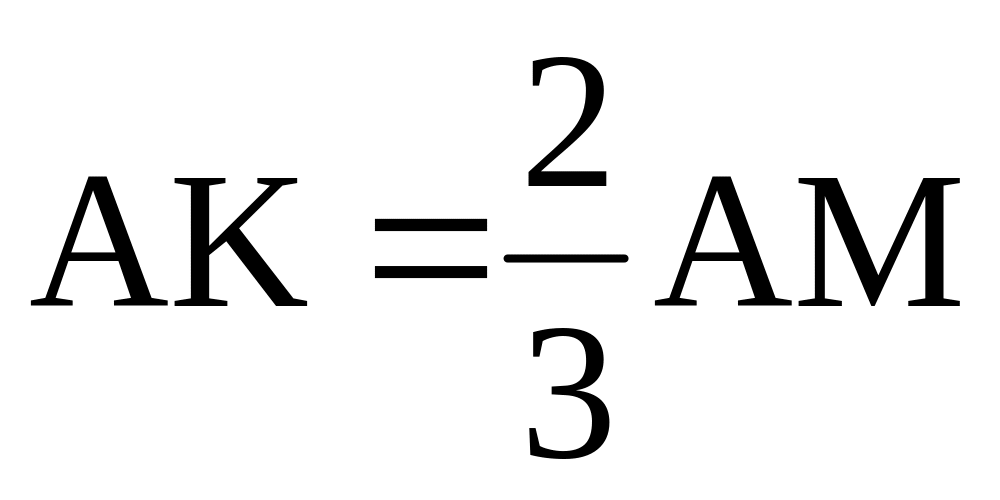 .
Gọi N là giao điểm của CK và AD, I là giao điểm của
BN và CD. Chứng minh rằng: CD = 3ID
.
Gọi N là giao điểm của CK và AD, I là giao điểm của
BN và CD. Chứng minh rằng: CD = 3ID
BÀI GIẢI
Bài 1: (2 điểm) Điều tra về điểm kiểm tra học kỳ II môn toán của học sinh lớp 7A, người điều tra có kết quả sau:
-
6
9
8
7
7
10
5
8
10
6
7
8
6
5
9
8
5
7
7
7
4
6
7
6
9
3
6
10
8
7
7
8
10
8
6
Lập bảng tần số, tính số trung bình cộng
Giải:
-
Giá trị (x)
Tần số (n)
Tích (x.n)
Số trung bình cộng
3
1
3
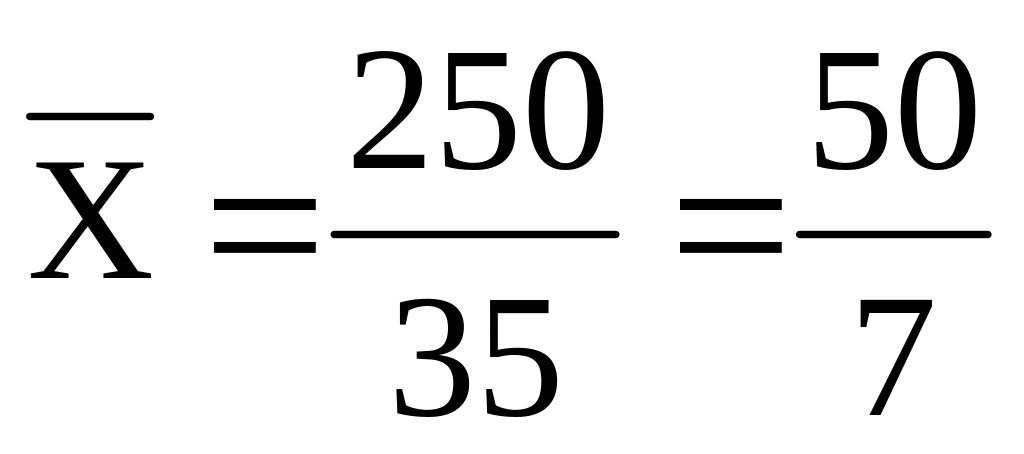
4
1
4
5
3
15
6
7
42
7
9
63
8
7
56
9
3
27
10
4
40
N = 35
Tổng: 250
Tìm mốt của dấu hiệu
Giải:
Mốt
của dấu hiệu là:
![]()
Bài
2: (1,5
điểm)
Cho đơn thức
![]() (a là hằng số khác 0)
(a là hằng số khác 0)
Thu gọn rồi cho biết phần hệ số và phần biến của A
Giải:
Ta
có
![]()
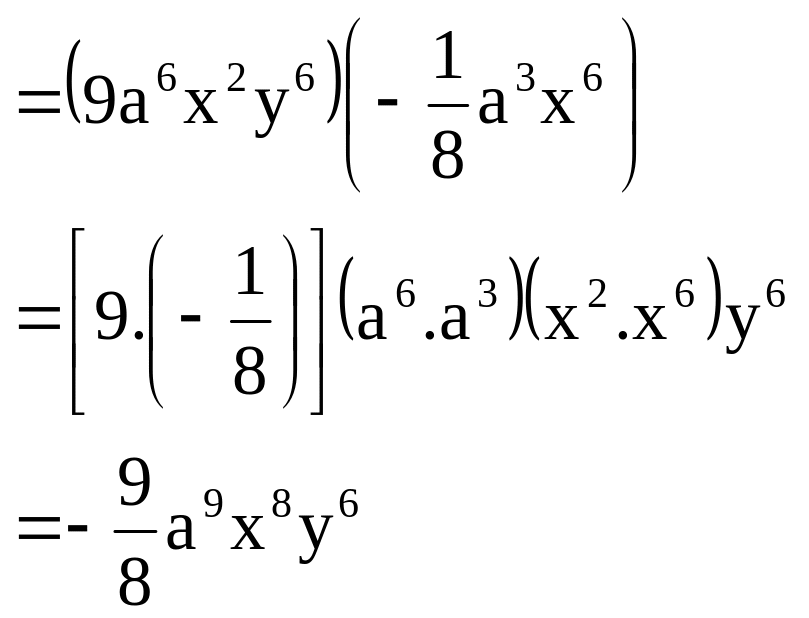
Phần
hệ số của A là:
![]()
Phần
biến của A là:
![]()
Tìm bậc của đơn thức A
Bậc
của đơn thức A là:
![]()
Bài 3: (2,5 điểm) Cho hai đa thức:
![]() và
và
![]()
Tính
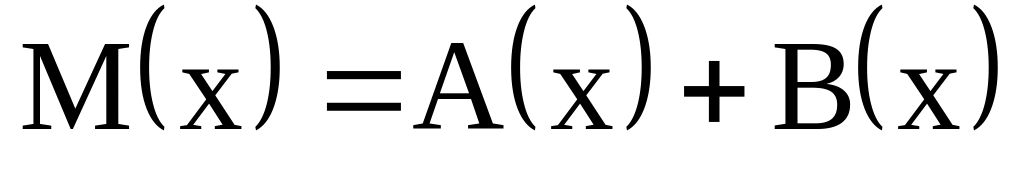 rồi
tìm nghiệm của đa thức
rồi
tìm nghiệm của đa thức
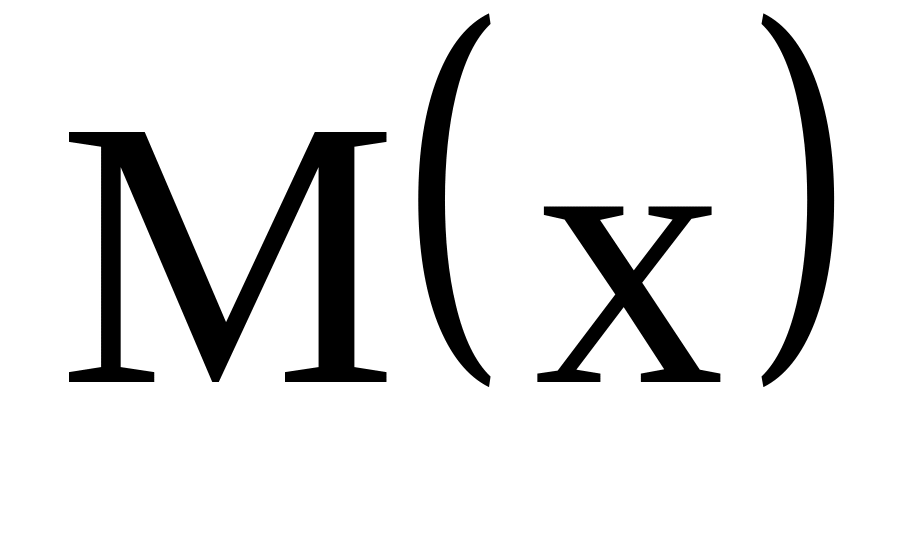
Giải:
Ta
có
![]()
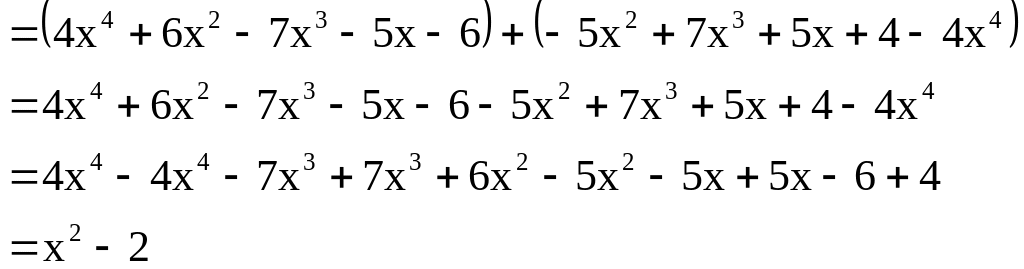
Ta
có
![]()
![]()
![]() hoặc
hoặc
![]()
![]() hoặc
hoặc
![]()
Vậy
nghiệm của đa thức M(x) là:
![]() hoặc
hoặc
![]()
Tìm đa thức
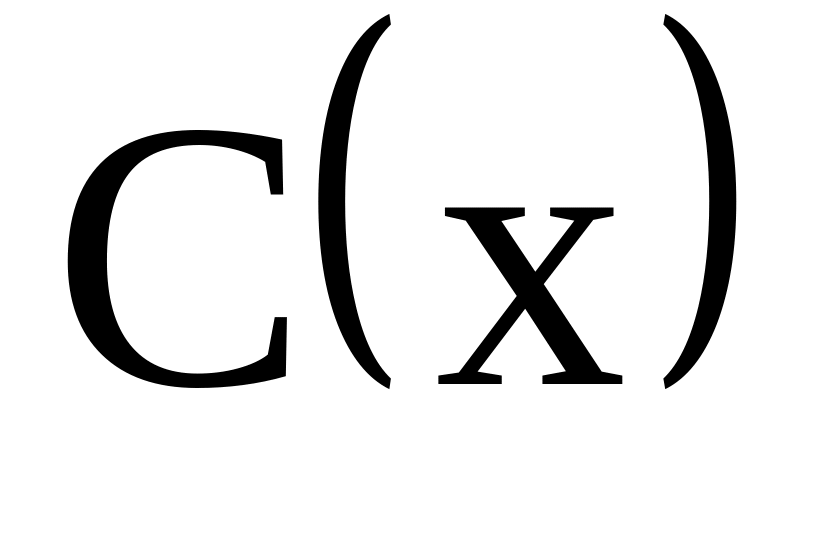 sao cho
sao cho
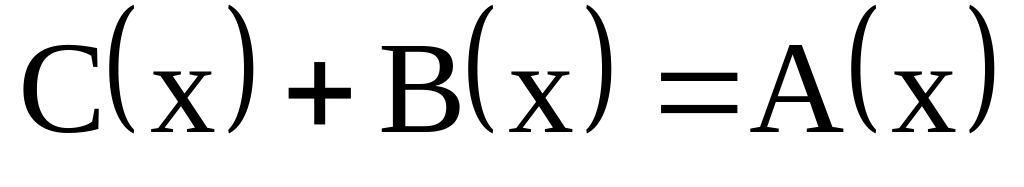
Giải:
Ta
có
![]()
![]()
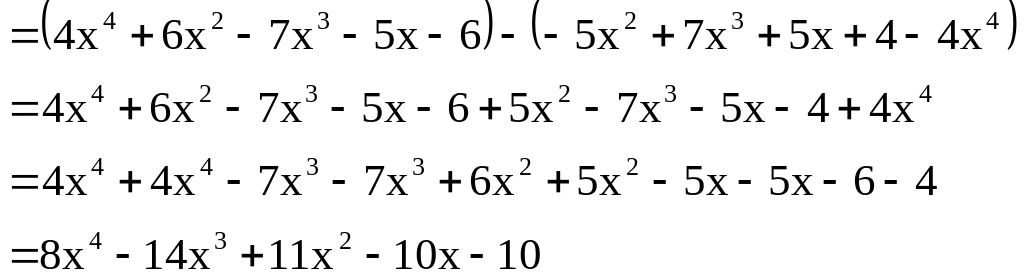
Bài
4: (0,5
điểm)
Cho
![]() .
Hỏi a có phải là nghiệm của đa thức
.
Hỏi a có phải là nghiệm của đa thức
![]() không? Vì sao?
không? Vì sao?
Giải:
Ta
có
![]()
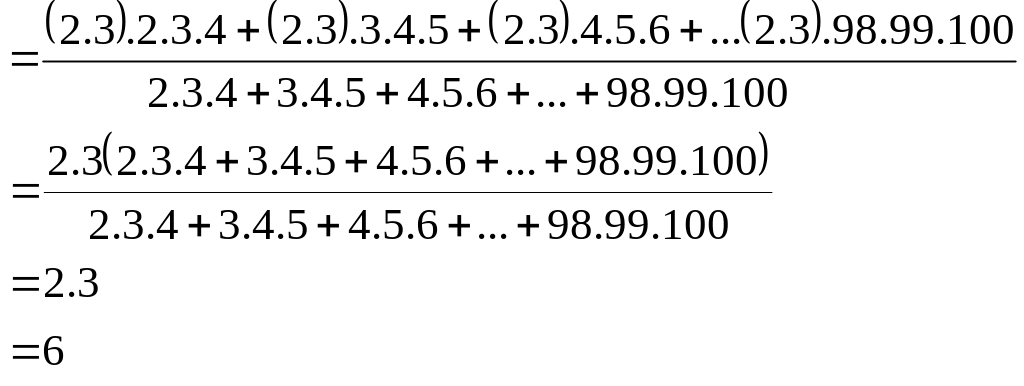
Thay a = 6 vào biểu thức P(x), ta được:
![]()
Vậy a = 6 không là nghiệm của đa thức P(x)
Bài 5: (3,5 điểm) Cho ΔABC vuông tại A, đường trung tuyến CM
Cho biết BC = 10cm, AC = 6cm. Tính độ dài đoạn thẳng AB, BM
Giải:
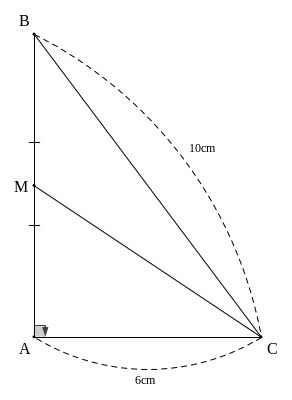
Ta có ΔABC vuông tại A
![]() (định lý Pytago)
(định lý Pytago)
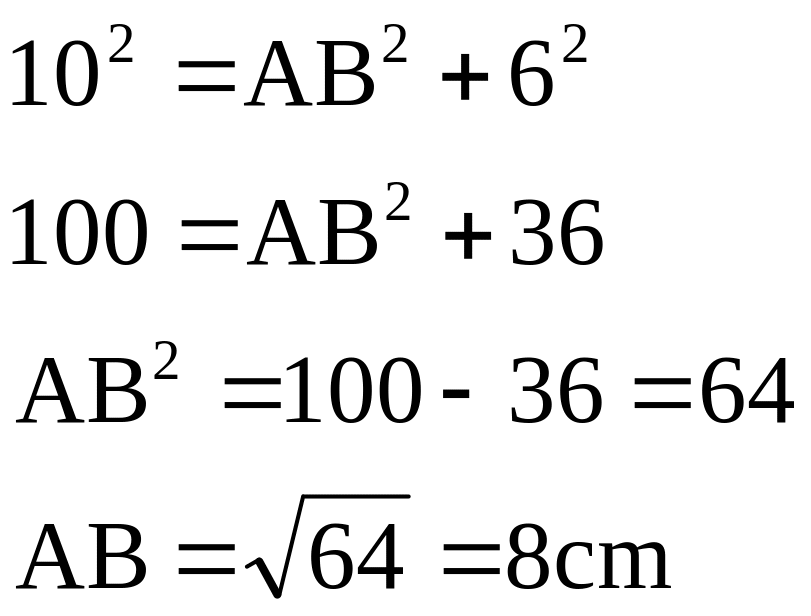
Ta
có
![]() (vì M là trung điểm của AB)
(vì M là trung điểm của AB)
Trên tia đối của tia MC lấy điểm D sao cho MD = MC. Chứng minh rằng ΔMAC = ΔMBD và AC = BD
Giải:
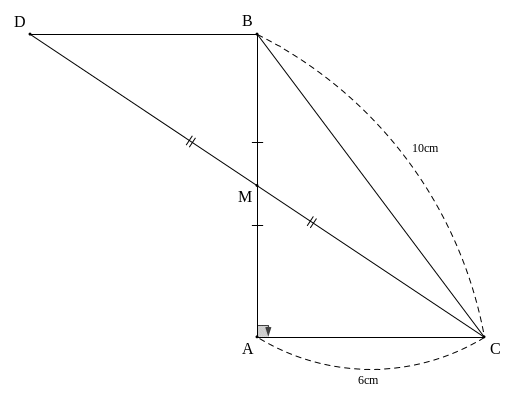
Xét ΔMAC và ΔMBD có:
![]() (2 góc đối đỉnh)
(2 góc đối đỉnh)
MA = MB (vì M là trung điểm của AB)
MC = MD (gt)
![]() ΔMAC ∽
ΔMBD (c.g.c)
ΔMAC ∽
ΔMBD (c.g.c)
![]() (2 cạnh tương ứng)
(2 cạnh tương ứng)
Chứng minh rằng AC + BC > 2CM
Giải:
Ta có AC + BC = BD + BC (1) (vì AC = BD)
Ta có 2CM = CD (2) (vì M là trung điểm của CD)
Xét ΔBCD có: BD + BC > CD (3) (bất đẳng thức tam giác)
Từ
(1), (2) và (3)
![]() AC + BC > 2CM
AC + BC > 2CM
Gọi K là điểm trên đoạn thẳng AM sao cho
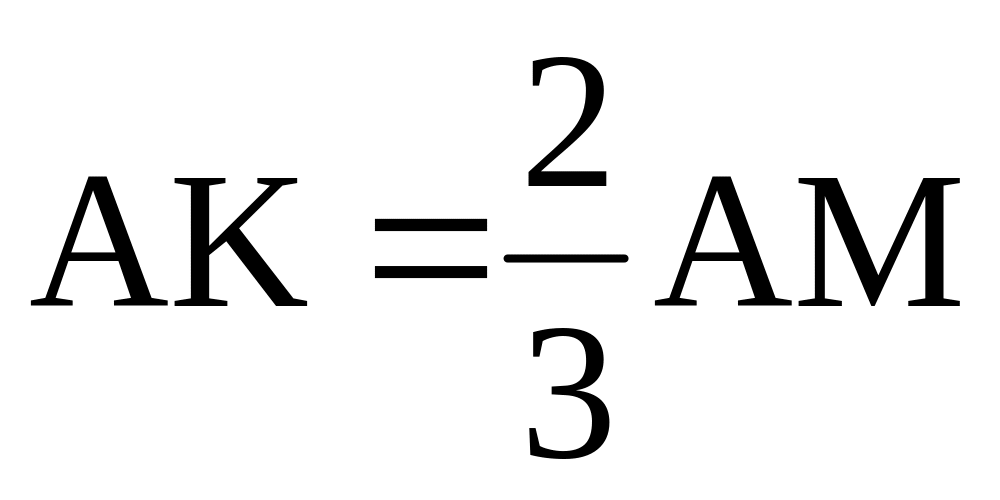 .
Gọi N là giao điểm của CK và AD, I là giao điểm của
BN và CD. Chứng minh rằng: CD = 3ID
.
Gọi N là giao điểm của CK và AD, I là giao điểm của
BN và CD. Chứng minh rằng: CD = 3ID
Giải:
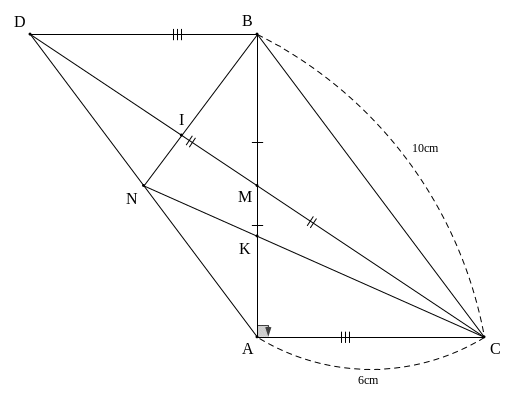
Xét
ΔACD có: AM là đường trung tuyến và
![]() (gt)
(gt)
![]() K là trọng tâm của ΔACD
K là trọng tâm của ΔACD
![]() CK cắt AD tại N là trung điểm của AD
CK cắt AD tại N là trung điểm của AD
Xét ΔABD có: DM và BN là 2 đường trung tuyến cắt nhau tại I
![]() I là trọng tâm ΔABD
I là trọng tâm ΔABD
![]()
![]() (vì M là trung điểm của DC)
(vì M là trung điểm của DC)
![]()
ĐỀ 8 |
ĐỀ THI HỌC KỲ II TOÁN 7 Thời gian: 90 phút |
A/ LÝ THUYẾT: (2 điểm)
Câu 1: (1 đ )
Bậc của đơn thức là gì?
b)
Thu gọn và tìm bậc đơn thức sau: -3x2y
. 4xy3
![]()
Câu 2:: (1 đ)
a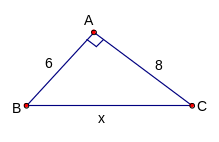 /
Phát biểu định lý Py-ta-go.
/
Phát biểu định lý Py-ta-go.
b/ Tìm x trên hình vẽ bên
B/ BÀI TẬP (8 điểm)
Câu 3 (2 đ) ) Thời gian giải xong một bài toán (tính bằng phút) của mỗi học sinh lớp 7 được ghi lại ở bảng sau:
-
10
13
15
10
13
15
17
17
15
13
15
17
15
17
10
17
17
15
13
15
a) Dấu hiệu điều tra ở đây là gì? Có bao nhiêu giá trị của dấu hiệu?
b)
Lập bảng tần số và tính số trung bình cộng của dấu
hiệu.
![]()
Câu 4 (3 đ ) Cho hai đa thức f(x) = 3x + x3 + 2x2 + 4
g(x) = x3 + 3x + 1 – x2
a)
Sắp xếp các đa thức trên theo lũy thừa giảm dần của
biến.
![]()
b) Tính f(x) + g(x) và f(x) – g(x)
c) Chứng tỏ f(x) – g(x) không có nghiệm .
Câu 5 (3 đ) Cho tam giác ABC cân tại A, đường cao AH. Biết AB = 10cm,
BC = 12cm.
a)
Chứng minh
![]() .
.
b) Tính độ dài đoạn thẳng AH.
c) Gọi G là trọng tâm của tam giác ABC. Chứng minh ba điểm A, G, H thẳng hàng.
Đ
Câu |
Nội dung |
Điểm |
||||||||||||
1 (1đ )
2 ( 1đ )
3 (2 đ) |
a)Bậc của đơn thức có hệ số khác 0 là tổng số mũ của tất cả các biến có trong đơn thức đó. b) -3x2y . 4xy3 = -12x3y4 a/ Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.
b/
hay
a)Dấu hiệu ở đây là thời gian làm một bài toán (tính bằng phút) của mỗi học sinh. Có 20 giá trị. b) Bảng “tần số”
Tính số trung bình cộng
|
0,5đ
0,5đ
0,5đ
0,5đ
0,5đ
1đ
0,5đ
|
||||||||||||
4 ( 3 đ) |
a) f(x) = 3x + x3 + 2x2 + 4 = x3 + 2x2 + 3x + 4 g(x) = x3 + 3x + 1 – x2 = x3 – x2 + 3x + 1
b) f(x) + g(x) = (x3 + 2x2 + 3x + 4) + (x3 – x2 + 3x + 1) = x3 + 2x2 + 3x + 4 + x3 – x2 + 3x + 1 = ( x3 + x3) + (2x2 – x2) + ( 3x + 3x) + (4 + 1) = 2x3 + x2 + 6x +5
f(x) – g(x) = (x3 + 2x2 + 3x + 4) – (x3 – x2 + 3x + 1) = x3 + 2x2 + 3x + 4 - x3 + x2 - 3x – 1 = ( x3 - x3) + (2x2 + x2) + ( 3x - 3x) + (4 - 1) = 3x2 + 3
Do đó không tìm được giá trị nào của x để 3x2 + 3 = 0 Vậy f(x) – g(x) = 3x2 + 3 không có nghiệm. |
0,25đ
0,25đ
1 đ
1 đ
0,5đ
|
||||||||||||
5(3 đ) |
Vẽ hình , ghi GT- KL
Góc AHB = Góc AHC = 900 (gt) AB = AC (vì ∆ABC cân tại A) Có cạnh AH chung Vậy ∆ABH = ∆ACH (cạnh huyền- cạnh góc vuông)
AB
= 10cm,
Áp dụng định lý pytago ta có :
|
0,5đ
1 đ
1 đ
0,5đ |
Lưu ý: Nếu học sinh giải theo cách khác đúng, vẫn cho điểm tối đa.
ĐỀ 9 |
ĐỀ THI HỌC KỲ II TOÁN 7 Thời gian: 90 phút |
Câu1: (1,5đ)
Điểm kiểm tra 1 tiết môn toán của lớp 7A được bạn lớp trưởng ghi lại như sau
-
5
8
4
8
6
6
5
7
4
3
6
7
7
3
8
6
7
6
5
9
7
9
7
4
4
7
10
6
7
5
4
7
6
5
2
8
Dấu hiệu ở đây là gì? Số các giá trị là bao nhiêu?
Lập bảng “tần số” và tìm Mốt của dấu hiệu.
Tính số trung bình cộng của dấu hiệu.
Câu2: (1đ)
Cho
đa thức M = 6 x6y
+
![]() x4y3
– y7
– 4x4y3
+ 10 – 5x6y
+ 2y7
– 2,5.
x4y3
– y7
– 4x4y3
+ 10 – 5x6y
+ 2y7
– 2,5.
Thu gọn và tìm bậc của đa thức.
Tính giá trị của đa thức tại x = -1 và y = 1.
Câu3: (2,5)
Cho hai đa thức:
P(x) = x2 + 5x4 – 3x3 + x2 + 4x4 + 3x3 – x + 5
Q(x) = x - 5x3– x2 – x4 + 4x3 - x2 + 3x – 1
Thu gọn rồi sắp xếp các đa thức trên theo luỹ thừa giảm dần của biến.
Tính P(x) + Q(x) và P(x) - Q(x)
Câu4: (1đ)
Tìm nghiệm của các đa thức
a. R(x) = 2x + 3 b. H(x) = (x – 1)( x+ 1)
C âu5:
(3đ)
âu5:
(3đ)
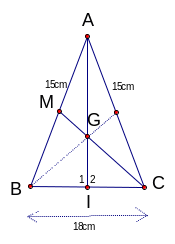
 Cho
ABC cân tại A ( A nhọn ). Tia phân giác góc của A cắt
BC tại I.
Cho
ABC cân tại A ( A nhọn ). Tia phân giác góc của A cắt
BC tại I.
 a.
Chứng minh AI BC.
a.
Chứng minh AI BC.
b. Gọi D là trung điểm của AC, M là giao điểm của BD với AI. Chứng minh rằng M là trọng tâm của tâm giác ABC.
c. Biết AB = AC = 5cm; BC = 6 cm. Tính AM.
Câu6: (1đ)
Trên tia phân giác góc A của tam giác ABC ( AB > AC) lấy điểm M.
 Chứng
minh MB - MC
Chứng
minh MB - MC
![]() <
AB – AC
<
AB – AC
………….. Hết ………….
ĐÁP ÁN VÀ THANG ĐIỂM
( Đáp án này gồm 02 trang )
Câu |
Ý |
Nội dung |
Điểm |
||||||||||||||||||||||
1 |
a
b
c |
- Dấu hiệu ở đây là điểm kiểm tra toán một tiết của mỗi học sinh - Số các giá trị là : N = 36 Bảng tần số:
M0 = 7
|
0,5
0,5
0,5 |
||||||||||||||||||||||
2 |
a
b |
- Thu gọn đa thức ta
được: M =
y7
+ x6y
-
- Thay x = -1 và y = 1 vào đa thức ta được : M(-1;
1) = 17
+ (-1)6.1
-
|
0,5
0,5 |
||||||||||||||||||||||
3 |
a
b |
- Thu gọn rồi săp xếp theo lũy thừa giảm dần của biến, ta được: P(x) = x2 + 5x4 - 3x3 + x2 + 4x4 + 3x3 - x + 5 = 9x4 + 2 x2 - x + 5 Q(x) = x - 5x3 - x2 - x4 + 4x3 - x2 + 3x - 1= - x4 - x3 - 2x2 + 4x - 1 P(x) + Q(x) = 8x4 - x3 + 3x + 4 P(x) - Q(x) = 10 x4 - x3 + 4x2 - 5x + 6 |
1
0,75 0,75 |
||||||||||||||||||||||
4 |
a
b |
Tìm được nghiệm của
đa thức a.
R(x) = 2x + 3 là x =
b. H(x) = (x – 1)( x+ 1) là x = 1 và x = -1
|
0,5
0,5 |
||||||||||||||||||||||
5 |
a
b
c
|
- -
- Ta có DA = DC => BD là đường trung tuyến ứng với cạnh AC. Trong tam giác cân ABC ( cân tại A), AI là đường phân giác ứng với đáy BC => AI cũng là đường trung tuyến => M là giao của AI và BD nên M là trọng tâm của tam giác ABC ( Tính chất ba đường trung tuyến của tam giác) đpcm Trong
tam giác cân ABC ( Cân tại A), AI là phân giác cũng là
trung tuyến => IB = IC =
=> IB = IC = 3 (cm) Áp dụng định lí Py-ta-go vào tam giác vuông AIB, ta có: AI2 = AB2 – IB2 = 52 – 32 = 16
=> AI = 4 (cm) M
là trọng tâm của tam giác ABC => AM =
|
0,5 0,5
0,5
0,5
|
||||||||||||||||||||||
6 |
|
- kẻ MI vuông góc với AB; MJ vuông góc với AC => MI = MJ (1) ( Tính chất tia phân giác của góc) - Ta lại có AB – AC = AI + IB – ( AJ + JC) => AB – AC = IB – JC (2) ( hai tam giác vuông AIM và AJM bằng nhau ( ch-gn) => AI = AJ). - Trong tam giác BMC’, ta có C’B > BM – MC’ ( BĐT tam giác) (4) - Từ (3), (4) và (5) suy ra AB – AC > MB - MC đpcm
|
0,25
0,25
0,25
0,25 |
||||||||||||||||||||||
|
|
|
|
ĐỀ 10 |
ĐỀ THI HỌC KỲ II TOÁN 7 Thời gian: 90 phút |
Câu1: (1,5đ)
Thời gian ( Tính bằng phút) giải một bài toán của học sinh lớp 7A được thầy giáo bộ môn ghi lại như sau
-
4
8
4
8
6
6
5
7
5
3
6
7
7
3
6
5
6
6
6
9
7
9
7
4
4
7
10
6
7
5
4
6
6
5
4
8
Dấu hiệu ở đây là gì? Số các giá trị là bao nhiêu?
Lập bảng “tần số” và tìm Mốt của dấu hiệu.
Tính số trung bình cộng của dấu hiệu.
Câu2: (1đ)
Cho
đa thức M = 3x6y
+
![]() x4y3
– 4y7
– 4x4y3
+ 11 – 5x6y
+ 2y7
- 2.
x4y3
– 4y7
– 4x4y3
+ 11 – 5x6y
+ 2y7
- 2.
Thu gọn và tìm bậc của đa thức.
Tính giá trị của đa thức tại x = 1 và y = -1.
Câu3: (2,5)
Cho hai đa thức:
R(x) = x2 + 5x4 – 2x3 + x2 + 6x4 + 3x3 – x + 15
H(x) = 2x - 5x3– x2 – 2 x4 + 4x3 - x2 + 3x – 7
Thu gọn rồi sắp xếp các đa thức trên theo luỹ thừa giảm dần của biến.
Tính R(x) + H(x) và R(x) - H(x)
Câu4: (1đ)
Tìm nghiệm của các đa thức
a. P(x) = 5x - 3 b. F(x) = (x +2)( x- 1)
C âu5:
(3đ)
âu5:
(3đ)
 Cho
ABC cân tại A ( A nhọn ). Tia phân giác góc của A cắt
BC tại I.
Cho
ABC cân tại A ( A nhọn ). Tia phân giác góc của A cắt
BC tại I.
 a.
Chứng minh AI BC.
a.
Chứng minh AI BC.
b. Gọi M là trung điểm của AB, G là giao điểm của CM với AI. Chứng minh rằng BG là đường trung tuyến của tam giác ABC.
c. Biết AB = AC = 15cm; BC = 18 cm. Tính GI.
Câu6: (1đ)
Cho đoạn thẳng AB. Gọi d là đường trung trực của AB. Trên đường thẳng d lấy điểm M bất kì. Trong mặt phẳng lấy đểm C sao cho BC < CA.
So sánh MB + MC với CA.
Tìm vị trí của M trên d sao cho MB + MC nhỏ nhất.
………….. Hết ………….
ĐÁP ÁN VÀ THANG ĐIỂM
( Đáp án này gồm 02 trang )
Câu |
Ý |
Nội dung |
Điểm |
||||||||||||||||||||||
1 |
a
b
c |
- Dấu hiệu ở đây là thời gian ( tính bằng phút) giải một bài toán toán của mỗi học sinh - Số các giá trị là : N = 36 Bảng tần số:
M0 = 6
|
0,5
0,5
0,5 |
||||||||||||||||||||||
2 |
a
b |
- Thu gọn đa thức ta
được: M = - 2y7
- 2x6y
- - Thay x = 1 và y = -1 vào đa thức ta được : M(1;
-1) = -2.17
-2 .16.(-1)
-
|
0,5
0,5 |
||||||||||||||||||||||
3 |
a
b |
- Thu gọn rồi săp xếp theo lũy thừa giảm dần của biến, ta được: R(x) = x2 + 5x4 – 2x3 + x2 + 6x4 + 3x3 – x + 15 = 11x4 + x3 +2x2 – x + 15 H(x) = 2x - 5x3– x2 – 2 x4 + 4x3 - x2 + 3x – 7 = -2x4 - x3 -2x2 + 5x - 7 R(x) + H(x) = 9x4 + 4x +8 R(x) - H(x) = 13x4 + 2x3+ 4x2 – 6x + 22 |
1
0,75 0,75 |
||||||||||||||||||||||
4 |
a
b |
Tìm nghiệm của các đa thức a.
P(x) = 5x - 3 có nghiệm <=> 5x - 3 = 0 <=> x =
b. F(x) = (x +2)( x- 1) có nghiệm <=> (x +2)( x- 1) = 0 <=> (x +2) = 0 hoặc ( x- 1) =0 <=> x= -2 hoặc x = 1
|
0,5
0,5 |
||||||||||||||||||||||
5 |
a
b
c
|
- -
- Ta có MA = MB => CM là đường trung tuyến ứng với cạnh AB. Trong tam giác cân ABC ( cân tại A), AI là đường phân giác ứng với đáy BC => AI cũng là đường trung tuyến => G là giao của AI và CM nên G là trọng tâm của tam giác ABC ( Tính chất ba đường trung tuyến của tam giác) => BG là đường trung tuyến của tam giác ABC. đpcm -
Trong tam giác cân ABC ( Cân tại A), AI là phân giác cũng
là trung tuyến => IB = IC =
- Áp dụng định lí Py-ta-go vào tam giác vuông AIB, ta có: AI2 = AB2 – IB2 = 152 – 92 = 144
=> AI = 12 (cm) G
là trọng tâm của tam giác ABC => GI =
|
0,5 0,5
0,5
0,5
0,5
0,5
|
||||||||||||||||||||||
6 |
a
b |
- M d nên MA = MB. Vậy MB + MC = MA + MC. Trong tam giác MAC, ta có : MA + MC > AC. Vậy MB + MC > AC Vì CB < CA nên C và B nằm trong cùng một nửa mặt phẳng bờ d. Do đó A và C nằm trong hai nửa mặt phẳng bờ d khác nhau. Do đó d cắt AC tại H. => MB + MC = AC Vậy ta có MB + MC ≥ AC - Khi M trùng với H thì HB + HC = AC. T
|
0,25
0,25
0,25
0,25 |
||||||||||||||||||||||
|
|
|
|
ĐỀ 11 |
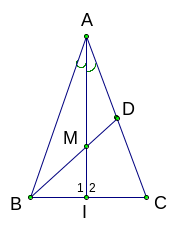
ĐỀ THI HỌC KỲ II TOÁN 7 Thời gian: 90 phút |

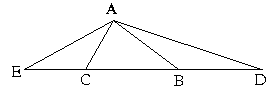
Câu 1: (2.0 điểm) Điểm kiểm tra một tiết môn Toán của học sinh một lớp 7 tại một trường THCS được cho trong bảng “tần số” sau:
Điểm số (x) |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Tần số (n) |
1 |
2 |
7 |
8 |
5 |
11 |
4 |
2 |
N = 40 |
Dấu hiệu điều tra ở đây là gì?
Có bao nhiêu học sinh làm kiểm tra? Số các giá trị khác nhau?
Tìm mốt của dấu hiệu và tính số trung bình cộng.
Câu 2: (1.0 điểm) Thu gọn và tìm bậc của các đơn thức sau:
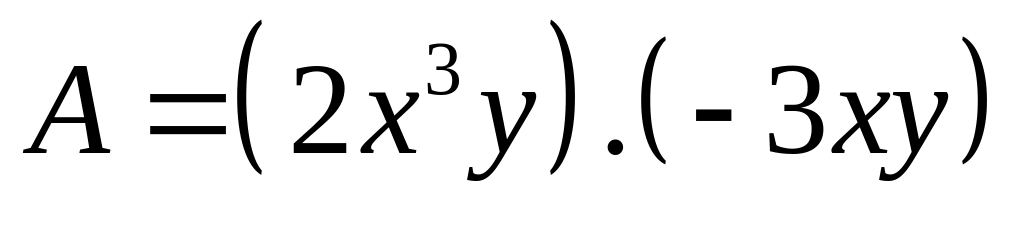 b)
b)
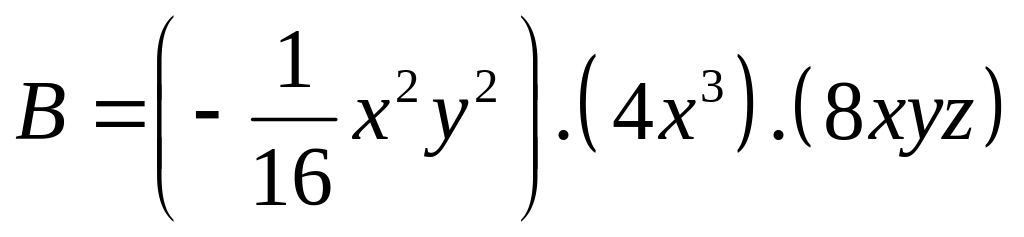
Câu 3: (1.0 điểm) Tìm đa thức M biết:
Câu
4:
(2 điểm) Cho các đa thức sau:
![]() và
và
![]()
Tính
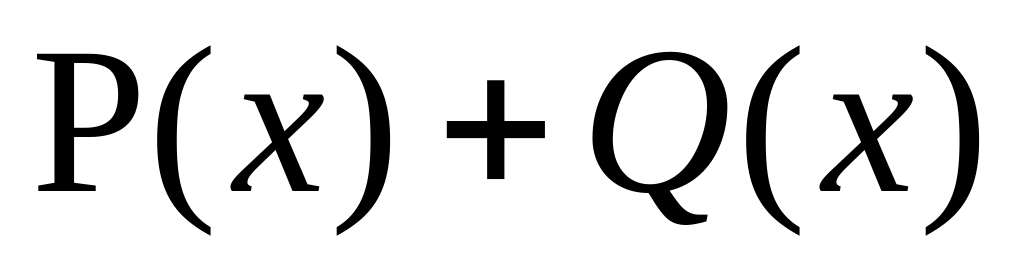
Tính
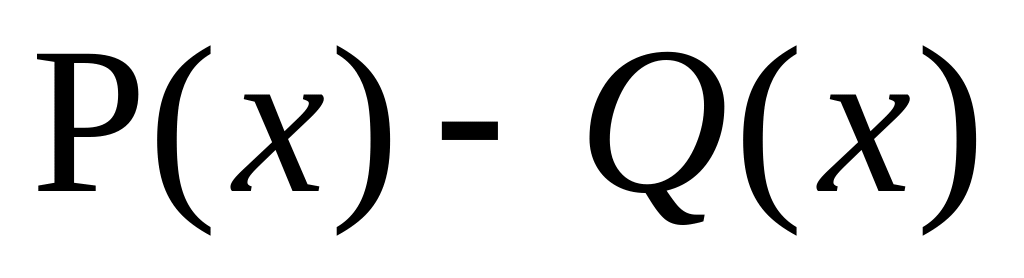
Tìm nghiệm của đa thức H(x) biết
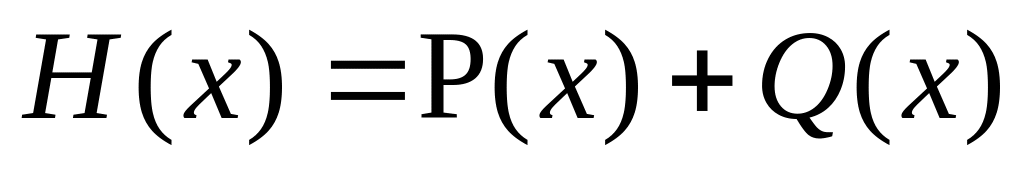 .
.
Câu
5: (1.0
điểm)
Cho hai đa thức
![]() và
và
![]() (a, b là hằng số).
(a, b là hằng số).
Tìm
các hệ số a, b sao cho
![]() và
và
![]()
Câu
6: (3.0
điểm)
Cho
![]() vuông
tại A, có AB = 6cm, AC = 8cm.
vuông
tại A, có AB = 6cm, AC = 8cm.
Tính độ dài cạnh BC và chu vi tam giác ABC.
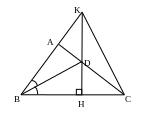
Đường phân giác của góc B cắt AC tại D. Vẽ
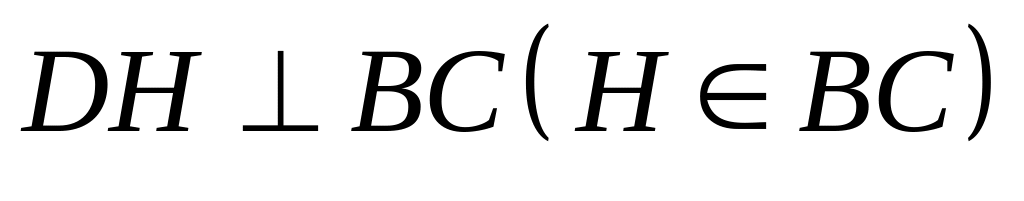 .
.
Chứng
minh:
![]()
Chứng minh: DA < DC.
----------HẾT----------
(Học sinh không được sử dụng máy tính)
ĐÁP ÁN – THANG ĐIỂM
Câu |
Ý |
Đáp án |
Thang điểm |
Câu 1 (2.0 điểm) |
a |
Dấu hiệu điều tra: “Điểm kiểm tra 1 tiết môn Toán của mỗi học sinh một lớp 7” |
0.5 |
b |
Có 40 học sinh làm kiểm tra. Có 8 giá trị khác nhau. |
0.5 |
|
c |
Mốt của dấu hiệu: 8 Số
trung bình cộng |
0.5 0.5 |
|
Câu 2 (1.0 điểm) |
a |
|
0.5 |
b |
|
0.5 |
|
Câu 3 (1.0 điểm) |
a |
|
0.5 |
b |
|
0.5 |
|
Câu 4 (2.0 điểm) |
a |
|
0.75 |
b |
|
0.75 |
|
c |
Vậy nghiệm của đa thức H(x) là x = 0; x = 1. |
0.5 |
|
Câu 5 (1.0 điểm) |
|
Theo đề bài ta có:
Thay (2) vào (1) ta được:
V |
0.25 0.25
0.25 0.25 |
Câu 6 (3.0 điểm)
|
a |
Áp dụng định lí Py-ta-go vào tam giác vuông ABC ta có:
Chu vi tam giác ABC: AB + AC + BC = 24 cm |
0.5 0.5 |
b |
Xét hai tam giác vuông ABD và HBD có: BD là cạnh chung
|
0.5
0.5 |
|
c |
Từ
câu b)
Xét tam giác vuông DHC có: DC > DH (DC là cạnh huyền) (2) Từ (1) và (2) suy ra: DC > DA |
0.25
0.25
0.5 |
ĐỀ 12 |
ĐỀ THI HỌC KỲ II TOÁN 7 Thời gian: 90 phút |
I) Trắc nghiệm: (2 điểm).
Hãy viết vào bài thi chỉ một chữ cái in hoa đứng trước đáp số đúng.
Câu
1: Thực hiện phép
tính:
![]() ta
được kết quả bằng:
ta
được kết quả bằng:
A.
![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
Câu
2: Đơn thức
![]() có bậc là:
có bậc là:
A. 3 B. 4 C. 5 D. 12.
Câu
3: Cho hai đa thức:
![]() và
và
![]() khi đó
khi đó
![]() bằng:
bằng:
A.
![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
Câu 4: Cho tam giác ABC với AD là trung tuyến, G là trọng tâm, AD= 12 cm. Khi đó độ dài đoạn GD bằng:
A. 8cm B. 9cm C. 6cm D. 4cm.
II) Tự luận (8 điểm).
Câu 5: Cho tam giác ABC với AC < AB. Trên tia đối của tia BC lấy điểm D sao cho
BD = AB. Trên tia đối của tia CB lấy điểm E sao cho CE = AC. Vẽ các đoạn thẳng AD, AE.
a) So sánh góc ADC và góc AEB.
b) So sánh các đoạn thẳng AD và AE.
Câu 6:
a) Tìm nghiệm của đa thức:
![]() .
.
b)
Chứng tỏ đa thức sau không có nghiệm:
![]()
----------------------------------------------------
ĐÁP ÁN
Phần |
Câu |
Nội dung |
Điểm |
Trắc nghiệm |
Câu 1 |
A |
0,5điểm |
Câu 2 |
D |
0,5 điểm |
|
Câu 3 |
B |
0,5 điểm |
|
Câu 4 |
D |
0,5 điểm |
|
Tự luận |
Câu 5
|
a)
xét
tam giác cân ACE đáy AE và tam giác ABD cân tại B ta có:
Từ
(1) và (2)
b)
Xét tam giác ADE có
|
hvẽ: 0,5đ
2 điểm
1,5 điểm |
Câu 6 |
a) Tìm được nghiệm y=-6 b)
Tại y=a bất kỳ ta có:
Vậy đa thức Q(y) không có nghiệm. |
2,0 điểm
2,0điểm.
|
ĐỀ 13 |
ĐỀ THI HỌC KỲ II TOÁN 7 Thời gian: 90 phút |
Câu 1 (2,0 điểm) Thực hiện các phép tính sau:
a)
![]() .
.
b)
![]() .
.
Câu 2 (3,0 điểm)
Tìm
 ,
biết
,
biết
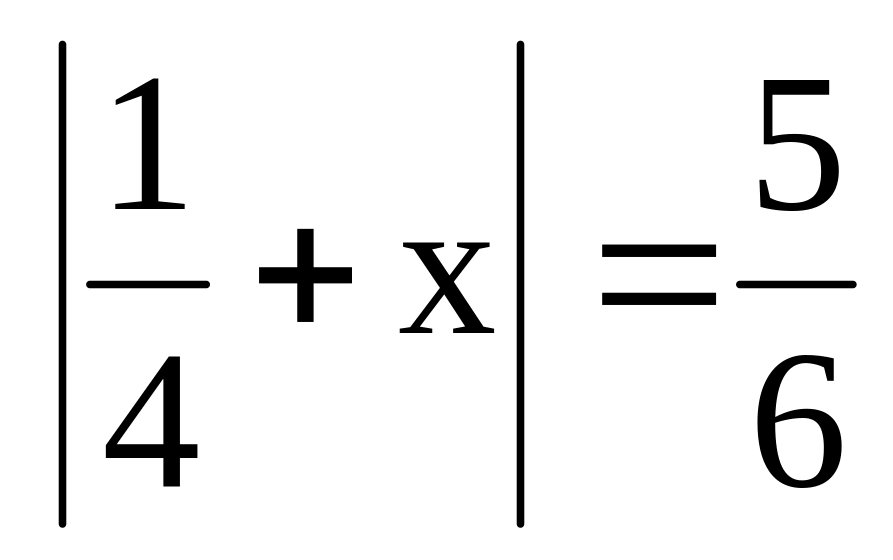 .
.
b)
Tính giá trị của biểu thức
![]() khi
khi
![]() .
.
c) Cho
đơn thức
![]() .
Hãy thu gọn và chỉ ra
hệ số, phần biến và bậc
của đơn thức A.
.
Hãy thu gọn và chỉ ra
hệ số, phần biến và bậc
của đơn thức A.
Câu 3 (1,5 điểm)
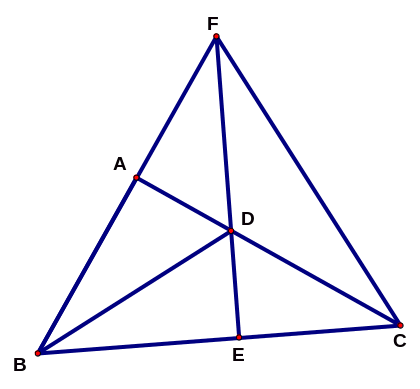
Cho hai đa
thức
![]() và
và
![]()
a)
Tìm
![]() .
.
b)
Tìm nghiệm của đa thức
![]() .
.
Câu 4 (3,0 điểm)
Cho tam giác ABC có AB = 6 cm; AC = 8 cm; BC = 10 cm.
a) Chứng minh tam giác ABC vuông tại A.
b) Vẽ tia phân giác BD của góc ABC (D thuộc AC), từ D vẽ DE BC (E BC).
Chứng minh DA = DE.
c) Kéo dài ED và BA cắt nhau tại F. Chứng minh DF > DE.
d) Chứng minh đường thẳng BD là đường trung trực của đoạn thẳng FC.
Câu 5. (0,5 điểm)
Cho
![]() trong đó
trong đó
![]() và thỏa mãn
và thỏa mãn
![]() Chứng minh rằng
Chứng minh rằng
![]() là bình phương của một số nguyên.
là bình phương của một số nguyên.
-----------------------Hết-----------------------
ĐÁP ÁN
Bài |
Sơ lược các bước giải |
Điểm |
Câu 1 |
|
2,0 |
Phần a 1 điểm |
|
0.5 |
|
0.5 |
|
Phần b 1 điểm |
|
0.25 |
|
0.75 |
|
Câu 2 |
|
3,0 |
Phần a 1 điểm |
|
0.5 |
+ HS xét
hai trường hợp tính được
|
0.25 |
|
KL:
|
0.25 |
|
Phần b 1 điểm |
Tính giá trị của biểu thức A = 5x2 – 3x – 16 tại x = -2 |
|
Thay x = -2 vào biểu thức A, ta được: A= 5.(-2)2 – 3.(-2) - 16 |
0. 5 |
|
A=5.4 + 6 – 16 = 10 |
0.25 |
|
Vậy A=10 khi x = -2. |
0.25 |
|
Phần c 1 điểm |
|
0.25 |
|
0.5 |
|
Đơn thức
A có: Hệ số là 16; phần biến là
|
0.25 |
|
Câu 3 |
|
1,5 |
Phần a 1 điểm |
|
0.25 |
HS làm đầy đủ, chi tiết
được h(x) =
|
0.75 |
|
Phần b 0,5 điểm |
|
0.25 |
Vậy
|
0.25 |
|
Câu 4 |
|
3,0 |
|
|
|
Phần a 1 điểm |
Ta có AB= 6(cm) (gt); AC = 8(cm) (gt) nên AB2 + AC2 = 62 + 82 =100 (cm) (1) Mà BC = 10(cm) (gt) nên BC2 = 102 = 100 (cm) (2) |
0.5
|
Từ (1) và (2) suy ra AB2 + AC2 = BC2 |
0.25 |
|
Xét tam giác ABC có AB2 + AC2 = BC2(chứng minh trên) nên tam giác ABC vuông tại A (Định lí pytago đảo) |
0.25 |
|
Phần b 1 điểm |
Vì BD là phân giác của góc ABC; DA, DE lần lượt là khoảng cách từ D đến AB, BC |
0.5 |
HS suy ra DA = DE |
0.5 |
|
Phần c 0.5 điểm |
* Tam giác ADF vuông tại A nên DF > AD |
0.25 |
* Lại có AD = DE (chứng minh trên) nên DF > DE |
0.25 |
|
Phần d 0.5 điểm |
* HS chứng minh BF = BC suy ra B thuộc đường trung trực FC (3) |
0.25 |
* HS chứng minh DF = DC suy ra D thuộc đường trung trực FC (4) * Từ (3) và (4) suy ra BD là đường trung trực của FC |
0.25 |
|
Câu 5 |
|
0,5 |
0.5 |
Ta có
|
0.25 |
Suy ra
Suy ra
|
0.25 |
|
|
Điểm toàn bài |
10 điểm |

ĐỀ 14 |
ĐỀ THI HỌC KỲ II TOÁN 7 Thời gian: 90 phút |
I/ PHẦN TRẮC NGHIỆM ( 2 điểm): Chọn đáp án đúng trong các câu sau:
Câu 1: Cho bảng sau
Giá trị (x) |
97 |
99 |
100 |
102 |
105 |
N= 40 |
Tần số (n) |
3 |
5 |
29 |
2 |
1 |
Mốt của dấu hiệu là: A. 29 B. 99 C. 100 D. 103
Câu 2: Cũng với bảng trên số trung bình cộng của dấu hiệu là:
-
A. 99,5
B. 99,875
C. 100,6
D.101,2
Câu 3: Đơn thức đồng dạng với đơn thức - 5ab2 là:
-
A. 2ab
B. 5a2b
C. 3b2a
D. a2b2
Câu
4:
Kết
quả phép tính
2x2y3z4.(![]() xy2)2
là:
xy2)2
là:
-
A. 2x4y3z4
B.
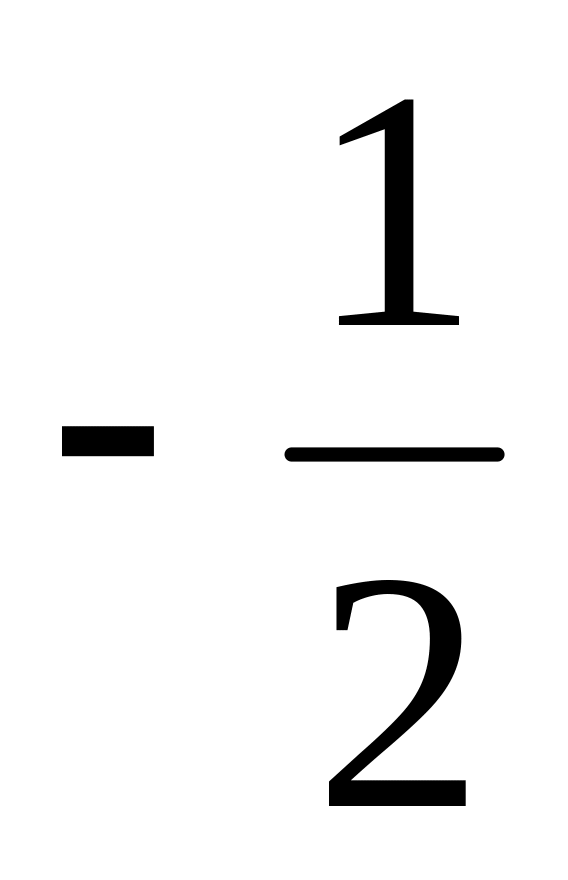 x4y5z4
x4y5z4C. - x3y5z4
D.
 x4y7z4
x4y7z4
Câu
5:
Bậc
của đơn thức
![]() x3yz5
là:
x3yz5
là:
-
A. 3
B. 5
C. 8
D. 9
Câu 6: Cho tam giác cân biết hai trong ba cạnh của tam giác có độ dài là 3,9 cm và 7,9 cm thì chu vi tam giác đó là:
-
A. 19,7 cm
B. 16 cm
C. 15,7 cm
D.11.8 cm
Câu
7:
Cho tam giác ABC vuông tại A biết
![]() =
400
khi đó:
=
400
khi đó:
A. BC>AC>AB |
B. BC>AB>AC |
C. AB>AC>BC |
D. AC>AB>BC |
Câu
8:
Cho tam giác MNP có
![]() =
900
biết MN= 9cm; MP= 15cm độ dài cạnh PN là:
=
900
biết MN= 9cm; MP= 15cm độ dài cạnh PN là:
-
A. 12cm
B. 144 cm
C. 306 cm
D.
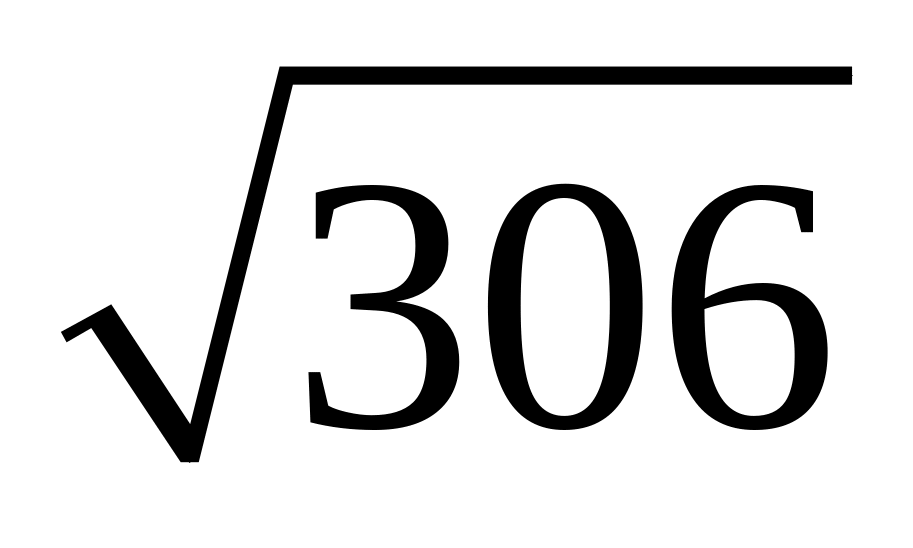 cm
cm
PHẦN II: TỰ LUẬN ( 8 điểm)
Bài 1 (1,5 điểm):
a) Tính giá trị của biểu thức sau bằng cách hợp lí (nếu có thể)
![]()
b)
Thu gọn biểu thức sau:
![]() .
.
![]()
Bài 2 (2,5 điểm): Cho đa thức A = x3 – 2x2 + 3x + 2 – x3 + x – 2
a)
Thu gọn đa thức A và tính giá trị của A tại
![]() =
=
![]()
b) Tính tổng M = A+ B và hiệu N = A – B biết B = 3x2 – 2x +1
Bài
3 (3,0 điểm):
Cho
![]() vuông tại A, kẻ tia phân giác của
vuông tại A, kẻ tia phân giác của
![]() cắt AC tại D. Kẻ DE vuông góc với BC tại E, gọi F là
giao điểm của BA và ED .
cắt AC tại D. Kẻ DE vuông góc với BC tại E, gọi F là
giao điểm của BA và ED .
a)
Chứng minh
![]()
b) So sánh AD và DC.
c) Gọi K là trung điểm của FC. Chứng minh ba điểm B; D; K thẳng hàng.
Bài
4 (1,0 điểm):
Cho
![]()
Tính
Q =
![]()
........HẾT.........
ĐÁP ÁN VÀ BIỂU ĐIỂM:
I, Phần trắc nghiệm(2đ). Mỗi ý đúng cho 0,25điểm
Câu 1 |
Câu 2 |
Câu 3 |
Câu 4 |
Câu 5 |
Câu 6 |
Câu 7 |
Câu 8 |
C |
B |
C |
D |
D |
A |
B |
A |
II, Tự luận(8đ)
Bài |
|
Nội dung |
Biểu điểm |
Bài 1 (1,5đ) |
Câu a 1,0đ
|
a)
=
=
=
=
|
0,25đ
0,25đ
0,25đ
0,25đ
|
|
Câu b 0,5 đ |
= =
|
0,25đ
0,25đ |
Bài 2 (2,5đ) |
Câu a 1,5đ |
a)-Thu gọn đa thức A = - 2x2 + 4x
+)Với
+)
Thay
=
Tại
+)
Thay
=
Tại
|
0,5đ
0,25đ
0,25đ
0,25đ
0,25đ |
|
Câu b 1,0đ |
+) M = – 2x2 + 4x + 3x2 – 2x+1 = x2 + 2x+1 +) N= – 2x2 + 4x – 3x2+ 2x – 1 = -5x2 + 6x –1
|
0.25đ 0.25đ 0.25đ 0.25đ |
Bài 3 ( 3 đ) |
Vẽ hình
|
|
Vẽ hình , ghi GT, KL :
0,25đ |
a) 1đ
b)0,75đ
c) 1đ |
a)
Chứng minh
+)
Chứng minh
+) Cạnh DB chung +)
b) So sánh AD và DC. Vì
Tam giác DEC vuông tại E
c)Chứng minh ba điểm B; D; K thẳng hàng Ta
có BD là tia phân giác của
Chứng
minh
Từ
đó chứng minh
Từ
1 và (2)
|
0,25 đ 0,25 đ 0,25 đ 0,25 đ
0,25đ
0.25đ 0,25đ
0,25đ 0.25đ 0.25đ
0,25đ |
|
Bài 4 (1,0đ) |
|
Từ
+) Nếu x+y+z+t=0
+)
Nếu x+y+z+t
|
0,25
0,25
0,25
0,25 |
ĐỀ 15 |
ĐỀ THI HỌC KỲ II TOÁN 7 Thời gian: 90 phút |
Câu 1: (2,0 điểm). Thời gian làm xong bài tập Toán (tính bằng phút) của 30 học sinh lớp 7B được giáo viên ghi lại trong bảng sau:
Thời gian (x) |
5 |
7 |
8 |
9 |
10 |
13 |
|
Tần số (n) |
4 |
3 |
9 |
7 |
5 |
2 |
N = 30 |
a/ Dấu hiệu ở đây là gì? Tìm mốt của dấu hiệu?
b/ Tính số trung bình cộng của dấu hiệu?
Câu 2: (3,5 điểm). Cho hai đa thức:
P(x) = 2x4 + 9x2 – 3x + 7 – x – 4x2 – 2x4
Q(x) = – 5x3 – 3x – 3 + 7x – x2 – 2
a/ Thu gọn các đa thức trên và sắp xếp các hạng tử theo lũy thừa giảm dần của biến. Tìm bậc của mỗi đa thức trên.
b/
Tính giá trị của các đa thức P(x) tại x =
![]() ; Q(x) tại x = 1.
; Q(x) tại x = 1.
c/ Tính Q(x) + P(x) và Q(x) – P(x)
d/ Tìm giá trị của x sao cho: Q(x) + P(x) + 5x2 – 2 = 0
Câu
3: (3,5
điểm). Cho
![]() ABC,
lấy M là trung điểm của BC. Trên tia đối của tia MA lấy
điểm E sao cho ME = MA. Chứng minh rằng:
ABC,
lấy M là trung điểm của BC. Trên tia đối của tia MA lấy
điểm E sao cho ME = MA. Chứng minh rằng:
a/ AC = EB và AC // BE
b/ Trên AC lấy điểm I, trên EB lấy điểm K sao cho AI = EK.
Chứng minh ba điểm: I, M, K thẳng hàng.
c/
Từ E kẻ EH
![]() BC (H
BC (H
![]() BC). Biết K là trung điểm của BE và HK = 5 cm; HE = 6 cm.
Tính độ dài đoạn thẳng BH.
BC). Biết K là trung điểm của BE và HK = 5 cm; HE = 6 cm.
Tính độ dài đoạn thẳng BH.
Câu 4: (3,0 điểm). Tìm số tự nhiên n có hai chữ số biết rằng 2n + 1 và 3n + 1 đồng thời là hai số chính phương.
BÀI LÀM
Câu 1: a/ Dấu hiệu ở đây là: " Thời gian làm xong bài tập Toán (tính bằng phút) của 30 học sinh lớp 7B".
Mốt của dấu hiệu là: M0 = 8
b/
Trung bình cộng của dấu hiệu là:
![]() =
=
![]() = 8,4
= 8,4
Câu 2: a/ Thu gọn và sắp xếp các đa thức theo lũy thừa giảm dần của biến:
P(x) = 2x4 + 9x2 – 3x + 7 – x – 4x2 – 2x4
P(x) = (2x4 – 2x4) + (9x2 – 4x2) + (– 3x – x) + 7
P(x) = 5x2 – 4x + 7
Q(x) = – 5x3 – 3x – 3 + 7x – x2 – 2
Q(x) = – 5x3 – x2 + (– 3x + 7x) + (– 3 – 2)
Q(x) = – 5x3 – x 2 + 4x – 5
Bậc của đa thức P(x) là 2, bậc của đa thức Q(x) là 3
b/ Ta có:
P(x) = 5x2 – 4x + 7
![]() =
=
![]()
Q(x) = – 5x3 – x 2 + 4x – 5
Q(1) = – 5.13 – 12 + 4.1 – 5 = – 7
c/ Ta có:
-
+
Q(x) = – 5x3 – x 2 + 4x – 5
P(x) = 5x2 – 4x + 7
Q(x) + P(x) = – 5x3+4x2 + 2
-
–
Q(x) = – 5x3 – x 2 + 4x – 5
P(x) = 5x2 – 4x + 7
Q(x) – P(x) = – 5x3–6x2 + 8x – 12
d/ Ta có: Q(x) + P(x) + 5x2 – 2 = 0
![]() (– 5x3 +
4x2
+ 2) + 5x2
– 2 = 0
(– 5x3 +
4x2
+ 2) + 5x2
– 2 = 0
![]() – 5x3
+ 9x2
= 0
– 5x3
+ 9x2
= 0
![]() x2(–
5x + 9) = 0
x2(–
5x + 9) = 0
![]()
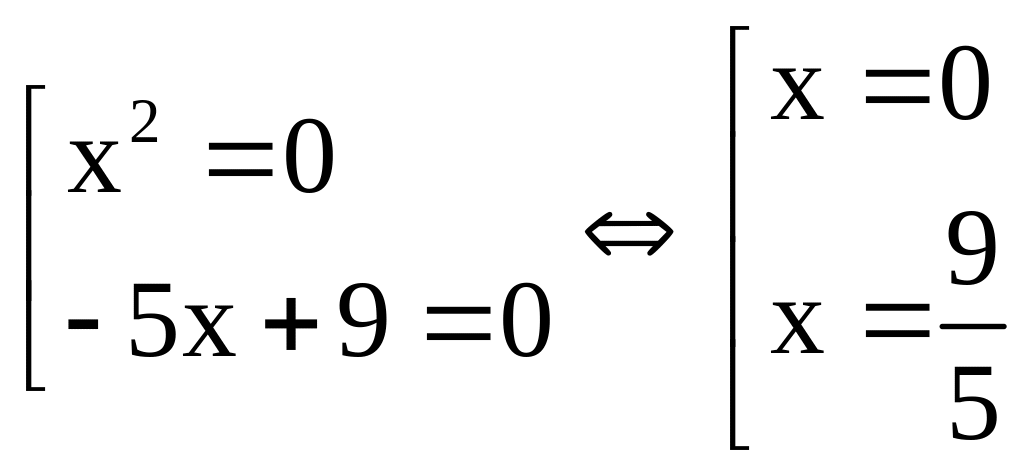
Vậy
x = 0 hoặc x =
![]()
C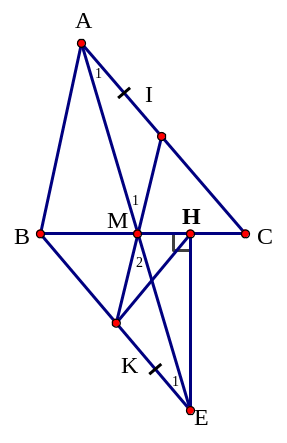 âu
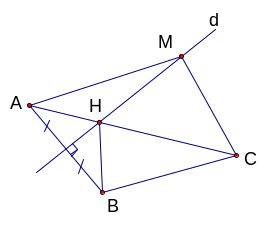
3:
âu
3:
GT |
HK = 5 cm; HE = 6 cm |
KL |
a/ AC = EB và AC // BE b/ I, M, K thẳng hàng c/ BH = ? |
a/
Xét
![]() AMC
và
AMC
và
![]() EMB
có:
EMB
có:
MA = ME (GT)
![]() (Hai góc đối đỉnh)
(Hai góc đối đỉnh)
MC = MB (GT)
![]()
![]() AMC
=
AMC
=
![]() EMB
(c – g – c)
EMB
(c – g – c)
![]() AC = EB (Hai cạnh
tương ứng)
AC = EB (Hai cạnh
tương ứng)
và
![]() (Hai
góc tương ứng) mà
(Hai
góc tương ứng) mà
![]() và
và
![]() ở vị trí so le trong nên AC // BE
ở vị trí so le trong nên AC // BE
b/
Vì
![]() AMC
=
AMC
=
![]() EMB
(Theo câu a)
EMB
(Theo câu a)
![]() MA = ME (Hai cạnh
tương ứng)
MA = ME (Hai cạnh
tương ứng)
Xét
![]() AMI
và
AMI
và
![]() EMK
có:
EMK
có:
AI = EK (GT)
![]() (CM ở câu a)
(CM ở câu a)
MA = ME (CM trên)
![]()
![]() AMI
và
AMI
và
![]() EMK
(c – g – c)
EMK
(c – g – c)
![]()
![]() (Hai
góc tương ứng)
(Hai
góc tương ứng)
Ta
có:
![]() = 1800 (Hai
góc kề bù) mà
= 1800 (Hai
góc kề bù) mà
![]() nên
nên
![]() = 1800
= 1800
![]() Ba điểm I, M, K thẳng hàng.
Ba điểm I, M, K thẳng hàng.
c/
Vì
![]() BHE
vuông tại H có HK là đường trung tuyến nên HK =
BHE
vuông tại H có HK là đường trung tuyến nên HK =
![]()
![]() BE = 2HK = 2.5 = 10 cm.
BE = 2HK = 2.5 = 10 cm.
Áp
dụng định lý Pythagoras vào
![]() BHE
vuông tại H:
BHE
vuông tại H:
BE2 = BH2 + HE2
![]() 102
= BH2
+ 62
102
= BH2
+ 62
![]() BH2
= 100 – 36
BH2
= 100 – 36
![]() BH2
= 64
BH2
= 64
![]() BH = 8 cm
BH = 8 cm
Câu
4: Vì n có hai
chữ số nên 10
![]() n
n
![]() 99
99
![]() 20
20
![]() 2n
2n
![]() 198
198
![]() 21
21
![]() 2n + 1
2n + 1
![]() 199.
199.
Vì
2n + 1 là số chính phương mà 21
![]() 2n + 1
2n + 1
![]() 199 nên 2n + 1
199 nên 2n + 1
![]() {25;
36; 49; 64; 81; 100; 121; 144; 169; 196}.
{25;
36; 49; 64; 81; 100; 121; 144; 169; 196}.
Vì
2n + 1 lẻ nên 2n + 1
![]() {25;
49; 81; 121; 169}
{25;
49; 81; 121; 169}
![]() n
n
![]() {12;
24; 40; 60; 84} (1)
{12;
24; 40; 60; 84} (1)
Vì
3n + 1 chia cho 3 dư 1 nên từ (1)
![]() n = 40
n = 40
Ngoài 15 Đề Thi kì 2 Toán 7 Có Đáp Án – Tài Liệu Toán thì các đề thi trong chương trình lớp 7 sẽ được cập nhật liên tục và nhanh nhất có thể sau khi kỳ thi diễn ra trên Danh mục Kho Đề Thi nhằm giúp các bạn đọc thuận tiện trong việc tra cứu và đối chiếu đáp án. Quý thầy cô và các bạn đọc có thể chia sẻ thêm những tài liệu học tập hữu ích đến địa chỉ email của chúng tôi, nhằm xây dựng nên kho đề thi phong phú, đa dạng cho các em học sinh tham khảo và rèn luyện.
Xem thêm







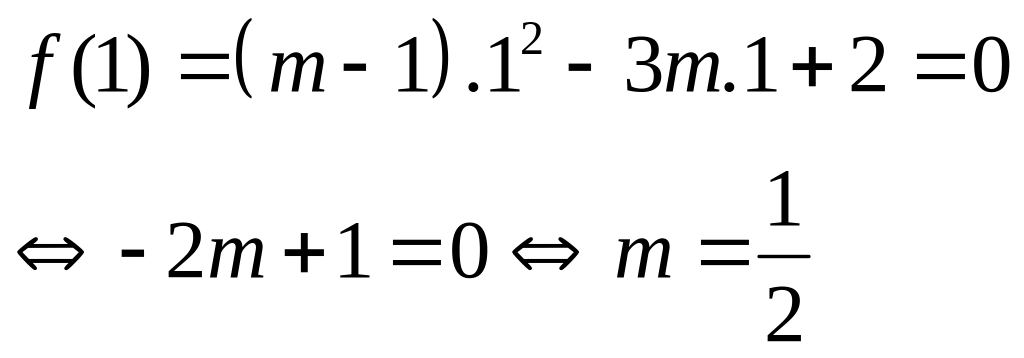
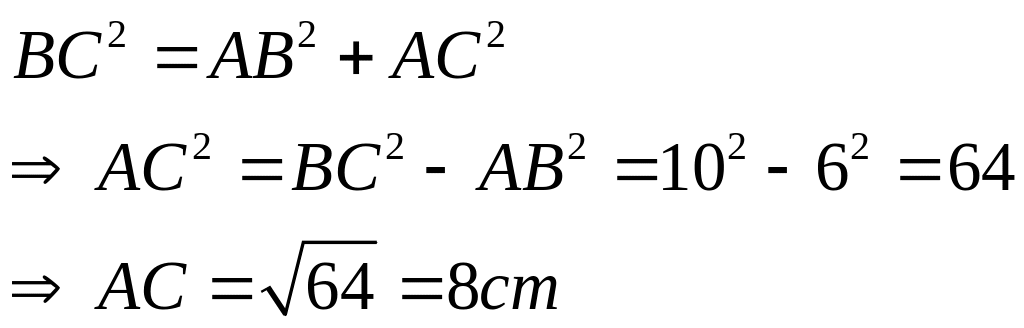

 (x)
+ B(x) = 2x
(x)
+ B(x) = 2x
 =
=
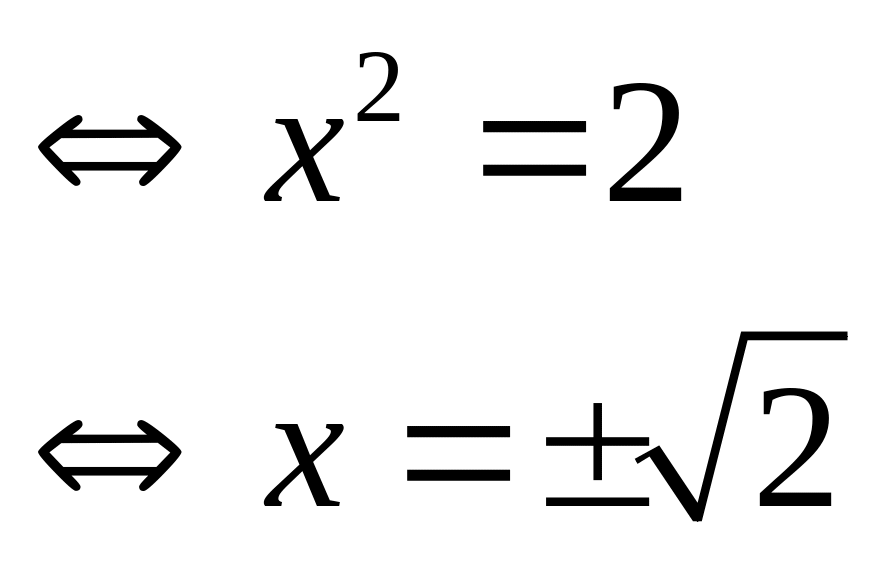
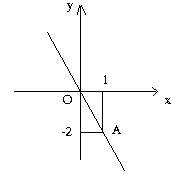 )
+ Với x=1; y=-2 vẽ A(1;-2)
)
+ Với x=1; y=-2 vẽ A(1;-2)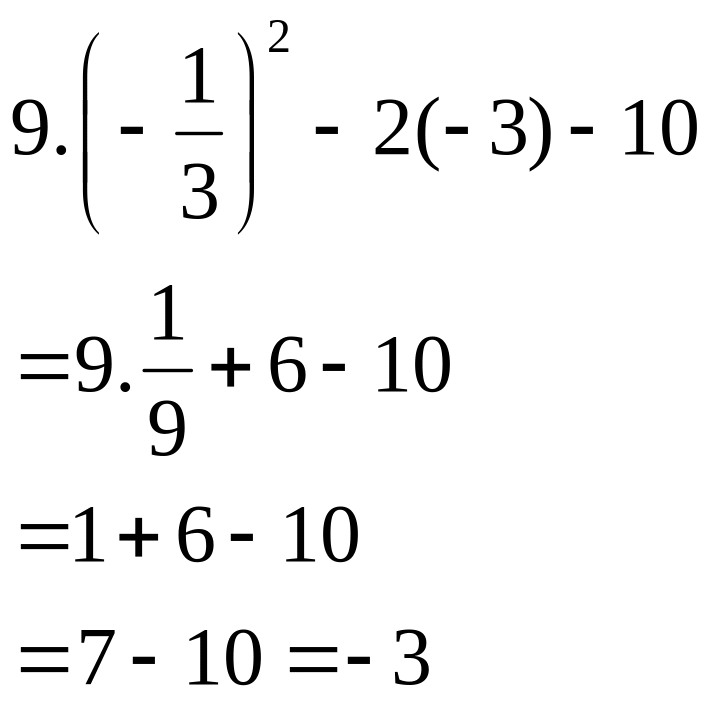
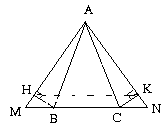 ét
hai tam giác cân
ét
hai tam giác cân





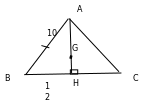

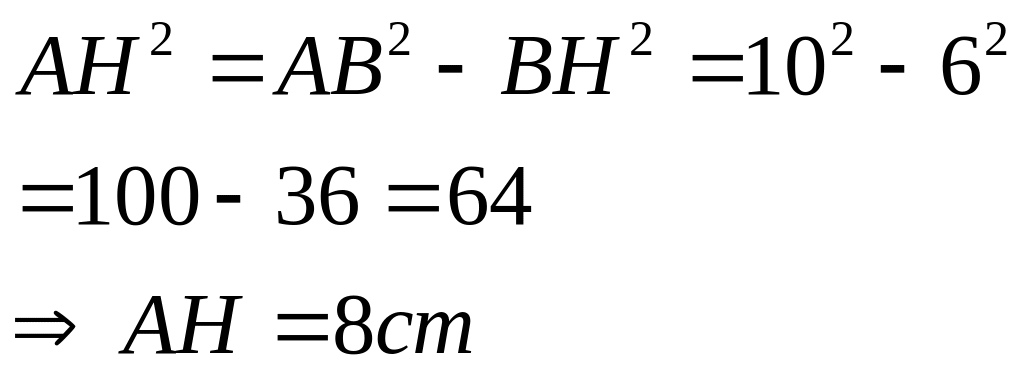




 Trên tia IB lấy điểm C’ sao cho IC’ = JC. Từ (2) suy
ra AB – AC = IB – IC’ = C’B (3)
Trên tia IB lấy điểm C’ sao cho IC’ = JC. Từ (2) suy
ra AB – AC = IB – IC’ = C’B (3)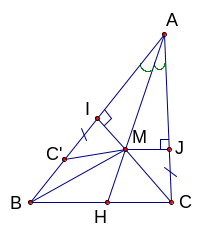

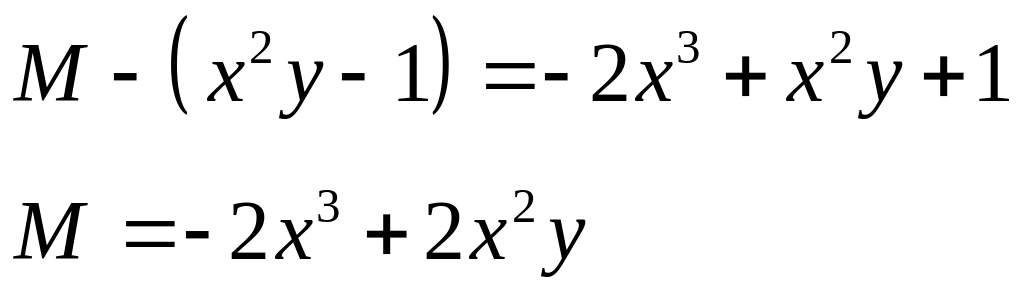
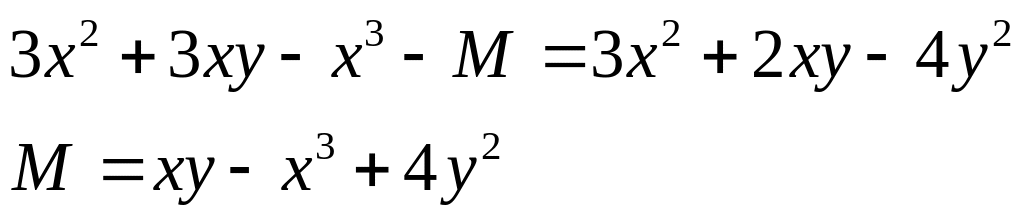
 ậy
ậy