15 Đề Thi HSG Toán 7 Cấp Trường Có Đáp Án
15 Đề Thi HSG Toán 7 Cấp Trường Có Đáp Án – Toán 7 được Trang Tài Liệu sưu tầm với các thông tin mới nhất hiện nay. Đề thi này sẽ giúp các em học sinh ôn tập, củng cố kiến thức, rèn luyện kĩ năng làm bài. Cũng như hỗ trợ thầy cô trong quá trình giảng dạy. Hy vọng những tài liệu này sẽ giúp các em trong quá trình ôn luyện và đạt kết quả cao trong bài thi sắp tới.
Trong hành trình chinh phục môn Toán, việc ôn tập và làm các đề thi là một phần quan trọng để rèn luyện kỹ năng và nắm vững kiến thức. Hôm nay, chúng ta sẽ khám phá một tài liệu đặc biệt – Bộ 15 đề thi HSG Toán lớp 7 cấp trường, với đáp án đi kèm.
Bộ 15 đề thi HSG Toán lớp 7 cấp trường là một kho tàng kiến thức và bài tập bổ ích để chúng ta ôn tập và đánh giá sự tiến bộ của mình. Được thiết kế theo định dạng của kỳ thi Học sinh giỏi, các đề thi trong bộ tài liệu này đảm bảo độ khó và đa dạng của các dạng bài toán.
Bộ 15 đề thi HSG Toán lớp 7 cấp trường không chỉ giúp chúng ta nắm vững kiến thức đã học mà còn giúp chúng ta khám phá các dạng bài toán mới và áp dụng kiến thức đã nắm vững vào thực tế. Qua việc làm các bài tập và kiểm tra đáp án, chúng ta có cơ hội rèn luyện khả năng tư duy logic, phân tích và giải quyết vấn đề.
Đề thi tham khảo
Dưới đây là bản đọc trực tuyến giúp thầy cô và các em học sinh có thể nghiên cứu Online hoặc bạn có thể tải miễn phí với phiên bản word để dễ dàng in ấn cũng như học tập Offline
ĐỀ 1 |
ĐỀ THI CHỌN HỌC SINH GIỎI MÔN TOÁN LỚP 7 Thời gian: 120 phút |
Bài
1:( 3 điểm) a)
Thực hiện phép tính:
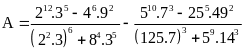
b)
Chứng minh rằng: Với mọi số nguyên dương n thì :
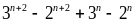 chia
hết cho 10
chia
hết cho 10
Bài
2:(2 điểm) Tìm
x
biết:
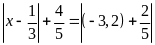
Bài
3: (2 điểm) Cho
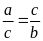 .
Chứng minh rằng:
.
Chứng minh rằng:
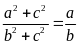
Bài
4: (3 điểm) Cho
tam giác ABC, M là trung điểm của BC. Trên tia đối của
của tia MA lấy điểm E sao cho ME = MA. Chứng minh rằng:
a) AC = EB và
 AC
// BE
AC
// BE
b) Gọi I là một điểm trên AC ; K là một điểm trên EB sao cho AI = EK . C.minh ba điểm I , M , K thẳng hàng
c)
Từ E kẻ
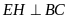
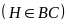 .
Biết
.
Biết
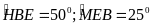 .
Tính
.
Tính
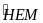 và
và
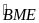
ĐỀ 2 |
ĐỀ THI CHỌN HỌC SINH GIỎI MÔN TOÁN LỚP 7 Thời gian: 120 phút |
Bài
1.
Tìm giá trị n nguyên dương: a)

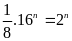 ;
b) 27 < 3n
< 243
;
b) 27 < 3n
< 243
Bài
2.
Thực hiện phép tính:
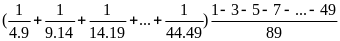
Bài
3.
a) Tìm x biết:
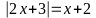
b)
Tìm giá trị nhỏ nhất của A =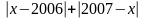 Khi x thay đổi
Khi x thay đổi
Bài 4. Hiện nay hai kim đồng hồ chỉ 10 giờ. Sau ít nhất bao lâu thì 2 kim đồng hồ nằm đối diện nhau trên một đường thẳng.
Bài 5. Cho tam giác vuông ABC ( A = 1v), đường cao AH, trung tuyến AM. Trên tia đối tia MA lấy điểm D sao cho DM = MA. Trên tia đối tia CD lấy điểm I sao cho CI = CA, qua I vẽ đường thẳng song song với AC cắt đường thẳng AH tại E. Chứng minh: AE = BC.
ĐỀ 3 |
ĐỀ THI CHỌN HỌC SINH GIỎI MÔN TOÁN LỚP 7 Thời gian: 120 phút |
Câu
1:
Tìm các cặp số (x; y) biết:
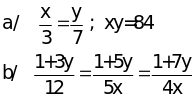
Câu
2:
Tìm giá trị nhỏ nhất hoặc lớn nhất của các biểu
thức sau : A =
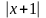 +5 ; B =
+5 ; B =
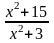
Câu
3:
Cho tam giác ABC có Â < 900.
Vẽ ra phía ngoài tam giác đó hai đoạn thẳng AD vuông góc
và bằng AB; AE vuông góc và bằng AC. a, Chứng minh: DC =
BE và DC
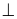 BE
BE
b, Gọi N là trung điểm của DE. Trên tia đối của tia NA lấy M sao cho NA = NM. C/minh: AB = ME và ABC= EMA
Chứng
minh: MA
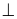 BC
BC
ĐỀ 4 |
ĐỀ THI CHỌN HỌC SINH GIỎI MÔN TOÁN LỚP 7 Thời gian: 120 phút |
Câu
1 ( 2 điểm)
Thực hiện phép tính : a-
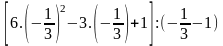 ;
b-
;
b-

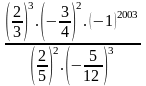
Câu
2 ( 2 điểm) a, Tìm
số nguyên a để
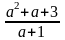 là số nguyên; b, Tìm số nguyên x,y sao cho x-2xy+y=0
là số nguyên; b, Tìm số nguyên x,y sao cho x-2xy+y=0
Câu
3 ( 2 điểm) a, Chứng
minh rằng nếu a+c=2b và 2bd = c (b+d) thì
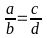 với b,d khác 0
với b,d khác 0
b, Cần bao nhiêu số hạng của tổng S = 1+2+3+… để được một số có ba chữ số giống nhau .
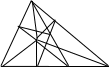
Câu 4 ( 3 điểm) Cho tam giác ABC có góc B bằng 450 , góc C bằng 1200. Trên tia đối của tia CB lấy điểm D sao cho CD=2CB . Tính góc ADE
Câu 5 ( 1điểm) Tìm mọi số nguyên tố thoả mãn : x2-2y2=1
ĐỀ 5 |
ĐỀ THI CHỌN HỌC SINH GIỎI MÔN TOÁN LỚP 7 Thời gian: 120 phút |
Bài
1: a)
So sánh hợp lý:
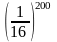 và
và
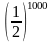 ;
b) Tính
A =
;
b) Tính
A =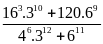
c) Cho x, y, z là các số khác 0 và x2 = yz , y2 = xz , z 2 = xy. Chứng minh rằng: x = y = z
Bài 2: Tìm x biết: a) (2x-1)4 = 16 b) (2x+1)4 = (2x+1)6
c)
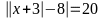 d)
d)
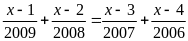
Bài 3: Tìm các số x, y, z biết : a) (3x - 5)2006 +(y2 - 1)2008 + (x - z) 2100 = 0
b)
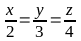 và x2
+ y2
+ z2
= 116
và x2
+ y2
+ z2
= 116
Bài 4 : a) Cho hai đại lượng tỉ lệ nghịch x và y ; x1, x 2 là hai giá trị bất kì của x; y1, y2 là hai giá trị tương ứng của y.Tính y1, y2 biết y12+ y22 = 52 và x1=2 , x 2= 3.
b) Cho hàm số : f(x) = a.x2 + b.x + c với a, b, c, d Z
Biết
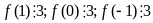 .Chứng
minh rằng a, b, c đều chia hết cho 3
.Chứng
minh rằng a, b, c đều chia hết cho 3
c)
Chứng
minh rằng : Với mọi số nguyên dương n thì :
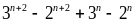 chia
hết cho 10
chia
hết cho 10
Bài 5: Cho tam giác ABC vuông cân tại A, M là trung điểm BC. Lấy điểm D bất kì thuộc cạnh BC. H và I thứ tự là hình chiếu của B và C xuống đường thẳng AD. Đường thẳng AM cắt CI tại N. Chứng minh rằng: a) BH = AI. b) BH2 + CI2 có giá trị không đổi.
c) Đường thẳng Dn vuông góc với AC. d) IM là phân giác của góc HIC.
ĐỀ 6 |
ĐỀ THI CHỌN HỌC SINH GIỎI MÔN TOÁN LỚP 7 Thời gian: 120 phút |
Câu
1.
Tìm x biết: a)
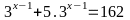 b) 3x +x2
= 0 c) (x-1)(x-3) < 0
b) 3x +x2
= 0 c) (x-1)(x-3) < 0
Câu
2.
a) Tìm ba số x, y, z thỏa mãn:
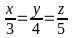 và
và
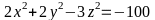
b)
Cho
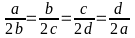 (a, b, c, d > 0)
(a, b, c, d > 0)
Tính
A =
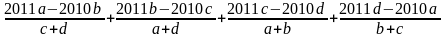
Câu 3. a) Tìm cặp số nguyên (x,y) thoả mãn x + y + xy =2.
b) Tìm giá trị lớn nhất của biểu thức Q =
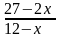 (với x nguyên)
(với x nguyên)
Câu 4. a) Cho đa thức f(x) = ax2 + bx + c. Chứng minh rằng nếu f(x) nhận 1 và -1 là nghiệm thì a và c là 2 số đối nhau.
b) Tìm giá trị nhỏ nhất của biểu thức P =
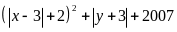
Câu
5.
Cho
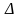 ABC
vuông tại A. M là trung điểm BC, trên tia đối của tia MA
lấy điểm D sao cho AM = MD. Gọi I và K lần lượt là chân
đường vuông góc hạ từ B và C xuống AD, N là chân đường
vuông góc hạ từ M xuống AC.
ABC
vuông tại A. M là trung điểm BC, trên tia đối của tia MA
lấy điểm D sao cho AM = MD. Gọi I và K lần lượt là chân
đường vuông góc hạ từ B và C xuống AD, N là chân đường
vuông góc hạ từ M xuống AC.
a) Chứng minh rằng BK = CI và BK//CI. b) Chứng minh KN < MC.
c)
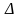 ABC
thỏa mãn thêm điều kiện gì để AI = IM = MK = KD.
ABC
thỏa mãn thêm điều kiện gì để AI = IM = MK = KD.
d) Gọi H là chân đường vuông góc hạ từ D xuống BC. Chứng minh rằng các đường thẳng BI, DH, MN đồng quy.
ĐỀ 7 |
ĐỀ THI CHỌN HỌC SINH GIỎI MÔN TOÁN LỚP 7 Thời gian: 120 phút |
Câu 1: Tìm các số a,b,c biết rằng: ab =c ;bc= 4a; ac=9b
Câu 2: Tìm số nguyên x thoả mãn:
a,5x-3 < 2 b,3x+1 >4 c, 4- x +2x =3
Câu3: Tìm giá trị nhỏ nhất của biểu thức: A =x +8 -x
Câu 4: Biết rằng :12+22+33+...+102= 385. Tính tổng : S= 22+ 42+...+202
Câu 5 :
Cho tam giác ABC ,trung tuyến AM .Gọi I là trung điểm của đoạn thẳng AM, BI cắt cạnh AC tại D.
a. Chứng minh AC=3 AD
b. Chứng minh ID =1/4BD
ĐỀ 8 |
ĐỀ THI CHỌN HỌC SINH GIỎI MÔN TOÁN LỚP 7 Thời gian: 120 phút |
Câu
1 . (
2đ) Cho:
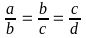 . Chứng minh:
. Chứng minh:
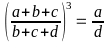 .
.
Câu
2.
(1đ). Tìm A biết rằng: A =
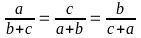 .
.
Câu
3. (2đ). Tìm
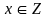 để
để
 A
Z và tìm giá trị đó.
A
Z và tìm giá trị đó.
a).
A =
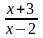 .
b). A =
.
b). A =
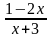 .
.
Câu 4. (2đ). Tìm x, biết:
a)
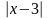 = 5 . b). ( x+ 2)
2
= 81. c). 5
x
+ 5
x+ 2
= 650
= 5 . b). ( x+ 2)
2
= 81. c). 5
x
+ 5
x+ 2
= 650
Câu 5. (3đ). Cho ABC vuông cân tại A, trung tuyến AM . E BC, BH AE, CK AE, (H,K AE). Chứng minh MHK vuông cân
ĐỀ 9 |
ĐỀ THI CHỌN HỌC SINH GIỎI MÔN TOÁN LỚP 7 Thời gian: 120 phút |
Bài
1:
(1,5 điểm) Tính
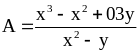 biết
biết
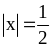 ;
y là số nguyên âm lớn nhất
;
y là số nguyên âm lớn nhất
Bài
2:
(2 điểm) Cho
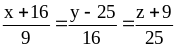 và
và
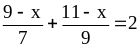 .Tìm
x+y+z
.Tìm
x+y+z
Bài
3:
(1,5 điểm) Tìm
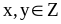 biết 2xy+3x = 4 ; 16
biết 2xy+3x = 4 ; 16![]() - 72
- 72![]() + 90.
+ 90.
Bài 4: (2 điểm) Cho đa thức: P = 3x3 + 4x2 - 8x+1
a/ Chứng minh rằng x= 1 là nghiệm của đa thức. b/ Tính giá trị của P biết x2+x-3 = 0
Bài 5: (3 điểm) Cho tam giác ABC có vuông tại A(AB<AC) trên cạnh Aclấy điểm Esao cho AE = AB. Tia phân giác của góc BAC cắt đường trung trực của CE tại F. a/ Chứng minh tam giác BFC
b/ Biết góc ACB bằng 300.Chứng minh tam giác BFE đều.
ĐỀ 10 |
ĐỀ THI CHỌN HỌC SINH GIỎI MÔN TOÁN LỚP 7 Thời gian: 120 phút |
Bài
1:
(1 điểm) Tìm số
![]() biết:
biết:
![]() =
=
![]() =
=
![]() ,
và x – y + z = 4
,
và x – y + z = 4
Bài
2:
(1 điểm) Biết
![]() + ab +
+ ab +
![]() = 25 ;
= 25 ;
![]() +
+
![]() = 9 ;
= 9 ;
![]() + ac +
+ ac +
![]() = 16 và a
= 16 và a
![]() 0; c ≠ 0; a ≠ -c.
0; c ≠ 0; a ≠ -c.
Chứng
minh rằng:
![]() =
=
![]() .
.
Bài 3: (2,5 điểm0 a/ Tìm giá trị của m để đa thức sau là đa thức bậc 3 theo biến x:
f
(x) = (![]() - 25)
- 25)![]() + (20 + 4m)
+ (20 + 4m)![]() + 7
+ 7![]() - 9
- 9
b/
Tìm giá trị nhỏ nhất của đa thức g(x) = 16![]() - 72
- 72![]() + 90.
+ 90.
Bài 4: (2 điểm) Tìm số chia và số dư biết rằng số bị chia bằng 112 và thương bằng 5.
Bài 5: (3 điểm) Cho tam giác ABC có ba góc nhọn, AB < AC < BC. Các tia phân giác của góc A và góc C cắt nhau tại O. Gọi F là hình chiếu của O trên BC; H là hình chiếu của O trên AC. Lấy điểm I trên đoạn FC sao cho FI = AH. Gọi K là giao điểm của FH và AI. a/ Chứng minh tam giác FCH cân và AK = KI.
b/ Chứng minh ba điểm B, O, K thẳng hàng.
ĐỀ 11 |
ĐỀ THI CHỌN HỌC SINH GIỎI MÔN TOÁN LỚP 7 Thời gian: 120 phút |
Bài
1:(2 đ)a.
Tìm x, y biết:
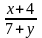 =
=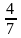 và x+ y = 22; b. Cho
và x+ y = 22; b. Cho
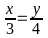 và
và
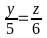 .
Tính M =
.
Tính M =
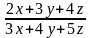
Bài
2: ( 2,0 điểm) a.
Cho H =
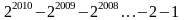 . Tính 2010H
. Tính 2010H
b.
Thực
hiện tính
M =
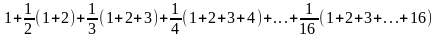
Bài
3: ( 2,5 điểm) Tìm
x biết:a.
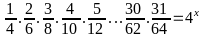
b.
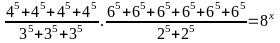 ;
c.
;
c.
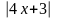 -
-
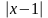 = 7
= 7
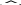
 Bài
4: ( 3,5đ) Cho
tam giác ABC có B < 900
và B = 2C. Kẻ đường cao AH. Trên tia đối của tia BA lấy
điểm E sao cho BE = BH. Đường thẳng HE cắt AC tại D. a.
Chứng minh BEH = ACB.
Bài
4: ( 3,5đ) Cho
tam giác ABC có B < 900
và B = 2C. Kẻ đường cao AH. Trên tia đối của tia BA lấy
điểm E sao cho BE = BH. Đường thẳng HE cắt AC tại D. a.
Chứng minh BEH = ACB.
b. Chứng minh DH = DC = DA. d. Chứng minh AE = HC.
c. Lấy B’ sao cho H là trung điểm của BB’. Chứng minh tam giác AB’C cân.
ĐỀ 12 |
ĐỀ THI CHỌN HỌC SINH GIỎI MÔN TOÁN LỚP 7 Thời gian: 120 phút |
Bài
1:(4 điểm)a)
Thực hiện phép tính:
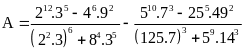
b)
Chứng minh rằng : Với mọi số nguyên dương n thì :
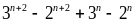 chia
hết cho 10
chia
hết cho 10
Bài
2:(4 điểm)Tìm
x
biết: a.
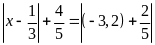 ;
b.
;
b.
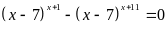
Bài
3: (4 điểm) a, Số
A được chia thành 3 số tỉ lệ theo
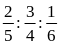 .
Biết rằng tổng các bình phương của ba số đó bằng
24309. Tìm số A. b, Cho
.
Biết rằng tổng các bình phương của ba số đó bằng
24309. Tìm số A. b, Cho
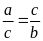 .
Chứng minh rằng:
.
Chứng minh rằng:
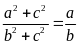
Bài
4: (4 điểm) Cho
tam giác ABC, M là trung điểm của BC. Trên tia đối của
của tia MA lấy điểm E sao cho ME = MA. Chứng minh rằng: a)
AC = EB và
 AC
// BE
AC
// BE
b) Gọi I là một điểm trên AC; K là một điểm trên EB sao cho AI = EK. C/m ba điểm I, M, K thẳng hàng
c)
Từ E kẻ
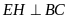
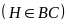 .
Biết
.
Biết
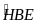 = 50o
;
= 50o
;
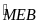 =25o
. Tính
=25o
. Tính
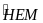 và
và
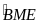
Bài
5: (4 điểm) Cho
tam giác ABC cân tại A có
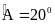 ,
vẽ tam giác đều DBC (D nằm trong tam giác ABC). Tia phân
giác của góc ABD cắt AC tại M. Chứng minh:
,
vẽ tam giác đều DBC (D nằm trong tam giác ABC). Tia phân
giác của góc ABD cắt AC tại M. Chứng minh:
a, Tia AD là phân giác của góc BAC ; b, AM = BC
ĐỀ 13 |
ĐỀ THI CHỌN HỌC SINH GIỎI MÔN TOÁN LỚP 7 Thời gian: 120 phút |
Câu
1.
(3 điểm) Rút gọn biểu thức
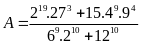
Câu
2.
(4 điểm) Chứng
minh: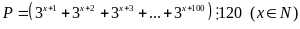
Câu
3.
(4 điểm) Cho hai hàm số
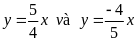
a. Vẽ đồ thị 2 h/số trên trên cùng hệ trục tọa độ Oxy. b. CMR:đồ thị của hai h/số trên vuông góc với nhau.
Câu
4.
(4,5điểm). Cho ∆ABC cân,
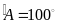 .
Gọi M là điểm nằm trong tam giác sao cho
.
Gọi M là điểm nằm trong tam giác sao cho
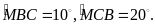 Trên tia đối của AC lấy điểm E sao cho CE = CB. a. Chứng
minh: ∆BME đều. b. Tính
Trên tia đối của AC lấy điểm E sao cho CE = CB. a. Chứng
minh: ∆BME đều. b. Tính
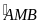
Câu
5.
(4,5điểm). Cho ∆ABC, trung tuyến BM. Trên tia BM lấy I và
K sao cho
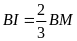 và M là trung điểm của IK. Gọi N là trung điểm của KC.
IN cắt AC tại O. Chứng minh:
và M là trung điểm của IK. Gọi N là trung điểm của KC.
IN cắt AC tại O. Chứng minh:
a.
O là trọng tâm của ∆IKC. b.
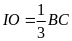 .
.
ĐỀ 14 |
ĐỀ THI CHỌN HỌC SINH GIỎI MÔN TOÁN LỚP 7 Thời gian: 120 phút |
Câu1:
(2 điểm) Cho dãy tỉ số bằng nhau:
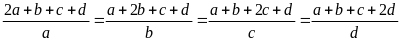
Tìm
giá trị biểu thức: M=
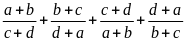
Câu2:
(1 điểm) . Cho S =
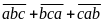 .
Chứng minh rằng S không phải là số chính phương.
.
Chứng minh rằng S không phải là số chính phương.
Câu3: (2 điểm) Một ô tô chạy từ A đến B với vận tốc 65 km/h, cùng lúc đó một xe máy chạy từ B đến A với vận tốc 40 km/h. Biết khoảng cách AB là 540 km và M là trung điểm của AB. Hỏi sau khi khởi hành bao lâu thì ôtô cách M một khoảng bằng 1/2 khoảng cách từ xe máy đến M.
Câu4: (2 điểm) Cho tam giác ABC, O là điểm nằm trong tam giác.
a.
Chứng minh rằng:
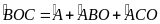
b.
Biết
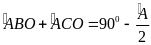 và tia BO là tia phân giác của góc B. CMR: Tia CO là tia phân
giác của góc C.
và tia BO là tia phân giác của góc B. CMR: Tia CO là tia phân
giác của góc C.
Câu 5: (1,5điểm). Cho 9 đường thẳng trong đó không có 2 đường thẳng nào song song. CMR ít nhất cũng có 2 đường thẳng mà góc nhọn giữa chúng không nhỏ hơn 200.
Câu 6: (1,5điểm). Khi chơi cá ngựa, thay vì gieo 1 con súc sắc, ta gieo cả hai con súc sắc cùng một lúc thì điểm thấp nhất là 2, cao nhất là 12. các điểm khác là 3; 4; 5 ;6… 11. Hãy lập bảng tần số về khả năng xuất hiện mỗi loại điểm nói trên? Tính tần xuất của mỗi loại điểm đó.
ĐỀ 15 |
ĐỀ THI CHỌN HỌC SINH GIỎI MÔN TOÁN LỚP 7 Thời gian: 120 phút |
Bài 1: Tính giá trị biểu thức:
A
=
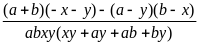 .
Với
a =
.
Với
a =
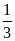 ; b = -2 ; x =
; b = -2 ; x =
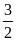 ; y = 1
; y = 1
Bài
2:
Chứng minh rằng: Nếu 0 < a1
< a2
< ….. <
a9
thì:
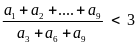
Bài 3: Có 3 mảnh đất hình chữ nhật: A; B và C. Các diện tích của A và B tỉ lệ với 4 và 5, các diện tích của B và C tỉ lệ với 7 và 8; A và B có cùng chiều dài và tổng các chiều rộng của chúng là 27m. B và C có cùng chiều rộng. Chiều dài của mảnh đất C là 24m. Hãy tính diện tích của mỗi mảnh đất đó.
Bài
4:
Cho 2 biểu thức: A =
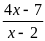 ; B =
; B =
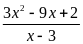
a) Tìm giá trị nguyên của x để mỗi biểu thức có giá trị nguyên
b) Tìm giá trị nguyên của x để cả hai biểu thức cùng có giá trị nguyên.
Bài 5: Cho tam giác cân ABC, AB = AC. Trên tia đối của các tia BC và CB lấy theo thứ tự hai điểm D và E sao cho BD = CE. a) Chứng minh tam giác ADE là tam giác cân.
b) Gọi M là trung điểm của BC. Chứng minh AM là tia phân giác của góc DAE
c) Từ B và C vẽ BH và CK theo thứ tự vuông góc với AD và AE. Chứng minh BH = CK
d) Chứng minh 3 đường thẳng AM; BH; CK gặp nhau tại 1 điểm.
ĐÁP ÁN
ĐÁP ÁN ĐỀ 1 THI CHỌN HỌC SINH GIỎI CẤP TRƯỜNG LỚP 7. Môn: TOÁN
Bài 1:(3 điểm): a) (1.5 điểm)
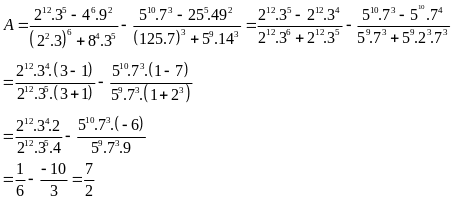
b)
(1.5 điểm)
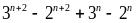 =
=
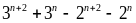 =
=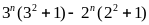
=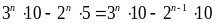 = 10( 3n
-2n)
= 10( 3n
-2n)
Vậy
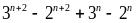
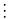 10 với mọi n là số nguyên dương.
10 với mọi n là số nguyên dương.
Bài 2:(2 điểm)
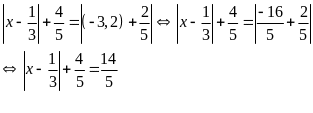
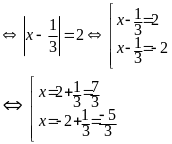
Bài
3: (2
điểm) Từ
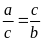 suy ra
suy ra
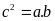 khi đó
khi đó
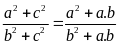 =
=
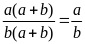
B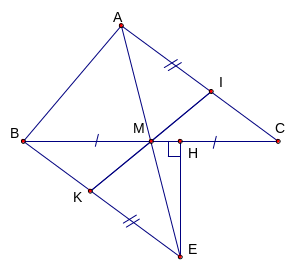 ài
4:
(3 điểm) a/
(1điểm) Xét
ài
4:
(3 điểm) a/
(1điểm) Xét
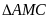 và
và
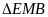 có :
có :
AM = EM (gt )
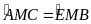 (đối
đỉnh )
(đối
đỉnh )
BM = MC (gt )
Nên
:
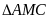 =
=
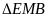 (c.g.c )
(c.g.c )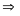 AC = EB
AC = EB
Vì
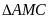 =
=
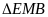
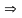
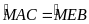 (2 góc có vị trí so le trong được tạo bởi đường
thẳng AC và EB cắt đường thẳng AE )
(2 góc có vị trí so le trong được tạo bởi đường
thẳng AC và EB cắt đường thẳng AE )
Suy ra AC // BE .
b/
(1 điểm ) Xét
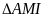 và
và
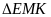 có :
có :
AM = EM (gt )
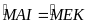 (
vì
(
vì
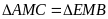 )
)
AI = EK (gt )
Nên
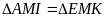 ( c.g.c ) Suy ra:
( c.g.c ) Suy ra:
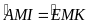
Mà
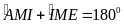 ( tính chất hai góc kề bù )
( tính chất hai góc kề bù )
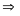
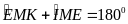
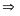 Ba
điểm I;M;K thẳng hàng
Ba
điểm I;M;K thẳng hàng
c/
(1 điểm ) Trong tam giác vuông BHE (
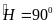 có
có
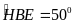
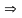
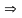
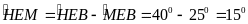
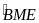 BME
là góc ngoài tại đỉnh M của
BME
là góc ngoài tại đỉnh M của
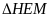
Nên
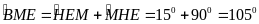
( định lý góc ngoài của tam giác )
( Học sinh giải theo cách khác đúng kết quả vẫn cho điểm tối đa)
ĐÁP ÁN ĐỀ 2 THI CHỌN HỌC SINH GIỎI CẤP TRƯỜNG LỚP 7. Môn: TOÁN
Bài 1. Tìm giá trị n nguyên dương: (4 điểm mỗi câu 2 điểm)
a)

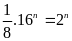 ;
=> 24n-3
= 2n
=> 4n – 3 = n => n = 1
;
=> 24n-3
= 2n
=> 4n – 3 = n => n = 1
b) 27 < 3n < 243 => 33 < 3n < 35 => n = 4
Bài 2. Thực hiện phép tính: (4 điểm)
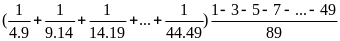
=
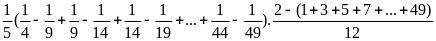
=
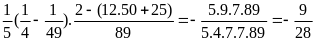
Bài 3. (4 điểm mỗi câu 2 điểm)
a)
Tìm x biết:
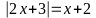
Ta
có: x + 2
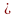 0 => x
0 => x
 - 2.
- 2.
+
Nếu x
 -
-
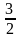 thì
thì
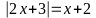 =>
2x + 3 = x + 2 => x = - 1 (Thoả mãn)
=>
2x + 3 = x + 2 => x = - 1 (Thoả mãn)
+
Nếu - 2
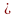 x < -
x < -
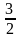 Thì
Thì
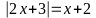 =>
- 2x - 3 = x + 2 => x = -
=>
- 2x - 3 = x + 2 => x = -
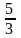 (Thoả
mãn)
(Thoả
mãn)
+ Nếu - 2 > x Không có giá trị của x thoả mãn
b)
Tìm giá trị nhỏ nhất của A =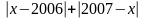 Khi x thay đổi
Khi x thay đổi
+ Nếu x < 2006 thì: A = - x + 2006 + 2007 – x = - 2x + 4013
Khi đó: - x > -2006 => - 2x + 4013 > – 4012 + 4013 = 1 => A > 1
+
Nếu 2006
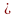 x
x
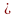 2007 thì: A = x – 2006 + 2007 – x = 1
2007 thì: A = x – 2006 + 2007 – x = 1
+ Nếu x > 2007 thì A = x - 2006 - 2007 + x = 2x – 4013
Do x > 2007 => 2x – 4013 > 4014 – 4013 = 1 => A > 1.
Vậy
A đạt giá trị nhỏ nhất là 1 khi 2006
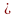 x
x
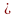 2007
2007
Bài 4. Hiện nay hai kim đồng hồ chỉ 10 giờ. Sau ít nhất bao lâu thì 2 kim đồng hồ nằm đối diện nhau trên một đường thẳng. (4 điểm mỗi)
Gọi x, y là số vòng quay của kim phút và kim giờ khi 10giờ đến lúc 2 kim đối nhau trên một đường thẳng, ta có:
x
– y =
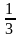 (ứng với từ số 12 đến số 4 trên đông hồ)
(ứng với từ số 12 đến số 4 trên đông hồ)
và x : y = 12 (Do kim phút quay nhanh gấp 12 lần kim giờ)
Do
đó:
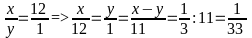
=>
x =
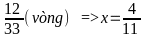 (giờ)
(giờ)
Vậy
thời gian ít nhất để 2 kim đồng hồ từ khi 10 giờ
đến lúc nằm đối diện nhau trên một đường thẳng là
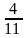 giờ
giờ
Bài 5. Cho tam giác vuông ABC ( A = 1v), đường cao AH, trung tuyến AM. Trên tia đối tia MA lấy điểm D sao cho DM = MA. Trên tia đối tia CD lấy điểm I sao cho CI = CA, qua I vẽ đường thẳng song song với AC cắt đường thẳng AH tại E. Chứng minh: AE = BC (4 điểm mỗi)
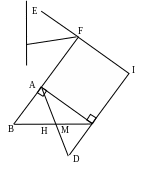 Đường
thẳng AB cắt EI tại F
Đường
thẳng AB cắt EI tại F
 ABM
=
ABM
=
 DCM
vì:
DCM
vì:
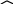
AM = DM (gt), MB = MC (gt),
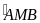 =
DMC (đđ) => BAM = CDM
=
DMC (đđ) => BAM = CDM
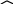
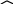
=>FB
// ID => ID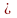 AC
AC
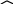
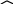
Và FAI = CIA (so le trong) (1)
IE // AC (gt) => FIA = CAI (so le trong) (2)
Từ
(1) và (2) =>
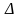 CAI
=
CAI
=
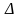 FIA
(AI chung)
FIA
(AI chung)
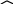
=> IC = AC = AF (3)
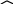
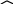
và E FA = 1v (4)
Mặt khác EAF = BAH (đđ),
BAH = ACB ( cùng phụ ABC)
=> EAF = ACB (5)
Từ
(3), (4) và (5) =>
 AFE
=
AFE
=
 CAB
CAB
=>AE = BC
ĐÁP ÁN ĐỀ 3 THI CHỌN HỌC SINH GIỎI CẤP TRƯỜNG LỚP 7. Môn: TOÁN
ĐÁP ÁN ĐỀ 3 TOÁN 7
Câu
1:
Tìm tất cả các số nguyên a biết
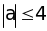 ;
0
;
0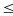
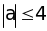 =>
=>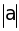 =
0; 1; 2; 3 ; 4
=
0; 1; 2; 3 ; 4
*
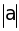 = 0 => a = 0; *
= 0 => a = 0; *
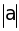 = 1 => a = 1 hoặc a = - 1 ; *
= 1 => a = 1 hoặc a = - 1 ; *
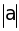 = 2 => a = 2 hoặc a = - 2
= 2 => a = 2 hoặc a = - 2
*
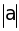 = 3 => a = 3 hoặc a = - 3; *
= 3 => a = 3 hoặc a = - 3; *
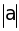 = 4 => a = 4 hoặc a = - 4
= 4 => a = 4 hoặc a = - 4
Câu
2:
Tìm phân số có tử là 7 biết nó lớn hơn
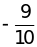 và nhỏ hơn
và nhỏ hơn
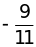
Gọi
mẫu phân số cần tìm là x. Ta có:
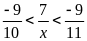 =>
=>
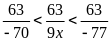
=>
-77 < 9x < -70. Vì 9x
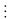 9
=> 9x = -72 => x = 8 . Vậy phân số cần tìm là
9
=> 9x = -72 => x = 8 . Vậy phân số cần tìm là
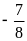
Câu
3.
Cho 2 đa thức: P
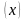 = x
= x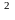 + 2mx + m
+ 2mx + m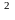 và Q
và Q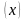 = x
= x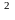 + (2m+1)x + m
+ (2m+1)x + m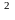 .
Tìm m biết P (1) = Q (-1)
.
Tìm m biết P (1) = Q (-1)
P(1) = 12 + 2m.1 + m2 = m2 + 2m + 1; Q(-1) = 1 – 2m – 1 +m2 = m2 – 2m
Để
P(1) = Q(-1) thì m2
+ 2m + 1 = m2
– 2m
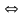 4m = -1
4m = -1
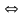 m = -1/4
m = -1/4
Câu
4:
Tìm các cặp số (x; y) biết:
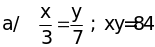 =>
=>
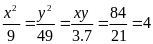
=>
x2
= 4.49 = 196 => x =
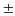 14
=> y2
= 4.4 = 16 => x =
14
=> y2
= 4.4 = 16 => x =
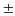 4
4
Do x,y cùng dấu nên: x = 6; y = 14 ; x = - 6; y = -14
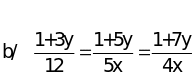
áp
dụng tính chất dãy tỉ số bằng nhau ta có:
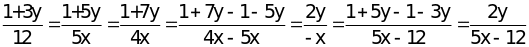
=>
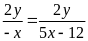 =>
-x = 5x -12 => x = 2. Thay x = 2 vào trên ta được:
=>
-x = 5x -12 => x = 2. Thay x = 2 vào trên ta được:
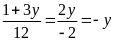
=>1+
3y = -12y => 1 = -15y => y =
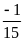 .
Vậy x = 2, y =
.
Vậy x = 2, y =
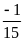 thoả mãn đề bài
thoả mãn đề bài
Câu
5:
Tìm giá trị nhỏ nhất hoặc lớn nhất của các biểu
thức sau : A =
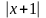 +5
+5

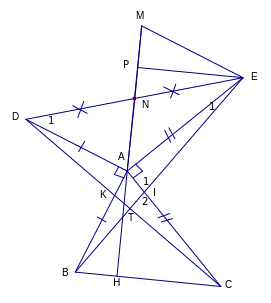
Ta
có :
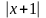
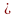 0. Dấu = xảy ra
0. Dấu = xảy ra
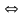 x= -1.
x= -1.
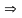 A
A
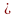 5.
5.
Dấu
= xảy ra
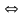 x= -1. Vậy: Min A = 5
x= -1. Vậy: Min A = 5
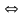 x= -1.
x= -1.
B =
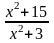 =
=
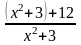 = 1 +
= 1 +
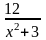
Ta
có: x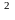
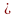 0. Dấu = xảy ra
0. Dấu = xảy ra
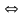 x = 0
x = 0
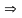 x
x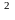 + 3
+ 3
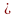 3 ( 2 vế dương )
3 ( 2 vế dương )
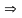
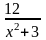
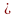
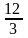
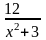
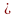 4
4
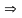 1+
1+
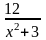
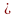 1+ 4
1+ 4
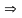 B
B
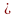 5
5
Dấu
= xảy ra
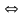 x = 0 . Vậy : Max B = 5
x = 0 . Vậy : Max B = 5
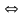 x = 0.
x = 0.
ĐA:ĐỀ 3- Câu 6:
a/ Xét ADC và BAF ta có:
DA = BA(gt); AE = AC (gt); DAC = BAE ( cùng bằng 900 + BAC )
=> DAC = BAE(c.g.c ) => DC = BE
Xét AIE và TIC
I1 = I2 ( đđ)
E1 = C1( do DAC = BAE)
=> EAI = CTI
=>
CTI = 900
=> DC
 BE
BE
b/ Ta có: MNE = AND (c.g.c)
=> D1 = MEN, AD = ME
mà AD = AB ( gt)
=> AB = ME (đpcm) (1)
Vì D1 = MEN => DA//ME => DAE + AEM = 1800 ( trong cùng phía )
mà BAC + DAE = 1800
=> BAC = AEM ( 2 )
Ta lại có: AC = AE (gt) ( 3). Từ (1),(2) và (3) => ABC = EMA ( đpcm)
c/
Kéo dài MA cắt BC tại H. Từ E hạ EP
 MH
MH
Xét AHC và EPA có:
CAH = AEP ( do cùng phụ với gPAE )
AE = CA ( gt)
PAE = HCA ( do ABC = EMA câu b)
=> AHC = EPA
=> EPA = AHC
=> AHC = 900
=>
MA
 BC (đpcm)
BC (đpcm)
ĐÁP ÁN ĐỀ 4 THI CHỌN HỌC SINH GIỎI CẤP TRƯỜNG LỚP 7. Môn: TOÁN
CÂU |
HƯỚNG DẪN CHẤM |
ĐIỂM |
||||||||||
1.a |
Thực hiện theo từng bước đúng kết quả -2 cho điểm tối đa |
1Điểm |
||||||||||
1.b |
Thực hiện theo từng bước đúng kết quả 14,4 cho điểm tối đa |
1Điểm |
||||||||||
2.a |
Ta
có :
vì
a là số nguyên nên
Vậy
với a |
0,25
0,25
0,25
0,25 |
||||||||||
2.b |
Từ : x-2xy+y=0 Hay (1-2y)(2x-1) = -1 Vì x,y là các số nguyên nên (1-2y)và (2x-1) là các số nguyên do đó ta có các trường hợp sau :
Hoặc
Vậy có 2 cặp số x, y như trên thoả mãn điều kiện đầu bài |
0,25
0,25
0,25
0,25 |
||||||||||
3.a |
Vì a+c=2b nên từ 2bd = c (b+d) Ta có: (a+c)d=c(b+d)
Hay
ad=bc Suy ra
|
0,5
0,5 |
||||||||||
3.b |
Giả
sử số có 3 chữ số là
Gọi số số hạng của tổng là n , ta có :
Vậy n(n+1) chia hết cho 37 , mà 37 là số nguyên tố và n+1<74 ( Nếu n = 74 không thoả mãn ) Do đó n=37 hoặc n+1 = 37
Nếu
n=37 thì n+1 = 38 lúc đó
Nếu
n+1=37 thì n = 36 lúc đó
Vậy số số hạng của tổng là 36 |
0,25
0,25
0,5 |
||||||||||
4 |
ĐA:ĐỀ 4 CAU 4:Kẻ DH Vuông góc với AC vì ACD =600 do đó CDH = 300
Tam
giác BCH cân tại C
Do đó tam giác AHD vuông cân tại H Vậy ADB = 450+300=750 |
0,5
0,5
1,0
1,0 |
||||||||||
5 |
Từ : x2-2y2=1suy ra x2-1=2y2 Nếu x chia hết cho 3 vì x nguyên tố nên x=3 lúc đó y= 2 nguyên tố thoả mãn Nếu x không chia hết cho 3 thì x2-1 chia hết cho 3 do đó 2y2 chia hết cho 3 Mà(2;3)=1 nên y chia hết cho 3 khi đó x2=19 không thoả mãn Vậy cặp số (x,y) duy nhất tìm được thoả mãn điều kiện đầu bài là (2;3)
|
0,25 0,25
0,25
0,25
|
ĐÁP ÁN ĐỀ 5 THI CHỌN HỌC SINH GIỎI CẤP TRƯỜNG LỚP 7. Môn: TOÁN
Bài 1: (1,5 điểm):
a)
Cách 1:
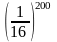 =
=
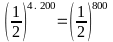 >
>
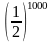
Cách
2:
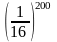 >
>
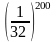 =
=
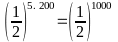
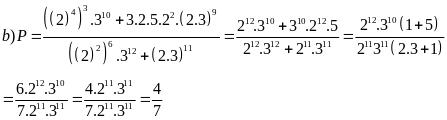
c)
Vì
x, y, z là các số khác 0 và x2
= yz , y2
= xz , z
2
= xy 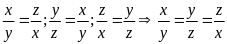 .áp
dụng tính chất dãy tỉ số bằng nhau
.áp
dụng tính chất dãy tỉ số bằng nhau
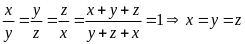
Bài 2: (1,5 điểm):
a) (2x-1)4 = 16 .Tìm đúng x =1,5 ; x = -0,5 (0,25điểm)
b) (2x+1)4 = (2x+1)6. Tìm đúng x = -0,5 ; x = 0; x = -15 (0,5điểm)
c)
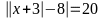
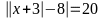
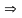
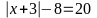 ;
;
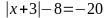
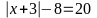
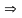
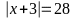
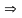 x
= 25; x = - 31
x
= 25; x = - 31
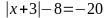
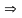
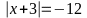 :
vô nghiệm
:
vô nghiệm
d)
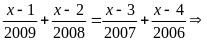
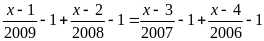
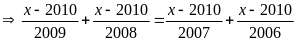
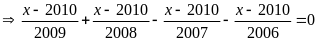
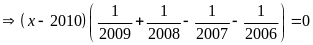
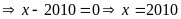
Bài 3:
a)
(3x - 5)2006
+(y2
-
1)2008
+ (x - z)
2100
= 0
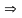 (3x
- 5)2006
=
0; (y2
-
1)2008
= 0; (x - z)
2100
= 0
(3x
- 5)2006
=
0; (y2
-
1)2008
= 0; (x - z)
2100
= 0
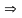 3x
- 5
=
0; y2
-
1 = 0 ; x - z
= 0
3x
- 5
=
0; y2
-
1 = 0 ; x - z
= 0
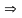 x = z =
x = z =
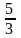 ;y
= -1;y = 1
;y
= -1;y = 1
b)
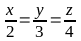 và x2
+ y2
+ z2
= 116
và x2
+ y2
+ z2
= 116
Từ
giả thiết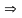
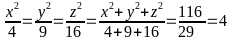
Tìm đúng: (x = 4; y = 6; z = 8 ); (x = - 4; y = - 6; z = - 8 )
Bài 4: a) Vì x, y là hai đại lượng tỉ lệ nghịch nên:
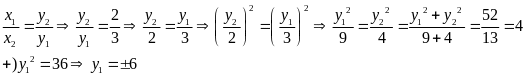
Với y1= - 6 thì y2 = - 4 ;
Với y1 = 6 thì y2= 4 .
b)Ta có: f(0) = c; f(1) = a + b + c; f(-1) = a - b +c
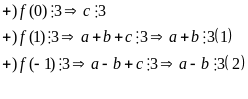
Từ
(1) và (2) Suy ra (a + b) +(a - b)
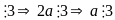 vì ( 2; 3) = 1
vì ( 2; 3) = 1
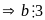
Vậy a , b , c đều chia hết cho 3
c)
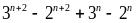 =
=
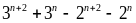
=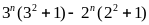 =
=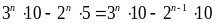 = 10( 3n
-2n-1)
= 10( 3n
-2n-1)
Vậy
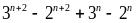
 10 với mọi n là số nguyên dương.
10 với mọi n là số nguyên dương.
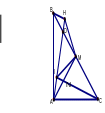
Bài 5:
AIC = BHA BH = AI (0,5điểm)
BH2 + CI2 = BH2 + AH2 = AB2 (0,75điểm)
AM, CI là 2 đường cao cắt nhau tại N N là trực tâm DN
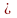 AC (0,75điểm)
AC (0,75điểm)BHM = AIM HM = MI và BMH = IMA (0,25điểm)
mà : IMA + BMI = 900 BMH + BMI = 900 (0,25điểm)
HMI vuông cân HIM = 450 (0,25điểm)
 mà
: HIC
= 900 HIM
=MIC=
450
IM là phân giác HIC
(0,25điểm)
mà
: HIC
= 900 HIM
=MIC=
450
IM là phân giác HIC
(0,25điểm)
*) Ghi chú:
Nếu học sinh có cách giải khác đúng, vẫn được điểm tối đa
ĐÁP ÁN ĐỀ 6 THI CHỌN HỌC SINH GIỎI CẤP TRƯỜNG LỚP 7. Môn: TOÁN
ĐÁP ÁN - BIỂU CHẤM
CÂU |
NỘI DUNG |
ĐIỂM |
|||||||||||||||||||
Câu 1 (4,5 đ) |
a) (1,5đ)
=> x-1= 3 => x = 4 |
0,75 0,75 |
|||||||||||||||||||
b) (1,5đ) 3x +x2 = 0 x(3 + x) = 0 x=0 hoặc x= -3 |
0,75 0,75 |
||||||||||||||||||||
c) (1,5đ) (x-1)(x-3) < 0 vì x-1 > x-3 nên (x-1)(x-3)
< 0
|
0,5 1,0 |
||||||||||||||||||||
Câu 2 (3,0 đ) |
a) (1,5đ) Từ
|
0,75
0,75
|
|||||||||||||||||||
b) (1,5 đ)
Ta
có
suy ra a = b = c= d Thay
vào tính được P =
|
0,5 0,5
0,5 |
||||||||||||||||||||
Câu 3 (3,0 đ) |
a) (1,5đ) Ta có x + y + xy =2 x + 1 + y(x + 1) = 3 (x+1)(y+1)=3 Do x, y nguyên nên x + 1 và y + 1 phải là ước của 3. Lập bảng ta có:
|
0,75 |
|||||||||||||||||||
Vậy các cặp (x,y) là: (0,2); (2,0); (-2,-4); (-4,-2) |
0,5
0,25 |
||||||||||||||||||||
b) (1,5 đ) Q
= A
lớn nhất khi
*
Xét x > 12 thì
*
Xét x < 12 thì
nhỏ
nhất A có giá trị lớn nhất là 5 khi x =11 |
0,25 0,25 0,25
0,25
0,25
0,25 |
||||||||||||||||||||
Câu 4 (4,0 đ) |
a) (2,0 đ) Ta có: 1 là nghiệm của f(x) => f(1) = 0 hay a + b + c = 0 (1) -1 là nghiệm của f(x) => f(-1) = 0 hay a - b + c = 0 (2) Từ (1) và (2) suy ra 2a + 2c = 0 => a + c = 0 => a = -c Vậy a và c là hai số đối nhau. |
0,75 0,75 0,5 |
|||||||||||||||||||
b) (2,0 đ) Ta
có
Vậy
P =
Dấu "=" xảy ra x = 3 và y = -3 Vậy giá trị nhỏ nhất của P = 2011 x = 3 và y = -3 |
0,5 0,5
0,5
0,5 |
||||||||||||||||||||
Câu 5 (5,5 đ) |
|
|
|||||||||||||||||||
a) (2,0 đ) -
Chứng minh
-
Chứng minh
=> CI = BK và góc MKB = góc MIC => BK//CI |
0,5 1,0 0,5 |
||||||||||||||||||||
b) (1,5 đ) Chỉ
ra được AM = MC =>
=>
đường cao MN đồng thời là đường trung tuyến của
=> N là trung điểm AC
Mặt
khác MC =
Lại
có
Vậy MC > KN (ĐPCM) |
0,5 0,25
0,25
0,5
|
||||||||||||||||||||
c) (1,0 đ) Theo CM ý a IM = MK mà AM = MD (gt) => AI = KD Vậy để AI = IM = MK = KD thì cần AI = IM Mặt
khác BI =>
Mà
Từ
(1) và (2) ruy ra
Vậy
vuông
|
0,5
0,5
|
||||||||||||||||||||
d) (1,0 đ) Xảy ra 2 trường hợp: Trường hợp 1: Nếu I thuộc đoạn AM => H thuộc đoạn MC => BI và DH cắt tia MN. Gọi O là giao điểm của BI và tia MN, O’ là giao điểm của DH và tia MN Dễ
dàng chứng minh
Suy ra BI, DH, MN đồng quy. Trường hợp 2: Nếu I thuộc đoạn MD => H thuộc đoạn MB => BI và BH cắt tia đối của tia MN. Chứng minh tương tự trường hợp 1 Vậy BI, DH, MN đồng quy. (Học sinh có thể sử dụng các cách khác để CM: VD sử dụng tính chất đồng quy của 3 đường cao...) |
0,5
0,5 |
Lưu ý:
- Lời giải chỉ trình bày tóm tắt, học sinh trình bày hoàn chỉnh, lý luận chặt chẽ mới cho điểm tối đa.
- Học sinh có thể trình bày nhiều cách giải khác nhau nếu đúng thì cho điểm tương ứng.
ĐÁP ÁN ĐỀ 7 THI CHỌN HỌC SINH GIỎI CẤP TRƯỜNG LỚP 7. Môn: TOÁN
Câu1: Nhân từng vế bất đẳng thức ta được : (abc)2=36abc
+, Nếu một trong các số a,b,c bằng 0 thì 2 số còn lại cũng bằng 0
+,Nếu cả 3số a,b,c khác 0 thì chia 2 vế cho abc ta được abc=36
+, Từ abc =36 và ab=c ta được c2=36 nên c=6;c=-6
+, Từ abc =36 và bc=4a ta được 4a2=36 nên a=3; a=-3
+, Từ abc =36 và ab=9b ta được 9b2=36 nên b=2; b=-2
-, Nếu c = 6 thì avà b cùng dấu nên a=3, b=2 hoặc a=-3 , b=-2
-, Nếu c = -6 thì avà b trái dấu nên a=3 b=-2 hoặc a=-3 b=2
Tóm lại có 5 bộ số (a,b,c) thoã mãn bài toán
(0,0,0); (3,2,6);(-3,-2,6);(3,-2,-6);(-3,2.-6)
Câu 2. (3đ)
a.(1đ) 5x-3<2=> -2<5x-3<2 (0,5đ)
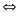 …
…
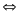 1/5<x<1
(0,5đ)
1/5<x<1
(0,5đ)
b.(1đ) 3x+1>4=> 3x+1>4hoặc 3x+1<-4 (0,5đ)
*Nếu 3x+1>4=> x>1
*Nếu 3x+1<-4 => x<-5/3
Vậy x>1 hoặc x<-5/3 (0,5đ)
c. (1đ) 4-x+2x=3 (1)
* 4-x0 => x4 (0,25đ)
(1)<=>4-x+2x=3 => x=-1( thoả mãn đk) (0,25đ)
*4-x<0 => x>4 (0,25đ)
(1)<=> x-4+2x=3 <=> x=7/3 (loại) (0,25đ)
Câu3. (1đ) Áp dụng a+b a+bTa có
A=x+8-xx+8-x=8
MinA =8 <=> x(8-x) 0 (0,25đ)
*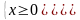 =>0x8
(0,25đ)
=>0x8
(0,25đ)
*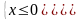 =>
=>
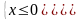 không thoã mãn(0,25đ)
không thoã mãn(0,25đ)
Vậy minA=8 khi 0x8(0,25đ)
Câu4. Ta có S=(2.1)2+(2.2)2+...+ (2.10)2(0,5đ) =22.12+22.22+...+22.102
=22(12+22+...+102) =22.385=1540(0,5đ)
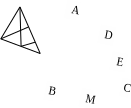 Câu5.(3đ)
Câu5.(3đ)
Chứng minh: a (1,5đ)
Gọi E là trung điểm CD trong tam giác BCD có ME là đường trung bình => ME//BD(0,25đ)
Trong tam giác MAE có I là trung điểm của cạnh AM (gt) mà ID//ME(gt)
Nên D là trung điểm của AE => AD=DE (1)(0,5đ)
Vì E là trung điểm của DC => DE=EC (2) (0,5đ)
So sánh (1)và (2) => AD=DE=EC=> AC= 3AD(0,25đ)
b.(1đ)
Trong tam giác MAE ,ID là đường trung bình (theo a) => ID=1/2ME (1) (0,25đ)
Trong tam giác BCD; ME là Đường trung bình => ME=1/2BD (2)(0,5đ)
So sánh (1) và (2) => ID =1/4 BD (0,25đ)
ĐÁP ÁN ĐỀ 8 THI CHỌN HỌC SINH GIỎI CẤP TRƯỜNG LỚP 7. Môn: TOÁN
Câu
1.
Ta có
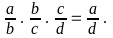 (1) Ta lại có
(1) Ta lại có
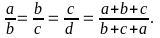 (2)
(2)
Từ
(1) và(2) =>
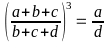 .
.
Câu
2.
A =
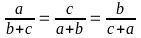 .=
.=
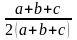 .
.
Nếu
a+b+c
0 => A =
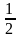 .
.
Nếu a+b+c = 0 => A = -1.
Câu
3.
a). A = 1 +
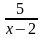 để A
Z thì x- 2 là ước của 5.
để A
Z thì x- 2 là ước của 5.
=> x – 2 = ( 1; 5)
* x = 3 => A = 6 * x = 7 => A = 2
* x = 1 => A = - 4 * x = -3 => A = 0
b)
A =
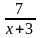 - 2 để A
Z thì x+ 3 là ước của 7.
- 2 để A
Z thì x+ 3 là ước của 7.
=> x + 3 = ( 1; 7)
* x = -2 => A = 5 * x = 4 => A = -1
* x = -4 => A = - 9 * x = -10 => A = -3 .
Câu
4.
a). x = 8 hoặc - 2

b). x = 7 hoặc - 11
c). x = 2.
Câu 5. ( Tự vẽ hình)
MHK là cân tại M .
Thật vậy: ACK = BAH. (gcg) => AK = BH .
AMK = BMH (g.c.g) => MK = MH.
Vậy: MHK cân tại M .
ĐÁP ÁN ĐỀ 9 THI CHỌN HỌC SINH GIỎI CẤP TRƯỜNG LỚP 7. Môn: TOÁN
Bài1: (1,5 điểm)
+
Tìm được: x =
![]()
![]() ;
y = -1 (0,5đ)
;
y = -1 (0,5đ)
+
Với x = -![]() ;
y = -1 Þ
A = -
;
y = -1 Þ
A = -
![]() (0,5đ)
(0,5đ)
+
Với x =
![]() ;
y = -1 Þ
A= -
;
y = -1 Þ
A= -
![]() (0,5đ)
(0,5đ)
Bài 2: (2 điểm)
+
Từ
![]() +
+
![]() = 2 Û
(2 – x)(
= 2 Û
(2 – x)(![]() +
+
![]() )
= 0 Û
x = 2 (0,75đ)
)
= 0 Û
x = 2 (0,75đ)
+
Thay x = 2 Þ
![]() =
=
![]() =
=
![]() =
=
![]() =
=
![]() = 2. (1đ)
= 2. (1đ)
+ Þ x + y + z = 100 (0,25đ)
Bài 3: (2 điểm)
+ Biến đổi được: x(2y + 3) = 4 (0,5đ)
+
Chỉ ra được x, y
![]() Z Þ
x
Z Þ
x
![]() Ư(4) và 2y + 3 lẻ (0,5đ)
Ư(4) và 2y + 3 lẻ (0,5đ)
+ Lập bảng. (1đ)
x |
-4 |
-2 |
-1 |
1 |
2 |
4 |
2y + 3 |
-1 |
-2 |
-4 |
4 |
2 |
1 |
y |
-2 |
loại |
loại |
loại |
loại |
-1 |
Bài 4: (2 điểm).
a) Chỉ được; a + b + c + d = 0 Þ đpcm. (0,5đ)
(hoặc tính được P(1) = 0 Þ đpcm).
b)
+ Rút được:
![]() + x = 3 (1) (0,25đ)
+ x = 3 (1) (0,25đ)
+
Biến đổi được P = (3![]() + 3
+ 3![]() )
+ (
)
+ (![]() + x) – 9x + 1
+ x) – 9x + 1
=
3x(![]() + x) + (
+ x) + (![]() + x) – 9x + 1 (1đ)
+ x) – 9x + 1 (1đ)
+ Thay (1) vào: P = 9x + 3 – 9x + 1 = 4(0,25đ)
(Học sinh có thể giải đúng bằng cách khác vẫn cho điểm)
Bài 5: (2,5 điểm)
+ Hình vẽ (phục vụ được câu 1): (0,25đ)
a) Chỉ ra được F là giao điểm 2 trung trực của D BEC (0,5đ)
Þ
F
![]() trung trực BC Þ
DBFC
cân (0,5đ)
trung trực BC Þ
DBFC
cân (0,5đ)
(học
sinh có thể chứng minh: FC = FE; FB = FE
![]() đpcm).
đpcm).
K F
 b)
+ Tính được
b)
+ Tính được
![]() EBC
= 15
EBC
= 15![]() .
(0,5đ)
.
(0,5đ)
+
Hạ FK
![]() AB Þ
DFKB
= DFHC
(ch + cgv) B (0,75đ)
AB Þ
DFKB
= DFHC
(ch + cgv) B (0,75đ)
ÞDBFC
vuông cân Þ
![]() FBC
= 45
FBC
= 45![]() .
(0,25đ)
.
(0,25đ)
+ Kết luận DBFE đều. (0,25đ)
A F H C
ĐÁP ÁN ĐỀ 10 THI CHỌN HỌC SINH GIỎI CẤP TRƯỜNG LỚP 7. Môn: TOÁN
Bài 1: (1điểm)
Þ
|
0,5đ 0,25đ 0,25đ |
||||||||||
Bài 2: (1,5 điểm) Ta
có:
Suy
ra: 2 Þ Þ
|
0,5đ 0,25đ 0,25đ
0,5đ
|
||||||||||
Bài 3: (2,5điểm) a/
(1 điểm) f(x) = ( biến
x khi:
Þ
m =
Vậy m = 5 thì f(x) là đa thức bậc 3 biến x.
|
0,5đ 0,25đ 0,25đ
|
||||||||||
b/
(1,5 điểm) g(x) = 16 g(x)
=
Với
mọi giá trị của x ta có:
Giá trị nhỏ nhất của g(x) là 9 Khi
và chỉ khi
Þ
|
0,25đ 0,25đ
0,25đ
0,25đ
0,5đ
|
||||||||||
Bài 4: (2 điểm) Gọi
số chia là a và số dư là r (a, r
Ta có: * 112 = 5a + r
Þ
5a < 112 Þ
a
*a > r Þ 5a + r < 5a + a 112 < 6a a > 112 : 6 a ≥ 19 (2) Từ (1) và (2) Þ a = 19; 20; 21; 22 lập bảng số:
|
0,5đ
0,5đ
0,5đ
|
||||||||||
Bài 5: (3 điểm) a/ (1,5 điểm) - Chứng minh DCHO = D CFO (cạnh huyền – góc nhọn) suy ra: CH = CF. Kết luận D FCH cân tại C. -Vẽ
IG //AC (G
-
Suy ra: AH = IG, và
- Chứng minh D AHK = D IGK (g-c-g). - Suy ra AK = KI.. |
0,25đ 0,25đ
0,25đ 0,25đ 0,25đ 0,25đ
|
||||||||||
b/ (1,5 điểm) Vẽ OE ^ AB tại E. Tương tự câu a ta có: D AEH, D BEF thứ tự cân tại A, B. Suy ra: BE = BF và AE = AH. BA = BE + EA = BF + AH = BF + FI = BI. Suy ra: D ABI cân tại B. Mà BO là phân giác góc B, và BK là đường trung tuyến của D ABI nên: B, O, K là ba điểm thẳng hàng.
E H K
O G
B F I C |
0,5đ 0,5đ
0,5đ
|
ĐÁP ÁN ĐỀ 11 THI CHỌN HỌC SINH GIỎI CẤP TRƯỜNG LỚP 7. Môn: TOÁN
Bài 1: (2,0 điểm)
|
0,25 |
|
0,25 |
|
0,25 |
|
|
|
0,25 |
(1)
|
0,25 |
(1)
|
0,25 |
|
0,25 |
|
0,25 |
Bài 2: ( 2,0 điểm)
Ta
có 2H =
|
0,25 |
2H-H
=
|
0,25 |
H
= |
0,25 |
H
|
0,25 |
|
|
Thực hiện tính: M
=
|
0,25 |
|
0,25 |
|
0,25 |
|
0,25 |
Bài 3: ( 2,5 điểm)
|
0,25 |
|
0,25 |
|
0,25 |
|
|
|
|
|
0,25 |
|
0,25 |
|
0,25 |
|
0,25 |
|
|
x
< - |
0,25 |
- |
0,25 |
x |
0,25 |
|
|
Bài 4: ( 3,5 điểm)
Câu a: 0,75 điểm |
Hình vẽ: |
|
BEH cân tại B nên E = H1 |
0,25 |
|
ABC = E + H1 = 2 E |
0,25 |
|
ABC = 2 C BEH = ACB |
0,25 |
|
Câu b: 1,0 điểm |
|
|
Chứng tỏ được DHC cân tại D nên DC = DH. |
0,25 |
|
DAH = 900 - C |
0,25 |
|
DHA = 900 - H2 =900 - C |
0,25 |
|
DAH cân tại D nên DA = DH. |
0,25 |
|
Câu c: 0,75 điểm |
||
ABB’ cân tại A nên B’ = B = 2C |
0,25 |
|
B’ = A1 + C nên 2C = A1 + C |
0,25 |
|
C = A1 AB’C cân tại B’ |
0,25 |
|
Câu d: 0,75 điểm |
||
AB = AB’ = CB’ |
0,25 |
|
BE = BH = B’H |
0,25 |
|
Có: AE = AB + BE HC = CB’ + B’H AE = HC |
0,25 |
|
ĐÁP ÁN ĐỀ 12 THI CHỌN HỌC SINH GIỎI CẤP TRƯỜNG LỚP 7. Môn: TOÁN
Bài 1:(4 điểm):
|
a) (2 điểm)
b) (2 điểm)
=
= = 10( 3n -2n) Vậy
|
Bài 2:(4 điểm)
|
a) (2 điểm)
b) (2 điểm)
|
Bài 3: (4 điểm)
|
a) (2,5 điểm) Gọi a, b, c là ba số được chia ra từ số A.
Theo
đề bài ta có: a : b : c =
và a2 +b2 +c2 = 24309 (2)
Từ
(1)
Do
đó (2)
+ Với k =180, ta được: a = 72; b = 135; c = 30. Khi đó ta có số A = a + b + c = 237.
+
Với k =
Khi
đó ta có só A = b) (1,5 điểm)
Từ
khi
đó
=
|
Bài 4: (4 điểm)

a/
(1điểm) Xét
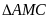 và
và
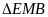 có :
có :
AM = EM (gt )
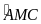 =
=
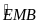 (đối đỉnh )
(đối đỉnh )
BM = MC (gt )
Nên
:
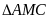 =
=
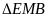 (c.g.c )
(c.g.c )
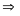 AC
= EB
AC
= EB
Vì
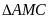 =
=
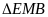
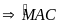 =
=
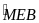
(2 góc có vị trí so le trong được tạo bởi đường thẳng AC và EB cắt đường thẳng AE )
Suy ra AC // BE .
b/ (1 điểm )
Xét
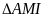 và
và
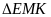 có :
có :
AM = EM (gt )
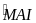 =
=
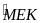 ( vì
( vì
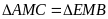 )
)
AI = EK (gt )
Nên
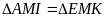 ( c.g.c )
( c.g.c )
Suy
ra
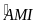 =
=
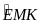
Mà
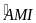 +
+
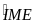 = 180o
( tính chất hai góc kề bù )
= 180o
( tính chất hai góc kề bù )
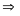
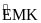 +
+
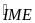 = 180o
= 180o
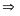 Ba
điểm I;M;K thẳng hàng
Ba
điểm I;M;K thẳng hàng
c/ (1,5 điểm )
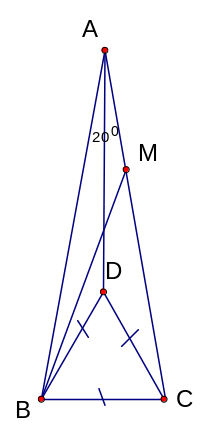
Trong
tam giác vuông BHE (
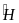 = 90o
) có
= 90o
) có
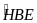 = 50o
= 50o
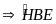 =
90o
-
=
90o
-
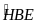 = 90o
-
50o
=40o
= 90o
-
50o
=40o

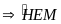 =
=
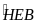 -
-
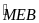 = 40o
-
25o
=
15o
= 40o
-
25o
=
15o
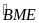 là
góc ngoài tại đỉnh M của
là
góc ngoài tại đỉnh M của
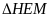
Nên
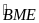 =
=
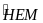 +
+
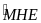 = 15o
+ 90o
= 105o
= 15o
+ 90o
= 105o
( định lý góc ngoài của tam giác )
Bài 5: (4 điểm)
a)
Chứng minh
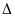 ADB
=
ADB
=
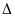 ADC
(c.c.c)
ADC
(c.c.c)
suy
ra
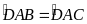
Do
đó
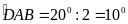
b)
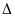 ABC
cân tại A, mà
ABC
cân tại A, mà
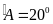 (gt)
nên
(gt)
nên
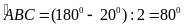
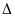 ABC
đều nên
ABC
đều nên
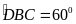
Tia
BD nằm giữa hai tia BA và BC suy ra
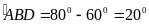 .
.
Tia BM là phân giác của góc ABD
nên
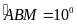
Xét tam giác ABM và BAD có:
AB
cạnh chung ;
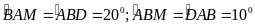
Vậy:
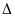 ABM
=
ABM
=
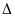 BAD
(g.c.g)
BAD
(g.c.g)
suy ra AM = BD, mà BD = BC (gt) nên AM = BC
ĐÁP ÁN ĐỀ 13 THI CHỌN HỌC SINH GIỎI CẤP TRƯỜNG LỚP 7. Môn: TOÁN
Câu1: (3 điểm)
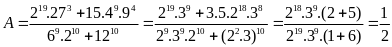 (mỗi
bước đúng 1điểm)
(mỗi
bước đúng 1điểm)
Câu 2: 4 điểm. (Phân tích đúng 1 bước 1điểm)
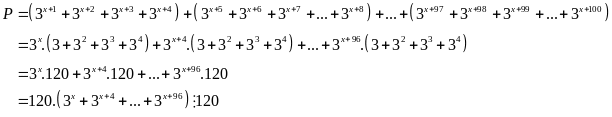
Câu 3: 4 điểm. Vẽ đồ thị 1điểm
|
0 |
4 |
|
0 |
5 |
|
0 |
5 |
|
0 |
-4 |
a) (mỗi bảng 0,25điểm)
Đồ
thị
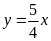 là đường thẳng qua điểm O(0;0) và điểm
A(4;5) (0,25điểm)
là đường thẳng qua điểm O(0;0) và điểm
A(4;5) (0,25điểm)
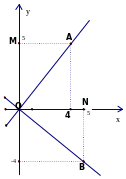 Đồ
thị
Đồ
thị
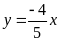 là đường thẳng qua điểm O(0;0) và điểm
B(5;-4) (0,25điểm)
là đường thẳng qua điểm O(0;0) và điểm
B(5;-4) (0,25điểm)
b)
Cần chứng minh
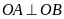
Xét ∆OMA và ∆ONB có:
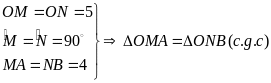 (1điểm)
(1điểm)
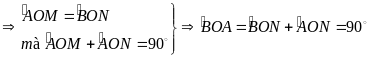 (1điểm)
(1điểm)
Vậy
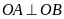
Câu 4: 4,5 điểm
Chứng minh ∆BME đều
∆ABC
cân (gt),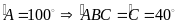 (0,25đ)
(0,25đ)
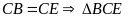 cân
tại C (0,25đ)
cân
tại C (0,25đ)
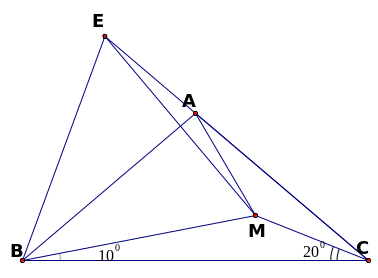
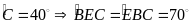 (0,25đ)
(0,25đ)
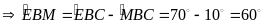 (1) (0,25đ)
(1) (0,25đ)
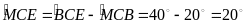 (0,25đ)
(0,25đ)
Vì
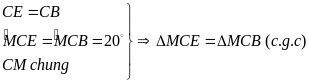 (1đ)
(1đ)
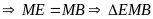 cân
tại M (2) (0,25đ)
cân
tại M (2) (0,25đ)
Từ
(1) và (2)
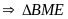 đều. (0,25đ)
đều. (0,25đ)
b)
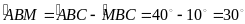 (0,25đ)
(0,25đ)
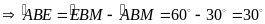 (0,25đ)
(0,25đ)
Vì
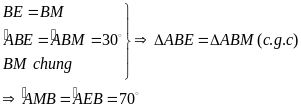 (1,25đ)
(1,25đ)
5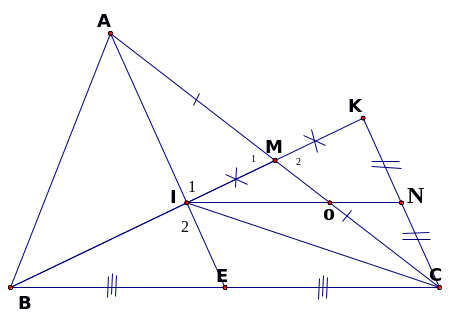 .
a) ∆IKC có MI =MK và NK= NC (gt) (0,5đ)
.
a) ∆IKC có MI =MK và NK= NC (gt) (0,5đ)
Nên CM và IN là hai trung tuyến. (0,25đ)
Mà CM cắt IN tại O nên O là trọng tâm. (0,25đ)
b) ∆AMI và ∆CMK có MI = MK (gt) (0,25đ)
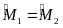 (đđ);
MA = MC (gt) (0,5đ)
(đđ);
MA = MC (gt) (0,5đ)
Nên ∆AMI = ∆CMK (c.g.c) (0,25đ)
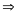
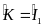 và
AI = KC (1) (0,25đ)
và
AI = KC (1) (0,25đ)
∆ABC
có I là trọng tâm
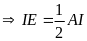 (2) (0,25đ)
(2) (0,25đ)
Mặt
khác
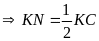 (3) (0,25đ)
(3) (0,25đ)
Từ
(1), (2) và (3)
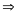 KN
= IE (0,25đ)
KN
= IE (0,25đ)
∆IBE và ∆KIN có KN = IE (cmt) (0,25đ)
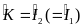 ;
IB =IK (0,25đ)
;
IB =IK (0,25đ)
Nên ∆IBE = ∆KIN (c.g.c) (0,25đ)
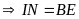 mà
mà
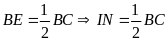 (4) (0,25đ)
(4) (0,25đ)
∆IKC
có O là trọng tâm nên
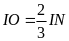 (5) (0,25đ)
(5) (0,25đ)
Từ
(4) và (5)
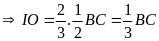 (0,25đ)
(0,25đ)
ĐÁP ÁN ĐỀ 14 THI CHỌN HỌC SINH GIỎI CẤP TRƯỜNG LỚP 7. Môn: TOÁN
Câu 1:
Mỗi tỉ số đã cho đều bớt đi 1 ta được:
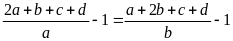 =
=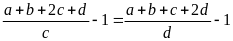
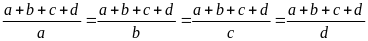
+, Nếu
a+b+c+d
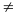 0
thì a = b = c = d lúc đó M = 1+1+1+1=4
0
thì a = b = c = d lúc đó M = 1+1+1+1=4
+, Nếu a+b+c+d = 0 thì a+b = - (c+d); b+c = - (d+a); c+d = - (a+b);
d+a = -(b+c), lúc đó M = (-1) + (-1) + (-1) + (-1) = -4.
Câu 2: S = (100a+10b+c)+(100b+10c+a)+ (100c+10a+b) = 111(a+b+c) = 37.3(a+b+c).
Vì
0 < a+b+c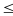 27
nên a+b+c
27
nên a+b+c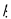 37. Mặt khác( 3; 37) =1 nên 3(a+b+c)
37. Mặt khác( 3; 37) =1 nên 3(a+b+c)
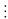 37
=> S không thể là số chính phương.
37
=> S không thể là số chính phương.
Câu 3:
 Quãng
đường AB dài 540 Km; nửa quảng dường AB dài 270 Km. Gọi
quãng đường ô tô và xe máy đã đi là S1,
S2.
Trong cùng 1 thời gian thì quãng đường tỉ lệ thuận với
vận tốc do đó
Quãng
đường AB dài 540 Km; nửa quảng dường AB dài 270 Km. Gọi
quãng đường ô tô và xe máy đã đi là S1,
S2.
Trong cùng 1 thời gian thì quãng đường tỉ lệ thuận với
vận tốc do đó
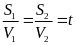 (t chính là thời gian cần tìm).
(t chính là thời gian cần tìm).
t=
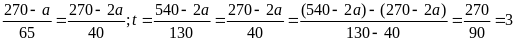
Vậy sau khi khởi hành 3 giờ thì ô tô cách M một khoảng bằng 1/2 khoảng cách từ xe máy đến M.
Câu 4:
a, Tia CO cắt AB tại D.
 +,
Xét
+,
Xét
 BOD
có
BOD
có
 là góc ngoài nên
là góc ngoài nên
 =
=
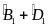
+,
Xét
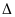 ADC
có góc D1
là góc ngoài nên
ADC
có góc D1
là góc ngoài nên
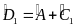
Vậy

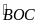 =
=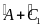 +
+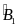
b,
Nếu
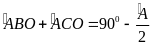 thì
thì
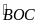 =
=
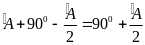
Xét
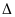 BOC
có:
BOC
có:
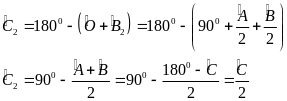
tia CO là tia phân giác của góc C.
Câu 5:
Lấy điểm O tuỳ ý.Qua O vẽ 9 đường thẳng lần lượt song song với 9 đường thẳng đã cho. 9 đường thẳng qua O tạo thành 18 góc không có điểm trong chung, mỗi góc này tương ứng bằng góc giữa hai đường thẳng trong số 9 đương thẳng đã cho. Tổng số đo của 18 góc đỉnh O là 3600 do đó ít nhất có 1 góc không nhỏ hơn 3600 : 18 = 200, từ đó suy ra ít nhất cũng có hai đường thẳng mà góc nhọn giữa chúng không nhỏ hơn 200.
Câu 6:
Tổng số điểm ghi ở hai mặt trên của hai con súc sắc có thể là:
2 = 1+1
3 = 1+2 = 2+1
4 = 1+3 =2 +2 = 3+1
5 = 1+4 =2+3=3+2=4+1.
6=1+5=2+4=3+3=4+2=5+1
7=1+6=2+5=3+4= 4+3=5+2=-6+1
8= 2+6=3+5=4+4=5+3=6+2
9=3+6=4+5=5+4=6+3
10=4+6=5+5=6+4
11=5+6=6+5
12=6+6.
 Như
vậy tổng số 7 điểm có khả năng xảy ra nhất tới
16,7%
Như
vậy tổng số 7 điểm có khả năng xảy ra nhất tới
16,7%
ĐÁP ÁN ĐỀ … THI CHỌN HỌC SINH GIỎI CẤP TRƯỜNG LỚP 7. Môn: TOÁN
Bài |
Cách giải |
Tổng |
1 |
A
=
=
=
Với
a =
|
2,5 |
2 |
Ta có: 0 < a1 < a2 < ….. < a9 nên suy ra: a1 + a2 + a3 < 3a3 (1) a4 + a5 + a6 < 3a6 (2) a7 + a8 + a9 < 3a9 (3) Cộng vế với vế của (1) (2) (3) ta được: a1 + a2 + ….. + a9 < 3(a3 + a6 + a9) Vì
a1
+ a2
+ ….. + a9
> 0 nên ta được:
|
2 |
3 |
Gọi
diện tích, chiều dài, chiều rộng của các mảnh đất
A, B, C theo thứ tự là SA,
dA,
rA,
SB,
dB,
rB,
SC,
dC,
rC.
Theo
bài ra ta có:
Hai
hình chữ nhật A và B có cùng chiều dài nên các diện
tích của chúng tỉ lệ thuận với các chiều rộng. Ta
có:
Hai
hình chữ nhật B và C có cùng chiều rộng nên các diện
tích của chúng tỉ lệ thuận với các chiều dài. Ta
có:
Do đó: SA = dA.rA = 21. 12 = 252 (m2) SB = dB. rB = 21. 15 = 315 (m2) SC = dC. rC = 24. 15 = 360 (m2) |
4,5 |
4 |
a)
Ta có: A =
Để
A nguyên thì
Ta có: x - 2 = 1 hoặc x - 2 = -1. Do đó: x = 3 hoặc x = 1 Vậy để A nguyên thì x = 3 hoặc x = 1 +)
B =
Với
x
Để
B nguyên thì
Ta
có: x - 3 =
Do đó x = 5 ; x = 1 ; x = 4 ; x = 2 Vậy để B nguyên thì x = 5 hoặc x = 1 hoặc x = 4 hoặc x = 2 b) Từ câu a) suy ra: Để A và B cùng nguyên thì x = 1 |
3 |
5 |
GT
DB = CE (D
a)
b)
MB = MC, chứng minh AM KL
là tia phân giác góc DAE c)
BH chứng
minh: BH = CK d)
AM
M D B C E O
Chứng minh: a)
Xét
AB = AC (gt)
DB = CE (gt)
Do
đó
b)
Xét
MD = ME (Do DB = CE và MB = MC theo gt) AM: Cạnh chung AD = AE (CM trên) Do
đó
c)
Vì
Xét
DB = CE (gt)
d) Gọi giao điểm của BH và CK là O. Xét
OA: Cạnh chung AH
= AK (Do AD = AE; DH = KE (vì
Do
đó
Mặt
khác theo câu b) AM là tia phân giác của
Do
đó AO
|
8 |
Ngoài 15 Đề Thi HSG Toán 7 Cấp Trường Có Đáp Án – Toán 7 thì các đề thi trong chương trình lớp 7 sẽ được cập nhật liên tục và nhanh nhất có thể sau khi kỳ thi diễn ra trên Danh mục Kho Đề Thi nhằm giúp các bạn đọc thuận tiện trong việc tra cứu và đối chiếu đáp án. Quý thầy cô và các bạn đọc có thể chia sẻ thêm những tài liệu học tập hữu ích đến địa chỉ email của chúng tôi, nhằm xây dựng nên kho đề thi phong phú, đa dạng cho các em học sinh tham khảo và rèn luyện.
Xem thêm







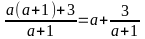
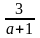 là
số nguyên hay a+1 là ước của 3 do đó ta có bảng sau
:
là
số nguyên hay a+1 là ước của 3 do đó ta có bảng sau
: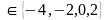 thì
thì
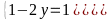
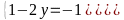
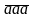 =111.a
( a là chữ số khác 0)
=111.a
( a là chữ số khác 0)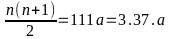 Hay
n(n+1) =2.3.37.a
Hay
n(n+1) =2.3.37.a
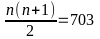 không thoả mãn
không thoả mãn
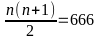 thoả mãn
thoả mãn
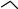
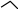 Nên
CH =
Nên
CH =
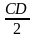
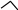
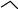 Mà
BAH = 150
nên tam giác AHB cân tại H
Mà
BAH = 150
nên tam giác AHB cân tại H
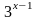 (1+5)
= 162
(1+5)
= 162 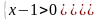
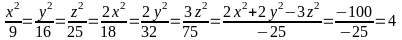
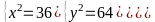 (
Vì x, y, z cùng dấu)
(
Vì x, y, z cùng dấu)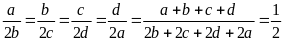 (do a,b,c,d > 0 => a+b+c+d >0)
(do a,b,c,d > 0 => a+b+c+d >0)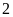
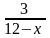

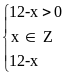
x = 11
x = 11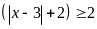 ,
,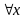 =>
=>
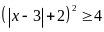 .
Dấu "=" xảy ra
x = 3
.
Dấu "=" xảy ra
x = 3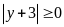 ,
,
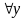 .
Dấu "=" xảy ra
y = -3
.
Dấu "=" xảy ra
y = -3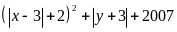
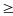 4
+ 2007 = 2011.
4
+ 2007 = 2011.
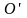
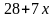 =
=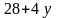
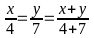
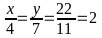
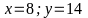
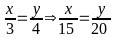 ;
;
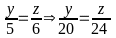
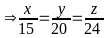 (1)
(1)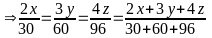
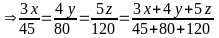
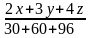 :
: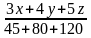 =
=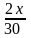 :
:
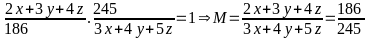
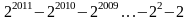
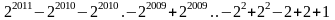
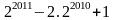
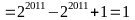
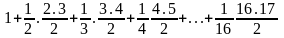
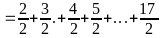
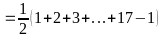
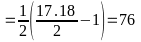
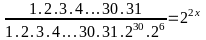
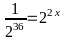
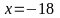
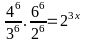
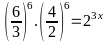
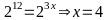
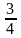
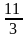 ( Thỏa mãn)
( Thỏa mãn)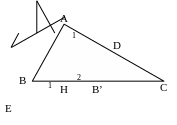
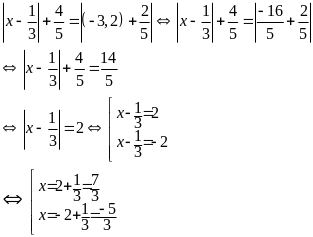
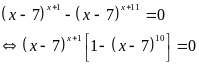
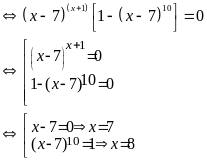
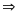
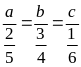 =
k
=
k
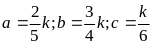
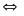
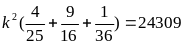
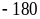
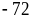
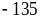
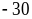
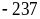
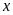
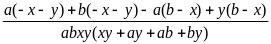
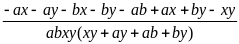 =
=
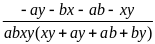
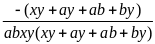 =
=
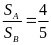
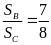
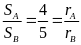
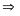
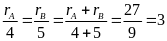
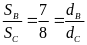
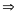
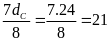
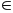
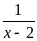 nguyên.
nguyên.
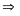
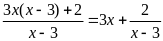
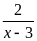 nguyên.
nguyên.
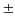

 ABC
có AB = AC.
ABC
có AB = AC.
 AD = H; CK
AD = H; CK AE
= K
AE
= K BH
BH CK
tại 1 điểm
CK
tại 1 điểm

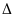
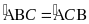
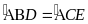
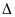 ACE
có:
ACE
có:
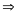 AD = AE (2 cạnh tương ứng).
AD = AE (2 cạnh tương ứng). 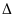
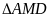 và
và
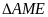 có:
có: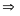
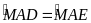
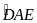
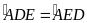
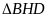
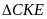
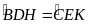
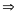
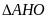 và
và
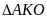 có:
có: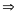
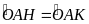
 AM, suy ra 3 đường thẳng AM; BH; CK cắt nhau tại O.
AM, suy ra 3 đường thẳng AM; BH; CK cắt nhau tại O.