Chuyên Đề Bồi Dưỡng HSG Toán 6 Chủ Đề Các Bài Toán Liên Quan Đến Số Và Chữ Số
>>> Mọi người cũng quan tâm:
Chuyên Đề Bồi Dưỡng HSG Toán 6 Chủ Đề Các Bài Toán Liên Quan Đến Số Và Chữ Số Có Lời Giải – Tài Liệu Toán là tài liệu học tập được Trang Tài Liệu biên soạn và sưu tầm từ những nguồn dữ liệu mới nhất hiện nay. Tài liệu này sẽ giúp các em luyện tập, củng cố kiến thức từ đó nâng cao điểm số cho môn học. Ngoài ra, cũng giúp các thầy cô giáo có nguồn tài nguyên phong phú để giảng dạy.
Dưới đây là bản đọc trực tuyến giúp thầy cô và các em học sinh có thể nghiên cứu Online hoặc bạn có thể tải miễn phí với phiên bản word để dễ dàng in ấn cũng như học tập Offline.
ĐS6.CHUYÊN ĐỀ 1-SỐ TỰ NHIÊN
CHỦ ĐỀ 1:PHƯƠNG PHÁP GIẢI CÁC BÀI TOÁN LIÊN QUAN ĐẾN SỐ VÀ CHỮ SỐ
PHẦN I.TÓM TẮT LÝ THUYẾT
Tập
hợp số tự nhiên:
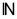
Tập
hợp số tự nhiên khác 0 (nguyên dương), ký hiệu là:
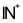
Có
10 chữ số:
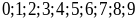 .
.
Số
tự nhiên có chữ số tận cùng là
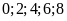 là các số chẵn.
là các số chẵn.
Số
tự nhiên có chữ số tận cùng là
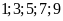 là các số lẻ.
là các số lẻ.
Hai số tự nhiên liên tiếp hơn (kém) nhau 1 đơn vị. Hai số hơn (kém) nhau 1 đơn vị là hai số tự nhiên liên tiếp.
Hai số chẵn liên tiếp hơn (kém) nhau 2 đơn vị. Hai số chẵn hơn (kém) nhau 2 đơn vị là hai số chẵn liên tiếp.
Hai số lẻ liên tiếp hơn (kém) nhau 2 đơn vị. Hai số lẻ hơn (kém) nhau 2 đơn vị là hai số lẻ liên tiếp.
2.CẤU TẠO CỦA MỘT SỐ TỰ NHIÊN
Phân tích một số tự nhiên theo các chữ số:
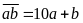
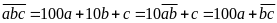
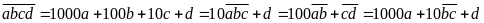
Với
điều kiện

3.SO SÁNH HAI SỐ TỰ NHIÊN
Trong hai số tự nhiên, số nào có chữ số nhiều hơn thì lớn hơn.
Nếu hai số có cùng chữ số thì số nào có chữ số đầu tiên kể từ trái sang phải lớn hơn thì số đó lớn hơn. Nếu hai số có tất cả các cặp chữ số ở từng hàng đều bằng nhau thì hai số đó bằng nhau.
PHẦN II.CÁC DẠNG BÀI
Dạng 1:Viết số tự nhiên từ giả thiết cho trước
I.Phương pháp giải
-
Khi viết một số tự nhiên ta sử dụng 10 chữ số
 .
Chữ số đầu tiên kể từ bên trái của một số tự
nhiên phải khác 0.
.
Chữ số đầu tiên kể từ bên trái của một số tự
nhiên phải khác 0.
- Thông qua việc phân tích và xét hết khả năng có thể xảy ra, đối chiếu với giả thiết đề bài để lập số.
II.Bài toán
Bài
1: Cho
bốn chữ số
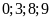 .
.
Tìm số lớn nhất, số nhỏ nhất có 4 chữ số khác nhau được viết từ 4 chữ số đã cho.
Tìm số lẻ lớn nhất, số chẵn nhỏ nhất có 4 chữ số khác nhau được viết từ 4 chữ số đã cho.
Lời giải:
a)Số lớn nhất có 4 chữ số khác nhau được viết từ 4 chữ số đã cho phải có chữ số hàng nghìn là chữ số lớn nhất. Vậy chữ số hàng nghìn phải tìm là 9.
Chữ số hàng trăm phải là chữ số lớn nhất trong 3 chữ số còn lại. Vậy chữ số hàng trăm phải tìm là 8.
Chữ số hàng chục là chữ số lớn nhất trong 2 chữ số còn lại. Vậy chữ số hàng chục là 3.
Vậy số cần tìm là 9830.
Tương tự số nhỏ nhất có bốn chữ số khác nhau từ 4 chữ số trên là 3089.
b)Tương tự số lẻ lớn nhất thỏa mãn điều kiện đầu bài là 9803.
Số chẵn nhỏ nhất thỏa mãn điều kiện đầu bài là 3098.
Bài
2: Tìm
số tự nhiên có ba chữ số
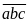 ,
thỏa mãn
,
thỏa mãn
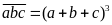
Lời giải:
Điều
kiện:
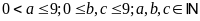
Nhận
thấy:

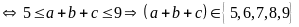
Nếu
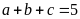 thì
thì
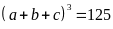 .
Thử lại
.
Thử lại
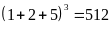 (không thỏa mãn)
(không thỏa mãn)
Nếu
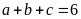 thì
thì
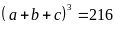 .
Thử lại
.
Thử lại
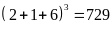 (không thỏa mãn)
(không thỏa mãn)
Nếu
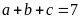 thì
thì
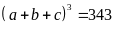 .
Thử lại
.
Thử lại
 (không thỏa mãn)
(không thỏa mãn)
Nếu
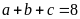 thì
thì
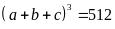 .
Thử lại
.
Thử lại
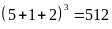 (thỏa mãn)
(thỏa mãn)
Nếu
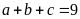 thì
thì
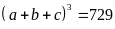 .
Thử lại
.
Thử lại
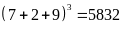 (không thỏa mãn)
(không thỏa mãn)
Vậy
số tự nhiên cần tìm là
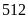 .
.
Bài
3: Tìm
hai số, biết rằng tổng của chúng gấp
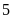 lần hiệu của chúng, tích của chúng gấp
lần hiệu của chúng, tích của chúng gấp
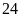 lần hiệu của chúng.
lần hiệu của chúng.
Phân tích: Bài toán có thể giải bằng “số phần” bằng cách biểu thị hiệu là 1 phần thì tổng là 5 phần và tích là 24 phần. Từ đó tính được số lớn ứng với bao nhiêu phần, số bé ứng với bao nhiêu phần.
Lời giải
Theo
đầu bài. Nếu biểu thị hiệu là
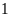 phần thì tổng là
phần thì tổng là
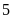 phần và tích là
phần và tích là
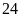 phần.
phần.
Số
lớn là:
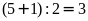 (phần).
(phần).
Số
bé là:
 (phần)
(phần)
Vậy
tích sẽ bằng
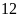 lần số bé.
lần số bé.
Ta
có: Tích
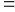 Số lớn
Số lớn
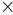 Số bé
Số bé
Tích
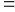
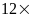 Số bé
Số bé
Số
lớn là
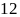 .
.
Số
bé là:
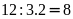
Vậy
hái số tự nhiên cần tìm là
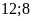 .
.
Bài
4: Tìm
thương của một phép chia, biết rằng nếu thêm
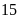 vào số bị chia và thêm
vào số bị chia và thêm
 vào số chia thì thương và số dư không đổi.
vào số chia thì thương và số dư không đổi.
Phân tích: Thực hiện biểu diễn số bị chia theo số chia, số thương và số dư, từ đó thiết lập được hai đẳng thức liên quan giữa số thương, số chia, và số dư. Cuối cùng tìm được thương.
Lời giải
Gọi
số bị chia, số chia, thương và số dư lần lượt là

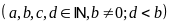 .
Ta có:
.
Ta có:
 (dư
(dư
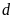 )
)
Theo
đề ta có:
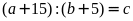 (dư
(dư
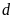 )
)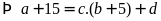
Hay
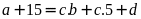
Mà
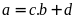 nên
nên

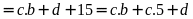
Suy
ra
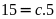 .
Vậy
.
Vậy
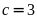 .
.
Bài 5: Hiệu của hai số là 4. Nếu tăng một số gấp ba lần, giữ nguyên số kia thì hiệu của chúng bằng 60. Tìm hai số đó.
Lời giải
Gọi
2 số đó là
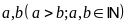
Theo
bài ra ta có:
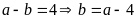
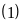
Nếu
tăng một số gấp ba lần, giữ nguyên số kia thì hiệu
của chúng bằng 60
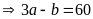
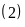
Thay
(1) vào (2) ta có
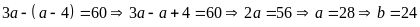
Vậy
số cần tìm là
 .
.
Bài 6: Tìm hai số biết rằng tổng của chúng gấp 5 lần hiệu của chúng và tích của chúng gấp 4008 lần hiệu của chúng.
Lời giải
Coi
hiệu của hai số là
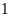 phần thì tổng của chúng là
phần thì tổng của chúng là
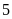 phần.
phần.
Do
đó số lớn là
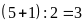 (phần).
(phần).
Số
bé là:
 (phần).
(phần).
Tích
của hai số là:
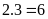 (phần)
(phần)
Mà
tích hai số là
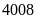 nên giá trị một phần là:
nên giá trị một phần là:
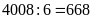 .
.
Số
bé là:
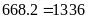
Số
lớn là:
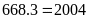 .
.
Vậy hai số cần tìm là 2004 và 1336.
Bài 7: Tìm hai số biết rằng tổng của chúng gấp 3 lần hiệu của chúng và tích của chúng gấp 124 lần hiệu của chúng.
Lời giải
Coi
hiệu của hai số là
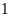 phần thì tổng của chúng là
phần thì tổng của chúng là
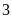 phần.
phần.
Do
đó số lớn là
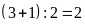 (phần).
(phần).
Số
bé là:
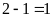 (phần).
(phần).
Tích
của hai số là:
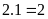 (phần)
(phần)
Mà
tích hai số là
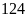 nên giá trị một phần là:
nên giá trị một phần là:
 .
.
Số
bé là:
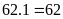
Số
lớn là:
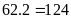 .
.
Vậy hai số cần tìm là 62 và 124.
Bài 8: Tổng của hai số tự nhiên gấp ba hiệu của chúng. Tìm thương của hai số tự nhiên ấy.
Lời giải
Gọi
hai số đó là
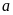 và
và
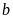

Ta
có
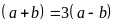
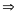
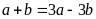
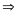

Suy
ra
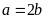 do đó
do đó
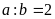
Vậy thương hai số tự nhiên cần tìm là 2.
Bài 9: Hiệu của hai số là 4. Nếu tăng một số gấp ba lần, giữ nguyên số kia thì hiệu của chúng bằng 60. Tìm hai số đó.
Lời giải
Gọi
số bị trừ là là
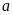 ,
số trừ là
,
số trừ là
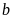

Theo
đề bài ta có :
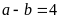
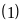
Tăng
số bị trừ lên 3 lần và giữ nguyên số chia vì hiệu
của chúng bằng 60 nên :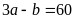
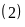
Từ
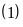 ta có
ta có
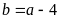 thay vào
thay vào
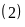 ta được :
ta được :
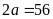 suy ra
suy ra
 suy ra
suy ra
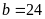 .
.
Vậy
hai số tự nhiên cần tìm là
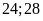 .
.
Bài 10: Tìm hai số, biết rằng tổng của chúng gấp 7 lần hiệu của chúng, tích của chúng gấp 192 lần hiệu của chúng.
Lời giải
Coi
hiệu của hai số là
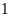 phần thì tổng của chúng là
phần thì tổng của chúng là
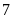 phần.
phần.
Do
đó số lớn là
 (phần).
(phần).
Số
bé là:
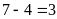 (phần).
(phần).
Tích
của hai số là:
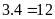 (phần)
(phần)
Mà
tích hai số là
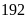 nên giá trị một phần là:
nên giá trị một phần là:
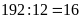 .
.
Số
bé là:
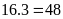
Số
lớn là:
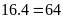 .
.
Vậy
hai số tự nhiên cần tìm là
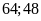 .
.
Bài
11: Viết
liên tiếp 15 số lẻ đầu tiên để được một số tự
nhiên. Hãy xoá đi 15 chữ số của số tự nhiên vừa nhận
được mà vẫn giữ nguyên thứ tự các chữ số còn lại
để được:
a, Số lớn nhất.
b, Số nhỏ nhất.
Lời giải
Viết
15 số lẻ đầu tiên liên tiếp ta được số tự nhiên:

Để sau khi xoá 15 chữ số ta nhận được số lớn
nhất thì chữ số giữ lại đầu tiên kể từ bên trái
phải là chữ số 9. Vậy trước hết ta xoá 4 chữ số
đầu tiên của dãy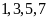 .
Số còn lại là:
.
Số còn lại là:
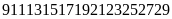
Ta phải xoá tiếp
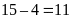 chữ số còn lại để được số lớn nhất. Để sau khi
xoá nhận được số lớn nhất thì chữ số thứ hai kể
từ bên trái phải là chữ số 9. Vậy tiếp theo ta phải
xoá tiếp những chữ số viết giữa hai chữ số 9 trong
dãy, đó là
chữ số còn lại để được số lớn nhất. Để sau khi
xoá nhận được số lớn nhất thì chữ số thứ hai kể
từ bên trái phải là chữ số 9. Vậy tiếp theo ta phải
xoá tiếp những chữ số viết giữa hai chữ số 9 trong
dãy, đó là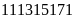 .
Số còn lại là:
.
Số còn lại là:
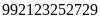 .
.
Ta
phải xoá tiếp
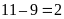 chữ số từ số còn lại để được số lớn nhất. Chữ
số thứ ba còn lại kể từ bên trái phải là 2, vậy để
được số lớn nhất sau khi xoá 2 chữ số ta phải xoá
số 12 hoặc 21. Vậy số lớn nhất phải là
chữ số từ số còn lại để được số lớn nhất. Chữ
số thứ ba còn lại kể từ bên trái phải là 2, vậy để
được số lớn nhất sau khi xoá 2 chữ số ta phải xoá
số 12 hoặc 21. Vậy số lớn nhất phải là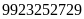 .
.
b,
Lập luận tương tự câu a. số phải tìm là
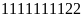 .
.
Bài
12: Tìm
số lớn nhất có các chữ số khác nhau và tổng các chữ
số bằng 6.
Lời
giải
Viết 6 thành tổng các chữ số khác nhau là
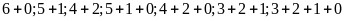 .
.
Vậy số lớn nhất có các chữ số khác nhau có tổng các chữ số bằng 6 cần tìm là 3210.
Bài
13: Tìm
số bé nhất có tổng các chữ số bằng 21.
Lời
giải
Số
có hai chữ số có tổng các chữ số lớn nhất là 99. Vì
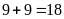 và 18 nhỏ hơn 21 nên số cần tìm phải có nhiều hơn hai
chữ số.
và 18 nhỏ hơn 21 nên số cần tìm phải có nhiều hơn hai
chữ số.
Xét
các số có ba chữ số có tổng các chữ số bằng 21. Số
bé nhất phải thỏa mãn có chữ số hàng trăm bé nhất.
Vì
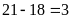 nên số cần tìm là 399.
nên số cần tìm là 399.
Bài
14:
Tìm số bé nhất, số lớn nhất có các chữ số khác
nhau và tích các chữ số bằng 30.
Lời
giải
Viết
30 thành tích các chữ số khác nhau là
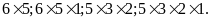
Vậy số bé nhất là 56, số lớn nhất là 5321.
Bài
15:
Trung bình cộng của n số chẵn nhỏ nhất có hai chữ số
là 14. Tìm
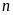 .
.
Lời
giải
Số
chẵn có hai chữ số và bé hơn 14 là
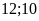 .
Hai số chẵn lớn hơn 14 là
.
Hai số chẵn lớn hơn 14 là
 .
Vậy
.
Vậy
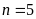 .
.
Dạng 2: Các bài toán giải bằng phân tích số
I.Phương pháp giải
- Phân tích một số tự nhiên theo các chữ số.
- Thông qua việc phân tích các giả thiết đề bài đề tìm số.
II.Bài toán
Bài 1: Tìm một số tự nhiên có hai chữ số biết rằng khi viết thêm số 12 vào bên trái số đó ta được số mới lớn gấp 26 lần số phải tìm.
Lời giải:
Gọi
số cần tìm là:
 (
(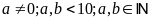 )
)
Viết
thêm số 12 vào bên trái số đó ta được:
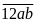
Theo
bài ra ta có:

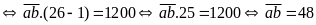
Thử
lại ta thấy
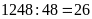 .
.
Vậy số tự nhiên cần tìm là 1248.
Bài 2: Cho số có hai chữ số. Nếu lấy số đó chia cho hiệu của chữ số hàng chục và hàng đơn vị của nó thì được thương là 18 và dư 4. Tìm số đã cho.
Lời giải:
Gọi
số phải tìm là:
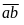
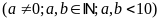
Theo
bài ra ta có: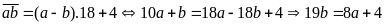
Vì
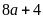 là số chẵn
là số chẵn
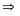
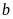 chẵn
chẵn
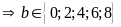
Với
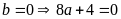 (vô lý)
(vô lý)
Tương
tự với các trường hợp
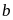 còn lại : ta
có
còn lại : ta
có
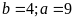 thỏa mãn bài toán
thỏa mãn bài toán
Vậy số cần tìm là 94.
Bài 3: Tìm một số tự nhiên có ba chữ số, biết rằng số đó gấp 5 lần tích các chữ số của nó.
Lời giải:
Gọi
số phải tìm là:
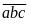
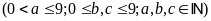

Nếu
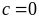 thì
thì
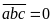 không thỏa mãn bài toán.
không thỏa mãn bài toán.
Nếu
 thì
thì


Số
có ba chữ số chia hết cho 25 khi

Ta
có: Vế trái (1)
là một số tự nhiên lẻ
nên vế phải cũng là một số tự nhiên lẻ
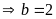 (loại) do đó
(loại) do đó
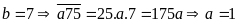
Vậy
số tự nhiên cần tìm là
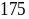 .
.
Bài 4: Tìm các chữ số a, b , c thỏa mãn:
a)
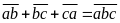 b)
b)
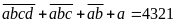
Lời
giải:
Điều kiện:
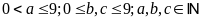
a)
Ta có
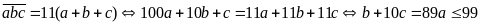
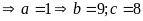

b)
Ta
có:
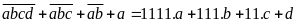
Vậy
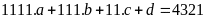
Nếu
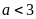 thì
thì
 (vô lý vì
(vô lý vì
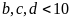 )
)
Nếu
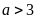 thì vế trái
thì vế trái
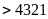 (không thỏa mãn)
(không thỏa mãn)
Vậy
 Suy ra
Suy ra
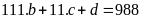
Nếu
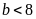 thì
thì
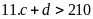 (vô lý vì
(vô lý vì
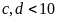 )
)
Nếu
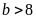 thì vế trái
thì vế trái
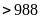 (không thỏa mãn)
(không thỏa mãn)
Vậy
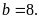 Suy ra
Suy ra
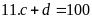
+
Nếu
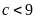 thì
thì
 (vô lý vì
(vô lý vì
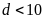 )
)
Do
đó
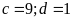
Vậy
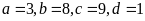 thỏa
thỏa

Bài
5: Tìm
số tự nhiên có năm chữ số, biết rằng nếu viết thêm
chữ số
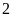 vào đằng sau số đó thì được số lớn gấp ba lần số
có được bằng cách viết thêm chữ số
vào đằng sau số đó thì được số lớn gấp ba lần số
có được bằng cách viết thêm chữ số
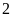 vào đằng trước số đó.
vào đằng trước số đó.
Phân
tích:
Gọi số cần tìm là
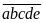 .
Khi viết thêm chữ số 2 vào đằng sau ta được
.
Khi viết thêm chữ số 2 vào đằng sau ta được
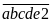
Khi
viết thêm chữ số 2 vào đằng trước ta được
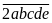 .
Do đó ta cần phân tích các số
.
Do đó ta cần phân tích các số
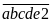 và
và
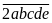 theo
theo
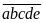 ,
từ đó theo mối quan hệ bài cho tìm được
,
từ đó theo mối quan hệ bài cho tìm được
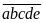 .
.
Lời giải
Gọi
số cần tìm là:
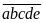
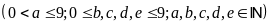
Theo
bài ra ta có:
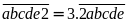
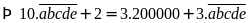
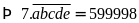

Thử
lại:
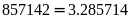
Vậy
số cần tìm là
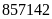 .
.
Bài
6: Tìm
số tự nhiên có tận cùng bằng
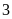 ,
biết rằng nếu xóa chữ số hàng đơn vị thì số đó
giảm đi
,
biết rằng nếu xóa chữ số hàng đơn vị thì số đó
giảm đi
 đơn vị.
đơn vị.
Phân
tích:
Gọi số cần tìm là
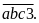 Khi xóa chữ số 3 ta được
Khi xóa chữ số 3 ta được
 ,
do đó ta cần phân tích cấu tạo số
,
do đó ta cần phân tích cấu tạo số
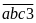 theo
theo
 ,
và theo mối quan hệ bài cho tìm được
,
và theo mối quan hệ bài cho tìm được
 rồi suy ra số cần tìm.
rồi suy ra số cần tìm.
Lời giải
Vì
rằng nếu xóa chữ số hàng đơn vị thì số đó giảm
đi
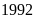 đơn vị nên số tự nhiên cần tìm có
đơn vị nên số tự nhiên cần tìm có
 chữ số.
chữ số.
Gọi
số tự nhiên cần tìm là
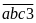
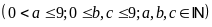
Theo
bài ra ta có:

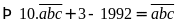
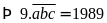
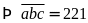
Vậy
số cần tìm là
 .
.
Bài
7:
Tìm ba chữ số khác nhau và khác
 ,
biết rằng nếu dùng cả ba chữ số này lập thành các
số tự nhiên có ba chữ số thì hai số lớn nhất có
tổng bằng
,
biết rằng nếu dùng cả ba chữ số này lập thành các
số tự nhiên có ba chữ số thì hai số lớn nhất có
tổng bằng
 .
.
Phân
tích:
Ba số cần tìm là
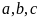
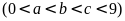 .
Như vậy tổng
.
Như vậy tổng
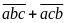 cần phân tích cấu tạo số theo a, b, c ta được
cần phân tích cấu tạo số theo a, b, c ta được
 việc còn lại ta phân tích số 1444 về dạng
việc còn lại ta phân tích số 1444 về dạng
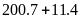
Rồi
đồng nhất với
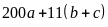 để tìm ra a, b, c
để tìm ra a, b, c
Lời giải
Gọi
ba chữ số cần tìm là

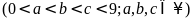 .
.
Theo bài ra ta có:
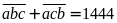
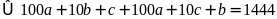
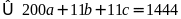
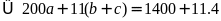
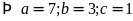 .
.
Vậy
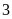 số cần tìm là:
số cần tìm là: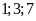 .
.
Bài
8: Cho
ba chữ số
 đôi một khác nhau và khác 0. Tổng của tất cả các số
có hai chữ số được lập từ ba chữ số
đôi một khác nhau và khác 0. Tổng của tất cả các số
có hai chữ số được lập từ ba chữ số
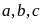 bằng 627. Tính tổng
bằng 627. Tính tổng
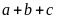 .
.
Lời giải:
Ta
có các số có hai chữ số được lập thành từ ba chữ
số
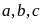 là:
là:
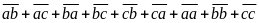
Theo
đầu bài ta có:
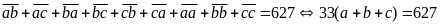
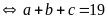
Vậy
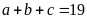 .
.
Bài
9: Tích
của hai số là
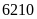 .
Nếu giảm một thừa số đi
.
Nếu giảm một thừa số đi
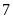 đơn vị thì tích mới là
đơn vị thì tích mới là
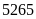 .
Tìm các thừa số của tích.
.
Tìm các thừa số của tích.
Phân tích: Từ mối liên hệ bài cho ta thiết lập được hai đẳng thức liên quan tới hai số, từ đó tìm được hai số.
Lời giải
Gọi
thừa số được giảm là
 ,
thừa số còn lại là
,
thừa số còn lại là
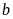 .
.
Theo đề bài ta có:
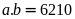
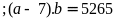
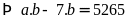
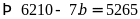
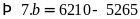
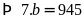
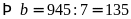
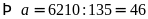
Vậy
hai thừa số cần tìm là
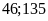 .
.
Bài 10: Một số có 3 chữ số, tận cùng bằng chữ số 7. Nếu chuyển chữ số 7 đó lên đầu thì ta được một số mới mà khi chia cho số cũ thì được thương là 2 dư 21. Tìm số đó.
Phân
tích:
Gọi
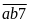 số tự nhiên có chữ số 7 là hàng đơn vị
số tự nhiên có chữ số 7 là hàng đơn vị
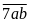 số
tự nhiên có chữ số 7 là hàng trăm
số
tự nhiên có chữ số 7 là hàng trăm
Bằng việc phân tích cấu tạo số ta có thể giải bài toán theo hai cách:
Phân
tích cấu tạo số theo
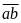
Lời giải
Gọi
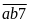 số tự nhiên có chữ số
số tự nhiên có chữ số
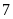 là hàng đơn vị.
là hàng đơn vị.

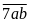 số
tự nhiên có chữ số
số
tự nhiên có chữ số
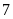 là số hàng trăm.
là số hàng trăm.
Theo
đề bài ta có:
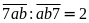 dư
dư
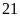
Hay:
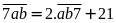
Ta
có:
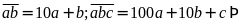
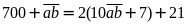
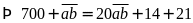
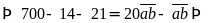
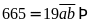
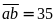 .
.
Vậy
số tự nhiên có ba chữ số đó là:
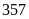 .
.
Bài 11: Tìm số tự nhiên có 5 chữ số, biết rằng nếu viết thêm chữ số 7 vào đằng trước số đó thì được một số lớn gấp 5 lần so với số có được bằng cách viết thêm chữ số 7 vào sau số đó
Phân
tích:
Gọi số cần tìm là
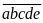 .
Khi viết thêm chữ số 7 vào đằng sau ta được
.
Khi viết thêm chữ số 7 vào đằng sau ta được
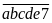
Khi
viết thêm chữ số 7 vào đằng trước ta được
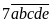 .
Do đó ta cần phân tích cấu tạo các số
.
Do đó ta cần phân tích cấu tạo các số
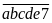 và
và
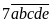 ,
từ đó theo mối quan hệ bài cho tìm được
,
từ đó theo mối quan hệ bài cho tìm được
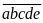 .
.
Lời giải
Gọi
số tiền có năm chữ số là:
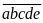
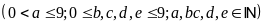
Theo
đề bài:
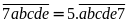
Ta
có:
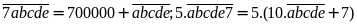
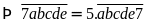
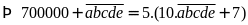
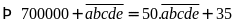
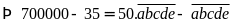

Vậy số tự nhiên cần tìm là 14285.
Bài 12: Tìm số tự nhiên có hai chữ số, biết rằng nếu viết thêm một chữ số 2 vào bên phải và một chữ số 2 vào bên trái của nó thì số ấy tăng gấp 36 lần.
Phân
tích:
Gọi số cần tìm là
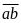 .
Khi
viết thêm chữ số 2 vào đằng trước và đằng sau ta
được
.
Khi
viết thêm chữ số 2 vào đằng trước và đằng sau ta
được
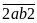 .
Do đó ta cần tìm cấu tạo số
.
Do đó ta cần tìm cấu tạo số
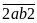 theo
theo
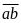 ,
từ đó theo mối liên hệ bài cho tìm được
,
từ đó theo mối liên hệ bài cho tìm được
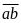
Lời giải
Gọi
số phải tìm là
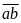 .
.

Viết
thêm một chữ số
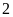 vào bên trái và bên phải ta được:
vào bên trái và bên phải ta được:
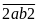 ,
số đo tăng lên gấp
,
số đo tăng lên gấp
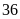 lần.
lần.
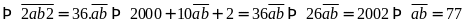
Vậy số tự nhiên cần tìm là 77.
Bài 13: Nếu ta viết thêm chữ số 0 vào giữa các chữ số của một số có hai chữ số ta được một số mới có 3 chữ số lớn hơn số đầu tiên 7 lần. Tìm số đó.
Phân
tích:
Gọi số cần tìm là
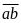 .
Khi viết thêm chữ số 0 vào giữa ta được
.
Khi viết thêm chữ số 0 vào giữa ta được
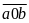 .
Vì hai chữ số a, b không có cạnh nhau, nên ta cần phân
tích cấu tạo số
.
Vì hai chữ số a, b không có cạnh nhau, nên ta cần phân
tích cấu tạo số
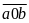 theo các chữ số
theo các chữ số
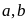 từ đó theo mối liên hệ bài cho tìm được các chữ số
a, b từ đó suy ra số
từ đó theo mối liên hệ bài cho tìm được các chữ số
a, b từ đó suy ra số
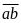
Lời giải
Số
tự nhiên có hai chữ số có dạng:
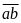

Thêm
chữ số
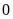 vào giữa hai chữ số:
vào giữa hai chữ số:
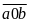
Theo
đề bài:
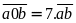
Hay
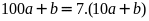
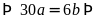
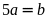
Khi
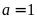 ,
ta được:
,
ta được:
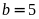 (nhận)
(nhận)
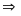
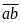 là
là

Khi
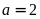 ,
ta được:
,
ta được:
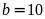 (loại)
(loại)
Vậy
số tự nhiên cần tìm là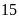 .
.
Bài 14: Nếu xen vào giữa các chữ số của một số có hai chữ số của chính số đó, ta được một số mới có bốn chữ số và bằng 99 lần số đầu tiên. Tìm số đó
Phân
tích:
Gọi số cần tìm là
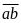 .
Xen vào giữa các chữ số của một số có hai chữ số
của chính số đó ta được
.
Xen vào giữa các chữ số của một số có hai chữ số
của chính số đó ta được
 ,
đến đây nhiều ý tưởng sẽ phân tích cấu tạo số
,
đến đây nhiều ý tưởng sẽ phân tích cấu tạo số
 theo
theo
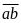 ,
tuy nhiên vì hai chữ số b, a ở hàng đơn vị và hàng
nghìn không cạnh nhau, nên việc phân tích cấu tạo số
theo
,
tuy nhiên vì hai chữ số b, a ở hàng đơn vị và hàng
nghìn không cạnh nhau, nên việc phân tích cấu tạo số
theo
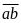 là không ra mà ta cần phân tích cấu tạo số theo các chữ
số a, b, từ đó theo mối liên hệ bài cho tìm được các
chữ số a, b từ đó suy ra số
là không ra mà ta cần phân tích cấu tạo số theo các chữ
số a, b, từ đó theo mối liên hệ bài cho tìm được các
chữ số a, b từ đó suy ra số
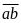 .
.
Lời giải
Gọi
số tự nhiên cần tìm là
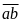

Theo
bài ra, ta có:
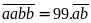
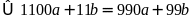
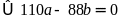
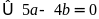
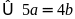
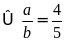
Mà
 là các số có
là các số có
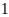 chữ số
chữ số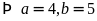 .
.
Vậy
số tự nhiên cần tìm là
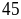 .
.
Bài 15: Nếu xen vào giữa các chữ số của một số có hai chữ số một số có hai chữ số kém số đó 1 đơn vị thì sẽ được một số có bốn chữ số lớn gấp 91 lần so với số đầu tiên. Hãy tìm số đó.
Lời giải:
Gọi
số cần tìm là
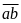

Ta
có:
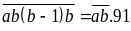
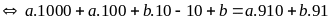
Bài 16: Tìm số tự nhiên có hai chữ số, biết rằng số mới viết theo thứ tự ngược lại nhân với số phải tìm thì được 3154; số nhỏ trong hai số thì lớn hơn tổng các chữ số của nó là 27
Lời giải:
Gọi
số cần tìm là:
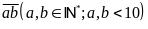
Thì
số mới có dạng:
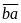
Giả
sử
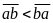
Theo đề ta có:
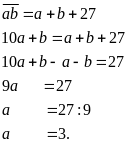
Từ
đó ta có
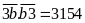
Vì
 có chữ số tận cùng là
có chữ số tận cùng là
 nên
nên
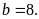
Vậy
số cần tìm là
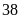 hoặc
hoặc
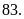
Bài 17: Cho số có hai chữ số . Nếu lấy số đó chia cho hiệu của chữ số hàng chục và hàng đơn vị của nó thì được thương là 18 và dư 4. Tìm số đã cho.
Lời giải:
Số
tự nhiên có
 chữ số là
chữ số là
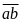
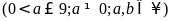 .
.
Ta
có
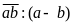 được thương là
được thương là
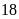 dư
dư
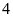 .
.
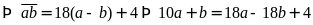
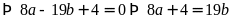
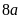 và
và
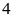 là hai số chẵn
là hai số chẵn
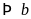 chẵn
chẵn
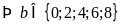
Với
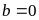
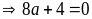 (loại vì
(loại vì
 )
)
Với
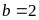
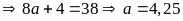 (loại vì
(loại vì
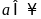 )
)
Với
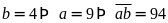 .
.
Với
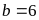
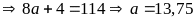 (loại vì
(loại vì
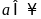 )
)
Với
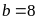
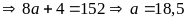 (loại vì
(loại vì
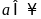 )
)
Vậy số tự nhiên cần tìm là 94.
Bài 18: Cho hai số có 4 chữ số và 2 chữ số mà tổng của hai số đó bằng 2750. Nếu cả hai số được viết theo thứ tự ngược lại thì tổng của hai số này bằng 8888 . Tìm hai số đã cho.
Lời giải:
Gọi
2 số cần tìm là:
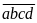 và
và
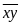
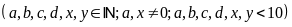
Theo
đề ta có:
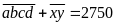


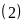
Cả
2 phép cộng đều không nhớ sang hàng nghìn nên từ
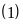 ta có
ta có
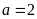 và từ
và từ
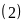 ta có
ta có
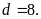
Cũng
từ
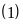 ta có
ta có
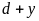 có tận cùng bằng
có tận cùng bằng
 mà
mà
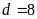 nên
nên
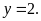
Từ
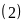 ta có
ta có
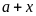 có tận cùng bằng
có tận cùng bằng
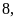 mà
mà
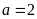 nên
nên
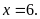
Từ
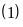 ta có
ta có
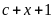 (vì có nhớ 1) có tận cùng bằng
(vì có nhớ 1) có tận cùng bằng
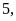 mà
mà
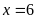 nên
nên
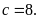
Từ
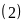 ta có
ta có
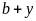 có tận cùng bằng
có tận cùng bằng
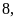 mà
mà
 nên
nên
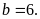
Vậy
hai số đó là:
 và
và
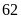 .
.
Bài 19: Tìm số có bốn chữ số khác nhau, biết rằng nếu viết thêm một chữ số 0 vào giữa hàng nghìn và hàng trăm thì được số mới gấp 9 lần số phải tìm.
Lời giải:
Gọi
số cần tìm là

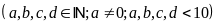
Số
mới là
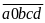
Ta
có
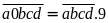
Hay
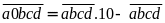
Hay
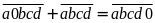
Vì
 có tận cùng bằng
có tận cùng bằng
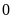 suy ra
suy ra
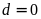 hoặc
hoặc
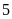
Nếu
 ta có
ta có
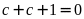 có tận cùng là
có tận cùng là
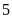 nên
nên
 hoặc
hoặc
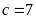 .
.
Nếu
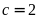 thì
thì
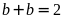 nên
nên
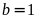 ,
do đó
,
do đó
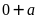 có tận cùng bằng
có tận cùng bằng
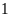 nên
nên
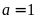 (loại vì
(loại vì
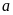 khác
khác
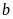 )
)
Nếu
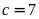 thì
thì
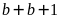 có tận cùng là
có tận cùng là
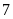 nên
nên
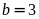 hoặc
hoặc
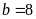 .
.
Nếu
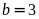 thì
thì
 nên
nên
 (loại).
(loại).
Nếu
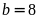 thì
thì
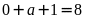 nên
nên
 (loại vì
(loại vì
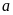 khác
khác
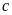 ).
).
Nếu
 suy ra
suy ra
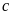 khác
khác
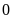 mà
mà
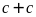 có tận cùng là
có tận cùng là
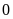 nên
nên
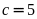 .
Khi đó
.
Khi đó
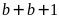 có tận cùng là
có tận cùng là
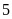 nên
nên
 hoặc
hoặc
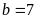
Nếu
 thì
thì
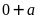 có tận cùng bằng
có tận cùng bằng
 nên
nên
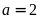 (loại)
(loại)
Nếu
 thì
thì
 có tận cùng là
có tận cùng là
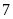 nên
nên
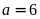
Vậy
số cần tìm là
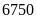 .
.
Bài 20: Tìm số tự nhiên có bốn chữ số, sao cho khi nhân số đó với 4 ta được số gồm bốn chữ số ấy viết theo thứ tự ngược lại.
Lời giải:
Gọi
số cần tìm là

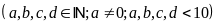
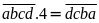
Ta
có
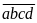 và
và
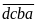 là số có
là số có
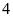 chữ số
chữ số
Nên
ta có:
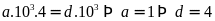 hoặc
hoặc

Xét
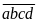 với
với
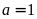 và
và
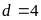
Để
có được
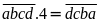 thì
thì
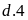 trước hết phải có chữ số tận cùng là
trước hết phải có chữ số tận cùng là
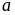
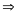 với
với
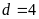 thì
thì
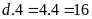 có chữ số tận cùng là
có chữ số tận cùng là
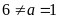 (loại)
(loại)
Xét
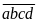 với
với
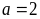 và
và
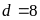 .
.
Do
đó
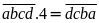 ta thấy:
ta thấy:
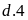 đã có chữ số lận cùng là
đã có chữ số lận cùng là
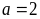 (1)
(1)
Vì
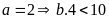

Với
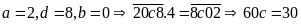 (không
thỏa mãn)
(không
thỏa mãn)
Với
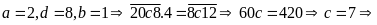 có số 2178.
có số 2178.
Với
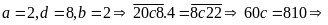 (không thỏa mãn)
(không thỏa mãn)
Vậy số cần tìm là 2178.
Bài 21: Tìm số tự nhiên có bốn chữ số, sao cho khi nhân số đó với 9 ta được số gồm bốn chữ số ấy viết theo thứ tự ngược lại
Lời giải:
Gọi
số cần tìm là

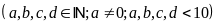
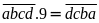
Ta
có
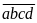 và
và
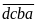 là số có
là số có
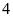 chữ số
chữ số
Nên
ta có:

Xét
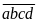 :
vì
:
vì
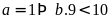
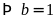 hoặc
hoặc
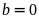
Với
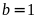 thì
thì
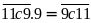
Vì
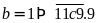 có
có
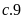 là số bé lớn hơn
là số bé lớn hơn
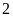 chữ số
chữ số
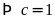 hoặc
hoặc
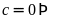 Vô lý.
Vô lý.
Với
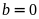 thì
thì
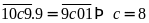
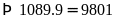 .
.
Vậy số tự nhiên cần tìm là 9801.
Bài 22: Tìm số tự nhiên có ba chữ số, biết rằng nếu xoá chữ số hàng trăm thì số ấy giảm 9 lần.
Lời giải:
Gọi
số cần tìm là
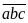
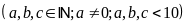
Khi
xóa chữ số hàng trăm ta có số
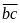
Ta
có:
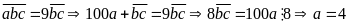 hoặc
hoặc
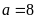
Vì
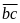 có hai chữ số
có hai chữ số
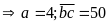
Vậy số cần tìm là 450.
Bài 23: Tìm số tự nhiên có bốn chữ số, biết rằng nếu xoá chữ số hàng nghìn thì số ấy giảm 9 lần.
Lời giải:
Gọi
số cần tìm là

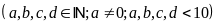
Xóa
chữ số hàng trăm ta có số

Ta
có:
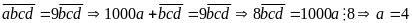 hoặc
hoặc
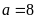
Vì
 có 3 chữ số
có 3 chữ số
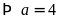 và
và
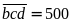
Vậy số cần tìm là 4500.
Bài 24: Tìm số tự nhiên có bốn chữ số, biết rằng chữ số hàng trăm bằng 0 và nếu xoá chữ số 0 đó thì số ấy giảm 9 lần.
Lời giải:
Gọi
số cần tìm là
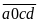
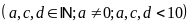
Xóa
chữ số hàng trăm ta có số
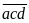
Ta
có:
 hoặc
hoặc
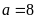
Vì
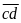 có 2 chữ số
có 2 chữ số
 và
và

Vậy số cần tìm là 4050 .
Bài 25: Một số tự nhiên có hai chữ số tăng gấp 9 lần nếu viết thêm một chữ số 0 vào giữa các chữ số hàng chục và hàng đơn vị của nó . Tìm số ấy.
Lời giải
Số
cần tìm là
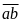
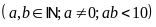 .
.
Viết
thêm một chữ số 0 vào giữa các chữ số hàng chục và
hàng đơn vị ta có số

Ta
có:
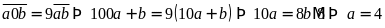 hoặc
hoặc
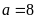
Vì
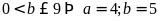
Vậy số cần tìm là 45 .
Bài
26:
Gọi
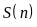 là tổng các chữ số của số tự nhiên
là tổng các chữ số của số tự nhiên
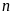 .
Tìm số tự nhiên
.
Tìm số tự nhiên
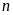 sao cho
sao cho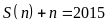 .
.
Chú ý: Có thể thay đầu bài bởi số khác
Lời giải
Nếu
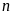 có 3 chữ số thì
có 3 chữ số thì
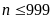 suy
ra
suy
ra
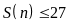 suy ra
suy ra
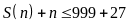
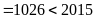 (loại)
(loại)
Nếu
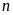 có nhiều hơn bốn chữ số: Suy ra
có nhiều hơn bốn chữ số: Suy ra
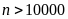 suy ra
suy ra
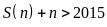 (loại )
(loại )
Vậy
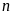 có bốn chữ số: Đặt
có bốn chữ số: Đặt
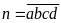
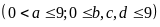
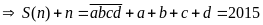
Nhận
thấy:
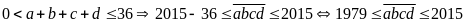
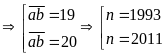
Nếu
 thì
thì
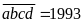 vì
vì
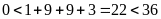 và
và
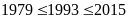
Nếu
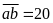 thì
thì
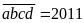 vì
vì
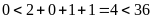 và
và
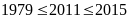
Vậy
số tự nhiên
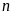 cần tìm là 1993 hoặc 2011.
cần tìm là 1993 hoặc 2011.
Bài
27:
Chứng minh rằng không tồn tại số tự nhiên có bốn chữ
số
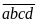 sao cho
sao cho
 .
.
Lời giải
Điều
kiện:
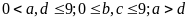
Ta có:

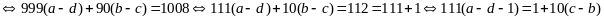
Nếu
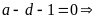
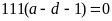 mà
mà
 là
số lẻ
là
số lẻ
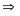 vô lý
vô lý
Nếu
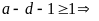
 mà
mà
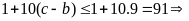 vô lý
vô lý
Vậy
không tồn tại số tự nhiên có bốn chữ số
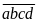 sao cho
sao cho
 .
.
Bài 28: Tìm một số tự nhiên có ba chữ số biết rằng khi viết thêm chữ số 2 vào bên phải số đó thì nó tăng thêm 4106 đơn vị.
Lời giải
Gọi
số cần tìm là

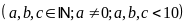
Viết
thêm chữ số 2 vào bên phải số đó, ta được:
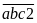
Theo
đề bài ta có:
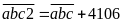
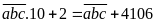 (phân
tích
(phân
tích
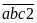 theo cấu tạo số)
theo cấu tạo số)
Ta
có:
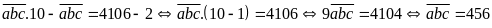
Thử
lại:
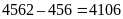 (đúng)
(đúng)
Vậy số tự nhiên cần tìm là 456.
Bài 29: Tìm số tự nhiên có 4 chữ số. Biết rằng nếu ta xóa đi chữ số hàng chục và hàng đơn vị thì số đó giảm đi 4455 đơn vị.
Lời giải
Gọi
số cần tìm là
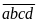

Xóa
đi chữ số hàng chục và hàng đơn vị của số đó, ta
được
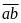
Theo
đề bài ta có:
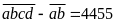
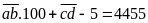 (phân
tích
(phân
tích
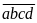 theo
cấu tạo số)
theo
cấu tạo số)
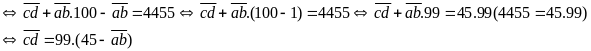
Ta
nhận thấy tích của 99 và 1 là một số tự nhiên bé hơn
100 nên
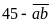 phải bằng 0 hoặc 1.
phải bằng 0 hoặc 1.
Nếu
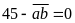 thì
thì
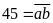 và
và
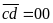
Nếu
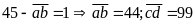
Thử
lại:
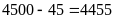 ;
;
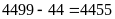
Vậy số cần tìm là 4500 hoặc 4499.
Bài 30: Chia một số tự nhiên có ba chữ số như nhau cho một số tự nhiên có ba chữ số như nhau ta được thương là 2 và có dư. Nếu xóa bớt một số ở số bị chia và xóa bớt một số ở số chia thì thương vẫn bằng 2 và số dư giảm đi 100. Tìm số bị chia và số chia lúc đầu.
Lời giải
Gọi
số cần tìm là
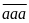
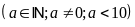
Ta
có:
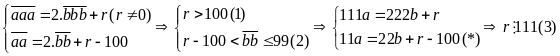
Từ
(1) ,(2) ,(3) suy ra
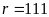 ,
thay vào (*) ta được
,
thay vào (*) ta được
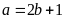
-

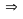 hai số là
hai số là
 và
và
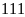 (loại vì
(loại vì
 không thỏa mãn)
không thỏa mãn)
-
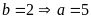
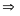 hai số là
hai số là
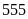 và
và
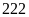 (nhận vì
(nhận vì
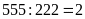 dư 111 thỏa mãn)
dư 111 thỏa mãn)
-
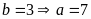
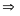 hai
số là
hai
số là
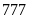 và
và
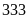 (nhận vì
(nhận vì
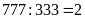 dư 111 thỏa mãn)
dư 111 thỏa mãn)
-

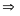 hai
số là
hai
số là
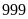 và
và
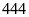 (nhận vì
(nhận vì
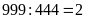 dư 111 thỏa mãn)
dư 111 thỏa mãn)
Vậy số bị chia và số chia lúc đầu là: 555 và 222; 777 và 333; 999 và 444.
Bài
31:
Tìm các số tự nhiên
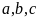 biết
biết
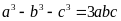 và
và
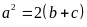
Lời giải
Điều
kiện:
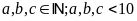
Ta
có
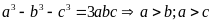
Do
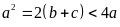 (do
(do
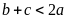 )
)
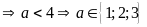
Thử
chọn
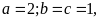 thay vào điều kiện của bài toán
thay vào điều kiện của bài toán
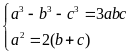 (thỏa mãn)
(thỏa mãn)
Vậy
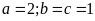 .
.
Bài 32: Tìm số tự nhiên có 5 chữ số, biết rằng nếu viết thêm chữ số 2 vào đằng sau số đó thì được số lớn gấp 3 lần số có được bằng cách viết thêm chữ số 2 vào đằng trước số đó.
Lời giải
Gọi
số cần tìm là:
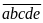
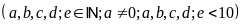
Ta
có phép nhân:
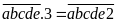
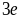 có
tận cùng là 2 suy ra
có
tận cùng là 2 suy ra
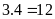 nhớ
1 sang hàng chục
nhớ
1 sang hàng chục
 tận
cùng là 4 suy ra
tận
cùng là 4 suy ra
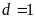
 tận
cùng là 1 suy ra
tận
cùng là 1 suy ra
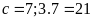 nhớ 2 sang hàng nghìn
nhớ 2 sang hàng nghìn
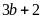 tận
cùng là 7 suy ra
tận
cùng là 7 suy ra
 nhớ 1 sang hàng chục nghìn
nhớ 1 sang hàng chục nghìn
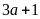 tận
cùng là 5 suy ra
tận
cùng là 5 suy ra
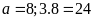 nhớ 2 sang hàng trăm nghìn
nhớ 2 sang hàng trăm nghìn
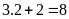 ,
được
,
được
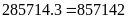 .
.
Vậy số tự nhiên cần tìm là 85741.
Bài 33: Tìm số tự nhiên có tận cùng bằng 3, biết rằng nếu xóa chữ số hàng đơn vị thì số đó giảm đi 1992 đơn vị.
Lời giải
Vì rằng nếu xóa chữ số hàng đơn vị thì số đó giảm đi 1992 đơn vị nên số tự nhiên cần tìm có 4 chữ số.
Gọi
số tự nhiên cần tìm là

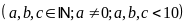
Theo
bài ta có:

Vậy số cần tìm là: 2213.
HẾT
Ngoài Chuyên Đề Bồi Dưỡng HSG Toán 6 Chủ Đề Các Bài Toán Liên Quan Đến Số Và Chữ Số Có Lời Giải – Tài Liệu Toán thì các tài liệu học tập trong chương trình 6 sẽ được cập nhật liên tục và nhanh nhất có thể sau khi kỳ thi diễn ra trên Danh mục Tài Liệu Học Tập nhằm giúp các bạn đọc thuận tiện trong việc nghiên cứu tài liệu. Quý thày cô và các bạn đọc có thể chia sẻ thêm những tài liệu học tập hữu ích đến địa chỉ email của chúng tôi, nhằm xây dựng nên kho đề thi phong phú, đa dạng cho các em học sinh tham khảo và rèn luyện.
Chuyên Đề Bồi Dưỡng HSG Toán 6 với chủ đề “Các bài toán liên quan đến số và chữ số” là một tài liệu quan trọng giúp học sinh lớp 6 nắm vững kiến thức và kỹ năng trong việc giải các bài toán liên quan đến số và chữ số.
Trong chuyên đề này, học sinh sẽ được làm quen với các loại bài toán liên quan đến số và chữ số, bao gồm: bài toán tìm số lớn nhất, tìm số bé nhất, tìm số có tính chất đặc biệt, xác định chữ số ở vị trí cụ thể trong số, thực hiện các phép tính và một loạt các bài toán khác.
Tài liệu bồi dưỡng HSG Toán 6 với chủ đề “Các bài toán liên quan đến số và chữ số” cung cấp một loạt các bài tập thực hành, từ các bài toán cơ bản đến những bài toán phức tạp hơn. Mỗi bài tập đi kèm với lời giải chi tiết, giúp học sinh hiểu rõ cách giải và áp dụng kỹ thuật vào từng bài toán cụ thể.
>>> Bài viết có liên quan:






