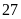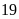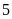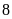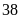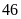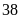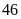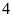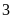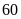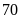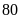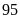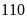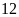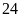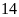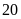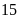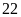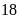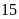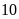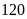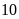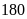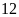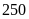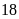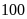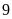Phương Pháp Tính Xác Suất Thực Nghiệm Có Lời Giải Chi Tiết
>>> Mọi người cũng quan tâm:
Phương Pháp Tính Xác Suất Thực Nghiệm Có Lời Giải Chi Tiết – Tài Liệu Toán là tài liệu học tập được Trang Tài Liệu biên soạn và sưu tầm từ những nguồn dữ liệu mới nhất hiện nay. Tài liệu này sẽ giúp các em luyện tập, củng cố kiến thức từ đó nâng cao điểm số cho môn học. Ngoài ra, cũng giúp các thầy cô giáo có nguồn tài nguyên phong phú để giảng dạy.
Dưới đây là bản đọc trực tuyến giúp thầy cô và các em học sinh có thể nghiên cứu Online hoặc bạn có thể tải miễn phí với phiên bản word để dễ dàng in ấn cũng như học tập Offline.
ĐS6.CHUYÊN ĐỀ - XÁC SUẤT
CHỦ ĐỀ 4: XÁC SUẤT THỰC NGHIỆM
PHẦN I. TÓM TẮT LÝ THUYẾT
Khi thực hiện thí nghiệm hoặc trò chơi, một sự kiện có thể xảy ra hoặc không xảy ra. Khả năng xảy ra một sự kiện được thể hiện bằng một con số từ 0 đến 1.
Khả năng bằng 0 (hay 0%) có nghĩa sự kiện đó không bao giờ xảy ra. Khả năng bằng 1 hay (100%) có nghĩa sự kiện đó chắc chắn xảy ra.
Xác suất thực nghiệm phụ thuộc vào người thực hiện thí nghiệm, trò chơi và số lần người đó thực hiện thí nghiệm trò chơi.
Thực
hiện lặp đi lặp lại một hoạt động nào đó
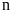 lần,
mỗi lần thực hiện hoạt động xảy ra một trong các sự
kiện A; B; C; ... . Gọi
lần,
mỗi lần thực hiện hoạt động xảy ra một trong các sự
kiện A; B; C; ... . Gọi
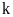 là số lần sự kiện A xảy ra trong
là số lần sự kiện A xảy ra trong
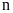 lần
đó. Khi đó, tỉ số
lần
đó. Khi đó, tỉ số
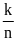 (
(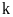 là
s
là
s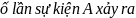 ,
,
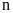 là tổng số lần thực hiện hoạt động) được
gọi là xác
suất thực nghiệm
của sự kiện A.
là tổng số lần thực hiện hoạt động) được
gọi là xác
suất thực nghiệm
của sự kiện A.
PHẦN II. CÁC DẠNG BÀI
Dạng 1: Tính xác suất thực nghiệm dựa vào số liệu đơn giản cho trước.
Dạng 2: Tính xác suất thực nghiệm dựa vào bảng thống kê.
Dạng 3: Tính xác suất thực nghiệm dựa vào dãy số liệu cho trước.
Dạng 4: Bài toán tổng hợp có tính xác suất thực nghiệm.
Dạng 1: Tính xác suất thực nghiệm dựa vào số liệu đơn giản cho trước.
I. Phương pháp giải
Bước
1: Từ số liệu đã cho xác định số lần thực hiện
hoạt động
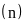
Bước
2: Từ số liệu đã cho xác định số lần sự kiện A
xảy ra
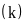
Bước
3: Tính xác suất thực nghiệm của sự kiện theo công
thức:
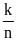
II.Bài toán
Bài
1:
Một
hộp có chứa
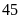 phiếu bốc thăm cùng loại. Trong đó có
phiếu bốc thăm cùng loại. Trong đó có
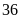 phiếu có nội dung “Chúc bạn may mắn lần sau”,
phiếu có nội dung “Chúc bạn may mắn lần sau”,
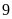 phiếu có nội dung “Quà tặng”. Bạn Việt thực hiện
bốc thăm lấy ngẫu nhiên một phiếu trong hộp.
phiếu có nội dung “Quà tặng”. Bạn Việt thực hiện
bốc thăm lấy ngẫu nhiên một phiếu trong hộp.
a) Liệt kê các kết quả có thể;
b) Lập bảng thống kê số lượng phiếu ở trên;
c) Hãy tính xác suất thực nghiệm của sự kiện lấy được phiếu “Quà tặng”.
Lời giải
Các kết quả có thể là: Chúc bạn may mắn lần sau, Quà tặng.
Bảng thống kê:
Loại phiếu
Chúc bạn may mắn lần sau
Quà tặng
Số lượng
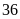
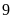
Xác suất thực nghiệm của sự kiện lấy được phiếu “Quà tặng”:
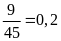
Bài
2:
Hùng
tập ném bóng vào rổ. Khi thực hiện ném
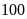 lần
thì có
lần
thì có
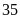 lần bóng vào rổ.
lần bóng vào rổ.
a) Lập bảng thống kê;
b) Tính xác suất thực nghiệm của sự kiện ném bóng vào rổ;
c) Theo em Hùng có thể tăng xác suất thực nghiệm của sự kiện ném bóng vào rổ không?
Lời giải
Số lần ném bóng không vào rổ là:
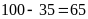 (lần).
(lần).
Bảng thống kê:
Kết quả |
Bóng vào rổ |
Bóng không vào rổ |
Số lần |
|
|
Xác suất thực nghiệm của sự kiện ném bóng vào rổ là:
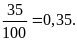
Hùng có thể tăng xác suất thực nghiệm của sự kiện ném bóng vào rổ nếu Hùng chăm chỉ luyện tập.
Bài 3: Trong buổi thực hành môn Khoa học tự nhiên đo thể tích của vật thể không xác định được hình dạng, lớp 6A có 40 học sinh thực hiện phép đo thì có 35 học sinh thực hiện thành công. Em hãy tính xác suất thực nghiệm của sự kiện Phép đo được thực hiện thành công.
Lời giải
Số
lần thực hiện phép đo là
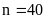
Sô
lần đo thành công là
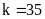
Xác
suất
thực nghiệm của sự kiện Phép đo được thực hiện
thành công là:
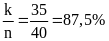
Bài 4: Tung một đồng xu 20 lần liên tiếp. Hãy ghi kết quả thống kê theo mẫu sau:
Lần tung |
Kết quả tung |
Số lần xuất hiện mặt N |
Số lần xuất hiện mặt S |
1 |
? |
|
|
... |
? |
Tính xác suất thực nghiệm:
a) Xuất hiện mặt N;
b) Xuất hiện mặt S;
Lời giải
Xác
suất thực nghiệm xuất hiện mặt N khi tung đồng xu 20
lần là: 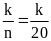
Xác
suất thực nghiệm xuất hiện mặt S khi tung đồng xu 20
lần là: 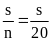
Bài 5.
a) Nếu tung một đồng xu 22 lần liên tiếp; có 13 lần xuất hiện mặt N thì xác suất thực nghiệm xuất hiện mặt N bằng bao nhiêu?
b) Nếu tung một đồng xu 25 lần liên tiếp; có 11 lần xuất hiện mặt S thì xác suất thực nghiệm xuất hiện mặt S bằng bao nhiêu?
c) Nếu tung một đồng xu 30 lần liên tiếp; có 14 lần xuất hiện mặt N thì xác suất thực nghiệm xuất hiện mặt S bằng bao nhiêu?
Lời giải
a) Nếu
tung một đồng xu 22 lần liên tiếp; có 13 lần xuất hiện
mặt N thì xác suất thực nghiệm xuất hiện mặt N bằng:
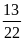
b)
Nếu tung một đồng xu 25 lần liên tiếp; có 11 lần xuất
hiện mặt S thì xác suất thực nghiệm xuất hiện mặt S
bằng: 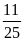
c)
Nếu tung một đồng xu 30 lần liên tiếp; có 14 lần xuất
hiện mặt N thì xác suất thực nghiệm xuất hiện mặt S
bằng: 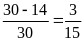
Bài 6: Một hộp có 10 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, .., 10; hai thẻ khác nhau thì ghi hai số khác nhau.
Rút ngẫu nhiên một chiếc thẻ từ trong hộp, ghi lại số của thẻ rút được và bỏ lại thẻ đó vào hộp. Sau 25 lần rút thẻ liên tiếp, hãy ghi kết quả thống kê theo mẫu sau:
Lần rút |
Kết quả rút |
Tổng số lần xuất hiện |
|||||||||
Số 1 |
Số 2 |
Số 3 |
Số 4 |
Số 5 |
Số 6 |
Số 7 |
Số 8 |
Số 9 |
Số 10 |
||
1 |
? |
? |
? |
? |
? |
? |
? |
? |
? |
? |
? |
... |
? |
||||||||||
Tính xác suất thực nghiệm:
a) Xuất hiện số 1;
b) Xuất hiện số 5;
c) Xuất hiện số 10.
Lời giải
a)
Gọi số lần xuất hiện số 1 là k thì xác suất thực
nghiệm xuất hiện số 1: 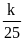
b)
Gọi số lần xuất hiện số 1 là k thì xác suất thực
nghiệm xuất hiện số 5: 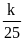
c)
Gọi số lần xuất hiện số 1 là k thì xác suất thực
nghiệm xuất hiện số 10: 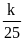
Bài
7.
Gieo
một xúc xắc
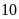 lần liên tiếp, bạn Cường có kết quả như sau:
lần liên tiếp, bạn Cường có kết quả như sau:
Lần gieo |
Kết quả gieo |
1 |
Xuất hiện mặt 2 chấm |
2 |
Xuất hiện mặt 1 chấm |
3 |
Xuất hiện mặt 6 chấm |
4 |
Xuất hiện mặt 4 chấm |
5 |
Xuất hiện mặt 4 chấm |
6 |
Xuất hiện mặt 5 chấm |
7 |
Xuất hiện mặt 3 chấm |
8 |
Xuất hiện mặt 5 chấm |
9 |
Xuất hiện mặt 1 chấm |
10 |
Xuất hiện mặt 1 chấm |
a) Hãy kiểm đếm số lần xuất hiện mặt 1 chấm và số lần xuất hiện mặt 6 chấm sau 10 lần gieo. Xác suất thực nghiệm xuất hiện
b) Tính xác suất thực nghiệm xuất hiện mặt 1 chấm.
c) Tính xác suất thực nghiệm xuất hiện mặt 6 chấm.
Lời giải
a) Số lần xuất hiện mặt 1 chấm: 3 lần
Số lần xuất hiện mặt 6 chấm: 1 lần
b)
Xác suất thực nghiệm xuất hiện mặt 1 chấm là: 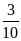
c)
Xác suất thực nghiệm xuất hiện mặt 6 chấm là: 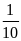
Bài 8
a) Nếu gieo một xúc xắc 11 lần liên tiếp, có 5 lần xuất hiện mặt 2 chấm thì xác suất thực nghiệm xuất hiện mặt 2 chấm bằng bao nhiêu?
b) Nếu gieo một xúc xắc 14 lần liên tiếp, có 3 lần xuất hiện mặt 6 chấm thì xác suất thực nghiệm xuất hiện mặt 6 chấm bằng bao nhiêu?
Lời giải
a)
Nếu gieo một xúc xắc 11 lần liên tiếp, có 5 lần xuất
hiện mặt 2 chấm thì xác suất thực nghiệm xuất hiện
mặt 2 chấm bằng: 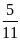
b)
Nếu gieo một xúc xắc 14 lần liên tiếp, có 3 lần xuất
hiện mặt 6 chấm thì xác suất thực nghiệm xuất hiện
mặt 6 chấm bằng:
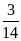
Dạng 2: Tính xác suất thực nghiệm dựa vào bảng thống kê.
I.Phương pháp giải
Bước
1: Từ bảng thống kê tính tổng số lần thực hiện
hoạt động
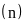
Bước
2: Từ bảng thống kê xác định số lần sự kiện A xảy
ra
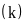
Bước
3: Tính xác suất thực nghiệm của sự kiện theo công
thức:
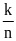
II.Bài toán
Bài 1. Số lượng khách hàng đến một cửa hàng mỗi ngày trong quý IV của năm 2020 được ghi lại ở bảng sau:
Số khách hàng |
0 -10 |
11-20 |
21 -30 |
31 - 40 |
41 - 50 |
51 -60 |
Số ngày |
|
|
|
|
|
|
Chọn
ngẫu nhiên một ngày trong quý IV. Tính xác suất thực
nghiệm của sự kiện “Trong ngày được chọn có không
quá
 khách hàng”.
khách hàng”.
Lời giải
Số
ngày mà trong ngày đó có không quá
 khách hàng (số khách hàng
khách hàng (số khách hàng
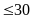 )
đến cửa hàng là:
)
đến cửa hàng là:
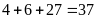 (ngày).
(ngày).
Tổng
số ngày của quý IV là:
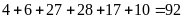 (ngày)
(ngày)
Xác
suất thực nghiệm của sự kiện “Trong ngày được chọn
có không quá 30 khách hàng” là:
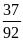 .
.
Bài 2. Số cuộc điện thoại một người nhận được trong một ngày của tháng 6 được ghi lại ở bảng sau:
Số cuộc điện thoại |
|
|
|
|
|
|
Số ngày |
|
|
|
|
|
|
Tính
xác suất thực nghiệm của sự kiện “Một ngày trong
tháng có ít nhất
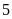 cuộc gọi”.
cuộc gọi”.
Lời giải
Một
ngày trong tháng có ít nhất
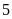 cuộc
gọi nghĩa là ngày đó sẽ có
cuộc
gọi nghĩa là ngày đó sẽ có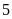 cuộc
gọi hoặc
cuộc
gọi hoặc
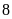 cuộc gọi. Vậy số ngày trong tháng có ít nhất
cuộc gọi. Vậy số ngày trong tháng có ít nhất
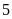 cuộc gọi là:
cuộc gọi là:
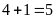 (ngày).
(ngày).
Tổng
số ngày của tháng 6 là:
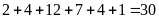 (ngày)
(ngày)
Xác
suất thực nghiệm của sự kiện “Một ngày trong tháng
có ít nhất
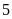 cuộc gọi” là:
cuộc gọi” là:
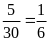 .
.
Bài
3.
Minh
gieo một con xúc xắc
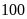 lần và ghi lại số chấm xuất hiện ở mỗi lần gieo
được kết quả như sau:
lần và ghi lại số chấm xuất hiện ở mỗi lần gieo
được kết quả như sau:
Số chấm xuất hiện |
1 |
2 |
3 |
4 |
5 |
6 |
Số lần |
|
|
|
|
|
|
Xác
suất thực nghiệm của sự kiện “Số chấm xuất hiện
chia cho
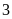 dư
dư
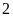 ”
là
”
là
Lời giải
Số
chấm xuất hiện chia cho
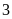 dư
dư
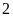 là
các số
là
các số
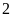 ,
,
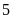 .
.
Nên
số lần gieo được mặt có số chấm chia cho
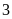 dư
dư
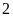 là:
là:
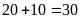 (lần)
(lần)
Xác
suất thực nghiệm của sự kiện “Số chấm xuất hiện
chia cho
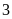 dư
dư
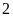 ”
là:
”
là:
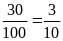 .
.
Bài 4. Một vận động viên nhảy xa thực hiện các lượt nhảy có kết quả như sau (đơn vị tính là mét):
Số mét |
|
|
Số lần nhảy |
|
|
a) Vận động viên trên thực hiện nhảy bao nhiêu lần?
b)
Có bao nhiêu lần nhảy được
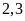 mét, bao nhiêu lần nhảy được
mét, bao nhiêu lần nhảy được
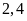 mét?
mét?
c)
Tính xác xuất thực nghiệm của các sự kiện thực hiện
lần nhảy được
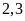 mét.
mét.
Lời giải
Số mét |
|
|
Số lần nhảy |
|
Vận động viên trên thực hiện
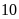 lần nhảy.
lần nhảy.Có
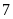 lần nhảy được
lần nhảy được
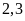 mét, có
mét, có
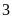 lần nhảy được
lần nhảy được
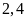 mét.
mét.Xác suất thực nghiệm của sự kiện thực hiện lần nhảy được
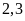 mét là:
mét là:
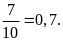
Bài 5. Sau đợt kiểm tra sức khỏe răng miệng của các em trong một lớp 6. Thống kê số lần đánh răng trong một ngày của các em được ghi lại ở bảng sau:
Số lần đánh răng |
|
|
|
Số học sinh |
|
|
|
Hãy tính xác suất thực nghiệm của các sự kiện:
a) Thực hiện đánh răng một lần;
b) Thực hiện đánh răng từ hai lần trở lên.
Lời giải
Số lần đánh răng |
|
|
|
Số học sinh |
|
|
|
Tổng số học sinh:
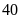
Xác
suất thực nghiệm của sự kiện đánh răng một lần là:
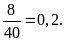
Số học sinh thực hiện đánh răng từ hai lần trở lên là:
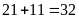 (Học sinh)
(Học sinh)
Xác
suất thực nghiệm của sự kiện đánh răng một lần là:
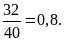
Bài 6. Thống kê số học sinh đi học trễ trong một tuần của lớp 6A được ghi lại ở bảng sau:
Thứ |
|
|
|
|
|
|
Số học sinh |
|
|
|
|
|
|
a) Có bao nhiêu học sinh đi học trễ trong tuần.
b)
Tính xác suất thực nghiệm của sự kiện số buổi có
học sinh đi trễ ít hơn
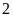 .
.
Lời giải
Số học sinh đi trễ trong tuần:
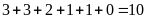 (Học sinh).
(Học sinh).Tổng số học sinh trong các buổi đi trễ ít hơn
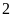 là:
là:
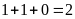 (Học sinh).
(Học sinh).
Xác
suất thực nghiệm của sự kiện số
buổi có học sinh đi trễ ít hơn
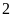 là:
là:
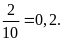
Bài 7. Hàng ngày Sơn đều đi xe buýt đến trường, Sơn ghi lại thời gian chờ xe của mình trong 20 lần liên tiếp như sau:
Thời gian chờ |
Dưới 1 phút |
Từ 1 phút đến dưới 5 phút |
Từ 5 phút trở lên |
Số lần |
|
|
|
Hãy
tính xác suất thực nghiệm của sự kiện Sơn phải chờ
xe từ
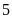 phút trở lên?
phút trở lên?
Lời giải
Xác
suất thực nghiệm của sự kiện Sơn phải chờ xe từ
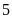 phút trở lên là:
phút trở lên là:
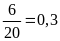
Bài 8. Minh gieo một con xúc xắc 100 lần và ghi lại số chấm xuất hiện ở mỗi lần gieo được kết quả như sau:
Số chấm xuất hiện |
1 |
2 |
3 |
4 |
5 |
6 |
Số lần |
15 |
20 |
18 |
22 |
10 |
15 |
Tính xác suất thực nghiệm của các sự kiện sau:
a. Số chấm xuất hiện là số chẵn.
b. Số chấm xuất hiện lớn hơn 2.
Lời giải
a.
Số chấm xuất hiện là số chẵn là:
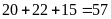
Xác
suất thực nghiệm của số chấm xuất hiện là số chẵn
là:
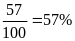
b.
Số chấm xuất hiện lớn hơn 2 là:
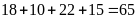
Xác
suất thực nghiệm của số chấm xuất hiện lớn hơn 2
là:
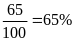
Bài 9. Trong túi có một số viên bi màu đen và một số viên bi màu đỏ. Thực hiện lấy ngẫu nhiên một viên bi từ túi, xem viên bi màu gì rồi trả lại viên bi vào túi. Khoa thực hiện thí nghiệm 30 lần. Số lần lấy được viên bi màu đỏ là 13. Hãy tính xác suất thực nghiệm của sự kiện Khoa lấy được viên bi màu đỏ.
Lời giải
Xác
suất thực nghiệm của sự kiện Khoa lấy được viên bi
màu đỏ là:
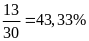
Bài 10: Một chiếc thùng kín có một số quả bóng màu xanh, đỏ, tím, vàng. Trong một trò chơi, người chơi 100 lần và được kết quả như bảng sau:
-
Màu
Số lần
Xanh
43
Đỏ
22
Tím
18
Vàng
17
Tính xác suất thực nghiệm của các sự kiện:
a. Bính lấy được quả bóng màu xanh
b. Qủa bóng được lấy ra không là màu đỏ.
Lời giải
Xác suất thực nghiệm của các sự kiện:
a.
Bính lấy được quả bóng màu xanh là: 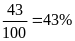
b.
Qủa bóng được lấy ra không là màu đỏ là:
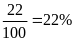
Bài 11. Một người ném một con xúc xắc ba lần và có kết quả tương ứng như sau. Xác định xác suất thực nghiệm để ném được mặt số 4.
Lần thử |
1 |
2 |
3 |
Kết quả |
2 |
5 |
1 |
Lời giải
Xác
suất thực nghiệm cho việc xuất hiện mặt số 4 là
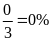
Bài 12: Một người tung một đồng xu ba lần và có kết quả tương ứng như sau. Xác định xác suất thực nghiệm để xuất hiện mặt ngửa.
Lần thử |
1 |
2 |
3 |
Kết quả |
Ngửa |
Ngửa |
Xấp |
Lời giải
Xác
suất thực nghiệm cho việc xuất hiện mặt ngửa là
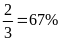
Bài 13: Gieo một con xúc sắc 4 mặt 50 lần và quan số ghi trên đỉnh của con xúc xắc, ta được kết quả như sau:
Số xuất hiện |
1 |
2 |
3 |
4 |
Số lần |
12 |
14 |
15 |
9 |
Hãy tính xác suất thực nghiệm để:
a) Gieo được đỉnh số 4.
b) Gieo được đỉnh có số chẵn.
Lời giải
a)
Xác suất thực nghiệm để gieo được đỉnh số 4 là: 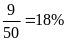
b)
Số lần gieo được đỉnh có số chẵn là:
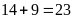
Xác
suất thực nghiệm để gieo được đỉnh có số chẵn:
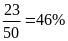
Bài 14: Trong hộp có một số bút xanh và một số bút đỏ. Lấy ngẫu nhiên 1 bút từ hộp, xem màu rồi trả lại. Lặp lại hoạt động trên 50 lần, ta được kết quả như sau:
-
Loại bút
Bút xanh
Bút đen
Số lần
42
8
a) Tính xác suất thực nghiệm của sự kiện lấy được bút xanh
b) Em hãy dự đoán xem trong hộp loại bút nào có nhiều hơn.
Lời giải
a)
Xác suất thực nghiệm của sự kiện lấy được bút
xanh là: 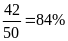
b) Dự đoán: Trong hộp loại bút xanh có nhiều hơn.
Bài 15: Tổng hợp kết quả xét nghiệm bệnh viêm gan ở một phòng khám trong một năm, ta được bảng sau:
Quý |
Số ca xét nghiệm |
Số ca dương tính |
I |
150 |
15 |
II |
200 |
21 |
III |
180 |
17 |
IV |
220 |
24 |
Hãy tính xác suất thực hiện của sự kiện một ca xét nghiệm có kết quả dương tính
a) Theo từng quý trong năm
b) Sau lần lượt từng quý tính từ đầu năm
Lời giải
a) Xác suất thực hiện một ca xét nghiệm có kết quả dương tính theo từng quý là:
Quý
I:
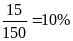
Quý
II:
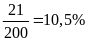
Quý
III:
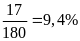
Quý
IV:
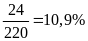
b) Tổng số ca xét nghiệm của cả năm là:
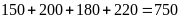 (ca)
(ca)
Xác suất thực hiện một ca xét nghiệm có kết quả dương tính từ đầu năm là:
Quý
I:
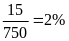
Quý
II:
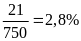
Quý
III:
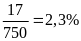
Quý
IV:
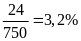
BÀI TẬP TỰ LUYỆN
Bài
1.
Bạn Toàn gieo một con xúc sắc
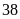 lần và ghi lại số chấm xuất hiện ở mỗi lần gieo
được như sau:
lần và ghi lại số chấm xuất hiện ở mỗi lần gieo
được như sau:
Số chấm xuất hiện |
|
|
|
|
|
|
Số lần |
|
|
|
|
|
|
Hãy tính xác suất thực nghiệm của các sự kiện sau:
Số chấm xuất hiện là chẵn.
Số chấm xuất hiện lớn hơn
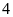 .
.
Lời giải
Bài 2. Một vận động viên nhảy cao thực hiện các lượt nhảy có kết quả như sau (đơn vị tính là mét):
Số mét |
|
|
|
|
|
|
|
Số lần |
|
|
|
|
|
|
|
Vận động viên trên thực hiện bao nhiêu lần nhảy?
Tính xác suất thực nghiệm của sự kiện số mét đạt được cao nhất.
Lời giải
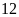 lần.
lần.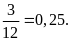 .
.
Bài
3.
Trong hộp có một số bóng xanh và một số bóng đỏ cùng
loại. Lấy ngẫu nhiên một bóng trong hộp, xem
màu rồi bỏ lại vào hộp. Lặp lại hoạt động trên
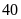 lần được kết quả như sau:
lần được kết quả như sau:
Bóng |
Bóng xanh |
Bóng đỏ |
Số lần |
|
|
Tính xác suất thực nghiệm của sự kiện bóng lấy ra có màu:
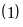 Xanh;
Xanh;
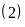 Đỏ.
Đỏ.
Lời giải
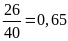 .
.
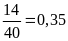 .
.
Bài
4.
Điều tra về việc tiêu thụ điện năng (tính theo kwh)
của
 hộ gia đình ở một tổ dân phố có kết quả sau:
hộ gia đình ở một tổ dân phố có kết quả sau:
Lượng điện tiêu thụ |
|
|
|
|
|
|
Số hộ |
|
|
|
|
|
|
Có bao nhiêu hộ gia gia đình có lượng tiêu thụ điện lớn hơn
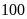 kwh?
kwh?Tính xác suất thực nghiệm của sự kiện lượng tiêu thụ điện lớn hơn
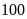 kwh.
kwh.
Lời giải
Bài
5.
Một
hộp kín có chứa một số bi có màu xanh, đỏ, vàng cùng
kích cỡ. Lấy ngẫu nhiên một bi trong hộp,
xem màu rồi bỏ lại vào hộp. Nam thực hiện lặp lại
hoạt động trên
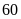 lần ta được kết quả như sau:
lần ta được kết quả như sau:
Bi |
Bi đỏ |
Bi xanh |
Bi vàng |
Số lần |
|
|
|
a) Hãy tính xác suất thực nghiệm của các sự kiện sau:
 Nam lấy được bi đỏ;
Nam lấy được bi đỏ;
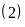 Viên bi lấy ra không phải màu xanh;
Viên bi lấy ra không phải màu xanh;
b) Em hãy dự đoán xem trong hộp loại bi nào nhiều hơn?
Lời giải
a)
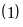
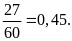
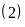
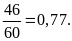
b) Trong hộp bi đỏ nhiều hơn.
Dạng 3: Tính xác suất thực nghiệm dựa vào dãy số liệu cho trước.
I.Phương pháp giải:
Bước 1: Từ dãy số liệu cho trước, lập bảng thống kê.
Bước
2: Dựa vào bảng thống kê tính tổng số lần thực
hiện hoạt động
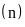 và
xác định số lần sự kiện A xảy ra
và
xác định số lần sự kiện A xảy ra
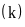
Bước
3: Tính xác suất thực nghiệm của sự kiện theo công
thức:
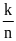
II.Bài toán:
Bài 1. Cho dãy số liệu về số lượng đạt tuần học tốt của các lớp trong một năm học của một trường THCS như sau:
6 |
5 |
8 |
6 |
7 |
6 |
7 |
7 |
6 |
8 |
5 |
6 |
a) Em hãy lập bảng thống kê theo mẫu sau:
Số tuần học tốt |
|
|
|
|
Số lớp đạt |
? |
? |
? |
? |
b)
Hãy tính xác suất thực nghiệm của sự kiện lớp đạt
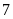 tuần học tốt.
tuần học tốt.
Lời giải
Bảng thống kê:
Số tuần học tốt
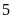
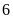
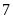
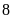
Số lớp đạt
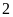
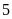
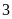
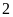
Tổng số lớp là:
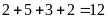
Xác
suất thực nghiệm của sự kiện lớp đạt
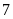 tuần học tốt là:
tuần học tốt là:
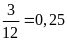 .
.
Bài 2. Số tuổi công nhân của một xí nghiệp được ghi lại như sau:
28 |
27 |
35 |
41 |
35 |
43 |
28 |
41 |
35 |
35 |
35 |
28 |
27 |
35 |
28 |
41 |
35 |
27 |
a) Hãy lập bảng thống kê biểu diễn dữ liệu đã thu thập;
b) Dựa vào bảng trên hãy cho biết công nhân ở tuổi nào có số lượng nhiều nhất;
c) Tính xác suất thực nghiệm của sự kiện công nhân có tuổi trẻ nhất.
Lời giải
Bảng thống kê:
Số tuổi
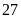
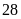
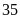
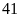
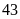
Số công nhân
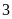
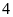
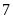
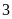
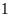
Công nhân ở độ tuổi
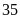 có số lượng nhiều nhất.
có số lượng nhiều nhất.Xác suất thực nghiệm của sự kiện công nhân có tuổi trẻ nhất là:
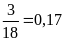
Bài 3. Trong đợt phát động “Trường học Xanh”. Số cây do các lớp trồng được ghi lại như sau:
35 |
46 |
46 |
46 |
35 |
38 |
46 |
38 |
46 |
38 |
35 |
46 |
46 |
35 |
a) Em hãy lập bảng thống kê theo mẫu sau:
Số cây |
|
|
|
Số lớp |
? |
? |
? |
b) Hãy tính xác suất thực nghiệm của sự kiện lớp trồng được nhiều cây xanh nhất.
Lời giải
a)
Số cây |
|
|
|
Số lớp |
|
|
|
b)
Xác
suất thực nghiệm của sự kiện lớp trồng được nhiều
cây xanh nhất là:
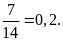
Bài 4. Một cửa hàng bán phụ kiện máy tính thống kê số sản phẩm bán hàng tháng của họ trong một năm như sau:
60 |
70 |
60 |
60 |
70 |
60 |
60 |
60 |
80 |
95 |
95 |
110 |
a) Hãy lập bảng thống kê biểu diễn dữ liệu đã thu thập;
b) Dựa vào bảng trên hãy cho biết có bao nhiêu tháng bán được nhiều nhất, có bao nhiêu tháng bán được ít nhất?
c) Tính xác suất thực nghiệm của sự kiện sản phẩm bán ra ít nhất.
Lời giải
a) Bảng thống kê
Sản phẩm bán ra |
|
|
|
|
|
Số tháng đạt |
|
|
|
|
|
b)
Có
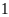 tháng bán
được nhiều nhất, có
tháng bán
được nhiều nhất, có
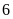 tháng bán được ít nhất.
tháng bán được ít nhất.
c)
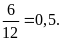
Bài
5.
Một
hộp có chứa
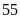 bút bi cùng loại. Trong đó có
bút bi cùng loại. Trong đó có
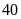 bút bi đỏ và
bút bi đỏ và
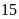 bút bi xanh. Mỗi lần Nam lấy
ra ngẫu nhiên một bút, xem bút đó có màu gì rồi lại
bỏ vào trong hộp. Nam đã thực hiện
bút bi xanh. Mỗi lần Nam lấy
ra ngẫu nhiên một bút, xem bút đó có màu gì rồi lại
bỏ vào trong hộp. Nam đã thực hiện
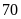 lần và thấy có
lần và thấy có
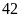 lần lấy được bút bi đỏ.
lần lấy được bút bi đỏ.
a) Em hãy cho biết số lần Nam lấy ra là bút bi xanh;
b) Lập bảng thống kê biểu diễn dữ liệu ở trên;
c) Hãy tính xác suất thực nghiệm của sự kiện bút lấy ra có màu:
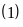 đỏ;
đỏ;
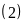 xanh.
xanh.
Lời giải
a)
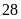 lần.
lần.
b)
Màu bút |
Đỏ |
Xanh |
Số lần |
|
|
c)
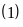
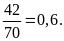
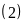
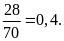
Bài
6.
Trong
trò chơi bánh xe quay số. Bánh xe số có
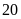 nấc điểm:
nấc điểm:
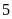 ;
;
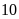 ;
;
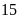 ;
;
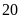 ;
…;
;
…;
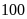 với các vạch chia
đều nhau và giả sử rằng khả năng chuyển từ nấc
điểm đã có tới các nấc điểm còn lại là như nhau.
Trong mỗi lượt chơi có hai người tham gia, mỗi người
được quay một lần và điểm của người chơi là điểm
quay được. Người nào có số điểm cao hơn sẽ thắng
cuộc, hòa nhau sẽ chơi lại lượt khác. Nam và Bình cùng
tham gia một lượt chơi. Nam chơi trước và được
với các vạch chia
đều nhau và giả sử rằng khả năng chuyển từ nấc
điểm đã có tới các nấc điểm còn lại là như nhau.
Trong mỗi lượt chơi có hai người tham gia, mỗi người
được quay một lần và điểm của người chơi là điểm
quay được. Người nào có số điểm cao hơn sẽ thắng
cuộc, hòa nhau sẽ chơi lại lượt khác. Nam và Bình cùng
tham gia một lượt chơi. Nam chơi trước và được
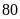 điểm. Hãy tính xác suất thực nghiệm của sự kiện
Bình thắng cuộc ở lượt chơi này.
điểm. Hãy tính xác suất thực nghiệm của sự kiện
Bình thắng cuộc ở lượt chơi này.
Lời giải
Để
Bình thắng ở lượt chơi này thì Bình phải quay vào các
nấc điểm là
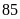 ;
;
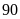 ;
;
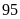 ;
;
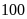 .
.
Xác
suất thực nghiệm của sự kiện Bình thắng ở lượt
chơi này là:
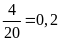 .
.
Bài
7.
Có
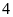 sinh viên trong cùng một phòng trọ nhưng họ chỉ được
tặng ba vé đi xem phim. Khi đó họ làm
sinh viên trong cùng một phòng trọ nhưng họ chỉ được
tặng ba vé đi xem phim. Khi đó họ làm
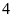 lá thăm trong đó
lá thăm trong đó
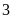 lá thăm được đánh dấu “X”. Mỗi người rút lần
lượt một lá thăm. Nếu ai rút được lá “X” thì được
đi. Hãy tính xác suất thực nghiệm của sự kiện được
đi xem phim của từng người.
lá thăm được đánh dấu “X”. Mỗi người rút lần
lượt một lá thăm. Nếu ai rút được lá “X” thì được
đi. Hãy tính xác suất thực nghiệm của sự kiện được
đi xem phim của từng người.
Lời giải
Xác
suất thực nghiệm của sự kiện được đi xem phim của
từng người là:
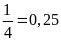 .
.
Dạng 4: Bài toán tổng hợp có tính xác suất thực nghiệm.
Bài
1:
Có
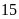 quyển sách trong đó có
quyển sách trong đó có
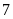 quyển
sách Toán,
quyển
sách Toán,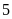 quyển
sách Vän và
quyển
sách Vän và
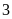 quyển
sách Lý. Tính xác suất để lấy được:
quyển
sách Lý. Tính xác suất để lấy được:
Hai quyển sách Toán.
Hai quyển sách trong đó có
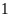 quyển Văn và
quyển Văn và
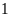 quyển L ý.
quyển L ý.Hai quyển sách trong đó có ít nhất
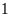 quyển Văn.
quyển Văn.
Lời giải
a)
Có
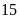 quyển sách, mỗi lần lấy ra
quyển sách, mỗi lần lấy ra
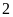 quyển. Vậy tổng số lần có thể lấy ra là:
quyển. Vậy tổng số lần có thể lấy ra là:
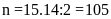
Xác
suất để lấy được hai quyển sách Toán là:
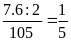
b)
Xác suất để lấy được hai quyển sách trong đó có
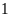 quyển Văn và
quyển Văn và
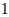 quyển Lý là:
quyển Lý là:
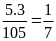
c)
Số cách chọn hai quyển Văn là :
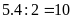
Số
cách chọn một quyển Văn và một quyển toán hoặc một
quyển Lý là :
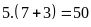
Xác
suất để lấy được hai quyển sách trong đó có ít nhất
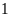 quyển Văn là:
quyển Văn là:
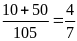
Bài
2.
Tung hai đồng xu cân đối
 lần ta được kết qủa như sau:
lần ta được kết qủa như sau:
Sự kiện |
Hai đồng sấp |
Một đồng sấp, một đồng ngửa |
Hai đồng ngửa |
Số lần |
|
|
|
Hãy tính xác suất thực nghiệm của sự kiện:
Có môt đồng xu sấp, một đồng xu ngửa;
Hai đồng xu đều ngửa.
Lời giải
a)
Xác suất thực nghiệm của sự kiện có một đồng xu
sấp, một đồng xu ngửa trong lần
tung là:
lần
tung là:
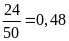
b)
Xác suất thực nghiệm của sự kiện cả hai đồng xu đều
ngửa trong
 lần
tung là:
lần
tung là:
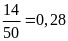
Bài
3: An
gieo một con xúc xắc
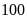 lần và ghi lại số chấm xuất hiện ở mỗi lần gieo
được kết qủa như sau:
lần và ghi lại số chấm xuất hiện ở mỗi lần gieo
được kết qủa như sau:
Số chấm xuất hiện |
1 |
2 |
3 |
4 |
5 |
6 |
Số lần |
|
|
|
|
|
|
Tính xác suất thực nghiệm của các sự kiện sau:
a) Số chấm xuất hiện là số lẻ;
b)
Số chấm xuất hiện là lớn hơn
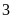 .
.
Lời giải
a) Xác suấtt thực nghiệm của sự kiện số chấm xuất hiện là số lẻ là:
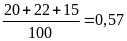
b) Xác suất thực nghiệm của sự kiện số chấm xuất hiện lớn hơn 3 là:
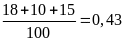
Bài
4. Trong
hộp có một số bút xanh và một số bút đỏ. Lấy ngẫu
nhiên
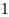 bút
từ hộp, xem màu rôi trả lại. Lặp
lại hoạt động trên
bút
từ hộp, xem màu rôi trả lại. Lặp
lại hoạt động trên
 lần, ta được kết qủa như sau:
lần, ta được kết qủa như sau:
-
Loại bút
Bút xanh
Bút đỏ
Số lần
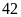
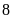
a) Tính xác suất thực nghiệm của sự kiện lấy được bút xanh.
b) Em hãy dự đoán xem trong hộp lọai bút nào có nhiều hơn.
Lời giải
a)
Xác suất thực nghiệm của sự kiện lấy được bút
xanh là:
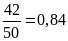
b) Không dự đoán được trong hộp bút lọai bút nào nhiều hơn.
Bài 5. Bảng sau là tổng hợp kết quả xét nghiệm người nhiễm Covíd 19 ở một bệnh viện trong một năm:
Quý |
Số ca xét nghiệm |
Số ca dương tính |
I |
|
|
II |
|
|
III |
|
|
IV |
|
|
Hãy tính xác suất thực nghiệm của sự kiện một ca xét nghiệm có kết quả dương tính:
Theo từng quý trong năm.
Theo năm.
Lời giải
a)
Xác suất thực nghiệm của sự kiện một ca xét nghiệm
có kết quả dương tính trong quý I là:
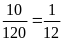
+
Xác
suất thực nghiệm của sự kiện một ca xét nghiệm có
kết quả dương tính trong quý II là:
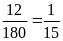
+
Xác
suất thực nghiệm của sự kiện một ca xét nghiệm có
kết quả dương tính trong quý III là:
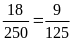
+
Xác
suất thực nghiệm của sự kiện một ca xét nghiệm có
kết quả dương tính trong quý IV là:
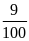
b)
Xác suất thực nghiệm của sự kiện một ca xét nghiệm
có kết quả dương tính trong 1 năm là:
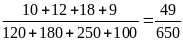
Bài 6. Kết qủa kiểm tra môn Toán và Ngữ văn của một số học sinh được lựa chọn ngẫu nhiên cho ở bảng sau:
-
Ngữ văn
Toán
Giỏi
Khá
Trung bình
Giỏi
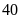
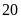
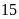
Khá
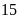

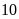
Trung bình
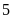
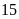
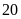
(Ví dụ: Số học sinh có kêt quả Toán — giỏi, Ngữ văn — khá là 20)
Hãy tính xác suất thực nghiệm của sự kiện một học sinh được chọn ra một cách ngẫu nhiên có kết quả:
a) Môn Toán đạt lọai giỏi.
b) Loại khá trở lên ở cả hai môn.
c) Loại trung bình ở ít nhất một môn.
Lời giải
Tổng
số học sinh được lựa chọn ngẫu nhiên là:
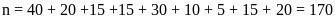
a) Xác suất thực nghiệm của sự kiện một học sinh Môn Toán đạt lọai giỏi là:
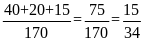
b)
Xác suất thực nghiệm cůa sự kiện một học sinh đạt
loại khá trở lên ở cả hai môn là::
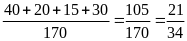
c) Xác suất thực nghiệm cůa sự kiện một học sinh đạt loại trung bình ít nhất một môn là:
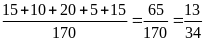
Ngoài Phương Pháp Tính Xác Suất Thực Nghiệm Có Lời Giải Chi Tiết – Tài Liệu Toán thì các tài liệu học tập trong chương trình 6 sẽ được cập nhật liên tục và nhanh nhất có thể sau khi kỳ thi diễn ra trên Danh mục Tài Liệu Học Tập nhằm giúp các bạn đọc thuận tiện trong việc nghiên cứu tài liệu. Quý thày cô và các bạn đọc có thể chia sẻ thêm những tài liệu học tập hữu ích đến địa chỉ email của chúng tôi, nhằm xây dựng nên kho đề thi phong phú, đa dạng cho các em học sinh tham khảo và rèn luyện.
Phương pháp tính xác suất thực nghiệm là một cách tiếp cận thực tế và linh hoạt để ước lượng xác suất dựa trên các quan sát và thử nghiệm thực tế. Thay vì dựa vào lý thuyết toán học, phương pháp này yêu cầu chúng ta thực hiện các thử nghiệm và đếm kết quả để ước lượng xác suất.
Việc áp dụng phương pháp tính xác suất thực nghiệm đòi hỏi sự quan sát kỹ lưỡng, việc thực hiện các thử nghiệm lặp đi lặp lại và việc đếm kết quả. Điều này giúp chúng ta có được một con số xác suất gần đúng cho sự kiện quan tâm.
Phương pháp này rất hữu ích trong nhiều lĩnh vực như xác suất trong trò chơi, xác suất trong thống kê, xác suất trong các thí nghiệm khoa học, và nhiều lĩnh vực khác. Nó giúp chúng ta hiểu rõ hơn về khả năng xảy ra của các sự kiện và đưa ra quyết định dựa trên dữ liệu thực tế.
Để hiểu rõ hơn về phương pháp tính xác suất thực nghiệm và cách áp dụng nó, bạn có thể tham khảo sách giáo trình, tài liệu học tập hoặc tìm hiểu trực tuyến. Ngoài ra, có thể tìm kiếm các bài tập và ví dụ để rèn kỹ năng tính toán xác suất thực nghiệm.
>>> Bài viết có liên quan







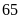
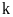
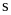
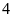
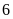
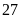
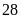
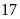
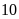
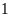
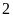
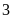
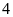
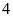
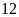
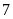
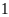
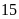
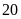
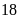
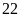
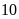
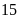
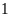
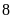
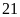
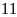
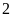
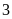
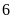
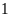
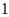
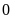
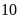
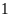
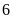
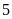
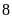
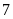
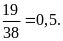
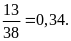
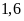
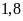
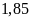
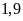
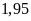
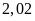
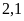
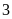
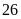
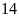


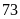
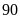
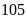
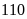
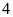
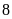
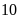
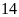
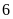
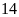 hộ.
hộ.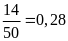 .
.