Phương Pháp Giải Bài 4 Toán 6 Bài Độ Dài Đoạn Thẳng Sách CTST
>>> Mọi người cũng quan tâm:
Phương Pháp Giải Bài 4 Toán 6 Bài Độ Dài Đoạn Thẳng Sách CTST – Toán 6 Chân Trời Sáng Tạo là tài liệu học tập được Trang Tài Liệu biên soạn và sưu tầm từ những nguồn dữ liệu mới nhất hiện nay. Tài liệu này sẽ giúp các em luyện tập, củng cố kiến thức từ đó nâng cao điểm số cho môn học. Ngoài ra, cũng giúp các thầy cô giáo có nguồn tài nguyên phong phú để giảng dạy.
Dưới đây là bản đọc trực tuyến giúp thầy cô và các em học sinh có thể nghiên cứu Online hoặc bạn có thể tải miễn phí với phiên bản word để dễ dàng in ấn cũng như học tập Offline.
Bài 4: ĐOẠN THẲNG. ĐỘ DÀI ĐOẠN THẲNG
KIẾN THỨC CẦN NHỚ
1. Đoạn thẳng. - Đoạn thẳng AB là hình gồm hai điểm A, B và tất cả các điểm nằm giữa A và B. - Đoạn thẳng AB còn gọi là đoạn thẳng BA. - Hai điểm A, B gọi là hai đầu mút ( hoặc hai đầu) của đoạn thẳng AB.
2. Độ dài đoạn thẳng. - Mỗi đoạn thẳng có một độ dài. Độ dài đoạn thẳng là một số dương. - Độ dài đoạn thẳng AB còn gọi là khoảng cách giữa hai điểm A và B. - Nếu hai điểm trùng nhau thì khoảng cách giữa chúng bằng 0. - Với điểm M nằm giữa hai điểm A, B ta luôn có AM + MB = AB.
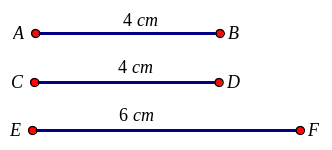
3. So sánh hai đoạn thẳng. Giả sử ta có ba đoạn thẳng AB = 4cm, CD = 4cm, EF = 6cm (xem hình bên dưới)
- Đoạn thẳng AB bằng đoạn thẳng CD và viết AB = CD. - Đoạn thẳng EF dài hơn đoạn thẳng AB và viết EF > AB. - Đoạn thẳng CD ngắn hơn đoạn thẳng EF và viết CD < EF. 4. Một số dụng cụ đo độ dài. - Thước dây, thước cuộn, thước xếp, thước mét, thước kẻ, …
|
B. BÀI TẬP CÓ HƯỚNG DẪN. (MẪU TỰ LUẬN)
DẠNG 1: Vẽ đoạn thẳng, đường thẳng, tia.
Bài 1. Hãy vẽ hình tương ứng trong mỗi trường hợp sau:
Đoạn thẳng AB; b) Đường thẳng AB; c) Tia AB; d) Tia BA.
Hướng dẫn: Chú ý giới hạn của đoạn thẳng, của đường thẳng, của tia.
a)
![]()
b)
![]()
c)
![]()
d)
![]()
Bài 2. Cho 3 điểm M, N, P không thẳng hàng. Vẽ đoạn thẳng MN, tia NP, đường thẳng MP.
Hướng dẫn: Vẽ đoạn thẳng, đường thẳng, tia qua 2 điểm: ...
Chú ý giới hạn của đoạn thẳng, của đường thẳng, của tia.

Bài 3. Trên thang chia của thước bị mờ chỉ còn các điểm chia 0 cm, 5 cm và 13 cm. Có thể chỉ sử dụng chiếc thước này để vẽ các đoạn thẳng có độ dài lần lượt dưới đây không?
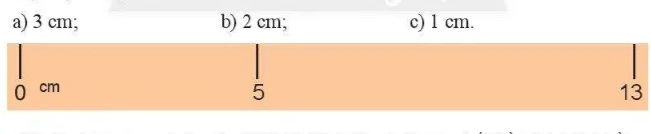
Hướng dẫn: Dựa vào tính chất cộng đoạn thẳng
3 cm = 13 cm – 5 cm – 5 cm
2 cm = 5 cm – 3 cm
1 cm = 13 cm – 5 cm – 5cm – 2 cm
DẠNG 2: Tính độ dài đoạn thẳng, so sánh hai đoạn thẳng.
Bài 4. Điểm M nằm giữa hai điểm C và D. Tính độ dài đoạn thẳng CD nếu:
a) CM = 2,5 cm và MD = 3,5 cm.
b) CM = 3,1 cm và MD = 4,6 cm.
Hướng
dẫn:
![]()
Vì điểm M nằm giữa hai điểm C và D nên CM + MD = CD. Thay độ dài CM và MD ta tính được CD.
Bài 5. Trên tia AB lấy điểm C. Tính độ dài đoạn BC nếu:
AB = 2,5 cm và AC = 1,5 cm.
AB = 2 cm và AC = 5cm.
Hướng dẫn:
Vì AC < AB nên điểm C nằm giữa 2 điểm A và B, sử dụng tính chất cộng đoạn thẳng để tính BC.
Vì AB < AC nên điểm B nằm giữa 2 điểm A và C, sử dụng tính chất cộng đoạn thẳng để tính BC.
Bài 6. Trong hình vẽ bên, các đoạn thẳng ME và NF bằng nhau. Hỏi các đoạn thẳng MF và NE có bằng nhau không? Vì sao?
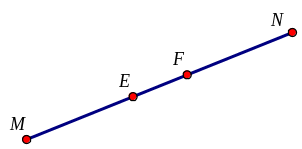
Hướng dẫn: Sử dụng tính chất cộng đoạn thẳng MF = ME + EF, NE = NF + FE để so sánh.
Bài 7. a) Đo và sắp xếp các đoạn thẳng HI, IK, KH trong hình vẽ theo thứ tự từ bé đến lớn.
b) Tính chu vi của tam giác HIK.
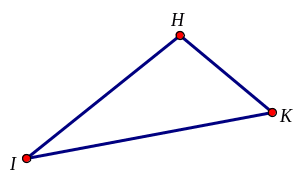
Hướng dẫn: Đo rồi sắp xếp.
DẠNG 3: Tính số đoạn thẳng
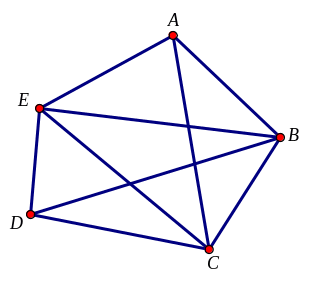
Bài 8. Cho 5 điểm A, B, C, D, E trong đó không có ba điểm nào thẳng hàng. Qua hai điểm vẽ được một đoạn thẳng. Cho biết có tất cả bao nhiêu đoạn thẳng? Hãy kể tên các đoạn thẳng đó?
Hướng dẫn:
- Xác định số đoạn thẳng kẻ từ một điểm đến các điểm còn lại. - Làm tương tự cho các điểm còn lại. Kẻ từ 1 điểm bất kì đến 4 điểm còn lại được 4 đoạn thẳng. Cứ làm như vậy với 5 điểm ta sẽ vẽ được 5.4 = 20 (đoạn thẳng) Nhưng như vậy mỗi đoạn thẳng đã được tính hai lần nên số đoạn thẳng thực vẽ được là 5.4:2 = 10 (đoạn thẳng) Các đoạn thẳng là: AB, AC, AD, AE, BC, BD, BE, CD, CE, DE.
|
|
DẠNG 4: Tổng hợp
Bài 9.
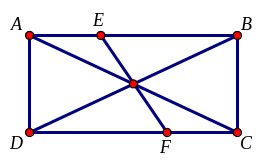
Cho hình chữ nhật ABCD như hình vẽ. a) Hãy kể tên tất cả các đoạn thẳng có trong hình vẽ. b) Dùng thước đo để kiểm tra xem những đoạn thẳng nào bằng nhau. c) So sánh đoạn thẳng AC và EF. |
|
Hướng dẫn:
Dựa vào hình vẽ để kể tên đoạn thẳng.
Đo rồi tìm các đoạn thẳng bằng nhau.
Đo rồi so sánh.
C. BÀI TẬP TỰ GIẢI CÓ ĐÁP SỐ.
Bài 1. Trên đường thẳng d lấy 4 điểm M, N, P, Q. Hỏi có tất cả bao nhiêu đoạn thẳng. Kể tên các đoạn thẳng đó.
Đáp số: 6 đoạn thẳng.
Bài 2. Lấy 3 điểm không thẳng hàng M, N, P. Vẽ hai tia PM, PN. Vẽ tia Px cắt đoạn thẳng MN tại I nằm giữa M, N. Gọi tên các đoạn thẳng có trên hình vẽ.
Đáp số: IM, IN, MN, PM, PN, PI
D. BÀI TẬP TRẮC NGHIỆM
Bài 1: Hãy nối mỗi hình vẽ ở cột A và tên của hình tương ứng ở cột B để được kết quả đúng.
A |
B |
Kết quả |
|
|
1) Tia QP |
|
|
|
2) Đoạn thẳng PQ |
|
|
|
3) Đường thẳng PQ |
|
|
4) Tia PQ |
|
Bài 2. Cho các đoạn thẳng AB = 4cm; MN = 5cm; EF = 3cm; PQ = 8cm; IK = 7cm . Sắp xếp độ dài các đoạn thẳng theo thứ tự tăng dần?
EF, AB, MN, IK, PQ
PQ, IK, MN, AB, EF
EF, AB, IK, PQ, MN
EF, MN, IK, PQ, AB Đáp án: A
Bài 3. Cho 20 điểm trong đó không có 3 điểm nào thẳng hàng. Biết cứ hai điểm nối với nhau được một đoạn thẳng. Hỏi vẽ được tất cả bao nhiêu đoạn thẳng?
A. 160
B. 170
C. 180
D. 190 Đáp án: D
Bài 4. Trên đường thẳng a lấy 4 điểm M, N, P, Q theo thứ tự đó. Cho biết MN = 2cm, MQ = 5cm và NP = 1cm. Tìm các cặp đoạn thẳng bằng nhau
A. MP = PQ
B. MP = NQ
C. MN = PQ
D. Cả B, C đều đúng Đáp án: D
Ngoài Phương Pháp Giải Bài 4 Toán 6 Bài Độ Dài Đoạn Thẳng Sách CTST – Toán 6 Chân Trời Sáng Tạo thì các tài liệu học tập trong chương trình 6 sẽ được cập nhật liên tục và nhanh nhất có thể sau khi kỳ thi diễn ra trên Danh mục Tài Liệu Học Tập nhằm giúp các bạn đọc thuận tiện trong việc nghiên cứu tài liệu. Quý thày cô và các bạn đọc có thể chia sẻ thêm những tài liệu học tập hữu ích đến địa chỉ email của chúng tôi, nhằm xây dựng nên kho đề thi phong phú, đa dạng cho các em học sinh tham khảo và rèn luyện.
Phương pháp giải bài 4 trong sách “Toán 6 – Bài Độ Dài Đoạn Thẳng” (CTST) là một công cụ hữu ích giúp học sinh hiểu và áp dụng các kiến thức về độ dài và đo đạc trong toán học.
Bài 4 tập trung vào khái niệm về độ dài đoạn thẳng, bao gồm các bài tập thực tế liên quan đến việc đo và so sánh độ dài đoạn thẳng. Phương pháp giải bài tập trong sách CTST đảm bảo cung cấp các bước cụ thể và logic để học sinh tiếp cận vấn đề và tìm ra câu trả lời chính xác.
Qua phương pháp giải này, học sinh sẽ được hướng dẫn cách đọc và hiểu bài toán, xác định thông tin quan trọng, áp dụng các công thức và quy tắc liên quan để giải quyết vấn đề. Bước giải được trình bày một cách rõ ràng và minh bạch, giúp học sinh dễ dàng theo dõi và hiểu quy trình giải quyết.
Ngoài ra, sách CTST cũng cung cấp ví dụ minh họa và lời giải chi tiết cho từng bài tập, giúp học sinh nắm vững các phương pháp và cải thiện kỹ năng toán học của mình. Qua việc luyện tập và áp dụng phương pháp giải này, học sinh sẽ phát triển khả năng tư duy logic, tính cẩn thận và kỹ năng giải quyết vấn đề trong lĩnh vực đo đạc và độ dài đoạn thẳng.
>>> Bài viết có liên quan