Phương Pháp Giải Toán 9 Góc Nội Tiếp Kèm Bài Luyện Tập & Đáp Án

CHỦ ĐỀ 9: GÓC NỘI TIẾP.

A. LÝ THUYẾT.

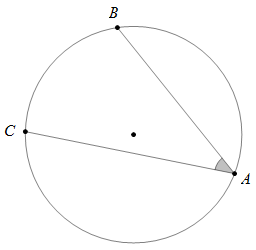
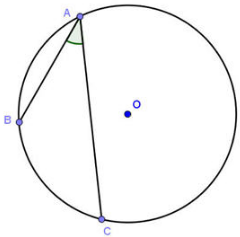
+ Góc nội tiếp là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn đó (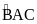 là góc nội tiếp chắn cung nhỏ )

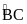+ Cung nằm bên trong góc gọi là cung bị chắn (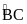 gọi là cung bị chắn).

2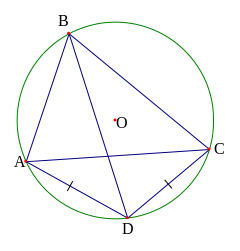 . Trong một đường tròn, số đo của góc nội tiếp bằng một nửa số đo của cung bị chắn.

3. Trong một đường tròn:

* Các góc nội tiếp bằng nhau chắn các cung bằng nhau.

Nếu

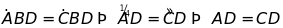
* Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.

Trên hình vẽ: .

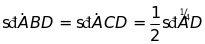Trên hình vẽ:

* Góc nội tiếp có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung.

* Góc nội tiếp chắn nửa đường tròn là góc vuông.

B/ BÀI TẬP VẬN DỤNG.

* Để chứng minh tích độ dài đoạn thẳng bằng nhau cần chứng minh hai tam giác giác đồng dạng liên quan đến tích đó.

* Để chứng minh hai tam giác đồng dạng cần chứng minh

+ Hai góc tương ứng của hai tam giác đó bằng nhau

+ Hai cặp cạnh của hai tam giác tương ứng tỉ lệ và góc sen giữa bằng nhau.

* Để chứng minh hai góc bằng nhau ta cần chú ý:

+ Xem góc cần chứng minh có phải là hai góc nội tiếp cùng chắn một cung, hai góc nội tiếp chắn hai cung bằng nhau (hai dây cung bằng nhau) trong một đường tròn.

+ Xem hai góc đó, mỗi góc bằng với góc nội tiếp nào và các góc nội tiếp đó có bằng nhau không

+ Xem hai góc đó có liên quan đến hai tam giác bằng nhau, góc có cạnh tương ứng vuông góc, góc sole trong, góc đồng vị không, góc của tam giác vuông…

I/ BÀI TẬP MẪU.

Bài 1: Cho hai đường tròn (O; R) và (O’; R’) cắt nhau tại A và B . Vẽ cát tuyến CAD vuông góc với AB . Tia CB cắt (O’) tại E, tia BD cắt (O) tại F. Chứng minh rằng:

a) ∠CAF = ∠DAE

b) AB là tia phân giác của ∠EAF

c) CA.CD = CB.CE

d) CD² = CB.CE + BD.CF

Hướng dẫn

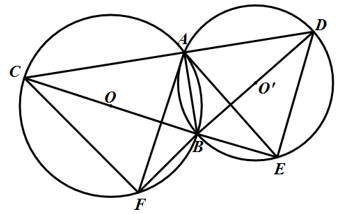
Vì CD ⊥ AB => ∠CAB = 90^o Mà ∠CAB = 1/2 sđ => sđ = 180^o

Vậy ba điểm B, O, C thằng hàng.

Chứng minh tương tự ta có B, O’, D thẳng hàng.

a) Chứng minh ∠CAF = ∠DAE

Trong (O) ta có: ∠CAF = ∠CBF (góc nội tiếp cùng chắn cung CF )

Trong (O’) ta có: ∠DAE = ∠DBE (góc nội tiếp cùng chắn cung DE )

Mà ∠CBF = ∠DBE (đối đỉnh)

=> ∠CAF = ∠DAE .

b) AB là tia phân giác của ∠EAF

Nối CF và DE ta có: ∠CFB = 90^o (góc nội tiếp chắn nửa đường tròn (O))

∠BED = 90^o (góc nội tiếp chắn nửa đường tròn (O’))

Xét ΔCFB và ΔDEB có:

∠CFB = ∠BED = 90^o

∠CBF = ∠DBE (đối đỉnh)

=> ∠FCB = ∠EDB

Mặt khác: ∠FAB = ∠FCB (góc nội tiếp (O) cùng chắn cung FB )

∠EAB = ∠EDB (góc nội tiếp (O’) cùng chắn cung EB )

=> ∠FAB = ∠EAB hay AB là phân giác của góc ∠EAF .

c) Chứng minh CA.CD = CB.CE

Xét ΔCAE và ΔCBD có:

∠C chung

∠CEA = ∠BDA (góc nội tiếp (O’) cùng chắn cung AB)

=> ΔCAE ∼ ΔCBD (g.g) => CA/CB = CE/CD hay CA.CD = CB.CE (1)

d) Chứng minh CD² = CB.CE + BD.CF

Chứng minh tương tự câu c) ta có: DA.DC = DB.DF (2)

Từ (1) và (2) suy ra:

CA.CD + DA.DC = CB.CE + DB.DF

⇔ (CA + DA)CD = CB.CE + DB.DF

⇔ CD² = CB.CE + DB.DF

Bài 2: Cho đường tròn (O; R) và một điểm M bên trong đường tròn đó. Qua M kẻ hai dây cung AB và CD vuông góc với nhau (C thuộc cung nhỏ AB). Vẽ đường kính DE. Chứng minh rằng:

a) MA.MB = MC.MD.

b) Tứ giác ABEC là hình thang cân.

c) Tổng có giá trị không đổi khi M thay đổi vị trí trong đường tròn (O).

Hướng dẫn

a) Chứng minh MA.MB = MC.MD.

Xét ΔAMC và ΔDMB có:

∠ACD = ∠ABD (góc nội tiếp cùng chắn cung AD)

∠AMC = ∠BMD = 90^o (gt)

=> ΔAMC ∼ ΔDMB (g.g)

=> MA/MD = MC/MB => MA.MB = MC.MD

b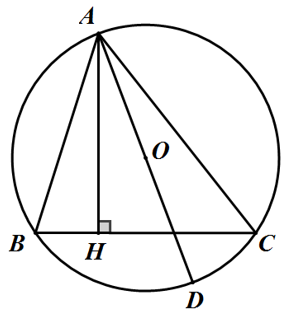 ) Chứng minh tứ giác ABEC là hình thang cân.

Vì ∠DCE = 90^o (góc nội tiếp chắn nửa đường tròn)

=> CD ⊥ CE CD ⊥ AB (gt) => AB // CE.

=> Tứ giác ABEC là hình thang (1).

Mặt khác: CE và AB là hai dây song song của đường tròn (O) chắn hai cung AC và BE

=> (2)

Từ (1) và (2) suy ra tứ giác ABEC là hình thang cân.

c) Tổng có giá trị không đổi khi M thay đổi vị trí trong đường tròn (O).

Ta có (cmt) => EA = BC .

Mặt khác: ∠DAE = 90^o (góc nội tiếp chắn nửa đường tròn)

Do đó: MA² + MB² + MC² + MD² = (MA²+ MD²) + (MB² + MC²)

= AD² + BC² = DE² = 4R² không đổi

Bài 4: Cho nửa đường tròn (O) đường kính AB và C là điểm chính giữa của cung AB. Lấy điểm M thuộc cung BC và điểm N thuộc tia AM sao cho AN = BM. Kẻ dây CD song song với AM.

a) Chứng minh ΔACN = ΔBCM .

b) Chứng minh ΔCMN vuông cân.

c) Tứ giác ANCD là hình gì? Vì sao?

H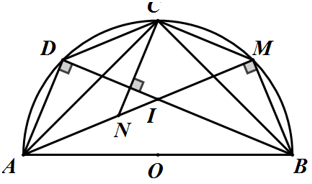 ướng dẫn

a) Chứng minh ΔACN = ΔBCM

Xét ΔACN và ΔBCM có:

AC = BC (vì C là điểm chính giữa cung AB)

∠CAN = ∠CBN (góc nội tiếp cùng chắn cung CM)

AN = BM (gt)

=> ΔACN = ΔBCM (c.g.c)

b) Chứng minh ΔCMN vuông cân

Vì ΔACN = ΔBCM (chứng minh a) => CN = CM => ΔCMN cân tại C (1)

Lại có ∠CMA = 1/2 sđ = 1/2. 90^o = 45^o (2)

Từ (1) và (2) => ΔCMN vuông cân tại C.

Vì CD // AM nên tứ giác ADCM là hình thang cân.

c) Tứ giác ANCD là hình gì? Vì sao?

Ta có: ∠DAM = ∠CMN = ∠CNM = 45^o

=> AD // CN. Vậy tứ giác ADCN là hình bình hành.

Bài 5: Cho ΔABC cân tại A nội tiếp đường tròn (O). M là một điểm bất kỳ thuộc cung nhỏ AC. Tia AM cắt BC tại N. Chứng minh rằng:

a) AB² = AM.AN

b) ∠ACM = ∠ANC

H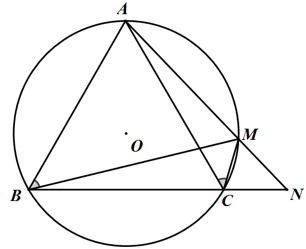 ướng dẫn

a) Chứng minh AB² = AM.AN

Vì ΔABC cân tại A =>∠ABC = ∠ACB

Lại có ∠ACB = ∠AMB (góc nội tiếp cùng chắn cung AB )

=> ∠ABN = ∠AMB

Do đó: ΔABM ∼ ΔANB (g.g) => AB/AN = AM/MB

=> AB² = AN. AM

b) Chứng minh ∠ACM = ∠ANC

Vì ΔABM ∼ ΔANB => ∠ABM = ∠ANB

Mà ∠ABM = ∠ACM (góc nội tiếp cùng chắn cung AM)

Do đó: ∠ACM = ∠ANC

Bài 6: Cho ΔABC có AD là tia phân giác trong của góc A. Qua D kẻ đường thẳng song song với AB cắt AC ở E và đường thẳng song song với AC cắt AB ở F.

a) Tứ giác AEDF là hình gì? Vì sao?

b) Đường tròn đường kính AD cắt AB và AC lần lượt tại các điểm M và N. Chứng minh: MN // EF.

Hướng dẫn

a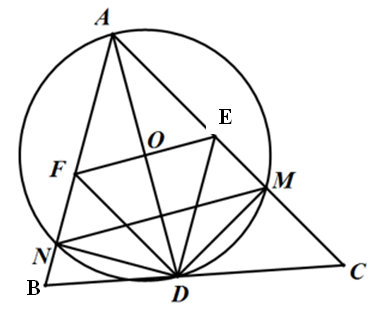 ) Chứng minh được Tứ giác AEDF là hình thoi.

b) Chứng minh: MN // EF.

ΔABC có AD là tia phân giác trong của góc A

=> ∠BAD = ∠CAD

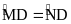=> => ∠DAC = ∠MND (hai góc nội tiếp chắn hai cung bằng nhau)

Lại có: ∠AND = 90^o (nội tiếp chắn nửa đường tròn)

=> ∠DAN + ∠ADN = 90^o => ∠MND + ∠ADN = 90^o

=> MN // AD

Vì tứ giác AEDF là hình thoi nên EF ⊥ AD => MN // EF

Bài 7: Cho hai đường tròn (O; R) và (O’; R’) tiếp xúc trong với nhau tại A, (R > R'). Qua điểm B bất kỳ trên (O’) vẽ tiếp tuyến với (O’) cắt (O) tại hai điểm M và N, AB cắt (O) tại C. Chứng minh rằng:

a) MN ⊥ OC

b) AC là tia phân giác của ∠MAN

Hướng dẫn

a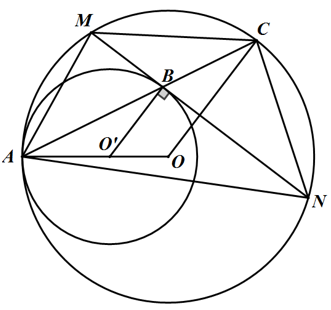 ) Chứng minh MN ⊥ OC

Vì Δ O'AB cân tại O’ nên ∠O'AB = ∠O'BA

=> Δ OAC cân tại O nên ∠OAC = ∠OCA

=> ∠O'BA = ∠OCA mà hai góc này ở vị trí đồng vị

=> O’B // OC.

Mặt khác MN là tiếp tuyến của (O’) tại B => O'B ⊥ MN.

Do đó OC ⊥ MN

b) Chứng minh AC là tia phân giác của ∠MAN

Trong đường tròn (O): => OC là đường trung trực của MN => CM = CN

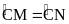=> => ∠MAC = ∠NAC Hay AC là tia phân giác của ∠MAN .

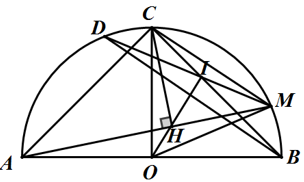
Bài 8: Cho nửa đường tròn (O) đường kính AB và C là điểm chính giữa cung AB. M là điểm bất kỳ trên cung BC, kẻ CH ⊥ AM.

a) Chứng minh ΔHCM vuông cân và OH là tia phân giác của ∠COM

b) Gọi I là giao điểm của OH với BC và D là giao điểm của MI với nửa đường tròn (O). Chứng minh MC // BD.

Hướng dẫn

a) Chứng minh ΔHCM vuông cân và OH là tia phân giác của ∠COM

Vì C là điểm chính giữa của cung AB

=> ∠CMA =

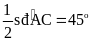
=> ΔHCM vuông cân tại H => CH = HM

Dễ thấy ΔCOH = ΔMOH (c.c.c) => ∠COH = ∠MOH

Vậy OH là tia phân giác của ∠COM

b) Chứng minh MC // BD.

Dễ thấy ΔCOI = ΔMOI (c.g.c) nên CI = MI => ΔCMI cân tại M.

Do đó ∠CMI = ∠MCI.

Lại có ∠CMD = ∠CBD (góc nội tiếp cùng chắn cung CD)

Suy ra ∠MCB = ∠CBD, mà hai góc này ở vị trí so le trong

=> MC // BD.

Bài 9: Qua điểm M nằm trong đường tròn (O) kẻ hai dây AB và CD vuông góc với nhau. Chứng minh rằng:

a) Đường cao MH của tam giác AMD đi qua trung điểm I của BC.

b) Đường trung tuyến MI của ΔBMC vuông góc với AD.

Hướng dẫn

a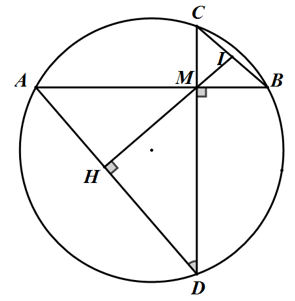 ) Chứng minh Đường cao MH của tam giác AMD đi qua trung điểm I của BC

Ta có ∠ADC = ∠ABC (góc nội tiếp cùng chắn cung AC) (1)

Lại có ∠AMH = ∠ADM (cùng phụ với góc ∠MAD)

Mà ∠AMH = ∠IMB (đối đỉnh) => ∠ADM = ∠IMB (2)

Do đó IM = IB.

Chứng minh tương tự ta có: IM = IC Suy ra IB = IC = IM

=> I là trung điểm của BC.

b) Học sinh tự chứng minh.

Bài 10: Cho AB và CD là hai đường kính vuông góc với nhau của đường tròn (O; R). Qua điểm M thuộc cung nhỏ AC (M ≠ A, M ≠ E)kẻ tiếp tuyến với đường tròn cắt AB, CD lần lượt tại E, F.

a) Chứng minh: ∠MFO = 2.∠MBO

b ) Xác định vị trí điểm M trên cung nhỏ AC sao cho ∠FEO = 30^o. Khi đó tính độ dài đoạn thẳng OE, ME, EF theo R.

Hướng dẫn

a) Chứng minh: ∠MFO = 2.∠MBO

Ta có: ∠MOA = 2∠MBO (cùng chắn cung MA)

Vì EF là tiếp tuyến với (O) tại M nên OM ⊥ EF

Ta có ∠MOA = ∠EFO (cùng phụ với góc ∠FEO )

Suy ra ∠EFO = 2∠MBO

b) Tính độ dài đoạn thẳng OE, ME, EF theo R.

Ta có: ∠FEO = 30^o ⇔ ∠MOA = 60^o ⇔ ΔAOM đều nên AM = OA = R.

Vậy nếu M ∈ (O) và AM = R thì ∠FEO = 30^o

Khi đó ΔOME vuông tại M nên ME = MO. tan∠MOA = 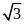R ; OE = 2MO = 2R

Vì ΔEOF vuông tại O nên cos ∠FEO = EO/EF => EF = EO/cos ∠FEO = 2R / cos30^o = 4R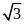 /3

II/ LUYỆN TẬP.

Bài 1 : Cho tam giác ABC nội tiếp đường tròn (O) . Tia phân giác của góc A cắt đường tròn tại M . Tia phân giác của góc ngoài tại đỉnh A cắt đường tròn tại N . Chứng minh rằng :

a) Tam giác MBC cân .

b) Ba điểm M , O , N thẳng hàng .

Bài 2 : Cho nửa đường tròn (O) đường kính AB . M là điểm tuỳ ý trên nửa đường tròn ( M khác A và B ) . Kẻ MH  AB ( H AB ) . Trên cùng nửa mặt phẳng bờ AB chứa nửa đường tròn (O) vẽ hai nửa đường tròn tâm O₁ đường kính AH và tâm O₂ đường kính BH . MA và MB cắt hai nửa đường tròn (O₁) và (O₂) lần lượt tại P và Q .

a) Chứng minh MH = PQ .

b) Chứng minh hai tam giác MPQ và MBA đồng dạng .

c) Chứng minh PQ là tiếp tuyến chung của hai đường tròn (O₁) và (O₂)

Bài 3 :Cho ABC đều , đường cao AH . M là điểm bất kỳ trên đáy BC . Kẻ

MP  AB và MQ  AC . Gọi O là trung của AM .

a) Chứng minh năm điểm A , P , M , H , Q cùng nằm trên một đường tròn .

b) Tứ giác OPHQ là hình gì ? chứng minh .

c) Xác định vị trí của M trên BC để PQ có độ dài nhỏ nhất .

Bài 4 : Cho đường tròn (O) đường kính AB . Lấy điểm M trên đường tròn (M khác A và B ) sao cho MA < MB . Lấy MA làm cạnh vẽ hình vuông MADE ( E thuộc đoạn thẳng MB ) . Gọi F là giao điểm của DE và AB .

a) Chứng minh ADF và BMA đồng dạng .

b) Lấy C là điểm chính giữa cung AB ( không chứa M ) . Chứng minh CA = CE = CB

c) Trên đoạn thẳng MC lấy điểm I sao cho CI = CA . Chứng minh I là tâm đường tròn nội tiếp tam giác AMB .

Bài 5 : Cho nửa đường tròn (O) đường kính AB = 2R và điểm C nằm ngoài nửa đường tròn . CA cắt nửa đường tròn ở M , CB cắt nửa đường tròn ở N . Gọi H là giao điểm của AN và BM .

a) Chứng minh CH  AB .

b) Gọi I là trung điểm của CH . Chứng minh MI là tiếp tuyến của nửa đường tròn (O)

c) Giả sử CH =2R . Tính số đo cung .

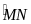Bài 6 : Trên cung nhỏ BC của đường tròn ngoại tiếp tam giác đều ABC lấy một điểm P tuỳ ý . Gọi Q là giao điểm của AP và BC

a) Chứng minh BC²= AP . AQ .

b) Trên AP lấy điểm M sao cho PM = PB . Chứng minh BP+PC= AP.

c) Chứng minh .

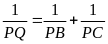Bài 7: Cho (O), đường kính AB, điểm D thuộc đường tròn. Gọi E là điểm đối xứng với A qua D.

a) Tam giác ABE là tam giác gì ?

b) Gọi K là giao điểm của EB với (O). Chứng minh rằng OD AK.

Bài 8: Cho hai đường tròn (O) và (O’) cắt nhau ở A, B, O nằm trên (O’). Dây AC của (O) cắt (O’) ở D, dây OE của (O’) cắt (O) ở F. Chứng minh :

a) OD  BC.

b) Điểm F cách đều ba cạnh của tam giác ABE.

Bài 9: Cho hai đường thẳng song song. Một đường tròn tiếp xúc với một đường thẳng tại A và cắt đường thẳng kia tại B, C. Trên đường tròn lấy một điểm D ( không trùng A, B, C ). Chứng minh rằng A cách đều hai đường thẳng BD và CD.

Bài 10: MA và MB là hai tiếp tuyến của (O). Vẽ (M;MA), C là một điểm nằm trên cung AB của (M) ( cung AB nằm trong đường tròn (O) ). Tia AC, BC cắt (O) ở P, Q. Chứng minh rằng : P và Q đối xứng với nhau qua O.

Bài 11: Trên cạnh CD của hình vuông ABCD ta lấy một điểm M khác C, D. Các đường tròn đường kính CD và AM cắt nhau tại điểm thứ hai N ( khác D ). Tia DN cắt BC tại P. Chứng minh rằng: AC  PM.