Hướng Dẫn Cách Giải Căn Bậc 3 Và Căn Bậc 2 Chi Tiết [2023]
>>> Mọi người cũng quan tâm:
Hướng Dẫn Cách Giải Căn Bậc 3 Và Căn Bậc 2 Chi Tiết [2023] – Toán 9 là tài liệu học tập được Trang Tài Liệu biên soạn và sưu tầm từ những nguồn dữ liệu mới nhất hiện nay. Tài liệu này sẽ giúp các em luyện tập, củng cố kiến thức từ đó nâng cao điểm số cho môn học. Ngoài ra, cũng giúp các thầy cô giáo có nguồn tài nguyên phong phú để giảng dạy.
Dưới đây là bản đọc trực tuyến giúp thầy cô và các em học sinh có thể nghiên cứu Online hoặc bạn có thể tải miễn phí với phiên bản word để dễ dàng in ấn cũng như học tập Offline.
A. KIẾN THỨC TRỌNG TÂM
Với số
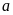 không âm, ta có
không âm, ta có
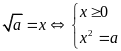 .
.Với
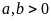 thì
thì
 .
.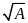 có
nghĩa khi và chỉ khi
có
nghĩa khi và chỉ khi
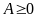 .
.Với mọi số thực
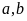 thì
thì
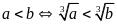 .
.Các công thức biến đổi căn thức
(1)
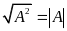 ; (2)
; (2)
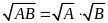 (với
(với
 );
);
(3)
 (với
(với
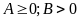 ); (4)
); (4)
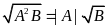 (với
(với
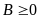 );
);
(5)
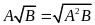 (với
(với
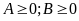 ); (6)
); (6)
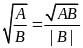 (với
(với
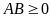 và
và
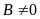 );
);
(7)
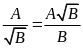 (với
(với
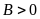 ); (8)
); (8)
 (với
(với
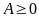 và
và
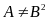 );
);
(9)
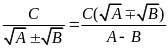 (với
(với
 ).
).
B. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
Dạng 1: Tìm điều kiện để căn thức xác định (hay có nghĩa) |
Với A, B là các biểu thức, ta có
|
Ví
dụ 1.
Tìm điều kiện của
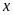 để các căn thức sau xác định
để các căn thức sau xác định
Ví
dụ 2.
Tìm điều kiện của
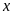 để các biểu thức sau xác định
để các biểu thức sau xác định
a)
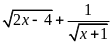 ; b)
; b)
 .
.
Dạng 2: Rút gọn biểu thức. Tính giá trị của biểu thức |
|
Ví dụ 3. Rút gọn các biểu thức sau
a)
 ;
;
b)
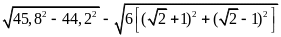 .
.
Ví dụ 4. Rút gọn các biểu thức sau
a)
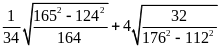 ;
;
b)
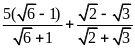 .
.
Ví
dụ 5.
Rút gọn biểu thức
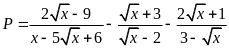 .
.
Ví
dụ 6.
Cho biểu thức
 .
.
a)
Rút gọn
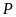 .
.
b)
Tính giá trị của
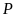 với
với
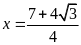 .
.
Ví
dụ 7.
Cho biểu thức
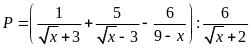 .
.
a)
Rút gọn
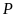 .
.
b)
Tính các giá trị nguyên của
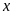 để
để
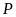 có giá trị nguyên.
có giá trị nguyên.
Dạng 3: Chứng minh biểu thức có một tính chất nào đó |
|
Ví
dụ 8.
Cho biểu thức
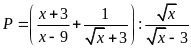 .
.
a)
Rút gọn
 .
.
b)
Chứng minh rằng
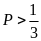 .
.
Ví
dụ 9.
Cho biểu thức
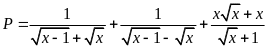 .
.
a)
Rút gọn
 .
.
b)
Chứng minh rằng biểu thức
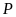 luôn luôn không âm với mọi giá trị của
luôn luôn không âm với mọi giá trị của
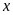 làm
làm
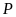 xác định.
xác định.
Ví
dụ 10.
Cho biểu thức
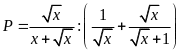 .
.
a)
Rút gọn
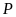 .
.
b)
Tìm giá trị lớn nhất của
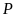 .
.
Dạng 4: Giải phương trình |
|
Ví dụ 11. Giải phương trình
a)
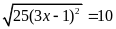 ; b)
; b)
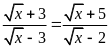 .
.
Ví dụ 12. Giải phương trình
a)
 ; b)
; b)
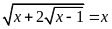 .
.
C. BÀI TẬP VẬN DỤNG
I. PHẦN TRẮC NGHIỆM
Câu
1.
Điều kiện xác định của biểu thức
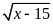 là
là
A.
 . B.
. B.
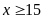 . C.
. C.
 . D.
. D.
 .
.
Câu
2.
Tìm
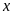 để biểu thức
để biểu thức
 có nghĩa.
có nghĩa.
A.
 . B.
. B.
 . C.
. C.
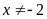 . D.
. D.
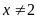 .
.
Câu
3.
Tìm nghiệm của phương trình
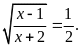
A.
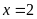 . B.
. B.
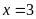 . C.
. C.
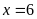 . D.
. D.
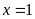 .
.
Câu
4.
Cho
 ,
rút gọn biểu thức
,
rút gọn biểu thức
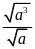 ta được kết quả
ta được kết quả
A.
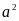 . B.
. B.
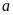 . C.
. C.
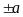 . D.
. D.
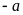 .
.
Câu
5.
Cho
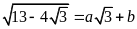 với
với
 ,
,
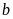 là các số nguyên. Tính giá trị của biểu thức
là các số nguyên. Tính giá trị của biểu thức
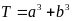 .
.
A.
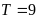 . B.
. B.
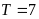 . C.
. C.
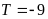 . D.
. D.
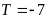 .
.
Câu
6.
Kết quả của phép tính
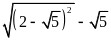 là
là
A.
 . B.
. B.
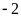 . C.
. C.
 . D.
. D.
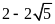 .
.
Câu
7.
Điều kiện để biểu thức
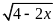 xác định là
xác định là
A.
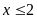 . B.
. B.
 . C.
. C.
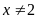 . D.
. D.
 .
.
Câu
8.
Cho biểu thức
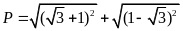 .
Khẳng định nào sau đây đúng.
.
Khẳng định nào sau đây đúng.
A.
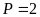 . B.
. B.
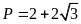 . C.
. C.
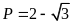 . D.
. D.
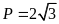 .
.
Câu
9.
Tìm điều kiện của
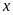 để biểu thức
để biểu thức
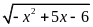 có nghĩa.
có nghĩa.
A.
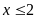 . B.
. B.
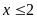 hoặc
hoặc
 .
.
C.
 . D.
. D.
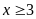 .
.
Câu
10.
Tìm điều kiện của
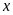 để đẳng thức
để đẳng thức
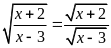 đúng.
đúng.
A.
 . B.
. B.
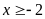 . C.
. C.
 . D.
. D.
 .
.
Câu
11.
Giá trị của
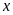 thỏa mãn
thỏa mãn
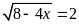 là
là
A.
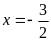 . B.
. B.
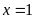 . C.
. C.
 . D.
. D.
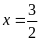 .
.
Câu
12.
Cho
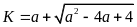 với
với
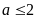 .
Khẳng định nào sau đây đúng?
.
Khẳng định nào sau đây đúng?
A.
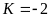 . B.
. B.
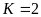 . C.
. C.
 . D.
. D.
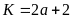 .
.
Câu
13.
Tìm tất cả các giá trị của
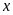 thỏa mãn
thỏa mãn
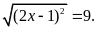
A.
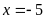 ,
,
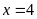 . B.
. B.
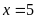 ,
,
 .
.
C.
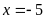 ,
,
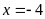 . D.
. D.
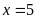 ,
,
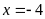 .
.
Câu 14. Chọn khẳng định \textbf{đúng} trong các khẳng định sau
A.
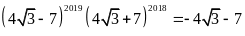 .
.
B.
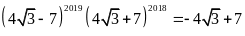 .
.
C.
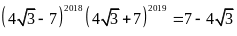 .
.
D.
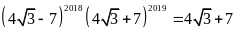 .
.
Câu
15.
Kết quả rút gọn biểu thức
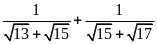 là
là
A.
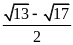 . B.
. B.
 . C.
. C.
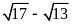 . D.
. D.
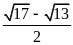 .
.
Câu
16.
Cho
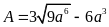 ,
với
,
với
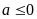 .
Khẳng định nào sau đây đúng?
.
Khẳng định nào sau đây đúng?
A.
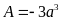 . B.
. B.
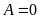 . C.
. C.
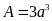 . D.
. D.
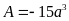 .
.
Câu
17.
Tìm các giá trị của
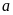 sao cho
sao cho
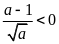 .
.
A.
 . B.
. B.
 . C.
. C.
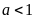 . D.
. D.
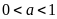 .
.
Câu
18.
Cho
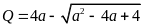 ,
với
,
với
 .
Khẳng định nào sau đây?
.
Khẳng định nào sau đây?
A.
 . B.
. B.
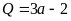 . C.
. C.
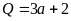 . D.
. D.
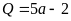 .
.
Câu
19.
Kết quả rút gọn biểu thức
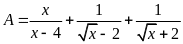 với
với
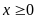 ,
,
 có dạng
có dạng
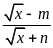 .
Tính giá trị của
.
Tính giá trị của
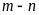 .
.
A.
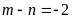 . B.
. B.
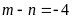 . C.
. C.
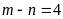 . D.
. D.
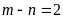 .
.
Câu
20.
Rút gọn biểu thức
 với
với
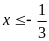 .
.
A.
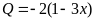 . B.
. B.
 . C.
. C.
 . D.
. D.
 .
.
Câu
21.
Kết quả rút gọn của biểu thức
 (với
(với
 ,
,
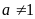 )
có dạng
)
có dạng
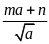 .
Tính giá trị
.
Tính giá trị
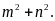
A.
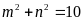 . B.
. B.
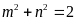 . C.
. C.
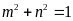 . D.
. D.
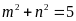 .
.
Câu
22.
Giá trị của biểu thức
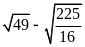 bằng
bằng
A.
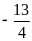 . B.
. B.
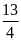 . C.
. C.
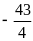 . D.
. D.
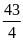 .
.
Câu 23. Đẳng thức nào dưới đây đúng?
A.
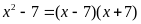 . B.
. B.
 .
.
C.
 . D.
. D.
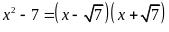 .
.
Câu
24.
Tính
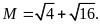
A.
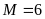 . B.
. B.
 . C.
. C.
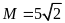 . D.
. D.
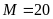 .
.
Câu
25.
Điều kiện của
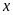 để
để
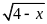 có nghĩa là
có nghĩa là
A.
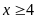 . B.
. B.
 . C.
. C.
 . D.
. D.
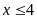 .
.
Câu
26.
Tìm tất cả các giá trị của
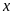 để biểu thức
để biểu thức
 có nghĩa.
có nghĩa.
A.
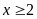 . B.
. B.
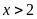 . C.
. C.
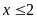 . D.
. D.
 .
.
Câu
27.
Đẳng thức nào sau đây đúng với mọi
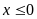 ?
?
A.
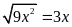 . B.
. B.
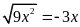 . C.
. C.
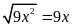 . D.
. D.
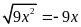 .
.
Câu
28.
Cho
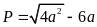 .
Khẳng định nào dưới đây đúng.
.
Khẳng định nào dưới đây đúng.
A.
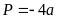 . B.
. B.
 . C.
. C.
 . D.
. D.
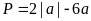 .
.
Câu
29.
Tính
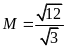 .
.
A.
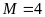 . B.
. B.
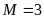 . C.
. C.
 . D.
. D.
 .
.
Câu
30.
Cho biểu thức
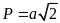 với
với
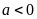 .
Khi đó biểu thức
.
Khi đó biểu thức
 bằng
bằng
A.
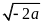 . B.
. B.
 . C.
. C.
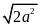 . D.
. D.
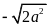 .
.
Câu
31.
Tính
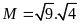 .
.
A.
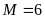 . B.
. B.
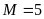 . C.
. C.
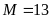 . D.
. D.
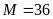 .
.
Câu
32.
Cho
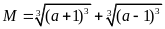 .
Khẳng định nào sau đây đúng?
.
Khẳng định nào sau đây đúng?
A.
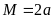 . B.
. B.
 . C.
. C.
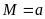 . D.
. D.
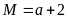 .
.
II. PHẦN TỰ LUẬN
Bài 1. Rút gọn các biểu thức sau
a)
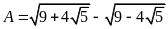 ; b)
; b)
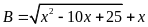 với
với
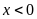 .
.
Bài 2. Tính
a)
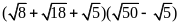 ; b)
; b)
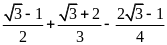 .
.
Bài
3.
Giải phương trình
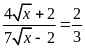 .
.
Bài
4.
Cho biểu thức
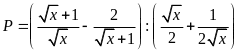 .
.
a)
Rút gọn
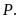
b)
Tính giá trị của
 khi
khi
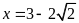 .
.
c)
Tìm
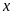 để
để

Bài
5.
Cho biểu thức
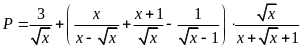 .
.
a)
Rút gọn
 .
.
b)
Tìm các giá trị của
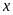 để
để
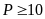 .
.
c)
Tìm các giá trị nguyên của
 để
để
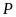 có giá trị nguyên.
có giá trị nguyên.
Bài
6.
[TS10
Hà Tĩnh, 2018-2019]
Rút gọn biểu thức
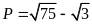 .
.
Bài 7. [TS10 Nghệ An, 2018-2019]
a)
So sánh
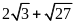 và
và
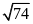 .
.
b)
Chứng minh đẳng thức
 ,
với
,
với
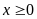 và
và
 .
.
Bài
8.
[TS10
Bắc Giang, 2018-2019] Tính
giá trị của biểu thức
 .
.
Bài
9.
[TS10
Trà Vinh, 2018-2019]
Rút gọn biểu thức

Bài
10.
[TS10
Phú Yên, 2018-2019]
So sánh
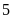 và
và
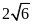 .
.
Bài
11.
[TS10
Quảng Trị, 2018-2019]
Rút gọn biểu thức
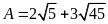 .
.
Bài
12.
[TS10
Hà Nam, 2018-2019]
Cho biểu thức
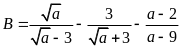 với
với
 .
.
a)
Rút gọn
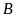 .
.
b)
Tìm các số nguyên
 để
để
 nhận giá trị nguyên.
nhận giá trị nguyên.
Bài 13. [TS10 Điện Biên, 2018-2019] Cho biểu thức

a)
Rút gọn biểu thức
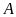 .
.
b)
Tìm giá trị lớn nhất của biểu thức
 .
.
Bài 14. [TS10 Hà Nội, 2018-2019]
Cho
hai biểu thức
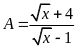 và
và
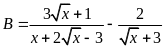 với
với
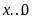 ,
,
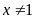 .
.
a)
Tính giá trị của biểu thức
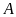 khi
khi
 .
.
b)
Chứng minh
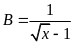 .
.
c)
Tìm tất cả giá trị của
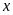 để
để
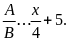
Bài
15.
[TS10
Bình Thuận, 2018-2019]
Rút gọn biểu thức
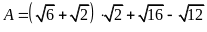 .
.
Bài 16. [TS10 Thái Nguyên, 2018-2019] Không dùng máy tính cầm tay, tính giá trị của biểu thức

Bài
17.
[TS10
Thanh Hóa, 2018-2019]
Cho biểu thức
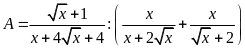 ,
với
,
với
 .
.
a)
Rút gọn biểu thức
 .
.
b)
Tìm tất cả các giá trị của
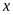 để
để
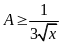 .
.
Bài 18. [TS10 Bắc Kạn, 2018-2019] Rút gọn biểu thức sau
 với
với
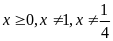 .
.
Bài
19.
[TS10
Đà Nẵng, 2018-2019]
Trục căn thức ở mẫu của biểu thức
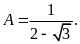
Bài
20.
[TS10
Tiền Giang, 2018-2019]
Tính giá trị của biểu thức
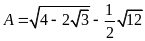 .
.
Bài
21.
[TS10
Đà Nẵng, 2018-2019]
Cho
 Chứng minh
Chứng minh
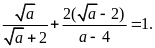
Bài 22. [TS10 Lai Châu, 2018-2019]
Cho
biểu thức
 (với
(với
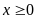 và
và
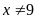 ).
).
a)
Rút gọn biểu thức
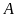 .
.
b)
Tìm giá trị lớn nhất của biểu thức
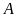 .
.
Bài
23.
[TS10
Lạng Sơn, 2018-2019]
Cho biểu thức
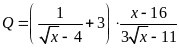 .
.
a)
Tính
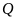 khi
khi
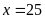 .
.
b)
Rút gọn biểu thức
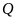 đã cho ở trên.
đã cho ở trên.
Bài 24. [TS10 Sóc Trăng, 2018-2019] Các đẳng thức sau đúng hay sai, giải thích?
a)
 . b)
. b)
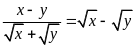 với
với
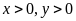 .
.
Bài
25.
[TS10
Đồng Tháp, 2018-2019]
Tính
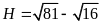 .
.
Bài
26.
[TS10
Đồng Tháp, 2018-2019]
Tìm điều kiện của
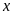 để
để
 có nghĩa.
có nghĩa.
Bài
27.
[TS10
Bắc Kạn, 2018-2019]
Rút gọn biểu thức
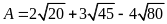 .
.
Bài
28.
[TS10
Hòa Bình, 2018-2019]
Rút gọn:
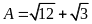 .
.
Bài 29. [TS10 Lạng Sơn, 2018-2019] Tính giá trị của các biểu thức sau
a)
 ; b)
; b)
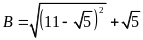 ; c)
; c)
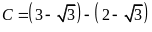 .
.
Bài
30.
[TS10
Cần Thơ, 2018-2019]
Rút gọn biểu thức
 .
.
Bài
31.
[TS10
Ninh Bình, 2018-2019]
Rút gọn biểu thức:
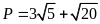 .
.
Bài 32. [TS10 Bình Phước, 2018-2019] Tính giá trị của các biểu thức
a)
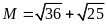 . b)
. b)
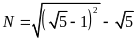 .
.
Bài 33. [TS10 Vĩnh Long, 2018-2019]
a)
Tính giá trị biểu thức
 .
.
b)
Rút gọn biểu thức
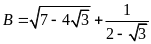 .
.
Bài
34.
[TS10
Hà Nam, 2018-2019]
Rút gọn các biểu thức
 .
.
Bài
35.
[TS10
Hưng Yên, 2018-2019]
Rút gọn biểu thức

Bài 36. [TS10 Lào Cai, 2018-2019] Tính giá trị của các biểu thức sau:
a)
 . b)
. b)
 .
.
Bài 37. [TS10 Bạc Liêu, 2018-2019] Rút gọn biểu thức
a)
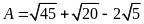 . b)
. b)
 ,
(với
,
(với
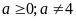 ).
).
Bài
38.
[TS10
Vũng Tàu, 2018-2019] Rút
gọn biểu thức
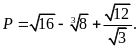
Bài
39.
[TS10
Bình Định, 2018-2019]
Cho biểu thức
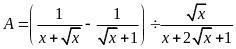 ,
với
,
với
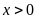 .
.
a)
Rút gọn biểu thức
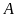 .
.
b)
Tìm các giá trị của
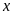 để
để
 .
.
Bài 40. [TS10 Nam Định, 2018-2019]
Cho
biểu thức
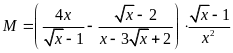 ,
với
,
với
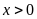 ,
,
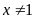 ,
,
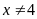 .
.
a)
Rút gọn
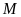 .
.
b)
Tìm
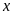 để
để
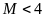 .
.
Bài
41.
[TS10
Bình Phước, 2018-2019] Cho
biểu thức
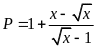 ,
với
,
với
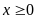 và
và
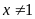 .
.
a)
Rút gọn biểu thức
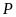 .
.
b)
Tìm các giá trị của
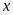 ,
biết
,
biết
 .
.
Bài
42.
[TS10
Thái Bình, 2018-2019]
Cho biểu thức
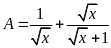 .
.
a)
Tính giá trị biểu thức
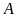 với
với
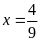 .
.
b)
Tìm điều kiện để biểu thức
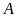 có nghĩa.
có nghĩa.
c)
Tìm
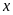 để
để
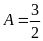 .
.
Bài 43. [TS10 Lào Cai, 2018-2019]
Cho
biểu thức
 với
với
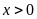 ,
,
 .
.
a)
Rút gọn biểu thức
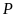 .
.
b)
Tìm
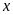 để
để
 .
.
Bài
44.
[TS10
Đắk Lắk, 2018-2019]
Tìm
 biết
biết
 .
.
Bài 45. [TS10 Long An, 2018-2019]
a)
Rút gọn biểu thức

b)
Rút gọn biểu thức
 với
với
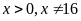 .
.
c)
Giải phương trình
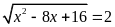 .
.
--- HẾT ---
Ngoài Hướng Dẫn Cách Giải Căn Bậc 3 Và Căn Bậc 2 Chi Tiết [2023] – Toán 9 thì các tài liệu học tập trong chương trình 9 sẽ được cập nhật liên tục và nhanh nhất có thể sau khi kỳ thi diễn ra trên Danh mục Tài Liệu Học Tập nhằm giúp các bạn đọc thuận tiện trong việc nghiên cứu tài liệu. Quý thày cô và các bạn đọc có thể chia sẻ thêm những tài liệu học tập hữu ích đến địa chỉ email của chúng tôi, nhằm xây dựng nên kho đề thi phong phú, đa dạng cho các em học sinh tham khảo và rèn luyện.
Bài tập liên quan đến căn bậc 3 và căn bậc 2 thường yêu cầu bạn tìm nghiệm, tính toán giá trị chính xác của căn, và áp dụng công thức hoặc phương pháp để giải quyết. Tài liệu này sẽ hướng dẫn bạn qua từng bước cụ thể để giải quyết các bài toán thực tế liên quan đến căn bậc 3 và căn bậc 2.
Mỗi phần trong tài liệu được giải thích chi tiết và kèm theo ví dụ minh họa giúp bạn hiểu rõ hơn về cách áp dụng kiến thức vào giải quyết các bài tập. Điều này giúp bạn nắm vững kỹ năng và tự tin hơn khi giải quyết các bài toán liên quan đến căn bậc 3 và căn bậc 2.
Hãy cùng tham gia và khám phá “Hướng Dẫn Cách Giải Căn Bậc 3 Và Căn Bậc 2 Chi Tiết [2023]”. Bằng sự nỗ lực và cố gắng trong việc học tập, bạn sẽ nắm vững kiến thức về căn bậc 3 và căn bậc 2, và có khả năng giải quyết các bài toán phức tạp liên quan đến chúng. Chúc bạn thành công và vui vẻ trong hành trình học tập toán học!
>>> Bài viết có liên quan:







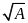 có
nghĩa khi và chỉ khi
có
nghĩa khi và chỉ khi
 .
.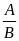 có
nghĩa khi và chỉ khi
có
nghĩa khi và chỉ khi
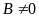 .
.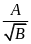 có
nghĩa khi và chỉ khi
có
nghĩa khi và chỉ khi
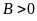 .
. ; b)
; b)
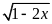 ; c)
; c)
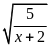 .
.