Phương Pháp Giải Bài 10 Tập Hợp Số Nguyên Tố Toán 6 Chân Trời Sáng Tạo
>>> Mọi người cũng quan tâm:
Phương Pháp Giải Bài 10 Tập Hợp Số Nguyên Tố Toán 6 Chân Trời Sáng Tạo – Toán 6 Chân Trời Sáng Tạo là tài liệu học tập được Trang Tài Liệu biên soạn và sưu tầm từ những nguồn dữ liệu mới nhất hiện nay. Tài liệu này sẽ giúp các em luyện tập, củng cố kiến thức từ đó nâng cao điểm số cho môn học. Ngoài ra, cũng giúp các thầy cô giáo có nguồn tài nguyên phong phú để giảng dạy.
Dưới đây là bản đọc trực tuyến giúp thầy cô và các em học sinh có thể nghiên cứu Online hoặc bạn có thể tải miễn phí với phiên bản word để dễ dàng in ấn cũng như học tập Offline.
§ 10: SỐ NGUYÊN TỐ.HỢP SỐ.
PHÂN TÍCH MỘT SỐ RA THỪA SỐ NGUYÊN TỐ
A. KIẾN THỨC CẦN NHỚ
1.Số nguyên tố.Hợp số
- Số nguyên tố là số tự nhiên lớn hơn 1, chỉ có 2 ước là 1 và chính nó.
- Hợp số là số tự nhiên lớn hơn 1, có nhiều hơn 2 ước
- Chú ý: Số 0 và số 1 không là số nguyên tố, và cũng không là hợp số
Phân tích một số ra thừa số nguyên tố
a.Thế nào là phân tích một số ra thừa số nguyên tố
- Phân tích một số tự nhiên lớn hơn 1 ra thừa số nguyên tố là viết số đó dưới dạng một tích các thừa số nguyên tố
-Chú ý:
+Mọi số tự nhiên lớn hơn 1 đều phân tích được thành tích các thừa số nguyên tố.
+ Mỗi số nguyên tố chỉ có một dạng phân tích ra thừa số nguyên tố là chính số đó.
+Có thể viết gọn dạng phân tích một số ra thừa số nguyên tố bằng cách dùng lũy thừa.
b.Cách phân tích một số ra thừa số nguyên tố.
Ta có thể phân tích một số ra thừa số nguyên tố theo “cột dọc” hoặc “sơ đồ cây”
Chú ý:
- Khi viết kết quả phân tích một số ra thừa số nguyên tố ta thường viết các ước nguyên tố theo thứ tự từ nhỏ đến lớn.
- Dù phân tích một số ra thừa số nguyên tố bằng cách nào thì ta cũng được cùng một kết quả.
B. BÀI TẬP CÓ HƯỚNG DẪN. (MẪU TỰ LUẬN)
DẠNG 1: Xác định số nguyên tố, hợp số
Bài 1. Các số sau là số nguyên tố hay hợp số ?
36; 37; 69; 75; 3311
Hướng dẫn:
Áp dụng dấu hiệu chia hết để xét xem số đó là nguyên tố hay hợp số
Bài 2. Gọi P là tập hơp các số nguyên tố. Điền kí hiệu ∈ , ∉ hoặc ⊂ vào ô trống cho đúng:
![]()
Hướng dẫn:
Áp dụng định nghĩa số nguyên tố, hợp số và dấu hiệu chia hết để xem các số đã cho là số nguyên tố hay hợp số
Bài 3. Tổng (hiệu) sau là số nguyên tố hay hợp số?
a) 3.4.5 + 6.7 ; b) 7.9.11.13 – 2.3.4.7
c) 3.5.7 + 11.13.17 ; d) 16 354 + 67 541
Hướng dẫn:
Áp
dụng tính chất chia hết của một tổng: - Nếu a
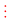 n và b
n và b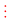 n
thì (a+b)
n
thì (a+b)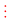 n
n
-Nếu a
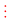 n và b
n và b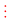 n
thì (a- b)
n
thì (a- b)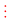 n
n
Bài
4.
Thay
chữ số vào dấu * để được hợp số: 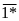 ;
;
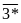
Hướng dẫn:
Tra bảng nguyên tố ta có 11, 13, 17, 19, 31, 37 là các số nguyên tố
DẠNG 2: Phân tích một số ra thừa số nguyên tố
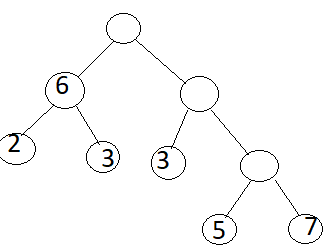
Bài 5. Tìm các số còn thiếu trong các sơ đồ phân tích một số ra thừa số nguyên tố sau:
? 3 35 ? ? 7 1 |
b,
|
Bài 6: Phân tích các số sau ra thừa số nguyên tố: 45, 78, 270, 299.
Hướng dẫn:
Phân tích ra thừa số nguyên tố có thể dùng “ Sơ đồ cây” hoặc “ theo cột dọc”
VD:
Phân tích số 45 bằng cách viết "theo cột dọc"
15 3 5 5 1
|
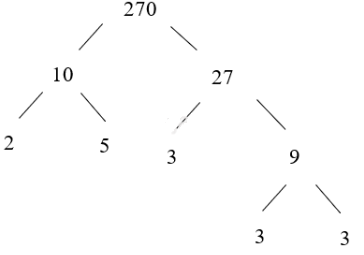
Phân tích số 270 bằng cách viết "Sơ đồ cây": Ta có: 270 = 10 . 27
|
Bài 7. Phân tích các số sau ra thừa số nguyên tố rồi tìm tập hợp các ước của mỗi số:
51; 75; 42; 30
Hướng dẫn:
VD: 51 = 3.17. Vậy Ư(51) = {1, 3, 17, 51}.
DẠNG 3: Vận dụng giải các bài toán có nội dung thực tiễn
Bài 8: Một lớp có 30 học sinh. Cô giáo muốn chia lớp thành các nhóm để thực hiện các dự án học tập nhỏ. Biết rằng, các nhóm đều có số người bằng nhau và có nhiều hơn 1 người trong mỗi nhóm. Hỏi mỗi nhóm có thể có bao nhiêu người?

Hướng dẫn:
Vì “Cô giáo muốn chia lớp 30 học sinh thành các nhóm nên số nhóm là ước của 30” nên tìm ước của 30 bằng cách phân tích 30 thành thừa số nguyên tố. Khi có số nhóm thì sẽ tính được số người trong mỗi nhóm
Bài 9: Bạn Hà đang ở ô tìm đường đến phòng chiếu phim. Biết rằng chỉ có thể đi từ một ô sang ô chung cạnh có chứa số nguyên tố. Em hãy giúp Hà đến được phòng chiếu phim nhé.
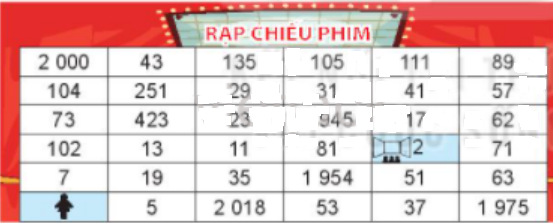
Hướng dẫn:
Với bước đi đầu tiên thì Hà chỉ có thể đi theo 2 cách là: Ô 5 hoặc ô 7 vì cả 2 số đều là số nguyên tố.
Vậy Hà sẽ có thể đi như sau: Hà → 7 → 19 → 13 → 11 → 23 → 29 → 31 → 41 → 17 → 2
Bài 10. Trong nghi lễ thượng cờ lúc 6 giờ sáng và hạ cờ lúc 21 giờ hàng ngày ở Quảng trường Ba Đình, đội tiêu binh có 34 người gồm 1 sĩ quan chỉ huy đứng đầu và 33 chiến sĩ. Hỏi có bao nhiêu cách sắp xếp 33 chiến sĩ thành các hàng, sao cho mỗi hàng có số người như nhau?
Hướng dẫn: Vì xếp 33 chiến sĩ thành các hàng thì số hàng là ước của 33. vậy phải tìm ước của 33
|
|
C. BÀI TẬP TỰ GIẢI CÓ ĐÁP SỐ.
Bài 11. Phân tích các số sau ra thừa số nguyên tố: 70; 115; 300; 432; 145.
Đáp
số :70 = 2.5.7 ; 115 = 5.23
; 300 =
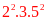 ; 432 =
; 432 =
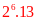 ;
145 = 5.29
;
145 = 5.29
Bài 12. Phân tích các số sau ra thừa số nguyên tố rồi tìm tập hợp các ước của mỗi số:
84 ; 50 ; 65
Đáp số
84
=
![]() .
3 . 7 nên Ư(84) = {1; 2; 3; 4; 6; 7; 12; 14; 21; 28; 42; 84}
.
3 . 7 nên Ư(84) = {1; 2; 3; 4; 6; 7; 12; 14; 21; 28; 42; 84}
50
=
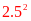 nên
Ư(50)
= {1;2; 10;25;50}
nên
Ư(50)
= {1;2; 10;25;50}
65= 13.5 nên Ư(65) = {1;5;13;65}
Bài 13: An phân tích các số 120; 306; 567 ra thừa số nguyên tố như sau:
120 = 2.3.4.5;
306 = 2.3.51;
567 = 92.7
An làm như trên có đúng không? Hãy sửa lại trong trường hợp An làm không đúng?
Đáp số :An làm như trên là sai vì vế phải còn chứa thừa số không phải là số nguyên tố
Bài 14:Tâm có 21 viên bi. Tâm muốn xếp số bi đó vào các túi sao cho số bi ở các túi đều bằng nhau. Hỏi Tâm có thể xếp 21 viên bi đó vào mấy túi? (kể cả trường hợp xếp vào một túi)

Đáp số:
Tâm có thể sắp xếp 21 viên bi vào 1 túi; 3 túi;7 túi; 21 túi
D. BÀI TẬP TRẮC NGHIỆM
Câu 1. Điền đúng (Đ) hoặc sai (S) vào các ô trống cho mỗi kết luận sau:
Kết luận |
Đ/S |
|
|
|
|
3.Tổng của 2 số nguyên tố lớn hơn 2 luôn là một hợp số |
|
4.Tổng của 2 hợp số là hợp số |
|
Đáp số: 1-S; 2-Đ; 3-Đ; 4-S
Câu 2: Phân tích số 18 ra thừa số nguyên tố
A. 18 = 18.1
B.. 18 = 10 + 8
C. 18 = 2.32
D.. 18 = 6 + 6 + 6
Câu 3: Cho a = 22.7, hãy viết tập hợp tất cả các ước của a
A. Ư(a) = {4; 7}
B.. Ư(a) = {1; 4; 7}
C. Ư(a) = {1; 2; 4; 7; 28}
D. Ư(a) = {1; 2; 4; 7; 14; 28}
Đáp số: D
Câu 4: Kết quả phân tích số 420 ra thừa số nguyên tố là:
22.3.7
22.5.7
22.3.5.7
2.3.5.7
Đáp số: C
Câu 5: An hỏi Bình số học sinh khối 6 của trường mình là bao nhiêu học sinh. Bình cho biết số học sinh khối 6 của trường mình là tích của bình phương số nguyên tố nhỏ nhất với ba số nguyên tố tiếp theo .Em hãy tìm số học sinh khối 6 của trường?
400 (học sinh)
410 (học sinh)
420 (học sinh)
430 ( học sinh)
Đáp số: C
Ngoài Phương Pháp Giải Bài 10 Tập Hợp Số Nguyên Tố Toán 6 Chân Trời Sáng Tạo – Toán 6 Chân Trời Sáng Tạo thì các tài liệu học tập trong chương trình 6 sẽ được cập nhật liên tục và nhanh nhất có thể sau khi kỳ thi diễn ra trên Danh mục Tài Liệu Học Tập nhằm giúp các bạn đọc thuận tiện trong việc nghiên cứu tài liệu. Quý thày cô và các bạn đọc có thể chia sẻ thêm những tài liệu học tập hữu ích đến địa chỉ email của chúng tôi, nhằm xây dựng nên kho đề thi phong phú, đa dạng cho các em học sinh tham khảo và rèn luyện.
Phương Pháp Giải Bài 10 Tập Hợp Số Nguyên Tố là một phần trong sách giải bài tập Toán lớp 6 theo chương trình sách Chân Trời Sáng Tạo (CTST). Bài tập này tập trung vào khái niệm về tập hợp và số nguyên tố.
Trong bài tập này, học sinh sẽ được yêu cầu giải các bài toán liên quan đến tập hợp và số nguyên tố. Họ sẽ áp dụng phương pháp và quy tắc để phân tích và tìm ra các số nguyên tố trong các tập hợp số.
Bài tập giúp học sinh rèn kỹ năng phân tích và phân loại số nguyên tố. Họ sẽ được thực hành áp dụng quy tắc kiểm tra số nguyên tố, tìm các số nguyên tố trong các tập hợp số đã cho và tìm cách biểu diễn tập hợp các số nguyên tố theo công thức hoặc thuật toán.
Phương Pháp Giải Bài 10 Tập Hợp Số Nguyên Tố trong sách CTST cung cấp các phương pháp giải chi tiết và các bước thực hiện để học sinh hiểu và áp dụng vào việc giải quyết các bài toán liên quan đến tập hợp và số nguyên tố. Nó là một nguồn tài liệu hữu ích cho giáo viên và học sinh lớp 6 trong quá trình học và ôn tập môn Toán, giúp họ nắm vững và làm chủ các khái niệm và kỹ năng liên quan đến tập hợp và số nguyên tố.
>>> Bài viết có liên quan