Ôn Thi HSG Toán 6: Các Bài Toán Nâng Cao Lớp 6 Về Lũy Thừa Kèm Giải
>>> Mọi người cũng quan tâm:
Ôn Thi HSG Toán 6: Các Bài Toán Nâng Cao Lớp 6 Về Lũy Thừa Kèm Giải – Toán 6 là tài liệu học tập được Trang Tài Liệu biên soạn và sưu tầm từ những nguồn dữ liệu mới nhất hiện nay. Tài liệu này sẽ giúp các em luyện tập, củng cố kiến thức từ đó nâng cao điểm số cho môn học. Ngoài ra, cũng giúp các thầy cô giáo có nguồn tài nguyên phong phú để giảng dạy.
Dưới đây là bản đọc trực tuyến giúp thầy cô và các em học sinh có thể nghiên cứu Online hoặc bạn có thể tải miễn phí với phiên bản word để dễ dàng in ấn cũng như học tập Offline.
ĐS6.CHUYÊN ĐỀ 2-LŨY THỪA VỚI SỐ MŨ TỰ NHIÊN
CHỦ ĐỀ 4: PHƯƠNG PHÁP BIẾN ĐỔI TƯƠNG ĐƯƠNG ĐỂ TÌM THÀNH PHẦN CHƯA BIẾT CỦA LŨY THỪA
PHẦN I. TÓM TẮT LÝ THUYẾT
1.
Lũy thừa bậc
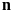 của số
của số
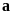 là
tích của
là
tích của
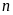 thừa số bằng nhau, mỗi thừa số bằng
thừa số bằng nhau, mỗi thừa số bằng

n thừa số
a
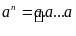
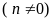 .
.
 gọi là cơ số,
gọi là cơ số,
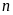 gọi là số mũ.
gọi là số mũ.
Chú ý:
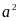 còn
được gọi là
còn
được gọi là
 bình phương (hay bình phương của
bình phương (hay bình phương của
 ).
).
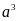 còn
được gọi là
còn
được gọi là
 lập
phương (hay lập phương của
lập
phương (hay lập phương của
 ).
).
Quy
ước:
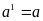
2.
Nhân
hai luỹ thừa cùng cơ số
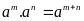
3.
Chia
hai luỹ thừa cùng cơ số

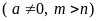
Quy
ước
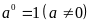
4.
Luỹ
thừa của luỹ thừa
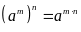
5.
Luỹ thừa một
tích
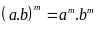
6.
Một số luỹ thừa của
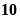 :
:
-
Một nghìn: 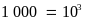
-
Một vạn: 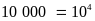
-
Một triệu: 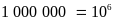
-
Một tỉ: 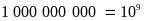
Tổng
quát: nếu
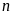 là số tự nhiên khác
là số tự nhiên khác
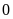 thì:
thì:
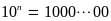 (có
(có
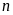 chữ số
chữ số
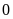 )
)
PHẦN II. CÁC DẠNG BÀI
Dạng 1: Tìm số mũ, thành phần trong số mũ của lũy thừa
I. Phương pháp giải
- Đưa hai luỹ thừa về cùng cơ số
- Sử dụng tính chất
Nếu
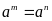 thì
thì

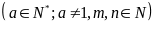
II. Bài toán
Bài
1: Tìm
số tự nhiên
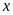 thoả mãn
thoả mãn
a)
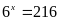
b)
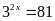
c)
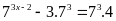
d)
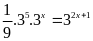
Lời giải:
a)
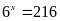
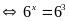
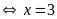
Vậy
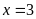
b)
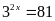

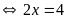
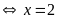
Vậy
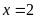 .
.
c)
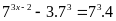
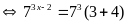
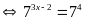
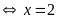
Vậy
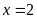 .
.
d)
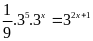

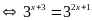
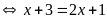
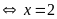
Vậy
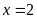 .
.
Bài
2:
Tìm
số tự nhiên
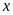 thoả mãn
thoả mãn
a)
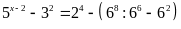
b)

Lời giải:
a)
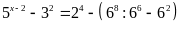
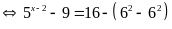
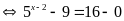
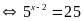
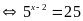
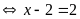
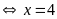
Vậy
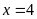 .
.
b)

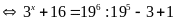
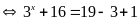

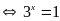
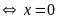
Vậy
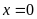
Bài
3: Tìm
số tự nhiên
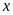 thoả mãn
thoả mãn
a)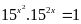
b)
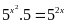
c)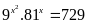
d)
Lời giải:
a)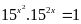

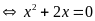
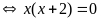
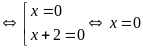
Vậy
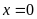
b)
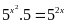
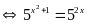
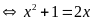

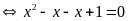
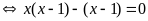
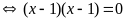

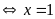
Vậy
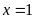
c)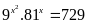
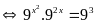
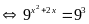
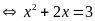
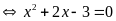
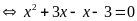
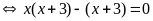
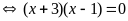
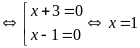
Vậy
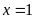
d)

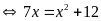
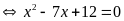
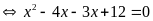
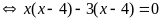
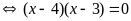
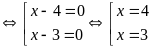
Vậy
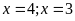
Bài
4: Tìm
số tự nhiên
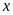 thoả mãn
thoả mãn
a)
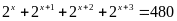
b)
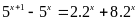
c)
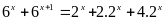
d)
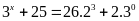
Lời giải:
a)
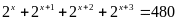
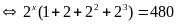
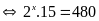
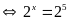
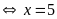
Vậy
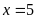
b)

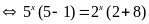
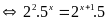
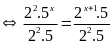
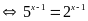
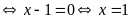
Vậy
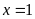
c)
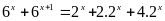
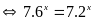
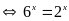
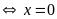
Vậy
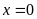
d)

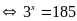
Vì
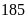 không viết được dưới dạng luỹ thừa của
không viết được dưới dạng luỹ thừa của
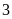 nên không có sô tự nhiên
nên không có sô tự nhiên
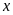 nào thoả mãn
nào thoả mãn
Vậy
không có giá trị nào của
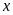 thoả mãn
thoả mãn
Bài 5: Tìm số tự nhiên x, biết
a)

b)
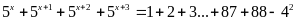
Lời giải:
a)
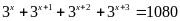
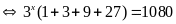
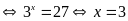
Vậy
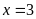 là giá trị cần tìm.
là giá trị cần tìm.
b)
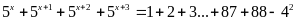
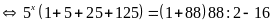
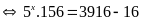
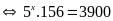
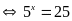
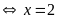
Vậy
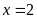 .
.
Bài
6:
Tìm
hai số tự nhiên
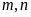 biết
biết
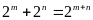
Lời giải:

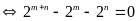
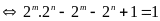
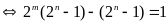
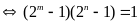
Vì
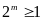 và
và
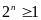 nên
nên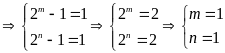
Vậy
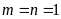
Bài
7:
Có
bao nhiêu số tự nhiên
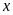 thoả mãn
thoả mãn
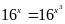
Lời giải:
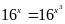
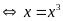

Vậy
có
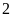 số tự nhiên
số tự nhiên
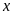 thoả mãn là
thoả mãn là
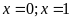
Bài 8:
a)
Cho
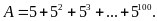 Tìm số tự nhiên
Tìm số tự nhiên
 biết
biết
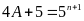
b)
Cho
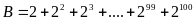 .
Tìm số tự nhiên n biết
.
Tìm số tự nhiên n biết

Lời giải:
a)Ta có
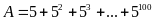
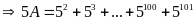
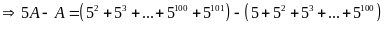
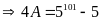
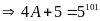
Theo đầu bài ta có:
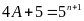
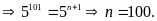
Vậy
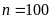 .
.
b) Ta có :
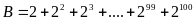
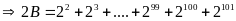
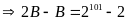
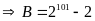
Mà
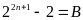
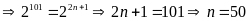
Vậy
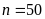
Bài 9:
a)
Cho
 .
Tìm số tự nhiên
.
Tìm số tự nhiên
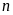 biết rằng
biết rằng
 .
.
b)
Cho
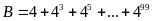 .
Tìm số tự nhiên
.
Tìm số tự nhiên
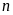 biết rằng
biết rằng
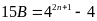 .
.
Lời giải
a)

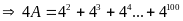
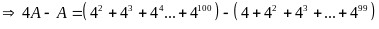
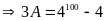
Có

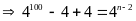
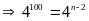
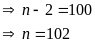
Vậy
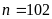 .
.
a)
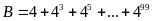
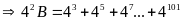

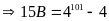
Có
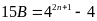
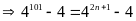
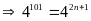
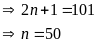
Vậy
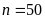 .
.
Bài
10:
Tìm
số tự nhiên
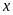 biết:
biết:
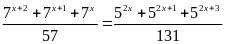
Lời giải:
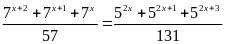
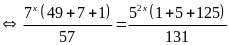
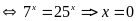
Vậy
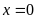
Bài
11:
Tìm số tự nhiên
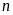 biết:
biết:
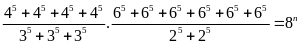
Lời giải:
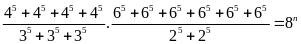
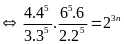
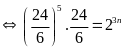
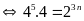
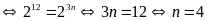
Vậy
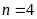
Bài
12:
Tìm
hai số tự nhiên
 thoả mãn
thoả mãn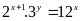
Lời giải:
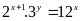
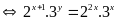
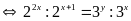
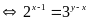
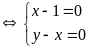
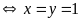
Vậy
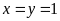
Bài 13: Tìm x biết:
a)
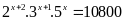
b)
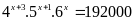
Lời giải:
a)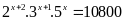

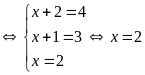
Vậy
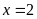 .
.
b)
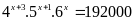
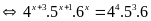
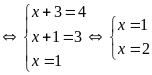
Vậy
không tìm được số tự nhiên
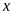 thoả mãn bài toán
thoả mãn bài toán
Bài
14:
Tìm
 biết
biết
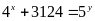
Lời giải:
Nếu
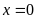 thì
thì
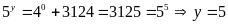
Nếu
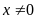 thì
vế trái là số chẵn, vế phải là số lẻ với mọi
thì
vế trái là số chẵn, vế phải là số lẻ với mọi
 (
vô lý)
(
vô lý)
Vậy
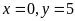
Dạng 2: Tìm cơ số, thành phần của cơ số trong lũy thừa.
I. Phương pháp giải
- Đưa về hai lũy thừa cùng số mũ
- Sử dụng tính chất
+)
Ta có
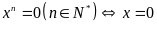
+)
Ta có

II. Bài toán
Bài 1: Tìm số tự nhiên x, biết:
a)
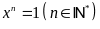
b)
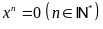
c)
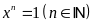
Lời giải:
a)
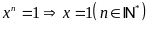
b)
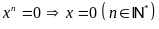
c)
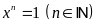
Nếu
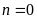 thì
thì
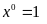
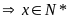
Nếu
 thì
thì
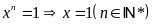 .
.
Bài 2: Tìm số tự nhiên x, biết:
a)
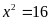 b)
b)
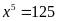 c)
c)
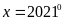
d)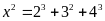 e)
e)
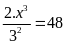
Lời giải:
a)
Ta có
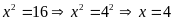
b)
Ta có
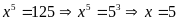
c)
Ta có
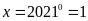
d)
Ta có
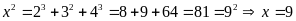
e)
Ta
có
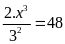
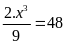
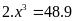

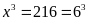

Vậy

Bài 3: Tìm số tự nhiên x, biết:
a)
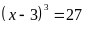
b)
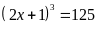
c)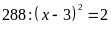
d)

Lời giải:
a)
Ta có
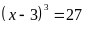
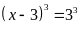
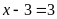
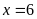
Vậy

b)
Ta có
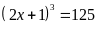
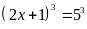
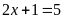
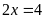
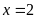
Vậy
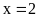
c)Ta
có
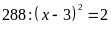
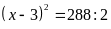
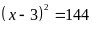
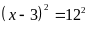
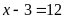
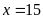
Vậy
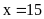
d)
Ta có


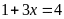
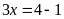
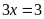
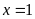
Vậy
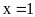
Bài 4: Tìm số tự nhiên x, biết:
a)
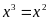
b)
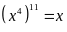
c)
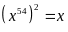
Lời giải:
a)
Ta có
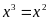 suy
ra
suy
ra
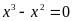

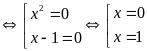
Vậy
 hoặc
hoặc
 .
.
b)
Ta có
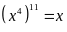 suy
ra
suy
ra
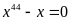
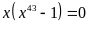
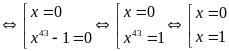
Vậy
 hoặc
hoặc
 .
.
c)
Ta có
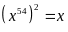 suy
ra
suy
ra

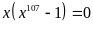
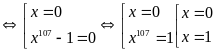
Vậy
 hoặc
hoặc
 .
.
Bài 5: Tìm số tự nhiên x, biết:
a)

b)
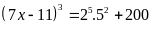
c)
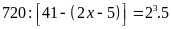
Lời giải:
a)
Ta có

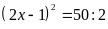
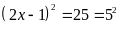
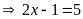
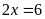
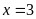
Vậy
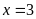
b)
Ta có:
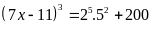
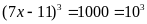
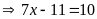
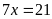

Vậy
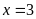
c)
Ta có:
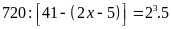
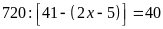
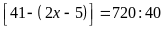
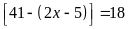
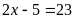
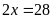
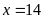
Vậy
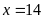 .
.
Bài 6: Tìm số tự nhiên x, biết:
a)
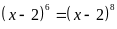
b)
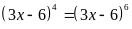
Lời giải:
a)
Ta có:
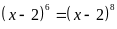
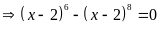
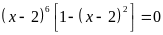
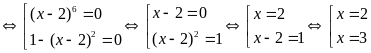
Vậy
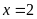 hoặc
hoặc
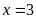 .
.
b)
Ta có:
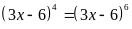
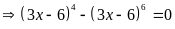
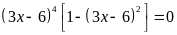
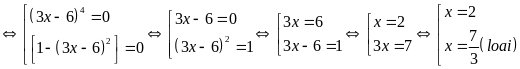
Vậy
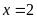 .
.
Bài
7: Tìm
số tự nhiên x, biết:

Lời giải:
Ta
có:

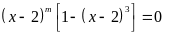
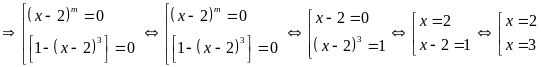
Vậy
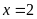 hoặc
hoặc
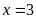 .
.
Bài
8: Tìm
số tự nhiên x, biết
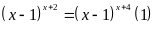
Lời giải:
Đặt
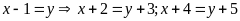
Ta
có
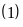 trở
thành
trở
thành
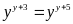
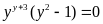
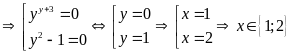
Vậy
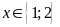 là giá trị cần tìm.
là giá trị cần tìm.
Bài
9:
Tìm các số tự nhiên x và y biết rằng:
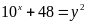
Lời giải:
Nếu
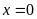 ta
có
ta
có
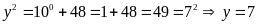 .
.
Nếu
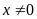 ta
có
ta
có
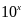 có chữ số tận cùng là 0, do đó
có chữ số tận cùng là 0, do đó
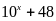 có chữ số tận cùng là 8 mà
có chữ số tận cùng là 8 mà
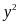 không
thể có chữ số tận cùng là 8.
không
thể có chữ số tận cùng là 8.
Vậy
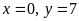 .
.
Bài 10: Tìm số tự nhiên x, biết:
a)

b)
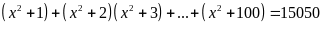
Lời giải:
a)
Ta có:
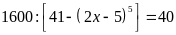
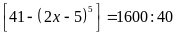
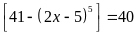
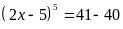
`
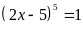

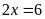
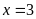
Vậy
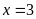 .
.
b)
Ta có:
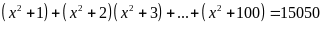

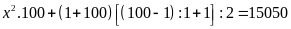
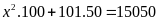

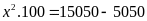
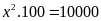
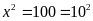
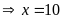
Vậy
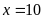 .
.
Bài 11: Tìm số tự nhiên x, biết:
a)
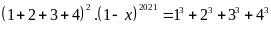
b)
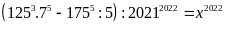
Lời giải:
a)
Ta có:
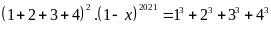
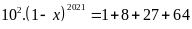
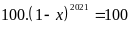
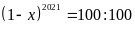
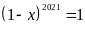
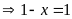
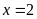
Vậy
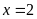 .
.
b)
Ta có:
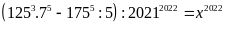
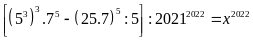
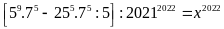
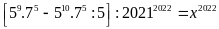
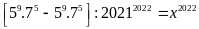
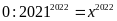
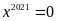
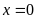
Vậy
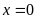 .
.
Bài
12.
Tìm
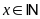 ,
biết:
,
biết:
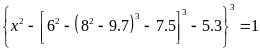
Lời giải:
Ta
có: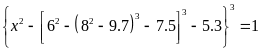
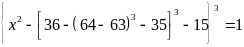
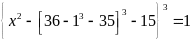
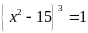
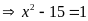
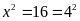
 .
.
Vậy
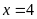 .
.
Bài
13.
Tìm
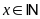 ,
biết:
,
biết:

Lời giải:
Ta
có
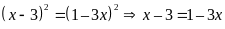

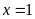
Vậy
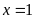
Bài
14.
Tìm số tự nhiên
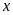 và
và
 ,
biết:
,
biết:
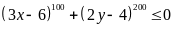
Lời giải:
Ta
có
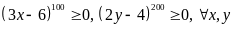
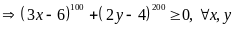
Mà
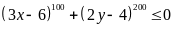
nên
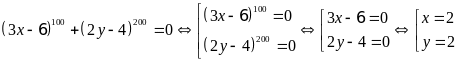
Vậy
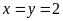 .
.
Bài
15.
Tìm số tự nhiên a và b, biết:
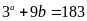
Lời giải:
Nếu
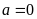 ta
có
ta
có
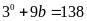
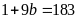
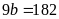
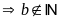
Nếu
 ta
có
ta
có
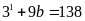
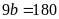

Nếu
 ta
có
ta
có
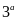 chia hết cho 9,
chia hết cho 9,
 chia hết cho 9
chia hết cho 9 chia
hết cho 9 nhưng 183 không chia hết cho 9.
chia
hết cho 9 nhưng 183 không chia hết cho 9.
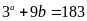 Vô
lý.
Vô
lý.
Vậy
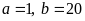 .
.
Bài
16.
Tìm số tự nhiên a và b, biết:
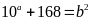
Lời giải:
Nếu
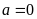 ta
có
ta
có
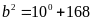
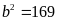
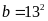
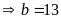
Nếu
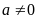 ta
có
ta
có
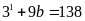
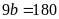

Nếu
 ta
có
ta
có
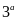 chia hết cho 9,
chia hết cho 9,
 chia hết cho 9
chia hết cho 9 chia
hết cho 9 nhưng 183 không chia hết cho 9.
chia
hết cho 9 nhưng 183 không chia hết cho 9.
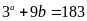 Vô
lý.
Vô
lý.
Vậy
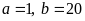 .
.
Bài
17.
Tổng bình phương của ba số tự nhiên là 2596. Biết rằng
tỉ số giữa số thứ nhất và số thứ hai là
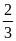 ,
giữa số thứ hai và số thứ ba là
,
giữa số thứ hai và số thứ ba là
 .
Tìm ba số đó.
.
Tìm ba số đó.
Lời giải:
Gọi
a, b, c là ba số tự nhiên phải tìm, ta có:
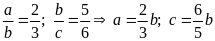
Có
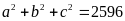 nên
nên
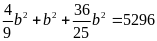
Hay
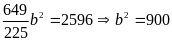
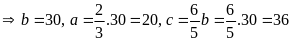
Vậy
ba số cần tìm lần lượt là 20, 30, 36.
Bài
18.
Tìm số tự nhiên
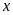 và
và
 ,
biết:
,
biết: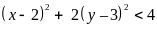
Ta
có
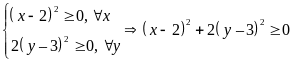
Mà
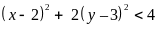
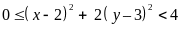 mà
mà
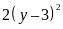 là số chẵn nên ta có các trường hợp:
là số chẵn nên ta có các trường hợp:
Xét trường hợp 1.
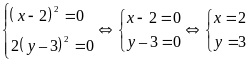
Xét trường hợp 2.
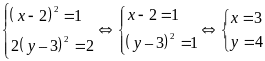
Vậy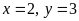 hoặc
hoặc
 .
.
PHẦN III. BÀI TOÁN THƯỜNG GẶP TRONG ĐỀ HSG. ( Khoảng 15 bài )
Bài 1: ĐỀ THI HUYỆN HOA LƯ
Tìm
x biết:
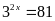
Lời giải:
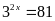

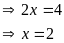
Bài 2: ĐỀ THI HUYỆN PHÙ CÁT
Tìm
số tự nhiên
 ,
biết:
,
biết:
a)
b)
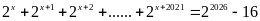
Lời giải:
a)
Ta có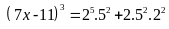
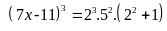
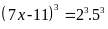
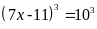
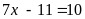
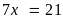
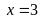
Vậy
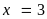
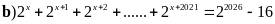
Đặt
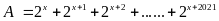
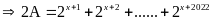
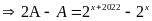
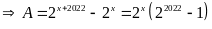
Từ (1):

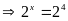
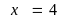
Vậy
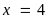
Bài 3: ĐỀ THI HUYỆN TP NINH BÌNH
Tìm các số nguyên x biết:
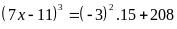
Lời giải:
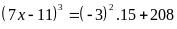
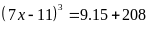
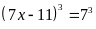

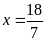
Bài 4: ĐỀ THI HUYỆN TIÊN DU
Tìm số tự nhiên x biết:
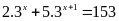
Lời giải:
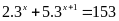
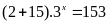

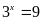
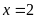
Vậy
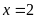
Bài 5: ĐỀ THI HUYỆN CHƯ SÊ
Tìm
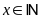 ,
biết:
,
biết:
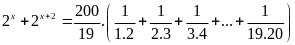
Lời giải:
Ta
có:
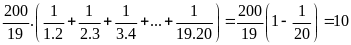
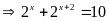
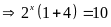
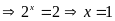
Bài 6: ĐỀ THI HƯNG HÀ
Tìm số tự nhiên x biết:
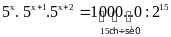 .
.
Lời giải:
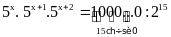
53x + 3 = 1015 : 215
53x + 3 = 515
Suy ra: 3x + 3 = 15
3x = 12
x = 4
Vậy x = 4
Bài 7: ĐỀ THI HUYỆN CHƯƠNG MỸ
Tìm
số nguyên x thỏa mãn:
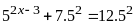
Lời giải:
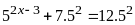
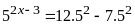
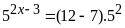
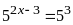
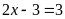
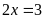
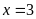
Vậy
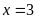
Bài 8: ĐỀ THI HUYỆN KIẾN XƯƠNG
Tìm
x biết:

Lời giải:
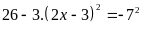
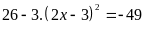
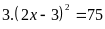
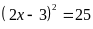
 hoặc
hoặc
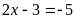
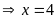 hoặc
hoặc
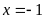
Vậy
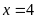 hoặc
hoặc
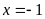
Bài 9: ĐỀ THI KỲ ANH
Tìm
 biết:
biết:
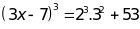
Lời giải:
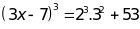
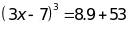

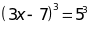


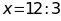
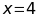
Bài 10: ĐỀ THI HUYỆN THANH TRÌ
Tìm
số tự nhiên
 ,
biết:
,
biết:
a)
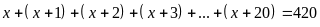 .
.
b)
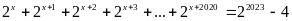 .
.
Lời giải
a)
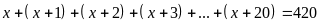
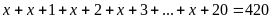
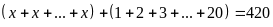

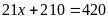
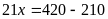
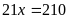
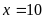
Vậy
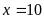 .
.
b)
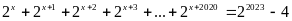 .
.
 (1)
(1)
Đặt
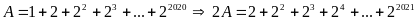
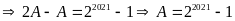
Từ
(1)
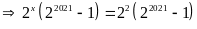
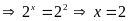
Vậy
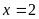 .
.
Bài 11: ĐỀ THI YÊN ĐỊNH
Tìm
 biết
biết
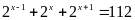
Lời giải
Ta
có:
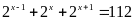
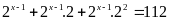
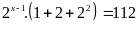
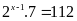
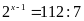
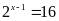
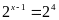

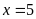
Bài 12: ĐỀ THI THANH BA
Cho
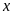 ,
,
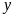 là các số tự nhiên thỏa mãn các hệ thức
là các số tự nhiên thỏa mãn các hệ thức
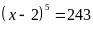 ;
;
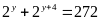 .
Khẳng định nào sau đây là đúng?
.
Khẳng định nào sau đây là đúng?
A.
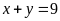 .
B.
.
B.
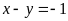 .
C.
.
C.
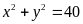 .
D.
.
D.
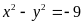 .
.
Lời giải
Ta
có

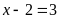

Ta
có
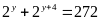
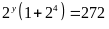
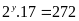
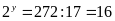
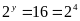

Vậy
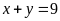
Bài 13. ĐỀ THI THỊ XÃ HOÀI NHƠN
Cho
 .
Tìm
.
Tìm
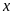 để
để
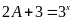
Lời giải

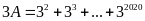
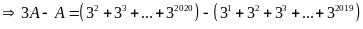
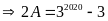
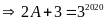
Mà
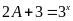
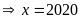
Vậy
 thì
thì
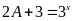
Bài 14. ĐỀ THI KIẾN XƯƠNG
Tìm
x biết:
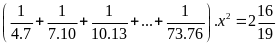
Lời giải
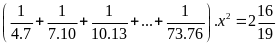
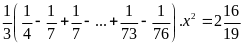
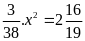
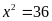
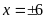
Vậy
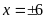
Bài 14. ĐỀ THI HUYỆN ĐÔNG HƯNG
Tìm x biết:
a)
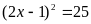 b)
b)
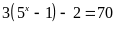
Lời giải
a)
Ta
có: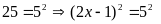 hoặc
hoặc
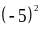
Trường
hợp 1: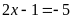
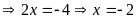
Trường
hợp 2:
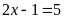
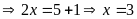
Vậy
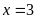 hoặc
hoặc
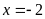
b,
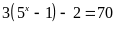
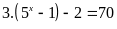
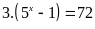
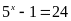
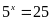
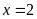
Vậy
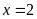
Bài 15. ĐỀ THI HUYỆN HƯNG HÀ
Tìm
số tự nhiên
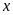 biết:
biết:
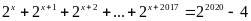 .
.
Lời giải
Tìm
số tự nhiên
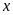 biết:
biết:
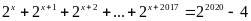 .
.
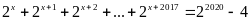
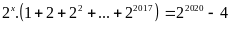

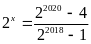
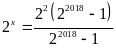
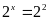
Vậy
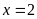 .
.
Ngoài Ôn Thi HSG Toán 6: Các Bài Toán Nâng Cao Lớp 6 Về Lũy Thừa Kèm Giải – Toán 6 thì các tài liệu học tập trong chương trình 6 sẽ được cập nhật liên tục và nhanh nhất có thể sau khi kỳ thi diễn ra trên Danh mục Tài Liệu Học Tập nhằm giúp các bạn đọc thuận tiện trong việc nghiên cứu tài liệu. Quý thày cô và các bạn đọc có thể chia sẻ thêm những tài liệu học tập hữu ích đến địa chỉ email của chúng tôi, nhằm xây dựng nên kho đề thi phong phú, đa dạng cho các em học sinh tham khảo và rèn luyện.
Ôn Thi HSG Toán 6 với chủ đề “Các bài toán nâng cao lớp 6 về lũy thừa” là một tài liệu ôn tập quan trọng giúp học sinh lớp 6 nắm vững kiến thức và kỹ năng giải các bài toán liên quan đến lũy thừa.
Trong chủ đề này, học sinh sẽ được làm quen với các bài toán nâng cao về lũy thừa, yêu cầu sử dụng kiến thức về tính chất và quy tắc của lũy thừa. Các bài toán này có tính chất ứng dụng cao và giúp học sinh rèn kỹ năng vận dụng kiến thức vào việc giải quyết các tình huống thực tế.
Tài liệu ôn thi HSG Toán 6 với chủ đề “Các bài toán nâng cao lớp 6 về lũy thừa” đi kèm với một loạt các bài toán thú vị và thử thách, từ những bài toán đơn giản đến những bài toán phức tạp hơn. Mỗi bài toán được giải thích chi tiết và cung cấp lời giải chi tiết, giúp học sinh hiểu rõ cách giải và áp dụng kiến thức vào thực tế.
Qua việc ôn tập các bài toán nâng cao về lũy thừa, học sinh sẽ phát triển khả năng tư duy logic, tính sáng tạo và kỹ năng giải quyết vấn đề. Đồng thời, tài liệu ôn thi cũng giúp học sinh làm quen với cấu trúc và định dạng của các câu hỏi trắc nghiệm và tự luận, chuẩn bị tốt cho các kỳ thi và cuộc thi HSG Toán.
>>> Bài viết có liên quan:






