Giáo Án Bồi Dưỡng HSG Toán Chủ Đề: Hình Chữ Nhật Có Lời Giải
>>> Mọi người cũng quan tâm:
Giáo Án Bồi Dưỡng HSG Toán Chủ Đề: Hình Chữ Nhật Có Lời Giải – Toán 6 là tài liệu học tập được Trang Tài Liệu biên soạn và sưu tầm từ những nguồn dữ liệu mới nhất hiện nay. Tài liệu này sẽ giúp các em luyện tập, củng cố kiến thức từ đó nâng cao điểm số cho môn học. Ngoài ra, cũng giúp các thầy cô giáo có nguồn tài nguyên phong phú để giảng dạy.
Dưới đây là bản đọc trực tuyến giúp thầy cô và các em học sinh có thể nghiên cứu Online hoặc bạn có thể tải miễn phí với phiên bản word để dễ dàng in ấn cũng như học tập Offline.
CHUYÊN ĐỀ 1 – MỘT SỐ HÌNH PHẲNG TRONG THỰC TIỄN
PHẦN I. TÓM TẮT LÝ THUYẾT
1. Một số tính chất của hình chữ nhật
Hình
chữ nhật
 có:
có:
*
Hai cạnh đối bằng nhau:
*
Hai cạnh đối
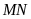 và
và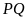 song song với nhau;
song song với nhau;
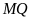 và
và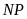 song song với nhau.
song song với nhau.
*
Hai đường chéo bằng nhau:
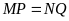 .
.
*
Bốn góc ở các đỉnh
 đều
là góc vuông.
đều
là góc vuông.
2. Công thức tính chu vi, diện tích của hình chữ nhật
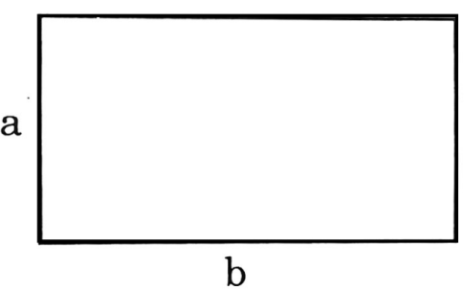
Hình
chữ nhật có chiều dài là
 và chiều rộng là
và chiều rộng là
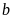 ,
ta có:
,
ta có:
*
Chu vi hình chữ nhật:
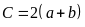
*
Diện tích hình chữ nhật:
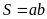
Chú ý:
*
Nếu chiều dài tăng
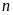 lần, chiều rộng không đổi thì diện tích hình chữ
nhật tăng lên
lần, chiều rộng không đổi thì diện tích hình chữ
nhật tăng lên
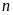 lần.
lần.
*
Nếu chiều rộng tăng lên
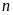 lần, chiều dài không đổi thì diện tích hình chữ nhật
tăng lên
lần, chiều dài không đổi thì diện tích hình chữ nhật
tăng lên
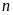 lần.
lần.
*
Nếu chiều dài và chiều rộng tăng lên
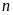 lần thì diện tích hình chữ nhật tăng
lần thì diện tích hình chữ nhật tăng
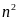 lần.
lần.
*
Nếu một chiều tăng
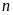 lần, chiều kia giảm
lần, chiều kia giảm
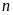 lần thì diện tích hình chữ nhật không đổi.
lần thì diện tích hình chữ nhật không đổi.
*
Nếu chiều dài của hình chữ nhật tăng thêm
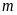 (đvđd), chiều rộng không đổi thì chu vi tăng thêm
(đvđd), chiều rộng không đổi thì chu vi tăng thêm
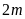 (đvđd).
(đvđd).
*
Nếu chiều rộng của hình chữ nhật tăng thêm
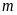 (đvđd), chiều dài không đổi thì chu vi tăng thêm
(đvđd), chiều dài không đổi thì chu vi tăng thêm
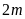 (đvđd).
(đvđd).
*
Nếu chiều rộng của hình chữ nhật tăng thêm
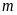 (đvđd), chiều dài giảm đi
(đvđd), chiều dài giảm đi
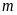 (đvđd) thì chu vi không đổi.
(đvđd) thì chu vi không đổi.
*
Nếu chiều dài của hình chữ nhật tăng thêm
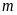 (đvđd), chiều rộng tăng thêm
(đvđd), chiều rộng tăng thêm
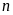 (đvđd) thì chu vi tăng thêm
(đvđd) thì chu vi tăng thêm
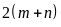 (đvđd).
(đvđd).
PHẦN II. CÁC DẠNG BÀI
Dạng 1: Các bài toán về chu vi hình chữ nhật.
I. Phương pháp giải
* HS nắm chắc công thức chu vi, các tính chất về cạnh, đường chéo của hình chữ nhật.
* HS phân tích kĩ đề bài để tìm mối quan hệ giữa các yếu tố đã cho và yếu tố cần tìm trong đề.
II. Bài toán
Bài
1:
Một
miếng bìa hình chữ nhật có chu vi
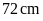 .
Người ta cắt bỏ đi
.
Người ta cắt bỏ đi
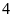 hình vuông bằng nhau ở
hình vuông bằng nhau ở
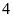 góc của hình chữ nhật.
góc của hình chữ nhật.
a) Tìm chu vi miếng bìa còn lại.
b)
Nếu phần chiều dài còn lại của miếng bìa hơn phần
còn lại của chiều rộng miếng bìa là
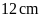 thì độ dài các cạnh của miếng bìa hình chữ nhật ban
đầu là bao nhiêu xăng-ti-mét?
thì độ dài các cạnh của miếng bìa hình chữ nhật ban
đầu là bao nhiêu xăng-ti-mét?
Lời giải:
a)

Từ
hình vẽ ta thấy chu vình của miếng bìa sau khi cắt vẫn
bằng chu vi hình chữ nhật ban đầu. Vậy chu miếng bìa
còn lại là
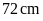
b)
Gọi chiều dài, rộng miếng bìa ban đầu lần lượt là
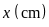 ,
,
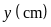 ,
cạnh hình vuông bị cắt đi là
,
cạnh hình vuông bị cắt đi là
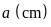
Vì
miếng bìa chữ nhật có chu vi
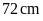 nên
nên
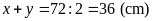
Chiều
dài còn lại của miếng bìa là
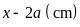
Chiều
rộng còn lại của miếng bìa là
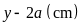
Vì
phần chiều dài còn lại của miếng bìa hơn phần còn
lại của chiều rộng miếng bìa là
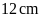 nên
nên
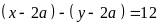 hay
hay
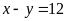 mà
mà
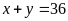
Suy
ra
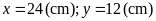 .
Vậy các cạnh của miếng bìa là
.
Vậy các cạnh của miếng bìa là
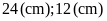
Bài
2: Một
đám đất hình chữ nhật có chiều dài và chiều rộng
là các số tự nhiên. Chiều dài gấp
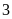 lần chiều rộng. Biết hình chữ nhật có diện tích từ
lần chiều rộng. Biết hình chữ nhật có diện tích từ
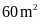 đến
đến
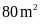 .
Tính chu vi đám đất.
.
Tính chu vi đám đất.
Lời giải:
Gọi
chiều rộng đám đất hình chữ nhật là
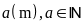
Vì
dài gấp
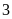 lần chiều rộng nên chiều dài là
lần chiều rộng nên chiều dài là
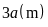
Diện
tích đám đất hình chữ nhật là
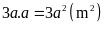
Vì
đám đất hình chữ nhật có diện tích từ
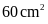 đến
đến
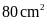 nên
nên
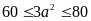
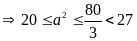
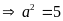 hay
hay
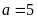
Chu
vi đám đất là
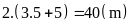
Bài
3:
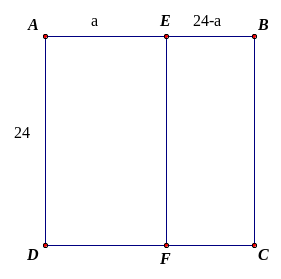
Cho
hình chữ nhật
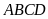 có chu vi
có chu vi
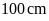 (
(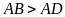 ).
Lấy điểm
).
Lấy điểm
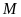 trên cạnh
trên cạnh
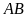 ,
điểm
,
điểm
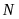 trên cạnh
trên cạnh
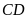 sao cho
sao cho
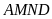 là
hình vuông còn
là
hình vuông còn
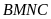 là hình chữ nhật có chu vi
là hình chữ nhật có chu vi
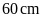 .
.
a)
Tính độ dài các cạnh của hình chữ nhật
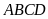
b)
Tính diện tích tam giác
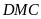
Lời giải:
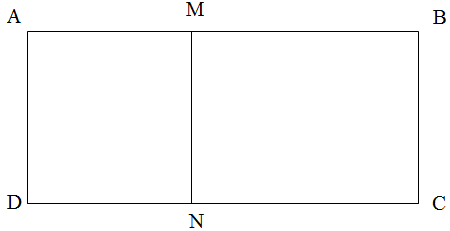
a)
Nửa chu vi hình chữ nhật
 là
là
Nửa
chu vi hình chữ nhật
 là
là
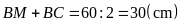
Suy
ra
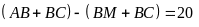 hay
hay
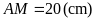
Chiều
rộng hình chữ nhật
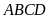 là
là
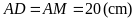 (do
(do
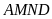 là
hình vuông)
là
hình vuông)
Chiều
dài hình chữ nhật
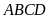 là
là
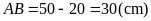
b)
Ta có
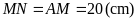 (do
(do
 là
hình vuông)
là
hình vuông)
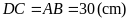 (do
(do
 là hình chữ nhật)
là hình chữ nhật)
Diện
tích tam giác
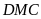 là
là
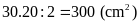
Bài
4:
Một
hình chữ nhật có chiều dài gấp
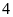 lần chiều rộng. Nếu tăng chiều rộng thêm
lần chiều rộng. Nếu tăng chiều rộng thêm
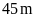 thì
được chiều dài của hình chữ nhật mới có chiều dài
vẫn gấp
thì
được chiều dài của hình chữ nhật mới có chiều dài
vẫn gấp
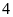 lần chiều rộng. Tính chu vi hình chữ nhật ban đầu.
lần chiều rộng. Tính chu vi hình chữ nhật ban đầu.
Lời giải:
Gọi
chiều rộng mảnh đất hình chữ nhật là
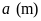 ,
,
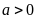
Vì
chiều dài gấp
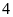 chiều rộng nên chiều dài là
chiều rộng nên chiều dài là
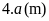
Chiều
rộng mới là
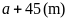
Khi
tăng chiều rộng thêm
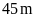 thì khi đó chiều rộng sẽ trở thành chiều dài của
hình chữ nhật mới, còn chiều dài ban đầu sẽ trở
thành chiều rộng của hình chữ nhật mới.
thì khi đó chiều rộng sẽ trở thành chiều dài của
hình chữ nhật mới, còn chiều dài ban đầu sẽ trở
thành chiều rộng của hình chữ nhật mới.
Theo
đề bài thì hình chữ nhật mới có chiều dài vẫn gấp
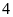 lần chiều rộng (tức là chiều dài cũ) nên ta có
lần chiều rộng (tức là chiều dài cũ) nên ta có
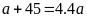
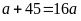
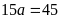 hay
hay
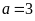
Chu
vi
hình chữ nhật ban đầu là
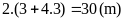
Bài
5: Người
ta ngăn thửa đất hình chữ nhật thành hai mảnh, một
mảnh hình vuông, một mảnh hình chữ nhật. Biết chu vi
thửa đất hình chữ nhật ban đầu hơn chu vi thửa đất
hình vuông là
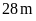 .
Diện tích của thửa đất ban đầu hơn diện tích thửa
đất hình vuông là
.
Diện tích của thửa đất ban đầu hơn diện tích thửa
đất hình vuông là
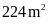 .
Tính chu vi thửa đất ban đầu.
.
Tính chu vi thửa đất ban đầu.
Lời giải:
Nửa
chu vi hình
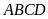 hơn nửa chu vi hình
hơn nửa chu vi hình
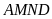 là
là
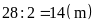 .
.
Nửa
chu vi hình
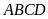 là
là
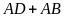 .
.
Nửa
chu vi hình
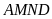 là
là
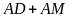 .
.
Do
đó
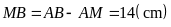 .
.
Diện
tích hình
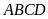 là
là
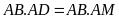 (do
(do
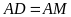 )
)
Diện
tích hình
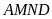 là
là
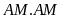
Theo
đề ta có
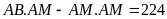 hay
hay
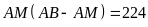
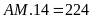
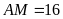
Chiều
rộng
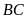 của hình
của hình
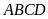 là:
là:
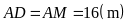
Chiều
dài
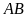 của hình
của hình
 là:
là:
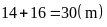
Chu
vi hình chữ nhật
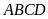 là:
là:
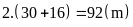 .
.
Bài
6: Một miếng bìa
hình chữ nhật, có chiều rộng
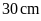 ,
chiều dài
,
chiều dài
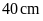 .
Người ta muốn cắt đi một hình chữ nhật nằm chính
giữa miếng bìa trên sao cho cạnh của hai hình chữ nhật
song song và cách đều nhau, đồng thời diện tích cắt đi
bằng
.
Người ta muốn cắt đi một hình chữ nhật nằm chính
giữa miếng bìa trên sao cho cạnh của hai hình chữ nhật
song song và cách đều nhau, đồng thời diện tích cắt đi
bằng
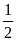 diện tích miếng bìa ban đầu. Hỏi hai cạnh tương ứng
của hai hình chữ nhật ban đầu và cắt đi cách nhau bao
nhiêu?
diện tích miếng bìa ban đầu. Hỏi hai cạnh tương ứng
của hai hình chữ nhật ban đầu và cắt đi cách nhau bao
nhiêu?
Lời giải:
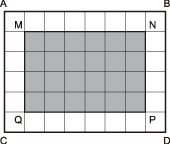
Chia
miếng bìa
 thành các ô vuông, mỗi ô vuông có cạnh là
thành các ô vuông, mỗi ô vuông có cạnh là
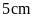 .
Số ô vuông của miếng bìa đó là:
.
Số ô vuông của miếng bìa đó là:
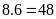 (ô vuông).
(ô vuông).
Số
ô vuông của hình chữ nhật
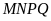 là:
là:
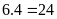 (ô vuông)
(ô vuông)
Vì
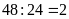 (lần) nên hình chữ nhật
(lần) nên hình chữ nhật
 có diện tích đúng bằng diện tích hình cắt đi. Mặt
khác các cạnh của hình chữ nhật
có diện tích đúng bằng diện tích hình cắt đi. Mặt
khác các cạnh của hình chữ nhật
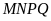 song song và cách đều các cạnh tương ứng của miếng
bìa
song song và cách đều các cạnh tương ứng của miếng
bìa
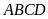 .
Vì vậy hình
.
Vì vậy hình
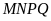 đúng là hình chữ nhật bị cắt đi. Mỗi cặp cạnh
tương ứng của hình
đúng là hình chữ nhật bị cắt đi. Mỗi cặp cạnh
tương ứng của hình
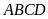 và
và
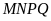 cách nhau
cách nhau
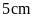 .
.
Bài
7:
Cho
một hình chữ nhật, biết nếu tăng chiều dài, chiều
rộng mỗi chiều
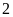 cm thì diện tích hình chữ nhật tăng thêm
cm thì diện tích hình chữ nhật tăng thêm
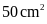 .
Tìm chu vi hình chữ nhật ban đầu.
.
Tìm chu vi hình chữ nhật ban đầu.
Lời giải:
Gọi
chiều dài và chiều rộng hình
chữ nhật
ban đầu lần lượt là
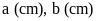 .
.
Diện
tích ban đầu hình chữ nhật là
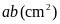
Diện
tích sau khi tăng mỗi chiều
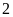 cm
là
cm
là
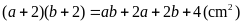
Theo
bài ra chiều dài và chiều rộng của hình
chữ nhật
tăng thêm
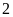 cm
thì diện tích tăng thêm
cm
thì diện tích tăng thêm
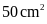 nên:
nên:
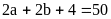
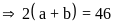
Vậy
chu vi hình chữ nhật
ban đầu là
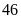 cm.
cm.
Dạng 2: Các bài toán về diện tích hình chữ nhật.
I. Phương pháp giải
* HS nắm chắc công thức diện tích của hình chữ nhật.
* HS phân tích kĩ đề bài để tìm mối quan hệ giữa các yếu tố đã cho và yếu tố cần tìm trong đề.
* HS vận dụng tốt tính chất tỉ số diện tích của hai tam giác có cùng chiều cao (chiều cao bằng nhau) hoặc cùng cạnh đáy (cạnh đáy bằng nhau).
II. Bài toán
Bài
1:
Cho mảnh đất hình chữ nhật có diện tích
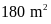 ,
chu vi
,
chu vi
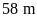 .
Hãy tính chiều dài và chiều rộng mảnh đất đó (biết
số đo các cạnh là số tự nhiên)?
.
Hãy tính chiều dài và chiều rộng mảnh đất đó (biết
số đo các cạnh là số tự nhiên)?
Lời giải:
Cách 1:
Ta
có tổng của chiều rộng và chiều dài là:
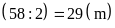
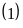
Ta phân tích diện tích hình chữ nhật thành tích của số đo chiều rộng và chiều dài được như sau:
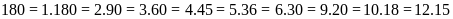
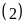
Dùng
phương pháp đối chiếu, từ
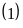 ta thấy tổng số đo của chiều rộng và chiều dài là
ta thấy tổng số đo của chiều rộng và chiều dài là
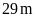 ,
đem đối chiếu với kết quả cặp số đo chiều rộng
và chiều dài ở
,
đem đối chiếu với kết quả cặp số đo chiều rộng
và chiều dài ở
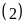 ta thấy cặp số
ta thấy cặp số
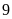 và
và
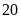 thỏa mãn yêu cầu.
thỏa mãn yêu cầu.
Như
vậy chiều rộng là
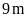 ;
chiều dài là
;
chiều dài là
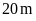 .
.
Cách 2:
Gọi
số đo chiều rộng là
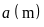 ;
số đo chiều dài là
;
số đo chiều dài là
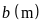
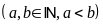
Theo
đề bài ta có:
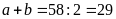
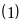 ,
suy ra
,
suy ra
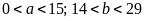
Lại
có
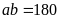
 ,
suy ra
,
suy ra
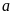 hoặc
hoặc
 phải chia hết cho
phải chia hết cho
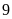 .
.
Xét
TH1:
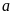 chia hết cho
chia hết cho
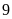 .
Vì
.
Vì
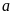 chia hết cho
chia hết cho
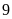 và
và
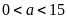 nên
nên
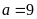 .
.
Với
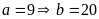 mà
mà
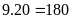 (thỏa mãn
(thỏa mãn
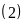 ).
).
Xét
TH2:
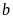 chia hết cho
chia hết cho
 ;
;
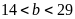 nên
nên
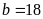 hoặc
hoặc
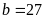 .
.
– Nếu
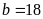 thì
thì
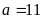 mà
mà
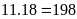 (không thỏa mãn
(không thỏa mãn
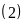 )
nên TH này ta loại.
)
nên TH này ta loại.
– Nếu
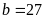 thì
thì
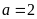 mà
mà
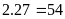 (không thỏa mãn
(không thỏa mãn
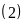 )
nên TH này ta cũng loại.
)
nên TH này ta cũng loại.
Vậy
chiều rộng là
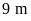 ;
chiều dài là
;
chiều dài là
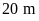 .
.
Bài
2:
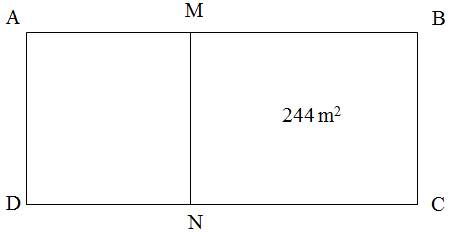
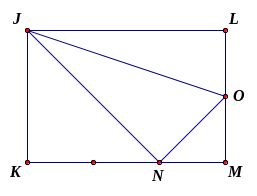
Cho hình chữ nhật
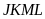 có
có
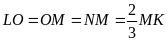 (như
hình vẽ). Tính diện tích hình chữ nhật
(như
hình vẽ). Tính diện tích hình chữ nhật
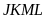 biết diện tích tam giác
biết diện tích tam giác
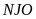 là
là
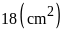
Lời giải:
Từ
đề
bài:
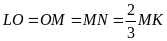 ta suy ra nếu
ta suy ra nếu
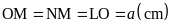 thì
thì
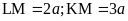
Ta
có
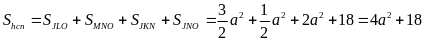
Mà
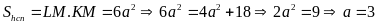
Vậy
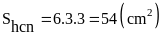 .
.
Bài
3: Một
hình chữ nhật có chu vi là
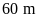 .
Tính diện tích của nó, biết rằng giữ nguyên chiều
rộng của hình chữ nhật đó và tăng chiều dài lên
.
Tính diện tích của nó, biết rằng giữ nguyên chiều
rộng của hình chữ nhật đó và tăng chiều dài lên
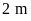 thì ta được một hình chữ nhật mới có diện tích tăng
thêm
thì ta được một hình chữ nhật mới có diện tích tăng
thêm
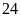 mét vuông.
mét vuông.
Lời giải:
Gọi
chiều dài và chiều rộng hình chữ nhật ban đầu lần
lượt là
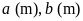 .
.
Diện
tích ban đầu hình chữ nhật là
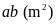
Diện
tích sau khi giữ nguyên chiều rộng và tăng chiều dài lên
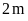 là
là
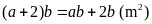
Vì
diện tích mới tăng
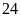 mét vuông nên
mét vuông nên
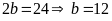
Chiều
rộng ban đầu của hình chữ nhật là:
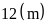
Chiều
dài ban đầu của hình chữ nhật là
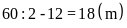
Diện
tích của hình chữ nhật là:
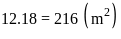 .
.
Bài
4: Một
hình chữ nhật có chiều dài gấp rưỡi chiều rộng. Nếu
mỗi chiều tăng thêm
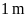 thì được hình chữ nhật mới có diện tích tăng thêm
thì được hình chữ nhật mới có diện tích tăng thêm
 mét vuông. Tính các kích thước của hình chữ nhật ban
đầu.
mét vuông. Tính các kích thước của hình chữ nhật ban
đầu.
Lời giải:
Gọi
chiều dài và chiều rộng hình chữ nhật ban đầu lần
lượt là
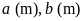 .
.
Diện
tích ban đầu hình chữ nhật là
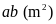
Diện
tích sau khi tăng mỗi chiều
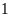 m
là
m
là
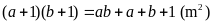
Theo
bài ra chiều dài và chiều rộng của hình chữ nhật tăng
thêm
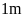 thì diện tích tăng thêm
thì diện tích tăng thêm
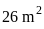 nên
nên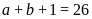
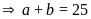
Theo
bài ra:
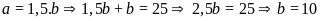
Từ
đó
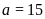
Vậy
hình
chữ nhật ban
đầu có chiều dài và chiều rộng lần lượt là
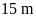 và
và
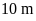 .
.
Bài
5:
Tính
tỉ số diện tích hình
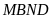 với
hình chữ nhật
với
hình chữ nhật
 .
Biết
.
Biết
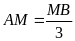 ,
,
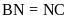 .
.
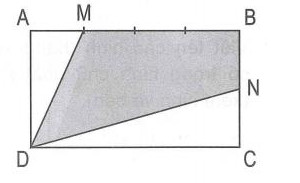
Lời giải:
Ta
có
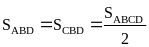 .
.
Ta
có
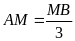
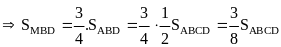
Tương
tự
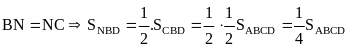
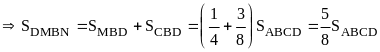
Vậy
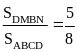 .
.
Bài
6: Một miếng bìa hình
vuông cạnh
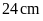 .
Cắt miếng bìa đó dọc theo một cạnh ta được hai hình
chữ nhật có tỉ số chu vi là
.
Cắt miếng bìa đó dọc theo một cạnh ta được hai hình
chữ nhật có tỉ số chu vi là 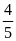 .
Tìm diện tích mỗi hình chữ nhật đó.
.
Tìm diện tích mỗi hình chữ nhật đó.
Lời giải:
Gọi
hình vuông là
 .
Cắt miếng bìa theo đường
.
Cắt miếng bìa theo đường
 .
.
Không
mất tính tổng quát ta giả sử hình chữ nhật
 có chu vi lớn hơn.
có chu vi lớn hơn.
Gọi
độ dài
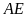 là
là
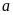 (cm)
(cm)
Khi
đó
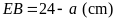
Theo
bài ra ta có:
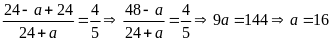 .
.
Diện
tích hình chữ nhật
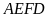 là
là
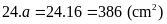
Diện
tích hình chữ nhật
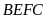 là
là
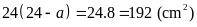
Vậy
diện tích mỗi hình chữ nhật là
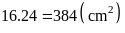 và
và
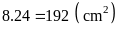
Bài
7:
Cho
(1), (2), (3), (4) là các hình thang vuông có kích thước
bằng nhau. Biết rằng
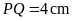 .
Tính diện tích hình chữ nhật
.
Tính diện tích hình chữ nhật
 .
.
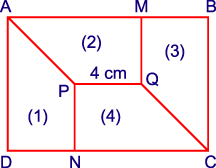
Lời giải:
Vì
các hình thang vuông
 ,
,
 ,
,
 ,
,
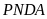 bằng nhau nên:
bằng nhau nên:
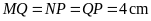 và
và
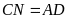 .
.
Mặt
khác
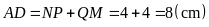 .
Do đó
.
Do đó
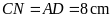 .
.
Diện
tích hình thang vuông
 là:
là:
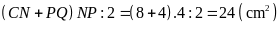
Suy
ra diện tích hình chữ nhật
 là:
là:
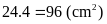 .
.
Bài
8:
Một
thửa ruộng hình chữ nhật được chia thành
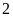 mảnh, một mảnh nhỏ trồng rau và mảnh còn lại trồng
ngô (hình
vẽ).
Diện tích của mảnh trồng ngô gấp
mảnh, một mảnh nhỏ trồng rau và mảnh còn lại trồng
ngô (hình
vẽ).
Diện tích của mảnh trồng ngô gấp
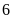 lần diện tích của mảnh trồng rau. Chu vi mảnh trồng
ngô gấp
lần diện tích của mảnh trồng rau. Chu vi mảnh trồng
ngô gấp
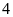 lần chu vi mảnh trồng rau. Tính diện tích thửa ruộng
ban đầu, biết chiều rộng của nó là
lần chu vi mảnh trồng rau. Tính diện tích thửa ruộng
ban đầu, biết chiều rộng của nó là
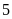 mét.
mét.

Lời giải:
Diện
tích mảnh trồng ngô gấp
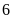 lần diện tích mảnh trồng rau mà hai mảnh có chung một
cạnh nên cạnh còn lại của mảnh trồng ngô gấp
lần diện tích mảnh trồng rau mà hai mảnh có chung một
cạnh nên cạnh còn lại của mảnh trồng ngô gấp
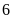 lần cạnh còn lại của mảnh trồng rau.
lần cạnh còn lại của mảnh trồng rau.
Gọi
cạnh còn lại của mảnh trồng rau là
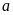 (m) thì cạnh còn lại của mảnh trồng ngô là
(m) thì cạnh còn lại của mảnh trồng ngô là
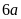 (m).
(m).
Chu
vi mảnh trồng rau là
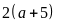 (m)
(m)
Chu
vi mảnh trồng ngô là
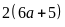 (m)
(m)
Vì
chu vi mảnh trồng ngô gấp
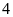 lần chu vi mảnh trồng rau nên
lần chu vi mảnh trồng rau nên
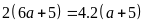
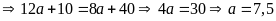
Độ
dài cạnh còn lại của mảnh trồng rau là:
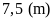
Độ
dài cạnh còn lại của mảnh trồng ngô là:
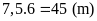
Diện
tích thửa ruộng ban đầu là:
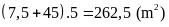 .
.
Bài
9:
Một
tờ giấy hình chữ nhật được gấp theo đường chéo
như hình vẽ. Diện tích hình nhận được bằng
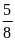 diện tích hình chữ nhật ban đầu. Biết diện tích phần
tô màu là
diện tích hình chữ nhật ban đầu. Biết diện tích phần
tô màu là
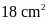 .
Tính diện tích tờ giấy ban đầu.
.
Tính diện tích tờ giấy ban đầu.

Lời giải:
Khi gấp tờ giấy hình chữ nhật theo đường chéo (đường nét đứt) thì phần hình tam giác được tô màu bị xếp chồng lên nhau. Do đó diện tích hình chữ nhật ban đầu lớn hơn diện tích hình nhận được chính là diện tích tam giác được tô màu.
Diện
tích hình chữ nhật ban đầu giảm đi bằng
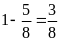 diện tích hình chữ nhật ban đầu.
diện tích hình chữ nhật ban đầu.
Do
vậy diện tích tam giác tô màu bằng
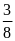 diện tích hình chữ nhật ban đầu, hay
diện tích hình chữ nhật ban đầu, hay
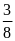 diện tích hình chữ nhật ban đầu bằng
diện tích hình chữ nhật ban đầu bằng
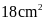 .
.
Vậy
diện tích hình chữ nhật ban đầu là:
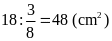
Bài
10:
Tính
diện tích hình chữ nhật
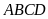 .
Biết rằng diện tích tứ giác
.
Biết rằng diện tích tứ giác
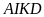 là
là
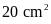 và
và
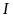 là điểm chia
là điểm chia
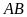 thành
thành
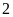 phần bằng nhau.
phần bằng nhau.
Lời giải:
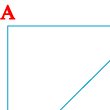
Kí
hiệu
 là diện tích của hình
là diện tích của hình
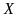 .
.
Nối
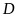 với
với
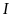 .
Qua
.
Qua
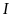 và
và
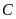 vẽ các đường thẳng
vẽ các đường thẳng
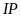 và
và
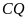 vuông góc với
vuông góc với
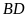 ,
,
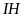 vuông góc với
vuông góc với
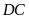 .
.
Ta
có
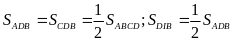 (vì có chung đường cao
(vì có chung đường cao
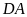 ,
,
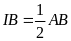 )
)
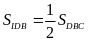 mà
hai tam giác này có chung đáy
mà
hai tam giác này có chung đáy
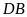 nên
nên
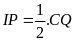
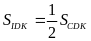
(vì
có chung đáy
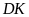 và
và
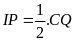 )
)
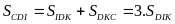 .
.
Ta
có
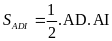 ,
,
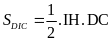 mà
mà
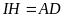 ,
,
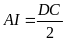
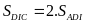
nên
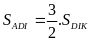
Vì
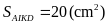
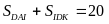
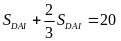
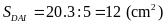
Mặt
khác
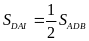 (cùng chung chiều cao
(cùng chung chiều cao
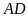 ,
,
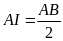 )
)
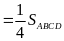
Suy
ra
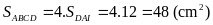 .
.
Bài
11:
Một
khu vườn hình chữ nhật có chu vi
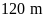 .
Người ta mở rộng khu vườn như hình vẽ để được
một vườn hình chữ nhật lớn hơn. Tính diện tích phần
mới mở thêm.
.
Người ta mở rộng khu vườn như hình vẽ để được
một vườn hình chữ nhật lớn hơn. Tính diện tích phần
mới mở thêm.
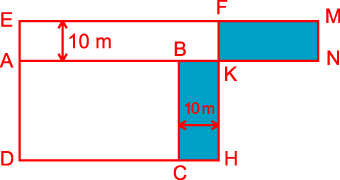
Lời giải:
Nếu
ta “dịch chuyển” khu vườn cũ
 vào một góc của khu vườn mới
vào một góc của khu vườn mới
 ta được hình vẽ bên. Kéo dài
ta được hình vẽ bên. Kéo dài
 về phía
về phía
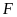 lấy
lấy
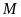 sao cho
sao cho
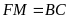 thì diện tích hình chữ nhật
thì diện tích hình chữ nhật
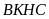 đúng bằng diện tích hình chữ nhật
đúng bằng diện tích hình chữ nhật
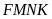 .
Do đó phần diện tích mới mở thêm chính là diện tích
hình chữ nhật
.
Do đó phần diện tích mới mở thêm chính là diện tích
hình chữ nhật
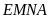 .
.
Ta
có
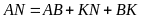 ,
vì
,
vì
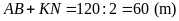 ;
;
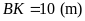 nên
nên
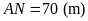 .
Vậy diện tích phần mới mở thêm là:
.
Vậy diện tích phần mới mở thêm là:
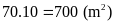 .
.
Bài
12:
Một
mảnh đất hình chữ nhật được chia thành
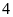 hình chữ nhật nhỏ hơn có diện tích được ghi như hình
vẽ. Tính diện tích hình chữ nhật còn lại .
hình chữ nhật nhỏ hơn có diện tích được ghi như hình
vẽ. Tính diện tích hình chữ nhật còn lại .
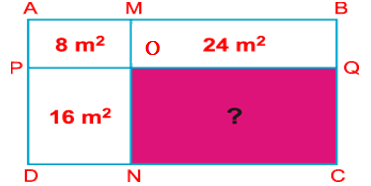
Lời giải:
Hai
hình chữ nhật
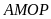 và
và
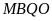 có chiều rộng bằng nhau và có diện tích hình
có chiều rộng bằng nhau và có diện tích hình
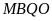 gấp 3 lần diện tích hình
gấp 3 lần diện tích hình
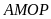 (
(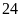 gấp
gấp
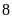 là
là
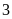 lần), do đó chiều dài hình chữ nhật
lần), do đó chiều dài hình chữ nhật
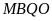 gấp
gấp
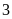 lần chiều dài hình chữ nhật
lần chiều dài hình chữ nhật
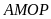
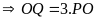
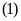 .
.
Hai
hình chữ nhật
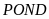 và
và
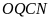 có chiều rộng bằng nhau và có chiều dài hình
có chiều rộng bằng nhau và có chiều dài hình
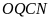 gấp
gấp
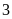 lần chiều dài hình
lần chiều dài hình
 (do
(do
 ). Do đó diện tích hình
). Do đó diện tích hình
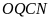 gấp
gấp
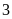 lần diện tích hình
lần diện tích hình
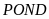 .
.
Vậy
diện tích hình chữ nhật
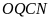 là:
là:
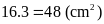 .
.
Bài
13:
Một
vườn trường hình chữ nhật có chu vi
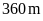 .
Tính diện tích của mảnh vườn đó biết nếu xóa chữ
số
.
Tính diện tích của mảnh vườn đó biết nếu xóa chữ
số
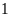 ở bên trái số đo chiều dài ta được số đo chiều
rộng.
ở bên trái số đo chiều dài ta được số đo chiều
rộng.
Lời giải:
Vì
xóa chữ số
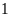 ở bên trái số đo chiều dài ta được số đo chiều
rộng nên chiều dài hơn chiều rộng là
ở bên trái số đo chiều dài ta được số đo chiều
rộng nên chiều dài hơn chiều rộng là
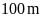
Nửa
chu vi hình chữ nhật là
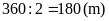
Gọi
chiều rộng mảnh đất hình chữ nhật là
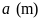 ,
,
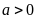 thì chiều dài hình chữ nhật là
thì chiều dài hình chữ nhật là
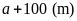
Ta
có
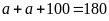
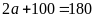
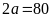 hay
hay
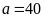
Diện
tích của mảnh vườn là
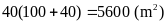
Bài
14:
Một
khu vườn hình chữ nhật có chiều dài gấp
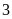 lần chiều rộng. Nếu giảm chiều dài đi
lần chiều rộng. Nếu giảm chiều dài đi
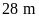 ,
tăng chiều rộng thêm
,
tăng chiều rộng thêm
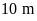 thì khu vườn đó trở thành hình vuông. Tính diện tích
khu vườn ban đầu.
thì khu vườn đó trở thành hình vuông. Tính diện tích
khu vườn ban đầu.
Lời giải:
Gọi
chiều rộng mảnh đất hình chữ nhật là
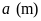 ,
,
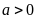
Vì
chiều dài gấp ba chiều rộng nên chiều dài là
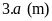
Vì
giảm chiều dài đi
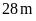 nên
chiều dài mới là
nên
chiều dài mới là
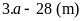
Vì
tăng chiều rộng thêm
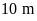 nên chiều rộng mới là
nên chiều rộng mới là
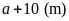
Theo
đề bài
thì mảnh vườn trở thành hình vuông nên ta có
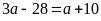
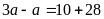
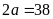 hay
hay
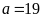
Diện
tích hình chữ nhật ban đầu là
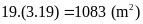
Bài
15:
Một
mảnh đất hình chữ nhật có chiều dài gấp đôi chiều
rộng. Nếu thêm vào chiều dài
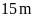 ,
thêm vào chiều rộng
,
thêm vào chiều rộng
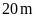 thì chiều dài mảnh đất mới gấp rưỡi chiều rộng
mảnh đất khi đó. Tính diện tích mảnh đất hình chữ
nhật ban đầu.
thì chiều dài mảnh đất mới gấp rưỡi chiều rộng
mảnh đất khi đó. Tính diện tích mảnh đất hình chữ
nhật ban đầu.
Lời giải:
Gọi
chiều rộng mảnh đất hình chữ nhật là
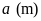 ,
,
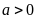
Vì
chiều dài gấp đôi chiều rộng nên chiều dài là
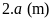
Chiều
dài mới là
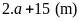
Chiều
rộng mới là
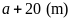
Theo
đề ta có
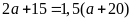
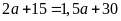
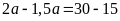
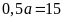 hay
hay
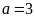
Diện
tích hình chữ nhật ban đầu là
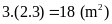
Bài
16:
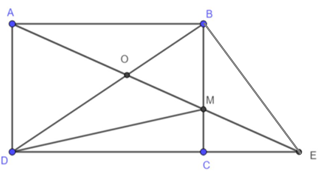
Cho
hình chữ nhật
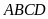 có chu vi là
có chu vi là
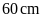 và
chiều dài
và
chiều dài
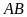 gấp rưỡi chiều rộng
gấp rưỡi chiều rộng
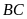 .
Lấy một điểm
.
Lấy một điểm
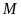 trên cạnh
trên cạnh
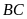 sao
cho
sao
cho
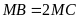 .
Nối
.
Nối
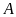 với
với
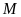 kéo dài cắt
kéo dài cắt
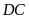 kéo dài tại điểm
kéo dài tại điểm
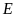 .
Nối
.
Nối
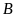 với
với
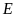 .
Nối
.
Nối
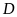 với
với
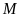 .
.
a)
Tính diện tích hình chữ nhật
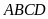 .
.
b)
Chứng tỏ rằng tam giác
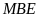 và tam giác
và tam giác
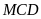 có
diện tích bằng nhau.
có
diện tích bằng nhau.
c)
Gọi
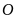 là
giao điểm của
là
giao điểm của
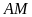 và
và
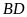 .
Tính tỷ số
.
Tính tỷ số
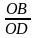
Lời giải:
a)
Gọi chiều rộng
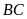 của hình chữ nhật là
của hình chữ nhật là
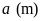
Vì
chiều dài
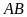 gấp rưỡi chiều rộng
gấp rưỡi chiều rộng
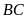 nên chiều dài
nên chiều dài
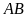 là
là
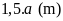
Ta
có
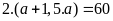
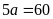 hay
hay
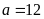
Diện
tích của hình chữ nhật
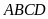 là:
là:
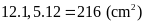
b)
Ta có
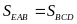 (vì có chiều cao hạ từ
(vì có chiều cao hạ từ
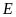 lên đáy
lên đáy
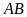 bằng chiều cao
bằng chiều cao
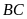 của tam giác
của tam giác
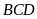 hạ từ
hạ từ
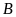 lên đáy
lên đáy
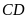 ,
đáy
,
đáy
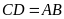 )
)
Ta
có
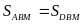 (vì có chiều
(vì có chiều
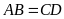 ,
chung đáy
,
chung đáy
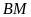 )
)
Do
đó
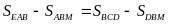 hay
hay
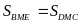
c)
Ta có
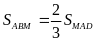 (vì có đường cao
(vì có đường cao
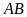 bằng đường cao hạ từ đỉnh
bằng đường cao hạ từ đỉnh
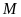 của ta giác
của ta giác
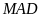 ,
đáy
,
đáy
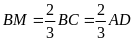 )
)
Mà
2 tam giác này chung đáy
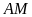 nên suy ra chiều cao hạ từ đỉnh
nên suy ra chiều cao hạ từ đỉnh
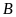 lên
lên
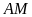 của tam giác
của tam giác
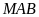 bằng
bằng 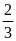 chiều
cao hạ từ đỉnh
chiều
cao hạ từ đỉnh
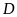 của tam giác
của tam giác
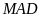 lên
đáy
lên
đáy
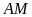 .
Đây cũng là chiều cao từ các đỉnh hạ lên đáy
.
Đây cũng là chiều cao từ các đỉnh hạ lên đáy
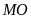 của
tam giác
của
tam giác
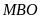 và tam giác
và tam giác
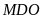
Chiều
cao hạ từ
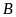 lên đáy
lên đáy
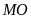 của tam giác
của tam giác
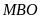 bằng
bằng 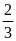 chiều
cao hạ từ đỉnh
chiều
cao hạ từ đỉnh 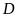 lên
đáy
lên
đáy
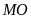 của tam giác
của tam giác
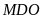
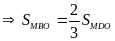 mà
hai tam giác này có chung chiều cao hạ từ M lên BD
mà
hai tam giác này có chung chiều cao hạ từ M lên BD
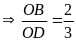 .
.
Dạng 3: Các bài toán có nội dung thực tiễn.
I. Phương pháp giải
* HS phân tích kỹ đề bài để tìm mối liên hệ giữa đề bài và các yếu tố thực tiễn.
* Áp dụng công thức tính chu vi, diện tích hình chữ nhật vào giải toán.
II. Bài toán
Bài
1:
Một
người rào xung quanh khu đất hình chữ nhật có chiều
dài
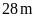 ,
chiều rộng
,
chiều rộng
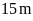 hết
hết
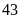 chiếc
cọc. Hỏi người đó rào xung quanh khu đất hình vuông có
cạnh
chiếc
cọc. Hỏi người đó rào xung quanh khu đất hình vuông có
cạnh
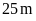 thì
hết bao nhiêu chiếc cọc? Biết khoảng cách giữa hai cọc
là như nhau.
thì
hết bao nhiêu chiếc cọc? Biết khoảng cách giữa hai cọc
là như nhau.
Lời giải:
Chu
vi hình chữ nhật là
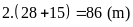
Khoảng
cách giữa hai cọc là
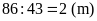
Chu
vi hình vuông là
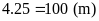
Số
cọ cần để rào xung quanh hình vuông là
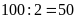 (cọc)
(cọc)
Bài
2:
Một
mảnh vườn hình chữ nhật có diện tích
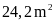 ,
chiều dài gấp
,
chiều dài gấp
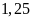 lần chiều rộng. Hỏi người ta cần bao nhiêu cọc để
đóng xung quanh khu vườn? Biết cứ
lần chiều rộng. Hỏi người ta cần bao nhiêu cọc để
đóng xung quanh khu vườn? Biết cứ
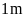 chôn một cọc và hai bên cửa ra vào rộng
chôn một cọc và hai bên cửa ra vào rộng
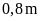 đều có cọc.
đều có cọc.
Lời giải:
Gọi
chiều rộng hình chữ nhật là
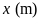 ,
,
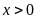
Vì
chiều dài gấp
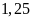 lần
chiều rộng nên chiều dài hình chữ nhật là
lần
chiều rộng nên chiều dài hình chữ nhật là
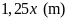
Theo
đề diện tích hình chữ nhật là
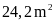 ,
ta có
,
ta có
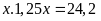 hay
hay
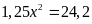
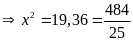 ,
suy ra
,
suy ra
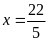
Chu
vi hình cữ nhật là
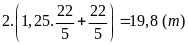
Chu
vi vườn cần đóng cọc là
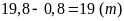
Số
cọ cần để đóng xung quanh vườn là
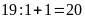 (cọc)
(cọc)
Bài
3:
Một
tấm biển quảng cáo hình chữ nhật có chiều dài gấp
bốn lần chiều rộng và diện tích bằng
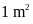 .
Hỏi phải dùng bao nhiêu mét nhôm để viền xung quanh tấm
biển đó?
.
Hỏi phải dùng bao nhiêu mét nhôm để viền xung quanh tấm
biển đó?
Lời giải:
Gọi
chiều rộng hình chữ nhật là
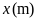 ,
,
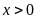
Vì
chiều dài gấp bốn lần chiều rộng nên chiều dài hình
chữ nhật là
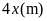
Theo
đề diện tích hình chữ nhật là
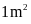 ,
ta có
,
ta có
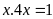 hay
hay
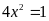
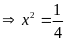 ,
suy ra
,
suy ra
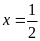
Số
mét nhôm để viền xung quanh tấm biển chính là chu vi của
tấm biển quảng cáo đó là
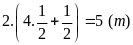
Bài
4:
Hợp
tác xã Hòa Bình dự định xây dựng một khu vui chơi cho
trẻ em trong xã. Vì thế họ đã mở rộng một mảnh đất
hình chữ nhật để diện tích gấp ba lần diện tích ban
đầu. Chiều rộng mảnh đất chỉ có thể tăng lên gấp
đôi nên phải mở rộng thêm chiều dài. Khi đó mảnh đất
trở thành hình vuông. Hãy tính diện tích khu vui chơi sau
khi mở rộng. Biết rằng chu vi mảnh đất ban đầu là
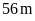 .
.
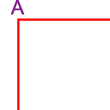
Lời giải:
Gọi
mảnh đất hình chữ nhật lúc đầu là
 ,
khi mở rộng mảnh đất hình chữ nhật để được mảnh
đất hình vuông
,
khi mở rộng mảnh đất hình chữ nhật để được mảnh
đất hình vuông
 có cạnh hình vuông gấp hai lần chiều rộng mảnh đất
hình chữ nhật
có cạnh hình vuông gấp hai lần chiều rộng mảnh đất
hình chữ nhật
 và diện tích gấp
và diện tích gấp
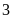 lần diện tích mảnh đất hình chữ nhật ấy. Khi đó
diện tích của các mảnh đất hình chữ nhật
lần diện tích mảnh đất hình chữ nhật ấy. Khi đó
diện tích của các mảnh đất hình chữ nhật
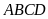 ,
,
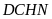 ,
,
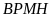 bằng nhau.
bằng nhau.
Mảnh
đất hình chữ nhật
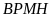 có độ dài cạnh
có độ dài cạnh
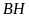 gấp
gấp
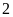 lần độ dài cạnh
lần độ dài cạnh
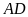
nên
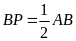 hay
hay
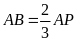
Ta
lại có
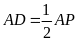 nên
nên
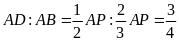
Nửa
chu vi mảnh đất ban đầu là
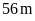 nên
nên
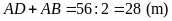 .
.
Ta
có : Chiều rộng mảnh đất ban đầu (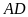 )
là:
)
là:
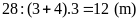 .
.
Cạnh
hình vuông
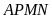 là:
là:
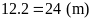 .
.
Diện
tích khu vui chơi là:
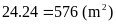 .
.
Bài
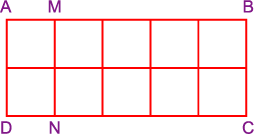
5:
Bác
Hà có hai tấm kính hình chữ nhật. Chiều rộng của mỗi
tấm kính bằng
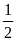 chiều dài của nó và chiều dài của tấm kính nhỏ đúng
bằng chiều rộng của tấm kính to. Bác ghép hai tấm kính
sát vào nhau và đặt lên bàn có diện tích
chiều dài của nó và chiều dài của tấm kính nhỏ đúng
bằng chiều rộng của tấm kính to. Bác ghép hai tấm kính
sát vào nhau và đặt lên bàn có diện tích
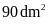 thì vừa khít. Hãy tính kích thước của mỗi tấm kính
đó.
thì vừa khít. Hãy tính kích thước của mỗi tấm kính
đó.
Lời giải:
Theo
đầu bài, coi chiều rộng của tấm kính nhỏ là
 đoạn thì chiều dài của nó là
đoạn thì chiều dài của nó là
 đoạn như vậy và chiều rộng của tấm kính to cũng là
đoạn như vậy và chiều rộng của tấm kính to cũng là
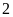 đoạn, khi đó chiều dài của tấm kính to là
đoạn, khi đó chiều dài của tấm kính to là
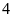 đoạn như vậy.
đoạn như vậy.
Nếu
bác Hà ghép khít hai tấm kính lại với nhau sẽ được
hình chữ nhật
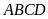 (hình
vẽ),
trong đó
(hình
vẽ),
trong đó
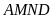 là tấm kính nhỏ,
là tấm kính nhỏ,
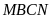 là tấm kính to. Diện tích
là tấm kính to. Diện tích
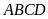 là
là
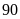 dm2.
dm2.
Chia
hình chữ nhật
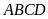 thành
thành
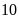 hình vuông nhỏ, mỗi cạnh là chiều rộng của tấm kính
nhỏ thì diện tích của mỗi hình vuông nhỏ là
hình vuông nhỏ, mỗi cạnh là chiều rộng của tấm kính
nhỏ thì diện tích của mỗi hình vuông nhỏ là
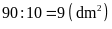 .
.
Ta
có
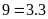 ,
do đó cạnh hình vuông là
,
do đó cạnh hình vuông là
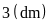 .
Tấm kính nhỏ có chiều rộng
.
Tấm kính nhỏ có chiều rộng
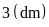 ,
chiều dài là
,
chiều dài là
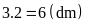 .
Tấm kính to có chiều rộng là
.
Tấm kính to có chiều rộng là
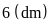 ,
chiều dài là
,
chiều dài là
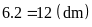 .
.
Bài
6:
Bác
Phong có một mảnh đất hình chữ nhật, chiều rộng mảnh
đất dài
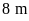 .
Bác ngăn mảnh đó thành hai phần, một phần để làm
nhà, phần còn lại để làm vườn. Diện tích phần đất
làm nhà bằng
.
Bác ngăn mảnh đó thành hai phần, một phần để làm
nhà, phần còn lại để làm vườn. Diện tích phần đất
làm nhà bằng
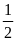 diện tích mảnh đất còn chu vi phần đất làm nhà bằng
diện tích mảnh đất còn chu vi phần đất làm nhà bằng
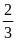 chu vi mảnh đất. Tính diện tích mảnh đất của bác
Phong.
chu vi mảnh đất. Tính diện tích mảnh đất của bác
Phong.
Lời giải:
Có hai cách chia mảnh đất hình chữ nhật thành hai phần có diện tích bằng nhau.
Cách chia 1: Như Hình 1.
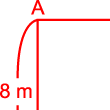
Hình 1
Gọi
mảnh đất hình chữ nhật là
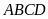 và
phần đất làm nhà là
và
phần đất làm nhà là
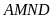 .
.
Vì
diện tích phần đất làm nhà bằng nửa diện tích mảnh
đất nên
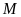 ,
,
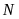 lần lượt là điểm chính giữa của
lần lượt là điểm chính giữa của
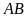 và
và
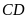 .
Do đó
.
Do đó
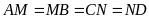 .
.
Chu
vi của phần đất làm nhà là:
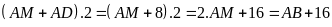 .
.
Chu
vi của mảnh đất là:
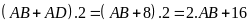 .
.
Hiệu
chu vi mảnh đất và chu vi phần đất làm nhà là:
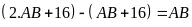 .
.
Hiệu
này so với chu vi mảnh đất thì chiếm:
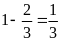 (chu vi mảnh đất)
(chu vi mảnh đất)
Do
đó ta có:
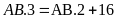 hay
hay
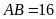 .
Vậy
diện tích mảnh đất là:
.
Vậy
diện tích mảnh đất là:
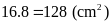
Cách chia 2 : Như Hình 2.
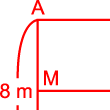
Hình 2
Lập
luận tương tự trường hợp trên, ta tìm được
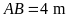 .
Điều này vô lí vì
.
Điều này vô lí vì
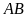 là chiều dài của mảnh đất hình chữ nhật là
là chiều dài của mảnh đất hình chữ nhật là
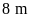 .
Do đó trường hợp này bị loại.
.
Do đó trường hợp này bị loại.
Bài
7:
Trên
một mặt bàn hình vuông, người ta đặt một lọ hoa có
đáy cũng là hình vuông sao cho một cạnh của đáy lọ
hoa trùng với một cạnh của bàn tại chính giữa bàn ấy
(như
hình vẽ).
Khoảng cách ngắn nhất từ cạnh mặt bàn đến đáy lọ
hoa là
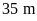 ,
biết diện tích còn lại của mặt bàn là
,
biết diện tích còn lại của mặt bàn là
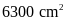 .
Tính cạnh của mặt bàn.
.
Tính cạnh của mặt bàn.
|
Lời giải:
Ta
có thể chuyển lọ hoa vào góc bàn, khi đó ta có
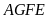 và
và
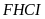 là hình vuông;
là hình vuông;
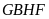 và
và
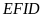 là các hình chữ nhật có diện tích bằng nhau.
là các hình chữ nhật có diện tích bằng nhau.
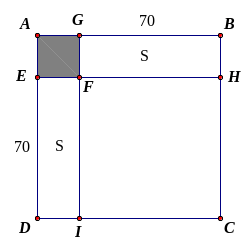
Độ
dài cạnh
 là:
là:
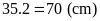
Diện
tích hình vuông
 là
là
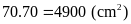
Diện
tích hình chữ nhật
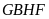 là
là
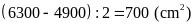
Độ
dài các cạnh hình vuông
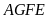 là
là
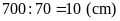
Vậy
cạnh mặt bàn là:
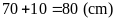
HẾT
Ngoài Giáo Án Bồi Dưỡng HSG Toán Chủ Đề: Hình Chữ Nhật Có Lời Giải – Toán 6 thì các tài liệu học tập trong chương trình 6 sẽ được cập nhật liên tục và nhanh nhất có thể sau khi kỳ thi diễn ra trên Danh mục Tài Liệu Học Tập nhằm giúp các bạn đọc thuận tiện trong việc nghiên cứu tài liệu. Quý thày cô và các bạn đọc có thể chia sẻ thêm những tài liệu học tập hữu ích đến địa chỉ email của chúng tôi, nhằm xây dựng nên kho đề thi phong phú, đa dạng cho các em học sinh tham khảo và rèn luyện.
Giáo Án Bồi Dưỡng HSG Toán với chủ đề “Hình Chữ Nhật” là một tài liệu dành riêng cho học sinh lớp 6 nhằm rèn luyện và nâng cao kỹ năng giải toán trong lĩnh vực hình học.
Trong giáo án này, học sinh sẽ tìm hiểu về các khái niệm và thuộc tính cơ bản của hình chữ nhật, bao gồm đường chéo, đường bán kính, đường trung trực, và các tính chất về cạnh, chu vi, diện tích. Giáo án cung cấp những bài tập thực hành giúp học sinh áp dụng kiến thức vào việc giải quyết các bài toán liên quan đến hình chữ nhật.
Ngoài ra, giáo án cũng cung cấp các phương pháp giải toán thông qua ví dụ và lời giải chi tiết, giúp học sinh hiểu rõ cách áp dụng kiến thức vào thực tế và phát triển khả năng tư duy logic và suy luận.
Giáo Án Bồi Dưỡng HSG Toán chủ đề “Hình Chữ Nhật” không chỉ giúp học sinh nắm vững kiến thức về hình chữ nhật mà còn rèn luyện kỹ năng giải toán, tư duy logic và sự linh hoạt trong việc áp dụng kiến thức vào các bài toán thực tế. Nó là một công cụ hữu ích để học sinh nâng cao khả năng toán học và chuẩn bị tốt hơn cho các kỳ thi hay các cuộc thi học sinh giỏi.
>>> Bài viết có liên quan