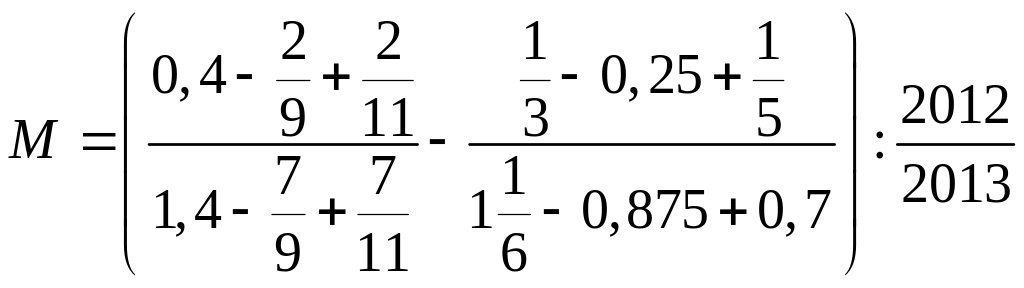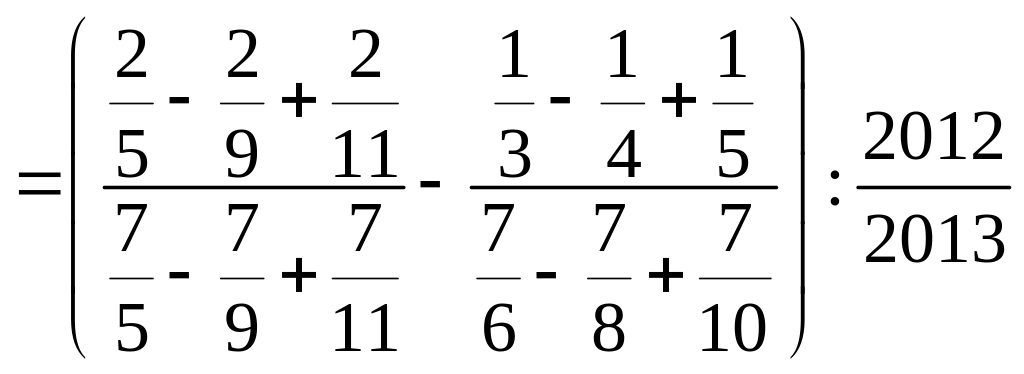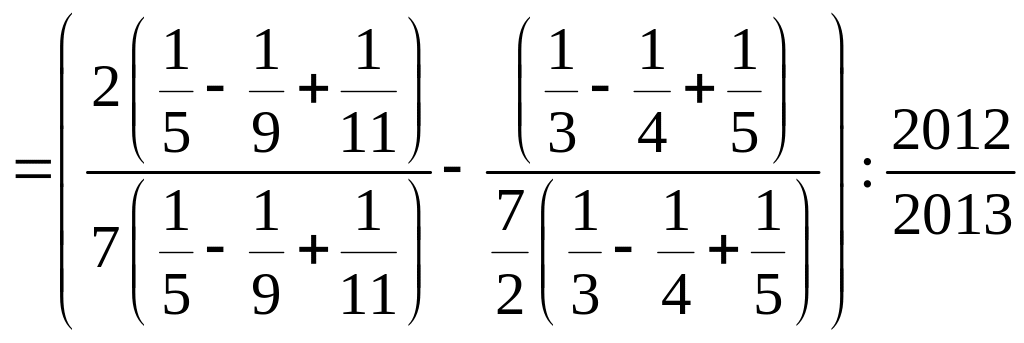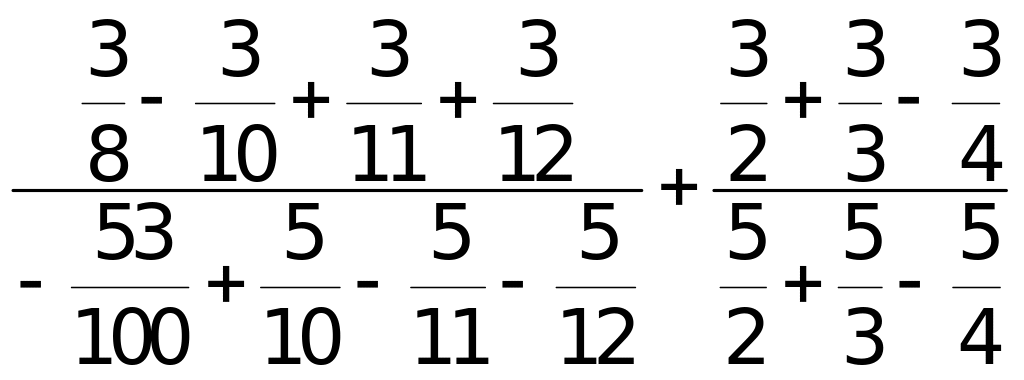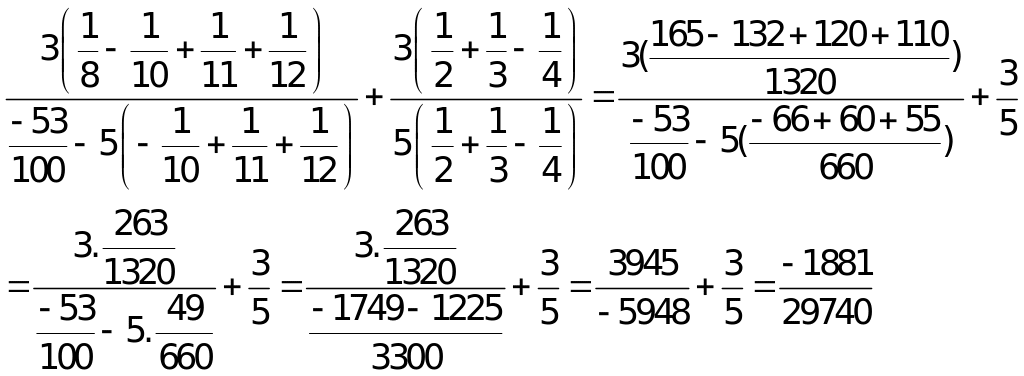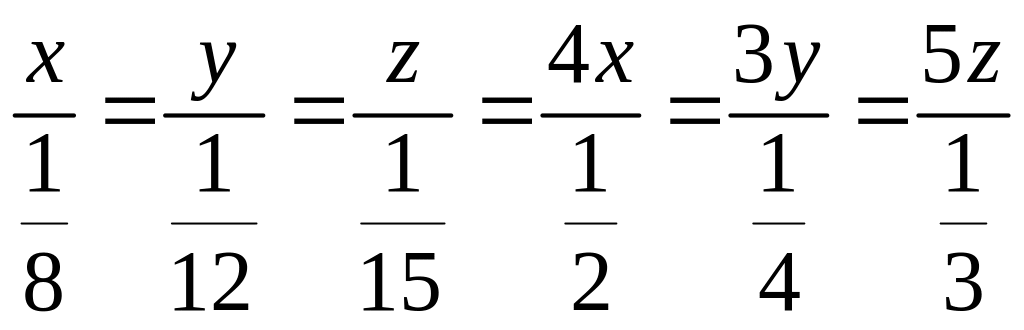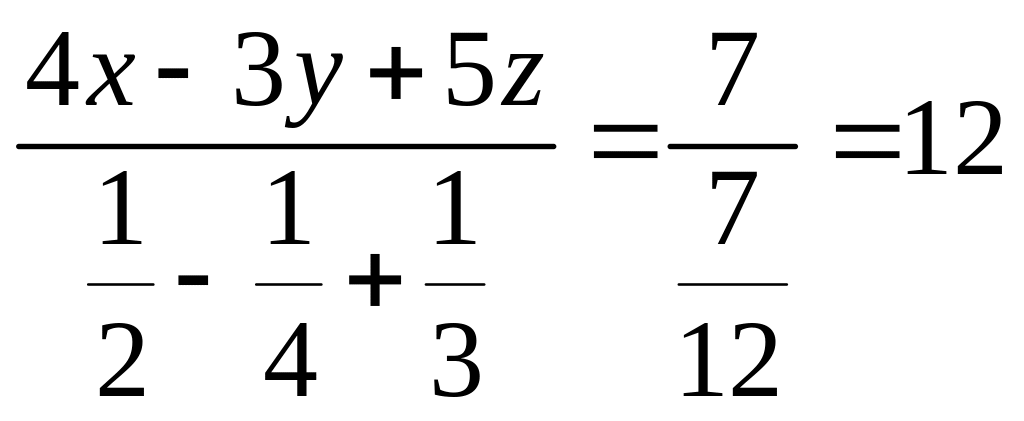Tổng Hợp 12 Đề Thi HGS Toán 7 Cấp Huyện Có Đáp Án – Toán 7
Tổng Hợp 12 Đề Thi HGS Toán 7 Cấp Huyện Có Đáp Án – Toán 7 được Trang Tài Liệu sưu tầm với các thông tin mới nhất hiện nay. Đề thi này sẽ giúp các em học sinh ôn tập, củng cố kiến thức, rèn luyện kĩ năng làm bài. Cũng như hỗ trợ thầy cô trong quá trình giảng dạy. Hy vọng những tài liệu này sẽ giúp các em trong quá trình ôn luyện và đạt kết quả cao trong bài thi sắp tới.
Tổng Hợp 12 Đề Thi HGS Toán 7 Cấp Huyện Có Đáp Án là một tài liệu vô cùng quý giá và hữu ích cho những ai đang chuẩn bị cho kỳ thi toán cấp huyện. Với đa dạng các đề thi và sự cung cấp đáp án chi tiết, bộ tài liệu này là một nguồn tư liệu tuyệt vời để rèn luyện và nâng cao khả năng giải toán của chúng ta.
Tổng Hợp 12 Đề Thi HGS Toán 7 Cấp Huyện Có Đáp Án không chỉ đơn thuần là một tập hợp các đề thi, mà nó còn là một cánh cửa để chúng ta tiếp cận với những bài toán thú vị và phong phú. Những câu hỏi và bài tập trong đề thi đòi hỏi chúng ta phải áp dụng kiến thức toán học đã học để giải quyết những tình huống thực tế. Điều này không chỉ giúp chúng ta rèn luyện kỹ năng toán học mà còn phát triển tư duy logic và khả năng giải quyết vấn đề.
Đặc biệt, sự có mặt của đáp án trong Tổng Hợp 12 Đề Thi HGS Toán 7 Cấp Huyện là một lợi thế lớn. Chúng ta không chỉ có thể tự kiểm tra và đánh giá kết quả làm bài của mình, mà còn có thể nắm bắt được cách giải quyết các bài toán một cách chi tiết và logic. Đáp án giúp chúng ta hiểu rõ hơn về các bước và quy trình giải quyết toán học, từ đó nâng cao khả năng giải toán và mở rộng hiểu biết của mình.
Tham gia Tổng Hợp 12 Đề Thi HGS Toán 7 Cấp Huyện Có Đáp Án, chúng ta không chỉ rèn luyện khả năng giải toán mà còn phát triển kỹ năng làm việc nhóm, tư duy linh hoạt và sự kiên nhẫn trong quá trình giải quyết các bài toán. Đây là cơ hội để chúng ta thử sức, vượt qua những thách thức và nâng cao trình độ toán học của mình.
Đề thi tham khảo
Dưới đây là bản đọc trực tuyến giúp thầy cô và các em học sinh có thể nghiên cứu Online hoặc bạn có thể tải miễn phí với phiên bản word để dễ dàng in ấn cũng như học tập Offline
PHÒNG GIÁO DỤC-ĐÀO TẠO ĐỀ THI CHỌN HỌC SINH GIỎI CẤP HUYỆN
ĐỨC PHỔ NĂM HỌC 2015 - 2016


ĐỀ CHÍNH THỨC
MÔN: TOÁN - LỚP 7 Thời gian: 120 phút (không kể thời gian giao đề).
Ngày thi: 10/4/2016
C âu
1: (5 điểm)
âu
1: (5 điểm)
a) Tính giá trị biểu thức P =
![]() ,
với
,
với
![]() .
.
b) Tìm số nguyên x để tích hai phân số
![]() và
và
![]() là một số nguyên.
là một số nguyên.
Câu 2: (5 điểm)
a )
Cho a > 2, b > 2. Chứng minh
)
Cho a > 2, b > 2. Chứng minh
![]()
b) Cho ba hình chữ nhật, biết diện tích của hình thứ nhất và diện tích của hình thứ hai tỉ lệ với 4 và 5, diện tích hình thư hai và diện tích hình thứ ba tỉ lệ với 7 và 8, hình thứ nhất và hình thứ hai có cùng chiều dài và tổng các chiều rộng của chúng là 27 cm, hình thứ hai và hình thứ ba có cùng chiều rộng, chiều dài của hình thứ ba là 24 cm. Tính diện tích của mỗi hình chữ nhật đó.
C âu
3: (3 điểm)
âu
3: (3 điểm)
Cho ∆DEF vuông tại D và DF > DE, kẻ DH vuông góc với EF (H thuộc cạnh EF). Gọi M là trung điểm của EF.
a) Chứng minh
![]()
b) Chứng minh EF - DE > DF - DH
C âu
4: (2 điểm)
âu
4: (2 điểm)
Cho các số
![]() .
Chứng minh rằng
.
Chứng minh rằng
![]()
C âu
5: (5 điểm)
âu
5: (5 điểm)
Cho ∆ABC có
![]() .
Các tia phân giác BE, CF của
.
Các tia phân giác BE, CF của
![]() và
và
![]() cắt nhau tại I (E, F lần lượt thuộc các cạnh AC, AB).
Trên cạnh BC lấy hai điểm M, N sao cho
cắt nhau tại I (E, F lần lượt thuộc các cạnh AC, AB).
Trên cạnh BC lấy hai điểm M, N sao cho
![]() .
.
a) Tính số đo của
![]() .
.
b) Chứng minh CE + BF < BC
------------------------------------------Hết---------------------------------------------
Cán bộ coi thi không giải thích gì thêm.
PHÒNG GD-ĐT ĐỨC PHỔ ĐỀ THI HỌC SINH GIỎI CẤP HUYỆN
MÔN: TOÁN - LỚP 7
ĐỀ CHÍNH THỨC NĂM HỌC 2015 - 2016

HƯỚNG DẪN CHẤM
Câu |
NỘI DUNG ĐÁP ÁN |
Điểm |
1
2.5 đ |
a) Tính giá trị biểu thức P =
Thay
Ta có P
P
P
P =
|
0.25
0.5
0.5
0.5 0.5 0.25
|
2.5 đ |
b) Tìm số nguyên x để tích hai phân số
Đặt A =
=
Để A nhận giá trị nguyên thì x + 1 là Ư(4) =
Suy ra x
|
0.25
0.25
0.25
0.25
0.5 |
2
2đ |
2. a
Từ
Suy ra
Vậy
|
0.5
0.5
0.5 0.5 |
3đ |
b) Cho ba hình chữ nhật, biết diện tích của hình thứ nhất và diện tích của hình thứ hai tỉ lệ với 4 và 5, diện tích hình thư hai và diện tích hình thứ ba tỉ lệ với 7 và 8, hình thứ nhất và hình thứ hai có cùng chiều dài và tổng các chiều rộng của chúng là 27 cm, hình thứ hai và hình thứ ba có cùng chiều rộng, chiều dài của hình thứ ba là 24 cm. Tính diện tích của mỗi hình chữ nhật đó.
Gọi diện tích ba hình chữ nhật lần lượt là
Vì hình thứ nhất và hình thứ hai cùng chiều dài
Suy
ra chiều rộng
Vì hình thứ hai và hình thứ ba cùng chiều rộng
Vậy
diện tích hình thứ hai
Diện tích hình thứ nhất
Diện tích hình thứ ba
|
0.5
0.5
0.25 0.25
0.25
0.25
0.25 0.25 0.25 0.25 |
3đ
|
Cho ∆DEF vuông tại D và DF > DE, kẻ DH vuông góc với EF (H thuộc cạnh EF). Gọi M là trung điểm của EF. a)
Chứng minh
Hình vẽ đúng, chính xác Vì M là trung điểm của EF suy ra MD = ME = MF
Mà
Ta
có
Vậy
b) Chứng minh EF - DE > DF - DH Trên cạnh EF lấy K sao cho EK = ED, trên cạnh DF lấy I sao cho DI = DH Ta có EF - DE = EF - EK = KF DF - DH = DF - DI = IF Ta cần chứng minh KF > IF
- EK = ED
-
- ∆DHK = ∆DIK (c-g-c)
Trong ∆KIF vuông tại I
|
0.5 0.25 0.25
0.25 0.25
0.25
0.25 0.25 0.25 0.25
0.25 |
4 (2đ) |
Cho các số
Chứng minh rằng
Ta có
Suy ra
Vậy
|
0.5 0.5
0.5
0.5 |
5 (5đ) |
Câu 5: (5 điểm)
Cho ∆ABC có
a) Tính số đo của
b) Chứng minh CE + BF < BC - Vẽ hình đúng, đủ, chính xác. a)
Tính số đo của
Ta
có
Mà
b) Chứng minh CE + BF < BC -
Suy
ra ∆BFI = ∆BMI ( g-c-g)
-
∆CNI = ∆CEI ( g-c-g)
Do đó CE + BF = BM + CN < BM + MN + NC = BC Vây CE + BF < BC |
0.5 0.5 0.5 0.5 0.5 0.25
0.25
0.5 0.5 0.5 0.25 0.25 |
- Một bài toán có thể có nhiều cách giải khác nếu đúng và phù hợp đều đạt điểm tối đa. Giám khảo cần thảo lụân, thống nhất đáp án và biểu điểm trước khi chấm.
PHÒNG GD-ĐT ĐỨC THỌ |
ĐỀ THI HỌC SINH GIỎI NĂM HỌC 2009-2010 MÔN TOÁN LỚP 7 (Thời gian làm bài: 120 phút) |
Câu 1. Tìm giá trị n nguyên dương:
a)
![]() ;
;
b) 8 < 2n < 64
Câu 2. Thực hiện phép tính:
![]()
Câu 3. Tìm các cặp số (x; y) biết:
![]() ;
;
![]()
Câu 4. Tìm giá trị nhỏ nhất hoặc lớn nhất của các biểu thức sau :
a) A =
![]() + 5
+ 5
b) B =
![]()
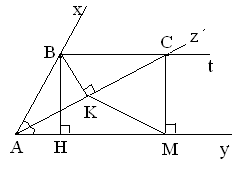
Câu 5. Cho tam giác ABC (CA < CB), trên BC lấy các điểm M và N sao cho BM = MN = NC. Qua điểm M kẻ đường thẳng song song với AB cắt AN tại I.
a) Chứng minh: I là trung điểm của AN
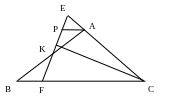
b) Qua K là trung điểm của AB kẻ đường thẳng vuông góc với đường phân giác góc ACB cắt đường thẳng AC tại E, đường thẳng BC tại F. Chứng minh AE = BF
ĐÁP ÁN VÀ HƯỚNG DẪN CHẤM TOÁN 7-ĐỨC THỌ
Câu 1. Tìm giá trị n nguyên dương:
a) (2điểm) ![]() ;
=> 34n-3 = 3n => 4n – 3 = n => n =
1
;
=> 34n-3 = 3n => 4n – 3 = n => n =
1
b) (2điểm) 8 < 2n < 64 => 23 < 2n < 26 => n = 4, n = 5
Câu 2. Thực hiện phép tính: (3điểm)
![]()
=
![]()
=
![]()
Câu 3. Tìm các cặp số (x; y) biết:
(2điểm) ![]() =>
=>
![]()
=> x2
= 9.25 = 152
=> x =
![]() 15
15
=> y2
= 9.81 = 272
=> y =
![]() 27
27
Do x, y cùng dấu nên:
x = 15; y = 27 và x = - 15; y = - 27
(2điểm) ![]()
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
![]()
![]()
=>
![]() => - 5x = 7x – 24 => x = 2
=> - 5x = 7x – 24 => x = 2
Thay x = 2 vào trên ta được:
![]() => - 5 - 25y = 24 y => - 49y = 5 => y =
=> - 5 - 25y = 24 y => - 49y = 5 => y =
![]()
Vậy x = 2, y =
![]() thoả mãn đề bài
thoả mãn đề bài
Câu 4. Tìm giá trị nhỏ nhất hoặc lớn nhất của các biểu thức sau:
a)
(2điểm) A
=
![]() + 5
+ 5
Ta
có :
![]()
![]() 0. Dấu “=” xẩy ra
0. Dấu “=” xẩy ra
![]() x = - 5.
x = - 5.
![]() A
A
![]() 5.
5.
Vậy:
Min A = 5
![]() x = - 5.
x = - 5.
b)
(2điểm) B
=
![]() =
=
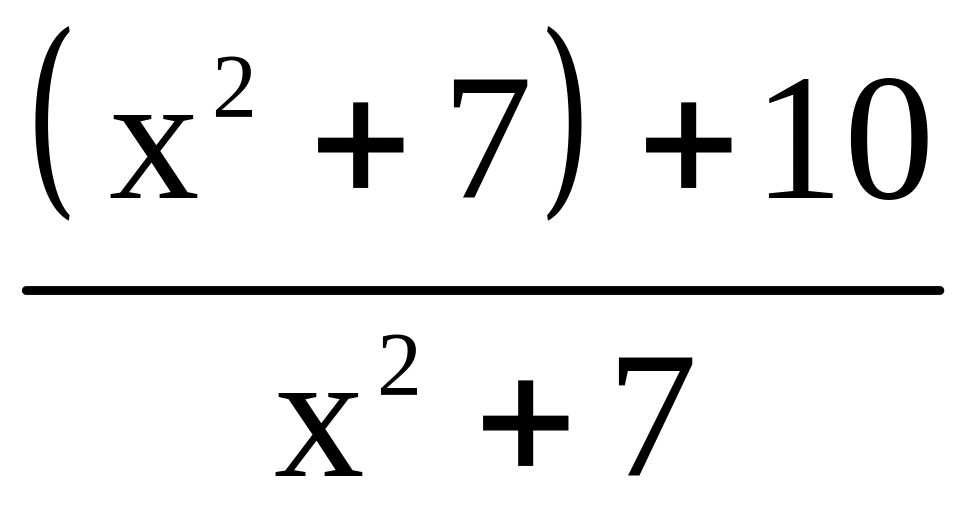 = 1 +
= 1 +
![]()
Ta
có: x![]()
![]() 0. Dấu = xảy ra
0. Dấu = xảy ra
![]() x = 0
x = 0
![]() x
x![]() + 7
+ 7
![]() 7 (2 vế dương)
7 (2 vế dương)
![]()
![]()
![]()
![]() => 1 +
=> 1 +
![]()
![]() 1 +
1 +
![]()
![]() B
B
![]()
![]()
Dấu
“=” xảy ra
![]() x = 0
x = 0
Vậy: Max B =
![]()
![]() x = 0.
x = 0.
Câu 5.
a) (3điểm) Từ I kẻ đường thẳng // BC cắt AB tại H. Nối MH.
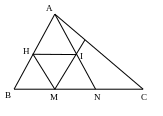 Ta có:
Ta có:
![]() BHM
=
BHM
=
![]() IMH
vì:
IMH
vì:
![]() (so
le trong)
(so
le trong)
![]() (so
le trong)
(so
le trong)
Cạnh HM chung =>BM = IH = MN
![]() AHI
=
AHI
=
![]() IMN
vì:
IMN
vì:
IH = MN (kết quả trên)
![]()
![]() (đồng vị)
(đồng vị)
=> AI = IN (đpcm)
b)
(2điểm) Từ A kẻ đường thẳng song song với BC
cắt EF tại P.
![]() PKA
=
PKA
=
![]() FKB
vì:
FKB
vì:
![]() (đối đỉnh)
(đối đỉnh)
![]() (so le trong)
(so le trong)
AK = KB (gt)
=> AP = BF (1)
![]() (đồng vị)
(đồng vị)
![]() (
(![]() CFE
cân)
CFE
cân)
=>
![]() =>
=>
![]() APE
cân
APE
cân
=> AP = AF (2). Từ (1) và (2) => AE = BF (đpcm)
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
H
Đ
Số báo danh …...............……
……………. …........................ |
ĐỀ GIAO LƯU HỌC SINH GIỎI CẤP HUYỆN Năm học: 2013-2014 Môn thi: Toán Lớp 7 THCS Ngày thi: 07 tháng 4 năm 2014 Thời gian : 150 phút (không kể thời gian giao đề) Đề này có 01 trang |
Câu 1(5 điểm):
a) Cho biểu thức: P = x -
4xy + y. Tính giá trị của P với
![]() y = -0,75
y = -0,75
b) Rút gọn biểu thức:
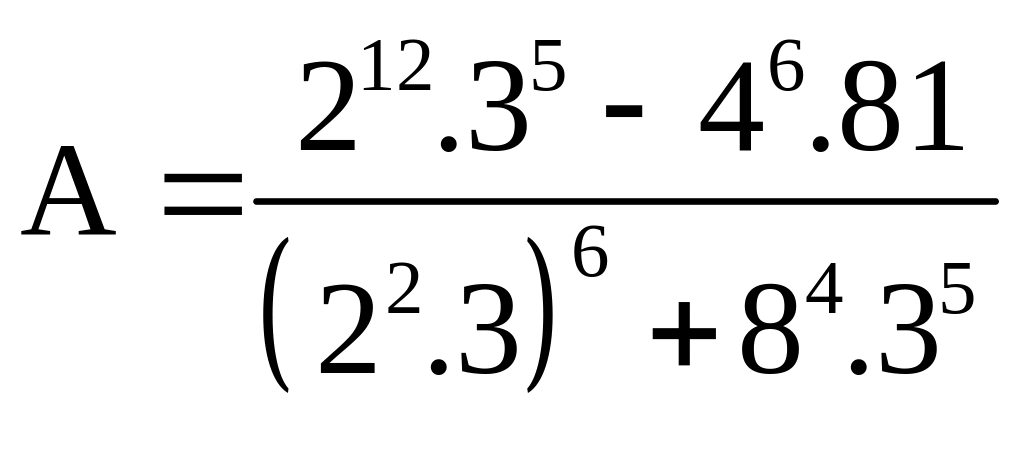
Câu 2 (4điểm):
Tìm x, y, z, biết:
2x = 3y; 4y = 5z và x + y + z = 11
Tìm x, biết:
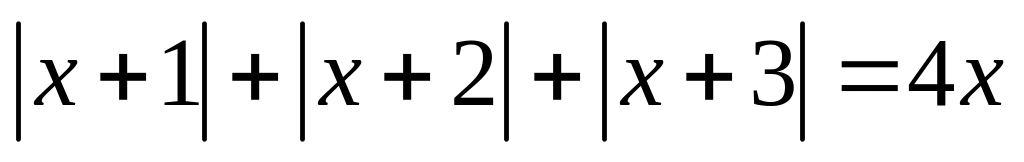
Câu 3(3 điểm). Cho hàm số: y = f(x) = -4x3 + x
Tính f(0), f(-0,5)
Chứng minh: f(-a) = -f(a).
Câu 4: (1,0 điểm): Tìm cặp số nguyên (x;y) biết: x + y = x.y
Câu
5(6
điểm):Cho
![]() ABC
có góc A nhỏ hơn 900.
Vẽ ra ngoài
tam giác ABC các tam giác vuông
cân tại A là
ABC
có góc A nhỏ hơn 900.
Vẽ ra ngoài
tam giác ABC các tam giác vuông
cân tại A là
![]() ABM
và
ABM
và
![]() ACN.
ACN.
Chứng minh rằng:
 AMC
=
AMC
=
 ABN;
ABN;Chứng minh: BN
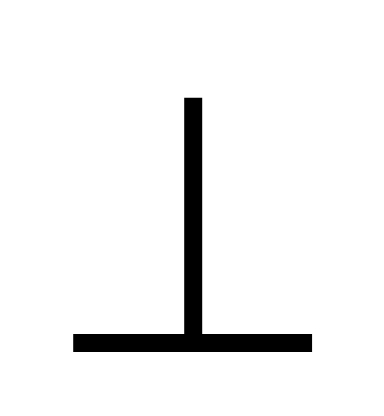 CM;
CM;Kẻ AH
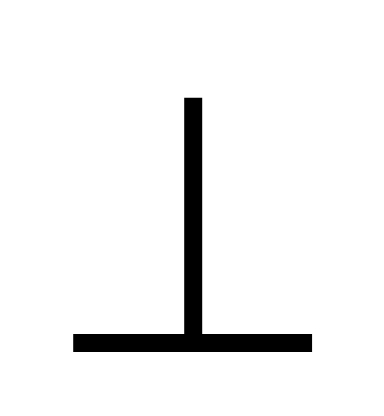 BC
(H
BC
(H
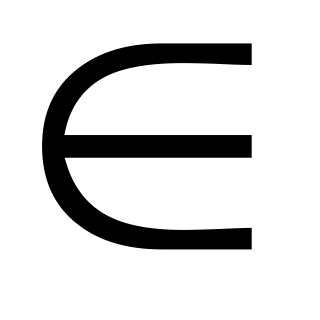 BC). Chứng minh AH đi qua trung điểm của MN.
BC). Chứng minh AH đi qua trung điểm của MN.
Câu
6 (1
điểm):Cho ba số
a, b, c thõa mãn:
![]() và a + b + c = 1. Tìm giá trị nhỏ nhất của c.
và a + b + c = 1. Tìm giá trị nhỏ nhất của c.

 Hết
Hết
Chú ý: - Giám thị không giải thích gì thêm.
- Học sinh không được dùng máy tính.
PHÒNG GIÁO DỤC VÀ ĐÀO
HUYỆN HẬU LỘC
HƯỚNG DẪN CHẤM ĐỀ THI HỌC SINH GIỎI TOÁN 7
NĂM HỌC 2013-2014
Câu |
Nội dung |
Điểm |
|
Câu 1 (5điểm) |
a)
Ta có:
+) Với x = 1,5 và y = -0,75 thì P = 1,5 -4.1,5(-0,75) -0,75 = 1,5(1 + 3) = 6 -0,75 = 5,25 +) Với x = -1,5 và y = - 0,75 thì P = -1,5 -4(-1,5).(-0,75) - 0,75 = -1,5(1+3) - 0,75 = -6,75
|
1,5
1,5 |
|
b)
|
2 |
||
Câu 2 (4 điểm) |
a) 2x
= 3y; 4y = 5z
|
1
1 |
|
b)
Vì
VT
(1)
|
1
1 |
||
Câu 3 (3điểm) |
f(-0,5)
= -4.(-
|
1 1 |
|
-
f(a) = -
|
0,5
0,5 |
||
Câu 4 (1 điểm) |
x + y = x.y
vì
do
đó y - 1 =
Nếu y = 2 thì x = 2 Nếu y = 0 thì x = 0 Vậy các cặp số nguyên (x;y) là: (0,0) và (2;2)
|
0,5
0,5 |
|
Câu 5 (6 điểm) |
a) Xét
AM
= AB ( AC
= AN (
Suy ra
|
|
1,0
1,0
0,5 |
|
b) Gọi I là giao điểm của BN với AC, K là giao điểm của BN với MC. Xét
|
1 1 0,5 |
|
|
c) Kẻ
ME
-
Ta có:
Lại
có
Xét
MA = AB Suy
ra
-
Chứng minh tương tự ta có
Xét
ME = NF (= AH)
Vậy AH đi qua trung điểm của MN. |
0,25
0,25
0,25
0,25 |
|
Câu 6 (1 điểm) |
Vì:
Hay
3c
Vậy
giá trị nhỏ nhất của c
là: - |
0,5
0,5 |
|
Chú ý: - Học sinh làm cách khác đúng vẫn cho điểm tối đa.
- Học sinh không vẽ hình hoặc vẽ sai cơ bản thì không chấm bài hình.
PHÒNG GD-ĐT HÒA BÌNH Đề chính thức Gồm 01 trang
|
KỲ THI CHỌN HỌC SINH GIỎI LỚP 6, 7 NĂM HỌC 2009 – 2010 Môn thi: Toán 7 Thời gian: 90 phút (không kể thời gian giao đề) |
Câu 1 (4đ):
Tính giá trị của biểu thức
A =
![]() +
+
![]() +
+
![]() + … +
+ … +
![]()
Tính:
24 + 8 [(-2)2 :
![]() ]0
– 2-2.4 + (-2)2
]0
– 2-2.4 + (-2)2
Câu 2 (4đ):
Hai lớp 7A và 7B đi lao động trồng cây. Biết rằng tỉ số giữa số cây trồng được của lớp 7A và 7B là 0,8. Lớp 7B trồng nhiều hơn lớp 7A là 20 cây. Tính số cây mỗi lớp trồng được?
Câu 3 (4đ):
Tìm x biết:
a)
![]() - x :
- x :
![]() = 2
= 2
b) 2![]() = 8
= 8
Câu 4 (4đ):
Ba đội máy ủi đất làm ba khối lượng công việc như nhau. Đội thứ nhất hoàn thành công việc trong 4 ngày, đội thứ hai hoàn thành trong 6 ngày, đội thứ ba hoàn thành trong 8 ngày. Hỏi mỗi đội có bao nhiêu máy (cùng công suất), biết rằng đội thứ nhất có nhiều hơn đội thứ hai 2 máy.
Câu 5 (4đ):
Cho góc
![]() .
Trên Ox lấy hai điểm A và B, trên Oy lấy hai điểm C và
D sao cho OA = OC, AB = CD. Chứng minh:
.
Trên Ox lấy hai điểm A và B, trên Oy lấy hai điểm C và
D sao cho OA = OC, AB = CD. Chứng minh:
ABC = ACD
ABD = BCD
- - - - - - - - - - - - - - - - - - Hết - - - - - - - - - - - - - - - - - -
HƯỚNG DẪN CHẤM-HÒA BÌNH
Câu 1 (4đ):
Tính giá trị của biểu thức
A =
![]() +
+
![]() +
+
![]() + … +
+ … +
![]()
Ta có:
![]() =
=
![]() -
-
![]() ;
; ![]() =
=
![]() -
-
![]() ; … ;
; … ;
![]() =
=
![]() -
-
![]() (1đ)
(1đ)
A = 1 + (![]() -
-
![]() )
+ (
)
+ (![]() -
-
![]() )
+ … + (
)
+ … + (![]() -
-
![]() )
-
)
-
![]() = 1 -
= 1 -
![]() =
=
![]() (1đ)
(1đ)
Tính:
24 + 8 [(-2)2 :
![]() ]0
– 2-2.4 + (-2)2 = 16 + 8.1 - 2-2.22
+ 4 (1đ)
]0
– 2-2.4 + (-2)2 = 16 + 8.1 - 2-2.22
+ 4 (1đ)
= 16 + 8 -20 + 4
= 16 + 8 – 1 + 4 = 27 (1đ)
Câu 2 (4đ):
Gọi x, y theo thứ tự là số cây trồng được của lớp 7A, 7B. Ta có:
y – x = 20 và
![]() = 0,8
= 0,8
![]()
![]() =
=
![]() =
=
![]() (1) (1đ)
(1) (1đ)
Từ (1) ta có tỉ lệ thức:
![]() =
=
![]() =
=
![]() =
=
![]() = 20 (2) (1đ)
= 20 (2) (1đ)
Từ (2) ta có:
![]() = 20
= 20
![]() x = 80 cây (lớp 7A) (1đ)
x = 80 cây (lớp 7A) (1đ)
![]() = 20
= 20
![]() y = 100 cây (lớp 7B) (1đ)
y = 100 cây (lớp 7B) (1đ)
Câu 3 (4đ):
a)
![]() - x :
- x :
![]() = 2
= 2
x :
![]() =
=
![]() - 2
(0,5đ)
- 2
(0,5đ)
x :
![]() =
=
![]() (0,5đ)
(0,5đ)
x =
![]() .
.
![]() (0,5đ)
(0,5đ)
x =
![]() (0,5đ)
(0,5đ)
b) 2![]() = 8
= 8
2![]() = 23
(0,5đ)
= 23
(0,5đ)
x +
![]() = 3
(0,5đ)
= 3
(0,5đ)
x = 3 -
![]() (0,5đ)
(0,5đ)
x =
![]() (0,5đ)
(0,5đ)
Câu 4 (4đ):
Gọi x, y, z theo thứ tự là số máy ủi của đội thứ nhất, thứ hai, thứ ba
Do các máy có cùng công suất, khối lượng công việc của ba đội như nhau
![]() Số máy và thời gian hoàn thành công việc là tỉ lệ
nghịch với nhau (1đ)
Số máy và thời gian hoàn thành công việc là tỉ lệ
nghịch với nhau (1đ)
Ta có:
![]() =
=
![]() =
=
![]() và x – y = 2
(1đ)
và x – y = 2
(1đ)
Theo tính chất của dãy tỉ số bằng nhau, ta có:
![]() =
=
![]() = 24
(1đ)
= 24
(1đ)
Từ đó:
![]() = 24
= 24
![]() x = 6 (số máy của đội thứ nhất)
x = 6 (số máy của đội thứ nhất)
![]() = 24
= 24
![]() y = 4 (số máy của đội thứ hai)
y = 4 (số máy của đội thứ hai)
![]() = 24
= 24
![]() z = 3 (số máy của đội thứ ba)
(1đ)
z = 3 (số máy của đội thứ ba)
(1đ)
C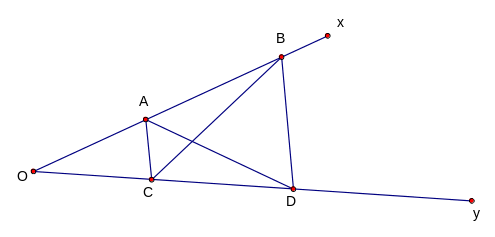 âu
5 (4đ):
âu
5 (4đ):
Già thiết: góc
![]() ;
OA=OC, AB=CD
;
OA=OC, AB=CD
Kết luận: a) ABC = ACD
b) ABD = BCD
(Hình vẽ và GT, KL 0,5đ)
Xét OAD và OCB có:
- Góc
![]() chung
chung
- OA = OC (gt)
- OB = OD
Do đó: OAD = OCB
(c-g-c)
![]() AD = BC (1,5đ)
AD = BC (1,5đ)
a) Xét ABC và ACD có
- AB = CD (gt)
- AC chung
- AD = BC
Do đó: ABC = ACD (1đ)
b) Xét ABD và BCD có
- AB = CD (gt)
- BD chung
- AD = BC
Do đó: ABD = BCD (1đ)
Ghi chú: Học sinh làm cách khác đúng vẫn được điểm tối đa của câu đó
- - - - - - - - - - - - - - - - - - Hết - - - - - - - - - - - - - - - - - -
phßng gi¸o dôc ®µo t¹o h¬ng khª
®Ò chÝnh thøc |
kú thi chän häc sinh giái huyÖn N¨m häc 2011 - 2012 M«n to¸n LíP 7 Khóa ngày 17.18.19 – 4 – 2012 Thời gian làm bài: 120 phút (không kể thời gian giao đề)
|
Bài 1:
Tìm x, biết
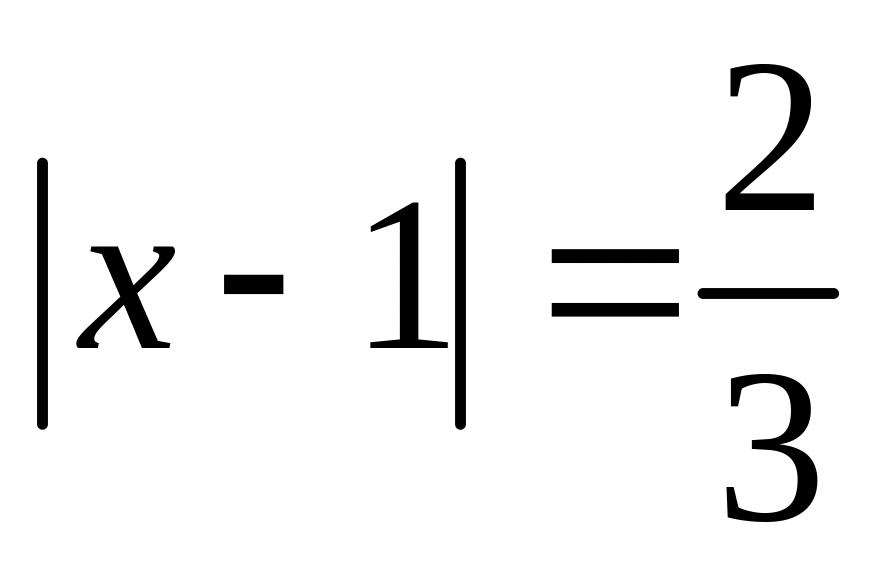 ;
;Tính giá trị của biểu thức sau:
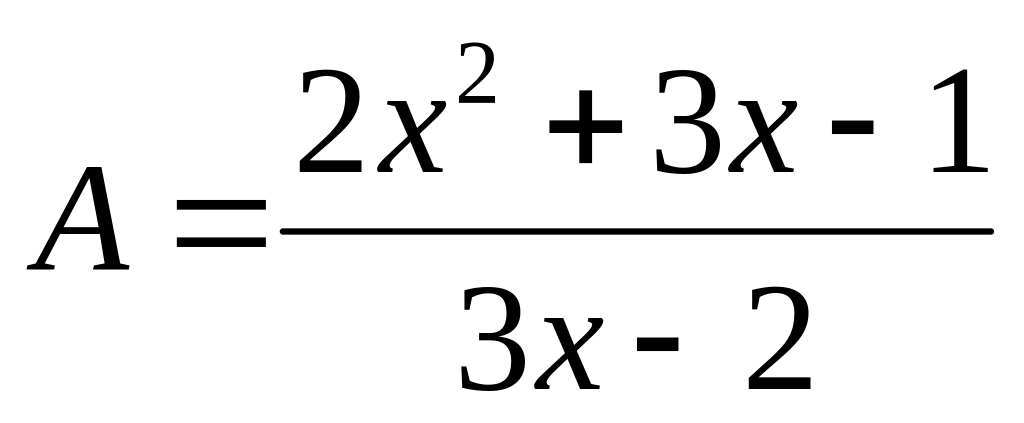 với
với
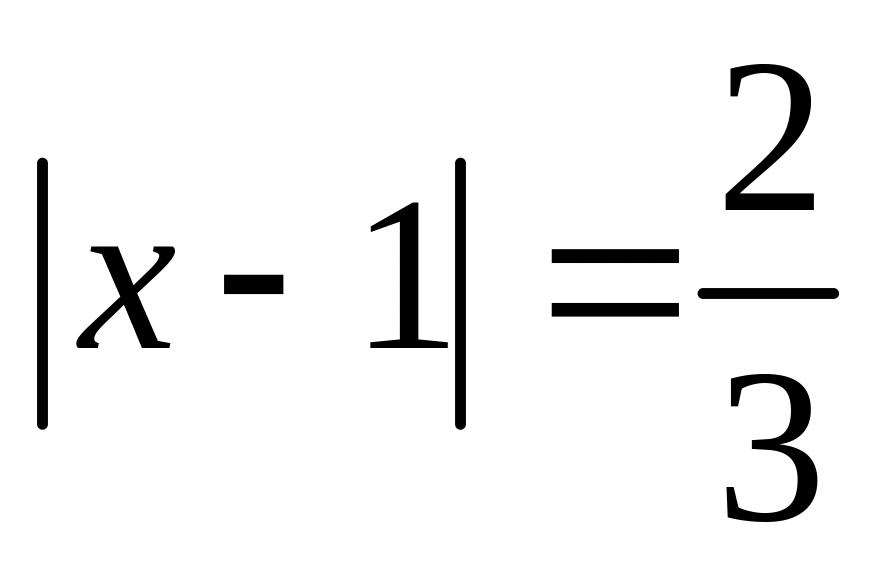
Bài 2:
Tìm chữ số tận cùng của A biết A = 3n+2 – 2n+2 + 3n – 2n
Tìm các giá trị nguyên của x để
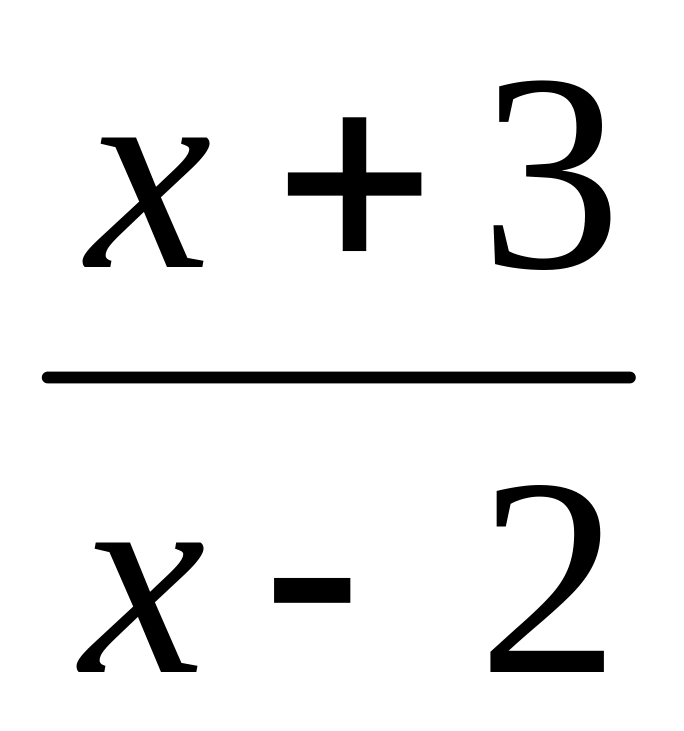 nhận
giá trị nguyên.
nhận
giá trị nguyên.
Bài 3: Cho đa thức f(x) xác định với mọi x thỏa mãn:
x.f(x + 2) = (x2 – 9).f(x).
Tính f(5).
Chứng minh rằng f(x) có ít nhất 3 nghiệm.
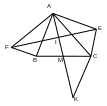
Bài 4: Cho tam giác ABC, trung tuyến AM. Trên nửa mặt phẳng chứa đỉnh C bờ là đường thẳng AB dựng đoạn AE vuông góc với AB và AE = AB. Trên nửa mặt phẳng chứa đỉnh B bờ là đường thẳng AC dựng đoạn AF vuông góc với AC và AF = AC. Chứng minh rằng:
a) FB = EC
b) EF = 2AM
c) AM EF.
Bài 5: Cho a, b, c, d là các số dương. Tìm giá trị nhỏ nhất của biểu thức:
![]()

HƯỚNG DẪN CHẤM BÀI THI HỌC SINH GIỎI HUYỆN NĂM HỌC 2011 - 2012
MÔN TOÁN LỚP 7
Khóa ngày 17.18.19 – 4 – 2012
Bài |
Hướng dẫn chấm |
Điểm |
|
1(6đ) |
|
4.0đ |
|
Với x = 1/3 thay vào A ta được A = -2/9
|
2.0đ |
||
2 (3đ) |
|
1.5đ |
|
|
1.5đ |
||
3(4đ) |
x = 3 f(5) = 0 x = 5 là một nghiệm x = -3 f(-1) = 0 x = -1 là một nghiệm Vậy f(x) có ít nhất là 3 nghiệm.
|
2.0đ
2.0đ |
|
4 (6đ) |
|
EAF và KCA có AE = AB = CK; AF
= AC (gt);
EAF = KCA (cgc) EF = AK = 2AM. c)
Từ EAF
= KCA
|
3.0đ
1.5đ
1.5đ |
5(1đ) |
Không
mất tính tổng quát, giả sử a
b
c
d. Áp dụng BĐT
Suy ra A ≥ c + d – a – b. Dấu “=” xảy ra khi và chỉ khi dấu “=” ở (1) và (2) xảy ra (x – a)(d – x) ≥ 0 và (x – b)(c – x) ≥ 0 a x d và b x c. Do đó minA = c + d –a – b b x c. |
1.0đ
|
|
Ghi chú: Các cách giải khác đầy đủ và chính xác vẫn cho điểm tối đa.
UBND HUYỆN KIM SƠN P |
KỲ KHẢO SÁT HỌC SINH GIỎI LỚP 7 CẤP HUYỆN NĂM HỌC 2010-2011 Môn: Toán - Lớp 7 Thời gian làm bài: 120 phút (Không kể thời gian giao đề) |
ĐỀ CHÍNH THỨC
Bài 1: ( 2,0 điểm)
a. Tìm x, y biết:
![]() =
=
![]() và x + y = 22
và x + y = 22
b. Cho
![]() và
và
![]() .
Tính M =
.
Tính M =
![]()
Bài 2: ( 2,0 điểm)
Thực hiện tính:
a. S =
![]()
b. P =
![]()
Bài 3: ( 2,0 điểm)
Tìm x biết:
a.
![]()
b.
![]()
B
 ài
4: ( 4,0 điểm)
ài
4: ( 4,0 điểm)
Cho tam giác ABC có B < 900 và B = 2C. Kẻ đường cao AH. Trên tia đối của tia BA lấy điểm E sao cho BE = BH. Đường thẳng HE cắt AC tại D.
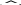
a. Chứng minh BEH = ACB.
b. Chứng minh DH = DC = DA.
c. Lấy B’ sao cho H là trung điểm của BB’. Chứng minh tam giác AB’C cân.
d. Chứng minh AE = HC.

UBND HUYỆN KIM SƠN P |
KỲ KHẢO SÁT HỌC SINH GIỎI LỚP 7 CẤP HUYỆN NĂM HỌC 2009-2010 Môn: Toán - Lớp 7 Thời gian làm bài: 120 phút (Không kể thời gian giao đề) |
HƯỚNG DẪN CHẤM
Bài 1: (2,0 điểm)
|
0,25 |
|
0,25 |
|
0,25 |
|
|
|
0,25 |
(1)
|
0,25 |
(1)
|
0,25 |
|
0,25 |
|
0,25 |
Bài 2: ( 2,0 điểm)
Thực hiện tính:
2S =
|
0,25 |
2S-S =
|
0,25 |
S = |
0,25 |
S
|
0,25 |
|
|
P =
|
0,25 |
|
0,25 |
|
0,25 |
|
0,25 |
Bài 3: ( 2,0 điểm)
|
0,25 |
|
0,25 |
|
0,25 |
|
0,25 |
|
|
|
0,25 |
|
0,25 |
|
0,25 |
|
0,25 |
Bài 4: ( 4,0 điểm)
Câu a: 0,75 điểm |
Hình vẽ: |
|
BEH cân tại B nên E = H1 |
0,25 |
|
ABC = E + H1 = 2 E |
0,25 |
|
ABC = 2 C BEH = ACB |
0,25 |
|
Câu b: 1,25 điểm |
|
|
Chứng tỏ được DHC cân tại D nên DC = DH. |
0,50 |
|
DAH = 900 - C |
0,25 |
|
DHA = 900 - H2 =900 - C |
0,25 |
|
DAH cân tại D nên DA = DH. |
0,25 |
|
Câu c: 1,0 điểm |
||
ABB’ cân tại A nên B’ = B = 2C |
0,25 |
|
B’ = A1 + C nên 2C = A1 + C |
0,50 |
|
C = A1 AB’C cân tại B’ |
0,25 |
|
Câu d: 1,0 điểm |
||
AB = AB’ = CB’ |
0,25 |
|
BE = BH = B’H |
0,25 |
|
Có: AE = AB + BE HC = CB’ + B’H AE = HC |
0,50 |
|
UBND HUYỆN QUẾ SƠN P |
KỲ KHẢO SÁT HỌC SINH GIỎI LỚP 6,7,8 CẤP HUYỆN NĂM HỌC 2009-2010 Môn: Toán - Lớp 7 Thời gian làm bài: 120 phút (Không kể thời gian giao đề) |
Bài 1: (2,0 điểm)
a. Tìm x,
y biết:
![]() =
=
![]() và x + y = 22
và x + y = 22
b. Cho
![]() và
và
![]() .
Tính M =
.
Tính M =
![]()
Bài 2: (2,0 điểm)
Thực hiện tính:
a. S =
![]()
b. P =
![]()
Bài 3: (2,0 điểm)
Tìm x biết:
a.
![]()
b.
![]()
B
 ài
4: (4,0 điểm)
ài
4: (4,0 điểm)
 Cho
tam giác ABC có B < 900
và B = 2C. Kẻ đường cao AH. Trên tia đối của tia BA lấy
điểm E sao cho BE = BH. Đường thẳng HE cắt AC tại D.
Cho
tam giác ABC có B < 900
và B = 2C. Kẻ đường cao AH. Trên tia đối của tia BA lấy
điểm E sao cho BE = BH. Đường thẳng HE cắt AC tại D.
a. Chứng minh BEH = ACB.
b. Chứng minh DH = DC = DA.
c. Lấy B’ sao cho H là trung điểm của BB’. Chứng minh tam giác AB’C cân.
d. Chứng minh AE = HC.

UBND HUYỆN QUẾ SƠN P |
KỲ KHẢO SÁT HỌC SINH GIỎI LỚP 6,7,8 CẤP HUYỆN NĂM HỌC 2009-2010 Môn: Toán - Lớp 7 Thời gian làm bài: 120 phút (Không kể thời gian giao đề) |
Bài 1: (2,0 điểm)
|
0,25 |
|
0,25 |
|
0,25 |
|
|
|
0,25 |
(1)
|
0,25 |
(1)
|
0,25 |
|
0,25 |
|
0,25 |
Bài 2: (2,0 điểm) Thực hiện tính:
2S =
|
0,25 |
2S-S =
|
0,25 |
S = |
0,25 |
S
|
0,25 |
|
|
P =
|
0,25 |
|
0,25 |
|
0,25 |
|
0,25 |
Bài 3: (2,0 điểm)
|
0,25 |
|
0,25 |
|
0,25 |
|
0,25 |
|
|
|
0,25 |
|
0,25 |
|
0,25 |
|
0,25 |
Bài 4: (4,0 điểm)
Câu a: 0,75 điểm |
Hình vẽ: |
|
BEH cân tại B nên E = H1 |
0,25 |
|
ABC = E + H1 = 2 E |
0,25 |
|
ABC = 2 C BEH = ACB |
0,25 |
|
Câu b: 1,25 điểm |
|
|
Chứng tỏ được DHC cân tại D nên DC = DH. |
0,50 |
|
DAH = 900 - C |
0,25 |
|
DHA = 900 - H2 =900 - C |
0,25 |
|
DAH cân tại D nên DA = DH. |
0,25 |
|
Câu c: 1,0 điểm |
||
ABB’ cân tại A nên B’ = B = 2C |
0,25 |
|
B’ = A1 + C nên 2C = A1 + C |
0,50 |
|
C = A1 AB’C cân tại B’ |
0,25 |
|
Câu d: 1,0 điểm |
||
AB = AB’ = CB’ |
0,25 |
|
BE = BH = B’H |
0,25 |
|
Có: AE = AB + BE HC = CB’ + B’H AE = HC |
0,50 |
|
UBND HUYỆN TIÊN YÊN PHÒNG GIÁO DỤC VÀ ĐÀO TẠO -------------------- |
KỲ THI CHỌN HỌC SINH GIỎI CẤP HUYỆN CÁC KHỐI LỚP 6-7-8 NĂM HỌC 2011-2012 |
MÔN: TOÁN 7 Ngày thi: 18/04/2012 Thời gian làm bài: 120 phút (Không kể thời gian giao đề) |
|
Câu 1: Thực hiện phép tính
a.
![]()
b.
![]()
c.
![]()
Câu 2:
a,
Cho tỉ lệ thức
![]() .
Chứng minh rằng : (a+2c)(b+d) = (a+c)(b+2d)
.
Chứng minh rằng : (a+2c)(b+d) = (a+c)(b+2d)
b. Tìm hai số nguyên biết: Tổng, hiệu (số lớn trừ số bé), thương (số lớn chia số bé) của hai số đó cộng lại bằng 38.
Câu 3: Tìm x biết:
a)
![]() b)
b)
![]()
Câu 4:
Cho tam giác ABC với M trung điểm BC. Trên nửa nặt phẳng bờ AB không chứa C vẽ tia Ax vuông góc AB và lấy D sao cho AD = AB. Trên nửa mặt phẳng bờ AC không chứa B vẽ Ay vuông góc AC và lấy AE = AC. Chứng minh:
a, AM =
![]() ED
ED
b, AM
![]() DE
DE
===== Hết =====
HƯỚNG DẪN CHẤM
MÔN: TOÁN 7
Ngày thi: 18/04/2012
Câu |
Hướng dẫn chấm |
điểm |
1 |
a.
b.
c.
|
1
1
1 |
2 |
a, Cho tỉ lệ thức
Ta
có:
Xét: (a+2c)(b+d) = ab+ad+2bc+2cd =ab+3bc+2cd Và (a+c)(b+2d) = ab+2ad+bc+2cd = ab+3bc+2cd Vậy: (a+2c)(b+d) = (a+c)(b+2d).
b. Tìm hai số nguyên biết : Tổng, hiệu (số lớn trừ số bé), thương (số lớn chia số bé) của hai số đó cộng lại bằng 38. Gọi hai số càn tìm là a và b ( a,b thuộc Z và b khác 0) Giả sử a > b, khi đó có: (a+b) + (a-b) + a:b = 38 => 2a + a: b = 38 => 2ab + a = 38b => a = 38 b : (2b + 1) = (38b +19 -19) : (2b +1) = 19- (19/(2b+1)) Để a thuộc Z thì 2b + 1 phải là ước của 19. => 2b+1 = 1 => b = 0 (loại) 2b+1 = - 1 => b = -1 => a = -38 (loại) 2b+1 = 19 => b = 9 => a = 18 2b+1 = - 19 => b = -10 => a = 20 Vậy có 2 cặp số thỏa mãn: (18:9) và (20; -10)
|
1
2 |
3 |
a)
x = -11/30 và x = -1/30 b)
Không có giá trị của x thỏa mãn.
|
0.5
0.5 |
4 |
a, Để chứng tỏ DE = 2AM tạo ra đoạn thẳng gấp đôi AM bằng cách trên tia đối MA lấy MK = MA và đi
Xét
Và
Vậy:
b, Gọi H là giao điểm AM&DE ; Ta có
|
2
1 |
Phßng Gi¸o dôc- §µo t¹o TRùC NINH *
®Ò
chÝnh thøc |
®Ò thi chän häc sinh giái cÊp huyÖn n¨m häc: 2008 - 2009 m«n: To¸n 7 (Thêi gian:120 phót, kh«ng kÓ thêi gian giao ®Ò)
|
§Ò thi nµy gåm 01 trang
Bµi 1: (3,5 ®iÓm)
Thùc hiÖn phÐp tÝnh:
a)
![]()
b)
![]()
Bµi 2: (3,5 ®iÓm)
T×m x; y; z biÕt:
a)
2009 –
![]() = x
= x
b)
![]()
Bµi 3: (3 ®iÓm)
T×m 3 sè a; b; c biÕt:
![]() vµ a + b + c = – 50
vµ a + b + c = – 50
Bµi 4: (7 ®iÓm)
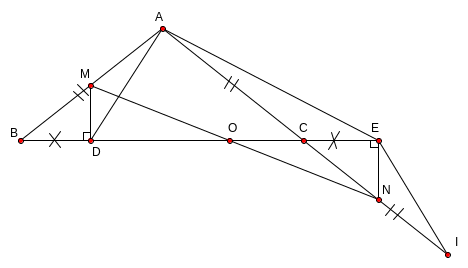
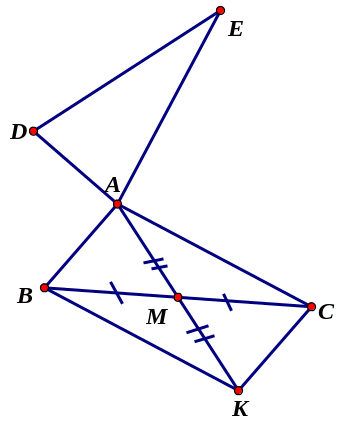
Cho tam gi¸c ABC c©n (AB = AC ; gãc A tï). Trªn c¹nh BC lÊy ®iÓm D, trªn tia ®èi cña CB lÊy ®iÓm E sao cho BD = CE. Trªn tia ®èi cña CA lÊy ®iÓm I sao cho CI = CA.
C©u 1: Chøng minh:
a)
![]()
b) AB + AC < AD + AE
C©u 2: Tõ D vµ E kÎ c¸c ®êng th¼ng cïng vu«ng gãc víi BC c¾t AB; AI theo thø tù t¹i M; N. Chøng minh BM = CN.
C©u 3: Chøng minh r»ng chu vi tam gi¸c ABC nhá h¬n chu vi tam gi¸c AMN.
Bµi 5 (3 ®iÓm):
T ×m
c¸c sè tù nhiªn a; b sao cho (2008.a + 3.b + 1).(2008a
+ 2008.a + b) = 225
×m
c¸c sè tù nhiªn a; b sao cho (2008.a + 3.b + 1).(2008a
+ 2008.a + b) = 225
§¸p ¸n §Ò thi HSG m«n To¸n 7-TRùC NINH
Bµi 1: 3 ®iÓm
C©u a: 1 ®iÓm (kÕt qu¶ = 0).
C©u b: 2 ®iÓm
![]()
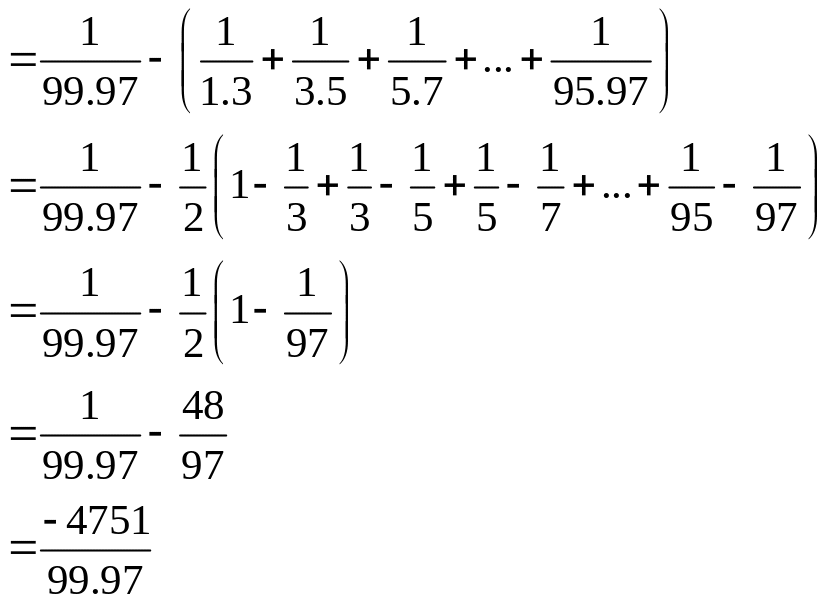
Bµi 2: 3,5 ®iÓm
C©u a: 2 ®iÓm
- NÕu x
![]() 2009
2009
![]() 2009 – x + 2009 = x
2009 – x + 2009 = x
![]() 2.2009 = 2x
2.2009 = 2x
![]() x = 2009
x = 2009
-
NÕu x < 2009
![]() 2009 – 2009 + x = x
2009 – 2009 + x = x
![]() 0 = 0
0 = 0
VËy
víi
![]() x
< 2009 ®Òu tho¶ m·n.
x
< 2009 ®Òu tho¶ m·n.
-
KÕt luËn : víi x
![]() 2009 th×
2009 th×
![]()
HoÆc c¸ch 2:
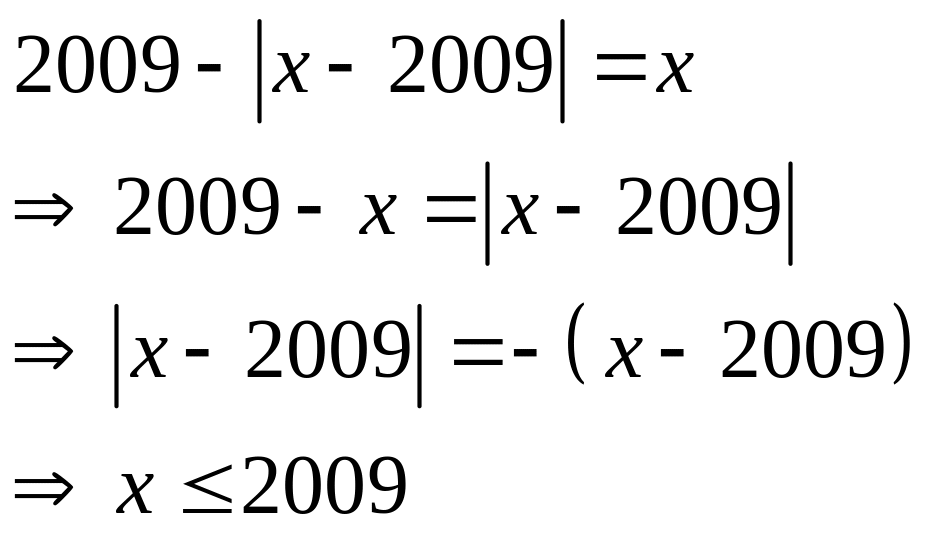
C©u b: 1,5 ®iÓm
![]() ;
;
![]() ;
;
![]()
Bµi 3: 2,5 ®iÓm
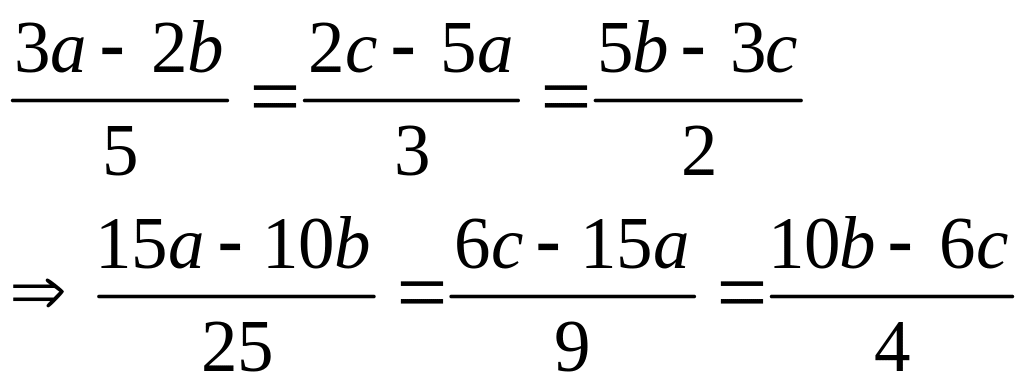
¸p dông tÝnh chÊt d·y tØ sè b»ng nhau cã:
![]()
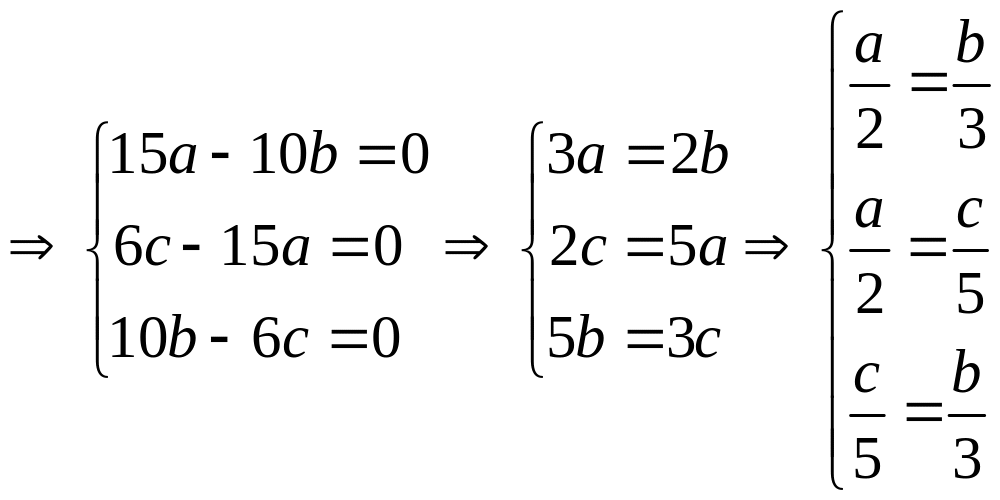
VËy
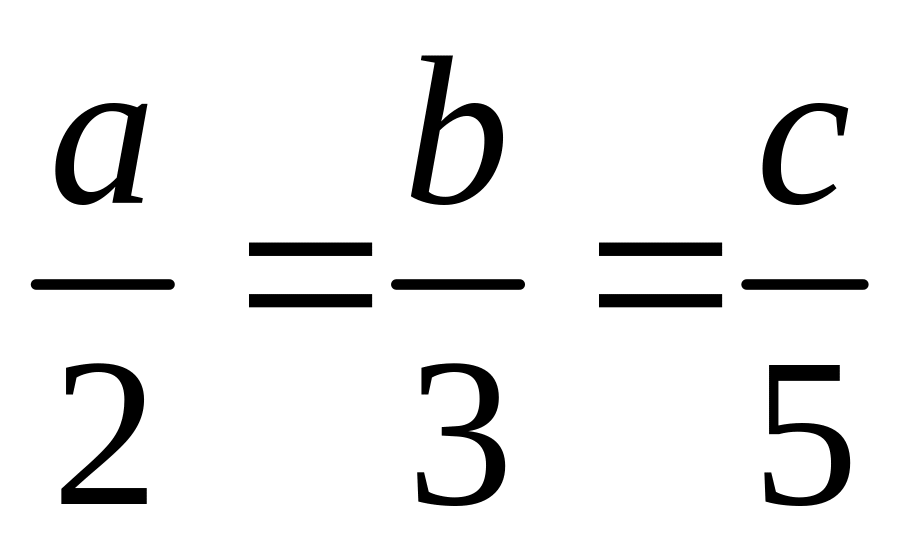
¸p
dông tÝnh chÊt d·y tØ sè b»ng nhau
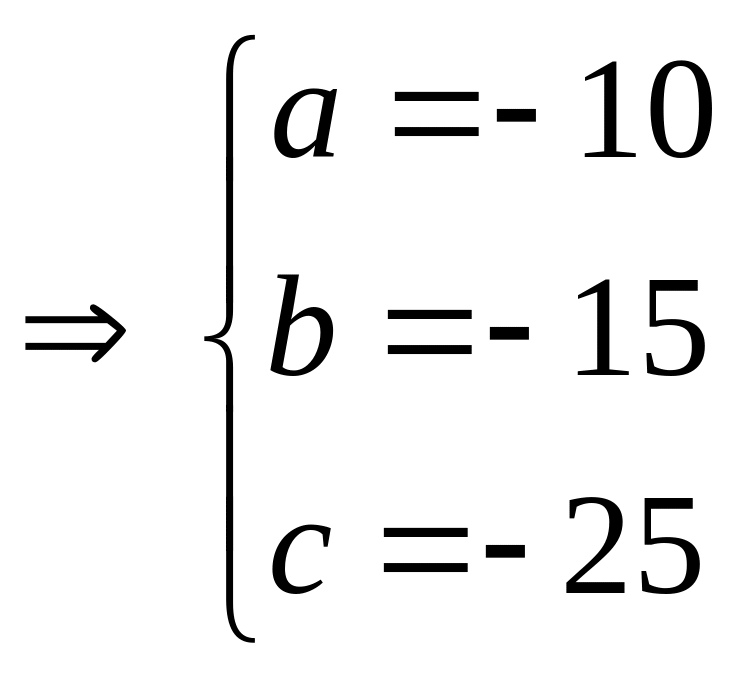
Bµi 4: 7 ®iÓm
C©u 1: mçi c©u cho 1,5 ®iÓm
C©u
a: Chøng minh
![]()
C©u b: cã AB + AC = AI
V×
![]() (2
c¹nh t¬ng øng)
(2
c¹nh t¬ng øng)
¸p
dông bÊt ®¼ng thøc tam gi¸c trong
![]() cã:
cã:
AE + EI > AI hay AE + AD > AB + AC
C©u 2: 1,5 ®iÓm
Chøng
minh
![]() vBDM
=
vBDM
=
![]() vCEN
(gcg)
vCEN
(gcg)
![]() BM = CN
BM = CN
C©u 3: 2,5 ®iÓm
V×
BM = CN
![]() AB + AC = AM + AN (1)
AB + AC = AM + AN (1)
cã
BD = CE (gt)
![]() BC = DE
BC = DE
Gäi giao ®iÓm cña MN víi BC lµ O ta cã:
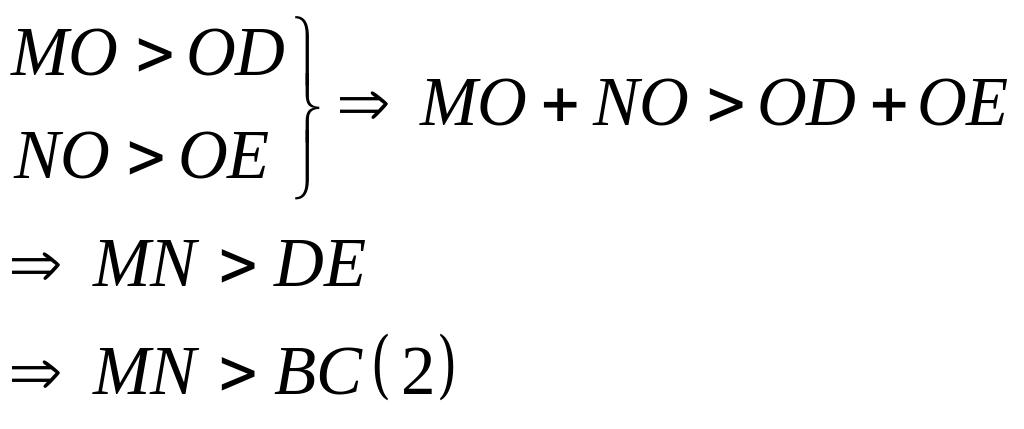
Tõ
(1) vµ (2)
![]() chu vi
chu vi
![]() nhá h¬n chu vi
nhá h¬n chu vi
![]()
Bµi 5: 2 ®iÓm
Theo ®Ò bµi
![]() 2008a + 3b + 1 vµ 2008a + 2008a + b lµ 2 sè lÎ.
2008a + 3b + 1 vµ 2008a + 2008a + b lµ 2 sè lÎ.
NÕu a
![]() 0
0
![]() 2008a + 2008a lµ sè ch½n
2008a + 2008a lµ sè ch½n
®Ó
2008a + 2008a + b lÎ
![]() b lÎ
b lÎ
NÕu
b lÎ
![]() 3b + 1 ch½n do ®ã
3b + 1 ch½n do ®ã
2008a + 3b + 1 ch½n (kh«ng tho¶ m·n)
VËy a = 0
Víi a = 0
![]() (3b + 1)(b + 1) = 225
(3b + 1)(b + 1) = 225
V×
b
![]() N
N
![]() (3b + 1)(b + 1) = 3.75 = 5. 45 = 9.25
(3b + 1)(b + 1) = 3.75 = 5. 45 = 9.25
3b + 1 kh«ng chia hÕt cho 3 vµ 3b + 1 > b + 1
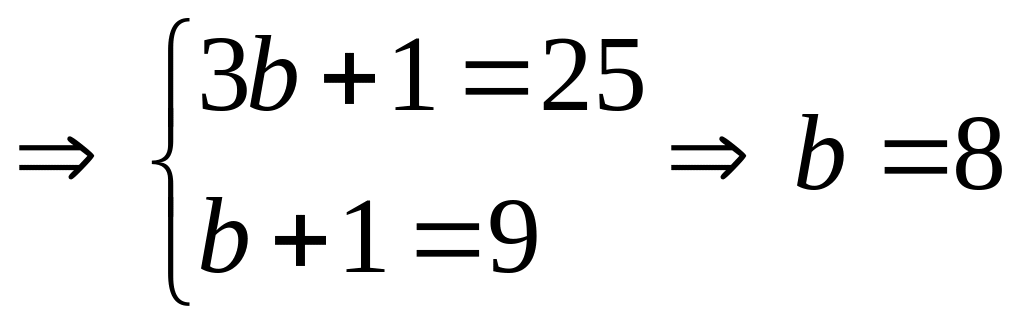
VËy a = 0 ; b = 8.
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO VIỆT YÊN
ĐỀ CHÍNH THỨC |
ĐỀ THI HỌC SINH GIỎI CẤP HUYỆN NĂM HỌC 2012-2013 MÔN THI: TOÁN 7 |
Câu 1. (4,0 điểm)
M =
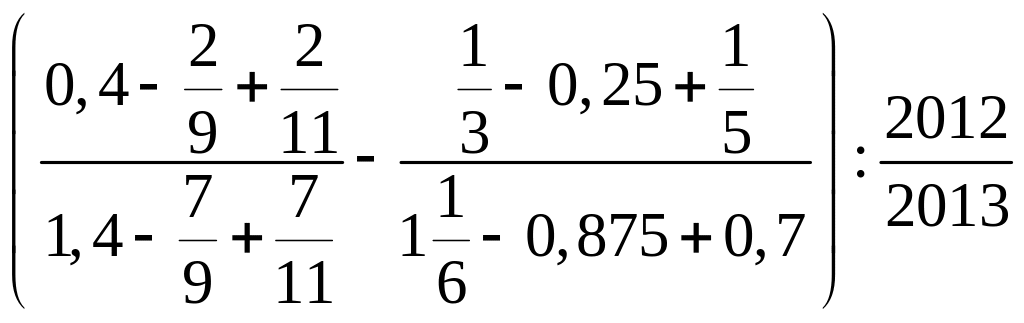
Tìm x, biết:
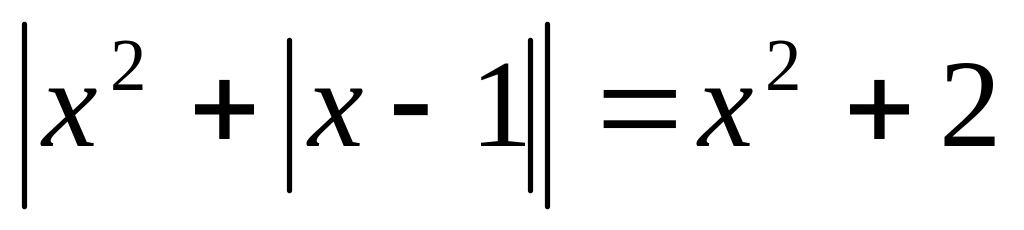 .
.
Câu 2. (5,0 điểm)
Cho a, b, c là ba số thực khác 0, thoả mãn điều kiện:
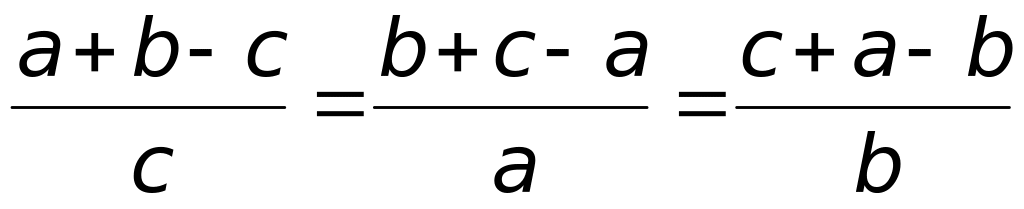 .
Hãy tính giá trị của biểu thức
.
Hãy tính giá trị của biểu thức
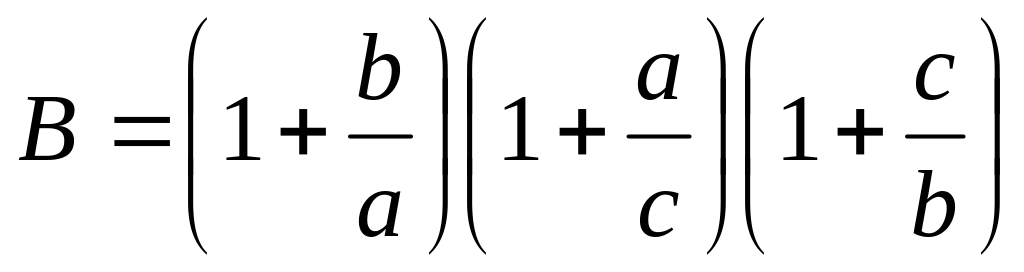 .
.
2) Ba lớp 7A, 7B, 7C cùng mua một số gói tăm từ thiện, lúc đầu số gói tăm dự định chia cho ba lớp tỉ lệ với 5:6:7 nhưng sau đó chia theo tỉ lệ 4:5:6 nên có một lớp nhận nhiều hơn dự định 4 gói. Tính tổng số gói tăm mà ba lớp đã mua.
Câu 3. (4,0 điểm)
Tìm giá trị nhỏ nhất của biểu thức A =
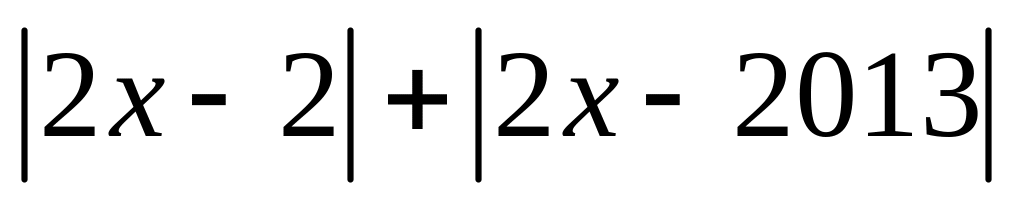 với x là số nguyên.
với x là số nguyên.Tìm nghiệm nguyên dương của phương trình
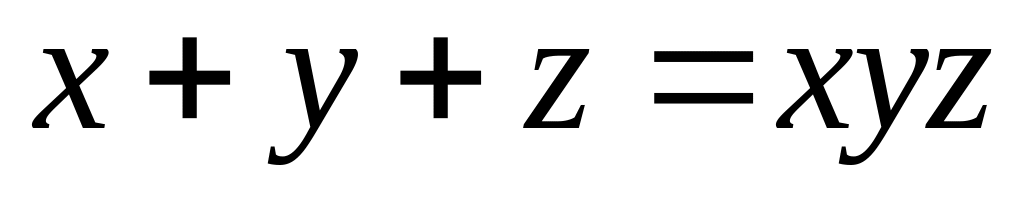 .
.
Câu 4. (6,0 điểm)
Cho
![]() =600
có tia phân giác Az . Từ điểm B trên Ax kẻ BH vuông góc
với Ay tại H, kẻ BK vuông góc với Az và Bt song song với
Ay, Bt cắt Az tại C. Từ C kẻ CM
=600
có tia phân giác Az . Từ điểm B trên Ax kẻ BH vuông góc
với Ay tại H, kẻ BK vuông góc với Az và Bt song song với
Ay, Bt cắt Az tại C. Từ C kẻ CM
vuông góc với Ay tại M . Chứng minh :
a ) K là trung điểm của AC.
b )
![]() KMC
là tam giác đều.
KMC
là tam giác đều.
c) Cho
BK = 2cm. Tính các cạnh
![]() AKM.
AKM.
Câu 5. (1,0 điểm)
Cho ba số dương 0![]() a
a![]() b
b![]() c
c![]() 1
chứng minh rằng:
1
chứng minh rằng:
![]()
--------------Hết----------------
Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh: .................................................................Số báo danh:.......................
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO VIỆT YÊN
|
HD CHẤM THI HỌC SINH GIỎI CẤP HUYỆN NĂM HỌC 2012-2013 MÔN THI: TOÁN 7 |
Câu |
Nội dung |
Điểm |
Câu 1 (4 điểm) |
1) Ta có:
KL:…….. |
0.5đ
0.5đ
0.5đ
0.5đ |
2) vì
+)
Nếu x
+) Nếu x <1 thì (*) = > x -1 = -2 => x = -1 KL:………….
|
0.5đ 0.5đ 0.5đ 0.5đ |
|
Câu 2 (5 điểm) |
1) +Nếu
a+b+c
Theo tính chất dãy tỉ số bằng nhau ,ta có:
mà
=>
Vậy B
= |
0.25đ 0.25đ 0.25đ
0.25đ |
+Nếu a+b+c = 0 Theo tính chất dãy tỉ số bằng nhau ,ta có:
mà
=>
Vậy B
= |
0.25đ 0.25đ 0.25đ
0.25đ |
|
2) Gọi tổng số gói tăm 3 lớp cùng mua là x ( x là số tự nhiên khác 0) Số gói tăm dự định chia chia cho 3 lớp 7A, 7B, 7C lúc đầu lần lượt là: a, b, c Ta
có:
Số gói tăm sau đó chia cho 3 lớp lần lượt là a’, b’, c’, ta có:
So sánh (1) và (2) ta có: a > a’; b=b’; c < c’ nên lớp 7C nhận nhiều hơn lúc đầu Vây:
c’ – c = 4 hay
Vậy số gói tăm 3 lớp đã mua là 360 gói.
|
0,5 đ
0,5đ
0,25đ
0,5đ
0,5đ
0,5đ 0,25đ |
|
Câu 3 (4 điểm) |
1) Ta có:
Dấu
“=” xảy ra khi
KL:…….. |
0,5đ
0,5đ 0,5đ
0,5đ |
2) Vì
x,y,z nguyên dương nên ta giả sử 1
Theo bài ra 1 =
=>
x 2 Thay
vào đầu bài ta có
=> y(1-z) - ( 1- z) + 2 =0 => (y-1) (z - 1) = 2 TH1: y -1 = 1 => y =2 và z -1 = 2 => z =3 TH2: y -1 = 2 => y =3 và z -1 = 1 => z =2 Vậy có hai cặp nghiệp nguyên thỏa mãn (1,2,3); (1,3,2) |
0,25đ 0,5đ
0,5đ 0,25đ 0,25đ 0,25đ |
|
Câu 4 (6 điểm) |
V ẽ h ình , GT _ KL
a,
b,
Ta
có : BH = CM ( t/c cặp đoạn chắn ) mà CK = BH =
Mặt
khác :
Từ
(1) và (2)
c)
Vì
Vì
AK =
Mà KC =
Theo phần b) AB = BC = 4 AH = BK = 2 HM = BC ( HBCM là hình chữ nhật) => AM = AH + HM = 6
|
0,25đ
1đ 1đ
0,5đ 0,25đ
0,25đ
0,25đ
0,5đ
0,25đ
0,25đ
0,25đ
0,25đ
0,25đ
0,5đ
0,25đ |
Câu 5 (1 điểm) |
Vì
Tương tự:
Do đó:
Mà
Từ (4) và (5) suy ra:
|
0,25đ
0,25đ
0,25đ
0,25đ |
Lưu ý: - Các tổ cần nghiên cứu kỹ hướng dẫn trước khi chấm.
- Học sinh làm bài các cách khác nhau mà đúng thì vẫn cho điểm tối đa.
- Bài hình không có hình vẽ thì không chấm.
- Tổng điểm của bài cho điểm lẻ đến 0,25đ ( ví dụ : 13,25đ , 14,5đ, 26,75đ).
PHÒNG GD & ĐT CHƯƠNG MỸ ĐỀ THI GIAO LƯU HỌC SINH GIỎI
NĂM HỌC: 2014 - 2015
ĐỀ CHÍNH THỨC
(Đề gồm 1 trang)
Thời gian: 120 phút (Không kể thời gian giao đề)

Câu 1.
a. Thực
hiện phép tính:
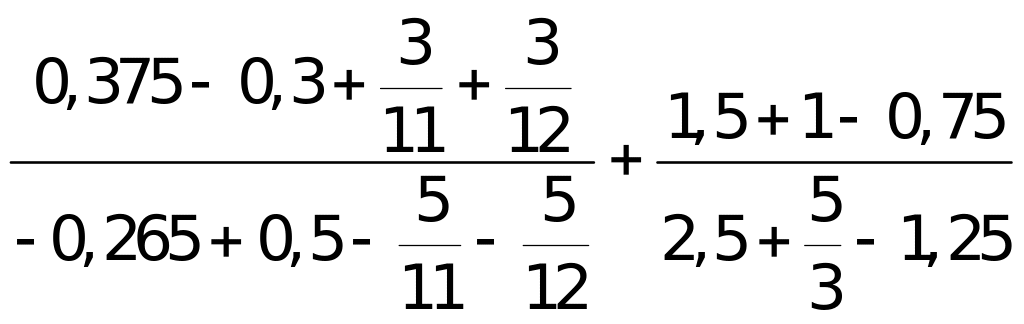
b. So
sánh:
![]() và
và
![]() .
.
Câu 2.
a. Tìm
![]() biết:
biết:
![]()
b. Tìm
![]() biết:
biết:
![]()
c. Tìm x; y; z biết: 2x = 3y; 4y = 5z và 4x - 3y + 5z = 7
Câu 3.
a. Tìm đa thức bậc hai biết f(x) - f(x-1) = x.
Từ đó áp dụng tính tổng S = 1+2+3+ ....+ n.
b. Cho
![]() Chứng minh:
Chứng minh:
![]() .
.
Câu 4.
Cho tam
giác ABC (![]() ),
đường cao AH. Gọi E; F lần lượt là điểm đối xứng
của H qua AB; AC, đường thẳng EF cắt AB; AC lần lượt
tại M và N. Chứng minh rằng:
),
đường cao AH. Gọi E; F lần lượt là điểm đối xứng
của H qua AB; AC, đường thẳng EF cắt AB; AC lần lượt
tại M và N. Chứng minh rằng:
a. AE = AF;
b. HA là
phân giác của
![]() ;
;
c. CM // EH; BN // FH.
Hết./.
Họ và tên: ...................................................Số báo danh:................................
PHÒNG GD & ĐT CHƯƠNG MỸ
ĐÁP ÁN THI GIAO LƯU HỌC SINH GIỎI. NĂM HỌC: 2012 - 2013
Môn thi: TOÁN 7
Câu |
Ý |
Nội dung |
Điểm |
|||||||||||||||||||
Câu 1 1,5 điểm |
a. 0,5 điểm |
A =
A= |
0.25
0.25
|
|||||||||||||||||||
b. 1 điểm |
Ta có:
Vậy:
|
0.5 0,5 |
||||||||||||||||||||
Câu 2 4 điểm |
a. 1 điểm |
Nếu x
>2 ta có: x - 2 + 2x - 3 = 2x + 1
Nếu
Nếu
x<
Vậy: x
= 6 ; x =
|
0.25 0.25
0.25
0.25 |
|||||||||||||||||||
b. 1.5 điểm |
Ta có:
xy + 2x - y = 5
|
0. 5 0. 5
0.5 |
||||||||||||||||||||
c. 1.5 điểm |
Từ:
2x= 3y; 4y = 5z
|
0. 5
0.5
0. 5 |
||||||||||||||||||||
Câu 3 1.5 điểm |
a. 0.5 điểm |
Đa thức bậc hai cần
tìm có dạng:
Ta
có :
Vậy
đa thức cần tìm là:
Áp dụng: +
Với x = 1 ta có :
+
Với x = 2 ta có :
…………………………………. +
Với x = n ta có :
|
0.25
0.25 |
|||||||||||||||||||
b. 1 điểm |
|
0.5
0.25
0.25 |
||||||||||||||||||||
Câu 4 3 điểm |
Hình vẽ 0. 5 đ |
|
0.25 |
|||||||||||||||||||
|
a. 1 điểm |
Vì AB là trung trực của EH nên ta có: AE = AH (1) Vì AC là trung trực của HF nên ta có: AH = AF (2) Từ (1) và (2) suy ra: AE = AF |
0.25 0.25 0. 5 |
|||||||||||||||||||
b. 1 điểm |
Vì M Vì
N Do
MB; NC cắt nhau tại A nên HA là phân giác trong góc H của
tam giác HMN hay HA
là phân giác của
|
0.25
0.25
0.25 0.25 |
||||||||||||||||||||
c. 1 điểm |
Ta có AH
MB
là phân giác ngoài góc M của tam giác HMN (cmt)
Chứng minh tương tự ta có: EH // CM |
0.25
0.25
0.25 |
UBND HUYỆN CHÂU THÀNH PHÒNG GD ĐT CHÂU THÀNH
ĐỀ THI CHÍNH THỨC (đề thi gồm 1 trang) |
KỲ THI HỌC SINH GIỎI CẤP HUYỆN LỚP 7 THCS - Năm học 2010 – 2011 MÔN : TOÁN Thời gian 150 phút (không kể thời gian giao đề) |
.
Câu 1: (2.0 điểm) Thực hiện tính:
A
=
![]() B
=
B
=
![]()
Câu 2: (2.0 điểm)
a. Tìm x,
y biết:
![]() =
=
![]() và x + y = 22
và x + y = 22
b. Cho
![]() và
và
![]() .
Tính M =
.
Tính M =
![]()
Câu 3: (2.0 điểm) Thực hiện tính:
a. S =
![]()
b. P =
![]()
Câu
4: (1.0 điểm) Vẽ đồ thị hàm số
![]() .
.
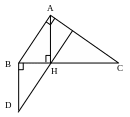
Câu 5: (3.0 điểm) Cho tam giác ABC có A = 900, B = 500. Đường thẳng AH vuông góc với BC tại H. Gọi d là đường thẳng vuông góc với BC tại B. Trên đường thẳng d thuộc nửa mặt phẳng bờ BC không chứa điểm A lấy điểm D sao cho BD = HA (Hình vẽ bên). a. Chứng minh ABH = DHB. b. Tính số đo góc BDH. |
|
c. Chứng minh đường thẳng DH vuông góc với đường thẳng AC.
_____________________ Hết _____________________
Họ và tên thí sinh: ……………………………………………... Số báo danh ………….
Chữ ký giám thị 1: ………………………..…. Giám thị 2 ………………………………
ĐÁP ÁN-CHÂU THÀNH
Câu 1: (Mỗi bước cho 0,25 điểm)
A =
= 1 - 1 + 0,5 = 0,5
|
= - 2 |
Câu 2:
a)
![]() =
=![]() 0,25
đ
0,25
đ
![]() 0,25
đ
0,25
đ
![]()
![]() 0,25
đ
0,25
đ
b)
![]() ;
;
![]()
![]() (1) 0,25
đ
(1) 0,25
đ
(1)
![]() 0,25
đ
0,25
đ
(1)
![]() 0,25
đ
0,25
đ
![]() :
:![]() =
=![]() :
:![]() 0,25
đ
0,25
đ
![]() 0,25
đ
0,25
đ
Câu 3:
a)
2S
=
![]() 0,25
đ
0,25
đ
2S-S
=
![]() 0,25
đ
0,25
đ
S
=![]() 0,25
đ
0,25
đ
S
![]() 0,25
đ
0,25
đ
b)
P
=
![]() 0,25
đ
0,25
đ
![]() 0,25
đ
0,25
đ
![]() 0,25
đ
0,25
đ
![]() 0,25
đ
0,25
đ
Câu 4: (Mỗi bước cho 0,25 điểm)
- Vẽ hệ trục toạ độ
-
Xác định toạ độ một điểm A
O thuộc đồ thị hàm số
![]()
- Biểu diễn điểm A.
-
Vẽ đồ thị hàm số
![]() (Đường thẳng OA)
(Đường thẳng OA)
C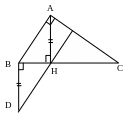 âu
5: (Mỗi
bước cho 0,25 điểm)
âu
5: (Mỗi
bước cho 0,25 điểm)
a. Xét ABH và DHB có:
![]() (= 900)
(= 900)
HB chung
BD = HA
ABH = DHB (c-g-c)
b.
Xét
ABH có
![]() = 500
và
= 500
và
![]() = 900
= 900
![]() = 180 - (
= 180 - (![]() )
= 400.
)
= 400.
Từ ABH = DHB có:
![]()
![]() = 400.
= 400.
c. Từ ABH = DHB có:
![]()
AB song song với DH.
AB AC
DH AC
Ngoài Tổng Hợp 1Tổng Hợp 12 Đề Thi HGS Toán 7 Cấp Huyện Có Đáp Án – Toán 7 Đề Thi Học Sinh Giỏi Toán Lớp 7 Cấp Huyện Có Đáp Án – Toán 7 thì các đề thi trong chương trình lớp 7 sẽ được cập nhật liên tục và nhanh nhất có thể sau khi kỳ thi diễn ra trên Danh mục Kho Đề Thi nhằm giúp các bạn đọc thuận tiện trong việc tra cứu và đối chiếu đáp án. Quý thầy cô và các bạn đọc có thể chia sẻ thêm những tài liệu học tập hữu ích đến địa chỉ email của chúng tôi, nhằm xây dựng nên kho đề thi phong phú, đa dạng cho các em học sinh tham khảo và rèn luyện.
Tổng Hợp 12 Đề Thi HGS Toán 7 Cấp Huyện Có Đáp Án đã hoàn thành một hành trình đầy thách thức và cung cấp cho chúng ta những kiến thức quý báu trong lĩnh vực toán học. Qua 12 đề thi đa dạng và bài giải chi tiết, chúng ta đã có cơ hội rèn luyện khả năng giải toán, mở rộng tầm nhìn và đạt được trình độ toán cao hơn.
Trong suốt quá trình tham gia Tổng Hợp 12 Đề Thi HGS Toán 7 Cấp Huyện Có Đáp Án, chúng ta đã đối mặt với những câu hỏi và bài tập đòi hỏi sự tư duy logic và sự sáng tạo. Chúng ta đã áp dụng những kiến thức đã học để giải quyết những vấn đề thực tế và phát triển khả năng phân tích, suy luận và giải quyết vấn đề một cách thông minh.
Sự có mặt của đáp án trong Tổng Hợp 12 Đề Thi HGS Toán 7 Cấp Huyện cung cấp cho chúng ta cơ hội kiểm tra và đánh giá kết quả làm bài của mình. Chúng ta không chỉ biết được câu trả lời đúng hay sai mà còn hiểu rõ cách giải quyết và quy trình làm bài một cách chi tiết. Điều này giúp chúng ta khắc phục những sai sót, nắm vững kiến thức và nâng cao kỹ năng giải toán của mình.
Tham gia Tổng Hợp 12 Đề Thi HGS Toán 7 Cấp Huyện Có Đáp Án không chỉ là một cơ hội để rèn luyện khả năng toán học mà còn là một bước tiến quan trọng trong hành trình học tập của chúng ta. Chúng ta đã trải qua những thử thách, vượt qua những khó khăn và đạt được sự tiến bộ trong lĩnh vực này. Sự kiên nhẫn, sự cống hiến và lòng đam mê đã trở thành những chìa khóa cho thành công của chúng ta.
Xem thêm







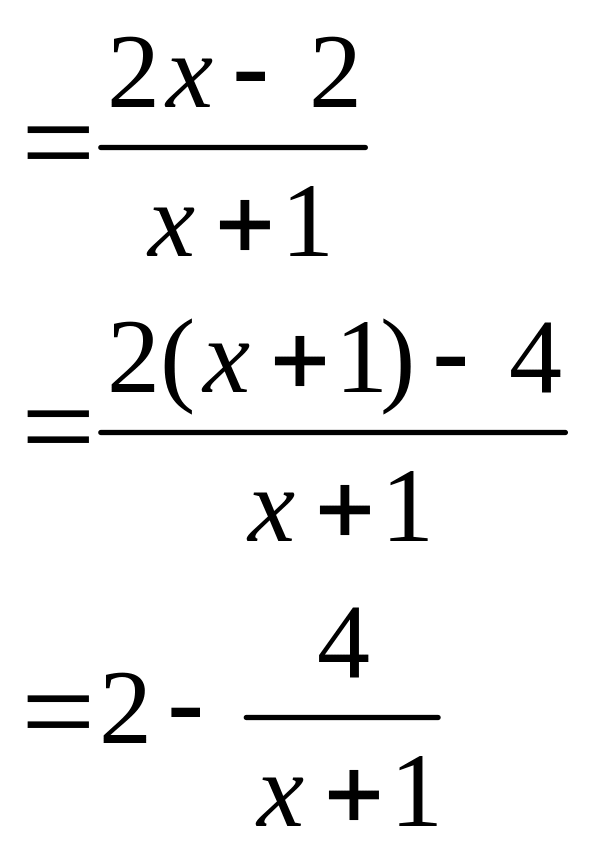
 ẬU
LỘC
ẬU
LỘC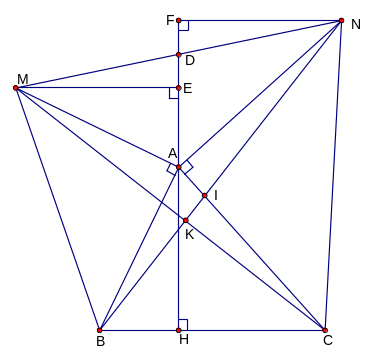
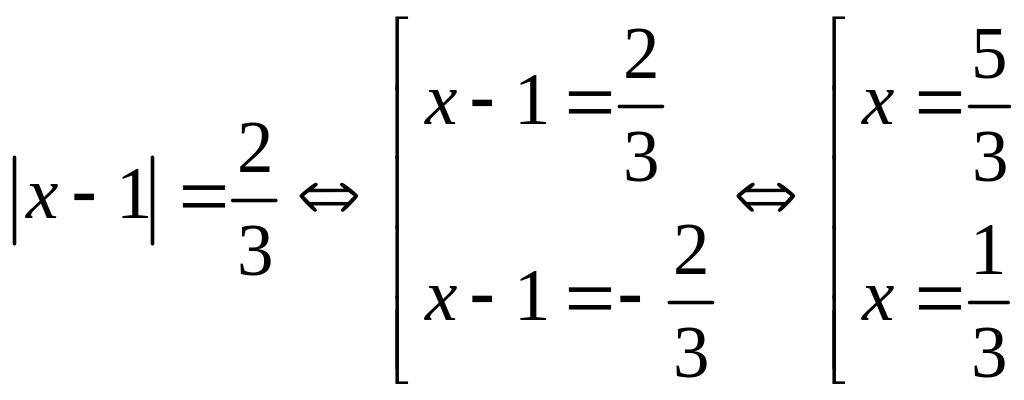
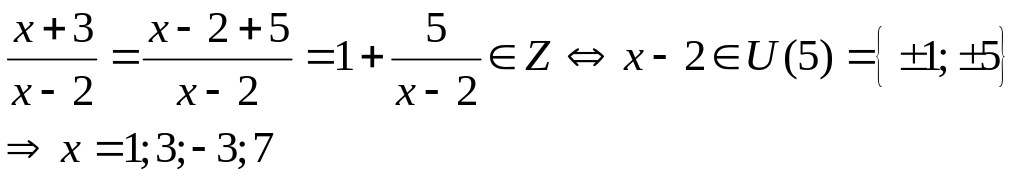
 HÒNG
GD&ĐT
HÒNG
GD&ĐT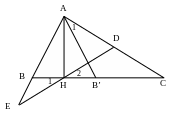
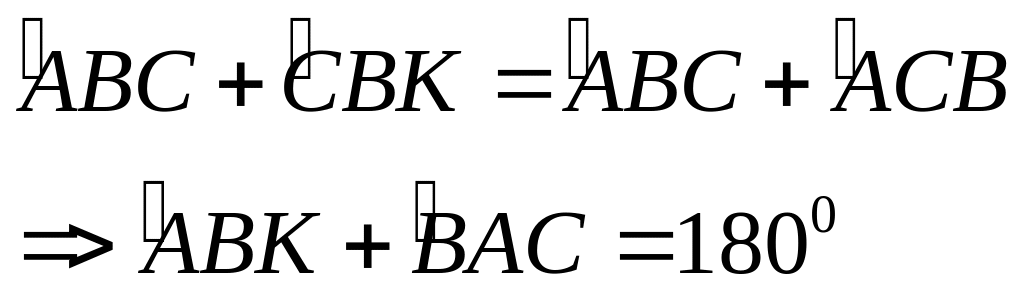 (2)
(2)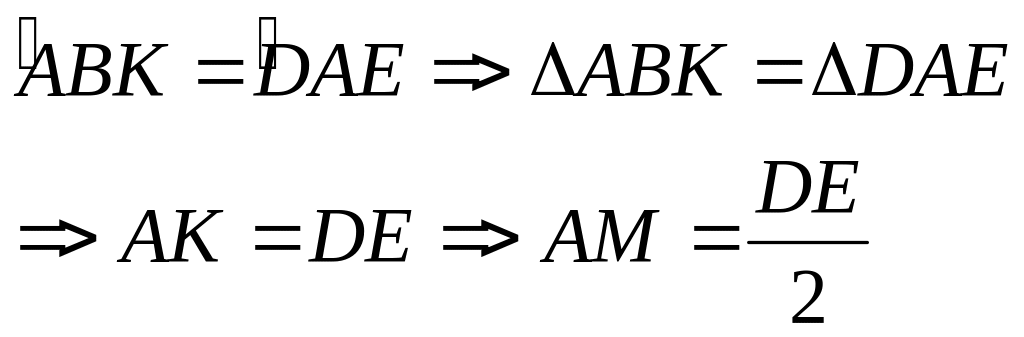


 Thời
gian làm bài:120 phút
Thời
gian làm bài:120 phút