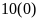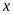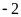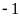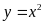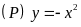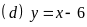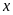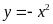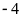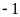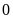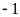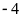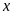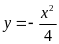Bộ Đề Tuyển Sinh Lớp 10 Môn Toán Quận 1 TPHCM 2022-2023 Có Lời Giải Chi Tiết
Bộ Đề Tuyển Sinh Lớp 10 Môn Toán Quận 1 TPHCM 2022-2023 Có Lời Giải Chi Tiết được Trang Tài Liệu sưu tầm với các thông tin mới nhất hiện nay. Đề thi này sẽ giúp các em học sinh ôn tập, củng cố kiến thức, rèn luyện kĩ năng làm bài. Cũng như hỗ trợ thầy cô trong quá trình giảng dạy. Hy vọng những tài liệu này sẽ giúp các em trong quá trình ôn luyện và đạt kết quả cao trong bài thi sắp tới.
Chuẩn bị cho kỳ thi tuyển sinh lớp 10 là một thử thách quan trọng đối với các em học sinh. Và trong hành trình này, bộ đề tuyển sinh môn Toán từ Quận 1, Thành phố Hồ Chí Minh cho năm học 2022-2023, với lời giải chi tiết, đã trở thành một nguồn tài liệu vô cùng quý giá. Đề thi này không chỉ là một công cụ hỗ trợ cho việc ôn tập, mà còn giúp các em hiểu rõ hơn về cấu trúc đề thi và nắm vững kiến thức toán học.
Bộ đề tuyển sinh môn Toán lớp 10 từ Quận 1, Thành phố Hồ Chí Minh cho năm học 2022-2023 có lời giải chi tiết là một tài liệu được biên soạn bởi những chuyên gia giáo dục có kinh nghiệm. Đề thi này bao gồm các dạng câu hỏi đa dạng, từ cơ bản đến nâng cao, giúp các em rèn luyện và áp dụng kiến thức một cách toàn diện. Lời giải chi tiết cung cấp các phương pháp giải quyết từng bài tập, giúp các em hiểu rõ hơn về cách áp dụng công thức và quy tắc trong giải toán.
Qua việc sử dụng bộ đề tuyển sinh môn Toán lớp 10 từ Quận 1, Thành phố Hồ Chí Minh cho năm học 2022-2023 có lời giải chi tiết, các em sẽ có cơ hội tự kiểm tra và đánh giá năng lực của mình. Bằng việc làm các câu hỏi và so sánh với lời giải, các em có thể nhận ra những điểm mạnh và yếu của mình, từ đó tìm cách cải thiện và phát triển kỹ năng toán học.
Bộ đề tuyển sinh môn Toán lớp 10 từ Quận 1, Thành phố Hồ Chí Minh cho năm học 2022-2023 có lời giải chi tiết là một nguồn tài liệu không thể thiếu trong quá trình ôn tập và chuẩn bị cho kỳ thi tuyển sinh. Hãy sử dụng bộ đề này một cách cẩn thận và cống hiến, và tin rằng sự nỗ lực và kiên nhẫn sẽ đem lại kết quả tốt trong bước ngoặt quan trọng này của học tập toán học.
Đề thi tham khảo
Dưới đây là bản đọc trực tuyến giúp thầy cô và các em học sinh có thể nghiên cứu Online hoặc bạn có thể tải miễn phí với phiên bản word để dễ dàng in ấn cũng như học tập Offline
SỞ GD & ĐT TP.HỒ CHÍ MINH ĐỀ THAM KHẢO TUYỂN SINH 10
PHÒNG GD & ĐT QUẬN 1 NĂM HỌC 2022-2023
ĐỀ THAM KHẢO MÔN : TOÁN 9
-------------------- Đề thi gồm 8 câu hỏi tự luận
MÃ ĐỀ : Quận 1 – 1 Thời gian: 120 phút (không kể thời gian phát đề)
Bài 1: (1.5
điểm).
Cho
 và
và
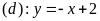
a)
Vẽ đồ thị
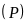 và
và
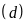 trên cùng hệ trục tọa độ;
trên cùng hệ trục tọa độ;
b) Tìm tọa
độ giao điểm của
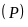 và
và
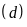 bằng phép toán.
bằng phép toán.
Bài 2: (1.0
điểm)
Cho
phương trình
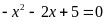 (1).
(1).
a) Chứng minh phương trình (1) luôn có hai nghiệm trái dấu.
b) Tìm
giá trị của biểu thức
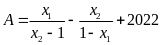 .
.
Bài 3: (0.75
điểm)
Một
người mua hai loại hàng và phải trả tổng cộng 2,17
triệu đồng, kể cả thuế giá trị gia tăng (VAT) với
mức
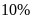 đối với loại hàng loạt hàng thứ nhất và
đối với loại hàng loạt hàng thứ nhất và
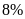 đối với loại hàng thứ hai. Nếu thuế VAT là
đối với loại hàng thứ hai. Nếu thuế VAT là
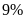 đối với cả hai loại hàng thì người đó phải trả
tổng cộng 2,18 triệu đồng. Hỏi nếu không kể thuế
VAT thì người đó phải trả bao nhiêu tiền cho mỗi loại
hàng?
đối với cả hai loại hàng thì người đó phải trả
tổng cộng 2,18 triệu đồng. Hỏi nếu không kể thuế
VAT thì người đó phải trả bao nhiêu tiền cho mỗi loại
hàng?
Bài 4: (0.75 điểm) Để tìm Hàng CHI của một năm ta dùng công thức sau rồi đối chiếu kết quả với bảng sau:

Để tìm Hàng CAN của một năm ta dùng công thức sau rồi đối chiếu kết quả với bảng sau:
Hàng CAN = Chữ số tận cùng
của năm dương lịch
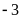
(Nếu chữ số tận cùng của năm đang xét nhỏ hơn 3 thì ta sẽ cộng thêm 10)
Hàng CAN |
Giáp |
Âtt |
Bính |
Đinh |
Mậu |
Kỷ |
Canh |
Tân |
Nhâm |
Quý |
Mã số |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Em hãy sử dụng quy tắc
trên để xác định CAN, CHI của năm
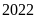 .
.
Bài 5: (1.0 điểm) Bác Bình An vay ở một ngân hàng 500 triệu đồng để sản xuất trong thời hạn 1 năm. Lẽ ra đúng 1 năm sau bác phải trả cả tiền vốn lẫn tiền lãi, song bác đã được ngân hàng cho kéo dài thời hạn thêm 1 năm nữa, số tiền lãi của năm đầu được gộp vào với tiền vốn để tính lãi năm sau và lãi suất vẫn như cũ. Hết 2 năm bác Bình An phải trả tất cả 605 triệu đồng. Hỏi lãi suất cho vay của ngân hàng đó là bao nhiêu phần trăm trong 1 năm?
Bài 6: (1.0 điểm)
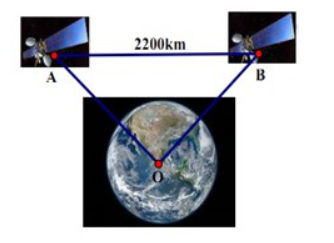
Sóng cực ngắn có tần
số
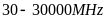 .
Năng lượng rất lớn, không bị tầng điện ly hấp thụ,
truyền đi rất xa
.
Năng lượng rất lớn, không bị tầng điện ly hấp thụ,
truyền đi rất xa
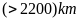 theo đường thẳng. Dùng trong thông tin liên lạc vũ trụ,
ra đa và truyền hình. Tại một thời điểm có hai vệ
tinh đang ở hai vị trí
theo đường thẳng. Dùng trong thông tin liên lạc vũ trụ,
ra đa và truyền hình. Tại một thời điểm có hai vệ
tinh đang ở hai vị trí
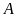 và
và
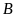 cùng cách mặt đất
cùng cách mặt đất
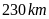 ,
một tín hiệu (truyền bằng sóng cực ngắn) được
truyền đi từ vệ tinh
,
một tín hiệu (truyền bằng sóng cực ngắn) được
truyền đi từ vệ tinh
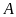 truyền đến vệ tinh
truyền đến vệ tinh
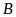 theo phương
theo phương
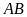 .
Hỏi vệ tinh
.
Hỏi vệ tinh
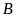 có nhận được tín hiệu đó không? Biết khoảng cách
giữa
có nhận được tín hiệu đó không? Biết khoảng cách
giữa
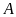 và
và
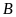 theo đường thẳng là
theo đường thẳng là
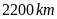 và bán kính Trái Đất là
và bán kính Trái Đất là
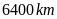 .
.
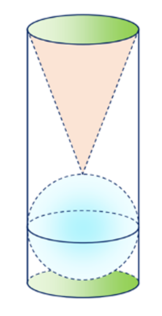
Bài 7: (1.0 điểm) Trên bàn có một cốc nước hình trụ chứa đầy nước, có chiều cao trong bằng 3 lần đường kính trong của đáy; một viên bi hình cầu và một khối nón đều bằng thủy tinh. Biết viên bi và khối nón đều có đường kính bằng đường kính trong của cốc nước. Người ta từ từ thả vào cốc nước viên bi và khối nón đó (như hình vẽ) thì thấy nước trong cốc tràn ra ngoài. Tính tỉ số thể tích của lượng nước còn lại trong cốc và lượng nước ban đầu.
Bài 8: (3.0 điểm)
Cho đường tròn tâm
 đường kính
đường kính
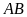 .
Trên đường tròn
.
Trên đường tròn
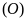 lấy điểm
lấy điểm
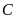 không trùng
không trùng
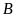 sao cho
sao cho
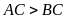 .
Các tiếp tuyến của đường tròn
.
Các tiếp tuyến của đường tròn
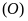 tại
tại
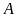 và tại
và tại
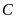 cắt nhau tại
cắt nhau tại
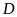 .
Gọi
.
Gọi
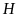 là hình chiếu vuông góc của
là hình chiếu vuông góc của
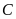 trên
trên
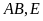 là giao điểm của hai đường thẳng
là giao điểm của hai đường thẳng
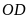 và
và
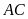 .
.
a) Chứng
minh
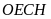 là tứ giác nội tiếp.
là tứ giác nội tiếp.
b) Gọi
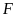 là giao điểm của hai đường thẳng
là giao điểm của hai đường thẳng
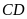 và
và
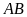 .
Chứng minh
.
Chứng minh
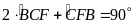 .
.
c) Gọi
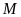 là giao điểm của hai đường thẳng
là giao điểm của hai đường thẳng
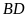 và
và
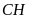 ;
gọi
;
gọi
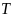 là hình chiếu vuông góc của
là hình chiếu vuông góc của
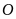 lên
lên
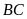 .
Chứng minh ba điểm
.
Chứng minh ba điểm
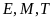 thẳng hàng.
thẳng hàng.
--------------------------------------------
HƯỚNG DẪN GIẢI
Bài 1: (1.5
điểm).
Cho
 và
và
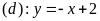
a)
Vẽ đồ thị
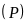 và
và
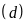 trên cùng hệ trục tọa độ;
trên cùng hệ trục tọa độ;
b) Tìm tọa
độ giao điểm của
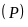 và
và
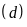 bằng phép toán.
bằng phép toán.
Lời giải
a)  Hàm số:
Hàm số:
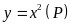 .
.
Bảng giá
trị tương ứng của
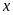 và
và
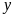 :
:
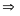 Đồ thị hàm số là một Parabol đi qua các điểm
Đồ thị hàm số là một Parabol đi qua các điểm
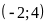 ;
;
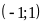 ;
;
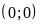 ;
;
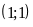 ;
;
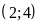
 Hàm số:
Hàm số:
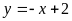
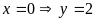
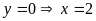
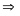 Đồ thị hàm số là đường thẳng đi qua
Đồ thị hàm số là đường thẳng đi qua
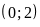 và
và
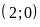
 Vẽ:
Vẽ:

b) Hoành độ giao điểm của
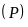 và
và
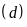 là nghiệm của phương trình:
là nghiệm của phương trình:
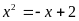
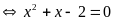
Vì
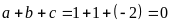
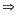 Phương
trình có hai nghiệm phân biệt:
Phương
trình có hai nghiệm phân biệt:
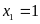 ;
;
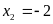
+ Với
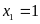
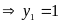
+ Với
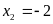
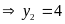
Vậy
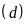 cắt
cắt
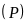 tại hai điểm phân biệt là
tại hai điểm phân biệt là
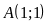 và
và
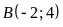 .
.
Bài 2: (1.0
điểm)
Cho
phương trình
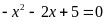 (1).
(1).
a) Chứng minh phương trình (1) luôn có hai nghiệm trái dấu.
b) Tìm
giá trị của biểu thức
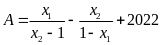 .
.
Lời giải
Xét phương
trình
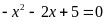 (1).
(1).
a) Phương
trình (1) có
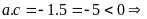 phương trình (1) luôn có hai nghiệm phân biệt trái dấu
phương trình (1) luôn có hai nghiệm phân biệt trái dấu
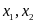 .
.
b) Phương
trình (1) luôn có hai nghiệm phân biệt trái dấu
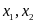 .
Theo hệ thức
Vi-et, ta có:
.
Theo hệ thức
Vi-et, ta có:
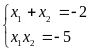 .
.
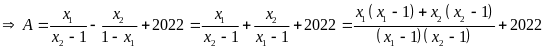
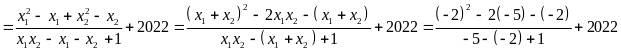
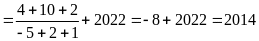
Bài 3: (0.75
điểm)
Một
người mua hai loại hàng và phải trả tổng cộng 2,17
triệu đồng, kể cả thuế giá trị gia tăng (VAT) với
mức
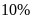 đối với loại hàng loạt hàng thứ nhất và
đối với loại hàng loạt hàng thứ nhất và
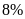 đối với loại hàng thứ hai. Nếu thuế VAT là
đối với loại hàng thứ hai. Nếu thuế VAT là
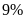 đối với cả hai loại hàng thì người đó phải trả
tổng cộng 2,18 triệu đồng. Hỏi nếu không kể thuế
VAT thì người đó phải trả bao nhiêu tiền cho mỗi loại
hàng?
đối với cả hai loại hàng thì người đó phải trả
tổng cộng 2,18 triệu đồng. Hỏi nếu không kể thuế
VAT thì người đó phải trả bao nhiêu tiền cho mỗi loại
hàng?
Lời giải
Gọi số
tiền không kể thuế của loại hàng thứ nhất là
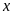 (triệu đồng), của loại hàng thứ hai là
(triệu đồng), của loại hàng thứ hai là
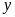 (triệu đồng) (
(triệu đồng) (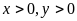 ).
).
Tổng số
tiền phải trả là 2,17
triệu đồng, kể cả thuế giá trị gia tăng (VAT) với
mức
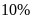 đối với loại hàng loạt hàng thứ nhất và
đối với loại hàng loạt hàng thứ nhất và
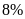 đối với loại hàng thứ hai nên ta có phương trình:
đối với loại hàng thứ hai nên ta có phương trình:
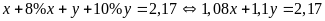 (1);
(1);
Nếu
thuế VAT là
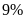 đối với cả hai loại hàng thì người đó phải trả
tổng cộng 2,18 triệu đồng nên ta có phương trình:
đối với cả hai loại hàng thì người đó phải trả
tổng cộng 2,18 triệu đồng nên ta có phương trình:
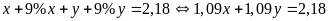 (2);
(2);
Vậy ta có
hệ:
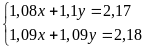 . Giải hệ phương trình ta được:
. Giải hệ phương trình ta được:
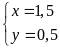 (thỏa mãn).
(thỏa mãn).
Vậy không kể thuế VAT thì loại hàng thứ nhất phải trả 1,5 triệu đồng, loại hàng thứ hai phải trả 0,5 triệu đồng.
Bài 4: (0.75 điểm) Để tìm Hàng CHI của một năm ta dùng công thức sau rồi đối chiếu kết quả với bảng sau:

Để tìm Hàng CAN của một năm ta dùng công thức sau rồi đối chiếu kết quả với bảng sau:
Hàng CAN = Chữ số tận cùng
của năm dương lịch
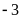
(Nếu chữ số tận cùng của năm đang xét nhỏ hơn 3 thì ta sẽ cộng thêm 10)
Hàng CAN |
Giáp |
Ất |
Bính |
Đinh |
Mậu |
Kỷ |
Canh |
Tân |
Nhâm |
Quý |
Mã số |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Em hãy sử dụng quy tắc
trên để xác định CAN, CHI của năm
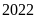 .
.
Lời giải
Vì
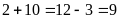 nên năm
nên năm
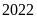 có CAN là Nhâm,
và
có CAN là Nhâm,
và
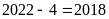 chia cho
chia cho
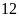 dư
dư
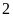 cộng 1
bằng 3 nên năm
cộng 1
bằng 3 nên năm
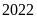 có CHI là Dần.
có CHI là Dần.
Bài 5: (1.0 điểm) Bác Bình An vay ở một ngân hàng 500 triệu đồng để sản xuất trong thời hạn 1 năm. Lẽ ra đúng 1 năm sau bác phải trả cả tiền vốn lẫn tiền lãi, song bác đã được ngân hàng cho kéo dài thời hạn thêm 1 năm nữa, số tiền lãi của năm đầu được gộp vào với tiền vốn để tính lãi năm sau và lãi suất vẫn như cũ. Hết 2 năm bác Bình An phải trả tất cả 605 triệu đồng. Hỏi lãi suất cho vay của ngân hàng đó là bao nhiêu phần trăm trong 1 năm?
Lời giải
Gọi
lãi suất của ngân hàng đó là
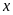 (
(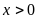 ).
).
Ta có: Số
tiền phải trả sau năm thứ nhất là:
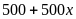 (triệu đồng).
(triệu đồng).
Số tiền
phải trả sau năm thứ hai là:
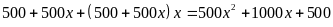 (triệu đồng).
(triệu đồng).
Vì sau hai năm bác Bình An phải trả 605 triệu đồng nên ta có phương trình:
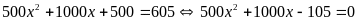 .
.
Giải phương
trình ta được
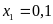 (thỏa mãn);
(thỏa mãn);
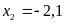 (loại).
(loại).
Vậy lãi
suất mỗi năm của ngân hàng đó là
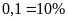 .
.
Bài 6: (1.0
điểm)
Sóng
cực ngắn có tần số
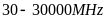 .
Năng lượng rất lớn, không bị tầng điện ly hấp thụ,
truyền đi rất xa
.
Năng lượng rất lớn, không bị tầng điện ly hấp thụ,
truyền đi rất xa
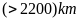 theo đường thẳng. Dùng trong thông tin liên lạc vũ trụ,
ra đa và truyền hình. Tại một thời điểm có hai vệ
tinh đang ở hai vị trí
theo đường thẳng. Dùng trong thông tin liên lạc vũ trụ,
ra đa và truyền hình. Tại một thời điểm có hai vệ
tinh đang ở hai vị trí
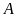 và
và
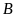 cùng cách mặt đất
cùng cách mặt đất
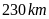 ,
một tín hiệu (truyền bằng sóng cực ngắn) được
truyền đi từ vệ tinh
,
một tín hiệu (truyền bằng sóng cực ngắn) được
truyền đi từ vệ tinh
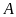 truyền đến vệ tinh
truyền đến vệ tinh
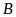 theo phương
theo phương
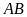 .
Hỏi vệ tinh
.
Hỏi vệ tinh
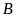 có nhận được tín hiệu đó không? Biết khoảng cách
giữa
có nhận được tín hiệu đó không? Biết khoảng cách
giữa
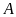 và
và
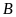 theo đường thẳng là
theo đường thẳng là
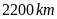 và bán kính Trái Đất là
và bán kính Trái Đất là
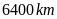 .
.

Lời giải
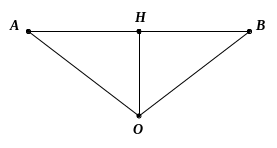
Kẻ
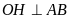 tại
tại
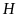 ,
,
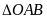 có
có
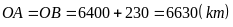 nên
nên
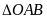 cân tại
cân tại
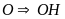 cũng là trung tuyến của
cũng là trung tuyến của
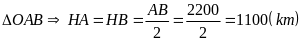 .
.
Áp dụng định
lý Pi-ta-go cho
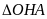 vuông tại
vuông tại
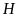 ,
ta có:
,
ta có:
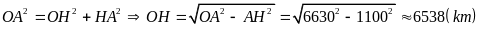 .
.
Vậy
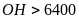 nên tín hiệu truyền từ vệ tinh A đến được vệ tinh
B mà không bị trái đất cản lại.
nên tín hiệu truyền từ vệ tinh A đến được vệ tinh
B mà không bị trái đất cản lại.
Bài 7: (1.0 điểm) Trên bàn có một cốc nước hình trụ chứa đầy nước, có chiều cao trong bằng 3 lần đường kính trong của đáy; một viên bi hình cầu và một khối nón đều bằng thủy tinh. Biết viên bi và khối nón đều có đường kính bằng đường kính trong của cốc nước. Người ta từ từ thả vào cốc nước viên bi và khối nón đó (như hình vẽ) thì thấy nước trong cốc tràn ra ngoài. Tính tỉ số thể tích của lượng nước còn lại trong cốc và lượng nước ban đầu.

Lời giải
Tỉ số thể tích của lượng nước còn lại trong cốc và lượng nước ban đầu là tỉ số thể tích của hiệu thể tích hình trụ với tổng thể tích hình nón và hình cầu với thể tích của hình trụ.
Chiều cao của hình trụ là :
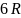
Chiều
cao của hình nón là :
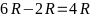
Ta có:
Thể tích hình
trụ là:
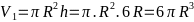 .
.
Thể tích viên
bi là:
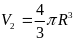 .
.
Thể tích hình
nón là:
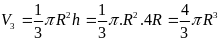 .
.
Thể tích nước
còn lại trong bình là:
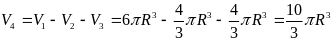 .
.
Tỉ số thể
tích của lượng nước còn lại trong cốc và lượng nước
ban đầu là:
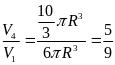 .
.
Bài 8: (3.0
điểm)
Cho
đường tròn tâm
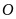 đường kính
đường kính
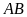 .
Trên đường tròn
.
Trên đường tròn
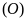 lấy điểm
lấy điểm
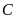 không trùng
không trùng
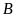 sao cho
sao cho
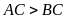 .
Các tiếp tuyến của đường tròn
.
Các tiếp tuyến của đường tròn
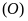 tại
tại
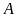 và tại
và tại
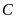 cắt nhau tại
cắt nhau tại
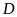 .
Gọi
.
Gọi
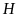 là hình chiếu vuông góc của
là hình chiếu vuông góc của
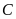 trên
trên
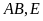 là giao điểm của hai đường thẳng
là giao điểm của hai đường thẳng
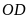 và
và
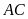 .
.
a) Chứng
minh
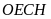 là tứ giác nội tiếp.
là tứ giác nội tiếp.
b) Gọi
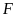 là giao điểm của hai đường thẳng
là giao điểm của hai đường thẳng
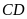 và
và
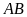 .
Chứng minh
.
Chứng minh
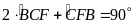 .
.
c) Gọi
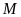 là giao điểm của hai đường thẳng
là giao điểm của hai đường thẳng
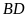 và
và
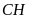 ;
gọi
;
gọi
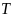 là hình chiếu vuông góc của
là hình chiếu vuông góc của
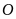 lên
lên
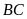 .
Chứng minh ba điểm
.
Chứng minh ba điểm
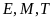 thẳng hàng.
thẳng hàng.
Lời giải
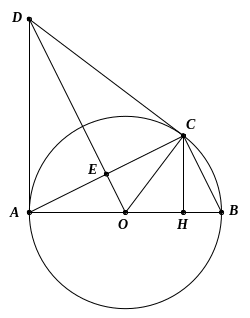
a) Chứng minh
 là tứ giác nội tiếp.
là tứ giác nội tiếp.
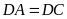 (tính chất hai tiếp tuyến
cắt nhau);
(tính chất hai tiếp tuyến
cắt nhau);
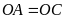 (bán kính
(bán kính
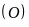 )
)
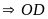 là trung trực của
là trung trực của
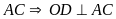 tại trung điểm
tại trung điểm
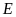 của
của
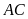
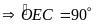 ;
;
Tứ giác
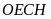 có:
có:
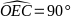 (chứng minh trên)
(chứng minh trên)
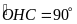 (
(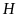 là hình chiếu vuông góc của
là hình chiếu vuông góc của
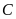 lên
lên
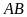 )
)
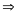 tứ giác
tứ giác
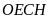 nội tiếp đường tròn đường kính
nội tiếp đường tròn đường kính
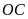 .
.
b) Gọi
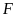 là giao điểm của hai đường thẳng
là giao điểm của hai đường thẳng
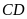 và
và
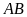 .
Chứng minh
.
Chứng minh
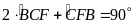 .
.
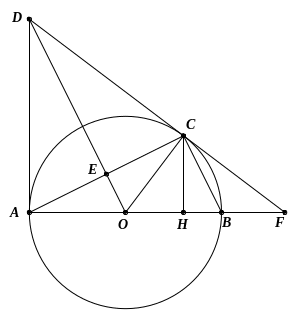
Ta có:
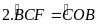 (góc tạo bởi tia tiếp tuyến và dây cung và góc ở tâm
cùng chắn
(góc tạo bởi tia tiếp tuyến và dây cung và góc ở tâm
cùng chắn
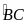 );
);
Mà
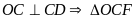 vuông tại
vuông tại
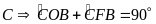 ;
;
Vậy
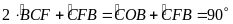 .
.
c) Gọi
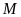 là giao điểm của hai đường thẳng
là giao điểm của hai đường thẳng
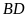 và
và
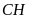 ;
gọi
;
gọi
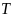 là hình chiếu vuông góc của
là hình chiếu vuông góc của
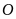 lên
lên
 .
Chứng minh ba điểm
.
Chứng minh ba điểm
 thẳng hàng.
thẳng hàng.
Gọi
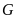 là giao điểm của
là giao điểm của
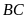 và
và
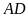 ;
Vì
;
Vì
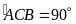 góc nội tiếp chắn nửa đường tròn
góc nội tiếp chắn nửa đường tròn
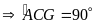 ;
;
Trong
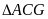 vuông tại
vuông tại
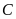 ,
ta có:
,
ta có:
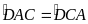 (
(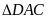 cân tại
cân tại
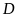 )
)
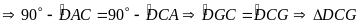 cân tại
cân tại
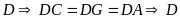 là trung điểm của
là trung điểm của
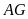 ;
;
Vì
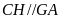 (cùng vuông góc với
(cùng vuông góc với
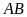 )
nên theo hệ quả của định lý T-let, ta có:
)
nên theo hệ quả của định lý T-let, ta có:
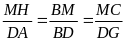 mà
mà
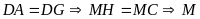 là trung điểm của
là trung điểm của
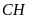 ;
;
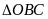 cân tại
cân tại
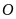 có
có
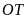 là đường cao nên cũng là trung tuyến
là đường cao nên cũng là trung tuyến
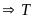 là trung điểm của
là trung điểm của
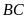 ;
;
Theo a) ta có
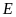 là trung điểm của
là trung điểm của
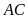 .
.
Vậy
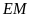 là đường trung bình của
là đường trung bình của
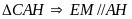 hay
hay
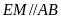 ;
;
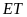 là đường
trung bình của
là đường
trung bình của
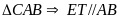 ;
;
Theo tiên
đề Ơ-clit
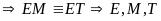 thẳng hàng.
thẳng hàng.
--------------------------------------------
SỞ GD & ĐT TP.HỒ CHÍ MINH ĐỀ THAM KHẢO TUYỂN SINH 10
PHÒNG GD & ĐT QUẬN 1 NĂM HỌC 2022-2023
ĐỀ THAM KHẢO MÔN : TOÁN 9
-------------------- Đề thi gồm 8 câu hỏi tự luận
MÃ ĐỀ: Quận 1 – 2 Thời gian: 120 phút (không kể thời gian phát đề)
a)
Vẽ đồ thị
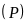 và
và
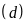 trên cùng hệ trục tọa độ.
trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm
của
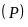 và
và
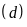 bằng phép tính.
bằng phép tính.
Câu 2: (1.0 điểm)
Gọi
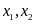 là các nghiệm của phương trình:
là các nghiệm của phương trình:
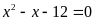 .
Không giải phương trình hãy tính giá trị của biểu thức
.
Không giải phương trình hãy tính giá trị của biểu thức
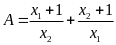 .
.
Câu 3: (0.75 điểm) Tốc độ của một chiếc ca nô và độ dài đường sóng nước để lại sau đuôi của nó được cho
bởi công thức
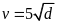 .
Trong đó
.
Trong đó
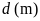 là độ dài đường sóng nước để lại sau đuôi ca nô,
là độ dài đường sóng nước để lại sau đuôi ca nô,
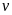 là vận
là vận
tốc ca nô (m/giây).
a)
Tính vận tốc ca nô biết độ dài đường sóng nước
để lại sau đuôi ca nô dài
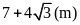 .
.
b) Khi ca nô chạy với vận
tốc
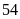 km/giờ thì đường
sóng nước để lại sau
đuôi ca nô dài bao nhiêu mét?
km/giờ thì đường
sóng nước để lại sau
đuôi ca nô dài bao nhiêu mét?
Câu 4: (0.75 điểm) Trong kết quả xét nghiệm lượng đường trong máu có bệnh viện tính theo đơn vị là
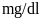 nhưng cũng có bệnh viện tính
theo đơn vị là
nhưng cũng có bệnh viện tính
theo đơn vị là
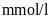 .
Công thức chuyển đổi là
.
Công thức chuyển đổi là
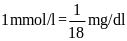 .
Hai bạn Châu và Lâm nhịn ăn sáng sau khi thử đường
huyết tại nhà có chỉ số đường huyết lần lượt là
.
Hai bạn Châu và Lâm nhịn ăn sáng sau khi thử đường
huyết tại nhà có chỉ số đường huyết lần lượt là
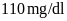 và
và
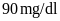 .
Căn cứ vào bảng sau, em hãy cho biết tình trạng
.
Căn cứ vào bảng sau, em hãy cho biết tình trạng
sức khỏe của hai bạn Châu và Lâm:
-
Tên xét nghiệm
Hạ đường huyết
Đường huyết bình thường
Giai đoạn tiền tiểu đường
Chuẩn đoán bệnh tiểu đường
Đường huyết lúc đói
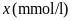
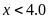
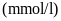
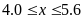
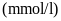
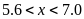
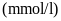
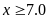
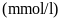
Câu 5: (1.0 điểm)
Một chiếc vòng nữ trang được làm từ vàng và bạc với
thể tích là
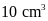 và cân nặng
và cân nặng
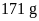 .
Biết vàng có khối lượng riêng là
.
Biết vàng có khối lượng riêng là
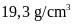 còn bạc có khối lượng riêng là
còn bạc có khối lượng riêng là
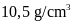 .
Hỏi
.
Hỏi
thể tích của vàng và bạc được sử dụng để làm chiếc vòng? Biết công thức tính khối lượng là
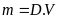 ,
trong đó
,
trong đó
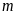 là khối lượng,
là khối lượng,
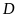 là khối lượng riêng và
là khối lượng riêng và
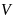 là thể tích.
là thể tích.
Câu 6: (1.0 điểm)
Một bình chứa nước hình hộp chữ nhật có diện tích
đáy là
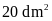 và chiều cao
và chiều cao
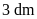 .
.
Người ta rót hết nước
trong bình ra những chai nhỏ mỗi chai có thể tích
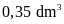 được tất cả
được tất cả
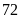
chai. Hỏi lượng nước có trong bình chiếm bao nhiêu phần trăm thể tích bình?
Câu 7: (1.0 điểm)
Trong tháng
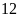 năm
năm
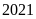 khi Thành phố Hồ Chí Minh cho các học sinh lớp
khi Thành phố Hồ Chí Minh cho các học sinh lớp
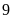 trở lại
trở lại
trường học trực tiếp sau những tháng ngày học trực tuyến, tôi đã về lại trường cũ để lãnh những
phần thưởng mà tôi đã gặt hái được trong năm học vừa qua do dịch bệnh nên không đến nhận phần
thưởng được. Vui mừng khi
tôi gặp lại thầy chủ nhiệm lớp
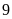 .
Qua chuyện thầy cho tôi biết lớp tôi sĩ số cuối năm
giảm
.
Qua chuyện thầy cho tôi biết lớp tôi sĩ số cuối năm
giảm
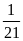 so với đầu năm, toàn bộ lớp đều tham gia xét tuyển
sinh lớp
so với đầu năm, toàn bộ lớp đều tham gia xét tuyển
sinh lớp
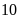 và kết quả có
và kết quả có
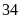 học sinh đã đậu vào lớp
học sinh đã đậu vào lớp
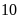 công lập đạt tỉ lệ
công lập đạt tỉ lệ
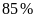 .
Các bạn hãy tính sĩ số đầu năm của lớp
.
Các bạn hãy tính sĩ số đầu năm của lớp
tôi là bao nhiêu?
Câu 8: (3.0 điểm)
Cho tam giác nhọn
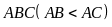 nội tiếp đường tròn
nội tiếp đường tròn
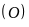 có đường cao
có đường cao
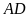 .
Vẽ
.
Vẽ
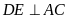 tại
tại
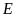 và
và
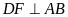 tại
tại
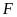 .
.
a) Chứng minh:
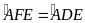 và tứ giác
và tứ giác
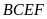 nội tiếp.
nội tiếp.
b) Tia
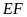 cắt tia
cắt tia
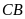 tại
tại
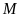 ,
đoạn thẳng
,
đoạn thẳng
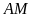 cắt đường tròn
cắt đường tròn
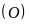 tại
tại
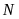 (khác
(khác
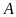 ).
Chứng minh
).
Chứng minh
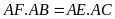 và
và
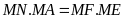 .
.
c) Tia
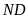 cắt đường tròn
cắt đường tròn
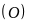 tại
tại
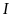 .
Chứng minh
.
Chứng minh
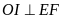 .
.
----------------------HẾT----------------------
HƯỚNG DẪN GIẢI
Câu 1: (1.5 điểm).
Cho
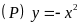 và
và
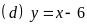
a)
Vẽ đồ thị
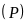 và
và
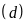 trên cùng hệ trục tọa độ.
trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm
của
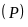 và
và
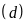 bằng phép tính.
bằng phép tính.
Lời giải
a) Vẽ đồ thị
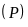 và
và
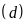 trên cùng hệ trục tọa độ.
trên cùng hệ trục tọa độ.
Đồ thị của parabol
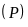 :
:
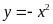
Bảng giá trị tương ứng
của
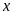 và
và
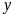 :
:
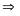 Đồ thị hàm số là một Parabol đi qua các điểm
Đồ thị hàm số là một Parabol đi qua các điểm
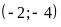 ;
;
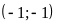 ;
;
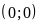 ;
;
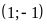 ;
;
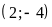
Đồ thị đường thẳng
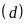 :
:
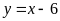
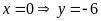
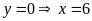
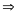 Đồ thị hàm số là đường thẳng đi qua
Đồ thị hàm số là đường thẳng đi qua
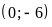 và
và
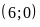
Vẽ đồ thị
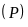 và
và
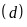 trên cùng hệ trục tọa độ:
trên cùng hệ trục tọa độ:
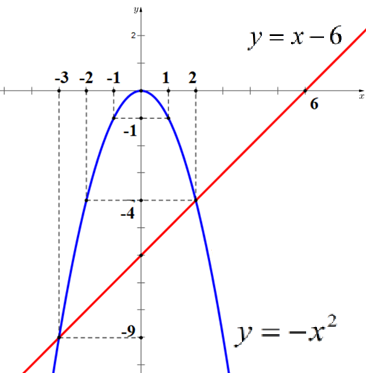
b) Hoành độ giao điểm của
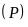 và
và
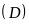 là nghiệm của phương trình:
là nghiệm của phương trình:
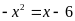
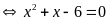
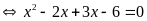
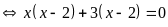
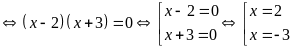
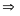 Phương
trình có hai nghiệm phân biệt:
Phương
trình có hai nghiệm phân biệt:
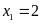 ;
;
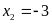
+ Với
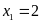
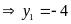
+ Với
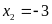
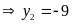
Vậy
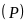 cắt
cắt
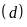 tại hai điểm phân biệt là
tại hai điểm phân biệt là
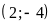 và
và
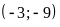 .
.
Câu 2: (1.0 điểm)
Gọi
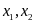 là các nghiệm của phương trình:
là các nghiệm của phương trình:
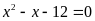 .
Không giải phương trình hãy tính giá trị của biểu thức
.
Không giải phương trình hãy tính giá trị của biểu thức
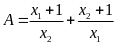 .
.
Lời giải
Phương trình đã cho là phương
trình bậc hai của
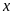 có các hệ số:
có các hệ số:
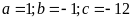
Gọi
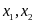 là các nghiệm của phương trình
là các nghiệm của phương trình
Theo định lý
Vi-et, ta có:
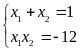
Ta có biểu
thức
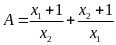
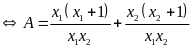
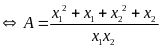
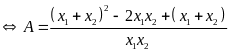
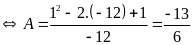
Vậy
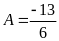
Câu 3: (0.75 điểm) Tốc độ của một chiếc ca nô và độ dài đường sóng nước để lại sau đuôi của nó được cho
bởi công thức
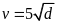 .
Trong đó
.
Trong đó
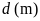 là độ dài đường sóng nước để lại sau đuôi ca nô,
là độ dài đường sóng nước để lại sau đuôi ca nô,
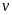 là vận
là vận
tốc ca nô (m/giây).
a)
Tính vận tốc ca nô biết độ dài đường sóng nước
để lại sau đuôi ca nô dài
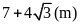 .
.
b) Khi ca nô chạy với vận
tốc
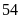 km/giờ thì đường
sóng nước để lại sau
đuôi ca nô dài bao nhiêu mét?
km/giờ thì đường
sóng nước để lại sau
đuôi ca nô dài bao nhiêu mét?
Lời giải
Tính vận tốc ca nô biết độ dài đường sóng nước để lại sau đuôi ca nô dài
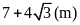 .
.
Theo đề bài, tốc độ của một chiếc ca nô và độ dài đường sóng nước để lại sau đuôi của nó được cho
bởi công thức
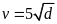
Khi độ dài đường sóng nước để lại sau đuôi ca nô
dài
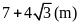 ,
ta có
,
ta có
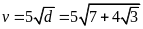
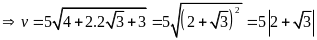
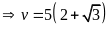 (m/giây)
(m/giây)
Khi ca nô chạy với vận tốc
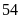 km/giờ thì đường sóng nước để lại sau đuôi ca nô
dài bao nhiêu mét?
km/giờ thì đường sóng nước để lại sau đuôi ca nô
dài bao nhiêu mét?
Đổi đơn vị:
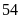 km/giờ =
km/giờ =
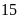 m/giây
m/giây
Ta có
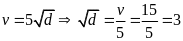
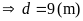
Câu 4: (0.75 điểm) Trong kết quả xét nghiệm lượng đường trong máu có bệnh viện tính theo đơn vị là
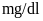 nhưng cũng có bệnh viện tính
theo đơn vị là
nhưng cũng có bệnh viện tính
theo đơn vị là
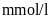 .
Công thức chuyển đổi là
.
Công thức chuyển đổi là
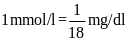 .
Hai bạn Châu và Lâm nhịn ăn sáng sau khi thử đường
huyết tại nhà có chỉ số đường huyết lần lượt là
.
Hai bạn Châu và Lâm nhịn ăn sáng sau khi thử đường
huyết tại nhà có chỉ số đường huyết lần lượt là
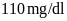 và
và
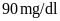 .
Căn cứ vào bảng sau, em hãy cho biết tình trạng
.
Căn cứ vào bảng sau, em hãy cho biết tình trạng
sức khỏe của hai bạn Châu và Lâm:
-
Tên xét nghiệm
Hạ đường huyết
Đường huyết bình thường
Giai đoạn tiền tiểu đường
Chuẩn đoán bệnh tiểu đường
Đường huyết lúc đói
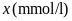
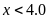
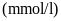
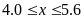
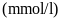
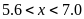
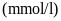
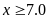
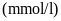
Lời giải
Theo đề bài, công thức
chuyển đổi là
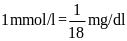
Bạn Châu và Lâm nhịn ăn sáng sau khi thử đường huyết tại nhà có chỉ số đường huyết lần lượt là
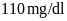 và
và
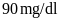 ,
nên ta có
,
nên ta có
Chỉ số lượng đường trong
máu của Bạn Châu tính theo đơn vị
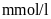 là:
là:
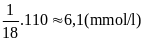
Chỉ số lượng đường trong
máu của Bạn Lâm tính theo đơn vị
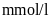 là:
là:
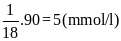
Căn cứ vào bảng trên, chỉ
số lượng đường trong máu của bạn Châu là
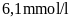 ,
tình trạng sức
,
tình trạng sức
khỏe của bạn Châu đang ở giai đoạn tiền tiểu đường. Chỉ số lượng đường trong máu của bạn Lâm là
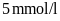 ,
bạn Lâm có mức đường huyết bình thường, sức khỏe
tốt.
,
bạn Lâm có mức đường huyết bình thường, sức khỏe
tốt.
Câu 5: (1.0 điểm)
Một chiếc vòng nữ trang được làm từ vàng và bạc với
thể tích là
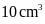 và cân nặng
và cân nặng
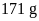 .
Biết vàng có khối lượng riêng là
.
Biết vàng có khối lượng riêng là
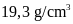 còn bạc có khối lượng riêng là
còn bạc có khối lượng riêng là
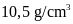 .
Hỏi
.
Hỏi
thể tích của vàng và bạc được sử dụng để làm chiếc vòng? Biết công thức tính khối lượng là
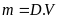 ,
trong đó
,
trong đó
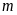 là khối lượng,
là khối lượng,
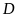 là khối lượng riêng và
là khối lượng riêng và
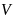 là thể tích.
là thể tích.
Lời giải
Gọi thể
tích vàng được sử dụng để làm chiếc vòng là
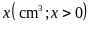
Gọi thể
tích bạc được sử dụng để làm chiếc vòng là
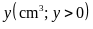
Theo đề
bài, chiếc vòng nữ trang có thể tích là
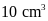 nên ta có phương trình:
nên ta có phương trình:
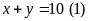
Khối lượng riêng của vàng
là
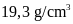 nên khối lượng vàng có trong chiếc vòng là
nên khối lượng vàng có trong chiếc vòng là
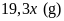
Khối lượng riêng của bạc
là
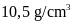 nên khối lượng bạc có trong chiếc vòng là
nên khối lượng bạc có trong chiếc vòng là
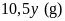
Chiếc vòng có cân nặng là
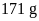 ,
nên ta có phương trình
,
nên ta có phương trình
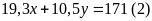
Từ
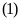 và
và
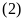 ta có hệ phương trình
ta có hệ phương trình
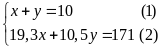
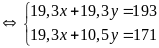
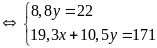
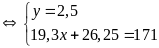
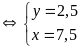 (Thỏa mãn)
(Thỏa mãn)
Vậy thể tích vàng được sử
dụng để là chiếc vòng là
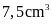
Thể tích bạc được sử
dụng để là chiếc vòng là
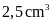
Câu 6: (1.0 điểm)
Một bình chứa nước hình hộp chữ nhật có diện tích
đáy là
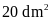 và chiều cao
và chiều cao
 .
.
Người ta rót hết nước
trong bình ra những chai nhỏ mỗi chai có thể tích
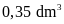 được tất cả
được tất cả
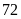
chai. Hỏi lượng nước có trong bình chiếm bao nhiêu phần trăm thể tích bình?
Lời giải
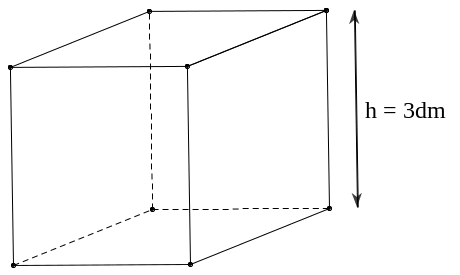
Bình chứa nước hình hộp
chữ nhật có diện tích đáy là
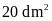 và chiều cao
và chiều cao
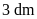
Thể tích của bình nước
hình hộp chữ nhật là
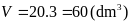
Người ta rót hết nước
trong bình ra những chai
nhỏ mỗi chai có thể tích
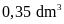 ,
được
,
được
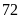 chai
chai
Thể tích lượng nước có
trong bình là
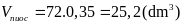
Lượng nước có trong bình
chiếm số phần trăm thể tích bình là
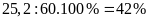
Vậy lượng
nước có trong bình chiếm
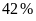 thể tích của bình.
thể tích của bình.
Câu 7: (1.0 điểm)
Trong tháng
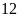 năm
năm
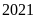 khi Thành phố Hồ Chí Minh cho các học sinh lớp
khi Thành phố Hồ Chí Minh cho các học sinh lớp
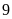 trở lại
trở lại
trường học trực tiếp sau những tháng ngày học trực tuyến, tôi đã về lại trường cũ để lãnh những
phần thưởng mà tôi đã gặt hái được trong năm học vừa qua do dịch bệnh nên không đến nhận phần
thưởng được. Vui mừng khi
tôi gặp lại thầy chủ nhiệm lớp
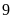 .
Qua chuyện thầy cho tôi biết lớp tôi sĩ số cuối năm
giảm
.
Qua chuyện thầy cho tôi biết lớp tôi sĩ số cuối năm
giảm
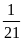 so với đầu năm, toàn bộ lớp đều tham gia xét tuyển
sinh lớp
so với đầu năm, toàn bộ lớp đều tham gia xét tuyển
sinh lớp
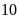 và kết quả có
và kết quả có
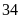 học sinh đã đậu vào lớp
học sinh đã đậu vào lớp
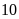 công lập đạt tỉ lệ
công lập đạt tỉ lệ
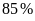 .
Các bạn hãy tính sĩ số đầu năm của lớp
.
Các bạn hãy tính sĩ số đầu năm của lớp
tôi là bao nhiêu?
Lời giải
Gọi sĩ số học sinh đầu
năm của lớp tôi là
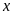 (bạn học sinh,
(bạn học sinh,
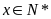 )
)
Theo đề bài, sĩ số học
sinh của lớp cuối năm giảm
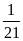 so với đầu năm, nên số bạn học sinh còn lại cuối
năm của lớp là
so với đầu năm, nên số bạn học sinh còn lại cuối
năm của lớp là
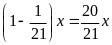 (bạn học sinh)
(bạn học sinh)
Toàn bộ lớp tham gia xét
tuyển sinh lớp
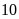 ,
có
,
có
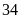 học sinh đã đậu vào lớp
học sinh đã đậu vào lớp
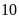 công lập đạt tỉ lệ
công lập đạt tỉ lệ
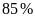 .
Đổi
.
Đổi
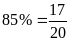
Ta có phương trình
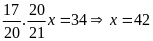 (thỏa mãn)
(thỏa mãn)
Vậy sĩ số học sinh đầu
năm của lớp tôi là
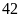 bạn học sinh.
bạn học sinh.
Câu 8: (3.0 điểm)
Cho tam giác nhọn
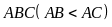 nội tiếp đường tròn
nội tiếp đường tròn
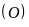 có đường cao
có đường cao
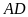 .
Vẽ
.
Vẽ
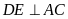 tại
tại
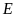 và
và
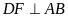 tại
tại
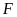 .
.
a) Chứng minh:
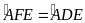 và tứ giác
và tứ giác
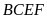 nội tiếp.
nội tiếp.
b) Tia
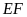 cắt tia
cắt tia
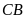 tại
tại
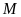 ,
đoạn thẳng
,
đoạn thẳng
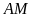 cắt đường tròn
cắt đường tròn
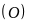 tại
tại
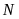 (khác
(khác
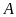 ).
Chứng minh
).
Chứng minh
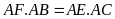 và
và
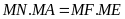 .
.
c) Tia
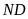 cắt đường tròn
cắt đường tròn
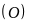 tại
tại
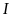 .
Chứng minh
.
Chứng minh
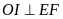 .
.
Lời giải
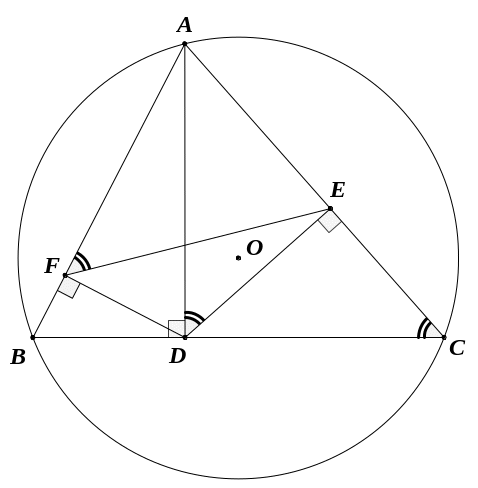
Chứng minh:
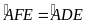 và tứ giác
và tứ giác
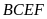 nội tiếp.
nội tiếp.
Theo giả thiết, ta có
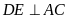 ,
,
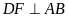 nên ta có
nên ta có
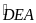 ,
,
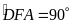
Xét tứ giác
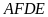 có
có
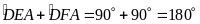 ,
mà hai góc
,
mà hai góc
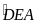 và
và
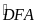 ở vị trí đối nhau
ở vị trí đối nhau
Nên suy ra tứ giác
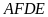 nội tiếp đường tròn (dấu hiệu nhận biết)
nội tiếp đường tròn (dấu hiệu nhận biết)
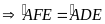 (góc nội tiếp cùng chắn
cung
(góc nội tiếp cùng chắn
cung
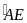 )
(đpcm)
)
(đpcm)
Ta có
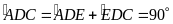
Trong tam giác
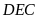 ,
vuông tại
,
vuông tại
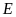 ,
nên ta có
,
nên ta có
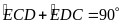
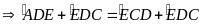
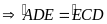
Mà
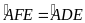 (cmt) nên ta có
(cmt) nên ta có
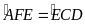 hay
hay
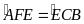
Xét tứ giác
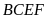 có
có
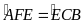 ,
,
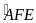 là góc ngoài tại đỉnh
là góc ngoài tại đỉnh
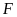 ,
,
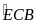 là góc trong tại đỉnh
là góc trong tại đỉnh
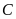 là
là
đỉnh đối với đỉnh
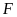
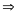 tứ giác
tứ giác
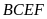 nội tiếp đường tròn (dấu hiệu nhận biết tứ giác
nội tiếp)
nội tiếp đường tròn (dấu hiệu nhận biết tứ giác
nội tiếp)
Tia
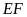 cắt tia
cắt tia
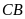 tại
tại
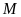 ,
đoạn thẳng
,
đoạn thẳng
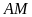 cắt đường tròn
cắt đường tròn
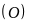 tại
tại
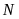 (khác
(khác
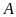 ).
Chứng minh
).
Chứng minh
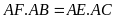 và
và
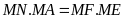 .
.
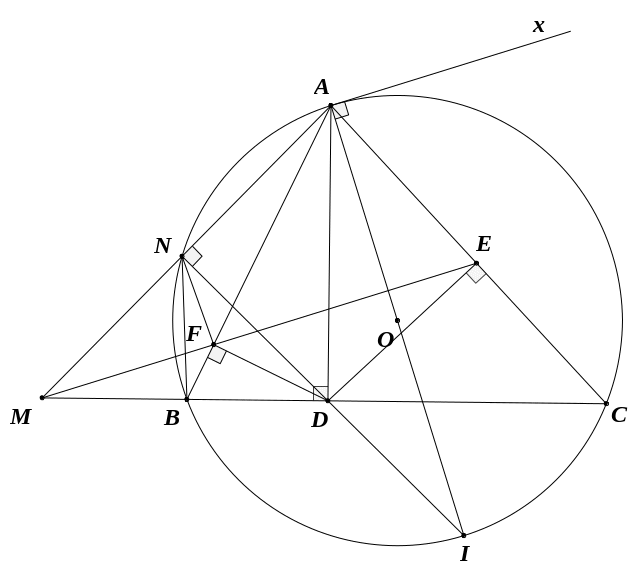
Xét hai tam giác
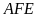 và tam giác
và tam giác
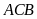 có
có
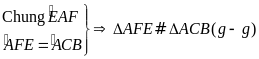
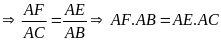 (đpcm)
(đpcm)
Xét tứ giác
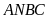 nội tiếp đường tròn
nội tiếp đường tròn
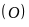 nên ta có
nên ta có
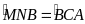 (góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối
của đỉnh đó), hay ta có
(góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối
của đỉnh đó), hay ta có
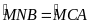
Xét hai tam giác
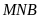 và tam giác
và tam giác
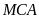 có
có
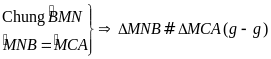
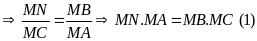
Ta có
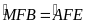 (đối đỉnh),
(đối đỉnh),
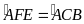 (cmt) nên ta có
(cmt) nên ta có
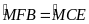
Xét hai tam giác
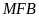 và tam giác
và tam giác
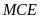 có
có
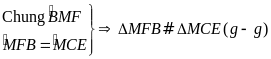
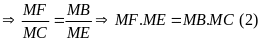
Từ
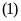 và
và
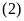 suy ra
suy ra
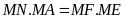 (đpcm)
(đpcm)
Tia
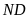 cắt đường tròn
cắt đường tròn
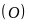 tại
tại
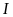 .
Chứng minh
.
Chứng minh
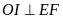 .
.
Cách 1:
Theo câu b, ta có
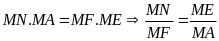
Xét hai tam giác
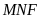 và tam giác
và tam giác
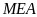 có
có
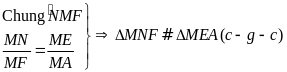
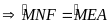
Xét tứ giác
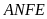 có
có
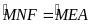 ,
,
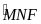 là góc ngoài tại đỉnh
là góc ngoài tại đỉnh
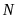 ,
,
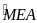 là góc trong tại đỉnh
là góc trong tại đỉnh
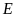
là đỉnh đối với đỉnh
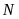
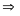 tứ giác
tứ giác
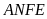 nội tiếp đường tròn (dấu hiệu nhận biết tứ giác
nội tiếp)
nội tiếp đường tròn (dấu hiệu nhận biết tứ giác
nội tiếp)
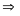 5 điểm
5 điểm
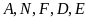 cùng thuộc một đường tròn
cùng thuộc một đường tròn
Xét tứ giác
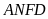 nội tiếp đường tròn có
nội tiếp đường tròn có
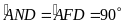 (góc nội tiếp cùng chắn
cung
(góc nội tiếp cùng chắn
cung
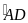 )
)
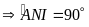 hay
hay
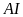 là đường kính của đường tròn
là đường kính của đường tròn
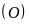 và ba điểm
và ba điểm
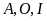 thẳng hàng
thẳng hàng
Dựng tia
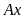 là tiếp tuyến với
là tiếp tuyến với
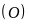 tại tiếp điểm A
tại tiếp điểm A
Ta có
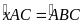 (góc tạo bởi tia tiếp tuyến và dây cung và góc nội
tiếp cùng chắn cung
(góc tạo bởi tia tiếp tuyến và dây cung và góc nội
tiếp cùng chắn cung
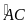
là bằng nhau), mà
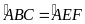 nên ta có
nên ta có
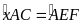
Hai góc
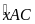 và
và
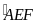 ở vị trí so le trong
ở vị trí so le trong
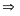
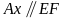
Mà
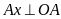 ,
AI là đường kính nên ta có
,
AI là đường kính nên ta có
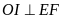 (đpcm)
(đpcm)
Cách 2:
Ta có
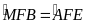 (đối đỉnh),
(đối đỉnh),
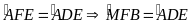
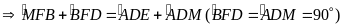
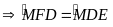
Xét hai tam giác
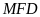 và tam giác
và tam giác
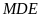 có
có
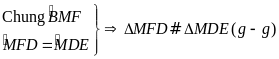
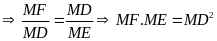
Mà
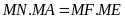 nên ta có
nên ta có
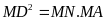
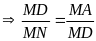
Xét hai tam giác
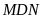 và tam giác
và tam giác
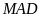 có
có
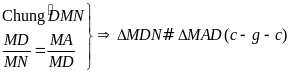
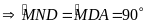
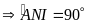
Chứng minh tương tự như Cách
1, ta được
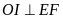 (đpcm)
(đpcm)
-------------------------------------------
SỞ GD & ĐT TP.HỒ CHÍ MINH ĐỀ THAM KHẢO TUYỂN SINH 10
PHÒNG GD & ĐT QUẬN 1 NĂM HỌC 2022-20232
ĐỀ THAM KHẢO MÔN : TOÁN 9
-------------------- Đề thi gồm 8 câu hỏi tự luận
MÃ ĐỀ : Quận 1 – 3 Thời gian: 120 phút (không kể thời gian phát đề)
Bài 1: (1.5
điểm).
Cho parabol
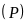 :
:
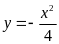 và đường thẳng
và đường thẳng
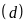 :
:
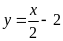
a)
Vẽ đồ thị
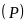 và
và
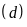 trên cùng hệ trục tọa độ;
trên cùng hệ trục tọa độ;
b) Tìm tọa
độ giao điểm của
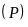 và
và
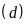 bằng phép toán.
bằng phép toán.
Bài 2: (1.0
điểm)
Cho phương trình
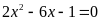 có hai nghiệm là
có hai nghiệm là
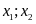 .
Không giải phương trình, hãy tính giá trị của biểu
thức:
.
Không giải phương trình, hãy tính giá trị của biểu
thức:
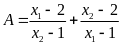 .
.
Bài 3: (0.75
điểm)
Càng lên cao không khí càng loãng nên áp suất khí quyển
càng giảm. Gọi
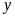 là đại lượng biểu thị cho áp suất khí quyển (tính
bằng mmHg) và
là đại lượng biểu thị cho áp suất khí quyển (tính
bằng mmHg) và
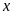 là đại lượng biểu thị cho độ cao so với mặt nước
biển (tính bằng mét). Người ta thấy với độ cao không
lớn lắm thì mối liên hệ giữa hai đại lượng này là
một hàm số bậc nhất
là đại lượng biểu thị cho độ cao so với mặt nước
biển (tính bằng mét). Người ta thấy với độ cao không
lớn lắm thì mối liên hệ giữa hai đại lượng này là
một hàm số bậc nhất
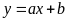 có đồ thị như hình vẽ sau:
có đồ thị như hình vẽ sau:
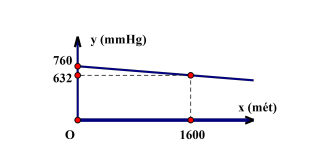
a) Hay xác định các hệ số
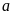 và
và
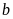 .
.
b) Một vận động viên leo núi đo được áp suất khí quyển là 540 mmHg. Hỏi vận động viên leo núi đang ở độ cao bao nhiêu mét so với mực nước biển.
Bài 4: (0.75 điểm) Bạn An đến siêu thị mua hai món hàng phải trả tổng cộng 480000 đồng, trong đó đã tính 40000 đồng thuế VAT (thuế giá trị gia tăng). Biết rằng thuế VAT đối với mặt hàng thứ nhất là 10% và thuế VAT với mặt hàng thứ hai là 8%. Hỏi nếu không tính thuế VAT thì giá niêm yết mỗi món hàng là bao nhiêu?
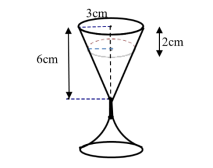
Bài 5: (1.0 điểm) Cho cốc rượu, phần phía trên là một hình nón có chiều cao 6 cm và đáy là đường tròn bán kính 3 cm. Biết trong cốc có chứa rượu với mực nước đang cách miệng cốc là 2 cm. Tính thể tích rượu trong ly. (kết quả làm tròn đến chữ số thập phân nhứ nhất)
Bài 6: (1.0 điểm) Một chiếc ti vi trong một đợt khuyến mãi, cửa hàng đã giảm giá 20% trên giá niêm yết. Đợt khuyến mãi thứ hai của hàng giảm giá tiếp 30% trên giá đã giảm ở đợt một. Nhưng đợt thứ ba cửa hàng tăng giá trở lại 25% trên giá đã giảm ở đợt hai và giá hiện tại của chiếc ti vi là 10500000 đồng. Hỏi giá niêm yết ban đầu của chiếc ti vi là bao nhiêu?
Bài 7: (1.0 điểm) Hai tổ của một nhà máy sản xuất khẩu trang trong một ngày sản xuất được 1500 chiếc khẩu trang. Để đáp ứng nhu cầu khẩu trang trong dịch cúm do chủng mới virut Corona gây ra nên mỗi ngày tổ một vượt mức 75%, tổ hai vượt mức 68%, cả hai tổ sản xuất được 2583 chiếc khẩu trang. Hỏi ban đầu trong một ngày mỗi tổ sản xuất được bao nhiêu chiếc khẩu trang?
Bài 8: (3.0 điểm)
Từ một điểm
 ở ngoài đường tròn
ở ngoài đường tròn
 ,
kẻ hai tiếp tuyến
,
kẻ hai tiếp tuyến
 (
(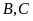 là tiếp điểm) và cát tuyến
là tiếp điểm) và cát tuyến
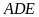 đến đường tròn (tia
đến đường tròn (tia
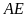 nằm trong góc
nằm trong góc
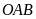 và điểm
và điểm
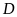 nằm giữa
nằm giữa
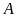 và
và
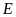 ).
).
a) Chứng minh:
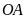 vuông góc với
vuông góc với
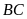 tại
tại
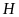 và
và
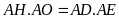 .
.
b) Chứng
minh: tứ giác
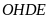 nội tiếp đường tròn và
nội tiếp đường tròn và
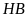 là tia phân giác của góc
là tia phân giác của góc
 .
.
c) Gọi
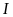 là giao điểm của
là giao điểm của
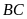 với
với
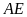 .
Qua
.
Qua
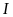 kẻ đường thẳng song song với
kẻ đường thẳng song song với
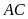 ,
cắt
,
cắt
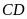 và
và
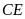 lần lượt tại
lần lượt tại
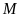 và
và
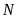 .
Chứng minh:
.
Chứng minh:
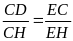 và
và
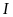 là trung điểm của
là trung điểm của
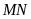 .
.
--------------------------------------------
HƯỚNG DẪN GIẢI
Bài 1: (1.5 điểm).
Cho parabol
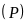 :
:
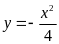 và đường thẳng
và đường thẳng
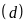 :
:
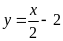
a)
Vẽ đồ thị
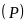 và
và
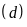 trên cùng hệ trục tọa độ;
trên cùng hệ trục tọa độ;
b) Tìm tọa độ giao điểm
của
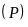 và
và
 bằng phép toán.
bằng phép toán.
Lời giải
a)  Hàm số:
Hàm số:
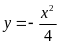
Bảng giá trị tương ứng
của
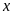 và
và
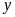 :
:
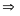 Đồ thị hàm số là một Parabol đi qua các điểm
Đồ thị hàm số là một Parabol đi qua các điểm
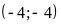 ;
;
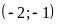 ;
;
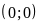 ;
;
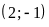 ;
;
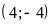
 Hàm số:
Hàm số:
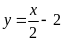
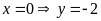
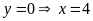
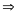 Đồ thị hàm số là đường thẳng đi qua
Đồ thị hàm số là đường thẳng đi qua
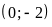 và
và
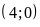
 Vẽ:
Vẽ:
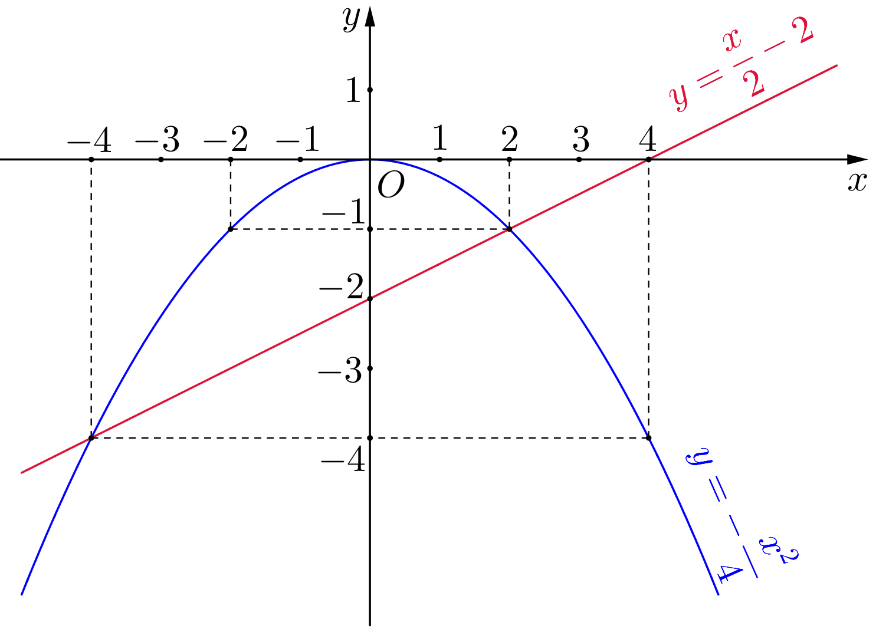
b) Hoành độ giao điểm của
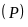 và
và
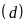 là nghiệm của phương trình:
là nghiệm của phương trình:
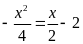
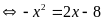
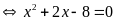
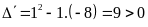
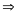 Phương
trình có hai nghiệm phân biệt:
Phương
trình có hai nghiệm phân biệt:
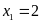 ;
;
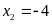
+ Với
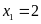
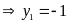
+ Với
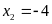
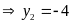
Vậy
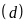 cắt
cắt
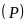 tại hai điểm phân biệt là
tại hai điểm phân biệt là
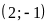 và
và
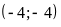 .
.
Bài 2: (1.0 điểm)
Cho phương trình
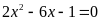 có hai nghiệm là
có hai nghiệm là
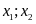 .
Không giải phương trình, hãy tính giá trị của biểu
thức:
.
Không giải phương trình, hãy tính giá trị của biểu
thức:
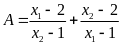 .
.
Lời giải
Phương trình đã cho là
phương trình bậc hai của
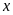 có:
có:
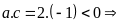 phương
trình đã cho có hai nghiệm
phương
trình đã cho có hai nghiệm
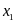 ;
;
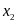
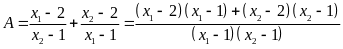
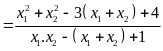
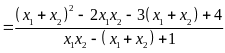
Theo
định lý Vi-et, ta có:
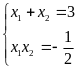
Suy
ra
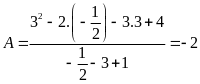 .
.
Bài 3: (0.75
điểm)
Càng lên cao không khí càng loãng nên áp suất khí quyển
càng giảm. Gọi
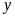 là đại lượng biểu thị cho áp suất khí quyển (tính
bằng mmHg) và
là đại lượng biểu thị cho áp suất khí quyển (tính
bằng mmHg) và
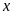 là đại lượng biểu thị cho độ cao so với mặt nước
biển (tính bằng mét). Người ta thấy với độ cao không
lớn lắm thì mối liên hệ giữa hai đại lượng này là
một hàm số bậc nhất
là đại lượng biểu thị cho độ cao so với mặt nước
biển (tính bằng mét). Người ta thấy với độ cao không
lớn lắm thì mối liên hệ giữa hai đại lượng này là
một hàm số bậc nhất
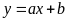 có đồ thị như hình vẽ sau:
có đồ thị như hình vẽ sau:

a) Hãy xác định các hệ số
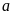 và
và
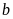 .
.
b) Một vận động viên leo núi đo được áp suất khí quyển là 540 mmHg. Hỏi vận động viên leo núi đang ở độ cao bao nhiêu mét so với mực nước biển.
Lời giải
a) Dựa vào đồ thị hàm số
ta thấy đồ thị hàm số
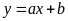 đi qua các điểm
đi qua các điểm
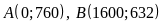
Ta có hệ phương trình:
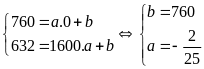 .
.
Vậy
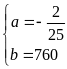 .
.
b) Theo phần a) ta có
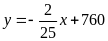 với
với
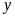 là đại lượng biểu thị cho áp suất khí quyển (tính
bằng mmHg) và
là đại lượng biểu thị cho áp suất khí quyển (tính
bằng mmHg) và
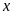 là đại lượng biểu thị cho độ cao so với mặt nước
biển (tính bằng mét).
là đại lượng biểu thị cho độ cao so với mặt nước
biển (tính bằng mét).
Một vận động viên leo núi đo được áp suất khí quyển là 540 mmHg
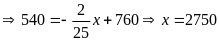 .
.
Vậy vận động viên leo núi đang ở độ 2750 mét so với mực nước biển.
Bài 4: (0.75 điểm) Bạn An đến siêu thị mua hai món hàng phải trả tổng cộng 480000 đồng, trong đó đã tính 40000 đồng thuế VAT (thuế giá trị gia tăng). Biết rằng thuế VAT đối với mặt hàng thứ nhất là 10% và thuế VAT với mặt hàng thứ hai là 8%. Hỏi nếu không tính thuế VAT thì giá niêm yết mỗi món hàng là bao nhiêu?
Lời giải
Gọi giá tiền niêm yết khi
không tính thuế VAT của mỗi món hàng lần lượt là
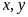 (đồng) với
(đồng) với
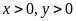 .
.
Bạn An đến siêu thị mua
hai món hàng phải trả tổng cộng 480000 đồng, trong đó
đã tính 40000 đồng thuế VAT
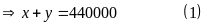 .
.
Biết rằng thuế VAT đối
với mặt hàng thứ nhất là 10% và thuế VAT với mặt
hàng thứ hai là 8%
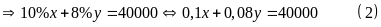 .
.
Từ
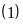 và
và
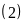 ta có hệ phương trình:
ta có hệ phương trình:
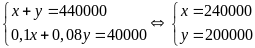 .
.
Vậy giá tiền niêm yết khi không tính thuế VAT của mỗi món hàng lần lượt là 240000 đồng và 200000 đồng.
Bài 5: (1.0 điểm) Cho cốc rượu, phần phía trên là một hình nón có chiều cao 6 cm và đáy là đường tròn bán kính 3 cm. Biết trong cốc có chứa rượu với mực nước đang cách miệng cốc là 2 cm. Tính thể tích rượu trong ly. (kết quả làm tròn đến chữ số thập phân nhứ nhất)

Lời giải
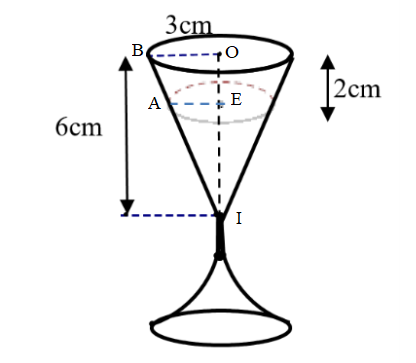
Thể tích rượu trong ly
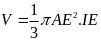
Có
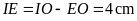
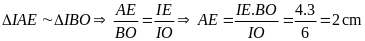
Thể tích rượu trong ly
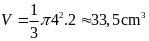 .
.
Bài 6: (1.0 điểm) Một chiếc ti vi trong một đợt khuyến mãi, cửa hàng đã giảm giá 20% trên giá niêm yết. Đợt khuyến mãi thứ hai cửa hàng giảm giá tiếp 30% trên giá đã giảm ở đợt một. Nhưng đợt thứ ba cửa hàng tăng giá trở lại 25% trên giá đã giảm ở đợt hai và giá hiện tại của chiếc ti vi là 10500000 đồng. Hỏi giá niêm yết ban đầu của chiếc ti vi là bao nhiêu?
Lời giải
Gọi giá niêm yết ban đầu
của chiếc ti vi là
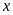 (đồng) (
(đồng) (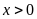 )
)
Đợt khuyến mãi thứ nhất
cửa hàng đã giảm giá 20% trên giá niêm yết suy
ra giá của chiếc ti vi trong đợt khuyến mãi thứ nhất
là :
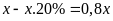 (đồng).
(đồng).
Đợt khuyến mãi thứ hai
cửa hàng giảm giá tiếp 30% trên giá đã giảm ở đợt
một suy ra giá của chiếc ti vi trong đợt khuyến mãi thứ
hai là :
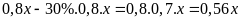 (đồng).
(đồng).
Đợt thứ ba cửa hàng tăng
giá trở lại 25% trên giá đã giảm ở đợt hai suy ra giá
hiện tại của chiếc ti vi là :
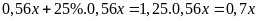 (đồng).
(đồng).
Theo
bài ra ta có :
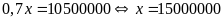 (đồng).
(đồng).
Vậy giá niêm yết ban đầu của chiếc ti vi là 15000000 đồng.
Bài 7: (1.0 điểm) Hai tổ của một nhà máy sản xuất khẩu trang trong một ngày sản xuất được 1500 chiếc khẩu trang. Để đáp ứng nhu cầu khẩu trang trong dịch cúm do chủng mới virut Corona gây ra nên mỗi ngày tổ một vượt mức 75%, tổ hai vượt mức 68%, cả hai tổ sản xuất được 2583 chiếc khẩu trang. Hỏi ban đầu trong một ngày mỗi tổ sản xuất được bao nhiêu chiếc khẩu trang?
Lời giải
Gọi
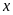 là số khẩu trang ban đầu tổ một sản xuất được mỗi
ngày
là số khẩu trang ban đầu tổ một sản xuất được mỗi
ngày
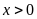 .
.
Gọi
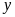 là số khẩu trang ban đầu tổ hai sản xuất được mỗi
ngày
là số khẩu trang ban đầu tổ hai sản xuất được mỗi
ngày
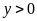 .
.
Hai tổ của
một nhà máy sản xuất khẩu trang trong một ngày sản
xuất được 1500 chiếc khẩu trang suy ra ta có phương
trình:
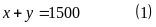
Nhưng mỗi
ngày tổ một vượt mức 75%, tổ hai vượt mức 68%, cả
hai tổ sản xuất được 2583 chiếc khẩu trang suy ra ta có
phương trình:
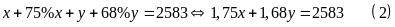
Từ
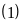 và
và
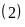 ta có hệ phương trình:
ta có hệ phương trình:
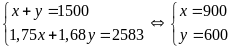 .
.
Vậy ban đầu trong một ngày tổ một sản xuất được 900 chiếc khẩu trang, tổ hai sản xuất được 600 chiếc khẩu trang.
Bài 8: (3.0
điểm)
Từ một điểm
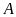 ở ngoài đường tròn
ở ngoài đường tròn
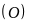 ,
kẻ hai tiếp tuyến
,
kẻ hai tiếp tuyến
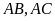 (
(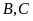 là tiếp điểm) và cát tuyến
là tiếp điểm) và cát tuyến
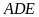 đến đường tròn (tia
đến đường tròn (tia
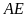 nằm trong góc
nằm trong góc
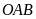 và điểm
và điểm
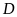 nằm giữa
nằm giữa
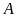 và
và
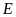 ).
).
a)
Chứng minh:
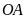 vuông góc với
vuông góc với
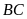 tại
tại
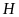 và
và
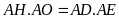 .
.
b) Chứng
minh: tứ giác
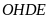 nội tiếp đường tròn và
nội tiếp đường tròn và
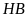 là tia phân giác của góc
là tia phân giác của góc
 .
.
c) Gọi
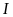 là giao điểm của
là giao điểm của
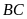 với
với
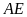 .
Qua
.
Qua
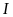 kẻ đường thẳng song song với
kẻ đường thẳng song song với
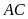 ,
cắt
,
cắt
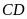 và
và
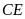 lần lượt tại
lần lượt tại
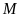 và
và
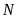 .
Chứng minh:
.
Chứng minh:
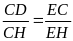 và
và
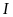 là trung điểm của
là trung điểm của
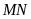 .
.
Lời giải
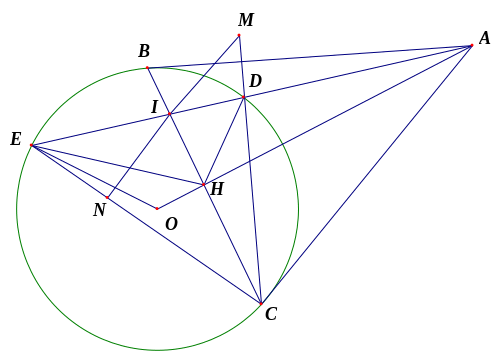
a) Ta có
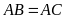 (tính chất hai đường tiếp tuyến cắt nhau)
(tính chất hai đường tiếp tuyến cắt nhau)
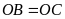 (cùng bằng bán kính)
(cùng bằng bán kính)
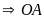 là trung trực của
là trung trực của
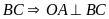 tại
tại
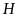 .
.
Xét
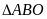 vuông tại
vuông tại
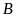 có
có
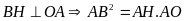 (1)
(1)
Xét
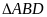 và
và
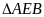 có
có
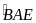 chung
chung
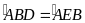 (cùng chắn
(cùng chắn
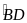 )
)
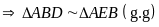
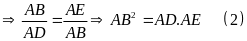
Từ (1) và (2) suy ra
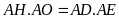 .
.
b) Xét
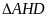 và
và
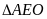 có:
có:
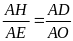 (câu a),
(câu a),
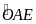 chung
chung
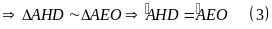
Có
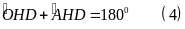
Từ (3) và (4)
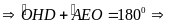 tứ giác
tứ giác
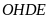 nội tiếp đường tròn.
nội tiếp đường tròn.
Tứ
giác
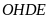 nội tiếp đường tròn
nội tiếp đường tròn
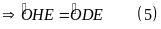
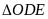 cân tại
cân tại
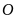
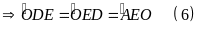
Từ (3), (5) và (6)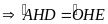 (7)
(7)
Lại có:
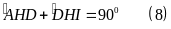
Và
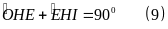
Từ (7), (8) và (9)
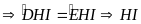 là tia phân giác của góc
là tia phân giác của góc
 .
.
c) Có
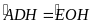 (cùng
bù với
(cùng
bù với
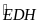 )
và
)
và
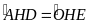 (chứng minh trên).
(chứng minh trên).
Suy ra
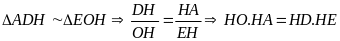 .
.
Xét trong tam giác vuông
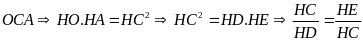 ,
mà
,
mà
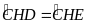 (do
(do
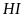 là tia phân giác của góc
là tia phân giác của góc
 )
)
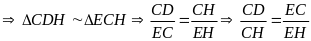 .
.
Có
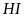 là
phân giác trong của tam giác
là
phân giác trong của tam giác
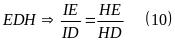
Mà
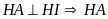 là phân giác ngoài của tam giác
là phân giác ngoài của tam giác
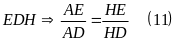
Từ (10) và (11) suy ra
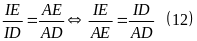
Có
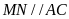 áp dụng định lý Talet ta có:
áp dụng định lý Talet ta có:
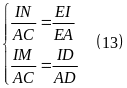
Từ (12) và (13) suy ra
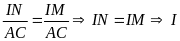 là trung điểm của
là trung điểm của
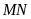 .
.
-------------------------------------------
Ngoài Bộ Đề Tuyển Sinh Lớp 10 Môn Toán Quận 1 TPHCM 2022-2023 Có Lời Giải Chi Tiết thì các đề thi trong chương trình lớp 9 sẽ được cập nhật liên tục và nhanh nhất có thể sau khi kỳ thi diễn ra trên Danh mục Kho Đề Thi nhằm giúp các bạn đọc thuận tiện trong việc tra cứu và đối chiếu đáp án. Quý thầy cô và các bạn đọc có thể chia sẻ thêm những tài liệu học tập hữu ích đến địa chỉ email của chúng tôi, nhằm xây dựng nên kho đề thi phong phú, đa dạng cho các em học sinh tham khảo và rèn luyện.
Cuối cùng, bộ đề tuyển sinh môn Toán lớp 10 từ Quận 1, Thành phố Hồ Chí Minh cho năm học 2022-2023 với lời giải chi tiết đã trở thành một nguồn tài liệu vô cùng quý giá và không thể thiếu trong quá trình ôn tập và chuẩn bị cho kỳ thi tuyển sinh. Đề thi này không chỉ là một bài kiểm tra, mà còn là một công cụ hỗ trợ quan trọng giúp các em rèn luyện và nắm vững kiến thức toán học.
Bộ đề tuyển sinh môn Toán lớp 10 từ Quận 1, Thành phố Hồ Chí Minh cho năm học 2022-2023 có lời giải chi tiết đã được biên soạn bởi những chuyên gia giáo dục có kinh nghiệm. Đề thi này bao gồm các dạng câu hỏi phong phú và đa dạng, từ những kiến thức cơ bản đến những bài toán khó hơn. Lời giải chi tiết không chỉ cung cấp đáp án chính xác, mà còn giải thích rõ ràng cách giải quyết từng bài tập, giúp các em hiểu rõ hơn về quy tắc và phương pháp giải toán.
Qua việc sử dụng bộ đề tuyển sinh môn Toán lớp 10 từ Quận 1, Thành phố Hồ Chí Minh cho năm học 2022-2023 có lời giải chi tiết, các em có cơ hội rèn luyện kỹ năng làm bài, nắm vững kiến thức và phát triển tư duy logic. Bằng việc tự kiểm tra và so sánh với lời giải, các em có thể xác định được những lỗ hổng và điểm yếu của mình, từ đó tập trung vào việc cải thiện và nâng cao khả năng giải toán.
Bộ đề tuyển sinh môn Toán lớp 10 từ Quận 1, Thành phố Hồ Chí Minh cho năm học 2022-2023 có lời giải chi tiết là một nguồn tài liệu đáng tin cậy và hữu ích để các em ôn tập và nâng cao kỹ năng toán học. Hãy sử dụng bộ đề này một cách chăm chỉ và kiên nhẫn, và tin rằng sự nỗ lực và cống hiến sẽ đem lại kết quả tốt trong hành trình tuyển sinh và học tập toán học của các em.
Xem thêm