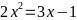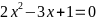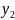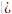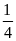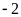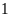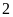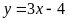Đề Thi Vào 10 Môn Toán Quận 3 TPHCM 2022-2023 Tham Khảo Có Lời Giải Chi Tiết – Toán 9
Đề Thi Vào 10 Môn Toán Quận 3 TPHCM 2022-2023 Tham Khảo Có Lời Giải Chi Tiết – Toán 9 được Trang Tài Liệu sưu tầm với các thông tin mới nhất hiện nay. Đề thi này sẽ giúp các em học sinh ôn tập, củng cố kiến thức, rèn luyện kĩ năng làm bài. Cũng như hỗ trợ thầy cô trong quá trình giảng dạy. Hy vọng những tài liệu này sẽ giúp các em trong quá trình ôn luyện và đạt kết quả cao trong bài thi sắp tới.
Trong quá trình học tập, việc chuẩn bị cho kỳ thi vào lớp 10 là một nhiệm vụ quan trọng của các bạn học sinh lớp 9. Đặc biệt, môn Toán được coi là một trong những môn thi quan trọng và đòi hỏi sự nắm vững kiến thức và kỹ năng giải toán. Để giúp các bạn học sinh tại Quận 3, Thành phố Hồ Chí Minh có một nguồn tài liệu tham khảo chất lượng, chúng tôi xin trình bày một đề thi vào 10 môn Toán năm 2022-2023, kèm theo lời giải chi tiết.
Bộ đề thi này được thiết kế dựa trên chương trình học Toán 9 và tuân thủ các yêu cầu của kỳ thi vào lớp 10. Mỗi câu hỏi trong đề thi đều được trình bày một cách cụ thể và kèm theo lời giải chi tiết, giúp các bạn học sinh hiểu rõ cách giải quyết từng bài toán. Điều này sẽ không chỉ giúp các bạn làm quen với cấu trúc đề thi mà còn rèn luyện tư duy logic và nắm vững kiến thức cần thiết.
Bộ đề thi và lời giải chi tiết này có thể được tìm kiếm và sử dụng như một nguồn tài liệu tham khảo trên các nguồn tài liệu trực tuyến hoặc thông qua việc liên hệ với nhà trường. Việc ôn tập và làm quen với bộ đề thi này sẽ giúp các bạn nắm vững kiến thức Toán học và tự tin hơn khi tiếp cận kỳ thi.
Chúng tôi hi vọng rằng đề thi và lời giải chi tiết môn Toán 9 dành cho kỳ thi vào lớp 10 tại Quận 3, TPHCM sẽ trở thành một nguồn tài liệu hữu ích trong quá trình ôn tập và chuẩn bị cho kỳ thi sắp tới. Qua sự cố gắng và cải thiện không ngừng, chúng ta tin rằng các bạn học sinh sẽ đạt được kết quả tốt và vượt qua thách thức của kỳ thi vào lớp 10 một cách thành công.
Chúc các bạn học tập hiệu quả và đạt được thành công với kỳ thi vào lớp 10!
Đề thi tham khảo
Dưới đây là bản đọc trực tuyến giúp thầy cô và các em học sinh có thể nghiên cứu Online hoặc bạn có thể tải miễn phí với phiên bản word để dễ dàng in ấn cũng như học tập Offline
SỞ GD & ĐT TP.HỒ CHÍ MINH ĐỀ THAM KHẢO TUYỂN SINH 10
PHÒNG GD & ĐT QUẬN 3 NĂM HỌC 2022-20232
ĐỀ THAM KHẢO MÔN : TOÁN 9
-------------------- Đề thi gồm 8 câu hỏi tự luận
MÃ ĐỀ : Quận 3 – 1 Thời gian: 120 phút (không kể thời gian phát đề)
Bài 1: (1.5
điểm).
Cho
 :
: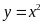 và đường thẳng
và đường thẳng
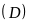 :
:
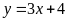
a)
Vẽ
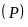 và
và
 trên cùng một hệ trục.
trên cùng một hệ trục.
b) Tìm tọa
độ giao điểm của
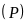 và
và
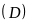 bằng phép tính.
bằng phép tính.
Bài 2: (1.0
điểm)
Cho phương trình bậc hai:

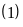
a) Chứng
minh rằng phương trình
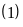 luôn
có hai nghiệm phân biệt
luôn
có hai nghiệm phân biệt
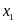 và
và
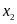 .
.
b) Tìm các
giá trị
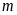 để
để
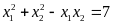 .
.
Bài 3: (1.0 điểm) Một cửa hàng đồng loạt giảm giá các sản phẩm. Trong đó có chương trình nếu mua một gói kẹo thứ hai trở đi sẽ được giảm 10% so với giá ban đầu là 50000 đồng.
a) Nếu gọi số gói kẹo đã mua là x, số tiền phải trả là y. Hãy biểu diễn diễn y theo x.
b) Bạn Thư muốn mua 10 gói kẹo thì hết bao nhiêu tiền.
Bài 4: (1.0 điểm) Trong kỳ thi HKII môn toán lớp 9. Một phòng thi của trường có 24 thí sinh dự thi. Các thí sinh đều phải làm bài trên giấy thi của trường phát. Cuối buổi thi, sau khi thu bài, giám thị coi thi đếm được tổng số tờ giấy thi là 53 tờ. Hỏi trong phòng thi đó có bao nhiêu thí sinh làm bài 2 tờ giấy thi, bao nhiêu thí sinh làm bài 3 tờ giấy thi? Biết rằng có 3 thí sinh chỉ làm 1 tờ giấy thi.
Bài 5: (1.0 điểm) Trong một phòng họp có 360 người họp, được sắp xếp ngồi đều trên các dãy ghế. Nếu bớt đi 3 dãy ghế thì mỗi dãy ghế phải xếp thêm 4 ghế mới đủ chỗ. Hỏi lúc đầu có bao nhiêu dãy ghế và mỗi dãy xếp mấy ghế?
B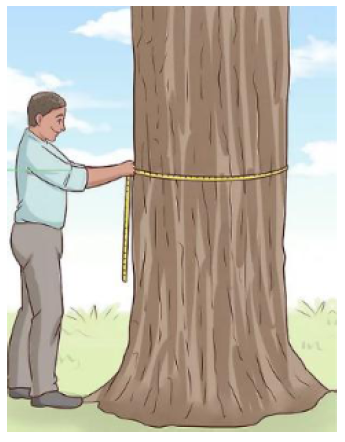 ài
6: (1.0 điểm) Để ước
lượng khối lượng của cây gỗ trồng trong rừng người
ta cần xác định chiều cao h
của cây (đo bằng mét) và chu vi C
của vòng tròn thân cây ngang tầm ngực (đo bằng mét).
Theo cách đo đạc trong lâm nghiệp, độ cao ngang tầm ngực
là 1,4 mét tính từ mặt đất. Từ đó người ta có thể
quấn thước dây vòng quanh thân cây ở độ cao này và
ghi lại số đo chu vi C.
ài
6: (1.0 điểm) Để ước
lượng khối lượng của cây gỗ trồng trong rừng người
ta cần xác định chiều cao h
của cây (đo bằng mét) và chu vi C
của vòng tròn thân cây ngang tầm ngực (đo bằng mét).
Theo cách đo đạc trong lâm nghiệp, độ cao ngang tầm ngực
là 1,4 mét tính từ mặt đất. Từ đó người ta có thể
quấn thước dây vòng quanh thân cây ở độ cao này và
ghi lại số đo chu vi C.
Áp dụng công thức thể tích hình trụ V = S.h trong đó S là diện tích vòng tròn thân cây có chu vi C nói trên và h là chiều cao của cây sẽ tính được thể tích của cây. Nếu một cây có chu vi C của vòng tròn thân cây ngang tầm ngực là 1,28m và chiều cao là 20,4m thì cây có thể tích bao nhiêu (làm tròn đến chữ số thập phân thứ nhất)?
Cho biết loại cây nói trên có khối lượng riêng là D = 1,05 tấn/m3 khối lượng m = V . D. Hãy ước lượng khối lượng của cây đó tính theo đơn vị là kg (làm tròn đến hàng trăm).
Bài 7: (1.0 điểm) Một cửa hàng Pizza có chương trình khuyến mãi: giảm 30% cho bánh Pizza hải sản có giá bán ban đầu là 210000 đồng/cái. Nếu khách hàng có thẻ VIP thì sẽ được giảm thêm 5% trên giá đã giảm. Hỏi một nhóm nhân viên văn phòng đặt mua 60 cái bánh Pizza hải sản ở cửa hàng trong đó có 25 cái dùng thẻ VIP thì phải trả tất cả bao nhiêu tiền (làm tròn nghìn đồng)?
Bài 8: (2.5 điểm)
Từ điểm A
ở ngoài đường tròn
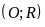 vẽ hai tiếp tuyến AB,
AC
với đường tròn
vẽ hai tiếp tuyến AB,
AC
với đường tròn
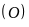
 là tiếp điểm
là tiếp điểm .
Gọi H
là giao điểm của AO
và BC.
Gọi I là
trung điểm của AB.
Từ B
kẻ đường thẳng vuông góc với OI
tại K,
đường thẳng này cắt đường tròn
.
Gọi H
là giao điểm của AO
và BC.
Gọi I là
trung điểm của AB.
Từ B
kẻ đường thẳng vuông góc với OI
tại K,
đường thẳng này cắt đường tròn
 tại D
(D
khác B).
tại D
(D
khác B).
a) Chứng minh tứ giác ABOC
nội tiếp và
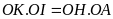 .
.
b) Đường
tròn
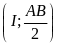 cắt AC
tại E.
Gọi F
là giao điểm của BE
và
OA. Chứng minh F
đối xứng với O
qua H.
cắt AC
tại E.
Gọi F
là giao điểm của BE
và
OA. Chứng minh F
đối xứng với O
qua H.
c) Chứng
minh đường tròn ngoại tiếp
 đi qua điểm K
đi qua điểm K
--------------------------------------------
HƯỚNG DẪN GIẢI
Bài 1: (1.5 điểm).
Cho
 :
: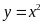 và đường thẳng
và đường thẳng
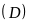 :
:
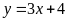
a)
Vẽ
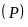 và
và
 trên cùng một hệ trục.
trên cùng một hệ trục.
b) Tìm tọa độ giao điểm
của
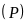 và
và
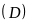 bằng phép tính.
bằng phép tính.
Lời giải
a)  Hàm số:
Hàm số:
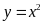
Bảng giá trị tương ứng
của
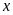 và
và
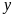 :
:
-
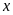
–2
-1
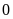
1
2

4
1
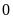
1
4
 Đồ thị hàm số là một Parabol đi qua các điểm
Đồ thị hàm số là một Parabol đi qua các điểm
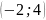 ;
;
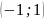 ;
;
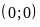 ;
;
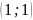 ;
;
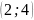
 Hàm số:
Hàm số:
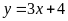
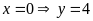
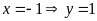
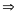 Đồ thị hàm số là đường thẳng đi qua
Đồ thị hàm số là đường thẳng đi qua
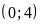 và
và
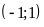
 Vẽ:
Vẽ:
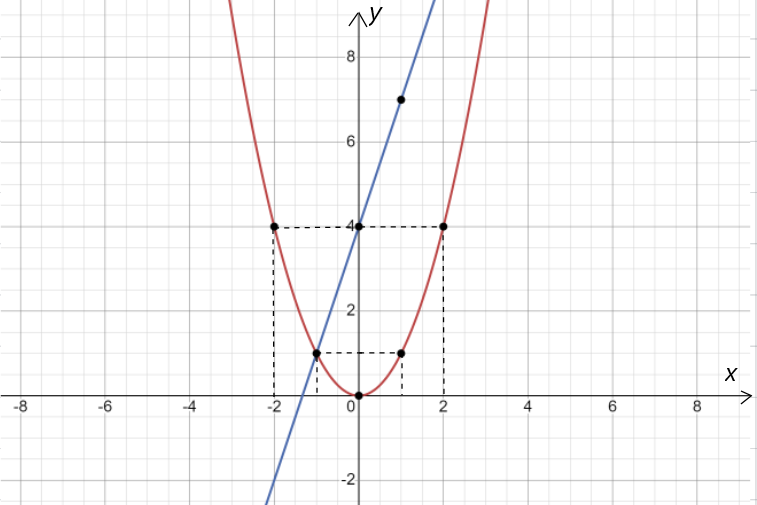
b) Hoành độ giao điểm của
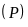 và
và
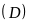 là nghiệm của phương trình:
là nghiệm của phương trình:
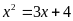

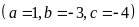
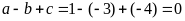
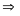 Phương
trình có hai nghiệm phân biệt:
Phương
trình có hai nghiệm phân biệt:
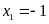 ;
;

+ Với
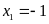
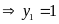
+ Với
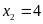
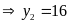
Vậy
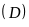 cắt
cắt
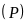 tại hai điểm phân biệt là
tại hai điểm phân biệt là
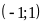 và
và
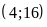 .
.
Bài 2: (1.0 điểm)
Cho phương trình bậc hai:

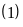
a) Chứng minh rằng phương
trình
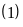 luôn
có hai nghiệm phân biệt
luôn
có hai nghiệm phân biệt
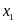 và
và
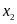 .
.
b) Tìm các giá trị
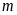 để
để
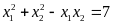 .
.
Lời giải
a)
Cách 1:
Phương trình đã cho là phương
trình bậc hai của
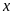 có:
có:
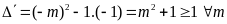
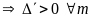
Vậy phương trình đã cho
luôn có hai nghiệm
 ;
;
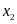 với mọi giá trị của
với mọi giá trị của
 .
.
Cách 2 : vì a, c trái dấu nên phương trình luôn có 2 nghiệm phân biệt
b)
Theo định lý Vi-et, ta có:
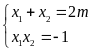
Do
đó:
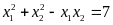
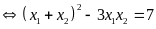
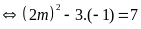
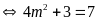


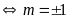
Vậy với
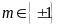 thì phương trình có hai nghiệm
thì phương trình có hai nghiệm
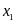 ;
;
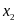 thỏa mãn
thỏa mãn
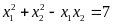 .
.
Bài 3: (1.0 điểm) Một cửa hàng đồng loạt giảm giá các sản phẩm. Trong đó có chương trình nếu mua một gói kẹo thứ hai trở đi sẽ được giảm 10% so với giá ban đầu là 50000 đồng.
a) Nếu gọi số gói kẹo đã mua là x, số tiền phải trả là y. Hãy biểu diễn diễn y theo x.
b) Bạn Thư muốn mua 10 gói kẹo thì hết bao nhiêu tiền.
Lời giải
Giá một gói kẹo thì gói thứ hai trở đi:
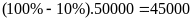 đồng
đồng
Số gói kẹo đã mua là x, số tiền phải trả là y. Theo đề bài ta có:
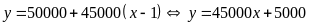
Bạn Thư mua 10 gói kẹo
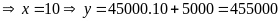
Vậy số tiền bạn Thư phải trả khi mua 10 gói kẹo là 455000 đồng
Bài 4: (1.0 điểm) Trong kỳ thi HKII môn toán lớp 9. Một phòng thi của trường có 24 thí sinh dự thi. Các thí sinh đều phải làm bài trên giấy thi của trường phát. Cuối buổi thi, sau khi thu bài, giám thị coi thi đếm được tổng số tờ giấy thi là 53 tờ. Hỏi trong phòng thi đó có bao nhiêu thí sinh làm bài 2 tờ giấy thi, bao nhiêu thí sinh làm bài 3 tờ giấy thi? Biết rằng có 3 thí sinh chỉ làm 1 tờ giấy thi.
Lời giải
Gọi x
là số thí sinh làm
bài 2 tờ giấy thi, y
là số thí sinh làm
bài 3 tờ giấy thi
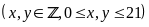
Vì có 3 thí sinh làm bài 1
tờ giấy thi nên ta có
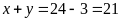
Tổng số tờ giấy thi của
các thí sinh làm 2 tờ và 3 tờ giấy thi là
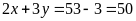
Ta có hệ phương trình:
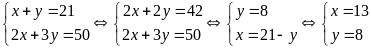 (thỏa
mãn)
(thỏa
mãn)
Vậy có 13 thí sinh làm bài 2 tờ giấy thi, có 8 thí sinh làm bài 3 tờ giấy thi.
Bài 5: (1.0 điểm) Trong một phòng họp có 360 người họp, được sắp xếp ngồi đều trên các dãy ghế. Nếu bớt đi 3 dãy ghế thì mỗi dãy ghế phải xếp thêm 4 ghế mới đủ chỗ. Hỏi lúc đầu có bao nhiêu dãy ghế và mỗi dãy xếp mấy ghế?
Lời giải
Gọi x là dãy ghế ban đầu (x nguyên dương, 3 < x < 360)
Số ghế mỗi dãy ban đầu
là

Số dãy ghế lúc sau là: x – 3.
Số ghế mỗi dãy lúc sau
là:
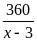
Vì mỗi dãy ghế phải xếp thêm 4 ghế so mới đủ chỗ nên ta có phương trình:
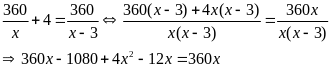
 (loại)
;
(loại)
;
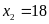 (nhận)
(nhận)
Vậy lúc đầu có 18 dãy ghế
và mỗi dãy có
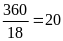 (ghế)
(ghế)
Bài 6: (1.0 điểm) Để ước lượng khối lượng của cây gỗ trồng trong rừng người ta cần xác định chiều cao h của cây (đo bằng mét) và chu vi C của vòng tròn thân cây ngang tầm ngực (đo bằng mét). Theo cách đo đạc trong lâm nghiệp, độ cao ngang tầm ngực là 1,4 mét tính từ mặt đất. Từ đó người ta có thể quấn thước dây vòng quanh thân cây ở độ cao này và ghi lại số đo chu vi C.
Áp dụng công thức thể tích hình trụ V = S.h trong đó S là diện tích vòng tròn thân cây có chu vi C nói trên và h là chiều cao của cây sẽ tính được thể tích của cây. Nếu một cây có chu vi C của vòng tròn thân cây ngang tầm ngực là 1,28m và chiều cao là 20,4m thì cây có thể tích bao nhiêu (làm tròn đến chữ số thập phân thứ nhất)?
Cho biết loại cây nói trên có khối lượng riêng là D = 1,05 tấn/m3 khối lượng m = V . D. Hãy ước lượng khối lượng của cây đó tính theo đơn vị là kg (làm tròn đến hàng trăm).
Lời giải
Gọi R (m) là bán kính vòng tròn thân cây ngang tầm ngực (R > 0)
Chu vi vòng tròn thân cây ngang tầm ngực là:

Diện tích vòng tròn thân cây ngang tầm ngực:
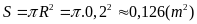
Thể tích cây là:
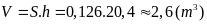
Khối lượng của cây:
 (tấn)
(tấn) (kg)
(kg)
Bài 7: (1.0 điểm) Một cửa hàng Pizza có chương trình khuyến mãi: giảm 30% cho bánh Pizza hải sản có giá bán ban đầu là 210000 đồng/cái. Nếu khách hàng có thẻ VIP thì sẽ được giảm thêm 5% trên giá đã giảm. Hỏi một nhóm nhân viên văn phòng đặt mua 60 cái bánh Pizza hải sản ở cửa hàng trong đó có 25 cái dùng thẻ VIP thì phải trả tất cả bao nhiêu tiền (làm tròn nghìn đồng)?
Lời giải
Giá một cái bánh Pizza hải sản trong chương trình khuyến mãi:
(100% – 30%).210000 = 147000 (đồng)
Giá một cái bánh Pizza hải hải trong chương trình khuyến mãi và có dùng thẻ VIP :
(100% – 5%).147000 = 139650 (đồng)
Nhóm nhân viên văn phòng đặt mua 60 cái bánh Pizza hải sản trong đó có 25 cái dùng thẻ VIP thì số tiền phải trả là : 147000.(60-25) + 139650.25 = 8636250 (đồng)
Bài 8: (2.5
điểm)
Từ điểm A
ở ngoài đường tròn
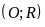 vẽ hai tiếp tuyến AB,
AC
với đường tròn
vẽ hai tiếp tuyến AB,
AC
với đường tròn
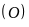
 là
tiếp điểm
là
tiếp điểm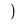 .
Gọi H
là giao điểm của AO
và
BC.
Gọi I
là
trung điểm của AB.
Từ B
kẻ đường thẳng vuông góc với OI
tại K,
đường thẳng này cắt đường tròn
.
Gọi H
là giao điểm của AO
và
BC.
Gọi I
là
trung điểm của AB.
Từ B
kẻ đường thẳng vuông góc với OI
tại K,
đường thẳng này cắt đường tròn
 tại D
(D
khác B).
tại D
(D
khác B).
a) Chứng
minh tứ giác ABOC
nội
tiếp và
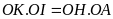 .
.
b) Đường
tròn
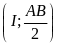 cắt AC
tại E.
Gọi F
là giao điểm của BE
và
OA.
Chứng minh F
đối xứng với O
qua H.
cắt AC
tại E.
Gọi F
là giao điểm của BE
và
OA.
Chứng minh F
đối xứng với O
qua H.
c) Chứng
minh đường tròn ngoại tiếp
 đi qua điểm K.
đi qua điểm K.
Lời giải
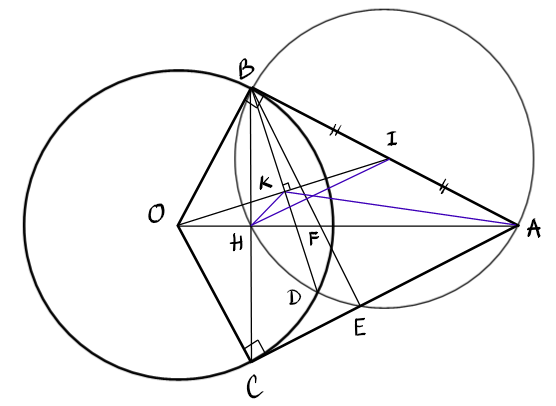
Ta có
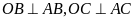 (AB,
AC là tiếp tuyến của (O)
)
(AB,
AC là tiếp tuyến của (O)
)
Suy ra
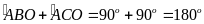
Do đó tứ giá ABOC nội tiếp.
Lại có: AO là phân giác góc BAC và AB = AC (AB, AC là tiếp tuyến của đường tròn (O))
Suy ra AO là phân giác cũng là đường cao của tam giác cân ABC
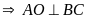 tại
H.
tại
H.
∆OBA vuông tại B có đường cao BH
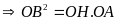
∆OBI vuông tại B có đường cao BK
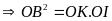
Vậy:
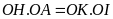
Xét đường tròn
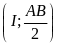 :
:
Ta có:
 (góc nội tiếp chắn cung HE)
(góc nội tiếp chắn cung HE)
Mà
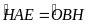 (cùng nhìn cạnh OC của tứ giác nội tiếp OBAC)
(cùng nhìn cạnh OC của tứ giác nội tiếp OBAC)
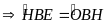
 BH
là phân giác
BH
là phân giác
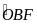
Mà
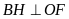
Do đó ∆OBF cân tại B có BH là phân giác cũng là đường cao và đường trung tuyến
Suy ra H là trung điểm OF hay F đối xứng O qua H.
Ta có
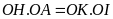 (chứng
minh ở câu a)
(chứng
minh ở câu a)
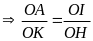
Đồng thời ∆OKA
và ∆OAI
có
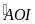 chung
nên
chung
nên
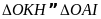 (c.g.c)
(c.g.c)
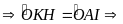 Tứ
giác AHKI nội
tiếp
Tứ
giác AHKI nội
tiếp
 (1)
(1)
Lại có
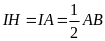 (∆ABH
vuông tại H,
HI là
trung tuyến) nên ∆IHA cân
tại I
(∆ABH
vuông tại H,
HI là
trung tuyến) nên ∆IHA cân
tại I
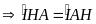
mà
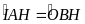 (cùng
phụ
(cùng
phụ
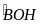 )
và
)
và
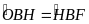 (chứng
minh trên)
(chứng
minh trên)
nên
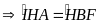 (2)
(2)
Từ (1) và (2)
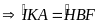
Mặt khác:
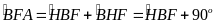 (góc
ngoài ∆BHF)
(góc
ngoài ∆BHF)
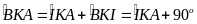
Do đó
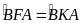 và cùng nhìn cạnh AB
và cùng nhìn cạnh AB
Vậy tứ giác BKFA nội tiếp hay đường tròn ngoại tiếp ∆BFA đi qua K.
-------------------------------------------
SỞ GD & ĐT TP.HỒ CHÍ MINH ĐỀ THAM KHẢO TUYỂN SINH 10
PHÒNG GD & ĐT QUẬN 3 NĂM HỌC 2022-2023
ĐỀ THAM KHẢO MÔN: TOÁN 9
------------------------- Đề thi gồm 8 câu hỏi tự luận
MÃ ĐỀ: Quận 3 – 2 Thời gian: 120 phút (không kể thời gian phát đề)
Bài 1: (1.5
điểm)
Cho
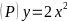 và
(D):
và
(D):
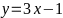
a) Vẽ (P) và (D) trên cùng một hệ trục tọa độ
b) Tìm tọa độ giao điểm của (P) và (D) bằng phép tính.
Bài 2: (1.0
điểm)
Cho
phương trình
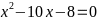 có hai nghiệm
có hai nghiệm
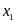 ,
,
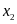 .
Không giải phương trình hãy tính giá trị của biểu thức
A
=
.
Không giải phương trình hãy tính giá trị của biểu thức
A
=
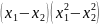 .
.
Bài 3: (1.0
điểm)
Các
nhà khoa học về thống kê đã thiết lập được hàm số
sau: A(t)
=
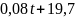 .
Trong đó A(t)
là độ tuổi trung bình các phụ nữ kết hôn lần đầu
của thế giới; t là số năm kết hôn, với gốc thời
gian là 1950. Hãy tính độ tuổi trung bình các phụ nữ
kết hôn lần đầu lần lượt vào các năm 1950, 2000,
2018, 2020 (làm tròn đến chữ số thập phân thứ hai).
.
Trong đó A(t)
là độ tuổi trung bình các phụ nữ kết hôn lần đầu
của thế giới; t là số năm kết hôn, với gốc thời
gian là 1950. Hãy tính độ tuổi trung bình các phụ nữ
kết hôn lần đầu lần lượt vào các năm 1950, 2000,
2018, 2020 (làm tròn đến chữ số thập phân thứ hai).
Bài 4: (1.0 điểm) Một trường học có tổng số giáo viên là 80 người, hiện tại tuổi trung bình của giáo viên là 35 tuổi. Trong đó, tuổi tuổi trung bình của giáo viên nữ là 32 tuổi và tuổi trung bình của giáo viên nam là 38 tuổi. Hỏi 3 trường đó có bao nhiêu giáo viên nam, bao nhiêu giáo viên nữ?
Bài 5: (1.0 điểm) Bé An sống trong gia đình ba thế hệ gồm ông bà nội, ba mẹ, bé An và em trai. Chủ nhật vừa rồi cả gia đình đi xem phim. Biết giá vé cho trẻ em (vé của bé An và em trai) được giảm giá 50%; vé người cao tuổi được giảm giá 25% (vé của ông bà nội). Vé của ba mẹ không được giảm giá. Ông nội bé An, người phải trả giá vé là 60 nghìn đồng, đang trả tiền cho mọi người. Hỏi ông nội phải trả bao nhiêu tiền?
Bài 6: (1.0
điểm)
Theo
năm Dương lịch, chu kỳ Trái Đất quay quanh Mặt Trời là
365 ngày và ngày (tức là 365,25 ngày). Khi đó,
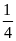 ngày này sẽ được tích lũy trong vòng 4 năm nên theo năm
Dương lịch thì cứ 4 năm lại có 1 năm là năm nhuận vào
các năm chia hết cho 4 (tháng 2 của năm này sẽ có 29 ngày
thay vì có 28 ngày như các năm không nhuận Dương lịch).
Tuy nhiên, vẫn có một số ngoại lệ đối với nguyên
tắc trên vì có khi một năm Dương lịch lại ngắn hơn
365,25 ngày nên với những năm có hai chữ số 0 ở cuối
thì năm đó phải chia hết cho 400 mới là năm nhuận Dương
lịch.
ngày này sẽ được tích lũy trong vòng 4 năm nên theo năm
Dương lịch thì cứ 4 năm lại có 1 năm là năm nhuận vào
các năm chia hết cho 4 (tháng 2 của năm này sẽ có 29 ngày
thay vì có 28 ngày như các năm không nhuận Dương lịch).
Tuy nhiên, vẫn có một số ngoại lệ đối với nguyên
tắc trên vì có khi một năm Dương lịch lại ngắn hơn
365,25 ngày nên với những năm có hai chữ số 0 ở cuối
thì năm đó phải chia hết cho 400 mới là năm nhuận Dương
lịch.
a) Từ năm 1900 đến năm 2000 có bao nhiêu năm nhuận Dương lịch? Vì sao?
 b)
Một nhà hộ sinh trong tháng 2 năm 2021 có 29 em bé chào
đời là con của 29 gia đình khác nhau. Có thể chắc chắn
rằng có ít nhất 2 em bé chào đời cùng ngày hay không?
Vì sao?
b)
Một nhà hộ sinh trong tháng 2 năm 2021 có 29 em bé chào
đời là con của 29 gia đình khác nhau. Có thể chắc chắn
rằng có ít nhất 2 em bé chào đời cùng ngày hay không?
Vì sao?
Bài 7: (1.0 điểm) Thớt là một dụng cụ sử dụng trong bếp của mỗi gia đình để
thái, chặt, ... Một cái thớt hình trụ có đường kính đáy 22cm,
cao 4cm.
a) Tính tổng diện tích hai mặt thớt (làm tròn đến cm2).
b) Cho biết loại gỗ làm thớt có khối lượng 500 kg/m3. Hỏi thớt nặng bao nhiêu gam?
Công thức tính thể tích hình trụ là V = S · h (S là diện tích đáy và h là chiều cao hình trụ).
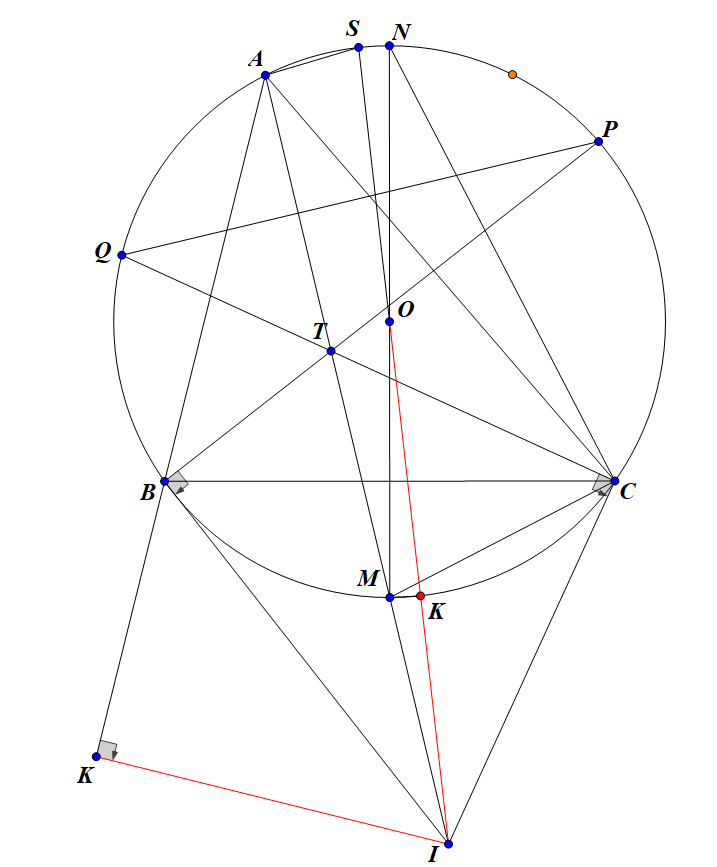
Bài 8: (3.0 điểm)
Cho
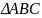 có 3 góc nhọn nội tiếp đường tròn (O; R). Gọi M,
P,
Q
lần lượt là điểm chính giữa các cung
có 3 góc nhọn nội tiếp đường tròn (O; R). Gọi M,
P,
Q
lần lượt là điểm chính giữa các cung
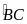 ,
,
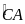 ,
,
 Gọi T
là giao điểm của BP
và CQ.
Đường thẳng vuông góc với BP
tại B
và đường thẳng vuông góc với CQ
tại C
cắt nhau ở I.
Vẽ đường kính MN
của (O).
Gọi K là
hình chiếu của I
trên AB.
Gọi T
là giao điểm của BP
và CQ.
Đường thẳng vuông góc với BP
tại B
và đường thẳng vuông góc với CQ
tại C
cắt nhau ở I.
Vẽ đường kính MN
của (O).
Gọi K là
hình chiếu của I
trên AB.
a) Chứng minh:
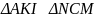 và tứ giác BICT
nội tiếp.
và tứ giác BICT
nội tiếp.
b) PQ cắt AC tại H, MQ cắt BC tại V. Chứng minh 3 điểm H, T, V thẳng hàng.
c) Gọi OI
= d, IK
= r. Chứng minh:
 .
.
----------------------HẾT----------------------
HƯỚNG DẪN GIẢI
Bài 1: (1.5 điểm)
Cho
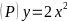 và (D):
và (D):
a) Vẽ (P) và (D) trên cùng một hệ trục tọa độ
b) Tìm tọa độ giao điểm của (P) và (D) bằng phép tính.
a)
 Hàm số (P):
Hàm số (P):
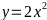
Bảng giá trị tương ứng
của
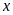 và
và
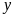 :
:
-

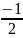
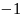
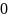
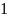
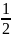
(P):
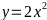
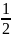
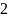
0
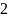
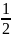
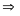 Đồ thị hàm số là một Parabol đi qua các điểm
Đồ thị hàm số là một Parabol đi qua các điểm
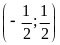 ;
;
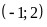 ;
;
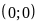 ;
;
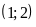 ;
;
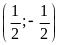
 Hàm số (D):
Hàm số (D):
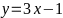
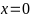 ⇒
⇒
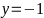
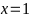 ⇒
⇒
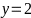
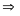 Đồ
thị hàm số là đường thẳng đi qua
Đồ
thị hàm số là đường thẳng đi qua
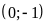 và
và
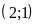 .
.
 Vẽ đồ thị hàm số
Vẽ đồ thị hàm số
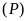 và (D)
trên cùng một hệ trục
tọa độ.
và (D)
trên cùng một hệ trục
tọa độ.
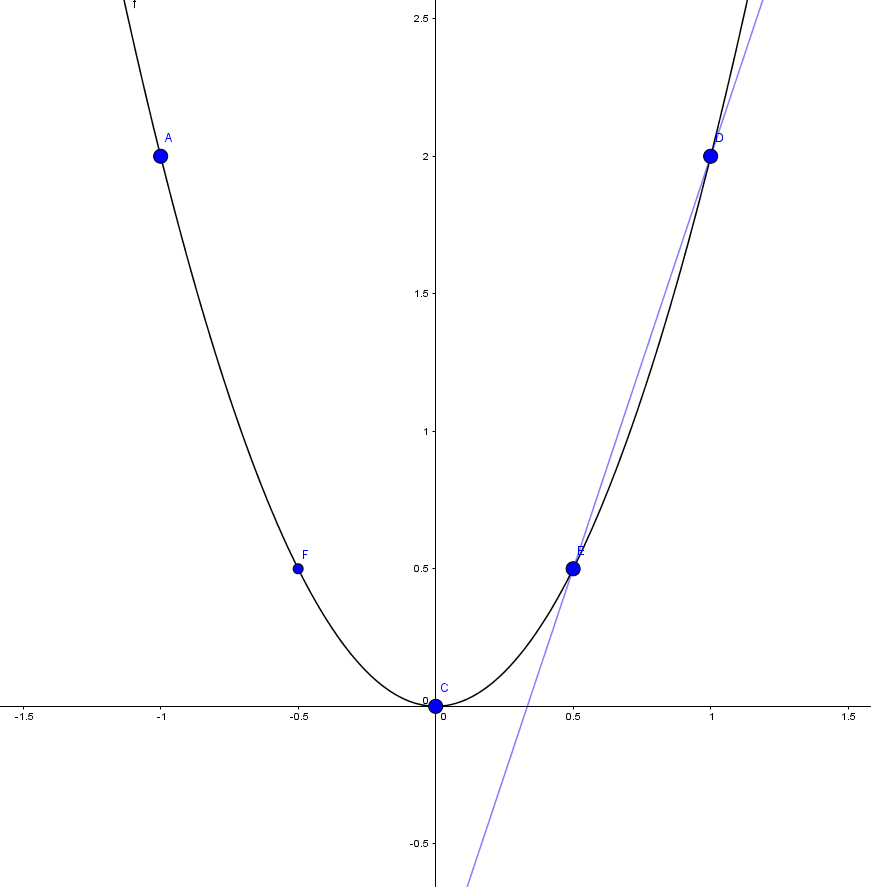
b) Hoành độ giao điểm của
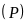 và
(D)
là nghiệm của phương trình:
và
(D)
là nghiệm của phương trình:
∆
= (–3)2
– 4.2.1 = 1 > 0
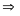 Phương trình có hai nghiệm
phân biệt:
Phương trình có hai nghiệm
phân biệt:
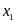 =
1;
=
1;
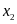 =
=
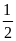

+
Với
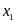 =
1
=
1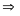
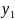 = 2.
= 2.
Vậy (D)
cắt
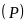 tại hai điểm phân biệt là
tại hai điểm phân biệt là
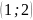 và
và
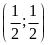 .
.
Bài 2: (1.0
điểm)
Cho
phương trình
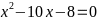 có hai nghiệm
có hai nghiệm
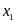 ,
,
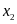 .
Không giải phương trình hãy tính giá trị của biểu thức
A
=
.
Không giải phương trình hãy tính giá trị của biểu thức
A
=
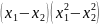 .
.
A
=
 =
=
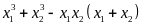
=
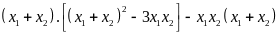
Do đó:
A
=
 =
1320.
=
1320.
Bài 3: (1.0
điểm)
Các
nhà khoa học về thống kê đã thiết lập được hàm số
sau: A(t)
=
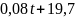 .
Trong đó A(t)
là độ tuổi trung bình các phụ nữ kết hôn lần đầu
của thế giới; t là số năm kết hôn, với gốc thời
gian là 1950. Hãy tính độ tuổi trung bình các phụ nữ
kết hôn lần đầu lần lượt vào các năm 1950, 2000,
2018, 2020 (làm tròn đến chữ số thập phân thứ hai).
.
Trong đó A(t)
là độ tuổi trung bình các phụ nữ kết hôn lần đầu
của thế giới; t là số năm kết hôn, với gốc thời
gian là 1950. Hãy tính độ tuổi trung bình các phụ nữ
kết hôn lần đầu lần lượt vào các năm 1950, 2000,
2018, 2020 (làm tròn đến chữ số thập phân thứ hai).
Lời giải
Số năm kết hôn của các phụ nữ kết hôn lần đầu ở các năm 1950, 2000, 2018, 2020 so với gốc thời gian 1950 lần lượt là: 0, 50, 68, 70 (năm).
Theo công thức tính độ tuổi trung bình các phụ nữ kết hôn lần đầu của thế giới, độ tuổi trung bình của các phụ nữ kết hôn lần đầu vào năm 1950, 2000, 2018, 2020 lần lượt là (làm tròn đến chữ số thập phân thứ hai):
A(0) = 0,08.0 + 19,7 = 19,70 (tuổi).
A(50) = 0,08.50 + 19,7 = 23,70 (tuổi).
A(68) = 0,08.68 + 19,7 = 25,14 (tuổi).
A(70) = 0,08.70 + 19,7 = 25,30 (tuổi).
Bài 4: (1.0 điểm) Một trường học có tổng số giáo viên là 80 người, hiện tại tuổi trung bình của giáo viên là 35 tuổi. Trong đó, tuổi tuổi trung bình của giáo viên nữ là 32 tuổi và tuổi trung bình của giáo viên nam là 38 tuổi. Hỏi 3 trường đó có bao nhiêu giáo viên nam, bao nhiêu giáo viên nữ?
Lời giải
Tổng số tuổi của 80 giáo viên là: 80 . 35 = 2800 (tuổi).
Gọi x là số giáo viên nữ, suy ra tổng số tuổi của các giáo viên nữ là: 32x (tuổi).
Gọi y là số giáo viên nam, suy ra tổng số tuổi của các giáo viên nam là: 38y (tuổi).
Theo tổng số tuổi của 80 giáo viên gồm nam và nữ, ta có phương trình:
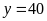
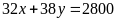 (1)
(1)
Theo tổng số giáo viên của trường học, ta có phương trình:
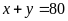 (2)
(2)
Từ (1),
(2), ta tìm được:
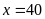 ;
;
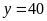 (giáo
viên).
(giáo
viên).
Bài 5: (1.0 điểm) Bé An sống trong gia đình ba thế hệ gồm ông bà nội, ba mẹ, bé An và em trai. Chủ nhật vừa rồi cả gia đình đi xem phim. Biết giá vé cho trẻ em (vé của bé An và em trai) được giảm giá 50%; vé người cao tuổi được giảm giá 25% (vé của ông bà nội). Vé của ba mẹ không được giảm giá. Ông nội bé An, người phải trả giá vé là 60 nghìn đồng, đang trả tiền cho mọi người. Hỏi ông nội phải trả bao nhiêu tiền?
Lời giải
Gọi x (nghìn đồng) là giá vé.
Ông nội được giảm giá vé 25% nên số tiền ông phải trả là: 0.75x.
Vì ông trả giá vé là 60 nghìn đồng, nên ta tính được giá vé là: 60 : 0.75 = 80 (nghìn đồng).
Gia đình bé An gồm có ông bà nội được giảm 25%, bé An và em được giảm 50%, ba mẹ không được giảm, ta có phép tính tổng tiền vé là:
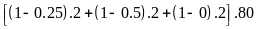 = 360
(nghìn đồng).
= 360
(nghìn đồng).
Bài 6: (1.0
điểm)
Theo
năm Dương lịch, chu kỳ Trái Đất quay quanh Mặt Trời là
365 ngày và ngày (tức là 365,25 ngày). Khi đó,
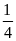 ngày
này sẽ được tích lũy trong vòng 4 năm nên theo năm Dương
lịch thì cứ 4 năm lại có 1 năm là năm nhuận vào các
năm chia hết cho 4 (tháng 2 của năm này sẽ có 29 ngày
thay vì có 28 ngày như các năm không nhuận Dương lịch).
Tuy nhiên, vẫn có một số ngoại lệ đối với nguyên
tắc trên vì có khi một năm Dương lịch lại ngắn hơn
365,25 ngày nên với những năm có hai chữ số 0 ở cuối
thì năm đó phải chia hết cho 400 mới là năm nhuận Dương
lịch.
ngày
này sẽ được tích lũy trong vòng 4 năm nên theo năm Dương
lịch thì cứ 4 năm lại có 1 năm là năm nhuận vào các
năm chia hết cho 4 (tháng 2 của năm này sẽ có 29 ngày
thay vì có 28 ngày như các năm không nhuận Dương lịch).
Tuy nhiên, vẫn có một số ngoại lệ đối với nguyên
tắc trên vì có khi một năm Dương lịch lại ngắn hơn
365,25 ngày nên với những năm có hai chữ số 0 ở cuối
thì năm đó phải chia hết cho 400 mới là năm nhuận Dương
lịch.
a) Từ năm 1900 đến năm 2000 có bao nhiêu năm nhuận Dương lịch? Vì sao?
b) Một nhà hộ sinh trong tháng 2 năm 2021 có 29 em bé chào đời là con của 29 gia đình khác nhau. Có thể chắc chắn rằng có ít nhất 2 em bé chào đời cùng ngày hay không? Vì sao?
a) Số năm có 2 chữ số 0 ở cuối là:
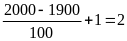 (năm)
(năm)
Vậy 2 năm đó là 1900 và 2000. Theo điều kiện của đề bài, ta có 2000 ⋮ 400, suy ra có 1 năm nhuận Dương lịch tận cùng là 2 chữ số 0. (1)
Số năm nhuận Dương lịch chia hết cho 4, không tính năm 1900, không tính năm 2000 là:
 (năm) (2)
(năm) (2)
Từ (1), (2), suy ra số năm nhuận Dương lịch là 24 + 1 = 25 (năm).
b) Vì năm 2021 không chia hết cho 4 nên được tính là năm không nhuận Dương lịch, suy ra tháng 2 năm 2021 có 28 ngày.
Giả sử mỗi ngày có 1 em bé sinh ra trong nhà hộ sinh, cả tháng 2 năm 2021 sẽ có tổng cộng 28 em bé sinh ra tương ứng với số ngày.
Mà số liệu ghi nhận 29 em bé, nên sẽ có ít nhất 2 em bé chào đời cùng ngày.

Bài 7: (1.0 điểm) Thớt là một dụng cụ sử dụng trong bếp của mỗi gia đình để
thái, chặt, ... Một cái thớt hình trụ có đường kính đáy 22cm,
cao 4cm.
a) Tính tổng diện tích hai mặt thớt (làm tròn đến cm2).
b) Cho biết loại gỗ làm thớt có khối lượng 500 kg/m3. Hỏi thớt nặng bao nhiêu gam?
Lời giải
a) Diện tích một mặt thớt hình tròn là:
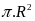 = 3.14 x 22 ≈
69 (cm2)
= 3.14 x 22 ≈
69 (cm2)
Diện tích hai mặt thớt là:
69 . 2 ≈ 138 (cm2)
b) Thể tích của thớt hình trụ là:
V = Smặt đáy . h ≈ 69 . 4 ≈ 276 (cm3) ≈ 0.000276 (m3)
Khối lượng của thớt là:
m = Dgỗ x Vthớt ≈ 500 x 0.000276 ≈ 0.138 (kg) ≈ 138 (g)
Bài 8: (3.0 điểm)
Cho
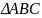 có 3 góc nhọn nội tiếp đường tròn (O; R). Gọi M,
P,
Q
lần lượt là điểm chính giữa các cung
có 3 góc nhọn nội tiếp đường tròn (O; R). Gọi M,
P,
Q
lần lượt là điểm chính giữa các cung
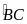 ,
,
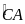 ,
,
 Gọi T
là giao điểm của BP
và CQ.
Đường thẳng vuông góc với BP
tại B
và đường thẳng vuông góc với CQ
tại C
cắt nhau ở I.
Vẽ đường kính MN
của (O).
Gọi K là
hình chiếu của I
trên AB.
Gọi T
là giao điểm của BP
và CQ.
Đường thẳng vuông góc với BP
tại B
và đường thẳng vuông góc với CQ
tại C
cắt nhau ở I.
Vẽ đường kính MN
của (O).
Gọi K là
hình chiếu của I
trên AB.
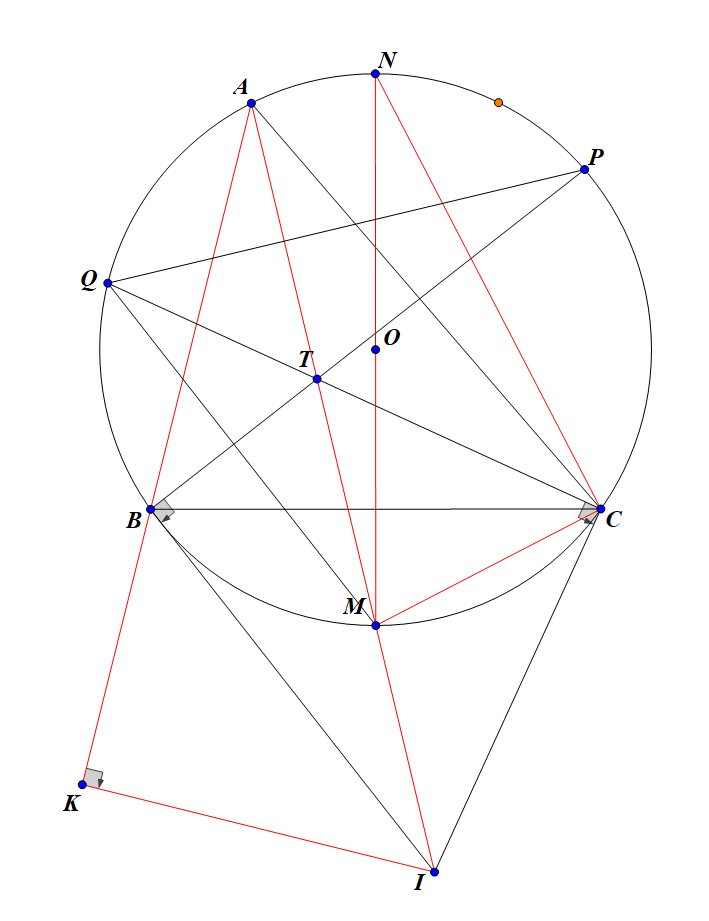
a) Chứng minh:
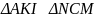 và tứ giác BICT
nội tiếp.
và tứ giác BICT
nội tiếp.
b) PQ cắt AC tại H, MQ cắt BC tại V. Chứng minh 3 điểm H, T, V thẳng hàng.
 c)
Gọi OI = d,
IK = r.
Chứng minh:
c)
Gọi OI = d,
IK = r.
Chứng minh:
 .
.
Lời giải
a) Xét tứ giác BICT, có:
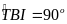 (gt)
(gt)
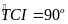 (gt)
(gt)
 BICT
nội tiếp.
BICT
nội tiếp.
Q
nằm chính giữa
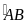
 sđ
sđ
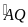 =
sđ
=
sđ
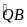

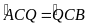
 CQ là phân giác góc C
của
CQ là phân giác góc C
của
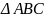 (1)
(1)
P
nằm chính giữa
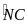
 sđ
sđ
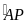 = sđ
= sđ
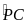

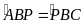
 BP
là phân giác góc B
của
BP
là phân giác góc B
của
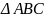 (2)
(2)
M
nằm chính giữa
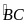
 sđ
sđ
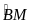 = sđ
= sđ
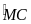

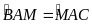
 AM
là phân giác góc A
của
AM
là phân giác góc A
của
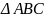 (3)
(3)
Mà CQ
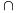 BP
= T (4)
BP
= T (4)
Từ (1), (2), (3), (4), suy ra T
tâm đường tròn nội tiếp
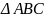 và AM,
CQ,
BP
đồng quy tại T.
và AM,
CQ,
BP
đồng quy tại T.
Đồng nghĩa với A, T, M thẳng hàng. (5)
Vì
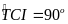 ,
ta có:
,
ta có:
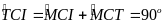 (6)
(6)
Xét
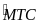 ,
có
,
có
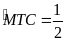 (sđ
(sđ
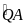 +
sđ
+
sđ
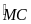 )
)
Mà
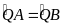 và
và
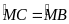 và
và
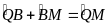

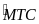 =
=
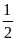 (sđ
(sđ
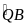 +
sđ
+
sđ
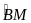 )
=
)
=
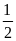 sđ
sđ
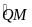 =
=
 =
=
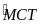 (7)
(7)

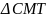 cân tại M
cân tại M

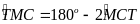 (góc
ngoài của
(góc
ngoài của
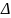 cân) (8)
cân) (8)
Từ (6), (7)
suy ra:
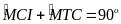 (9)
(9)
Xét
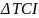 vuông tại C,
có:
vuông tại C,
có:
 (10)
(10)
Từ (9), (10)
suy ra
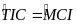

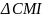 cân tại M
cân tại M

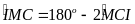 (góc ngoài của
(góc ngoài của
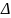 cân) (11)
cân) (11)
Từ
(6), (8), (11)

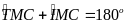
 T,
M,
I
thẳng hàng. (12)
T,
M,
I
thẳng hàng. (12)
Từ (5), (12), suy ra A, T, M, I thẳng hàng.
Xét
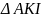 và
và
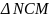 ,
có:
,
có:
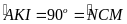
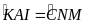 (2 góc chắn 2 cung bằng
nhau,
(2 góc chắn 2 cung bằng
nhau,
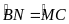 )
)
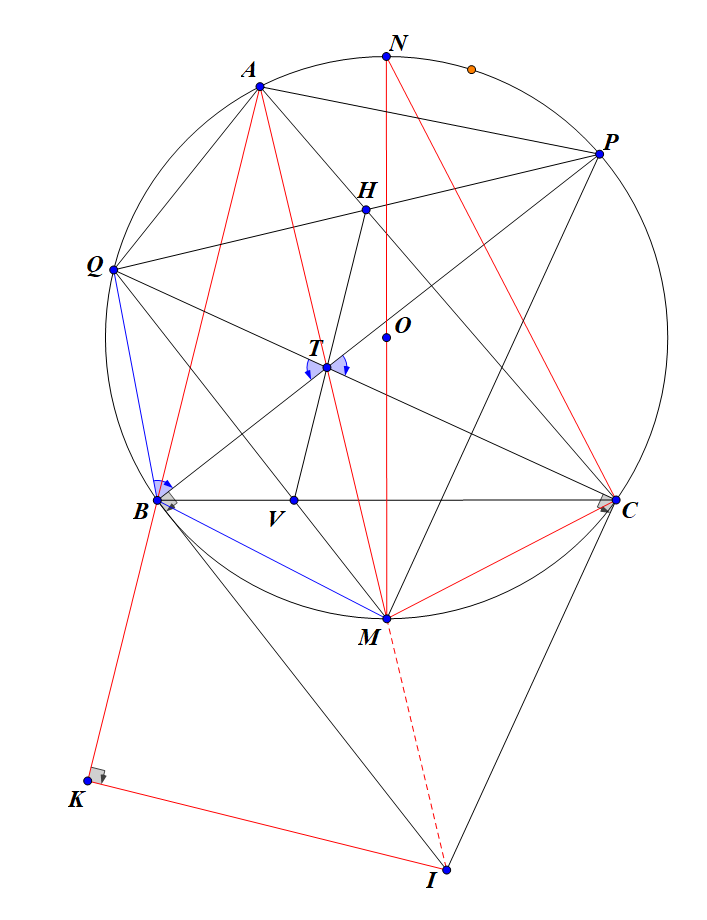 b) CÁCH
1:
b) CÁCH
1:
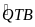 =
=
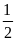 (sđ
(sđ
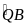 + sđ
+ sđ
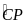 )
)
Mà
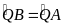 và
và
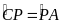 và
và
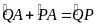

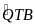 =
=
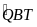 =
=
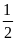 sđ
sđ
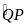

 cân tại Q
cân tại Q
 QB
= QT (13)
QB
= QT (13)
Chứng minh tương tự với
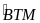 ,
ta có:
,
ta có:
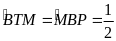 sđ
sđ
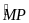

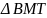 cân tại M
cân tại M
 BM =
MT (14)
BM =
MT (14)
Từ (13), (14) suy ra QM là đường trung trực của BT.
 BV
= VT
(V
= QM
BV
= VT
(V
= QM
 BC,
V
BC,
V
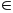 QM)
QM)

 cân tại V
cân tại V

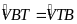 mà BP
là phân giác
mà BP
là phân giác
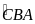

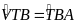 mà 2 góc này ở vị trí
so le trong.
mà 2 góc này ở vị trí
so le trong.
 VT
// AB. (15)
VT
// AB. (15)
Chứng minh tương tự với
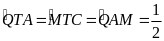 sđ
sđ
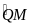
Suy ra
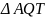 cân tại Q.
cân tại Q.
 QA
= QT (16)
QA
= QT (16)
Chứng minh tương tự với
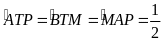 sđ
sđ
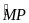
Suy ra
 cân tại P.
cân tại P.
 PA
= PT (17)
PA
= PT (17)
Từ (16), (17) suy ra QP
là đường trung trực AT,
mà H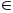 AC
AC
 HA
= HT
và
HA
= HT
và
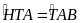
Mà AM là phân giác
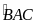

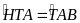
 HT
// AB. (18)
HT
// AB. (18)
Từ (15), (18), theo tiên đề Ơ-clit:
 H, V, T thẳng hàng.
H, V, T thẳng hàng.
b) CÁCH 2:
Xét tứ giác TCPH có:
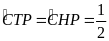 .
(sđ
.
(sđ
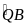 + sđ
+ sđ
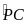 )
=
)
=
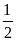 .
(sđ
.
(sđ
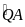 + sđ
+ sđ
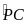 )
(do
)
(do
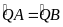 )
)
 TCPH là
tứ giác nội tiếp.
TCPH là
tứ giác nội tiếp.

 (13)
(13)
Xét tứ giác VTCM có:
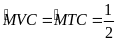 .
(sđ
.
(sđ
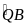 + sđ
+ sđ
 )
=
)
=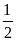 .
(sđ
.
(sđ
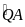 + sđ
+ sđ
 )
(do
)
(do
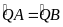 )
)
 VTCM là tứ giác nội tiếp.
VTCM là tứ giác nội tiếp.

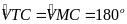 (14)
(14)
Xét
tứ giác MQPC
nội tiếp
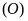 ,
có:
,
có:
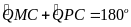 (15)
(15)
 và
và
Từ
(13), (14), (15) suy ra
 H,
T,
V
thẳng hàng.
H,
T,
V
thẳng hàng.
c)
Ta có:
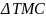 cân
tại M
(cmt)
cân
tại M
(cmt)
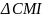 cân
tại M
(cmt)
cân
tại M
(cmt)
 MT
= MC
= MI
MT
= MC
= MI
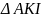

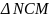 (cmt)
(cmt)

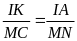

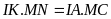

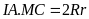

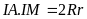 (do MC
=
MI)
(do MC
=
MI)
Gọi
K,
S
lần lượt là giao điểm của IO và
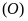
Xét
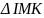 và
và
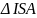 ,
có:
,
có:
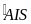 chung
chung
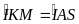 (do tứ giác MKSA nội
tiếp
(do tứ giác MKSA nội
tiếp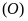 )
)

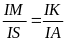

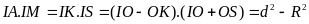
Mà
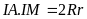

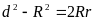
SỞ GD & ĐT TP.HỒ CHÍ MINH ĐỀ THAM KHẢO TUYỂN SINH 10
PHÒNG GD & ĐT QUẬN 3 NĂM HỌC 2022-2023
ĐỀ THAM KHẢO MÔN : TOÁN 9
-------------------- Đề thi gồm 8 câu hỏi tự luận
MÃ ĐỀ : Quận 3 – 3 Thời gian: 120 phút (không kể thời gian phát đề)
Bài 1: Cho
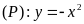 và đường thẳng
và đường thẳng
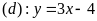 .
.
a) Vẽ
 và
và
 trên cùng mặt phẳng tọa độ.
trên cùng mặt phẳng tọa độ.
b) Tìm tọa
độ giao điểm của
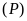 và
và
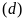 bằng phép tính.
bằng phép tính.
Bài 2: Cho
phương trình
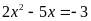 có hai nghiệm
có hai nghiệm
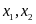 .
Không giải phương trình hãy tính giá trị của biểu thức
.
Không giải phương trình hãy tính giá trị của biểu thức
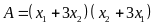 .
.
Bài 3: Tổng
điều tra dân số và nhà ở năm 2019 được tiến hành
vào thời điểm 0 giờ ngày 1/4/2019 theo Quyết định số
772/QD-TTg ngày 26/6/2018 của Thủ tướng Chính phủ. Đây
là cuộc Tổng điều tra dân số và nhà ở lần thứ năm
ở Việt Nam kể từ khi đất nước thống nhất vào năm
1975. Theo kết quả của cuộc tổng điều tra nói trên,
tổng dân số của Việt Nam là 96.208.984 người, trong đó
nam ít hơn nữ là 446.862 người và dân tộc Kinh chiếm
 dân số cả nước.
dân số cả nước.
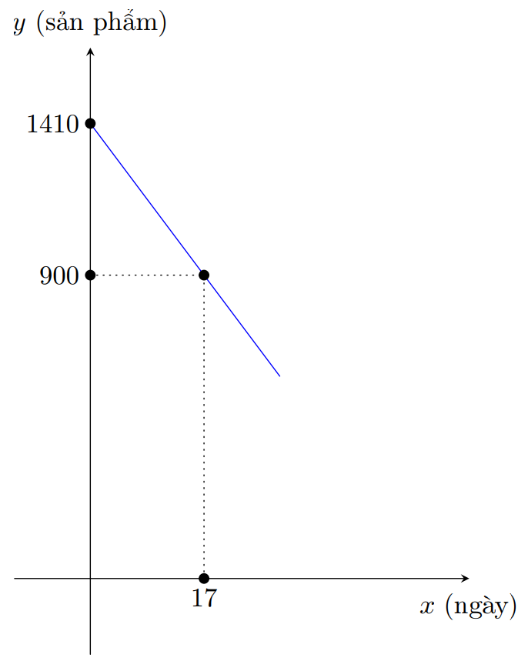 a) Dân
tộc Kinh có bao nhiêu người (làm tròn đến hàng đơn
vị)?
a) Dân
tộc Kinh có bao nhiêu người (làm tròn đến hàng đơn
vị)?
b) Tính số nam và số nữ của Việt Nam.
Bài 4: Một xí
nghiệp cần bán thanh lý
 sản phẩm. Số sản phẩm
sản phẩm. Số sản phẩm
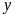 còn lại sau
còn lại sau
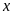 ngày bán được xác định bởi hàm số:
ngày bán được xác định bởi hàm số:
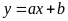 có đồ thị như bên
có đồ thị như bên
a) Hãy dựa vào đồ thị hãy
xác định
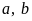 và hàm số
và hàm số
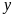 .
.
b) Xí nghiệp cần bao nhiêu ngày để bán hết số sản phẩm cần thanh lý?
Bài 5: Các bạn
học sinh của lớp 9A dự định đóng góp một số tiền
để mua tặng cho mỗi em ở Mái ấm tình thương ba món
quà (giá tiền các món quà đều như nhau). Khi các bạn
đóng đủ số tiền như dự trù thì Mái ấm đã nhận
chăm sóc thêm 9 em và giá tiền mỗi món quà lại tăng
thêm
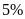 nên số tiền có được vừa đủ để tặng mỗi em hai
món quà. Hỏi có bao nhiêu em ở Mái ấm lúc tặng quà?
nên số tiền có được vừa đủ để tặng mỗi em hai
món quà. Hỏi có bao nhiêu em ở Mái ấm lúc tặng quà?
B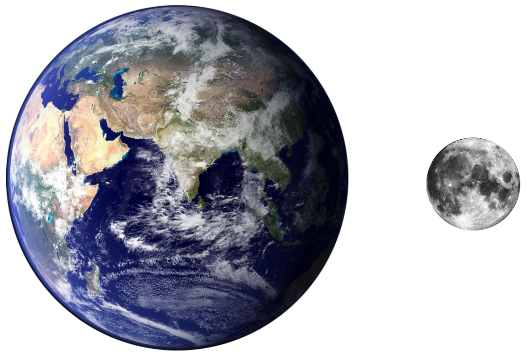 ài
6: Coi cả Trái Đất
và Mặt Trăng đều có dạng hình cầu và biết bán kính
của Trái Đất là khoảng
ài
6: Coi cả Trái Đất
và Mặt Trăng đều có dạng hình cầu và biết bán kính
của Trái Đất là khoảng
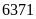 km, bán kính của mặt trăng là khoảng
km, bán kính của mặt trăng là khoảng
 km.
km.
a) Hãy tính diện tích bề mặt của Trái Đất và diện tích bề mặt của Mặt Trăng.
b) Biết
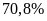 diện tích bề mặt Trái Đất là nước. Hãy tính phần
diện tích này? (Làm tròn kết quả đến
diện tích bề mặt Trái Đất là nước. Hãy tính phần
diện tích này? (Làm tròn kết quả đến
hàng triệu)
Bài 7: Giá của
một mặt hàng là
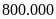 đồng. Nếu bán mặt hàng này với giá bằng một nửa
giá niêm yết thì lợi nhuận là
đồng. Nếu bán mặt hàng này với giá bằng một nửa
giá niêm yết thì lợi nhuận là
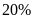 .
Hỏi phải bán với giá bao nhiêu thì được lợi nhuận
.
Hỏi phải bán với giá bao nhiêu thì được lợi nhuận
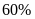 ?
?
Bài 8: Cho tam giác
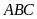 nhọn
nhọn
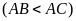 nội tiếp đường tròn tâm
nội tiếp đường tròn tâm
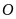 có ba đường cao
có ba đường cao
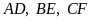 cắt nhau tại
cắt nhau tại
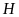 .
.
a) Chứng minh
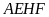 và
và
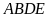 là các tứ giác nội tiếp.
là các tứ giác nội tiếp.
b) Đường thẳng
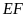 cắt đường tròn
cắt đường tròn
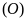 tại các điểm
tại các điểm
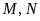 (
(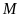 thuộc
cung nhỏ
thuộc
cung nhỏ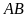 ).
Kẻ đường kính
).
Kẻ đường kính 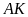 của đường tròn
của đường tròn
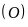 .
Chứng minh tia
.
Chứng minh tia
 là tia phân giác của góc
là tia phân giác của góc
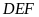 và
và
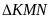 cân.
cân.
c) Đường trung trực của
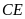 cắt
cắt
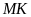 tại
tại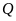 .
Chứng minh
.
Chứng minh
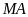 là tiếp tuyến của
là tiếp tuyến của
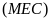 và
và
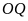 vuông góc với
vuông góc với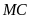 .
.
HƯỚNG DẪN GIẢI
Bài 1: Cho
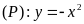 và đường thẳng
và đường thẳng
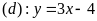 .
.
a) Vẽ
 và
và
 trên cùng mặt phẳng tọa độ.
trên cùng mặt phẳng tọa độ.
b) Tìm tọa độ giao điểm
của
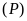 và
và
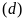 bằng phép tính.
bằng phép tính.
Lời giải
a)  Hàm số:
Hàm số:
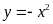
Bảng giá trị tương ứng
của
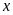 và
và
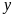 :
:
|
|
|
|
|
|
|
|
|
|
|
|
 Đồ thị hàm số là một Parabol đi qua các điểm
Đồ thị hàm số là một Parabol đi qua các điểm
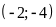 ;
;
 ;
;
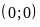 ;
;
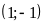 ;
;
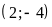 .
.
 Hàm số:
Hàm số:
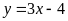
|
|
|
|
|
|
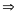 Đồ thị hàm số là đường thẳng đi qua
Đồ thị hàm số là đường thẳng đi qua
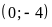 và
và
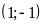 .
.
 Vẽ:
Vẽ:
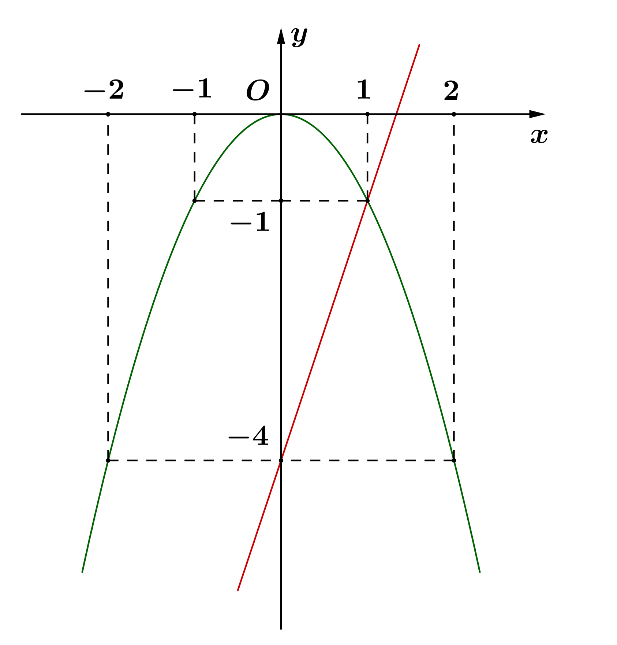
b) Hoành độ giao điểm của
 và
và
 là nghiệm của phương trình:
là nghiệm của phương trình:
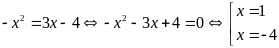
+ Với
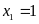

+ Với
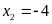
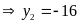
Vậy
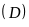 cắt
cắt
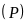 tại hai điểm phân biệt là
tại hai điểm phân biệt là
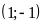 và
và
 .
.
Bài 2: Cho phương
trình
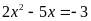 có hai nghiệm
có hai nghiệm
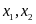 .
Không giải phương trình hãy tính giá trị của biểu thức
.
Không giải phương trình hãy tính giá trị của biểu thức
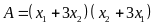 .
.
Lời giải
Ta
có:
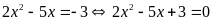 .
.
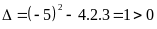
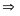 Phương trình có hai nghiệm
phân biệt.
Phương trình có hai nghiệm
phân biệt.
Theo
định lí Vi-et:
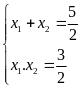 .
.
Khi đó:
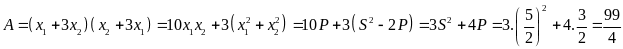 .
.
Bài 3: Tổng điều
tra dân số và nhà ở năm 2019 được tiến hành vào thời
điểm 0 giờ ngày 1/4/2019 theo Quyết định số 772/QD-TTg
ngày 26/6/2018 của Thủ tướng Chính phủ. Đây là cuộc
Tổng điều tra dân số và nhà ở lần thứ năm ở Việt
Nam kể từ khi đất nước thống nhất vào năm 1975. Theo
kết quả của cuộc tổng điều tra nói trên, tổng dân
số của Việt Nam là 96.208.984 người, trong đó nam ít hơn
nữ là 446.862 người và dân tộc Kinh chiếm
 dân số cả nước.
dân số cả nước.
a) Dân tộc Kinh có bao nhiêu người (làm tròn đến hàng đơn vị)?
b) Tính số nam và số nữ của Việt Nam.
Lời giải
a)
Số người dân tộc
Kinh là:
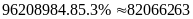 người.
người.
b) Gọi
số nam và số nữ lần lượt là
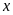 và
và
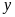
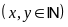 .
.
Ta
có hệ phương trình:
 .
.
Vậy
số nam là
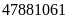 và số nữ là
và số nữ là
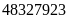 .
.
B ài
4: Một
xí nghiệp cần bán thanh lý
ài
4: Một
xí nghiệp cần bán thanh lý
 sản phẩm. Số sản phẩm
sản phẩm. Số sản phẩm
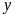 còn lại sau
còn lại sau
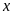 ngày bán được xác định bởi hàm số:
ngày bán được xác định bởi hàm số:
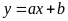 có đồ thị như bên
có đồ thị như bên
a) Hãy dựa
vào đồ thị hãy xác định
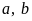 và hàm số
và hàm số
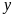 .
.
b) Xí nghiệp cần bao nhiêu ngày để bán hết số sản phẩm cần thanh lý?
Lời giải
a) Nhìn
vào hình ta có đồ thị hàm số
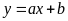 đi qua hai điểm
đi qua hai điểm
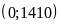 và
và
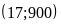 .
.
Thay
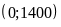 vào
vào
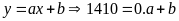
Thay (17; 900) vào y = ax +b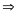 900
= 17a +b
900
= 17a +b
Ta có hệ pt:
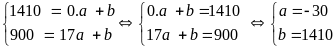 .
.
Vậy
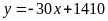 .
.
b)
Số ngày xí nghiệp bán hết số sản phẩm cần thanh lý:
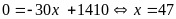
Vậy số ngày xí nghiệp bán hết số sản phẩm cần thanh lý là 47 ngày.
Bài 5: Các bạn
học sinh của lớp 9A dự định đóng góp một số tiền
để mua tặng cho mỗi em ở Mái ấm tình thương ba món
quà (giá tiền các món quà đều như nhau). Khi các bạn
đóng đủ số tiền như dự trù thì Mái ấm đã nhận
chăm sóc thêm 9 em và giá tiền mỗi món quà lại tăng
thêm
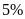 nên số tiền có được vừa đủ để tặng mỗi em hai
món quà. Hỏi có bao nhiêu em ở Mái ấm lúc tặng quà?
nên số tiền có được vừa đủ để tặng mỗi em hai
món quà. Hỏi có bao nhiêu em ở Mái ấm lúc tặng quà?
Lời giải
Gọi
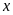 là số em ở mái ấm lúc chưa có thêm 9 em
là số em ở mái ấm lúc chưa có thêm 9 em
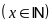 .
.
Gọi
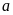 là giá tiền một món quà lúc chưa tăng giá.
là giá tiền một món quà lúc chưa tăng giá.
Ta có phương trình:
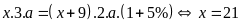
Vậy có 21 em ở Mái ấm lúc tặng quà.
B ài
6: Coi cả Trái Đất
và Mặt Trăng đều có dạng hình cầu và biết bán kính
của Trái Đất là khoảng
ài
6: Coi cả Trái Đất
và Mặt Trăng đều có dạng hình cầu và biết bán kính
của Trái Đất là khoảng
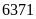 km, bán kính của mặt trăng là khoảng
km, bán kính của mặt trăng là khoảng
 km.
km.
a) Hãy tính diện tích bề mặt của Trái Đất và diện tích bề mặt của Mặt Trăng.
b) Biết
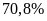 diện tích bề mặt Trái Đất là nước. Hãy tính phần
diện tích này? (Làm tròn kết quả đến hàng triệu)
diện tích bề mặt Trái Đất là nước. Hãy tính phần
diện tích này? (Làm tròn kết quả đến hàng triệu)
Lời giải
a) Diện tích bề mặt của Trái Đất:
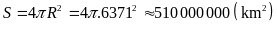
Diện tích bề mặt của Mặt Trăng:
b) Diện tích nước bao phủ bề mặt Trái Đất là:
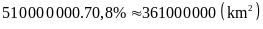
Bài 7: Giá của
một mặt hàng là
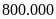 đồng. Nếu bán mặt hàng này với giá bằng một nửa
giá niêm yết thì lợi nhuận là
đồng. Nếu bán mặt hàng này với giá bằng một nửa
giá niêm yết thì lợi nhuận là
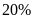 .
Hỏi phải bán với giá bao nhiêu thì được lợi nhuận
.
Hỏi phải bán với giá bao nhiêu thì được lợi nhuận
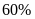 ?
?
Lời giải
Giá
gốc của mặt hàng đó:
 (đồng).
(đồng).
Giá
bán lần sau:
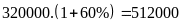 (đồng).
(đồng).
Bài 8: Cho tam giác
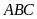 nhọn
nhọn
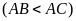 nội tiếp đường tròn tâm
nội tiếp đường tròn tâm
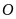 có ba đường cao
có ba đường cao
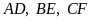 cắt nhau tại
cắt nhau tại
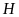 .
.
a) Chứng minh
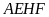 và
và
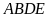 là các tứ giác nội tiếp.
là các tứ giác nội tiếp.
b) Đường thẳng
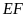 cắt đường tròn
cắt đường tròn
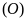 tại các điểm
tại các điểm
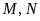 (
(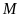 thuộc
cung nhỏ
thuộc
cung nhỏ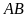 ).
Kẻ đường kính
).
Kẻ đường kính 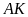 của đường tròn
của đường tròn
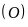 .
Chứng minh tia
.
Chứng minh tia
 là tia phân giác của góc
là tia phân giác của góc
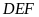 và
và
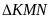 cân.
cân.
c) Đường trung trực của
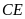 cắt
cắt
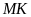 tại
tại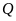 .
Chứng minh
.
Chứng minh
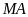 là tiếp tuyến của
là tiếp tuyến của
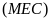 và
và
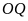 vuông góc với
vuông góc với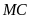 .
.
Lời giải
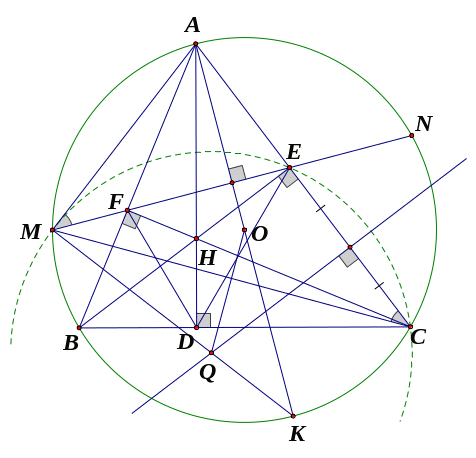
a) Xét
tứ giác
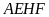 có
có
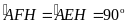 (
(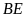 và
và
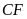 là các đường cao)
là các đường cao)
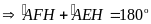
 Tứ giác
Tứ giác
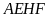 nội tiếp đường tròn đường kính
nội tiếp đường tròn đường kính
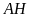 .
.
Xét tứ giác
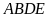 có
có
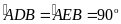 (
(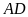 và
và
 là các đường cao)
là các đường cao)
 Tứ giác
Tứ giác
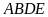 nội tiếp đường tròn đường kính
nội tiếp đường tròn đường kính
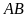 .
.
b) Tứ giác
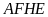 nội tiếp
nội tiếp
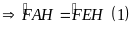 .
.
Tứ giác
 nội tiếp
nội tiếp
 .
.
Từ
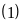 và
và

 hay
hay
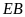 là tia phân giác của góc
là tia phân giác của góc
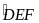 .
.
Xét tứ giác
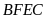 có
có
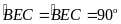
 Tứ giác
Tứ giác
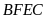 nội tiếp đường tròn đường kính
nội tiếp đường tròn đường kính
 .
.
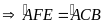
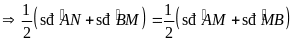
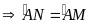
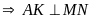 tại trung điểm của
tại trung điểm của
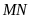
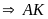 là đường trung trực của
là đường trung trực của
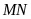
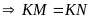 hay
hay
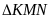 cân
tại
cân
tại
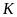
c) Ta có:
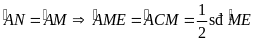
 là dây của đường tròn
là dây của đường tròn
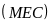
 là tiếp tuyến của
là tiếp tuyến của
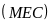 .
.
 tại
tại

Tâm đường tròn (MEC) thuộc MK
mà Q là giao điểm MK và đường trung trực của EC
Q là tâm đường tròn (MEC) QM = QC
mà OM = OC (= bk(O)) OQ là đường trung trực MC
Vậy OQ MC.
Ngoài Đề Thi Vào 10 Môn Toán Quận 3 TPHCM 2022-2023 Tham Khảo Có Lời Giải Chi Tiết – Toán 9 thì các đề thi trong chương trình lớp 9 sẽ được cập nhật liên tục và nhanh nhất có thể sau khi kỳ thi diễn ra trên Danh mục Kho Đề Thi nhằm giúp các bạn đọc thuận tiện trong việc tra cứu và đối chiếu đáp án. Quý thầy cô và các bạn đọc có thể chia sẻ thêm những tài liệu học tập hữu ích đến địa chỉ email của chúng tôi, nhằm xây dựng nên kho đề thi phong phú, đa dạng cho các em học sinh tham khảo và rèn luyện.\
Trên đây là những thông tin về đề thi và lời giải chi tiết môn Toán 9 dành cho kỳ thi vào lớp 10 tại Quận 3, Thành phố Hồ Chí Minh trong năm học 2022-2023. Bộ đề thi này là một nguồn tài liệu tham khảo hữu ích để các bạn học sinh chuẩn bị cho kỳ thi quan trọng này.
Đề thi vào lớp 10 môn Toán đóng vai trò quan trọng trong việc đánh giá năng lực và kiến thức của các bạn học sinh. Việc làm quen với cấu trúc và dạng đề thi, cùng việc rèn luyện kỹ năng giải toán và nắm vững kiến thức Toán 9 là yếu tố quan trọng để đạt kết quả tốt trong kỳ thi.
Bộ đề thi và lời giải chi tiết này không chỉ giúp các bạn học sinh làm quen với từng dạng bài toán và phương pháp giải quyết, mà còn giúp hiểu rõ cách suy nghĩ và lý thuyết đằng sau từng bài toán. Lời giải chi tiết cung cấp cách giải từng bước một, giúp các bạn học sinh hiểu rõ quy trình giải quyết vấn đề và áp dụng vào các bài tương tự.
Để thuận tiện trong việc sử dụng bộ đề thi và lời giải, các bạn có thể tìm kiếm trên các nguồn tài liệu trực tuyến hoặc liên hệ với nhà trường để có thể tiếp cận và sử dụng tài liệu này một cách hiệu quả.
Hy vọng rằng đề thi và lời giải chi tiết môn Toán 9 dành cho kỳ thi vào lớp 10 tại Quận 3, TPHCM sẽ giúp các bạn học sinh rèn luyện và nắm vững kiến thức, cũng như tự tin và sẵn sàng để đối mặt với kỳ thi sắp tới.
Chúng tôi chúc các bạn thành công và đạt được kết quả cao trong kỳ thi vào lớp 10. Hãy tiếp tục nỗ lực và học tập một cách chăm chỉ để xây dựng nền tảng vững chắc cho tương lai!
Xem thêm