Phiếu Học Tập Môn Toán 6 Phân Theo Từng Dạng Kèm Hướng Dẫn Giải
>>> Mọi người cũng quan tâm:
Phiếu Học Tập Môn Toán 6 Phân Theo Từng Dạng Kèm Hướng Dẫn Giải – Toán 6 là tài liệu học tập được Trang Tài Liệu biên soạn và sưu tầm từ những nguồn dữ liệu mới nhất hiện nay. Tài liệu này sẽ giúp các em luyện tập, củng cố kiến thức từ đó nâng cao điểm số cho môn học. Ngoài ra, cũng giúp các thầy cô giáo có nguồn tài nguyên phong phú để giảng dạy.
Dưới đây là bản đọc trực tuyến giúp thầy cô và các em học sinh có thể nghiên cứu Online hoặc bạn có thể tải miễn phí với phiên bản word để dễ dàng in ấn cũng như học tập Offline.
Buổi 1:
TẬP HỢP – PHẦN TỬ CỦA TẬP HỢP – TẬP HỢP CON
MỤC TIÊU
- Rèn HS kỉ năng viết tập hợp, viết
tập hợp con của một tập hợp cho trước, sử dụng
đúng, chính xác các kí hiệu
![]() .
.
- Sự khác nhau giữa tập hợp
![]()
- Biết tìm số phần tử của một tập hợp được viết dưới dạng dãy số cóquy luật.
- Vận dụng kiến thức toán học vào một số bài toán thực tế.
NỘI DUNG
I. Ôn tập lý thuyết.
Câu 1: Hãy cho một số VD về tập hợp thường gặp trong đời sống hàng ngày và một số VD về tập hợp thường gặp trong toán học?
Câu 2: Hãy nêu cách viết, các ký hiệu thường gặp trong tập hợp.
Câu 3: Một tập hợp có thể có bao nhiêu phần tử?
Câu 4: Có
gì khác nhau giữa tập hợp
![]() và
và
![]() ?
?
II. Bài tập
Dạng 1: Rèn kĩ năng viết tập hợp, viết tập hợp con, sử dụng kí hiệu
Bài 1: Cho tập hợp A là các chữ cái trong cụm từ “Thành phố Hồ Chí Minh”
Hãy liệt kê các phần tử của tập hợp A.
Điền kí hiệu thích hợp vào ô vuông
a
Hướng dẫn
a/ A = {a, c, h, I, m, n, ô, p, t}
b/
![]()
![]()
![]()
Lưu ý HS: Bài toán trên không phân biệt chữ in hoa và chữ in thường trong cụm từ đã cho.
Bài 2: Cho tập hợp các chữ cái X = {A, C, O}
a/ Tìm chụm chữ tạo thành từ các chữ của tập hợp X.
b/ Viết tập hợp X bằng cách chỉ ra các tính chất đặc trưng cho các phần tử của X.
Hướng dẫn
a/ Chẳng hạn cụm từ “CA CAO” hoặc “CÓ CÁ”
b/ X = {x: x-chữ cái trong cụm chữ “CA CAO”}
Bài 3: Chao các tập hợp
A = {1; 2; 3; 4; 5; 6} ; B = {1; 3; 5; 7; 9}
a/ Viết tập hợp C các phần tử thuộc A và không thuộc B.
b/ Viết tập hợp D các phần tử thuộc B và không thuộc A.
c/ Viết tập hợp E các phần tử vừa thuộc A vừa thuộc B.
d/ Viết tập hợp F các phần tử hoặc thuộc A hoặc thuộc B.
Hướng dẫn:
a/ C = {2; 4; 6}
b/ D = {5; 9}
c/ E = {1; 3; 5}
d/ F = {1; 2; 3; 4; 5; 6; 7; 8; 9}
Bài 4: Cho tập hợp A = {1; 2; a; b}
a/ Hãy chỉ rõ các tập hợp con của A có 1 phần tử.
b/ Hãy chỉ rõ các tập hợp con của A có 2 phần tử.
c/ Tập hợp B = {a, b, c} có phải là tập hợp con của A không?
Hướng dẫn
a/ {1} { 2} { a } { b}
b/ {1; 2} {1; a} {1; b} {2; a} {2; b} { a; b}
c/ Tập hợp B không phải là tập hợp con
của tập hợp A bởi vì c
![]() nhưng c
nhưng c
![]()
Bài 5: Cho tập hợp B = {x, y, z} . Hỏi tập hợp B có tất cả bao nhiêu tập hợp con?
Hướng dẫn
- Tập hợp con của B không có phần từ
nào là
![]() .
.
- Tập hợp con của B có 1phần từ là {x} { y} { z }
- Các tập hợp con của B có hai phần tử là {x, y} { x, z} { y, z }
- Tập hợp con của B có 3 phần tử chính là B = {x, y, z}
Vậy tập hợp A có tất cả 8 tập hợp con.
Ghi chú. Một tập hợp A bất kỳ luôn có
hai tập hợp con đặc biệt. Đó là tập hợp rỗng
![]() và chính tập hợp A. Ta quy ước
và chính tập hợp A. Ta quy ước
![]() là tập hợp con của mỗi tập hợp.
là tập hợp con của mỗi tập hợp.
Bài 6: Cho A = {1; 3; a; b} ; B = {3; b}
Điền các kí hiệu
![]() thích hợp vào ô vuông
thích hợp vào ô vuông
1 ý A ; 3 ý A ; 3 ý B ; B ý A
Bài 7: Cho các tập hợp
![]() ;
;
![]()
Hãy điền dấu
![]() hay
hay![]() vào
các ô dưới đây
vào
các ô dưới đây
N ý N* ; A ý B
Dạng 2: Các bài tập về xác định số phần tử của một tập hợp
Bài 1: Gọi A là tập hợp các số tự nhiên có 3 chữ số. Hỏi tập hợp A có bao nhiêu phần tử?
Hướng dẫn:
Tập hợp A có (999 – 100) + 1 = 900 phần tử.
Bài 2: Hãy tính số phần tử của các tập hợp sau:
a/ Tập hợp A các số tự nhiên lẻ có 3 chữ số.
b/ Tập hợp B các số 2, 5, 8, 11, …, 296.
c/ Tập hợp C các số 7, 11, 15, 19, …, 283.
Hướng dẫn
a/ Tập hợp A có (999 – 101):2 +1 = 450 phần tử.
b/ Tập hợp B có (296 – 2 ): 3 + 1 = 99 phần tử.
c/ Tập hợp C có (283 – 7 ):4 + 1 = 70 phần tử.
Cho HS phát biểu tổng quát:
Tập hợp các số chẵn từ số chẵn a đến số chẵn b có (b – a) : 2 + 1 phần tử.
Tập hợp các số lẻ từ số lẻ m đến số lẻ n có (n – m) : 2 + 1 phần tử.
Tập hợp các số từ số c đến số d là dãy số các đều, khoảng cách giữa hai số liên tiếp của dãy là 3 có (d – c ): 3 + 1 phần tử.
Bài 3: Cha mua cho em một quyển số tay dày 256 trang. Để tiện theo dõi em đánh số trang từ 1 đến 256. HỎi em đã phải viết bao nhiêu chữ số để đánh hết cuốn sổ tay?
Hướng dẫn:
- Từ trang 1 đến trang 9, viết 9 số.
- Từ trang 10 đến trang 99 có 90 trang, viết 90 . 2 = 180 chữ số.
- Từ trang 100 đến trang 256 có (256 – 100) + 1 = 157 trang, cần viết 157 . 3 = 471 số.
Vậy em cần viết 9 + 180 + 471 = 660 số.
Bài 4: Các số tự nhiên từ 1000 đến 10000 có bao nhiêu số có đúng 3 chữ số giống nhau.
Hướng dẫn:
- Số 10000 là số duy nhất có 5 chữ số, số này có hơn 3 chữ số giống nhau nên không thoả mãn yêu cầu của bài toán.
Vậy số cần tìm chỉ có thể có dạng:
![]() ,
,
![]() ,
,
![]() ,
,
![]() với a
với a
![]() b
là cá chữ số.
b
là cá chữ số.
- Xét số dạng
![]() ,
chữ số a có 9 cách chọn ( a
,
chữ số a có 9 cách chọn ( a
![]() 0)
0)
![]() có 9 cách chọn để b khác a.
có 9 cách chọn để b khác a.
Vậy có 9 . 8 = 71 số có dạng
![]() .
.
Lập luận tương tự ta thấy các dạng còn lại đều có 81 số. Suy ta tất cả các số từ 1000 đến 10000 có đúng 3 chữ số giống nhau gồm 81.4 = 324 số.
Ngày dạy: ……………...
Buổi 2:
PHÉP CỘNG VÀ PHÉP NHÂN – PHÉP TRỪ VÀ PHÉP CHIA
MỤC TIÊU
- Ôn tập lại các tính chất của phép cộng và phép nhân, phép trừ và phép chia.
- Rèn luyện kỹ năng vận dụng các tính chất trên vào các bài tập tính nhẩm, tính nhanh và giải toán một cách hợp lý.
- Vận dụng việc tìm số phần tử của một tập hợp đã được học trước vào một số bài toán.
- Hướng dẫn HS cách sử dụng máy tính bỏ túi.
NỘI DUNG
I. Ôn tập lý thuyết.
Câu 1: Phép cộng và phép nhân có những tính chất cơ bản nào?
Câu 2: Phép trừ và phép chia có những tính chất cơ bản nào?
II. Bài tập
Dạng 1: Các bài toán tính nhanh
Bài 1: Tính tổng sau đây một cách hợp lý nhất.
a/ 67 + 135 + 33
b/ 277 + 113 + 323 + 87
ĐS: a/ 235 b/ 800
Bài 2: Tính nhanh các phép tính sau:
a/ 8 x 17 x 125
b/ 4 x 37 x 25
ĐS: a/ 17000 b/ 3700
Bài 3: Tính nhanh một cách hợp lí:
a/ 997 + 86
b/ 37. 38 + 62. 37
c/ 43. 11; 67. 101; 423. 1001
d/ 67. 99; 998. 34
Hướng dẫn
a/ 997 + (3 + 83) = (997 + 3) + 83 = 1000 + 80 = 1083
Sử dụng tính chất kết hợp của phép cộng.
Nhận xét: 997 + 86 = (997 + 3) + (86 -3) = 1000 + 83 = 1083. Ta có thể thêm vào số hạng này đồng thời bớt đi số hạng kia với cùng một số.
b/ 37. 38 + 62. 37 = 37.(38 + 62) = 37.100 = 3700.
Sử dụng tính chất phân phối của phép nhân đối với phép cộng.
c/ 43. 11 = 43.(10 + 1) = 43.10 + 43. 1 = 430 + 43 = 4373.
67. 101= 6767
423. 1001 = 423 423
d/ 67. 99 = 67.(100 – 1) = 67.100 – 67 = 6700 – 67 = 6633
998. 34 = 34. (100 – 2) = 34.100 – 34.2 = 3400 – 68 = 33 932
Bái 4: Tính nhanh các phép tính:
a/ 37581 – 9999
b/ 7345 – 1998
c/ 485321 – 99999
d/ 7593 – 1997
Hướng dẫn:
a/ 37581 – 9999 = (37581 + 1 ) – (9999 + 1) = 37582 – 10000 = 89999 (cộng cùng một số vào số bị trừ và số trừ
b/ 7345 – 1998 = (7345 + 2) – (1998 + 2) = 7347 – 2000 = 5347
c/ ĐS: 385322
d/ ĐS: 5596
Dạng 2: Các bài toán có liên quan đến dãy số, tập hợp
Bài 1: Tính 1 + 2 + 3 + … + 1998 + 1999
Hướng dẫn
- Áp dụng theo cách tích tổng của Gauss
- Nhận xét: Tổng trên có 1999 số hạng
Do đó
S = 1 + 2 + 3 + … + 1998 + 1999 = (1 + 1999). 1999: 2 = 2000.1999: 2 = 1999000
Bài 2: Tính tổng của:
a/ Tất cả các số tự nhiên có 3 chữ số.
b/ Tất cả các số lẻ có 3 chữ số.
Hướng dẫn:
a/ S1 = 100 + 101 + … + 998 + 999
Tổng trên có (999 – 100) + 1 = 900 số hạng. Do đó
S1= (100+999).900: 2 = 494550
b/ S2 = 101+ 103+ … + 997+ 999
Tổng trên có (999 – 101): 2 + 1 = 450 số hạng. Do đó
S2 = (101 + 999). 450 : 2 = 247500
Bài 3: Tính tổng
a/ Tất cả các số: 2, 5, 8, 11, …, 296
b/ Tất cả các số: 7, 11, 15, 19, …, 283
ĐS: a/ 14751
b/ 10150
Các giải tương tự như trên. Cần xác định số các số hạng trong dãy sô trên, đó là những dãy số cách đều.
Bài 4: Cho dãy số:
a/ 1, 4, 7, 10, 13, 19.
b/ 5, 8, 11, 14, 17, 20, 23, 26, 29.
c/ 1, 5, 9, 13, 17, 21, …
Hãy tìm công thức biểu diễn các dãy số trên.
ĐS:
a/ ak = 3k + 1 với k = 0, 1, 2, …, 6
b/ bk = 3k + 2 với k = 0, 1, 2, …, 9
c/ ck
= 4k + 1 với k = 0, 1, 2, … hoặc
ck
= 4k + 1 với k
![]() N
N
Ghi chú:
Các số tự nhiên lẻ là những số không chia hết cho 2,
công thức biểu diễn là
![]() ,
k
,
k
![]() N
N
Các số tự nhiên chẵn là những số chia
hết cho 2, công thức biểu diễn là
![]() ,
k
,
k
![]() N
N
Dạng 3: Ma phương
C
9
19
5
7
11
15
17
3
10
Các số đặt trong hình vuông có tính chất rất đặc biệt. đó là tổng các số theo hàng, cột hay đường chéo đều bằng nhau. Một bảng ba dòng ba cột có tính chất như vậy gọi là ma phương cấp 3 (hình vuông kỳ diệu)
B
15
10
12
15
10
17
16
14
12
11
18
13
Hướng dẫn:
Bài 2: Điền các số 1, 2, 3, 4, 5, 6, 7, 8, 9 vào bảng có 3 dòng 3 cột để được một ma phương cấp 3?
1
4
2
7
5
3
8
6
9
4
9
2
3
5
7
8
1
6
Hướng dẫn: Ta vẽ hình 3 x 3 = 9 và đặt thêm 4o ô phụ vào giữa các cạnh hình vuông và ghi lại lần lượt các số vào các ô như hình bên trái. Sau đó chuyển mỗi số ở ô phụ vào hình vuông qua tâm hình vuông như hình bên phải.
8 |
9 |
24 |
36 |
12 |
4 |
6 |
16 |
18 |
T
10
a
50
100
b
c
d
e
40
ĐS: a = 16, b = 20, c = 4, d = 8, e = 25
Ngày dạy: ……………...
Buổi 3:
LUỸ THỪA VỚI SỐ MŨ TỰ NHIÊN
A> MỤC TIÊU
- Ôn lại các kiến thức cơ bản về luỹ thừa với số mũ tự nhiên như: Lũy thừa bậc n của số a, nhân, chia hai luỹ thừa cùng có số, …
- Rèn luyện tính chính xác khi vận dụng các quy tắc nhân, chia hai luỹ thừa cùng cơ số
- Tính bình phương, lập phương của một số. Giới thiệu về ghi số cho máy tính (hệ nhị phân).
- Biết thứ tự thực hiện các phép tính, ước lượng kết quả phép tính.
B> NỘI DUNG
I. Ôn tập lý thuyết.
1. Lũy thừa bậc n của số a là tích của n thừa số bằng nhau, mỗi thừa số bằng a
an=
a.a.a.a……a( n thừa số a, n
![]() 0).
a gọi là cơ số, n gọi là số mũ.
0).
a gọi là cơ số, n gọi là số mũ.
2. Nhân
hai luỹ thừa cùng cơ số
![]()
3. Chia
hai luỹ thừa cùng cơ số
![]() ( a
( a![]() 0,
m
0,
m
![]() n)
n)
Quy ước a0
= 1 ( a![]() 0)
0)
4. Luỹ
thừa của luỹ thừa
![]()
5. Luỹ thừa một
tích
![]()
6. Một số luỹ thừa của 10:
- Một nghìn: 1 000 = 103
- Một vạn: 10 000 = 104
- Một triệu: 1 000 000 = 106
- Một tỉ: 1 000 000 000 = 109
T
n thừa số 0
![]()
II. Bài tập
Dạng 1: Các bài toán về luỹ thừa
Bài 1: Viết các tích sau đây dưới dạng một luỹ thừa của một số:
a/ A = 82.324
b/ B = 273.94.243
ĐS: a/ A = 82.324 = 26.220 = 226. hoặc A = 413
b/ B = 273.94.243 = 322
Bài 2: Tìm các số mũ n sao cho luỹ thừa 3n thảo mãn điều kiện: 25 < 3n < 250
Hướng dẫn
Ta có: 32 = 9, 33 = 27 > 25, 34 = 41, 35 = 243 < 250 nhưng 36 = 243. 3 = 729 > 250
Vậy với số mũ n = 3,4,5 ta có 25 < 3n < 250
Bài 3: So sách các cặp số sau:
a/ A = 275 và B = 2433
b/ A = 2 300 và B = 3200
Hướng dẫn
a/ Ta có A = 275 = (33)5 = 315 và B = (35)3 = 315
Vậy A = B
b/ A = 2 300 = 33.100 = 8100 và B = 3200 = 32.100 = 9100
Vì 8 < 9 nên 8100 < 9100 và A < B.
Ghi chú: Trong hai luỹ thừa có cùng cơ số, luỹ thừa nào có cơ số lớn hơn thì lớn hơn.
Dạng 2: Bình phương, lập phương
Bài 1: Tính và so sánh
a/ A = (3 + 5)2 và B = 32 + 52
b/ C = (3 + 5)3 và D = 33 + 53
ĐS: a/ A > B ; b/ C > D
Lưu ý HS tránh sai lằm khi viết (a + b)2 = a2 + b2 hoặc (a + b)3 = a3 + b3
Dạng 3: Ghi số cho máy tính - hệ nhị phân
- Nhắc lại về hệ ghi số thập phân
VD: 1998 = 1.103 + 9.102 +9.10 + 8
![]() trong đó a, b, c, d, e là một trong các số
0, 1, 2, …, 9 vớ a khác 0.
trong đó a, b, c, d, e là một trong các số
0, 1, 2, …, 9 vớ a khác 0.
- Để ghi các sô dùng cho máy điện toán
người ta dùng hệ ghi số nhị phân. Trong hệ nhị phân
số
![]() có giá trị như sau:
có giá trị như sau:
![]()
Bài 1: Các số được ghi theo hệ nhị phân dưới đây bằng số nào trong hệ thập phân?
a/
![]() b/
b/
![]()
ĐS: A = 93 B = 325
Bài 2: Viết các số trong hệ thập phân dưới đây dưới dạng số ghi trong hệ nhị phân:
a/ 20 b/ 50 c/ 1335
ĐS: 20 =
![]() 50
=
50
=
![]() 1355 =
1355 =
![]()
GV hướng dẫn cho HS 2 cách ghi: theo lý thuyết và theo thực hành.
Bài 3: Tìm tổng các số ghi theo hệ nhị phân:
a/ 11111(2) + 1111(2)
b/ 10111(2) + 10011(2)
H
+
0
1
0
0
1
1
1
10
a/ Ta dùng bảng cộng cho các số theo hệ nhị phân
Đặt phép tính như làm tính cộng các số theo hệ thập phân
1
1
1
1
1(2)
+
1
1
1
1(2)
1
0
1
1
1
0(2)
b/ Làm tương tự như câu a ta có kết quả 101010(2)
Dạng 4: Thứ tự thực hiện các phép tính - ước lượng các phép tính
- Yêu cầu HS nhắc lại thứ tự thực hiện các phép tính đã học.
- Để ước lượng các phép tính, người ta thường ước lượng các thành phần của phép tính
Bài 1: Tính giá trị của biểu thức:
A = 2002.20012001 – 2001.20022002
Hướng dẫn
A = 2002.(20010000 + 2001) – 2001.(20020000 + 2002)
= 2002.(2001.104 + 2001) – 2001.(2002.104 + 2001)
= 2002.2001.104 + 2002.2001 – 2001.2002.104 – 2001.2002
= 0
Bài 2: Thực hiện phép tính
a/ A = (456.11 + 912).37 : 13: 74
b/ B = [(315 + 372).3 + (372 + 315).7] : (26.13 + 74.14)
ĐS: A = 228 B = 5
Bài 3: Tính giá trị của biểu thức
a/ 12:{390: [500 – (125 + 35.7)]}
b/ 12000 –(1500.2 + 1800.3 + 1800.2:3)
ĐS: a/ 4 b/ 2400
Dạng 5: Tìm x
Tìm x, biết:
a/ 541 + (218 – x) = 735 (ĐS: x = 24)
b/ 96 – 3(x + 1) = 42 (ĐS: x = 17)
c/ ( x – 47) – 115 = 0 (ĐS: x = 162)
d/ (x – 36):18 = 12 (ĐS: x = 252)
e/ 2x = 16 (ĐS: x = 4)
f) x50
= x (ĐS: x
![]() )
)
Ngày dạy:
Buổi 4:
ĐIỂM. ĐƯỜNG THẲNG. BA ĐIỂM THẲNG HÀNG. ĐƯỜNG THẲNG ĐI QUA HAI ĐIỂM. HAI ĐƯỜNG THẲNG CẮT NHAU
A) Mục tiêu
-HS biết biết
khái niệm điểm thuộc đường thẳng, điểm không thuộc
đường thẳng, dùng các kí hiệu
![]()
- Biết khái niệm ba điểm thẳng hàng, ba điểm không thẳng hàng, điểm nằm giữa hai điểm, biết sử dụng thước để vẽ và kiểm tra ba điểm thẳng hàng.
- vẽ được đường thẳng đi qua hai điểm, biết vị trí tương đối của hai đường thẳng: cắt nhau, trùng nhau, song song.
B) Nội dung
I. lí thuyết
Câu 1: thế nào là một điểm, hai điểm phân biệt, đường thẳng và điểm thuộc đường thẳng
Câu 2: thế nào là ba điểm thẳng hàng, ba điểm không thẳng hàng, quan hệ giữa ba điểm thẳng hàng?
Câu 3: Vẽ đường thẳng đi qua hai điểm A và B, vẽ được bao nhiêu đường thẳng như thế?
Câu 4: Vẽ hình theo diễn đạt sau:
đường thẳng AB, AC trùng nhau
đường thẳng AB, AC căt nhau
Đường thẳng AB, AC song song
II. Bài tập
Bài 1: Điền từ hoặc cụm từ thích hợp vào chỗ chấm:
1, Bất cứ hình nào cũng là một tập hợp …
2, Người ta dùng các chữ cái … để đặt tên cho điểm và các chữ cái thường để đặt tên cho…
3,
Điểm A thuộc đường thẳng d ta kí hiệu …, điểm B …
ta kí hiệu B![]() d
d
4, Khi 3 điểm M, N, P cùng thuộc một đường thẳng ta nói chúng…
5, 3 điểm A, B, C không thẳng hàng khi …
6, Trong 3 điểm thẳng hàng, có…và chỉ… nằm giữa … còn lại
7, Có một … và chỉ một đường thẳng đi qua 2… AvàB
8, Hai đường thẳng cắt nhau khi chúng có… chumg
9, Hai đường thẳng song song khi chúng… nào
10, Hai đường thẳng … còn được gọi là hai đường thẳng phân biệt
11, Mỗi điểm trên đường thẳng là gốc chung của…
12, Hình tạo bởi điểm … và một phần đường thẳng bị chia ra bởi điểm A được gọi … gốc A
Cho học sinh đứng tại chỗ đọc từng câu một và nêu từ cần điền
Bài tập tự luận
Bài 1: Cho hình vẽ. Hãy trả lời các câu hỏi sau:
M
N
P
Q



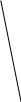
a, Điểm M thuộc các đườngthẳng nào?
b, Điểm N nằm trên đường thẳng nào? Nằm ngoài ngoài đường thẳng nào?
c, Trong bốn điểm M, N, P, Q, ba điểm nào thẳng hàng? ba điểm nào không thẳng hàng? Điểm nào giữa hai điểm còn lại
d, Có bao nhiêu đường thẳng ở hình trên , mỗi đường thẳng đó có bao nhiêu cách gọi tên
Gọi học sinh đứng tại chỗ trả lời câu a
a, Điểm M thuộc các đường thẳng a, b, c
Ta có M![]() a,
M
a,
M![]() b,
M
b,
M![]() c
c
GV: Tôi nói: M thuộc đường thẳng MN đúng hay sai?
HS:
M![]() MN
là đúng vì đưởng thẳng MN chính là đường thẳng c
MN
là đúng vì đưởng thẳng MN chính là đường thẳng c
b, Gọi học sinh đứng tại chỗ trả lời
Điểm N nằm trên các đường thẳng a và d, điểm N không nằm trên đường thẳng b và c
GV:
Ta nói điểm N![]() MP
đúng hay sai?
MP
đúng hay sai?
HS:
N![]() MP
là đúng vì đường thẳng MP chính là đường thẳng b
MP
là đúng vì đường thẳng MP chính là đường thẳng b
c, Trong 4 điểm M, N, P, Q thì:
- 3 điểm N, P, Q thẳng hàng
GV: Vì sao kết luận 3 điểm N, P, Q thẳng hàng?
HS: Vì 3 điểm N, P, Q cùng thuộc đường thẳng d
- 3 điểm M, N, P; 3 điểm M, N, Q; 3 điểm M, P, Q không thẳng hàng
d, Có 4 đường thẳng ở hình trên
- Mỗi đường thẳng a, b, c có 3 cách gọi tên
- Đường thẳng d có 7 cách gọi tên
Giáo viên yêu cầu học sinh viết các cách gọi tên đường thẳng
Giáo viên phát triển thêm:
e, Hãy chỉ ra các tia phân biệt có ở hình trên?
HS: tia MN, NM, MP, PM, MQ, QM, QN, NQ, PN, PQ
f, Hãy chỉ ra 2 tia đối nhau gốc P?
HS: Hai tia đối nhau gốc P là: PN và PQ
h, Hãy kể tên giao điểm của các cặp đường thẳng ?
Gọi học sinh trả lời
Giáo viên lưu ý: Khi viết các giao điểm các em viết lần lượt giao của 1 đường thẳng với các đường thẳng còn lại thì không bị sót
Ví dụ: Giao điểm của đường thẳng a với đường thẳng b là M
Giao điểm của đường thẳng a với đường thẳng c là M
Giao điểm của đường thẳng a với đường thẳng d là N
Ngày dạy:
Buổi 5:
THỨ TỰ THỰC HIỆN CÁC PHÉP TÍNH- KIỂM TRA 1 TIẾT
A. Kiến thức cần nhớ :
1. Đối với biểu thức không có dấu ngoặc :
- Nếu phép tính chỉ có cộng, trừ hoặc chỉ có nhân, chia, ta thực hiện phép tính theo thứ tự từ trái sang phải.
- Nếu phép tính có cả cộng , trừ, nhân, chia, nâng lên lũy thừa, ta thực hiện phép nâng lên lũy thừa trước, rồi đến nhân chia, cuối cùng đến cộng trừ.
2. Đối với biểu thức có dấu ngoặc.
Nếu biểu thức có các dấu ngoặc : ngoặc tròn ( ), ngoặc vuông [ ], ngoặc nhọn { }, ta thực hiện phép tính theo thứ tự : { } [ ] ( )
B. BÀI TẬP
Bài toán 1 : Thực hiện phép tính.
a) 5 . 22 – 18 : 32
b) 23 . 17 – 23 . 14
c) 17 . 85 + 15 . 17 – 120
d) 20 – [ 30 – (5 – 1)2 ]
e) 75 – ( 3.52 – 4.23 )
f) 2.52 + 3: 710 – 54: 33
g) 150 + 50 : 5 - 2.32
h) 5.32 – 32 : 42
Bài toán 2 : Thực hiện phép tính.
a) 27 . 75 + 25 . 27 – 150 b) 12 : { 400 : [500 – (125 + 25 . 7)]}
c) 13 . 17 – 256 : 16 + 14 : 7 – 1 d) 18 : 3 + 182 + 3.(51 : 17)
e) 15 – 25 . 8 : (100 . 2) f) 25 . 8 – 12.5 + 170 : 17 - 8
Bài toán 3 : Thực hiện phép tính.
a) 23 – 53 : 52 + 12.22 d) (62007 – 62006) : 62006
b) 5[(85 – 35 : 7) : 8 + 90] – 50 e) (52001 - 52000) : 52000
c) 2.[(7 – 33 : 32 ) : 22 + 99] – 100 f) (72005 + 72004) : 72004
Bài toán 4 : Tìm số tự nhiên x, biết.
a) 70 – 5.(x – 3) = 45 b) 12 + (5 + x) = 20 h) 14x + 54 = 82 c) 130 – (100 + x) = 25 k) 15x – 133 = 17
d) 175 + (30 – x) = 200 l) 155 – 10(x + 1) = 55
e) 5(x + 12) + 22 = 92 m) 6(x + 23 ) + 40 = 100
f) 95 – 5(x + 2) = 45 g) 10 + 2x = 45 : 43
n) 22 .(x + 32 ) – 5 = 55
Bài toán 5 : Tìm x, biết.
a) 5.22 + (x + 3) = 52 f) 5x – 52 = 10
b) 23 + (x – 32 ) = 53 – 43 g) 9x – 2.32 = 34
c) 4(x – 5) – 23 = 24 .3 h) 10x + 22 .5 = 102
d) 5(x + 7) – 10 = 23 .5 k) 125 – 5(4 + x) = 15
e) 72 – 7(13 – x) = 14 l) 26 + (5 + x) = 34
Bài toán 6 : Tìm x, biết.
a) 15 : (x + 2) = 3
b) 20 : (1 + x) = 2 f) 12x - 33 = 32 . 33
c) 240 : (x – 5) = 22 .52 – 20
d) 96 - 3(x + 1) = 42 h) 1230 : 3(x - 20) = 10
e) 5(x + 35) = 515
g) 541 + (218 - x) = 73
Bài toán 7 : Thực hiện phép tính.
a) 27 . 75 + 25 . 27 - 150; b) 142 - [50 - (23 .10 - 23 .5)]
c) 375 : {32 – [ 4 + (5. 32 – 42)]} – 14
d) {210 : [16 + 3.(6 + 3. 22 )]} – 3
e) 500 – {5[409 – (2³.3 – 21)²] - 1724}
Bài toán 8 : Thực hiện phép tính.
a) 80 - (4.52 - 3.23 ) b) 56 : 54 + 23 .22 – 12017
c) 125 - 2.[56 - 48 : (15 - 7)] d) 23.75 + 25.10 + 25.13 + 180
e) 2448: [119 -(23 -6)] f) [36.4 - 4.(82 - 7.11)2 : 4 – 20160
g) 303 - 3.{[655 - (18 : 2 + 1).43 + 5]} : 100
Bài toán 9 : Tìm x, biết.
a) 48 - 3(x + 5) = 24 e) 4x + 18 : 2 = 13
b) 2x+1 - 2x = 32 g) 2x - 20 = 35 : 33
c) (15 + x) : 3 = 315 : 312 h) 525.5x-1 = 525
d) 250 - 10(24 - 3x) : 15 = 244 k) x - 48 : 16 = 37
Bài toán 10 : Tìm x, biết.
a) [(8x - 12) : 4] . 33 = 36 g) 52x – 3 – 2 . 52 = 52 . 3
b) 41 - 2x+1 = 9 h) 52x – 3 – 2 . 52 = 52 . 3
c) 32x-4 - x 0 = 8 k) 30 - [4(x - 2) + 15] = 3
d) 65 - 4x+2 = 20140 l) 740:(x + 10) = 102 – 2.13
e) 120 + 2.(3x - 17) = 214 m) [(6x - 39) : 7].4 = 12
Bài toán 11 : Tính tổng sau.
a) S = 4 + 7 + 10 + 13 +………………+ 2014 + 2017
b) S = 35 + 38 + 41 +……….+ 92 + 95
c) S = 10 + 12 + 14 +……….+ 96 + 98
Gợi ý bài toán 11 : Tổng của dãy số cách đều.
Bước 1 : tính số số hạng qua công thức : n = (số cuối - số đầu) : d + 1 Với d là khoảng cách giữa hai số hạng liên tiếp.
Bước 2 : Tính tổng S qua công thức :
S =( (số cuối + số đầu ) . n): 2
KIỂM TRA 1 TIẾT
Bài 1 : Thực hiện phép tính.
a) 5 . 22 – 18 : 32
b) 23 . 17 – 23 . 14
c) 17 . 85 + 15 . 17 – 120
d) 20 – [ 30 – (5 – 1)2 ]
Bài 2 : Tìm x, biết.
a) 5.22 + (x + 3) = 52 f) 5x – 52 = 10
b) 23 + (x – 32 ) = 53 – 43 g) 9x – 2.32 = 34
c) 4(x – 5) – 23 = 24 .3 h) 10x + 22 .5 = 102
d) 5(x + 7) – 10 = 23 .5 k) 125 – 5(4 + x) = 15
Bài 3:
a, (x- 6)2= 9
b, 5 x+1= 125
c, 5 2x- 3- 2. 52= 52. 3
d, 128- 3(x+ 4)= 23
Bài 4: Cha mua cho em một quyển số tay dày 256 trang. Để tiện theo dõi em đánh số trang từ 1 đến 256. Hỏi em đã phải viết bao nhiêu chữ số để đánh hết cuốn sổ tay?
Bài 5: Tính tổng sau.
S = 4 + 7 + 10 + 13 +………………+ 2014 + 2017
Ngày dạy:
Buổi 6:
TÍNH CHẤT CHIA HẾT CỦA MỘT TỔNG
DẤU HIỆU CHIA HẾT CHO 2, 5
A) Mục tiêu
- HS củng cố kiến thức tính chất chia hết của 1 tổng, dấu hiệu chia hết cho 2 và 5
- Vận dụng thành thạo các dấu hiệu chia hết để nhanh chóng nhận ra 1 số có chia hết cho 2 và 5 hay không?
B) Nội dung
I) Ôn tập lí thuyết
Câu 1: nêu tính chất chia hết của 1 tổng
Câu 2: Nêu dấu hiệu chia hết cho 2 và 5
Câu 3: Những số như thế nào thì chia hết cho 2 và 5? Cho ví dụ?
II) Bài tập
Bài 1: Không làm tính , xét xem tổng sau có chia hết cho 12 không ? Vì sao ?
120 + 36
120a + 36b ( với a ; b
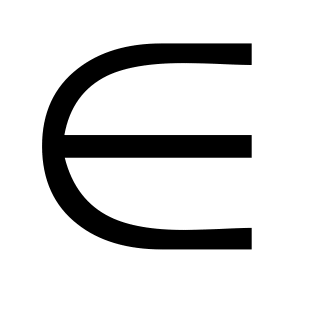 N
)
N
)
Bài
2: Cho A = 2.4.6.8.10.12
![]() 40 . Hỏi A có chia hết cho 6 ; cho 8 ; cho 20 không ? Vì sao?
40 . Hỏi A có chia hết cho 6 ; cho 8 ; cho 20 không ? Vì sao?
Bài 3: Khi chia số tự nhiên a cho 36 ta được số dư 12 . Hỏi a có chia hết cho 4 ; cho 9 không vì sao ?
Bài 4:
Điền dấu X và ô thích hợp :
Câu |
Đ |
S |
Nếu a
|
|
|
Nếu a
|
|
|
Nếu tổng của hai số chia hết cho 9 và một trong hai số chia hết cho 3 thì số còn lại chia hết cho 3 |
|
|
Nếu hiệu của hai số chia hết cho 6 và số thứ nhất chia hết cho 6 thì số thứ hai chia hết cho 3 |
|
|
Nếu a
|
|
|
Nếu a
|
|
|
125.7 – 50 chia hết cho 25 |
|
|
1001a + 28b – 22 không chia hết cho 7 |
|
|
Nếu cả hai số hạng của một tổng không chia hết cho 5 thì tổng không chia hết cho 5 |
|
|
Để tổng n + 12
|
|
|
Bài
5: Cho
![]() và
và
![]() .
Chứng minh rằng:
.
Chứng minh rằng:
![]() với m ; n
với m ; n
![]() N
N
Bài 6: Chứng minh rằng tổng của ba số tự nhiên liên tiếp chia hết cho 3, tổng của 5 số tự nhiên liên tiếp không chia hết cho 5.
Bài 7: Chứng minh rằng :
a) Tổng của ba số chẵn liên tiếp thì chia hết cho 6,
b) Tổng ba số lẻ liên tiếp không chia hết cho 6
c) Nếu a chia hết cho b và b chia hết cho c thì a chia hết cho c
Bài 8: Viết 5 số có 5 chữ số khác nhau:
a. Chia hết cho 2 ; b. Chia hết cho 5 ; c. chia hết cho cả 2 và 5;
Bài 9: Hãy lập tất cả các số có 3 chữ số khác nhau từ 4 chữ số: 0; 5; 4; 9 và thoả mãn điều kiện:
a. Chia hết cho 2. b. Chia hết cho 4. c. Chia hết cho cả 2 và 5.
Bài 10: Cho 3 chữ số: 0; 1; 2. Hãy lập tất cả các số có 3 chữ số vừa chia hết cho 2; vừa chia hết cho 5.
Bài 11: Cho 4 chữ số: 0; 1; 2; 3. Hãy lập tất cả các số có 4 chữ số vừa chia hết cho 2; vừa chia hết cho5 sao cho mỗi số đều có đủ 4 chữ số đã cho.
Bài
12: Tìm chữ số a để thay số
![]()
a, chia hết cho 2
b, chia hết cho 5
c, chia hết cho 2 và 5
Bài 13: Cho số
![]() ,
thay dấu * bởi chữ số nào để:
,
thay dấu * bởi chữ số nào để:
a/ A chia hết cho 2
b/ A chia hết cho 5
c/ A chia hết cho 2 và cho 5
Bài 14: Cho số
![]() ,
thay dấu * bởi chữ số nào để:
,
thay dấu * bởi chữ số nào để:
a/ B chia hết cho 2
b/ B chia hết cho 5
c/ B chia hết cho 2 và cho 5
Bài 15: Viết tập hợp các số x chia hết cho 2, thoả mãn:
a/ 52 < x < 60
b/ 105
![]() x < 115
x < 115
c/ 256 < x
![]() 264 d/ 312
264 d/ 312
![]() x
x
![]() 320
320
Hướng dẫn
a/
![]()
b/
![]()
c/
![]()
d/
![]()
Bài 16: Viết tập hợp các số x chia hết cho 5, thoả mãn:
a/ 124 < x < 145
b/ 225
![]() x < 245
x < 245
c/ 450 < x
![]() 480 d/ 510
480 d/ 510
![]() x
x
![]() 545
545
Hướng dẫn
a/
![]()
b/
![]()
c/
![]()
d/
![]()
Ngày dạy:
Buổi 7:
DẤU HIỆU CHIA HẾT CHO 3, 9
A) Mục tiêu
- HS được khắc sâu các kiến thức về dấu hiệu chia hêt cho 3 và 9
- Vận dụng thành thạo các dấu hiệu chia hết để nhanh chóng nhận ra 1 số có chia hết cho 3 và 9 hay không?
B) Nội dung
I) Lí thuyêt
Câu 1: Nêu dấu hiệu chia hết cho 3 và 9?
Câu 2: Những số như thế nào thì chia hết cho cả 3 và 9? Cho ví dụ?
II) Bài tập vận dụng
Bài 1(SGK 4 trang 98): Với bốn chữ số 0; 6; 1 ; 2.
Hãy viết ít nhất ba số có ba chữ số khác nhau và chia hết cho 9.
Hãy viết một số có ba chữ số khác nhau chia hết cho 3 nhưng không chia hết cho 9.
Bài 2: Hãy tìm số tự nhiên nhỏ nhất có 6 chữ số khác nhau và chia hết cho 5.
Bài 3: Hãy viết vào bên phải và bên trái số 2009 mỗi bên một chữ số để được một số:
Chia hết cho 2 ;
Chia hết cho 3 ;
Chia hết cho 4 ;
Chia hết cho 5;
Chia hết cho 30;
Chia hết cho 3 nhưng không chia hết cho 9.
Bài 4: Tìm a , b biết:
a =
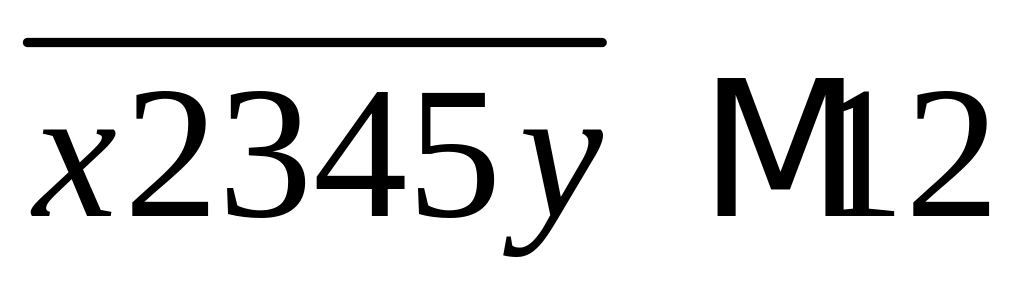 ;
;b =
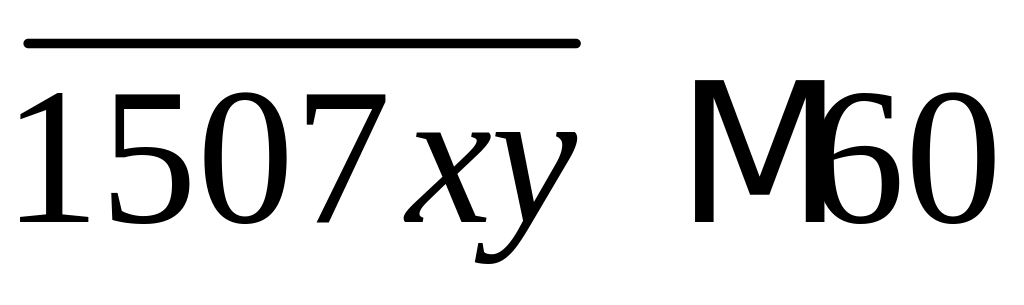 .
.
Bài 5: Trong các số 2485 ; 8553 ; 152007 ; 12408 ; 1948 ; 65308 ; 11200.
Số nào chia hết cho 2 ?
Số nào chia hết cho cả 2 và 5 ?
Số nào chia hết cho 8 ?
Số nào chia hết cho cả 3 và 4 ?
Số nào chia hết cho 2 và 3 ?
Bài 6:
Một số có 2 chữ số chia hết cho 3 và 5 thì chữ số hàng chục của nó có thể là những số nào ?
Một số có 3 chữ số chia hết cho 3 và 4 thì chữ số hàng trăm của nó có thể là những số nào ?
Bài 7 (Đề thi học sinh giỏi lớp 5): Cho một số có hai chữ số, trong đó, chữ số hàng đơn vị gấp 3 lần chữ số hàng chục. Nếu đổi vị trí các số cho nhau thì số đó tăng thêm 36 đơn vị. Tìm số đó.
Bài 8 (Đề thi học sinh giỏi lớp 5): Cho một số có hai chữ số. Nếu thêm số 0 vào giữa số đó ta được số mới gấp 9 lần số đã cho. Tìm số đã cho.
Bài 9: Tìm các số chia hết cho 25 trong:
a. 1000 số tự nhiên đầu tiên.
b. 2009 số tự nhiên đầu tiên.
Bài 10:
Tìm dấu hiệu chia hết cho 2, 3 và cho 6 của các số ghi trong hệ 7 – phân.
Tìm dấu hiệu chia hết cho 2, 4 và cho 8 của các số ghi trong hệ 9 – phân.
Bài 11: Trong các câu sau, câu nào đúng, câu nào sai ?
Những số chia hết cho 2 và 5 thì có chữ số tận cùng bằng 0.
Những số nguyên tố lớn hơn 2 thì chia cho 2 dư 1.
Hiệu của hai số chia hết cho 2 thì 2 số đó có cùng chữ số hàng đơn vị.
Hiệu của hai số chia hết cho 10 thì hai số đó có cùng chữ số hàng đơn vị.
Một số chia hết cho 25 thì chia hết cho 5.
Một số chia hết cho 3 thì bình phương số đó chia hết cho 9.
Một số chia hết cho 5 thì bình phương số đó chia hết cho 25.
Bài 12: Chứng minh rằng:
a. A = m3
+ 5m
![]() 6
6
b. B = m5
- m
![]() 30.
30.
c. C = p2
– 1
![]() 3 , với p là số nguyên tố lớn hơn 3.
3 , với p là số nguyên tố lớn hơn 3.
Bài 13:
a. Cho a là số tự nhiên có 2 chữ số. Viết các số a theo thứ tự ngược lại ta được số tự nhiên b. Hỏi hiệu của hai số đó có chia hết cho 3 không ? Vì sao ?
b. Cho a là số tự nhiên có 3 chữ số. Viết các số của a theo thứ tự ngược lại ta được số tự nhiên b. Hỏi hiệu của hai số đó có chia hết cho 9 không ? Vì sao ?
Bài 14: Hai bạn Hải và Linh đi mua 9 gói bánh và 6 gói kẹo để liên hoan. Linh đưa cho cô bán hàng 100.000 đồng và cô bán hàng trả lại 36.000 đồng. Hải nói ngay: “Cô tính sai rồi!” Bạn hãy cho biết Hải nói đúng hay sai biết số tiền mỗi gói bánh, kẹo là một số nguyên đồng.
Hướng dẫn:
Bài 1:
Tương tự các ví dụ của dạng 2.
Viết số có 3 chữ số khác nhau có tổng chia hết cho 3 nhưng không chia hết cho 9.
Bài 2: Số tự nhiên nhỏ nhất có 6 chữ số khác nhau chia hết cho 5 thì chữ số tận cùng là 0 hoặc 5.
Đáp số: 102345.
Bài 3: Dựa vào các dấu hiệu chia hết cho 2; 3 ; 4 ; 5.
Bài 4:
Tìm x; y để a chia hết cho 3 và 4.
Tìm x; y để a chia hết cho 3; 4 và 5.
Bài 5: Dựa vào các dấu hiệu chia hết.
Bài 6: Dựa vào các dấu hiệu chia hết.
Bài 7: Chữ số hàng đơn vị gấp 3 lần chữ số hàng chục nên chữ số hàng đơn vị chia hết cho 3. Do đó, chữ số hàng đơn vị chỉ có thể là 3; 6 hoặc 9.
Đáp số: 26.
Bài 8: Thêm 0 vào giữa số phải tìm được số mới gấp 9 lần số đã cho nên số mới chia hết cho 9. Do đó tổng các chữ số của số ban đầu chia hết cho 9.
Đáp số: 45.
Bài 10:
Biểu diễn số tự nhiên a trong hệ 7 – phân từ đó suy ra kết quả.
Biểu diễn số tự nhiên a trong hệ 9 – phân từ đó suy ra kết quả.
Bài 12:
Chứng minh A chia hết cho 2 và 3 (dựa vào bổ đề 1 và 2).
Chứng minh B chia hết cho 2; 3 và 5 (dựa vào bổ đề 1 và 2).
Bài 13:
a. Gọi số có hai chữ số là
![]() .
Khi đó số viết theo thứ tự ngược lại là
.
Khi đó số viết theo thứ tự ngược lại là
![]() .
.
Ta có:
![]() = 10x + y
= 10x + y
![]() = 10y + x.
= 10y + x.
Từ đó suy ra điều phải chứng minh.
b. Tương tự ý a.
Bài 14: Gọi số tiền một gói bánh là a (đồng).
Số tiền một gói kẹo là b (đồng).
Tổng số tiền mua bánh và kẹo là : 9a + 6b.
Như vậy số tiền mua bánh kẹo là một số chia hết cho 3.
Vì 100.000 không chia hết cho 3 nên số tiền trả lại phải là một số không chia hết cho
3. Nhưng 36.000 chia hết cho 3. Do đó, bạn Hải nói đúng.
Ngày dạy:
Buổi 8:
ƯỚC VÀ BỘI – SỐ NGUYÊN TỐ - HỢP SỐ
A> MỤC TIÊU
- HS biết kiểm tra một số có hay không là ước hoặc bội của một số cho trước, biết cách tìm ước và bội của một số cho trước .
- Biết nhận ra một số là số nguyên tố hay hợp số.
- Biết vận dụng hợp lý các kiến thức về chia hết đã học để nhận biết hợp số.
B> NỘI DUNG
I. Ôn tập lý thuyết.
Câu 1: Thế nào là ước, là bội của một số?
Câu 2: Nêu cách tìm ước và bội của một số?
Câu 3: Định nghĩa số nguyên tố, hợp số?
Câu 4: Hãy kể 20 số nguyên tố đầu tiên?
II. Bài tập
Dạng 1:
Bài 1: Tìm các ước của 4, 6, 9, 13, 1
Bài 2: Tìm các bội của 1, 7, 9, 13
Bài 3: Chứng tỏ rằng:
a/ Giá trị của biểu thức A = 5 + 52 + 53 + … + 58 là bội của 30.
b/ Giá trị của biểu thức B = 3 + 33 + 35 + 37 + …+ 329 là bội của 273
Hướng dẫn
a/ A = 5 + 52 + 53 + … + 58 = (5 + 52) + (53 + 54) + (55 + 56) + (57 + 58)
= (5 + 52) + 52.(5 + 52) + 54(5 + 52) + 56(5 + 52)
=
30 + 30.52
+ 30.54
+ 30.56
= 30 (1+ 52
+ 54 +
56)
![]() 3
3
b/
Biến đổi ta được B = 273.(1 + 36
+ … + 324 )![]() 273
273
Bài
4: Biết số tự nhiên
![]() chỉ có 3 ước khác 1. tìm số đó.
chỉ có 3 ước khác 1. tìm số đó.
Hướng dẫn
![]() = 111.a = 3.37.a chỉ có 3 ước số khác 1
là 3; 37; 3.37 khia a = 1.
= 111.a = 3.37.a chỉ có 3 ước số khác 1
là 3; 37; 3.37 khia a = 1.
Vậy số phải tìm là 111
(Nết
a
![]() 2
thì 3.37.a có nhiều hơn 3 ước số khác 1).
2
thì 3.37.a có nhiều hơn 3 ước số khác 1).
Dạng 2:
Bài 1: Tổng (hiệu) sau là số nguyên tố hay hợp số:
a/ 3150 + 2125
b/ 5163 + 2532
c/ 19. 21. 23 + 21. 25 .27
d/ 15. 19. 37 – 225
Hướng dẫn
a/ Tổng lớn hơn 5 và chia hết cho 5, nên tổng là hợp số.
b/ Hiệu lớn hơn 3 và chia hết cho 3, nên hiệu là hợp số.
c/ Tổng lớn hơn 21 và chia hết cho 21 nên tổng là hợp số.
d/ Hiệu lớn hơn 15 và chia hết cho 15 nên hiệu là hợp số.
Bài 2: Chứng tỏ rằng các số sau đây là hợp số:
a/ 297; 39743; 987624
b/ 111…1 có 2001 chữ số 1 hoặc 2007 chữ số 1
c/ 8765 397 639 763
Hướng dẫn
a/ Các số trên đều chia hết cho 11
Dùng dấu hiệu chia hết cho 11 đê nhận biết: Nếu một số tự nhiên có tổng các chữ số đứng ở vị trí hàng chẵn bằng tổng các chữ số ở hàng lẻ ( số thứ tự được tính từ trái qua phải, số đầu tiên là số lẻ) thì số đó chia hết cho 11. Chẳng hạn 561, 2574,…
b/ Nếu số đó có 2001 chữ số 1 thì tổng các chữ số của nó bằng 2001 chia hết cho 3. Vậy số đó chia hết cho 3. Tương tự nếu số đó có 2007 chữ số 1 thì số đó cũng chia hết cho 9.
c/ 8765 397 639 763 = 87654.100001 là hợp số.
Bài 3: Chứng minh rằng các tổng sau đây là hợp số
a/
![]()
b/
![]()
c/
![]()
Hướng dẫn
a/
![]() = a.105
+ b.104
+ c.103
+ a. 102
+ b.10 + c + 7
= a.105
+ b.104
+ c.103
+ a. 102
+ b.10 + c + 7
= 100100a + 10010b + 1001c + 7
= 1001(100a + 101b + c) + 7
Vì
1001![]() 7
7
![]() 1001(100a + 101b + c)
1001(100a + 101b + c)
![]() 7 và 7
7 và 7![]() 7
7
Do
đó
![]()
![]() 7, vậy
7, vậy
![]() là hợp số
là hợp số
b/
![]() = 1001(100a + 101b + c) + 22
= 1001(100a + 101b + c) + 22
1001![]() 11
11
![]() 1001(100a + 101b + c)
1001(100a + 101b + c)
![]() 11 và 22
11 và 22![]() 11
11
Suy
ra
![]() = 1001(100a + 101b + c) + 22 chia hết cho 11 và
= 1001(100a + 101b + c) + 22 chia hết cho 11 và
![]() >11 nên
>11 nên
![]() là hợp số
là hợp số
c/
Tương tự
![]() chia
hết cho 13 và
chia
hết cho 13 và
![]() >13
nên
>13
nên
![]() là hợp số
là hợp số
Bài 4: a/ Tìm số tự nhiên k để số 23.k là số nguyên tố
b/ Tại sao 2 là số nguyên tố chẵn duy nhất?
Hướng dẫn
a/ Với k = 0 thì 23.k = 0 không là số nguyên tố
với k = 1 thì 23.k = 23 là số nguyên tố.
Với
k>1 thì 23.k
![]() 23 và 23.k > 23 nên 23.k là hợp số.
23 và 23.k > 23 nên 23.k là hợp số.
b/ 2 là số nguyên tố chẵn duy nhất, vì nếu có một số chẵn lớn hơn 2 thì số đó chia hết cho 2, nên ước số của nó ngoài 1 và chính nó còn có ước là 2 nên số này là hợp số.
Bài 5: Tìm một số nguyên tố, biết rằng số liền sau của nó cũng là một số nguyên tố
Hướng dẫn
Ta biết hai số tự nhiên liên tiếp bao giờ cũng có một số chẵn và một số lẻ, muốn cả hai là số nguyên tố thì phải có một số nguyên tố chẵn là số 2. Vậy số nguyên tố phải tìm là 2.
Dạng 3: Dấu hiệu để nhận biết một số nguyên tố
Ta có thể dùng dấu hiệu sau để nhận biết một số nào đó có là số nguyên tố hay không:
“ Số tự nhiên a không chia hết cho mọi số nguyên tố p mà p2 < a thì a là số nguyên tố.
VD1: Ta đã biết 29 là số nguyên tố.
Ta ó thể nhận biết theo dấu hiệu trên như sau:
- Tìm các số nguyên tố p mà p2 < 29: đó là các số nguyên tố 2, 3, 5 (72 = 49 19 nên ta dừng lại ở số nguyên tố 5).
- Thử các phép chia 29 cho các số nguyên tố trên. Rõ ràng 29 không chia hết cho số nguyên tố nào trong các số 2, 3, 5. Vậy 29 là số nguyên tố.
VD2: Hãy xét xem các số tự nhiên từ 1991 đến 2005 số nào là số nguyên tố?
Hướng dẫn
- Trước hết ta loại bỏ các số chẵn: 1992, 1994, 1996, …, 2004
- Loại bỏ tiếp các số chia hết cho 3: 1995, 2001
- Ta còn phải xét các số 1991, 1993, 1997, 1999, 2003 ố nguyên tố p mà p2 < 2005 là 11, 13, 17, 19, 23, 29, 31, 37, 41, 43.
- Số 1991 chia hết cho 11 nên ta loại.
- Các số còn lại 1993, 1997, 1999, 2003 đều không chia hết cho các số nguyên tố tên.
Vậy từ 1991 đến 2005 chỉ có 4 số nguyên tố là 1993, 1997, 1999, 2003
Ngày dạy:
Buổi 9:
PHÂN TÍCH MỘT SỐ RA THỪA SỐ NGUYÊN TỐ
A> MỤC TIÊU
- HS biết phân tích một số ra thừa số nguyên tố.
- Dựa vào việc phân tích ra thừa số nguyên tố, HS tìm được tập hợp của các ước của số cho trước
- Giới thiệu cho HS biết số hoàn chỉnh.
- Thông qua phân tích ra thừa số nguyên tổ để nhận biết một số có bao nhiêu ước, ứng dụng để giải một vài bài toán thực tế đơn giản.
B> NỘI DUNG
I. Ôn tập lý thuyết.
Câu 1: Thế nào là phân tích một số ra thừa số nguyên tố?
Câu 2: Hãy phân tích số 250 ra thừa số nguyên tố bằng 2 cách.
II. Bài tập
Bài 1: Phân tích các số 120, 900, 100000 ra thừa số nguyên tố
ĐS: 120 = 23. 3. 5
900 = 22. 32. 52
100000 = 105 = 22.55
Bài 2. Một số tự nhiên gọi là số hoàn chỉnh nếu tổng tất cả các ước của nó gấp hai lần số đó. Hãy nêu ra một vài số hoàn chỉnh.
VD 6 là số hoàn chỉnh vì Ư(6) = {1; 2; 3; 6} và 1 + 2 + 3 + 6 = 12
Tương tự 48, 496 là số hoàn chỉnh.
Bài 3: Học sinh lớp 6A được nhận phần thưởng của nhà trường và mỗi em được nhận phần thưởng như nhau. Cô hiệu trưởng đã chia hết 129 quyển vở và 215 bút chì màu. Hỏi số học sinh lớp 6A là bao nhiêu?
Hướng dẫn
Nếu gọi x là số HS của lớp 6A thì ta có:
129![]() x
và 215
x
và 215![]() x
x
Hay nói cách khác x là ước của 129 và ước của 215
Ta có 129 = 3. 43; 215 = 5. 43
Ư(129) = {1; 3; 43; 129}
Ư(215) = {1; 5; 43; 215}
Vậy
x
![]() {1; 43}. Nhưng x không thể bằng 1. Vậy x = 43.
{1; 43}. Nhưng x không thể bằng 1. Vậy x = 43.
MỘT SỐ CÓ BAO NHIÊU ƯỚC?
VD: - Ta có Ư(20) = {1, 2, 4, 5, 10, 20}. Số 20 có tất cả 6 ước.
- Phân tích số 20 ra thừa số nguyên tố, ta được 20 = 22. 5
So sánh tích của (2 + 1). (1 + 1) với 6. Từ đó rút ra nhận xét gì?
Bài 1: a/ Số tự nhiên khi phân tích ra thừa số nguyên tố có dạng 22 . 33. Hỏi số đó có bao nhiêu ước?
b/ A = p1k. p2l. p3m có bao nhiêu ước?
Hướng dẫn
a/ Số đó có (2+1).(3+1) = 3. 4 = 12 (ước).
b/ A = p1k. p2l. p3m có (k + 1).(l + 1).(m + 1) ước
Ghi nhớ: Người ta chứng minh được rằng: “Số các ước của một số tự nhiên a bằng một tích mà các thừa số là các số mũ của các thừa số nguyên tố của a cộng thêm 1”
a = pkqm…rn
Số phần tử của Ư(a) = (k+1)(m+1)…(n+1)
Bài 2: Hãy tìm số phần tử của Ư(252):
ĐS: 18 phần tử.
Ngày dạy:
Buổi 10:
ĐOẠN THẲNG. ĐỘ DÀI ĐOẠN THẲNG. CỘNG ĐOẠN THẲNG
A )Kiến
thức cơ bản:
)Kiến
thức cơ bản:
1, Đoạn thẳn AB là hình gồm điểm A, điểm B
và tất cả các điểm nằm giữa A và B h9.
2, Mỗi đoạn thẳng có một đọ dài độ dài đoạn thẳng là một số dương.
3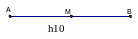 AB = CD <=> AB và CD có cùng độ dài.
AB = CD <=> AB và CD có cùng độ dài.
AB < CD <=> AB ngắn hơn CD.
AB > CD <=> AB dài hơnCD.
4, Nếu điểm m nằm giữa hai điểm A và B thì
AM + MB = AB
Ngược lai nếu AM+ MB = AB thì điểm M nằm giữa hai điểm A và B h10.
N
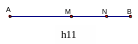 âng
cao:
âng
cao:
1, Mệnh đề sau tương đương với tính chất trên:
Nếu AM+ MB ≠ AB thì M không nằm giữa A và B.
2, Cộng liên tiếp(h11)
Nếu điểm M nằm giữa hai điểm A và B; điểm N nằm giữa hai điểm m và B thì:
AM + MN + NM = AB
Thí dụ 3:
Cho điểm M nằm giữa hai điểm A và B. Giải thích vì sao AM < AB; MB<AB.
 Giải:(h3.1)
Giải:(h3.1)
Vì điểm M nằm giữa hai điểm A và B
nên AM + MB =AB
Do AM > 0; BM > 0; nên AM < AB; MB<AB.
Thí dụ 4:
Cho biết điểm M nằm giữa hai điểm A và B. Có AB = 11cm; BM= 7 cm. Tính MA?
Giải: (h4.1)
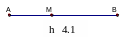 Vì
M nằm giữa hai điểm A và B nên ta có:
Vì
M nằm giữa hai điểm A và B nên ta có:
AM + MB =AB
AM = AB – MB
AM= 11- 7
AM= 4
Vậy AM = 4 cm.
Thí dụ 5:
Cho ba điểm M;O;N thẳng hàng. Điểm N không nằm giữa hai điểm M và O.
c ho
biết MN = 3 cm; ON = 1cm, hãy so sánh OM và ON.
ho
biết MN = 3 cm; ON = 1cm, hãy so sánh OM và ON.
Giải: (h4.1)
Nếu điểm M nằm giữa hai điểm O và N thì:
OM + MN = ON
thay số: OM + 3 = 1(vô lý) vậy điểm M không nằm giữa O và N
điểm N không nằm giữa O và M(đề bài) => điểm O nằm giữa hai điểm M và N.
ta có: MO+ ON = MN=> MO + 1 =3 => MO = 2 cm.
Do đó OM > ON (2 > 1).
Thí dụ 6:
Cho ba điểm A;B;C biết AB= 9 cm;AC= 4,9 cm; BC= 4,1 cm. Trong ba điểm A;B;C điểm nào nằm giữa hai điểm còn lại?
Giải:
Ta có 4,9+ 4,1 = 9 => AC+ CB = AB
=> C nằm giữa A và B.
B) Bài tập
Bài 13. Cho biết D là điểm nằm giữa hai điểm M và N. Biết MD = 12 cm; MN = 5 cm
Tính DN?
Bài 14. Biết M là điểm thuộc đoạn Thẳng AB có MA= 3 cm;MB= 7cm. Tính độ dài đoạn thẳng MN?
Bài 15. Cho 5 điểm A, B, C, D, E trong đó không có 3 điểm nào thẳng hàng. Vẽ các đoạn thẳng đi qua các cặp điểm. Hỏi vẽ được bao nhiêu đoạn thẳng, là những đoạn thẳng nào.
Kết quả trên có thay đổi không nếu cả 5 điểm A, B, C, D, E thẳng hàng.
Bài 16. Cho trước n điểm (n € N ; ≥ 2). Vẽ các đoạn thẳng đi qua các cặp điểm được tất cả 28 đoạn thẳng. Tìm n.
Bài 17. Vẽ 5 đoạn thẳng đôi một cắt nhau sao cho tổng số giao điểm là 10. Giải thích vì sao số giao điểm không thể quá 10 ?
B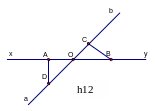 ài
18. Xem hình 12 rồi cho biết:
ài
18. Xem hình 12 rồi cho biết:
a) Hình này có mấy tia?
b) Hình này có mấy đoạn thẳng ?
c) Những cặp đoạn thẳng nào
không cắt nhau ?
d) Vì sao có thể khẳng định tia Ox
không cắt đoạn thẳng BC ?
Bài 19. Cho hai tia chung gốc Ox, Oy.
Trên tia Ox lấy hai điểm B và C sao cho B nằm giữa O và C. Trên tia Oy lấy điểm A sao cho OA>OC.
a) So sánh OA với OB.
b) So sánh OA- OB với OA.
Bài 20. Trên đường thẳng a lấy 4 điểm E, F, H theo thứ tự đó. Giả sử EH =7 cm;
EF = 2cm ; FG = 3cm.
a) So sánh FG với GH.
b) Tìm những căp đoạn thẳng bằng nhau.
Bài 21. Cho đạon thẳng AB. Trên tia đối của Ab lấy điểm E, trên tia đối của tia BA lấy điểm F sao cho AE<BF. Hãy so sánh à với BE.
Bài 22. Cho ba điểm A, B, C.
a) Giả sử AB = 2cm ; BC = 3cm ; CA = 5cm, hãy chứng tỏ A, B, C thẳng hàng.
b) Giả sử AB = 2cm ; BC = 3cm ; CA = 4cm, hãy chứng tỏ A, B, C không thẳng hàng.
Bài 23. Cho đoạn thẳng AB. Lấy điểm O nẵm giữa A và B, lấy điểm I nằm giữa O và B.
a) Giả sử AB = 5cm ; BI = 2cm, tính OI.
b) Giả sử AO = a ; BI = b, tìm điều kiện của a và b để AI = OB.
Bài 24. Cho ba điểm A,B,C thẳng hàng. Hỏi điểm nào nằm giữa hai điểm còn lại nếu:
AC + CB = AB
AB + BC = AC
BA+ AC= BC
Bài 25. Trong mỗi trường hợp sau, hãy vẽ hình và cho biết ba điểm A,B,M có thẳng hàng không?
AM= 3,1 cm; MB= 2,9 cm; AB= 6 cm.
AM= 3,1 cm; MB= 2,9 cm; AB= 5 cm
AM= 3,1 cm; MB= 2,9 cm; AB= 7 cm
Ngày dạy:
Buổi 11:
ƯỚC CHUNG VÀ BỘI CHUNG
ƯỚC CHUNG LỚN NHẤT - BỘI CUNG NHỎ NHẤT
A> MỤC TIÊU
- Rèn kỷ năng tìm ước chung và bội chung: Tìm giao của hai tập hợp.
- Biết tìm ƯCLN, BCNN của hai hay nhiều số bằng cách phân tích các số ra thừa số nguyên tố.
- Biết vận dụng ƯC, ƯCLN, BC, BCNN vào các bài toán thực tế đơn giản.
B> NỘI DUNG
I. Ôn tập lý thuyết.
Câu
1: Ước chung của hai hay nhiều số là gi? x
![]() ƯC(a; b) khi nào?
ƯC(a; b) khi nào?
Câu 2: Bội chung nhỏ nhất của hai hay nhiều số là gi?
Câu 3: Nêu các bước tìm UCLL
Câu 4: Nêu các bước tìm BCNN
II. Bài tập
Dạng 1:
Bài 1: Viết các tập hợp
a/ Ư(6), Ư(12), Ư(42) và ƯC(6, 12, 42)
b/ B(6), B(12), B(42) và BC(6, 12, 42)
ĐS:
a/
Ư(6) =
![]()
Ư(12)
=
![]()
Ư(42)
=
![]()
ƯC(6,
12, 42) =
![]()
b/
B(6) =
![]()
B(12)
=
![]()
B(42)
=
![]()
BC
=
![]()
Bài 2: Tìm ƯCLL của
a/ 12, 80 và 56
b/ 144, 120 và 135
c/ 150 và 50
d/ 1800 và 90
Hướng dẫn
a/ 12 = 22.3 80 = 24. 5 56 = 33.7
Vậy ƯCLN(12, 80, 56) = 22 = 4.
b/ 144 = 24. 32 120 = 23. 3. 5 135 = 33. 5
Vậy ƯCLN (144, 120, 135) = 3.
c/ ƯCLN(150,50) = 50 vì 150 chia hết cho 50.
d/ ƯCLN(1800,90) = 90 vì 1800 chia hết cho 90.
Bài 3: Tìm
a/ BCNN (24, 10)
b/ BCNN( 8, 12, 15)
Hướng dẫn
a/ 24 = 23. 3 ; 10 = 2. 5
BCNN (24, 10) = 23. 3. 5 = 120
b/ 8 = 23 ; 12 = 22. 3 ; 15 = 3.5
BCNN( 8, 12, 15) = 23. 3. 5 = 120
Dạng 2: Dùng thuật toán Ơclit để tìm ƯCLL (không cần phân tích chúng ra thừa số nguyên tố)
1/ GV giới thiệu Ơclit: Ơclit là nhà toán học thời cổ Hy Lạp, tác giả nhiều công trình khoa học. Ông sống vào thế kỷ thứ III trước CN. Cuốn sách giáo kha hình học của ông từ hơn 2000 nưam về trước bao gồm phần lớn những nội dung môn hình học phổ thông của thế giới ngày nay.
2/ Giới thiệu thuật toán Ơclit:
Để tìm ƯCLN(a, b) ta thực hiện như sau:
- Chia a cho b có số dư là r
+ Nếu r = 0 thì ƯCLN(a, b) = b. Việc tìm ƯCLN dừng lại.
+ Nếu r > 0, ta chia tiếp b cho r, được số dư r1
- Nếu r1 = 0 thì r1 = ƯCLN(a, b). Dừng lại việc tìm ƯCLN
- Nếu r1 > 0 thì ta thực hiện phép chia r cho r1 và lập lại quá trình như trên. ƯCLN(a, b) là số dư khác 0 nhỏ nhất trong dãy phép chia nói trên.
VD: Hãy tìm ƯCLN (1575, 343)
Ta có: 1575 = 343. 4 + 203
343 = 203. 1 + 140
203 = 140. 1 + 63
140 = 63. 2 + 14
63 = 14.4 + 7
14 = 7.2 + 0 (chia hết)
Vậy: Hãy tìm ƯCLN (1575, 343) = 7
Trong thực hành người ta đặt phép chia đó như sau:
1575
343
343
203
4
203
140
1
140
63
1
63
14
2
14
7
4
0
2
Suy ra ƯCLN (1575, 343) = 7
Bài tập1: Tìm ƯCLN(702, 306) bằng cách phân tích ra thừa số nguyên tố và bằng thuật toán Ơclit.
ĐS: 18
Bài tập 2: Dùng thuật toán Ơclit để tìm
a/ ƯCLN(318, 214)
b/ ƯCLN(6756, 2463)
ĐS: a/ 2 b/ 1 (nghĩa là 6756 và 2463 là hai số nguyên tố cùng nhau).
Dạng 2: Tìm ước chung thông qua ước chung lớn nhất
Dạng
Dạng 3: Các bài toán thực tế
Bài 1: Một lớp học có 24 HS nam và 18 HS nữ. Có bao nhiêu cách chia tổ sao cho số nam và số nữ được chia đều vào các tổ?
Hướng dẫn
Số tổ là ước chung của 24 và 18
Tập
hợp các ước của 18 là A =
![]()
Tập
hợp các ước của 24 là B =
![]()
Tập
hợp các ước chung của 18 và 24 là C = A
![]() B =
B =
![]()
Vậy có 3 cách chia tổ là 2 tổ hoặc 3 tổ hoặc 6 tổ.
Bài 2: Một đơn vị bộ đội khi xếp hàng, mỗi hàng có 20 người, hoặc 25 người, hoặc 30 người đều thừa 15 người. Nếu xếp mỗi hàng 41 người thì vừa đủ (không có hàng nào thiếu, không có ai ở ngoài hàng). Hỏi đơn vị có bao nhiêu người, biết rằng số người của đơn vị chưa đến 1000?
Hướng dẫn
Gọi
số người của đơn vị bộ đội là x (x![]() N)
N)
x
: 20 dư 15
![]() x – 15
x – 15
![]() 20
20
x
: 25 dư 15
![]() x – 15
x – 15
![]() 25
25
x
: 30 dư 15
![]() x – 15
x – 15
![]() 30
30
Suy ra x – 15 là BC(20, 25, 35)
Ta có 20 = 22. 5; 25 = 52 ; 30 = 2. 3. 5; BCNN(20, 25, 30) = 22. 52. 3 = 300
BC(20,
25, 35) = 300k (k![]() N)
N)
x
– 15 = 300k
![]() x
= 300k + 15 mà x < 1000 nên
x
= 300k + 15 mà x < 1000 nên
300k
+ 15 < 1000
![]() 300k
< 985
300k
< 985
![]() k
<
k
<
![]() (k
(k![]() N)
N)
Suy ra k = 1; 2; 3
Chỉ
có k = 2 thì x = 300k + 15 = 615
![]() 41
41
Vậy đơn vị bộ đội có 615 người
Ngày dạy:
Buổi 12:
ÔN TẬP – KIỂM TRA 1 TIẾT
A> MỤC TIÊU
- Ôn tập các kiến thức đã học về cộng , trừ, nhân, chia và nâng lên luỹ thừa.
- Ôn tập các kiến thức đã học về tính chất chia hết của một tổng, các dấu hiệu chia hết
- Biết tính giá trị của một biểu thức.
- Vận dụng các kiến thức vào các bài toán thực tế
- Rèn kỷ năng tính toán cho HS.
B> NỘI DUNG
I. Các bài tập trắc nghiệm tổng hợp
Câu 1: Cho hai tập hợp: X = {a; b; 1; 2}, Y = {2; 3; 4; 5; 7}. Hãy điền ký hiệu thích hợp vào ô vuông:
a/ a ý X b/ 3 ý X
c/ b ý Y d/ 2 ý Y
Câu 2: Cho tập hợp A các số tự nhiên lớn hơn 2 và nhỏ hơn 10, tập hợp B các số tự nhiên chẵn nhỏ hơn 12. Hãy điền kí hiệu thích hợp vào ô vuông:
a/
12
![]() B b/ 2
B b/ 2
![]() A
A
a/
5
![]() B a/ 9
B a/ 9
![]() A
A
Câu 3: Cho tập hợp A = {2; 3; 4; 5; 6}. Hãy điền chữ Đ(đúng), S (sai) vào các ô vuông bên cạnh các cách viết sau:
a/
A = {2; 4; 6; 3 ; 5} ![]()
b/
A = {![]() }
} ![]()
c/
A = {![]() }
} ![]()
d/
A = {![]() }
} ![]()
Câu 4: Hãy điền vào chỗ trống các số để mỗi dòng tạo nên các số tự nhiên liên tiếp tăng dần:
a/ …, …, 2
b/ …, a, …
c/ 11, …, …, 14
d/ x – 1, … , x + 1
Câu 5: Cho ba chữ số 0, 2, 4. Số các số tự nhiên có ba chữ số khác nhau được viết bởi ba chữ số đó là:
a/ 1 số
b/ 2 số
c/ 4 số
d/ 6 số
Câu 6: Cho tập hợp X = {3; 4; 5; …; 35}. Tập hợp X có mấy phần tử?
a/ 4
b/ 32
c/ 33
d/ 35
Câu 7: Hãy tính rồi điền kết quả vào các phép tính sau:
a/ 23.55 – 45.23 + 230 = …
b/ 71.66 – 41.71 – 71 = …
c/ 11.50 + 50.22 – 100 = …
d/ 54.27 – 27.50 + 50 =
Câu 8: Diền dấu X thích hợp để hoàn thành bảng sau:
STT
Câu
Đúng
Sai
1
33.
37
= 321
2
33.
37
= 310
3
72.
77
= 79
4
72.
77
= 714
Câu 9: Diền dấu X thích hợp để hoàn thành bảng sau:
STT
Câu
Đúng
Sai
1
310:
35
= 32
2
49:
4
= 48
3
78:
78
= 1
4
53:
50
= 53
Câu 10: Hãy điền các dấu thích hợp vào ô vuông:
a/
32
![]() 2 + 4
2 + 4
b/
52
![]() 3 + 4 + 5
3 + 4 + 5
c/
63
![]() 93 –
32.
93 –
32.
d/
13 +
23 =
33
![]() (1 + 2 + 3 + 4)2
(1 + 2 + 3 + 4)2
Câu 11: Điên chữ đúng (Đ), sai (S) cạnh các khẳng định sau:
a/
(35 + 53 )![]() 5
5 ![]()
b/
28 – 77
![]() 7
7 ![]()
c/
(23 + 13)
![]() 6
6 ![]()
d/
99 – 25
![]() 5
5 ![]()
Câu 12: Điên chữ đúng (Đ), sai (S) cạnh vào các ô vuông cạnh các câu sau:
a/
Tổng của hai số tự nhiên liên tiếp chia hết cho 2 ![]()
b/
Tổng của ba số tự nhiên liên tiếp chia hết cho 3 ![]()
c/
Tích của hai số tự nhiên liên tiếp chia hết cho 2 ![]()
d/
Tích của ba số tự nhiên liên tiếp chia hết cho 3 ![]()
Câu 13: Hãy điền các số thích hợp để được câu đúng
a/ Số lớn nhất có 3 chữ số khác nhau chia hết cho 2 lập được từ các số 1, 2, 5 là …
b/ Số lớn nhất có 3 chữ số khác nhau chia hết cho 5 lập được từ các số 1, 2, 5 là …
c/ Số nhỏ nhất có 3 chữ số khác nhau chia hết cho 2 lập được từ các số 1, 2, 5 là …
d/ Số nhỏ nhất có 3 chữ số khác nhau chia hết cho 5 lập được từ các số 1, 2, 5 là …
Câu 14: Hãy điền số thích hợp vào dấu * để được câu đúng
a/
![]() chia hết cho 3
chia hết cho 3
b/
![]() chia hết cho 9
chia hết cho 9
c/
![]() chia hết cho 3 mà không chia hết cho 9
chia hết cho 3 mà không chia hết cho 9
d/
![]() vừa chia hết cho 3 vừa chia hết cho 5
vừa chia hết cho 3 vừa chia hết cho 5
Câu 15: Hãy điền các số thích hợp để được câu đúng
a/ Từ 1 đến 100 có … số chia hết cho 3.
b/ Từ 1 đến 100 có … số chia hết cho 9
c/ Từ 1 đến 100 có … số chia hết cho cả 2 và 5
d/ Từ 1 đến 100 có … số chia hết cho cả 2, 3, 5 và 9
Câu 16: Chọn câu đúng
a/ Ư(24) = {0; 1; 2; 3; 4; 6; 12}
b/ Ư(24) = {1; 2; 3; 4; 6;8; 12; 24}
c/ Ư(24) = {0; 1; 2; 3; 4; 6; 12; 24}
d/ Ư(24) = {0; 1; 2; 3; 4; 6; 12; 24; 48}
Câu 16: Điền đúng (Đ), sai (S) vào các ô thích hợp để hoàn thành bảng sau:
STT
Câu
Đúng
Sai
1
Có
hai số tự nhiên liên tiếp là số nguyên tố
2
Mọi
số nguyên tố đều là số lẻ
3
Có
ba số lẻ liên tiếp là số nguyên tố
4
Mọi
số nguyên tố đều có chữ số tận cùng là một
trong các chữ số 1, 3, 5, 7, 9
Câu 17:
Hãy nối các số ở cột A với các thừa số nguyên tố ở B được kết quả đúng:
Cột
A
Cột
B
225
22.
32.
52
900
24.
7
112
32.
52
63
32.7
Câu 18: Hãy tìm ước chung lớn nhất và điền vào dấu …
a/ ƯCLN(24, 29) = …
b/ƯCLN(125, 75) = …
c/ƯCLN(13, 47) = …
d/ƯCLN(6, 24, 25) = …
Câu 19: Hãy tìm bội chung lớn nhất và điền vào dấu …
a/ BCNN(1, 29) = …
b/BCNN(1, 29) = …
c/BCNN(1, 29) = …
d/BCNN(1, 29) = …
Câu 20: Học sinh khối 6 của trường khi xếp hàng 2, hàng 3, hàng 4, hàng 5, hàng 6 đều thừa ra một em nhưng khi xếp hàng 7 thì vừa đủ. Biết rằng số HS khối 6 ít hơn 350. Số HS của kkhối 6 là:
a/ 61 em.
b/ 120 em
c/ 301 em
d/ 361 em
II. Bài toán tự luận
Bài 1 Chứng tỏ rằng:
a/ 85 + 211 chia hết cho 17
b/ 692 – 69. 5 chia hết cho 32.
c/ 87 – 218 chia hết cho 14
Hướng dẫn
a/
85 +
211 =
215 +
211 =
211(22
+ 1) = 2 11.
17
![]() 17.
Vậy 85
+ 211
chia hết cho 17
17.
Vậy 85
+ 211
chia hết cho 17
b/
692 –
69. 5 = 69.(69 – 5) = 69. 64
![]() 32
(vì 64
32
(vì 64![]() 32).
Vậy 692
– 69. 5 chia hết cho 32.
32).
Vậy 692
– 69. 5 chia hết cho 32.
c/
87 –
218 =
221 –
218 =
218(23
– 1) = 218.7
= 217.14
![]() 14.
14.
Vậy 87 – 218 chia hết cho 14
Bài 2: Tính giá trị của biểu thức:
A = (11 + 159). 37 + (185 – 31) : 14
B = 136. 25 + 75. 136 – 62. 102
C= 23. 53 - {72. 23 – 52. [43:8 + 112 : 121 – 2(37 – 5.7)]}
Hướng dẫn
A = 170. 37 + 154 : 14 = 6290 + 11 = 6301
B = 136(25 + 75) – 36. 100 = 136. 100 – 36. 100 = 100.(136 – 36) = 100. 100 = 10000
C= 733.
Bài 3: Số HS của một trường THCS là số tự nhiên nhỏ nhất có 4 chữ số mà khi chia số đó cho 5 hoặc cho 6, hoặc cho 7 đều dư 1.
Hướng dẫn
Gọi
số HS của trường là x (x![]() N)
N)
x
: 5 dư 1
![]() x – 1
x – 1
![]() 5
5
x
: 6 dư 1
![]() x – 1
x – 1
![]() 6
6
x
: 7 dư 1
![]() x – 1
x – 1
![]() 7
7
Suy ra x – 1 là BC(5, 6, 7)
Ta có BCNN(5, 6, 7) = 210
BC(5,
6, 7) = 210k (k![]() N)
N)
x
– 1 = 210k
![]() x
= 210k + 1 mà x số tự nhiên nhỏ nhất có 4 chữ số nên
x
x
= 210k + 1 mà x số tự nhiên nhỏ nhất có 4 chữ số nên
x
![]() 1000
1000
suy
ra 210k + 1
![]() 1000
1000
![]() k
k
![]()
![]() (k
(k![]() N)
nên k nhỏ nhất là k = 5.
N)
nên k nhỏ nhất là k = 5.
Vậy số HS trường đó là x = 210k + 1 = 210. 5 + 1 = 1051 (học sinh)
Ngày dạy:
Buổi 13:
TẬP HỢP Z CÁC SÔ NGUYÊN – THỨ TỰ TẬP HỢP CÁC SỐ NGUYÊN
A> MỤC TIÊU
- Củng cố khái niệm Z, N, thứ tự trong Z.
- Rèn luyện về bài tập so sánh hai só nguyên, cách tìm giá trị tuyệt đối, các bài toán tìm x.
B> NỘI DUNG
I. Câu hỏi ôn tập lý thuyết
Câu 1: Lấy VD thực tế trong đó có số nguyên âm, giải thích ý nghĩa của số nguyên âm đó.
Câu 2: Tập hợp Z các số nguyên bao gồm những số nào?
Câu 3: Cho biết trên trục số hai số đối nhau có đặc điểm gì?
Câu 4: Nói tập hợp Z bao gồm hai bộ phận là số tự nhiên và số nguyên âm đúng không?
Câu 5: Nhắc lại cách so sánh hai số nguyên a và b trên trục số?
II. Bài tập
Bài 1: Cho tập hợp M = { 0; -10; -8; 4; 2}
a/ Viết tập hợp N gồm các phần tử là số đối của các phần tử thuộc tập M.
b/ Viết tập hợp P gồm các phần tử của M và N
Hướng dẫn
a/ N = {0; 10; 8; -4; -2}
b/ P = {0; -10; -8; -4; -2; 10; 8; 4; 2}
Bài 2: Trong các câu sau câu nào đúng? câu nào sai?
a/ Mọi số tự nhiên đều là số nguyên.
b/ Mọi số nguyên đều là số tự nhiên.
c/ Có những số nguyên đồng thời là số tự nhiên.
d/ Có những số nguyên không là số tự nhiên.
e/ Số đối của 0 là 0, số đối của a là (–a).
g/ Khi biểu diễn các số (-5) và (-3) trên trục số thì điểm (-3) ở bên trái điểm (-5).
h/ Có những số không là số tự nhiên cũng không là số nguyên.
ĐS: Các câu sai: b/ g/
Bài 3: Trong các câu sau câu nào đúng? câu nào sai?
a/ Bất kỳ số nguyên dương nào xũng lớn hơn số nguyên ân.
b/ Bất kỳ số tự nhiên nào cũng lớn hơn số nguyên âm.
c/ Bất kỳ số nguyên dương nào cũng lớn hơn số tự nhiên.
d/ Bất kỳ số tự nhiên nào cũng lớn hơn số nguyên dương.
e/ Bất kỳ số nguyên âm nào cũng nhỏ hơn 0.
ĐS: Các câu sai: d/
Bài 4: a/ Sắp xếp các số nguyên sau theo thứ tự tăng dần
2, 0, -1, -5, -17, 8
b/ Sắp xếp các số nguyên sau theo thứ tự giảm dần
-103, -2004, 15, 9, -5, 2004
Hướng dẫn
a/ -17. -5, -1, 0, 2, 8
b/ 2004, 15, 9, -5, -103, -2004
Bài 5: Trong các cách viết sau, cách viết nào đúng?
a/ -3 < 0
b/ 5 > -5
c/ -12 > -11
d/ |9| = 9
e/ |-2004| < 2004
f/ |-16| < |-15|
ĐS: Các câu sai: c/ e/ f/
Bài 6: Tìm x biết:
a/ |x – 5| = 3
b/ |1 – x| = 7
c/ |2x + 5| = 1
Hướng dẫn
a/ |x – 5| = 3 nên x – 5 = ± 3
x – 5 = 3
 x = 8
x = 8x – 5 = -3
 x
= 2
x
= 2
b/ |1 – x| = 7 nên 1 – x = ± 7
1 – x = 7
 x = -6
x = -61 – x = -7
 x
= 8
x
= 8
c/ x = -2, x = 3
Bài 7: So sánh
a/ |-2|300 và |-4|150
b/ |-2|300 và |-3|200
Hướng dẫn
a/ Ta có |-2|300 = 2300
| -4 |150 = 4150 = 2300 Vậy |-2|300 = |-4|150
b/ |-2|300 = 2300 = (23)100 = 8100
-3|200
= 3200
= (32)100
= 9100
Vì
8 < 9 nên 8100
< 9100
suy ra |-2|300
< |-3|200
Ngày dạy:
Buổi 14:
CỘNG, TRỪ HAI SỐ NGUYÊN
TÍNH CHẤT CỦA PHÉP CỘNG CÁC SỐ NGUYÊN
A> MỤC TIÊU
- ÔN tập HS về phép cộng hai số nguyên cùng dấu, khác dấu và tính chất của phép cộng các số nguyên
- HS rèn luyện kỹ năng trừ hai số nguyên: biến trừ thành cộng, thực hiện phép cộng.
- Rèn luyện kỹ năng tính toán hợp lý, biết cách chuyển vế, quy tắc bỏ dấu ngoặc.
B> NỘI DUNG
I. Câu hỏi ôn tập lí thuyết:
Câu 1: Muốn cộng hai số nguyên dương ta thực hiện thế nằo? Muốn cộng hai số nguyên âm ta thực hiện thế nào? Cho VD?
Câu 2: Nếu kết quả tổng của hai số đối nhau? Cho VD?
Câu 3: Muốn cộng hai số nguyên khác dấu không đối nhau ta làm thế nào?
Câu 4: Phát biểu quy tắc phép trừ số nguyên. Viết công thức.
II. Bài tập
Dạng 1:
Bài 1: Trong các câu sau câu nào đúng, câu nào sai? Hãy chưũa câu sai thành câu đúng.
a/ Tổng hai số nguyên dương là một số nguyên dương.
b/ Tổng hai số nguyên âm là một số nguyên âm.
c/ Tổng của một số nguyên âm và một số nguyên dương là một số nguyên dương.
d/ Tổng của một số nguyên dương và một số nguyên âm là một số nguyên âm.
e/ Tổng của hai số đối nhau bằng 0.
Hướng dẫn
a/ b/ e/ đúng
c/ sai, VD (-5) + 2 = -3 là số âm.
Sửa câu c/ như sau:
Tổng của một số nguyên âm và một số nguyên dương là một số nguyên dương khi và chỉ khi giá trị tuyệt đối của số dương lớn hơn giá trị tuyệt đối của số âm.
d/ sai, sửa lại như sau:
Tổng của một số dương và một số âm là một số âm khi và chỉ khi giá trị tuyệt đối của số âm lớn hơn giá trị tuyệt đối của số dương.
Bài 2: Điền số thích hợp vào ô trống
(-15) + ý = -15; (-25) + 5 = ý
(-37) + ý = 15; ý + 25 = 0
Hướng dẫn
(-15)
+
![]() = -15; (-25) + 5 =
= -15; (-25) + 5 =
![]()
(-37)
+
![]() = 15;
= 15; ![]() + 25 = 0
+ 25 = 0
Bài 3: Tính nhanh:
a/ 234 - 117 + (-100) + (-234)
b/ -927 + 1421 + 930 + (-1421)
ĐS: a/ 17 b/ 3
Bài 4: Tính:
a/ 11 - 12 + 13 – 14 + 15 – 16 + 17 – 18 + 19 – 20
b/ 101 – 102 – (-103) – 104 – (-105) – 106 – (-107) – 108 – (-109) – 110
Hướng dẫn
a/ 11 - 12 + 13 – 14 + 15 – 16 + 17 – 18 + 19 – 20
= [11 + (-12)] + [13 + (-14)] + [15 + (-16)] + [17 + (-18)] + [19 + (-20)]
= (-1) + (-1) + (-1) + (-1) + (-1) = -5
b/ 101 – 102 – (-103) – 104 – (-105) – 106 – (-107) – 108 – (-109) – 110
= 101 – 102 + 103 – 104 + 105 – 106 + 107 – 108 + 109 – 110
= (-1) + (-1) + (-1) + (-1) + (-1) = -5
Bài 5: Thực hiện phép trừ
a/ (a – 1) – (a – 3)
b/
(2 + b) – (b + 1) Với a, b
![]()
Hướng dẫn
a/ (a – 1) – (a – 3) = (a – 1) + (3 - a) = [a + (-a)] + [(-1) + 3] = 2
b/ Thực hiện tương tự ta được kết quả bằng 1.
Bài 6: a/ Tính tổng các số nguyên âm lớn nhất có 1 chữ số, có 2 chữ số và có 3 chữ số.
b/ Tính tổng các số nguyên âm nhỏ nhất có 1 chữ số, có 2 chữ số và có 3 chữ số.
c/ Tính tổng các số nguyên âm có hai chữ số.
Hướng dẫn
a/ (-1) + (-10) + (-100) = -111
b/ (-9) + (-99) = (-999) = -1107
Bài 7: Tính tổng:
a/ (-125) +100 + 80 + 125 + 20
b/ 27 + 55 + (-17) + (-55)
c/ (-92) +(-251) + (-8) +251
d/ (-31) + (-95) + 131 + (-5)
Bài 8: Tính các tổng đại số sau:
a/ S1 = 2 -4 + 6 – 8 + … + 1998 - 2000
b/ S2 = 2 – 4 – 6 + 8 + 10- 12 – 14 + 16 + … + 1994 – 1996 – 1998 + 2000
Hướng dẫn
a/ S1 = 2 + (-4 + 6) + ( – 8 + 10) + … + (-1996 + 1998) – 2000
= (2 + 2 + … + 2) – 2000 = -1000
Cách 2:
S1 = ( 2 + 4 + 6 + … + 1998) – (4 + 8 + … + 2000)
= (1998 + 2).50 : 2 – (2000 + 4).500 : 2 = -1000
b/ S2 = (2 – 4 – 6 + 8) + (10- 12 – 14 + 16) + … + (1994 – 1996 – 1998 + 2000)
= 0 + 0 + … + 0 = 0
Dạng 2: BT áp dụng quy tắc bỏ dấu ngoặc, chuyển vế
Bài 1: Rút gọn biểu thức
a/ x + (-30) – [95 + (-40) + (-30)]
b/ a + (273 – 120) – (270 – 120)
c/ b – (294 +130) + (94 + 130)
Hướng dẫn
a/ x + (-30) – 95 – (-40) – 5 – (-30)
= x + (-30) – 95 + 40 – 5 + 30
= x + (-30) + (-30) + (- 100) + 70 = x + (- 60).
b/ a + 273 + (- 120) – 270 – (-120)
= a + 273 + (-270) + (-120) + 120 = a + 3
c/ b – 294 – 130 + 94 +130
= b – 200 = b + (-200)
Bài 2: 1/ Đơn giản biểu thức sau khi bỏ ngoặc:
a/ -a – (b – a – c)
b/ - (a – c) – (a – b + c)
c/ b – ( b+a – c)
d/ - (a – b + c) – (a + b + c)
Hướng dẫn
1. a/ - a – b + a + c = c – b
b/ - a + c –a + b – c = b – 2a.
c/ b – b – a + c = c – a
d/ -a + b – c – a – b – c = - 2a -2c.
Bài 3: So sánh P với Q biết:
P = a {(a – 3) – [( a + 3) – (- a – 2)]}.
Q = [ a + (a + 3)] – [( a + 2) – (a – 2)].
Hướng dẫn
P = a – {(a – 3) – [(a + 3) – (- a – 2)]
= a – {a – 3 – [a + 3 + a + 2]} = a – {a – 3 – a – 3 – a – 2}
= a – {- a – 8} = a + a + 8 = 2a + 8.
Q = [a+ (a + 3)] – [a + 2 – (a – 2)]
= [a + a + 3] – [a + 2 – a + 2] = 2a + 3 – 4 = 2a – 1
Xét hiệu P – Q = (2a + 8) – (2a – 1) = 2a + 8 – 2a + 1 = 9 > 0
Vậy P > Q
Bài 4: Chứng minh rằng a – (b – c) = (a – b) + c = (a + c) – b
Hướng dẫn
Áp dụng quy tắc bỏ dấu ngoặc
Bài 5: Chứng minh:
a/ (a – b) + (c – d) = (a + c) – (b + d)
b/ (a – b) – (c – d) = (a + d) – (b +c)
Áp dung tính
1. (325 – 47) + (175 -53)
2. (756 – 217) – (183 -44)
Hướng dẫn:
Áp dụng quy tắc bỏ dấu ngoặc.
Dạng 3: Tìm x
Bài 1: Tìm x biết:
a/ -x + 8 = -17
b/ 35 – x = 37
c/ -19 – x = -20
d/ x – 45 = -17
Hướng dẫn
a/ x = 25
b/ x = -2
c/ x = 1
d/ x = 28
Bài 2: Tìm x biết
a/ |x + 3| = 15
b/ |x – 7| + 13 = 25
c/ |x – 3| - 16 = -4
d/ 26 - |x + 9| = -13
Hướng dẫn
a/ |x + 3| = 15 nên x + 3 = ±15
x + 3 = 15
 x = 12
x = 12x + 3 = - 15
 x
= -18
x
= -18
b/ |x – 7| + 13 = 25 nên x – 7 = ±12
x = 19
x = -5
c/ |x – 3| - 16 = -4
|x – 3| = -4 + 16
|x – 3| = 12
x – 3 = ±12
x - 3 = 12
 x = 15
x = 15x - 3 = -12
 x
= -9
x
= -9
d/ Tương tự ta tìm được x = 30 ; x = -48
Bài
3. Cho a,b
![]() Z. Tìm x
Z. Tìm x
![]() Z sao cho:
Z sao cho:
a/ x – a = 2 b/ x + b = 4
c/ a – x = 21 d/ 14 – x = b + 9.
Hướng dẫn
a/ x = 2 + a
b/ x = 4 – b
c/ x = a – 21
d/ x = 14 – (b + 9)
x = 14 – b – 9
x = 5 – b.
Ngày dạy:
Buổi 15:
VẼ ĐOẠN THẲNG CHO BIẾT ĐỘ DÀI – TRUNG ĐIỂM CỦA ĐOẠN THẲNG
A)Kiến thức cơ bản:
1. Trên tia Ox bao giờ cũng vẽ được một và chỉ
một điểm M sao cho OM = a ( đơn vị dài ) (H.13)
2. Trên tia Ox, OM = a, ON = b nếu 0 < a < b thì điểm M nằm giữa hai điểm O và N.(H.14)
Nâng cao:
Trên tia Ox có ba điểm M, N, P: OM = a; ON = b; OP = c nếu a < b < c thì điểm N nằm giữa hai điểm M và P. (h.15)
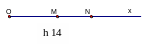
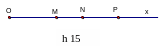
Thí dụ 7:
Trên tia Ox lấy hai điểm A và B sao cho OA= 7 cm; OB = 5 cm. Tính độ dài đoạn thẳng AB.
Giải: (h.7.1)
T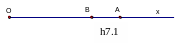 rên
tia Ox vì OB < OA
rên
tia Ox vì OB < OA
nên điểm B nằm giữa hai điểm O và A
OB+ BA =OA
AB= OA – OB
AB= 7- 5
AB= 2
AB= 2 cm.
Thí dụ 8:
Trên tia Ox lấy điểm P và Q sao cho OP = 3 cm; PQ = 2 cm. Tính OQ.
G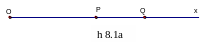 iải:(h.8.1a,b)
iải:(h.8.1a,b)
Ta xét hai trường hợp:
a) Trường hợp Q nằm trên tia đối của
tia PO. Lúc đó P nằm giữa hai điểm O và Q,
s uy
raOQ = OP + PQ = 3 + 2 = 5 (cm)
uy
raOQ = OP + PQ = 3 + 2 = 5 (cm)
b) Trường hợp Q nằm trên tia PO (h.24b)
vì PQ < PO (2<3) nên Q nằm giữa P vàO
do đó PQ + QO = OP. Suy ra:
OQ = OP – PQ = 3 – 2 = 1 (cm).
Nhận xét:
Trên tia Ox lấy P sao cho OP = 3 cm, điểm P là điểm duy nhất, còn điểm Q thì không duy nhất. Tại sao như vậy?
Điểm Q không duy nhất trên tia Ox vì điểm Q không cách gốc O của tia Ox một khoảng 2 cm; điểm P chỉ là một điểm thuộc tia Ox chứ P không phải là gốc của tia Ox.
Thí dụ 9:
Gọi M, N, P là ba điểm trên tia Ox; OM = a, ON = b; OP = c; Giải thích vì sao nếu a<b<c thì điểm N nằm giữa hai điểm M và P.
Giải: (h.9.1)

Hai điểm M và N thuộc tia Ox mà OM< ON
(a<b) nên điểm M nằm giữa hai điểm O và
N suy ra hai tia NM, NO trùng nhau (1)
Hai điểm N và P thuộc tia Ox mà ON < OP (b<c) nên điểm N nằm giữa hai điểm O và P, suy ra hai tia NO và NP đối nhau. (2)
Từ (1) và (2) suy ra hai tia NM, NP đối nhau, do đó điểm N nằm giữa hai điểm M và P.
Bài tập.
Bài 26.
Trên tia Ox vẽ đoạn thẳng OM= 3 Cm
Cho điểm A. Vẽ đoạn thẳng AB= 2,5 Cm
Vẽ đoạn thẳn CD = 3,5 Cm.
Bài 27 Gọi M, N, P là ba điểm trên tia Ox sao cho OM = 2cm, ON=3cm, OP = 5 cm. So sánh MN và NP.
Bài 28. Gọi A và B là hai điểm trên tia Ox sao cho OA = 4 cm, OB = 6cm. Trên tia BA lấy điểm C sao cho BC = 3 cm. So sánh AB với AC.
Bài 29. Trên tia Ox:
Đặt OA= 2 Cm
Trên tia Ax đặt AB= 4 Cm
Trên tia BA đặt BC= 3 Cm
Hỏi trong ba điểm A,B,C thì điểm nào nằm giữa hai điểm còn lại.
Bài 30. Cho A và B là hai điểm trên Ox sao cho OA = a (cm) với a>0; AB = 2 cm. Tính OB.
Bài 31.
Vẽ đoạn thẳng AB = 5 cm. Lấy hai điểm E và F nằm giữa Avà B sao cho AE + BF = 7 cm.
a) Chứng tỏ rằng điểm E nằm giữa hai điểm B và F.
b) Tính EF.
Bài 32. Trên tia Ox vẽ các điểm A, B sao cho OA= 7 Cm, AB= 3,5 Cm. Tính OB?
Bài 33. Vẽ tia Ox.
Vẽ )A= 1 Cm; OB = 2 Cm. Hỏi trong ba điểm O,A,B thì điểm nào nằm giữa hai điểm còn lại?
Vẽ OC = 3 Cm. Hỏi trong ba điểm A,B,C thì điểm nào nằm giữa hai điểm còn lại?
Vẽ OD = 4 Cm. Quan sát thứ tự các điểm A,B,C,D trên tia Ox.
Trung điểm của đoạn thẳng.
Kiến thức cơ bản:
1. Trung điểm của một đoạn thẳng là điểm nằm giữa hai đầu đoạn thẳng và cách đều hai đầu đoạn thẳng đó. (h.16)
2 .
Nếu M là trung điểm của một đoạn thẳng AB
.
Nếu M là trung điểm của một đoạn thẳng AB
thì
MA = MB =
![]()
Nâng cao:
1.
Nếu M nằm giữa hai đầu đoạn thẳng AB và AM =
![]() thì M là trung điểm của AB.
thì M là trung điểm của AB.
2. Mỗi đoạn thẳng có một trung điểm duy nhất.
Thí dụ 10:
Cho đoạn thẳng AB = a. Điểm O nằm giữa Avà B, gọi M và N thứ tự là trung điểm của OA và OB. Tính MN.
Giải: (h.10.1)
M là trung điểm của OA nên M nằm giữa
là trung điểm của OA nên M nằm giữa
A
và O; OM =
![]()
N Là trung điểm của OB nên N nằm giữa O
và
B: ON =
![]() .
.
Vì có O nằm giữa A và B (đề bài) nên O nằm giữa M và N ( xem thí dụ 5 ).
Vậy
MN = OM + ON =
![]() +
+![]() =
=![]() hay MN =
hay MN =
![]()
Nhận xét:
Độ
dài MN là một số không đổi , nó không phụ thuộc vào
vị trí của điểm O trên đoạn thẳng AB. Ta luôn có MN =
![]()
Thí dụ 11:
Cho
điểm M nằm giữa hai đầu đoạn thẳng AB và AM =
![]() .
Giải thích vì sao M là trung điểm của AB.
.
Giải thích vì sao M là trung điểm của AB.
Giải: (h.11.1)
Đ iểm
M nằm giữa A và B (1)
iểm
M nằm giữa A và B (1)
nên AM + MB = AB
MB = AB – AM
MB
= AB -
![]() =
=![]()
Do đó: AM = MB.
Từ (1) và (2) suy ra M là trung điểm của AB.
Bài tập.
Bài 34:
Cho ba điểm M, N, O sao cho OM = 2cm; ON = 2cm và MN = 4cm. Vì sao có thể khẳng định O là trung điểm của đoạn thẳng MN.
Bài 35:
Trên tia Ox lấy hai điểm A và M sao cho OA = 3 cm, OM = 4,5 cm. Trên tia Ax lấy điểm B sao cho M là trung điểm của AB. Hỏi điểm A có phải là trung điểm của đoạn thẳng OB không? Vì sao?
Bài 36;
Trên đường thẳng a lấy 6 điểm M, N, O, P, Q, R theo thứ tự đó. Biết MN = NO = OP = PQ = QR. Tìm những điểm là trung điểm của đoạn thẳng.
Bài 37.
Cho đoạn thẳng AB = 6 cm. Lấy hai điểm C, D thuộc đoạn thẳng AB sao cho AC = BD = 2cm. Gọi M là trung điểm của AB.
Giải thích tại sao M cũng là trung điểm của CD.
Tìm trên hình vẽ những điểm khác cũng là trung điểm của đoạn thẳng.
Bài 38:
Trên tia Ax lấy điểm O và B sao cho AO = 2cm; AB = 5 cm. Gọi I là trung điểm của OB. Tính AI.
Bài 39:
Trên đường thẳng xy lấy điểm O và hai điểm M, N sao cho OM = 2 cm; ON = 3 cm; Vẽ các điểm A và B trên đường thẳng xy sao cho M là trung điểm của OA; N là trung điểm của OB. Tính độ dài AB.
Bài 40:
Cho đoạn thẳng CD= 5 cm. Trên đoạn thẳng này lấy hai điểm I và k sao cho CI= 1 cm; DK= 3 cm.
Điểm K có là trung điểm của đoạn thẳng CD không?
Chứng tỏ rằng I là trung điểm của đoận thẳng CK.
Ngày dạy:
Buổi 16:
ÔN VỀ QUY TẮC DẤU NGOẶC – QUY TẮC CHUYỂN VẾ
A. TÓM TẮT LÍ THUYẾT.
1. Tính chất của đẳng thức :
Nếu a = b thì a + c = b + c ;
Nếu a + c = b + c thì a = b ;
Nếu a = b thì b = a
2. Quy tắc chuyển vế:
Khi chuyển một số hạng từ vế này sang vế kia của một đẳng thức, ta phải đổi dấu số hạng
đó : dấu “+” đổi thành dấu và dấu đổi thành dấu
3. Quy tắc dấu ngoặc
- Nếu biểu thức có các dấu ngoặc : ngoặc tròn ( ), ngoặc vuông [ ], ngoặc nhọn { }, ta thực hiện phép tính theo thứ tự : { } [ ] ( )
B. CÁC DẠNG TOÁN.
Bài toán 1 : Thực hiện phép tính.
a) 5 . 22 – 18 : 32
b) 23 . 17 – 23 . 14
c) 17 . 85 + 15 . 17 – 120
d) 20 – [ 30 – (5 – 1)2 ]
e) 75 – ( 3.52 – 4.23 )
f) 2.52 + 3: 710 – 54: 33
g) 150 + 50 : 5 - 2.32
h) 5.32 – 32 : 42
Bài toán 2 : Thực hiện phép tính.
a) 27 . 75 + 25 . 27 – 150 b) 12 : { 400 : [500 – (125 + 25 . 7)]}
c) 13 . 17 – 256 : 16 + 14 : 7 – 1 d) 18 : 3 + 182 + 3.(51 : 17)
e) 15 – 25 . 8 : (100 . 2) f) 25 . 8 – 12.5 + 170 : 17 - 8
Bài toán 3 : Thực hiện phép tính.
a) 23 – 53 : 52 + 12.22 d) (62007 – 62006) : 62006
b) 5[(85 – 35 : 7) : 8 + 90] – 50 e) (52001 - 52000) : 52000
c) 2.[(7 – 33 : 32 ) : 22 + 99] – 100 f) (72005 + 72004) : 72004
Bài toán 4 : Tìm số tự nhiên x, biết.
a) 70 – 5.(x – 3) = 45 b) 12 + (5 + x) = 20 h) 14x + 54 = 82 c) 130 – (100 + x) = 25 k) 15x – 133 = 17
d) 175 + (30 – x) = 200 l) 155 – 10(x + 1) = 55
e) 5(x + 12) + 22 = 92 m) 6(x + 23 ) + 40 = 100
f) 95 – 5(x + 2) = 45 g) 10 + 2x = 45 : 43
n) 22 .(x + 32 ) – 5 = 55
Bài toán 5 : Tìm x, biết.
a) 5.22 + (x + 3) = 52 f) 5x – 52 = 10
b) 23 + (x – 32 ) = 53 – 43 g) 9x – 2.32 = 34
c) 4(x – 5) – 23 = 24 .3 h) 10x + 22 .5 = 102
d) 5(x + 7) – 10 = 23 .5 k) 125 – 5(4 + x) = 15
e) 72 – 7(13 – x) = 14 l) 26 + (5 + x) = 34
Bài toán 6 : Tìm x, biết.
a) 15 : (x + 2) = 3
b) 20 : (1 + x) = 2 f) 12x - 33 = 32 . 33
c) 240 : (x – 5) = 22 .52 – 20
d) 96 - 3(x + 1) = 42 h) 1230 : 3(x - 20) = 10
e) 5(x + 35) = 515
g) 541 + (218 - x) = 73
Bài toán 7 : Thực hiện phép tính.
a) 27 . 75 + 25 . 27 - 150; b) 142 - [50 - (23 .10 - 23 .5)]
c) 375 : {32 – [ 4 + (5. 32 – 42)]} – 14
d) {210 : [16 + 3.(6 + 3. 22 )]} – 3
e) 500 – {5[409 – (2³.3 – 21)²] - 1724}
Bài toán 8 : Thực hiện phép tính.
a) 80 - (4.52 - 3.23 ) b) 56 : 54 + 23 .22 – 12017
c) 125 - 2.[56 - 48 : (15 - 7)] d) 23.75 + 25.10 + 25.13 + 180
e) 2448: [119 -(23 -6)] f) [36.4 - 4.(82 - 7.11)2 : 4 – 20160
g) 303 - 3.{[655 - (18 : 2 + 1).43 + 5]} : 100
Bài toán 9 : Tìm x, biết.
a) 48 - 3(x + 5) = 24 e) 4x + 18 : 2 = 13
b) 2x+1 - 2x = 32 g) 2x - 20 = 35 : 33
c) (15 + x) : 3 = 315 : 312 h) 525.5x-1 = 525
d) 250 - 10(24 - 3x) : 15 = 244 k) x - 48 : 16 = 37
Bài toán 10 : Tìm x, biết.
a) [(8x - 12) : 4] . 33 = 36 g) 52x – 3 – 2 . 52 = 52 . 3
b) 41 - 2x+1 = 9 h) 52x – 3 – 2 . 52 = 52 . 3
c) 32x-4 - x 0 = 8 k) 30 - [4(x - 2) + 15] = 3
d) 65 - 4x+2 = 20140 l) 740:(x + 10) = 102 – 2.13
e) 120 + 2.(3x - 17) = 214 m) [(6x - 39) : 7].4 = 12
Ngày dạy:
Buổi 17:
KIỂM TRA VÀ LUYỆN VỀ CÁC QUY TẮC
I. Trắc nghiệm (5 đ)
Câu 1: Điền chữ Đ (đúng), chữ S (sai) vào ô vuông vạnh các cách viết sau:
a/
5
![]() N
N ![]()
b/
-5
![]() N
N ![]()
c/
0
![]() N
N ![]()
d/
-3
![]() Z
Z ![]()
Câu 2: Hãy điền số thích hợp vào chỗ thiếu (…) để được các câu đúng
a/ Số đối của – 1 là số:…
b/ Số đối của 3 là số…
c/ Số đối của -25 là số…
d/ Số đối của 0 là số…
Câu 3: Điền dấu (>, <, =) thích hợp vào ô vuông
a/
5
![]() -3
-3
b/
-5
![]() -3
-3
c/
|-2004|
![]() |2003|
|2003|
d/
|-10|
![]() |0|
|0|
Câu 4: Sắp xếp các số nguyên sau theo thứ tự tăng dần:
a/ 12; -12; 34; -45; -2
b/ 102; -111; 7; -50; 0
c/ -21; -23; 77; -77; 23
d/ -2003; 19; 5; -45; 2004
Câu 5: Điền số thích hợp vào ô trống để hoàn thành bảng sao
x
y
x
+ y
|x
+ y|
a/
27
-28
b/
-33
89
c/
123
-22
d
/
-321
222
Câu 6: Viết tiếp 3 số của mỗi dãy số sau:
a/ 3, 2, 1, …, …, …
b/ …, …, …., -19, -16, -13
c/ -2, 0, 2, …, …, …
d/ …, …, …, 1, 5, 9
C
Cột
A
Cột
B
(-12)-(-15)
-3
-28
11
+ (-39)
27
-30
43-54
4
+ (-15)
3
Câu 8: Giá trị của biểu thức A = 23. 3 + 23.7 – 52 là:
a/ 25
b/ 35
c/ 45
d/ 55
II. Bài tập tự luận: (5 đ)
Bài 1: Tính (1 đ)
a/ (187 -23) – (20 – 180)
b/ (-50 +19 +143) – (-79 + 25 + 48)
Bài 2: Tính tổng: (1, 5đ)
a/ S1 = 1 + (-2) + 3 + (-4) + … + 2001 + ( -2002)
b/ S2 = 1 + (-3) + 5 + (-7) + … + (-1999) + 2001
c/ S 3 = 1 + (-2) + (-3) + 4 + 5 + (-6) + (-7) + 8 + … + 1997 + (-1008) + (-1999) + 2000
Bài 3: Bỏ dấu ngoặc rồi thu gọn biểu thức: (1 đ)
a/ A = (a + b) – (a – b) + (a – c) – (a + c)
b/ B = (a + b – c) + (a – b + c) – (b + c – a) – (a – b – c)
Bài 4: 1/ Tìm x biết: (1, 5 đ)
a/ 5 – (10 – x) = 7
b/ - 32 - (x – 5) = 0
c/ - 12 + (x – 9) = 0
d/ 11 + (15 – x) = 1
HƯỚNG DẪN CHẤM
I.
Trắc nghiệm: 5 điểm
- Mỗi ý đúng trong câu 1, 2, 3, 4, 6, 7, 8 đạt 0.15 điểm.
- Các câu 1, 2, 3, 4, 6, 7, 8 mỗi câu đúng đủ 4 ý đạt 0,6 đ.Câu 5 đúng tất cả 8 ý đạt 0,8 đ
Câu 1: Điền chữ Đ (đúng), chữ S (sai) vào ô vuông vạnh các cách viết sau:
a/
5
![]() N
N ![]() Đ
Đ
b/
-5
![]() N
N ![]() S
S
c/
0
![]() N
N ![]() S
S
d/
-3
![]() Z
Z ![]() Đ
Đ
Câu 2: Hãy điền số thích hợp vào chỗ thiếu (…) để được các câu đúng
a/ Số đối của – 1 là số:…1
b/ Số đối của 3 là số…-3
c/ Số đối của -25 là số…-25
d/ Số đối của 0 là số…0
Câu 3: Điền dấu (>, <, =) thích hợp vào ô vuông
a/
5
![]() -3
-3
b/
-5
![]() -3
-3
c/
|-2004|
![]() |2003|
|2003|
d/
|-10|
![]() |0|
|0|
Câu 4: Sắp xếp các số nguyên sau theo thứ tự tăng dần:
a/ -45; -12; -2; 12; 34
b/ -111; -50; 0; 7; 102
c/ -77; -23; -21; 23; 77
d/ -2003; -45; 5; 19; 2004
Câu 5: Điền số thích hợp vào ô trống để hoàn thành bảng sao
x
y
x
+ y
|x
+ y|
a/
27
-28
-1
1
b/
-33
89
56
56
c/
123
-22
121
121
d
/
-321
222
99
99
Câu 6: Viết tiếp 3 số của mỗi dãy số sau:
a/ 3, 2, 1, 0, -1, -2
b/ -28, -25, -22, -19, -16, -13
c/ -2, 0, 2, 4, 6, 8
d/ -11, -7, -3, 1, 5, 9
Câu 7: Nối cột A và B để được kết quả đúng
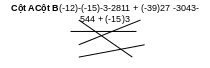
Câu 8: Giá trị của biểu thức A = 23. 3 + 23.7 – 52 là:
a/ 25
b/ 35
c/ 45
d/ 55
II. Bài tập tự luận ( 5 đ)
Bài 1: (1 đ)
a/ 324 b/ 118
Mỗi câu đúng 0, 5 đ.
Bài 2: (1, 5 đ)
a/ S1 = [1 + (-2)] + [3 + (-4)] + … + [2001 + ( -2002)] = (-1) + (-1) + …+ (-1) = -1001
b/ S2 = [1 + (-3)] + [5 + (-7]) + … + [1997 + (-1999)] + 2001 = (-1000) + 2001 =1001
Mỗi câu đúng 0.75 đ.
Nết nhóm các số hạng đúng: 0.25 đ, nếu tính được tổng mỗi cặp đúng 0.25 đ, kết quả đúng 0.25 đ.
Bài 3: (1 đ)
Hướng dẫn
a/ A = a + b – a + b + a – c – a – c = 2b
-2c
b/ B = a + b – c + a – b + c – b – c + a – a + b + c
= a + a + a – a + b – b – b + b –c + c –c +c = 2a
Bỏ dấu ngoặc đúng 0.5 đ.
Rút gọn đúng 0.5 đ
Bài 4: (1, 5 đ)
1.
a/ 5 – (10 – x) = 7
![]() 5
– 10 + x = 7
5
– 10 + x = 7
![]() -
5 + x = 7
-
5 + x = 7
![]() x
= 7 + 5 = 12.
x
= 7 + 5 = 12.
Thử lại 5 – (10 – 12) = 5 – 10 + 12 = 7
Vậy x = 12 đúng là nghiệm.
b/
- 32 – (x -5) = 0
![]() -
32 – x + 5 = 0
-
32 – x + 5 = 0
![]() -
27 – x = 0
-
27 – x = 0
![]() x = - 27
x = - 27
c/ x = 21
d/ x = 25
Mỗi câu đúng 0.75 đ.
Mỗi câu chuyển vế đúng 0.5 đ.
Kết quả 0.25 đ.
Ngày dạy:
Buổi 18:
BỘI VÀ ƯỚC CỦA MỘT SỐ NGUYÊN
A> MỤC TIÊU
- Ôn tập lại khái niệm về bội và ước của một số nguyên và tính chất của nó.
- Biết tìm bội và ước của một số nguyên.
- Thực hiện một số bài tập tổng hợp.
B> NỘI DUNG
I. Câu hỏi ôn tập lí thuyết:
Câu 1: Nhắc lại khái niệm bội và ước của một số nguyên.
Câu 2: Nêu tính chất bội và ước của một số nguyên.
Câu 3: Em có nhận xét gì xề bội và ước của các số 0, 1, -1?
II. Bài tập
Dạng 1:
Bài 1: Tìm tất cả các ước của 5, 9, 8, -13, 1, -8
Hướng dẫn
Ư(5) = -5, -1, 1, 5
Ư(9) = -9, -3, -1, 1, 3, 9
Ư(8) = -8, -4, -2, -1, 1, 2, 4, 8
Ư(13) = -13, -1, 1, 13
Ư(1) = -1, 1
Ư(-8) = -8, -4, -2, -1, 1, 2, 4, 8
262. Viết biểu thức xác định:
a/ Các bội của 5, 7, 11
b/ Tất cả các số chẵn
c/ Tất cả các số lẻ
Hướng dẫn
a/
Bội của 5 là 5k, k![]() Z
Z
Bội
của 7 là 7m, m![]() Z
Z
Bội
của 11 là 11n, n![]() Z
Z
b/
2k, k![]() Z
Z
c/
2k
![]() 1, k
1, k![]() Z
Z
Bài 2: Tìm các số nguyên a biết:
a/ a + 2 là ước của 7
b/ 2a là ước của -10.
c/ 2a + 1 là ước của 12
Hướng dẫn
a/ Các ước của 7 là 1, 7, -1, -7 do đó:
a + 2 = 1
 a
= -1
a
= -1a + 2 = 7
 a
= 5
a
= 5a + 2 = -1
 a
= -3
a
= -3a + 2 = -7
 a
= -9
a
= -9
b/
Các ước của 10 là
![]() 1,
1,
![]() 2,
2,
![]() 5,
5,
![]() 10,
mà 2a là số chẵn do đó: 2a =
10,
mà 2a là số chẵn do đó: 2a =
![]() 2,
2a =
2,
2a =
![]() 10
10
2a = 2
 a
= 1
a
= 12a = -2
 a
= -1
a
= -12a = 10
 a
= 5
a
= 52a = -10
 a
= -5
a
= -5
c/
Các ước của 12 là
![]() 1,
1,
![]() 2,
2,
![]() 3,
3,![]() 6,
6,
![]() 12,
mà 2a + 1 là số lẻ do đó: 2a +1 =
12,
mà 2a + 1 là số lẻ do đó: 2a +1 =
![]() 1,
2a + 1 =
1,
2a + 1 =
![]() 3
3
Suy ra a = 0, -1, 1, -2
Bài
3: Chứng minh rằng nếu a
![]() Z thì:
Z thì:
a/ M = a(a + 2) – a(a – 5) – 7 là bội của 7.
b/ N = (a – 2)(a + 3) – (a – 3)(a + 2) là số chẵn.
Hướng dẫn
a/ M= a(a + 2) – a(a - 5) – 7
= a2 + 2a – a2 + 5a – 7
= 7a – 7 = 7 (a – 1) là bội của 7.
b/ N= (a – 2) (a + 3) – (a – 3) (a + 2)
= (a2 + 3a – 2a – 6) – (a2 + 2a – 3a – 6)
= a2
+ a – 6 – a2
+ a + 6 = 2a là số chẵn với a![]() Z.
Z.
Bài 4: Cho các số nguyên a = 12 và b = -18
a/ Tìm các ước của a, các ước của b.
b/ Tìm các số nguyên vừa là ước của a vừa là ước của b/
Hướng dẫn
a/ Trước hết ta tìm các ước số của a là số tự nhiên
Ta có: 12 = 22. 3
Các ước tự nhiên của 12 là:
Ư(12) = {1, 2, 22, 3, 2.3, 22. 3} = {1, 2, 4, 3, 6, 12}
Từ
đó tìm được các ước của 12 là:
![]() 1,
1,
![]() 2,
2,
![]() 3,
3,
![]() 6,
6,
![]() 12
12
Tương tự ta tìm các ước của -18.
Ta có |-18| = 18 = 2. 33
Các ước tự nhiên của |-18| là 1, 2, 3, 9, 6, 18
Từ
đó tìm được các ước của 18 là:
![]() 1,
1,
![]() 2,
2,
![]() 3,
3,
![]() 6,
6,
![]() 9
9
![]() 18
18
b/
Các ước số chung của 12 và 18 là:
![]() 1,
1,
![]() 2,
2,
![]() 3,
3,
![]() 6
6
Ghi chú: Số c vừa là ước của a, vừa là ước của b gọi là ước chung của a và b.
Dạng 2: Bài tập ôn tập chung
Bài 1: Trong những câu sau câu nào đúng, câu nào sai:
a/ Tổng hai số nguyên âm là 1 số nguyên âm.
b/ Hiệu hai số nguyên âm là một số nguyên âm.
c/ Tích hai số nguyên là 1 số nguyên dương
d/ Tích của hai số nguyên âm là 1 số nguyên dương.
Hướng dẫn
a/ Đúng
b/ Sai, chẳng hạn (-4) – (-7) = (-4) + 7 = 3
c/ Sai, chẳng hạn (-4).3 = -12
d/ Đúng
Bài 2: Tính các tổng sau:
a/ [25 + (-15)] + (-29);
b/ 512 – (-88) – 400 – 125;
c/ -(310) + (-210) – 907 + 107;
d/ 2004 – 1975 –2000 + 2005
Hướng dẫn a/ -19
b/ 75
c/ -700
d/ 34
274. Tìm tổng các số nguyên x biết:
a/
![]()
b/
![]()
Hướng dẫn
a/
![]()
Từ đó ta tính được tổng này có giá trị bằng 0
b/ Tổng các số nguyên x bằng
![]()
Bài 3. Tính giá strị của biểu thức
A = -1500 - {53. 23 – 11.[72 – 5.23 + 8(112 – 121)]}. (-2)
Hướng dẫn
A = 302
Ngày dạy:
Buổi 19:
GÓC – SỐ ĐO GÓC – CỘNG SỐ ĐO GÓC
A) Mục tiêu
- HS được
củng cố kiến thức thế nào là nửa mặt phẳng bờ a,
góc, số đo góc, khi nào thì
![]()
![]() +
+
![]() =
=
![]() ?
?
- HS vẽ được góc khi biết số đo, so sánh được hai góc, biết được thế nào là góc vuông, góc nhọn, góc tù, góc bẹt.
- HS biết được thế nào là hai góc phụ nhau, hai góc bù nhau và hai góc kề bù. Từ đó tính được số đo của 1 góc khi biết số đo của 1 góc khác.
B) Nội dung
Bài 1: Trên cùng một nửa mặt phẳng bờ chứa tia OA ta vẽ ba tia OB, OC, OD sao cho AÔB = 40 độ ;
AÔC = 90 độ ; AÔD = 120 độ .
a) Xét ba tia OA, OB, OC, tia nào nằm giữa hai tia còn lại ? Tính số đo của góc BOC.
b) Xét ba tia OA,OC , OD, tia nào nằm giữa hai tia còn lại ? Tính số đo của góc COD.
Bài 2: Cho hai tia đối nhau Ox, Oy. Trên cùng một nửa mặt phẳng bờ là đường thẳng xy ta vẽ hai tia Om và
On sao cho xÔm = 45 độ , yÔn = 75 độ . Hãy so sánh góc mOn với góc xÔm và yÔn.
Bài 3: Cho tia Ox. Vẽ hai tia Oy, Oz sao cho xÔy = 40 độ ; xÔz – 70 độ. Tính số đo của góc yOz.
Bài 4: Cho tia Ox. Vẽ hai tia Oy và Oz sao cho xÔy = 110 độ ; xÔz = 150 độ. Tính số đo của góc yOz.
Bài 5: Cho góc xOy có số đo 130 độ. Ở trong đó ta vẽ hai tia Om, On sao cho xÔm + yÔn = 100 độ.
a) Trong ba tia Ox, Om, On, tia nào nằm giữa hai tia còn lại ?
B) Tính mÔn.
ĐÁP SỐ:
Bài 1
Hình 10.
a) Tia OB nằm giữa hai tia OA và OC ( vì AÔB < AOC ) do đó AÔB +BÔC = AÔC, từ đó được BÔC = 500
b) Tia OC nằm giữa hai tia OA và OD ( vì AÔC < AÔD ) do đó AÔC + CÔD = AÔD , từ đó được CÔD = 300
Bài 2
Hình 11.
Trước hết hãy tính góc yOm để suy ra tia ON nằm giữa hai tia Oy , Om sau đó dùng tính chất cộng góc để tính được mÔn = 600. Suy ra xÔm < mÔn yÔn.
Bài 3
Ta phải xét hai trường hợp:
– Trường hợp hai tia Oy và Oz cùng thuộc một nửa mặt phẳng bờ chứa tia Ox ,
lúc đó yÔz = 700 – 400 – 300 .
– Trường hợp hai tia Oy, Oz thuộc hai nửa mặt phẳng đối nhau bờ chứa tia Ox, lúc đó yÔz = 400 + 700 = 1100.
Bài 4
Hướng dẫn :
– Trường hợp hai tia Oy, Oz cùng thuộc một nửa mặt phẳng bờ chứa tia Ox, lúc đó yÔz = 1500 – 1100=400.
– Trường hợp hai tia Oy, Oz thuộc hai nửa mặt phẳng đối nhau bờ chứa tia Ox (Hình 12’).
Lúc đó tia Ox’ là tia đối của tia Ox nằm giữa hai tia Oy, Oz do đó yOz = yÔx’ + x’Ôz = 700+300 =1000.

Bài 5
(Hình 13’)
Tia On nằm trong góc xOy nên :
xÔn + yÔn = xÔy = 130 0 (1)
Mặt khác xÔm + yÔm = 100 0 (2)
Từ (1) và (2) suy ra xÔm < xÔn ; do đó tia Om nằm giữa hai tia Ox và On.
Ta có : xÔm + mÔn + yÔn = xÔn + yÔn = xÔy = 130 0 .
Mà xÔm + yÔn = 100 0 nên mÔn = 130 0 -100 0 = 30 0.
Bài 6.
Cho góc xÔy = 130 độ. Vẽ tia Ot nằm giữa hai tia Ox, Oy. Tính số đo các góc xOt và yOt nếu biết :
a) xÔt = yÔt ;
b) xÔt – yÔt = 30 độ ;
c) xÔt = 2/3 yÔt .
Bài 7.
Cho góc vuông xOz. Vẽ tia Oy nằm giữa hai tia Ox, Oz ; vẽ tia ot nằm giữa hai tia Oy, Oz. Chứng tỏ rằng trong ba góc xOy, yOt, tOz có ít nhất một góc có số đo lớn hơn hoặc bằng 30 độ.
Bài 8.
Cho góc O nhọn. Hãy so sánh hai góc A và B biết góc A phụ với góc O; góc B bù với góc O.
Bài 9.
Trên đường thẳng xy lấy một điểm o. Vẽ hai tia Om và On thuộc hai nửa mặt phẳng đối nhau bờ là đường thẳng xy. Cho biết mÔy < nÔy , hãy so sánh hai góc mÔx và nÔx .
Bài 10.
Trong hình 34 biết AÔC = 90°. Hãy cho biết :
a) Những cặp góc bằng nhau ;
b) Những cặp góc phụ nhau ;
c) Những cặp góc bù nhau.
Bài 11.
Tia Om có nằm giữa hai tia Ox và Oy không nếu xÔy = 50 độ và xÔm = 70 độ.
Bài 12.
Cho hai góc kề AOM và AON. Biết AÔM = 70 độ ; AÔN = 50 độ.
a) Trong ba tia OA, OM, ON tia nào nằm giữa hai tia còn lại ?
b) Tính MÔN.
Bài 13.
Cho góc xÔy, tia Om nằm giữa hai tia Ox và Oy. Hãy chứng tỏ rằng :
a) Các góc mÔx, mÔy là các góc nhọn.
b) Tia Ox không nằm giữa hai tia Om và Oy.
ĐÁP SỐ:
Bài 6.
a) Đáp số : 65 °.
b) Đây là bài toán tìm hai số biết tổng và hiệu.
Đáp số : 80 ° và 50 ° .
c) Đây là bài toán tìm hai số biết tổng và tỉ số.
Đáp số : 52 ° và 78 °.
Bài 7.
(Hình 6’)
Ta có xÔy + yÔt + yÔz = xÔz = 90 ° (1)
Giả sử cả ba góc xOy, yOt, tOz, mỗi góc đều nhỏ hon 30 ° thì xÔy + yÔt + tÔz < 90 °
mâu thuẫn với (1) do đó phải có ít nhất một góc có số đo lớn hơn hoặc bằng 30 °
Bài 8.
Góc A phụ với góc O nên  + Ô = 90 ° (1)
Góc B bù với góc O nên góc B + góc O = 180 ° (2)
Từ ( 1) và (2) suy ra A < B.
Bài 9.
(Hình 7’)
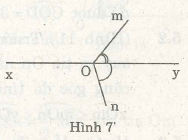
mÔy + mÔx = 180° (1)
nÔy + nÔx = 180° (2)
mà mÔy < nÔy (đề bài)
nên từ (1) và (2) suy ra mÔx > nÔx.
Bài 10.
(Hình 34 SGK)
a) AÔC = BÔC = 90 °;
b) BÔD và CÔD phụ nhau ;
c) AÔC và BÔC bù nhau; AÔD và BÔD bù nhau.
Bài 11.
Nếu tia Om nằm giữa hai tia Ox và Oy thì xÔm + mÔy = xÔy.
Thay số : 70 ° + mÔy = 50 ° .
Điều này vô lí, suy ra tia Om không nằm giữa hai tia Ox và Oy.
Bài 12.
(Hình 8’)
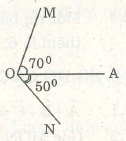
a) Hai góc AOM và AON là hai góc kề mà
AÔM + AÔN = 70 ° + 50 ° = 120 ° < 180 ° nên tia OA nằm giữa hai tia OM và ON.
b) MÔN = AÔM + AÔN = 120 ° .
Bài 13. Hình (9’)
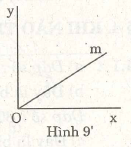
a) Tia Om nằm giữa hai tia Ox và Oy nên xÔm + mÔy = xÔy = 90 ° .
Suy ra xÔm < 90 ° , yÔm < 90 °. Do đó các góc xOm, yOm nhọn.
b) Giả sử tia Ox nằm giữa hai tia Om và Oy
ta có mÔx + xÔy = mÔy hay mÔx + 90 ° = mÔy
ta có mÔx + xÔy = mOy hay mÔx + 90 ° = mÔy
không nằm giữa hai tia Om, Oy.
Ngày dạy:
Buổi 20:
ÔN TẬP
A) Mục tiêu:
- Học sinh ôn tập kiến thức đó học
- Rèn kỹ năng làm bài kiểm tra
B) Nội dung
I. Ôn tập
Bài 1: Viết tập hợp A các số tự nhiên không vượt quá 5 theo 2 cách?
Bài 2: Thực hiện phộp tớnh:
3.52 + 15.22 – 26:2
53.2 – 100 : 4 + 23.5
47 – [(45.24 – 52.12):14]
50 – [(20 – 23) : 2 + 34]
102 – [60 : (56 : 54 – 3.5)]
Bài 3: Tìm x, biết:
71 – (33 + x) = 26
(x + 73) – 26 = 76
11(x – 9) = 77
5(x – 9) = 350
2x – 49 = 5.32
Bài 4: Cho A = 963 + 2493 + 351 + x với x N. Tìm điều kiện của x để A chia hết cho 9, để A không chia hết cho 9.
Bài 5: Lớp 6A có 18 bạn nam và 24 bạn nữ. Trong một buổi sinh hoạt lớp, bạn lớp trưởng dự kiến chia các bạn thành từng nhóm sao cho số bạn nam trong mỗi nhóm đều bằng nhau và số bạn nữ cũng vậy. Hỏi lớp có thể chia được nhiều nhất bao nhiêu nhóm? Khi đó mỗi nhóm có bao nhiêu bạn nam, bao nhiêu bạn nữ?
II. KiÓm tra: MA TRẬN CỦA ĐỀ KIỂM TRA:
Cấp độ
Chủ đề
|
Nhận biết |
Thông hiểu |
Vận dụng |
Cộng |
|
Cấp độ thấp |
Cấp độ cao |
||||
1. Lũy thừa với số mũ Tự Nhiên, Thứ tự thực hiện các phép tính ( 6 tiết ) |
Nhận biết được biểu thức nhân hai lũy thừa cùng cơ số |
Thông hiểu được thứ tự thực hiện các phép tính trong biểu thức |
|
Vận dụng được các KT về lũy thừa, thứ tự các phép tính để tìm x |
|
Số câu: Số điểm Tỉ lệ % |
1 1 |
1 2 |
|
1 2 |
3 5 50% |
2. Dấu hiệu chia hết cho 2, 3, 5, 9 ( 3 tiết ) |
Nhận biết được các số chia hết cho 3, cho 9 |
|
|
|
|
Số câu Số điểm Tỉ lệ % |
1 1 |
|
|
|
1 1 10% |
3. Ước và bội ( 1 tiết ) |
|
Thông hiểu được cách tìm ước và bội của một số |
|
|
|
Số câu Số điểm Tỉ lệ % |
|
1 1 |
|
|
1 1 10% |
4. Điểm. Đường thẳng ( 5 tiết ) |
|
|
Vận dụng được các KT điểm, đường thẳng, tia để vẽ hình |
|
|
Số câu Số điểm Tỉ lệ % |
|
|
1 3 |
|
1 3 30% |
Tổng số câu Tổng số điểm Tỉ lệ % |
2 2 20 % |
2 3 30 % |
2 5 50 % |
13 10 |
|
ĐỀ KIỂM TRA
1.\ Lý thuyết(2 điểm)
Câu 1( 1điểm).
Viết biểu thức tổng quát của phép nhân hai lũy thừa
cùng cơ số. Áp dụng tính:
![]()
![]()
![]()
Câu 2( 1điểm). Nêu dấu hiệu chia hết cho 3. Áp dụng: trong các tổng sau tổng nào chia hết cho 3: 1236 + 36 ; 122 + 120
2.\ Bài tập(8 điểm)
Tìm số tự nhiên x sao cho:
a/
![]() và
và
![]() b/
b/
![]() và
và
![]()
Bài 2(2 điểm). Tính:
a/ 23.5 – 23.3 b/ 10 – [ 30 – (3+2)2]
Bài 3(2 điểm). Tìm số tự nhiên x, biết:
a/ (x – 11) . 4 = 43 : 2 b/ (3 + x) . 5 = 102 : 4
Bài 4(3 điểm). Lấy ba điểm không thẳng hàng A,B, C. Vẽ hai tia AB và AC, sau đó vẽ tia Ax cắt đoạn thẳng BC tại điểm K nằm giữa hai điểm B và C.
ĐÁP ÁN VÀ THANG ĐIỂM
1.\ Lý thuyết(2 điểm)
Câu 1: (1 đ)
![]() ;
;
![]()
Câu 2: (1 đ) Các số có tổng các chữ số chia hết cho 3 thì số đó chia hết cho 3 và chỉ những số đó mới chia hết cho 3.
* Áp dụng: 1236+50 chia hết cho 3 vì 1236 chia hết cho3 (1+2+3+6=12 chia hết cho 3) và chia hết cho 3(3+6=9 chia hết cho3) ;
122 + 120 chia hết cho 3 vì 122 chia hết cho 3(1+2+2=5 chia hết cho 3) và 120 chia hết cho 3(1+2+0=3)
2.\ Bài tập(8 điểm)
Bài 1(1 điểm).
a)
![]() b)
b)
![]()
Bài 2(2 điểm). Tính
a/ 23.5 – 23.3 = 23(5-3) = 23.2 = 24 = 16
b/ 10 – [ 30 – (3+2)2] = 10 - [ 30 – 25 ] = 10 – 5 = 5
Bài 3(2 điểm). Tìm số tự nhiên x, biết:
-
a. (x – 11) . 4 = 43 : 2
(x – 11) . 4 = 32
x – 11 = 32 : 4
x – 11 = 8
x = 19
0, 25
0, 25
0, 25
0, 25
b. (3 + x) . 5 = 102 : 4
(3 + x) . 5 = 25
3 + x = 25 : 5
3 + x = 5
x = 2
0, 25
0, 25
0, 25
0, 25
Bài 4(3 điểm).
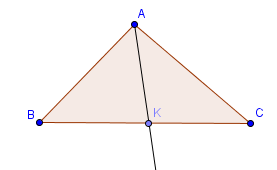
Ngày dạy:
Buổi 21:
Phân số - Phân số bằng nhau- Tính chất cơ bản của phân số
Rút gọn phân số
A. Mục tiờu
- Học ôn tập khái niệm phân số, định nghĩa hai phân số bằng nhau.
- Luyện tập viết phân số theo điều kiện cho trước, tìm hai phân số bằng nhau
- Rèn luyện kỹ năng tính toán.
B.Nội dung
I.Các kiến thức cơ bản cần nhớ:
1.Phõn số
: số cú dạng
![]() trong đó a,b
trong đó a,b
![]() Z , B
Z , B
![]() 0
;
0
;
a được gọi là tử số ,b được gọi là mẫu số
2. Định nghĩa hai phân số bằng nhau.
hai phân số được gọi là bằng nhau nếu a.d = b.c
3.Tính chất cơ bản của phân số:
![]() =
=
![]() (n
(n
![]() 0 ) ;
0 ) ;
![]() =
=
![]() ( m
( m
![]() ƯC(a;b)
ƯC(a;b)
Chú ý:
*Mỗi 1 số nguyên đều được viết dưới dạng 1 phân số có mẫu số bằng 1
* Mỗi 1 phân số thì có vô số bằng nó
*Mọi phân số đều được viết dưới dạng có mẫu số dương
*các phân số bằng nhau là có cùng 1 giá trị ‘giá trị này được gọi là số hữu tỷ
4/ Cách rút gọn phân số :
a)ta chia cả tử và mẫu của phân số đã cho cho cùng 1 số khác 0
Tổng
quát
![]() =
=
![]() ( m ≠ 0 )
( m ≠ 0 )
b). phân số tối giản: là phân số không thể rút gọn được nữa (tử và mẫu chỉ có ƯC là ± 1)
c) Cách rút gọn phân số về dạng tối giản :
- Tìm ƯCLN của tử và mẫu
- Chia tử và mẫu cho UCLN của chúng
5.Quy đồng mẫu số nhiều phân số :
a)Các bước quy đồng
Muốn quy đồng nhiều phân số với mẫu số dương ta làm như sau :
Bước 1 : Tìm một bội chung của các mẫu ( thương là BCNN) để làm mẫu chung.
Bước 2 : Tìm thừa số phụ của mỗi mẫu (bằng cách chia mẫu chung cho từng mẫu).
Bước 3 : Nhân tử và mẫu của mỗi phân số với thừa số phụ tương ứng.
b)Chú ý :
+Cần rút gọn phân số rồi mới quy đồng
+Nếu mẫu số là các số nguyên tố cùng nhau thì MSC bằng tích các mẫu
II.Bài tập áp dụng:
Bµi 1:Trong các số sau số nào không phải là phân số?
A:
![]() ;
B:
;
B:![]() ;
C:
;
C:
![]() ;
D:
;
D:![]() ;
E:
;
E:![]() ;
;
Bài 2: Dùng hai trong ba số sau 2, 3, 5 để viết thành phân số (tử số và mấu số khác nhau)
Có các phân số:
![]()
Bài 3: 1/ Số nguyên a phải có điều kiện gì để ta có phân số?
a/
![]() b/
b/
![]()
2/ Số nguyên a phải có điều kiện gì để các phân số sau là số nguyên:
a/
![]() b/
b/
![]()
3/ Tìm số nguyên x để các phân
số sau là số nguyên:
![]()
giải
1/ a/ a
![]() 1 b/
1 b/
![]()
2/ a/
![]()
![]() Z
Z
![]() a + 1
a + 1
![]() 3
3
![]() a
+ 1 = 3k (k
a
+ 1 = 3k (k
![]() Z). Vậy a = 3k – 1 (k
Z). Vậy a = 3k – 1 (k
![]() Z)
Z)
b/
![]()
![]() Z
Z
![]() a
- 2 = 5k (k
a
- 2 = 5k (k
![]() Z).
Z).
![]() a = 5k +2 (k
a = 5k +2 (k
![]() Z)
Z)
3/
![]()
![]() Z
Z
![]() x
– 1 là ước của 13.
x
– 1 là ước của 13.
Các ước của 13 là 1; -1; 13; -13
S
x - 1
-1
1
-13
13
x
0
2
-12
14
Bài 4: Tìm x biết:
a/
![]() b/
b/
![]() c/
c/
![]() d/
d/
![]() e/
e/
![]() f/
f/
![]()
Hướng dẫn
a/
![]()
![]() b/
b/
![]()
![]()
c/
![]()
![]() d/
d/
![]()
![]()
e/
![]()
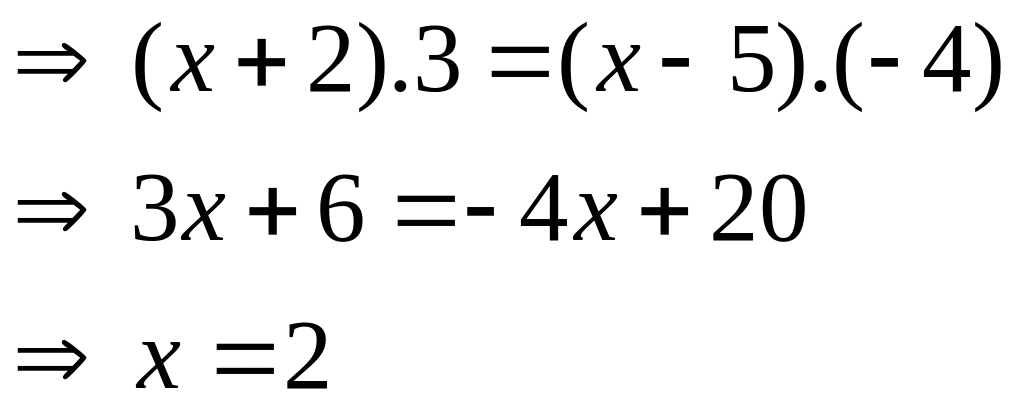
f/
![]()
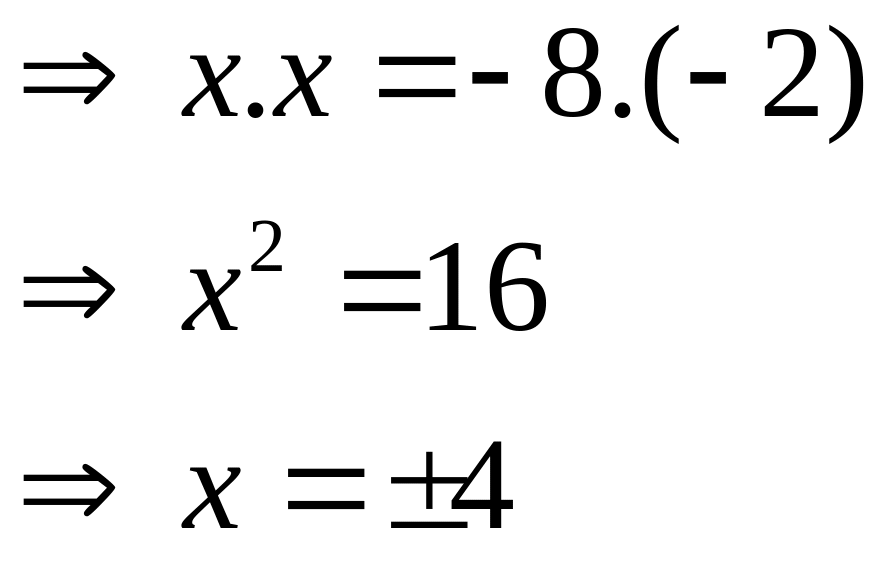
Bài 5:
a/ Chứng minh rằng
![]() thì
thì
![]()
2/ Tìm x và y biết
![]() và x + y = 16
và x + y = 16
giải a/
Ta có
![]()
![]()
![]()
b/ Ta có:
![]()
![]() x
= 10, y = 6
x
= 10, y = 6
Bài 6:
1/ Chứng tỏ rằng các phân số sau đây bằng nhau: Giải
a/
![]() ;
;
![]() và
và
![]()
b/
![]() ;
;
![]() và
và
![]()
2/
Tìm phân số bằng phân số
![]() và biết rằng hiệu của mẫu và tử của nó bằng 6.
và biết rằng hiệu của mẫu và tử của nó bằng 6.
Giải
1/ a/ Ta có:
![]() =
=
![]()
![]() =
=
![]()
b/ Tương tự
2/ Gọi phân số cần tìm có dạng
![]() (x
(x![]() -6),
theo đề bài thì
-6),
theo đề bài thì
![]() =
=![]()
Từ đó suy ra x = 33, phân số cần tìm là
![]()
Bài 7: Điền số thích hợp vào ô vuông
a/
![]() =…………………………..
=…………………………..
b/
![]() =…………………………..
=…………………………..
Giải
a/
![]()
b/
![]()
Bài 8. Giải thích vì sao các phân số sau bằng nhau:
a/
![]() ;
b/
;
b/
![]()
Giải
a/
![]() ;
;
![]() =
=
![]() =
=![]()
b/ HS giải tương tự
Bài 9.
a) Rút gọn các phân số sau:
![]()
Giải
![]()
b)Rút gọn các phân số sau:
a/
![]() b/
b/
![]()
Giải
a/
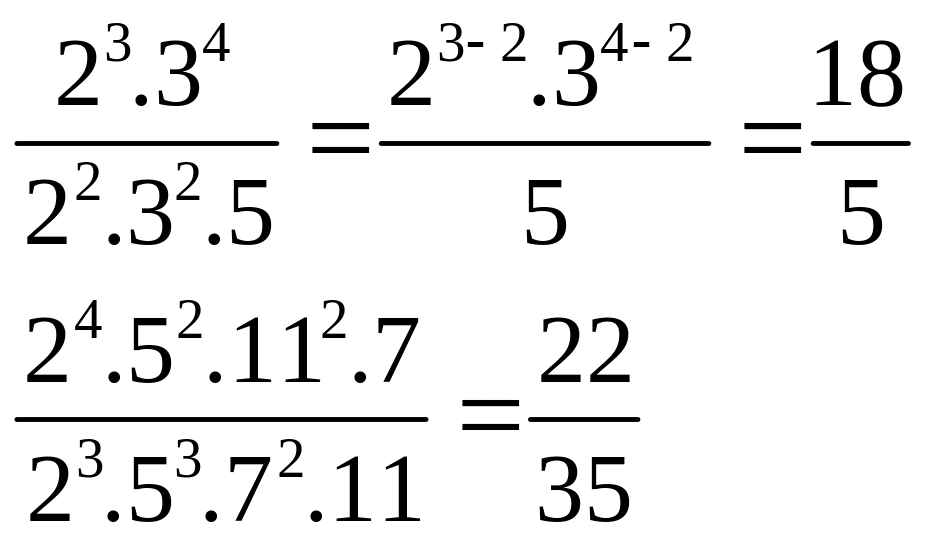
b/
![]()
Bài 10. Rút gọn các phân số sau:
a/
![]() b/
b/
![]()
c/
![]() d/
d/
![]()
Giải
a/
![]()
c/
![]()
Bài 11.
Tổng
của tử và mẫu của phân số bằng 4812. Sau khi rút gọn
phân số đó ta được phân số
![]() .
Hãy tìm phân số chưa rút gọn.
.
Hãy tìm phân số chưa rút gọn.
Giải
Tổng số phần bằng nhau là 12
Tổng của tử và mẫu bằng 4812
Do đó: tử số bằng 4811:12.5 = 2005
Mẫu số bằng 4812:12.7 = 2807.
Vậy phân số cần tìm là
![]()
Bài 12.
Mẫu
số của một phân số lớn hơn tử số 14 đơn vị. Sau
khi rút gọn phân số đó ta được
![]() .
Hãy tìm phân số ban đầu.
.
Hãy tìm phân số ban đầu.
Hiệu số phần của mẫu và tử là 1000 – 993 = 7
Do đó tử số là (14:7).993 = 1986
Mẫu số là (14:7).1000 = 2000
Vạy phân số ban đầu là
![]()
Bài 13:
a/
Với a là số nguyên nào thì phân số
![]() là tối giản.
là tối giản.
b/
Với b là số nguyên nào thì phân số
![]() là tối giản.
là tối giản.
Giải
a/ Ta có
![]() là phân số tối giản khi a là số nguyên khác 2 và 37
là phân số tối giản khi a là số nguyên khác 2 và 37
b/
![]() là phân số tối giản khi b là số nguyên khác 3 và 5
là phân số tối giản khi b là số nguyên khác 3 và 5
Ngày dạy:
Buổi 22:
QUY ĐỒNG MÃU NHIỀU PHÂN SỐ - SO SÁNH PHÂN SỐ
A. Mục tiêu:
- Ôn tập về các bước quy đồng mẫu hai hay nhiều phân số.
- Ôn tập về so sánh hai phân số.
- Rèn luyện HS ý thức làm việc theo quy trình, thực hiện đúng, đầy đủ các bước quy đồng, rèn kỹ năng tính toán, rút gọn và so sánh phân số.
B. Nội dung
*Lý thuyết:
Câu 1: Phát biểu quy tắc quy đồng mẫu hai hay nhiều phân số có mẫu số dương?
Câu
2: Nêu cách so sánh hai phân số cùng mẫu. AD so sánh hai
phân số
![]() và
và
![]()
Câu
3: Nêu cách so sánh hai phân số không cùng mẫu. So sánh:
![]() và
và
![]() ;
;
![]() và
và
![]()
Câu 4: Thế nào là phân số âm, phân số dương? Cho VD.
*Bµi tËp:
Bài 1: a/ Quy đồng mẫu các phân số sau:
![]()
b/ Rút gọn rồi quy đồng mẫu các phân số sau:
![]()
Hướng dẫn
a/ 38 = 2.19; 12 = 22.3
BCNN(2, 3, 38, 12) = 22. 3. 19 = 228
![]()
b/
![]()
BCNN(10, 40, 200) = 23. 52 = 200
![]()
Bài 2: Các phân số sau có bằng nhau hay không?
a/
![]() và
và
![]() ; b/
; b/
![]() và
và
![]()
c/
![]() và
và
![]() d/
d/
![]() và
và
![]()
Hướng dẫn
- Có thể so sánh theo định nghĩa hai phân số bằng nhau hoặc quy đồng cùng mẫu rồi so sánh
- Kết quả:
a/
![]() =
=
![]() ; b/
; b/
![]() =
=
![]()
c/
![]() >
>
![]() d/
d/
![]() >
>
![]()
Bài 3: Rút gọn rồi quy đồng mẫu các phân số:
a/
![]() và
và
![]()
b/
![]() và
và
![]()
Hướng dẫn
![]() =
=
![]() ;
;
![]() =
=
![]()
b/
![]() ;
;
![]()
Bài
4: Tìm tất cả các phân số có
tử số là 15 lớn hơn
![]() và nhỏ hơn
và nhỏ hơn
![]()
Hướng dẫn
Gọi phân số phải tìm là
![]() (a
(a
![]() ),
theo đề bài ta có
),
theo đề bài ta có
![]() .
Quy đồng tử số ta được
.
Quy đồng tử số ta được
![]()
Vậy ta được các phân số cần tìm là
![]() ;
;
![]() ;
;
![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]()
Bài
5: Tìm tất cả các phân số có
mẫu số là 12 lớn hơn
![]() và nhỏ hơn
và nhỏ hơn
![]()
Hướng dẫn
Cách thực hiện tương tự
Ta được các phân số cần tìm là
![]() ;
;
![]() ;
;![]() ;
;![]()
Bài 6: Sắp xếp các phân số sau theo thứ tự
a/ Tăng dần:
![]()
b/ Giảm dần:![]()
Hướng dẫn
a/ ĐS:
![]()
b/
![]()
Bài
8: Cho phân số
![]() là phân số tối giản. Hỏi phân số
là phân số tối giản. Hỏi phân số
![]() có phải là phân số tối giản không?
có phải là phân số tối giản không?
Hướng dẫn:Giả sử a, b là các số tự
nhiên và ƯCLN(a, b) = 1 (vì
![]() tối giản)
tối giản)
nếu d là ước chung tự nhiên a của a + b thì
(a + b)![]() d
và a
d
và a
![]() d
d
Suy ra: [(a + b) – a ] = b
![]() d, tức là d cũng bằng 1.
d, tức là d cũng bằng 1.
kết luận: Nếu phân số
![]() là phân số tối giản thì phân số
là phân số tối giản thì phân số
![]() cũng là phân số tối giản - BTVN:
cũng là phân số tối giản - BTVN:
Bài 1: Quy đồng mẫu các phân số sau:
a/
![]() ,
,
![]() và
và
![]()
b/
![]() ,
,
![]() và
và
![]()
Bài
2: Tìm tất cả các phân số có
mẫu số là 5 lớn hơn
![]()
![]() và nhỏ hơn
và nhỏ hơn
![]()
Bài
3: Tìm tất cả các phân số có
tử số là 10 lớn hơn
![]() và nhỏ hơn
và nhỏ hơn
![]()
Ngày dạy:
Buổi 23:
Céng, trõ Ph©n sè
TÍNH CHẤT CƠ BẢN CỦA PHÉP CỘNG PHÂN SỐ
A. Môc tiªu:
- Ôn tập về phép cộng, trừ hai phân số cùng mẫu, không cùng mẫu.
- Rèn luyện kỹ năng cộng, trừ phân số. Biết áp dụng các tính chất của phép cộng, trừ phân số vào việc giải bài tập.
- Áp dụng vào việc giải các bài tập thực tế
B. Nội dung
*Lý thuyÕt:
Câu 1: Nêu quy tắc cộng hai phân số cùng
mẫu. Tính
![]()
Câu 2: Muốn cộng hai phân số không cùng mẫu ta thực hiện thế nào?
Câu 3 Phép cộng hai phân số có những tính chất cơ bản nào?
Câu 4: Thế nào là hai số đối nhau? Cho VD hai số đối nhau.
Câu 5: Muốn thực hiện phép trừ phân số ta thực hiện thế nào?
*Bµi tËp:
Bài 1: Cộng các phân số sau:
a/
![]() b/
b/
![]()
c/
![]() d/
d/
![]()
Hướng dẫn
ĐS: a/
![]() b/
b/
![]() c/
c/
![]() d/
d/
![]()
Bài 2: Tìm x biết:
a/
![]() b/
b/
![]() c/
c/
![]()
Hướng dẫn
ĐS: a/
![]() b/
b/
![]() c/
c/
![]()
Bài
3: Cho
![]() và
và
![]()
So sánh A và B
Hướng dẫn
![]()
![]()
Hai phân số có từ số bằng nhau, 102005 +1 < 102006 +1 nên 10A > 10 B. Từ đó suy ra A > B
Bài 4: Có 9 quả cam chia cho 12 người. Làm cách nào mà không phải cắt bất kỳ quả nào thành 12 phần bằng nhau?
Hướng dẫn:-
Lấy 6 quả cam cắt mỗi quả thành 2 phần bằng nhau, mỗi
người được ½ quả. Còn lại 3 quả cắt làm 4 phần
bằng nhau, mỗi người được ¼ quả. Như vạy 9 quả cam
chia đều cho 12 người, mỗi người được
![]() (quả).
(quả).
Chú ý 9 quả cam chia đều cho 12 người thì mỗi người được 9/12 = ¾ quả nên ta có cách chia như trên.
Bài 5: Tính nhanh giá trị các biểu thức sau:
![]()
![]()
Hướng dẫn
![]()
![]()
Bài 6: Tính theo cách hợp lí:
a/
![]()
b/
![]()
Hướng dẫn
a/
![]()

b/
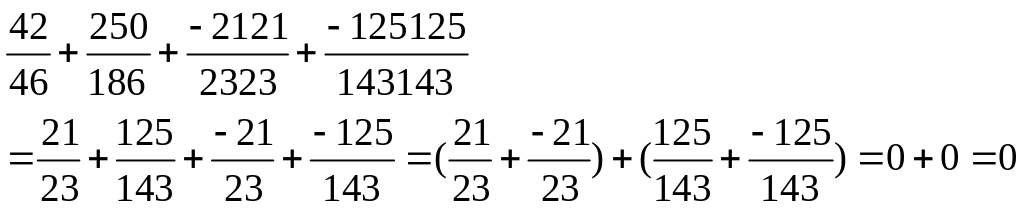
Bài 7: Tính:
a/
![]() b/
b/
![]()
ĐS: a/
![]() b/
b/
![]()
Bài 9: Tìm x, biết:
a/
![]() b/
b/
![]() c/
c/
![]() d/
d/
![]()
ĐS: a/
![]() b/
b/
![]() c/
c/
![]() d/
d/
![]()
Bài 10: Tính tổng các phân số sau:
a/
![]()
b/
![]()
Hướng dẫn
a/ GV hướng dẫn chứng minh công thức sau:
![]()
HD: Quy đồng mẫu VT, rút gọn được VP.
Từ công thức trên ta thấy, cần phân tích bài toán như sau:
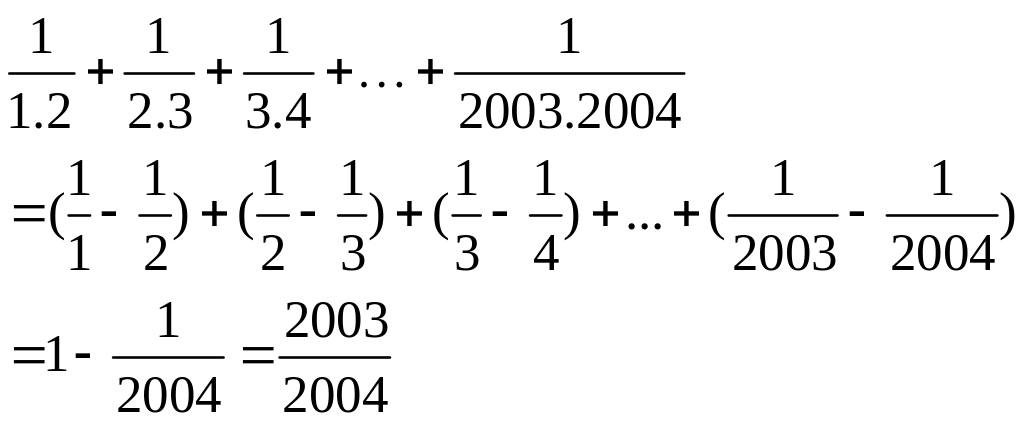
b/ Đặt B =
![]()
Ta có 2B =
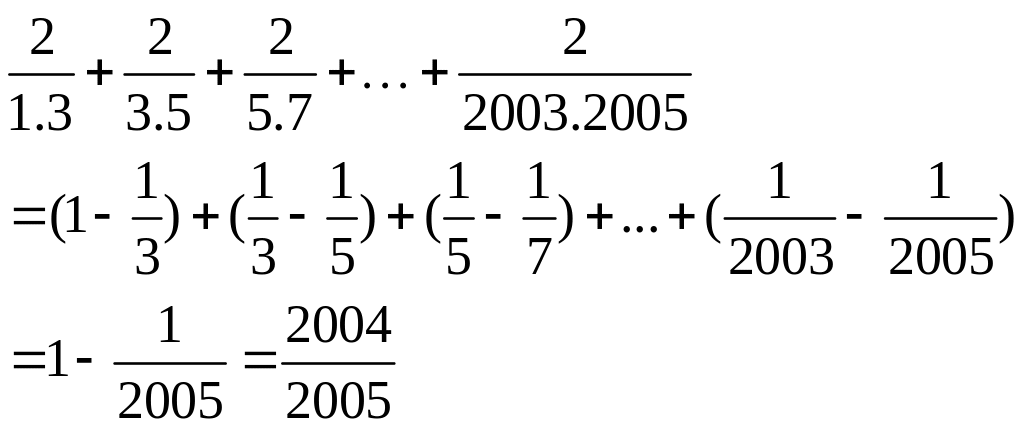
Suy ra B =
![]()
Bài
11: Hai can đựng 13 lít nước.
Nếu bớt ở can thứ nhất 2 lít và thêm vào can thứ hai
![]() lít, thì can thứ nhất nhiều hơn can thứ hai
lít, thì can thứ nhất nhiều hơn can thứ hai
![]() lít.
Hỏi lúc đầu mỗi can đựng được bao nhiêu lít nước?
lít.
Hỏi lúc đầu mỗi can đựng được bao nhiêu lít nước?
Hướng dẫn
- Dùng sơ đồ đoạn thẳng để dể dàng thấy cách làm.
-Ta có: Số nước ở can thứ nhất nhiều
hơn can thứ hai là:
![]()
Số nước ở can thứ hai là (13-7):2 = 3
![]()
Số nước ở can thứ nhất là 3 +7 = 10
![]()
BTVN:
Bài 1:Thực hiện phép tính một cách hợp lí , tính các tổng sau:
A =
![]() +
+![]() +
+![]() +
+![]() +
+![]() +
+
![]() +
+
![]()
B =
![]() +
+![]() +
+![]() +
+![]() +
+![]() +
+
![]() +
+
![]()
C = =
![]() +
+![]() +
+![]() +
+![]() +
+![]() +
+
![]() +
+
![]()
Bài 2. Tìm các số nguyên x biết :
a)
![]() +
+
![]() +
+![]() +
+![]() ≤ x <
≤ x <
![]() +
+
![]() +
+![]() +
+![]() +
+![]() .
.
b)
![]() +
+![]() +
+![]() +
+![]() +
+![]() <
x ≤
<
x ≤
![]() +
+![]() +
+![]() +
+![]() +
+![]()
Bài 3. Cho S =
![]() +
+![]() +
+![]() +….+
+….+![]() +
+![]() .
Hãy so sánh S với
.
Hãy so sánh S với
![]()
Bài 4. Ba vòi nước cùng chảy vào một chiếc bể không chứa nước. Nếu mở riêng từng vòi thì vòi thứ nhất chảy đầy bể trong 3 giờ , vòi thứ hai chảy trong 4 giờ và vòi thứ ba trong 5 giờ.Hỏi: a) Trong 1 giờ, nõi vòi chảy được mấy phần của bể?
b) Trong 1 giờ,cả ba vòi cùng chảy thì được mấy phần của bể?
Ngày dạy:
Buổi 24:
PHÉP NHÂN VÀ PHÉP CHIA PHÂN SỐ
TÍNH CHẤT CƠ BẢN CỦA PHÉP NHÂN PHÂN SỐ
KIỂM TRA
A. Môc tiªu:
- HS biết thực hiện phép nhân và phép chia phân số.
- Nắm được tính chất của phép nhân và phép chia phân số. Áp dụng vào việc giải bài tập cụ thể.
- Ôn tập về số nghịch đảo, rút gọn phân số
- Rèn kỹ năng làm toán nhân, chia phân số.
B. Nội dung
*Lý thuyÕt:
Câu 1: Nêu quy tắc thực hiện phép nhân phân số? Cho VD
Câu 2: Phép nhân phân số có những tính chất cơ bản nào?
Câu 3: Hai số như thế nào gọi là hai số nghịch đảo của nhau? Cho VD.
Câu 4. Muốn chia hai phân số ta thực hiện như thế nào?
*Bµi tËp:
Bài 1: Thực hiện phép nhân sau:
a/
![]() b/
b/
![]()
![]() c/
c/
![]() d/
d/
![]()
Hướng dẫn
ĐS: a/
![]() b/
b/
![]() c/
c/
![]() d/
d/
![]()
Bài 2: Tìm x, biết:
a/ x -
![]() =
=
![]() b/
b/
![]()
c/
![]() d/
d/
![]()
Hướng dẫn
a/ x -
![]() =
=
![]() b/
b/
![]()
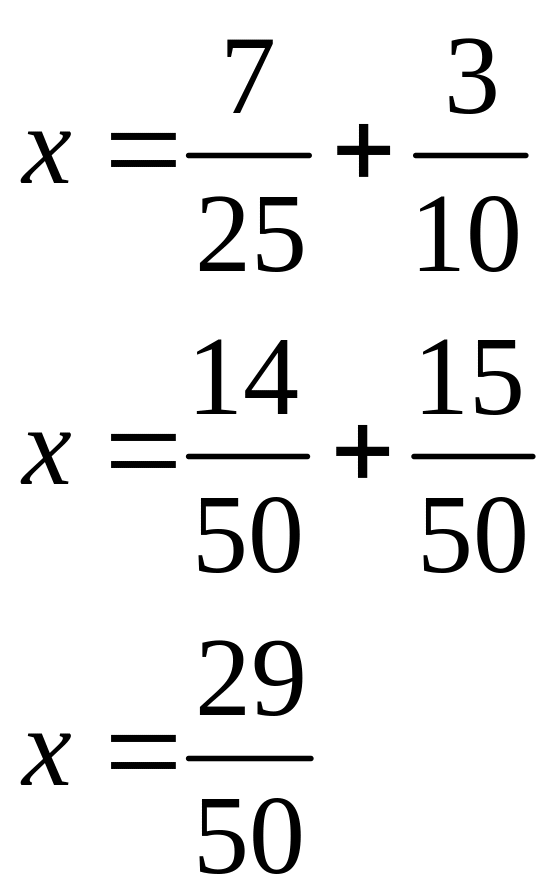
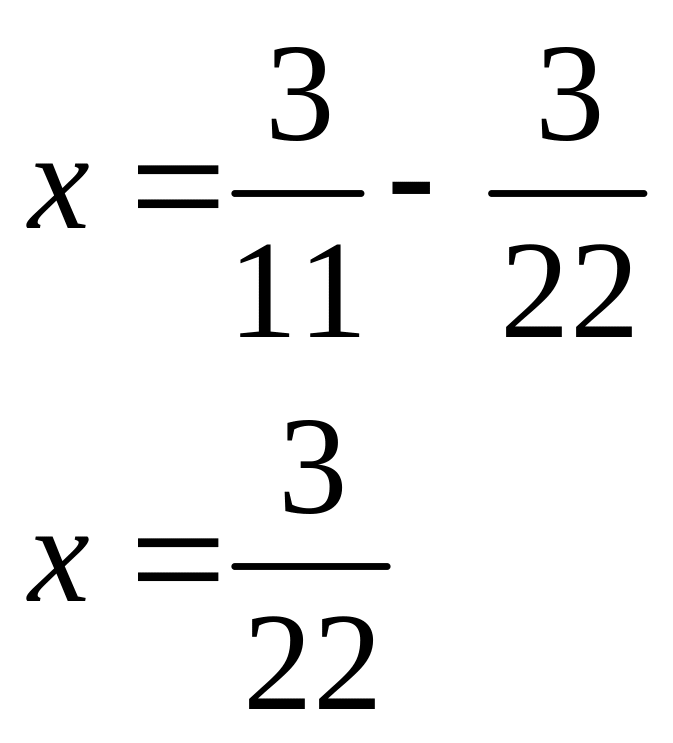
c/
![]() d/
d/
![]()
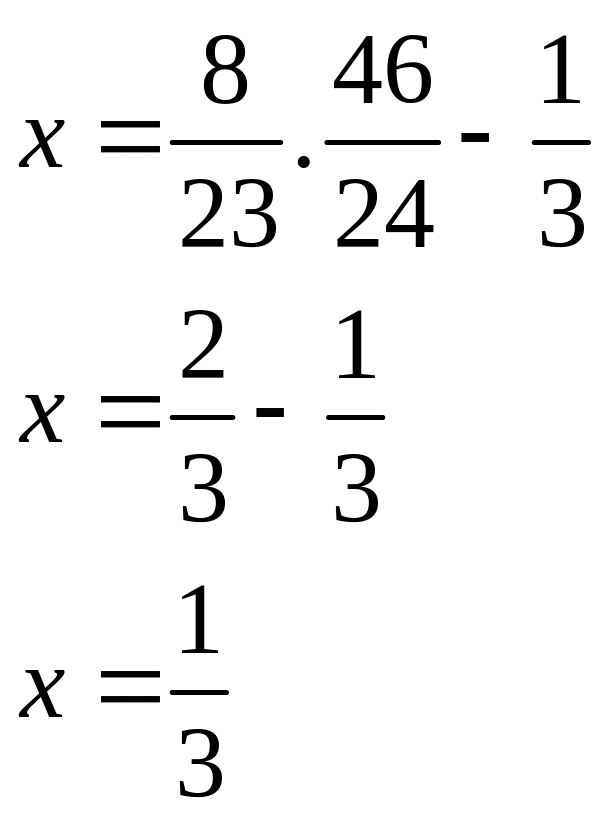
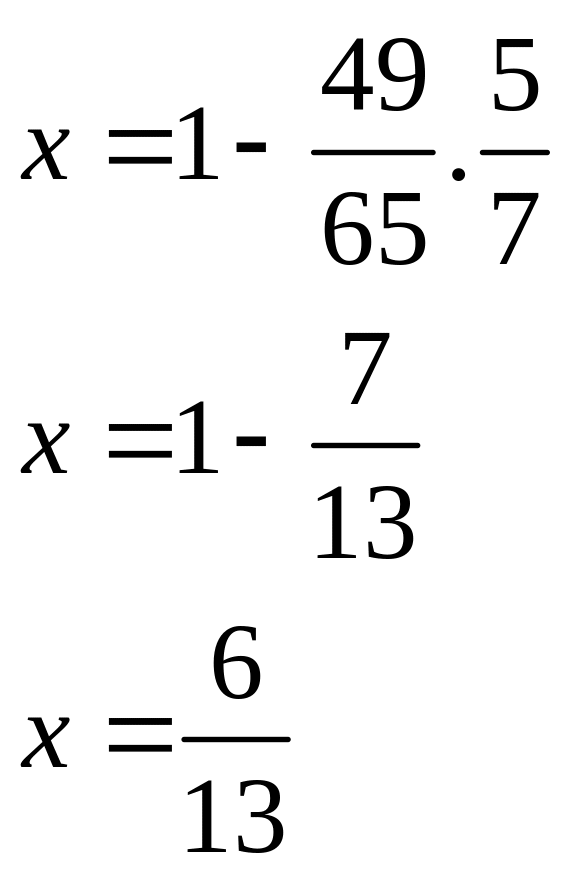
Bài 3: Lớp 6A có 42 HS được chia làm 3 loại: Giỏi, khá, Tb. Biết rằng số HSG bằng 1/6 số HS khá, số HS Tb bằng 1/5 tổng số HS giỏi và khá. Tìm số HS của mỗi loại.
Hướng dẫn
Gọi số HS giỏi là x thì số HS khá là 6x,
số học sinh trung bình là (x + 6x).![]()
Mà lớp có 42 học sinh nên ta có:
![]()
Từ đó suy ra x = 5 (HS)
Vậy số HS giỏi là 5 học sinh.
Số học sinh khá là 5.6 = 30 (học sinh)
SÁô học sinh trung bình là (5 + 30):5 = 7 (HS)
Bài 4: Tính giá trị của cắc biểu thức sau bằng cach tính nhanh nhất:
a/
![]() b/
b/
![]() c/
c/
![]()
Hướng dẫn
a/
![]()
b/
![]()
c/
![]()
Bài 5: Tìm các tích sau:
a/
![]() b/
b/
![]()
Hướng dẫn
a/
![]() b/
b/
![]()
Bài 6: Tính nhẩm
a/
![]() b.
b.
![]()
c/
![]() d/
d/
![]()
Bài 7: Chứng tỏ rằng:
![]()
Đặt H =
![]()
Vậy
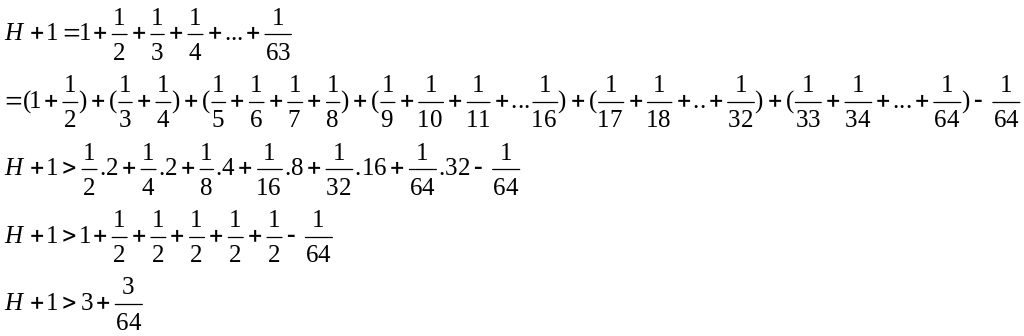
Do đó H > 2
Bài
9: Tìm A biết:
![]()
Hướng dẫn :Ta có (A -
![]() ).10
= A. VẬy 10A – 7 = A suy ra 9A = 7 hay A =
).10
= A. VẬy 10A – 7 = A suy ra 9A = 7 hay A =
![]()
Bài 10: Lúc 6 giờ 50 phút bạn Việt đi xe đạp từ A đến B với vận tốc 15 km/h. Lúc 7 giờ 10 phút bạn Nam đi xe đạp từ B đến A với vận tốc 12 km/h/ Hai bạn gặp nhau ở C lúc 7 giờ 30 phút. Tính quãng đường AB.
Hướng dẫn
Thời gian Việt đi là: 7 giờ 30 phút –
6 giờ 50 phút = 40 phút =
![]() giờ
giờ
Quãng đường Việt đi là:![]() =10
(km)
=10
(km)
Thời gian Nam đã đi là: 7 giờ 30 phút –
7 giờ 10 phút = 20 phút =
![]() giờ
giờ
Quãng đường Nam đã đi là
![]() (km)
(km)
Bài 11: . Tính giá trị của biểu thức:
![]() biết x + y = -z
biết x + y = -z
Hướng dẫn
![]()
Bài 12: Tính gí trị các biểu thức A, B, C rồi tìm số nghịch đảo của chúng.
a/ A =
![]() b/
B =
b/
B =
![]() c/
C =
c/
C =
![]()
Hướng dẫn
a/ A =
![]() nên số nghịch đảo của A là 2003
nên số nghịch đảo của A là 2003
b/ B =
![]() nên số nghịc đảo cảu B là
nên số nghịc đảo cảu B là
![]()
c/ C =
![]() nên số nghịch đảo của C là
nên số nghịch đảo của C là
![]()
Bài 13: Một canô xuôi dòng từ A đến B mất 2 giờ và ngược dòng từ B về A mất 2 giờ 30 phút. Hỏi một đám bèo trôi từ A đến B mất bao lâu?
Hướng dẫn
Vận tốc xuôi dòng của canô là:
![]() (km/h)
(km/h)
Vân tốc ngược dòng của canô là:
![]() (km/h)
(km/h)
Vận tốc dòng nước là:
![]() :
2 =
:
2 =
![]() :
2 =
:
2 =
![]() (km/h)
(km/h)
Vận tốc bèo trôi bằng vận tốc dòng nước, nên thời gian bèo trôi từ A đến B là:
AB:
![]() = AB :
= AB :
![]() = 20 (giờ)
= 20 (giờ)
BTVN::
Bài 1: Thực hiện phép tính chia sau:
a/
![]() ; b/
; b/
![]() c/
c/
![]() d/
d/
![]()
Bài 2: Tìm x biết:
a/
![]() b/
b/
![]() c/
c/
![]()
Bài 3: Đồng hồ chỉ 6 giờ. Hỏi sau bao lâu kim phút và kim giờ lại gặp nhau?
KIỂM TRA
Bài 1: Thực hiện phép tính: (3đ)
a)
![]() b)
b)
![]() c)
c)
![]()
Bài 2: Tìm x, biết: (3đ)
a)
![]() b)
b)
![]() c)
8x = 7,8.x + 25
c)
8x = 7,8.x + 25
Bài 3:
(2đ) Một quyển sách dày 36 trang. Ngày đầu An đọc được
![]() số trang sách. Ngày thứ hai An đọc tiếp 50% số trang
sách còn lại. Hỏi An còn bao nhiêu trang sách chưa đọc?
số trang sách. Ngày thứ hai An đọc tiếp 50% số trang
sách còn lại. Hỏi An còn bao nhiêu trang sách chưa đọc?
Bài 4:
Cho 2 tia OB và OC cùng nằm trên một nửa mặt phẳng bờ
chứa tia OA. Biết
![]() và
và
![]()
a) Tia OB có nằm giữa 2 tia OA và OC không? Vì sao? (0,5đ)
b) Tia OB có phải là tia phân giác của![]() không? Vì sao? (1đ)
không? Vì sao? (1đ)
c) Vẽ OD là tia đối của tia OA và OE là
tia phân giác của
![]() .Tính
.Tính
![]() (0,5đ)
(0,5đ)
Ngoài Phiếu Học Tập Môn Toán 6 Phân Theo Từng Dạng Kèm Hướng Dẫn Giải – Toán 6 thì các tài liệu học tập trong chương trình 6 sẽ được cập nhật liên tục và nhanh nhất có thể sau khi kỳ thi diễn ra trên Danh mục Tài Liệu Học Tập nhằm giúp các bạn đọc thuận tiện trong việc nghiên cứu tài liệu. Quý thày cô và các bạn đọc có thể chia sẻ thêm những tài liệu học tập hữu ích đến địa chỉ email của chúng tôi, nhằm xây dựng nên kho đề thi phong phú, đa dạng cho các em học sinh tham khảo và rèn luyện.
Phiếu học tập môn Toán 6 phân theo từng dạng kèm hướng dẫn giải là một tài liệu hữu ích giúp học sinh nắm vững kiến thức và kỹ năng toán học trong lớp 6. Phiếu học tập này được thiết kế theo từng dạng bài toán phổ biến trong chương trình học, giúp học sinh tiếp cận và làm quen với các dạng bài tập khác nhau.
Phiếu học tập môn Toán 6 phân theo từng dạng cung cấp cho học sinh một bộ đề bài toán đa dạng, từ các bài toán cơ bản đến những bài toán phức tạp hơn. Mỗi dạng bài toán được giải thích rõ ràng và cung cấp hướng dẫn giải chi tiết, từ cách phân tích bài toán, áp dụng công thức và phương pháp giải, cho đến các bước thực hiện và kết quả cuối cùng.
Đặc biệt, phiếu học tập môn Toán 6 phân theo từng dạng cung cấp cho học sinh các ví dụ minh họa và bài tập thực hành, giúp họ áp dụng kiến thức và rèn kỹ năng toán học một cách thực tế. Hướng dẫn giải cụ thể từng bước giúp học sinh hiểu rõ cách áp dụng kiến thức vào từng dạng bài tập và nắm vững phương pháp giải quyết.
>>> Bài viết có liên quan






