Hướng Dẫn Giải Toán 6 Chân Trời Sáng Tạo Bài 6 Chi Tiết Nhất

§ 6: GÓC

A. KIẾN THỨC CẦN NHỚ

1. Góc

* Hai tia chung gốc Ox và Oy tạo nên một góc xOy ( H.8.23). Điểm O gọi là đỉnh của góc xOy , hai tia Ox và Oy gọi là hai cạnh của góc xOy.

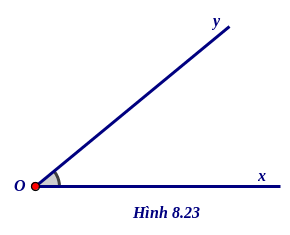
* Khi Ox và Oy là hai tia đối nhau thì góc xOy là một góc bẹt (H.8.24)

2. Điểm trong của góc

Trên hình 8.25 , ta có :

* Điểm M nằm trong góc xOy . Ta còn nói M là một điểm trong của góc xOy .

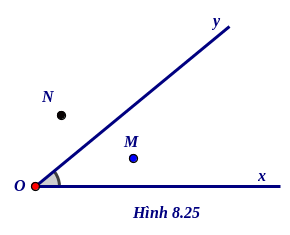
_{* Các điểm như điểm N và các điểm nằm trên cạnh của góc xOy không phải là điểm trong của góc xOy}

B. BÀI TẬP CÓ HƯỚNG DẪN.

 DẠNG 1: Nhận biết hình vẽ và gọi tên : góc, đỉnh, và cạnh của góc

Xem hình 8.28 và thực hiện các yêu cầu sau ( các bài từ bài 1 đến bài 4 )

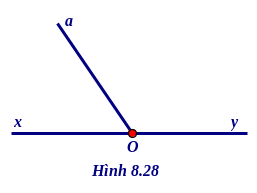
Bài 1. Kể tên các góc mà em thấy trên hình . Trong đó góc nào là góc bẹt ?

Hướng dẫn:

Tìm hai tia bất kì có chung gốc ở trên hình để kể tên các góc . Góc bẹt là góc có 2 cạnh là 2 tia đối nhau.

Bài 2. Hãy nêu nhận xét về quan hệ giữa các cạnh của hai góc aOx và aOy .

Hướng dẫn:

Quan sát hai góc aOx và aOy tìm cạnh chung. Hai cạnh còn lại như thế nào với nhau ?

Bài 3. Một điểm trong của góc aOx có thể cũng là điểm trong của góc aOy hay không ? Hãy nêu một nhận xét tương tự đối với các điểm trong của góc aOy

Hướng dẫn:

Tự lấy 1 điểm trong của góc aOy rồi dùng kiến thức trong phần lí thuyết để trả lời .

Bài 4 . Điền vào chỗ trống trong các phát biểu sau :

1. Góc xOy là hình gồm ……………..

2. Góc yOz được kí hiệu ……………..

c) Góc bẹt là góc có …………….

Hướng dẫn:

a) Nêu đỉnh, hai cạnh của góc.

b) Thêm dấu mũ vào góc.

c) Định nghĩa góc bẹt.

Bài 5 . Gọi A là một điểm trong tùy ý của góc xOy không bẹt . Trên tia OA , ta lấy điểm M tùy ý khác O

a) Vẽ hình và cho biết M có là điểm trong của góc xOy không ?

b) Điền từ thích hợp vào chỗ chấm trong nhận xét sau đây :

Nếu tia OA chứa một …………của góc xOy thì mọi điểm khác O của tia OA đều …………của góc xOy .

Hướng dẫn:

a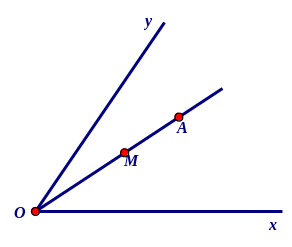 ) Vẽ hình . Trả lời M có nằm trong góc xOy không ?

b) Điểm trong

 DẠNG 2: Nhận biết trên hình vẽ điểm trong của một góc.

Cho góc xOy không bẹt . Hãy trả lời các câu hỏi sau : ( các bài từ 5 đến 7 )

Bài 6. Vẽ góc xOy không bẹt và điểm M là điểm trong của góc đó . Qua M, vẽ một đường thẳng cắt hai cạnh của góc tại A và B sao cho 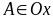và 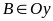. Hỏi trong ba điểm A, B và M, điểm nào nằm giữa hai điểm còn lại ?

H ướng dẫn:

Vẽ hình :

Nhìn vào hình vẽ để trả lời điểm nằm giữa hai điểm còn lại .

Bài 7. Trên hai cạnh của góc xOy, ta lấy hai điểm A và B không trùng với O sao cho 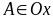và 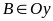. Gọi M là một điểm tùy ý nằm giữa hai điểm A và B . Hỏi M có phải là một điểm trong của góc xOy hay không?

Hướng dẫn:

Quan sát lại hình vẽ bài 5 và trả lời

Bài 8. Từ hai bài 5 và 6, hãy nêu nhận xét về quan hệ giữa hai khái niệm : điểm trong của một góc và điểm nằm giữa hai điểm.

Hướng dẫn:

Từ hai bài 5 và 6 ta có kết luận : cho góc xOy không bẹt . Khi đó :

- Nếu M là một điểm trong của góc xOy, còn A và B là hai điểm nằm trên hai cạnh của góc xOy sao cho A, M, B thẳng hàng thì điểm M nằm giữa hai điểm A và B

- Ngược lại, nếu M là điểm nằm giữa hai điểm A và B với 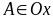và 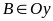( A, B khác O) thì M là một điểm trong của góc xOy

C. BÀI TẬP TỰ GIẢI CÓ ĐÁP SỐ.

Bài 9.  Vẽ hình theo cách diễn đạt bằng lời trong mỗi trường hợp sau đây

a) Vẽ góc xOy không phải là góc bẹt;

b) Vẽ góc bẹt tBz;

c) Vẽ góc jGk và điểm M nằm bên trong góc đó;

d) Vẽ góc nCm và nCt sao cho tia Cm nằm giữa hai tia Cn và Ct;

e) Vẽ các góc xOy, yOz, zOt sao cho tia Oz nằm trong góc xOy, tia Oy nằm trong góc zOt và xOt là góc bẹt.

Đáp số:

Tự vẽ hình theo các diễn đạt.

Bài 10. Cho  4 tia chung gốc Ox, Oy, Oz, Ot. Hỏi có bao nhiêu góc tạo thành ? Kể tên các góc.

Đáp số: tự vẽ hình.

Ghép hai tia được một góc, có 6 góc tạo thành :

Bài 11. Cho góc bẹt xOy, ba tia Om, On, Op cùng thuộc một nửa mặt phẳng có bờ là đường thẳng xy. Có bao nhiêu góc đỉnh O, kể tên các góc đó?

Đáp số: tự vẽ hình.

Có 10 góc đỉnh O. Đó là các góc xOm, góc xOn, góc xOp, góc xOy, góc mOn, góc mOp, góc mOy, góc nOp, góc nOy, góc pOy.

Bài 12: Gọi O là giao điểm của ba đường thẳng xy, zt và uv

a) Có bao nhiêu góc bẹt đỉnh O? Kể tên các góc đó?

b) Kể tên tất cả các góc có chung đỉnh O.

Đáp số: tự vẽ hình.

a) Có 3 góc bẹt đỉnh O. Đó là các góc xOy, zOt và uOv

b) Có 15 góc có chung đỉnh O. Đó là các góc xOz, xOu, xOy, xOt, xOv, zOu, zOy, zOt, zOv, uOy, uOt, uOv, yOt, yOv, tOv

B ài 13: Tìm các góc có trong các hình vẽ sau :

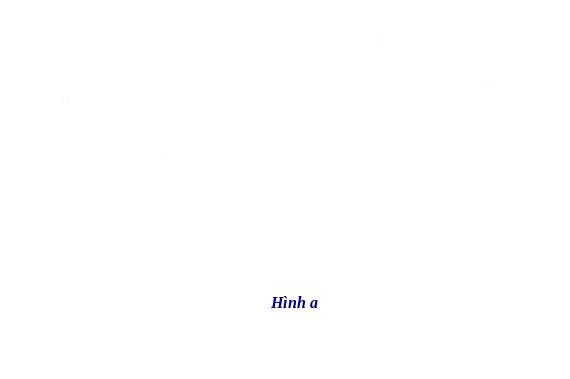
D. BÀI TẬP TRẮC NGHIỆM

Câu 1.  Chọn câu trả lời đúng

A. Hai tia chung gốc tạo thành góc bẹt

B. Góc là hình gồm hai tia chung gốc

C. Một góc có nhiều đỉnh khác nhau

D. Hai đường thẳng cắt nhau tạo thành 2 góc

A B C D

Đáp án : B

Câu 2. Số góc có chung đỉnh O trong hình vẽ dưới đây là:

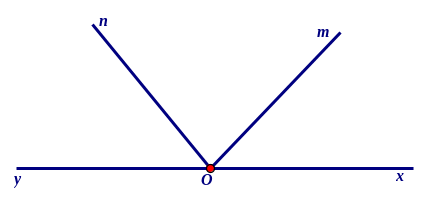
A. 3 B. 4 C. 5 D. 6

Đáp án : D

Câu 3. Gọi O là giao điểm của ba đường thẳng xy, zt và uv. Có bao nhiêu góc bẹt đỉnh O?

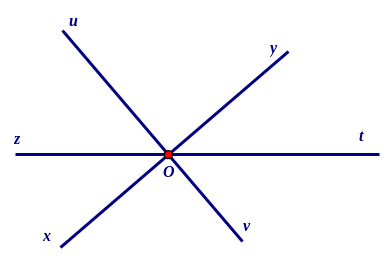
A. 3 B. 2 C. 1 D. 0

Đáp án : A

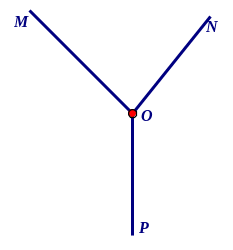
Câu 4 . Cho hình vẽ . Tìm câu đúng

A. Tia OM nằm giữa hai tia ON và OP.

B. Tia ON nằm giữa hai tia OM và OP

C. Tia Op nằm giữa hai tia OM và ON

D. Cả ba câu a, b, c đều đúng.

E. Cả ba câu a, b, c đều sai.

Đáp án : E

Câu 5. Hình vẽ này có bao nhiêu góc tại đỉnh của ngôi sao

A. 3 B. 4 C. 5 D. 6

Đáp án : C