Phương Pháp Giải Toán Lớp 6 Bài 2 Xác Suất Thực Nghiệm Đầy Đủ Nhất
>>> Mọi người cũng quan tâm:
Phương Pháp Giải Toán Lớp 6 Bài 2 Xác Suất Thực Nghiệm Đầy Đủ Nhất – Toán 6 Chân Trời Sáng Tạo là tài liệu học tập được Trang Tài Liệu biên soạn và sưu tầm từ những nguồn dữ liệu mới nhất hiện nay. Tài liệu này sẽ giúp các em luyện tập, củng cố kiến thức từ đó nâng cao điểm số cho môn học. Ngoài ra, cũng giúp các thầy cô giáo có nguồn tài nguyên phong phú để giảng dạy.
Dưới đây là bản đọc trực tuyến giúp thầy cô và các em học sinh có thể nghiên cứu Online hoặc bạn có thể tải miễn phí với phiên bản word để dễ dàng in ấn cũng như học tập Offline.
§ 2: XÁC SUẤT THỰC NGHIỆM
A. KIẾN THỨC CẦN NHỚ
1. Khả năng xảy ra của một sự kiện:
- Để nói về khả năng xảy ra của một sự kiện, ta dùng một con số có giá trị từ 0 đến 1.
- Một sự kiện không thể xảy ra có khả năng xảy ra bằng 0.
- Một sự kiện chắc chắn xảy ra có khả năng xảy ra bằng 1.
2. Xác suất thực nghiệm:
Thực hiện lặp đi lặp lại một hoạt động nào đó n lần. Gọi n(A) là số lần sự kiện A xảy ra trong n lần đó. Tỉ số
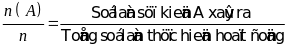
được gọi là xác suất thực nghiệm của sự kiện A sau n hoạt động vừa thực hiện.
B. BÀI TẬP CÓ HƯỚNG DẪN.
 DẠNG
1: Xác định khả năng xảy ra của một sự kiện
DẠNG
1: Xác định khả năng xảy ra của một sự kiện
Bài 1. Hai bạn Mận và Xoài cùng chơi với nhau 20 ván cờ tướng.
Mận đã thắng 10 ván, hòa 8 ván và thua 2 ván. Xoài rất muốn gỡ,
nhưng hai bạn chỉ thi đấu với nhau 25 ván. Theo em trong hai bạn,
bạn nào có khả năng giành chiến thắng cao hơn?
Hướng dẫn:
Quan sát kỹ số bàn thắng thua của mỗi bạn, sau đó em đưa ra dự đoán
Bạn Mận có khả năng giành chiến thắng cao hơn.
Bài 2. Trong một hộp có 8 viên bi đen, 2 viên bi trắng. Không nhìn
vào hộp, lấy ngẫu nhiên 1 viên bi trong hộp. Xét các sự kiện sau:
a) Viên bi chọn ra có màu trắng. b) Viên bi chọn ra có màu đỏ.
c) Viên bi chọn ra không có màu vàng. d) Viên bi chọn ra có màu đen.
Hướng dẫn:
a) Có khả năng xảy ra. b) Chắc chắn không xảy ra.
c) Chắc chắn xảy ra. d) Có khả năng xảy ra.
Bài 3. Gieo đồng thời 2 con xúc xắc 6 mặt. Quan sát số chấm xuất hiện và cho biết sự kiện nào có khả năng xảy ra?
a) Tổng số chấm xuất hiện trên hai con xúc xắc là số chẵn.
b) Tổng số chấm xuất hiện trên hai con xúc xắc lớn hơn 8.
Hướng dẫn:
a) Có khả năng xảy ra. b) Chắc chắn không xảy ra.
DẠNG 2: Tính xác suất thực nghiệm
Bài 4. Để theo dõi việc học tập của mình, bạn Khang đã ghi lại số lần phát biểu của mình trong tuần ở bảng sau:
Phát biểu đúng |
Phát biểu sai |
45 |
20 |
Hãy tính xác suất thực nghiệm của sự kiện bạn Khang phát biểu đúng trong tuần.
Hướng dẫn:
- Tính tổng số lần phát biểu trong tuần của bạn Khang.
-
Tính xác suất thực nghiệm của sự kiện bạn Khang phát
biểu đúng trong tuần là:
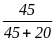
Bài 5. Gieo một con xúc xắc 20 mặt 150 lần , quan sát số ghi trên mặt của con xúc xắc, ta được kết quả như sau:
Số xuất hiện |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
Số lần |
4 |
12 |
10 |
6 |
14 |
5 |
5 |
10 |
8 |
6 |
4 |
4 |
12 |
2 |
11 |
1 |
3 |
4 |
19 |
10 |
H ãy
tính xác suất thực nghiệm của sự kiện:
ãy
tính xác suất thực nghiệm của sự kiện:
a) Gieo được mặt có số lẻ.
b) Gieo được mặt có số chẵn.
c) Gieo được mặt từ số 5 đến số 10.
Hướng dẫn:
a) Các mặt có số lẻ là: 1, 3, 5, 7, 9, 11, 13, 15, 17, 19.
Xác suất thực nghiệm của sự kiện gieo được mặt có số lẻ là:
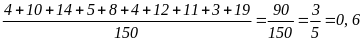
b) Các mặt có số chẵn là: 2; 4; 6; 8; 10; 12; 14; 16; 18; 20.
Xác suất thực nghiệm của sự kiện gieo được mặt có số chẵn là:
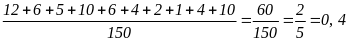
C. BÀI TẬP TỰ GIẢI CÓ ĐÁP SỐ.
Bài 6. Lớp 6A trong lớp học luôn có 1 hộp đựng thẻ là số thứ tự của 35 bạn. Cứ mỗi lần kiểm tra bài cũ hay lên bảng làm bài giáo viên sẽ bốc thăm theo số thứ tự đó. Đúng là bài hoàn chỉnh không có sai sót , Sai là bài vẫn còn thiếu sót.
Tổ 2 có 10 bạn, bạn tổ trưởng rất có trách nhiệm và siêng năng, bạn ấy đã ghi lại số lần phát biểu của mỗi thành viên trong tổ mình và tổng kết mỗi tuần. Dưới đây là bảng thống kê của bạn:
Tên |
Mai |
Cường |
Vy |
Tường |
Anh |
Thư |
Lan |
Kỳ |
Tỷ |
Ngọc |
|
Số lần phát biểu |
Đúng |
27 |
32 |
10 |
7 |
10 |
20 |
40 |
38 |
12 |
15 |
Sai |
10 |
5 |
3 |
5 |
8 |
10 |
2 |
5 |
7 |
8 |
|
a) Tính xác suất thực nghiệm số lần phát biểu đúng của tổ 2.
b) Tính xác suất thực nghiệm số lần phát biểu sai của tổ 2.
Đ áp
số: a)
áp
số: a)
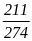 b)
b)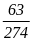
Bài 7. Khang và Hiếu cùng nhau chơi bắn bi và ghi lại
các bàn thắng của mỗi bạn như sau:
Hiếu |
|
Khang |
|
Em hãy tìm xác suất thực nghiệm của sự kiện bàn thắng của bạn Khang trong 50 trận đấu của hai bạn.
Đáp
số:
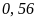
 Bài
8. Bảng điểm tổng kết
HKI của lớp 6A gồm 3 môn Toán, Văn, Anh như sau:
Bài
8. Bảng điểm tổng kết
HKI của lớp 6A gồm 3 môn Toán, Văn, Anh như sau:
-
Môn
Xếp loại
Toán
Văn
Anh
Giỏi
35
20
20
Khá
0
10
8
Trung bình
0
5
7
Em hãy tính xác suất thực nghiệm xếp loại giỏi của ba môn Toán, Văn, Anh.
Đáp
số:
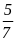
Bài 9. Gieo một con xúc xắc 6 mặt liên tiếp 20 lần, bạn An đã có kết quả thống kê như sau:
Xuất hiện mặt |
1 |
2 |
3 |
4 |
5 |
6 |
Số lần |
4 |
5 |
7 |
1 |
1 |
2 |
a) Tính xác xuất thực nghiệm xuất hiện mặt 1 chấm.
b) Tính xác suất thực nghiệm các mặt không lớn hơn 4.
c) Tính xác suất thực nghiệm các mặt lớn hơn 6.
Đáp
số: a)
 b)
b)
 c)
c)
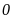
Bài 10. Nếu gieo một con xúc xắc 6 mặt 20 lần liên tiếp, có 5 lần xuất hiện mặt 3 chấm, 8 lần xuất hiện mặt 5 chấm. Tính xác suất thực nghiệm của sự kiện gieo được mặt 3 chấm và 5 chấm.
Đáp
số:
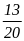
D .
BÀI TẬP TRẮC NGHIỆM
.
BÀI TẬP TRẮC NGHIỆM
Tung hai đồng xu cân đối 20 lần ta được 2 lần xuất hiện hai
mặt sấp, 8 lần xuất hiện 1 mặt sấp và 1 mặt ngửa, 10 lần xuất
hiện hai mặt ngửa.
Câu 1. Xác suất thực nghiệm 1 đồng xu có mặt sấp và 1 đồng xu có mặt ngửa là:
A.
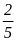 B.
B.
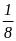 C.
C.
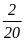 D.
D.

Câu 2. Xác suất thực nghiệm có 2 đồng xu đều sấp là:
A.
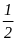 B.
B.
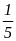 C.
C. D.
D.
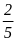
Câu 3. Xác suất thực nghiệm không có xuất hiện hai mặt sấp là:
Câu 1 |
Câu 2 |
Câu 3 |
A |
C |
D |
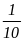 B.
B.
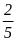 C.
C.
 D.
D.
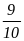
Đáp số:
Ngoài Phương Pháp Giải Toán Lớp 6 Bài 2 Xác Suất Thực Nghiệm Đầy Đủ Nhất – Toán 6 Chân Trời Sáng Tạo thì các tài liệu học tập trong chương trình 6 sẽ được cập nhật liên tục và nhanh nhất có thể sau khi kỳ thi diễn ra trên Danh mục Tài Liệu Học Tập nhằm giúp các bạn đọc thuận tiện trong việc nghiên cứu tài liệu. Quý thày cô và các bạn đọc có thể chia sẻ thêm những tài liệu học tập hữu ích đến địa chỉ email của chúng tôi, nhằm xây dựng nên kho đề thi phong phú, đa dạng cho các em học sinh tham khảo và rèn luyện.
Phương pháp giải toán lớp 6 Bài 2 về xác suất thực nghiệm là một tài liệu hữu ích giúp học sinh nắm vững và áp dụng kiến thức về xác suất vào việc giải các bài toán thực tế. Bài toán xác suất thực nghiệm là một trong những chủ đề quan trọng trong môn Toán lớp 6, và phương pháp giải toán đầy đủ nhất sẽ giúp học sinh hiểu rõ về cách tiếp cận và giải quyết các bài toán liên quan đến xác suất.
Phương pháp giải toán lớp 6 Bài 2 về xác suất thực nghiệm sẽ giới thiệu cho học sinh các bước cơ bản để giải quyết một bài toán xác suất. Từ việc xác định không gian mẫu, tính số phần tử của không gian mẫu và các biến cố, đến việc tính xác suất của một biến cố dựa trên số phần tử của biến cố và không gian mẫu. Ngoài ra, phương pháp cũng sẽ giới thiệu các công thức và quy tắc cần thiết để giải quyết các bài toán xác suất phức tạp hơn.
Phương pháp giải toán lớp 6 Bài 2 xác suất thực nghiệm đầy đủ nhất cung cấp cho học sinh nhiều ví dụ minh hoạ và bài tập thực hành, giúp họ áp dụng kiến thức vào việc giải quyết các bài toán thực tế. Đồng thời, phương pháp này cũng giúp học sinh phát triển kỹ năng tư duy logic, khả năng phân tích và suy luận, cũng như rèn luyện khả năng làm việc nhóm và ghi chú thông tin quan trọng.
>>> Bài viết có liên quan










