Đề Cương Ôn Tập Học Kì 2 Toán 9 Năm Học 2021-2022 Có Lời Giải
>>> Mọi người cũng quan tâm:
Đề Cương Ôn Tập Toán 9 Học Kỳ 2 Năm 2021-2022 Có Lời Giải – Toán 9 là tài liệu học tập được Trang Tài Liệu biên soạn và sưu tầm từ những nguồn dữ liệu mới nhất hiện nay. Tài liệu này sẽ giúp các em luyện tập, củng cố kiến thức từ đó nâng cao điểm số cho môn học. Ngoài ra, cũng giúp các thầy cô giáo có nguồn tài nguyên phong phú để giảng dạy.
Dưới đây là bản đọc trực tuyến giúp thầy cô và các em học sinh có thể nghiên cứu Online hoặc bạn có thể tải miễn phí với phiên bản word để dễ dàng in ấn cũng như học tập Offline.
ĐỀ CUƠNG ÔN TẬP MÔN TOÁN 9
HỌC KÌ II
I. LÝ THUYẾT:
A. HỆ HAI PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN:
Câu 1: Nêu khái niệm phương trình bậc nhất hai ẩn.
Áp dụng cho phương trình x+3y=4, tìm nghiệm tổng quát của phương trình.
Trả lời:
Phương
trình bậc nhất hai ẩn x và y có dạng ax+by=c, trong đó
a, b và c là các số đã biết a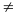 0
hoặc b
0
hoặc b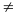 0.
0.
Áp
dụng: nghiệm tổng quát của phương trình là
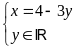
Câu 2: a) Nêu định nghĩa hệ phương trình bậc nhất hai ẩn x và y. Cho ví dụ
b) Trong trường hợp nào thì (x0; y0) là nghiệm của hệ phương trình hai ẩn.
Trả lời:
Cho hai phương trình bậc nhất hai ẩn ax+by=c và a’x+b’y=c’. Khi đó, ta có hệ phương trình bậc nhất hai ẩn.
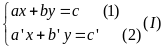
Ví
dụ:

Nếu hai phương trình (1) và (2) có nghiệm chung (x0; y0) thì (x0; y0) được gọi là nghiệm của hệ (I)
Câu 3: Nêu các bước giải hệ phương trình bậc nhất hai ẩn bằng phương pháp thế.
Áp
dụng giải hệ
phương trình
Trả lời:
Các bước giải hệ phương trình bằng phương pháp thế:
Dùng guy tắc thế biến đổi hệ phương trình đã cho để được một hệ phương trình mới, trong đó có một phương trình một ẩn.
Giải phương trình một ẩn vừa có rồi suy ra nghiệm của hệ đã cho.
Áp dụng:

Hệ phương trình có nghiệm duy nhất (-1; 0)
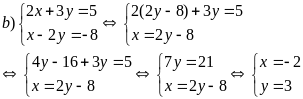
Hệ phương trình có nghiệm duy nhất (-2;3)
Câu 4: Nêu các bước giải hệ phương trình bằng phương pháp cộng.
Áp dụng giải các hệ phương trình sau:

Trả lời:
Các bước giải hệ phương trình bằng phương pháp cộng
Nhân hai vế của mỗi phương trình với một số thích hợp (Nếu cần) sao cho các hệ số của cùng một ẩn nào đó trong hai phương trình của hệ là bằng nhau hoặc đối nhau.
Áp dụng quy tắc cộng đại số để được một hệ phương trình mới, trong đó một phương trình có hệ số của một trong hai ẩn bằng 0 (Tức là phương trình một ẩn)
Giải phương trình một ẩn vừa có rồi suy ra nghiệm của hệ đã cho.
Áp dụng

Hệ phương trình có nghiệm duy nhất (2; 1)
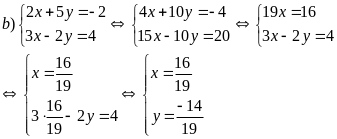
Hệ
phương trình có nghiệm duy nhất

Câu 5: Nêu các bước giải bài toán bằng cách lập hệ phương trình
Trả lời:
Bước 1: Lập hệ phương trình
Chọn 2 ẩn và đặt điều kiện thích hợp cho ẩn
Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết
Lập hệ phương trình
Bước 2: Giải hệ phương trình
Bước 3: Trả lời: Kiểm tra xem trong các nghiệm của hệ phương trình, nghiệm nào thỏa điều kiện bài toán rồi kết luận.
B.
HÀM SỐ y=ax2
(a
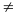 0)
– PHƯƠNG TRÌNH BẬC HAI MỘT ẨN:
0)
– PHƯƠNG TRÌNH BẬC HAI MỘT ẨN:
Câu
1: Nêu các
tính chất của hàm số y=ax2
(a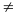 0).
0).
Áp dụng: nêu tính chất của hàm số y=-2x2.
Trả lời
Hàm
số y=ax2
(a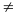 0)
được xác định với mọi giá trị của x thuộc
0)
được xác định với mọi giá trị của x thuộc

Tính
chất của hàm số y=ax2
(a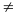 0)
0)
a>0 |
a<0 |
Hàm số đồng biến khi x>0 và nghịch biến khi x<0 |
Hàm số đồng biến khi x<0 và nghịch biến khi x>0 |
y=0 là giá trị nhỏ nhất (khi x=0) |
y=0 là giá trị lớn nhất (khi x=0) |
Áp dụng:
Hàm số y=-2x2 có dạng y=ax2 với a=-2<0
Hàm
số xác định với mọi x
Hàm số đồng biến khi x<0 và nghịch biến khi x>0
y=0 là giá trị lớn nhất của hàm số (khi x=0)
Câu
2: Nêu nhận
xét đồ thị của hàm số y=ax2
(a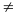 0)
0)
Áp dụng vẽ đồ thị của hàm số y=2x2.
Trả lời:
Nhận xét
Đồ
thị của hàm số y=ax2
(a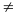 0)
là một đường cong đi qua gốc tọa độ và nhận trục
Oy làm trục đối xứng. Đường cong đó được gọi là
một parabol với đỉnh O.
0)
là một đường cong đi qua gốc tọa độ và nhận trục
Oy làm trục đối xứng. Đường cong đó được gọi là
một parabol với đỉnh O.
Nếu a>0 thì đồ thị nằm phía trên trục hoành, O là điểm thấp nhất của đồ thị.
Nếu a<0 thì đồ thị nằm phía dưới trục hoành, O là điểm cao nhất của đồ thi
Áp dụng:
x |
-2 |
-1 |
0 |
1 |
2 |
y=-2x2 |
-8 |
-2 |
0 |
-2 |
-8 |
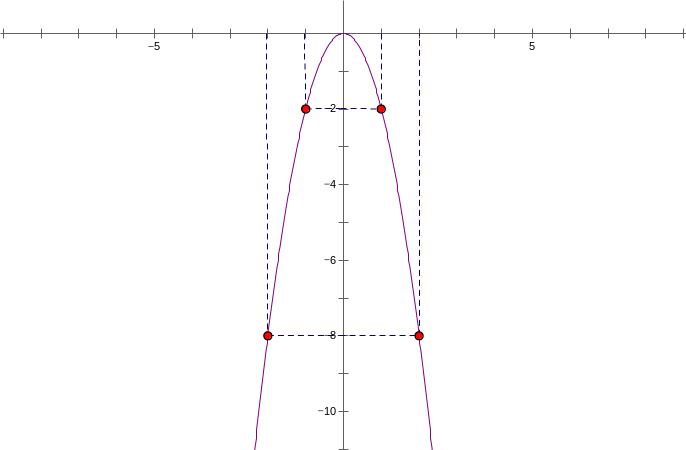
Câu 3: Nêu định nghĩa phương trình bậc hai một ẩn. Cho ba ví dụ về phương trình bậc hai.
Áp dụng: Với giá trị nào của a thì phương trình (4 – a2)x2+ax – 3=0 là phương trình bậc hai.
Trả lời:
Định nghĩa:
Phương
trình bậc hai một ẩn là phương trình có dạng
ax2+bx+c=0,
x là ẩn số; a, b, c là những số cho trước gọi là các
hệ số và a
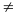 0.
0.
Ví dụ: -3x2 – 7x+10=0
Áp dụng: phương trình (4 – a2)x2+ax – 3=0 là phương trình bậc hai.
 4
– a2
4
– a2
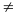 0
0 4
4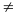 a2
a2 a
a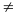
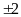
Câu
4: Trình
bày công thức nghiệm của phương trình bậc hai ax2+bx+c=0
(a
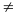 0)
0)
Áp dụng giải phương trình -3x2 – 7x+10=0
Trả lời:
Công
thức tính nghiệm của phương trình ax2
+ bx +c =
0
 .
.
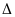 =
b2
– 4ac
=
b2
– 4ac
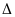 >
0 phöông trình coù hai nghieäm phaân bieät: x1
=
>
0 phöông trình coù hai nghieäm phaân bieät: x1
=
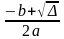 ; x1
=
; x1
=
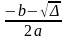

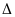 =
0 phöông trình coù nghieäm keùp 😡1
= x2
=
=
0 phöông trình coù nghieäm keùp 😡1
= x2
=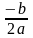
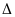 <
0 phöông trình voâ nghieäm
<
0 phöông trình voâ nghieäm
Áp dụng:

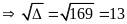
Phương trình có hai nghiệm phân biệt
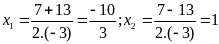
Câu
5: Trình
bày công thức nghiệm thu gọn của phương trình ax2+bx+c=0
(a
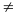 0)
0)
Áp dụng: Giải phương trình x2+6x – 7=0
Trả lời:
Phương
trình: ax2
+bx + c = 0 (a
0) có
hệ số b là số chẵn, ta có thể sử dụng công thức
nghiệm thu gọn với b’
=
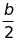 ;
’
= b’2 – ac
;
’
= b’2 – ac
’ > 0 phöông trình coù hai nghieäm phaân bieät: x1 =
 ; x2 =
; x2 =
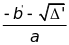
’ =0 phöông trình coù nghieäm keùp :x1 = x2 =

’ < 0 phöông trình voâ nghieäm
Áp dụng: x2+6x – 7=0

Phương trình có hai nghiệm phân biệt
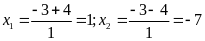
Câu
6: Phát
biểu hệ thức Vi et về tổng và tích hai nghiệm của
phương trình ax2+bx+c=0
(a
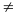 0)
0)
Áp dụng: Trong các phương trình sau, phương trình nào có nghiệm? Đối với phương trình có nghiệm, hãy tính tổng và tích các nghiệm của phương trình mà không giải phương trình đó.
a) 2x2 – 3x+2=0 b) 3x2+x – 10=0 c)-9x2 – 6x – 1=0
Trả lời
a)
Ñònh lyù thuaän: Neáu phöông trình baäc hai ax2
+ bx + c = 0 (a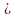 0
) coù hai nghieäm x1,
x2
thì toång vaø tích cuûa chuùng laø :
0
) coù hai nghieäm x1,
x2
thì toång vaø tích cuûa chuùng laø :
b
) Ñònh lyù ñaûo : Neáu hai soá x1
vaø
x2
maø toång x1
+
x2
=
S vaø tích x1.x2
=P và S2 – 4P
 0
thì
hai soá naøy laø nghieäm cuûa phöông trình: X2
– SX + P = 0.
0
thì
hai soá naøy laø nghieäm cuûa phöông trình: X2
– SX + P = 0.
Áp dụng:
2x2 – 3x+2=0 (1) (a=2, b=-3, c=2)
 =(-3)2
– 4.2.2=9 – 16=-7<0
=(-3)2
– 4.2.2=9 – 16=-7<0
Vậy phương trình (1) vô nghiệm
3x2+x – 10=0 (2) (a=3, b=1, c=-10)
 =12
– 4.3.(-10)=1+120=121>0
=12
– 4.3.(-10)=1+120=121>0
Vậy phương trình có hai nghiệm phân biệt x1, x2 và
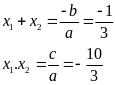
-9x2 – 6x – 1=0 (3) (a=-9, b=-6, c=-1)
 =(-6)2
– 4.(-9).(-1)=36 – 36=0
=(-6)2
– 4.(-9).(-1)=36 – 36=0
Vậy phương trình (3) có nghiệm kép
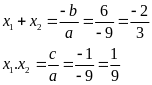
Câu 6: Định nghĩa và cách giải phương trình trùng phương
Áp dụng: Giải phương trình 3x4+4x2 – 7=0
Trả lời:
Phương trình trùng phương là phương trình có dạng ax4+bx2+c=0
Đặt
t=x2
(điều kiện t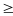 0),
ta có phương trình at2+bt+c=0
(*)
0),
ta có phương trình at2+bt+c=0
(*)
Giải
(*) rồi chọn nghiệm t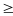 0,
lúc đó x=
0,
lúc đó x=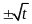
Áp dụng: 3x4+4x2 – 7=0
Đặt
t=x2 (điều
kiện t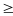 0)
0)
Ta có phương trình 3t2+4t – 7=0 (*)
Vì (*) có a+b+c=3+4+(-7)=0 nên phương trình (*) có hai nghiệm
t1=1>0 (nhận)
t2=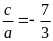 (loại)
(loại)
Với
t=1
 x2=1
x2=1 x=
x=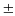 1
1
Câu
7:
Cho phương trình
: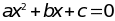
 có hai nghiệm x1
và x2
.Chứng
minh :
có hai nghiệm x1
và x2
.Chứng
minh :

Trả lời: ta có
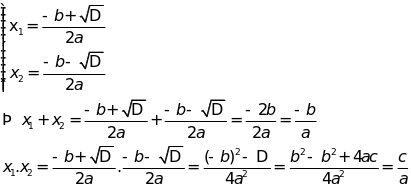
Câu 8: Nêu các bước giải bài toán bằng cách lập phương trình
Trả lời:
Bước 1: Lập phương trình
Chọn ẩn và đặt điều kiện thích hợp cho ẩn
Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết
Lập phương trình
Bước 2: Giải phương trình
Bước 3: Trả lời: Kiểm tra xem trong các nghiệm của phương trình, nghiệm nào thỏa điều kiện bài toán rồi kết luận.
C. GÓC VỚI ĐƯỜNG TRÒN:
Câu 1: Giữa hai đường tròn có mấy vị trí tương đối? Kể ra và vẽ hình mô tả.
Trả lời:
Giữa hai đường tròn (O) và (O’) có ba vị trí tương đối
Hai đường tròn không giao nhau (không có điểm chung)
Hai đường tròn ở ngoài nhau
Hai đường tròn đựng nhau

Hai đường tròn tiếp xúc nhau (có một điểm chung)
Hai đường tròn tiếp xúc ngoài
Hai đường tròn tiếp xúc trong

Hai đường tròn cắt nhau (có hai điểm chung)

Câu 2: Hãy cho biết vị trí tương đối của hai đường tròn (O) và (O’) khi hai đường tròn này có:
4 tiếp tuyến chung
3 tiếp tuyến chung
Không có tiếp tuyến chung
Vẽ hình mô tả mỗi trường hợp
Trả lời:
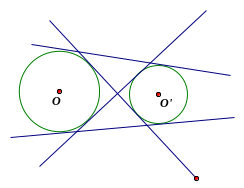
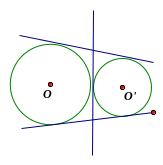

Hình 1 Hình 2 Hình 3
Số tiếp tuyến của hai đường tròn |
Vị trí tương đối của (O) và (O’) |
4 |
Ngoài nhau (Hình 1) |
3 |
Tiếp xúc ngoài (Hình 2) |
0 |
Đựng nhau (Hình 3) |
Câu 3: Nêu các vị trí tương đối của hai đường tròn. Ứng với mỗi vị trí đó, viết hệ thức giữa đoạn nối tâm d với các bán kính R, r.
Trả lời:
Vị trí tương đối của hai đường tròn (O;R) và (O’;r) (R>r) |
Số điểm chung |
Hệ thức giữa d với R và r |
Hai đường tròn cắt nhau |
2 |
R – r<OO’<R+r |
Hai đường tròn tiếp xúc nhau
|
1 |
d=R+r d=R – r |
Hai đường tròn không giao nhau
|
0 |
d>R+r d<R – r d=0 |
Câu 4: a) Nêu định nghĩa góc ở tâm. Vẽ hình
b) Định nghĩa số đo của một cung trên trên một đường tròn.
Áp
dụng: Trên đường tròn (O) lấy ba điểm A, B, C sao cho
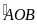 =900
và số đo của cung nhỏ BC bằng 300
(Điểm C nằm trên cung nhỏ AB). Tính số đo của góc AOC
và số đo cung lớn AB
=900
và số đo của cung nhỏ BC bằng 300
(Điểm C nằm trên cung nhỏ AB). Tính số đo của góc AOC
và số đo cung lớn AB
Trả lời:
Góc có đỉnh trùng với tâm của đường tròn được gọi là góc ở tâm.

S
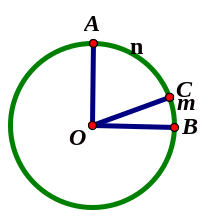 ố
đo của cung nhỏ bằng số đo của góc ở tâm chắn cung
đó
ố
đo của cung nhỏ bằng số đo của góc ở tâm chắn cung
đó
Số đo cung lớn bằng hiệu giữa 3600 và số đo của cung nhỏ (Có chung hai mút với cung lớn)
Số đo của nửa đường tròn bằng 1800
Áp dụng:
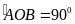
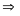 sđ
sđ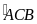 =900
=900
Vậy
sđ
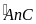 =sđ
=sđ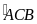 - sđ
- sđ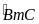 =900
– 300=600
=900
– 300=600
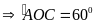
Số
đo cung lớn AB bằng 3600
- sđ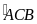 =3600
– 900=2700.
=3600
– 900=2700.
Câu
5: Trên
đường tròn (O) cho hai điểm A và B và điểm C nằm trên
cung nhỏ AB. Chứng minh sđ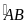 =sđ
=sđ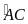 +sđ
+sđ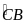
Áp
dụng: Trên đường
tròn (O) cho ba điểm I, J, K sao cho tam giác OIJ đều và
OJ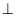 OK.
Tính số đo cung lớn IK.
OK.
Tính số đo cung lớn IK.
Trả lời:
Chứng
minh sđ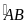 =sđ
=sđ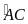 +sđ
+sđ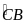
Ta có điểm C nằm trên cung AB
D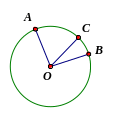 o
đó OC nằm giữa hai tia OA, OB
o
đó OC nằm giữa hai tia OA, OB
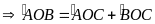
Hay
sđ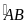 =sđ
=sđ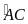 +sđ
+sđ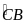 (đpcm)
(đpcm)
Á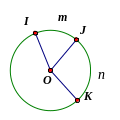 p
dụng:
p
dụng:
Ta có tam giác OIJ đều
Do
đó
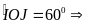 sđ
sđ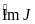 =600
=600
Mặt
khác ta có OJ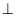 OK
OK
Do
đó
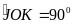
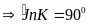
sđ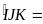 sđ
sđ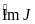 +sđ
+sđ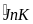 =600+900=1500.
=600+900=1500.
Số đo cung lớn IK là 3600 – 1500=2100.
Câu 6:Phát biểu các định lí liên hệ giữa cung và dây.
Áp
dụng: Cho tam giác ABC nội tiếp đường tròn tâm (O). Biết
Â=500
và
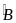 =650.
So sánh hai cung nhỏ AB và AC.
=650.
So sánh hai cung nhỏ AB và AC.
Trả lời:
Định lí 1:
Với hai cung nhỏ trong một đường tròn hay trong hai đường tròn bằng nhau:
Hai cung bằng nhau căng hai dây bằng nhau
Hai dây bằng nhau căng hai cung bằng nhau
Định lí 2:
Với hai cung nhỏ trong một đường tròn hay trong hai đường tròn bằng nhau:
Cung lớn hơn căng dây lớn hơn
Dây lớn hơn căng cung lớn hơn
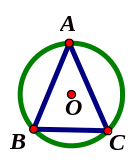
Áp dụng:
Trong tam giác ABC, có
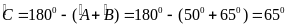
Do
đó
 cân tại A
cân tại A
Nên AB=AC
Vậy hai cung nhỏ AB và AC bằng nhau
Câu 7: Chứng minh định lí: “Với hai cung nhỏ trong một đường tròn hay trong hai đường tròn bằng nhau:
Hai cung bằng nhau căng hai dây bằng nhau
Hai dây bằng nhau căng hai cung bằng nhau”
Trả lời:
Xét
 OAB
và
OAB
và
 OCD
có
OCD
có
OA=OC (bán kính)
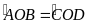 (vì
(vì
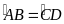 )
)
OB=OD (bán kính)
D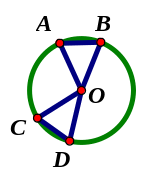 o
đó
o
đó
 OAB=
OAB= OCD
(c – g – c)
OCD
(c – g – c)
 AB=CD
(hai cạnh tương ứng)
AB=CD
(hai cạnh tương ứng)
Xét
 OAB
và OCD có
OAB
và OCD có
AB=CD (gt)
OA=OC (bán kính)
OB=OD (bán kính)
Do
đó
 OAB=
OAB= OCD
(c – c – c)
OCD
(c – c – c)
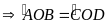 (hai
góc tương ứng)
(hai
góc tương ứng)
Vậy

Câu 8: Định nghĩa góc nội tiếp và phát biểu (không chứng minh) định lí tính số đo của góc nội tiếp.
Áp
dụng: Xem hình bên (hai đường tròn có tâm O và tâm B,
Điểm B nằm trên đường tròn tâm O). Số đo của góc
JOI bằng bao nhiêu biết

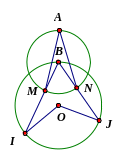
Trả lời:
Định nghĩa:
Góc nội tiếp là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn đó
Cung nằm bên trong góc gọi là cung bị chắn
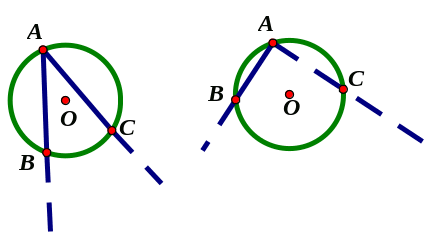
Định lí: Trong một đường tròn, số đo góc nội tiếp bằng nửa số đo cung bị chắn
Áp dụng:
Đối
với đường tròn (B), ta có
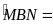 sđ
sđ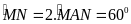
Đối
với đường tròn (O), ta có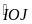 =sđ
=sđ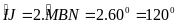
Câu 9: Chứng minh định lí “Trong một đường tròn, số đo của góc nội tiếp bằng nửa số đo của cung bị chắn” (trường hợp O nằm trên một cạnh của góc)
Trả lời:
T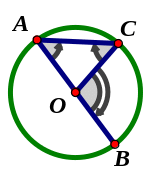 a
có
a
có
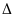 OAC
cân tại O (OA=OC=bán kính)
OAC
cân tại O (OA=OC=bán kính)
Do
đó
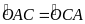
Mặt
khác ta có
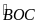 là
góc ngoài của
là
góc ngoài của
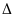 OAC
OAC
Do
đó
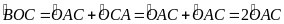
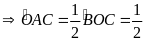 sđ
sđ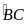
Hay
 sđ
sđ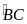 (đpcm)
(đpcm)
Câu 10: Phát biểu các tính chất về góc nội tiếp trong một đường tròn
Trả lời:
Trong một đường tròn:
Các góc nội tiếp bằng nhau chắn các cung bằng nhau.
Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.
Góc nội tiếp (nhỏ hơn hoặc bằng 900) có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung.
Góc nội tiếp chắn nửa đường tròn là góc vuông.
Câu 11: Chứng minh định lí “Số đo của góc tạo bởi tia tiếp tuyến và dây cung bằng nửa số đo của cung bị chắn” (trường hợp tâm nằm bên ngoài góc)
T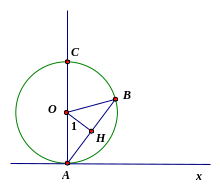 rả
lời:
rả
lời:
Kẻ
OH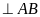
Ta
có
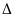 OAB
cân tại O
OAB
cân tại O
Do đó OH là tia phân giác của góc AOB
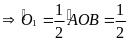 sđ
sđ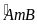
Mà
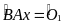 (cùng
phụ với
(cùng
phụ với
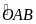 )
)
Nên
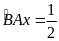 sđ
sđ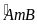
Câu 12: Chứng minh định lí :Góc có đỉnh ở bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn”.
T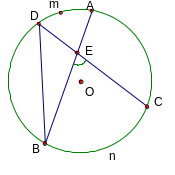 rả
lời:
rả
lời:
Ta
có
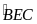 là
góc ngoài của
là
góc ngoài của
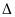 BDE
BDE
Do
đó

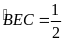
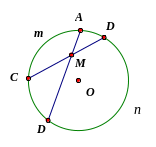 sđ
sđ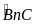 +
+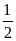 sđ
sđ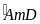 =
=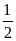 (
sđ
(
sđ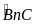 +sđ
+sđ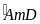 )
)
Câu 13: Phát biểu (không chứng minh) định lí về số đo của góc có đỉnh ở bên trong đường tròn.
Áp
dụng: Tính số đo của góc
 trong hình bên, biết sđ
trong hình bên, biết sđ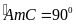 và
sđ
và
sđ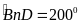
Trả lời:
Định lí: Góc có đỉnh ở bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.
Áp dụng:
Ta
có
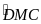 là góc có đỉnh bên trong đường tròn
là góc có đỉnh bên trong đường tròn
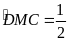 (sđ
(sđ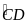 +sđ
+sđ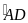 )=
)=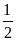 (3600
– sđ
(3600
– sđ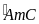 - sđ
- sđ
 )=
)=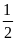 (3600
– 900
– 2000)=350.
(3600
– 900
– 2000)=350.
Câu 14: Chứng minh định lí “Góc có đỉnh bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn”
Trả lời:

B
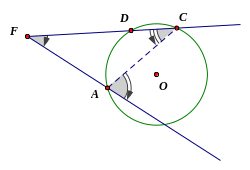
Ta
có
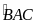 là
góc ngoài của
là
góc ngoài của
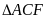
Do
đó
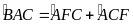
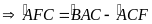 =
=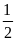 sđ
sđ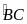 -
-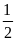 sđ
sđ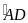 =
=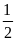 (sđ
(sđ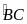 -sđ
-sđ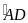 )
)
C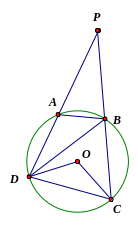 âu
15: Phát
biểu (không chứng minh) định lí về số đo của góc có
đỉnh ở bên ngoài đường tròn.
âu
15: Phát
biểu (không chứng minh) định lí về số đo của góc có
đỉnh ở bên ngoài đường tròn.
Áp
dụng: Cho tứ giác ABCD nội tiếp đường tròn (O), AD và
BC kéo dài cắt nhau tại P. Tính số đo của
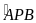 biết
biết
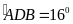 và
và
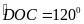
Trả lời:
Định lí: Góc có đỉnh bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn
Áp
dụng: ta có
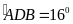
Do
đó sđ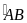 =2.
=2.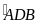 =2.160=320.
=2.160=320.
Mặt
khác ta có
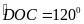
Do
đó sđ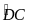 =
=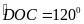
 (sđ
(sđ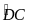 -sđ
-sđ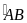 )=
)=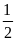 (1200
– 320)=440
(1200
– 320)=440
Câu 16: Chứng minh định lí “Trong một tứ giác nội tiếp, tổng số đo hai góc đối nhau bằng 1800”
-
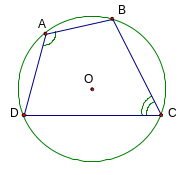
GT
. Cho đường tròn (O) . ABCD nội tiếp (O)
KL
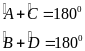
Ta
có:
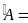
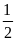 sđ
sđ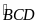 ( sđ góc nội tiếp bằng nửa sđ cung bị chắn)
( sđ góc nội tiếp bằng nửa sđ cung bị chắn)

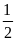 sđ
sđ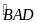 ( sđ góc nội tiếp bằng nửa sđ cung bị chắn)
( sđ góc nội tiếp bằng nửa sđ cung bị chắn)
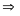
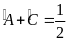 sđ(
sđ(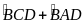 )
=
)
=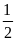 .
. =
=
Tương
tự:
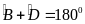 ( hoặc
( hoặc
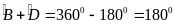 :
tính chất tổng 4 góc của tứ giác)
:
tính chất tổng 4 góc của tứ giác)
Câu 17: Tứ giác nội tiếp là gì? Phát biểu một số dấu hiệu nhận biết tứ giác nội tiếp. Định lí về tứ giác nội tiếp.
Trả lời:
* Định nghĩa:
Một tứ giác có 4 đỉnh nằm trên đường tròn được gọi là tứ giác nội tiếp đường tròn.
* Dấu hiệu nhận biết tứ giác nội tiếp:
Tứ
giác có tổng hai góc đối bằng 1800
Tứ
giác có góc ngoài tại một đỉnh bằng góc trong của
đỉnh đối diện.
Tứ giác có 4 đỉnh cách đều một điểm (mà ta có thể xác định được) điểm đó là tâm của đường tròn ngoại tiếp tứ giác.
Tứ
giác có hai đỉnh kề nhau cùng nhìn cạnh chứa hai đỉnh
còn lại dưới một góc
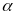
* Định lí thuận: Trong một tứ giác nội tiếp, tổng số đo hai góc đối diện bằng 1800
* Định lí đảo: Nếu một tứ giác có tổng số đo hai góc đối diện bằng 1800 thì tứ giác đó nội tiếp được đường tròn.
Câu 18:Viết công thức tính chu vi của đường tròn
Á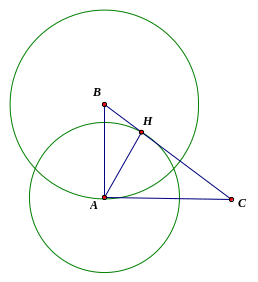 p
dụng: Cho tam giác ABC vuông tại A có đường cao AH với
BH=2
p
dụng: Cho tam giác ABC vuông tại A có đường cao AH với
BH=2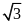 cm
và CH=6
cm
và CH=6 cm.
Tính chu vi của các đường tròn (B;BA) và (A; AH)
cm.
Tính chu vi của các đường tròn (B;BA) và (A; AH)
Trả lời:
Công thức tính chu vi của đường tròn
C=2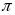 R
hay C=
R
hay C=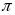 d
d
Trong đó R là bán kính của đường tròn, d là đường kính đường tròn
Áp dụng:
Theo hệ thức giữa cạnh và đường cao trong tam giác vuông ABC
AB2=BH.BC=2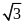 .(2
.(2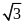 +6
+6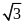 )=2
)=2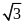 .8
.8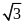 =16.3=48
=16.3=48
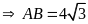 cm
cm
AH2=HB.CH=2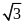 .6
.6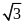 =12.3=36
=12.3=36
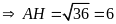 cm
cm
Chu vi của đường tròn (B; BA) là
2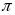 .BA=2.
.BA=2.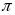 4
4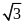 =8
=8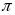
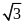 (cm)
(cm)
Chu vi của đường tròn (A, AH) là
2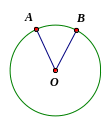
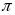 .AH=2
.AH=2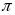 .6=12
.6=12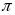 (cm)
(cm)
Câu 19: Viết công thức tính diện tích hình tròn và hình quạt tròn.
Áp
dụng: Tính diện tích của phần hình quạt AOB và hình
tròn trong hình vẽ bên, biết OA=5cm,
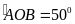 .
.
Trả lời:
Công
thức tính diện tích hình tròn S=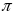 R2
R2
Trong đó: S là diện tích của hình tròn, R là bán kính của hình tròn
Công
thức tính diện tích hình quạt tròn bán kính R, cung n0
là
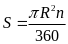 hay
hay
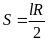
Trong đó: l là độ dài cung của hình quạt tròn
Áp dụng:
Diện tích hình tròn
S=
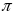 .OA2=
.OA2=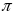 .52=25
.52=25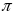 (cm2)
(cm2)
Diện tích hình quạt
SAOB=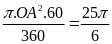 (cm2)
(cm2)
Câu 20 : Chứng minh rằng trong một đường tròn, hai cung bị chắn giữa hai dây song song thì bằng nhau. (Chú ý: Học sinh chỉ chứng minh một trường hợp: một trong hai dây, có một dây đi qua tâm cuả đường tròn)
Trả lời:
-

GT
Cho đường tròn (O) CD: dây cung AB: đường kính AB // CD
KL
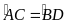
Ta
có:
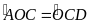
 (
So le trong)
(
So le trong)
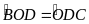 (
So le trong)
(
So le trong)
Mà
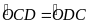 (
(
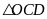 cân tại O)
cân tại O)
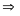
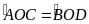
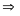
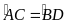 (
2 góc ở tâm bằng nhau thì chắn 2 cung bằng nhau)
(
2 góc ở tâm bằng nhau thì chắn 2 cung bằng nhau)
II/ CÁC PHƯƠNG PHÁP GIẢI BÀI TẬP:
ĐẠI SỐ:
1. HỆ PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN:
a)
Hệ phương trình bậc nhất hai ẩn có dạng
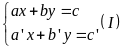
Hệ (I) có nghiệm duy nhất
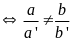
Hệ (I) vô nghiệm

Hệ (I) có vô số nghiệm khi

b) Các bước giải hệ pt bằng phương pháp thế:
Bước 1: Biểu thị một ẩn (Giả sử ẩn x) theo ẩn kia từ một trong hai phương trình (Lưu ý chọn các ẩn có hệ số bằng 1 hoặc -1)
Bước 2: Thay biểu thức của x vào pt kia rồi tìm giá trị của y.
Bước 3: Thay giá trị của y vừa tìm được vào biểu thức của x để tìm giá trị của x.
Bước 4: Kết luận nghiệm của hệ pt.
c) Các bước giải hệ pt bằng phương pháp cộng:
Bước 1: Biến đổi các hệ số của một ẩn (Giả sử x) có giá trị tuyệt đối bằng nhau.
Bước 2: Cộng hoặc trừ từng vế của hai pt để khử ẩn của x. (Hệ số của ẩn x ở hai pt có dấu giống nhau ta làm phép trừ, có dấu khác nhau ta làm phép cộng)
Bước 3: Giải pt tìm giá trị của y.
Bước 4: Thay giá trị của y vừa tìm được vào một trong hai pt ban đầu để tìm giá trị của x (Lưu ý chọn pt đơn giản)
Bước 5: Kết luận nghiệm của hệ pt.
d) Các bước giải bài toán bằng cách lập pt:
Bước 1:Lập hệ pt
Chọn các ẩn và đặt điều kiện thích hợp cho ẩn. Chú ý phải ghi rõ đơn vị của ẩn.
Biểu thị các đại lượng chưa biết theo ẩn và các đại lượng đã biết.
Lập hệ pt biểu thị mối quan hệ giữa các đại lượng.
Bước 2: Giải hệ pt.
Bước 3: Kiểm tra xem trong các nghiệm của hệ pt nghiệm nào thích hợp với điều kiện bài toán rồi kết luận.
2.
HÀM SỐ y=ax2
(a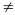 0),
PHƯƠNG TRÌNH BẬC HAI MỘT ẨN:
0),
PHƯƠNG TRÌNH BẬC HAI MỘT ẨN:
Hàm số y=ax2 (a
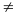 0)
0)
Tính chất
Nếu a>0
Hàm số nghịch biến khi x<0, đồng biến khi x>0
y=0 là giá trị nhỏ nhất của hàm số, đạt được khi x=0
Nếu a<0
Hàm số hàm số nghịch biến khi x>0, đồng biến khi x<0
y=0 là giá trị lớn nhất của hàm số, đạt được khi x=0
Đồ thị của hàm số y=ax2 (a
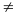 0)
0)
*
Cách vẽ đồ thị hàm số y=ax2
(a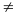 0)
0)
Lập bảng giá trị gồm có 5 cặp giá trị
Vẽ đồ thị
*
Xác định giao điểm của hai đồ thị Parabol (P) y=ax2
(a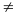 0)
và đường thẳng (d) y=bx+c (b
0)
và đường thẳng (d) y=bx+c (b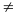 0)
0)
Lập pt hoành độ giao điểm
a2x=bx+c
Chuyển tất cả các hạng tử sang một vế, rồi giải pt bậc hai để tìm x
Thay các giá trị x vừa tìm được vào một trong hai pt của (P) hoặc (d) để tìm giá trị y
Kết luận tọa độ giao điểm của hai đồ thị.
*
Biện luận giao điểm của Parabol (P) y=ax2
(a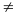 0)
và đường thẳng (d) y=bx+c (b
0)
và đường thẳng (d) y=bx+c (b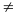 0)
0)
Bước 1: Lập pt hoành độ giao điểm, chuyển các hạng tử sang vế trái, vế phải bằng 0 ta được pt bậc hai một ẩn.
Bước
2: Tính hệ thức
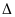 hoặc
hoặc
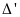
Bước 3: Biện luận
Nếu
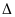 >0
hoặc
>0
hoặc
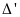 >0
thì (P) cắt (d)
>0
thì (P) cắt (d)Nếu
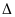 =0
hoặc
=0
hoặc
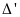 =0
thì (P) tiếp xúc (d)
=0
thì (P) tiếp xúc (d)Nếu
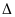 <0
hoặc
<0
hoặc
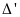 <0
thì (P) không cắt (d)
<0
thì (P) không cắt (d)
Công thức nghiệm của pt bậc hai:
* Công thức nghiệm:
Pt
bậc hai ax2+bx+c=0
(a 0)
0)
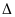 =b2
– 4ac
=b2
– 4ac
Nếu
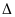 >0
thì pt có hai nghiệm phân biệt
>0
thì pt có hai nghiệm phân biệt
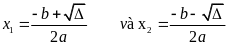
Nếu
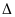 =0
thì pt có nghiệm kép
=0
thì pt có nghiệm kép
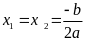
Nếu
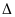 <0
thì pt vô nghiệm
<0
thì pt vô nghiệm
* Công thức nghiệm thu gọn
Pt
bậc hai ax2+bx+c=0
(a 0)
và b=2b’ (hay b’=b:2)
0)
và b=2b’ (hay b’=b:2)
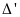 =b’2
– ac
=b’2
– ac
Nếu
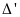 >0
thì pt có hai nghiệm phân biệt
>0
thì pt có hai nghiệm phân biệt
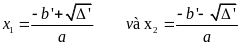
Nếu
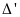 =0
thì pt có nghiệm kép
=0
thì pt có nghiệm kép
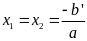
Nếu
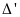 <0
thì pt vô nghiệm
<0
thì pt vô nghiệm
* Các phương pháp giải pt bậc hai:
Phương pháp 1: Dùng công thức nghiệm hoặc công thức nghiệm thu gọn.
Phương pháp 2: Trong các trường hợp đặc biệt:
Nếu a+b+c=0 thì pt có hai nghiệm x1=1 và
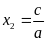
Nếu a – b+c=0 thì pt có hai nghiệm x1=-1 và x2=
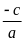
* Lưu ý trước khi giải pt bậc hai ta phải xét xem pt đó có ở dạng đặc biệt nào không, rồi mới áp dụng để giải.
Điều kiện có nghiệm của pt bậc hai:
*
Pt bậc hai ax2+bx+c=0
(a 0)
0)
Pt vô nghiệm khi
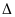 <0
hoặc
<0
hoặc
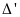 <0
<0Pt có nghiệm khi
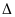
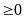 hoặc
hoặc
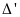
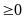
Pt có nghiệm kép khi
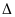 =0
hoặc
=0
hoặc
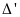 =0
=0Pt có hai nghiệm phâm biệt khi
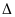 >0
hoặc
>0
hoặc
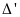 >0
>0
* Lưu ý trong trường hợp hệ số a có chứa tham số, ta cần xét hai trường hợp
Trường hợp 1: a=0, ta có pt bx+c=0, giải pt bậc nhất
Trường hợp 2:
Điều kiện để pt có hai nghiệm phân biệt
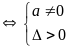 hoặc
hoặc
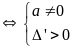
Điều kiện để pt có nghiệm kép
 hoặc
hoặc
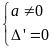
Hệ thức Viet và các ứng dụng:
Pt
bậc hai ax2+bx+c=0
(a 0)
có hai nghiệm x1,
x2
0)
có hai nghiệm x1,
x2
* Hệ thức Vi ét
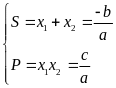
* Tìm hai số biết tổng và tích của chúng:
Nếu hai số u+v=S và uv=P
Thì u và v là hai nghiệm của pt x2 – Sx+P=0
* Tìm giá trị của biếu thức đối xứng giữa các nghiệm:
Bước
1: Tính
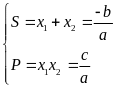
Bước 2: Tính
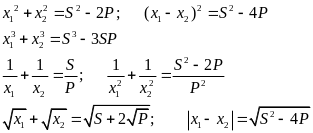
Tìm hệ thức liên hệ giữa các nghiệm không phụ thuộc vào tham số:
Bước
1: Tìm điều
kiện của m để pt có hai nghiệm x1,
x2
Bước
2: Áp dụng hệ
thức Viet ta được
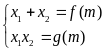 (I)
(I)
Bước 3: Khử m từ hệ (I) ta được hệ thức cần tìm
Xét dấu các nghiệm:
Pt
bậc hai ax2+bx+c=0
(a 0)
0)
Bước
1: Dùng hệ thức
Vi et tính
Bước 2: Lập luận
Pt có hai nghiệm trái dấu
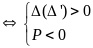
Pt có hai nghiệm cùng dấu
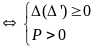
Pt có hai nghiệm dương
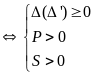
Pt có hai nghiệm âm
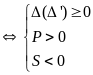
Pt có hai nghiệm là hai số nghịch đảo của nhau
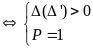
Pt có hai nghiệm là hai số đối nhau khi
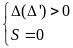
Tìm điều kiện của m để các nghiệm của pt thỏa mãn một điều kiệm K cho trước.
Bước
1: Tìm điều
kiệm của m để pt có hai nghiệm x1,
x2
khi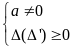
Bước
2: Áp dụng hệ
thức Viet, ta được
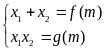 (I)
(I)
Bước 3: Biểu diễn điều kiện K thông qua (I)
Bước 4: Kết luận
Tìm nghiệm còn lại của pt và tìm tham số m
Nếu cho nghiệm x1, tìm nghiệm x2 dùng hệ thức Viet
Tìm m có hai cách:
Cách 1: Dùng hệ thức Viet
Cách 2: Thay giá trị x1 vào pt bậc hai để tìm giá trị m
Phương trình quy về pt bậc hai:
* Pt chứa ẩn ở mẫu:
Bước 1: Tìm ĐKXĐ của pt
Bước 2: Quy đồng mẫu hai vế, rồi khử mẫu
Bước 3: Giải pt vừa nhận được
Bước 4: Kiểm tra các giá trị tìm được ở trên có thõa mãn ĐKXĐ không rồi kết luận
* Giải pt bậc ba: ax3+bx2+cx+d=0 (1)
Bước 1: Dự đoán nghiệm x0 của pt (1)
Các phương pháp dự đoán nghiệm:
Nếu a+b+c+d=0 thì (1) có nghiệm x=1
Nếu a-b+c-d=0 thì pt (1) có nghiệm x=-1
Nếu a,b,c,d nguyên và (1) có nghiệm hữu tỉ
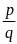 thì p,q theo thứ tự là ước của d và a
thì p,q theo thứ tự là ước của d và aNếu ac3=bd3 (a, d
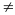 0)
thì pt (1) có nghiệm x=
0)
thì pt (1) có nghiệm x=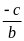
Bước
2: Phân tích (1)
thành (x – x0)(ax2+b1x+c1)=0
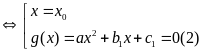
Lưu ý: để phân tích (1) thành (x – x0)(ax2+b1x+c1)=0, ta lấy (1) đem chia cho x – x0 ta được ax2+b1x+c1
Bước 3: Giải (2) rồi kết luận nghiệm của pt (1)
* Giải pt trùng phương ax4+bx2+c=0 (1)
Bước
1: Đặt t=x2
điều kiện t 0
0
Bước 2: Khi đó pt(1) được biến đổi về dạng at2+bt+c=0 (2)
Bước 3: Giải (2) để tìm nghiệm t, từ đó suy ra nghiệm x cho pt (1) (Lưu ý nghiệm t khi giải xong phải kiểm tra xem có thỏa mãn điều kiện hay không)
Chú
ý: nếu pt (2) có nghiệm t0
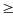 0
thì pt (1) có hai nghiệm x=
0
thì pt (1) có hai nghiệm x=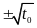
* Phương trình tích:
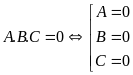
Giải bài toán bằng cách lập pt:
Bước 1:Lập pt
Chọn các ẩn và đặt điều kiện thích hợp cho ẩn. Chú ý phải ghi rõ đơn vị của ẩn.
Biểu thị các đại lượng chưa biết theo ẩn và các đại lượng đã biết.
Lập pt biểu thị mối quan hệ giữa các đại lượng.
Bước 2: Giải pt.
Bước 3: Kiểm tra xem trong các nghiệm của pt nghiệm nào thích hợp với điều kiện bài toán rồi kết luận.
*HÌNH HỌC:
Các phương pháp giải bài toán hình học:
Dạng 1: Chứng minh hai đoạn thẳng bằng nhau:
Vận dụng yếu tố độ dài của đoạn thẳng
Vận dụng hai tam giác bằng nhau
Vận dụng định nghĩa các hình
Vận dụng tính chất các hình
Dạng 2: Chứng minh hai góc bằng nhau
Vận dụng yếu tố số đo của góc
Vận dụng hai tam giác bằng nhau, hai tam giác đồng dạng
Vận dụng định nghĩa các hình
Vận dụng tính chất các hình
Dạng 3: Chứng minh hai cung bằng nhau (Lưu ý trong một đường tròn hay hai đường tròn bằng nhau)
Hai cung có cùng số đo
Hai cung (Nhỏ hơn nửa đường tròn) có dây trương cung bằng nhau
Hai cung (nhỏ hơn nửa đường tròn) có góc ở tâm bằng nhau
Hai cung bị chằn bởi hai góc nội tiếp bằng nhau
Hai cung bị chắn bởi hai dây song song thì bằng nhau
Đường kính vuông góc với một dây thì chia cung bị trương thành hai phần bằng nhau
Đường kính đi qua trung điểm của một dây không đi qua tâm thì chia cung bị trương thành hai phần bằng nhau
Dạng 4: Chứng minh hai đường thẳng song song
Vận dụng dấu hiệu nhận biết hai đường thẳng song song
Vận dụng quan hệ giữa tính vuông góc và tính song song
Vân dụng tính chất đường trung bình của tam giác của hình thang
Vận dụng tính chất của các tứ giác đặc biệt
Vận dụng định lí Talet đảo
Dạng 5: Chứng minh hai đường thẳng vuông góc
Chứng minh góc tạo bởi hai đường thẳng là góc vuông
Vận dụng tính chất hai tia phân giác của hai góc kề bù
Vận dụng tính chất của tam giác cân, tam giác vuông
Vận dụng tính chất các đường đặc biệt trong tam giác
Vận dụng tính chất các đường chéo của hình thoi, hình vuông
Vận dụng định lí Pytago đảo
Vận dụng đường kính đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây đó
Vận dụng tiếp tuyến của đường tròn thì vuông góc với bán kính đi qua tiếp điểm
Vận dụng đường nối tâm của hai đường tròn cắt nhau là đường trung trực của dây chung, từ đó đường nối tâm thì vuông góc với dây chung
Vận dụng góc nội tiếp chắn nửa đường tròn là góc vuông
Dạng 6: Chứng minh ba điểm thẳng hàng
Vận dụng tính chất của hai tia đối nhau
Vận dụng hai đường thẳng cùng đi qua một điểm và song song hoặc vuông góc với một đường thẳng thì trùng nhau
Vận dụng tính chất các đường đặc biệt trong tam giác
Vận dụng tính chất các đường chéo các tứ giác đặc biệt
Vận dụng hai mút của đường kính và tâm của đường tròn là ba điểm thẳng hàng
Vận dụng hai tâm của đường tròn tiếp xúc nhau và tiếp điểm là ba điểm thẳng hàng
Dạng 7: Chứng minh tứ giác nội tiếp
Tứ giác có tổng hai góc đối nhau bằng 1800
Tứ giác có góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối của đỉnh đó
Tứ giác có 4 đỉnh cách đều một điểm (mà ta có thể xác định). Điểm đó là tâm của đường tròn ngoại tiếp tứ giác
Tứ giác có hai đỉnh kề nhau cùng nhìn cạnh chứa hai đỉnh còn lại dưới một góc a
Dạng 8: Chứng minh ba đường thẳng đồng quy
Giao điểm của hai đường thẳng nằm trên đường thẳng còn lại
Chỉ ra một điểm thuộc cả ba đường thẳng
Vận dụng tính chất đồng quy của ba đường cùng tên của một tam giác
Vận dụng tính chất về đường chéo của hình bình hành
Dạng 9: Chứng minh đường thẳng là tiếp tuyến của đường tròn
Đường thẳng vuông góc với bán kính đi qua tiếp điểm
Đường thẳng đi qua một điểm và vuông góc với bán kính đi qua điểm đó
Khoảng cách từ tâm đường tròn đến đường thẳng bằng bán kính của đường tròn
Phương pháp phản chứng
Dạng 10: Tính toán
Vận dụng kiến thức về định lí, hệ quả của định lí Talet, tam giác đồng dạng
Vận dụng hệ thức lượng trong tam giác vuông
Vận dụng các công thức tính diện tích hình phẳng
Vận dụng tỉ số lượng giác của góc nhọn
Vận dụng hệ thức về cạnh
Dạng 11: Chứng minh đẳng thức a.b=c.d
Chứng minh hai tam giác đồng dạng
Vận dụng các hệ thức về cạnh và đường cao trong tam giác.
III/ BÀI TẬP:
Câu 1: Giải các hệ phương trình sau:
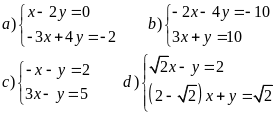
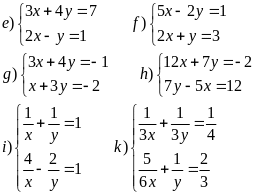
Câu 2: Giải các hệ phương trình sau:

Câu
3: Cho hệ phương trình: 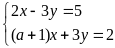
Tìm giá trị của a để hệ pt có nghiệm, vô nghiệm
Câu
4: Cho hệ pt
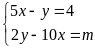
Tìm m để hệ vô nghiệm, vô số nghiệm
Câu 5: Cho hai hàm số (P): y=x2 và (d): y= -2x+3
Vẽ (P) và (d) trên cùng một hệ trục tọa độ
Tìm tọa độ giao điểm của (P) và (d)
Câu
6:Cho
(P) y=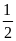 x2
và (d) y=
x2
và (d) y=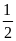 x+1
x+1
a) Vẽ (P) và (d) trên cùng một hệ trục tọa độ
Tìm tọa độ giao điểm A, B của (P) và (d)
Gọi C là một điểm trên (P) có hoành độ là 1. Tính diện tích tam giác ABC
Câu 7: Cho hàm số y=ax2 có đồ thị là (P)
a)
Tìm hệ số a cho biết
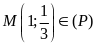
b) Tìm tung độ của điểm N thuộc (P) có hoành độ x= -2
c) Tìm các điểm thuộc (P) có tung độ y=3
d) Vẽ (P)
Câu 8: Cho (P): y=2x2 và (d): y=3x+m+1
Cho m= -1, Vẽ (P) và (d) trên cùng hệ trục tọa độ và xác định tọa độ giao điểm của chúng.
Với giá trị nào của m thì (P) cắt (d); (P) tiếp xúc (d); (P) không cắt (d)
Câu
9: Cho (P): y=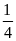 x2
và đường thẳng (d) đi qua A và B trên (P) có hoành độ
lần lượt là -2 và 4.
x2
và đường thẳng (d) đi qua A và B trên (P) có hoành độ
lần lượt là -2 và 4.
Vẽ đồ thị (P)
Viết phương trình đường thẳng (d)
Câu 10: giải phương trình
x2 – 4x – 5=0
x2+8x+15=0
3x2+8x+3=0
2x4 – 5x2 – 7=0
x4 – 4x2 – 8=0
(3x+4)2 – 9(x – 2)2=0
5x4+2x2 - 16=10 – x2
(2x+
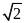 )2
– 1=(x+1)(x – 1)
)2
– 1=(x+1)(x – 1)

k)
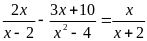
l)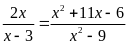
m)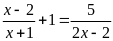
Câu 11: Dùng hệ thức Viet để tìm nghiệm x2 của phương trình rồi giá trị của m trong mỗi trường hợp sau:
x2 – (m – 1)x – 21=0, biết x1=3
2x2 – mx+4=0, biết x1=
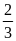
x2 – 2(m+4)x – 3=0, biết x1=
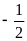
x2+x+m=0, biết x1=-2
Câu 12: Cho pt: x2 – (m+2)x+3m – 4=0 (1)
Tìm m để pt có một nghiệm x=2
Tìm m để pt có hai nghiệm đối nhau. Tính hai nghiệm đó.
Câu 13: Cho pt 3x2 – 9x +5=0 có hai nghiệm x1 và x2. Không giải pt, hãy dùng hệ thức Viet để tính:
x12 + x22
x13 + x23
x1 - x2
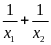
Câu 14: Với giá trị nào của m thì pt x2 – 2(m+3)x+m2 – 15=0
Có hai nghiệm phân biệt
Có nghiệm kép. Tính nghiệm kép đó
Câu 15: Cho pt x2 – 3mx+2m+4=0 (1)
Chứng tỏ pt (1) luôn có hai nghiệm phân biệt
Không giải pt, dùng hệ thức Viet tính tổng và tích các nghiệm x1, x2
Cho pt (1) có một nghiệm x1=2. Hãy tính giá trị của m rồi tính nghiệm x2
Tìm m để pt (1) có hai nghiệm đối nhau
Tìm m để pt (1) có hai nghiệm là hai số nghịch đảo
Câu 16: Cho pt x2 – (m – 1)x – m2+m – 2=0 (2)
Giải pt (2) khi m=0
CMR pt (2) có hai nghiệm với mọi m
Tìm m để A= x12+x22 đạt giá trị nhỏ nhất
Câu 17: Cho pt x2 – 2(1+2m)x+3+4m=0 (3)
Giải pt (3) khi m=1
CMR pt (3) luôn có hai nghiệm phân biệt với mọi m
Tìm m để A=x12+x22 đạt giá trị nhỏ nhất
Câu 18: Cho pt x2 – 2(m – 1)x+m – 5=0 (4)
Tìm m để pt (4) có một nghiệm x1= -1. Tìm nghiệm còn lại
CMR pt (4) luôn có hai nghiệm phân biệt với mọi m
Tìm m để A=x12+x22 đạt giá trị nhỏ nhất
Tìm m để pt (4) có hai nghiệm là hai số nghịch đảo của nhau
Tìm m để pt (4) có hai nghiệm là hai số đối nhau
Tìm m để pt (4) có hai nghiệm trái dấu
Tìm m để pt (4) có hai nghiệm cùng dấu
Câu 19: Cho pt x2 +2x – (m+1)=0 (5)
Giải pt (5) khi m=2
Tìm m để pt (5) có nghiệm
Tìm m để pt (5) có hai nghiệm x1, x2 thỏa (x1 – x2)2 =10
Tìm m để A=x13x2+x1x23 đạt giá trị lớn nhất
Câu 20: Cho pt x2 – 4x+m – 1=0 (6)
Tìm m để pt (6) có hai nghiệm phân biệt
Tìm m để pt (6) có nghiệm kép. Tính nghiệm kép
Tìm m để pt (6) vô nghiệm
Câu 21:Cho pt x2 – 4x+2m+1=0 (7)
Giải pt (7) khi m=1
Tìm điều kiện của m để (7) có nghiệm
Tìm giá trị của m sao cho (7) có hai nghiệm x1, x2 thỏa mãn x12+x22=13
Câu 22: Cho pt bậc hai: x2+2x+m=0 (8)
Tìm điều kiện của m để pt (8) có nghiệm
Giải pt với m=-8.
Tìm giá trị của m để pt (8) có hai nghiệm x1, x2 thỏa mãn x12+x22=5.
Câu 23: Cho tam giác ABC vuông tại A, AH là đường cao và AM là trung tuyến (H, M thuộc BC). Đường tròn tâm H, bán kính HA cắt tia AB tại D và tia AC tại E.
Chứng minh ba điểm D, H, E thẳng hàng
Chứng minh MA vuông góc với DE
Giả sử C=300, AH=4cm. Tính diện tích tam giác HEC.
Câu 24: Cho tam giác ABC vuông tại A. Gọi M là trung điểm của cạnh AC. Đường tròn tâm O đường kính MC cắt BC tại N. Đường nối BM kéo dài gặp đường tròn tại D.
Chứng minh tứ giác BADC nội tiếp đường tròn. Xác định tâm I của đường tròn này.
Chúng minh DB là phân giác của góc ADN
Kéo dài BA cà CD gặp nhau tại S. Chứng minh ba điểm S, M, N thẳng hàng.
Câu 25: Cho nửa đường tròn tâm O, đường kính AB. Cho C, D là hai điểm nằm trên nửa đường tròn ấy và C, D khác với A, B (D nằm giũa C và B), AC cắt BD tại E, AD cắt BC ở F.
Chứng minh tứ giác ECFD nội tiếp. Xác định tâm của đường tròn đó.
CMR: Góc AEF bằng góc ABC. Suy ra EF vuông góc với AB.
Cho EF=AB=2R (cm) và AC=R (cm). Chứng minh tam giác ABC bằng tam giác FEC. Có nhận xét gì về tam giác ACF?
Tính diện tích tam giác ABE theo R
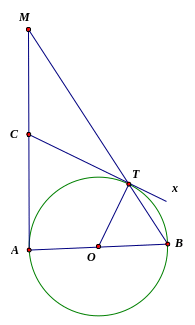
Câu 26: Cho nửa đường tròn tâm O, đường kính AB=2R. Trên tiếp tuyến của đường tròn (O) tại A, lấy điểm C rồi vẽ tiếp tuyến thứ hai CT. Đường thẳng BT cắt AC tại M.
CMR: Từ giác AOTC nội tiếp. Xác định tâm của đường tròn đó.
CMR: Tam giác CTM cân tại C
Tính diện tích tứ giác OBMC theo R nếu AC=
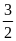 R
R
Câu 27: Cho đường tròn (O,R) AB là đường kính. Trên đường tròn lấy hai điểm M và N (theo thứ tự A, M, N, B). AM cắt BN tại S, BM cắt AN tại H
CM: Tứ giác SMHN nội tiếp
Gọi K là giao điểm của SH và AB. Chứng minh SH vuông góc với AB tại K, suy ra AM.AS=AK.AB
Giả sử MN//AB và MN=R. Tính diện tích hình phẳng được giới hạnh bởi SM, SN và cung nhỏ MN theo R.
Câu 28: Cho tam giác ABC vuông tại A(AB<AC) và nội tiếp trong đường tròn tâm O. Gọi M, N lần lượt là trung điểm của AB và AC.
Chứng minh tứ giác AMON là hình chữ nhật
Vẽ đường cao AH và tia phân giác trong góc A của tam giác ABC, tia phân giác này cắt BC tại tại I và đường tròn tâm O tại E. Chứng minh rằng E là điểm chính giữa của cung BC và OE vuông góc với BC
Chứng minh AE cũng là tia phân giác của góc OAH
Tiếp tuyến tại A của đường tròn tâm O cắt CB kéo dài tại S. Chứng minh tam giác SAI cân tại S
Câu 29: Một khu vườn hình chữ nhật có diện tích bẳng 675m2 và chu vi bằng 120m. Tìm chiều dài và chiều rộng của khu vườn.
Câu 30:Giải bài toán sau bằng cách lập phương trình: Tính độ dài hai cạnh góc vuông của một tam giác vuông nội tiếp đường tròn bán kính 6,5cm.Biết rằng hai cạnh góc vuông của tam giác hơn kém nhau 7cm .
Câu 31: Một ca nô xuôi một khúc sông dài 50km, rồi ngược dòng trở lại 32km hết tất
cả 4giờ 30phút.
Tính vận tốc dòng nước biết vận tốc thực của ca nô là 18km/giờ.
Câu 32: Tìm số tự nhiên có hai chữ số. Biết rằng số đó có tổng các chữ số bằng 8 và nếu đổi vị trí hai chữ số cho nhau thì số tự nhiên đó tăng lên 18 đơn vị.
Câu 33: Tìm số tự nhiên có hai chữ số. Biết chữ số hàng chục lớn hơn chữ số hàng đơn vị là 5, nếu viết xen chữ số 0 vào giữa chữ số hàng chục và chữ số hàng đơn vị thì số tự nhiên đó tăng 630 đơn vị.
Câu 34: Một người đi xe đạp dự định đi hết quãng đường AB với vận tốc 10km/h. Sau khi đi được nữa quãng đường với vận tốc dự định người ấy nghĩ 30 phút. Vì muốn đến B kịp giờ nên người ấy phải đi với vận tốc 15 km/h trên quãng đường còn lại. Tính quãng đường AB.
Câu
35: Hai máy
bơm cùng bơm nước vào một bể sau
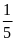 giờ thì đầy bể. Nếu máy bơm I bơm trong 10 phút, máy
bơm II bơm trong 6 phút thì hai máy bơm được
giờ thì đầy bể. Nếu máy bơm I bơm trong 10 phút, máy
bơm II bơm trong 6 phút thì hai máy bơm được
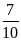 bể. Hỏi mỗi máy bơm làm việc một mình mất bao nhiêu
giờ?
bể. Hỏi mỗi máy bơm làm việc một mình mất bao nhiêu
giờ?
Câu 36: Tìm hai số biết hiệu của chúng bằng 5 và tổng các bình phương của chúng bằng 125.
Câu 37: Một ô tô dự định đi quãng đường AB dài 60km. Trong một thời gian nhất định, trên nửa quãng đường AB do đường xấu nên ô tô chỉ đi với vận tốc ít hơn dự định 6km/h, Để đến B đúng dự định, ô tô phải đi quãng đường còn lại với vận tốc nhanh hơn vận tốc dự định 10km/h. Tính thời gian dự định đi hết quãng đường.
Câu 38: Đồng lúa của xã Đại Đồng rộng hơn đồng lúa của xã Bình Minh là 12ha. Trong vụ thu hoạch, xã Đại Đồng thu được 1470 tấn, còn xã Bình Minh thu được 1440 tấn. Tuy nhiên, năng suất lúa ở xã Bình Minh cao hơn ở xã Đại Đồng là 1 tạ/ha. Tính năng suất lúa ở mỗi xã. (49, 50)
Câu 39: Một xe khách và một xe du lịch khởi hành đồng thời từ TP Hồ Chí Minh đi Tiền Giang. Xe du lịch có vận tốc hơn vận tốc của xe khách là 20 km/h, do đó nó đến Tiền Giang trước xe khách 25 phút. Tính vận tốc của mỗi xe, biết rằng khoảng cách giữa TP Hồ Chí Minh và Tiền Gaing là 100km. (Khách: 60, du lịch: 80)
HƯỚNG DẪN VÀ ĐÁP ÁN:
Câu 1:
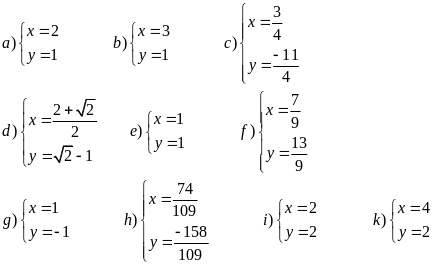
Câu 2:
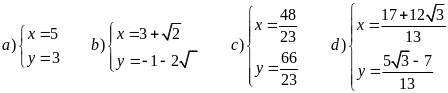
Đặt

Giải
hệ phương trình được
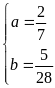
Sau
đó giải hệ phương trình theo ẩn x, y ta được
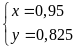
Câu
3: có
nghiệm
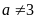 ;
a=3
;
a=3
Câu
4: Vô
nghiệm m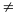 -8;
có vô số nghiệm m=-8
-8;
có vô số nghiệm m=-8
Câu 5:
Đồ thị HS tự vẽ
(1;1); (-3;9)
Câu 6:
HS tự vẽ
A(-1; 0,5); B(2;2)
C(1; 0,5)
Câu 7:
a)
a=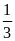 b)
yN=
b)
yN=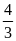 c)
x=
c)
x= 3
3
Câu 8:
(0;0); (1,5; 18)
(P) cắt (d) khi m>
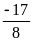 ;
(P) tiếp xúc (d) khi m=
;
(P) tiếp xúc (d) khi m=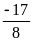 ;
(P) không cắt (d) khi m<
;
(P) không cắt (d) khi m<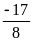
Câu 9:
HS tự vẽ
Tìm A(-2; 1) và B(4;4), rồi viết phương trình đường thẳng y=
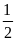 x+2
x+2
Câu 10:
a)
5; -1 b) -3; -5 c)
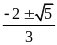 d)
d)
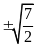
e)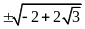 f)
f)
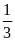 g)
g)
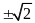 h)
h)
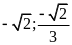
i)
4 j)4;
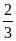 k)3 l)
2 m)3;
k)3 l)
2 m)3;

Câu 11: sử dụng hệ thức viet để tìm x2, thay x1 vào phương trình để tìm m
a) x2=-7; m=-3
b)
x2=3;
m=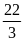
c)
x2=6;
m=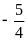
d) x2=1; m=-2
Câu 12:
a)
m=4 b)m=-2 x1,2=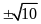
Câu 13:
a)
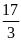 b)12 c)
b)12 c) d)
d)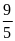
Câu 14:
a) m>-4 b) m=-4; x1=x2=-1
Câu 15:
Chứng minh
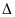 >0
với mọi m
>0
với mọi mS=3m; P=2m+4
m=2; x2=4
m=0
m=
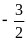
Câu 16:
a)
1; -2 b)
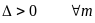 c)GTNN
c)GTNN
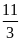 khi m=
khi m=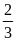
Câu 17:
a)
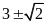 b)
Chứng minh
b)
Chứng minh
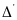 >0
với mọi m
>0
với mọi m
c) GTNN -6 khi m=1
Câu 18:
a)
m=2; x2=3 b)
Chứng minh
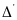 >0
với mọi m
>0
với mọi m
c)
GTNN:
 d)
m=6
d)
m=6
e) m=1 f) m<5 g) m>5
Câu 19:
a)
1; -3 b) m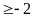
c)
m=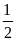 d)
GTLN: 2 khi m=-2
d)
GTLN: 2 khi m=-2
Câu 20:
a) m<5 b) m=5 nghiệm kép x=2 c) m>5
Câu 21:
a)
1; 3 b) m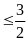 c)
m=
c)
m=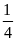
Câu 22:
a)
m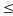 1 b)-4;
2 c) m=
1 b)-4;
2 c) m=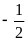
Câu 23:
a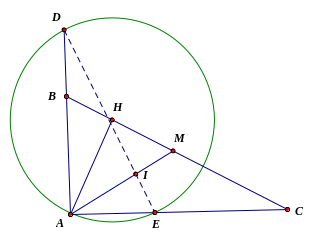 )
Vận dụng hai mút của đường kính và tâm của đường
tròn là ba điểm thẳng hàng
)
Vận dụng hai mút của đường kính và tâm của đường
tròn là ba điểm thẳng hàng
b) Chứng minh


Chứng
minh
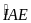 =
=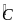 và
và
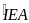 =
=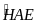
Chứng minh AE=4cm, tính AC (hệ thức giữa cạnh và góc trong tam giác vuông AHC); tính EC=AC – AE; Tính đường cao HF của tam giác HEC (áp dụng hệ thức giữa cạnh và góc trong tam giác vuông AHF); Tính SHCE=
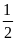 EC.HF
EC.HF
C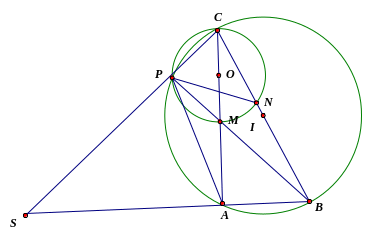 âu
24:
âu
24:
Sử dụng dấu hiệu 4
Chứng minh
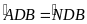 bằng cách sử dụng góc trung gian
bằng cách sử dụng góc trung gian
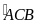
Chứng minh SM, MN cùng vuông góc với BC (cách thứ hai trong chứng minh ba điểm thẳng hàng)
C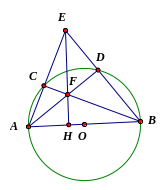 âu
25:
âu
25:
Sử dụng dấu hiệu một
Tìm góc trung gian là góc ADC
Hai tam giác ABC và tam giác FEC bằng nhau (Cạnh huyền – góc nhọn). Tam giác ACF vuông cân tại C
S
 ABE=
ABE=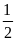 HE.
AB; Tính HE áp dụng hệ thức giữa cạnh và góc trong tam
giác vuông AEH
HE.
AB; Tính HE áp dụng hệ thức giữa cạnh và góc trong tam
giác vuông AEH
Câu 26:
Dấu hiệu 1
Chứng minh
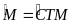
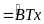
SOBMC=SABM – SACO.
C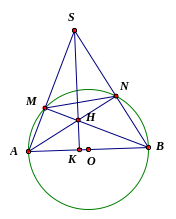 âu
27:
âu
27:
Dấu hiệu 1
SH là đường cao thứ ba của tam giác SAB; Chứng minh hai tam giác ASK và ABM đồng dạng
SOMSN - SquạtMON.
C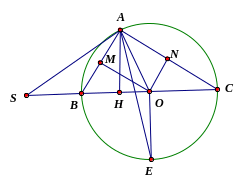 âu
28:
âu
28:
Hình bình hành có một góc vuông
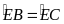 ,
từ đó suy ra OE vuông góc với BC
,
từ đó suy ra OE vuông góc với BC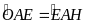 (góc
trung gian
(góc
trung gian
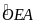 )
)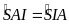
Ngoài Đề Cương Ôn Tập Toán 9 Học Kỳ 2 Năm 2021-2022 Có Lời Giải – Toán 9 thì các tài liệu học tập trong chương trình 9 sẽ được cập nhật liên tục và nhanh nhất có thể sau khi kỳ thi diễn ra trên Danh mục Tài Liệu Học Tập nhằm giúp các bạn đọc thuận tiện trong việc nghiên cứu tài liệu. Quý thày cô và các bạn đọc có thể chia sẻ thêm những tài liệu học tập hữu ích đến địa chỉ email của chúng tôi, nhằm xây dựng nên kho đề thi phong phú, đa dạng cho các em học sinh tham khảo và rèn luyện.
Đề cương ôn tập học kỳ 2 môn Toán lớp 9 năm học 2021-2022 là một tài liệu quan trọng để bạn ôn tập và chuẩn bị cho kỳ thi học kỳ cuối. Đề cương này bao gồm các chủ đề đã học trong học kỳ, nhằm giúp bạn củng cố và nắm vững kiến thức cơ bản.
Đề cương này tập trung vào các chủ đề như đại số, hình học, giải tích và xác suất. Bạn sẽ được ôn tập các công thức, quy tắc và phương pháp giải quyết bài tập liên quan đến các chủ đề này.
Lời giải chi tiết trong đề cương giúp bạn hiểu rõ cách giải quyết từng bài tập. Nó cung cấp các bước giải chi tiết và giải thích logic để bạn có thể áp dụng vào các bài tương tự.
>>> Bài viết có liên quan:






