Giải bài tập toán lớp 5 trang 175 | Tìm x, Nhân chia cộng trừ phân số

Toán lớp 5 trang 175 Luyện tập chung bao gồm các bài tập tự luyện SGK có phương pháp giải và lời giải chi tiết cho từng dạng bài tập cho các em học sinh tham khảo, nắm được cách giải các dạng toán có lời văn, nhân chia cộng trừ số tự nhiên, phân số, bài toán tìm x, toán có nội dung hình học, hệ thống lại các kiến thức Toán 5 chương 5 Ôn tập cuối năm. Cùng Trang Tài Liệu xem thêm dưới đây

Giải Toán lớp 5 trang 175 bài 1

Câu 1: Tính

a) 85793 – 36841 + 3826

b)  ;

c) 325,97 + 86,54 + 103,46.

Hướng dẫn giải

– Biểu thức chỉ có phép cộng và phép trừ thì ta tính lần lượt từ trái sang phải.

– Thực hiện phép tính đối với số tự nhiên và phân số

Đáp án

a) 85793 – 36841 + 3826

= 48952 + 3826

= 52778

b)

= =;

c) 325,97 + 86,54 + 103,46

= 412,51 + 103,46

= 515,97.

Giải Toán lớp 5 trang 175 bài 2

Câu 2: Tìm x:

a) x + 3,5 = 4,72 + 2,28

b) x – 7,2 = 3,9 + 2,5

Hướng dẫn giải

– Tính giá trị vế phải.

– Tìm x dựa vào các quy tắc đã học:

+ Muốn tìm số hạng chưa biết ta lấy tổng trừ đi số hạng đã biết.

+ Muốn tìm số bị trừ ta lấy hiệu cộng với số trừ.

Đáp án

a) x + 3,5 = 4,72 + 2,28

x + 3,5 = 7

x = 7 – 3,5

x = 3,5

b) x – 7,2 = 3,9 + 2, 5

x – 7,2 = 6,4

x = 6,4 + 7,2

x = 13,6.

Giải Toán lớp 5 trang 175 bài 3

Câu 3: Một mảnh đất hình thang có đáy bé là 150m, đáy lớn bằng  đáy bé, chiều cao bằng đáy lớn. Hỏi diện tích mảnh đất bằng bao nhiêu mét vuông, bao nhiêu héc-ta?

Hướng dẫn giải

– Tính đáy lớn = đáy bé × .

– Tính chiều cao = đáy lớn × .

– Tính diện tích = (đáy lớn + đáy bé) × chiều cao : 2.

– Đổi số đo diện tích sang đơn vị héc-ta, lưu ý rằng 1ha = 10000m²

Đáp án

Hình thang có đáy bé = 150m, mà đáy lớn bằng đáy bé.

Độ lớn của mảnh đất hình thang là:

Chiều cao của mảnh đất hình thang là:

Hình thang có: đáy lớn = 250m , đáy bé = 150m, chiều cao = 100m

Diện tích mảnh đất hình thang là:

20000m² = 2 ha

Đáp số: 20000m^2; 2 ha.

Giải Toán lớp 5 trang 175 bài 4

Câu 4: Lúc 6 giờ, một ô tô chở hàng đi từ A với vận tốc 45km/giờ. Đến 8 giờ, một ô tô du lịch cũng đi từ A với vận tốc 60km/giờ và đi cùng chiều với ô tô chở hàng. Hỏi đến mấy giờ thì ô tô du lịch đuổi kịp ô tô chở hàng?

Hướng dẫn giải

Hai xe chuyển động cùng chiều và xuất phát không cùng lúc. Để giải bài toán này ta có thể làm như sau:

Bước 1: Tính thời gian ô tô chở hàng chở hàng đi trước ô tô du lịch = 8 giờ – 6 giờ = 2 giờ.

Bước 2: Tính số ki-lô-mét ô tô chở hàng đi trước ô tô du lịch (chính là quãng đường ô tô chở hàng đi được trong 2 giờ).

Bước 3: Tính số ki-lô-mét mà mỗi giờ ô tô du lịch gần ô tô du lịch chở hàng.

Bước 4: Tính thời gian đi để ô tô du lịch đuổi kịp ô tô chở hàng = số ki-lô-mét ô tô chở hàng đi trước ô tô du lịch : số ki-lô-mét mà mỗi giờ ô tô du lịch gần ô tô chở hàng.

Bước 5: Thời gian lúc ô tô du lịch đuổi kịp ô tô chở hàng = thời gian lúc ô tô du lịch xuất phát + thời gian đi để ô tô du lịch đuổi kịp ô tô chở hàng.

Đáp án

Ô tô chở hàng đi từ A lúc 6 giờ, ô tô du lịch đi từ A lúc 8 giờ.

Thời gian ô tô chở hàng đi trước ô tô du lịch là:

8 giờ – 6 giờ = 2 giờ.

Ô tô chở hàng đi với v = 45km/giờ.

Quãng đường ô tô chở hàng đi trong 2 giờ là:

45 x 2 = 90 (km)

v_{ô tô chở hàng} = 45km/giờ ; v_{ô tô du lịch} = 60km/giờ

Sau mỗi giờ ô tô du lịch đến gần ô tô chở hàng là:

60 – 45 = 15 (km)

Ô tô chở hàng đi trước 90km, mà mỗi giờ ô tô du lịch gần ô tô chở hàng thêm 15km.

Thời gian ô tô du lịch đi để đuổi kịp ô tô chở hàng là:

90 : 15 = 6 (giờ)

Ô tô du lịch đuổi kịp ô tô chở hàng lúc:

8 giờ + 6 giờ = 14 (giờ)

Đáp số: 14 giờ.

Giải toán lớp 5 trang 175 bài 5

Câu 5: Tìm số tự nhiên thích hợp của x sao cho:

Hướng dẫn giải

Áp dụng tính chất cơ bản của phân số: Nếu nhân cả tử số và mẫu số của một phân số với cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.

Đáp án

Cách 1:

Ta có: 

Do đó: .

Suy ra: x = 20 (Hai phân số bằng nhau có tử số bằng nhau thì mẫu số cũng bằng nhau).

Cách 2: 

hay 4 : x = 

x = 4 : 

x = 20

Cách 3:

hay 4 : x = 0,2

x = 4 : 0,2

x = 20

Cách 4:

Tỉ số giữa 4 và x là 

Vậy x gấp 5 lần 4

Suy ra x = 4 x 5

x = 20

Ôn luyện với Bài tập toán lớp 5 trang 176

Giải Toán lớp 5 trang 176 bài 1

Câu 1: Tính

a) 683 x 35

1954 x 425

2438 x 306

b)

;

;

;

c) 36,66 : 7,8

15,7 : 6,28

27,63 : 0,45

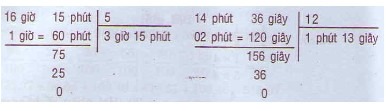
d) 16 giờ 15 phút : 5

14 phút 36 giây : 12.

Hướng dẫn giải

– Đặt tính rồi tính theo các quy tắc đã học về phép nhân hoặc phép chia số tự nhiên.

– Muốn nhân hai phân số ta lấy tử số nhân với tử số, mẫu số nhân với mẫu số.

– Muốn chia hai phân số ta lấy phân số thứ nhất nhân với phân số thứ hai đảo ngược.

– Cách chia số đo thời gian

• Ta đặt tính như đối với phép chia các số tự nhiên.
• Chia từng số đo ở số bị chia cho số chia (theo thứ tự từ trái sang phải).
• Khi tính sau mỗi kết quả ta phải ghi đơn vị đo tương ứng.

Đáp án

a) 683 x 35 = 23905

1954 x 425 = 830450

2438 x 306 = 746028

Ta đặt tính như sau:

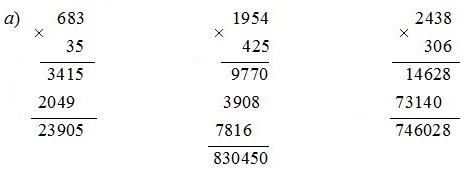
b)

c)

36,66 : 7,8 = 4,7

15,7 : 6,28 = 2,5

27,63 : 0,45 = 61,4

Ta đặt tính như sau

c)

16 giờ 15 phút : 5 = 3 giờ 15 phút

14 phút 36 giây : 12 = 1 phút 13 giây

Ta đặt tính như sau

Giải Toán lớp 5 trang 176 bài 2

Câu 2: Tìm x:

a)

b) 

c) 5,6 : x = 4;

d) 

Hướng dẫn giải

Áp dụng các quy tắc:

– Muốn tìm thừa số chưa biết ta lấy tích chia cho thừa số đã biết.

– Muốn tìm số bị chia ta lấy thương nhân với số chia.

– Muốn tìm số chia ta lấy số bị chia chia cho thương.

Đáp án

a) 0,12 x X = 6

X = 6 : 0,12

X = 50.

b) x : 2,5 = 4

x = 4 x 2,5

x = 10.

c) 5,6 : x = 4

x = 5,6 : 4

x = 1,4

d)

Giải Toán lớp 5 trang 176 bài 3

Câu 3: Trong ba ngày một cửa hàng bán được 2400kg đường. Ngày thứ nhất bán được 35% số đường đó, ngày thứ hai bán được 40% số đường đó. Hỏi ngày thứ ba cửa hàng đó bán được bao nhiêu ki-lô-gam đường?

Hướng dẫn giải

Cách 1:

– Tìm số đường bán ngày thứ nhất, ngày thứ hai theo quy tắc:

Muốn tìm a% của B ta có thể lấy B chia cho 100 rồi nhân với a hoặc lấy B nhân với a rồi chia cho 100.

– Số đường bán ngày thứ ba = số đường bán trong ba ngày − số đường bán ngày thứ nhất − số đường bán ngày thứ hai.

Cách 2:

– Tìm tỉ số phần trăm của số đường bán ngày thứ ba so với tổng số đường bán trong ba ngày.

– Tìm số đường bán ngày thứ ba theo quy tắc:

Muốn tìm a% của B ta có thể lấy B chia cho 100 rồi nhân với a hoặc lấy B nhân với a rồi chia cho 100.

Đáp án

Cách 1

Số ki-lô-gam đường cửa hàng đó đã bán trong ngày đầu là:

2400 x 35 : 100 = 840 (kg)

Số ki-lô-gam đường cửa hàng đó đã bán trong ngày thứ hai là:

2400 x 40 : 100 = 960 (kg)

Số ki-lô-gam đường cửa hàng đó đã bán trong ngày thứ ba là:

2400 – (840 + 960) = 600 (kg)

Đáp số: 600kg đường.

Cách 2:

Số đường bán được ngày thứ ba chiếm số phần trăm số đường bán được trong cả ba ngày là:

100% – (35% + 40%) = 25%

Trong ngày thứ nhất cửa hàng bán được số ki-lô-gam đường là:

2400 : 100 × 25 = 600 (kg)

Đáp số: 600kg đường.

Giải Toán lớp 5 trang 176 bài 4

Câu 4: Một cửa hàng bán hoa quả (trái cây) thu được 1 800 000 đồng. Tính ra số tiền lãi bằng 20% số tiền mua. Hỏi tiền vốn để mua số hoa quả đó là bao nhiêu đồng

Hướng dẫn giải

Áp dụng công thức: tiền bán = tiến vốn + tiền lãi.

Bước 1: Nếu coi số tiền mua là 100%, tìm tỉ số phần trăm của số tiền bán hàng so với tiền mua hàng

Bước 2: Tính số tiền vốn bỏ ra để mua hoa quả

Bằng số tiền bán hàng chia cho 120% (hay chia cho 120 rồi nhân với 100)

Đáp án

Coi số tiền mua là 100% số tiền bán hàng:

100 % + 20% = 120% (số tiền mua)

Số tiền vốn để mua số hoa quả đó là:

1 800 000 : 120% = 1 500 000 (đồng)

Đáp số: 1 500 000 (đồng)

Có thể lập luận theo cách sau

Tiền lãi = 20% số tiền mua, mà tiền mua (vốn) + tiền lãi = 1 800 000 đồng

1 800 000 đồng bằng số phần trăm tiền mua là:

100% + 20% = 120%

Số tiền vốn để mua hoa quả là:

 (đồng)

Đáp số: 1500000 đồng

Tham khảo và luyện tập bài tập SBT Toán 5 ở bên dưới đây. Luyện tập chung để biết thêm các cách giải bài tập toán ôn tập tổng hợp học kì 1, 2. Hy vọng với những tài liệu học tập này, các em học sinh sẽ học tốt môn Toán lớp 5 hơn mà không cần sách giải. Chúc các bạn học tốt.