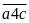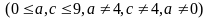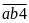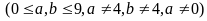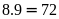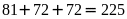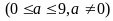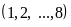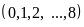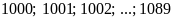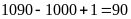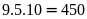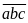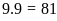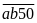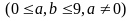Chuyên Đề Bồi Dưỡng HSG Toán 6 – Phương Pháp Giải Các Bài Toán Đếm
>>> Mọi người cũng quan tâm:
Chuyên Đề Bồi Dưỡng HSG Toán 6 – Phương Pháp Giải Các Bài Toán Đếm Có Đáp Án – Toán 6 là tài liệu học tập được Trang Tài Liệu biên soạn và sưu tầm từ những nguồn dữ liệu mới nhất hiện nay. Tài liệu này sẽ giúp các em luyện tập, củng cố kiến thức từ đó nâng cao điểm số cho môn học. Ngoài ra, cũng giúp các thầy cô giáo có nguồn tài nguyên phong phú để giảng dạy.
Dưới đây là bản đọc trực tuyến giúp thầy cô và các em học sinh có thể nghiên cứu Online hoặc bạn có thể tải miễn phí với phiên bản word để dễ dàng in ấn cũng như học tập Offline.
ĐS6. CHUYÊN ĐỀ 1: TẬP HỢP SỐ TỰ NHIÊN
CHỦ ĐỀ 2: PHƯƠNG PHÁP GIẢI CÁC BÀI TOÁN ĐẾM
PHẦN I. TÓM TẮT LÝ THUYẾT
*) Nhận xét: Đối với “Bài toán đếm số” thì không có phương pháp chung nào cho mọi bài toán ở dạng này. Mà khi gặp mỗi bài toán có liên quan tới việc đếm số, đếm chữ số.... đòi hỏi sự tư duy, tố chất thông minh kết hợp với những kiến thức đã học về tập hợp số tự nhiên để giải bài toán. Qua mỗi bài toán cụ thể, học sinh sẽ tích lũy được những phương pháp giải, giúp hỗ trợ cho việc giải các bài toán khác ở dạng này được tốt hơn.
*)
Đếm số tự nhiên lập được từ m số cho trước lấy
ra từ tập hợp số
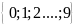 ta làm như sau:
ta làm như sau:
+ Chọn một trong m số làm chữ số hàng cao nhất, rồi lập sơ đồ hình cây, sau đó đếm số lập được
+ Ví dụ: Từ các số 3, 6, 9 lập được bao nhiêu số có 3 chữ số khác nhau?
Bước 1: Chọn chữ số 3 làm hàng trăm, ta có 2 số 369 và 396.
Bước 2: Từ sơ đồ, ta thấy từ 3 chữ số đã cho ta lập được 2 số có 3 chữ số khác nhau mà chữ số hàng trăm bằng 3. Tương tự, ta lập được 2 số có 3 chữ số khác nhau mà chữ số hàng trăm bằng 6, lập được 2 số có 3 chữ số khác nhau mà có chữ số hàng trăm bằng 9.
Bước
3: Vậy từ 3 chữ số đã cho ta lập được
 (số).
(số).
*) Để tìm số tự nhiên chưa biết, ta vận dụng hai phương pháp cơ bản sau:
- Phân tích cấu tạo số của một số tự nhiên.
Ta
có:
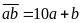
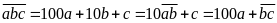
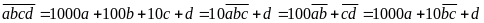
- Từ đặc điểm của số cần tìm và dữ kiện của bài toán ta lập luận, nhận xét để lựa chọn chữ số (thường sẽ nhận xét để chỉ ra chữ số của hàng đơn vị và chữ số hàng cao nhất).
PHẦN II. BÀI TẬP:
I.Phương pháp giải
- Liệt kê: Các phần tử thỏa mãn điều kiện cho trước ⇒ dùng phương pháp đếm (ít phần tử)
- Dựa vào quy luật hình thành các phần tử để đếm (chia hết cho 2, 3, … hoặc thỏa mãn điều kiện nào đó).
II.Bài toán
Dạng 1: Đếm số các chữ số của dãy số
Bài
1:
Viết
dãy số tự nhiên từ 1 đến 999 ta được một số tự
nhiên
 .
.
a) Số A có bao nhiêu chữ số?
b)
Tính tổng các chữ số của số
 ?
?
c) Chữ số 1 được viết bao nhiêu lần?
d) Chữ số 0 được viết bao nhiêu lần?
Phân tích:
a) Cần đếm số chữ số của các dãy số sau: Dãy các số tự nhiên có 1 chữ số, dãy các số tự nhiên có 2 chữ số, dãy các số tự nhiên có 3 chữ số. Sau đó cộng các kết quả lại với nhau
b)
Viết số
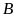 là
các số tự nhiên từ 000 đến 999 (mỗi số đều viết
bởi 3 chữ số), thì tổng các chữ số của
là
các số tự nhiên từ 000 đến 999 (mỗi số đều viết
bởi 3 chữ số), thì tổng các chữ số của
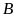 cũng bằng tổng các chữ số của
cũng bằng tổng các chữ số của
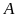 .
Số
.
Số
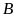 có:
có:
 chữ số mà mỗi chữ số từ 0 đến 9 đều có mặt 300
lần
chữ số mà mỗi chữ số từ 0 đến 9 đều có mặt 300
lần
Lời giải:
a)
Số
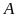 có bao nhiêu chữ số?
có bao nhiêu chữ số?
Từ 1 đến 9 có 9 số gồm: 9 (chữ số)
Từ
10
đến 99
số có 90
số gồm:
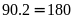 (chữ
số)
(chữ
số)
Từ
100
đến 999
có 900
số gồm:
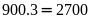 (chữ
số)
(chữ
số)
Số
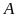 có:
có:
 (chữ
số).
(chữ
số).
b)
Tính tổng các chữ số của số
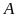 ?
?
Giả
sử ta viết số
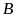 là các số tự nhiên từ 000
đến 999
(mỗi số đều viết bởi 3
chữ số), thế thì tổng các chữ số của
là các số tự nhiên từ 000
đến 999
(mỗi số đều viết bởi 3
chữ số), thế thì tổng các chữ số của
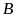 cũng bằng tổng các chữ số của A.B
có:
cũng bằng tổng các chữ số của A.B
có:
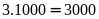 chữ số, mỗi chữ số từ 0
đến 9
đều có mặt:
chữ số, mỗi chữ số từ 0
đến 9
đều có mặt:
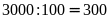 (lần)
(lần)
Tổng
các chữ số của
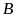 (cũng là của
(cũng là của
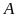 ):
):
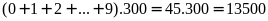 (chữ
số)
(chữ
số)
c) Chữ số 1 được viết bao nhiêu lần?
Cần
đếm số chữ số 1
trong 11
dãy:
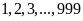
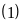
Số
chữ số 1
trong hai dãy như nhau. Ở đây dãy
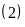 có
1000
số, mỗi số gồm 3
chữ số, số lượng mỗi chữ số từ 0
đến 9
đều như nhau. Mỗi chữ số (từ 0
đến 9)
đều có mặt
có
1000
số, mỗi số gồm 3
chữ số, số lượng mỗi chữ số từ 0
đến 9
đều như nhau. Mỗi chữ số (từ 0
đến 9)
đều có mặt
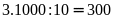 (lần).
(lần).
Vậy
ở đây
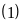 chữ
số 1
cũng được viết 300
lần.
chữ
số 1
cũng được viết 300
lần.
d) Chữ số 0 được viết bao nhiêu lần?
Ở
dãy
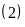 chữ
số 0
có mặt 300
lần.
chữ
số 0
có mặt 300
lần.
So
với dãy
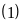 thì
ở dãy
thì
ở dãy
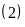 ta
viết thêm các chữ số 0:
ta
viết thêm các chữ số 0:
- Vào hàng trăm 100 lần (chữ số hàng trăm của các số từ 000 đến 099);
-Vào hàng chục 10 lần (chữ số hàng chục của các số từ 000 đến 009);
-Vào hàng đơn vị 1 lần (chữ số hàng đơn vị của 000).
Vậy
chữ số
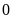 ở dãy
ở dãy
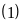 được
viết là:
được
viết là:
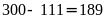 (lần).
(lần).
Bài
2:
Viết
dãy số tự nhiên từ 1 đến 999 ta được một số tự
nhiên
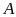 .
.
a)
Số
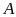 có bao nhiêu chữ số?
có bao nhiêu chữ số?
b)
Tính tổng các chữ số của số
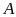 ?
?
c) Chữ số 1 được viết bao nhiêu lần?
d) Chữ số 0 được viết bao nhiêu lần?
Phân tích:
a) Cần đếm số chữ số của các dãy số sau: Dãy các số tự nhiên có 1 chữ số, dãy các số tự nhiên có 2 chữ số, dãy các số tự nhiên có 3 chữ số. Sau đó cộng các kết quả lại với nhau
b)
Viết số
 là các số tự nhiên từ 000 đến 999 (mỗi số đều viết
bởi 3 chữ số), thì tổng các chữ số của
là các số tự nhiên từ 000 đến 999 (mỗi số đều viết
bởi 3 chữ số), thì tổng các chữ số của
 cũng bằng tổng các chữ số của
cũng bằng tổng các chữ số của
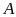 .
Số
.
Số
 có:
có:
 chữ số mà mỗi chữ số từ 0 đến 9 đều có mặt 300
lần
chữ số mà mỗi chữ số từ 0 đến 9 đều có mặt 300
lần
Lời giải:
a)
Số
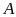 có bao nhiêu chữ số?
có bao nhiêu chữ số?
Từ 1 đến 9 có 9 số gồm: 9 (chữ số)
Từ
10
đến 99
số có 90
số gồm:
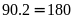 (chữ
số)
(chữ
số)
Từ
100
đến 999
có 900
số gồm:
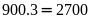 (chữ
số)
(chữ
số)
b)
Tính tổng các chữ số của số
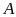 ?
?
Giả
sử ta viết số
 là các số tự nhiên từ 000
đến 999
(mỗi số đều viết bởi 3
chữ số), thế thì tổng các chữ số của
là các số tự nhiên từ 000
đến 999
(mỗi số đều viết bởi 3
chữ số), thế thì tổng các chữ số của
 cũng bằng tổng các chữ số của
cũng bằng tổng các chữ số của
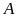 .Số
.Số
 có:
có:
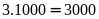 chữ số, mỗi chữ số từ 0
đến 9
đều có mặt:
chữ số, mỗi chữ số từ 0
đến 9
đều có mặt:
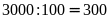 (lần)
(lần)
Tổng
các chữ số của
 (cũng là của
(cũng là của
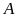 ):
):
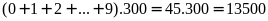 (chữ
số)
(chữ
số)
c) Chữ số 1 được viết bao nhiêu lần?
Cần
đếm số chữ số 1
trong 11
dãy:
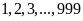
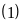
Ta
xét dãy:
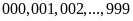
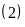
Số
chữ số 1
trong hai dãy như nhau. Ở đây dãy
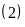 có
1000
số, mỗi số gồm 3
chữ số, số lượng mỗi chữ số từ 0
đến 9
đều như nhau. Mỗi chữ số (từ 0
đến 9)
đều có mặt
có
1000
số, mỗi số gồm 3
chữ số, số lượng mỗi chữ số từ 0
đến 9
đều như nhau. Mỗi chữ số (từ 0
đến 9)
đều có mặt
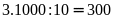 (lần).
(lần).
Vậy
ở đây
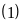 chữ
số 1
cũng được viết 300
lần.
chữ
số 1
cũng được viết 300
lần.
d) Chữ số 0 được viết bao nhiêu lần?
Ở
dãy
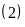 chữ
số 0
có mặt 300
lần.
chữ
số 0
có mặt 300
lần.
So
với dãy
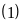 thì
ở dãy
thì
ở dãy
 ta
viết thêm các chữ số 0:
ta
viết thêm các chữ số 0:
- Vào hàng trăm 100 lần (chữ số hàng trăm của các số từ 000 đến 099);
-Vào hàng chục 10 lần (chữ số hàng chục của các số từ 000 đến 009);
-Vào hàng đơn vị 1 lần (chữ số hàng đơn vị của 000).
Vậy
chữ số
 ở dãy
ở dãy
 được
viết là:
được
viết là:
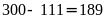 (lần).
(lần).
Bài 3: Để đánh số trang của một cuốn sách, người ta viết dãy số tự nhiên bắt đầu từ 1và phải dùng tất cả 1998 chữ số.
a) Hỏi cuốn sách có bao nhiêu trang?
b) Chữ số thứ 1010 là chữ số nào?
Phân tích: Để đếm số trang sách ta cần phân số trang sách theo 3 loại
Loại 1: Số trang sách mà mỗi số có 1 chữ số
Loại 2: Số trang sách mà mỗi số có 2 chữ số
Loại 3: Số trang sách mà mỗi số có 3 chữ số
Từ đó tính số chữ còn lại để đánh dấu các trang có 3 chữ số, rồi tính được số trang sách
b) Nhận thấy số 100 là số thứ nhất có 3 chữ số. Bằng việc dùng phép chia dư ta cần tìm xem chữ số thứ 1010 thuộc số thứ bao nhiêu có 3 chữ số
Lời giải
a) Hỏi cuốn sách có bao nhiêu trang?
Ta có: Từ trang 1 đến trang 9 phải dùng 9 chữ số (viết tắt chữ số).
Từ
trang 10
đến trang 99
cần
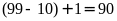 số có 2
chữ số, phải dùng 180 (chữ số)
số có 2
chữ số, phải dùng 180 (chữ số)
Vì còn các trang gồm các số có 3 chữ số
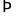 Còn
lại:
Còn
lại:
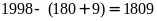 (chữ
số)
là đánh dấu các trang có 3
chữ số.
(chữ
số)
là đánh dấu các trang có 3
chữ số.
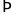 Có:
Có:
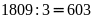 số có 3
chữ số.
số có 3
chữ số.
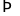 Cuốn
sách đó có:
Cuốn
sách đó có:
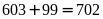 (vì trang
(vì trang
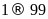 có 99
trang).
có 99
trang).
Cuốn sách có 702 trang.
b)
Vì
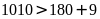 nên chữ số thứ 1010 nằm trong các số có 3 chữ số
nên chữ số thứ 1010 nằm trong các số có 3 chữ số
Ta
có:
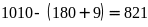 (chữ số) đánh dấu các trang có 3 chữ số tính từ
trang 100 (số thứ nhất có 3 chữ số) nên có
(chữ số) đánh dấu các trang có 3 chữ số tính từ
trang 100 (số thứ nhất có 3 chữ số) nên có
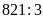 được 273 và dư 2
được 273 và dư 2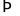 Chữ
số thứ 1010 sẽ nằm ở số thứ 274 có 3 chữ số.
Chữ
số thứ 1010 sẽ nằm ở số thứ 274 có 3 chữ số.
Số
thứ 274 có 3 chữ số là 374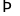 Chữ
số thứ 1010
là chữ số 7
của 374.
Chữ
số thứ 1010
là chữ số 7
của 374.
Bài
4: Bạn
Tâm đánh số trang của một cuốn vở có 110 trang bằng
cách viết dãy số tự nhiên
 Bạn Tâm phải viết tất cả bao nhiêu chữ số?
Bạn Tâm phải viết tất cả bao nhiêu chữ số?
Lời giải:
Ta có: Từ trang 1 đến trang 9 có 9 trang, phải dùng 9 chữ số.
Từ
trang 10 đến trang 99 có
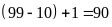 (trang), phải dùng 180 (chữ số).
(trang), phải dùng 180 (chữ số).
Từ
trang
100
đến
trang 110
có
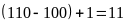 (trang),
phải dùng
(trang),
phải dùng
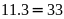 (chữ
số).
(chữ
số).
Vậy
bạn Tâm phải viết tất cả:
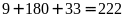 (chữ
số).
(chữ
số).
Bài
5: Một
cô nhân viên đánh máy liên tục dãy số chẵn bắt đầu
từ 2: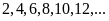 Cô
phải đánh tất cả 2000 chữ số. Tìm chữ số cuối cùng
mà cô đã đánh.
Cô
phải đánh tất cả 2000 chữ số. Tìm chữ số cuối cùng
mà cô đã đánh.
Lời giải:
Đánh
từ
số
2
đến số
8
cần
 số
chẵn có 1 chữ số, phải
đánh
4
(chữ
số).
số
chẵn có 1 chữ số, phải
đánh
4
(chữ
số).
Đánh
từ số
10
đến số
98
cần
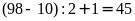 số chẵn
có
2
chữ số, phải đánh
số chẵn
có
2
chữ số, phải đánh
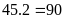 (chữ
số).
(chữ
số).
Đánh
từ số
100
đến số
998
cần
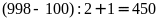 số chẵn
có
3
chữ số, phải đánh
số chẵn
có
3
chữ số, phải đánh
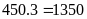 (chữ
số).
(chữ
số).
Vì còn các số chẵn phải đánh gồm các số chẵn có 4 chữ số
 Còn
lại:
Còn
lại:
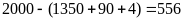 chữ số là đánh các
số chẵn có 4 chữ số
chữ số là đánh các
số chẵn có 4 chữ số
Có:
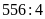 được 139
được 139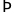 chữ
số thứ
chữ
số thứ
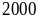 sẽ nằm ở số chẵn thứ 139 có 4 chữ số
sẽ nằm ở số chẵn thứ 139 có 4 chữ số
Số
chẵn thứ 139 có 4 chữ số là: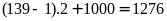 .
.
 Chữ
số thứ 2000
là chữ số 6
của số
1276.
Chữ
số thứ 2000
là chữ số 6
của số
1276.
Bài
6:
Bạn
Mai viết dãy số lẻ
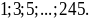
a) Bạn Mai phải viết tất cả bao nhiêu chữ số?
b) Nếu mỗi chữ số viết mất một giây thì viết đến số 245 mất bao nhiêu giây? Sau 5 phút, bạn Mai viết đến chữ số nào?
Lời giải:
a)
Viết
từ
số
1 đến số
9 cần
 số
lẻ có 1 chữ số, phải
viết
5
chữ số.
số
lẻ có 1 chữ số, phải
viết
5
chữ số.
Viết
từ số 11
đến số
99
cần
 số lẻ
có
2
chữ số, phải viết
số lẻ
có
2
chữ số, phải viết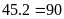 chữ
số.
chữ
số.
Viết
từ số
101
đến số
245
cần
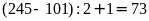 số lẻ
có
3
chữ số, phải viết
số lẻ
có
3
chữ số, phải viết
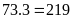 chữ
số.
chữ
số.
Vậy
bạn Mai phải viết tất cả:
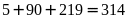 (chữ
số).
(chữ
số).
b) Nếu mỗi chữ số viết hết một giây thì viết đến số 245 mất 314 giây.
Đổi:
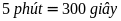 .
.
Sau 5 phút, bạn Mai viết đến chữ số thứ 300.
Vì
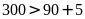 nên chữ số thứ 300 nằm trong các số lẻ có 3 chữ số.
nên chữ số thứ 300 nằm trong các số lẻ có 3 chữ số.
Ta
có:
 chữ số để viết các số lẻ có 3 chữ số tính từ số
101 (số lẻ thứ nhất có 3 chữ số) mà có
chữ số để viết các số lẻ có 3 chữ số tính từ số
101 (số lẻ thứ nhất có 3 chữ số) mà có
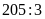 được 68 và dư 1.
được 68 và dư 1.
 Chữ
số thứ 300 sẽ nằm ở số lẻ thứ 69 có 3 chữ số.
Chữ
số thứ 300 sẽ nằm ở số lẻ thứ 69 có 3 chữ số.
Số
lẻ thứ 69 có 3 chữ số là
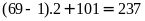
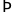 Chữ
số thứ 300
là chữ số 2
của số
237.
Chữ
số thứ 300
là chữ số 2
của số
237.
Dạng 2: Đếm số thỏa mãn điều kiện cho trước
Bài 1: Có bao nhiêu số tự nhiên chia hết cho 4 gồm bốn chữ số, chữ số tận cùng bằng 2?
Phân
tích:
Đây
là bài toán đếm số tự nhiên có liên quan tới dấu
hiệu chia hết cho 4. Trước hết ta cần viết số tự
nhiên cầ n tìm dưới dạng
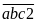 ,
sau đó đếm số cách chọn mỗi chữ số tập hợp
,
sau đó đếm số cách chọn mỗi chữ số tập hợp
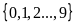 .
Việc thực hiện số cách chọn các chữ số
.
Việc thực hiện số cách chọn các chữ số
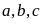 có sự dang buộc lẫn nhau. Do đó nếu chữ số
có sự dang buộc lẫn nhau. Do đó nếu chữ số
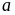 có
có
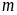 cách chọn, chữ số
cách chọn, chữ số
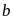 có
có
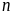 cách chọn, chữ số
cách chọn, chữ số
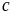 có
có
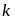 cách chọn thì ta sẽ có
cách chọn thì ta sẽ có
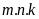 số có bốn chữ số thỏa mãn bài toán. Việc chọn chữ
số
số có bốn chữ số thỏa mãn bài toán. Việc chọn chữ
số
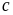 phải thỏa mãn điều kiện chi chia hết cho 4 là
phải thỏa mãn điều kiện chi chia hết cho 4 là

Lời giải:
Các
số phải đếm có dạng:
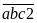
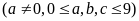 .
.
Chữ
số
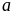 có 9
cách chọn.
có 9
cách chọn.
Với
mỗi cách chọn
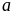 ,
chữ số
,
chữ số
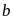 có 10
cách chọn.
có 10
cách chọn.
Với
mỗi cách chọn
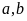 chữ số c
có 5
cách chọn
chữ số c
có 5
cách chọn
 để tạo với chữ số 2
tận cùng làm thành số chia hết cho 4.
để tạo với chữ số 2
tận cùng làm thành số chia hết cho 4.
Tất
cả có:
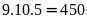 (số).
(số).
Bài 2: Có bao nhiêu số tự nhiên có ba chữ số trong đó có đúng một chữ số 5?
Phân
tích:
Số
tự nhiên có ba chữ số trong đó có đúng một chữ số
5, ta cần hiểu chữ số 5 có thể là chữ số hàng đơn
vị, chữ số hàng chục, chữ số hàng trăm nên ta cần
chia ra ba loại số có 3 chữ số thỏa mãn là:
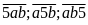 .
Ở mỗi loại số ta thực hiện đếm số cách chọn mỗi
chữ số từ tập hợp
.
Ở mỗi loại số ta thực hiện đếm số cách chọn mỗi
chữ số từ tập hợp
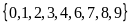 giống như bài 2.
giống như bài 2.
Lời giải:
Ta chia ra 3 loại số:
Số
đếm có dạng
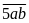
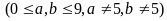 :
chữ số a
có 9
cách chọn, chữ số b
có 9
cách chọn các số thuộc loại này có:
:
chữ số a
có 9
cách chọn, chữ số b
có 9
cách chọn các số thuộc loại này có:
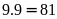 (số).
(số).
Số
đếm
có dạng
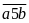
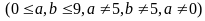 :
chữ số a
có 8
cách chọn, chữ số b
có 9
cách chọn, các số thuộc loại này có:
:
chữ số a
có 8
cách chọn, chữ số b
có 9
cách chọn, các số thuộc loại này có:
 (số).
(số).
Số
đếm có dạng
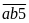
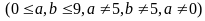 :
các số thuộc loại này có:
:
các số thuộc loại này có:
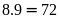 (số).
(số).
Vậy
số tự nhiên có ba chữ số trong đó có đúng một chữ
số 5
là
 (số).
(số).
Bài 3: Trong các số tự nhiên có ba chữ số, có bao nhiêu số:
a) Chứa đúng một chữ số 4?
b) Chứa đúng hai chữ số 4?
c) Chia hết cho 5, có chứa chữ số 5?
d) Chia hết cho 3, không chứa chữ số 3?
Lời giải:
a) Chứa đúng một chữ số 4?
Các số phải đếm có 3 dạng:
-
Dạng
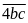
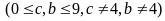 có
có
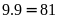 (số).
(số).
b) Chứa đúng hai chữ số 4?
Các số phải đếm gồm 3 dạng:
-
Dạng
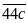
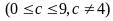 có
9
(số).
có
9
(số).
-
Dạng
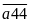
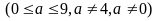 có
8
(số).
có
8
(số).
-
Dạng
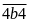
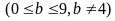 có 9
(số).
có 9
(số).
Tất
cả có:
 (số).
(số).
c) Chia hết cho 5, có chứa chữ số 5?
Số
có ba chữ số, chia hết cho 5
gồm 180
số, trong đó số không chứa chữ số 5
có dạng
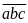
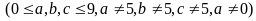 ,
,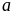 có 8
cách chọn,
có 8
cách chọn,
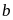 có 9
cách chọn,
có 9
cách chọn,
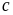 có 1
cách chọn (là 0)
gồm
có 1
cách chọn (là 0)
gồm
 (số).
(số).
Vậy
có
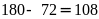 (số)
phải đếm.
(số)
phải đếm.
d) Chia hết cho 3, không chứa chữ số 3?
Số
phải tìm có dạng
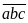
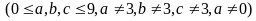 ,
a
có 8
cách chọn, b
có 9
cách chọn, c
có 3
cách chọn
(nếu
,
a
có 8
cách chọn, b
có 9
cách chọn, c
có 3
cách chọn
(nếu
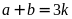 thì
thì
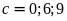 ,
nếu
,
nếu
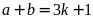 thì
thì
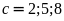 ,
nếu
,
nếu
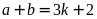 thì
thì
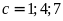 )
có
)
có
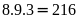 (số).
(số).
Bài 4: Có bao nhiêu số tự nhiên có 4 chữ số chia hết cho 3 và có tận cùng bằng 5?
Phân tích: Những số có tận cùng bằng 5 luôn cách nhau 10 đơn vị, tuy nhiên bài toán đòi hỏi số tự nhiên có 4 chữ số và chia hết cho 3. Do đó ta cần xác định: Số nhỏ nhất có 4 chữ số chia hết cho 3 và có tận cùng bằng 5. Khoảng cách trong dãy này sẽ là 30. Từ đó vận dụng công thức “Số số hạng = (số cuối – số đầu): Khoảng cách + 1”.
Lời giải:
Số lớn nhất có 4 chữ số chia hết cho 3 và có tận cùng bằng 5 là 9975
Số nhỏ nhất có 4 chữ số chia hết cho 3 và có tận cùng bằng 5 là 1005
Ta có dãy số: 1005; 1035; 1065;....; 9975
Khoảng cách của dãy là 30
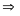 Số
số tự nhiên có 4 chữ số chia hết cho 3 và có tận cùng
bằng 5 là:
Số
số tự nhiên có 4 chữ số chia hết cho 3 và có tận cùng
bằng 5 là:

Vậy có 300 số thỏa mãn yêu cầu bài toán.
Bài 5: Trong các số tự nhiên từ 1 đến 100, có bao nhiêu số:
a) Chia hết cho 2 mà không chia hết cho 3?
b) Chia hết cho ít nhất một trong hai số 2 và 3?
c) Không chia hết cho 2 và không chia hết cho 3?
Lời giải:
a) Chia hết cho 2 mà không chia hết cho 3?
Các
số chia hết cho 2 là:
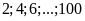
Số các số chia hết cho 2 là:
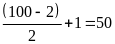 (số)
(số)
Các
số chia hết cho 2 và 3:
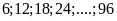
Số các số chia hết cho cả 2 và 3 là:
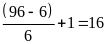 (số)
(số)
Vậy
từ 1 đến 100 có
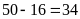 số chia hết cho 2 mà không chia hết cho 3.
số chia hết cho 2 mà không chia hết cho 3.
b) Chia hết cho ít nhất một trong hai số 2 và 3?
Các
số chia hết cho 3 là:
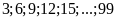
Số các số chia hết cho 3 là:
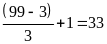 (số)
(số)
Vậy các số chia cho ít nhất một trong hai số 2 và 3 là:
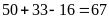 (số)
(số)
c) Không chia hết cho 2 và không chia hết cho 3?
Số các số không chia hết cho 2 và cho 3 là:
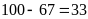 (số).
(số).
Bài 6: Trong các số tự nhiên từ 1 đến 1000, có bao nhiêu số:
a) Chia hết cho ít nhất một trong các số 2, 3, 5?
b) Không chia hết cho tất cả các số tự nhiên từ 2 đến 5?
Lời giải:
a) Chia hết cho ít nhất một trong các số 2, 3, 5?
Gọi
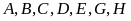 là tập hợp các số từ 1 đến 1000 mà theo thứ tự
chia hết cho 2, chia hết cho 3, chia hết cho 5, chia hết cho
2 và 3, chia hết cho 2 và 5, chia hết cho 3 và 5, chia hết
cho cả 3 số. Số
phần tử của các tập hợp đó theo thứ tự bằng
là tập hợp các số từ 1 đến 1000 mà theo thứ tự
chia hết cho 2, chia hết cho 3, chia hết cho 5, chia hết cho
2 và 3, chia hết cho 2 và 5, chia hết cho 3 và 5, chia hết
cho cả 3 số. Số
phần tử của các tập hợp đó theo thứ tự bằng
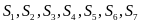
Ta
có:
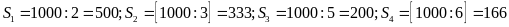
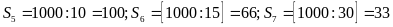
Số
các
số phải tìm gồm:
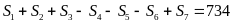 (số)
(số)
b) Không chia hết cho tất cả các số tự nhiên từ 2 đến 5?
Còn
lại
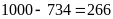 (số).
(số).
Bài
7: Có
bao nhiêu số
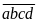 mà
mà
 ?
?
Lời
giải:
Điều
kiện: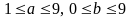
Xét các trường hợp sau:
Nếu
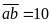 thì
thì
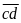
 có thể bằng:
có thể bằng:
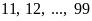 ,
có 89 số.
,
có 89 số.
Nếu
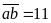 thì
thì
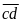
 có
thể bằng:
có
thể bằng:
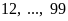 ,
có 88 số.
,
có 88 số.
........................................
Nếu
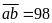 thì
thì
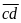
 có
thể bằng:
có
thể bằng:
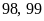 ,
có 2 số.
,
có 2 số.
Nếu
ab = 98 thì
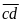
 bằng: 99, có 1 số.
bằng: 99, có 1 số.
Vậy
có tất cả:
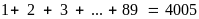 (số).
(số).
Bài
8:
Có
bao nhiêu số tự nhiên có bốn chữ số
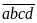 ,
trong đó
,
trong đó
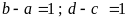 ?
?
Lời giải:
Chữ
số b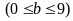 có 1 cách chọn
có 1 cách chọn
 .
.
Chữ
số d có
1 cách chọn
có
1 cách chọn
 .
.
Tất
cả có:
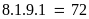 (số).
(số).
Bài 9: Có bao nhiêu số chứa ít nhất một chữ số 1 trong các số tự nhiên:
a) Có ba chữ số.
b) Từ 1 đến 999.
Lời giải:
a) Ta đếm các số tự nhiên có ba chữ số rồi bớt đi các số có ba chữ số không chứa chữ số 1.
Số
có ba chữ số là:
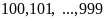 ,
có 900 số (1).
,
có 900 số (1).
Trong
các số trên, số không chứa chữ số 1 có dạng
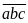
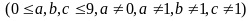 trong
đó a có 8 cách chọn (từ 2 đến 9), b có 9 cách chọn (từ
0 đến 9 nhưng khác 1), c có 9 cách chọn (từ 0 đến 9
nhưng khác 1), có:
trong
đó a có 8 cách chọn (từ 2 đến 9), b có 9 cách chọn (từ
0 đến 9 nhưng khác 1), c có 9 cách chọn (từ 0 đến 9
nhưng khác 1), có:
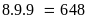 (số) (2).
(số) (2).
Từ
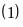 và
và
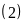 ⇒
Số các số phải đếm là:
⇒
Số các số phải đếm là:
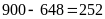 (số).
(số).
b)
Ta thêm chữ số 0 vào dãy
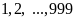 thành
dãy mới
thành
dãy mới
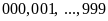 để đếm số được dễ dàng.
để đếm số được dễ dàng.
Trước
hết, ta đếm các số không chứa chữ số 1 của dãy này:
đó là các số có dạng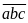
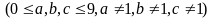 trong
đó mỗi chữ số
trong
đó mỗi chữ số
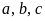 đều có 9 cách chọn (từ 0 đến 9 nhưng khác 1), tất cả
có: 9.9.9 = 729 (số). Vậy số lượng các số từ 1 đến
999 không chứa chữ số 1 có:
đều có 9 cách chọn (từ 0 đến 9 nhưng khác 1), tất cả
có: 9.9.9 = 729 (số). Vậy số lượng các số từ 1 đến
999 không chứa chữ số 1 có:
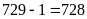 (số).
(số).
Số lượng các số từ 1 đến 999 có chứa chữ số 1 là:
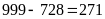 (số).
(số).
Bài 10: Tìm số lượng các số tự nhiên có bốn chữ số mà:
a) Số tạo bởi hai chữ số đầu (theo thứ tự ấy) cộng với số tạo bởi hai chữ số cuối (theo thứ tự ấy) nhỏ hơn 100.
b) Số tạo bởi hai chữ số đầu (theo thứ tự ấy) lớn hơn số tạo bởi hai chữ số cuối (theo thứ tự ấy)?
Lời giải:
a)
Các số cần tìm có dạng: 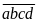
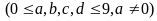 trong đó:
trong đó:
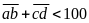 .
.
Ta có các số sau thỏa mãn đề bài:
+)
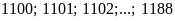 ⇒
Gồm:
⇒
Gồm:
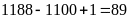 (số).
(số).
…………………………………….
+)
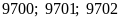 ⇒
gồm: 3 (số).
⇒
gồm: 3 (số).
+)
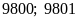 ⇒
gồm: 2 (số).
⇒
gồm: 2 (số).
+) 9900 ⇒gồm: 1 (số).
Vậy
có tất cả: 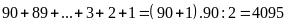 (số).
(số).
b)
Các số cần tìm có dạng: 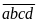
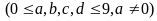 trong
đó:
trong
đó:
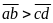 .
.
Ta có các số sau thỏa đề bài:
+)
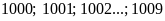 ⇒
gồm:
⇒
gồm:
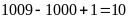 (số).
(số).
+)
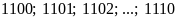 ⇒
gồm:
⇒
gồm:
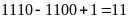 (số).
(số).
………………………………….
+)
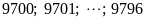 ⇒
gồm:
⇒
gồm:
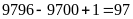 (số).
(số).
+)
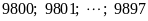 ⇒
gồm:
⇒
gồm:
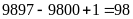 (số).
(số).
+)
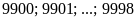 ⇒
gồm
⇒
gồm
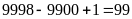 (số).
(số).
Số
các số thỏa đề bài là:
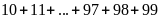
Tổng
trên gồm
 (số).
(số).
Vậy
số các số thỏa đề bài là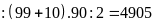 (số).
(số).
Bài 11: Trong các số tự nhiên từ 1 đến 252, xoá các số chia hết cho 2 nhưng không chia hết cho 5, rồi xoá các số chia hết cho 5 nhưng không chia hết cho 2. Còn lại bao nhiêu số?
Lời giải:
Các
số phải xóa có tận cùng
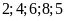 .Mỗi
chục xóa 5 số, còn lại 5 số. Từ 1 đến 250 có 25 chục,
còn lại:
.Mỗi
chục xóa 5 số, còn lại 5 số. Từ 1 đến 250 có 25 chục,
còn lại:
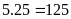 (số).
(số).
Xét
các số
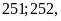 số 251 được giữ lại.
số 251 được giữ lại.
Bài 12: Có bao nhiêu số tự nhiên có ba chữ số mà:
a) Các chữ số đểu chẵn?
b) Chữ số hàng chục là chữ số lẻ?
Lời giải:
a)
Các số phải đếm có dạng
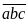
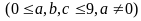 ,
trong
đó:
,
trong
đó:
Chữ
số a
có 4
cách chọn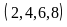 .
.
Với
mỗi cách chọn a,
chữ số b
có 5
cách chọn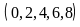 .
.
Với
mỗi cách chọn
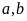 chữ số c
có 5
cách chọn
chữ số c
có 5
cách chọn
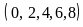 .
.
Tất
cả có:
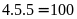 (số).
(số).
b)
Các số phải đếm có dạng
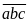
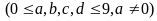 ,
trong
đó:
,
trong
đó:
Chữ
số a
có 9
cách chọn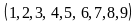 .
.
Với
mỗi cách chọn a,
chữ số b
có 5
cách chọn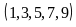 .
.
Với
mỗi cách chọn
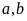 chữ số c
có 10
cách chọn
chữ số c
có 10
cách chọn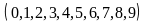 .
.
Bài 13: Có bao nhiêu số tự nhiên có bốn chữ số trong đó:
a) Mỗi chữ số đều chẵn?
b) Tổng các chữ số là số chẵn?
Lời giải:
a)
Các số phải đếm có dạng
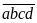
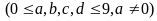 ,
trong
đó:
,
trong
đó:
Chữ
số a
có 4
cách chọn
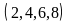 .
.
Với
mỗi cách chọn a,
chữ số b
có 5
cách chọn
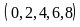 .
.
Với
mỗi cách chọn
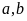 chữ số c
có 5
cách chọn
chữ số c
có 5
cách chọn
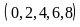 .
.
Với
mỗi cách chọn
 chữ số d
có 5
cách chọn
chữ số d
có 5
cách chọn
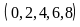 .
.
Tất
cả có:
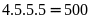 (số).
(số).
b)
Các số phải đếm có dạng

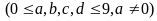 ,
trong
đó:
,
trong
đó:
Chữ
số a
có 9
cách chọn
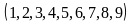 .
.
Với
mỗi cách chọn a,
chữ số b
có 10
cách chọn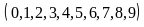 .
.
Với
mỗi cách chọn
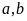 chữ số c
có 10
cách chọn
chữ số c
có 10
cách chọn
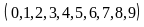 .
.
Với
mỗi cách chọn
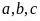 chữ số d
có 5
cách chọn:
chữ số d
có 5
cách chọn:
+
Nếu
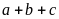 lẻ thì
lẻ thì
 .
.
+
Nếu
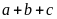 chẵn
thì
chẵn
thì
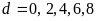 .
.
Tất
cả có:
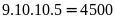 (số).
(số).
Bài 14: Có bao nhiêu số tự nhiên có ba chữ số, biết rằng cộng nó với số gồm ba chữ số ấy viết theo thứ tự ngược lại thì được một số chia hết cho 5?
Lời giải:
Các
số phải đếm có dạng
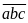
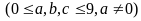 .
.
Theo
đề bài, ta có :
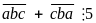 .
.
Với
mỗi cách chọn
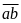 (từ 10 đến 99) thì c có 2 cách chọn phụ thuộc vào a
:
(từ 10 đến 99) thì c có 2 cách chọn phụ thuộc vào a
:
Nếu a = 5k thì c bằng 0 hoặc 5
Nếu a = 5k + 1 thì c bằng 4 hoặc 9
Nếu a = 5k + 2 thì c bằng 3 hoặc 8
Nếu a = 5k + 3 thì c bằng 2 hoặc 7
Nếu a = 5k + 4 thì c bằng 1 hoặc 6
Vậy
có:
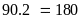 (số).
(số).
Bài 15: Có bao nhiêu số chẵn có ba chữ số, các chữ số khác nhau?
Lời giải:
Nếu
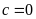 thì
a có 9 cách
chọn (từ 1 đến 9), b có 8 cách chọn (từ 1 đến 9, khác
a).
thì
a có 9 cách
chọn (từ 1 đến 9), b có 8 cách chọn (từ 1 đến 9, khác
a).
Nếu
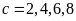 thì
a có 8 cách chọn (từ 1 đến 9, khác c), b có 8 cách chọn
(từ 0 đến 9, khác a và c).
thì
a có 8 cách chọn (từ 1 đến 9, khác c), b có 8 cách chọn
(từ 0 đến 9, khác a và c).
Vậy
có:
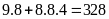 (số).
(số).
Bài 16: Có bao nhiêu số tự nhiên có ba chữ số trong đó có ít nhất hai chữ số như nhau?
Lời giải:
Ta đếm các số tự nhiên có ba chữ số rồi bớt đi các số ba chữ số khác nhau.
Số
có ba chữ số là:
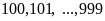 ,
có 900 số.
,
có 900 số.
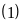
Trong
các số trên, số có 3 chữ số khác nhau dạng
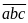
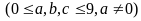 ,
trong đó a có 9 cách chọn (từ 1 đến 9), b có 9 cách chọn
(từ 0 đến 9 nhưng khác a), c có 8 cách chọn (từ 0 đến
9 nhưng khác a và b),có:
,
trong đó a có 9 cách chọn (từ 1 đến 9), b có 9 cách chọn
(từ 0 đến 9 nhưng khác a), c có 8 cách chọn (từ 0 đến
9 nhưng khác a và b),có:
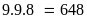 (số)
(số)
Từ
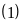 và
và
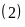 ⇒
Số lượng số phải đếm là:
⇒
Số lượng số phải đếm là:
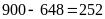 (số).
(số).
Bài 17: Trong các số tự nhiên có bốn chữ số, có bao nhiêu số trong đó có đúng ba chữ số như nhau?
Lời giải:
Các số phải đếm gồm bốn dạng:
Dạng
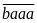
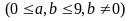 :
Chữ số b có 9 cách chọn (từ 1 đến 9), chữ số a có 9
cách chọn (từ 0 đến 9 nhưng khác b). Có:
:
Chữ số b có 9 cách chọn (từ 1 đến 9), chữ số a có 9
cách chọn (từ 0 đến 9 nhưng khác b). Có:
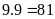 (số).
(số).
Dạng
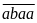
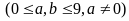 ,
dạng
,
dạng
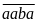
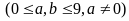 ,
dạng
,
dạng
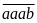
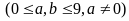 :
ở mỗi dạng này, chữ số a có
9
cách chọn, chữ số b có 9 cách chọn (khác a). Mỗi dạng
có:
:
ở mỗi dạng này, chữ số a có
9
cách chọn, chữ số b có 9 cách chọn (khác a). Mỗi dạng
có:
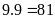 (số).
(số).
Tất
cả có:
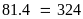 (số).
(số).
Bài 18: Trong các số tự nhiên có ba chữ số, có bao nhiêu số chứa ít nhất một chữ số 4?
Lời giải:
Ta đếm các số tự nhiên có ba chữ số rồi bớt đi các số ba chữ số không chứa chữ số 4.
Số
có ba chữ số là:
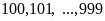 ,
có 900
số.
,
có 900
số.
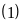
Trong
các số trên, số có 3
chữ số không chứa chữ số 4
dạng
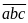 .
.
Trong
đó
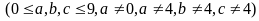 ,
trong đó
,
trong đó
 có 8
cách chọn (từ 1
đến 9
nhưng khác
4),
có 8
cách chọn (từ 1
đến 9
nhưng khác
4),
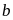 có
9
cách chọn (từ 0 đến 9
nhưng khác 4),
có
9
cách chọn (từ 0 đến 9
nhưng khác 4),
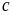 có
9
cách chọn (từ 0 đến 9
nhưng khác 4), có:
có
9
cách chọn (từ 0 đến 9
nhưng khác 4), có:
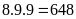 (số).
(số).
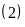
Từ
 và
và
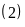 ⇒
Số lượng số phải đếm là:
⇒
Số lượng số phải đếm là:
 (số).
(số).
Bài 19: Trong các số tự nhiên từ 1 đến 10000
a) Có bao nhiêu số chứa chữ số 0?
b) Số chứa chữ số 1 hay số không chứa chữ số 1 có nhiều hơn?
Lời giải:
a) Ta đếm các số tự nhiên từ 1 đến 10000 rồi bớt đi các số không chứa chữ số 0.
Các số tự nhiên từ 1 đến 10000 có 10000 số.
Ta đếm các số không chứa chữ số 0:
+ Từ 1 đến 9 có 9 (số).
+
Từ
100 đến 999 có
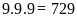 (số).
(số).
+
Từ
1000 đến 9999 có
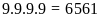 (số).
(số).
Vậy
số lượng số phải đếm là:
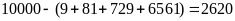 (số) có chứa chữ số 0.
(số) có chứa chữ số 0.
b) Các số tự nhiên từ 1 đến 10000 có 10000 số.
Ta đếm các số không chứa chữ số 1:
+ Từ 1 đến 9 có 8 số.
+
Từ 10 đến 99 có
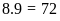 số.
số.
+
Từ
100 đến 999 có
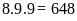 số.
số.
+
Từ
1000 đến 9999 có
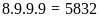 số.
số.
⇒Có
tất cả:
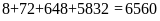 (số)
không chứa chữ số 1.
(số)
không chứa chữ số 1.
Còn
lại:
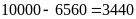 (số) có chứa chữ số 1.
(số) có chứa chữ số 1.
Vậy số không chứa chữ số 1 có nhiều hơn số chứa c số 1.
Bài 20: Có bao nhiêu số tự nhiên từ 10 đến 24 chia hết cho ít nhất một trong hai số 2 và 3?
Lời giải: Trong các số tự nhiên từ 10 đến 24:
Các
số tự nhiên chia hết cho 2 là:
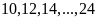 ,
gồm:
,
gồm: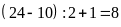 (số).
(số).
Các
số chia hết cho 3 là:
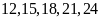 ,
gồm 5 số.
,
gồm 5 số.
Có
những số có mặt ở hai dãy trên, đó là các bội của
6 :
 ,
gồm 3 số.
,
gồm 3 số.
Vậy
có:
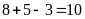 (số) chia hết cho ít nhất một trong hai số 2 và 3.
(số) chia hết cho ít nhất một trong hai số 2 và 3.
Bài 21: Có bao nhiêu số tự nhiên chia hết cho 5, có bốn chữ số, có đúng một chữ số 5?
Lời giải:
Các số phải đếm có 4 dạng:
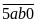
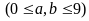 có
có
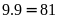 (số)
(số)

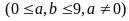 có
có
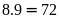 (số)
(số)
Tất
cả có:
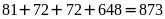 (số).
(số).
Bài 22: Trong các số tự nhiên từ 1 đến 200, có bao nhiêu số:
a. Chia hết cho 2 mà không chia hết cho 3?
b. Chia hết cho ít nhất một trong hai số 2 và 3?
c. Không chia hết cho 2 và không chia hết cho 3?
Lời giải:
a) Chia hết cho 2 mà không chia hết cho 3?
Các
số chia hết cho
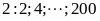
Số các số chia hết cho 2 là:
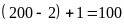 (số)
(số)
Các
số chia hết cho 2
và 3
là:
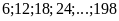
Số các số chia hểt cho cả 2 và 3 là:
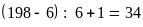 (số)
(số)
Vậy
từ 1
đến 200
có
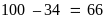 số chia hết cho 2
mà không chia hết cho 3.
số chia hết cho 2
mà không chia hết cho 3.
b)
Các số chia hết cho 3
là:
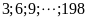
Số các số chia hết cho 3 là:
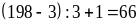 (số)
(số)
Vậy các số chia hết cho ít nhất một trong hai số 2 và 3 là:
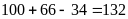 (số)
(số)
c) Không chia hết cho 2 và cho 3 là:
 (số)
(số)
Bài
23: Tuấn
muốn đến nhà bạn, nhưng không nhớ số nhà, chỉ biết
rằng số nhà của bạn là só chia hết cho 3 và có hai chữ
số. Biết số nhà cuối của dãy phố đó là 135. Hỏi
Tuấn phải gõ cửa nhiều nhất bao nhiêu số nhà? (các số
nhà không đánh số
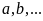 ).
).
Lời giải:
Dãy
số lẻ chia hết cho 3 và có hai chữ số là:
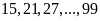 gồm
gồm
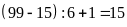 (số).
(số).
Vậy Tuấn phải gõ cửa nhiều nhất 15 số nhà.
Bài 24: Có bao nhiêu biển số xe máy khác nhau, mỗi số xe lập bởi hai chữ cái đứng đầu và ba chữ số đứng sau? (bảng chữ cái có 25 chữ, không có biển số 000).
Lời giải:
Vì
bảng chữ cái có 25 chữ số nên có
 cách
lập kí hiệu đứng đầu gồm 2 chữ cái.
cách
lập kí hiệu đứng đầu gồm 2 chữ cái.
Ta
có: 999 cách lập số từ 001 đến 999 ⇒
có
tất cả:
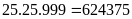 (biển
số xe).
(biển
số xe).
Dạng 3: Dạng khác
Bài 1: Trong số 100 học sinh có 75 học sinh thích học Toán, 60 học sinh thích Văn.
a) Nếu có 5 học sinh không thích cả Toán lẫn Văn thì có bao nhiêu học sinh thích cả hai môn Văn và Toán?
b) Có nhiều nhất bao nhiêu học sinh thích cả hai môn Văn và Toán?
c) Có ít nhất bao nhiêu học sinh không thích cả hai môn Văn và Toán?
Lời giải:
Gọi
số học sinh thích cả hai môn Văn và Toán là x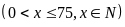 ,
số học sinh thích Toán mà
,
số học sinh thích Toán mà
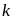 thích Văn là
thích Văn là
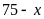 .
.
a) Nếu có 5 học sinh không thích cả Toán lẫn Văn thì có bao nhiêu học sinh thích cả hai môn Văn và Toán?
Ta
có:
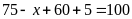
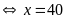
Vậy có 40 học sinh thích cả hai môn.
a)
Vì
trong 100 học sinh có 75 học sinh thích toán và 60 học sinh
thích văn nên số học sinh nhiều nhất thích cả toán và
văn không thể vượt 60 học sinh.
Vậy số học sinh
thích cả 2 môn nhiều nhất là 60 học sinh.
b)
Ta có: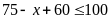
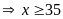 .
.
Có ít nhất 35 học sinh thích cả hai môn Văn và Toán.
Bài 2: Kết quả điều tra ở một lớp học cho thấy: có 20 học sinh thích bóng đá, 17 học sinh thích bơi, 36 học sinh thích bóng chuyển,14 học sinh thích bóng đá và bơi,13 học sinh thích bơi và bóng chuyền, 15 học sinh thích bóng đá và bóng chuyền,10 học sinh thích cả ba môn,12 học sinh không thích một môn nào. Tính xem lớp học đó có bao nhiêu học sinh?
Lời giải:
Số học sinh thích đúng 2môn bóng đá và bơi:
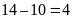 (học
sinh)
(học
sinh)
Số học sinh thích đúng hai môn bơi và bóng chuyền:
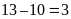 (học
sinh).
(học
sinh).
Số học sinh thích đúng hai môn bóng đá và bóng chuyền:
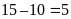 (học
sinh)
(học
sinh)
Số học sinh chỉ thích bóng đá:
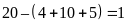 (học
sinh)
(học
sinh)
Số học sinh chỉ thích bơi:
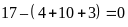 (học
sinh)
(học
sinh)
Số học sinh chỉ thích bóng chuyền:
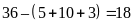 (học
sinh)
(học
sinh)
Số học sinh của lớp là:
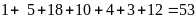 (học
sinh)
(học
sinh)
Vậy số học sinh của lớp học là 53 học sinh.
Bài 3: Tổng kết đợt thi đua "100 điểm 10 dâng tặng thầy cô", lớp 6A có 43 bạn được từ 1 điểm 10 trở lên, 39 bạn được từ 2 điểm 10 trở lên, 14 bạn được từ 3 điểm 10 trở lên, 5 bạn được 4 điểm 10, không có ai được trên 4 điểm 10. Tính xem trong đợt thi đua đó, lớp 6A có bao nhiêu điểm 10?
Lời giải:
Số
học sinh đạt 1 điểm 10 là:
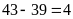 (học
sinh).
(học
sinh).
Só
học sinh đạt 2 điểm 10 là:
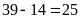 (học
sinh).
(học
sinh).
Số
học sinh đạt 3 điểm 10 là:
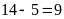 (học
sinh).
(học
sinh).
Số điểm 10 của lớp 6A đạt được là:
 (điểm
10).
(điểm
10).
Bài 4: Trong số 200 học sinh có 150 học sinh thích học Toán, 120 học sinh thích Văn.
a) Nếu có 5 học sinh không thích cả Toán lẫn Văn thì có bao nhiêu học sinh thích cả hai môn Văn và Toán?
b) Có nhiều nhất bao nhiêu học sinh thích cả hai môn Văn và Toán?
c) Có ít nhất bao nhiêu học sinh thích cả hai môn Văn và Toán?
Lời giải:
Gọi
số học sinh thích cả hai môn Văn và Toán là x , số học sinh thích Toán mà không thích Văn là
, số học sinh thích Toán mà không thích Văn là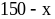 .
.
a)
Ta có:
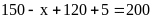

Vậy có 75 học sinh thích cả hai môn.
b) Có nhiều nhất 120 học sinh ( nếu tất cả số thích văn đều thích toán)
c)
Ta có: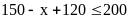
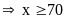
Có ít nhất 70 học sinh thích cả hai môn Văn và Toán.
Ngoài Chuyên Đề Bồi Dưỡng HSG Toán 6 – Phương Pháp Giải Các Bài Toán Đếm Có Đáp Án – Toán 6 thì các tài liệu học tập trong chương trình 6 sẽ được cập nhật liên tục và nhanh nhất có thể sau khi kỳ thi diễn ra trên Danh mục Tài Liệu Học Tập nhằm giúp các bạn đọc thuận tiện trong việc nghiên cứu tài liệu. Quý thày cô và các bạn đọc có thể chia sẻ thêm những tài liệu học tập hữu ích đến địa chỉ email của chúng tôi, nhằm xây dựng nên kho đề thi phong phú, đa dạng cho các em học sinh tham khảo và rèn luyện.
Chuyên Đề Bồi Dưỡng HSG Toán 6 với chủ đề “Phương pháp giải các bài toán đếm” là một tài liệu quan trọng giúp học sinh lớp 6 nắm vững kiến thức và kỹ năng trong việc giải các bài toán đếm.
Trong chuyên đề này, học sinh sẽ được làm quen với các phương pháp giải các bài toán đếm, bao gồm: phương pháp quy tắc cộng, phương pháp quy tắc nhân, phương pháp quy tắc chia, và các phương pháp kết hợp khác. Các bài toán đếm có thể liên quan đến xếp hàng, chọn lựa, phân chia, hoán vị, tổ hợp, và nhiều loại bài toán khác.
Tài liệu bồi dưỡng HSG Toán 6 với chủ đề “Phương pháp giải các bài toán đếm” cung cấp một loạt các bài tập thực hành, từ các bài toán cơ bản đến những bài toán phức tạp hơn. Mỗi bài tập đi kèm với lời giải chi tiết, giúp học sinh hiểu rõ cách giải và áp dụng phương pháp vào từng bài toán cụ thể.
>>> Bài viết có liên quan: