Chuyên Đề Tỉ Lệ Thức Lớp 7 Môn Toán Có Lời Giải Chi Tiết
Có thể bạn quan tâm
Chuyên Đề Tỉ Lệ Thức Lớp 7 Môn Toán Có Lời Giải Chi Tiết là tài liệu học tập được Trang Tài Liệu biên soạn và sưu tầm từ những nguồn dữ liệu mới nhất hiện nay. Tài liệu này sẽ giúp các em luyện tập, củng cố kiến thức từ đó nâng cao điểm số cho môn học. Ngoài ra, cũng giúp các thầy cô giáo có nguồn tài nguyên phong phú để giảng dạy.
Cùng với lời giải chi tiết, chuyên đề tỉ lệ thức lớp 7 môn toán cũng cung cấp các bước giải thích logic và các phương pháp tính toán cụ thể. Điều này giúp các bạn học sinh hiểu rõ cách suy nghĩ và tiếp cận các bài toán tỉ lệ thức một cách tổng quát, từ đó nâng cao khả năng vận dụng và giải quyết các bài toán tương tự.
Dưới đây là bản đọc trực tuyến giúp thầy cô và các em học sinh có thể nghiên cứu Online hoặc bạn có thể tải miễn phí với phiên bản word để dễ dàng in ấn cũng như học tập Offline.
CHUYÊN ĐỀ : TỈ LỆ THỨC
PHẦN I. TÓM TẮT LÝ THUYẾT
1. Định nghĩa
Tỉ lệ thức là đẳng thức của hai tỉ số
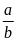 và
và
 ,
viết là
,
viết là
 .
.
Tính chất
PHẦN II. CÁC DẠNG BÀI.
Dạng 1. Lập tỉ lệ thức
Phương pháp giải:
Tỉ lệ thức
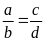 còn được viết là
còn được viết là
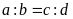 từ đó thay tỉ số giữa các số hữu tỉ thành tỉ số
giữa các số nguyên.
từ đó thay tỉ số giữa các số hữu tỉ thành tỉ số
giữa các số nguyên.Dựa vào định nghĩa nếu có
 thì tỉ số
thì tỉ số
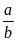 và
và
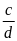 lập thành được một tỉ lệ thức
lập thành được một tỉ lệ thứcNếu
 và
và
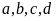 đều khác 0 thì ta có các tỉ lệ thức
đều khác 0 thì ta có các tỉ lệ thức

Để lập tỉ lệ thức từ các số đã cho ta cần xác định bộ bốn số
 sao cho
sao cho
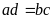 rồi áp dụng tính chất 2 của tỉ lệ thức để lập
được 4 tỉ lệ thức
rồi áp dụng tính chất 2 của tỉ lệ thức để lập
được 4 tỉ lệ thức
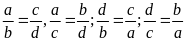
Bài toán.
Bài
1. Thay các tỉ số sau bằng tỉ số giữa các số
nguyên.
a) 3,5:5,04
b)
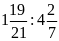
c)
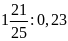
d)

Lời giải:
b)

a)
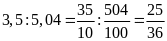
c)

d)
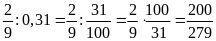
Bài
2. Thay các tỉ số sau bằng tỉ số giữa các số
nguyên.
b)
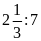
a)
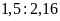
c)
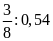
d)

Lời giải:
a)

b)

d)
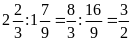
c)
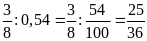
Bài
3. Thay các tỉ số sau bằng tỉ số giữa các số
nguyên.
b)
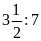
a)
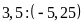
c)
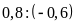
d)
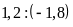
Lời giải:
a)
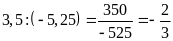
b)
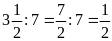
c)

d)
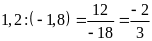
Bài
4. Thay các tỉ số sau bằng tỉ số giữa các số
nguyên.
b)
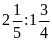
a)

d)
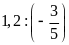
c)
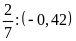
Lời giải:
b)
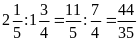
a)

c)
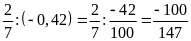
d)
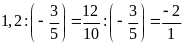
Bài
5. Thay các tỉ số sau bằng tỉ số giữa các số
nguyên.
b)

a)
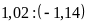
с)
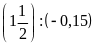
d)
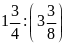
Lời giải:
b)
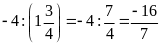
a)

c)
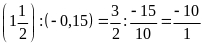
d)
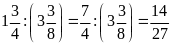
Bài
6 . Từ các tỉ số sau đây có lập được tỉ lệ thức
hay không?
a)
 và
và

b)
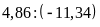 và
và

c)
 và
và
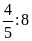
d)
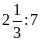 và
và

LỜI giải:
a) Ta có:
 và
và
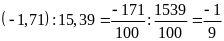
Hai
tỉ số đã cho đều bằng
 .
.
Vậy
ta có tỉ lệ thức
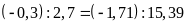
b) Ta có:
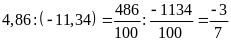 và
và
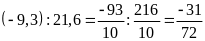
Vì
 nên
nên
Hai
tỉ số đã cho không bằng nhau nên ta không có tỉ lệ
thức từ hai tỉ số đó.
c) Ta có:
 và
và
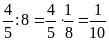
Hai
tỉ số đã cho đều bằng
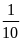 .
Vậy ta có tỉ lệ thức
.
Vậy ta có tỉ lệ thức

d)
Ta có:
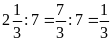 và
và
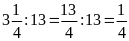
Hai
tỉ số đã cho không bằng nhau nên ta không có tỉ lệ
thức từ hai tỉ số đó.
Bài 7. Từ các tỉ số sau
đây có lập được tỉ lệ thức hay không?
a)
 và
và
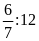
b)
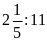 và
và
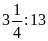
c)
 và
và
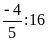
d)
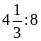 và
và

Lời giải:
a)
Ta có:
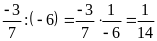 và
và
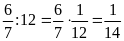
Hai
tỉ số đã cho đều bằng
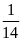 .
.
Vậy
ta có tỉ lệ thức

b)
Ta có:
 và
và
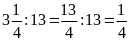
Hai
tỉ số đã cho không bằng nhau nên ta không có tỉ lệ
thức từ hai tỉ số đó.
c)
Ta có:
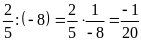 và
và

Hai
tỉ số đã cho đều bằng
 .
Vậy ta có tỉ lệ thức
.
Vậy ta có tỉ lệ thức

d)
Ta có:
 và
và

Hai tỉ số đã cho không bằng nhau nên ta không có tỉ lệ thức từ hai tỉ số đó.
Bài 8. Từ các tỉ số sau đây có lập được tỉ lệ thức hay không?
a)
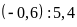 và
và
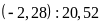
b)
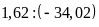 và
và
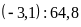
c)
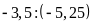 và
và
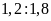
d)
 và
và
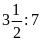
LỜI giải:
a)
Ta có:
 và
và

Hai
tỉ số đã cho đều bằng
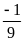 .
.
Vậy
ta có tỉ lệ thức
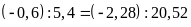
b)
Ta có:
 và
và
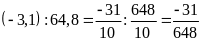
Hai tỉ số đã cho không bằng nhau nên ta không có tỉ lệ thức từ hai tỉ số đó.
c) Ta có:
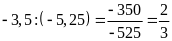 và
và

Hai
tỉ số đã cho đều bằng
 .
Vậy ta có tỉ lệ thức
.
Vậy ta có tỉ lệ thức
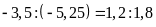
d) Ta có:
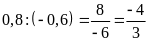 và
và
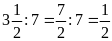
Hai tỉ số đã cho không bằng nhau nên ta không có tỉ lệ thức từ hai tỉ số đó.
Cách khác:
Vì
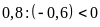 còn
còn
 nên ta không có tỉ lệ thức từ hai số đó.
nên ta không có tỉ lệ thức từ hai số đó.
Bài 9. Từ các tỉ số
sau đây có lập được tỉ lệ thức hay không?
a)
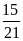 và
và
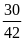
b)
 và
và
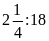
c)
 và
và

d)
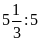 và
và
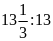
Lời giải:
a) Ta có:
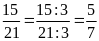 và
và
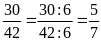
Hai
tỉ số đã cho đều bằng
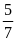 .
.
Vậy
ta có tỉ lệ thức
 .
.
b) Ta có:
 và
và

Hai tỉ số đã cho không bằng nhau nên ta không có tỉ lệ thức từ hai tỉ số đó. C) Ta Có:
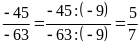 và
và
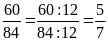
Hai
tỉ số đã cho đều bằng
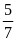 .Vậy
ta có tỉ lệ thức
.Vậy
ta có tỉ lệ thức
 .
.
d) Ta có:
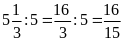 và
và

Hai tỉ số đã cho không bằng nhau nên ta không có tỉ lệ thức từ hai tỉ số đó.
Bài
10 . Từ các tỉ số sau đây có lập được tỉ lệ thức
hay không?
a)
 và
và
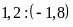
b)
 và
và
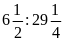
c)
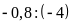 và
và
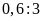
d)
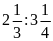 và
và

Lò̀i giải:
a) Ta có:
 và
và
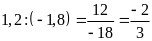
Hai tỉ số đã cho không bằng nhau nên ta không có tỉ lệ thức từ hai tỉ số đã cho.
b) Ta có:
 và
và

Hai
tỉ số đã cho đều bằng
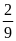 .
Vậy ta có tỉ lệ thức
.
Vậy ta có tỉ lệ thức
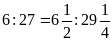 .
.
c) Ta có:
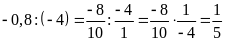 và
và

Hai
tỉ số đã cho đều bằng
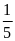 .
Vậy ta có tỉ lệ thức
.
Vậy ta có tỉ lệ thức
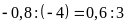 .
.
d) Ta có:
 và
và

Hai tỉ số đã cho không bằng nhau nên ta không có tỉ lệ thức từ hai tỉ số đã cho.
Bài
11. Lập tất cả các tỉ lệ thức có thể từ các đẳng
thức sau
a)
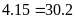
b)
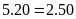
c)
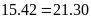
Lời giải:
a)
Vì
 nên ta có các tỉ lệ thức sau
nên ta có các tỉ lệ thức sau
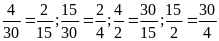
b)
Vì
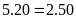 nên ta có các tỉ lệ thức sau
nên ta có các tỉ lệ thức sau

c)
Vì
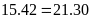 nên ta có các tỉ lệ thức sau
nên ta có các tỉ lệ thức sau

Bài
12. Lập tất cả các tỉ lệ thức có thể từ đẳng
thức sau
a)
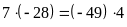
b)

c)

Lời giải:
a)
Vì 7.(-28)=(-49).4 nên ta có các tỉ lệ thức sau:

b)
Vì
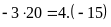 nên ta có các tỉ lệ thức sau
nên ta có các tỉ lệ thức sau
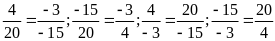
c)
Vì -2.(-27)=(-9).(-6) nên ta có các tỉ lệ thức sau
 ;
;
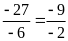
Bài
13. Lập tất cả các tỉ lệ thức có thể từ các đẳng
thức sau
a)
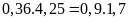
b)

c)

Lời giải:
a)
Vì
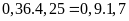 nên ta có các tỉ lệ thức sau:
nên ta có các tỉ lệ thức sau:

b)
Vì
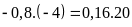 nên ta có các tỉ lệ thức sau
nên ta có các tỉ lệ thức sau
 ;
;
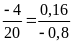
c)
Vì
 nên ta có các tỉ lệ thức sau
nên ta có các tỉ lệ thức sau
 .
.
Bài
14. Lập tất cả các tỉ lệ thức có thể từ các đẳng
thức sau
a)

b)

C)
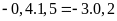
Lời giải:
a)
Vì 4,4.1,89=9,9.0,84 nên ta có các tỉ lệ thức sau
 ;
;
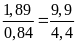
b)
Vì
 nên ta có các tỉ lệ thức sau
nên ta có các tỉ lệ thức sau

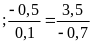 c) Vì
c) Vì
 nên ta có các tỉ lệ thức sau
nên ta có các tỉ lệ thức sau
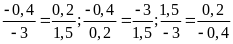 ;
;

Bài
15. Lập tất cả các tỉ lệ thức có thể từ các đẳng
thức sau
a)
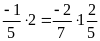
b)

c)
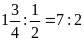
Lời giải:
a)
Vì
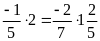 nên ta có các tỉ lệ thức sau
nên ta có các tỉ lệ thức sau
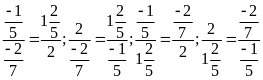
b)
Vì
 nên ta có các tỉ lệ thức sau
nên ta có các tỉ lệ thức sau
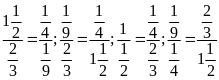
c)
Vì
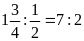 nên ta có các tỉ lệ thức sau
nên ta có các tỉ lệ thức sau
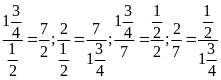
Bài
16. Có thể lập được tỉ lệ thức từ nhóm bốn số
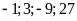 không? Nếu lập được hãy viết các tỉ lệ thức từ
nhóm bốn số đó.
không? Nếu lập được hãy viết các tỉ lệ thức từ
nhóm bốn số đó.
Lời giải:
Ta
có
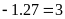 .
.
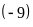 nên lập được tỉ lệ thức từ nhóm bốn số
nên lập được tỉ lệ thức từ nhóm bốn số
 là
là
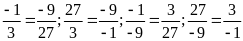
Bài
17. Có thể lập được tỉ lệ thức từ nhóm bốn số
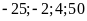 không? Nếu lập được hãy viết các tî̉ lệ thức từ
nhóm bốn số đó.
không? Nếu lập được hãy viết các tî̉ lệ thức từ
nhóm bốn số đó.
Lời giải:
Ta
có
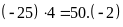 nên lập được tỉ lệ thức từ nhóm bốn số là
nên lập được tỉ lệ thức từ nhóm bốn số là

Bài
18. Có thể lập được tỉ lệ thức từ nhóm bốn số
0, không? Nếu lập được hãy viết các tỉ lệ thức từ
nhóm bốn số đó.
không? Nếu lập được hãy viết các tỉ lệ thức từ
nhóm bốn số đó.
Lời giải:
Ta
có
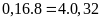 nên lập được tỉ lệ thức từ nhóm bốn số 0,
nên lập được tỉ lệ thức từ nhóm bốn số 0, là
là

Bài 19. Với năm số 1;2;6;8;16. Hãy lập các tỉ lệ thức có thể được từ nhóm năm số đó.
Lời giải:
Ta
có
 nên lập được tỉ lệ thức từ nhóm là
nên lập được tỉ lệ thức từ nhóm là
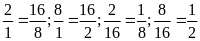
Bài
20. Với năm số
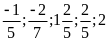 .
Hãy lập các tỉ lệ thức có thể được từ nhóm năm
số đó.
.
Hãy lập các tỉ lệ thức có thể được từ nhóm năm
số đó.
Lời giải:
Ta
có
 nên lập được tỉ lệ thức từ nhóm là
nên lập được tỉ lệ thức từ nhóm là
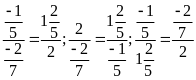 ;
;

Dạng 2. Tìm số chưa biết của một tỉ lệ thức
Phương pháp giải:
Từ tỉ lệ thức
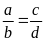 suy ra
suy ra
 .
.
hoặc
từ tỉ lệ thức
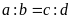 suy ra
suy ra
 .
.
Bài toán.
Bài
1. Tìm số hữu tỉ
 trong các tỉ lệ thức sau:
trong các tỉ lệ thức sau:
b)

a)
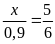
c)
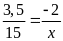
d)
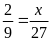
Lời giải:
b)
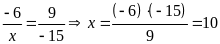
a)
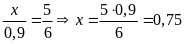
c)
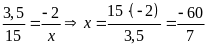
d)
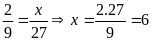
Bài
2. Tìm số hữu tỉ
 trong các tỉ lệ thức sau:
trong các tỉ lệ thức sau:
b)

a)
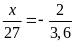
c)
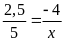
d)

Lời giải:
b)

a)
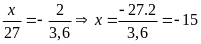
c)
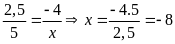
d)
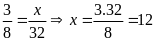
Bài
3. Tìm số hữu tỉ
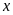 trong các tỉ lệ thức sau:
trong các tỉ lệ thức sau:
b)
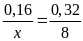
a)
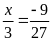
c)

d)
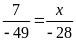
Lời giải:
b)

a)

d)

c)

Bài
4. Tìm số hữu tỉ
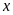 trong các tỉ lệ thức sau:
trong các tỉ lệ thức sau:
a)
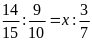
b)
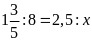
c)
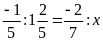
d)

Lời giải:
a)
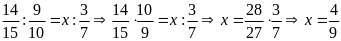
b)
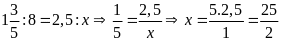
c)

d)
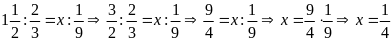
Bài
5. Tìm số hữu tỉ
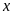 trong các tỉ lệ thức sau:
trong các tỉ lệ thức sau:
b)
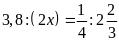
a)
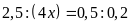
c)
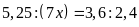
d)
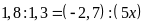
Lời giải:
a)
2,5:
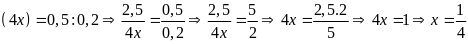
b)
3,8:
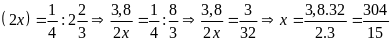
c)

d)
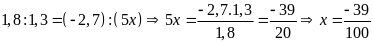
Bài
6. Tìm số hữu tỉ
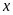 trong các tỉ lệ thức sau:
trong các tỉ lệ thức sau:
a)
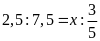
b)

c)
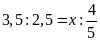
d)
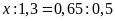
Lời giải:
a)

b)
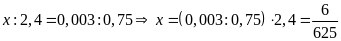
c)
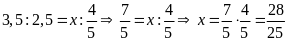
d)
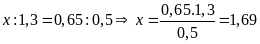
Bài
7. Tìm số hữu tỉ
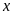 trong các tỉ lệ thức sau:
trong các tỉ lệ thức sau:
a)
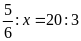
b)

d)
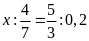
c)
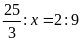
Lời giải:
a)
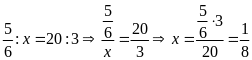
b)
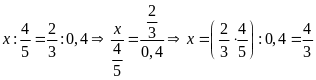
c)
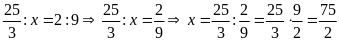
d)
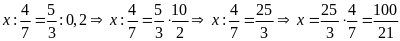
Bài
8. Tìm số hữu tỉ
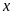 trong các tỉ lệ thức sau:
trong các tỉ lệ thức sau:
a)
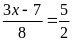
b)
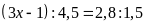
c)
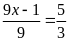
d)
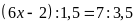
Lời giải:
a)

b)
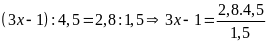
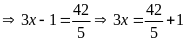

c)
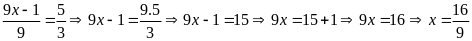
d)

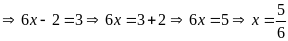
Bài
9. Tìm số hữu tỉ
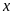 trong các tỉ lệ thức sau:
trong các tỉ lệ thức sau:
a)
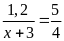
b)

c)
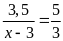
d)
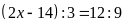
Lời giải:
a)
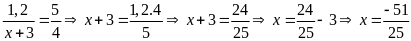
b)
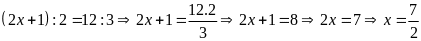
c)

d)
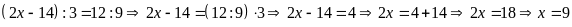
Bài
10. Tìm số hữu tỉ
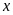 trong các tỉ lệ thức sau:
trong các tỉ lệ thức sau:
a)
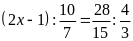
b)

c)

d)
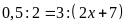
Lời giải:
a)
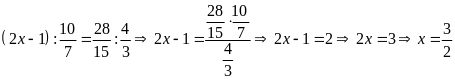
b)
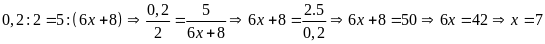
c)
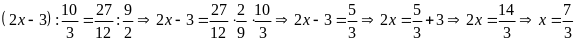
d)
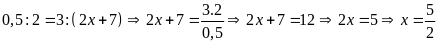
Bài
11. Tìm số hữu tỉ
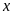 trong các tỉ lệ thức sau:
trong các tỉ lệ thức sau:
a)
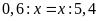
b)
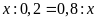
c)
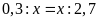
d)
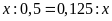
Lời giải:
a)

b)

c)
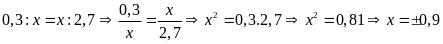
d)
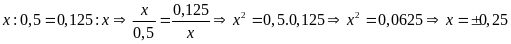
Bài
12. Tìm số hữu tỉ
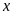 trong các tỉ lệ thức sau:
trong các tỉ lệ thức sau:
a)

b)

c)

d)

Lời giải:
a)

b)

c)
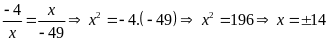
d)
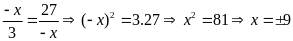
Bài
13. Tìm số hữu tỉ
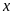 trong các tỉ lệ thức sau:
trong các tỉ lệ thức sau:
a)
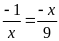
b)
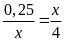
d)
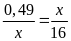
c)
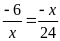
Lời giải:
a)
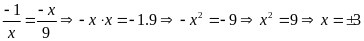
b)

c)

d)
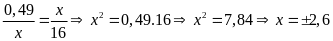
Bài
14. Tìm số hữu tỉ
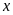 trong các tỉ lệ thức sau
trong các tỉ lệ thức sau
a)

b)

C)

d)
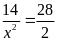
Lời giải:
a)
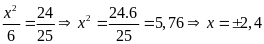
b)

c)
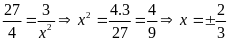
d)
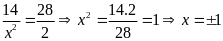
Bài
15. Tìm số hữu tỉ
 trong các tỉ lệ thức sau
trong các tỉ lệ thức sau
a)

b)

c)
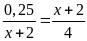
Lời giải:
a)
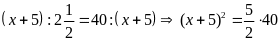
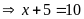 hoặc
hoặc

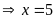 hoặc
hoặc
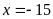
b)
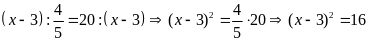
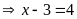 hoặc
hoặc
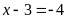
 hoặc
hoặc

c)
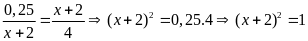
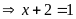 hoặc
hoặc

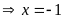 hoặc
hoặc
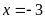
Bài
16. Tìm số hữu tỉ
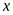 trong các tỉ lệ thức
trong các tỉ lệ thức
a)

b)
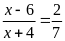
Lời giải:
a)
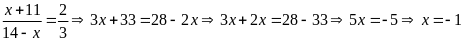
b)

Bài
17. Tìm số hữu tỉ
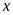 trong các tỉ lệ thức
trong các tỉ lệ thức
a)
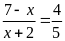
b)

Lời giải:
a)

b)

Bài
18. Tìm số hữu tỉ
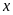 trong tỉ lệ thức
trong tỉ lệ thức
a)

b)

Lời giải:
a)
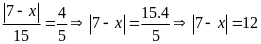
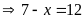 hoặc
hoặc
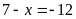
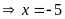 hoặc
hoặc
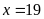
b)

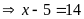 hoặc
hoặc
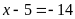
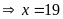 hoặc
hoặc
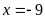
Bài
19. Tìm số hữu tỉ
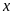 trong các tỉ lệ thức
trong các tỉ lệ thức
a)
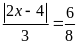
b)

Lời giải:
a)
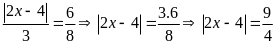
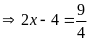 hoặc
hoặc
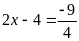
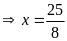 hoặc
hoặc
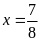
b)
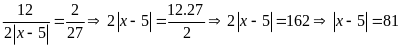
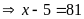 hoạc
hoạc
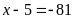
 hoăc
hoăc
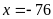
Bài
20. Tìm số hữu tỉ
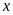 trong các tỉ lệ thức
trong các tỉ lệ thức
a)

b)
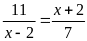
Lời giải:
a)

b)
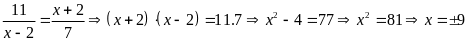 .
.
Dạng 3. Các bài tập ứng dụng
Phương pháp giải:
Tỉ lệ thức
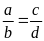 còn được viết là
còn được viết là
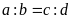 .
.Dựa vào định nghĩa nếu có
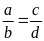 thì tỉ số
thì tỉ số
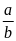 và
và
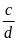 lập thành được một tỉ lệ thức
lập thành được một tỉ lệ thức
Bài toán.
Bài
1. Trong giờ thí nghiệm, bạn Hùng dùng hai quả cân
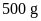 và
và
 thì đo được trọng lượng tương ứng là
thì đo được trọng lượng tương ứng là
 và
và
 .
.
a) Tính tỉ số giữa khối lượng của quả cân thứ nhất và khối lượng quả cân thứ hai; tỉ số giữa trọng lượng của quả cân thứ nhất và trọng lượng của quả cân thứ hai.
b) Hai tỉ số trên có lập thành tỉ lệ thức hay không?
Lời giải:
a)
Tỉ số giữa khối lượng của quả cân thứ nhất và
khối lượng quả cân thứ hai là
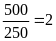 .
.
Tỉ
số giữa trọng lượng của quả cân thứ nhất và trọng
lượng quả cân thứ hai là
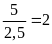 .
.
b)
Hai tỉ số trên bằng nhau, nên hai tỉ số trên lập được
thành một tỉ lệ thức là
 .
.
Bài
2. Hai máy tính có kích thước màn hình 20 inch, (inch là gì
một đơn vị đo lường được sử dụng chủ yếu ở
Hoa Kỳ và phổ biến ở các nước Canada, Anh...) tỉ lệ
chuẩn là 1680 x1050
 và màn hình 24 inch tỉ lệ chuẩn là 1920 x1200
và màn hình 24 inch tỉ lệ chuẩn là 1920 x1200
 .
.
a) Tính tỉ số giữa chiều rộng và chiều dài của mỗi màn hình.
b) Hai tỉ số giữa chiều rộng và chiều dài của mỗi màn hình trên có lập thành tỉ lệ thức hay không?
Lời giải:
a)
Tỉ số giữa chiều rộng và chiều dài của màn hình 20
inch là
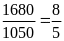 .
.
Tỉ
số giữa chiều rộng và chiều dài của màn hình 24 inch
là
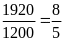 .
b) Hai tỉ số trên bằng nhau, nên hai tỉ số giữa chiều
rộng và chiều dài của mỗi màn hình trên lập được
thành một tỉ lệ thức là
.
b) Hai tỉ số trên bằng nhau, nên hai tỉ số giữa chiều
rộng và chiều dài của mỗi màn hình trên lập được
thành một tỉ lệ thức là
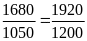 .
.
Bài
3. Lá quốc kỳ trên cột cờ Lũng Cú là hình chữ nhật
có kích thước là 6x9(m), lá cờ quốc kỳ lớp
 treo tại lớp trong các giờ sinh hoạt là hình chữ nhật
có kích thước là
treo tại lớp trong các giờ sinh hoạt là hình chữ nhật
có kích thước là
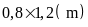 .
.
a) Tính tỉ số giữa chiều rộng và chiều dài của mỗi lá cờ.
b) Hai tỉ số giữa chiều rộng và chiều dài của mỗi lá cờ trên có lập thành tỉ lệ thức hay không?
Lời giải:
a)
Tỉ số giữa chiều rộng và chiều dài của lá quốc kỳ
trên cột cờ Lũng Cú là
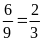 .
.
Tỉ
số giữa chiều rộng và chiều dài của lá quốc kỳ lớp
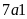 là
là
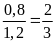 .
.
b)
Hai tỉ số trên bằng nhau, nên hai tỉ số giữa chiều
rộng và chiều dài của mỗi lá cờ trên lập được
thành một tỉ lệ thức là
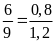 .
.
Bài
4. Theo tiêu chuẩn của Liên đoàn bóng chuyền quốc tế
FIVB sân bóng chuyền là hình chữ nhật có kích thước là
9x18 (m). Lan vẽ mô phỏng mặt sân bóng chuyền là hình
chữ nhật có kích thước là
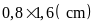 .
.
a) Tính tỉ số giữa chiều rộng và chiều dài của sân bóng chuyền.
b) Lan đã vẽ mô phỏng mặt sân đúng tỉ lệ hay chưa?
Lời giải:
a)
Tỉ số giữa chiều rộng và chiều dài của sân bóng
chuyền là
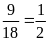 .
.
b)
Tỉ số giữa chiều rộng và chiều dài của bản vẽ mô
phỏng mặt sân bóng chuyền là
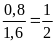 .
.
Hai
tỉ số trên bằng nhau, ta có một tỉ lệ thức là
 .
Vậy Lan đã vẽ mô phỏng mặt sân đúng tỉ lệ.
.
Vậy Lan đã vẽ mô phỏng mặt sân đúng tỉ lệ.
Bài 5. Lan đọc một cuốn sách trong ba ngày. Ngày thứ nhất Lan đọc 20 trang, ngày thứ hai lan đọc 40 trang, ngày thứ 3 Lan đọc 80 trang.
a) Tính tỉ số giữa trang sách Lan đọc được trong ngày thứ nhất và thứ hai.
b) Tính tỉ số giữa trang sách Lan đọc được trong ngày thứ hai và thứ ba.
c) Hai tỉ số trên có lập thành tỉ lệ thức hay không?
Lời giải:
a)
Tỉ số giữa trang sách Lan đọc được trong ngày thứ
nhất và thứ hai là
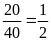 .
.
b)
Tỉ số giữa trang sách Lan đọc được trong ngày thứ
hai và thứ ba là
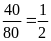 .
.
c)
Hai tỉ số trên bằng nhau, nên lập được thành một tỉ
lệ thức là
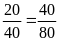 .
.
Bài
6. Tỉ số của hai số là
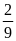 .
Biết số lớn là 135 . Tìm số bé?
.
Biết số lớn là 135 . Tìm số bé?
Lời giải:
Gọi
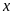 là số bé cần tìm
là số bé cần tìm
 .
.
Theo
bài ra tỉ số giữa số bé và số lớn là
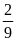 nên
nên
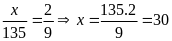 (TMĐK).
(TMĐK).
Vậy số bé cần tìm là 30 .
Bài
7. Tỉ số của hai số là
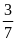 .
Biết số bé là 12 . Tìm số lớn?
.
Biết số bé là 12 . Tìm số lớn?
Lời giải:
Gọi
 là số lớn cần tìm
là số lớn cần tìm
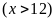 .
.
Theo
bài ta tỉ số giữa số bé và số lớn là
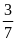 nên
nên
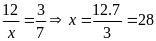 (TMĐK).
(TMĐK).
Vậy số lớn cần tìm là 28
Bài 8. Người ta làm mứt dâu bằng cách trộn 6 phần dâu với 4 phần đường. Hỏi cần bao nhiêu kg đường để trộn hết 45 kg dâu theo cách pha nhiên trộn như trên?
Lời giải:
Gọi
 là số kg đường cần để trộn hết 45 kg dâu theo cách
pha trộn như trên
là số kg đường cần để trộn hết 45 kg dâu theo cách
pha trộn như trên
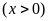 .
.
Theo
bài ta có trộn 6 phần dâu với 4 phần đường nên
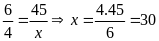 (TMĐK)
(TMĐK)
Vậy
số kg đường cần để trộn là
 .
.
Bài 9. Người ta pha nhiên liệu cho một loại động cơ bằng cách trộn 2 phần dầu với 7 phần xăng. Hỏi cần bao nhiêu lít xăng để trộn hết 8 lít dầu theo cách pha nhiên liệu như trên?
Lời giải:
Gọi
 là số lít xăng cần để trộn hết 8 lít dầu theo cách
pha nhiên liệu như trên
là số lít xăng cần để trộn hết 8 lít dầu theo cách
pha nhiên liệu như trên
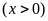 .
.
Theo
bài ta có trộn 2 phần dầu với 7 phần xăng nên
 (TMĐK)
(TMĐK)
Vậy số lít xăng cần để trộn là 28 lít.
Bài
10. Lá quốc kỳ Việt Nam là hình chữ nhật có tỉ lệ
kích thước rộng và dài là
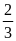 .
Nam làm lá cờ quốc kỳ bằng giấy đảm bảo đúng tỉ
lệ quy định để tham gia cổ vũ đá bóng Sea Games có
chiều dài là
.
Nam làm lá cờ quốc kỳ bằng giấy đảm bảo đúng tỉ
lệ quy định để tham gia cổ vũ đá bóng Sea Games có
chiều dài là
 .
Tính chiều rộng của lá cờ Nam làm
.
Tính chiều rộng của lá cờ Nam làm
Lời giải:
Gọi
 là chiều rộng của lá cờ Nam làm
là chiều rộng của lá cờ Nam làm
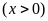 .
.
Theo
bài ra: tỉ số giữa chiều rộng và chiều dài của lá
quốc kỳ là
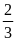 nên
nên
 (TMĐK)
(TMĐK)
Vậy
chiều rộng của lá cờ Nam làm
 .
.
Bài
11. Tỉ lệ nấu bánh chưng ngon nhất là 4 gạo:1 đậu
xanh, vậy gói bánh chưng ngon với tỉ lệ như trên thì
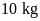 gạo cần bao nhiêu đậu xanh.
gạo cần bao nhiêu đậu xanh.
Lời giải:
Gọi
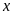 là số kg đậu xanh cần tìm để gói bánh chưng
là số kg đậu xanh cần tìm để gói bánh chưng

Theo
bài ta tỉ lệ thức giữa số gạo và đậu xanh gói bánh
là
 (TMĐK) Vậy cần khối lượng đậu xanh là 2,5kg.
(TMĐK) Vậy cần khối lượng đậu xanh là 2,5kg.
Bài
12. Tính độ dài hai cạnh của hình chữ nhật, biết tỉ
số giữa các cạnh là 0,6 và chu vi bằng

Lời giải:
Gọi
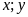 là độ dài hai cạnh của hình chữ nhật
là độ dài hai cạnh của hình chữ nhật
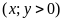 .
.
Nửa
chu vi bằng
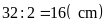 suy ra
suy ra

Tỉ
số giữa các cạnh là
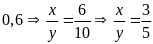
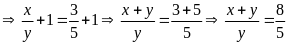 (2)
(2)
Từ
(1) và (2) ta có
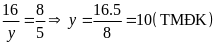

Vậy
hình chữ nhật có kích thước là
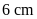 và
và
 .
.
Bài
13. Tính độ dài 2 cạnh của một vườn hoa hình chữ
nhật, biết tỉ số giữa chiều rộng và chiều dài là
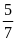 và chu vi bằng
và chu vi bằng
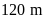
Lời giải:
Gọi
 là độ dài chiều rộng và chiều dài của hình chữ
nhật.
là độ dài chiều rộng và chiều dài của hình chữ
nhật.
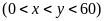 .
.
Nửa
chu vi bằng 120:
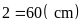 suy ra
suy ra
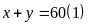
Tỉ
số giữa các cạnh là

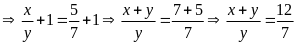 (2)
(2)
Từ
(1) và (2) ta có
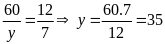 (TMĐK)
(TMĐK)
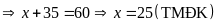
Vậy
hình chữ nhật có hai kích thước là
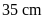 và
và
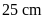 .
.
Bài
14. Thông thường, một thùng sơn có thể tích
 và theo quy định của nhà sản xuất tất cả các loại
sơn đều pha theo tỉ lệ nhỏ hơn hoặc bằng
và theo quy định của nhà sản xuất tất cả các loại
sơn đều pha theo tỉ lệ nhỏ hơn hoặc bằng
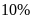 .
Như vậy, nếu một thùng sơn
.
Như vậy, nếu một thùng sơn
 sẽ pha cùng với
sẽ pha cùng với
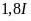 nước sạch thì để có
nước sạch thì để có
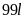 sơn nước thì cần bao nhiêu thùng sơn và bao nhiêu lít
nước sạch?
sơn nước thì cần bao nhiêu thùng sơn và bao nhiêu lít
nước sạch?
Lời giải:
Gọi
số sơn và số nước sạch cần tìm là
 ( đơn vị: lít ; đk:
( đơn vị: lít ; đk:
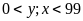 )
)
Ta
có:
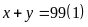 Vì tỉ số sơn và số nước sạch là
Vì tỉ số sơn và số nước sạch là

 (2)
(2)
Từ
(1) và (2) ta có:
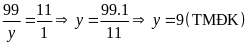
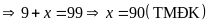
Ta
có

Vậy số thùng sơn cần dùng là 5 thùng, số nước sạch cần là 91 .
Bài
15. An cần lăn sơn phòng, diện tích phòng 1 là
 ,
ở phòng 2 là
,
ở phòng 2 là
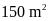 .
Cả hai phòng An lăn hết
.
Cả hai phòng An lăn hết
 sơn. Tính số lượng sơn cần dùng cho mỗi phòng ?
sơn. Tính số lượng sơn cần dùng cho mỗi phòng ?
Lời giải:
Gọi
số lượng sơn cần dùng cho phòng 1 và phòng 2 lần lượt
là
 (đơn vị:
(đơn vị:
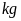 ;
đk:
;
đk:
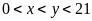 )
)
Ta
có:
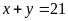 (1)
(1)
Vì
tỉ số diện tích giữa hai phòng là
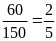
 (2)
(2)
Từ
(1) và
 ta có:
ta có:


Vậy
số lượng sơn cần dùng phòng 1 là
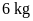 ,
ở phòng 2 là
,
ở phòng 2 là
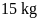 .
.
Bài
16. Hai lớp
 và
và
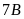 đi lao động trồng cây. Biết rằng tỉ số giữa số cây
trồng được của lớp
đi lao động trồng cây. Biết rằng tỉ số giữa số cây
trồng được của lớp
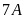 và
và
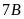 là
là
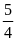 và lớp
và lớp
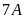 trồng nhiều hơn lớp
trồng nhiều hơn lớp
 là 20 cây. Tính số cây mỗi lớp đã trồng.
là 20 cây. Tính số cây mỗi lớp đã trồng.
Lời giải:
Gọi
số cây trồng được của lớp
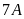 và
và
 thứ tự là
thứ tự là
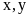 (đơn vị: cây; đk:
(đơn vị: cây; đk:
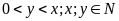 ) Ta có lớp
) Ta có lớp
 trồng nhiều hơn lớp
trồng nhiều hơn lớp
 là 20 cây
là 20 cây
 (1)
(1)
Vì
tỉ số giữa số cây trồng được của lớp
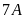 và
và
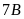 là
là
 nên
nên
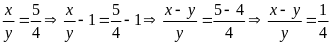 (2) Từ (1) và (2) ta có:
(2) Từ (1) và (2) ta có:
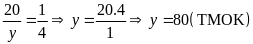
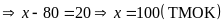
Vậy
số cây trồng được của lớp
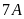 là 100 cây và
là 100 cây và
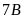 là 80 cây.
là 80 cây.
Bài
17. Hai lớp
 và
và
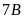 đi lao động trồng cây. Biết rằng tỉ số giữa số cây
trồng được của lớp
đi lao động trồng cây. Biết rằng tỉ số giữa số cây
trồng được của lớp
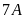 và
và
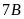 là
là
 và lớp
và lớp
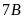 trồng nhiều hơn lớp
trồng nhiều hơn lớp
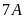 là 20 cây. Tính số cây mỗi lớp đã trồng.
là 20 cây. Tính số cây mỗi lớp đã trồng.
Lời giải:
Gọi
số cây trồng được của lớp
 và
và
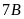 thứ tự là
thứ tự là
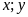 (đơn vị: cây; đk:
(đơn vị: cây; đk:
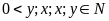 )
)
Ta
có:
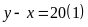
Vì
tỉ số giữa số cây trồng được của lớp
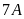 và
và
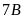 là
là
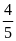 nên
nên
 (2)
(2)
Từ
(1) và (2) ta có:
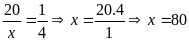 (TMĐK)
(TMĐK)

Vậy
số cây trồng được của lớp
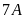 là 80 cây và
là 80 cây và
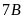 là 100 cây.
là 100 cây.
Bài
18. Biết rằng 17 lít dầu hỏa nặng
 .
Hỏi
.
Hỏi
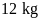 dầu hỏa thì có chứa hết được vào chiếc can 16 lít
hay không?
dầu hỏa thì có chứa hết được vào chiếc can 16 lít
hay không?
Lời giải:
Gọi
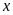 là số lít dầu hỏa nặng
là số lít dầu hỏa nặng
 .
.
Theo
bài ta tỉ lệ thức giữa thể tích dầu và khối lượng
dầu là
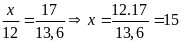 (TMĐK)
(TMĐK)
Vậy
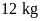 dầu hỏa thì có thể tích là 15 lít nên chứa hết được
vào chiếc can 16 lít.
dầu hỏa thì có thể tích là 15 lít nên chứa hết được
vào chiếc can 16 lít.
Bài
19. Tỉ số của hai số là
 ,
nếu thêm 2 đơn vị vào số thứ nhất thì tỉ số của
chúng sẽ bằng
,
nếu thêm 2 đơn vị vào số thứ nhất thì tỉ số của
chúng sẽ bằng
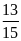 .
Tìm hai số đó.
.
Tìm hai số đó.
Lời giải:
Gọi
hai số cần tìm là
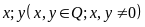 .
.
Theo
đề bài tỉ số của hai số là
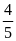 ,
ta có:
,
ta có:
 (1) Nếu thêm 2 đơn vị vào số thứ nhất thì tỉ số
của chúng sẽ bằng
(1) Nếu thêm 2 đơn vị vào số thứ nhất thì tỉ số
của chúng sẽ bằng

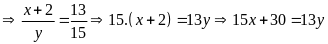 (2)
(2)
Từ
(1) và (2) ta có:
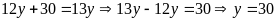 (TMĐK)
(TMĐK)
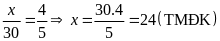
Vậy
hai số đó là

Bài
20. Tìm hai phân số tối giản biết tổng của chúng là
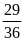 ,
các tử theo thứ tự tỉ lệ với 7 và 5 ; các mẫu theo
thứ tự tỉ lệ với 3 và 2 .
,
các tử theo thứ tự tỉ lệ với 7 và 5 ; các mẫu theo
thứ tự tỉ lệ với 3 và 2 .
Lời giải:
Gọi
hai phân số tối giản cần tìm là
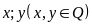 .
.
Theo
đề bài ta có tử số của chúng tỉ lệ với
 và các mẫu số tỉ lệ với 3; 2 , nên ta có:
và các mẫu số tỉ lệ với 3; 2 , nên ta có:
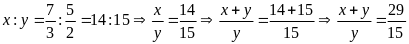
Mà:

Vậy:
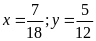
Dạng 4. Chứng minh đẳng thức
Phương pháp giải:
Từ tỉ lệ thức
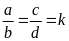 suy ra
suy ra
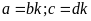 .
.Từ tỉ lệ thức
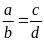 suy ra
suy ra
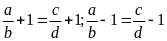
Bài toán.
Bài
1. Cho tỉ lệ thức
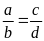 .
Chứng minh rằng ta có tỉ lệ thức:
.
Chứng minh rằng ta có tỉ lệ thức:
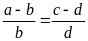
Lời giải:
Từ
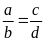 suy ra
suy ra
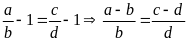 .
.
Bài
2. Cho tỉ lệ thức
 .
Chứng minh rằng ta có tỉ lệ thức:
.
Chứng minh rằng ta có tỉ lệ thức:
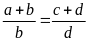
Lời giải:
Từ
 suy ra
suy ra
 .
.
Bài
3. Cho tỉ lệ thức
 .
Chứng minh rằng ta có tỉ lệ thức:
.
Chứng minh rằng ta có tỉ lệ thức:
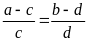
Lời giải:
Từ
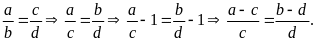
Bài
4. Cho tỉ lệ thức
 .
Chứng minh rằng ta có tỉ lệ thức:
.
Chứng minh rằng ta có tỉ lệ thức:
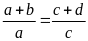
Lời giải:
Từ
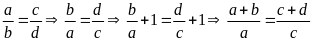
Bài
5. Cho tỉ lệ thức
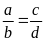 .
Chứng minh rằng ta có tỉ lệ thức:
.
Chứng minh rằng ta có tỉ lệ thức:
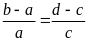
Lời giải:
Từ
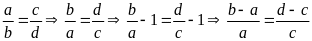
Bài
6. Cho tỉ lệ thức
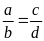 .
Chứng minh rằng ta có tỉ lệ thức:
.
Chứng minh rằng ta có tỉ lệ thức:
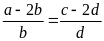
Lời giải:
Từ
 suy ra
suy ra
 .
.
Bài
7. Cho tỉ lệ thức
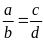 .
Chứng minh rằng ta có tỉ lệ thức:
.
Chứng minh rằng ta có tỉ lệ thức:

Lời giải:
Từ
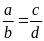 suy ra
suy ra
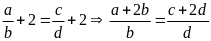 .
.
Bài
8. Cho tỉ lệ thức
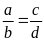 .
Chứng minh rằng ta có tỉ lệ thức:
.
Chứng minh rằng ta có tỉ lệ thức:
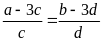
Lời giải:
Từ
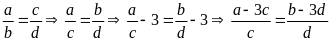 .
.
Bài
9. Cho tỉ lệ thức
 .
Chứng minh rằng ta có tỉ lệ thức:
.
Chứng minh rằng ta có tỉ lệ thức:

Lời giải:
Từ
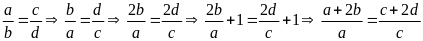
Bài
10. Cho tỉ lệ thức
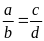 .
Chứng minh rằng ta có tỉ lệ thức:
.
Chứng minh rằng ta có tỉ lệ thức:
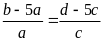
Lời giải:
Từ

Bài
11. Chứng tỏ rằng: Nếu
 (trong đó
(trong đó
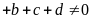 ) thì
) thì
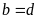
Lời giải:
Từ
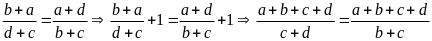
mà
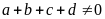
nên

Bài
12. Chứng tỏ rằng: Nếu
 (trong đó
(trong đó
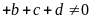 ) thì
) thì

Lời giải:
Từ
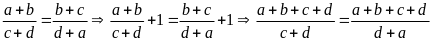 mà
mà
 nên
nên
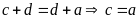
Bài
13. Cho tỉ lệ thức
 .
Chứng minh tỉ lệ thức:
.
Chứng minh tỉ lệ thức:
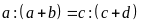 (Giả thiết các tỉ lệ thức đều có nghĩa).
(Giả thiết các tỉ lệ thức đều có nghĩa).
Lời giải:
Từ
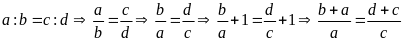

Bài
14. Cho tỉ lệ thức
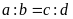 .
Chứng minh tỉ lệ thức:
.
Chứng minh tỉ lệ thức:
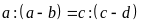 (Giả thiết các tỉ lệ thức đều có nghĩa).
(Giả thiết các tỉ lệ thức đều có nghĩa).
Lời giải:
Từ
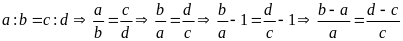
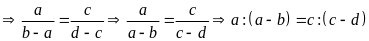
Bài
15. Cho tỉ lệ thức
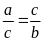 .
Chứng minh rằng ta có tỉ lệ thức
.
Chứng minh rằng ta có tỉ lệ thức
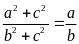
Lời giải:
Từ
tỉ lệ thức
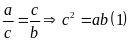
Đặt
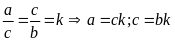 .
Do đó
.
Do đó
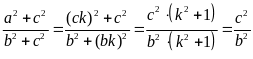
Từ
(1) và (2) suy ra
 .
Vậy
.
Vậy

Bài
16. Cho tỉ lệ thức
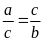 .
Chứng minh rằng ta có tỉ lệ thức
.
Chứng minh rằng ta có tỉ lệ thức
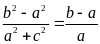
Lời giải:
Áp dụng bài 15 ta có:
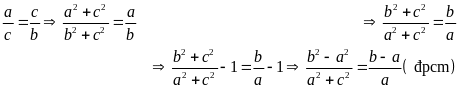
Bài
17. Cho tỉ lệ thức
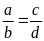 .
Chứng minh rằng ta có tỉ lệ thức
.
Chứng minh rằng ta có tỉ lệ thức
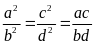
Lời giải:
Đặt
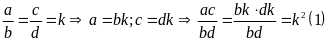
Từ
tỉ lệ thức

Từ
(1) và (2) suy ra
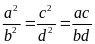 Bài 18. Cho tỉ lệ thức
Bài 18. Cho tỉ lệ thức
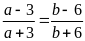 .
Chứng minh
.
Chứng minh
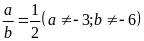
Lời giải:
Từ
tỉ lệ thức
 ,
ta có:
,
ta có:
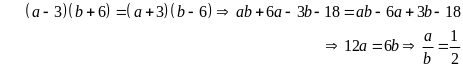
Bài
19. Cho tỉ lệ thức:
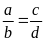 .
Chứng minh đẳng thức sau:
.
Chứng minh đẳng thức sau:
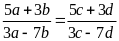
Lời giải:
Đặt
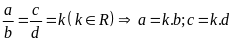
Ta có:

Từ
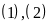 suy ra đpcm
suy ra đpcm
Bài
20. Chứng minh rằng nếu
 thì
thì
 hoặc
hoặc
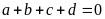 .
.
Lời giải:
Vì
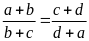 nên
nên

Suy
ra:
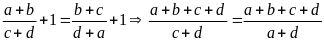
Nếu
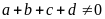 thì từ
thì từ
 suy ra:
suy ra:
 .
.
Nếu
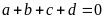 thì ta có tỉ lệ thức luôn đúng (
thì ta có tỉ lệ thức luôn đúng (
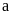 có thể bằng hay không bằng
có thể bằng hay không bằng
 ).
).
Phần III. BÀI TẬP TỰ LUYỆN
Dạng 1. Lập tỉ lệ thức
Bài
1. Thay các tỉ số sau bằng tỉ số giữa các số
nguyên.
c)

b)
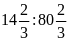
a)
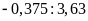
Bài
2. Thay các tỉ số sau bằng tỉ số giữa các số
nguyên.
a)

b)

c)
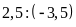 Bài 3. Từ các tỉ số sau đây có lập được tỉ lệ
thức hay không?
Bài 3. Từ các tỉ số sau đây có lập được tỉ lệ
thức hay không?
a)

và
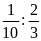
b)
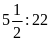 và
và
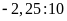
Bài
4. Từ các tỉ số sau đây có lập được tỉ lệ thức
hay không?
b)
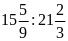 và
và

a)
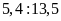 và
và
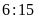
Bài
5. Lập tất cả các tỉ lệ thức có thể từ các đẳng
thức sau
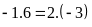
Bài
6. Lập tất cả các tỉ lệ thức có thể từ các đẳng
thức sau

Bài
7. Có thể lập được tỉ lệ thức từ nhóm bốn số
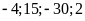 không? Nếu lập được hãy viết các tỉ lệ thức từ
nhóm bốn số đó.
không? Nếu lập được hãy viết các tỉ lệ thức từ
nhóm bốn số đó.
Bài
8. Với năm số
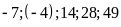 .
Hãy lập các tỉ lệ thức có thể được từ nhóm năm
số đó.
.
Hãy lập các tỉ lệ thức có thể được từ nhóm năm
số đó.
Dạng 2. Tìm số chưa biết trong tỉ lệ thức
Bài
1. Tìm số hữu tỉ
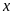 trong các tỉ lệ thức sau:
trong các tỉ lệ thức sau:
a)

b)

c)
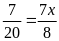
Bài
2. Tìm số hữu tỉ
 trong các tỉ lệ thức sau:
trong các tỉ lệ thức sau:
a)
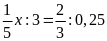
b)
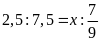
c)
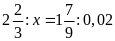
Bài
3. Tìm số hữu tỉ
 trong các tỉ lệ thức sau:
trong các tỉ lệ thức sau:
a)
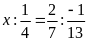
b)

Bài
4. Tìm số hữu tỉ
 trong các tỉ lệ thức sau:
trong các tỉ lệ thức sau:
a)
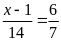
b)
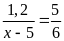
Bài
5. Tìm số hữu tỉ
 trong tỉ lệ thức
trong tỉ lệ thức
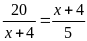
Bài
6. Tìm số hữu tỉ
 trong tỉ lệ thức
trong tỉ lệ thức

Dạng 3. Các bài tập ứng dụng
Bài
1. Trong giờ thí nghiệm, bạn Hùng dùng hai quả cân
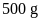 và
và
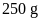 thì đo được trọng lượng tương ứng là
thì đo được trọng lượng tương ứng là
 và
và
 .
.
a)
Tính tỉ số giữa khối lượng của quả cân thứ nhất
và khối lượng quả cân thứ hai; tỉ số giữa trọng
lượng của quả cân thứ nhất và trọng lượng của quả
cân thứ hai.
b) Hai tỉ số trên có lập thành tỉ lệ thức hay không? Bài 2. Người ta pha nhiên liệu cho một loại động cơ bằng cách trộn 5 phần dầu với 8 phần xăng. Hỏi cần bao nhiêu lít xăng để trộn hết 15 lít dầu theo cách pha nhiên liệu như trên?
Bài
3. Tìm độ dài hai cạnh của một hình chữ nhật, biết
tỉ số giữa hai cạnh của nó là
 và chu vi bằng 28 mét.
và chu vi bằng 28 mét.
Bài
4. Tìm diện tích của một hình chữ nhật, biết tỉ số
giữa hai cạnh của nó là
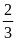 và chu vi bằng 90 mét.
và chu vi bằng 90 mét.
Bài
5. Hải muốn gói bánh chưng, gói xong mỗi bánh nặng
khoảng 0,75kg . Tính sơ mỗi bánh sẽ khoảng
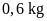 gạo nếp và
gạo nếp và
 đỗ xanh. Chú ý, đây là gạo đã ngâm và đỗ xanh đã
được ngâm và nấu chín. Cứ
đỗ xanh. Chú ý, đây là gạo đã ngâm và đỗ xanh đã
được ngâm và nấu chín. Cứ
 gạo nếp sau khi ngâm nặng khoảng
gạo nếp sau khi ngâm nặng khoảng
 đậu sau khi ngâm và nấu chín cũng được khoảng
đậu sau khi ngâm và nấu chín cũng được khoảng
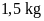 .
Vậy để làm 10 cái bánh chưng cần bao nhiêu gạo, bao
nhiêu đậu?
.
Vậy để làm 10 cái bánh chưng cần bao nhiêu gạo, bao
nhiêu đậu?
Dạng 4. Chứng minh đẳng thức
Bài
1. Cho tỉ lệ thức
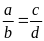 .
Chứng minh rằng ta có tỉ lệ thức:
.
Chứng minh rằng ta có tỉ lệ thức:
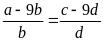
Bài
2. Cho tỉ lệ thức
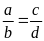 .
Chứng minh rằng ta có tỉ lệ thức:
.
Chứng minh rằng ta có tỉ lệ thức:

Bài
3. Cho tỉ lệ thức
 .
Chứng minh rằng ta có tỉ lệ thức
.
Chứng minh rằng ta có tỉ lệ thức
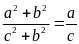
Bài
4. Cho tỉ lệ thức:
 .
Chứng minh đẳng thức sau:
.
Chứng minh đẳng thức sau:

ĐÁP SÔ BÀI TẬP TỤ̉ LUYỆN
Dạng 1. Lập tỉ lệ thức
Bài

a)
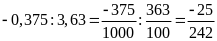
b)
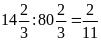
c)
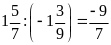
Bài
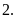
a)

b)
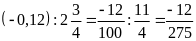
c)
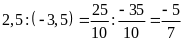
Bài
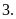
a) Ta có

Hai tỉ số đã cho không bằng nhau nên ta không có tỉ lệ thức từ hai tỉ số đó.
b) Ta có

Hai tỉ số đã cho không bằng nhau nên ta không có tỉ lệ thức từ hai tỉ số đó.
Bài
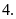
a) Ta có
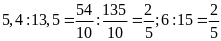
Hai
tỉ số đã cho đều bằng
 .
.
Vậy
ta có tỉ lệ thức
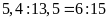 .
.
b) Ta có
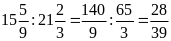 và
và
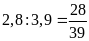
Hai
tỉ số đã cho đều bằng
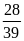 .
.
Vậy
ta có tỉ lệ thức
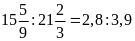 .
.
Bài 5. Lập tất cả các tỉ lệ thức có thể từ các đẳng thức sau -1.6 = 2.(-3)
Ta
có các tỉ lệ thức sau
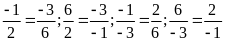
Bài
6. Lập tất cả các tỉ lệ thức có thể từ các đẳng
thức sau
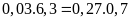
Ta
có các tỉ lệ thức sau

Bài
7. Có thể lập được tỉ lệ thức từ nhóm bốn số
 không? Nếu lập được hãy viết các tỉ lệ thức từ
nhóm bốn số đó.
không? Nếu lập được hãy viết các tỉ lệ thức từ
nhóm bốn số đó.
Ta
có
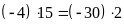 nên lập được tỉ lệ thức từ nhóm bốn số
nên lập được tỉ lệ thức từ nhóm bốn số
 là
là
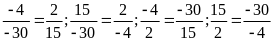
Bài
8. Với năm số
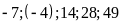 .
Hãy lập các tỉ lệ thức có thể được từ nhóm năm
số đó.
.
Hãy lập các tỉ lệ thức có thể được từ nhóm năm
số đó.
Ta
có
 nên lập được tỉ lệ thức từ nhóm là
nên lập được tỉ lệ thức từ nhóm là

Dạng 2 . Tìm số chưa biết trong tỉ lệ thức
Bài
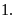
a)
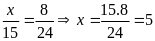
b)
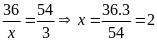
c)
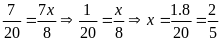
Bài
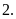
a)

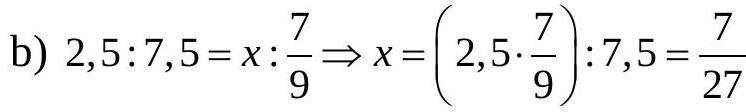
c)

Bài

a)
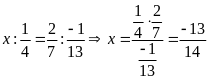
b)
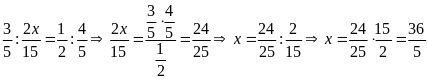
Bài
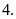
a)
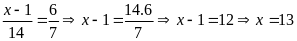
b)

Bài
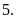

Bài
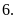
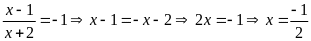
Dạng 3. Các bài tập ứng dụng
Bài
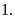
a)
Tỉ số giữa khối lượng của quả cân thứ nhất và
khối lượng quả cân thứ hai là
 .
.
Tỉ
số giữa trọng lượng của quả cân thứ nhất và trọng
lượng quả cân thứ hai là
 .
.
b)
Ta có
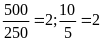 .
Nên hai tỉ số trên lập được thành một tỉ lệ thức
là
.
Nên hai tỉ số trên lập được thành một tỉ lệ thức
là
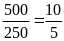 .
.
Bài
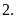
Gọi
x là số lít xăng cần để trộn hết 8 lít dầu theo cách
pha nhiên liệu như trên
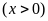 .
.
Theo
bài ta có trộn 5 phần dầu với 8 phần xăng nên
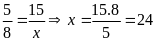 (TMĐK)
(TMĐK)
Vậy số lít xăng cần để trộn là 24 lít.
Bài

Nửa
chu vi của hình chữ nhật là: 28:
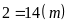
Gọi
độ dài hai cạnh của hình chữ nhật đó là
 (đơn vị: mét; đk:
(đơn vị: mét; đk:
 ) Ta có:
) Ta có:

Vì
tỉ số giữa hai cạnh của nó là
 (2)
(2)
Từ
(1) và (2) ta có:
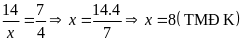

Vậy chiều dài hình chữ nhật là 8 mét, chiều rộng hình chữ nhật là 6 mét.
Bài
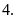
Nửa
chu vi của hình chữ nhật là:
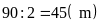
Gọi
chiều dài và chiều rộng của hình chữ nhật đó thứ
tự là
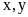 (đơn vị: mét; đk:
(đơn vị: mét; đk:
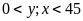 )
)
Ta
có:
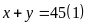
Vì
tỉ số giữa hai cạnh của nó là
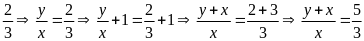 (2)
(2)
Từ
(1) và (2) ta có:
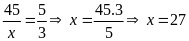 (TMĐK)
(TMĐK)
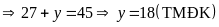
Vậy
diện tích của một hình chữ nhật là
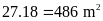 .
.
Bài
10
cái bánh chưng có khối lượng là: 10.0,75=7,5(
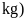
Gọi
khối lượng gạo nếp và đậu xanh sau khi đã ngâm cần
để gói 10 cái bánh chưng theo thứ tự là
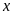 ;
;
 (đơn vị:
(đơn vị:
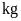 ;
đk:
;
đk:
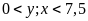 )
)
Ta
có:

Vì
tỉ số giữa khối lượng gạo nếp và đậu xanh của
bánh là
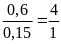
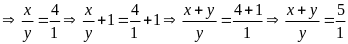 (2)
(2)
Từ
(1) và (2) ta có:

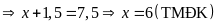
Vì
cứ
 gạo nếp sau khi ngâm nặng khoảng
gạo nếp sau khi ngâm nặng khoảng
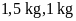 đậu sau khi ngâm và nấu chín cũng được khoảng
đậu sau khi ngâm và nấu chín cũng được khoảng
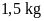 .
Nên khối lượng gạo nếp cần là
.
Nên khối lượng gạo nếp cần là
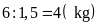 ;
khối lượng đậu xanh cần là
;
khối lượng đậu xanh cần là

Dạng 4. Chứng minh đẳng thức
Bài
1. Cho tỉ lệ thức
 .
Chứng minh rằng ta có tỉ lệ thức:
.
Chứng minh rằng ta có tỉ lệ thức:
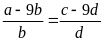 Từ
Từ
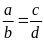 suy ra
suy ra
 .
.
Bài
2. Cho tỉ lệ thức
 .
Chứng minh rằng ta có tỉ lệ thức:
.
Chứng minh rằng ta có tỉ lệ thức:
 Từ
Từ
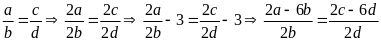 .
.
Bài
3. Cho tỉ lệ thức
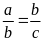 .
Chứng minh rằng ta có tỉ lệ thức
.
Chứng minh rằng ta có tỉ lệ thức
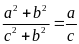
Từ
tỉ lệ thức
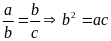 (1)
(1)
Đặt
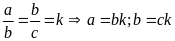 .
Do đó
.
Do đó
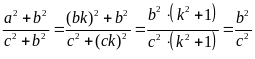 (2)
(2)
Từ
(1) và (2) suy ra
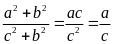 .
Vậy
.
Vậy
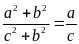
Bài
4. Cho tỉ lệ thức:
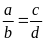 .
Chứng minh đẳng thức sau:
.
Chứng minh đẳng thức sau:

Đặt
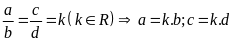
Ta có:
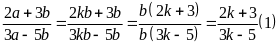
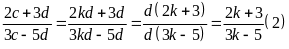
Từ
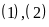 suy ra đpcm
suy ra đpcm
PHIẾU BÀI TẬP
( Nội dung là toàn bộ bài tập đã có trên )
Dạng 1. Lập tỉ lệ thức
Bài
1. Thay các tỉ số sau bằng tỉ số giữa các số
nguyên.
b)

a)

c)
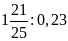
d)
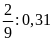
Bài
2. Thay các tỉ số sau bằng tỉ số giữa các số
nguyên.
b)

a)
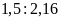
d)
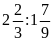
c)

Bài 3. Thay các tỉ số sau bằng tỉ số giữa các số nguyên.
b)
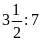
a)
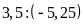
C)
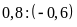
d)
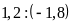
Bài
4. Thay các tỉ số sau bằng tỉ số giữa các số
nguyên.
b)
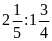
a)
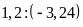
d)
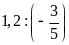
c)

Bài
5 . Thay các tỉ số sau bằng tỉ số giữa các số
nguyên.
b)

a)
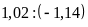
c)

d)

Bài
6 . Từ các tỉ số sau đây có lập được tỉ lệ thức
hay không?
a)
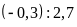 và
và
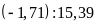
b)
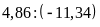 và
và
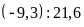
c)
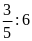 và
và
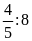
d)
 và
và
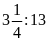
Bài
7. Từ các tỉ số sau đây có lập được tỉ lệ thức
hay không?
a)
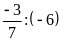 và
và
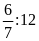
b)
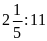 và
và

c)
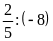 và
và
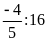
d)
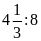 và
và
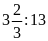
Bài
8. Từ các tỉ số sau đây có lập được tỉ lệ thức
hay không?
a)
 và
và
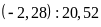
b)
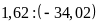 và
và
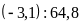
c)
 và
và
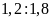
d)
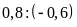 và
và
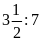
Bài
9. Từ các tỉ số sau đây có lập được tỉ lệ thức
hay không?
a)
 và
và
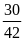
b)
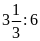 và
và

c)
 và
và

d)
 và
và
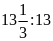
Bài
10. Từ các tỉ số sau đây có lập được tỉ lệ thức
hay không?
a)
 và
và
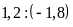
b)
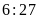 và
và
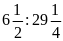
c)
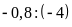 và
và
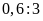
d)
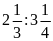 và
và

Bài
11. Lập tất cả các tỉ lệ thức có thể từ các đẳng
thức sau
a)

b)
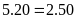
c)
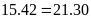
Bài
12. Lập tất cả các tỉ lệ thức có thể từ đẳng
thức sau
a)
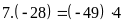
b)

c)

Bài
13. Lập tất cả các tỉ lệ thức có thể từ các đẳng
thức sau
a)
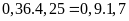
b)

c)

Bài
14. Lập tất cả các tỉ lệ thức có thể từ các đẳng
thức sau
a) 4,4.1,89=9,9.0,84
b)

c)
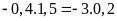
Bài
15. Lập tất cả các tỉ lệ thức có thể từ các đẳng
thức sau
a)
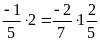
b)

c)

Bài
16. Có thể lập được tỉ lệ thức từ nhóm bốn số
 không? Nếu lập được hãy viết các tỉ lệ thức từ
nhóm bốn số đó.
không? Nếu lập được hãy viết các tỉ lệ thức từ
nhóm bốn số đó.
Bài
17. Có thể lập được tỉ lệ thức từ nhóm bốn số
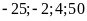 không? Nếu lập được hãy viết các tỉ lệ thức từ
nhóm bốn số đó.
không? Nếu lập được hãy viết các tỉ lệ thức từ
nhóm bốn số đó.
Bài
18. Có thể lập được tỉ lệ thức từ nhóm bốn số
0,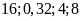 không? Nếu lập được hãy viết các tỉ lệ thức từ
nhóm bốn số đó.
không? Nếu lập được hãy viết các tỉ lệ thức từ
nhóm bốn số đó.
Bài 19. Với năm số 1; 2;6;8;16. Hãy lập các tỉ lệ thức có thể được từ nhóm năm số đó.
Bài
20. Với năm số
 .
Hãy lập các tỉ lệ thức có thể được từ nhóm năm
số đó.
.
Hãy lập các tỉ lệ thức có thể được từ nhóm năm
số đó.
Dạng 2. Tìm số chưa biết của một tỉ lệ thức
Bài
1. Tìm số hữu tỉ
 trong các tỉ lệ thức sau:
trong các tỉ lệ thức sau:
a)

b)

c)

d)
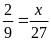 Bài 2. Tìm số hữu tỉ
Bài 2. Tìm số hữu tỉ
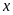 trong các tỉ lệ thức sau:
trong các tỉ lệ thức sau:
a)
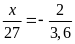
b)
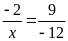
c)

d)
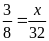
Bài
3. Tìm số hữu tỉ
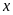 trong các tỉ lệ thức sau:
trong các tỉ lệ thức sau:
b)

a)
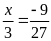
c)
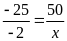
d)
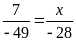
Bài
4. Tìm số hữu tỉ
 trong các tỉ lệ thức sau:
trong các tỉ lệ thức sau:
b)
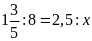
a)

c)
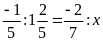
d)
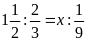
Bài
5. Tìm số hữu tỉ
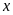 trong các tỉ lệ thức sau:
trong các tỉ lệ thức sau:
b)
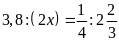
a)

c)
5, 25:
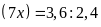
d)

Bài
6. Tìm số hữu tỉ
 trong các tỉ lệ thức sau:
trong các tỉ lệ thức sau:
a)
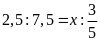
b)

c)
3,5: 2,5

d)
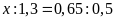
Bài
7. Tìm số hữu tỉ
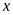 trong các tỉ lệ thức sau:
trong các tỉ lệ thức sau:
b)
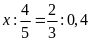
a)

c)

d)
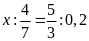
Bài
8. Tìm số hữu tỉ
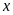 trong các tỉ lệ thức sau:
trong các tỉ lệ thức sau:
a)
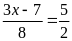
b)

c)
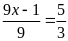
d)

Bài
9. Tìm số hữu tỉ
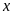 trong các tỉ lệ thức sau:
trong các tỉ lệ thức sau:
a)

b)

c)
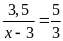
d)
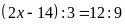
Bài
10. Tìm số hữu tỉ
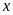 trong các tỉ lệ thức sau:
trong các tỉ lệ thức sau:
a)
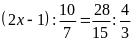
b)

c)

d)
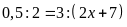
Bài
11. Tìm số hữu tỉ
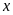 trong các tỉ lệ thức sau:
trong các tỉ lệ thức sau:
a)
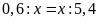
b)

c)
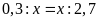
d)
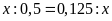
Bài
12. Tìm số hưư tỉ
 trong các tỉ lệ thức sau:
trong các tỉ lệ thức sau:
a)
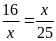
b)

c)

d)
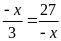
Bài
13. Tìm số hữu tỉ
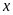 trong các tỉ lệ thức sau:
trong các tỉ lệ thức sau:
a)
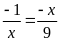
b)
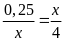
c)
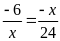
d)

Bài
14. Tìm số hữu tỉ
 trong các tỉ lệ thức sau
trong các tỉ lệ thức sau
b)

a)

d)
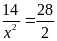
c)
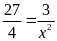
Bài
15. Tìm số hữu tỉ x trong các tỉ lệ thức sau
a)

b)
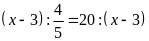
c)
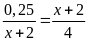
Bài
16. Tìm số hữu tỉ
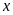 trong các tỉ lệ thức
trong các tỉ lệ thức
a)
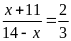
b)
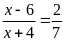
Bài
17. Tìm số hữu tỉ
 trong các tỉ lệ thức
trong các tỉ lệ thức
a)
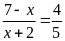
b)
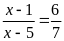
Bài
18. Tìm số hữu tỉ
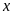 trong tỉ lệ thức
trong tỉ lệ thức
a)
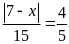
b)
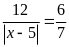
Bài
19. Tìm số hữu tỉ
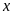 trong các tỉ lệ thức
trong các tỉ lệ thức
a)
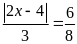
b)

Bài
20. Tìm số hữu tỉ
 trong các tỉ lệ thức
trong các tỉ lệ thức
a)

b)
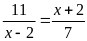
Dạng 3. Các bài tập ứng dụng
Bài
1. Trong giờ thí nghiệm, bạn Hùng dùng hai quả cân
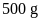 và
và
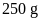 thì đo được trọng lượng tương ứng là
thì đo được trọng lượng tương ứng là
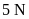 và
và
 .
.
a) Tính tỉ số giữa khối lượng của quả cân thứ nhất và khối lượng quả cân thứ hai; tỉ số giữa trọng lượng của quả cân thứ nhất và trọng lượng của quả cân thứ hai.
b) Hai tỉ số trên có lập thành tỉ lệ thức hay không?
Bài
2. Hai máy tính có kích thước màn hình 20 inch, (inch là gì
một đơn vị đo lường được sử dụng chủ yếu ở
Hoa Kỳ và phổ biến ở các nước Canada, Anh...) tỉ lệ
chuẩn là 1680 x1050
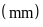 và màn hình 24 inch tỉ lệ chuẩn là 1920 x1200
và màn hình 24 inch tỉ lệ chuẩn là 1920 x1200
 .
.
a) Tính tỉ số giữa chiều rộng và chiều dài của mỗi màn hình.
b) Hai tỉ số giữa chiều rộng và chiều dài của mỗi màn hình trên có lập thành tỉ lệ thức hay không?
Bài
3. Lá quốc kỳ trên cột cờ Lũng Cú là hình chữ nhật
có kích thước là
 ,
lá cờ quốc kỳ lớp
,
lá cờ quốc kỳ lớp
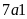 treo tại lớp trong các giờ sinh hoạt là hình chữ nhật
có kích thước là
treo tại lớp trong các giờ sinh hoạt là hình chữ nhật
có kích thước là
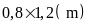 .
.
a) Tính tỉ số giữa chiều rộng và chiều dài của mỗi lá cờ.
b) Hai tỉ số giữa chiều rộng và chiều dài của mỗi lá cờ trên có lập thành tỉ lệ thức hay không?
Bài
4. Theo tiêu chuẩn của Liên đoàn bóng chuyền quốc tế
FIVB sân bóng chuyền là hình chữ nhật có kích thước là
9x18 (m). Lan vẽ mô phỏng mặt sân bóng chuyền là hình
chữ nhật có kích thước là
 .
.
a) Tính tỉ số giữa chiều rộng và chiều dài của sân bóng chuyền.
b) Lan đã vẽ mô phỏng mặt sân đúng tỉ lệ hay chưa?
Bài 5. Lan đọc một cuốn sách trong ba ngày. Ngày thứ nhất Lan đọc 20 trang, ngày thứ hai lan đọc 40 trang, ngày thứ 3 Lan đọc 80 trang.
a) Tính tỉ số giữa trang sách Lan đọc được trong ngày thứ nhất và thứ hai.
b) Tính tỉ số giữa trang sách Lan đọc được trong ngày thứ hai và thứ ba.
c) Hai tỉ số trên có lập thành tỉ lệ thức hay không?
Bài
6. Tỉ số của hai số là
 .
Biết số lớn là 135 . Tìm số bé?
.
Biết số lớn là 135 . Tìm số bé?
Bài
7. Tỉ số của hai số là
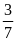 .
Biết số bé là 12 . Tìm số lớn?
.
Biết số bé là 12 . Tìm số lớn?
Bài 8. Người ta làm mứt dâu bằng cách trộn 6 phần dâu với 4 phần đường. Hỏi cần bao nhiêu kg đường để trộn hết 45 kg dâu theo cách pha nhiên trộn như trên?
Bài 9. Người ta pha nhiên liệu cho một loại động cơ bằng cách trộn 2 phần dầu với 7 phần xăng. Hỏi cần bao nhiêu lít xăng để trộn hết 8 lít dầu theo cách pha nhiên liệu như trên?
Bài
10. Lá quốc kỳ Việt Nam là hình chữ nhật có tỉ lệ
kích thước rộng và dài là
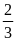 .
Nam làm lá cờ quốc kỳ bằng giấy đảm bảo đúng tỉ
lệ quy định để tham gia cổ vũ đá bóng Sea Games có
chiều dài là
.
Nam làm lá cờ quốc kỳ bằng giấy đảm bảo đúng tỉ
lệ quy định để tham gia cổ vũ đá bóng Sea Games có
chiều dài là
 .
Tính chiều rộng của lá cờ Nam làm
.
Tính chiều rộng của lá cờ Nam làm
Bài 11. Tỉ lệ nấu bánh chưng ngon nhất là 4 gạo:1 đậu xanh, vậy gói bánh chưng ngon với tỉ lệ như trên thì 10kg gạo cần bao nhiêu đậu xanh.
Bài
12. Tính độ dài hai cạnh của hình chữ nhật, biết tỉ
số giữa các cạnh là 0,6 và chu vi bằng
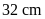
Bài
13. Tính độ dài 2 cạnh của một vườn hoa hình chữ
nhật, biết tỉ số giữa chiều rộng và chiều dài là
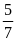 và chu vi bằng
và chu vi bằng
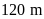
Bài
14. Thông thường, một thùng sơn có thể tích
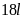 và theo quy định của nhà sản xuất tất cả các loại
sơn đều pha theo tỉ lệ nhỏ hơn hoặc bằng
và theo quy định của nhà sản xuất tất cả các loại
sơn đều pha theo tỉ lệ nhỏ hơn hoặc bằng
 .
Như vậy, nếu một thùng sơn
.
Như vậy, nếu một thùng sơn
 sẽ pha cùng với
sẽ pha cùng với
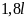 nước sạch thì để có
nước sạch thì để có
 sơn nước thì cần bao nhiêu thùng sơn và bao nhiêu lít
nước sạch?
sơn nước thì cần bao nhiêu thùng sơn và bao nhiêu lít
nước sạch?
Bài
15. An cần lăn sơn phòng, diện tích phòng 1 là
 ,
ở phòng 2 là
,
ở phòng 2 là
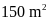 .
Cả hai phòng An lăn hết
.
Cả hai phòng An lăn hết
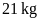 sơn. Tính số lượng sơn cần dùng cho mỗi phòng ?
sơn. Tính số lượng sơn cần dùng cho mỗi phòng ?
Bài
16. Hai lớp
 và
và
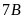 đi lao động trồng cây. Biết rằng tỉ số giữa số cây
trồng được của lớp
đi lao động trồng cây. Biết rằng tỉ số giữa số cây
trồng được của lớp
 và
và
 là
là
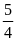 và lớp
và lớp
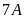 trồng nhiều hơn lớp
trồng nhiều hơn lớp
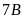 là 20 cây. Tính số cây mỗi lớp đã trồng.
là 20 cây. Tính số cây mỗi lớp đã trồng.
Bài
17. Hai lớp
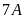 và
và
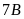 đi lao động trồng cây. Biết rằng tỉ số giữa số cây
trồng được của lớp
đi lao động trồng cây. Biết rằng tỉ số giữa số cây
trồng được của lớp
 và
và
 là
là
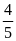 và lớp
và lớp
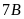 trồng nhiều hơn lớp
trồng nhiều hơn lớp
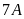 là 20 cây. Tính số cây mỗi lớp đã trồng.
là 20 cây. Tính số cây mỗi lớp đã trồng.
Bài
18. Biết rằng 17 lít dầu hỏa nặng
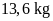 .
Hỏi
.
Hỏi
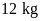 dầu hỏa thì có chứa hết được vào chiếc can 16 lít
hay không?
dầu hỏa thì có chứa hết được vào chiếc can 16 lít
hay không?
Bài
19. Tỉ số của hai số là
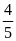 ,
nếu thêm 2 đơn vị vào số thứ nhất thì tỉ số của
chúng sẽ bằng
,
nếu thêm 2 đơn vị vào số thứ nhất thì tỉ số của
chúng sẽ bằng
 .
Tìm hai số đó.
.
Tìm hai số đó.
Bài
20. Tìm hai phân số tối giản biết tổng của chúng là
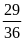 ,
các tử theo thứ tự tỉ lệ với 7 và 5 ; các mẫu theo
thứ tự tỉ lệ với 3 và 2 .
,
các tử theo thứ tự tỉ lệ với 7 và 5 ; các mẫu theo
thứ tự tỉ lệ với 3 và 2 .
Dạng 4. Chứng minh đẳng thức
Bài
1. Cho tỉ lệ thức
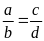 .
Chứng minh rằng ta có tỉ lệ thức:
.
Chứng minh rằng ta có tỉ lệ thức:
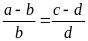
Bài
2. Cho tỉ lệ thức
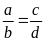 .
Chứng minh rằng ta có tỉ lệ thức:
.
Chứng minh rằng ta có tỉ lệ thức:
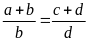
Bài
3. Cho tỉ lệ thức
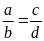 .
Chứng minh rằng ta có tỉ lệ thức:
.
Chứng minh rằng ta có tỉ lệ thức:
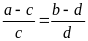
Bài
4. Cho tỉ lệ thức
 .
Chứng minh rằng ta có tỉ lệ thức:
.
Chứng minh rằng ta có tỉ lệ thức:
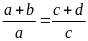
Bài
5. Cho tỉ lệ thức
 .
Chứng minh rằng ta có tỉ lệ thức:
.
Chứng minh rằng ta có tỉ lệ thức:
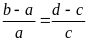
Bài
6. Cho tỉ lệ thức
 .
Chứng minh rằng ta có tỉ lệ thức:
.
Chứng minh rằng ta có tỉ lệ thức:
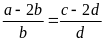
Bài
7. Cho tỉ lệ thức
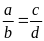 .
Chứng minh rằng ta có tỉ lệ thức:
.
Chứng minh rằng ta có tỉ lệ thức:

Bài
8. Cho tỉ lệ thức
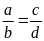 .
Chứng minh rằng ta có tỉ lệ thức:
.
Chứng minh rằng ta có tỉ lệ thức:
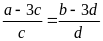
Bài
9. Cho tỉ lệ thức
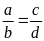 .
Chứng minh rằng ta có tỉ lệ thức:
.
Chứng minh rằng ta có tỉ lệ thức:

Bài
10. Cho tỉ lệ thức
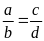 .
Chứng minh rằng ta có tỉ lệ thức:
.
Chứng minh rằng ta có tỉ lệ thức:

Bài
11. Chứng tỏ rằng: Nếu
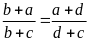 (trong đó
(trong đó
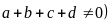 thì
thì

Bài
12. Chứng tỏ rằng: Nếu
 (trong đó
(trong đó
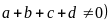 thì
thì

Bài
13. Cho tỉ lệ thức
 .
Chứng minh tỉ lệ thức
.
Chứng minh tỉ lệ thức
 thiết các tỉ lệ thức đều có nghĩa).
thiết các tỉ lệ thức đều có nghĩa).
Bài
14. Cho tỉ lệ thức
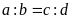 .
Chứng minh tỉ lệ thức
.
Chứng minh tỉ lệ thức
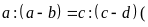 Giả thiết các tỉ lệ thức đều có nghĩa).
Giả thiết các tỉ lệ thức đều có nghĩa).
Bài
15. Cho tỉ lệ thức
 .
Chứng minh rằng ta có tỉ lệ thức
.
Chứng minh rằng ta có tỉ lệ thức
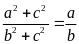
Bài
16. Cho tỉ lệ thức
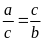 .
Chứng minh rằng ta có tỉ lệ thức
.
Chứng minh rằng ta có tỉ lệ thức

Bài
17. Cho tỉ lệ thức
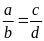 .
Chứng minh rằng ta có tỉ lệ thức
.
Chứng minh rằng ta có tỉ lệ thức
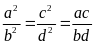
Bài
18. Cho tỉ lệ thức
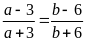 .
Chứng minh
.
Chứng minh

Bài
19. Cho tỉ lệ thức:
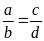 .
Chứng minh đẳng thức sau:
.
Chứng minh đẳng thức sau:

Bài
20. Chứng minh rằng nếu
 thì
thì
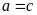 hoặc
hoặc
 .
.
Phần III. BÀI TẬP TƯƠNG TỤ' TỤ' GIẢI
Dạng 1. Lập tỉ lệ thức
Bài
1. Thay các tỉ số sau bằng tỉ số giữa các số
nguyên.
a)

b)
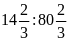
c)
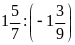
Bài
2. Thay các tỉ số sau bằng tỉ số giữa các số
nguyên.
a)
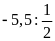
b)
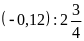
c)
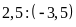
Bài
3. Từ các tỉ số sau đây có lập được tỉ lệ thức
hay không?
a)
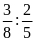
và

b)
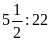 và
và
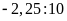
Bài
4. Từ các tỉ số sau đây có lập được tỉ lệ thức
hay không?
a)
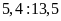 và
và

b)
 và
và
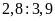
Bài
5. Lập tất cả các tỉ lệ thức có thể từ các đẳng
thức sau

Bài 6. Lập tất cả các tỉ lệ thức có thể từ các đẳng thức sau 0,03.6,3=0, 27.0,7
Bài
7. Có thể lập được tỉ lệ thức từ nhóm bốn số
 không? Nếu lập được hãy viết các tỉ lệ thức từ
nhóm bốn số đó.
không? Nếu lập được hãy viết các tỉ lệ thức từ
nhóm bốn số đó.
Bài
8. Với năm số
 .
Hãy lập các tỉ lệ thức có thể được từ nhóm năm
số đó.
.
Hãy lập các tỉ lệ thức có thể được từ nhóm năm
số đó.
Dạng 2. Tìm số chưa biết trong tỉ lệ thức
Bài
1 . Tìm số hữu tỉ
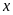 trong các tỉ lệ thức sau:
trong các tỉ lệ thức sau:
a)
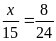
b)
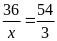
c)
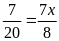
Bài
2. Tìm số hữu tỉ
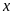 trong các tỉ lệ thức sau:
trong các tỉ lệ thức sau:
a)
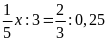
b)
2,5:7,5

c)
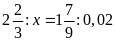
Bài
3. Tìm số hữu tỉ
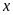 trong các tỉ lệ thức sau:
trong các tỉ lệ thức sau:
a)
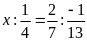
b)

Bài
4. Tìm số hữu tỉ
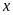 trong các tỉ lệ thức sau:
trong các tỉ lệ thức sau:
a)
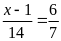
b)

Bài
5. Tìm số hữu tỉ
 trong tỉ lệ thức
trong tỉ lệ thức
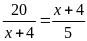
Bài
6. Tìm số hữu tỉ
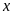 trong tỉ lệ thức
trong tỉ lệ thức
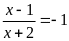
Dạng
 Các
Các
bài
tập
ứng
Bài
1. Trong giờ thí nghiệm, bạn Hùng dùng hai quả cân
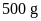 và
và
 thì đo được trọng lượng tương ứng là
thì đo được trọng lượng tương ứng là
 và
và
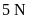 .
.
a)
Tính tỉ số giữa khối lượng của quả cân thứ nhất
và khối lượng quả cân thứ hai; tỉ số giữa trọng
lượng của quả cân thứ nhất và trọng lượng của quả
cân thứ hai.
b) Hai tỉ số trên có lập thành tỉ lệ thức hay không?
Bài 2. Người ta pha nhiên liệu cho một loại động cơ bằng cách trộn 5 phần dầu với 8 phần xăng. Hỏi cần bao nhiêu lít xăng để trộn hết 15 lít dầu theo cách pha nhiên liệu như trên?
Bài
3. Tìm độ dài hai cạnh của một hình chữ nhật, biết
tỉ số giữa hai cạnh của nó là
 và chu vi bằng 28 mét.
và chu vi bằng 28 mét.
Bài
4. Tìm diện tích của một hình chữ nhật, biết tỉ số
giữa hai cạnh của nó là
 và chu vi bằng 90 mét.
và chu vi bằng 90 mét.
Bài
5. Hải muốn gói bánh chưng, gói xong mỗi bánh nặng
khoảng 0,75kg . Tính sơ mỗi bánh sẽ khoảng
 gạo nếp và
gạo nếp và
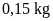 đỗ xanh. Chú ý, đây là gạo đã ngâm và đỗ xanh đã
được ngâm và nấu chín. Cứ
đỗ xanh. Chú ý, đây là gạo đã ngâm và đỗ xanh đã
được ngâm và nấu chín. Cứ
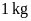 gạo nếp sau khi ngâm nặng khoảng
gạo nếp sau khi ngâm nặng khoảng
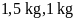 đậu sau khi ngâm và nấu chín cũng được khoảng
đậu sau khi ngâm và nấu chín cũng được khoảng
 .
Vậy để làm 10 cái bánh chưng cần bao nhiêu gạo, bao
nhiêu đậu?
.
Vậy để làm 10 cái bánh chưng cần bao nhiêu gạo, bao
nhiêu đậu?
Dạng 4. Chứng minh đẳng thức
Bài
1. Cho tỉ lệ thức
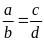 .
Chứng minh rằng ta có tỉ lệ thức:
.
Chứng minh rằng ta có tỉ lệ thức:
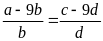
Bài
2. Cho tỉ lệ thức
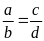 .
Chứng minh rằng ta có tỉ lệ thức:
.
Chứng minh rằng ta có tỉ lệ thức:
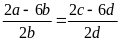
Bài
3. Cho tỉ lệ thức
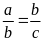 .
Chứng minh rằng ta có tỉ lệ thức
.
Chứng minh rằng ta có tỉ lệ thức
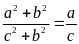
Bài
4. Cho tỉ lệ thức:
 .
Chứng minh đẳng thức sau:
.
Chứng minh đẳng thức sau:
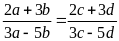
Ngoài Chuyên Đề Tỉ Lệ Thức Lớp 7 Môn Toán Có Lời Giải Chi Tiết thì các tài liệu học tập trong chương trình 7 sẽ được cập nhật liên tục và nhanh nhất có thể sau khi kỳ thi diễn ra trên Danh mục Tài Liệu Học Tập nhằm giúp các bạn đọc thuận tiện trong việc nghiên cứu tài liệu. Quý thày cô và các bạn đọc có thể chia sẻ thêm những tài liệu học tập hữu ích đến địa chỉ email của chúng tôi, nhằm xây dựng nên kho đề thi phong phú, đa dạng cho các em học sinh tham khảo và rèn luyện.
Xem thêm







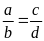 thì
thì
 .
.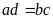 và
và
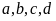 đều khác 0 thì ta có các tỉ lệ thức
đều khác 0 thì ta có các tỉ lệ thức