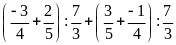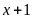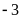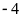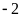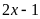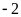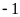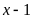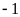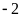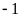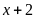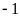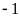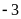Chuyên Đề Nhân Chia Số Hữu Tỉ Toán 7 Có Lời Giải Chi Tiết
Có thể bạn quan tâm
Chuyên Đề Nhân Chia Số Hữu Tỉ Toán 7 Có Lời Giải Chi Tiết là tài liệu học tập được Trang Tài Liệu biên soạn và sưu tầm từ những nguồn dữ liệu mới nhất hiện nay. Tài liệu này sẽ giúp các em luyện tập, củng cố kiến thức từ đó nâng cao điểm số cho môn học. Ngoài ra, cũng giúp các thầy cô giáo có nguồn tài nguyên phong phú để giảng dạy.
Chuyên Đề Nhân Chia Số Hữu Tỉ là một phần quan trọng trong chương trình học toán lớp 7. Nó giúp chúng ta hiểu rõ về cách nhân và chia các số hữu tỉ, từ đó áp dụng vào việc giải quyết các bài toán thực tế và phát triển khả năng tư duy logic và suy luận.
Dưới đây là bản đọc trực tuyến giúp thầy cô và các em học sinh có thể nghiên cứu Online hoặc bạn có thể tải miễn phí với phiên bản word để dễ dàng in ấn cũng như học tập Offline.
CHƯƠNG 1: SỐ HỮU TỈ
I. LÍ THUYẾT TRỌNG TÂM
1. Nhân, chia hai số hữu tỉ
a) Ta có thể nhân, chia hai số hữu tỉ bằng cách viết chúng dưới dạng phân số rồi áp dụng quy tắc nhân, chia phân số.
Với
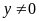 ,
ta có:
,
ta có:

b) Phép nhân số hữu tỉ cũng có các tính chất như phép nhân phân số: giao hoán, kết hợp, nhân với 1 và tính chất phân phối của phép nhân đối với phép cộng.
Với
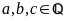 ,
ta có:
,
ta có:
+
Tính chất giao hoán:
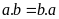
+
Tính chất kết hợp:
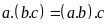
+
Tính chất nhân với 1:
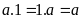
+
Tính chất phân phối:

*) Chú ý: Nếu hai số hữu tỉ đều được cho dưới dạng số thập phân thì ta có thể áp dụng quy tắc nhân và chia đối với số thập phân.
c) Mọi số hữu tỉ khác 0 đều có một số nghịch đảo
Với
 .
Số nghịch đảo của a
là
.
Số nghịch đảo của a
là
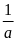 .
.
Ví
dụ: Nghịch
đảo của
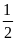 là
là
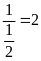
d)
Tỉ số: Thương
của phép chia x
cho y
(với
 )
gọi là tỉ số của hai số x
và y,
kí hiệu là
)
gọi là tỉ số của hai số x
và y,
kí hiệu là
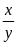 hoặc
hoặc
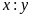 .
.
Ví
dụ:
Nghịch đảo
của
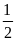 là
là
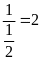
II. CÁC DẠNG BÀI TẬP
Dạng 1: Nhân, chia hai số hữu tỉ
*) Phương pháp giải: Để nhân, chia hai số hữu tỉ ta thực hiện các bước sau:
Bước 1. Viết hai số hữu tỉ dưới dạng phân số.
Bước 2. Áp dụng quy tắc nhân, chia phân số.
Bước 3. Rút gọn kết quả (nếu có thể).
Bài 1:
Tính:
a)
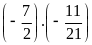 b)
b)

c)
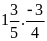 d)
d)
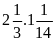
Lời giải
a)
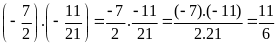
b)

c)
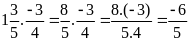
d)
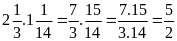
Bài 2:
Tính:
a)
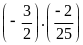 b)
b)
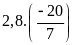
c)
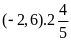 d)
d)
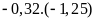
Lời giải
a)
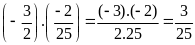
b)

c)

d)
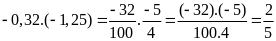
Bài 3:
Tính:
a)
 b)
b)
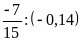
c)
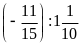 d)
d)
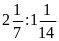
Lời giải
a)
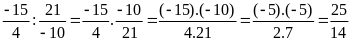
b)
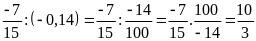
c)
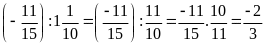
d)

Bài 4:
Tính:
a)
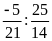 b)
b)
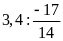
c)
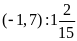 d)
d)
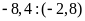
Lời giải
a)
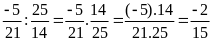
b)
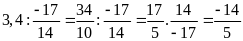
c)

d)

Bài 5:
Tính:
a)
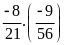 b)
b)
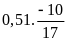
c)
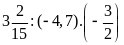 d)
d)

Lời giải
a)
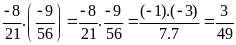
b)

c)

d)
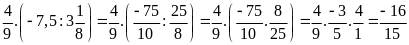
Bài 6:
Tính
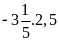
Lời giải
Ta
có:

Bài 7:
Thực hiện phép tính:
a)
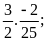 b)
b)

c)
 d)
d)
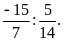
Lời giải
a)

b)
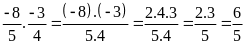
c)
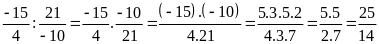
d)
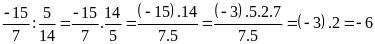
Bài 8:
Thực hiện phép tính:
a)
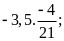 b)
b)
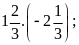
c)
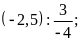 d)
d)
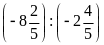
Lời giải
a)
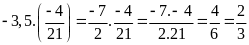
b)
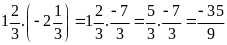
c)
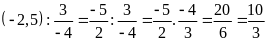
d)
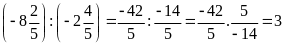
Bài 9:
Giá trị
của
 bằng:
bằng:
A)
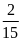 B)
B)

C)
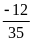 D)
D)
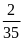
Lời giải
Chọn A.
Ta có:
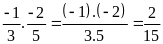 .
.
Bài 10:
Giá trị
của
 bằng:
bằng:
A)
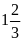 B)
B)
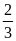
C)
 D)
D)

Lời giải
Chọn B.
Ta có:
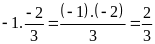 .
.
Bài 11:
Giá trị
của
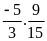 bằng:
bằng:
A.
 B.
B.
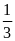
C. 3. D. 1.
Lời giải
Chọn A.
Ta có:
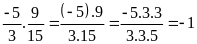 .
.
Bài 12:
Giá trị
của
 bằng:
bằng:
A.
1. B.

C.
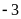 D.
D.
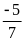
Lời giải
Chọn D.
Ta có:
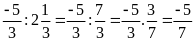
Bài 13:
Tính:
A.
 B.
B.

C.
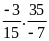 D.
D.
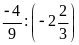
Lời giải

Dạng 2: Tính giá trị biểu thức
*) Phương pháp giải:
+ Để tính giá trị biểu thức, ta căn cứ vào thứ tự thực hiện phép tính: trong ngoặc trước, ngoài ngoặc sau; nhân chia trước, cộng trừ sau.
+ Ngoài ra ta có thể sử dụng các quy tắc phép tính cộng, trừ, nhân, chia số hữu tỉ kết hợp các tính chất của các phép tính cộng và nhân để tính hợp lí (nếu có thể).
+ Chú ý dấu của kết quả và rút gọn.
Ví
dụ: Tính

Lời giải
Ta
có:
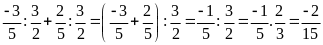
Bài 1:
Tính giá trị các biểu thức sau:
a)
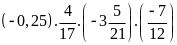 b)
b)
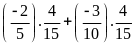
c)
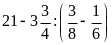 d)
d)
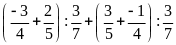
Lời giải
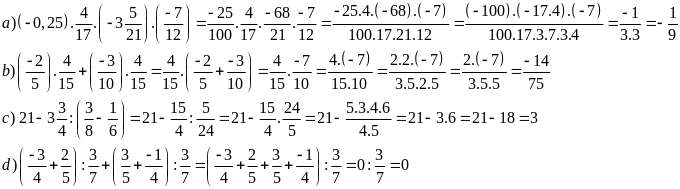
Bài 2:
Tính giá trị các biểu thức sau:
a)
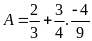 b)
b)

c)
 d)
d)

Lời giải
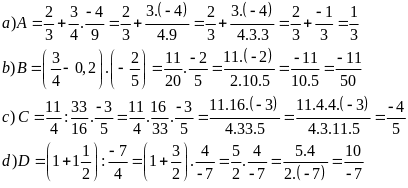
Bài 3:
Thực hiện phép tính (hợp lí nếu có thể):
a)
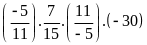 b)
b)
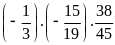
c)
 d)
d)
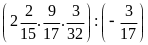
Lời giải
a)

b)

c)
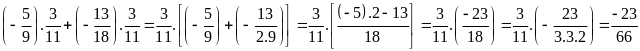
d)

Bài 4:
Giá trị
của
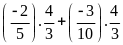 bằng:
bằng:
A.
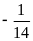 B.
B.
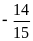
C.
 D.
D.
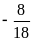
Lời giải
Chọn B.

Bài 5:
Giá trị
của
 bằng
bằng
A.
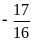 B.
B.
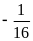
C.
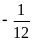 D.
D.

Lời giải
Chọn A.
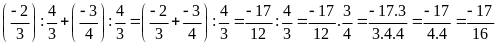
Bài 6:
Tính
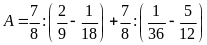 .
.
Lời giải
Ta
có

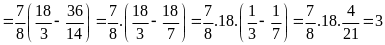
Vậy

Bài 7:
Tính
nhanh

Lời giải
Ta
có:
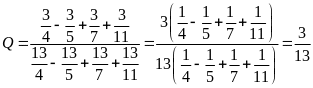
Vậy

Bài 8:
Tính hợp lí (nếu có thể)
a)
 b)
b)
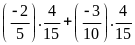
c)
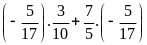 d)
d)
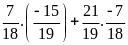
Lời giải
a)
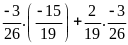

b)

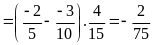
c)
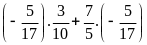
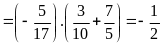
d)
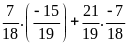

Bài 9:
Tính hợp lí (nếu có thể)
a)
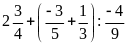 b)
b)
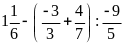
c)
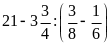 d)
d)
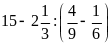
Lời giải
a)
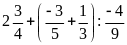

b)
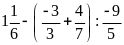
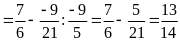
c)
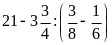
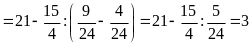
d)

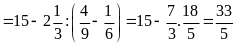
Bài 10:
Tính hợp lí (nếu có thể)
a)
 b)
b)
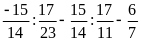
c)
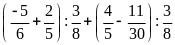 d)
d)

Lời giải
a)


b)
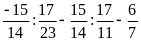

c)


Bài 11:
Tính hợp lí (nếu có thể)
a)
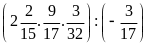 b)
b)
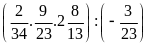
c)
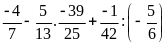 d)
d)
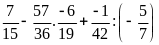
Lời giải
a)

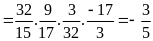
b)
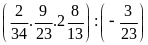

c)
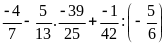
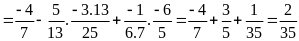
d)
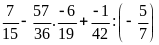

Bài 12:
Tính hợp lí (nếu có thể)
a)
 b)
b)
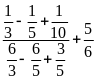
c)
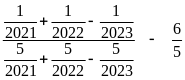 d)
d)

Lời giải
a)
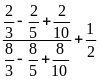
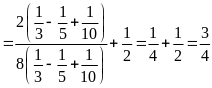
b)
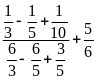

c)
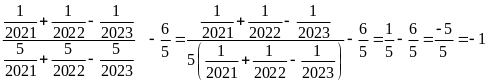
d)
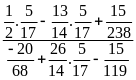
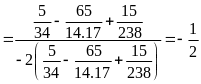
Bài 13:
Tính hợp lí (nếu có thể)
a)
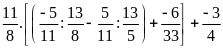 b)
b)
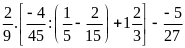
c)
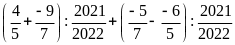 d)
d)
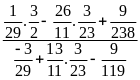
Lời giải
a)
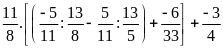
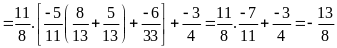
b)
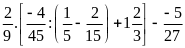

c)
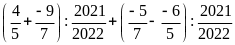
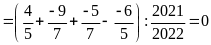
d)
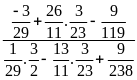
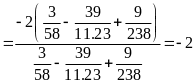
Bài 14:
Tính:
a)
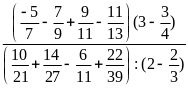
b)
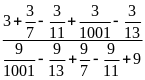
Lời giải
a)
Ta có :
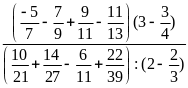 =
=
b)
Ta có :
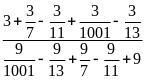 =
=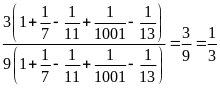
Bài 15:
Tính

Lời giải
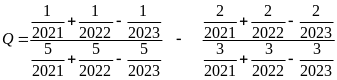
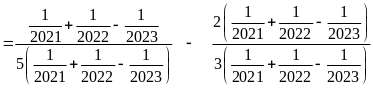

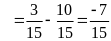
Bài 16:
Tính

Lời giải
Ta
có :
 và
và
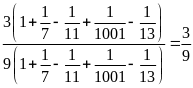
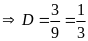
Bài 17:
Tính

Lời giải

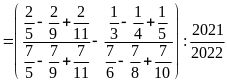
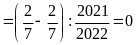
Bài 18:
Tính
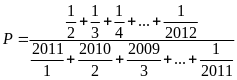
Lời giải

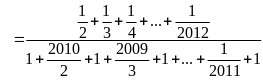
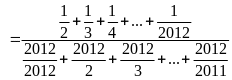
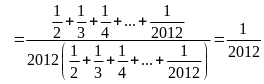
Bài 19:
Tính
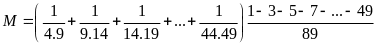
Lời giải
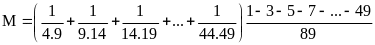
=

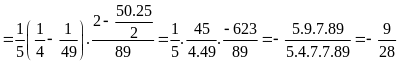
Bài 20:
Tính
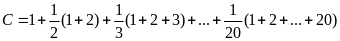
Lời giải

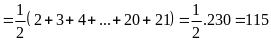
Bài 21:
Tính
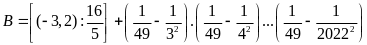
Lời giải
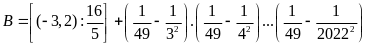

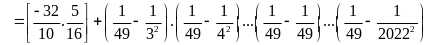
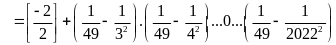
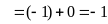
BÀI TẬP TỰ LUYỆN
Bài 1:
Tính:
a)
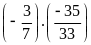 b)
b)

c)
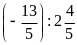 d)
d)
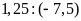
Lời giải
a)
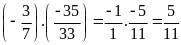
b)
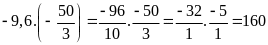
c)
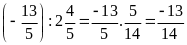
d)
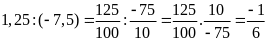
Bài 2:
Tính:
a)
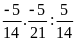 b)
b)
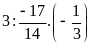
c)
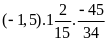 d)
d)
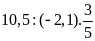
Lời giải
a)
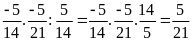
b)
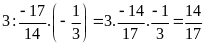
c)
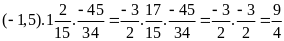
d)
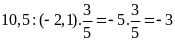
Bài 3:
Tính:
a)
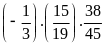 b)
b)
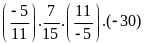
c)
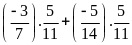 d)
d)
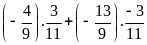
Lời giải
a)
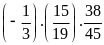
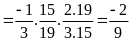
b)
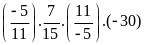
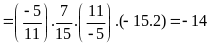
c)

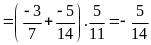
d)
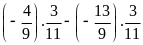
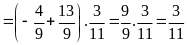
Bài 4:
Tính hợp lí (nếu có thể)
a)
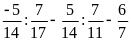 b)
b)
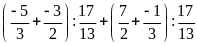
c)
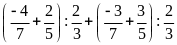 d)
d)
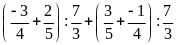
Lời giải
a)
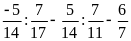
b)
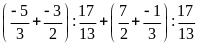

c)
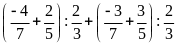
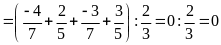
d)

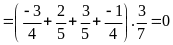
Bài 5:
Tính hợp lí (nếu có thể)
a)
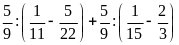 b)
b)
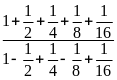
c)
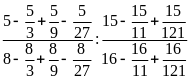
Lời giải
a)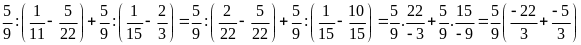
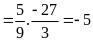
b)
 =
=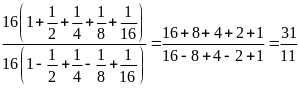
c)
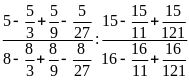 =
=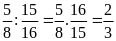
Bài 6:
Tính
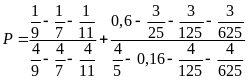
Lời giải
Ta
có:
 =
=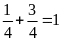
Bài 7:
Tính
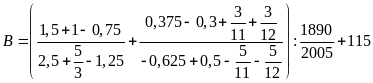
Lời giải
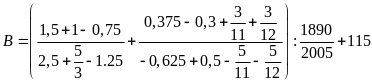
=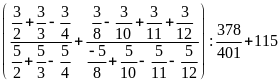 =
=
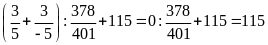
Bài 8:
Tính
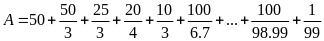
Lời giải
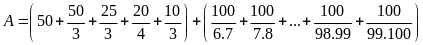
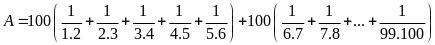
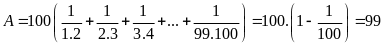
Dạng 3: Viết một số hữu tỉ dưới dạng tích hoặc thương của hai số hữu tỉ
*) Phương pháp giải
Để viết một số hữu tỉ dưới dạng tích hoặc thương của hai số hữu tỉ ta thực hiện các bước sau:
Bước 1. Viết số hữu tỉ dưới dạng phân số.
Bước 2. Viết tử và mẫu của phân số dưới dạng tích của hai số nguyên.
Bước 3. “Tách” ra hai phân số có tử và mẫu là các số nguyên thỏa mãn yêu cầu đề bài.
Bước 4. Lập tích hoặc thương của các phân số đó.
Ví
dụ: Viết
số hữu tỉ
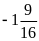 dưới dạng tích của hai số hữu tỉ có một thừa số
là
dưới dạng tích của hai số hữu tỉ có một thừa số
là
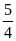 .
.
Hướng dẫn giải
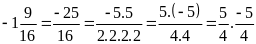
Bài 1:
Viết
số hữu tỉ
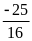 dưới các dạng sau:
dưới các dạng sau:
a) Tích
của hai số hữu tỉ có một thừa số là

b)
Thương của hai số hữu tỉ, trong đó số bị chia là
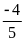
Lời giải
a)
Ta có
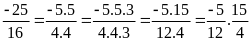
b)
Ta có:
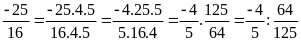
Bài 2:
Viết
số hữu tỉ
 dưới các dạng sau:
dưới các dạng sau:
a) Tích
của hai số hữu tỉ có một thừa số là
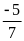
b)
Thương của hai số hữu tỉ, trong đó số bị chia là
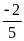
Lời giải
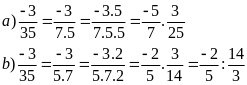
Bài 3:
Viết
số hữu tỉ
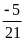 dưới dạng sau
dưới dạng sau
a) Tích của hai số hữu tỉ;
b) Thương của hai số hữu tỉ;
c) Tích
của hai số hữu tỉ trong đó có một số bằng
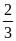 ;
;
d)
Thương của hai số hữu tỉ trong đó số bị chia bằng
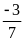 .
.
Lời giải
a) Tích của hai số hữu
tỉ:
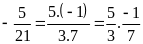
b) Thương của hai số hữu
tỉ:

c) Tích của hai số hữu
tỉ trong đó có một số bằng
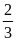 :
:
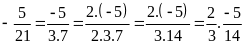
d) Thương của hai số hữu tỉ trong đó số bị chia bằng
 :
:
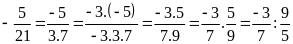
Dạng 4: Tìm số hữu tỉ x thỏa mãn điều kiện cho trước
*) Phương pháp giải
Với bài toán tìm x, ta thường làm như sau:
Bước 1. Ta xác định vai trò và tính chất của x trong đẳng thức hoặc điều kiện ở đề bài.
Bước 2. Sử dụng các quy tắc và tính chất đã biết về phép tính số hữu tỉ để tìm x.
Chú ý: Ta thường sử dụng quy tắc và tính chất sau để biến đổi tìm x.
Quy tắc “chuyển vế” biến đổi số hạng tự do sang một vế, số hạng chứa x sang một vế khác.
Sử dụng các tính chất các phép tính nhân, chia các số hữu tỉ.
Sử dụng tính chất tích hai số bằng 0 thì một trong hai số đó bằng 0.
*)
Cách làm rút gọn: Thực
hiện phá ngoặc theo thứ tự thực hiện phép tính để
đưa đẳng thức về các dạng: 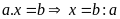


Chú
ý: Nếu
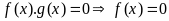 hoặc
hoặc
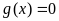
Ví
dụ. Tìm x
biết:
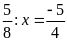
Hướng dẫn giải
Bước 1. x đóng vai trò là số chia.
Bước
2.
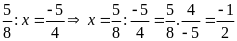 .
.
Vậy
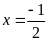
Bài 1:
Tìm x biết:
a)
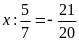 b)
b)
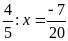
c)
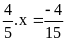 d)
d)
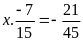
Lời giải
a)

b)
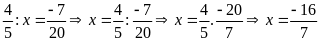
c)

d)

Bài 2:
Tìm x biết:
a)
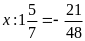 b)
b)
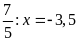
c)
 d)
d)

Lời giải
a)

b)
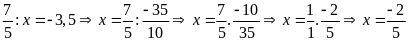
c)
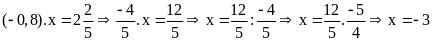
d)
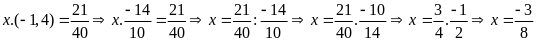
Bài 3:
Tìm x biết:
a)
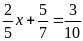 b)
b)
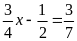
c)
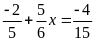 d)
d)
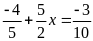
Lời giải
a)
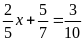
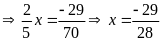
b)

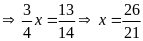
c)

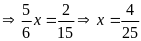
d)
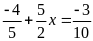
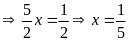
Bài 4:
Tìm x biết:
a)
 b)
b)
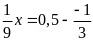
c)
 d)
d)
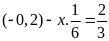
Lời giải
a)
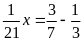
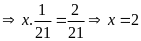
b)


c)
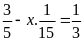
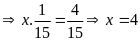
d)

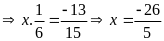
Bài 5:
Tìm x biết:
a)
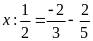 b)
b)
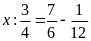
c)
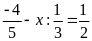 d)
d)

Lời giải
a)
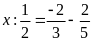
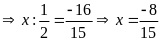
b)


c)
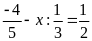
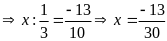
d)
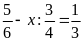
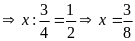
Bài 6:
Tìm x biết:
a)
 b)
b)
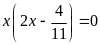
c)
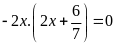 d)
d)

Lời giải
a)
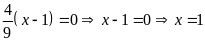
b)
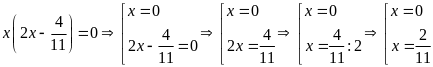
c)
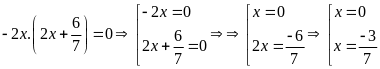
d)
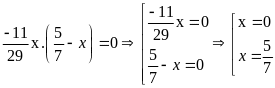
Bài 7:
Tìm x biết:
a)
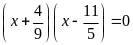 b)
b)
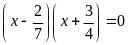
c)
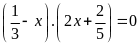 d)
d)

Lời giải
a)


b)
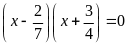
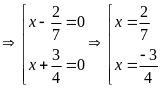
c)
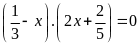

d)
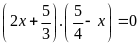

Bài 8:
Tìm x biết:
a)
 b)
b)
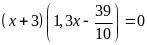
c)
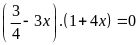 d)
d)

Lời giải
a)
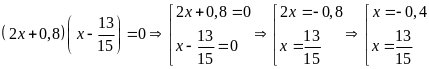
b)
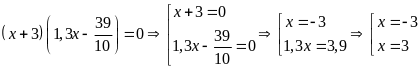
c)
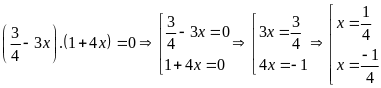
d)

Bài 9:
Tìm x biết:
a)
 b)
b)
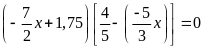
c)
 d)
d)
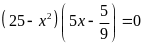
Lời giải
a)
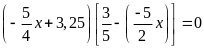
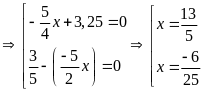
b)
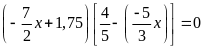
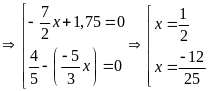
c)

d)
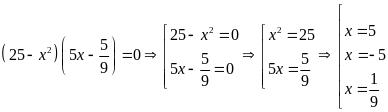
Bài 10:
Tìm x biết:
a)
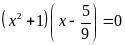 b)
b)

c)
 d)
d)
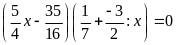
Lời giải
a)
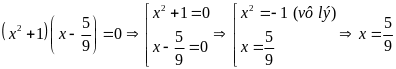
b)

c)
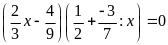
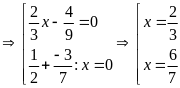
d)
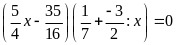
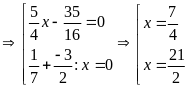
Bài 11:
Tìm x biết:
a)
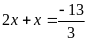 b)
b)
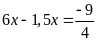
c)
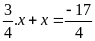 d)
d)
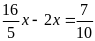
Lời giải
a)

b)
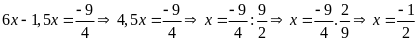
c)

d)
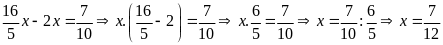
Bài 12:
Tìm x biết:
a)
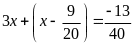 b)
b)

c)
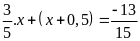 d)
d)

Lời giải
a)
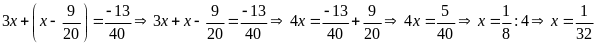
b)
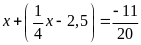
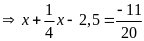
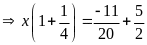
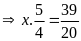
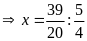
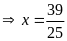

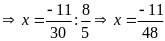
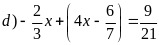

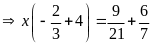
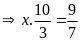
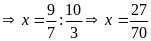
Bài 13:
Tìm x biết:
a)
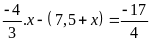 b)
b)

c)
 d)
d)
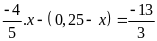
Lời giải
a)
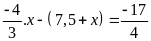
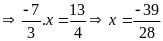
b)

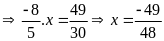
c)
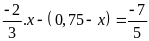
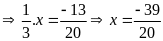
d)
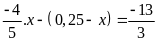
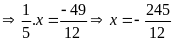
Bài 14:
Tìm x biết:
a)
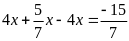 b)
b)

c)
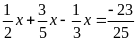 d)
d)
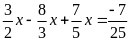
Lời giải
a)
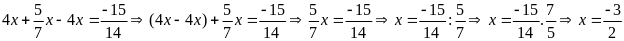
b)
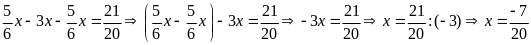
c)

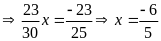
d)
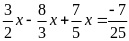
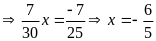
Bài 15:
Tìm x biết:
a)
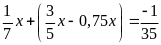 b)
b)

c)
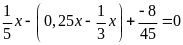 d)
d)

Lời giải
a)

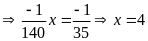
b)


c)
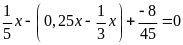
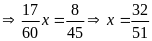
d)
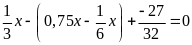
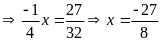
Bài 16:
Tìm x
biết:
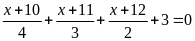
Lời giải
Ta
có:


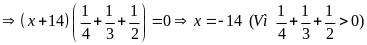
Bài 17:
Tìm x
biết:

Lời giải
Ta
có:
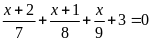

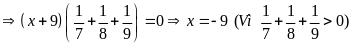
Bài 18:
Tìm x biết:
a)

b)

Lời giải
a)

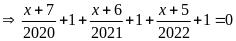
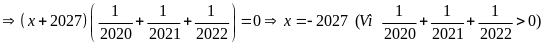
b)


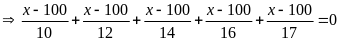
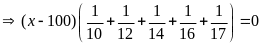
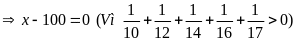

Bài 19:
Tìm x
biết:

Lời giải
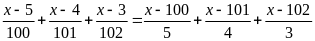
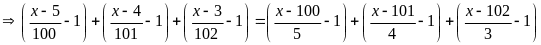
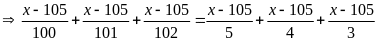
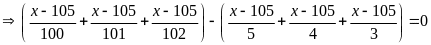
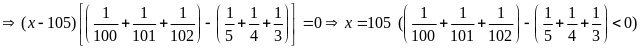
Bài 20:
Tìm x
biết:

Lời giải
Ta
có: Tách
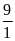 thành
thành
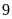 số
số

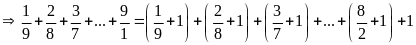

Khi đó:
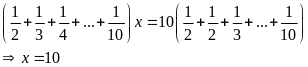
Bài 21:
Tìm x biết:
a)
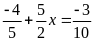 b)
b)
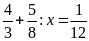
Lời giải
a)


Vậy
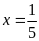 .
.
b)

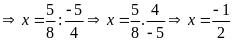
Vậy
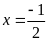 .
.
Bài 22:
Tìm x biết:
a)
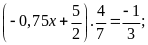 b)
b)

Lời giải
a)

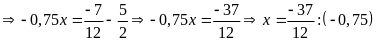
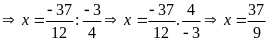
Vậy

b)
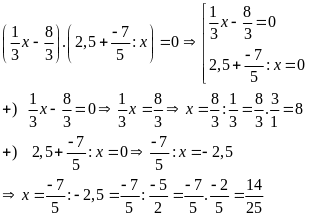
Vậy
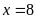 hoặc
hoặc
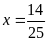
Bài 23:
Tìm x biết:
a)
 b)
b)
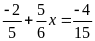
c)
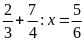 d)
d)
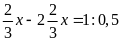
Lời giải
a)
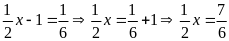
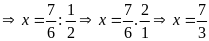
Vậy

b)

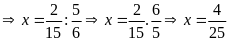
Vậy
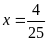 .
.
c)


Vậy
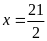 .
.
d)
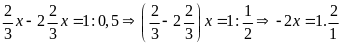
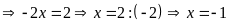
Vậy
 .
.
Bài 24:
Tìm x biết:
a)
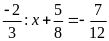 b)
b)

Lời giải
a)

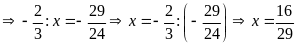
Vậy
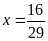
b)
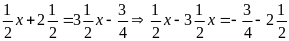

Vậy
 .
.
Bài 25:
Tìm x biết:
a)
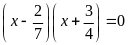 b)
b)
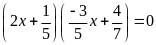
c)

Lời giải
a)
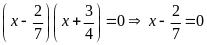 hoặc
hoặc
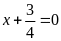 .
.
 hoặc
hoặc

Vậy
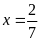 hoặc
hoặc
 .
.
b)
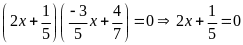 hoặc
hoặc
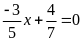
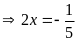 hoặc
hoặc
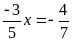
 hoặc
hoặc
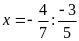
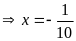 hoặc
hoặc

Vậy
 hoặc
hoặc
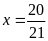 .
.
c)
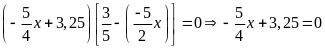 hoặc
hoặc

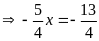 hoặc
hoặc
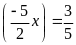
 hoặc
hoặc
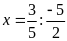
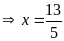 hoặc
hoặc

Vậy
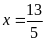 hoặc
hoặc
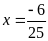 .
.
BÀI TẬP TỰ LUYỆN
Bài 1:
Tìm x biết:
a)
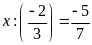 b)
b)
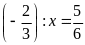
c)
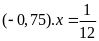 d)
d)

Lời giải
a)
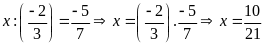
b)
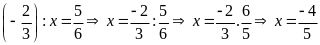
c)

d)
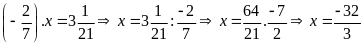
Bài 2:
Tìm x biết:
a)
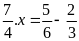 b)
b)
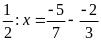
c)
 d)
d)

Lời giải
a)
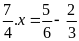

b)
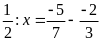

c)
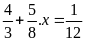
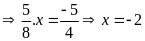
d)
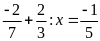

Bài 3:
Tìm x biết:
a)
 b)
b)
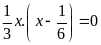
c)
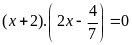 d)
d)

Lời giải
a)
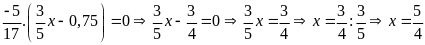
b)
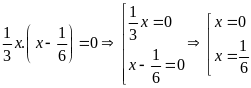
c)

d)
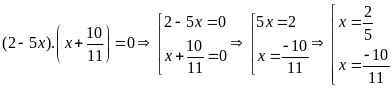
Bài 4:
Tìm x biết:
a)
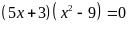 b)
b)

c)
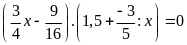 d)
d)
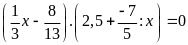
Lời giải
a)
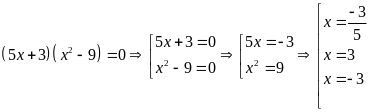
b)
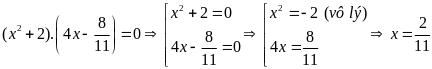
c)
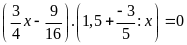
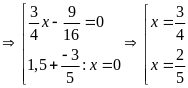
d)
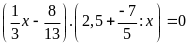

Bài 5:
Tìm x biết:
a)
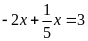 b)
b)
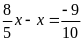
c)
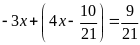 d)
d)

Lời giải
a)
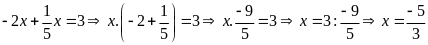
b)

c)
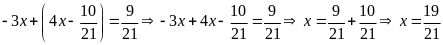
d)
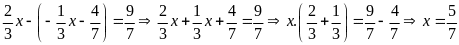
Bài 6:
Tìm x biết:
a)
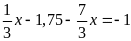 b)
b)

c)
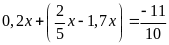 d)
d)
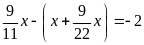
Lời giải
a)
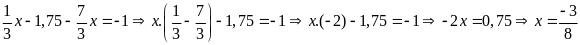
b)
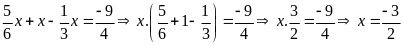
c)
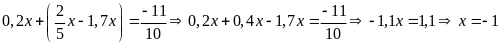
d)
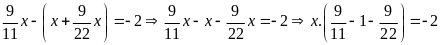
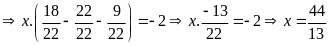
Bài 7:
Tìm x
biết:

Lời giải
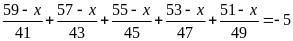


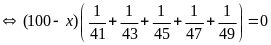
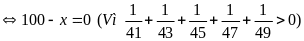
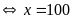
Bài 8:
Tìm
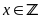 để biểu thức sau nhận giá trị nguyên:
để biểu thức sau nhận giá trị nguyên:
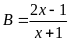
Lời giải
Ta
có:
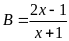
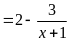
Với
 thì
thì
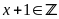
Để
B nguyên thì
 nguyên
nguyên
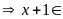 Ư
Ư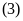
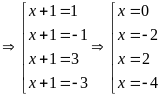
Dạng 5: Tìm điều kiện của x để biểu thức nhận giá trị nguyên
*) Phương pháp giải
Tìm điều kiện của x để biểu thức nhận giá trị nguyên, ta thường làm như sau:
Bước 1. Tách phần nguyên.
Tách tử theo mẫu sao cho A có dạng tổng của một số nguyên và một phân số có tử nguyên.
Bước 2. Tìm x.
Vận
dụng tính chất sau:
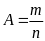 với
với
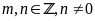
Để
A
nhận giá trị nguyên thì
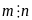 hay
hay
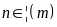 .
.
Bước 3. Đối chiếu với điều kiện và kết luận.
Ví
dụ:
Với
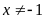 ,
tìm
,
tìm
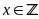 để
để
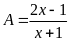 nhận giá trị là số nguyên.
nhận giá trị là số nguyên.
Hướng dẫn giải
Bước 1. Tách phần nguyên.
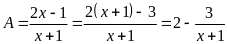
Bước
2.
Để A
là số nguyên thì
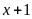 là ước của 3.
là ước của 3.
Suy
ra

|
|
|
1 |
3 |
x |
|
|
0 |
2 |
Bước 3.
Các
giá trị của x
đều nguyên và khác
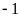 .
.
Vậy
 thì A
nhận giá trị nguyên.
thì A
nhận giá trị nguyên.
Bài 1:
Tìm x
nguyên để biểu thức
 nhận giá trị nguyên.
nhận giá trị nguyên.
Lời giải
P
nhận giá trị nguyên khi
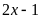 là ước của 2. Suy ra
là ước của 2. Suy ra
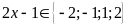
Ta có bảng sau:
|
|
|
1 |
2 |
x |
|
0 |
1 |
|
Vì
x
nguyên nên
 .
.
Vậy
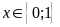 thì P
nhận giá trị nguyên.
thì P
nhận giá trị nguyên.
Bài 2:
Cho
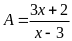 .
Tìm
.
Tìm
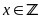 để A
là số nguyên.
để A
là số nguyên.
Lời giải
Điều
kiện:
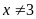 .
.
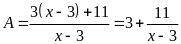
Để
A
là số nguyên thì
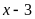 là ước của 11. Ta có bảng sau:
là ước của 11. Ta có bảng sau:
|
|
|
1 |
11 |
x |
|
2 |
4 |
14 |
Các giá trị của x đều nguyên và thỏa mãn điều kiện.
Vậy
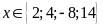 thì A nhận
giá trị nguyên.
thì A nhận
giá trị nguyên.
Bài 3:
Với
 và
và
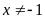 .
Tìm điều kiện để các biểu thức sau nhận giá trị
nguyên:
.
Tìm điều kiện để các biểu thức sau nhận giá trị
nguyên:
a)
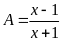 b)
b)
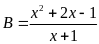
Lời giải
a) Với
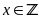 và
và
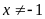 ta có
ta có
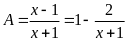 .
.
A
nguyên nếu
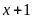 là ước của 2. Khi đó
là ước của 2. Khi đó

b) Với
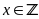 và
và
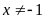 ta có
ta có
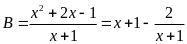 .
.
B
nguyên nếu
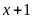 là ước của 2. Khi đó:
là ước của 2. Khi đó:
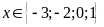
Bài 4:
Cho
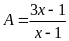 và
và
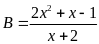
a) Tìm
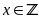 để
để
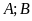 là số nguyên
là số nguyên
b) Tìm
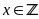 để
để
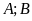 cùng là số nguyên.
cùng là số nguyên.
Lời giải
a) Xét biểu thức A:
Điều kiện:
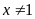 .
.

Để A
là số nguyên với x
nguyên thì
 là ước của 2. Ta có bảng sau:
là ước của 2. Ta có bảng sau:
|
1 |
|
2 |
|
x |
2 |
0 |
3 |
|
Vậy
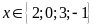 thì A
nguyên.
thì A
nguyên.
Xét biểu thức B. Điều
kiện:
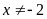 .
.
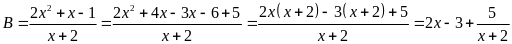
Để B
là một số nguyên với x nguyên thì
 là ước của 5. Ta có bảng sau:
là ước của 5. Ta có bảng sau:
|
1 |
|
5 |
|
x |
|
|
3 |
|
Vậy
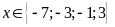 thì B nguyên.
thì B nguyên.
b) Để A
và B cùng
là số nguyên thì
 hoặc
hoặc
 .
.
Dạng 6: Bài toán thực tế
I. Phương pháp giải: Để giải một bài toán thực tế liên quan đến nhân, chia số hữu tỉ, ta thường làm như sau:
Bước 1: Phân tích bài toán, từ các dữ kiện đề bài xác định các giá trị của cùng một đại lượng (ví dụ: các giá trị của một đoạn đường, một chiếc bánh, một quyển sách, một đơn vị thời gian...) và thiết lập mối quan hệ giữa các đại lượng trong bài toán.
Bước 2: Dựa vào quy tắc nhân, chia số hữu tỉ, thực hiện các phép toán tương ứng.
Bước 3: Kết luận.
II. Bài toán:
Bài 1:
Tính
diện tích và chu vi một mảnh vườn đồ chơi hình chữ
nhật có chiều dài
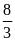 m
và chiều rộng
m
và chiều rộng
 m.
m.
Lời giải
Diện
tích mảnh vườn là:
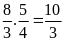 (m2)
(m2)
Chu
vi mảnh vườn là:
 (m)
(m)
Bài 2:
Một
cửa hàng có bán một số bao hạt giống, mỗi bao nặng
 kg,
biết của hàng đã bán được
kg,
biết của hàng đã bán được
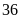 kg
hạt giống, hỏi cửa hàn đã bán được bao nhiêu bao hạt
giống?
kg
hạt giống, hỏi cửa hàn đã bán được bao nhiêu bao hạt
giống?
Lời giải
Cửa
hàng đã bán được số bao hạt giống là: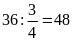 (bao hạt)
(bao hạt)
Vậy
cửa hàng đã bán được
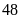 bao hạt giống.
bao hạt giống.
Bài 3:
Lúc
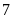 giờ An đi xe đạp từ A đến B
với vận tốc
giờ An đi xe đạp từ A đến B
với vận tốc
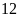 km/h.
Cùng
thời điểm đó thì Bình đi bộ từ B
về A
với vận tôc
km/h.
Cùng
thời điểm đó thì Bình đi bộ từ B
về A
với vận tôc
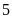 km/h.
Hai bạn gặp nhau tại điểm hẹn lúc
km/h.
Hai bạn gặp nhau tại điểm hẹn lúc
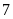 giờ
giờ
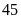 phút. Tính độ dài quãng đường AB?
phút. Tính độ dài quãng đường AB?
Lời giải
Thời
gian An và Bình đi đến khi gặp nhau là:
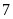 giờ
giờ
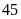 phút -
phút -
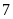 giờ =
giờ =
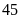 phút =
phút =
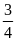 giờ.
giờ.
Quãng
đường An đi:
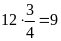 (km)
(km)
Quãng
đường Bình đi: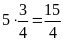 (km)
(km)
Độ
dài quãng đường AB
là:
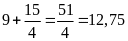 (km)
(km)
Bài 4:
Một
tấm bìa hình chữ nhật có diện tích là
 cm2,
chiều rộng là
cm2,
chiều rộng là
 cm.Tính
chu vi của tấm bìa đó.
cm.Tính
chu vi của tấm bìa đó.
Lời giải
Chiều
dài của tấm bìa là:
 (cm)
(cm)
Chu
vi tấm bìa
là:
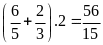 (cm)
(cm)
Bài 5:
Một
ô tô đi từ A
đến B
với vận tốc
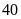 km/h
hết
km/h
hết
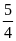 giờ. Sau đó ôtô đi từ B
đến A
với
vận
tốc
giờ. Sau đó ôtô đi từ B
đến A
với
vận
tốc km/h.
Tính thời gian cả đi và về của ô tô?
km/h.
Tính thời gian cả đi và về của ô tô?
Lời giải
Quãng
đường AB
bằng: (km)
(km)
Thời
gian ô tô đi từ B
đến
A là: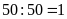 (giờ).
(giờ).
Vậy
thời gian cả đi và về của ô tô là: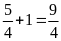 giờ
giờ
Bài 6:
Một
tam giác có độ dài một cạnh
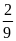 m
và chiều cao tương ứng với cạnh đó bằng nửa cạnh
đó. Tính diện tích của tam giác đã cho.
m
và chiều cao tương ứng với cạnh đó bằng nửa cạnh
đó. Tính diện tích của tam giác đã cho.
Lời giải
Chiều
cao của tam giác là:
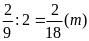
Diện
tích tam giác là:

Vậy
diện tích tam giác đã cho là

Bài 7:
Lúc
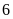 giờ
giờ
 phút bạn Việt đi xe đạp từ A đến B với vận tốc
phút bạn Việt đi xe đạp từ A đến B với vận tốc
 km/h. Lúc
km/h. Lúc
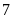 giờ
giờ
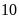 phút bạn Nam đi xe đạp từ B đến A với vận tốc
phút bạn Nam đi xe đạp từ B đến A với vận tốc
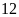 km/h. Hai bạn gặp nhau ở C lúc
km/h. Hai bạn gặp nhau ở C lúc
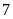 giờ
giờ
 phút. Tính quãng đường AB.
phút. Tính quãng đường AB.
Lời giải
Thời
gian Việt đi là:
 giờ
giờ
 phút –
phút –
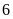 giờ
giờ
 phút =
phút =
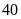 phút =
phút =
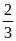 giờ
giờ
Quãng
đường Việt đi là:

Thời
gian Nam đã đi là:
 giờ
giờ
 phút –
phút –
 giờ
giờ
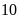 phút =
phút =
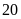 phút =
phút =
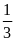 giờ
giờ
Quãng
đường Nam đã đi là: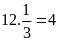 (km)
(km)
Quãng
đường AB dài là:
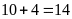 (km)
(km)
Bài 8:
Bảo
và Bình cùng đi từ nhà lúc
 h
h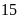 phút
sáng để đến trường. Nhà Bảo cách trường
phút
sáng để đến trường. Nhà Bảo cách trường
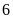 km và Bảo đi với vận tốc
km và Bảo đi với vận tốc
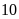 km/h.
Còn Bình đi với vận tốc
km/h.
Còn Bình đi với vận tốc
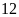 km/h.
Hai bạn cùng đến trường một lúc. Tính quãng đường
từ nhà Bình đến trường?
km/h.
Hai bạn cùng đến trường một lúc. Tính quãng đường
từ nhà Bình đến trường?
Lời giải
Thời
gian Bảo đi là:
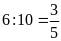 (giờ)
(giờ)
Vì
Bảo và Bình cùng đi, cùng đến trường nên thời gian đi
của Bình là
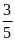 giờ.
giờ.
Quãng
đường Bình đi là:
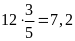 (km)
(km)
Vậy
quãng đường từ nhà Bình đến trường dài
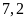 km.
km.
Bài 9:
Hai
người thợ cùng làm một công việc. Nếu làm riêng thì
người thứ nhất phải mất
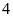 giờ, người thứ hai phải mất
giờ, người thứ hai phải mất
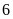 giờ mới hoàn thành công việc. hỏi nếu làm chung trong
giờ mới hoàn thành công việc. hỏi nếu làm chung trong
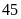 phút thì hai người làm được mấy phần công việc?
phút thì hai người làm được mấy phần công việc?
Lời giải
Đổi
 phút =
phút =
 giờ
giờ
Một
giờ người thứ nhất làm được
 công
việc
công
việc
Một
giờ người thứ hai làm được
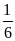 công
việc
công
việc
Một
giờ cả hai người làm được:
 (công
việc)
(công
việc)
Trong
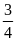 giờ cả hai người làm được:
giờ cả hai người làm được:
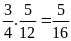 (công
việc)
(công
việc)
Vậy
trong
 phút cả hai người làm được
phút cả hai người làm được
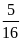 công việc.
công việc.
Bài 10:
Ba
người thợ cùng làm một công việc. Nếu làm riêng thì
người thứ nhất phải mất
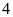 giờ, người thứ hai phải mất
giờ, người thứ hai phải mất
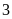 giờ, người thứ ba phải mất
giờ, người thứ ba phải mất
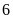 giờ mới hoàn thành công việc. hỏi nếu làm chung trong
giờ mới hoàn thành công việc. hỏi nếu làm chung trong
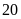 phút thì cả ba người làm được mấy phần công việc?
phút thì cả ba người làm được mấy phần công việc?
Lời giải
Đổi
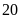 phút =
phút =
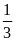 giờ
giờ
Một
giờ người thứ nhất làm được
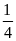 công
việc
công
việc
Một
giờ người thứ hai làm được
 công
việc
công
việc
Một
giờ người thứ ba làm được
 công
việc
công
việc
Một
giờ cả ba người làm được:
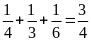 (công
việc)
(công
việc)
Trong
 giờ cả ba người làm được:
giờ cả ba người làm được:
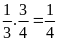 (công
việc)
(công
việc)
Vậy
trong
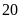 phút cả ba người làm được
phút cả ba người làm được
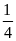 công việc.
công việc.
Bài 11:
Có
 bao đường, bao thứ nhất nặng
bao đường, bao thứ nhất nặng
 kg,
bao thứ hai nặng hơn bao thứ nhất
kg,
bao thứ hai nặng hơn bao thứ nhất
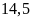 kg,
bao thứ ba bằng
kg,
bao thứ ba bằng
 bao thứ hai. Hỏi ba bao nặng bao nhiêu kilogam?
bao thứ hai. Hỏi ba bao nặng bao nhiêu kilogam?
Lời giải
Bao thứ
hai nặng số kg là:
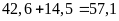 (kg)
(kg)
Bao thứ
ba nặng số kg là:
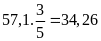 (kg)
(kg)
Ba bao
đường nặng số kg là:
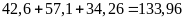 (kg)
(kg)
Bài 12:
Một
công trường xây dựng cần chuyển về
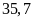 tấn sắt. Lần đầu chở được
tấn sắt. Lần đầu chở được
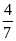 số
sắt đó về bằng xe tải, mỗi xe tải chở được
số
sắt đó về bằng xe tải, mỗi xe tải chở được
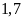 tấn
sắt, lần thứ hai chở hết số sắt còn lại với số
xe tải bằng
tấn
sắt, lần thứ hai chở hết số sắt còn lại với số
xe tải bằng
 số
xe lúc đầu. Hỏi mỗi xe lúc sau chở được bao nhiêu tấn
sắt?
số
xe lúc đầu. Hỏi mỗi xe lúc sau chở được bao nhiêu tấn
sắt?
Lời giải
Số tấn
sắt lần đầu chở được là:
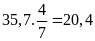 (tấn)
(tấn)
Số tấn
sắt chở lần
hai
là:
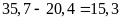 (tấn)
(tấn)
Số xe tải
sử dụng lần đầu là:
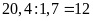 (xe)
(xe)
Số xe tải
sử dụng lần hai là:
 (xe)
(xe)
Mỗi xe
lúc sau chở được số tấn sắt là:
 (tấn)
(tấn)
Bài 13:
Một
người trung bình mỗi phút hít thở
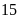 lần,
mỗi lần hít thở
lần,
mỗi lần hít thở
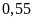 lít không khí, biết
lít không khí, biết
 lít không khí nặng
lít không khí nặng
 g.
Hãy tính khối lượng không khí
g.
Hãy tính khối lượng không khí
 người hít thở trong
người hít thở trong
 giờ?
giờ?
Lời giải
Đổi
 giờ =
giờ =
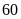 phút
phút
Số lần
hít thở của một người trong
 giờ là:
giờ là:
 (lần)
(lần)
Số lần
hít thở của sáu người trong
 giờ là:
giờ là:
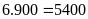 (lần)
(lần)
Số lít
không khí sáu người hít thở trong
 giờ là:
giờ là:
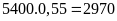 (lít)
(lít)
Khối
lượng không khí sáu người hít thở trong
 giờ là:
giờ là:
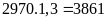 (gam)
(gam)
Bài 14:
Bác
Hà có một thửa ruộng hình chữ nhật với chiều dài
 ,
chiều rộng
,
chiều rộng
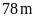 .
Bác Hà cấy lúa trên thửa ruộng đó, cứ
.
Bác Hà cấy lúa trên thửa ruộng đó, cứ
 thu
hoạch được
thu
hoạch được
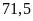 tạ thóc. Hỏi cả thửa ruộng đó, bác Hà thu hoạch được
bao nhiêu tạ thóc?
tạ thóc. Hỏi cả thửa ruộng đó, bác Hà thu hoạch được
bao nhiêu tạ thóc?
Lời giải
Diện
tích thửa ruộng đó là:
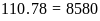 (m2)
=
(m2)
=
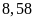 (ha)
(ha)
Bác
Hà thu hoạch được số tạ thóc là:
 (tạ)
(tạ)
Bài 15:
Để
di chuyển các tầng của tòa nhà bệnh viện, người ta sử
dụng thang máy tải trọng tối đa
 tấn.
tấn.
 người gồm bệnh nhân và nhân viên y tế, trung bình mỗi
người cân nặng
người gồm bệnh nhân và nhân viên y tế, trung bình mỗi
người cân nặng
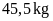 ,
có thể đi cùng thang máy đó trong một lần được không?
Vì sao?
,
có thể đi cùng thang máy đó trong một lần được không?
Vì sao?
Lời giải
 người
gồm bệnh nhân và nhân viên y tế nặng số kg là
người
gồm bệnh nhân và nhân viên y tế nặng số kg là (kg)
(kg)
Đổi
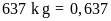 tấn.
tấn.
Vì
 .
Vậy
.
Vậy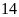 người đó có thể đi cùng thang máy đó trong một lần.
người đó có thể đi cùng thang máy đó trong một lần.
Bài 16:
Một
đội sản xuất gồm
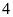 người được trả
người được trả
 triệu đồng tiền công. Sau khi tính lao động của từng
người thì số tiền người thứ nhất, thứ hai, thứ ba
lần lượt bằng
triệu đồng tiền công. Sau khi tính lao động của từng
người thì số tiền người thứ nhất, thứ hai, thứ ba
lần lượt bằng
 tổng số tiền thu được. Tính tiền công mà người thứ
tổng số tiền thu được. Tính tiền công mà người thứ
 nhận được.
nhận được.
Lời giải
Tiền
công của người thứ nhất là:
 (triệu
đồng)
(triệu
đồng)
Tiền
công của người thứ hai là:
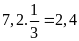 (triệu
đồng)
(triệu
đồng)
Tiền
công của người thứ ba là:
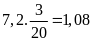 (triệu
đồng)
(triệu
đồng)
Tiền
công của người thứ tư là:
 (triệu đồng)
(triệu đồng)
Bài 17:
Lớp
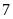 A
cuối năm chỉ có
A
cuối năm chỉ có
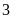 loại học sinh là: giỏi, khá, trung bình (không có học
sinh yếu, kém). Số học sinh trung bình chiếm
loại học sinh là: giỏi, khá, trung bình (không có học
sinh yếu, kém). Số học sinh trung bình chiếm
 số
học sinh cả lớp. Số học sinh khá bằng
số
học sinh cả lớp. Số học sinh khá bằng
 số
học sinh giỏi. Tính số học sinh mỗi loại biết lớp
số
học sinh giỏi. Tính số học sinh mỗi loại biết lớp
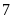 A
có
A
có
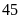 em.
em.
Lời giải
Số
học sinh trung bình là:
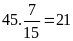 (học
sinh)
(học
sinh)
Số học sinh giỏi và khá là:
 (học sinh)
(học sinh)
Số
học sinh khá chiếm:
 (số
học sinh giỏi và khá)
(số
học sinh giỏi và khá)
Số
học sinh khá là:
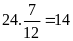 (học
sinh)
(học
sinh)
Số
học sinh giỏi là:
 (học sinh)
(học sinh)
Bài 18:
Điểm
kiểm tra trung bình của lớp
 là
là
 điểm và điểm trung bình của học sinh nữ là
điểm và điểm trung bình của học sinh nữ là
 điểm. Biết lớp
điểm. Biết lớp
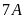 có
có
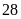 học sinh, số học sinh nam nhiều hơn số học sinh nữ là
học sinh, số học sinh nam nhiều hơn số học sinh nữ là
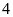 học
sinh. Tính tổng số điểm của các học sinh nam đạt
được.
học
sinh. Tính tổng số điểm của các học sinh nam đạt
được.
Lời giải
Lớp
 có số học sinh nam là:
có số học sinh nam là: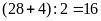 (học sinh)
(học sinh)
Lớp
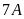 có số học sinh nữ là:
có số học sinh nữ là: 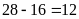 (học sinh)
(học sinh)
Tổng số
điểm của cả lớp đạt được là: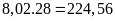 (điểm)
(điểm)
Tổng số
điểm của học sinh nữ đạt được là:
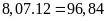 (điểm)
(điểm)
Tổng số
điểm của học sinh nam đạt được là: 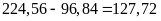 (điểm)
(điểm)
Bài 19:
Hai
xe ô tô chở tất cả
 kg
hàng hóa. Nếu chuyển
kg
hàng hóa. Nếu chuyển
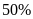 số hàng ở xe thứ nhất sang xe thứ hai thì xe thứ hai
chở gấp
số hàng ở xe thứ nhất sang xe thứ hai thì xe thứ hai
chở gấp
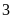 lần xe thứ nhất. Mỗi xe chở bao nhiêu ki-lô-gam hàng
hóa?
lần xe thứ nhất. Mỗi xe chở bao nhiêu ki-lô-gam hàng
hóa?
Lời giải
Khi
chuyển
 số
hàng ở xe thứ nhất sang xe thứ hai thì xe thứ nhất còn
chở số hàng hóa là:
số
hàng ở xe thứ nhất sang xe thứ hai thì xe thứ nhất còn
chở số hàng hóa là:
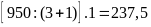 (kg)
(kg)
Thực
tế xe thứ nhất chở là:
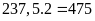 (kg)
(kg)
Xe
thứ hai chở là:
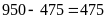 (kg)
(kg)
Bài 20:
Nhà
Hoa và nhà Hồng cách nhau
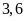 km.
Cùng một lúc Hoa đi xe đạp đến nhà Hồng, Hồng đi bộ
đến nhà Hoa. Hai bạn gặp nhau sau khi khởi hành
km.
Cùng một lúc Hoa đi xe đạp đến nhà Hồng, Hồng đi bộ
đến nhà Hoa. Hai bạn gặp nhau sau khi khởi hành
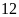 phút.
Tính vận tốc của mỗi bạn, biết rằng vận tốc của
Hoa hơn vận tốc của Hồng là
phút.
Tính vận tốc của mỗi bạn, biết rằng vận tốc của
Hoa hơn vận tốc của Hồng là
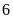 km/h.
km/h.
Lời giải
Đổi
 phút =
phút =
 giờ
giờ
Tổng
vận tốc của Hoa và Hồng là:
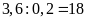 (km/h)
(km/h)
Vận
tốc của Hoa là:
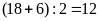 (km/h)
(km/h)
Vận
tốc của Hồng là:
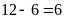 (km/h)
(km/h)
BÀI TẬP TỰ LUYỆN
B ài
1. Loài
chó nhỏ nhất thế giới: Chó Chihuahua là một giống chó
của Mexico. Nguồn gốc của chúng vẫn là một bí ẩn,
người ta chỉ mới đưa ra suy đoán rằng những hình vẽ
trong các bức tranh được tìm thấy ở Mexico có niên đại
ài
1. Loài
chó nhỏ nhất thế giới: Chó Chihuahua là một giống chó
của Mexico. Nguồn gốc của chúng vẫn là một bí ẩn,
người ta chỉ mới đưa ra suy đoán rằng những hình vẽ
trong các bức tranh được tìm thấy ở Mexico có niên đại
 năm trước công nguyên là của tổ tiên của Chihuahua ngày
nay.
năm trước công nguyên là của tổ tiên của Chihuahua ngày
nay.
Cân
nặng trung bình của một chú chó Chihuahua khoảng
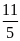 kg.
kg.
E nglish
Mastiff có tên tiếng Việt là chó ngao Anh, là một trong
những giống chó to nhất thế giới. Cân nặng của chó
ngao Anh được xem là nặng nhất thế giới. Chiều cao
trung bình của chúng cũng xếp thứ
nglish
Mastiff có tên tiếng Việt là chó ngao Anh, là một trong
những giống chó to nhất thế giới. Cân nặng của chó
ngao Anh được xem là nặng nhất thế giới. Chiều cao
trung bình của chúng cũng xếp thứ
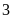 thế giới, vào khoảng
thế giới, vào khoảng
 cm.
cm.
Tuy to lớn là thế nhưng chó ngao Anh khá “hiền”. Chúng khá trầm tĩnh, ngoan ngoãn và không thích sủa giống như những chú chó khác. Đặc biệt chúng cực thích chơi với trẻ em. Chó ngao Anh trước đây thường được huấn luyện để đấu chó hoặc làm chó nghiệp vụ.
Trung
bình cân nặng của một chú chó ngao Anh gấp
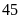 lần chó
Chihuahua.
lần chó
Chihuahua.
Tính cân nặng trung bình của chó ngao Anh?
Lời giải
Trung bình
cân nặng của một chú chó ngao Anh gấp
 lần chó
Chihuahua.
lần chó
Chihuahua.
Cân
nặng của chó ngao Anh
là:
 (kg)
(kg)
Bài 2:
Một
hình chữ nhật có chu vi là
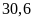 cm,
chiều rộng là
cm,
chiều rộng là
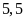 cm.
Tính diện tích của hình chữ nhật đó?
cm.
Tính diện tích của hình chữ nhật đó?
Lời giải
Chiều
dài của hình chữ nhật là:
 (cm)
(cm)
Diện
tích của hình chữ nhật là:
 (cm2)
(cm2)
Vậy
diện tích của hình chữ nhật đó là

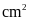 .
.
Bài 3:
Một
cửa hàng có
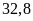 tạ
gạo, ngày thứ nhất cửa hàng bán được
tạ
gạo, ngày thứ nhất cửa hàng bán được
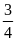 số gạo, ngày thứ hai cửa hàng bán được
số gạo, ngày thứ hai cửa hàng bán được
 số gạo còn lại. Hỏi cửa hàng còn lại bao nhiêu kg gạo
chưa bán?
số gạo còn lại. Hỏi cửa hàng còn lại bao nhiêu kg gạo
chưa bán?
Lời giải
Số
gạo cửa hàng bán ngày thứ nhất là:
 (tạ)
(tạ)
Số
gạo còn lại sau ngày thứ nhất là:
 (tạ)
(tạ)
Số
gạo cửa hàng chưa bán là:
 (tạ) = 205(kg)
(tạ) = 205(kg)
Vậy
cửa hàng còn lại
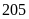 kg
gạo.
kg
gạo.
Bài 4:
Bạn
Nam đạp xe từ nhà tới trường với vận tốc
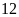 km/h hết
km/h hết
 phút. Khi về, Nam đạp xe với vận tốc
phút. Khi về, Nam đạp xe với vận tốc
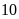 km/h. Thời gian Nam đi từ trường về nhà là bao nhiêu
phút?
km/h. Thời gian Nam đi từ trường về nhà là bao nhiêu
phút?
Lời giải
Đổi:
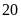 phút
=
phút
=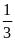 giờ
giờ
Quãng
đường từ nhà Nam đến trường là:
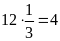 (km)
(km)
Thời
gian Nam đi từ trường về nhà là:
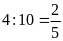 (giờ)
(giờ)
Đổi:
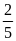 giờ
=
giờ
=
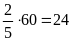 phút.
phút.
Vậy
thời gian Nam đi từ trường về nhà là
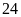 phút.
phút.
Bài 5:
Một
mảnh vườn hình chữ nhật có chiều dài là
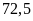 m, chiều rộng kém chiều dài
m, chiều rộng kém chiều dài
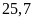 m.
Người ta trồng dâu tây trên mảnh vườn đó, trung bình
cứ
m.
Người ta trồng dâu tây trên mảnh vườn đó, trung bình
cứ
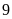 m2
thì thu được
m2
thì thu được
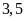 kg
dâu tây. Vậy trên mảnh vườn đó người ta thu được
tất cả bao nhiêu tấn dâu tây?
kg
dâu tây. Vậy trên mảnh vườn đó người ta thu được
tất cả bao nhiêu tấn dâu tây?
Lời giải
Chiều
rộng mảnh vườn đó là:
 (m)
(m)
Diện tích
mảnh vườn đó là:
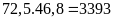 (m2)
(m2)
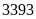 m2
gấp
m2
gấp
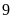 m2
số lần là:
m2
số lần là:
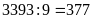 (lần)
(lần)
Trên mảnh
vườn đó người ta thu được tất cả số tấn dâu tây
là:
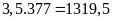 (kg)
(kg)
 (tấn)
(tấn)
Bài 6:
Một
vườn cây hình chữ nhật có diện tích
 m2,
chiều dài
m2,
chiều dài
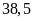 m.
Người ta muốn rào xung quanh vườn và làm cửa vườn.
Hỏi hàng rào xung quanh dài bao nhiêu mét, biết cửa vườn
rộng
m.
Người ta muốn rào xung quanh vườn và làm cửa vườn.
Hỏi hàng rào xung quanh dài bao nhiêu mét, biết cửa vườn
rộng
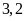 m.
m.
Lời giải
Chiều
rộng của vườn cây là: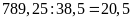 (m)
(m)
Chu vi của
vườn cây là: (m)
(m)
Độ dài
của hàng rào xung quanh vườn là: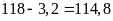 (m)
(m)
Bài 7:
Năm
 ,
tổng diện tích đất trồng lúa của nước ta đạt
,
tổng diện tích đất trồng lúa của nước ta đạt
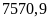 (nghìn ha); giảm
(nghìn ha); giảm
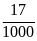 so
với năm trước. Em hãy tính diện tích đất trồng lúa
của Việt Nam năm
so
với năm trước. Em hãy tính diện tích đất trồng lúa
của Việt Nam năm
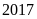 là bao nhiêu hécta (sử dụng máy tính cầm tay rồi làm
tròn đến hàng đơn vị).
là bao nhiêu hécta (sử dụng máy tính cầm tay rồi làm
tròn đến hàng đơn vị).
Lời giải
Diện tích
trồng lúa năm
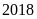 bằng:
bằng:
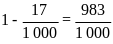 (diện
tích trồng lúa năm 2017)
(diện
tích trồng lúa năm 2017)
Vì vậy
năm
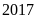 ,
diện tích trồng lúa của Việt Nam là:
,
diện tích trồng lúa của Việt Nam là:
 (nghìn
ha)
(nghìn
ha)
 (ha)
(ha)
Bài 8:
Một
bánh xe hình tròn có đường kính là
 mm chuyển động trên một đường thẳng từ điểm A đến
điểm B sau
mm chuyển động trên một đường thẳng từ điểm A đến
điểm B sau
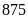 vòng. Quãng đường AB dài khoảng bao nhiêu ki-lô-mét? (làm
tròn kết quả đến hàng phần mười và lấy
vòng. Quãng đường AB dài khoảng bao nhiêu ki-lô-mét? (làm
tròn kết quả đến hàng phần mười và lấy  )?
)?
Lời giải
Ta có:

Chu vi bánh
xe là:
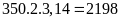 (mm)
(mm)
Quãng
đường AB dài là:

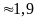 (km).
(km).
Ngoài Chuyên Đề Nhân Chia Số Hữu Tỉ Toán 7 Có Lời Giải Chi Tiết thì các tài liệu học tập trong chương trình 7 sẽ được cập nhật liên tục và nhanh nhất có thể sau khi kỳ thi diễn ra trên Danh mục Tài Liệu Học Tập nhằm giúp các bạn đọc thuận tiện trong việc nghiên cứu tài liệu. Quý thày cô và các bạn đọc có thể chia sẻ thêm những tài liệu học tập hữu ích đến địa chỉ email của chúng tôi, nhằm xây dựng nên kho đề thi phong phú, đa dạng cho các em học sinh tham khảo và rèn luyện.
Xem thêm







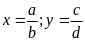 ,
với
,
với
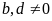 ta có:
ta có:
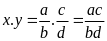 .
.