Chuyên Đề Toán Chia Hết Lớp 8 Của Số Nguyên Bồi Dưỡng Học Sinh Giỏi

CHUYÊN ĐỀ - CÁC BÀI TOÁN VỀ SỰ CHIA HẾT CỦA SỐ NGUYÊN

I. Dạng 1: Chứng minh quan hệ chia hết

1. Kiến thức:

* Để chứng minh A(n) chia hết cho một số m ta phân tích A(n) thành nhân tử có một nhân tử làm hoặc bội của m, nếu m là hợp số thì ta lại phân tích nó thành nhân tử có các đoi một nguyên tố cùng nhau, rồi chứng minh A(n) chia hết cho các số đó

* Chú ý:

+ Với k số nguyên liên tiếp bao giờ củng tồn tại một bội của k

+ Khi chứng minh A(n) chia hết cho m ta xét mọi trường hợp về số dư khi chia A(n) cho m

+ Với mọi số nguyên a, b và số tự nhiên n thì:

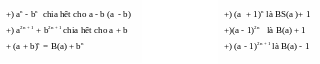
2. Bài tập:

2. Các bài toán

Bài 1: chứng minh rằng

a) 2⁵¹ - 1 chia hết cho 7 b) 2⁷⁰ + 3⁷⁰ chia hết cho 13

c) 17¹⁹ + 19¹⁷ chi hết cho 18 d) 36⁶³ - 1 chia hết cho 7 nhưng không chia hết cho 37

e) 2⁴ⁿ -1 chia hết cho 15 với nÎ N

Giải

a) 2⁵¹ - 1 = (2³)¹⁷ - 1 2³ - 1 = 7

b) 2⁷⁰ + 3⁷⁰ (2²)³⁵ + (3²)³⁵ = 4³⁵ + 9³⁵ 4 + 9 = 13

c) 17¹⁹ + 19¹⁷ = (17¹⁹ + 1) + (19¹⁷ - 1)

17¹⁹ + 1 17 + 1 = 18 và 19¹⁷ - 1 19 - 1 = 18 nên (17¹⁹ + 1) + (19¹⁷ - 1)

hay 17¹⁹ + 19¹⁷ 18

d) 36⁶³ - 1 36 - 1 = 35 7

36⁶³ - 1 = (36⁶³ + 1) - 2 chi cho 37 dư - 2

e) 2 ⁴ⁿ - 1 = (2⁴) ⁿ - 1 2⁴ - 1 = 15

Bài 2: chứng minh rằng

a) n⁵ - n chia hết cho 30 với n Î N ;

b) n⁴ -10n² + 9 chia hết cho 384 với mọi n lẻ nÎ Z

c) 10ⁿ +18n -28 chia hết cho 27 với nÎ N ;

Giải:

a) n⁵ - n = n(n⁴ - 1) = n(n - 1)(n + 1)(n² + 1) = (n - 1).n.(n + 1)(n² + 1) chia hết cho 6 vì

(n - 1).n.(n+1) là tích của ba số tự nhiên liên tiếp nên chia hết cho 2 và 3 (*)

Mặt khác n⁵ - n = n(n² - 1)(n² + 1) = n(n² - 1).(n² - 4 + 5) = n(n² - 1).(n² - 4 ) + 5n(n² - 1)

= (n - 2)(n - 1)n(n + 1)(n + 2) + 5n(n² - 1)

Vì (n - 2)(n - 1)n(n + 1)(n + 2) là tích của 5 số tự nhiên liên tiếp nên chia hết cho 5

5n(n² - 1) chia hết cho 5

Suy ra (n - 2)(n - 1)n(n + 1)(n + 2) + 5n(n² - 1) chia hết cho 5 (**)

Từ (*) và (**) suy ra đpcm

b) Đặt A = n⁴ -10n² + 9 = (n⁴ -n² ) - (9n² - 9) = (n² - 1)(n² - 9) = (n - 3)(n - 1)(n + 1)(n + 3)

Vì n lẻ nên đặt n = 2k + 1 (k Z) thì

A = (2k - 2).2k.(2k + 2)(2k + 4) = 16(k - 1).k.(k + 1).(k + 2) A chia hết cho 16 (1)

Và (k - 1).k.(k + 1).(k + 2) là tích của 4 số nguyên liên tiếp nên A có chứa bội của 2, 3, 4 nên A là bội của 24 hay A chia hết cho 24 (2)

Từ (1) và (2) suy ra A chia hết cho 16. 24 = 384

c) 10 ⁿ +18n -28 = ( 10 ⁿ - 9n - 1) + (27n - 27)

+ Ta có: 27n - 27 27 (1)

+ 10 ⁿ - 9n - 1 = [( + 1) - 9n - 1] = - 9n = 9( - n) 27 (2)

vì 9 9 và - n 3 do - n là một số có tổng các chữ số chia hết cho 3

Từ (1) và (2) suy ra đpcm

3. Bài 3: Chứng minh rằng với mọi số nguyên a thì

a) a³ - a chia hết cho 3

b) a⁷ - a chia hết cho 7

Giải

a) a³ - a = a(a² - 1) = (a - 1) a (a + 1) là tích của ba số nguyên liên tiếp nên tồn tại một số là bội của 3 nên (a - 1) a (a + 1) chia hết cho 3

b) ) a⁷ - a = a(a⁶ - 1) = a(a² - 1)(a² + a + 1)(a² - a + 1)

Nếu a = 7k (k Z) thì a chia hết cho 7

Nếu a = 7k + 1 (k Z) thì a² - 1 = 49k² + 14k chia hết cho 7

Nếu a = 7k + 2 (k Z) thì a² + a + 1 = 49k² + 35k + 7 chia hết cho 7

Nếu a = 7k + 3 (k Z) thì a² - a + 1 = 49k² + 35k + 7 chia hết cho 7

Trong trường hợp nào củng có một thừa số chia hết cho 7

Vậy: a⁷ - a chia hết cho 7

Bài 4: Chứng minh rằng A = 1³ + 2³ + 3³ + ...+ 100³ chia hết cho B = 1 + 2 + 3 + ... + 100

Giải

Ta có: B = (1 + 100) + (2 + 99) + ...+ (50 + 51) = 101. 50

Để chứng minh A chia hết cho B ta chứng minh A chia hết cho 50 và 101

Ta có: A = (1³ + 100³) + (2³ + 99³) + ... +(50³ + 51³)

= (1 + 100)(1² + 100 + 100²) + (2 + 99)(2² + 2. 99 + 99²) + ... + (50 + 51)(50² + 50. 51 + 51²) = 101(1² + 100 + 100² + 2² + 2. 99 + 99² + ... + 50² + 50. 51 + 51²) chia hết cho 101 (1)

Lại có: A = (1³ + 99³) + (2³ + 98³) + ... + (50³ + 100³)

Mỗi số hạng trong ngoặc đều chia hết cho 50 nên A chia hết cho 50 (2)

Từ (1) và (2) suy ra A chia hết cho 101 và 50 nên A chi hết cho B

Bài tập về nhà

Chứng minh rằng:

a) a⁵ – a chia hết cho 5

b) n³ + 6n² + 8n chia hết cho 48 với mọi n chẵn

c) Cho a l à số nguyên tố lớn hơn 3. Cmr a² – 1 chia hết cho 24

d) Nếu a + b + c chia hết cho 6 thì a³ + b³ + c³ chia hết cho 6

e) 2009²⁰¹⁰ không chia hết cho 2010

f) n² + 7n + 22 không chia hết cho 9

II. Dạng 2: Tìm số dư của một phép chia

Bài 1:

Tìm số dư khi chia 2¹⁰⁰

a)cho 9, b) cho 25, c) cho 125

Giải

a) Luỹ thừa của 2 sát với bội của 9 là 2³ = 8 = 9 - 1

Ta có : 2¹⁰⁰ = 2. (2³)³³ = 2.(9 - 1)³³ = 2.[B(9) - 1] = B(9) - 2 = B(9) + 7

Vậy: 2¹⁰⁰ chia cho 9 thì dư 7

b) Tương tự ta có: 2¹⁰⁰ = (2¹⁰)¹⁰ = 1024¹⁰ = [B(25) - 1]¹⁰ = B(25) + 1

Vậy: 2¹⁰⁰ chia chop 25 thì dư 1

c)Sử dụng công thức Niutơn:

2¹⁰⁰ = (5 - 1)⁵⁰ = (5⁵⁰ - 5. 5⁴⁹ + … + . 5² - 50 . 5 ) + 1

Không kể phần hệ số của khai triển Niutơn thì 48 số hạng đầu đã chứa thừa số 5 với số mũ lớn hơn hoặc bằng 3 nên đều chia hết cho 5³ = 125, hai số hạng tiếp theo: . 5² - 50.5 cũng chia hết cho 125 , số hạng cuối cùng là 1

Vậy: 2¹⁰⁰ = B(125) + 1 nên chia cho 125 thì dư 1

Bài 2:

Viết số 1995¹⁹⁹⁵ thành tổng của các số tự nhiên . Tổng các lập phương đó chia cho 6 thì dư bao nhiêu?

Giải

Đặt 1995¹⁹⁹⁵ = a = a₁ + a₂ + …+ a_n.

Gọi = + a - a

= (a₁ ³ - a₁) + (a₂ ³ - a₂) + …+ (a_n ³ - a_n) + a

Mỗi dấu ngoặc đều chia hết cho 6 vì mỗi dấu ngoặc là tích của ba số tự nhiên liên tiếp. Chỉ cần tìm số dư khi chia a cho 6

1995 là số lẻ chia hết cho 3, nên a củng là số lẻ chia hết cho 3, do đó chia cho 6 dư 3

Bài 3: Tìm ba chữ số tận cùng của 2¹⁰⁰ viết trong hệ thập phân

giải

Tìm 3 chữ số tận cùng là tìm số dư của phép chia 2¹⁰⁰ cho 1000

Trước hết ta tìm số dư của phép chia 2¹⁰⁰ cho 125

Vận dụng bài 1 ta có 2¹⁰⁰ = B(125) + 1 mà 2¹⁰⁰ là số chẵn nên 3 chữ số tận cùng của nó chỉ có thể là 126, 376, 626 hoặc 876

Hiển nhiên 2¹⁰⁰ chia hết cho 8 vì 2¹⁰⁰ = 16²⁵ chi hết cho 8 nên ba chữ số tận cùng của nó chia hết cho 8

trong các số 126, 376, 626 hoặc 876 chỉ có 376 chia hết cho 8

Vậy: 2¹⁰⁰ viết trong hệ thập phân có ba chữ số tận cùng là 376

Tổng quát: Nếu n là số chẵn không chia hết cho 5 thì 3 chữ số tận cùng của nó là 376

Bài 4: Tìm số dư trong phép chia các số sau cho 7

a) 22²² + 55⁵⁵ b)3¹⁹⁹³

c) 1992¹⁹⁹³ + 1994¹⁹⁹⁵ d)

Giải

a) ta có: 22²² + 55⁵⁵ = (21 + 1)²² + (56 – 1)⁵⁵ = (BS 7 +1)²² + (BS 7 – 1)⁵⁵

= BS 7 + 1 + BS 7 - 1 = BS 7 nên 22²² + 55⁵⁵ chia 7 dư 0

b) Luỹ thừa của 3 sát với bội của 7 là 3³ = BS 7 – 1

Ta thấy 1993 = BS 6 + 1 = 6k + 1, do đó:

3¹⁹⁹³ = 3 ^{6k + 1} = 3.(3³)^2k = 3(BS 7 – 1)^2k = 3(BS 7 + 1) = BS 7 + 3

c) Ta thấy 1995 chia hết cho 7, do đó:

1992¹⁹⁹³ + 1994¹⁹⁹⁵ = (BS 7 – 3)¹⁹⁹³ + (BS 7 – 1)¹⁹⁹⁵ = BS 7 – 3¹⁹⁹³ + BS 7 – 1

Theo câu b ta có 3¹⁹⁹³ = BS 7 + 3 nên

1992¹⁹⁹³ + 1994¹⁹⁹⁵ = BS 7 – (BS 7 + 3) – 1 = BS 7 – 4 nên chia cho 7 thì dư 3

d) = 3²⁸⁶⁰ = 3^{3k + 1} = 3.3^3k = 3(BS 7 – 1) = BS 7 – 3 nên chia cho 7 thì dư 4

Bài tập về nhà

Tìm số d ư khi:

a) 2¹⁹⁹⁴ cho 7

b) 3¹⁹⁹⁸ + 5¹⁹⁹⁸ cho 13

c) A = 1³ + 2³ + 3³ + ...+ 99³ chia cho B = 1 + 2 + 3 + ... + 99

III. Dạng 3: Tìm điều kiện để xảy ra quan hệ chia hết

Bài 1: Tìm n Z để giá trị của biểu thức A = n³ + 2n² - 3n + 2 chia hết cho giá trị của biểu thức B = n² - n

Giải

Chia A cho B ta có: n³ + 2n² - 3n + 2 = (n + 3)(n² - n) + 2

Để A chia hết cho B thì 2 phải chia hết cho n² - n = n(n - 1) do đó 2 chia hết cho n, ta có:

n	1	- 1	2	- 2
n - 1	0	- 2	1	- 3
n(n - 1)	0	2	2	6
	loại			loại

Vậy: Để giá trị của biểu thức A = n³ + 2n² - 3n + 2 chia hết cho giá trị của biểu thức

B = n² - n thì n

Bài 2:

a) Tìm n N để n⁵ + 1 chia hết cho n³ + 1

b) Giải bài toán trên nếu n Z

Giải

Ta có: n⁵ + 1 n³ + 1 n²(n³ + 1) - (n² - 1) n³ + 1 (n + 1)(n - 1) n³ + 1

(n + 1)(n - 1) (n + 1)(n² - n + 1) n - 1 n² - n + 1 (Vì n + 1 0)

a) Nếu n = 1 thì 0 1

Nếu n > 1 thì n - 1 < n(n - 1) + 1 < n² - n + 1 nên không thể xẩy ra n - 1 n² - n + 1

Vậy giá trụ của n tìm được là n = 1

b) n - 1 n² - n + 1 n(n - 1) n² - n + 1 (n² - n + 1 ) - 1 n² - n + 1

1 n² - n + 1. Có hai trường hợp xẩy ra:

+ n² - n + 1 = 1 n(n - 1) = 0 (Tm đề bài)

+ n² - n + 1 = -1 n² - n + 2 = 0 (Vô nghiệm)

Bài 3: Tìm số nguyên n sao cho:

a) n² + 2n - 4 11 b) 2n³ + n² + 7n + 1 2n - 1

c) n⁴ - 2n³ + 2n² - 2n + 1 n⁴ - 1 d) n³ - n² + 2n + 7 n² + 1

Giải

a) Tách n² + 2n - 4 thành tổng hai hạng tử trong đó có một hạng tử là B(11)

n² + 2n - 4 11 (n² - 2n - 15) + 11 11 (n - 3)(n + 5) + 11 11

(n - 3)(n + 5) 11

b) 2n³ + n² + 7n + 1 = (n² + n + 4) (2n - 1) + 5

Để 2n³ + n² + 7n + 1 2n - 1 thì 5 2n - 1 hay 2n - 1 là Ư(5)

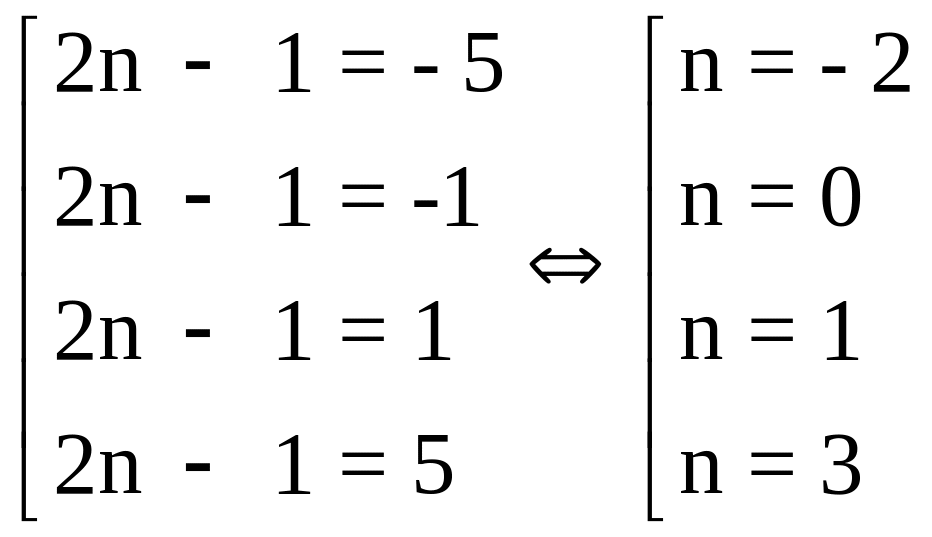
Vậy: n thì 2n³ + n² + 7n + 1 2n - 1

c) n⁴ - 2n³ + 2n² - 2n + 1 n⁴ - 1

Đặt A = n⁴ - 2n³ + 2n² - 2n + 1 = (n⁴ - n³) - (n³ - n²) + (n² - n) - (n - 1)

= n³(n - 1) - n²(n - 1) + n(n - 1) - (n - 1) = (n - 1) (n³ - n² + n - 1) = (n - 1)²(n² + 1)

B = n⁴ - 1 = (n - 1)(n + 1)(n² + 1)

A chia hết cho b nên n 1 A chia hết cho B n - 1 n + 1 (n + 1) - 2 n + 1

2 n + 1

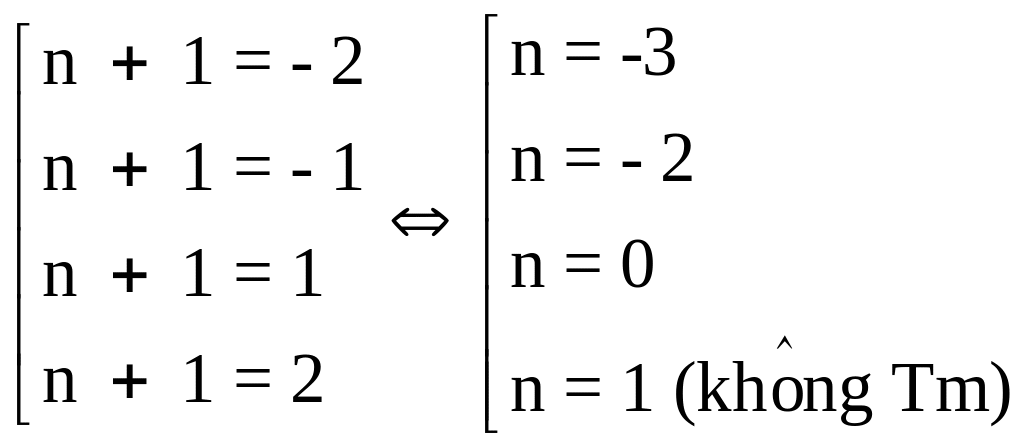
Vậy: n thì n⁴ - 2n³ + 2n² - 2n + 1 n⁴ - 1

d) Chia n³ - n² + 2n + 7 cho n² + 1 được thương là n - 1, dư n + 8

Để n³ - n² + 2n + 7 n² + 1 thì n + 8 n² + 1 (n + 8)(n - 8) n² + 1 65 n² + 1

Lần lượt cho n² + 1 bằng 1; 5; 13; 65 ta được n bằng 0; 2; 8

Thử lại ta có n = 0; n = 2; n = 8 (T/m)

Vậy: n³ - n² + 2n + 7 n² + 1 khi n = 0, n = 8

Bài tập về nhà:

Tìm số nguyên n để:

a) n³ – 2 chia hết cho n – 2

b) n³ – 3n² – 3n – 1 chia hết cho n² + n + 1

c)5ⁿ – 2ⁿ chia hết cho 63

IV. Dạng 4: Tồn tại hay không tồn tại sự chia hết

Bài 1: Tìm n N sao cho 2ⁿ – 1 chia hết cho 7

Giải

Nếu n = 3k ( k N) thì 2ⁿ – 1 = 2^3k – 1 = 8^k - 1 chia hết cho 7

Nếu n = 3k + 1 ( k N) thì 2ⁿ – 1 = 2^{3k + 1} – 1 = 2(2^3k – 1) + 1 = BS 7 + 1

Nếu n = 3k + 2 ( k N) thì 2ⁿ – 1 = 2^{3k + 2} – 1 = 4(2^3k – 1) + 3 = BS 7 + 3

V ậy: 2ⁿ – 1 chia hết cho 7 khi n = BS 3

Bài 2: Tìm n N để:

a) 3ⁿ – 1 chia hết cho 8

b) A = 3^{2n + 3} + 2^{4n + 1} chia hết cho 25

c) 5ⁿ – 2ⁿ chia hết cho 9

Giải

a) Khi n = 2k (k N) thì 3ⁿ – 1 = 3^2k – 1 = 9^k – 1 chia hết cho 9 – 1 = 8

Khi n = 2k + 1 (k N) thì 3ⁿ – 1 = 3^{2k + 1} – 1 = 3. (9^k – 1 ) + 2 = BS 8 + 2

Vậy : 3ⁿ – 1 chia hết cho 8 khi n = 2k (k N)

b) A = 3^{2n + 3} + 2^{4n + 1} = 27 . 3²ⁿ + 2.2⁴ⁿ = (25 + 2) 3²ⁿ + 2.2⁴ⁿ = 25. 3²ⁿ + 2.3²ⁿ + 2.2⁴ⁿ

= BS 25 + 2(9ⁿ + 16ⁿ)

Nếu n = 2k +1(k N) thì 9ⁿ + 16ⁿ = 9^{2k + 1} + 16^{2k + 1} chia hết cho 9 + 16 = 25

Nếu n = 2k (k N) thì 9ⁿ có chữ số tận cùng bằng 1 , còn 16ⁿ có chữ số tận cùng bằng 6

suy ra 2((9ⁿ + 16ⁿ) có chữ số tận cùng bằng 4 nên A không chia hết cho 5 nên không chia hết cho 25

c) Nếu n = 3k (k N) thì 5ⁿ – 2ⁿ = 5^3k – 2^3k chia hết cho 5³ – 2³ = 117 nên chia hết cho 9

Nếu n = 3k + 1 thì 5ⁿ – 2ⁿ = 5.5^3k – 2.2^3k = 5(5^3k – 2^3k) + 3. 2^3k = BS 9 + 3. 8^k

= BS 9 + 3(BS 9 – 1)^k = BS 9 + BS 9 + 3

Tương tự: nếu n = 3k + 2 thì 5ⁿ – 2ⁿ không chia hết cho 9