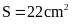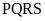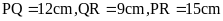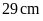Ôn Tập Chương 3 Các Hình Học Trực Quan Trong Thực Tiễn Toán 6
>>> Mọi người cũng quan tâm:
Ôn Tập Chương 3 Các Hình Học Trực Quan Trong Thực Tiễn Toán 6 – Toán 6 Chân Trời Sáng Tạo là tài liệu học tập được Trang Tài Liệu biên soạn và sưu tầm từ những nguồn dữ liệu mới nhất hiện nay. Tài liệu này sẽ giúp các em luyện tập, củng cố kiến thức từ đó nâng cao điểm số cho môn học. Ngoài ra, cũng giúp các thầy cô giáo có nguồn tài nguyên phong phú để giảng dạy.
Dưới đây là bản đọc trực tuyến giúp thầy cô và các em học sinh có thể nghiên cứu Online hoặc bạn có thể tải miễn phí với phiên bản word để dễ dàng in ấn cũng như học tập Offline.
§5. ÔN TẬP CHƯƠNG III (tiết 1)
A. KIẾN THỨC CẦN NHỚ

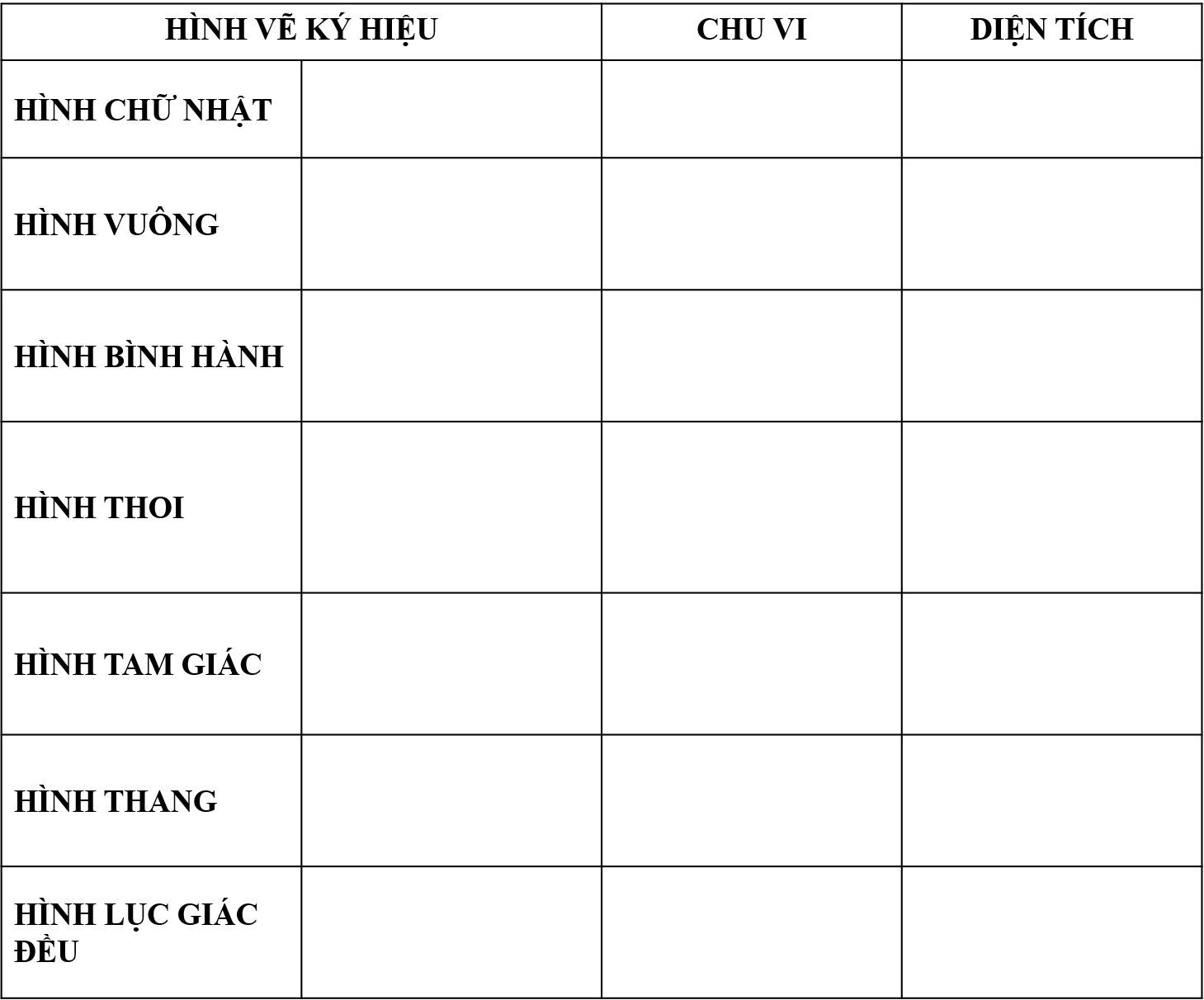
![]()


![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
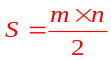
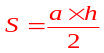
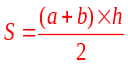
B. BÀI TẬP CÓ HƯỚNG DẪN.
DẠNG 1: Dạng toán nhận biết các công thức tính chu vi, diện tích
Bài
1.
Cho
hình vuông
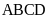 có
có
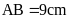 .
Tính độ dài các đoạn thẳng
.
Tính độ dài các đoạn thẳng
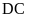 và
và
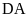 .
.
Hướng dẫn: Áp dụng kiến thức của hình vuông.
Bài
2.
Cho
lục giác đều
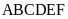 với cạnh
với cạnh
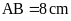 và
đường chéo
và
đường chéo
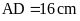 .
Tính độ dài đoạn thẳng
.
Tính độ dài đoạn thẳng
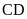 và
và
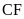 .
.
Hướng dẫn: Áp dụng các kiến thức của hình lục giác đều.
Bài
3. Cho hình thoi
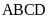 với
với
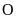 là giao điểm của hai đường chéo. Biết
là giao điểm của hai đường chéo. Biết
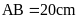 ,
OA = 16 cm,
,
OA = 16 cm,
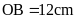 .
Tính độ dài các cạnh và các đường chéo của hình
thoi.
.
Tính độ dài các cạnh và các đường chéo của hình
thoi.
Hướng dẫn: Áp dụng các kiến thức của hình thoi.
Bài
4. Cho hình chữ nhật
 có
có
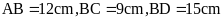 .
Tính cạnh
.
Tính cạnh
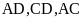 .
.
Hướng dẫn: Áp dụng các kiến thức của hình chữ nhật.
DẠNG 2: Dạng toán tính chu vi, diện tích
Bài
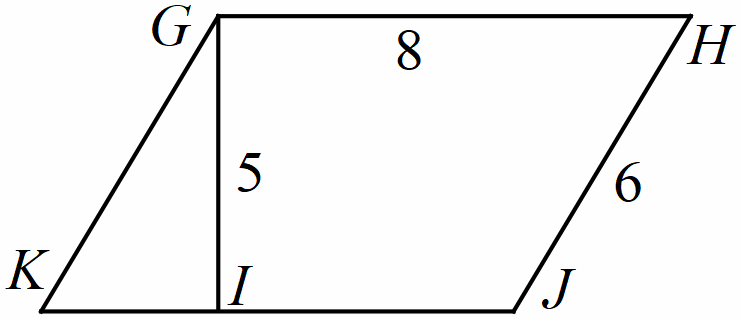
5. Tính diện tích của hình
vuông, biết chu vi của hình vuông đó bằng
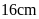 .
.
Hướng dẫn: Tìm cạnh của hình vuông rồi sau đó áp dụng công thức tính diện tích.
Đáp số:
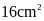
Bài
6. Một hình vuông có chu vi
bằng
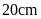 ,
một hình chữ nhật có chiều rộng bằng cạnh hình vuông
và có chu vi
,
một hình chữ nhật có chiều rộng bằng cạnh hình vuông
và có chu vi
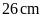 .
Tính diện tích hình chữ nhật?
.
Tính diện tích hình chữ nhật?
Hướng dẫn: Tìm cạnh của hình vuông, chiều rộng của hình chữ nhật, rồi sau đó áp dụng công thức tính diện tích.
Đáp số:
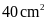
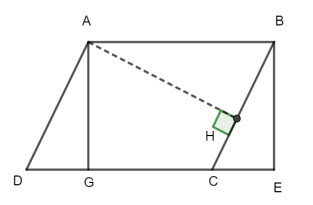
Bài 7. Tính
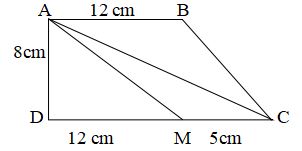
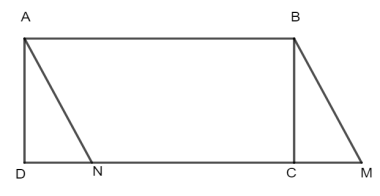
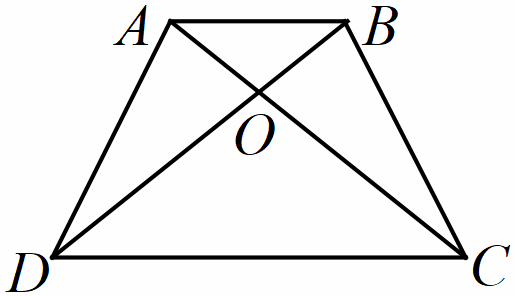
chu vi và diện tích của hình bình hành ABCD (như hình
bên). Biết
Hướng dẫn: Áp dụng công thức tính chu vi, diện tích hình bình hành.
|
Đáp số:
|
|
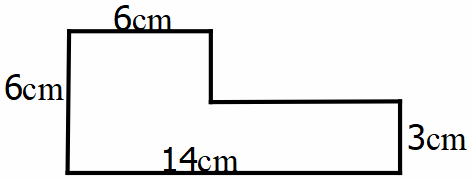
Bài 8. Tính chu vi và diện tích của hồ bơi có kích thước như hình vẽ sau: Hướng dẫn: Áp dụng công thức tính chu vi, diện tích chữ nhật. Có thể chia nhỏ các hình để tính.
|
Đáp số:
|
|
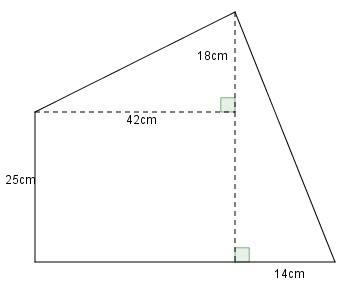
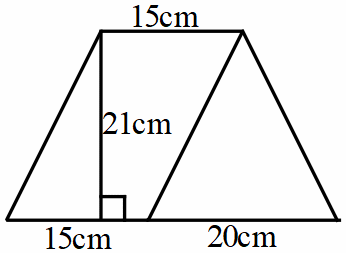
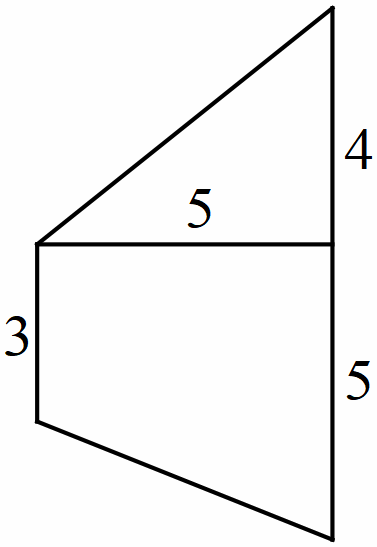
Bài 9. Hình
thang
Hướng dẫn: Áp dụng công thức tính diện tích hình thang, hình tam giác. Lấy diện tích hình thang trừ diện tích tam giác.
|
Đáp số:
|
|
Bài 10. Tính diện tích hình bên: Hướng dẫn: Áp dụng công thức tính diện tích hình thang. |
Đáp số:
|
Bài
11. Tính tổng độ dài hai
đáy của hình thang. Biết diện tích là
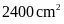 và
chiều cao là
và
chiều cao là
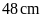 .
.
Hướng
dẫn: Áp dụng công thức
tính diện tích hình thang.
Đáp số:
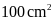
Bài
12. Tìm chiều cao hình
thang. Biết diện tích là
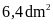 ,
đáy lớn là
,
đáy lớn là
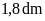 ,
đáy bé là
,
đáy bé là
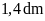 .
.
Hướng
dẫn: Áp dụng công thức
tính diện tích hình thang.
Đáp số:
Bài
13. Cho tam giác
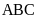 ,
trên
,
trên
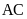 lấy
điểm
lấy
điểm
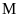 sao
cho
sao
cho
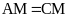 .
Hãy so sánh diện tích hai tam giác
.
Hãy so sánh diện tích hai tam giác
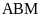 và
và
 .
.
Hướng
dẫn: Áp dụng công thức
tính diện tích hình tam giác. So sánh.
Đáp số:
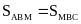
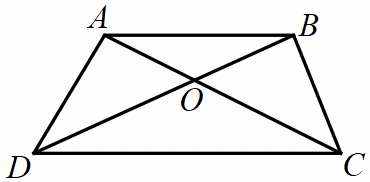
Bài 14. Cho
hình thang
diện
tích tam giác
Hướng dẫn: Áp dụng công thức tính diện tích hình tam giác. So sánh. |
Đáp số:
|
DẠNG 3: Dạng toán nâng cao
C. BÀI TẬP TỰ GIẢI CÓ ĐÁP SỐ.
Bài 1. Hình
vẽ bên gồm hình bình hành
|
Đáp số:
|
Bài 2. Hình
vẽ bên gồm hình chữ nhật
|
Đáp số:
|
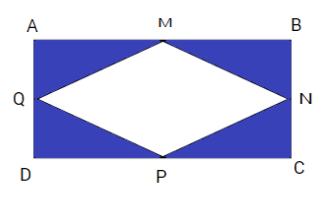
Bài 3. Trung
điểm các cạnh của hình chữ nhật
|
Đáp số:
|
D. BÀI TẬP TRẮC NGHIỆM
Câu 1. Một
hình bình hành có cạnh đáy dài
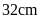 ,
chiều cao là
,
chiều cao là
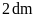 .
Tính diện tích hình bình hành đó:
.
Tính diện tích hình bình hành đó:
A.
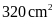 . B.
. B.
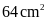 . C.
. C.
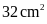 . D.
. D.
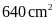 .
.
Câu 2. Chu vi của hình bên là:
A.
C.
|
|
Câu 3.
Một hình thoi có diện tích là
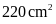 và
độ dài đường chéo lớn là
và
độ dài đường chéo lớn là
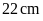 .
Độ dài đường chéo nhỏ là:
.
Độ dài đường chéo nhỏ là:
A.
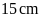 . B.
. B.
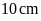 . C.
. C.
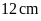 . D.
. D.
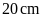 .
.
Câu 4. Hãy cho biết trong các câu sau, câu nào là hình có diện tích lớn nhất:
A. Hình
vuông có cạnh
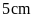 .
.
B.
Hình chữ nhật có chiều dài
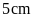 và
chiều rộng
và
chiều rộng
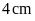 .
.
C.
Hình bình hành có diện tích
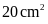 .
.
D.
Hình thoi có độ dài các đường chéo là
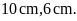
Câu 5: Hình thoi A có độ dài hai đường chéo gấp đôi độ dài hai đường chéo của hình thoi B. Hỏi hình thoi A có diện tích gấp mấy lần diện tích hình thoi B?
A.
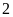 . B.
. B.
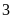 . C.
. C.
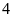 . D.
. D.
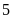 .
.
Câu 6: Một
hình thang có đáy nhỏ là
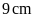 ,
chiều cao là
,
chiều cao là
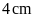 ,
diện tích là
,
diện tích là
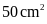 .
Đáy lớn là:
.
Đáy lớn là:
A.
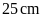 .
B.
.
B.
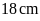 . C.
. C.
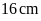 . D.
. D.
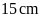 .
.
Câu 7: Diện tích của hình bên là:
A.
C.
|
|
Câu 8: Một
sân chơi hình chữ nhật có chiều dài
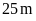 ,
chiều rộng
,
chiều rộng
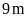 .
Người ta xây một bồn hoa hình vuông cạnh
.
Người ta xây một bồn hoa hình vuông cạnh
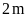 .
Diện tích còn lại của sân chơi là:
.
Diện tích còn lại của sân chơi là:
A.
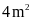 . B.
. B.
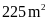 . C.
. C.
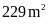 . D.
. D.
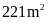 .
.
Câu 9: Trong
tam giác
A.
Cạnh
C.
Cạnh |
|
Câu 10: Tính
diện tích hình tam giác
A.
C.
|
|
§5. ÔN TẬP CHƯƠNG III (tiết 2)
A. KIẾN THỨC CẦN NHỚ
1. Các hình học phẳng trong thực tiễn:
a) T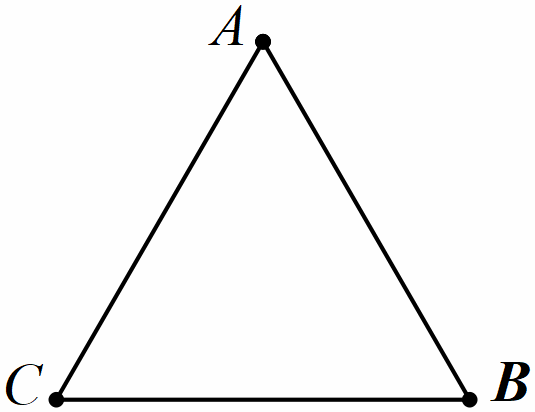 am
giác đều:
am
giác đều:
Tam giác đều ABC có:
- Ba đỉnh A, B, C
- Ba cạnh bằng nhau: AB=AC=BC
- Ba góc đỉnh A, B, C bằng nhau
b) Tứ giác (Hình vuông, hình chữ nhật, hình bình hành, hình thang cân, hình thoi):
Hình vuông Hình vuông ABCD có: - Bốn đỉnh A, B, C, D. - Bốn cạnh bằng nhau: AB=BC=CD=DA - Bốn góc bằng nhau và bằng góc vuông - Hai đường chéo bằng nhau: AC=BD |
|
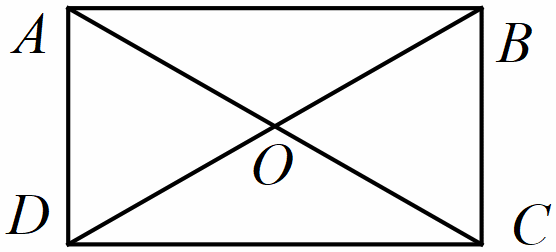
Hình chữ nhật Hình chữ nhật ABCD có: - Bốn đỉnh A, B, C, D. - Hai cặp cạnh đối diện bằng nhau: AB=CD, BC=DA - Hai cặp cạnh đối diện song song với nhau: AB song song với CD, BC song song với DA - Bốn góc bằng nhau và bằng góc vuông - Hai đường chéo bằng nhau và cách nhau tại chung điểm của mỗi đường: AC=BD và OA=OC=OB=OD |
|
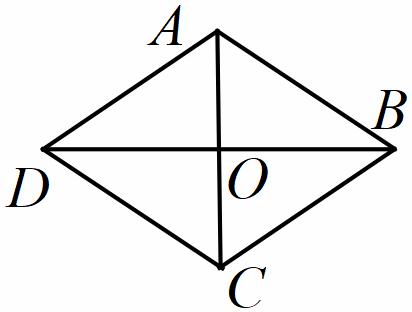
Hình thoi Hình thoi ABCD có: - Bốn đỉnh A, B, C, D. - Bốn cạnh bằng nhau: AB=CD=BC=DA - Hai cặp cạnh đối diện song song với nhau: AB song song với CD, BC song song với DA - Hai đường chéo AC và BD vuông góc với nhau |
|
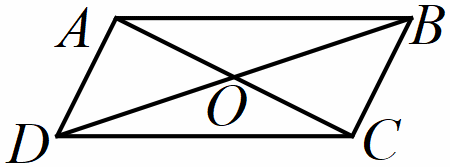
Hình bình hành Hình bình hành ABCD có: - Bốn đỉnh A, B, C, D. - Hai cặp cạnh đối diện bằng nhau: AB=CD, BC=DA - Hai cặp cạnh đối diện song song với nhau: AB song song với CD, BC song song với DA - Hai đường chéo cách nhau tại chung điểm của mỗi đường: OA=OC; OB=OD - Hai góc đối diện bằng nhau: góc đình A bằng góc đỉnh C, góc đỉnh B bằng góc đỉnh D. |
|
Hình thang cân Hình thang cân ABCD có: - Hai đáy song song với nhau: AB song song với CD - Hai cạnh bên bằng nhau: AD = BC - Hai góc kề 1 đáy bằng nhau: Góc đỉnh A bằng góc đỉnh B, góc đỉnh C bằng góc đỉnh D - Hai đường chéo bằng nhau: AC=BD
|
|
c) Lục giác đều :
L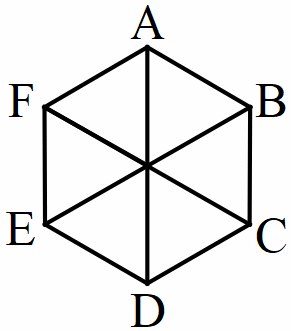 ục
giác đều ABCDÈ có:
ục
giác đều ABCDÈ có:
- Sáu đỉnh A, B, C, D, E, F
- Sáu cạnh bằng nhau:
AB=AC=BC=CD=DE=EF=FA
- Sáu góc đỉnh A, B, C, D, E, F bằng nhau
- Ba đường chéo chính bằng nhau:
AD = BE =CF
2. Công thức tính chu vi diện tích của các hình:
-
Tên
Hình minh họa
Chu vi
Diện tích
Hình vuông

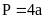
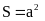
Chữ nhật
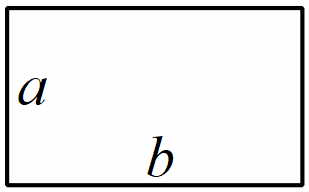
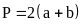
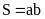
T
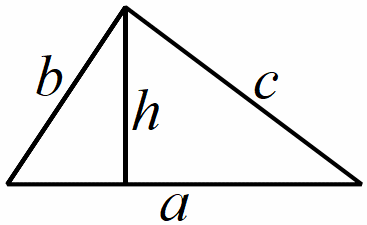 am
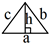
giác
am
giác
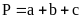
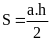
Hình bình hành
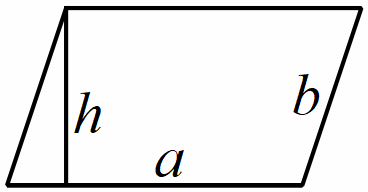
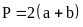
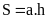
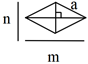
Hình thoi
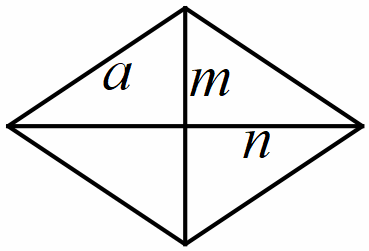
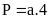
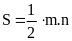
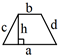
Hình thang
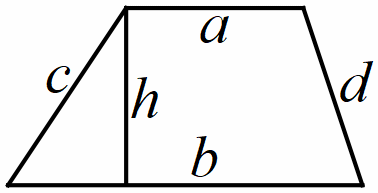
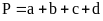
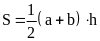
B. BÀI TẬP CÓ HƯỚNG DẪN.
DẠNG 1: Dạng toán nhận biết cạnh, đường chéo của các hình
Bài
1.
Cho
hình vuông
 có
có
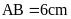 .
Tính độ dài các đoạn thẳng BC,
.
Tính độ dài các đoạn thẳng BC,
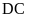 và
và
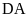 .
.
Hướng
dẫn: Áp
dụng kiến thức của hình vuông. .
Đáp số:
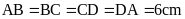
Bài
2.
Cho
lục giác đều
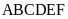 với cạnh
với cạnh
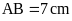 và
đường chéo
và
đường chéo
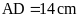 .
.
a) Tính độ dài cạnh BC, CD, DE, EF, FA
b) Tính độ dài đường chéo BE, CF.
Hướng dẫn: Áp dụng các kiến thức của hình lục giác đều. .
Đáp
số:
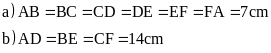
Bài
3. Cho hình thoi
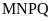 với
với
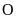 là giao điểm của hai đường chéo. Biết
là giao điểm của hai đường chéo. Biết
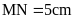 ,
OM = 3cm,
,
OM = 3cm,
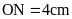 .
Tính độ dài các cạnh và các đường chéo của hình
thoi.
.
Tính độ dài các cạnh và các đường chéo của hình
thoi.
Hướng dẫn: Áp dụng các kiến thức của hình thoi. Đáp số:
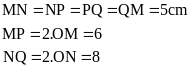
DẠNG 2: Tính chu vi, diện tích
Bài
1. Tính diện tích của hình
vuông, biết chu vi của hình vuông đó bằng
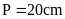 .
.
Hướng
dẫn: Tìm cạnh của hình
vuông rồi sau đó áp dụng công thức tính diện tích.
Đáp số:
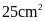
Bài 2. Một hình chữ nhật có chiều dài 8m và chiều rộng 5m. Tính chu vi và diện tích hình chữ nhật đó?
Hướng dẫn: áp dụng công thức tính chu vi và diện tích hình chữ nhật.
Đáp số:
chu vi 26m, diện tích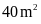
Bài 3. Tính chu vi và diện tích của hình bình hành GHJK (như
hình bên). Biết
Hướng dẫn: Áp dụng công thức tính chu vi, diện tích hình bình hành. |
Đáp số:
|
B
Hướng dẫn: Tính đáy lớn rồi áp dụng công thức tính diện tích hình thang.. |
Đáp số:
|
DẠNG 3: Dựng hình
Bài 1. Dùng thước và compa vẽ tam giác đều có độ dài cạnh 5cm.
Bài 2. Dùng thước và êke vẽ hình vuông có độ dài cạnh 6cm. Dùng compa so sánh độ dài hai đường chéo của hình vuông đó.
Bài
3. Nêu cách vẽ hình chữ
nhật ABCD có
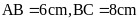
HD: Học sinh tự vẽ hình
DẠNG 4: Bài tập liên quan đến yếu tố phân tích hình
B
Hướng dẫn: Áp dụng công thức tính diện tích hình chữ nhật và hình tam giác. |
Đáp số:
|
B
Hướng dẫn: + Kéo dài đoạn GF tới AB và kéo đài đoạn BC tới EF ta được các hình chữ nhật +Áp dụng công thức tính diện tích hình chữ nhật. |
Đáp số:
|
C. BÀI TẬP TỰ GIẢI CÓ ĐÁP SỐ.
Bài 1. Cho
hình chữ nhật
Đáp số:
|
Bài
2. Tìm đường chéo còn lại
của hình thoi. Biết diện tích là
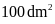 và một đường chéo dài
và một đường chéo dài
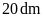 .
.
Đáp số:
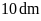
Bài
3. Cho tam giác
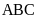 ,
trên
,
trên
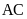 lấy
điểm
lấy
điểm
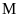 sao
cho
sao
cho
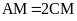 .
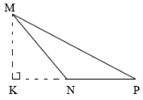
Tính diện tích tam giác AMC biết đường cao
.
Tính diện tích tam giác AMC biết đường cao
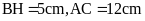
Đáp số:
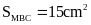
Bài
4. Nêu cách vẽ hình bình
hành MNPQ có
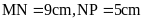
Bài 5. Nêu cách vẽ hình thoi GHJK có cạnh bằng 10 và đường chéo bằng 16
D. BÀI TẬP TRẮC NGHIỆM
Câu 1. Chu vi của hình bên là:
A.
C.
|
|
Câu 2.
Một hình thoi có diện tích là
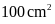 và
độ dài đường chéo lớn là
và
độ dài đường chéo lớn là
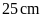 .
Độ dài đường chéo nhỏ là:
.
Độ dài đường chéo nhỏ là:
A.
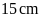 . B.
. B.
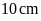 . C.
. C.
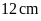 . D.
. D.
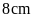 .
.
Câu 3: Công thức tính diện tích hình chữ nhật là:
A.
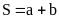 .
B.
.
B.
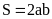 . C.
. C.
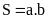 . D.
. D.
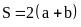 .
.
§ 5: ÔN TẬP CHƯƠNG 3 (Tiết 3)
A. KIẾN THỨC CẦN NHỚ
B. BÀI TẬP CÓ HƯỚNG DẪN.
DẠNG 1: Áp dụng công thức tính chu vi và diện tích
Bài
1. Một
hình thoi có cạnh
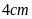 thì chu vi của nó bằng bao nhiêu?
thì chu vi của nó bằng bao nhiêu?
Hướng dẫn: Áp dụng công thức tính chu vi của hình thoi .
Bài
2. Một
hình vuông có chu vi là
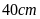 thì cạnh của nó bằng bao nhiêu?
thì cạnh của nó bằng bao nhiêu?
Hướng dẫn: Áp dụng công thức tính chu vi của hình vuông.
Bài
3. Một hình chữ nhật có
chu vi
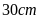 và chiều rộng là
và chiều rộng là
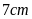 thì chiều dài của nó bằng bao nhiêu?
thì chiều dài của nó bằng bao nhiêu?
Hướng dẫn: Áp dụng công thức tính chu vi của hình chữ nhật.
Bài
4. Tính chu vi và diện
tích của hình bình hành ABCD (như hình bên). Biết rằng
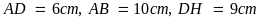
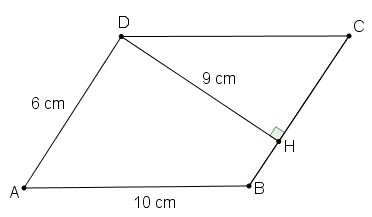
Hướng dẫn:
Áp dụng công thức tính chu vi, diện tích của hình bình hành
Chu
vi của hình bình hành
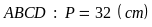
Diện
tích của hình bình hành
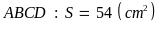
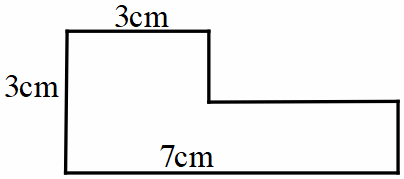
Bài 5. Tính diện tích của hình dưới đây:
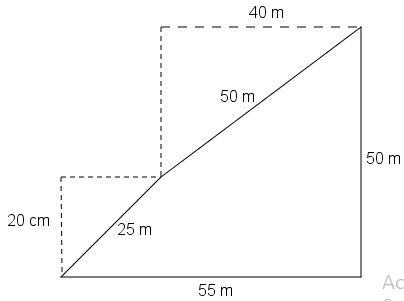
Hướng dẫn:
Chia nhỏ hình thành: tam giác, hình chữ nhật
Áp dụng công thức tính diện tích hình chữ nhật, tam giác
Diện tích cần tìm là
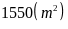
Bài 6. Tính diện tích của hình dưới đây:
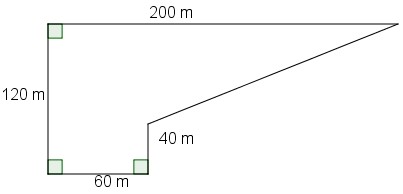
Hướng dẫn:
Chia nhỏ hình thành: tam giác, hình chữ nhật
Áp dụng công thức tính diện tích hình chữ nhật, tam giác
Diện tích cần tìm là
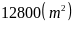
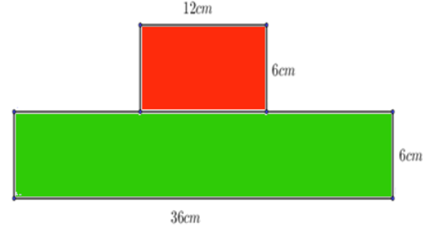
Bài 7. Tính chu vi và diện tích của hồ bơi có kích thước như hình vẽ sau:
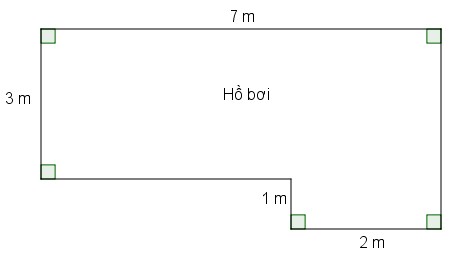
Hướng dẫn:
Chia nhỏ hình thành các hình chữ nhật
Áp dụng công thức tính chu vi, diện tích hình chữ nhật
Diện tích hồ bơi là
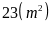
Chu vu hồ bơi
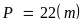
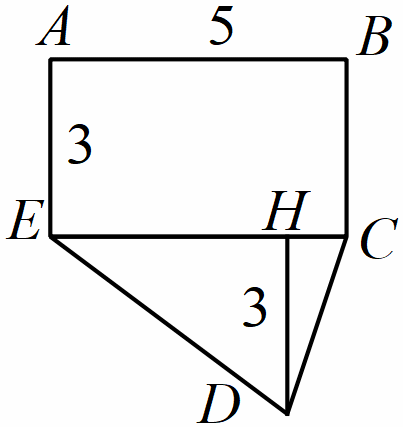
Bài 8. . Tính diện tích của hình dưới đây:
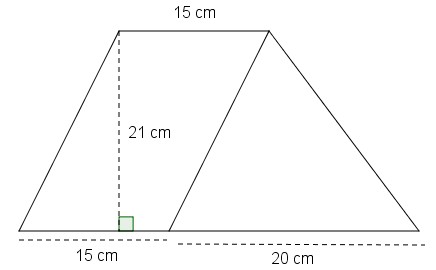
Hướng dẫn:
Áp dụng công thức tính diện tích hình thang
Diện tích cần tìm là:
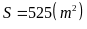
DẠNG 2: Dạng toán có lời văn
Bài
9. Một mảnh vườn hình chữ nhật có
chiều dài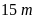 ,
chiều rộng
,
chiều rộng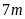 .
Người ta làm các lối đi rộng
.
Người ta làm các lối đi rộng
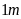 ở giữa vườn, phần đất còn lại để trồng hoa và
cây cảnh. Tính diện tích phần đất để trồng hoa và
cây cảnh.
ở giữa vườn, phần đất còn lại để trồng hoa và
cây cảnh. Tính diện tích phần đất để trồng hoa và
cây cảnh.

Hướng dẫn:
Áp dụng công thức tính diện tích hình chữ nhật
- Diện tích mảnh vườn hình chữ nhật
- Ta có lối đi rộng
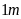 và dài
và dài
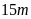
Diện tích lối đi ở giữa vườn
- Diện tích phần đất để trồng hoa và cây cảnh
Đáp
án:
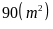
Bài
10. Một mảnh đất
hình chữ nhật có chiều dài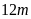 ,
chiều rộng
,
chiều rộng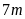 .
Người ta xây một bồn hình thoi để trồng hoa (như hình
vẽ). Tính diện tích phần đất còn lại.
.
Người ta xây một bồn hình thoi để trồng hoa (như hình
vẽ). Tính diện tích phần đất còn lại.

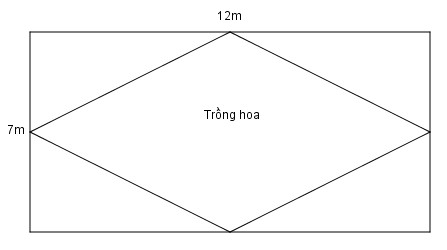
Hướng dẫn:
Áp dụng công thức tính diện tích hình chữ nhật, hình thoi
- Diện tích mảnh đất hình chữ nhật
- Diện tích phần đất trồng hoa
- Diện tích phần đất còn lại
Đáp
án:
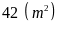
Bài
11. Trên một
thửa đất hình chữ nhật có chiều dài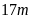 ,
chiều rộng
,
chiều rộng
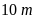 dùng
để ươm cây giống. Người ta chia làm 6 luống dài rộng
như nhau. Xung quanh mỗi luống có lối đi rộng 1m. Tính
diện tích các lối đi xung quanh các luống rau. Biết chiều
rộng có 3 luống chiều dài có 2 luống.
dùng
để ươm cây giống. Người ta chia làm 6 luống dài rộng
như nhau. Xung quanh mỗi luống có lối đi rộng 1m. Tính
diện tích các lối đi xung quanh các luống rau. Biết chiều
rộng có 3 luống chiều dài có 2 luống.

Hướng dẫn:
Áp dụng công thức tính diện tích hình chữ nhật
Vì xung quanh
các luống đều có lối đi rộng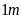 ,
chiều rộng có 3 luống nên có 4 lối đi.
,
chiều rộng có 3 luống nên có 4 lối đi.
Vậy chiều
rộng của thử đất dùng để ươm cây còn lại là:
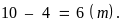
Chiều dài có 2 luống nên có 3 lối đi
Vậy chiều dài
của thửa đất dùng để ươm cây là:
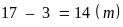
- Diện tích của thửa đất :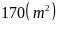
- Diện tích đất ươm cây:
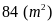
- Diện tích các lối đi
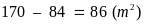
Đáp
án:
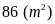
C. BÀI TẬP TỰ GIẢI CÓ ĐÁP SỐ.
Bài 1. Tính diện tích của hình dưới đây:
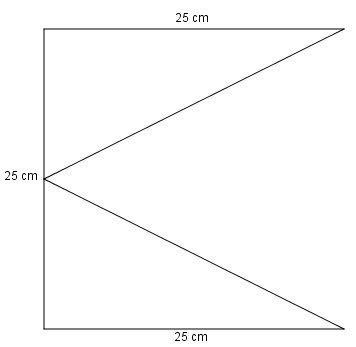
Đáp án:
Bài 2. Tính diện tích của hình dưới đây:
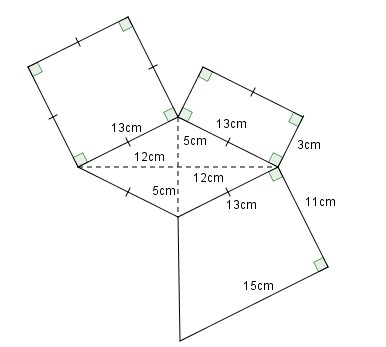
Đáp án:
Bài 3. Tính diện tích của hình dưới đây:
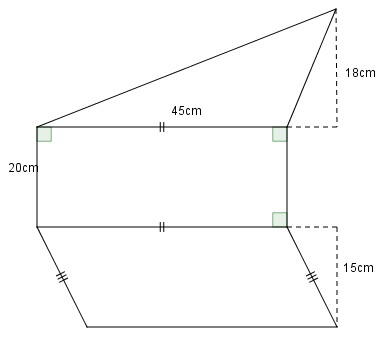
Đáp án:
Bài 4. Một mảnh vườn hình chữ nhật có chiều dài 50m, chiều rộng 40m với lối đi hình bình hành rộng 1m (xem hình bên). Tính diện tích phần mảnh vườn không tính lối đi.
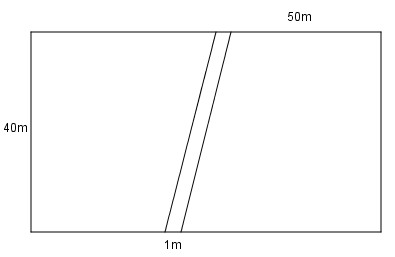
Đáp án:
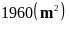
D. BÀI TẬP TRẮC NGHIỆM
Câu 1. Cho hình vẽ như bên dưới:
Biết hình
chữ nhật có diện tích là
 Diện tích của hình tam giác là:
Diện tích của hình tam giác là:
A. 600cm2 B. 750cm2
C. 900cm2. D. 1200cm2.
Đáp án: A
Câu 2. Tính diện tích mảnh đất có kích thước như hình vẽ:
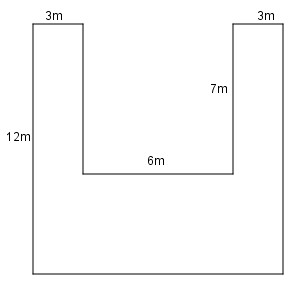
A. 60m2. B. 102m2. C. 132m2. D. 144m2.
Đáp án: B
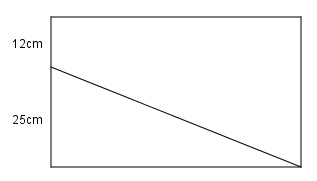
Câu 3. Một miếng bìa có hình dạng như hình vẽ dưới đây. Diện tích miếng bìa đó là:
A. 1200cm2. B. 1700cm2. C. 1729cm2. D. 729cm2.
Đáp án: C
.
.
Ngoài Ôn Tập Chương 3 Các Hình Học Trực Quan Trong Thực Tiễn Toán 6 – Toán 6 Chân Trời Sáng Tạo thì các tài liệu học tập trong chương trình 6 sẽ được cập nhật liên tục và nhanh nhất có thể sau khi kỳ thi diễn ra trên Danh mục Tài Liệu Học Tập nhằm giúp các bạn đọc thuận tiện trong việc nghiên cứu tài liệu. Quý thày cô và các bạn đọc có thể chia sẻ thêm những tài liệu học tập hữu ích đến địa chỉ email của chúng tôi, nhằm xây dựng nên kho đề thi phong phú, đa dạng cho các em học sinh tham khảo và rèn luyện.
Chương 3 của môn học Toán lớp 6 đem lại cho chúng ta một cái nhìn tổng quan về các hình học trực quan và cách chúng áp dụng vào thực tiễn. Đây là một chương quan trọng, vì hình học không chỉ tồn tại trong sách giáo trình mà còn là một phần không thể thiếu trong cuộc sống hàng ngày của chúng ta.
Trong chương này, chúng ta sẽ ôn lại các hình học cơ bản như hình vuông, hình chữ nhật, hình tam giác, và hình tròn. Chúng ta sẽ tìm hiểu về cấu trúc và đặc điểm của mỗi hình, cách tính toán chu vi và diện tích của chúng, cũng như cách áp dụng kiến thức này vào các tình huống thực tế.
Trong thực tế, chúng ta gặp các hình học này hằng ngày. Khi chúng ta xây dựng một ngôi nhà, chúng ta cần tính toán diện tích của mảnh đất, diện tích các phòng, và số lượng vật liệu cần thiết. Khi chúng ta mua sơn để tô lại căn phòng, chúng ta cần biết diện tích của các bức tường để mua đúng lượng sơn cần thiết. Những ví dụ này chỉ là một phần nhỏ trong việc áp dụng hình học vào cuộc sống thực.
>>> Bài viết có liên quan







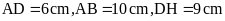
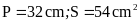
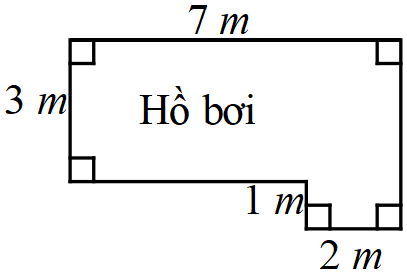
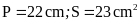
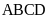
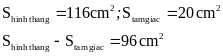
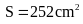
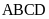
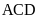
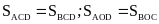
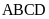 và
hình chữ nhật
và
hình chữ nhật
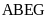 .
Biết
.
Biết
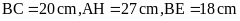 .
Tính chu vi hình chữ nhật
.
Tính chu vi hình chữ nhật
 .
.
 và hình bình hành
và hình bình hành
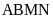 .
Biết chu vi hình chữ nhật
.
Biết chu vi hình chữ nhật
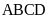 là
là
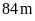 ,
chiều dài hơn chiều rộng
,
chiều dài hơn chiều rộng
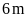 .
Tính diện tích hình bình hành
.
Tính diện tích hình bình hành
 .
.
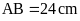
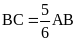
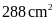
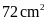
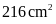
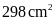 .
.

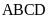
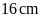
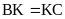
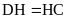
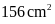
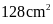
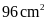
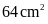 .
.

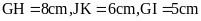
 ài
4.
ài
4. 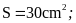
 ài
1.
ài
1. 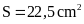
 ài
2.
ài
2.