Giáo Án Bồi Dưỡng HSG Môn Lý 8 Cả Năm
Có thể bạn quan tâm
Giáo Án Bồi Dưỡng HSG Môn Lý 8 Cả Năm là tài liệu học tập được Trang Tài Liệu biên soạn và sưu tầm từ những nguồn dữ liệu mới nhất hiện nay. Tài liệu này sẽ giúp các em luyện tập, củng cố kiến thức từ đó nâng cao điểm số cho môn học. Ngoài ra, cũng giúp các thầy cô giáo có nguồn tài nguyên phong phú để giảng dạy.
Dưới đây là bản đọc trực tuyến giúp thầy cô và các em học sinh có thể nghiên cứu Online hoặc bạn có thể tải miễn phí với phiên bản word để dễ dàng in ấn cũng như học tập Offline.
Tuần 02:
Ngày soạn: 10/9/2019
Ngày dạy: 13/9/2019
Tiết: 1+2+3
CHỦ ĐỀ CƠ HỌC
PHẦN I: CHUYỂN ĐỘNG CƠ HỌC
I. MỤC TIÊU:
1. Kiến thức: HS nắm chắc được các kiến thức cơ bản về:
- Chuyển động cơ học; CĐ trên cạn (cùng chiều, ngược chiều), CĐ trên sông nước;
- Chuyển động đều; Chuyển động không đều.
2. Kỹ năng:
- Bước đầu làm quen với các bài tập về chuyển động
- Thu thập và sử lí thông tin.
3. Thái độ: Rèn tính độc lập, tính tập thể, tinh thần tự giác trong học tập.
4. Năng lực cần đạt:
- Phát triển năng lực tự học , tự tìm hiểu.
- Phát triển năng lực phát hiện và giải quyết vấn đề.
II. PHƯƠNG PHÁP: Nêu và giải quyết vấn đề. vấn đáp gợi mở, thuyết trình
III. CHUẨN BỊ:
1. Giáo viên:
- Giáo án, SGK, thước.
2. Học sinh:
- Đọc lại bài Vật lí đã học trong chương trình Lí 8. Ôn lại các công thức đã học.
IV. QUÁ TRÌNH TỔ CHỨC CÁC HOẠT ĐỘNG CHO HỌC SINH:
A. TÓM TẮT KIẾN THỨC CƠ BẢN
I. Định nghĩa chuyển động cơ học
- Sự thay đổi vị trí của vật so với vật khác theo thời gian gọi là chuyển động cơ học
- Một vật được gọi là đứng yên so với vật này, nhưng lại là chuyển động so với vật khác. Đối với vật này thì chuyển động nhanh, nhưng đối với vật kia thì chuyển động chậm.
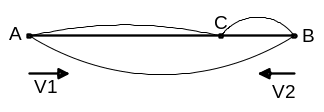
- Xét hai vật A và B cùng tham gia chuyển động.
1. Chuyển động của vật A và B khi ở trên cạn
- Vận tốc của vật A và vật B so với vật làm mốc gắn với trái đất lần lượt là v1 và v2 và v12 là vận tốc của vật A so với vật B và ngược lại.
a) Chuyển động cùng chiều
N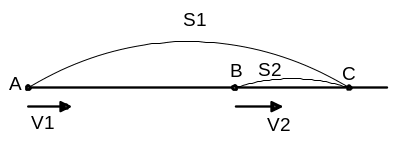 ếu
hai vật chuyển động cùng chiều thì khi gặp nhau thì
hiệu quãng đường hai vật đã đi bằng khoảng cách ban
đầu giữa hai vật
ếu
hai vật chuyển động cùng chiều thì khi gặp nhau thì
hiệu quãng đường hai vật đã đi bằng khoảng cách ban
đầu giữa hai vật
sAB = s1 - s2
v12
=
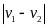
b) Chuyển động ngược chiều
N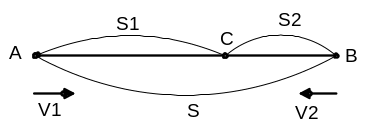 ếu
hai vật chuyển động ngược chiều thì khi gặp nhau
tổng quãng đường
hai vật đã đi bằng khoảng cách ban đầu giữa hai vật
ếu
hai vật chuyển động ngược chiều thì khi gặp nhau
tổng quãng đường
hai vật đã đi bằng khoảng cách ban đầu giữa hai vật
sAB = s1+ s2
v12 = v1 + v2
2. Chuyển động của vật A và vật B trên sông
- Vận tốc của ca nô là v1, dòng nước là v2 thì v12 là vận tốc của ca nô so với bờ (Bờ gắn với trái đất)
a) Chuyển động cùng chiều ( Xuôi theo dòng nước)
v12 = v1 + v2 ( Hoặc v = vvật + vnước)
b) Chuyển động ngược chiều( Vật chuyển động ngược dòng nước)
v12 = v1 - v2 ( Hoặc v = vvật - vnước)
* Chú ý chuyển động trên cạn nếu một vật chuyển động là gió thì ta cũng vận dụng công thức như trên sông.
II. Chuyển động đều
- Vận tốc của một chuyển động đều được xác định bằng quãng đường đi được trong một đơn vị thời gian và không đổi trên mọi quãng đường đi
![]() với s: Quãng đường đi
với s: Quãng đường đi
t: Thời gian vật đi quãng đường s
v: Vận tốc
III. Chuyển động không đều
- Vận tốc trung bình của chuyển động không đều trên một quãng đường nào đó (tương ứng với thời gian chuyển động trên quãng đường đó) được tính bằng công thức:
![]() với
s: Quãng đường đi
với
s: Quãng đường đi
t: Thời gian đi hết quãng đường S
- Vận tốc trung bình của chuyển động không đều có thể thay đổi theo quãng đường đi.
* Chú ý: Khi giải bài tập chuyển động nên sử dụng đơn vị hợp pháp
+ Quãng đường (m); Thời gian (s) thì vận tốc ( m/s)
+ Quãng đường (km); Thời gian (h) thì vận tốc ( km/h)
B. Bài tập
*Bài tập1: Một ô tô đi 5 phút trên con đường bằng phẳng v ới vận tốc 60km/h, sau đó lên dốc 3 phút với vận tốc 40km/h. Coi ô tô chuyển động đều. Tính quãng đường ô tô đi trong cả hai giai đoạn.
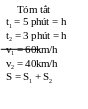
Bài giải
Quãng đường bằng phẳng có độ dài là
Từ
công thức v1
=
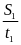
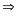 S1
= v1.t1
= 60.
S1
= v1.t1
= 60.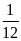 = 5(km)
= 5(km)
Quãng đường bằng phẳng có độ dài là
Từ
công thức v2
=
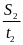
 S2
= v2.t2
= 40.
S2
= v2.t2
= 40.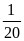 = 2(km)
= 2(km)
Quãng đường ô tô đi trong 2 giai đoạn là
S = S1 + S2 = 5 + 2 = 7(km)
Đáp số S = 7(km)
*Bài tập 2: Từ điểm A đến điểm B một ô tô chuyển động đều với vận tốc v1 = 30km/h. Đến B ô tô quay ngay về A, ô tô cũng chuyển động đều nhưng với vận tốc
v2 = 40km/h. Tính vận tốc trung bình của chuyển động cả đi lẫn về

Bài giải
Thời
gian ô tô đi từ A đến B là t1
=
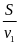 ;
Thời gian ô tô đi từ A đến B là t2
=
;
Thời gian ô tô đi từ A đến B là t2
=
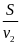
Thời
gian cả đi lẫn về của ô tô là t = t1
+ t2
=
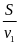 +
+
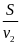
Vận tốc trung bình trên cả đoạn đường cả đi lẫn về là
vtb
=
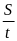 =
=
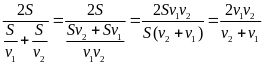
Thay
số ta được vtb
=
 34,3 ( km/h)
34,3 ( km/h)
Đáp
số vtb
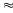 34,3 ( km/h)
34,3 ( km/h)
*Bài tập 3: Một ô tô chuyển động từ địa điểm A đến địa điểm B cách nhau 180 km. Trong nửa đoạn đường đầu xe đi với vận tốc v1 = 45km/h, nửa đoạn đường còn lại xe đi với vận tốc v2 = 30 km/h.
a) Sau bao lâu xe đến B
b) tính vận tốc trung bình của xe trên cả đoạn đường AB
c)
Áp dụng công thức
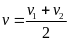 tìm kết quả và so sánh kết quả của câub. từ đó rút
ra nhận xét.
tìm kết quả và so sánh kết quả của câub. từ đó rút
ra nhận xét.
 Bài
giải
Bài
giải
a) Thời gian xe đi nửa quãng đường đầu là
t1
=
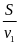 =
=
 = 2(h)
= 2(h)
Thời gian xe đi nửa quãng đường còn lại là
t2
=
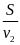 =
=
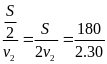 = 3(h)
= 3(h)
Thời gian xe đi hết quãng đường AB là
t = t1 + t2= 2+3 = 5(h)
Vậy từ khi xuất phát thì sau 5 giờ xe mới đến B
b) Vận tốc trung bình của xe là
vtb
=
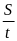 =
=
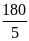 = 36(km/h)
= 36(km/h)
c)
Ta có
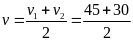 = 37,5(km/h)
= 37,5(km/h)
Ta
thấy v
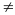 vtb
( 36
vtb
( 36
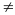 37,5 )
37,5 )
Vậy vận tốc trung bình hoàn toàn khác với trung bình cộng các vận tốc.
C. Bài tập về nhà
*Bài tập 1: Hai người cùng xuất phát 1 lúc từ hai địa điểm A và B cách nhau 60km. Người thứ nhất đi xe máy từ A đến B với vận tốc v1 = 30km/h, người thứ 2 đi xe đạp từ B về A với vận tốc v2 = 10km/h. Hỏi sau bao lâu hai người gặp nhau và xác định vị trí gặp nhau đó. Coi chuyển động của hai xe là đều.
*Bài tập 2: Hai xe ô tô khởi hành cùng một lúc từ hai địa điểm A và B chuyển động về đến địa điểm C. Biết AC = 120km; BC = 96km. Xe khởi hành từ A đi với vận tốc 50km/h, Muốn hai xe đến C cùng một lúc thì xe khởi hành từ B phải chuyển động với vận tốc v2 bằng bao nhiêu?
D. Rút kinh nghiệm
………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………*********************************************
Tuần: 03
Ngày soạn: 14/9/2019
Ngày dạy: 17/9/2019
Tiết : 4+5+6
LUYỆN TẬP BÀI TOÁN CHUYỂN ĐỘNG
I. MỤC TIÊU:
1. Kiến thức: HS được củng cố các kiến thức cơ bản về:
- Chuyển động cơ học; CĐ trên cạn (cùng chiều, ngược chiều), CĐ trên sông nước;
- Chuyển động đều; Chuyển động không đều.
2. Kỹ năng:
- Có kỹ năng trình bày các bài tập về chuyển động
- Thu thập và sử lí thông tin.
3. Thái độ: Rèn tính độc lập, tính tập thể, tinh thần tự giác trong học tập.
4. Năng lực cần đạt:
- Phát triển năng lực tự học , tự tìm hiểu.
- Phát triển năng lực phát hiện và giải quyết vấn đề.
II. PHƯƠNG PHÁP: Nêu và giải quyết vấn đề. vấn đáp gợi mở, thuyết trình
III. CHUẨN BỊ:
1. Giáo viên:
- Giáo án, SGK, thước.
2. Học sinh: Làm các bài tập giao về nhà. Ôn lại các công thức đã học.
IV. QUÁ TRÌNH TỔ CHỨC CÁC HOẠT ĐỘNG CHO HỌC SINH:
A. Chữa bài tập về nhà
 *
Bài tập1
*
Bài tập1
Bài giải
Gọi quãng đường người 1 đo từ A đến điểm gặp nhau C là S1 ( km)
Quãng đường người 2 đi từ B đến C là S2 ( km)
Ta có :Quãng đường người 1 đi được là
S1 = t1. v1
Quãng đường người 2 đi được là
S2 = t2. v2
Mà thời gian hai người đi đến lúc gặp nhau là như nhau
Nên t1 = t2 = t
Mà
S = S1
+ S2
= ( v1
+ v2
) .t Hay S = t . 40
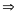 t
=
t
=
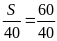 = 1,5
= 1,5
Vậy sau 1,5 ( h) thì hai xe gặp nhau
Chỗ gặp nhau cách A bằng quãng đường S1 = 1,5 . 30 = 45 ( km)
* Bài tập 2
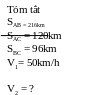
Bài giải
Thời
gian xe thứ nhất đi từ A đến C là t1
=
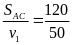 = 2,4(h)
= 2,4(h)
Muốn hai xe đến C cùng một lúc. Do hai xe xuất phát cùng một lúc, nên thời gian xe 2 đi từ B đến C bằng thời gian xe 1 đi từ A đến C
Do đó ta có t = t1 = t2 = 2,4 ( h)
Vậy
vận tốc của xe 2 là v2
=
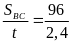 = 40(km/h)
= 40(km/h)
B. Bài tập luyện tập
* Bài tập1: Đổi vận tốc v1 = 5m/s ra km/h và vận tốc v2 = 36km/h ra m/s. Từ đó so sánh độ nhanh, chậm của hai chuyển động có vận tốc nói trên
Bài giải
Ta
biết 1m =
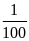 km
= 0,001km 1km = 1000m
km
= 0,001km 1km = 1000m
1s
=
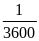 h = 0,00028 s 1h = 3600s
h = 0,00028 s 1h = 3600s
Vậy:
v1
= 5m/s = 5.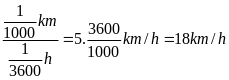
V2
= 36km/h = 36.
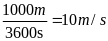
Ta
có v1
= 5m/s
 V2
= 36km/h = 10m/s
V2
= 36km/h = 10m/s
Vậy v1 > v2 nên chuyển động 2 nhanh hơn chuyển động 1.
* Bài tập2: Một người công nhân đạp xe đều trong 20 phút đi được 3 km.
a) Tính vận tốc của người đó ra m/s và km/h
b) Biết quãng đường từ nhà đến xí nghiệp là 3600m. hỏi người đó đi từ nhà đến xí nghiệp hết bao nhiêu phút
c) Nếu đạp xe liền trong 2 giờ thì người này từ nhà về tới quê mình. Tính quãng đường từ nhà đến quê?
a) Bài giải
Vận
tốc của người công nhân là v =
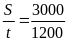
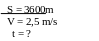 =
2,5m/s = 9km/h
=
2,5m/s = 9km/h
b) Bài giải
Thời gian người công nhân đi từ nhà đến xí nghiệp là
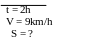 Từ
v =
Từ
v =
 = 1440(s) = 24( phút)
= 1440(s) = 24( phút)
c) Bài giải
Quãng đường từ nhà về quê dài là
Từ
v =
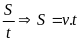 = 9.2 = 18(km)
= 9.2 = 18(km)
* Bài tập 3: Một người đi xe đạp xuống dốc dài 120m. Trong 12 giây đầu đi được 30m, đoạn dốc còn lại đi hết 18 giây. Tính vận tốc trung bình:
a) Trên mỗi đoạn dốc b) Trên cả đoạn dốc
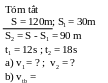 Bài
giải
Bài
giải
a) Vận tốc trung bình trên đoạn dốc thứ nhất là
v1
=
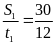 = 2,5( m/s)
= 2,5( m/s)
Vận tốc trung bình trên đoạn dốc còn lại là
v2
=
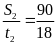 = 5(m/s)
= 5(m/s)
b) Vận tốc trung bình trên cả đoạn dốc là
vtb
=
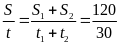 = 4( m/s)
= 4( m/s)
* Bài tập 4: Một ô tô lên dốc có vận tốc 40km/h, khi xuống dốc xe có vận tốc 60km/h. Tính vận tốc trung bình của ô tô trong suốt quá trình chuyển động
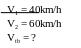
Bài giải
Thời
gian ô tô đi lên dốc là t1
=

Thời
gian ô tô đi lên dốc là t2
=
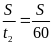
Vận tốc trung bình trên suốt quá trình lên dốc v à xuống dốc là
Vtb
=
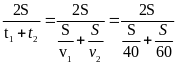 = 48(km/h)
= 48(km/h)
* Bài tập: Một đầu tầu di chuyển trong 10 giờ. Trong 4 giờ đầu tầu chạy với vận tốc trung bình 60km/h; trong 6 giờ sau tầu chạy với vận tốc trung bình 50km/h. Tính vận tốc trung bình của đoàn tầu trong suốt thời gian chuyển động.
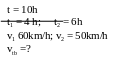 Bài
giải
Bài
giải
Quãng đường tầu đi trong 4 giờ đầu là
S1 = v1.t1 = 60.4 = 240(km)
Quãng đường tầu đi trong 6giờ sau là
S2 = v2.t2 = 50.6 = 300(km)
Vận tốc trung bình của đoàn tầu trong suất thời gian chuyển động là
Vtb
=
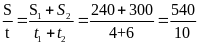 = 54( km/h)
= 54( km/h)
C. Bài tập về nhà
Bài tập1: Hai thành phố A và B cách nhau 300km. Cùng một lúc ô tô xuất phát từ A đến B với vận tốc 55 km/h, xe máy chuyển động từ B về A với vận tốc 45 km/h
a) Sau bao lâu hai xe gặp nhau
b) Nơi gặp nhau cách A bao nhiêu km
Bài tập2: Một HS chạy từ nhà ga tới một trường học với vận tốc 12 km/h. Một HS khác cũng chạy trên quãng đường đó với vận tốc 5km/h. Hai bạn cùng khởi hành một lúc nhưng một bạn đến trường lúc 7h54 ph còn bạn kia đến trường lúc 8h06ph (và bị muộn). Tính quãng đường từ nhà ga đến trường.
D. Rút kinh nghiệm
………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………*********************************************
Tuần :04
Ngày soạn: 20/9/2019
Ngày dạy: 24/9/2019
Tiết: 7+8+9
LUYỆN TẬP TOÁN CHUYỂN ĐỘNG (tiếp)
I. MỤC TIÊU:
1. Kiến thức: HS tiếp tục được củng cố các kiến thức cơ bản về:
- Chuyển động cơ học; CĐ trên cạn (cùng chiều, ngược chiều), CĐ trên sông nước;
- Chuyển động đều; Chuyển động không đều.
2. Kỹ năng:
- Có kỹ năng trình bày các bài tập về chuyển động
- Thu thập và sử lí thông tin.
3. Thái độ: Rèn tính độc lập, tính tập thể, tinh thần tự giác trong học tập.
4. Năng lực cần đạt:
- Phát triển năng lực tự học , tự tìm hiểu.
- Phát triển năng lực phát hiện và giải quyết vấn đề.
II. PHƯƠNG PHÁP: Nêu và giải quyết vấn đề. vấn đáp gợi mở, thuyết trình
III. CHUẨN BỊ:
1. Giáo viên:
- Giáo án, SGK, thước.
2. Học sinh: Làm các bài tập giao về nhà. Ôn lại các công thức đã học.
IV. QUÁ TRÌNH TỔ CHỨC CÁC HOẠT ĐỘNG CHO HỌC SINH:
A. Chữa bài tập về nhà
* Bài tập 1
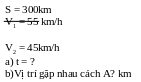 Bài
giải
Bài
giải
Quãng đường mà ô tô đi đến khi gặp nhau là
S1 = v1.t1 = 55 .t1
Quãng đường mà xe máy đi đến khi gặp nhau là
S2 = v1.t2 = 45 .t2
Do hai xe chuyển động ngược chiều gặp nhau
nên ta có S = S1 + S2
Hay 300 = 55 .t1 + 45t2
Mà thời gian hai xe đi đến khi gặp nhau là bằng nhau nên
t1
= t2
= t Suy ra 300 = 55 .t + 45t = 100t
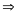 t = 3(h)
t = 3(h)
Vậy sau 3 giờ thì hai xe gặp nhau
b) Vị trí gặp nhau cách A một khoảng bằng quãng đường mà ô tô đi cho đến khi gặp nhau nên ta có S1 = v1.t1 = 55 .t1 = 55 . 3 = 165(km)
* Bài tập2
 Bài giải
Bài giải
Gọi thời gian HS1 đi đến trường là ta ( h) của HS2 là tb ( h)
ta > tb và ta >0 ; tb >0
Thời
gian HS1 đi từ nhà ga đến trường là ta
=
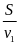
Thời
gian HS2 đi từ nhà ga đến trường là tb
=
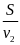
Do
HS1 đến trường lúc t1
= 7h 54ph; HS 2 đến trường lúc t2
= 8h06ph,
nên
thời gian HS1 đến trường sớm hơn HS 2 là 12 phút =
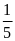 (h)
(h)
Do
đó ta
+
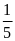 = tb
Hay
= tb
Hay
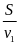 +
+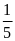 =
=
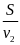
 +
+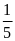 =
=
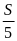
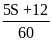 =
=
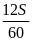
 12
= 7S
12
= 7S
 S = 1,7(km)
S = 1,7(km)
Vậy quãng đường từ nhà ga đến trường dài 1,7 (km)
II. Bài tập luyện tập
* Bài tập1: Một vật xuất phát từ A chuyển động đều về B cách A là 240m với vận tốc 10m/s. Cùng lúc đó một vật khác chuyển động đều từ B về A, sau 15 giây 2 vật gặp nhau. Tìm vận tốc của người thứ 2 và vị ytí gặp nhau?
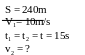 Bài
giải
Bài
giải
Quãng đường vật 1 đi đến lúc gặp nhau là
S1 = v1 .t1= 10.15 = 150(m)
Quãng đường vật 2 đi đến lúc gặp nhau là
S2 = v2 .t2 = v2 .15 = 15v2 (m)
Do hai vật chuyển động ngược chiều để gặp nhau nên ta có
S = S1 + S2
Hay
240 = 150 + 15v2
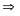 v2
= 6(m/s)
v2
= 6(m/s)
Vậy vận tốc của người 2 là 6(m/s)
Vị trí gặp nhau cách A là 150(m)
* Bài tập 2: Hai xe cùng khởi hành lúc 8h từ 2 địa điểm A và B cách nhau 100km. Xe 1 đi từ A về B với vận tốc 60km/h. Xe thứ 2 đi từ B về A với vận tốc 40km/h. Xác định thời điểm và vị trí 2 xe gặp nhau.
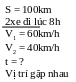 Bài
giải
Bài
giải
Quãng đường xe 1 đi từ A đến lúc gặp xe 2 là
S1 = v1 .t1= 60.t1
Quãng đường xe 2 đi từ A đến lúc gặp xe 1 là
S2 = v2 .t2 = 40 .t2
Do hai xe chuyển động ngược chiều gặp nhau nên ta có
S = S1 + S2
Hay
60.t1
+40 .t2
= 100 Mà t = t1
= t2
Nên 60t + 40t = 100 t = 1(h)
t = 1(h)
Vậy sau 1(h) hai xe gặp nhau và lúc gặp nhau là 8 (h) khi đó vị trí 2 xe gặp nhaucách A một khoảng
S1 = v1 .t1= 60. 1 = 60( km)
* Bài tập 3
Lúc 10 giờ hai xe máy cùng khởi hành từ hai địa điểm A và B cách nhau 96 km và đi ngược chiều nhau. Vận tốc xe đi từ A là 36km/h của xe đi từ B là 28km/h
a) Xác định vị trí và thời điểm hai xe gặp nhau
b) Sau bao lâu thì hai xe cách nhau 32 km kể từ lúc gặp nhau
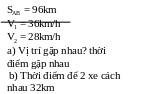 Bài
giải
Bài
giải
Quãng đường xe đi từ A đến khi gặp nhau là
S1 = v1.t1 = 36.t1
Quãng đường xe đi từ B đến khi gặp nhau là
S2 = v2.t2 = 28.t2
Do 2 xe chuyển động ngược chiều gặp nhau
nên ta có: S = S1 + S2 Hay 96 = 36.t1+28.t2
Mà thời gian 2 xe chuyển động đến khi gặp nhau là bằng nhau nên t = t1 = t2
Nên
ta có 96 = 36.t+28.t = 64t
 t = 1,5(h)
t = 1,5(h)
Vậy sau 1,5(h) thì 2 xe gặp nhau và lúc gặp nhau là 10 + 1,5 = 11,5 ( h)
Khi đó vật đi từ A đến khi gặp nhau đã đi được quãng đường là
S1 = v1.t1 = 36. 1,5 = 54(km)
Vậy vị trí gặp nhau cách A là 54 ( km) và cách B là 42(km)
b) Sau khi gặp nhau lúc 11,5(h). Để hai xe cách nhau 32km thì
Xe I đi được quãng đường là S/1 = v1.t/1
Xe II đi được quãng đường là S/2 = v2.t/2
Mà S/1 + S/2 = 32 và t/1 = t/2 =t/
Nên ta có 32 = v1.t/1 + v2.t/2 hay 32 = 36.t/1 +28.t/2
Giải ra tìm được t/ = 0,5(h)
Vậy sau lần gặp thứ nhất để hai xe cách nhau 32 km thì hai xe cùng đi với thời gian là 0,5(h) và lúc đó là 11,5 + 0,5 = 12(h)
* Bài tập 4: Một động tử xuất phát từ A chuyển động thẳng đều về B cách A là 120m với vận tốc 8m/s. Cùng lúc đó 1 động tử khác chuyển động thẳng đều từ B về A. Sau 10 giây hai động tử gặp nhau. Tính vận tốc của động tử 2 và vị trí hai động tử gặp nhau.
Bài giải
Quãng đường động tử 1 đi từ A đến khi gặp nhau là
S1 = v1.t1 = 8.10 = 80(m)
 Quãng đường động tử 2 đi từ B đến khi gặp nhau
là
Quãng đường động tử 2 đi từ B đến khi gặp nhau
là
S2 = v2.t2 =10.t2
Do hai động tử chuyển động ngược chiều gặp nhau nên
S = S1 + S2 Hay 120 = 80+10.v2
Giải ra tìm được v2 = 4(m/s)
Vị trí gặp nhau cách A một đoạn đúng bằng quãng đường động tử 1 đi được đến khi gặp nhau và bằng 80m
Đáp số:4(m/s) và 80m
*
Bài tập 5:
Hai vật xuất phát từ A đến B, chuyển động cùng chiều
theo hướng A B.
Vật thứ nhất chuyển động từ A với vận tốc 36km/h,
vật thứ 2 chuyển động đều từ B với v ận tốc
18km/h. Sau bao lâu hai vật gặp nhau? Chỗ gặp nhau cách
A?km
B.
Vật thứ nhất chuyển động từ A với vận tốc 36km/h,
vật thứ 2 chuyển động đều từ B với v ận tốc
18km/h. Sau bao lâu hai vật gặp nhau? Chỗ gặp nhau cách
A?km
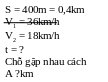 Bài
giải
Bài
giải
Quãng đường xe đi từ A đến khi gặp nhau là
S1 = v1. t1 = 36.t1
Quãng đường xe đi từ B đến khi gặp nhau là
S2 = v2 .t2= 18. t2
Do 2 xe chuyển động ngược chiều nê ta có
S = S1 - S2 và t1 = t2 = t
0,4 = 36.t1 - 18. t2
Giải
ra tìm được t =
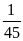 h
= 80(s)
h
= 80(s)
Vậy
vị trí gặp nhau cách A là S1
= v1.
t1
= 36.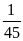 = 0,8(km) = 800(m)
= 0,8(km) = 800(m)
C. Bài tập về nhà
* Bài tập1: Cùng một lúc 2 xe xuất phát từ 2 địa điểm A và B cách nhau 60km, chúng chuyển động thẳng đều và cùng chiều từ A đến B. Xe thứ nhất đi từ A với vận tốc 30km/h, xe thứ hai đi từ B với vận tốc 40km/h
a) Tìm khoảng cách giữa 2 xe sau 30 phút kể từ lúc xuất phát
b) Hai xe có gặp nhau không? Tại sao?
c) Sau khi xuất phát 1h. Xe thứ nhất ( Đi từ A) tăng tốc và đạt tới vận tốc 50km/h. Hãy xác định thời điểm 2 xe gặp nhauvà vị trí chúng gặp nhau?
* Bài tập2: Cùng một lúc có 2 xe xuất phát từ 2 địa điểm A và B cách nhau 60km, chúng chuyển động cùng chiều từ A đến B. Xe thứ nhất đi từ A v ới vận tốc 30km/h, xe thứ 2 đi từ Bvới vận tốc 40km/h( Cả 2 xe chuyển động thẳng đều)
a) Tính khoảng cách 2 xe sau 1 giờ kể từ lúc xuất phát
b) Sau khi xuất phát được 1h30ph xe thứ nhất đột ngột tăng tốc và đạt tới vận tốc 50km/h. Hãy xác định thời điểm và vị trí 2 xe gặp nhau.
D. Rút kinh nghiệm
………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………
******************************
Tuần :05
Ngày soạn: 28/9/2019
Ngày dạy: 01/10/2019
Tiết: 10+11+12
LUYỆN TẬP TOÁN CHUYỂN ĐỘNG (tt)
I. MỤC TIÊU:
1. Kiến thức: HS tiếp tục được củng cố các kiến thức cơ bản về:
- Chuyển động cơ học; CĐ trên cạn (cùng chiều, ngược chiều), CĐ trên sông nước;
- Chuyển động đều; Chuyển động không đều.
2. Kỹ năng:
- Có kỹ năng trình bày các bài tập về chuyển động
- Thu thập và sử lí thông tin.
3. Thái độ: Rèn tính độc lập, tính tập thể, tinh thần tự giác trong học tập.
4. Năng lực cần đạt:
- Phát triển năng lực tự học , tự tìm hiểu.
- Phát triển năng lực phát hiện và giải quyết vấn đề.
II. PHƯƠNG PHÁP: Nêu và giải quyết vấn đề. vấn đáp gợi mở, thuyết trình
III. CHUẨN BỊ:
1. Giáo viên:
- Giáo án, SGK, thước.
2. Học sinh: Làm các bài tập giao về nhà. Ôn lại các công thức đã học.
IV. QUÁ TRÌNH TỔ CHỨC CÁC HOẠT ĐỘNG CHO HỌC SINH:
A. Chữa bài về nhà
* Bài tập1 Bài giải
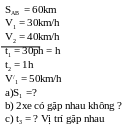 Sau
30ph xe đi từ A đi được quãng đường
Sau
30ph xe đi từ A đi được quãng đường
S1 = v1 .t1 = 30.0,5 = 15(km)
Sau 30 ph xe đi từ B đi được quãng đường
S2 = v2 .t1= = 40.0,5 = 20(km)
Sau 30 phút hai xe cách nhau
S = SAB - S1 + S2 = 60-15+20 =65(km)
b) Do xe 1 đi sau xe 2 mà v1 < v2 nên 2 xe không
gặp nhau
c) Sau 1h 2 xe đi được quãng đường là
Xe1: S/1 = v1 .t2 = 30.1 =30(km)
Xe 2: S/2 = v2 .t2 = 40.1 = 40(km)
Khoảng cách giữa 2 xe lúc đó là
S/ = SAB - S/1 +S/2 = 60 - 30 +40 = 70(km)
Sau 1 h xe 1 tắng vận tốc đạt tới V/1 = 50km/h. Gọi t là thời gian 2 xe đi đến lúc gặp nhau
Quãng đường 2 xe đi đến lúc gặp nhau là
Xe1: S//1 = v/1 .t = 50.t (km)
Xe 2: S//2 = v/2 .t = 40.t (km
Do 2 xe chuyển động cùng chiều gặp nhau nên ta có
S/ = S//1 - S//2 Hay 70 = 50.t - 40.t
Giải ra tìm được t = 7(h)
Vậy sau 7h kể từ lúc tăng tốc thì 2 xe gặp nhau
Vị trí gặp nhau cách A một khoảng
L = S//1 + S/1 = 50.t + 30.t2 = 380(km)
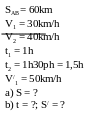 *
Bài tập 2
*
Bài tập 2
Bài giải
Sau 1h 2 xe đi được quãng đường là
Xe1: S1 = v1 .t1 = 30.1 =30(km)
Xe 2: S2 = v2 .t2 = 40.1 = 40(km)
Sau 1h 2 xe cách nhau một khoảng là
S = SAB - S1 + S2 = 60 - 30 +40 = 70(km)
b) Sau 1h30ph hai xe đi được quãng đường là
Xe1: S/1 = v1 .t2 = 30.1,5 = 45(km)
Xe 2: S/2 = v2 .t2 = 40.1,5 = 60(km)
Khoảng cách 2 xe lúc đó là
S/ = SAB - S/1 +S/2 = 60 -45 +60 =75(km)
Sau 1,5h xe 1 tăng tốc tới V/1 = 50km/h . Gọi t là thời gian 2 xe đi đến lúc gặp nhau( Tính từ lúc xe 1 tăng vận tốc)
Quãng đường 2 xe đi đến lúc gặp nhau là
Xe1: S//1 = v/1 .t = 50.t (km)
Xe 2: S//2 = v/2 .t = 40.t (km)
Do 2 xe chuyển động cùng chiều gặp nhau nên ta có
S/ = S//1 = S//2 Hay 75 = 50.t - 40.t
Giải ra tìm được t = 7,5(h)
Vậy sau 7,5h thì hai xe gặp nhau
Khi đó vị trí gặp nhau cách A một khoảng
L = S//1 + S/1 = 50.t + S/1 = 50 .7,5 +45 = 420(km)
B. Bài tập luyện tập
* Bài tập 1: Một người đi từ A chuyển động thẳng đều về B cách A một khoảng 120m với vận tốc 8m/s. Cùng lúc đó người 2 chuyển động thẳng đều từ B về A. Sau 10 giây 2 người gặp nhau. Tính vận tốc của người thứ 2 và vị trí 2 người gặp nhau.
 Bài
giải
Bài
giải
SAB
=120m V1
= 8m/s t
= 10s v2
= ? Vị
trí gặp nhau? 
Người 1: S1 = v1 .t = 50.t = 8.10 = 80(m)
Người 2: S2 = v2 .t = v2 .10 = 10v2(m)
Khi 2 vật gặp nhau ta có
SAB= S1 + S2 hay 120 = 80 +10v2
Giải ra tìm được v2 = 4(m/s)
Vậy người thứ hai có vận tốc v2 = 4(m/s) và vị trí gặp nhau cách A một đoạn
L = S1 = 80(m)
*
Bài tập2:
Một người đi xe máy từ A đến B cách nhau 400m. Nửa
quãng đường đầu xe đi trên đường nhựa với vận tốc
v1,
nửa quãng đường còn lại xe chuyển động trên cát nên
có vận tốc v2
=
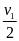 .
Hãy xác định các vận tốc v1
và v2
sao cho sau 1 phút người ấy đến được B.
.
Hãy xác định các vận tốc v1
và v2
sao cho sau 1 phút người ấy đến được B.
 Bài
giải
Bài
giải
Thời gian xe đi trên đường nhựa là
t1
=
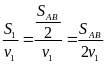
Thời gian xe đi trên đường cát là
t2
=
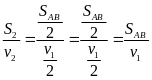
Sau t = 1 phút thì đến được B nê ta có
t
= t1
+ t2
=
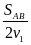 +
+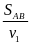 hay 60 =
hay 60 =
 +
+
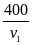
Giải ra tìm được v1 = (10m/s)
Suy ra v2 = (5m/s)
* Bài tập 3: Một người đi xe đạp đi nửa quãng đường đầu với vận tốc 12 km/h và nửa quãng đường còn lại với vận tốc 20km/h. Hãy xác định vận tốc trung bình của người đi xe đạp trên cả quãng đường.
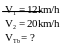 Bài
giải
Bài
giải
Thời gian để đi hết nửa quãng đường đầu là
t1
=
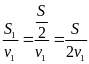
Thời gian để đi hết nửa quãng đường đầu là
t2
=
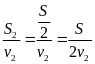
Vận tốc trung bình trên cả đoạn đường là
vTb
=
 =
15(km/h)
=
15(km/h)
* Bài tập 4: Một ô tô chuyển động trên đoạn đường AB dài 120km với vận tốc trung bình 40km/h. Biết nửa thời gian đầu vận tốc của ô tô là 55km/h. Tính vận tốc của ô tô trong nửa thời gian sau. Cho rằng trong các giai đoạn ô tô chuyển động đều.
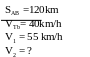 Bài
giải
Bài
giải
Thời gian đô tô đi hết quãng đường là
vTb
=
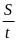
 t =
t =
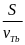 =
=
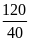 = 3(h)
= 3(h)
Quãng đường ô tô đi trong nửa thời gian đầu là :
S1
= v1.t1
= v1
.
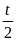 =
55.
=
55.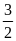 = 82,5(km)
= 82,5(km)
Quãng đường ô tô đi trong nửa thời gian sau là :
S2 = SAB - S1 = 120 - 82,5 = 37,5(km)
Vận tốc của ô tô trong nửa thời gian sau là
V2
=
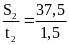 =
25(km)
=
25(km)
* Bài tập 5: Lúc 7h 2 ô tô cùng khởi hành từ 2 địa điểm A và B cách nhau 140km và đi ngược chiều nhau. Vận tốc xe đi từ A là 38km/h. Của xe 2 đi từ B là 30km/h.
a) Tìm khoảng cách giữa 2 xe lúc 9h
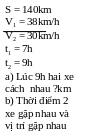 b)
Xác định thời điểm 2 xe gặp nhau và vị trí gặp nhau?
b)
Xác định thời điểm 2 xe gặp nhau và vị trí gặp nhau?
Bài giải
Do 2 xe cùng xuất phát lúc 7h nên tính đến 9h thì 2 xe cùng đi được thời gian là t = t2 - t1 = 2(h)
Sau 2 h xe đi từ A đi được quãng đường
S1 = v1 .t = 38.2 = 76(km)
Sau 2 h xe đi từ B đi được quãng đường
S2 = v2 .t = 30.2 = 60(km)
Sau 2 giờ 2 xe đi được quãng đường là
S/ = S1 +S2 = 76 +36 =136(km)
Và khi đó 2 xe cách nhau là S - S/ = 140 -136 = 4(km)
b) Quãng đường xe đi từ A đến khi gặp nhau là
S/1 = v1. t/ = 38.t/
Quãng đường xe đi từ B đến khi gặp nhau là
S/2 = v2 .t/= 30. t/
Do 2 xe chuyển động ngược chiều nê ta có
S = S/1 + S/2 hay 140 = 38.t/ + 30. t/
Giải
ra tìm được t/ 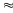 2,06(h)
2,06(h)
Vậy sau gần 2,09(h) thì 2 xe gặp nhau và lúc gặp nhau cách A một khoảng
S/1
= 38.2,06
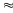 78,3(km)
78,3(km)
Đáp
số:
a)
4km b) 78,3(km)
và
78,3(km)
và
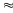 2,06(h)
2,06(h)
C. Bài tập về nhà
* Bài tập1: Một vật chuyển động trên đoạn đường thẳng AB. Nửa đoạn đường đầu với vận tốc v1 = 25km/h. Nửa đoạn đường sau vật chuyển động theo hai giai đoạn. Trong nửa thời gian đầu vật đi với vận tốc v2 = 18km/h, nửa thời gian sau vật đi với vận tốc v3 = 12km/h. Tính vận tốc trung bình của vật trên cả đoạn đường AB
*
Bài tập2:
Một
người đi xe đạp trên đoạn thẳng AB. Trên
 đoạn đường đầu đi với vận tốc 14km/h,
đoạn đường đầu đi với vận tốc 14km/h,
 đoạn đường tiếp theo đi với vận tốc 16km/h,
đoạn đường tiếp theo đi với vận tốc 16km/h,
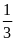 đoạn đường cuối cùng đi với vận tốc 8km/h. Tính vận
tốc trung bình của xe đạp trên cả đoạn đường AB.
đoạn đường cuối cùng đi với vận tốc 8km/h. Tính vận
tốc trung bình của xe đạp trên cả đoạn đường AB.
D. Rút kinh nghiệm
…………………………………………………………………………………………………………………………………………………………………………
Tuần :06
Ngày soạn: 05/10/2019
Ngày dạy: 08/10/2019
Tiết: 13+14+15
LUYỆN TẬP CHỦ ĐỀ 1
VỀ TOÁN CHUYỂN ĐỘNG DƯỚI NƯỚC
I. MỤC TIÊU:
1. Kiến thức: HS tiếp tục được củng cố các kiến thức cơ bản về: Chuyển động cơ học; CĐ trên trên sông nước;
2. Kỹ năng:
- Rèn kỹ năng suy luận và trình bày các bài tập về chuyển động
- Thu thập và sử lí thông tin.
3. Thái độ: Rèn tính độc lập, tính tập thể, tinh thần tự giác trong học tập.
4. Năng lực cần đạt:
- Phát triển năng lực tự học, tự tìm hiểu.
- Phát triển năng lực phát hiện và giải quyết vấn đề.
II. PHƯƠNG PHÁP: Nêu và giải quyết vấn đề. vấn đáp gợi mở, thuyết trình
III. CHUẨN BỊ:
1. Giáo viên:
- Giáo án, SGK, thước.
2. Học sinh: Làm các bài tập giao về nhà. Ôn lại các công thức đã học.
IV. QUÁ TRÌNH TỔ CHỨC CÁC HOẠT ĐỘNG CHO HỌC SINH:
A. Chữa bài về nhà
 *
Bài tập 1: Bài
giải
*
Bài tập 1: Bài
giải
Thời
gian đi nửa đoạn đường đầu là : t1
=
 =
=
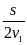
Thời
gian đi với vận tốc v2
và v3
là
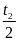
Quãng
đường đi được ứng với các thời gian
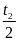 này là s2
= v2
.
này là s2
= v2
.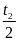 và s3
= v3
.
và s3
= v3
.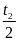
Theo
điều kiện bài ra ta có s2
+ s3
=
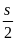
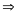 t2
=
t2
=
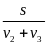
Thời
gian đi hết quãng đường là t = t1
= t2
=
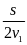 +
+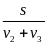 =
=
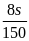
Vận
tốc trung bình trên cả đoạn đường là vTb
=
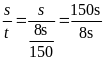 = 18,75(km/h)
= 18,75(km/h)
* Bài tập2: Bài giải
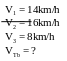 Thời
gian để đi hết
Thời
gian để đi hết
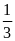 quãng đường liên tiếp là
quãng đường liên tiếp là
t1
=
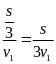 ; t2
=
; t2
=
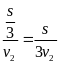 ;
t2
=
;
t2
=
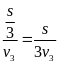
Thời
gian tổng cộng đi hết quãng đường là t = t1
+ t2
+ t3
=
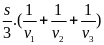
Vận tốc trung bình trên cả quãng đường là
vTb
=
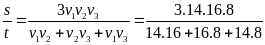 = 11,6(km/h)
= 11,6(km/h)
B. Bài tập luyện tập
* Bài tập1: Một ca nô chạy xuôi dòng sông dài 150km. Vận tốc của ca nô khi nước không chảy là 25km/h, vận tốc của dòng nước chảy là 5km/h. Tính thời gian ca nô đi hết đoạn sông đó.
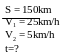 Bài
giải
Bài
giải
Vận tốc thực của ca nô khi đi hết quãng đường xuôi là
v = v1 + v2 = 25 + 5 = 30 (km/h)
Thời gian ca nô đi hết đoạn sông đó là
t
=
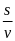 =
=
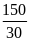 = 5 (h)
= 5 (h)
Đáp số: 5 (h)
* Bài tập2: Một chiếc xuồng chạy trên một dòng sông. Nếu xuồng chạy xuôi dòng từ A đến B thì mất 2 giờ, còn nếu xuồng chạy ngược dòng từ B đến A thì phải mất 6 giờ. Tính vận tốc của xuồng khi nước yên lặng và vận tốc của dòng nước. Biết khoảng cách AB là 120km
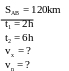 Bài
giải
Bài
giải
Khi xuồng chạy xuôi dòng thì vận tốc thực của xuồng là
v1 = vx + vn
Thời gian xuồng chạy xuôi dòng
t1
=
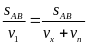
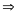 vx
+ vn
=
vx
+ vn
=
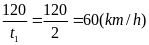 ( 1)
( 1)
Khi xuồng chạy ngược dòng vận tốc thực của xuồng là
v2 = vx - vn
Thời gian xuồng chạy ngược dòng
t2
=
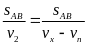
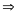 vx
- vn
=
vx
- vn
=
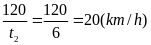 (2)
(2)
Từ (1) suy ra vn = 60 - vx (3)
Thay ( 3) vào (2) ta được vx - 60 + vx = 20
Giải ra tìm được vx = 40(km/h)
Vậy vận tốc của xuồng là 40 ( km/h) vận tốc của nước là
vn = 60 - vx = 60 - 40 = 20 ( km/h)
* Bài tập 3: Hai bến sông AB cách nhau 36 km. Dòng nước chảy từ A đến B với vận tốc 4km/h. Một ca nô chuyển động đều từ A về B hết 1giờ. Hỏi ca nô đi ngược từ B về A trong bao lâu.
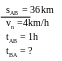
Bài giải
Vận tốc thực của ca nô khi xuôi dòng là
v1 = vcn + vn = vcn + 4 ( km/h)
Ta có quãng đường AB là sAB =v1.t = (vcn +4).tAB
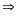 vcn
+ 4 =
vcn
+ 4 =
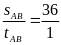
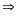 vcn
= 36 -4 =32 (km/h)
vcn
= 36 -4 =32 (km/h)
Khi ngược dòng, vận tốc thực của ca nô là
v2 = vcn - vn = 32-4=28(km/h)
Thời gian ca nô chuyển động ngược dòng là
tBA
=
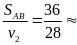 1,2(h)
1,2(h)
C: bài tập về nhà
* Bài tập1: Một chiếc xuồng máy chạy từ bến A đến B cách nhau 120 km. Vận tốc của xuồng khi nước yên lặng là 30 km/h. Sau bao lâu xuồng đến B nếu
a) Nước sông không chảy
b) Nước chảy từ A đến B với vận tốc 5km/h
* Bài tập 2: Một chiếc xuồng khi xuôi dòng mất thời gian t1, khi ngược dòng mất thời gian t2. Hỏi nếu thuyền trôi theo dòng nước trên quãng đường trên sẽ mất thời gian bao lâu?
D. Rút kinh nghiệm
…………………………………………………………………………………………………………………………………………………………………………
****************************
Tuần: 07
Ngày soạn: 12/10/2019
Ngày dạy: 15/10/2019
Tiết: 16+17+18
LUYỆN TẬP CHỦ ĐỀ 1
VỀ TOÁN CHUYỂN ĐỘNG DƯỚI NƯỚC
I. MỤC TIÊU:
1. Kiến thức: HS tiếp tục được củng cố các kiến thức cơ bản về: Chuyển động cơ học; CĐ trên cạn;
2. Kỹ năng:
- Rèn kỹ năng suy luận và trình bày các bài tập về chuyển động
- Thu thập và sử lí thông tin.
3. Thái độ: Rèn tính độc lập, tính tập thể, tinh thần tự giác trong học tập.
4. Năng lực cần đạt:
- Phát triển năng lực tự học, tự tìm hiểu.
- Phát triển năng lực phát hiện và giải quyết vấn đề.
II. PHƯƠNG PHÁP: Nêu và giải quyết vấn đề. vấn đáp gợi mở, thuyết trình
III. CHUẨN BỊ:
1. Giáo viên:
- Giáo án, SGK, thước.
2. Học sinh: Làm các bài tập giao về nhà. Ôn lại các công thức đã học.
IV. QUÁ TRÌNH TỔ CHỨC CÁC HOẠT ĐỘNG CHO HỌC SINH:
A. Chữa bài về nhà
sAB
=120km v1
= 30km/h v2
= 5km/h a)
t1
= ? b)
t2
=?

a) Thời gian đi từ A đến B khi nước không chảy
t1
=
 = 4(h)
= 4(h)
b) Vận tốc thực của xuồng khi xuôi là
v = v1 + v2 = 30 + 5 = 35(km/h)
Thời gian xuồng đi từ A đến B là
t2
=

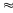 3,4(h)
3,4(h)
* Bài tập2:
Gọi quãng đường là s(km) ( s > 0)
v1; v2 là vận tốc của thuyền đối với nước và của nước đối với bờ ta có.
Khi
xuôi dòng vận tốc thực của thuyền là vx
= v1
+ v2
hay
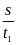 = v1
+ v2
(1)
= v1
+ v2
(1)
Khi
ngược dòng vận tốc thực của thuyền là vn
= v1
- v2
hay
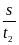 = v1
- v2
(2)
= v1
- v2
(2)
Từ
(1) suy ra
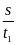 - v2=
v1
( 3)
- v2=
v1
( 3)
Thay
(3) vào (2) ta được
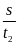 =
=
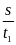 - v2
-
v2
- v2
-
v2
 -2v2
=
-2v2
=
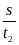 -
-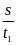
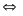 v2
=
v2
=
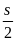 .(
.(
 -
-
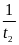 )
)
Vậy
khi trôi theo dòng nước thuyền mất thời gian là t =
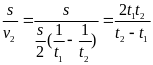
B. Bài tập luyện tập
* Bài tập1: Một người đi xe đạp nửa quãng đường đầu với vận tốc v1 = 15km/h; đi nửa quãng đường còn lại với vận tốc v2 không đổi. Biết các đoạn đường mà người ấy đi là thẳng và vận tốc trung bình trên cả quãng đường là 10km/h. tính vận tốc v2
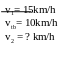 Bài
giải
Bài
giải
Thời
gian đi hết nửa quãng đường đầu là t1
=
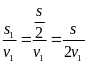 (1)
(1)
Thời
gian đi hết nửa quãng đường đầu là t2
=
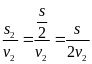 (2)
(2)
Vận
tốc trung bình trên cả quãng đường là : vtb
=
 (3)
(3)
Thay
(1) và (2) vào (3) ta được
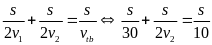
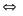 sv2
+ 15s = 3v2s
sv2
+ 15s = 3v2s
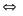 v2
+ 15 = 3v2
v2
+ 15 = 3v2
Giải
ra tìm được
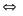 v2
= 7,5
v2
= 7,5
Vậy vận tốc v2 = 7,5( km/h)
* Bài tập 2: Một chiếc thuyền đi ngược dòng sông được 6km, sau đó đi xuôi về điểm xuất phát hết 3 giờ. vận tốc chảy của dòng nước là 1,5 km/h. Tính vận tốc của thuyền trong nước không chảy.
 Bài
giải
Bài
giải
Thời
gian thuyền đi ngược dòng là t1
=
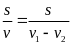
Thời
gian thuyền đi ngược dòng là t2
=
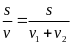
Do thuyền đi hết 3h nên ta có t = t1 + t2
Hay
3=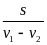 +
+
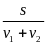
Thay
số ta có 3 = +
+
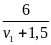 Chia cả hai vế cho 3 ta được
Chia cả hai vế cho 3 ta được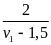 +
+
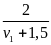 =
1
=
1
 2(
v1
+ 1,5) +2( v1
- 1,5) = ( v1
+ 1,5) ( v1
- 1,5)
2(
v1
+ 1,5) +2( v1
- 1,5) = ( v1
+ 1,5) ( v1
- 1,5)
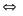 4v1
= v21
- 1,52
4v1
= v21
- 1,52
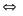 4v1
- v21
+ 1,52
= 0 Nhân cả hai vế với -1 ta được
4v1
- v21
+ 1,52
= 0 Nhân cả hai vế với -1 ta được
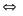 v21
- 4v1
+ 1,52
v21
- 4v1
+ 1,52
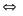 v21
-
4,5 v1
+ 0,5v1
- 2,25 = 0
v21
-
4,5 v1
+ 0,5v1
- 2,25 = 0
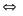 v1(v1
-
4,5 )+ 0,5 ( v1
- 4,5) = 0
v1(v1
-
4,5 )+ 0,5 ( v1
- 4,5) = 0
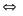 (v1
-
4,5 ) ( v1
+ 0,5) = 0
(v1
-
4,5 ) ( v1
+ 0,5) = 0
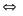 v1
-
4, = 0
v1
-
4, = 0
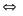 v1
=
4,5 ( Nhận)
v1
=
4,5 ( Nhận)
hoặc
v1
+ 0,5 = 0
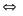 v1
= - 0,5 ( Loại)
v1
= - 0,5 ( Loại)
Vậy vận tốc của thuyền trong nước là v1 = 4,5 (km/h)
* Bài tập 3: Một người đi từ A đến B. Nửa đoạn đường đầu người đó đi với vận tốc v1, nửa thời gian còn lại đi với vận tốc v2, quãng đường cuối cùng đi với vận tốc v3. tính vận tốc trung bình của người đó trên cả quãng đường.
Bài giải
Gọi s(km) là chiều dài cả quãng đường
t1 (h) là thời gian đi nửa đoạn đường đầu
t2 (h) là thời gian đi nửa đoạn đường cuối
( Điều kiện: s; t1; t2 >0)
Thời
gian đi hết nửa quãng đường đầu là t1
=
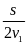
Thời
gian đi với vận tốc v2
là t3
=
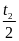 .
Thời gian đi với vận tốc v3
là t4
=
.
Thời gian đi với vận tốc v3
là t4
=
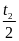
Quãng
đường đi với vận tốc v2
là s2
= v2.t3
= v2.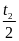
Quãng
đường đi với vận tốc v3
là s3
= v3.t4
= v3.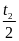
Theo
điều kiện đề bài ta có s1
+ s2
=
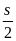
Hay
v2.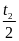 + v3.
+ v3.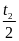 =
=
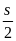 Giải ra tìm được t2
=
Giải ra tìm được t2
=
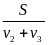
Thời
gian đi hết quãng đường là t = t1
+ t2
=
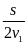 +
+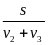
Vậy
vận tốc trung bình là Vtb
=

* Bài tập 4: Một ca nô và một bè thả trôi cùng xuất phát từ A đến B. Khi ca nô đến B lập tức nó quay lại ngay và gặp bè ở C cách A 4km. Ca nô tiếp tục chuyển động về A rồi quay lại ngay và gặp bè ở D. Tính khoảng cách AD biết AB = 20 km
Bài giải
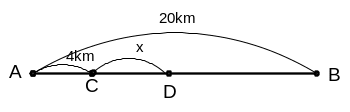
Gọi vận tốc của bè ( Vận tốc dòng nước) là v1 ( km/h); Vận tốc của ca nô so với dòng nước là v2 ( km/h) ; Khoảng cách từ C đến D là x(km)
( Điều kiện:v1; v2; x >0)
Vận tốc thực của ca nô khi xuôi dòng là v2 + v1
Vận tốc thực của ca nô khi ngược dòng là v2 - v1
Đoạn đường ca nô đi từ A đến B là 20 (km)
Đoạn đường từ B đến C là 16 (km)
Thời
gian bè trôi từ A đến C là
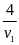
Thời
gian ca nô đi từ A đến B là
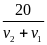
Thời
gian ca nô đi ngược từ B đến C là
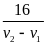
Theo
đề bài ra ta có phương trình
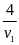 =
=
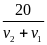 +
+
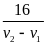 (1)
(1)
Ca
nô đi từ C đến A rồi quay ngược lại trở về đến
điểm D thì hết thời gian là
 +
+
Thời
gian bè trôi từ C đến D là

Theo
bài ra ta có phương trình
 =
=
 +
+
 (2)
(2)
Từ (1) giải ra tìm được v2 = 9v1 ( 3)
Thay (3) vào (2) tìm được x = 1
C. Bài tập về nhà
Hai xe chuyển động thẳng đều từ A đến B cách nhau 60 km và đi liên tục không nghỉ. Xe thứ nhất khởi hành xớm hơn 1 giờ nhưng dọc đường phải ngừng nghỉ 2 giờ. Hỏi xe thứ 2 phải có vận tốc bằng bao nhiêu để đến B cùng một lúc với xe thứ nhất. Biết xe 1 đi với vận tốc 15km/h
D. Rút kinh nghiệm
…………………………………………………………………………………………………………………………………………………………………………
*************************
Tuần: 08
Ngày soạn: 19/10/2019
Ngày dạy: 22/10/2019
Tiết: 19+20+21
LUYỆN TẬP CHỦ ĐỀ 1
I. MỤC TIÊU:
1. Kiến thức: HS tiếp tục được củng cố các kiến thức cơ bản về: Chuyển động cơ học; CĐ trên cạn; CĐ trên sông nước.
2. Kỹ năng:
- Rèn kỹ năng suy luận và trình bày các bài tập về chuyển động
- Thu thập và sử lí thông tin.
3. Thái độ: Rèn tính độc lập, tính tập thể, tinh thần tự giác trong học tập.
4. Năng lực cần đạt:
- Phát triển năng lực tự học, tự tìm hiểu.
- Phát triển năng lực phát hiện và giải quyết vấn đề.
II. PHƯƠNG PHÁP: Nêu và giải quyết vấn đề. vấn đáp gợi mở, thuyết trình
III. CHUẨN BỊ:
1. Giáo viên:
- Giáo án, SGK, thước.
2. Học sinh: Làm các bài tập giao về nhà. Ôn lại các công thức đã học.
IV. QUÁ TRÌNH TỔ CHỨC CÁC HOẠT ĐỘNG CHO HỌC SINH:
A. Chữa bài về nhà
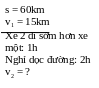 Bài
giải
Bài
giải
Thời gian mà xe 1 đi hết đoạn đường AB là
t1
=
 = 4(h)
= 4(h)
Để đi đến B cùng lúc với xe 1 thì xe 2 mất thời gian là
t2 = 1 + t1 -2 = 1 + 4 - 2 = 3(h)
Vận
tốc của xe 2 là v2
=
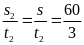 = 20 (km/h)
= 20 (km/h)
Vậy xe 2 phải đi với vận tốc 20km/h thì đến B cùng lúc với xe 1
B: Bài tập luyện tập
* Bài tập1: Một người dự định đi xe đạp trên quãng đường 60km với vận tốc 20km/h. Vì tăng tốc nên người đó đã đến sớm hơn dự định 36 phút. Hỏi người đó đã tăng thêm vận tốc là bao nhiêu?
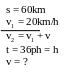 Bài
giải
Bài
giải
Thời gian dự định đi hết quãng đường với vận tốc v1 là
t1
=
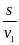
Thời
gian thực tế đã đi là t2
=

Do người đó đến sớm hơn dự định là 36phút nên ta có
t
= t1
- t2
Hay
 -
-
 =
=

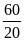 -
-
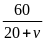 =
=

Giải phương trìnhg tìm được v = 5(km/h)
Vậy vận tốc người đó đã tăng thêm là v = 5(km/h)
* Bài tập 2: Một ca nô chạy từ bến A đến bến B rồi trở về bến A trên một dòng sông. Hỏi nước chảy nhanh hay chảy chậm thì vận tốc trung bình của ca nô trong suốt thời gian cả đi lẫn về sẽ lớn hơn( Coi vận tốc ca nô với so với nước có độ lớn không đổi.)
Bài giải
Gọi vận tốc ca nô là v1 ( km/h), của dòng nước là v2 (km/h); chiều dài quãng đường là s ( Điều kiện: v1 ; v2; s >0)
Vận tốc thực của ca nô khi xuôi dòng là v1 + v2
Vận tốc thực của ca nô khi ngược dòng là v1 - v2
Thời
gian ca nô xuôi dòng từ A đến B là t1
=
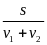
Thời
gian ca nô đi ngược từ B đến A là t2
=

Thời gian ca nô đi từ A đến B rồi lại về A là t = t1 + t2
Hay
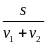 +
+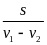 =
=
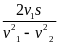
Vận tốc trung bình của ca nô trong cả đoạn đường từ A đến B rồi về A là
vtb
=
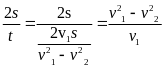
Do đó khi v2 càng lớn ( nước chảy càng nhanh) thì vtb càng nhỏ.
* Bài tập 3: Một người dự định đi xe đạp trên quãng đường 60km với vận tốc v. Nếu tăng vận tốc thêm 5km/h thì xẽ đến sớm hơn dự định 36 phút. Hỏi vận tốc dự định là bao nhiêu?
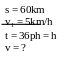 Bài
giải
Bài
giải
Thời gian đi hết quãng đường 60km với vận tốc dự định v là
t1
=
 (h)
(h)
Thời gian đi hết quãng đường 60km với vận tốc thực tế là
t2
=
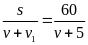 (h)
(h)
Theo
đề bài ta có t = t1
- t2
Hay
 =
=
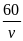 -
-
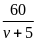 Giải ra ta được v2
+ 5v - 500 = 0
Giải ra ta được v2
+ 5v - 500 = 0
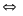 v2
- 20v + 25v - 500 = 0
v2
- 20v + 25v - 500 = 0
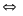 (
v - 20 ) ( v + 25) = 0
(
v - 20 ) ( v + 25) = 0
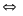 v
- 20 = 0
v
- 20 = 0
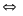 v = 20 ( Thỏa mãn) Hoặc v+25 = 0
v = 20 ( Thỏa mãn) Hoặc v+25 = 0
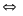 v
= -25 ( Loại)
v
= -25 ( Loại)
Vậy vận tốc dự định của người đó là 20(km/h)
* Bài tập 4: Một người dự định đi bộ một quãng đường với vận tốc 5km/h. Nhưng đi đến đúng nửa đường thì nhờ được bạn đèo xe đạp đi tiếp với vận tốc 12 km/h, do đó đã đến sớm hơn dự định 28 phút. hỏi người ấy đã đi hết toàn bộ quãng đường mất bao lâu?
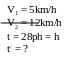 Bài
giải
Bài
giải
Gọi S(km) là chiều dài quãng đường
t1; t2 (h) lần lượt là thời gian đi hết nửa quãng đường đầu
và cuối ( ĐK: S; t1; t2 >0 và t1> t2 )
Thời gian người ấy đi nửa quãng đường đầu với vận tốc
dự
định là: t1
=

Thời
gian người ấy đi nửa quãng đường còn lại với vận
tốc 12km/h là: t2
=
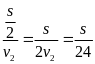
Theo
bài ra ta có phương trình t1
- t2
= t Hay
 -
-
 =
=
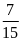
Giải ra tìm được S = 8(km)
Vậy
thời gian người ấy đi hết quãng đường là t/
= t1+t2
=
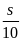 -
-
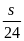 =
=
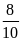 -
-
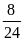 =
=
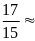 1,1(h)
1,1(h)
Bài
tập 5:
Một người đi từ A đến B. Đoạn đường AB bao gồm
một đoạn lên dốc và một đoạn xuống dốc. Đoạn
lên dốc đi với vận tốc 30km/h, đoạn xuống dốc đi
với vận tốc 50km/h. Thời gian đoạn lên dốc bằng
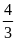 thời gian đoạn xuống dốc.
thời gian đoạn xuống dốc.
a) So sánh độ dài đoạn đường lên dốc với đoạn xuống dốc.
b) Tính vận tốc trung bình trên cả đoạn đường AB.
Bài giải
Gọi s1; s2 lần lượt là độ dài quãng đường lên dốc và xuống dốc
t1; t2 lần lượt là thời gian đi đoạn lên dốc và đoạn xuống dốc ( s1; s2;t1; t2 > 0 và t1> t2 )
a)
Đoạn đường lên dốc là: s1
= v1.t1
= 30t1
Mà
ta có t1
=
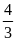 t2
t2
Nên
s1
= 30.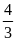 t2
= 40 t2
t2
= 40 t2
Đoạn đường xuống dôc là s2 = v2.t2 = 50.t2
Lập
tỷ số
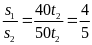 suy ra s1
=
suy ra s1
=
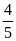 s2
s2
b) Vận tốc trung bình trên đoạn AB là
vtb
=
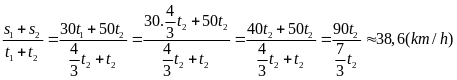
C: Bài tập về nhà
* Bài tập1: Hai bến A và B ở bên một con sông mà nước chảy với vận tốc 1m/s. Một ca nô đi từ A đến B mất 2h30phút và đi từ B về A mất 3h45phút. Biết rằng vận tốc riêng của ca nô ( Tức là vận tốc đối với nước yên lăng) không thay đổi. Hãy tính vận tốc ấy và khoảng cách giữa 2 bến sông.
* Bài tập2: Trong một cuộc đua thuyền trên sông, mỗi thuyền phải đi từ một bến A xuôi xuống tới một cột mốc B, vòng quanh cột đó rồi về A. Vận tốc dòng nước là 2m/s. Một thuyền có vận tốc riêng là 18km/h đã về nhất với tổng thời gian là 1h30phút. Tính khoảng cách AB
D. Rút kinh nghiệm
…………………………………………………………………………………………………………………………………………………………………………
*************************
Tuần: 09
Ngày soạn: 25/10/2019
Ngày dạy: 29/10/2019
Tiết: 22+23+24
CHỦ ĐỀ 2: LỰC VÀ KHỐI LƯỢNG
I. MỤC TIÊU:
1. Kiến thức: HS được củng cố kiến thức cơ bản về: Lực và khối lượng; Áp suất
2. Kỹ năng:
- Rèn kỹ năng suy luận và trình bày các bài tập về Quan hệ giữa khối lượng, trọng lượng, KLR, trọng lượng riêng
3. Thái độ: Rèn tính độc lập, tinh thần tự giác trong học tập.
4. Năng lực cần đạt:
- Phát triển năng lực tự học, tự tìm hiểu.
- Phát triển năng lực phát hiện và giải quyết vấn đề.
II. PHƯƠNG PHÁP: Nêu và giải quyết vấn đề. vấn đáp gợi mở, thuyết trình
III. CHUẨN BỊ:
1. Giáo viên: Giáo án, SGK, thước.
2. Học sinh: Làm các bài tập giao về nhà. Ôn lại các kiến thức đã học về Lực và khối lượng; Áp suất
IV. QUÁ TRÌNH TỔ CHỨC CÁC HOẠT ĐỘNG CHO HỌC SINH:
A. Kiến thức cơ bản cần nhớ
1.1: Lực là một đại lượng có hướng. Muốn xác định lực đầy đủ thì phải có:
+ Điểm đặt
+ Hướng (Phương, chiều)
+ Độ lớn (Cường độ)
*Lưu ý: Khi xác định phương của lực ta phải chỉ rõ
+ Phương thẳng đứng, phương nằm ngang, phương xiên nghiêng bao nhiêu độ (Hợp với phương nào)
+ Chiều từ trái qua phải và ngược lại, từ trên xuống và ngược lại.
+ Riêng phương xiên: Chiều hướng lên trên( Xuống dưới). Từ trái qua phải(Phải qua trái)
1.2: Trọng lực
Là lực hút của trái đất tác dụng lên một vật gọi là trọng lực
1.3: Lực đàn hồi
+Lực do vật bị biến dạng đàn hồi sinh ra gọi là lực đàn hồi
+ Công thức tính lực đàn hồi : f = k(l - lo)
1.4: Lực ma sát
+ Lực ma sát sinh ra khi vật này tiếp xúc với vật kia
+ Có 3 loại lực ma sát
Lực ma sát lăn
Lực ma sát trượt
Lực ma sát nghỉ
+ Lực ma sát phụ thuộc vào
Trọng lượng của vật
Tính chất và chất liệu của mặt tiếp xúc
* Lưu ý
+ Nếu một vật đang trượt (lăn) đều, dưới tác dụng của một lực có độ lớn F thì lực ma sát trượt (lăn) trong trường hợp này cũng có độ lớn bằng F
+ Khi vật đứng yên, nếu có xuất hiện lực ma sát nghỉ thì lực ma sát nghỉ và lực tác dụng lên vật khi đó là 2 lực cân bằng
+ Nếu vật đứng yên mà chịu tác dụng của 2 lực cân bằng thì không có lực ma sát nghỉ
1.5: Cân bằng lực
- Hai lực cân bằng khi chúng có : Cùng phương, ngược chiều, cùng độ lớn
- Hợp của hai lực cân bằng thì bằng 0
- Một vật chịu tác dụng của 2 lực cân bằng thì độ lớn của vấn tốc không thay đổi
- Một vật chịu tác dụng của nhiều lực (Nhiều hơn 2 lực). Nếu vật đứng yên mà vấn đứng yên hoặc vật đang chuyển động mà vẫn tiếp tục chuyển động thẳng đều thì các lực đó cân bằng nhau. Khi đó phương của các lực đó cùng đi qua một điểm và hợp lực bằng 0.
1.6: Mối quan hệ giữa khối lượng và trọng lượng
P = m.g hay P = 10m
1.7: Khối lượng riêng, trọng lượng riêng
D
=
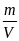 ( Đơn vị kg/m3)
( Đơn vị kg/m3)
d
=
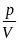 = 10 .D ( Đơn vị N/m3)
= 10 .D ( Đơn vị N/m3)
B: Bài tập luyện tập
Bài tập 1: Treo một vật vào lực kế, thấy lực kế chỉ 12N. Móc thêm vật B vào lực kế thấy lực kế chỉ 18N. Tính khối lượng của vật B.
Giải:
Khi chỉ treo vật A, số chỉ của lực kế bằng trọng lượng của vật:
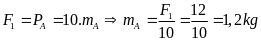
Khi treo thêm vật B, số chỉ của lực kế bằng tổng trọng lượng của hai vật:
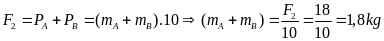
Khối lượng vật B: mB = 1,8 - 1,2 = 0,6kg
Bài tập 2: Một quả cân có khối lượng 1kg được đặt trên một miếng gỗ nằm trên bàn. Miếng gỗ vẫn giữ nguyên trạng thái đứng yên mặc dù có lực ép từ quả cân lên nó. Điều này có mâu thuẫn gì với tác dụng của lực hay không? Hãy giải thích.
Giải:
Không mâu thuẫn gì, vì ngoài lực ép của quả cân, còn có lực đàn hồi của mặt bàn chống lại sự biến dạng, lực này cân bằng với lực ép tác dụng lên miếng gỗ làm cho miếng gỗ vẫn đứng yên.
Bài tập 3: Một học sinh kéo chiếc hộp gỗ trên bàn thông qua lực kế. Ban đầu, lực kéo nhỏ hộp gỗ không nhúc nhích, tăng dần lực kéo một chút hộp gỗ vẫn không nhúc nhích. Khi lực kéo đạt đến một giá trị F nào đó (bằng số chỉ trờn lực kế thì thấy hộp gỗ bắt đầu nhúc nhích.
a) Giải thích vì sao khi lực kéo còn nhỏ hơn giá trị F thì hộp gỗ không nhúc nhích. Lực ma sát xuất hiện trong trường hợp này là lực ma sát gì?
b) Khi hộp gỗ bắt đầu nhúc nhích, lực ma sát trong trường hợp này là lực ma sát gì?
c) So sánh độ lớn của lực ma sát trong hai trường hợp a và b.
Giải:
a) Khi lực kéo còn nhỏ hơn giá trị F thì giữa hộp gỗ và mặt bàn xuất hiện lực ma sát nghỉ, lực ma sát nghỉ này cân bằng với lực F làm cho hộp gỗ vẫn đứng yên. Khi lực kéo tăng nhưng vẫn nhỏ hơn F thì lực ma sát nghỉ cũng tăng theo để cân bằng với lực kéo và hộp gỗ vẫn không chuyển động.
b) Khi hộp gỗ bắt đầu nhúc nhích, lực ma sát trong trường hợp này là lực ma sát trượt. Độ lớn của lực ma sát trượt nhỏ hơn so với độ lớn của lực kéo F.
Bài tập 4: (Quan hệ giữa khối lượng, trọng lượng, KLR, trọng lượng riêng)
Một vật cân bằng cân đĩa ở Hà Nội được 4kg. Biết khối lượng riêng của chất làm vật là 2,7 g/Cm3 ( g = 9,793 N/kg)
a) Tìm trọng lượng của vật và trọng lượng riêng của chất làm vật
b) Đem vật đến TPHCM thì khối lượng riêng và trọng lượng riêng của vật thay đổi như thế nào?Cho rằng thể tích của vật không thay đổi
Bài giải
Cân đĩa cho biết khối lượng của vật là m = 4kg. Khối lượng này không thay đổi dù ở HN hay TPHCM
a) Ở Hà Nội
+ Trọng lượng của vật là P = m.g = 4 . 9,793 = 39,172(N)
Mà
trọng lượng riêng của vật là d =
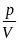 và khối lượng riêng của vật là D =
và khối lượng riêng của vật là D =
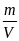
Lập
tỷ số
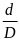 =
=
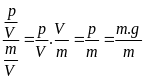 = g
= g
Do đó d = D.g = 2700kg/m3 . 9,793 = 26441,10(N/m3)
b) Đem vật đến TPHCM thì khối lượng và thể tích của vật không đổi nếu khối lượng riêng của vật không đổi
Mặt khác hệ số (g) giảm đi nên trọng lượng của vật giảm. Vì vậy trọng lượng riêng d = D.g sẽ giảm
Bài tập 2: (Xác định các thành phần của hợp kim có khối lượng riêng cho trước)
Một thỏi hợp kim có thể tích 1dm3 và khối lượng 9,850 kg tạo bởi bạc và thiếc. Xác định khối lượng của bạc và thiếc có trong thỏi hợp kim đó. Biết rằng khối lượng riêng của bạc là 10500kg/m3 và của thiếc là 2700kg/m3
(Phương pháp giải : Dựa vào định nghĩa KLR lập công thức tính khối lượng riêng D1 của bạc, D2 của thiếc và D của hợp kim. Biết thêm rằng khối lượng của thỏi hợp kim bằng tổng các khối lượng thành phần m = m1 + m2 và V = V1 + V2)
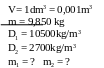 Bài
giải
Bài
giải
Khối lượng riêng D1 của bạc là
D1
=
 (1)
(1)
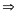 V1
=
V1
=
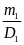
Khối lượng riêng D2 của thiếc là
D2
=
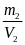 (2)
(2)
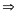 V2
=
V2
=
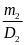
Khối lượng riêng D của thỏi hợp kim là
D =
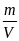 =
=
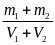 (3)
(3)
Thay
(1) và (2) vào (3) tính ra ta được D =
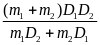 (4)
(4)
Mà
m = m1
+ m2
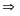 m2
= m - m1
( 5)
m2
= m - m1
( 5)
Thay
(5) vào (4) ta được D =
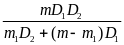 mà D =
mà D =
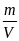
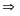
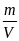 =
=
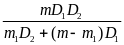
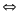 m(m1D2
+ mD1
- m1D1)
= mD1D2V
m(m1D2
+ mD1
- m1D1)
= mD1D2V
Chia cả hai vế cho m ta được m1D2 + mD1 - m1D1 = VD1D2
Giải
ra tìm được m1
=
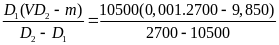 = 9,625(kg)
= 9,625(kg)
Vậy m1 = 9,625(kg) và m2 = 9,850 - 9,625 = 0,225(kg)
C: Bài tập về nhà
* Bài tập 1: Người ta cần chế tạo 1 hợp kim có khối lượng riêng 5g/Cm3 bằng cách pha trộn đồng có KLR 8900kg/m3 với nhôm có KLR là 2700kg/m3. Hỏi tỷ lệ giữa khối lượng đồng và khối lượng nhôm cần phải pha trộn
* Bài tập 2: Tìm khối lượng thiếc cần thiết để pha trộn với 1 kg bạc để được 1 hợp kim có KLR là 10 000kg/m3. Biết KLR của bạc là 10,5g/Cm3 của thiếc là 7,1g/Cm3
D. Rút kinh nghiệm
…………………………………………………………………………………………………………………………………………………………………………
*************************
Tuần: 10
Ngày soạn: 02/11/2019
Ngày dạy: 05/11/2019
Tiết: 25+26+27
LUYỆN TẬP CHỦ ĐỀ 2
I. MỤC TIÊU:
1. Kiến thức:
- Củng cố kiến thức về lực và khối lượng
- Sử dụng các công thức liên quan về lực và khối lượng đẻ giải bài tập liên quan.
2. Kỹ năng:
- Rèn kỹ năng suy luận và trình bày các bài tập về Quan hệ giữa khối lượng, trọng lượng, KLR, trọng lượng riêng
3. Thái độ: Rèn tính độc lập, tinh thần tự giác trong học tập.
4. Năng lực cần đạt:
- Phát triển năng lực tự học, tự tìm hiểu.
- Phát triển năng lực phát hiện và giải quyết vấn đề.
II. PHƯƠNG PHÁP: Nêu và giải quyết vấn đề. vấn đáp gợi mở, thuyết trình
III. CHUẨN BỊ:
1. Giáo viên: Giáo án, SGK, thước.
2. Học sinh: Làm các bài tập giao về nhà. Ôn lại các kiến thức đã học về Lực và khối lượng; Áp suất
IV. QUÁ TRÌNH TỔ CHỨC CÁC HOẠT ĐỘNG CHO HỌC SINH:
A. Chữa bài về nhà
 *
Bài tập 1:
*
Bài tập 1:
Bài giải
Khối
lượng riêng D1
của đồng là : D1
=

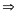 V1
=
V1
=
 và m1
= D1.V1
và m1
= D1.V1
Khối
lượng riêng D2
của nhôm là : D2
=
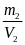
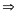 V2
=
V2
=
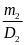 và m2
= D2.V2
và m2
= D2.V2
Khối
lượng riêng D của thỏi hợp kim là : D =
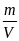 =
=
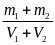 (1)
(1)
Gọi
tỷ lệ khối lượng của đồng và nhôm là:
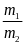 = k
= k
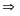 m1
= m2.k
(2)
m1
= m2.k
(2)
Thay (2) vào (1) ta được
D=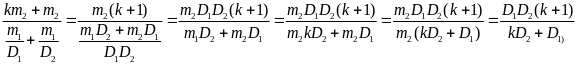
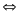 DkD2
+ DD1
= D1D2
- DD1
DkD2
+ DD1
= D1D2
- DD1
Giải
ra ta được k =
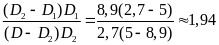
Vậy
tỷ lệ giữa khối lượng của đồng và nhôm cần pha
trộn là : k
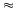 1,94
1,94
* Bài tập 2:

Bài giải
Khối
lượng riêng D1
của bạc là : D1
=

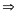 V1
=
V1
=
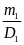 và m1
= D1.V1
và m1
= D1.V1
Khối
lượng riêng D2
của thiếc là : D2
=
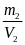
 V2
=
V2
=
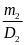 và m2
= D2.V2
và m2
= D2.V2
Khối lượng riêng D của thỏi hợp kim là :
D
=
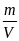 =
=
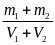 =
=
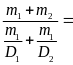
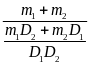 =
=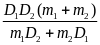
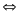 DD2m1+DD1m2
= D1D2(m1
+m2)
DD2m1+DD1m2
= D1D2(m1
+m2)
Giải
ra tìm được m2
=
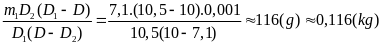
Vậy khối lượng thiếc cần dùng là gần 116 gam
B. Bài tập luyện tập
* Bài tập1: Một mẩu hợp kim thiếc - chì có khối lượng m = 664gam, khối lượng riêng D = 8,3g/Cm3. Hãy xác định khối lượng thiếc và chì trong hợp kim. Biết KLR của thiếc là D1 = 7300kg/m3 và của chì là D2 = 11300kg/m3 và coi rằng thể tích của hợp kim bằng tổng thể tích các kim loại thành phần
Bài giải
Khối
lượng riêng D1
của thiếc là : D1
=

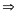 V1
=
V1
=
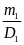 (1)
(1)
Khối
lượng riêng D2
của chì là : D2
=
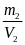
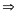 V2
=
V2
=
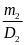 (2)
(2)
Khối
lượng riêng D của thỏi hợp kim là : D =
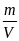 =
=
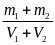 (3)
(3)
Thay (1) và (2) vào (3) ta được
D
=
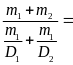
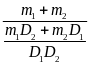 =
=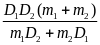 (4)
(4)
m1
+ m2
= m
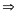 m1
= m - m2
(5)
m1
= m - m2
(5)
Thay (5) vào (4) và giải ra ta tìm được
m2
=
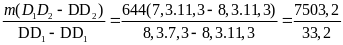 = 226
= 226
 Vậy
khối lượng của chì là 226(g) của thiếc là m1
= m - m2
= 664 - 226 = 438(g)
Vậy
khối lượng của chì là 226(g) của thiếc là m1
= m - m2
= 664 - 226 = 438(g)
* Bài tập 2: Một thanh nhẹ AB có thể quay tự do
quanh một điểm O cố định, OA = 2.OB. Bên đầu
A có treo một vật có khối lượng m1 = 8kg.
Hỏi phải treo ở đầu B một vật có khối lượng m2
bằngbao nhiêu để thanh cân bằng (Thanh ở vị trí nằm ngang, xem hình vẽ bên), cho biết trọng lượng P của vật có khối lượng m tính theo công thức P = 10m
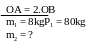
Bài giải
Để thanh cân bằng thì vật m2 phải có trọng lượng P2 sao cho hợp lực của P1 và P2 có điểm đặt đúng tại O. Theo điều kiện cân bằng của đòn bẩy ta có
P1.OA
= P2
.OB
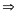
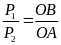 (1)
Do OA = 2.OB nên
(1)
Do OA = 2.OB nên
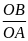 =
=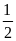 (2)
(2)
Từ
(1) và (2) ta có

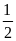
 P2
= 2P1
mà P1
= 80(N) nên P2
= 160(N)
P2
= 2P1
mà P1
= 80(N) nên P2
= 160(N)
Vậy tại đầu B phải treo một vật có khối lượng m2 là
Từ
P2
= 10.m2
 m2
=
m2
=
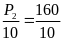 =
16(kg)
=
16(kg)
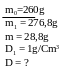 *
Bài tập 3:
Một cốc chứa đầy nước có khối lượng tổng cộng
là mo
= 260,cho vào cốc một hòn sỏi có khối lượng m = 28,8g
rồi đem cân thì thấy khối lượng tổng cộng lúc này
là 276,8g. Tính khối lượng riêng D của sỏi, biết KLR
của nước là 1g/Cm3
*
Bài tập 3:
Một cốc chứa đầy nước có khối lượng tổng cộng
là mo
= 260,cho vào cốc một hòn sỏi có khối lượng m = 28,8g
rồi đem cân thì thấy khối lượng tổng cộng lúc này
là 276,8g. Tính khối lượng riêng D của sỏi, biết KLR
của nước là 1g/Cm3
Bài giải
Do cốc nước ban đầu chứa đầy nước nên khi thả sỏi vào cốc
nước sẽ có một lượng nước m’ tràn ra ngoài cốc
nên ta có m’ = (m0 + m) - m1 = 12(g)
Thể
tích của phần nước tràn ra ngoài cũng chính là thể
tích của hòn sỏi,
nên
ta có: V =
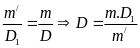 = 2,4(g/Cm3)
= 2,4(g/Cm3)
* Bài tập 4: Hãy tính thể tich V, khối lượng m, khối lượng riêng D của một vật rắn. Biết rằng khi thả nó vào một bình nước đầy thì khối lượng của cả bình tăng thêm m1 = 21,75g. Còn nếu thả nó vào một bình đựng đầy dầu thì khối lượng của cả bình tằng thêm m2 = 51,75g( Trong cả hai trường hợp vật đều chìm hoàn toàn). Biết KLR của nước là D1 = 1g/Cm3, của dầu D2 = 0,9g/Cm3
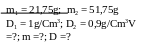
Bài giải
Do cốc nước và cốc dầu đều đầy, nên khi thả 1 vật rắn vào cốc nước hoặc cốc dầu thì sẽ có một lượng nước hoặc dầu tràn ra khỏi cốc. Phần thể tích nước hoặc dầu tràn ra ngoài có cùng thể tích với vật rắn.
+ Độ tăng khối lượng của cả bình khi thả vật rắn vào cốc nước là
m1
= m - D1V
 m = m1
+ D1V
(1) ( D1V
là khối lượng nước đã tràn ra ngoài)
m = m1
+ D1V
(1) ( D1V
là khối lượng nước đã tràn ra ngoài)
+ Độ tăng khối lượng của cả bình khi thả vật rắn vào cốc dầu là
m2 = m - D2V (2) ( D1V là khối lượng nước đã tràn ra ngoài)
Thay
(1) vào (2) ta được m2
= m1
+ D1V
- D2V
 m2
- m1
= D1V
- D2V
m2
- m1
= D1V
- D2V
 V
=
V
=
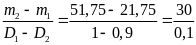 = 300 (3)
= 300 (3)
Vậy thể tích của vật rắn là 300(Cm3)
Thay (3) vào (1) ta được khối lượng của vật rắn là:
m = 21,75 + 1.300 = 321,75(g)
Khối
lượng riêng của vật rắn là D =
 = 1,07(g/Cm3)
= 1,07(g/Cm3)
III: Bài tập về nhà
*Bài tập 1: Một thỏi sắt và một thỏi nhôm có cùng khối lượng 400gam. Hỏi thể tích của thỏi nhôm gấp mấy lần thể tích của thỏi sắt. Biết KLR của sắt là 7,8g/Cm3; của nhôm là 2,7g/Cm3
* Bài tập 2: Một lỗ thép có lỗ hổng ở bên trong. Dùng lực kế đo trọng lượng của miếng thép trong không khí thấy lực kế chỉ 370N. Nhúng miếng thép vào nước thấy lực kế chỉ 320N. Hãy xác định thể tích lỗ hổng, biết trọng lượng riêng của nước là 10000N/m3, của thép là 78000N/m3
D. Rút kinh nghiệm
…………………………………………………………………………………………………………………………………………………………………………
*************************
Tuần: 11
Ngày soạn: 9/11/2019
Ngày dạy: 12/11/2019
Tiết: 28+29+30
CHỦ ĐỀ 3: ÁP SUẤT CỦA CHẤT LỎNG VÀ CHẤT KHÍ
I. MỤC TIÊU:
1. Kiến thức: HS được củng cố kiến thức cơ bản về Áp suất
2. Kỹ năng:
- Rèn kỹ năng suy luận và trình bày các bài tập về Áp suất, Áp suất chất lỏng, áp suất của chất khí, Định luật Paxcan, Định luật Ác - Si - mét,
3. Thái độ: Rèn tính độc lập, tinh thần tự giác trong học tập.
4. Năng lực cần đạt:
- Phát triển năng lực tự học, tự tìm hiểu.
- Phát triển năng lực phát hiện và giải quyết vấn đề.
II. PHƯƠNG PHÁP: Nêu và giải quyết vấn đề. vấn đáp gợi mở, thuyết trình
III. CHUẨN BỊ:
1. Giáo viên: Giáo án, SGK, thước.
2. Học sinh: Làm các bài tập giao về nhà. Ôn lại các kiến thức đã học về Lực và khối lượng; Áp suất
IV. QUÁ TRÌNH TỔ CHỨC CÁC HOẠT ĐỘNG CHO HỌC SINH:
A. Chữa bài tập về nhà
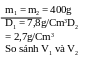 *
Bài tập 1:
*
Bài tập 1:
Bài giải
Khối
lượng riêng D1
của thỏi sắt là D1
=

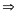 m1
= D1.V1
m1
= D1.V1
Khối
lượng riêng D2
của nhôm là D2
=
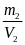
 m2
= D2.V2
m2
= D2.V2
Mà m1 = m2 Nên ta có D1.V1 = D2.V2
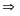
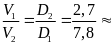 0,35
Vậy V1
= 0,35 V2
0,35
Vậy V1
= 0,35 V2
* Bài tập 2:
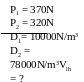 Bài
giải
Bài
giải
Lực đẩy Ác - Si - Mét tác dụng lên miếng thép là
FA = P1 - P2 = 370 -320 = 50(N)
Mà ta có FA = d.V ( V gồm thể tích của thép đặc và lỗ hổng
trong thép)
Suy
ra V =
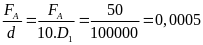 ( m3)
( m3)
Lại
có Vlh
= V - Vthép
= V -
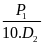 = 0,005 -
= 0,005 -
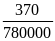
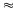 0,00026(m3)
0,00026(m3)
Vậy
lỗ hổng trong miếng thép có thể tích là V
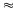 0,00026(m3)
0,00026(m3)
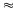 260(m3)
260(m3)
B. Kiến thức cơ bản cần nhớ
1: Áp suất
a) Áp lực là lực ép có phương vuông góc với mặt bị ép
b) Để xác định tác dụng của áp lực lên mặt bị ép người ta đưa ra khái niệm áp suất:
Áp suất được tính bằng độ lớn của áp lực trên một đơn vị diện tích bị ép.
p
=

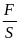
d) Đơn vị áp suất là paxcan(Pa): 1Pa = 1N/m2
2: Áp suất chất lỏng và chất khí
a) Chất lỏng tĩnh và chất khí tĩnh luôn gây lực ép lên thành bình và bề mặt các vật nhúng trong nó. Lực ép này tỷ lệ với diện tích bị ép
b) Tại mỗi điểm trong chất lỏng và chất khí, áp suất theo mọi hướng đều có giá trị như nhau.
2.3: Nguyên lý thủy tĩnh
Độ chênh lệch áp suất giữa 2 điểm trong lòng chất lỏng tĩnh được đo bằng tích của trọng lượng riêng của chất lỏng với khoảng cách theo phương thẳng đứng giữa hai điểm đó.
PA
- PB
= d.h
* Hệ quả
+ Trong chất lỏng tất cả những điểm cùng nằm trên một mặt phẳng nằm ngang đều chịu chung một áp suất
P
= d.h
2.4: Định luật Paxcan
a) Định luật: Áp suất tác dụng lên mặt chất lỏng truyền đi nguyên vẹn theo mọi hướng
F1.S2
= F2.S1
2.5: Lực đẩy Ác - Si - Mét
FA = d .V
2.6: Bình thông nhau
- Khi các nhánh của bình thông nhau có miệng hở và chứa cùng một chất lỏng thì mặt thoáng trong các nhánh đều nằm trên cùng một mặt phẳng nằm ngang
- Nếu trong các nhánh của bình thông nhau chứa các chất lỏng có trọng lượng riêng khác nhau thì mực chất lỏng trong các nhánh sẽ khác nhau.
- Nhánh chứa chất lỏng có trọng lượng riêng lớn hơn sẽ có mực chất lỏng cao hơn.
2.7: Áp suất chất khí
- Trong một bình kín chứa khí, áp suất của chất khí lên thành bình ở ở mọi điểm đều bằng nhau.
+ Khi bị nén giảm thể tích, áp suất của chất khí tăng lên
+ Chất khí cũng truyền áp suất nguyên vẹn đi theo mọi hướng như chất lỏng
- Áp suất của khí quyển trên mặt biển(Ở độ cao số 0 ) có giá trị bằng áp suất của cột thủy ngân cao 760mmHg = 10336N/m2
+ Áp suất của khí quyển thay đổi theo độ cao
2.8: Định luật Ác - Si - mét
a) Định luật:Chất lỏng tác dụng lên vật nhúng trong nó một lực hướng thẳng đứng từ dưới lên, có độ lớn bằng trọng lượng của phần chất lỏng bị vật chiếm chỗ
FA
= V.d = V.Dg
b) Hệ quả:
+ Khi vật chuyển động lên trên (nổi lên mặt thoáng) trong chất lỏng hay chất khí thì lực đẩy ác si mét lớn hơn trọng lượng của vật: FA > P
+ Khi vật đứng yên (nằm lơ lửng) trong chất lỏng hay chất khí thì lực đẩy ác si mét bằng trọng lượng của vật: FA = P
+ Khi vật chuyển động xuống dưới(chìm xuống đáy bình) thì lực đẩy ác si mét nhỏ hơn trọng lượng của vật: FA < P
C. Bài tập luyện tập
* Bài tập 1: Chiều cao tính từ đáy tới miệng một cái ống nhỏ là 140Cm
a) Người ta đổ thủy ngân vào ống sao cho mặt thủy ngân cách miệng ống 25Cm, tính áp suất do thủy ngân tác dụng lên đáy ống và lên điểm A cách miệng ống 100cm.
b) Để tạo ra một áp suất ở đáy ống như câu a, có thể đổ nước vào ống được không ? Đổ đến mức nào?
Cho biết trọng lượng riêng của thủy ngân là 136000N/m3, của nước là 10000N/m3
h1




h
h3
A
.




Bài giải
a) Độ sâu của đáy ống so với mặt thoáng của thủy ngân là
h5 = h - h1 = 140 -25 = 115 (cm) = 1,15(m)
Vậy áp suất của thủy ngân tác dụng lên đáy ống là
Pđ = h5.d = 1,15 .136000 = 156400(N/m2)
Độ sâu của điểm A so với mặt thoáng của thủy ngân là
h6 = h5 - ( h - h3 ) = 115 - 140 + 100 = 75 (cm) = 0,75(m)
Vậy áp suất của thủy ngân tác dụng lên điểm A là
PA = h6.d = 0,75 . 136000 = 102000(N/m2)
b) Khi thay thủy ngân bằng nước, muốn có áp suất đáy bằng áp suất được tính như câu a thì độ cao cột nước h4 phải thỏa mãn
Pđ
= dn.h4
 h4
=
h4
=
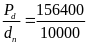 =15,64(m)
=15,64(m)
Vì h4 > h ( 15,64 >1,4 ) nên không thể thực hiện được yêu cầu đề bài nêu ra
* Bài tập 2: Một cái cốc hình trụ, chứa một lượng nước và thủy ngân cùng khối lượng. Độ cao tổng cộng của chất lỏng trong cốc là H = 150cm. Tính áp suất của các chất lỏng lên đáy cốc, biết KLR của nước là D1 = 1g/cm3 và của thủy ngân là D2 = 13,6g/cm3

Bài giải
Gọi h1 là độ cao cột nước; h2 là độ cao cột thủy ngân
S là diện tích đáy bình
Ta có H = h1 + h2 (1)
Khối lượng của nước là: m1 = V1.D1 mà V1 = h1.S Nên m1 = h1.S.D1
Khối lượng của thủy ngân là : m2 = V2.D2 mà V2 = h2.S Nên m2 = h2.S.D2
Do 2 vật có khối lượng bằng nhau nên ta có : h1.S.D1= h2.S.D2(2)
Áp suất của thủy ngân và của nước lên đáy bình là
P
=
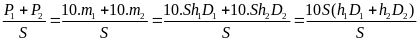 = 10(h1.D1+h2.D2)
(3)
= 10(h1.D1+h2.D2)
(3)
Từ
(2) h1.S.D1=
h2.S.D2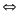 h1.D1=
h2.D2
h1.D1=
h2.D2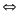
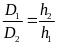
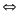
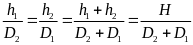
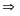 h1
=
h1
=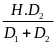 và h2
=
và h2
=
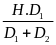
Thay h1 và h2 vào (3) ta được
P
=
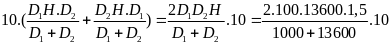 = 27945,2(N/m2)
= 27945,2(N/m2)
* Bài tập 3: Bình A hình trụ tiết diện 8cm2 chứa nước đến độ cao 24cm. Bình hình trụ B có tiết diện 12cm2 chứa nước đến độ cao 50cm. Người ta nối chúng thông với nhau ở đáy bằng một ống dẫn nhỏ có dung tích không đáng kể, tìm độ cao cột nước ở mỗi bình. Coi đáy của hai bình ngang nhau

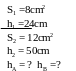
Bài giải
Khi nối 2 bình bởi một ống có dung tích không đáng kể thì nước từ bình B chảy sang bình A
Thể tích nước chảy từ bình B sang bình A là VB = ( h2- h ) S2
Thể tích nước bình A nhận từ bình B là VA = ( h - h1 ) S1
Mà VA = VB nê ta có ( h2- h ) S2 = ( h - h1 ) S1
Biến
đổi ta được h =
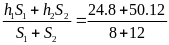 = 39,6
= 39,6
Vậy độ cao của cột nước trong 2 ống lúc cân bằng là 39,6(cm)
 D.
Bài tập về nhà
D.
Bài tập về nhà
* Bài tập 1: Một ô tô có khối lượng 1400kg, hai trục
bánh xe cách một khoảng O1O2 = 2,80m. Trọng tâm G
của xe cách trục bánh sau 1,2m (Hình vẽ)
a)Tính áp lực của mỗi bánh xe lên mặt đường nằm ngang
b)Nếu đặt thêm lên sàn xe tại trung điểm của O1O2 một vật có khối lượng 200kg thì áp lực của hai bánh xe lên mặt đường là bao nhiêu?
*
Bài tập 2:
Móc
một vật A vào một lực kế thì thấy lực kế chỉ 7N,
nhưng khi nhúng vật vào trong nước thì lực kế chỉ 4N.
Hãy xác định thể tích của vật và trọng lượng riêng
của nó. Biết trọng lượng riêng của nước là
10000N/m3
E.
Rút kinh nghiệm
…………………………………………………………………………………………………………………………………………………………………………
*************************
Tuần: 12
Ngày soạn: 16/11/2019
Ngày dạy: 19/11/2019
Tiết: 31+32+33
LUYỆN TẬP CHỦ ĐỀ 3
I. MỤC TIÊU:
1. Kiến thức: HS được củng cố kiến thức cơ bản về Áp suất
2. Kỹ năng: Rèn kỹ năng suy luận và trình bày các bài tập về Áp suất, Áp suất chất lỏng, áp suất của chất khí, Định luật Paxcan, Định luật Ác - Si - mét,
3. Thái độ: Rèn tính độc lập, tinh thần tự giác trong học tập.
4. Năng lực cần đạt:
- Phát triển năng lực tự học, tự tìm hiểu.
- Phát triển năng lực phát hiện và giải quyết vấn đề.
II. PHƯƠNG PHÁP: Nêu và giải quyết vấn đề. vấn đáp gợi mở, thuyết trình
III. CHUẨN BỊ:
1. Giáo viên: Giáo án, SGK, thước.
2. Học sinh: Làm các bài tập giao về nhà. Ôn lại các kiến thức đã học về Lực và khối lượng; Áp suất
IV. QUÁ TRÌNH TỔ CHỨC CÁC HOẠT ĐỘNG CHO HỌC SINH:
A. Chữa bài tập về nhà
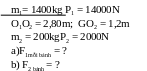
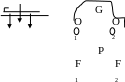 *
Bài tập 1
*
Bài tập 1
Bài giải
a) Trọng lượng P của xe phân tích thành 2 phần song song F1 và F2 đặt ở 2 trục bánh xe và đó cũng à áp lực của 2 bánh xe lên mặt đường
Ta có : P = F1 + F2 (1)
Áp dụng điều kiện cân bằng của đòn bẩy ta có
F1.O1G
= F2.O2G

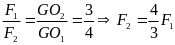 (2)
(2)
Thay
(2) vào (1) ta được : F1
+
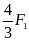 = P
= P
Hay
F1=
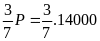 = 600(N) và F2=
= 600(N) và F2=
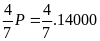 = 8000(N)
= 8000(N)
b) Nếu đặt ở trung điểm O1O2 một vật m2 = 200kg thì bánh xe tác dụng lên mặt đường áp lực là
F1’
=
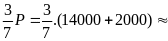 6857(N)
và F2’
=
6857(N)
và F2’
=
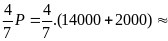 9142(N)
9142(N)
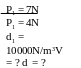 *
Bài tập 2:
*
Bài tập 2:
Bài giải
Khi vật bị nhúng ngập trong nước nó chịu tác dụng của
Hai lực là trọng lực P và lực đẩy FA
Ta có FA = P1 - P2 = 7 - 4 = 3(N)
Mà
FA=
V.d1 V =
V =
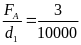 = 0,0003(m3)
= 0,0003(m3)
Vậy
trọng lượng riêng của vật là : Từ P1
= d.V
 d =
d =
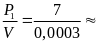 23333(N/m3)
23333(N/m3)
B. Bài tập luyện tập
* Bài tập 1: Trên hai đầu một thanh cứng nhẹ có treo hai vật khối lượng lần lượt là m1 = 6kg và m2 = 9kg. Người ta dùng lực kế để móc vào một điểm O trên thanh. Hãy xác địnhvị trí của điểm O để khi hệ thống cân bằng thì thanh nằm ngang. Tìm số chỉ của lực kế khi đó, biết chiều dài của thanh bằng 50cm
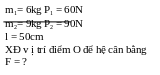
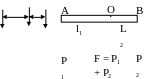
Bài giải
Muốn hệ cân bằng và thnah nằm ngang thì điểm O phải trùng với điểm đặt cảu hợp lực của 2 lực P1 v à P2
Theo
điều kiện cân bằng của đòn bẩy ta có
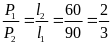
Khi thanh nằm ngang thì l = l1 + l2 = 50(cm)
Ta
có
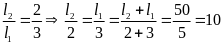
Vậy:
 (cm)
và
(cm)
và
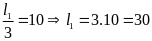 (cm)
(cm)
Do đó điểm O cách A một khoảng bẳng l1= 30(cm)
Khi đó số chỉ của lực kế đúng bằng độ lớn của hợp lực : F = P1 + P2 = 150(N)
* Bài tập 2:Trong một máy ép dùng chất lỏng, mỗi lần pít tông nhỏ đi xuống một đoạn h = 0,2m thì pít tông lớn được nâng lên một đoạn H = 0,01m. Tính lực nén vật lên pít tông lớn nếu tác dụng vào pít tông nhỏ một lực f = 500N

Bài giải
Gọi s và S lần lượt là diện tích của pít tông nhỏ và lớn.
Xem chất lỏng không chịu nẽ thì thể tích chất lỏng chuyển
Từ xi lanh nhỏ sang xi lanh lớn là :
V
= h.s = H.S
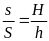
Do áp suất được truyền đi nguyên vẹn nên ta có
P
=

 F
=
F
=
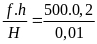 =
10000(N)
=
10000(N)

C. Bài tập về nhà
* Bài tập 1: Một thanh mảnh đồng chất, phân bố
đều khối lượng có thể quay quanh trục O ở phía
trên. Phần dưới của thanh nhúng trong nước, khi
cân bằng thanh nằm nghiêng như hình vẽ bên, một
nửa chiều dài nằm trong nước. Hãy xác định khối
lượng riệng của chất làm thanh.
* Bài tập 2: Phía dưới 2 đĩa cân, bên trái treo một vật bằng chì, bên phải treo một vật hình trụ bằng đồng được khắc vạch chia độ từ 0 đến 100. Có 2 cốc đựng 2 chất lỏng A và B khác nhau(Hình vẽ). Ban đầu khi chưa nhúng 2 vật vào chất lỏng thì cân ở trạng thái cân bằng.
 -
Khi cho vật bằng chì chìm hẳn trong chất lỏng A,
-
Khi cho vật bằng chì chìm hẳn trong chất lỏng A,
và hình trụ trong chất lỏng B thì phải nâng cốc chứa
chất lỏng B đến khi mặt thoáng ngang với vạch 87
thì cân mới cân bằng
- Khi cho vật bằng chì chìm hẳn trong chất lỏng B
và hình trụ trong chất lỏng A thì mặt thoảng của
chất lỏng A phỉa ngang vạch 79 thì cân mới thăng
bằng.
Tính tỷ số các khối lượng riêng của hai chất
lỏng A và B, từ đó nêu ra một phương pháp đơn giản nhằm xác định KLR của một chất lỏng
D. Rút kinh nghiệm
…………………………………………………………………………………………………………………………………………………………………………
****************************
Tuần: 13
Ngày soạn: 23/11/2019
Ngày dạy: 26/11/2019
Tiết: 34+35+36
ÔN TẬP CHUNG CHỦ ĐỀ 1
I. MỤC TIÊU:
1. Kiến thức: HS tiếp tục được củng cố các kiến thức cơ bản về: Chuyển động cơ học; CĐ trên cạn; CĐ trên sông nước.
2. Kỹ năng:
- Rèn kỹ năng suy luận và trình bày các bài tập về chuyển động
- Thu thập và sử lí thông tin.
3. Thái độ: Rèn tính độc lập, tính tập thể, tinh thần tự giác trong học tập.
4. Năng lực cần đạt:
- Phát triển năng lực tự học, tự tìm hiểu.
- Phát triển năng lực phát hiện và giải quyết vấn đề.
II. PHƯƠNG PHÁP: Nêu và giải quyết vấn đề. vấn đáp gợi mở, thuyết trình
III. CHUẨN BỊ:
1. Giáo viên:
- Giáo án, SGK, thước.
2. Học sinh: Làm các bài tập giao về nhà. Ôn lại các công thức đã học.
IV. QUÁ TRÌNH TỔ CHỨC CÁC HOẠT ĐỘNG CHO HỌC SINH:
A. Chữa bài tập về nhà
* Bài tập1: Hai bến A và B ở bên một con sông mà nước chảy với vận tốc 1m/s. Một ca nô đi từ A đến B mất 2h30phút và đi từ B về A mất 3h45phút. Biết rằng vận tốc riêng của ca nô ( Tức là vận tốc đối với nước yên lăng) không thay đổi. Hãy tính vận tốc ấy và khoảng cách giữa 2 bến sông.
* Bài tập2: Trong một cuộc đua thuyền trên sông, mỗi thuyền phải đi từ một bến A xuôi xuống tới một cột mốc B, vòng quanh cột đó rồi về A. Vận tốc dòng nước là 2m/s. Một thuyền có vận tốc riêng là 18km/h đã về nhất với tổng thời gian là 1h30phút. Tính khoảng cách AB
* Bài tập1:

Bài giải
Thời gian ca nô đi xuôi là
t1
=
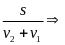 s = t1
( v2
+ v1)
= 9000(v2
+1 ) (1)
s = t1
( v2
+ v1)
= 9000(v2
+1 ) (1)
Thời gian ca nô đi ngược là
t2
=
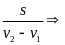 s = t2
( v2
- v1)
= 13500(v2
+1 ) (2)
s = t2
( v2
- v1)
= 13500(v2
+1 ) (2)
Mà quãng đường khi xuôi bằng quãng đường khi ngược nên ta có phương trình.
9000(vV2 +1 ) = 13500(v2 +1 )
Giải ra tìm được v2 = 5m/s
Vật quãng đường AB là 9000(5 +1 ) = 54000(m/s) = 54(km/h)
* Bài tập 2: Bài giải
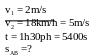 Thời
gian thuyền đi xuôi từ A đến B là t1
=
Thời
gian thuyền đi xuôi từ A đến B là t1
=
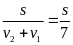
Thời
gian thuyền đi xuôi từ A đến B là t2
=
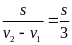
Theo
bài ra ta có phương trình: t = t1
+ t2
Hay
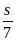 +
+
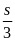 =5400
=5400
Giải ra tìm được s = 11340
Vậy quãng đường AB là 11340 (m) = 11,340(km).
B. Bài tập luyện tập
*
Bài tập 1:
Một người đi từ A đến B. Đoạn đường AB bao gồm
một đoạn lên dốc và một đoạn xuống dốc. Đoạn
lên dốc đi với vận tốc 30km/h, đoạn xuống dốc đi
với vận tốc 50km/h. Thời gian đoạn lên dốc bằng
 thời gian đoạn xuống dốc.
thời gian đoạn xuống dốc.
a) So sánh độ dài đoạn đường lên dốc với đoạn xuống dốc.
b) Tính vận tốc trung bình trên cả đoạn đường AB.
Bài giải
Gọi s1; s2 lần lượt là độ dài quãng đường lên dốc và xuống dốc
t1; t2 lần lượt là thời gian đi đoạn lên dốc và đoạn xuống dốc ( s1; s2;t1; t2 > 0 và t1> t2 )
a)
Đoạn đường lên dốc là: s1
= v1.t1
= 30t1
Mà
ta có t1
=
 t2
t2
Nên
s1
= 30.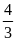 t2
= 40 t2
t2
= 40 t2
Đoạn đường xuống dôc là s2 = v2.t2 = 50.t2
Lập
tỷ số
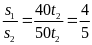 suy ra s1
=
suy ra s1
=
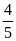 s2
s2
b) Vận tốc trung bình trên đoạn AB là
vtb
=
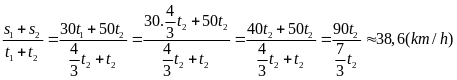
* Bài tập 2: Hai ô tô cùng xuất phát từ A đến B, ô tô thứ nhất chạy nhanh hơn ô tô thứ hai mỗi giờ 10km, nên đến B sớm hơn ô tô thứ hai 1 giờ. Tính vận tốc hai xe ô tô, biết quãng đường AB dài 300km. Bài giải
Gọi x(km/h) là vận tốc của xe thứ nhất ( x >10 )
Vận tốc ô tô thứ hai là x - 10 (km/h)
Thời
gian ô tô thứ nhất đi hết quãng đường AB là
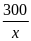 (h)
(h)
Thời
gian ô tô thứ hai đi hết quãng đường AB là
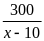 (h)
(h)
Theo
bài ra ta có phương trình
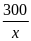 +1
=
+1
=
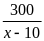
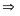 x2
- 10x - 3000 = 0
x2
- 10x - 3000 = 0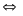 x2
- 60x + 50x - 3000
x2
- 60x + 50x - 3000
Giải ra tìm được x = 60 ( nhận) và x = -50 ( loại)
Vậy vận tốc của xe thứ nhất là 60km/h của xe thứ hai là 50km/h
* Bài tập 3: Từ thành phố A đến thành phố B cách nhau 60km, vào lúc 12 giờ một xe đạp xuất phát với vận tốc không đổi 10km/h. Một ô tô xuất phát từ B đi tới A cũng với vận tốc không đổi bằng 30km/h. Họ gặp nhau tại chỗ cách đều A và B. Hỏi hai xe cách nhau bao nhiêu lúc 14h và 16h.
 Bài
giải
Bài
giải
Vì chỗ gặp nhau là điểm chính giữa A và B nên theo sơ đồ ta có
SAC
= SCB
=
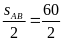 = 30(km)
= 30(km)
Thời
gian xe đạp đi từ A đến chỗ gặp nhau tại C là t1
=
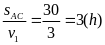
Lúc đó là 12 + 3 = 15(h)
Thời
gian ô tô đi từ B đến chỗ gặp nhau C là t2
=

Vậy ô tô xuất phát sau xe đạp thời gian là 3 - 1 = 2(h), Tức là lúc 14 h
Lúc 14h xe đạp ở D và cách A là sAD = v1.( 14 - 12 ) = 10.2 = 20(km)
Và ô tô ở B. Ta có sBD = sAB- sAD = 60 - 20 = 40(km).
Vậy lúc 14h hai xe cách nhau 40(km)
Sau 1 giờ kể từ lúc hai xe gặp nhau( Lúc đó là 16h) xe đạp ở E cách C là
SCE = v1.1 = 10(km) và ô tô ở G cách C là sCG = v2.1 = 30(km) Suy ra G trùng A
Vậy lúc 16h hai xe cách nhau AE = AC + CE = 30 + 10 = 40(km)
* Bài tập 4: Một người đang ngồi trên một xe ô tô đang chuyển động đều với vận tốc 18km/h. Thì thấy một xe du lịch ở cách xa mình 300m và chuyển động ngược chiều, sau 20 giây thì hai xe gặp nhau. a) Tính vận tốc của xe du lịch so với đường
b) 40 giây sau khi gặp nhau thì hai ô tô cách nhau bao nhiêu?
Bài giải
a)Gọi v1(m/s) và v2(m/s) lần lượt là vận tốc của xe tải và xe du lịch
Vận tốc của xe du lịch đối với xe tải là v21
Khi
chuyển động ngược chiều thì v21
= v2
+ v1(1)
Mà v21
=
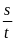 (2)
(2)
Từ
(1) và (2)
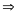 v2
+ v1
=
v2
+ v1
=
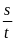
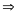 v2
=
v2
=
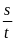 -
v1
Thay số ta có v2
=
-
v1
Thay số ta có v2
=
 = 10(m/s)
= 10(m/s)
b) Khoảng cách sau 40 giây kể từ lúc hai xe gặp nhau là
l = v21 .t = ( v2 + v1) .t = (5 + 10) .40 = 600(m)
C. Bài tập về nhà
* Bài tập 1: Một ca nô đi ngược dòng thì gặp một bè đang trôi xuôi. Sau khi gặp bè 30 phút thì động cơ ca nô bị hỏng. Sau 15 phút thì sửa xong, ca nô lập tức quay lại đuổi theo bè (Vận tốc của ca nô đối với nước là không đổi) và gặp lại bè ở điểm gặp cách điểm gặp trước một đoạn là l = 2,5 km. Tìm vận tốc của dòng nước
* Bài tập 2: Một người đi du lịch bằng xe đạp, xuất phát lúc 5h 30 phút với vận tốc 15 km/h. Người đó dự định đi được nửa quãng đường sẽ nghỉ 30 phút và đến 10h thì sẽ tới nơi. Nhưng sau khi nghỉ 30 phút thì phát hiện xe bị hỏng nên phải sửa xe mất 20 phút. Trên đoạn đường còn lại người đó phải đi với vận tốc bao nhiêu để đến đích đúng giờ dự định.
D. Rút kinh nghiệm
…………………………………………………………………………………………………………………………………………………………………………
***********************************
Ngày soạn: 01/12/2019
Ngày dạy: 03/12/2019
Tiết: 37+38+39
ÔN TẬP CHUNG CHỦ ĐỀ 2,3
I. MỤC TIÊU:
1. Kiến thức:
- Tái hiện lại điều kiện cân bằng của đòn bẩy vào giải bài tập liên quan
- Tái hiện lại kiến thức về bình thông nhau để giải bài tập về bình thông nhau
2. Kỹ năng: Rèn kỹ năng suy luận và trình bày các bài tập.
3. Thái độ: Rèn tính độc lập, tinh thần tự giác trong học tập.
4. Năng lực cần đạt:
- Phát triển năng lực tự học, tự tìm hiểu.
- Phát triển năng lực phát hiện và giải quyết vấn đề.
II. PHƯƠNG PHÁP: Nêu và giải quyết vấn đề. vấn đáp gợi mở, thuyết trình
III. CHUẨN BỊ:
1. Giáo viên: Giáo án, SGK, thước.
2. Học sinh: Làm các bài tập giao về nhà. Ôn lại các kiến thức đã học về Lực và khối lượng; Áp suất
IV. QUÁ TRÌNH TỔ CHỨC CÁC HOẠT ĐỘNG CHO HỌC SINH:
A. Chữa bài tập về nhà
 *
Bài tập
*
Bài tập
Gọi: m1; m2 lần lượt là khối lượng của chì và đồng
V1; V2 lần lượt là thể tích của chì và đồng
+ Khi chưa nhúng vào chất lỏng thì hệ cân bằng nghĩa
là m1 = m2 suy ra P1 = P2
+ Khi nhúng chì vào bình chất lỏng A, đồng vào
bình chất lỏng B, thì các vật chịu tác dụng của lực
đẩy Ác - Si - Mét là
F1 = dA.V1 = 10.DAV1
F1
= dB.V2
= 10.DB.V2
=
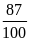 .10.DB.V2
.10.DB.V2
Do
thanh cân bằng nên ta có F1
= F2
hay 10.DA.V1
=
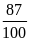 .10.DB.V2(1)
.10.DB.V2(1)
+ Khi nhúng chì vào bình chất lỏng B, đồng vào bình đựng chất lỏng A thì lực đẩy Ác - Si - Mét tác dụng lên các vật khi đó là
F1’
= dB.V1
= 10 .DB.V1
và
F2’
= dA.V2
= 10.DA.V2
=
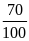 .10.DA.V2
.10.DA.V2
Do
thanh cân bằng nên ta có :F1’
=
F2’
Hay 10 .DB.V1
=
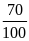 .10.DA.V2(2)
.10.DA.V2(2)
Lập
tỷ số
 70D2A=
87D2B
70D2A=
87D2B

B. Bài tập luyện tập
* Bài tập 1: Hai hình trụ thông nhau đặt thẳng đứng có tiết diện thẳng bên trong là 20cm2 và 10cm2 đựng thủy ngân, mực thủy ngân ở độ cao 10cm trên một thước chia khoảng đặt thẳng đứng giữa 2 bình
a) Đổ vào bình lớn một cột nước nguyên chất cao 27,2 cm. Hỏi độ chênh lệch giữa độ cao của mặt trên cột nước và mặt thoáng của thủy ngân trong bình nhỏ?
b) Mực thủy ngân trong bình nhỏ đã dâng lên đến độ cao bao nhiêu trên thước chia độ
c) Cần phải đổ thêm vào bình nhỏ một lượng nước muối có chiều cao bao nhiêu để mực thủy ngân trong bình trở lại ngang nhau? Biết KLR của thủy ngân là
13600 kg/m3, của nước muối là 1030kg/m3, của nước nguyên chất 1000kg/m3
Phương pháp giải toán bình thông nhau
+ Chất lỏng trong hai bình thông nhau cân bằng khi áp suất của các cột nước trong hai bình lên những điểm ở trên cùng một mặt phẳng nằm ngang bằng nhau. Áp suất đó tính bởi công thức p = h.d
+Khi có dịch chuyển thì thể tích chất lỏng giảm đi trong bình này sẽ truyền nguyên vẹn sang bình kia
+ Áp suất khí quyển trên mặt thoáng của chất lỏng trong 2 bình coi bằng nhau
+ Dựa vào 3 đặc điểm trên lập các phương trình cần thiết
Bài giải
a)Khi đổ nước nguyên chất vào bình lớn(H.vẽ)
nước này gây áp suất lên mặt thủy ngân
p1 = d1.h1
Khi đó một phần thủy ngân bị dồn sang bình
nhỏ, khi đó độ chênh lệch thủy ngân là h2
+ Áp suất của cột thủy ngân tác dụng lên một điểm
Trên mặt phẳng nằm ngang CD trùng với mặt dưới
Của cột nước trong bình lớn. Áp suất này bằng áp suất của cột nước tác dụng lên mặt đó nên ta có: d1h1 = d2h2
 h2
=
h2
=
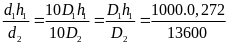 =
0,02(m) = 2(cm)
=
0,02(m) = 2(cm)
Vậy độ chênh lệch giữa mặt nước trong bình lớn và mặt thủy ngân trong bình nhỏ là
H = h1 - h2 = 27,2 - 2 = 25,2(cm)
b) Mực thủy ngân trong 2 bình lúc đầu nằm trên mặt phẳng ngang AB, sau khi đổ nước vào bình lớn, mực thủy ngân trong bình lớn hạ xuống 1 đoạn AC = a và dâng lên trong bình nhỏ 1 đoạn BE = b
Vì thể tích thủy ngân trong bình lớn giảm được chuyển cả sang bình nhỏ nên ta có
S1a
= S2b
 a =
a =
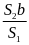
Mặt khác ta có h2 = DE = DB + BE = a + b
Từ
đó h2
=
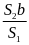 + b = b(
+ b = b(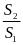 + 1); BE = b mà b =
+ 1); BE = b mà b =
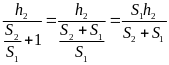
Suy
ra BE = b =
 =
1,3(cm)
=
1,3(cm)
Vậy trên thước chia khoảng mực thủy ngân trong bình nhỏ chỉ
10 + 1,3 = 11,3(cm)
c) Khi đổ nước muối lên mặt thủy ngân trong bình nhỏ, muốn cho mực thủy ngân trở lại ngang nhau trong 2 bình thì áp suất do cột muối gây ra trêm mặt thủy ngân trong bình nhỏ phải bằng áp suất do cột nước nguyên chất gây ra trong bình lớn
d1h1
= d3h3 h3
=
h3
=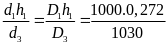 =0,264(m)
= 264(cm)
=0,264(m)
= 264(cm)
* Bài tập 2: Hai bình thông nhau một bình đựng nước, một bình đựng dầu không hòa lẫn được. Người ta đọc trên một thước chia đặt giữa 2 bình số liệu sau( số 0 của thước ở phía dưới)
a)Mặt phân cách nước và dầu ở mức 3cm
b) Mặt thoáng của nước ở mức 18cm
c)Mặt thoáng của dầu ở mức 20cm.
Tính trọng lượng riêng của dầu biết KLR của nước là 1000kg/m3
Bài giải
Nước có KLR lớn hơn dầu nên chiếm phần dưới.
Khi cân bằng áp suất của cột dầu bằng áp suất của
cột nước lên một điểm trên mặt phẳng nằm ngang MN
trùng với mặt phân cách cảu dàu và nước
Ta
có h1.d1
= h2.d2
 d2
=
d2
=
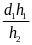
Lại có h1 = 18 - 3 =15(cm) = 0,15(m)
h2
= 20 - 3 = 17(cm) = 0,17(m) Do đó d2
=
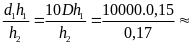 8824(N/m3)
8824(N/m3)
C. Bài tập về nhà
* Bài tập: Hai bình thông nhau và chứa một chất lỏng không hòa tan trong nước có trọng lượng riêng là 12700N/m3. Người ta đổ nước vào một bình cho tới khi mặt nước cao hơn 30cm so với mặt chất lỏng trong bình ấy. Hãy tìm chiều cao cột chất ở bình khia so với mặt ngăn cách của hai chất lỏng. Cho biết trọng lượng riêng của nước là 10000N/m3
D. Rút kinh nghiệm
…………………………………………………………………………………………………………………………………………………………………………
Ngày soạn: 07/12/2019
Ngày dạy: 10/12/2019
Tiết: 40 + 41 + 42
KIỂM TRA LẦN 1
I. MỤC TIÊU:
1. Kiến thức: Kiểm tra lại kiến thức về toán chuyển động và
2. Kỹ năng: Kiểm tra kỹ năng suy luận và trình bày các dạng bài tập.
3. Thái độ: Rèn tính nghiêm túc, tinh thần tự giác trong học tập.
4. Năng lực cần đạt: Phát triển năng lực phát hiện và giải quyết vấn đề.
II. HÌNH THỨC: Đề tự luận
III. CHUẨN BỊ:
1. Giáo viên: Đề kiểm tra
2. Học sinh: Ôn lại các kiến thức đã học và các dạng bài tập về chuyển động, Lực và khối lượng; Áp suất
IV. ĐỀ
Bài tập 1: Một chiếc xuồng chạy trên một dòng sông. Nếu xuồng chạy xuôi dòng từ A đến B thì mất 2 giờ, còn nếu xuồng chạy ngược dòng từ B đến A thì phải mất 6 giờ. Tính vận tốc của xuồng khi nước yên lặng và vận tốc của dòng nước. Biết khoảng cách AB là 120km
Bài
tập 2:
Một người đi từ A đến B. Đoạn đường AB bao gồm
một đoạn lên dốc và một đoạn xuống dốc. Đoạn
lên dốc đi với vận tốc 30km/h, đoạn xuống dốc đi
với vận tốc 50km/h. Thời gian đoạn lên dốc bằng
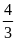 thời gian đoạn xuống dốc.
thời gian đoạn xuống dốc.
a) So sánh độ dài đoạn đường lên dốc với đoạn xuống dốc.
b) Tính vận tốc trung bình trên cả đoạn đường AB.
Bài tập 3: Chiều cao tính từ đáy tới miệng một cái ống nhỏ là 140Cm
a) Người ta đổ thủy ngân vào ống sao cho mặt thủy ngân cách miệng ống 25cm, tính áp suất do thủy ngân tác dụng lên đáy ống và lên điểm A cách miệng ống 100cm.
b) Để tạo ra một áp suất ở đáy ống như câu a, có thể đổ nước vào ống được không ? Đổ đến mức nào?
Cho biết trọng lượng riêng của thủy ngân là 136000N/m3, của nước là 10000N/m3
V. ĐÁP ÁN, BIỂU ĐIỂM
Bài tập 1:
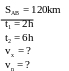 Bài
giải
Bài
giải
Khi xuồng chạy xuôi dòng thì vận tốc thực của xuồng là
v1 = vx + vn
Thời gian xuồng chạy xuôi dòng
t1
=
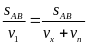
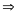 vx
+ vn
=
vx
+ vn
=
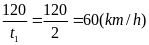 ( 1)
( 1)
Khi xuồng chạy ngược dòng vận tốc thực của xuồng là
v2 = vx - vn
Thời gian xuồng chạy ngược dòng
t2
=
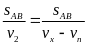
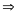 vx
- vn
=
vx
- vn
=
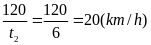 (2)
(2)
Từ (1) suy ra vn = 60 - vx (3)
Thay ( 3) vào (2) ta được vx - 60 + vx = 20
Giải ra tìm được vx = 40(km/h)
Vậy vận tốc của xuồng là 40 ( km/h) vận tốc của nước là
vn = 60 - vx = 60 - 40 = 20 ( km/h)
Bài tập 2:
Gọi s1; s2 lần lượt là độ dài quãng đường lên dốc và xuống dốc
t1; t2 lần lượt là thời gian đi đoạn lên dốc và đoạn xuống dốc ( s1; s2;t1; t2 > 0 và t1> t2 )
a)
Đoạn đường lên dốc là: s1
= v1.t1
= 30t1
Mà
ta có t1
=
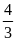 t2
t2
Nên
s1
= 30.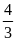 t2
= 40 t2
t2
= 40 t2
Đoạn đường xuống dôc là s2 = v2.t2 = 50.t2
Lập
tỷ số
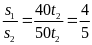 suy ra s1
=
suy ra s1
=
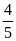 s2
s2
b) Vận tốc trung bình trên đoạn AB là
vtb
=
Bài tập 3:
h1




h
h3
A
.




Bài giải
a) Độ sâu của đáy ống so với mặt thoáng của thủy ngân là
h5 = h - h1 = 140 -25 = 115 (cm) = 1,15(m)
Vậy áp suất của thủy ngân tác dụng lên đáy ống là
Pđ = h5.d = 1,15 .136000 = 156400(N/m2)
Độ sâu của điểm A so với mặt thoáng của thủy ngân là
h6 = h5 - ( h - h3 ) = 115 - 140 + 100 = 75 (cm) = 0,75(m)
Vậy áp suất của thủy ngân tác dụng lên điểm A là
PA = h6.d = 0,75 . 136000 = 102000(N/m2)
b) Khi thay thủy ngân bằng nước, muốn có áp suất đáy bằng áp suất được tính như câu a thì độ cao cột nước h4 phải thỏa mãn
Pđ
= dn.h4
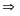 h4
=
h4
=
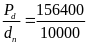 =15,64(m)
=15,64(m)
PHÒNG GD&ĐT CAO LỘC
|
KIỂM TRA HSG
|
MÔN: VẬT LÍ LỚP 8
Thời gian làm bài: 90 phút (không kể thời gian giao đề)
(Đề gồm 1 trang 3 bài)
Bài tập 1: Một chiếc xuồng chạy trên một dòng sông. Nếu xuồng chạy xuôi dòng từ A đến B thì mất 2 giờ, còn nếu xuồng chạy ngược dòng từ B đến A thì phải mất 6 giờ. Tính vận tốc của xuồng khi nước yên lặng và vận tốc của dòng nước. Biết khoảng cách AB là 120km
Bài
tập 2:
Một người đi từ A đến B. Đoạn đường AB bao gồm
một đoạn lên dốc và một đoạn xuống dốc. Đoạn
lên dốc đi với vận tốc 30km/h, đoạn xuống dốc đi
với vận tốc 50km/h. Thời gian đoạn lên dốc bằng
 thời gian đoạn xuống dốc.
thời gian đoạn xuống dốc.
a) So sánh độ dài đoạn đường lên dốc với đoạn xuống dốc.
b) Tính vận tốc trung bình trên cả đoạn đường AB.
Bài tập 3: Chiều cao tính từ đáy tới miệng một cái ống nhỏ là 140Cm
a) Người ta đổ thủy ngân vào ống sao cho mặt thủy ngân cách miệng ống 25cm, tính áp suất do thủy ngân tác dụng lên đáy ống và lên điểm A cách miệng ống 100cm.
b) Để tạo ra một áp suất ở đáy ống như câu a, có thể đổ nước vào ống được không ? Đổ đến mức nào?
Cho biết trọng lượng riêng của thủy ngân là 136000N/m3, của nước là 10000N/m3
Ngày soạn: 10/01/2020
Ngày dạy: 14/01/2020
Tiết: 43 + 44 + 45
BÀI TẬP VỀ LỰC ĐẨY ACSIMET- SỰ NỔI
ĐIỀU KIỆN VẬT NỔI, CHÌM, LƠ LỬNG
I. MỤC TIÊU:
1. Kiến thức:
- Củng cố điều kiện để vật nổi, vật chìm, vật lơ lửng
- Sử dụng các điều kiện để vật nổi, vật chìm, vật lơ lửng vào giải bài tập liên quan
2. Kỹ năng: Rèn kỹ năng suy luận và trình bày các bài tập.
3. Thái độ: Rèn tính độc lập, tinh thần tự giác trong học tập.
4. Năng lực cần đạt:
- Phát triển năng lực tự học, tự tìm hiểu.
- Phát triển năng lực phát hiện và giải quyết vấn đề.
II. PHƯƠNG PHÁP: Nêu và giải quyết vấn đề. vấn đáp gợi mở, thuyết trình
III. CHUẨN BỊ:
1. Giáo viên: Giáo án, SGK, thước.
2. Học sinh: Làm các bài tập giao về nhà. Ôn lại các kiến thức đã học về Lực và khối lượng; Áp suất
IV. QUÁ TRÌNH TỔ CHỨC CÁC HOẠT ĐỘNG CHO HỌC SINH:
A. Chữa bài về nhà
 *
Bài tập:
Hai bình thông nhau và chứa một chất lỏng không hòa tan
trong nước có trọng lượng riêng là 12700N/m3.
Người ta đổ nước vào một bình cho tới khi mặt nước
cao hơn 30cm so với mặt chất lỏng trong bình ấy. Hãy tìm
chiều cao cột chất ở bình khia so với mặt ngăng cách
của hai chất lỏng. Cho biết trọng lượng riêng của
nước là 10000N/m3
*
Bài tập:
Hai bình thông nhau và chứa một chất lỏng không hòa tan
trong nước có trọng lượng riêng là 12700N/m3.
Người ta đổ nước vào một bình cho tới khi mặt nước
cao hơn 30cm so với mặt chất lỏng trong bình ấy. Hãy tìm
chiều cao cột chất ở bình khia so với mặt ngăng cách
của hai chất lỏng. Cho biết trọng lượng riêng của
nước là 10000N/m3

Bài giải
Ban đầu mặt chất lỏng ở hai nhánh ngang nhau ( aa/). Khi đổ nước lên trên mặt thoáng chất lỏng bên nhánh (I) đến độ cao h1 = 30cm thì chất lỏng trong bình được dồn sang nhánh (II)- (Do mặt chất lỏng nhánh(I) chịu áp suất của cột nước h1 gây lên)
Xét áp suất do cột nước gây lên tại điểm b nhánh(I) bằng áp suất do cột chất lỏng gây ra tại b/ ở nhánh (II) - (bb/ ở mặt phẳng nằm ngang)
Nên
ta có p1
= d2.h1
; p2
= d1.h2
Hay d2.h1
= d1.h2
 h2
=
h2
=
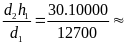 23,6(c3)
23,6(c3)
Vậy chiều cao cột chất lỏng cần tìm là 23,6(cm)
B. Bài tập luyện tập
* Phương pháp giải : So sánh trọng lượng P của vật với lực đẩy Ác-Si-mét
+ Khi vật nổi thì P < FA
+ Khi vật chìm thì P > FA
+ Khi vật lơ lửng trong lòng chất lỏng (Vật nổi lên mặt thoáng chất lỏng cân bằng )
thì P = FA
* Bài tập 1: Một vật bằng kim loại, nếu bỏ vào bình chứa có vạch chia thể tích thì làm cho nước trong bình dâng lên thêm 50cm3. Nếu treo vật vào một lực kế thì lực kế chỉ 3,9N. cho biết trọng lượng riêng của nước là 10000N/m3.
a)Tính lực đẩy Ác-Si-Mét tác dụng lên vật
b) Xác định khối lượng riêng của chất làm lên vật
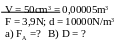
Bài giải
a) Khi thả vật vào bình thì thể tích nước dâng lên thêm 50cm3 đó chính là thể tích của vật.
Do đó lực đẩy Ác-Si-Mét tác dụng lên vật là:
FA = d.V = 10000.0,00005 = 0,5(N)
b) Khi treo vật vào một lực kế thì lực kế chỉ 3,9N đó cũng là trọng lượng của vật do đó ta có P = F = 3,9(N)
Từ
công thức p = d.V
 d
=
d
=
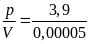 = 78000(N/m3)
= 78000(N/m3)
Vậy khối lượng riêng của chất làm vật là
Từ
d = 10D
 D
=
D
=
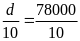 = 7800(kg/m3)
= 7800(kg/m3)
* Bài tập 2: Một cục nước đá có thể tích V = 500cm3 nổi trên mặt nước. Tính thể tích của phần ló ra khỏi mặt nước biết KLR của nước đá là 0,92g/cm3 và trọng lượng riêng của nước là 10000N/m3
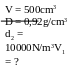
Bài giải
Do cục nước đá nổi trên mặt nước nên trọng lượng của
cục đá đúng bằng trọng lượng của nước bị chiếm chỗ, tức là
bằng lực đẩy Ác-Si-Mét nên ta có
P = FA= d2.V2 ( V2 là thể tích phần chìm trong nước)
 V2
=
V2
=
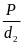 Mà P = 10m, mặt khác m = V.D = 500.0,92 = 460(g) = 0,46(kg)
Mà P = 10m, mặt khác m = V.D = 500.0,92 = 460(g) = 0,46(kg)
Vậy P = 10.0,46 = 4,6(N)
Do đó thể tích phần nhúng chìm trong nước là
V2
=
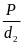 =
=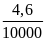 =
0,00046(m3=
460(cm3)
=
0,00046(m3=
460(cm3)
Vậy thể tích phần cục đá nhô ra khỏi nước là
V1 = V - V2 = 500 - 460 = 40(cm3)
* Bài tập 3: Một qủa cầu có trọng lượng riêng d1 = 8200N/m3, thể tích V1 = 100m3, nổi trên mặt một bình nước, Người ta rót dầu vào phủ kín hoàn toàn quả cầu.
a) Tính thể tích phần quả cầu ngập trong nước khi đã đổ dầu
b) Nếu tiếp túc rót thêm dầu thì thể tích phần ngập trong nước của quả cầu có thay đổi không?
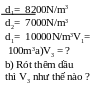 Cho
biết trọng lượng riêng của dầu d2
=7000N/m3,
của nước d3
= 10000N/m3
Cho
biết trọng lượng riêng của dầu d2
=7000N/m3,
của nước d3
= 10000N/m3
Bài giải
a)Gọi V2; V3 lần lượt là thể tích của quả cầu ngập
trong dầu và trong nước, theo bài ra ta có
V1
= V2
+ V3
 V2
= V1
- V3
(1)
V2
= V1
- V3
(1)
Do quả cầu cân bằng trong dầu và trong nước nên
ta có trọng lượng của quả cầu bằng lực đẩy Ác-Si-Mét
V1d1 = V2d2 + V3d3 (2)
Thai (1) vào (2) ta được V1d1 = (V1 - V3 )d2 + V3d3
Hay
V1d1
= v1d2
+ (d3
- d2)
V3
 V3
=
V3
=
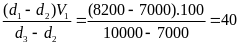 (cm3)
(cm3)
Vậy thể tích phần quả cầu ngập trong nước khi đã đổ dầu là 40(cm3)
b)
Từ biểu thức V3
=
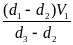 ta thấy V3 chỉ phụ thuốc vào V1, d1,d2,
d3.
Tức là không phụ thuộc vào độ sâu của quả cầu
trong dầu cũng như lượng dầu đã đổ thêm. Do đó nếu
tiếp tục rót thêm dầu thì phần ngập trong nước của
quả cầu vẫn không thay đổi.
ta thấy V3 chỉ phụ thuốc vào V1, d1,d2,
d3.
Tức là không phụ thuộc vào độ sâu của quả cầu
trong dầu cũng như lượng dầu đã đổ thêm. Do đó nếu
tiếp tục rót thêm dầu thì phần ngập trong nước của
quả cầu vẫn không thay đổi.
 *
Bài tập 4: Một
khối kình hộp đáy vuông chiều
*
Bài tập 4: Một
khối kình hộp đáy vuông chiều
cao h = 10cm nhỏ hơn cạnh đáy, bằng gỗ có
KLR là D1 = 880kg/m3 được thả nổi trong một
bình nước (Hình vẽ)
a) Tính chiều cao của phần nhô lên khỏi mặt nước của hình hộp
b)Đổ thêm vào bình 1 chất dầu không trộn lẫn được với nước có KLR là D2= 700kg/m3. Tính chiều cao của phần chìm trong nước, trong dầu của gỗ
Bài giải
a) Gọi V là thể tích của vật, V1 là thể tích phần chìm trong nước, vì vật nổi nên ta có
P = FA
Mà P = 10m = 10.V.D1 và FA = dn.V1 = 10.V1.Dn
Nên
ta có 10.V.D1
= 10.V1.Dn
Hay V.D1
= V1.Dn

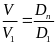 Điều này chứng tỏ thể tích của vật tỷ lệ nghịch
với KLR của chúng.
Điều này chứng tỏ thể tích của vật tỷ lệ nghịch
với KLR của chúng.
Gọi h1 là chiều cao của phần chìm trong nước của vật, tức là của khối lượng chất lỏng bị vật chiếm chỗ. Thì V; V1 chính là thể tích của 2 hình hộp chữ nhật có cùng đáy và độ cao tương ứng là h và h1
Vậy h; h1 phải tỷ lệ nghịch với V và V1
nên
ta có
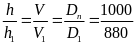
 h1
=
h1
=
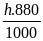 = 0,08.h
= 0,08.h
Vậy phần chìm trong nước của khối gỗ có chiều cao là
h1 = 0,88h = 0,88 . 10 = 8,8 (cm)
và phần nhô ra khỏi mặt nước có chiều cao là : h - h1 = 10 - 8,8 = 1,2(cm)
b) Gọi h2; h3 là chiều cao của khối gỗ gập trong nước và trong dầu ta có
V2; V3 là thể tích của khối gỗ ngập trong nước và trong dầu
d2; d3 là trọng lượng riêng của nước và của dầu
h
= h2
+ h3
 h2
= h - h3
(1)
h2
= h - h3
(1)
Do khối gỗ cân bằng trong dầu và nước nên P = FA
Mà P = 10.m = 10.D1.V = 10.D1.S.h và
FA = d2 .V2 + d3.V3 = 10.D2.S.h2 + 10.D3.S.h3
Do đó ta có 10.D1.S.h = 10.D2.S.h2 + 10.D3.S.h3
Hay D1.h = D2.h2 + D3.h3 (2)
Thay (2) vào (1) ta được D1.h = D2(h - h3 ) + D3h3
Giải
ra tìm được h3
=
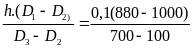 = 0,04(m) = 4(cm)
= 0,04(m) = 4(cm)
Vậy chiều cao khối khỗ chìm trong dầu là h3 = 4(cm)
Chiều cao khối gỗ chìm trong nước là h2 = h - h3 = 10 - 4 = 6(cm)
C: Bài tập về nhà: Hai quả cầu A,B có trọng lượng bằng nhau nhưng làm bằng hai chất khác nhau, được treo vào 2 đầu của 1 đòn có trọng lượng không đáng kể và chiều dài l = 84cm. Lúc đầu, đòn cân bằng. Sau đó đem nhúng cả hai quả cầu ngập trong nước. Người ta thấy phải dịch chuyển điểm tựa đi 6cm về phía B để đòn trở lại cân bằng. tính trọng lượng riêng của quả cầu B nếu trọng lượng riêng của quả cầu A là dA = 3.104N/m3 của nước dn = 104N/m3
D. RÚT KINH NGHIỆM:
.................................................................................................................................................................................................................................................................................................................................................................................................
* Bài tập 2: Một cái thớt bằng gỗ, khối lượng riêng D1 = 850kg/m3, có hai mặt phẳng song song cách nhau một khoảng h = 8cm được đặt trong một cái chậu.
a) Người ta đổ nước vào chậu, cho đến kho áp suất do nước và do cái thớt tác dụng lên đáy chậu bằng nhau. Tính độ cao của cột nước.
b) Sau đó từ từ rót vào chậu một chất lỏng không trộn lẫn được với nước cho đến khi mặt trên của thớt ngang với mặt thoáng của chất lỏng, thì thấy lớp chất lỏng dày 4,8cm. Xác định khối lượng riêng của chất lỏng đó.
c) Nếu lại tiếp tục rót thêm chất lỏng đó cho mực chất lỏng cao thêm 3cm, thì phần chìm trong chất lỏng của thớt tằng hay giảm bao nhiêu?
******************************
Phần Quang học
Yêu cầu:
Kiến thức : Củng cố và nâng cao kiến thức về 3 loại gương, tính chất về ảnh của vật tạo bởi gương;cách vẽ ảnh của một vật tạo bởi gương phẳng.
Kĩ năng : Rèn kĩ năng vẽ hình và giải bài tập phần quang học
Nội dung:
Phần lí thuyết:
Chữa bài tập về nhà:
Bài tập :
Bài 1: Cho hai điểm sáng S1 và S2 trước một gương phẳng như a/ Hãy vẽ ảnh S1’ và S2’ cña các điểm sáng S1; S2 qua gương phẳng. b/ Xác định các miền mà nếu ta đặt mắt ở đó thì chØ cã thể quan s¸t được ¶nh S'1 ; ¶nh S'2 ; c¶ hai ¶nh S'1 , S'2 vµ kh«ng quan s¸t ®îc bất cứ ảnh nào.
|
|
|
Vẽ được ảnh S’1; S’2 ( có thể bằng Phương pháp đối xứng) Chỉ ra được: + vùng chỉ nhìn thấy S’1 là vùng II + Vùng chỉ nhìn thấy S’2 là vùng I + Vùng nhìn thấy cả hai ảnh là vùng III + Vùng không nhìn thấy ảnh nào là vùng IV
|
|
|
Bài
2:
 Hai tia tới SI và SK vuông góc với nhau chiếu tới một
gương phẳng tại hai điểm I và K như hình vẽ (H1).
Hai tia tới SI và SK vuông góc với nhau chiếu tới một
gương phẳng tại hai điểm I và K như hình vẽ (H1).
a) Vẽ tia phản xạ của 2 tia tới SI và SK.
b) Chứng minh rằng 2 tia phản xạ ấy
cũng hợp với nhau 1 góc vuông.
c) Giả sử góc tạo bởi tia tới SK với gương phẳng
bằng 300. Chiếu một tia sáng từ S tới gương đi qua trung điểm M của đoạn thẳng nối hai điểm I và K. Xác định góc tạo bởi tia phản xạ của hai tia SK và SM.
Bài giải:
giải:
- Lấy S’ đối xứng với S qua gương
- S’ là ảnh của S qua gương
- Vì tia phản xạ có đường kéo dài đi qua
ảnh nên nối S’I, S’K kéo dài lên mặt
gương ta được tia IR và KR’ cần vẽ
b)
Chứng
minh được
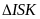 =
=
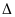
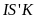 Suy ra gúc
Suy ra gúc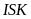 =
gúc
=
gúc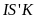 =900.
Vậy S’R
=900.
Vậy S’R
 S’R’
S’R’
c) - Dựng được tia phản xạ MM’ của tia SM qua gương
- Tớnh được gúc SIM = 600
Xột
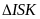 vuụng
tại S, SM là trung tuyến => SM = 1/2IK = MK
vuụng
tại S, SM là trung tuyến => SM = 1/2IK = MK
 =>
=>
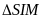 cõn tại M, mà gúc SIM = 600=>
cõn tại M, mà gúc SIM = 600=>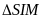 đều
=> gúc SMI = 600
đều
=> gúc SMI = 600
=> gúc KMM’ = 600 suy ra gúc S’MK = 1200
Chỉ ra được gúc MKS’ = 300.
Xột
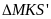 cú gúc S’MK = 1200,
gúc MKS’ = 300
cú gúc S’MK = 1200,
gúc MKS’ = 300
Suy ra gúc MS’K = 1800- 1200 - 300 = 300
Bµi
3:
Cho
hai g¬ng ph¼ng hîp víi nhau mét gãc
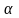 =
50o
vµ mét ®iÓm s¸ng S trong kho¶ng hai g¬ng nh h×nh 1.
BiÕt r»ng mÆt ph¼ng h×nh vÏ vu«ng gãc víi hai mÆt g¬ng.
=
50o
vµ mét ®iÓm s¸ng S trong kho¶ng hai g¬ng nh h×nh 1.
BiÕt r»ng mÆt ph¼ng h×nh vÏ vu«ng gãc víi hai mÆt g¬ng.
VÏ mét tia s¸ng ph¸t ra tõ S ph¶n x¹ lÇn lît trªn G1 t¹i I, råi trªn G2 t¹i J vµ sau ®ã qua S. TÝnh gãc hîp bëi tia tíi SI vµ tia ph¶n x¹ JS.
VÏ mét tia s¸ng ph¸t ra tõ S ph¶n x¹ lÇn lît trªn G1 t¹i K, råi trªn G2 t¹i H vµ quay trë l¹i trïng víi tia tíi SK. TÝnh gãc hîp bëi SK vµ G1


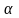
I1 = I3 Vµ J1 = J3 (
Trong tam gi¸c SIJ, ta cã :
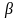 =
180 – (J2
+ I2)
)
=
180 – (J2
+ I2)
)
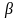 =
180 – {[180 – (I1
+ J3)]
+ [180 - (I1
+ I3)]}
=
180 – {[180 – (I1
+ J3)]
+ [180 - (I1
+ I3)]}
 =
180 – [(180 – 2J1)
+ (180 – 2I3)]
=
180 – [(180 – 2J1)
+ (180 – 2I3)]
 =
180 – [360 – 2(J1+
I3)]
=
180 – [360 – 2(J1+
I3)]
 =
180 – [360 – 2(180 -
=
180 – [360 – 2(180 - )]
)]
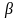 =
180 - 2
=
180 - 2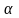
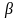 = 180 – 2.60 = 60O
= 180 – 2.60 = 60O
 b.
V× tia s¸ng khi ®Õn G2
th× quay trë l¹i ®êng cò nªn tia ph¶n x¹ KH vu«ng gãc
víi G2.
b.
V× tia s¸ng khi ®Õn G2
th× quay trë l¹i ®êng cò nªn tia ph¶n x¹ KH vu«ng gãc
víi G2.
Tõ ®Þnh luËt ph¶n x¹ ¸nh s¸ng, ta cã :
Gãc K1 = gãc K2
Trong tam gi¸c vu«ng HOK, ta cã :
K1
= 90 -
= 90 – 60 = 30o
Bài 4
 Một
tia sáng mặt trời tạo góc 360
với
Một
tia sáng mặt trời tạo góc 360
với
mặt phẳng nằm ngang, chiếu tới một gương phẳng
đặt trên miệng một cái giếng và cho tia phản xạ có
phương thẳng đứng xuống đáy giếng. Hỏi gương phải đặt nghiêng một góc bao nhiêu so với phương thẳng đứng ?
- Ta thấy; I1 = I2 (Theo định luật phản xạ)
Mặt khác; I3 = I5 (cùng phụ với góc tới và góc phản xạ)
I5 = I4 (đối đỉnh)
=> I3 = I4 = I5
Và
 SIP + I3
+ I4
= 900
=> I3
= I4
= (900
– 360)
: 2 = 270
SIP + I3
+ I4
= 900
=> I3
= I4
= (900
– 360)
: 2 = 270
Ta lại có: I1 + I2 + I3 + I5 = 1800 => I1 = I2 = (1800 - 2 I3) : 2 = 630
V ậy
: - Góc hợp bởi mặt gương với phương thẳng đứng là
270
ậy
: - Góc hợp bởi mặt gương với phương thẳng đứng là
270
- Góc tới bằng góc phản xạ và bằng 630
Bài 5: Cho hai gương phẳng vuông góc với nhau, một tia sáng chiếu đến gương thứ nhất, phản xạ truyền tới gương thứ hai, rồi phản xạ,
a, Vẽ hình minh họa?
b, Chứng minh tia phản xạ cuối cùng song song với tia tới ban đầu?
c, Cho một điểm sáng S đặt trước hai gương trên. Hãy vẽ hình minh họa số ảnh của S tạo bởi hai gương?
Bài giải: a, Hình vẽ: G1

 M
M
 M1
P
R
M1
P
R
 H
H
O K G2
H1
Trong đó:
- M1 đối xứng với M qua G1
- H1 đối xứng với H qua G2
- Đường MHKR là đường truyền cần dựng
b, Hai đường pháp tuyến ở H và K cắt nhau tại P. Theo định luật phản xạ ánh sáng ta có:
![]()
Mà
![]()
Mặt khác
![]()
( Hai góc này lại ở vị trí so le trong ). Nên MH//KR
c, Vẽ hình:

 G1
G1
S1 S
H O
G2
S3 S2
KL: Hệ gương này cho 3 ảnh S1 , S2 , S3
Bài 6: Điểm sáng S nằm giữa 2 gương phẳng có mặt phẳng phản xạ quay vào nhau. Gọi S1, S2 lần lượt là ảnh của S qua gương M và N. Chứng tỏ rằng S, S1, S2 cùng nằm trên đường tròn tâm 0 bàn kính 0S.
Bài
giải:
- Dựng S1 đối xứng với S qua gương M
- Dựng S2 đối xứng với S qua gương N.
- Nối 0 với S . Do ảnh và vật đối xứng nhau qua gương phẳng nên
+ 0 nằm trên đường trung trực của SS1 nên 0S= 0S1 (1)
+ 0 nằm trên đường trung trực của SS2 nên 0S=0S2 (2)
Từ 1,2 suy ra 0S=0S1=0S2
hay 3 điểm S,S1,S2 nẳm trên đường tròn tâm 0 bán kính 0S
 Bài
7: Hai gương
phẳng G1
và G2 hợp
với nhau một góc
Bài
7: Hai gương
phẳng G1
và G2 hợp
với nhau một góc
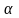 ,
hai mặt phản xạ hướng vào nhau. G1
,
hai mặt phản xạ hướng vào nhau. G1
x S
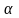
G2
Điểm sáng S đặt trong khoảng 2 gương . Gọi S1 là ảnh của S qua G1 và S2 là ảnh của S1 qua G2. Hãy nêu cách vẽ đường đi của tia sáng từ S phản xạ lần lượt qua G1 và G2 rồi đi qua S. Chứng tỏ rằng độ dài của đường đi đó bằng SS2.
Bài giải:
|
1,- Dựng S1 đối xứng với S qua G1 - Dựng S2 đối xứng với S1 qua G2 - Nối S2 với S cắt G2 tại I. - Nối I với S1 cắt G1 tại K. - Nối K với S . -
Vậy đường đi là: S |
2, CM : SK + KI + IS = SS2 Ta có : SK + KI + IS = S1K + KI + SI = S1I + SI S1I + SI = S2I + IS = SS2 ( ĐPCM)
|
|
Bài 8: Cho một điểm sáng S và một điểm M trước gương phẳng như hình vẽ:
xM
x S












 G
G
1, Trình bày cách vẽ một tia sáng đi từ S tới gương rồi phản xạ qua M.
Bài giải:
G
S’ |
1, - Dựng S’ đối xứng S qua G - Nối S’ với M cắt G tại I. - Nối S với I. - Dễ ràng chứng minh được SI là tia tới , IM là tia phản xạ. |
2, Lấy điểm E tùy ý trên G , nối SE, EM Ta có SE + EM = ES’+ EM > S’M
|
|
, Chứng minh rằng trong vô số con đường đi từ S tới G rồi tới M thì ánh sáng đi theo con đường ngắn nhất.
Bài
9: Tia sáng Mặt
Trời nghiêng 1 góc
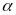 =480
so với phương ngang. Cần đặt một gương phẳng như thế
nào để đổi phương của tia sáng thành phương nằm
ngang
=480
so với phương ngang. Cần đặt một gương phẳng như thế
nào để đổi phương của tia sáng thành phương nằm
ngang
Bài
giải: Gọi
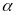 ,
, lần lượt là góc hợp bởi tia sáng mặt trời với
phương ngang và góc hợp bởi tia tới với tia phản xạ.
lần lượt là góc hợp bởi tia sáng mặt trời với
phương ngang và góc hợp bởi tia tới với tia phản xạ.
Trường hợp 1: Tia sáng truyền theo phương ngang cho tia phản xạ từ trái sang phải.
Từ
hình 1,
Ta có:
 +
+ = 1800
= 1800
= >
> = 1800
-
= 1800
- = 1800
– 480
= 1320
= 1800
– 480
= 1320
D ựng
phân giác IN của góc
ựng
phân giác IN của góc
 như hình 2.
như hình 2.
Dễ dang suy ra: i’ = i = 660
Vì IN là phân giác cũng là pháp tuyến nên ta kẻ đường thẳng vuông góc với IN tại I ta sẽ được nét gương PQ như hình 3.
Xét hình 3:
Ta
có:
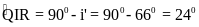
Vậy
ta phải đặt gương phẳng hợp với phương ngang một góc
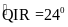
Trường hợp 2: Tia sáng truyền theo phương ngang cho tia phản xạ từ phải sang trái.
T ừ
hình 4,
Ta có:
ừ
hình 4,
Ta có:
 =
= = 480
= 480
Dựng
phân giác IN của góc
 như
như
hình 5.
D ễ
dang suy ra: i’ = i = 240
ễ
dang suy ra: i’ = i = 240
Vì IN là phân giác cũng là pháp tuyến nên ta kẻ đường thẳng vuông góc với IN tại I ta sẽ được nét gương PQ như hình 6.

Xét hình 6:
Ta
có:
Vậy
ta phải đặt gương phẳng hợp với phương ngang một góc
Vậy có hai trường hợp đặt gương:
TH1: đặt gương hợp với phương ngang một góc 240.
TH2: đặt gương hợp với phương ngang một góc 660.
Bài 10: Một nguồn sáng điểm và hai gương nhỏ đặt ở ba đỉnh của một tam giác đều. Tính góc gợp bởi hai gương để một tia sáng đi từ nguồn sau khi phản xạ trên hai gương:
a) đi thẳng đến nguồn.
b) quay lại nguồn theo đường củ
B ài
giải: a) Để tia
phản xạ trên gương thứ hai đi thẳng đến nguồn, đường
đi của tia sáng có dạng như hình
1.
ài
giải: a) Để tia
phản xạ trên gương thứ hai đi thẳng đến nguồn, đường
đi của tia sáng có dạng như hình
1.
Theo định luật phản xạ ánh sáng ta có:
I1=I2=> SIJ=600
Tương tự ta có: SJI=600
Do đó: IOJ=600
Vậy: hai gương hợp với nhau một góc 600
b) Để tia sáng phản xạ trên gương thứ hai rồi quay lại nguồn theo phương cũ, đường đi của tia sáng có dạng như hình 2
Theo định luật phản xạ ánh sáng ta có:
I1=I2 => IJO=600
Trong
 ta có:O=900-I=300
ta có:O=900-I=300
Vây: hai gương hợp với nhau một góc 300
guồn theo đường đi cũ
Bài 11: Hai gương phẳng G1 và G2 đặt vuông góc với nhau mặt phản xạ quay vào nhau (hv).S và M là hai điểm sáng đặt trước hai gương.
 a)
Nêu cách vẽ một tia sáng xuất phát
(G1)
a)
Nêu cách vẽ một tia sáng xuất phát
(G1)


 từ
S phản xạ lần lượt qua G1,
G2
rồi đi qua M.
.S
từ
S phản xạ lần lượt qua G1,
G2
rồi đi qua M.
.S

 b)
Có bao nhiêu ảnh của S và M
b)
Có bao nhiêu ảnh của S và M

 cho
bởi hệ thống hai gương? Vẽ hình
cho
bởi hệ thống hai gương? Vẽ hình
 c)
Nếu em đứng ở S sẽ quan sát được gì?
c)
Nếu em đứng ở S sẽ quan sát được gì?





 .M
.M











 (G2)
(G2)
G1
Bước 1:Dựng cảnh S1 cuả S qua G1
Bước 2: Dựng cảnh S2 của S1 qua G2
Bước 3: Nối S2 với M cắt G2 ở đâu là điểm J
Bước 4 : Nối J với S1 cắt G1 ở đâu là điểm I
Bước 5 : Nối S với I rồi vẽ chiều mũi tên đường truyền ánh sáng
b) Hệ gương có 4 ảnh của S .Trong đó có 2 ảnh trùng nhau ,4 ảnh của M trong đó có 2 ảnh trùng nhau (0,5đ)
M




 hv(
1đ)
hv(
1đ)
c) Nếu em đứng ở S sẽ quan sát được 3 ảnh của mình qua gương (0,5đ)
Bài 12: Tia sáng mặt trời chiếu nghiêng một góc 300 so với phương nằm ngang. Hỏi phải đặt gương phẳng nghiêng bao nhiêu độ so với phương nằm ngang để hắt tia sáng xuống đáy giếng theo phương thẳng đứng
Bài
giải:

Ta
có = +
= 300
+ 900
=
1200
Mà
 = +
= 2 ( = ;định luật phản xạ ánh sáng )
= \f(,2
= \f(1200,2
= 600
= +
= 2 ( = ;định luật phản xạ ánh sáng )
= \f(,2
= \f(1200,2
= 600
Mà = - = 900 - 600 = 300 = + = 300 + 300 = 600
Vậy góc hợp bởi mặt phẳng với gương phẳng là 600
Soạn:20/10/2011 Tiết:49+50+51
Dạy:22/10/
Soạn: Tiết:
Dạy: LUYỆN TẬP
 I:
Chữa bài tập về nhà
I:
Chữa bài tập về nhà
 *
Bài tập1
*
Bài tập1
Bài giải
Vì
trọng lượng hai quả cầu bằng nhau nên lúc đầu điểm
tựa O ở chính giữa thanh, nên ta có : OA = OB =
 = 42(cm)
= 42(cm)
Khi nhúng A và B vào nước thì phải dịch chuyển O đến vị trí O1 thì thanh cân bằng nên ta có : O1A = 42 + 6 = 48(cm) và O1B = 42 - 6 = 36(cm)
Khi đó lực đẩy Ác-Si-Mét tác dụng lên vật A và B là
FA
= dn.VA
mà VA
=
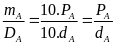 .
Nên FA
=
.
Nên FA
=
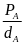 .dn
(1)
.dn
(1)
FB
= dn.VB
mà VB
=
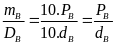 .
Nên FB
=
.
Nên FB
=
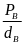 .dn
(2)
.dn
(2)
Theo điều kiện cân bằng của đòn bẩy ta có
(PA - FA) . O1A = (PB - FB) . O1B (3)
Thay (1) và(2) vào (3) ta được
(PA
-
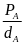 .dn
).O1A
= (PB
-
.dn
).O1A
= (PB
-
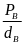 .dn
). O1B
mà PA
= PB
= P nên ta có
.dn
). O1B
mà PA
= PB
= P nên ta có
(P
-
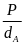 .dn
).O1A
= (P -
.dn
).O1A
= (P -
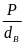 .dn
). O1B
.dn
). O1B
Biến
đổi ta được kết quả dB
=
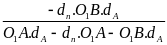
Thay
số vào ta được dB
=
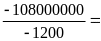 90000(N/m3)
90000(N/m3)
Vậy trọng lượng riêng của vật B là dB = 90000(N/m3)
* Bài tập 2:
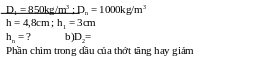
Bài giải
a) Áp suất của thớt tác dụng lên đáy chậu là
p1
=
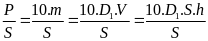 = 10.D1.h
= 10.D1.h
Thay số ta được p1 = 10.850.0,08 = 680(N/m3)
Áp suất do cột nước đổ vào gây ra cho đáy bình là P2 = dn . hn = 10.Dn.hn
Mà Áp suất của thớt và của nướ tác dụng lên đáy bình là bằng nhau nên ta có
P1
= p2
hay 680 = 10.Dn.hn
 hn
=
hn
=
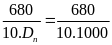 = 0,068(m) = 6,8(cm)
= 0,068(m) = 6,8(cm)
b) Do mặt trên của thớt ngang với mặt thoáng của dầu chứng tỏ thớt lơ lửng trong dầu và nước, Vậy lực đẩy Ác-Si-Mét của dầu và nước tác dụng lên thớt là
FA = 10S.D2.h1 + 10.S.dn.h2 ( h1 = 8 -4,8 = 3,2 cm)
Trọng lượng của vật là P = 10.m = 10.D1.V = 10.D1.S.h
Theo điều kiện vật lơ lửng ta có: FA = P hay 10S.D2.h1 + 10.S.dn.h2 = 10.D1.S.h
Biến
đổi ta được D2
=
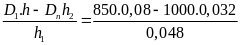 = 750(kg/m3)
= 750(kg/m3)
c) Do rót lần 1 thớt đã chìm hẳn trong dầu và đứng cân bằng. Vậy có rót thêm dầu vào thì thớt vẫn chỉ chìm trong dầu và nước như lần 1.
Lực P hướng xuống không thay đổi. Nên độ cao của hai phần chìm trong dầu và nước không thay đổi
 II:
Bài tập luyện tập
II:
Bài tập luyện tập
* Bài tập 1: Trên đĩa cân bên trái có một bình
chứa nước, bên phải là giá đỡ có treo vật (A)
bằng sợi dây mảnh, nhẹ. Khi vật chưa chạm nước,
cân ở vị trí cân bằng. Nối dài sợi dây để vật(A)
chìm hoàn toàn trong nước. Trạng thái cân bằng
của cân bị phá vỡ. Hỏi phải đặt một quả cân có
trọng lượng bao nhiêu vào đĩa cân nào , để 2 đĩa
cân được cân bằng trở lại. Cho thể tích vật(A)
bằng V, trọng lượng riêng của nước bằng d
(Hệ thống biểu diễn trên hình vẽ)
Bài giải
Khi nối dài sợi dây để vật(A) ngập hoàn toàn trong nước thì vật A chịu tác dụng của lực đẩy Ác-Si-Mét là: FA = d.V
Do đó đĩa cân bên phải mất đi một trọng lượng P đúng bằng lực đẩy Ác-Si-Mét là
Nên ta có P = FA
Mặt khác khi vật A nhúng trong nước thì v ật A cũng chịu một lực tác dụng ngược lại đúng bằng FA. Lực này được truyền và ép xuống đĩa cân bên trái làm đĩa cân này thêm đúng bằng FA
Kết quả đĩa cân bên trái nặng hơn là 2FA = 2d.V
Muốn cân được thăng bằng trở lại thì phải đặt trên đĩa cân bên phải 1 quả cân có trọng lượng đúng bằng 2dV
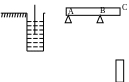 *Bài
tập 2:
Một thanh đồng chất tiết diện đều,
*Bài
tập 2:
Một thanh đồng chất tiết diện đều,
có khối lượng 10kg, chiều dài l được đặt trên
hai giá đỡ A và B như hình vẽ bên. Khoảng
cách
BC =
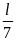 .
Ở đầu C người ta buộc một vật
.
Ở đầu C người ta buộc một vật
nặng hình trụ có bán kính đáy là 10cm, chiều
cao 32cm, trọng lượng riêng của chất làm hình trụ
là d = 35000N/m3. Lực ép của thanh lên giá đỡ A
bị triệt tiêu. Tính trọng lượng riêng của chất lỏng trong bình

Bài giải
Vì lực ép của thanh lên điểm A bị triệt tiêu nên khi đó B chính là điểm tựa và thanh đồng chất lúc này chịu tác dụng của các lực sau
+ Lực F của vật nặng tác dụng vào đầu C
+ Trọng lượng P1 đặt vào trung điểm của BC
+ Trọng lượng P2 đặt vào trung điểm của AB
Gọi l1; l2; l3 lần lượt là cánh tay đòn của lực P1; P2 và F
Theo điều kiện cân bằng của đòn bẩy ta có : P2.l2 = P1.l1 + F.l3 (3)
Do
BC =
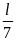 nên AB =
nên AB =
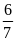 l
l
Khi
đó ta có l3
=
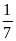 l
; l1
=
l
; l1
=
 =
=
 ; l2=
; l2=
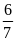 l
: 2 =
l
: 2 =
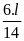 =
=
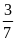 l
l
Vì
trọng lượng P1
của thanh đặt ở trung điểm của BC nên P1
=
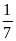 P
P
Trọng
lượng P2
đặt ở trung điểm của AB nên P2
=
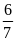 P
P
Mà F là hợp của FA và P nên F = V.d - V.dn = V ( d - dn)
Khi
đó (1) trở thành
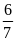 P.
P.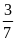 l
=
l
=
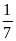 P.
P.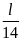 + V ( d - dn).
+ V ( d - dn).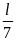
Biến
đổi ta được kết quả dn
= d -
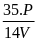 Mà V = S.h =
Mà V = S.h =
 .R2.h
( Với
.R2.h
( Với
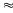 3,14)
3,14)
Khi
đó dn
= d -
 = 10000(N/m3)
= 10000(N/m3)
(
Với
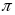 .R2.h
= 3,14.(0,1)2.0,32
= 0,01(m3)
.R2.h
= 3,14.(0,1)2.0,32
= 0,01(m3)
III: Bài tập về nhà
* Bài tập 1: Trong một bình nước có một hộp sắt rỗng nổi, dưới đáy hộp có một dây chỉ treo một hòn bi thép, hòn bi không chạm đáy bình. Độ cao của cột nước thay đổi như thế nào nếu dây treo quả cầu bị đứt.
* Bài tập 2:Người ta thả một hộp sắt rỗng nổi trong một bình nước. Ở tâm của đáy hộp có một lỗ hổng nhỏ được bịt kín bằng một cái nút có thể tan trong nước. Khi đó mực nước so với đáy bình là H. Sau một thời gian ngắn, cái nút bị tan trong nước và hộp bị chìm xuống. Hỏi mực nước trong bình có thay đổi không? Thay đổi như thế nào?
***********************
Soạn: Tiết :
Dạy: LUYỆN TẬP
 I:
Chữa bài về nhà
I:
Chữa bài về nhà
* Bài tập 1:
Gọi H là độ cao của nước trong bình
Khi dây chưa đứt thì khối nước gây ra một áp suất lên đáy bình là
F1 = dn.S.H ( S là diện tích đáy bình
dn là trọng lượng riêng của nước )
Khi dây bị đứt. Lúc này đáy bình chịu tác dụng của 2 lực đó là của nước và của viên bi nên ta có
F2 = dn.S.h + Fbi ( h là độ cao của nước khi dây đứt )
Do trọng lượng của hộp + bi + nước không thay đổi nên
F1 = F2 hay dn.S.H = dn.S.h + Fbi
Vì bi có trọng lượng nên Fbi > 0 suy ra dn.S.H > dn.S.h
Suy ra H > h vậy mực nước giảm
 *Bài
tập 2:
*Bài
tập 2:
Khi hộp nổi, lực ép của nước lên đáy bình là
F1 = dn.S.H
Khi hộp chìm lực ép là
F2 = dn.S.h + Fhộp
Do trọng lượng của nước và hộp không đổi trong cả hai trường hợp nên ta có
F1 = F2 hay dn.S.H = dn.S.h + Fhộp
Mà Fhộp > 0 nên suy ra H > h điều đó chứng tỏ mực nước giảm
II: Bài tập luyện tập
* Bài tập 1: Tiết diện của pittông nhỏ của một cái kích dùng dầu là 1,35cm2, của pittông lớn là 170cm2. Người ta dùng kích để nâng một vật có trọng lượng 42000N. Hỏi phải tác dụng lên pít tông nhỏ một lực bằng bao nhiêu?
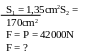
Bài giải
Áp dụng công thức về máy ép dùng chất lỏng ta có
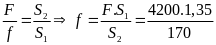 =
333,5(N)
=
333,5(N)
Vậy cần tác dụng lên pít tông nhỏ là f = 333,5(N)
* Bài tập 2: Đường kính pit tông nhỏ của một máy dùng chất lỏng là 2cm. Hỏi diện tích tối thiểu của pít tông lớn là bao nhiêu để tác dụng một lực 120N lên pít tông nhỏ có thể nâng được một ô tô có trọng lượng 24000N
Bài giải
Diện tích pít tông nhỏ là
s
=
 .
. = 3,14(cm2)
= 3,14(cm2)
Diện tích tối thiểu của pít tông lớn là
Từ
công thức
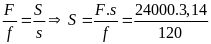 = 628 (cm2)
= 628 (cm2)
* Bài tập 3: Trong một máy ép dùng chất lỏng, mỗi lần pít tông nhỏ đi xuống một đoạn h = 0,2m thì pít tông lớn được nâng lên một đoạn H = 0,01m. Tính lực nén vật lên pít tông lớn nếu tác dụng vào pít tông nhỏ một lực f = 500N
 Bài
giải
Bài
giải
Xem chất lỏng không bị nén thì thể tích chất lỏng chuyển từ xi
lanh
nhỏ sang xi lanh lớn là V = h.s = H.S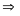
Áp suất được truyền đi nguyên vẹn nên ta có
P
=
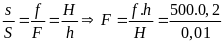 = 10000(N)
= 10000(N)
Vậy lực nén lên pít tông lớn là 10000(N)
* Bài tập 4: Dưới đáy của một thùng có lỗ hình tròn đường kính 2cm. Lỗ này được đạy kín bằng một lắp phẳng được ép từ ngoài vào bằng một lò so tác dụng một lực ép bằng 40N. Người ta đổ thủy ngân vào thùng. Hỏi độ cao cực đại của mực thủy ngân để nắp không bị bật ra? Biết KLR của thủy n gân là 13600kg/m3
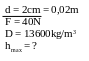
Bài giải
Lực ép của thủy ngân lên nắp ở đáy bình có diện tích s là
Từ
p =
 F
= p.S (1)
F
= p.S (1)
Áp suất của thủy ngân lên đáy bình khi mực thủy ngân có độ cao h là
p = d.h = 10.D.h (2)
Thay (2) vào (1) ta được F = 10.D.h.S
Nắp
đậy sẽ không bị bật ra khi F < 40N nên ta có 10.D.h.S
< 40 Trong đó S =
 r2
r2
Vậy
10.D.h. r2
< 40
r2
< 40
Suy
ra h <
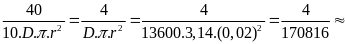 0,234(m)
0,234(m)
Vậy độ cao cực đại của mực thủy ngân để nắp không bị bật ra là 0,234(m)
* Bài tập 5: Một người thợ lặn mặc bộ áo lặn chỉ chịu được áp suất tối đa là 300000N/m2
a) Hỏi thợi lặn có thể lặn sâu nhất là bao nhiêu trong nước biển có d = 10300N/m3
b)Tính lực của nước biển tác dụng lên cửa kính quan sát của áo lặn có diện tích là 200cm2 khi lặn sâu 25m
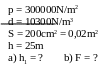
Bài giải
a) Khi người thợ lặn xuống đến độ sâu h1 thì bề mặt
áo lặn chịu một áp suất là p = d.h1
Để cho an toàn p phải nhỏ hơn áp suất tối đa
mà áo lặn có thể chịu được 300000N/m2
Vậy
ta có p < 300000 dh1
< 300000
dh1
< 300000
 h1
<
h1
<
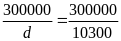
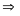 h1
< 29,1(m)
h1
< 29,1(m)
b) Lực ép của nước biển lên mặt kính quan sát là
F = p.S = d.h.S = 10300.25.0,02 = 5150(N)
III: Bài tập về nhà
* Bài tập1: Một máy ép dùng dầu có 2 xi lanh A và B thẳng đứng nối với nhau bằng một ống nhỏ. Tiết diện thẳng của xi lanh A là 200cm2 và của xi lanh B là 4cm2. Trọng lượng riêng của dầu là 8000N/m3. Đầu tiên mực dầu ở trong hai xi lanh ở cùng một độ cao.
a) Đặt lên mặt dầu trong A một pít tông có trọng lượng 40N. Hỏi sau khi cân bằng thì độ chênh lệch giữa hai mặt chất lỏng trong hai xi lanh là bao nhiêu?
b) Cần phải đặt lên mặt chất lỏng trong B một pít tông có trọng lượng bao nhiêu để hai mặt dưới của 2 pít tông nằm trên cùng một mặt phẳng
c) Cần tác dụng lên pít tông trong nhánh B một lực là bao nhiêu để có thể nâng được một vật có khối lượng 200kg đặt lên pít tông trên nhánh A? Coi như lực ma sát không đáng kể.
* Bài tập 2: Bán kính của 2 xi lanh của 1cái kích dùng dầu lần lượt là 10cm và 2cm.
a)Đặt lên pít tông lớn của kích 1 vật có khối lượng 250kg. Cần phải tác dụng lên pít tông nhỏ một lực là bao nhiêu để nâng được vật nặng lên?
b) Người ta chỉ có thể tác dụng lên pít tông nhỏ một lực lớn nhất là 500N. Vậy phải chế tạo pít tông lớn có tiết diện thẳng là bao nhiêu để có thể nâng được một ô tô có khối lượng 2500kg
********************************
Soạn: Tiết
Dạy: LUYỆN TẬP
I: Chữa bài tập về nhà
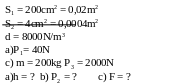
 *
Bài tập 1:
*
Bài tập 1:
Bài giải
a) Khi đặt pít tông có trọng lương P1 lên mặt chất lỏng trong nhánh A có tiết diện S1 thì lúc đó chất lỏng trong nhánh A được dồn sang nhánh B, làm cho cột chất lỏng trong nhánh B được dâng lên.
Áp
suất của pít tông tác dụng lên mặt chất lỏng ở
nhánh A là : p1
=
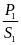
Áp suất của cột chất lỏng trong nhánh B lên một điểm trên mặt phẳng nằm ngang với mực chất lỏng trong nhánh A là: p2 = d.h
Do
có cân bằng nên ta có p1
= p2
hay
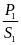 = d.h
= d.h
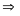 h
=
h
=
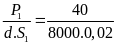 =0,25(m)
= 25(cm)
=0,25(m)
= 25(cm)
b)
Khi đặt lên mặt chất lỏng trong nhánh B một pít tông
có trọng lượng P2
thì pít tông này tác dụng lên mặt chất chất lỏng một
áp suất là : p3
=
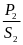
Khi cân bằng, mặt dưới của 2 pít tông cùng nằm trên 1 mặt phẳng nằm ngang. Vậy áp suất 2 pít tông tác dụng lên mặt chất lỏng bằng nhau nên ta có p1 = p3
Hay
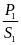 =
=
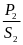
 p2
=
p2
=
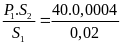 = 0,8(N)
= 0,8(N)
c)
Khi đặt vật có khối lượng 20kg lên pít tông ở nhánh
A thì vật này gây áp suất lên pít tông A là p4
=
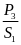
Vậy muốn nâng vật này lên phải tác dụng lên pít tông B một lực F sao cho áp suất gây ra lên trên pít tông B lớn hơn áp suất do vật gây ra lên trên pít tông A
Nên
ta có
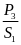
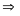 F
F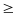
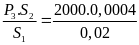 = 40(N)
= 40(N)
* Bài tập 2:

Bài giải
a)
Muốn nâng được pít tông lớn lên thì áp suất tác dụng
lên pít tông nhỏ ít nhất phải bằng áp suất tác dụng
lên pít tông lớn nên ta có
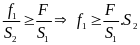
Mà
S1
=
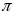 R12
;
S2
=
R12
;
S2
=
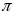 R22
; F = P1
= 2500N
R22
; F = P1
= 2500N
Nên
f1
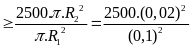 = 100(N)
= 100(N)
Vậy phải tác dụng lên pít tông nhỏ một lực lớn hơn hoặc bằng 100N thì sẽ nâng được vật lên.
b)
Từ
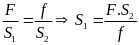
Vậy để nâng được vật lên thì pít tông lớn phải có tiết diện là
S1
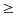
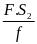 =
=
 = 0,0628(m2)
= 628(cm2
= 0,0628(m2)
= 628(cm2
II: Bài tập luyện tập:
* Bài tập 1: Một phanh ô tô dùng dầu gồm 2 xi lanh nối với nhau bằng một ống nhỏ dẫn dầu. Pít tông A của xi lanh ở đầu bàn đạp có tiết diện 4cm2, còn pít tông nối với 2 má phanh có tiết diện 8cm2. Tác dụng lên bàn đạp một lực 100N. Đòn bẩy của bàn đạp làm cho lực đẩy tác dụng lên pít tông giảm đi 4 lần. Tính lực đã truyền đến má phanh
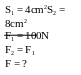 Bài
giải
Bài
giải
Áp
lực tác dụng lên pít tông là F2
=
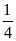 F1
=
F1
=
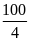 = 25(N)
= 25(N)
Khi
đó áp suất lên pít tông bàn đạp là p1
=
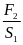 được truyền
được truyền
nguyên
vẹn đến pít tông phanh có diện tích S2
là p2
=
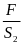
 Nên
Nên
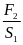 =
=
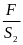
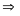 F =
F =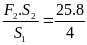 = 50(N)
= 50(N)
Vậy lực đã truyền đến má phanh là F = 50(N)
* Bài tập 2: Thả một khối đồng hình hộp chữ nhật
Vào một chậu bên dưới đựng thủy ngân, bên trên
là nước nguyên chất. Một phần khối đồng nằm trong
thủy ngân(H.vẽ). Chứng minh rằng lực đẩy Ác-Si-Mét
tổng cộng tác dụng lên khối gỗ bằng tổng trọng lượng của phần nước bị chiếm chỗ và trọng lượng của thủy ngân bị chiếm chỗ.
 Bài
giải
Bài
giải
Mặt trên của khối đồng có tiết diện S cách mặt nước độ cao h,
do đó áp lực của nước lên mặt khối đồng là
F1 = p.S = d.S.h
Khối đồng chịu áp suất chất lỏng gây ra lên đáy khối đồng là
p = d.h + d.h1 + d2.h2
Do đó áp lực tác dụng lên đáy dưới của khối đồng là
F2 = (d.h + d.h1 + d2.h2).S = d.h.S + d.h1.S + d2.h2.S
Vậy lực đẩy Ác-Si-Mét tác dụng lên toàn bộ khối đồng là
F = F2 - F1 = d.h.S + d.h1.S + d2.h2.S - d.S.h = d.h1.S + d2.h2.S = d.V1 + d2.V2
Mà trọng lượng của phần nước bị vật chiếm chỗ là
P1 = 10.m1 = 10.D.V1 = d.V1
Trọng lượng của phần thủy ngân bị vật chiếm chỗ là
P2 = 10.m2 = 10.D2.V2 = d2.V1
Vậy F = d.V1+d2.V1 = P1 + P2
* Bài tập 3: Một quả cầu bằng đồng đặc có KLR là 8900kg/m3 và thể tích là 10cm3 được thả trong một chậu thủy ngân bên trên là nước. Khi quả cầu cân bằng, một phần ngập trong thủy ngân, một phần trong nước. Tìm thể tích chìm trong thủy ngân và thể tích chìm trong nước của quả cầu? Biết KLR của nước và thủy ngân lần lượt là 1000kg/m3 và 13600kg/m3
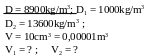

Bài giải
Ta đã chứng minh được trong bài 2 thì lực đẩy Ác-Si-Mét tác dụng lên quả cầu bằng tổng trọng lượng của phần thủy ngân và nước bị vật chiếm chỗ nên ta có:
FA = P1 + P2 = ( P1;P2 lần lượt là trọng lượng của phần nước và thủy ngân bị quả cầu chiếm chỗ )
Hay FA = d1.V1 + d2.V2
Mà trọng lượng của quả cầu ngoài không khí là : P = d.V
Vì quả cầu lơ lửng trong chất lỏng nên FA = P
Hay d.V = d1.V1 + d2.V2 (1)
Mặt khác V = V1 + V2 Suy ra V2 = V - V1 (2)
Thay (2) vào (1) ta được d.V = d1.V1 + d2 ( V - V1)
Biến
đổi ta được V1
=
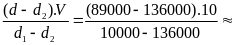 3,73(cm3)
3,73(cm3)
 Vậy
phần ngập trong nước có thể tích là V1
Vậy
phần ngập trong nước có thể tích là V1
 3,73(cm3)
3,73(cm3)
Phần
thể tích ngập trong thủy ngân là V2 6,27(cm3)
6,27(cm3)
* Bài tập 4: Hai xi lanh có tiết diện S1 và S2 thông với
nhau và có chứa nước. Trên mặt nước có đặt các
pít tông mỏng có khối lượng riêng khác nhau nên
mực nước ở 2 bên cheeng nhau một đoạn h(H.vẽ).
Đổ 1 lớp dầu lên pít tông S1 sao cho mực nước nước
ở 2 bên ngang nhau. Tính độ chênh lệch x của mực nước ở 2 xi lanh ( Theo S1; S2 và h ) Nếu lấy lượng dầu đó từ bên S1 đổ lên pít tông S2
Bài giải
Gọi P1; P2 lần lượt là trọng lượng của pít tông S1; S2
d1; d2 lần lượt là trọng lượng riêng của dầu và nước
h1 ; h2 lần lượt là chiều cao của dầu trên pít tông có tiết diện S1 ; S2
Ban
đầu khi mực nước ở 2 bênh chênh nhau 1 đoạn h nên ta
có
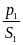 + d2.h
=
+ d2.h
=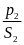 (1)
(1)
Khi
đổ dầu vào S1
ta có
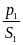 + d1.h1
=
+ d1.h1
=
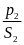 (2)
(2)
Khi
đổ dầu vào S2
ta có
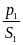 + d2.x
=
+ d2.x
=
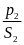 + d1.h2
+ d1.h2
 + d2.x
- d1.h2
=
+ d2.x
- d1.h2
=
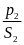 (3)
(3)
Từ
(1) và (2) suy ra
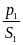 + d2.h
=
+ d2.h
=
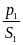 + d1.h1
+ d1.h1
 d2.h
= d1.h1
d2.h
= d1.h1
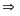 h1
=
h1
=
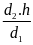 (4)
(4)
Từ
(1) và (3) suy ra
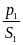 +
d2.h
=
+
d2.h
=
 + d2.x
- d1.h2
+ d2.x
- d1.h2
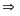 d2.h
+d1.h2
=
d2.x
d2.h
+d1.h2
=
d2.x
 x
=
x
=
 (5)
(5)
Vì
thể tích dầu không đổi nên V1
= V2
Hay h1.S1
= h2.S2
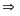 h2
=
h2
=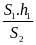 (6)
(6)
Thế
(4) vào (6) ta được h2=
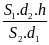 (7)
(7)
Thế
(7) vào (5) ta được x =
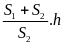
III: Bài tập về nhà
* Bài tập 1:
a) Một khí cầu có thể tích 10m3 chứa khí hiđrô, có thể kéo lên trên không một vật nặng bằng bao nhiêu?Biết trọng lượng của vỏ khí cầu là 100N, trọng lượng riêng của không khí là 12,9N/m3, của khí hiđrô là 0,9N/m3
b) Muốn kéo một người nặng 6okg lên thì khí cầu phải có thể tích tối thiểu là bao nhiêu, nếu coi trọng lượng của vỏ khí cầu vẫn không đổi
* Bài tập 2: Trên bàn em chỉ có những dụng cụ và vật liệu sau: Lực kế, bình nước
( Nước đựng trong bình có khối lượng riêng Do )
Làm thế nào, chỉ bằng các dụng cụ trên mà em có thể xác định được khối lượng riêng của một vật kim loại có hình dạng bất kỳ ? Hãy trình bầy cách làm đó.
****************************
Soạn: Tiết :
Dạy: LUYỆN TẬP
I: Chữa bài tập về nhà
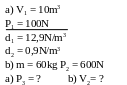 *
Bài tập 1:
*
Bài tập 1:
Bài giải
a) Trọng lượng của khí hiđrô trong khí cầu là
PH = d2.V1 = 0,9 .10 = 9(N)
Trọng lượng của khí cầu là
P = PH + P1 = 9 + 100 = 109 (N)
Lực đẩy Ác-Si-Mét tác dụng lên khí cầu là
F1 = d1.V1 = 12,9.10 = 129(N)
Vậy trọng lượng tối đa của vật mà khí cầu có thể kéo lên là
P3 = F1 - P = 129 - 109 = 20(N)
b) Trọng lượng của khí cầu trong trường hợp này là : P’H = d2.V2
Trọng lượng của người là P2 = 600(N)
Lực đẩy Ác-Si-Mét lúc này là: F2 = d1.V2
Muốn bay lên được thì khí cầu phải thỏa mãn điều kiện sau
F2
> P1
+ P’H
+ P2
Hay d1.V2
> 100 + d2.V2+
600
 V2
( d1
- d2
) > 700
V2
( d1
- d2
) > 700
 V2
>
V2
>
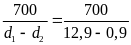 = 58,33(m3)
= 58,33(m3)
* Bài tập 2:
Để xác định KLR của vật kim loại ta cần biết khối lương m và thể tích V của nó.
+ Dùng lực kế xác định trọng lượng P1 của vật trong không khí và P2 trong nước.
Khi đó ta có : FA = P1 - P2
Mặt
khác FA
= d1.V
= 10D1.V
 V =
V =
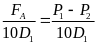
Vậy
khối lượng riêng của vật là D =
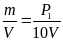 ( Vì m = 10P nên P =
( Vì m = 10P nên P =
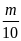 )
)
Do
đó D =
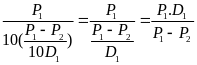
Làm như vậy sẽ xác định được khối lượng riêng của vật
 II:
Bài tập luyện tập:
II:
Bài tập luyện tập:
* Bài tập 1: Ba ống giống nhau và thông nhau chứa
nước chưa đầy ( H.vẽ), Đổ vào bên trái một cột dầu
cao h1 = 20cm và đổ vào bên phải một cột dầu cao
h2 = 25cm. Hỏi mực nước ở ống giữa sẽ dâng cao bao
nhiêu so với lúc đầu. Biết trọng lượng riêng của nước,
dầu lần lượt là d1 = 10000N/m3 và d2 = 8000N/m3.
Bài giải
Khi chưa đổ nước vào 2 nhánh thì áp suất của 3 nhánh đều bằng nhau nên ta có
p1 = p2 = p3
Khi đổ dầu vào 2 nhánh thì áp suất tổng cộng của 2 cột dầu này gây ra là.
p = d2.h1 + d2.h2 = d2 (h1 + h2) = 8000.0,45 = 3600(N)
Khi đã ở trạng thái cân bằng thì áp suất ở 3 nhánh lúc này lại bằng nhau nên ta có
P1’ = p2’ = p3’ = 3600:3 = 1200(N)
Do dầu nhẹ hơn nước nên ở nhánh giữa không có dầu và như vậy áp suất do cột nước ở nhánh giữa gây lên so với lúc đầu là :
p2’
= h’.d1
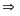 h’
=
h’
=
 = 0,12(m)
= 0,12(m)
Vậy mực nước ở nhánh giữa sẽ dâng lên thêm 0,12(m)
* Bài tập 2: Một thanh gỗ dài 15cm thả v ào trong một chậu nước thì nổi ở tư thế thẳng đứng, phần nhô khỏi mặt nước cao 3cm. Người ta rót vào chậu 1 chất dầu không trộn lẫn được vào nước có KLR là 700kg/m3. Dầu làm thành 1 lớp dầy 2cm. Hỏi phần nhô lên khỏi dầu lúc này là bao nhiêu. Biết KLR của nước là 100kg/m3


Bài giải
Vì thanh nổi trong nước nên KLR của thanh và KLR của nước phải tỷ lệ với độ dài của phần chìm trong nước của thanh và độ dài của thanh.
Vì FA = d2.V1 = 10D2.S.h’ ( V1 là phần chất lỏng bị vật chiếm chỗ, h’ là phần thanh chìm trong nước)
Ta có trọng lượng của thanh P = 10.m = 10D.V = 10D.S.h
Do vật cân bằng trong chất lỏng nên ta có
F1
= P hay 10D2.S.h’
=10D.S.h D2.h’
= D.h
D2.h’
= D.h
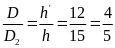
 D
=
D
=
 = 800kg/m3
= 800kg/m3
Lực đẩy Ác-Si-Mét tác dụng lên thanh khi đã đổ dầu là
F2 = 10.D2.S.h’ + 10.D1.S.h2
Do thanh nổi cân bằng nên ta có F2= P
Hay
10.D2.S.h’
+ 10.D1.S.h2
= 10D.S.h D2.h’
+ D1.h2
= D.h
D2.h’
+ D1.h2
= D.h
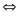 h’
=
h’
=
 = 0,106(m)
= 0,106(m)
Vậy phần thanh nhô ra khỏi dầu lúc này là
h3 = h - h’ - h2 = 0,15 - 0,02 - 0,106 = 0,024(`m) = 2,4 (m)
* Bài tập 3: Một ống nghiệm cao chứa ba chất lỏng không trộn lẫn vào nhau được có KLR lần lượt là D1 = 1080kg/m3; D2 = 900kg/m3 ; D3 = 840kg/m3. Chất lỏng D2 làm thành 1 lớp dày 4cm ở giữa 2 lớp chất lỏng kia( Mỗi lớp đều có độ dầy 10cm). Thả vào đó 1 thanh có tiết diện S1 = 1cm2, độ dai l = 16cm có KLR là D = 960kg/m3 thì thanh nổi lơ lửng ở tư thế thẳng đứng( Vì trọng tâm ở gần 1 đầu thanh). Tìm độ cao các khúc chìm trong 3 chất lỏng của thanh

Bài giải
Do lớp chất lỏng D2 làm thành một lớp dày h = 4cm nên phần thanh chìm trong chất lỏng D2 là: h2 = h = 4(cm)
Do thanh lơ lửng nên ta có FA = P
Hay 10.D1.S.h1 + 10.D2.S.h2 + 10.D3.S.h3 = 10.D.S.l
 D1.h1
+ D2.h2
+ D3.h3
= D.l (1)
D1.h1
+ D2.h2
+ D3.h3
= D.l (1)
Mà l = h1 + h2 + h3 Suy ra h3 = l - h1 - h2 = 0,16 - 0,04 - h1 = 0,12 - h1 (2)
Thay (2) vào (1) ta được D1.h1 + D2.h2 + D3. 0,12 - D3. h1 = D.l
Biến đổi ta được
h1=
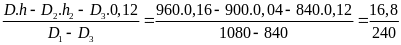 = 0,07(m)
= 0,07(m)
Vậy h3 = 0,12 - 0,07 = 0,05(m)
* Bài tập 4: Một cái cốc chứa 150g nước. Người ta thả 1 quả trứng vào cốc thì quả trứng chìm tới đáy cốc. Từ từ rót thêm nước mối có khối lượng riêng D = 1150kg/m3 vào cốc đồng thời khuấy cho đều thì lúc rót được 60ml nước muối thì thấy quả trứng rời khỏi đáy cốc nhưng không nổi lên mặt nước. Xác định KLR của quả trứng
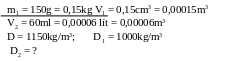
Bài giải
Khối lượng nước muối được rót thêm vào là
Từ
D =
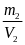
 m2=
D.V2
= 1150 . 0,00006 =0,069(kg)
m2=
D.V2
= 1150 . 0,00006 =0,069(kg)
Khi đó hỗn hợp có khối lượng là: m = m1 + m2 = 0,15 + 0,069 = 0,219(kg)
Thể tích của hỗn hợp là: V = V1 + V2 = 0,00015 + 0,00006 = 0,00021(m3)
Mà
do vật lơ lửng nên ta có: D2
= D + D1
Hau D2
=
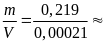 1043(kg/m3)
1043(kg/m3)
III: Bài tập về nhà
* Bài tập 1: Treo một miếng nhựa đặc vào đầu dưới của m ột lực kế, trong không khí lực kế chỉ 8N. Nhúng miếng nhựa ngập trong nước, lực kế chỉ 4N. Tính thể tích miếng nhựa và trọng lượng riêng của nó
* Bài tập 2: Một quả cầu rỗng khối lượng 1g, thể tích ngoài 6cm, chiều dày của vỏ không đáng kể, một phần chứa nước còn lại chứa 0,1g không khí, quả cầu lơ lửng trong nước. tính thể tích phần chứa không khí
*******************************
Soạn: Tiết:
Dạy: LUYỆN TẬP
I: Chữa bài tập về nhà
 *
Bài tập 1:
Bài giải
*
Bài tập 1:
Bài giải
Do ở ngoài lực kế chỉ F1 = 8N, khi nhúng vào nước lực
Kế chỉ F2 = 4N, khi đó miếng nhựa chịu lực đẩy là
FA = F1 - F2 = 8 - 4 = 4(N)
Mà FA = d.V = 10.D.V
Suy
ra thể tích miếng nhựa là: V =
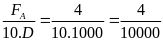 = 0,0004(m3)
= 0,0004(m3)
Trọng lượng riêng của miếng nhựa là
Từ
P1
= 10.m = 10.D.V = = d.V Suy ra d =
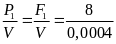 = 20000(N/m3)
= 20000(N/m3)
* Bài tập 2:
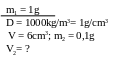
Bài giải
Khi quả cầu lơ lửng trong nước thì lực đẩy Ác-Si-Mét bằng tổng trọng lượng P1 của vỏ quả cầu ; P2 của không khí bên trong và P3 của nước bên trong nên ta có
FA = P1 + P2 + P3 Hay 10.D.V = 10.m1 + 10.m2 + 10.D3.V’(D là KLR của nước,V’ là thể tích phần nước trong quả cầu)
Suy ra thể tích cảu nước trong quả cầu là
V’
=
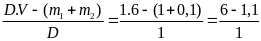 = 4,9(cm3)
= 4,9(cm3)
Vậy thể tích phần chứa không khí là : V2= V - V’ = 6 - 4,9 = 1,1(cm3)
II: Bài tập luyện tập
* Bài tập 1: Một quả cầu làm bằng kim loại có KLR là 7500kg/m3, nổi trên mặt nước,tâm của quả cầu nằm trên cùng mặt phẳng với mặt thoáng của nước. Quả cầu có một phần rỗng có dung tích 1dm3. Tính trọng lượng của quả cầu
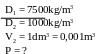

Bài giải
Thể
tích của quả cầu chìm trong nước là :

Lực
đẩy Ác-Si-Mét tác dụng lên quả cầu là: FA
= d2.V
=
d2..
Trọng lượng của quả cầu là : P = d1.V1 = d1 (V - V2) = d1.V - d1.V2
Khi
quả cầu cân bằng ta có : FA
= P hay d2.. = d1.V
- d1.V2
= d1.V
- d1.V2
Biến
đổi ta được V =
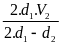
Thể
tích phần kim loại của quả cầu chìm trong nước là V1
= V = V2
=
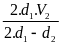 - V
- V
Biến
đổi ta được V1
=
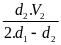
Vậy
trọng lượng của quả cầu là: P = d1.V1
=
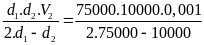
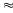 5,36(N)
5,36(N)
 *
Bài tập 2:
Một ống chữ U có 2 nhánh hình trụ tiết diện khác
nhau và chứa thủy ngân. Đổ nước vào nhánh nhỏ đến
khi cân bằng thì thấy mực thủy ngân ở 2 nhánh chênh
nhau h = 4cm. Tính chiều cao cột nước cho biết trọng
lượng riêng của thủy ngân là d1
= 136000N/m3,
của nước là d2
= 10000N/m3.
Kết quả có thay đổi không nếu đổ nước vào nhánh to
*
Bài tập 2:
Một ống chữ U có 2 nhánh hình trụ tiết diện khác
nhau và chứa thủy ngân. Đổ nước vào nhánh nhỏ đến
khi cân bằng thì thấy mực thủy ngân ở 2 nhánh chênh
nhau h = 4cm. Tính chiều cao cột nước cho biết trọng
lượng riêng của thủy ngân là d1
= 136000N/m3,
của nước là d2
= 10000N/m3.
Kết quả có thay đổi không nếu đổ nước vào nhánh to
Bài giải
Xét áp suất tại các điểm có mức ngang mặt thủy ngân
Bên có nhánh nước ở 2 nhánh ta có
P1 = p2 hay d1.h = d2.d2 ( h1;h2 lần lượt là chiều cao của
Cột thủy ngân và nước ở nhánh I và II )
Suy
ra h2
=
 = 0,544(m) = 54,4(cm)
= 0,544(m) = 54,4(cm)
Kết quả trên không phụ thuộc việc nước được đổ vào nhánh to hay nhánh nhỏ
* Bài tập 3: Có 1 cái vại, đáy bình tròn diện tích S1 = 1200cm2 và 1 cái thớt gỗ mặt hình tròn diện tích S2 = 800cm2, bề dày h = 7,5cm. Phải rót nước vào vại tới độ cao ít nhất là bao nhiêu để khi thả nhẹ thớt vào vại thì thớt nổi được? Cho biết KLR của nước và gỗ lần lượt là D1 = 100kg/m3 và D2 = 1600kg/m3
 Bài
giải
Bài
giải
Khi thớt nổi, thể tích nước bị chiếm chỗ(V1) có
trọng lượng bằng trọng lượng của thớt nên ta có
P1
= P2
hay V1.d1
= V2.d2
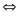 V1.D1
= V2.D2
V1.D1
= V2.D2
Vì V = S.h là thể tích của thớt nên độ cao của
Phần thớt chìm trong nước là
h’
=

Sau khi thả thớt vào, nếu độ cao cảu nước trong vại là h’ thì thớt bắt đầu nổi được vậy thể tích nước ít nhất sẽ là:
V’ = h’.S’ = h’.(S1 - S2) = 4,7.(1200 - 800) = 1880(cm3)
Trước khi thả thớt vào thì thể tích nước ấy trong vại có độ cao là
h1
=
 III:
Bài tập về nhà
III:
Bài tập về nhà
Hai bình thông nhau có tiết diện S1 = 12cm2 và
S2 = 240cm2 chứa nước và được đậy bằng 2
pít tông P1 và P2 (H.vẽ)có khối lượng không đáng kể
a)Đặt lên đĩa Đ1 của pít tông P1 một vật m có khối
lượng 420g. Hỏi pít tông P2 bị đẩy lên cao thêm bao
nhiêu xentimét
b)Để 2 pít tông vẫn ngang bằng nhau, phải đặt lên đĩa Đ2 của pít tông P2 một vật có khối lượng bằng bao nhiêu
c) Nếu đặt vật m lên đĩa Đ2 thì P1 bị đẩy lên cao thêm bao nhiêu xentimét?
******************************
Soạn: Tiết
Dạy: LUYỆN TẬP
I: Chữa bài về nhà
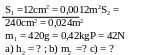
Bài giải
a)
Khi đặt lên đĩa cân Đ1
của pít tông P1
một vật có khối lượng 420g thì áp suất do vật gây ra
lên mặt chất lỏng ở pít tông là (Áp suất trên mặt
nước trong bình nhỏ tăng thêm) p1
=
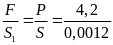 = 3500(N/m2)
= 3500(N/m2)
Khi đó pít tông lớn sẽ dâng lên một đoạn sao cho cột nước ở pít tông 2cao hơn cột nước ở pít tông 1. Khi đó áp suất do cột nước h gây ra là : p2 = d.h
Mà
p1
= p2
nên 3500 = 10000.h
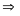 h =
h =
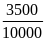 = 0,35(m) = 35(cm)
= 0,35(m) = 35(cm)
Do thể tích nước ở xi lanh tiết diện S1 dồn sang xi lanh tiết diện S2 nên ta có
V1 = V2 hay S1.( h - h2 ) = S2.h2 ( h2 là độ cao của pít tông được dâng lên )
Do diện tích S2 = 20.S1 nên ta có S1.h - S1.h1 = 20.S1.h2
Biến đổi ta được h = 21.h2
Vậy pít tông P2 bị đẩy lên độ cao của h2 chỉ bằng
h2
= h.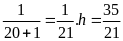
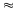 1,666...(cm)
1,666...(cm)
 1,67(cm)
1,67(cm)
b) Để 2 pít tông vẫn ngang nhau thì phải tăng áp suất trên mặt nước trong bình lớn thêm 3500N/m2 tức là phải tạo một áp lực là
F2 = p1.S1 = 3500.0,024 = 84(N)
Vậy
phải đặt lên pít tông P2
một vật có khối lượng là: m2
=
 =
8,4(kg)
=
8,4(kg)
c)
Nếu đặt vật m = 420g lên đĩa của P2
thì áp suất gây ra lên mặt chất lỏng ở pít tông là
:
 = 175(N/m2)
= 175(N/m2)
Khi đó độ chênh lệch của mực nước trong 2 bình là
Từ
:
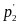 =
=
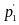 hay 175 = 10000.h’
hay 175 = 10000.h’
 h’ =
h’ =
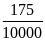 = 0,0175(m) = 1,75(cm)
= 0,0175(m) = 1,75(cm)
Và
pít tông P1
đẩy lên cao thêm
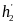 =
=
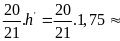 1,67(cm)
=
1,67(cm)
=
 0,0167(m)
0,0167(m)
********************************
QUANG HỌC
1. Nguån s¸ng, vËt s¸ng.
2. §Þnh luËt truyÒn th¼ng cña ¸nh s¸ng
3. Tia s¸ng vµ chïm s¸mg
4. Bãng tèi vµ bãng nöa tèi
5. §Þnh luËt ph¶n x¹ ¸nh s¸ng
6. G¬ng ph¼ng.
Bµi tËp VËt lý
Chuyªn ®Ò: §Þnh luËt truyÒn th¼ng cña ¸nh s¸ng bãng ®en - nöa tèi - G¬ng ph¼ng
PhÇn I : Bµi tËp vÒ Bãng ®en - nöa tèi.
Bµi
1. Mét ®iÓm s¸ng S
c¸ch têng mét kho¶ng ST = d. T¹i vÞ trÝ M trªn ST c¸ch
M mét kho¶ng SM =
 ngêi
ta ®Æt mét tÊm b×a h×nh trßn vu«ng gãc víi ST cã b¸n kÝnh
R vµ cã t©m trïng víi M
ngêi
ta ®Æt mét tÊm b×a h×nh trßn vu«ng gãc víi ST cã b¸n kÝnh
R vµ cã t©m trïng víi M
a. T×m b¸n kÝnh bãng ®en trªn têng.
b. CÇn di chuyÓn tÊm b×a theo ph¬ng vu«ng gãc víi mµn mét ®o¹n b»ng bao nhiªu ? Theo chiÒu nµo ®Ó b¸n kÝnh vïng tèi gi¶m ®i mét nöa. T×m tèc ®é thay ®æi cña b¸n kÝnh bãng ®en biÕt tÊm b×a di chuyÓn ®Ìu víi vËn tèc v.
c. VÞ trÝ tÊm b×a nh ë c©u b) thay ®iÕm s¸ng S b»ng mét nguån s¸ng h×nh cÇu cã b¸n kÝnh r.
- T×m diÖn tÝch bãng ®en trªn têng.
- T×m diÖn tÝch cña bãng nöa tèi trªn têng.
Bµi gi¶i
|
Gi¸o viªn ph©n tÝch vµ yªu cÇu häc sinh vÏ h×nh |
a) B¸n kÝnh vïng tèi trªn têng lµ PT
 SIM
vµ
SIM
vµ
 SPT
lµ 2 tam gi¸c vu«ng ®ång d¹ng nªn
SPT
lµ 2 tam gi¸c vu«ng ®ång d¹ng nªn
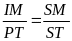
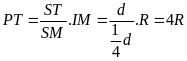
b) Tõ h×nh vÏ ta thÊy ®Ó b¸n kÝnh vïng tèi gi¶m xuèng ta ph¶i di chuyÓn tÊm b×a vÒ phÝa têng
Gäi
P1T
lµ b¸n kÝnh bãng ®en lóc nµy P1T
=
 PT
= 2R
PT
= 2R
 SIM
vµ
SIM
vµ
 SPT
lµ 2 tam gi¸c vu«ng ®ång d¹ng nªn
SPT
lµ 2 tam gi¸c vu«ng ®ång d¹ng nªn
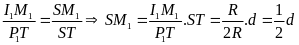
VËy
cÇn di chuyÓn tÊm b×a vÒ phÝa têng mét ®o¹n M1M
= SM1
- SM =
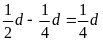
Khi
tÊm b×a di chuyÓn ®Òu víi vËn tèc v vµ ®i ®îc
qu·ng ®êng M1M
=
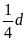 th× mÊt thêi gian
th× mÊt thêi gian
t
=
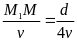 .
.
Còng trong kho¶ng thêi gian ®ã b¸n kÝnh cña vïng tèi thay ®æi mét ®o¹n lµ
PP1 = PT – P1T = 4R – 2R = 2R
VËy
tèc ®é thay ®æi cña b¸n kÝnh vïng tèi lµ v’ =
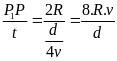
c) Thay ®iÓm s¸ng S b»ng nguån s¸ng h×nh cÇu.

Gäi AB lµ ®êng kÝnh nguån s¸ng, O lµ t©m nguån s¸ng. Theo kÕt qu¶ c©u b) M lµ trung ®iÓm cña ST.
B¸n
kÝnh vïng tèi lµ PT, ta cã
 (g.c.g)
(g.c.g)
 PD
= BC.
PD
= BC.
Mµ ta l¹i cã BC = OC – OB = MI – OB = R-r.
PT = PD + DT = BC + IM = (R-r) + R = 2R – r
VËy
diÖn tÝch vïng tèi trªn têng lµ: STèi
=
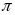 (2R
– r)2
(2R
– r)2
Vïng nöa tèi lµ diÖn tÝch h×nh vµnh kh¨n cã b¸n kÝnh lín lµ P’T, b¸n kÝnh nhá lµ PT
Ta
cã:
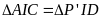 (g.c.g)
(g.c.g)
 P’D
= AC = R+r
P’D
= AC = R+r
Mµ: P’T = P’D + IM = AC + IM = R+r + R = 2R+r
Tõ ®ã ta cã: DiÖn tÝch vïng nöa tèi lµ:
SNöa
tèi
=
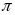 (2R
+ r)2
-
(2R
+ r)2
-
 (2R
- r)2
= 8
(2R
- r)2
= 8 Rr
Rr
Bµi 2.
Mét ®Üa trßn t©m O1 b¸n kÝnh R1 = 20cm, ph¸t s¸ng vµ ®îc ®Æt song song víi mét mµn ¶nh vµ c¸ch mµn ¶nh mét kho¶ng D = 120 cm. Mét ®Üa trßn kh¸c t©m O2 b¸n kÝnh R2 = 12 cm ch¾n s¸ng cóng ®îc ®Æt song song víi mµn ¶nh vµ ®êng nèi t©m O1O2 vu«ng gãc víi mµn ¶nh.
a) T×m vÞ trÝ ®Æt O2 ®Ó vïng tèi trªn mµn cã ®êng kÝnh R = 4 cm. Khi ®ã b¸n kÝnh R’ cña ®êng trßn giíi h¹n ngoµi cïng cña bãng nöa tèi trªn mµnlµ bao nhiªu?
b) Tõ vÞ trÝ O2 ®îc x¸c ®Þnh ë c©u a), cÇn di chuyÓn ®Üa ch¾n s¸ng nh thÕ nµo ®Ó trªn mµn võa vÆn kh«ng cßn vïng tèi

a) Tõ h×nh vÏ ta cã: Oa lµ b¸n kÝnh cña vïng tèi trªn mµn, OA = R = 4 cm
- OP lµ b¸n kÝnh cña ®êng trßn giíi h¹n ngoµi cïng cña vung nöa tèi OP =R’
Ta
cã:
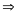
 =
=
 =
=
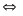
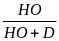 =
=
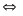
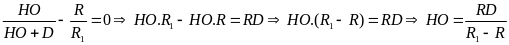
Thay
sè ta cã HO =
 cm
cm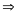 HO1
=120+30=150 cm
HO1
=120+30=150 cm
MÆt kh¸c:
Ta
cã:
 =
=
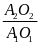
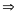 HO2
=
HO2
=
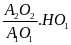 =
=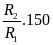 =
=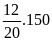 =
90 cm.
=
90 cm.
VËy ®Üa ch¾n s¸ng ph¶i ®Æt c¸ch ®Üa ph¸t s¸ng mét kho¶ng O1O2 = HO1 – HO=90-30=60 cm th× vïng tèi trªn mµn cã b¸n kÝnh lµ 4 cm.
TÝnh R’:
Ta
cã:
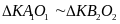
 =
=
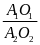
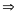
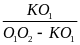 =
=
 -
- =0
=0
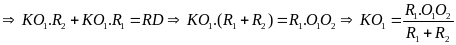
Thay
sè ta cã KO1
=
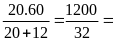 cm
cm KO1
= 37.5 cm
KO1
= 37.5 cm
MÆt kh¸c:
Ta
cã:

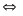
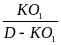 =
=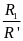
 R’=
R’=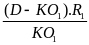 thay sè ta cã:
thay sè ta cã:
R’
=
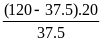 =
44 cm
=
44 cm
|
Tõ h×nh vÏ ta cã ®Ó trªn nµm h×nh võa vÆn kh«ng cßn bãng tèi th× ph¶i di chuyÓn ®Üa ch¾n s¸ng vÒ phÝa O1 mét ®o¹n O2O’2 . Ta
cã :
|
Thay
sè ta cã: Mµ O1O2 = OO1-OO’2 = 120-72 = 48 cm nªn O2O’2 = O1O2 – O1O’2 = 60-48 = 12 cm VËy ph¶i di chuyÓn ®Üa ch¾n s¸ng ®i mét ®o¹n 12 cm th× trªn mµn võa vÆn kh«ng cßn vïng tèi |
|
C¸c bµi tËp t¬ng tù.
Bµi 1 Mét ®iÓm s¸ng c¸ch mµn ¶nh mét kho¶ng SH = 1m. t¹i trung ®iÓm M cña SH ngêi ta ®Æt mét tÊm b×a h×nh trßn vu«ng gãc víi SH.
a) T×m b¸n kÝnh vïng tèi trªn mµn nÕu b¸n kÝnh tÊm b×a lµ R = 10 cm.
b) Thay ®iÓm s¸ng S b»ng nguån s¸ng h×nh cÇu cã b¸n kÝnh r = 2cm. T×m b¸n kÝnh vungd tèi vµ vïng nöa tèi.
Gi¶i
Tãm t¾t SH = 1m = 100cm IM = R = 10 cm r = 2cm
|
|
a) B¸n kÝnh vïng tèi trªn têng lµ PH
 SIM
SIM
 SPH
SPH
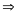
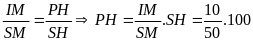 =20 cm
=20 cm
Ta cã: PH’ = AA’ () AA’ = SA’ – SA = MI – SA = R – r = 10 – 2 = 8 cm
T¬ng tù ta cã: A’B = HO= AA’ + AB = AA’ +2r = 8+4 = 12 cm VËy PO = HO –HP = 12-8 = 4 cm Vïng nöa tèi lµ h×nh vµnh kh¨n cã bÒ réng lµ 4 cm.
|
|
Bµi 2 Mét ®iÓm s¸ng c¸ch mµn ¶nh mét kho¶ng D = 4.5m. §Æt mét qu¶ cÇu ch¾n s¸ng t©m O, b¸n kÝnh r = 0,3 m gi÷a S vµ mµn sao cho SO vu«ng gãc víi mµn vµ OS = d
a) T×m b¸n kÝnh R cña vïng tèi trªn mµn khi d = 0,5m vµ d=4m.
b) TÝnh d ®Ó R = 1,5m.
Gi¶i
a)
Ta cã
mµ
nªn
ta cã thay sè ta cã: Khi d= 0,5m th× b¸n kÝnh vïng tèi trªn mµn lµ R=3.38m Khi d= 4m th× b¸n kÝnh vïng tèi trªn mµn lµ R=0.34m |
|
b)
Tõ biÓu thøc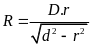 ta cã:
ta cã:
 Thay
sè ta cã ®Ó R = 1,5m th× d = 0.95m
Thay
sè ta cã ®Ó R = 1,5m th× d = 0.95m
Bµi 3. Mét ®iÓm s¸ng ®Æt c¸ch mµn 2m. Gi÷a ®iÓm s¸ng vµ mµn ngêi ta ®Æt mét ®Üa ch¾n s¸ng h×nh trßn sao cho ®Üa song song víi mµn vµ ®iÓm s¸ng m»n trªn trôc cña ®Üa.
T×m ®êng kÝnh bãng ®en trªn mµn biÕt ®êng kÝnh cña ®Üa d =20 cm vµ ®Üa c¸ch ®iÓm s¸ng 50 cm.
CÇn di chuyÓn ®Üa theo ph¬ng vu«ng gãc víi mµn mét kho¶ng b»ng bao nhiªu vµ theo chiÒu nµo ®Ó ®êng kÝnh cña ®Üa gi¶m ®i mét nöa.
BiÕt ®Üa di chuyÓn ®Òu víi vËn tèc v = 2m/s t×m tèc ®é thay ®æi ®êng kÝnh cña bãng ®en.
Gi÷ nguyªn vÞ trÝ cña ®Üa vµ mµn nh c©u b) thay ®iÓm s¸ng b»ng vËt s¸ng h×nh cÇu ®êng kÝnh d1 =8cm. T×m vÞ trÝ ®Æt vËt s¸ng ®Ó ®êng kÝnh cña bãng ®en vÉn nh c©u a). T×m diÖn tÝch cña vïng nöa tèi xung quanh bãng ®en.
HD
a); b) Nh c©u a,b bµi 1. KÕt qu¶
§êng kÝnh bãng ®en trªn mµn lµ: 80 cm
CÇn di chuyÓn ®Üa ch¾n s¸ng mét kho¶ng lµ 50 cm
c) T×m vËn tèc thay ®æi cña bãng ®en:
|
Do
®Üa di chuyÓn víi vËn tèc v = 2m/s vµ ®i ®îc qu¶ng
®êng MM1
= 0.5 m nªn mÊt th× gian lµ t=
Tõ
®ã ta cã tèc ®é thay ®æi bãng ®en lµ
|
d)
|
Gäi O lµ t©m, MN lµ ®êng kÝnh vËt s¸ng h×nh cÇu, P lµ giao cña MA’ vµ NB’ Ta cã
Ta
l¹i cã:
mµ
OI1
= PI1
– PO =
|
VËy cÇn ®Æt ®Üa ch¾n s¸ng c¸ch t©m vËt s¸ng h×nh cÇu lµ 20 cm
*) Gäi K lµ giao ®iÓm cña NA2 vµ MB2
Ta
cã
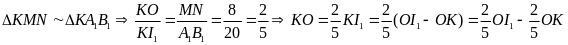

MÆt kh¸c ta cã:
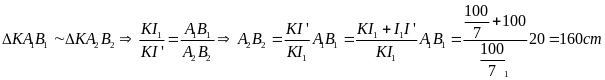
VËy diÖn tÝch vïng nöa tèi lµ
S
=
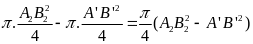 =
=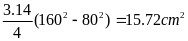
Bµi 4.
Mét ngêi cã ®é cao h ®øng ngay díi bãng ®Ìn treo ë ®é cao H (H>h). NÕu ngêi ®ã ®i ®Òu víi vËn tèc v. H·y x¸c ®Þnh chuyÓn ®éng cña bãng cña ®Ønh ®Çu in trªn mÆt ®Êt.
S |
C¸c tia s¸ng ph¸t ra tõ bãng ®Ìn bÞ ngêi chÆn l¹i t¹o ra mét kho¶ng tèi trªn ®Êt ®ã lµ bãng cña ngêi ®ã. Trong kho¶ng thíi gian t, ngêi di chuyÓn mét qu¶ng ®êng S = BB’ = v.t. Khi ®ã bãng cña ®Ønh ®Çu di chuyÓn mét ®o¹n ®êng S’ = BB” Ta
cã:
|
MÆt
kh¸c ta l¹i cã: B”B’= BB’+B’B” VËy
vËn tèc cña bãng cña ®Ønh ®Çu lµ
|
|
PhÇn II: Bµi tËp vÒ G¬ng ph¼ng.
Bµi 1.
|
|
HD
a)
|
Tõ h×nh vÏ ta cã vïng quan s¸t ®îc ¶nh M’ cña M ®îc giíi h¹n bëi G¬ng PQ vµ c¸c tia PC; QD. Vïng quan s¸t ®îc ¶nh N’ cña N ®îc giíi h¹n bëi G¬ng PQ vµ c¸c tia PA; QB VÞ trÝ cuØa mçi ngêi ®Òu kh«ng n»m trong vïng quan s¸t ¶nh cña ngêi kia nªn hä kh«ng nh×n thÊy nhau trong g¬ng. |
b) NÕu hai ngêi cïng tiÕn ®Õn g¬ng theo ph¬ng vu«ng gãc víi vËn tèc nh nhau th× kho¶ng c¸ch tõ hä ®Õn g¬ng kh«ng thay ®æi nªn hä vÉn kh«ng nh×n thÊy nhau trong g¬ng.
c) Khi mét trong hai ngêi tiÕn ®Õn g¬ng theo ph¬ng vu«ng gãc
XÐt 2 trêng hîp.
1) Ngêi M di chuyÓn, ngêi N ®øng yªn.
Tõ h×nh vÏ ta thÊy: §Ó nh×n thÊy ¶nh N’ cña ngêi N trong g¬ng th× ngêi M ph¶i tiÕn vµo gÇn g¬ng ®Õn vÞ trÝ M1 th× b¾t ®Çu nh×n thÊy N’ trong g¬ng.
Tõ
®ã ta cã:
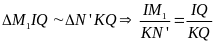 thay sè ta cã: IM1
= 0,5m
thay sè ta cã: IM1
= 0,5m
2) Ngêi N di chuyÓn, ngêi M ®øng yªn.
Tõ h×nh vÏ ta thÊy: §Ó nh×n thÊy ¶nh M’ cña ngêi M trong g¬ng th× ngêi N ph¶i tiÕn ra xa g¬ng ®Õn vÞ trÝ N1 th× b¾t ®Çu nh×n thÊy M’ trong g¬ng.
Tõ
®ã ta cã:
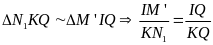 thay sè ta cã: IN1
= 2 m
thay sè ta cã: IN1
= 2 m
Bµi
2.
ChiÕu mét chïm s¸ng SI vµo g¬ng ph¶ng G. Tia ph¶n x¹
IR. Gi÷ tia tíi cè ®Þnh, quay g¬ng mét gãc
 quang
mét trôc
quang
mét trôc
 víi
mÆt ph¼ng tíi. TÝnh gãc quay cña tia ph¶n x¹ t¹o bëi tia IR
vµ IR’.
víi
mÆt ph¼ng tíi. TÝnh gãc quay cña tia ph¶n x¹ t¹o bëi tia IR
vµ IR’.
|
a) Trêng hîp trôc quay qua I Gäi gãc t¹o bëi tia IR vµ IR’ lµ Theo ®Þnh luËt ph¶n x¹ AS ta cã: i1 = i’1; i2 = i’2
Thay
(2) vµo (1) ta ®îc:
VËy
|
|
|
b) Trêng hîp trôc quay bÊt kú +)
XÐt
+)
XÐt
Thay (2) vµo (1) ta cã:
VËy.
|
|
VËy
khi g¬ng quay ®i mét gãc
 th× tia ph¶n x¹ quay ®i cïng chiÒu mét gãc
th× tia ph¶n x¹ quay ®i cïng chiÒu mét gãc
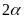
Bµi 3. Cho g¬ng ph¼ng h×nh vu«ng c¹nh a ®Æt th¼ng ®øng trªn nÒn nhµ, mÆt híng vµo têng vµ song song víi têng. Trªn sµn nhµ s¸t ch©n têng, tríc g¬ng cã ®iÓm s¸ng ®iÓm S
a) X¸c ®Þnh kÝch thíc cña vÖt s¸ng trªn têng do chïm tia ph¶n x¹ tõ g¬ng t¹o nªn.
b) Khi g¬ng dÞch chuyÓn víi vËn tèc v vu«ng gãc víi têng (Sao cho g¬ng lu«n ë vÞ trÝ th¼ng ®øng vµ song song víi têng) th× kÝch thíc cña vÖt s¸ng trªn têng thay ®æi nh thÕ nµo ? gi¶i thÝch. T×m vËn tèc cña ¶nh S’
HD
a)
|
XÐt sù ph¶n x¹ ¸nh s¸ng n»m trong mÆt ph¼ng th¼ng ®øng Ta
cã S’ lµ ¶nh cña Svµ ®èi xøng víi S qua g¬ng,
T¬ng tù víi c¸c c¹nh cßn l¹i vËy vÖt s¸ng trªn têng lµ h×nh vu«ng cã c¹nh =2a
|
b)
|
Khi nguån s¸ng S ë s¸t ch©n têngvµ di chuyÓn g¬ng theo ph¬ng vu«ng gãc víi têng(®Õn gÇn hoÆc ra xa têng)th× kÝch thíc cña vÖt s¸ng kh«ng thay ®æi. Lu«n lµ hinhg vu«ng c¹nh lµ 2a. V× SC lu«n b»ng 2AB = 2a
|
Trong kho¶ng thêi gian t g¬ng di chuyÓn víi vËn tèc v vµ ®i ®îc qu·ng ®êng BB’ = vt.
Còng trong thêi gian ®ã ¶nh S’ cña S dÞch chuyÓn víi vËn tèc v’ vµ ®i ®îc qu·ng ®êng S’S” = v’t
Theo tÝnh chÊt ¶nh vµ vËt ®èi xøng nhau qua g¬ng ta cã:
SB’ = B’S” <=>SB + BB’ = B’S’+S’S” (1)
SB = BS’ <=> SB = BB’ + B’S’ (2)
Thay (2) vµ (1) ta cã: BB’ + B’S’+ BB’ = B’S’+S’S” <=> 2BB’ = S’S” Hay v’t = 2vt <=> v’ =2v
Bµi 4
Mét ®iÓm s¸ng S ®Æt tríc mét g¬ng ph¼ng G cè ®Þnh vµ chuyÓn ®éng víi vËn tèc v ®èi víi g¬ng. X¸c ®Þnh vËn tèc cña ¶nh S’ ®èi víi g¬ng vµ ®èi víi S trong trêng hîp.
S chuyÓn ®éng song song víi g¬ng
S chuyÓn ®éng vu«ng gãc víi g¬ng.
S chuyÓn ®éng theo ph¬ng hîp víi mÆt ph¼ng g¬ng mét gãc
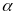
Gi¶i
|
|
|
a) Trêng hîp S chuyÓn ®éng song song víi g¬ng.
V× S’ ®èi xøng víi S qua g¬ng nªn vËn tèc cña S’ ®èi víi g¬ng cãcïng ®é lín, song song vµ cïng chiÒu víi v ®èi víi g¬ng. Cßn vËn tèc cña S’ ®èi víi S b»ng 0.
b) Trêng hîp S chuyÓn ®éng vu«ng gãc víi g¬ng.
VËn tèc cña S’ ®èi víi g¬ng cã cïng ®é lín, cïng ph¬ng vµ ngîc chiÒu víi v. VËn tèc cña S’ ®èi víi S cïng ph¬ng vµ ngîc chiÒu vµ cã ®é lín b»ng 2v.
c)
S chuyÓn ®éng theo ph¬ng hîp víi mÆt ph¼ng g¬ng
mét gãc
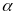
Lóc nµy cã thÓ coi S võa chuyÓn ®éng song song víi g¬ng (víi vËn tèc v1), võa chuyÓn ®éng vu«ng gãc víi g¬ng (víi vËn tèc v2)
Ta
cã v1
= v.cos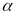 vµ v2
= v.sin
vµ v2
= v.sin
VËy
vËn tèc cña S’ ®èi víi g¬ng lµ v1
= v.cos cßn
vËn tèc cña S’ ®èi víi S lµ 2.v2=
2v.sin
cßn
vËn tèc cña S’ ®èi víi S lµ 2.v2=
2v.sin theo
ph¬ng vu«ng gãc víi g¬ng.
theo
ph¬ng vu«ng gãc víi g¬ng.
Bµi 5
|
Cho
h×nh vÏ, S lµ 1 ®iÓm s¸ng cè ®Þnh n»m tríc 2 g¬ng
Gi¸o viªn vµ G2.
G¬ng G1
quay quanh I1,
G¬ng G2
quay quanh I2
(§iÓm I1
vµ I2
cè ®Þnh). BiÕt
|
HD
V× vËt vµ ¶nh ®èi xøng nhau qua g¬ng nªn. Khi hai g¬ng quay ta cã S1 ch¹y trªn ®êng trßn t©m I1 b¸n kÝnh I1S vµ S2 ch¹y trªn ®êng trßn t©m I2 b¸n kÝnh I2S
Ha) |
Hb) |
a)
S1S2
nhá nhÊt khi S1 vµ
S2
trïng nhau t¹i giao ®iÓm thøc 2 S’ cña hai ®êng trßn.
Khi ®ã, mÆt ph¼ng ph¶n x¹ cña 2 g¬ng trïng nhau vËy
b) S1S2 lín nhÊt khi S1 vµ S2 n»m ë hai ®Çu ®êng nèi t©m cña hai ®êng trßn. Khi ®ã I1 vµ I2 lµ ®iÓm tíi cña c¸c tia s¸ng trªn mçi g¬ng.
Trong
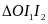 ta
cã:
ta
cã:
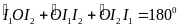
Hay

* Bài 6:
Chiếu một tia sáng hẹp vào một gương phẳng. Nếu cho gương quay đi một góc a quanh một trục bất kì nằm trên mặt gương và vuông góc với tia tới thì tia phản xạ sẽ quay đi một góc bao nhiêu? Theo chiều nào?
* Bài 7::
Hai gương phẳng M1 , M2 đặt song song có mặt phản xạ quay vào nhau. Cách nhau một đoạn d. Trên đường thẳng song song với hai gương có hai điểm S, O với các khoảng cách được cho như hình vẽ a) Hãy trình bày cách vẽ một tia sáng từ S đến gương M1 tại I, phản xạ đến gương M2 tại J rồi phản xạ đến O b) Tính khoảng cách từ I đến A và từ J đến B
|
|
* Bài 8: Một người cao 1,65m đứng đối diện với một gương phẳng hình chữ nhật được treo thẳng đứng. Mắt người đó cách đỉnh đầu 15cm.
a) Mép dưới của gương cách mặt đất ít nhất là bao nhiêu để người đó nhìn thấy ảnh của chân trong gương?
b) Mép trên của gương cách mặt đất nhiều nhất bao nhiêu để người đó thấy ảnh của đỉnh đầu trong gương?
c) Tìm chiều cao tối thiểu của gương để người đó nhìn thấy toàn thể ảnh của mình trong gương.
d) Các kết quả trên có phụ thuộc vào khỏng cách từ người đó tới gương không? vì sao?
* Bài 9:Người ta dự định đặt bốn bóng điện tròn ở bốn góc của một trần nhà hình vuông mỗi cạnh 4m và một quạt trần ở chính giữa trần nhà. Quạt trần có sải cánh (Khoảng cách từ trục quay đến đầu cánh) là 0,8m. Biết trần nhà cao 3,2m tính từ mặt sàn. Em hãy tính toán thiết kế cách treo quạt để sao cho khi quạt quay. Không có điểm nào trên mặt sàn bị sáng loang loáng.
* Bài 10:
Ba gương phẳng (G1), (G21), (G3) được lắp thành một lăng trụ đáy tam giác cân như hình vẽ Trên gương (G1) có một lỗ nhỏ S. Người ta chiếu một chùm tia sáng hẹp qua lỗ S vào bên trong theo phương vuông góc với (G1). Tia sáng sau khi phản xạ lần lượt trên các gương lại đi ra ngoài qua lỗ S và không bị lệch so với phương của tia chiếu đi vào. Hãy xác định góc hợp bởi giữa các cặp gương với nhau |
|
HƯỚNG DẪN GIẢI
* Bài 6:
* Xét gương quay quanh trục O từ vị trí M1 đến vị trí M2 (Góc M1O M1 = a) lúc đó pháp tuyến cũng quay 1 góc N1KN2 = a (Góc có cạnh tương ứng vuông góc). * Xét DIPJ có: Góc
IJR2
=
2i’ = 2i + b Þ b = 2(i’-i) (1) * Xét DIJK có
i’ = i + a Þ a = 2(i’-i) (2) Từ (1) và (2) ta suy ra b = 2a Tóm lại: Khi gương quay một góc a quanh một trục bất kì thì tia phản xạ sẽ quay đi một góc 2a theo chiều quay của gương |
|
* Bài 7:
a) Chọn S1 đối xứng S qua gương M1 ; Chọn O1 đối xứng O qua gương M2 , nối S1O1 cắt gương M1 tại I , gương M2 tại J. Nối SIJO ta được tia cần vẽ b) DS1AI ~ D S1BJ Þ
Þ
AI =
Xét DS1AI ~ D S1HO1 Þ
|
|
Þ
AI =
 thau vào (1) ta được BJ =
thau vào (1) ta được BJ =

* Bài 8: a) Để mắt thấy được ảnh của chân thì mép dưới của gương cách mặt đất nhiều nhất là đoạn IK Xét DB’BO có IK là đường trung bình nên : IK
=
b) Để mắt thấy được ảnh của đỉnh đầu thì mép trên của gương cách mặt đất ít nhất là đoạn JK Xét DO’OA có JH là đường trung bình nên : JH
=
Mặt khác : JK = JH + HK = JH + OB |
|
Þ JK = 0,075 + (1,65 – 0,15) = 1,575m
c) Chiều cao tối thiểu của gương để thấy được toàn bộ ảnh là đoạn IJ.
Ta có : IJ = JK – IK = 1,575 – 0,75 = 0,825m
d) Các kết quả trên không phụ thuộc vào khoảng cách từ người đến gương do trong các kết quả không phụ thuộc vào khoảng cách đó. Nói cách khác, trong việc giải bài toán dù người soi gương ở bất cứ vị trí nào thì các tam giác ta xét ở phần a, b thì IK, JK đều là đường trung bình nên chỉ phụ thuộc vào chiều cao của người đó.
* Bài 9:
Để khi quạt quay, không một điểm nào trên sàn bị sáng loang loáng thì bóng của đầu mút quạt chỉ in trên tường và tối đa là đến chân tường C và D. Vì nhà hình hộp vuông, ta chỉ xét trường hơph cho một bóng, các bóng còn lại là tương tự (Xem hình vẽ bên) Gọi L là đường chéo của trần nhà : L
= 4 Khoảng cách từ bóng đèn đến chân tường đối diện là : |
|
S1D
=
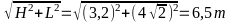
T
là điểm treo quạt, O là tân quay của cánh quạt. A, B là
các đầu mút khi cánh quạt quay. Xét DS1IS3
ta có :
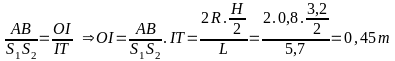
Khoảng cách từ quạt đến điểm treo là : OT = IT – OI = 1,6 – 0,45 = 1,15m
Vậy quạt phải treo cách trần nhà tối đa là 1,15m
* Bài 10:Vì sau khi phản xạ lần lượt trên các gương, tia phản xạ ló ra ngoài lỗ S trùng đúng với tia chiếu vào. Điều đó cho thấy trên từng mặt phản xạ có sự trùng nhau của tia tới và tia ló. Điều này chỉ xảy ra khi tia KR tới gương G3 theo hướng vuông góc với mặt gương. Trên hình vẽ ta thấy : Tại
I :
Tại
K:
Mặt
khác
Do
KR^BC
Þ
Trong
DABC
có
|
|
Û
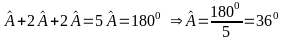

KHÔNG ÔN (KHÔNG CÓ TRONG PHẠM VI ĐỀ)
Phần NHIỆT HỌC
Tóm tắt lý thuyết:
1. Định nghĩa nhiệt lượng:Phần nội năng mà vật nhận được hay mất đi trong quá trình truyền nhiệt gọi là nhiệt lượng.
2. Định nghĩa nhiệt dung riêng:Nhiệt lượng cần cung cấp cho 1kg của một chất để nó tăng thêm 1oK gọi là nhiệt dung riêng của chất đó.
3.Cáccông thức
a. Tính nhiệt lượng thu vào để tăng nhiệt độ từ t1 t2:Qthu = mc(t2 –t1) ( t2>t1)
b. Tính nhiệt lượng tỏa ra khi hạ nhiệt từ t2 t1: Qtỏa = mc ( t1 – t2) (t1>t2)
c. Phương trình cân bằng nhiệt: Qtỏa = Qthu.
d.
Tính nhiệt lượng thu vào khi nóng chảy và tỏa ra khi
đông đặc ở NĐNC ( NĐĐĐ): Q = m.
e. Tính nhiệt lượng thu vào khi hóa hơi và tỏa ra khi ngưng tụ ở nhiệt độ hóa hơi( NĐNT): Q = L.m
f. Tính nhiệt luợng tỏa ra khi đốt cháy nhiên liệu: Q = q.m.
4. Đơn vị của các đại lượng:
Q là nhiệt lượng, đơn vị J
m là khối lượng, đơn vị kg
t là nhiệt độ, dơn vị là 0C hoặc 0K ( 10C = 10K)
c là nhiệt dung riêng, đơn vị J/kg.K
 là
nhiệt nóng chảy, đơn vị J/kg
là
nhiệt nóng chảy, đơn vị J/kg
L là nhiệt hóa hơi, đơn vị J/kg.
Q là năng suất tỏa nhiệt của nhiên liệu , đơn vị là J/kg
5.
Hiệu suất tỏa nhiệt với thu nhiệt, hiệu suất của
động cơ nhiệt: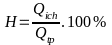
A. Phương pháp giải bài tập:
1. Một nồi đồng có khối lượng 300g chứa 1 lít nước. Tính nhiệt lượng cần thiết để cung cấp cho nồi nước tăng nhiệt độ từ 350C đến 1000C
Giải:
Nhiệt lượng cần cung cấp cho nồi đồng để nó tăng nhiệt độ từ 350C đếân1000C.
Q1 = m1c1(t2 – t1) = 0,3.380.( 100 – 35) = 7410J
Nhiệt lượng cần cung cấp cho nồi đồng để nó tăng nhiệt độ từ 350C đếân1000C.
Q1 = m2.c2( t2 – t1) = 1.4200.( 100 – 35) = 273000J
Nhiệt lượng cần cung cấp cho ấm nước:
Q = Q1 + Q2 = 7410 + 273000 = 280410 J
2. Một quả cầu nhôm có khối lượng 0,105kg được đun nóng tới 1420C rồi thả vào chậu nước ở nhiệt độ 200C. Sau một thời gian nhiệt độ của cả hệ thống là 420C. Xem như nhiệt lượng chỉ trao đổi cho nhau. Xác định khối lượng của nước.
Giải:
Nhiệt lượng quả cầu nhôm tỏa ra khi hạ nhiệt từ 1420C xuống 420C.
Qtỏa = m1c1( t1 – t2) = 0,105.880.(142-42) =9240J
Nhiệt lượng nước thu vào để nó tăng nhiệt độ từ 200C đếân420C.
Q2 = m2.c2 ( t2 – t1) = m2.4200(42 – 20) = 92400m2J
Theo phương trình cân bằng nhiệt , ta có:
Q1 = Q2 9240 = 92400m2 => m2 = 0,1kg.
3. Có 20kg nước 200C, phải pha vào thêm bao nhiêu kg nước ở 1000C để được nước ở 500C
Giải:
Nhiệt lượng 20kg nước thu vào để tăng nhiệt độ từ 200C đến 500C
Q1 = m1.c1 ( t2 – t1) = 20.4200.(50 – 20) = 2520000J
Nhiệt lượng do khối nước nóng tỏa ra khi hạ nhiệt từ 1000C xuống 500C.
Q2 = m2.c2.( t’1 – t2) = m2.4200.( 100 – 50) = 210000J.
Theo phương trình cân bằng nhiệt , ta có:
Q1 = Q2 2520000J = m2.210000J => m2 = 12kg.
Vậy cần 12kg nước ở nhiệt độ 1000C.
4. Vật A có khối lượng 0,1kg ở nhiệt độ 1000C được bỏ vào một nhiệt lượng kế B làm bằng đồng có khối lượng 0,1kg chứa 0,2kg nước có nhiệt độ ban đầu 200C. Khi cân bằng , nhiệt độ cuối cùng của hệ là 240C. Tính nhiệt dung riêng của vật A. Biết nhiệt dung riêng của vật B là 380J/kg.K , của nước là 4200J/kg.K.
Giải :
Nhiệt lượng của vật A tỏa ra: Q1 = m1c1( t1 – t2) = 0,1c1.(100 – 24)= 7,6c1
Nhiệt lượng vật B thu vào: Q2 = m2.c2( t2 – t’1) = 0,1.380.(24 – 20) = 152J
Nhiệt lượng nước thu vào: Q3 = m3.c3.( t2 –t’1) = 0,2.4200 ( 24 – 20) = 3360J
Theo phương trình cân bằng nhiệt ta có:Q = Q1 + Q2 + Q3 7,6c = 152 + 3360
c1 = 462J/kg.K
5. Người ta thả một miếng đồng có khối lượng 0,5kg vào 500g nước. Miếng đồng nguội đi từ 1200C xuống 600C. Hỏi nước nhận một nhiệt lượng là bao nhiêu? Tìm nhiệt độ ban đầu của nước.
Giải:
Nhiệt lượng miếng đồng tỏa ra khi hạ nhiệt từ 1200C xuống 600C
Q1 = m1c1 ( t2 – t1) = 0,5.380. ( 120 – 60) = 11400J
Nhiệt
lượng mà nước hấp thụ:Q2
= m2.c2.(
t2
–t’1)
= 0,5.4200. t’=
2100
t’=
2100 t’
t’
Theo phương trình cân bằng nhiệt ta có: Q1 = Q2
11400J
= 2100 t’
=>
t’
=>
 t’
= 5,4290C
t’
= 5,4290C
t’1 = t2 -
 t’
= 600C
– 5,4290C
= 54,530C
t’
= 600C
– 5,4290C
= 54,530C
Vậy nước nhận thêm một nhiệt lượng 11400J và nhiệt độ ban đầu của nước là 54,530C
6. Người ta trộn 1500g nước ở 150C với 100g nước ở 370C. Tính nhiệt độ cuối cùng của hỗn hợp.
Giải:
Nhiệt lượng 1500g nước thu vào:Q1 = m1.c1.( t2 – t1) = 1,5.4200.( t2 – 15)
Nhiệt lượng 100g nước tỏa ra: Q2 = m2.c2.(t’1 – t2) = 0,1.4200.(37 – t2)
Theo phương trình cân bằng nhiệt ta có: Q1 = Q2
1,5.4200. (t2 – 15) = 0,1.4200.( 37 – t2) => t2 = 16,3750C.
Vậy nhiệt độ cuối cùng của hệ thống là:16,3750C.
7. Một nhiệt lượng kế bằng đồng có khối lượng 0,1kg chứa 0,5kg nước ở 200C. Người ta thả vào nhiệt lượng kế nói trênmột thỏi đồng có khối lượng 0,2kg đã được đun nóng đến 2000C. Xác định nhiệt độ cuối cùng của hệ thống.
Giải:
Nhiệt lượng mà nhiệt lượng kế thu vào:Q1= m1c1(t2–t1)=0,1.380(t2–20)=38(t2 – 20)
Nhiệt lượng nước thu vào: Q2 = m2.c2( t2 – 20) = 0,5.4200( t2- 20) = 2100( t2 – 20).
Nhiệt lượng đồng tỏa ra: Q3 = m3.c3.( t”1 – t2) = 1,2.380.( 200 – t2) = 76( 200 – t2)
Theo phương trình cân bằng nhiệt ta có: Q = Q1 + Q2
38t2 – 760 + 2100t2 – 4200 = 15200 – t2 => t2 = 26,10C
8. Dùng một bếp dầu để đun một ấm nước bằng nhôm khối lượng 500g chứa 5 lít nước ở nhiệt độ 200C.
a/ Tính nhiệt độ cần thiết để đun ấm nước đến sôi.
b/ Bếp có hiệu suất 80%, tính thể tích dầu cần dùng. Biết khối lượng riêng của dầu là
D = 800kg/m3.
Giải:
a. Nhiệt lượng cần thiết để đun ấm nước:
Q = Q1 + Q2 = m1.c1.( t2 – t1) + m2.c2.(t2 – t1) = ( t2 –t1).( m1.c1 + m2.c1)
= (100 – 20) ( 0,5.880 + 5.4200) = 1725200J
b.
Năng lượng do bếp tỏa ra ( năng suất tỏa nhiệt):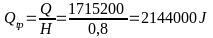
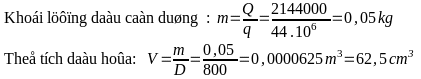
9. Tính nhiệt lượng cần thiết cung cấp cho một miếng nhôm có khối lượng 100g ở nhiệt độ 200C đến nóng chảy hoàn toàn ở nhiệt độ nóng chảy. Cho biết nhiệt độ nóng chảy của nhôm là 6580C, nhiệt nóng chảy của nhôm là 3,9.105J/kg.K.
Giải:
Nhiệt lượng cần thiết cung cấp cho 100g nhôm tăng nhiệt độ từ 200C đến 6580C:
Q1 = m.c.(t2 – t1 ) = 0,1.880.( 658 – 20) = 56114J
Nhiệt lượng cần thiết cung cấp cho 100g nhôm nóng chảy hoàn toàn ở 6580C:
Q2
=
 .m
= 3,9.105.0,1
= 39000J
.m
= 3,9.105.0,1
= 39000J
Nhiệt lượng cần thiết cung cấp cho miếng nhôm:
Q = Q1 + Q2 = 56114J + 39000J = 95114J
10. Đun nóng 10kg đồng ở nhiệt độ 380C đến nóng chảy hoàn toàn.
a/ Xác định nhiệt lượng cần thiết để thực hiện quá trình trên.
b/ Nhiệt lượng trên được cung cấp bởi một lượng than củi. Cho biết hiệu suất của bếp than củi này là 40%. Xác định lượng than củi cần dùng.
Biết nhiệt nóng chảy của đồng là 1,8.105J/kg, đồng nóng chảy ở nhiệt độ 10830C, năng suất tỏa nhiệt của than củi là 10.106J/kg.
Giải:
a. Nhiệt lượng dùng để đun nóng đồng từ 380C đến 10830C:
Q1 = m.c (t2 – t1) = 10.380.( 1083 – 38) = 3971000J
Nhiệt lượng cung cấp cho 10kg đồng nóng chảy hoàn toàn ở nhiệt độ nóng chảy:
Q2
=
 .m
= 10.1,8.105
= 18.105J
.m
= 10.1,8.105
= 18.105J
Nhiệt lượng cung cấp cho cả quá trình :
Q = Q1 + Q2 = 3971000J + 1800000J = 5771000J

11. Đun 15kg nước đá ở -100C đến sôi.
a/ Tính nhiệt lượng cần cung cấp cho lượng nước nói trên.
b/ Với lượng củi than 1,5kg, có thể thực hiện quá trình trên được không? Biết hiệu suất của bếp là 50%, năng suất tỏa nhiệt của than củi là 10.106J/kg.
Giải:
Nhiệt lượng cần cung cấp cho 15kg nước đá ở -100C đến 00C:
Q1 = m.c1. ( t2 – t1) = 15.1800.[ 0 – (-10)] = 270000J
Nhiệt lượng cần cung cấp cho 15kg nước đá nóng chảy hoàn toàn ở 00C:
Q2
=
 .
m = 15.3,4.105
= 5100000J
.
m = 15.3,4.105
= 5100000J
Nhiệt lượng cần cung cấp cho 15kg nước tăng nhiệt độ từ 00C đến 1000C:
Q3 = m.c2.( t3 – t2) = 15.4200.(100 – 0) = 6300000J
Nhiệt lượng cần cung cấp cho 15kg nước đá từ -100C đến sôi:
Qthu = Q1 + Q2 + Q3 = 270000J + 5100000J + 6300000J = 11670000J
Nhiệt lượng do đốt cháy than củi tỏa ra là nhiệt lượng toàn phần:
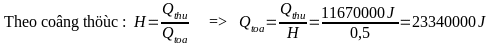
Nhiệt lượng tỏa ra khi đốt cháy 1,5kg than củi: Q’tỏa = q.m = 10.106.1,5 = 15000000J
Ta thấy Q’tỏa < Qtỏa. Vậy với 1,5kg than củi thì không thực hiện được quá trình này.
12. Tính nhiệt lượng cần cung cấp cho 1kg nước tăng nhiệt độ từ -200C biến thành hơi.
Giải:
Nhiệt lượng cần cung cấp cho 1kg nước tăng nhiệt độ từ -200C đến 00C.
Q1 = m.c1.( t2 –t1) = 1.1800.{ 0 – (-20)] = 36000J
Nhiệt lượng cần cung cấp cho 1kg nước đá nóng chảy hoàn toàn ở nhiệt độ nóng chảy:
Q2
=
 .m
= 3,4.105.1
= 340000J
.m
= 3,4.105.1
= 340000J
Nhiệt lượng cần cung cấp cho 1kg nước tăng nhiệt độ từ 00C đến sôi ở 1000C:
Q3 = m.c2.(t3 –t2 ) = 1.42000.(100 – 0) = 42000J
Nhiệt lượng cần cung cấp cho 1kg nước hóa hơi hoàn toàn ở nhiệt độ sôi:
Q4 = L.m = 2.3.106.1 = 2300000J
Nhiệt lượng cần cung cấp để thực hiện quá trình trên:
Q = Q1 + Q2 + Q3 + Q4 = 36kJ + 340kJ + 420kJ + 2300kJ = 3096kJ.
13. Bỏ một quả cầu bằng đồng thau có khối lượng 1kg được đun nóng đến 1000C vào thùng sắt có khối lượng 500g đựng 2kg nước ở 200C. Bỏ qua sự trao đổi nhiệt với môi trường.
a/ Tìm nhiệt độ cuối cùng của nước. Biết nhiệt dung riêng của đồng thau, sắt và nước lần lượt là c1 = 3,8.103J/kg.K ; c2 = 0,46.103J/kg.K ; c3 = 4,2.103J/kg.K.
b/ Tìm nhiệt lượng cần thiết để đun nước từ nhiệt độ ở câu a ( có cả quả cầu) đến 500C.
Giải:
a. Nhiệt lượng quả cầu bằng đồng thau tỏa ra khi hạ nhiệt từ 1000C đến t0C
Q1 = m1.c1.( t1 – t)
Nhiệt lượng thùng sắt và nước nhận được để tăng nhiệt độ từ 200C đến t0C:
Q2 = m2.c2.( t –t2)
Q3 = m3.c1.( t-t2)
Theo phương trình cân bằng nhiệt , ta có: Q1 = Q2 + Q3
m1.c1.( t1 –t) = m2.c2.( t –t2) + m3.c3.(t – t2)
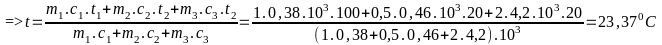
b. Nhiệt lượng cần cung cấp để nước, thùng sắt, quả cầu tăng nhiệt độ từ 23,370C đến 500C:
Q = ( m1.c1 + m2.c2 + m3.c3) ( t’ – t)
= (1.0,28.103 + 0,5.0,46.103 + 2.4,2.103) (50 – 23,37) = 239,9.103J = 240kJ
14. Bỏ 100g nước đá ở 00C vào 300g nước ở 200C.
a/
Nước đá tan hết không ? Cho biết nhiệt nóng chảy của
nước đá
 = 3,4.105J/kg
và nhiệt dung riêng của nước là 4200J/kg.K.
= 3,4.105J/kg
và nhiệt dung riêng của nước là 4200J/kg.K.
b/ Nếu không tan hết, tính khối lượng nước đá còn lại.
Giải:
a. Nhiệt lượng nước đá thu vào để nóng chảy ( tan )hoàn toàn ở 00C
Q1
= m1.
 = 0,1.3,4.105
= 34.103J
= 0,1.3,4.105
= 34.103J
Nhiệt lượng nước tỏa ra khi hạ nhiệt từ 200C xuống 00C
Q2 = m2.c2.( t2 – t1 ) = 0,3.4200.( 20 – 0)= 25,2.103J
Ta thấy Q2 < Q1 nên nước đá chỉ tan một phần.
b. Gọi m’ là lượng nước đá tan ra.
Q2
= m’.
 => m’ =
=> m’ =
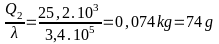
Khối lượng nước đá còn lại: m” = m1 – m’ = 100g – 74g = 26g.
15. Dẫn 100g hơi nước vào bình cách nhiệt đựng nước đá ở -40C. Nước đá tan hoàn toàn và lên đến 100C.
a/
Tìm khối lượng nước đá có trong bình. Biết nhiệt
nóng chảy của nước đá là
 =3,4.105J/kg,
nhiệt hóa hơi của nước là 2,3.106J/kg,
nhiệt dung riêng của nước là c1
= 4200J/kg.K , của nước đá là c2
= 1800J/kg.K.
=3,4.105J/kg,
nhiệt hóa hơi của nước là 2,3.106J/kg,
nhiệt dung riêng của nước là c1
= 4200J/kg.K , của nước đá là c2
= 1800J/kg.K.
b/ Để tạo nên 100g hơi nước ở nhiệt độ 1000C từ nước có nhiệt độ ban đầu 200C bằng bếp dầu có hiệu suất H = 40%. Tìm lượng dầu cần dùng, biết năng suất tỏa nhiệt của dầu là q = 4,5.107J/kg.
Giải:
Nhiệt lượng nước tỏa ra khi ngưng tụ ở 1000C và hạ nhiệt từ 1000C xuống 100C:
Q1 = L.m1 + m1.c1 ( t1 –t)
Nhiệt lượng nước đá thu vào để tăng nhiệt độ từ -40C đến 00C sau đó nóng chảy hoàn toàn thành nước ở 00C và tăng nhiệt độ từ 00C đến 100C:
Q2
= m2.c2.
( t3
– t2)
+ m2.
 + m2.c1.(
t –t3)
+ m2.c1.(
t –t3)
Theo phương trình cân bằng nhiệt, ta có:
L.m1
+ m1.c1.(t1
–t) = m2
{ c2(
t3
– t2)
+
 + c1.(t
–t3)}
+ c1.(t
–t3)}
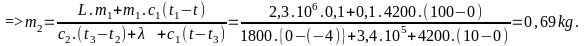
b. Lượng dầu cần dùng:
Nhiệt lượng cần cung cấp cho 100g nước từ 200C biến thành hơi nước ở 1000C:
Qthu = m1.c1.( t1 – t4) + m1.L = 0,1.4200.(100 – 20) + 0,1.2,3.106 = 263,6.103J
Nhiệt
lượng do dầu đốt cháy tỏa ra: Qtỏa
=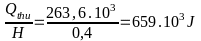
Lượng
dầu cần dùng:
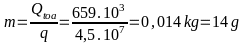
16*.
Để xác định nhiệt độ của một bếp lò người ta
làm như sau; Bỏ vào lò một khối đồng hình lập phương
có cạnh a = 2cm, sau đó lấy khối đồng bỏ trên một
tảng nước đá ở 00C.
Khi có cân bằng nhiệt, mặt trên của khối đồng chìm
dưới mặt nước đá 1 đoạn b = 1cm. Biết khối lượng
riêng của đồng là Do
= 8900kg/m3,
nhiệt dung riêng của đồng co
= 400J/kg.k, nhiệt nóng chảy của nước đá = 3,4.105J/kg.K
, khối lượng riêng của nước đá D = 900kg/m3.
Giả sử nước đá chỉ tan có dạng hình hộp có tiết
diện bàng tiết diện khối đồng.
= 3,4.105J/kg.K
, khối lượng riêng của nước đá D = 900kg/m3.
Giả sử nước đá chỉ tan có dạng hình hộp có tiết
diện bàng tiết diện khối đồng.
Giải:
Cho biết: a = 2cm = 2.10-2m b= 1cm = 1.10-2m
Do = 8900kg/m3 D = 900kg/m3
 =
3,4.105J/kg
co
= 400J/kg.K
=
3,4.105J/kg
co
= 400J/kg.K
t2 = 00C t1 =?
Nhiệt lượng đồng tỏa ra khi hạ nhiệt từ t1 xuống t2:
Qtỏa = mđ.co.( t1 – t2) Trong đó : mđ = Do.Vđ = Do.a3
Nhiệt
lượng nước đá thu vào khi nóng chảy: Q thu
=
 . mnước
=
. mnước
=
 .D.a2(
a + b)
.D.a2(
a + b)
Vì xem hai vật chỉ trao đổi nhiệt cho nhau nên ta có: Qtỏa = Qthu
Hay
: Do.a3.co.
( t1-t2)
=
 .D.a2.(a
+b)
.D.a2.(a
+b)
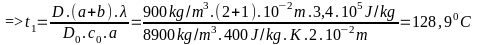
Vậy nhiệt độ ban đầu của thỏi đồng là 128,90C.
17*. Một thỏi hợp kim chì kẽm có khối lượng 500g ở nhiệt độ 1200C được thả vào một nhiệt lượng kế có nhiệt dung 300J/độ chứa 1lít nước ở 200C. Nhiệt độ khi cân bằng là 220C. Tìm khối lượng chì kẽm có trong hợp kim. Biết nhiệt dung riêng của chì kẽm lần lượt là 130J/kg.K , 400J/kg.k và nhiệt dung riêng của nước là 4200J/kg.K.
Giải:
Cho biết: mhk = 500g = 0,5kg t1 = 1200C
mnước = 1kg t2 = 200C
m3.c3 = 300J/độ t = 220C
cc = 130J/kg.K ck = 400J/kg.K
cnước = 4200J/kg.K
mc và mk =?
Gọi mc và mk lần lượt là khối lượng của chì và kẽm có trong hợp kim. Ta có:
mc + mk = mhk = 0,5kg (1)
Mặc khác, hợp kim chì kẽm tỏa nhiệt còn nhiệt lượng kế và nước thu nhiệt. Do đó khi cân bằng nhiệt , ta có:
(mc.cc + mk.ck )(t1 – t) = (m3.c3 + mnước.cnước)( t – t2)
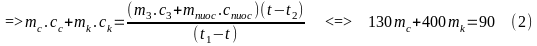
Giải phương trình (1) và (2) ta được: mc = 407,4g ; mk = 92,6g
18*. Một thau nhôm có khối lượng 0,5kg đựng 2kg nước ở nhiệt độ 200C.
a/ Thả vào thau nước một thỏi đồng có khối lượng 200g lấy ở lò ra. Nước nóng đến 21,20C. Tìm nhiệt độ của bếp lò. Biết nhiệt dung riêng của nhôm, nước, đồng lần lượt là c1 = 800J/kg.K ; c2 = 4200J/kg.K ; c3 = 380J/kg.K, bỏ qua sự trao đổi nhiệt ra môi trường.
b/ Thực ra trong trường hợp này , nhiệt lượng tỏa ra môi trường là 10%. Tìm nhiệt độ thực của bếp lò.
c/
Nếu tiếp tục bỏ vào thau nước một cục nước đá có
khối lượng 100g ở 00C.
Nước đá tan hết không? Tìm nhiệt độ cuối cùng của
hệ thống hoặc lượng nước đá còn sót lại nếu nó
không tan hết. Biết nhiệt nóng chảy của nước đá là
 = 3,4.105J/kg.
= 3,4.105J/kg.
Giải:
a. Gọi t0C là nhiệt độ của bếp lò cũng là nhiệt độ ban đầu của thỏi đồng.
Nhiệt lượng thau nhôm nhận được để tăng nhiệt độ từ t1 = 200C đến t2= 21,20C
Q1 = m1.c1.( t2 – t1)
Nhiệt lượng nước nhận được để tăng nhiệt độ từ t1 đến t2: Q2 = m2.c2.(t2 – t1).
Nhiệt lượng khối đồng tỏa ra để hạ nhiệt từ t0C xuống 21,20C: Q3 = m3.c3.( t – t2)
Do bỏ qua mất mát nhiệt, theo phương trình cân bằng nhiệt ta có:
Q3 = Q1 + Q2 m3.c3.(t – t2) = ( m1.c1 + m2.c2)(t2 –t1)
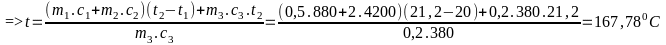
b. Thực tế do sự tỏa nhiệt ra môi trường nên ta có:Qthu = 90%Qtỏa
Q1 + Q2 = 90% Q3 hay 0,9Q3 = Q1 + Q2
0,9.m3.c3 (t’ – t2) = (m1.c1 + m2.c2) ( t2 –t1)
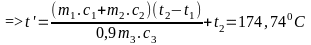
c. Nhiệt lượng thỏi nước đá thu vào để nóng chảy hoản toàn ở 00C.
Q
=
 . m = 3,4.105.0,1
= 34000J
. m = 3,4.105.0,1
= 34000J
Nhiệt lượng cả hệ thống gồm thau nhôm, nước, thỏi đồng tỏa ra để giảm nhiệt độ từ 21,20C xuống 00C.
Q’= ( m1.c1 + m2.c2 + m3.c3)( 21,2 – 0) = ( 0,5.880 + 2.4200 + 0,2.380).21,2 = 189019,2J
Do nhiệt lượng nước đá thu vào để làm tan hoàn toàn nhỏ hơn nhiệt lượng của hệ thống tỏa ra nên nước đá tan hết và cả hệ thống tăng nhiệt độ đến t”.
Gọi Q” là nhiệt lượng thừa lại dụng cho cả hệ thống tăng nhiệt độ từ 00C đến t”0C.
Q” = Q’ –Q = [ m1.c1 + (m2 + m).c2 + m3.c3].t”
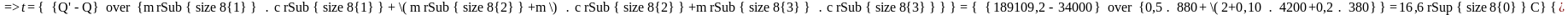
19*.Một thỏi nước đá có khối lượng m1 = 200g ở -100C.
a/
Tính nhiệt lượng cần cung cấp để thỏi nước đá
biến thành hơi hoàn toàn ở 1000C.
Cho nhiệt dung riêng của nước đá c1
= 1800J/kg.K, của nước c2
= 4200J/kg.K; nhiệt nóng chảy của nước đá ở 00C
là
 = 3,4.105J/kg;
nhiệt hóa hơi của nước là L = 2,3.106J/kg.
= 3,4.105J/kg;
nhiệt hóa hơi của nước là L = 2,3.106J/kg.
b/ Nếu bỏ thỏi nước đá trên vào sô nhôm chứa nước ở 200C. Sau khi có cân bằng nhiệt , người ta thấy nước đá còn sót lại là 50g. Tính lượng nước có trong sô lúc đầu. Biết sô nhôm có khối lượng m2 = 100g và nhiệt dung riêng của nhôm là c3 = 880J/kg.K
Giải:
a. Gọi Q là nhiệt lượng nược thu vào để tăng nhiệt độ từ t1 = -100c đến t2 = 00C:
Q1 = m1.c1.( t2 – t1) = 0,2.1800.[0 – (-10)]= 3600J = 3,6kJ
Nhiệt lượng nước đá thu vào để nóng chảy hoàn toàn ở 00C:
Q2
=
 .m1
= 3,4.105.0,2
= 68000J = 68kJ
.m1
= 3,4.105.0,2
= 68000J = 68kJ
Nhiệt lượng nước thu vào để tăng nhiệt độ từ 00C đến 1000C:
Q3 = m1.c2.(t3 –t2) = 0,2.4200.(100 – 0) = 84000J = 84kJ
Nhiệt lượng nước thu vào để hóa hơi hoàn toàn ở 1000C:
Q4 = L.m1 = 2,3.106.0,2 = 460000J = 460kJ.
Nhiệt lượng tổng cộng cần cung cấp để nước đá ở -100C đến khi hóa hơi hoàn toàn ở 1000C
Q = Q1 + Q2 + Q3 + Q4 = 3,6kJ + 68kJ + 84kJ + 460kJ = 615,6kJ
b. Gọi mx là lượng nước đá đã tan thành nước khi bỏ nó vào sô nhôm:
mx = 200 – 50 = 150g
Do nước đá không tan hết nên nhiệt độ cuối cùng của hệ thống là 00C.
Nhiệt lượng mà toàn khối nước đá nhận được để tăng nhiệt độ đến 00C:
Q’ = m1.c1. (t2 –t1) = Q1 = 3600J
Nhiệt lượng mà mx khối nước đá nhận được để tan hoàn toàn:
Q”
= mx
.
 = 0,15.3,4.105
= 51000J
= 0,15.3,4.105
= 51000J
Toàn bộ nhiệt lượng này là do nước có khối lượng M và sô nhôm tỏa ra để giảm nhiệt độ từ 200C xuống 00C.
Q = ( M.c2 + m2.c3 )( 200 – 0) = (M.4200 + 0,1.880) .20.
Theo phương trình cân bằng nhiệt , ta có:Q = Q’ +Q”
Hay : ( M.4200 + 0,1.880).20 = 3600 + 51000 = 54600 M.4200 + 88 = 2730

20*.Môt bếp dầu dùng để đun nước, khi đun 1kg nước ở 200C thì sau 10phút nước sôi. Biết nhiệt được cung cấp một cách đều đặn.
a/ Tìm thời gian cần thiết để cung cấp lượng nước nói trên bay hơi hoàn toàn. Biết nhiệt dung riêng và nhiệt hóa hơi của nước là c = 4200J/kg.K , L = 2,3.106J/kg.Bỏ qua sự trao đổi nhiệt với đồ dúng của nước.
b/ Giải lại câu a nếu tính đến ấm nhôm có khối lượng 200g , có nhiệt dung riêng 880J/kg.K
Giải:
a. Nhiệt lượng nước thu vào để tăng nhiệt độ từ t1 = 200C đến sôi ở 1000C
Q1 = m1.c1.( t2 – t1) = 1.4200.( 100 – 20) = 336000J = 336kJ
Nhiệt lượng nước thu vào để hóa hơi hoàn toàn ở 1000C:
Q2 = L.m1 = 2,3.106.1 = 2300000J = 2300kJ
Do bếp cung cấp nhiệt đều đặn, Sau 10phút nước thu được nhiệt lượng Q1.
Gọi t’1 và t’2 là thời gian đun nước.Thời gian đun để nước thu được nhiệt lượng Q2 là:
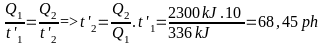
Thời gian tổng cộng kể từ lúc đun nước đến khi nó hóa hơi hoàn toàn:
t’ = t’1 + t’2 = 10ph + 68,45ph = 78,45ph
b. Nếu kể đến phần nhiệt lượng do ấm nhôm thu vào thì sau 10ph bếp dầu cung cấp một nhiệt lượng: Q = Q1 + Q’1 ( với Q’ là nhiệt lượng do ấm nhôm thu vào để nó tăng nhiệt độ từ 200C đến 1000C):
Q’1 = m2.c2 .(t2 – t1) = 0,2.880. (100 – 20) = 14080J = 14,08J
Q = Q1 +Q’1 = 336kJ + 14,08kJ = 350,08kJ.
Kể từ lúc nước sôi, ấm nhôm không nhận thêm nhiệt lượng nữa ( vì nó không tăng nhiệt độ). Nhiệt lượng do bếp dầu cung cấp vẫn là nhiệt lượng Q2 = 2300kJ. Do đó thời gian để bếp cung cấp nhiệt lượng Q2 là:

Thời gian tổng cộng để đun ấm nước: t” = t’1 + t”2 = 10ph + 65,08ph = 75,70ph
21*.Thả một quả cầu bằng thép có khối lượng m1 = 2kg được nung tới nhiệt độ 6000C vào một hỗn hợp nước đá ở 00C. Hỗn hợp có khối lượng tổng cộng là m2 = 2kg.
a/
Tính khối lượng nước đá có trong hỗn hợp. Biết
nhiệt độ cuối cùng có trong hỗn hợp là 500C,
Nhiệt dung riêng của thép c1
= 460J/kg.K và của nước là 4200J/kg.K, nhiệt nóng chảy
của nước đá là
 = 3,4.105J/kg.
= 3,4.105J/kg.
b/ Thực ra trong quá trình trên có một lớp nước tiếp xúc với quả cầu bị hóa hơi nên nhiệt độ cuối cùng của hỗn hợp chỉ là 480C. Tính lượng nước đã hóa thành hơi. Cho biết nhiệt hóa hơi của nước L = 2,3.106J/kg.
Giải:
Nhiệt lưọng do quả cầu thép tỏa ra khi hạ nhiệt từ 6000C xuống 500C.
Q1 = m1.c1.( 600 – 50) = 2.4200.550 = 506000J
Gọi
mx
là lượng nước đá có trong hỗn hợp. Nhiệt lượng
nước đá nhận được để nóng chảy hoàn toàn ở 00C:
Qx
= mx.

Nhiệt lượng cả hỗn hợp nhận được để tăng nhiệt độ từ 00C đến 500C là :
Q2 = m2.c2.( 50 – 0) = 2.4200.50 = 420000J
Theo phương trình cân bằng nhiệt , ta có: Qx + Q2 = Q1 Hay:
mx.
 + 420000 = 506000 => mx
=
+ 420000 = 506000 => mx
=
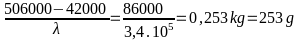
b. Gọi my là lượng nước đã hóa thành hơi. Theo bài toán ta có:
Nhiệt lượng do quả cầu thép cung cấp dùng để làm nóng chảy hoàn toàn mx gam nước đá ở 00C, nâng nhiệt độ của hỗn hợp từ 00C đến 480C; nâng my gam nước từ 480C đến 1000C và hóa hơi ở 1000C. Do đó:
Q1 = Qx + m2.c2.( 48 – 0) + my.c2.(100 – 48) + my.L
Hay: my[ c2.52 + L] = Q1 – Qx – m2.c2.48
= 506000 – 86000 – 2.4200.48 = 16800J
my =
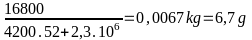
Chú ý: Có thể giải theo cách khác câu b: Phần nhiệt lượng mất đi do hỗn hợp chỉ tăngnhiệt độ đến 480C thay vì 500C được dùng để làm tăng my gam nước từ 480C đến 1000C và hóa hơi hoàn toàn ở 1000C. Nghĩa là ta có phương trình cân bằng nhiệt như sau:
m2.c2.(50 – 48) = my.c2.( 100 – 48) +my.L
m2.c2.2
= my.(
c2.52
+ L) =>my
=
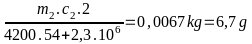
22.
Rót 0,5kg nước ở nhiệt độ t1
= 200C
vào một nhiệt lượng kế. Thả trong nước một cục
nước đá có khối lượng m2
= 0,5kg có nhiệt độ ban đầu là -150C.
Hãy tìm nhiệt độ của hỗn hợp sau khi cân bằng nhiệt.
Cho nhiệt dung riêng của nước c1
= 4200J/kg.K, của nước đá là c2
= 2100J/kg.K, nhiệt nóng chảy của nước đá là
 = 3,4.105J/kg.
Bỏ qua khối lượng của nhiệt lượng kế.
= 3,4.105J/kg.
Bỏ qua khối lượng của nhiệt lượng kế.
Giải:
Nhiệt lượng 0,5kg nước tỏa ra khi hạ nhiệt từ 200C xuống 00C:
Q1 = m1.c1.( t1 – 0) = 0,5.4200.20 = 42000J
Khi nước đá tăng nhiệt độ từ -150C đến 00C , nước đá cần một nhiệt lượng:
Q2 = m2.c2.[0 – (-15)}= 0,5.2100.15 = 15750J
Muốn cho 0,5kg nước đá nóng chảy hoàn toàn cần một nhiệt lượng:
Q3
=
 . m2
= 3,4.105.0,5
= 170000J.
. m2
= 3,4.105.0,5
= 170000J.
Từ kết quả trên cho thấy:
- Q1 > Q2: Nước đá có thể tăng nhiệt độ tới 00C.
- Q1 – Q2 < Q3: Nước đá không thể tan hoàn toàn mà chỉ tan một phần.
Vậy : Sau khi cân bằng nhiệt, nước đá không tan hoàn toàn mà nhiệt độ chung của hỗn hợp là 00C.
23*.Trong một bình đậy kín có một cúc nước đá khối lượng M = 0,1kg nổi trên nước; trong cục nước đá có một viên chì có khối lượng 5g. Hỏi phải tốn một nhiệt lượng bao nhiêu để cục chì bắt đầu chìm xuống nước.
Biết khối lượng riêng của chì là 11,3g/cm3; của nước đá là 0,9g/cm3; nhiệt nóng chảy của nước là 3,4.105J/kg, nhiệt độ nước trung bình là 00C.
Giải:
Để cục chì bắt đầu chìm thì không cần toàn bộ cục nước đá tan hết, chỉ cần khối lượng riêng trung bình của nước đá và chì bằng khối lượng riêng của nước.
Gọi M1 là khối lượng còn lại của cục nước đá khi bắt đầu chìm.
Dhh là khối lượng riêng trung bình của nước đá và chì.
V là thể tích của cục nước đá và chì.
m là khối lượng của viên chì.
Để cục nước đá có viên chì bắt đầu chìm, ta có:
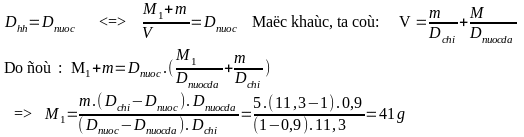
Khối lượng nước phải tan: M’ = M – M1 = 100g – 41g = 59g
Nhiệt
lượng cần dùng: Q =
 . M’ = 3,4.105.59.10-3
= 200600J
. M’ = 3,4.105.59.10-3
= 200600J
24*.Có hai bình cách nhiệt. Bình thứ nhất chứa 5 lít nước ở nhiệt độ t1 = 600C, bình thứ hai chứa 1 lít nước ở nhiệt độ t2 = 200C. Đầu tiên rót một phần nước từ bình thứ nhất sang bình thứ hai, sau khi trong bình thứ hai đã đạt cân bằng nhiệt, người ta lại rót trở lại từ bình thứ hai sang bình thứ nhất một lượng nước để cho trong hai bình có dung tích nước bằng lúc ban đầu. Sau các thao tác đó, nhiệt độ nước trong bình thứ nhất là t’1 = 590C. Hỏi đã rót bao nhiêu nước từ bình thứ nhất sang bình thứ hai và ngược lại.
Giải:
Do
chuyển nước từ bình 1 sang bình 2 và từ bình 2 sang bình
1. Giá trị khối lượng nước trong mỗi bình vẫn như
cũ, còn nhiệt độ trong bình thứ 1 hạ xuống 1 lượng
 t1.
t1.
 t1
= 600C
– 590C
= 10C
t1
= 600C
– 590C
= 10C
Vậy
nước trong bình đã mất đi một nhiệt lượng : Q1
= m1.c.
 t1
t1
Nhiệt lượng trên đã truyền sang bình 2. Do đó:
m2.c.
 t2
= Q1
= m1.c.
t2
= Q1
= m1.c.
 t1
(1) (
t1
(1) ( t2
là độ biến thiên nhiệt độ trong bình 2)
t2
là độ biến thiên nhiệt độ trong bình 2)
Từ
(1) ta có:
 t2
=
t2
=
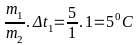
Như
vậy khi chuyển một lượng nước
 m
từ bình 1 sang bình 2 nhiệt độ nước trong bình 2 là:
m
từ bình 1 sang bình 2 nhiệt độ nước trong bình 2 là:
t’2
= t2
+
 t2
= 20 +5 = 250C
t2
= 20 +5 = 250C
Theo phương trình cân bằng nhiệt ta có:
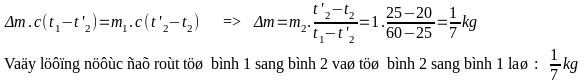
25*. a/ Tính lượng dầu cần dùng để đun sôi 2 lít nước ở 200C đựng trong ấm bằng nhôm có khối lượng 200g. Biết nhiệt dung riêng của nước và của nhôm lần lượt là: c1 = 4200J/kg.K và c2 = 880J/kg.K, năng sấut tỏa nhiệt của dầu là q = 44.106J/kg, hiệu suất của bếp là 30%.
b/ Cần đun thêm bao lâu nữa thì nước hóa hơi hoàn toàn. Biết bếp dầu cung cấp nhiệt một cách đều đặn và kể từ lúc đun đến khi sôi mất 15ph, nhiệt hóa hơi của nước là L = 2,3.106J/kg.
Giải:
a. Nhiệt lượng cần cung cấp cho nước để nó tăng nhiệt độ từ 200C đến 1000C.
Q1 = m1.c1 ( t2 – t1) = 2.4200.( 100 – 20) = 672000J = 672kJ
Nhiệt lượng cần cung cấp cho ấm nhôm tăng nhiệt độ từ 200C đến 1000C
Q2 = m2.c2.( t2 – t1) = 2.880 ( 100 – 20) = 14080J = 14,08kJ
Nhiệt lượng tổng cộng cần cung cấp cho ấm nhôm để tăng nhiệt độ từ 200C đến sôi.
Q = Q1 + Q2 = 672000J + 14080J = 686080J = 686,08kJ
Do hiệu suất của bếp là 30% nên thực tế nhiệt cung cấp do bếp dầu tỏa ra:
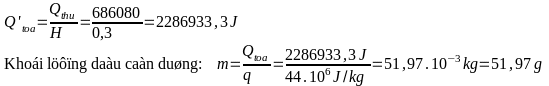
Nhiệt lượng cần dùng để nước hóa hơi hoàn toàn ở 1000C
Q3 = L.m = 2,3.106.2 = 4,6.106 J = 4,6.103kJ
Khi nước sôi ấm nhôm không nhận nhiệt lượng. Trong 15phút bếp dầu cung cấp nhiệt lượng 686,08kJ. Vậy để cung cấp nhiệt lượng 4600kJ cần tốn thời gian:
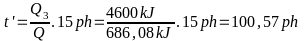
26*. Một khối nước đá có khối lượng m1 = 2kg ở nhiệt độ -50C.
a/
Tính nhiệt lượng cần cung cấp cho khối nước đá trên
biến thành hơi hoàn toàn ở 1000C.
Cho biết nhiệt dung riêng của nước đá là c1
= 1800J/kg.K, của nước là 4200J/kg.K nhiệt nóng chảy của
nước đá là
 = 3,4.105J/kg
nhiệt hóa hơi của nước là 2,3.106J/kg.
= 3,4.105J/kg
nhiệt hóa hơi của nước là 2,3.106J/kg.
b/ Nếu bỏ khối đá trên vào sô nhôm chứa nước ở 500C, sau khi cân bằng nhiệt người ta thấy còn sót lại 100g nước đá chưa tan hết. Tính lượng nước có trong sô nhôm. Biết sô nhôm có khối lượng m2 = 500g và nhiệt dung riêng của nhôm là 880J/kg.K
Giải:
a. Nhiệt lượng Q1 nước thu vào để tăng nhiệt độ từ -50c đến 00C:
Q1 = m1.c1.( t2 – t1) = 2.1800.[ 0 –(-5)] = 18000J = 18kJ
Nhiệt lượng Q2 nước đá thu vào để nóng chảy hoàn toàn:
Q2
=
 .m = 3,4.105.2
= 6,7.105J
= 680kJ
.m = 3,4.105.2
= 6,7.105J
= 680kJ
Nhiệt lượng Q3 nước thu vào để tăng nhiệt độ từ 00C đến 1000C:
Q3 = m1.c2.( t3 – t2) = 2.4200.( 100 – 0) = 840000J = 840kJ
Nhiệt lượng Q4 nước thu vào để hóa hơi hoàn toàn ở 1000C
Q4 = L.m1 = 2,3.106.2 = 4600000J = 4600kJ
Nhiệt lượng tổng cộng để nước đá ở -50C biến thành hơi hoàn toàn ở 1000C:
Q = Q1 + Q2 + Q3 + Q4 = 18kJ + 680kJ + 840kJ + 4600 = 6138kJ
b. Gọi mx là lượng nước đá đã tan thành nước: mx = 2 - 0,1 = 1,9kg.
Do nước đá không tan hết nên nhiệt đô cuối cùng của hệ thống là 00C.
Nhiệt lượng khối nước nhận vào để tăng nhiệt độ đến 00C: Q1 = 18000J
Nhiệt lượng mx kg nước đá tan hoàn toàn ở 00C:
Qx
= mx.
 = 1,9.3,4.106
= 646000J
= 1,9.3,4.106
= 646000J
Nhiệt lượng này do nước ( có khối lượng M) và sô nhôm ( có khối lượng m3) cung cấp do giảm nhiệt từ 500C xuống 00C. Do đó;
Q = ( M.c2 + m3.c3)( 50 – 0) = ( M.4200 + 0,5.880).50
Theo phương trình cân bằng nhiệt ta có:
Q = Q1 + Qx Hay ( M.4200 + 0,5.880).50 = 18000 + 646000 => M = 3,05kg.
27*. Có hai bình cách nhiệt, bình 1 chứa 2kg nước ở t1 = 200C, bình 2 chứa 40kg nước ở t2 = 600C. Người ta rót một lượng nước từ bình 1 sang bình 2. Sau khi cân bằng nhiệt người ta rót một lượng nước m như thế từ bình 2 vào bình 1. Nhiệt độ cân bằng của bình 1 lúc này là t’1 = 21,950C.
a/ Tính lượng nước m trong mỗi lần rót và nhiệt độ cân bằng t’2 của bình 2.
b/ Nếu tiếp tục thực hiện lần 2, tìm nhiệt độ cân bằng của mỗi bình.
Giải:
Sau khi rót lượng nước từ bình 1 sang bình 2 nhiệt dộ cân bằng của bình 2 là t’2, Ta có:
m.c(t’2 – t1) = m2.c ( t2 –t’2) => m( t’2 – t1) = m2 ( t2 – t’2) (1)
Sau khi rót một lượng nước từ bình 2 sang bình 1, nhiệt độ cân bằng của bình 1 là t’1. Lúc này lượng nước trong bình 1 chỉ còn ( m1 – m). Do đó:
m. ( t’2 – t’1) = ( m1 – m) ( t’1 – t1) => m( t’2 – t1) = m1.(t’1 – t1) (2)
Từ (1) và (2) ta suy ra: m2.( t2 – t’2) = m1 ( t’1 – t1)
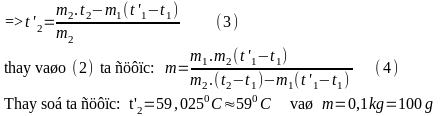
28*.
a/ Một ống nghiệm hình trụ đựng nước đá đến độ
cao h1
= 40cm, một ống nghiệm khác có cùng tiết diện đựng
nước ở nhiệt độ 40C
độ cao h2
= 10cm. Người ta rót hết nước trong ống nghiệm thứ hai
vào ống nghiệm thứ nhất. Sau khi cân bằng nhiệt, mực
nước trong ống nghiệm cao dâng thêm một đoạn
 h1
= 0,2cm so với lúc vừa rót xong. Tính nhiệt độ ban đầu
của nước đá, biết nhiệt dung riêng của nước là
4200J/kg .K , của nước đá là 2000J/kg.K nhiệt nóng chảy
của nước đá là
h1
= 0,2cm so với lúc vừa rót xong. Tính nhiệt độ ban đầu
của nước đá, biết nhiệt dung riêng của nước là
4200J/kg .K , của nước đá là 2000J/kg.K nhiệt nóng chảy
của nước đá là
 = 3,4.105J/kg,
khối lượng riêng của nước 1000kg/m3
và của nước đá là 900kg/m3.
Bỏ qua sự trao đổi nhiệt ra môi trường.
= 3,4.105J/kg,
khối lượng riêng của nước 1000kg/m3
và của nước đá là 900kg/m3.
Bỏ qua sự trao đổi nhiệt ra môi trường.
b/
Sau đó người ta nhúng ống nghiệm đó vào một ống
nghiệm khác có tiết diện gấp đôi đựng chất lỏng có
độ cao h3
= 20cm ở nhiệt độ t3
= 100C.
Khi cân bằng nhiệt, mực nước trong ống nghiệm nhỏ hạ
xuống một đoạn
 h2
= 2,4cm. Tính nhiệt dung riêng của chất lỏng. Cho biết
khối lượng riêng chất lỏng D3
= 800kg/m3,
bỏ qua nhiệt dung của ống nghiệm.
h2
= 2,4cm. Tính nhiệt dung riêng của chất lỏng. Cho biết
khối lượng riêng chất lỏng D3
= 800kg/m3,
bỏ qua nhiệt dung của ống nghiệm.
Giải:
a.
Mực nước dâng thêm chứng tỏ có một phần nước bị
đông đặc.( do khối lượng riêng của phần đó giảm
nên thể tích tăng). Gọi S là tiết diện của ống
nghiệm, x là chiều cao của cột nước bị đông đặc.
Sau khi đông đặc nó có chiều cao x+ h,
nhưng khối lượng vẫn không thay đổi. Nghĩa là:
h,
nhưng khối lượng vẫn không thay đổi. Nghĩa là:
S.x.D1
= S.(x+ h1).D2
=> x =
h1).D2
=> x =
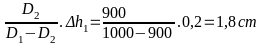
Do nước chỉ đông đặc một phần nên nhiệt độ cuối cùng của hệ thống là 00C.
Nhiệt lượng nước tỏa ra để giảm nhiệt từ 40C đến 00C:
Q1 = m1.c1.(t1 – 0) = D1.S.h2.c1(t1 – 0)
Nhiệt lượng của phần nước có độ cao x tỏa ra để đông đặc ở nhiệt độ 00C:
Q2
= m.
 = D1.S.x.
= D1.S.x.
 .
.
Nhiệt lượng nước đá thu vào để tăng nhiệt độ từ t2 đến 00C:
Q3 = D1.S.h1.c2 ( 0 – t2)
Theo phương trình cân bằng nhiệt ta có: Q1 + Q2 = Q3 Hay:
D1.S.h2.c1(t1
– 0) + D1.S.x.
 = D1.S.h1.c2
( 0 – t2)
= D1.S.h1.c2
( 0 – t2)
D1.S.h2.c2.t1
+
 .S.D1.x
= -D2.S.h1.c2.t2
.S.D1.x
= -D2.S.h1.c2.t2
t2 =
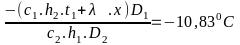
b.
Mực nước hạ xuống do một phần nước đá tan trong ống
nghiệm nhỏ đã nóng chảy. Gọi y là chiều cao của cột
nước đã bị nóng chảy. Sau khi nóng chảy phần đó có
chiều cao y -
 h2.
Nên ta có:
h2.
Nên ta có:
S.y.D2
= S.( y -
 h2).D1
=>
h2).D1
=>
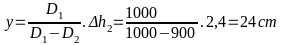
Nhiệt độ cuối cùng của hệ thống vẫn là 00C. Phần nhiệt lượng do chất lỏng tỏa ra bằng phần nhiệt lượng nước đá hấp thụ nóng chảyï . Ta có:
S.y.D2.
 = c3.2S.h3.D3(t3
– 0) =>
= c3.2S.h3.D3(t3
– 0) =>
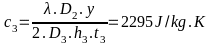
29*. Người ta trộn lẫn hai chất lỏng có nhiệt dung riêng, khối lượng, nhiệt độ ban đầu lần lượt là: c1; m1; t1 và c2; m2; t2. Tính tỉ số khối lượng của hai chất lỏng trong các trường hợp sau đây:
a/ Độ biến thiên nhiệt độ của chất lỏng thứ hai gấp đôi so với độ biến thiên nhiệt độ chất lỏng thứ nhất sau khi đã cân bằng nhiệt.
b/ Hiệu nhiệt độ ban đầu của hai chất lỏngso với hiệu giữa nhiệt độ cân bằng và nhiệt độ đầu của chất lỏng thu nhiệt bằng tỉ số a/b.
Giải:
Khi cân bằng nhiệt ta có: Qtỏa = Qthu Hay:
m1.c1.
 t1
= m2.c2.
t1
= m2.c2.
 t2
(
t2
( t1
= t – t1
;
t1
= t – t1
;
 t2
= t2
– t)
t2
= t2
– t)
Vì
 t2
= 2.
t2
= 2. t1
nên: m1.c1
= 2.m2.c2
=>
t1
nên: m1.c1
= 2.m2.c2
=>
Hiệu
nhiệt độ ban đầu của hai chất lỏng: t2
– t1
=
 t2
+
t2
+
 t1.
t1.
Hiệu
nhiệt độ cân bằng với nhiệt độ đầu của chất
lỏng thu nhiệt:
 t1
= t1
-
t
t1
= t1
-
t
Theo điều kiện bài toán:

30*.
Nước trong một ống chia độ được làm đông đặc
thành nước đá ở 00C
, người ta nhúng ống này vào một chất lỏng có khối
lượng m = 50g ở nhiệt độ to
= 150C.
Khi hệ thống đạt tới trạng thái cân bằng ở 00C
người ta thấy thể tích trong ống giảm đi 0,42cm3
. Tính nhiệt dung riêng của chất lỏng trên. Cho khối
lượng riêng của nước đá Do=900kg/m3;
của nước là 1000kg/m3;
nhiệt nóng chảy của nước đá là = 3,4.105J/kg.(
Bỏ qua sự trao đổi nhiệt với môi trường bên ngoài và
với ống đựng nước đá)
= 3,4.105J/kg.(
Bỏ qua sự trao đổi nhiệt với môi trường bên ngoài và
với ống đựng nước đá)
( Đề thi HSG cấp tỉnh năm học 2005 – 2006)
Giải:
Nhiệt lượng 50g chất lỏng tỏa ra khi hạ nhiệt từ 150C xuống 00C
Qtỏa = mcl.c ( t2 – t1) = 0,5.15.c = 0,75c (1)
Nhiệt lượng nước đá thu vào để nóng chảy
Qthu
= mn. ( 2)
( 2)
Mà
ta có: mn
= Dn.V.
 (3) và V = Vo
– Vg
( Vg
= 0,42)
(3) và V = Vo
– Vg
( Vg
= 0,42)
Nên : mn= Dn ( Vo – Vg)
Thay mn = 3,87.10-3kg vào (2) ta được:
Qthu= 3,87.10-3. 3,4.105 = 1285,2J
Vì bỏ qua mất mát nhiệt nên Qtỏa = Qthu
0,75c = 1285,2 =>c = 1713,6J/kg.K
31. Một ô tô có công suất 15000w. Tính công của máy sinh ra trong 1 giờ. Biết hiệu suất của máy là 25%. Hãy tính lượng xăng tiêu thụ để sinh ra công đó. Biết năng suất tỏa nhiệt của xăng là 46.106J/kg.
Giải:
Công của động cơ sinh ra trong 1giờ cũng chính là công có ích của động cơ:
A = p.t = 15.103W.36.102s = 540.105J
Năng lượng toàn phần do đốt cháy xăng tỏa ra:
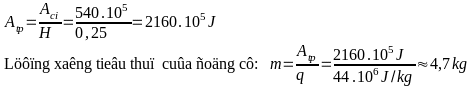
32. Tính lượng than mà động cơ tiêu thụ trong mỗi giờ. Biết rằng mỗi giờ động cơ thực hiện một công là 405.105J, năng suất tỏa nhiệt của than là 36.106J/kg, hiệu suất của động cơ là 10%.
Giải:
Theo đề ta có công có ích của động cơ là 405.105J
Công toàn phần là năng lượng do đốt cháy than tỏa ra:
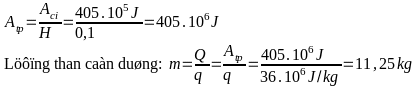
33. Một ô tô chạy 100km với lực kéo không đổi là 700N thì tiêu thụ hết 5lít xăng. Tính hiệu suất của động cơ, cho khối lượng riêng của xăng là 700kg/m3.
Giải:
Công có ích của động cơ: Aci = F.S = 700.100.103 = 7.107J
Công toàn phần của động cơ chính là năng lượng toàn phần do xăng cháy tỏa ra.
Atp = q.m = q.D.V = 46.105J/kg.700kg/m3.0,005m3 = 161.106J
Hiệu
suất của động cơ:
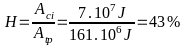
34. Một chiếc xe máy có công suất 1,4kW chuyển động với vận tốc 36km/h. Khi sử dụng hết 2 lít xăng thì đi được quãng đường dài bao nhiêu? Cho biết hiệu suất của động cơ 30%, khối lượng riêng của xăng là 700kg/m3 và năng suất tỏa nhiệt của xăng là 46.106J/kg.
Giải:
Khối lượng của 2 lít xăng: m = D.V = 700kg/m3.0,002m3 = 1,4kg
Công toàn phần của động cơ cũng chính là năng lượng toàn phần do xăng cháy tỏa ra.
Atp = Q = m.q = 1,4kg.46.106J/kg = 64,4.106J
Công có ích của động cơ: Aci = Atp. H = 64,4.106J . 30% = 19,32.106J
Thời
gian đi xe máy:
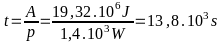
Quãng đường xe đi được: S = v.t = 10m/s.13,8.103s = 138.103s = 138km
35. Một xe Hon đa chạy với vận tốc 36km/h thì máy phải sinh ra một công suất p = 3220W. Hiệu suất của máy là H = 40%. Hỏi 1 lít xăng xe đi được bao nhiêu km, biết khối lượng riêng của xăng là 700kg/m3, năng suất tỏa nhiệt của xăng là 4,6.107J/kg.
Giải:

HẾT
Ngoài Giáo Án Bồi Dưỡng HSG Môn Lý 8 Cả Năm – Vật Lí Lớp 8 thì các tài liệu học tập trong chương trình 8 sẽ được cập nhật liên tục và nhanh nhất có thể sau khi kỳ thi diễn ra trên Danh mục Tài Liệu Học Tập nhằm giúp các bạn đọc thuận tiện trong việc nghiên cứu tài liệu. Quý thày cô và các bạn đọc có thể chia sẻ thêm những tài liệu học tập hữu ích đến địa chỉ email của chúng tôi, nhằm xây dựng nên kho đề thi phong phú, đa dạng cho các em học sinh tham khảo và rèn luyện.
Trên đây là giáo án bồi dưỡng học sinh giỏi môn Lý lớp 8 cả năm. Giáo án này đã được thiết kế nhằm giúp các học sinh nắm vững kiến thức và kỹ năng trong môn Lý, từ những khái niệm cơ bản đến các bài toán và vấn đề phức tạp hơn.
Qua giáo án bồi dưỡng HSG môn Lý, các em được tiếp cận với các chủ đề quan trọng như động lực học, áp suất, điện trường và từ trường, quang học và nhiệt độ. Các hoạt động trong giáo án bao gồm giải toán, thảo luận nhóm, làm thí nghiệm và trình bày báo cáo. Điều này giúp các em rèn luyện kỹ năng phân tích, suy luận, vận dụng kiến thức và tư duy khoa học.
Tuy nhiên, giáo án bồi dưỡng HSG chỉ là một phần trong quá trình học tập. Để đạt được thành tích cao hơn và phát triển sự đam mê với môn Lý, các em cần tiếp tục tự học, thực hành và tìm hiểu sâu hơn về các khái niệm và ứng dụng của vật lý trong cuộc sống hàng ngày.
Xem thêm












 K
K










 nªn
nªn

 PH
= PH’ + HH’= PH’ + MI= 8+10= 18 cm
PH
= PH’ + HH’= PH’ + MI= 8+10= 18 cm
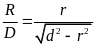
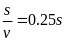
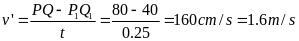
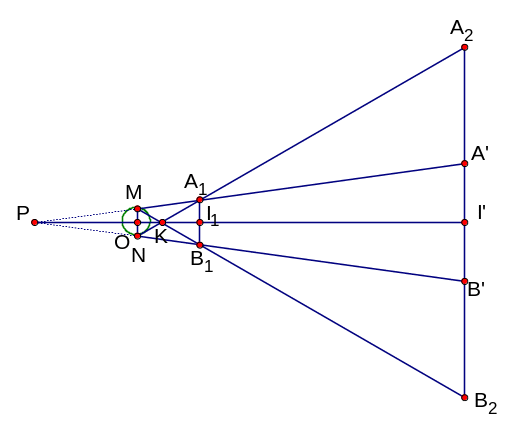
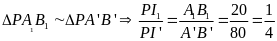
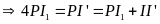
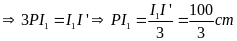
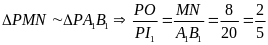
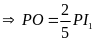
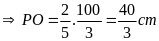
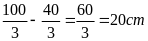

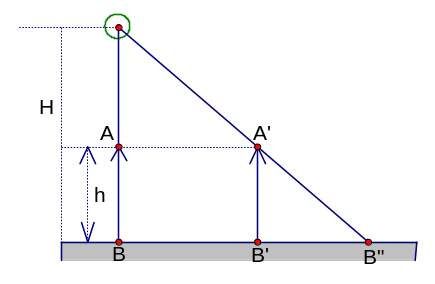
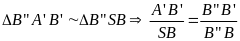
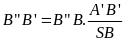 =
=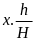
 x=
vt+
x=
vt+
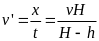
 hay
hay
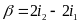 (1)
(1)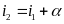 (2)
(2)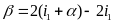 =
=
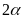
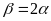


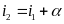
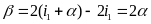
 S’SC
cã AB lµ ®êng trung b×nh nªn SC = 2Ab = 2a.
S’SC
cã AB lµ ®êng trung b×nh nªn SC = 2Ab = 2a.



 hay
hay
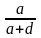
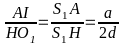
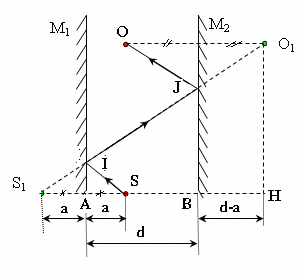
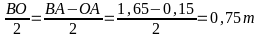


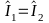 =
=
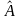
 =
=