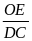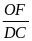SKKN Các Bài Toán Về Tam Giác Đồng Dạng
Có thể bạn quan tâm
| Chuyên Đề Văn Thuyết Minh Lớp 8 |
SKKN Các Bài Toán Về Tam Giác Đồng Dạng là tài liệu học tập được Trang Tài Liệu biên soạn và sưu tầm từ những nguồn dữ liệu mới nhất hiện nay. Tài liệu này sẽ giúp các em luyện tập, củng cố kiến thức từ đó nâng cao điểm số cho môn học. Ngoài ra, cũng giúp các thầy cô giáo có nguồn tài nguyên phong phú để giảng dạy.
Dưới đây là bản đọc trực tuyến giúp thầy cô và các em học sinh có thể nghiên cứu Online hoặc bạn có thể tải miễn phí với phiên bản word để dễ dàng in ấn cũng như học tập Offline.
SỰ PHONG PHÚ CỦA
TAM GIÁC ĐỒNG DẠNG
I/MỞ ĐẦU:
* Người ta thường nói:’’Bí như hình ‘’thật không sai ;bởi vì phần lớn học sinh đều ngán ngẫm môn học này do sự phong phú và phức tạp của ‘’tam giác đồng dạng’’ .Nhưng nếu các em nắm chắc được lí thuyết và vận dụng tốt thì trí tuệ phát triển rất nhanh.
*Trong chương trình hình học phẳng THCS, đặc biệt là chương 3 hình học 8, phương pháp“Tam giác đồng dạng” là một công cụ quan trọng nhằm giải quyết các bài toán hình học . Làm cơ sở để học sinh vận dụng giaỉ các bài toán về hình học phẳng ở các lớp trên .
*Phương pháp “ Tam giác đồng dạng” là phương pháp ứng dụng tính chất đồng dạng của tam giác, tỷ lệ các đoạn thẳng, trên cơ sở đó tìm ra hướng giải các dạng toán hình học.
*Trên thực tế, việc áp dụng phương pháp “Tam giác đồng dạng” trong giải toán có các thuận lợi và khó khăn chứng như sau:
* Thuận lợi:
+ Phương pháp “ Tam giác đồng dạng” là công cụ chính giúp ta tính toán nhanh chóng các dạng toán đặc trưng về tính tỷ lệ, chứng minh hệ thức, các bài tập ứng dụng các định lý sau Thales....
+ Với một số dạng toán quen thuộc như chứng minh đoạn thẳng bằng nhau, góc bằng nhau, chứng minh song song, chứng minh thẳng hàng, phương pháp “ Tam giác đồng dạng” có thể cho ta những cách giải quyết gọn gàng, ngắn hơn các phương pháp truyền thống khác nhau sử dụng tính chất tam giác, tính chất tứ giác đặc biệt...Học sinh sẽ vận dụng linh hoạt, nhuần nhuyễn khi giải toán .
+ Phương pháp “ Tam giác đồng dạng” giúp rèn luyện tốt khả năng tư duy logic của học sinh, rèn luyện tính sáng tạo, phát triển trí tuệ cho học sinh một cách hiệu quả. Từ đó học sinh đam mê học toán .
* Khó khăn:
+ Phương pháp “ Tam giác đồng dạng” còn lạ lẫm với học sinh. Các em chưa quen với việc sử dụng một phương pháp mới để giải toán thay cho các cách chứng minh truyền thống, đặc biệt là với các học sinh lớp 8 mới.
+ Việc sử dụng các tỷ số cạnh rất phức tạp dễ dẫn đến nhầm lẫn trong tính toán, biến đổi vòng quanh luẩn quẩn, không rút ra ngay được các tỷ số cần thiết, không có kỹ năng chọn cặp tam giác cần thiết phục vụ cho hướng giải bài toán.
*Từ những nhận định trên, sáng kiến kinh nghiệm này giải quyết giúp cho giáo viên dạy lớp 8 và các em học sinh một số vấn đề cụ thể là :
- Hệ thống lại các kiến thức thường áp dụng trong phương pháp.
- Hệ thống các dạng toán hình học thường áp dụng phương pháp “ Tam giác đồng dạng”.
- Định hướng giải quyết các dạng toán này bằng Phương pháp “ Tam giác đồng dạng”
- Hệ thống một số bài tập luyện tập.
*Trong sáng kiến kinh nghiệm này tôi đã có rất nhiều cố gắng nhằm làm rõ thêm một số phương pháp hình học đặc trưng, tuy nhiên do hạn chế về kiến thức về thực tế giảng dạy chắc chắn sáng kiến kinh nghiệm còn nhiều thiếu sót. Kính mong các thầy giáo, cô giáo có nhiều năm kinh nghiệm trong giảng dạy, các bạn đồng nghiệp tham gia góp ý bổ sung làm cho sáng kiến kinh nghiệm trở nên hoàn chỉnh hơn. Tôi xin chân thành cảm ơn tất cả các quý vị .
II/ KẾT QUẢ :
Để có kết quả tốt khi học về tam giác đồng dạng thì các em cần nắm vững khái niệm về tam giác đồng dạng . Từ đó mới phân tích, biến đổi thành thạo trong mọi trường hợp.
* LÝ THUYẾT : Học sinh cần nắm chắc và hiểu kỹ những kiến thức về tam giác đồng dạng sau để vận dụng cho tốt trong mọi trường hợp cụ thể .
1. Đinh lý Talet trong tam giác.
N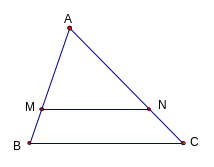 ếu
một đường thẳng song song với một cạnh của tam giác
và cắt hai cạnh còn lại thì nó định ra trên cạnh đó
những đoạn thẳng tương ứng tỷ lệ.
ếu
một đường thẳng song song với một cạnh của tam giác
và cắt hai cạnh còn lại thì nó định ra trên cạnh đó
những đoạn thẳng tương ứng tỷ lệ.
MN // BC
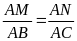

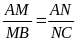
2. Khái niệm tam giác đồng dạng.
Tam giác A’B’C’ gọi là đồng dạng với tam giác ABC nếu:
+
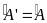 ;
;
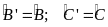
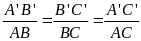
3. Các trường hợp đồng dạng của tam giác:
a) Trường hợp thứ nhất (ccc):
Nếu 3 cạnh của tam giác này tỷ lệ với 3 cạnh của tam giác kia thì 2 tam giác đó đồng dạng.
b) Trường hợp thứ 2(cgc):
Nếu 2 cạnh của tam giác này tỷ lệ với 2 cạnh của tam giác kia và 2 góc tạo bởi tạo các cặp cạnh đó bằng nhau thì hai tam đó giác đồng dạng.
c) Trường hợp thứ 3(gg):
Nếu 2 góc của tam giác này lần lượt bằng 2 góc của tam giác kia thì hai tam giác đó đồng dạng.
d) Các trường hợp đồng dạng của tam giác vuông.
+ Tam giác vuông này có một góc nhọn bằng góc nhọn của tam giác vuông kia thì hai tam giác đó đồng dạng.
+ Tam giác vuông này có hai cạnh góc vuông tỷ lệ với hai cạnh góc vuông của tam giác vuông kia thì hai tam giác đó đồng dạng.
+ Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này tỷ lệ với cạnh huyền và cạnh góc vuông của tam giác vuông kia thì hai tam giác đó đồng dạng.
* ÁP DỤNG:Để dễ sử dụng kiến thức khi tính toán, so sánh, chứng minh .Tôi tạm chia thành các dạng toán cơ bản sau:
&.DẠNG1:Tính độ dài đoạn thẳng, góc, tỷ số, diện tích, chu vi:
_ Loại1: Tính độ dài đoạn thẳng:
_Ví dụ:1) Cho ABC vuông ở A, có AB = 24cm; AC = 18cm; đường trung trực của BC cắt BC , BA, CA lần lượt ở M, E, D. Tính độ dài các đoạn BC, BE, CD.
2) Hình thoi BEDF nội tiếp ABC (E AB; D AC; F AC)
Tính cạnh hình thoi biết AB = 4cm; BC = 6cm. Tổng quát với AB = a, BC = c.
Chứng minh rằng BD <
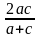 với AB = c; BC = a.
với AB = c; BC = a.Tính độ dài AB, BC biết AD = m; DC = n. Cạnh hình thoi bằng d.
3)a)
Tam giác ABC có
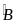 = 2
= 2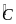 ;
AB = 4cm; BC = 5cm.
;
AB = 4cm; BC = 5cm.
Tính độ dài AC?
b)
Tính độ dài các cạnh của ABC
có
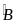 = 2
= 2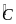 biết rằng số đo các cạnh là 3 số tự nhiên liên tiếp.
biết rằng số đo các cạnh là 3 số tự nhiên liên tiếp.
G iảI
:3)
iảI
:3)
a) Trên tia đối của tia BA lấy BD = BC
ACD
và ABC
có
 chung;
chung;
 =
=
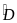 =
=
ACD P ABC (g.g)
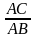 =
=
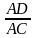
AC2
= AB. AD
AC2
= AB. AD
= 4 . 9 = 36
AC = 6(cm)
b) Gọi số đo của cạnh BC, AC, AB lần lượt là a, b, c.
Theo câu (a) ta có.
AC2 = AB. AD = AB(AB+BC) b2 = c(c+a) = c2 + ac (1)
Ta có b > c (đối diện với góc lớn hơn) nên chỉ có 2 khả năng là:
b = c + 1 hoặc b= c + 2
* Nếu b = c + 1 thì từ (1) (c + 1)2 = c2 + ac 2c + 1 = ac
c(a-2) = 1 (loại) vì c= 1 ; a = 3; b = 2 không là các cạnh của 1 tam giác
* Nếu b = c + 2 thì từ (1) (c + 2)2 = c2 + ac 4c + 4 = ac
c(a – 4) = 4
Xét c = 1, 2, 4 chỉ có c = 4; a = 5; 5 = 6 thỏa mãn bài toán.
Vậy AB = 4cm; BC = 5cm; AC = 6cm.
_Loại2:Tính góc:
_Ví
dụ:1)
Cho
ABH
vuông tại H có AB = 20cm; BH = 12cm. Trên tia đối của HB
lấy điểm C sao cho AC =
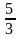 AH.
Tính
AH.
Tính
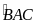 .
.
2) Cho hình thoi ABCD cạnh a, có A = 600. Một đường thẳng bất kỳ đi qua C cắt tia đối của các tia BA, DA tương ứng ở M, N. Gọi K là giao điểm của BN và DM. Tính BKD?
3) ABC có AB: AC : CB = 2: 3: 5 và chu vi bằng 54cm; DEF có DE = 3cm;
Chứng minh AEF P ABC
Biết A = 1050; D = 450. Tính các góc còn lại của mỗi
Giải:1)
T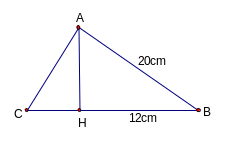 a
có
a
có
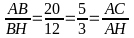
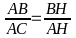
Xét ABH và CAH có :
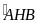 =
=
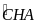 = 900
= 900
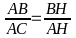 (chứng minh trên)
(chứng minh trên)
ABH
P
CAH
(CH cạnh gv)
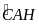 =
=
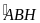
Lại
có
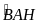 +
+
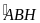 = 900
nên
= 900
nên
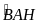 +
+
 = 900
Do đó :
= 900
Do đó :
 = 900
= 900
Giải:2)
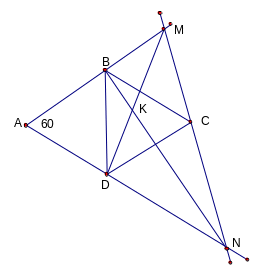 Do
BC // AN (vì N
AD) nên ta có :
Do
BC // AN (vì N
AD) nên ta có :
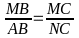 (1)
(1)
Do
CD // AM (vì M
AB) nên ta có :
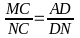 (2)
(2)
Từ
(1) và (2)
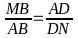
ABD
có AB = AD (đ/n hình thoi) và
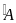 = 600
nên là
đều
= 600
nên là
đều
AB = BD = DA
Từ
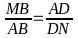 (cm trên)
(cm trên)
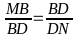
Mặt
khác :
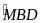 =
=
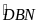 = 1200
= 1200
Xét
2MBD
và BDN
có :
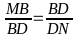 ;
;
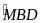 =
=
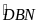
MBD P BDN (c.g.c)
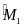 =
=
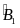
MBD
và KBD
có
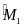 =
=
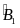 ;
;
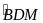 chung
chung
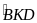 =
=
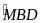 = 1200
= 1200
Vậy
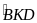 =
1200
=
1200
_ Loại3 :Tính tỉ số đoạn thẳng, tỉ số chu vi, tỉ số diện tích:
_Ví
dụ: 1)
Cho ABC,
D là điểm trên cạnh AC sao cho
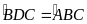 .
Biết AD = 7cm;
.
Biết AD = 7cm;
DC
= 9cm. Tính tỷ số
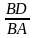
2)
Cho hình vuông ABCD, gọi E và F theo thứ tự là trung điểm
của AB, BC, CE cắt DF ở M. Tính tỷ số
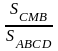 ?
?
3) Cho ABC, D là trung điểm của BC, M là trung điểm của AD.
BM cắt AC ở P, P’ là điểm đối xứng của P qua M. Chứng minh rằng PA = P’D. Tính tỷ số
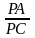 và
và
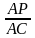
Chứng minh AB cắt Q, chứng minh rằng PQ // BC. Tính tỷ số
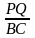 và
và
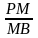
Chứng minh rằng diện tích 4 tam giác BAM, BMD, CAM, CMD bằng nhau. Tính tỷ số diện tích MAP và ABC.
Giải:1)
CAB
và CDB
có C chung ;
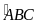 =
=
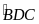 (gt)
(gt)
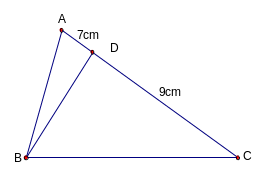 CAB
P
CDB
(g.g)
CAB
P
CDB
(g.g)
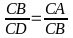 do đó ta có :
do đó ta có :
CB2 = CA.CD
Theo gt CD = 9cm; DA = 7cm nên CA = CD + DA = 9 + 7 = 16 (cm)
Do đó CB2 = 9.16 = 144 CB = 12(cm)
Mặt
khác lại có :
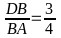
Giải:2)
Xét DCF
và CBE
có DC = BC (gt);
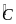 =
=
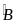 = 900;
BE = CF
= 900;
BE = CF
DCF = CBE (c.g.c)
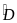 1
=
1
=
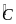 2
2
Mà
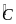 1
+
1
+
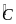 2
= 1v
2
= 1v
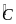 1
+
1
+
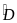 1
= 1v
CMD
vuông ở M
1
= 1v
CMD
vuông ở M
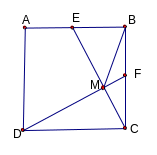 CMD
P
FCD
(vì
CMD
P
FCD
(vì
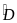 1
=
1
=
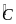 2
;
2
;
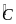 =
=
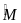 )
)
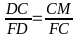
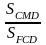 =
=
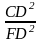
SCMD
=
SCMD
=
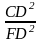 .
SFCD
.
SFCD
Mà
SFCD
=
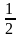 CF.CD
=
CF.CD
=
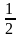 .
.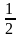 BC.CD
=
BC.CD
=
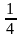 CD2
CD2
Vậy
SCMD
=
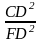 .
.
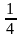 CD2
=
CD2
=
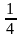 .
.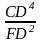 (*)
(*)
Áp dụng định lý pitago vào tam giác vuông DFC, ta có:
DF2
= CD2
+ CF2
= CD2
+ (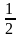 BC)2
= CD2
+
BC)2
= CD2
+
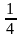 CD2
=
CD2
=
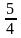 CD2
CD2
Thay
DF2
=
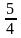 CD2
ta
có : SCMD
=
CD2
ta
có : SCMD
=
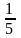 CD2
=
CD2
=
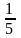 SABCD
SABCD
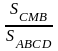 =
=
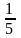
_Loại 4: Tính chu vi các hình:
_Ví dụ:1) Cho ABC, D là một điểm trên cạnh AB, E là 1 điểm trên cạnh AC sao cho DE // BC.
Xác
định vị trí của điểm D sao cho chu vi ADE
=
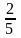 chu vi ABC.
chu vi ABC.
Tính chu vi của 2 tam giác đó, biết tổng 2 chu vi = 63cm
2)
A’B’C’
P
ABC
theo tỷ số đồng dạng K =
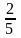 .Tính chu vi của mỗi tam giác, biết hiệu chu vi của 2 tam
giác đó là 51dm.
.Tính chu vi của mỗi tam giác, biết hiệu chu vi của 2 tam
giác đó là 51dm.
3) Tính chu vi ABC vuông ở A biết rằng đường cao ứng với cạnh huyền chia tam giác thành 2 tam giác có chu vi bằng 18cm và 24cm.
G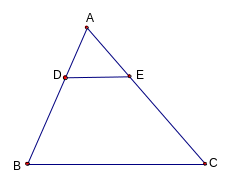 iải:1)
Do DE // BC nên ADE
PABC
theo tỷ số đồng dạng. K =
iải:1)
Do DE // BC nên ADE
PABC
theo tỷ số đồng dạng. K =
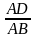 =
=
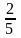 . Ta có .
. Ta có .
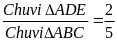
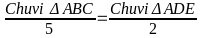 =
=
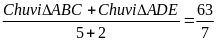 = 9
= 9
Do đó: Chu vi ABC = 5.9 = 45 (cm)
Chu vi ADE = 2.9 = 18 (cm)
_Loại 5:Tính diện tích các hình:
_Ví dụ :1)Cho hình vuông ABCD có độ dài = 2cm. Gọi E, F theo thứ tự là trung điểm của AD, DC. Gọi I, H theo thứ tự là giao điểm của AF với BE, BD. Tính diện tích tứ giác EIHD
2) Cho tứ giác ABCD có diện tích 36cm2, trong đó diện tích ABC là 11cm2. Qua B kẻ đường thẳng // với AC cắt AD ở M, cắt CD ở N. Tính diện tích MND.
3) Cho ABC có các B và C nhọn, BC = a, đường cao AH = h. Xét hình chữ nhật MNPQ nội tiếp tam giác có M AB; N AC; PQ BC.
Tính diện tích hình chữ nhật nếu nó là hình vuông.
Tính chu vi hình chữ nhật a = h
c) Hình chữ nhật MNPQ có vị trí nào thì diện tích của nó có giá trị lớn nhất
4) Cho ABC và hình bình hành AEDF có E AB; D BC, F AC.
Tính diện tích hình bình hành biết rằng : SEBD = 3cm2; SFDC = 12cm2;
Giải:4)
Xét
EBD
và FDC
có
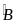 =
=
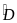 1
(đồng vị do DF // AB) (1)
1
(đồng vị do DF // AB) (1)
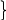

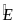 1
=
1
=
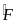 1
(2)
1
(2)
E1 = D2 ( so le trong do AB // DF)
D2 = E1 ( so le trong do DE // AC)
T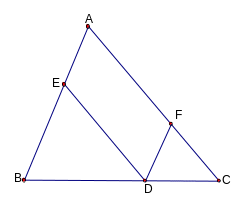 ừ
(1) và (2)
EBD
P
FDC
(g.g)
ừ
(1) và (2)
EBD
P
FDC
(g.g)
Mà
SEBD
: SFDC
= 3 : 12 = 1 : 4 = (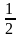 )2
)2
Do
đó :
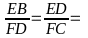
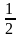
FD = 2EB và ED =
FD = 2EB và ED =
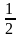 FC
FC
AE = DF = 2BE ( vì AE = DF)
AF
= ED =
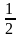 EC
( vì AF = ED)
EC
( vì AF = ED)
Vậy SADE = 2SBED = 2.3 = 6(cm2)
SADF
=
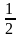 SFDC
=
SFDC
=
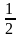 .
12 = 6(cm2)
.
12 = 6(cm2)
SAEDF = SADE + SADF = 6 + 6 = 12(cm2)
&.DẠNG 2: Chứng minh hệ thức, đẳng thức nhờ tam giác đồng dạng:
A. Các ví dụ và định hướng giải:
1. Ví dụ 1: Cho hình thang ABCD(AB // CD). Gọi O là giao điểm của 2đường chéo AC và BD
Chứng minh rằng: OA. OD = OB. OC.
Đường thẳng qua O vuông góc với AB và CD theo thứ tự tại H và K.
C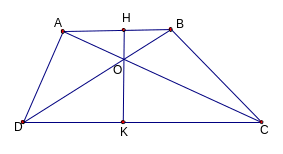 MR:
MR:
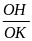 =
=
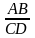
* Tìm hiểu bài toán : Cho gì?
Chứng minh gì?
* Xác định dạng toán:
? Để chứng minh hệ thức trên ta cần chứng minh điều gì?
TL:
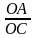 =
=
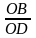
? Để có đoạn thẳng trên ta vận dụng kiến thức nào.
TL: Chứng minh tam giác đồng dạng
a) OA. OD = OB.OC
Sơ đồ :
+
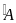 1
=
1
=
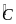 1
(SLT l AB // CD)
1
(SLT l AB // CD)
+
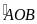 =
=
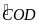 ( Đối đỉnh)
( Đối đỉnh)
OAB P OCD (g.g)
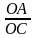 =
=
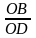
OA.OD = OB.OC
b)
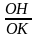 =
=
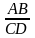
Tỷ
số
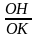 bằng tỷ số nào?
bằng tỷ số nào?
TL
:
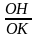 =
=
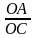
?
Vậy để chứng minh
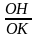 =
=
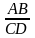 ta cần chứng minh điều gì.
ta cần chứng minh điều gì.
TL:
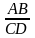 =
=
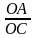
Sơ đồ :
+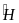 =
=
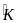 = 900
= 900
+
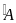 1
=
1
=
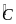 1.(SLT;
AB // CD) Câu a
1.(SLT;
AB // CD) Câu a
OAH P OCK(gg) OAB P OCD

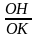 =
=
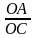
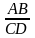 =
=
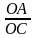
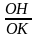 =
=
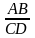
2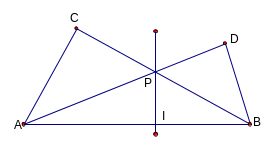 .
Ví dụ 2: Cho
hai tam gíac vuông ABC và ABD có đỉnh góc vuông C và D nằm
trên cùng một nửa mặt phẳng bờ AB. Gọi P là giao điểm
của các cạnh AC và BD. Đường thẳng qua P vuông góc với
AB tại I.CMR : AB2
= AC. AP + BP.PD
.
Ví dụ 2: Cho
hai tam gíac vuông ABC và ABD có đỉnh góc vuông C và D nằm
trên cùng một nửa mặt phẳng bờ AB. Gọi P là giao điểm
của các cạnh AC và BD. Đường thẳng qua P vuông góc với
AB tại I.CMR : AB2
= AC. AP + BP.PD
Định hướng:
- Cho HS nhận xét đoạn thẳng AB (AB = AI + IB)
AB2 = ? (AB.(AI + IB) = AB . AI + AB. IB)
- Việc chứng minh bài toán trên đưa về việc chứng minh các hệ thức
AB.AI = AC.AP
AB.IB = BP. PD
- HS xác định kiến thức vận dụng để chứng minh hệ thức ( P)
Sơ
đồ : +
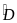 =
=
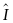 = 900 +
= 900 +
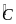 =
=
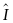 = 900
= 900
+
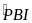 chung +
chung +
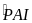 chung
chung
ADB P PIB ACB P AIP (gg)
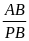 =
=
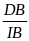
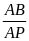 =
=
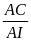
AB.AI = PB.DB AB . AI = AC . AP
AB . IB + AB . AI = BP . PD + AC . AP
AB (IB + IA) = BP . PD + AC . AP
AB2 = BP . PD + AC . AP
3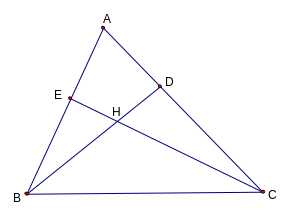 .
Ví dụ 3:
Trên cơ sở ví dụ 2 đưa ra bài toán sau:
.
Ví dụ 3:
Trên cơ sở ví dụ 2 đưa ra bài toán sau:
Cho nhọn ABC, các đường cao BD và CE cắt nhau tại H.
CMR: BC2 = BH . BD + CH.CE
Định hướng: Trên cơ sở bài tập 2
Học sinh đưa ra hướng giải quyết bài tập này.
Vẽ hình phụ (kẻ KH BC; K BC).
Sử dụng P chứng minh tương tự ví dụ 2
4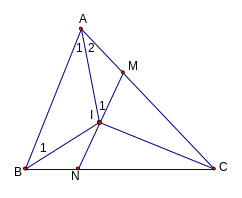 .
Ví dụ 4:
Cho
ABC, I là giao điểm của 3 đường phân giác, đường
thẳng vuông góc với CI tại I cắt AC và BC lần lượt ở
M và N. Chứng minh rằng.
.
Ví dụ 4:
Cho
ABC, I là giao điểm của 3 đường phân giác, đường
thẳng vuông góc với CI tại I cắt AC và BC lần lượt ở
M và N. Chứng minh rằng.
a) AM . BI = AI. IM
b) BN . IA = BI . NI
c)
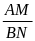 =
=
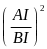
* Định hướng:
a) ? Để chứng minh hệ thức AM. BI = AI.IM ta cần chứng minh điều gì ?
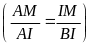
b) Để chứng minh đẳng thức trên ta cần chứng minh điều gì ?
( AMI P AIB)
Sơ đồ:
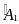 =
=
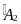 (gt)
(gt) 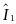 =
=
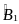 *
CM:
*
CM:
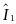 =
=
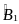

 v
MIC:
v
MIC:
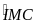 = 900
-
= 900
-
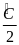
AMI
P
AIB
(gg) ABC:
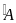 +
+ 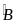 +
+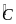 = 1800(t/c
tổng...)
= 1800(t/c
tổng...)
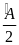 +
+
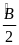 +
+
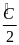 = 900
= 900
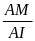 =
=
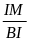 Do
đó:
Do
đó:
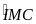 =
=
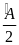 +
+
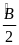 (1)
(1)
Mặt
khác:
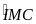 =
=
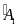 +
+
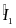 (t/c
góc ngoài )
(t/c
góc ngoài )
AM.
BI = AI . IM hay
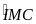 =
=
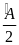 +
+
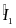 (2) Từ (1) và (2)
(2) Từ (1) và (2)
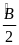 =
=
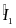 hay
hay
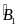 =
=
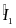
AMI
P
AIB
(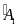 =
=
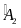 ;
;
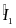 =
=
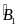 )
)
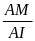 =
=
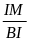
AM . BI = AI. IM
AM . BI = AI. IM
b) Tương tự ý a.
Chứng minh BNI P BIA (gg)
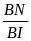 =
=
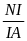
BN . IA = BI. IN
BN . IA = BI. IN
c) (Câu a) (Câu b)
-
HS nhận xét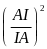 =
=
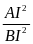 AMI
P
AIB
BNI
P
BIA
AMI
P
AIB
BNI
P
BIA
Tính
AI2
; BI2
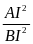
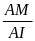 =
=
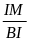
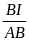 =
=
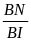
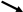
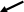 (Tính
AI2
; BI2
nhờ P) AI2
= AM . AB BI2
= BN . AB
(Tính
AI2
; BI2
nhờ P) AI2
= AM . AB BI2
= BN . AB
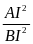 =
=
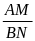
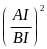 =
=
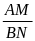
B.Bài tập đề nghị:
1)
Cho hình thanh ABCD (AB // CD), gọi O là giao điểm của 2
đường chéo. Qua O kẻ đường thẳng song song với 2 đáy
cắt BC ở I cắt AD ở J.CMR : a)
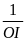 =
=
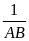 +
+
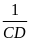
b)
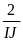 =
=
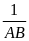 +
+
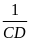
2) Cho ABC, phân giác AD (AB < AC). trên tia đối của tia DA lấy điểm I sao cho
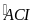 =
=
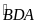 .
CMR: a) AD . DI = BD . DC
.
CMR: a) AD . DI = BD . DC
b) AD2 = AB . AC - BD . DC
&.DẠNG3: Chứng minh quan hệ song song:
+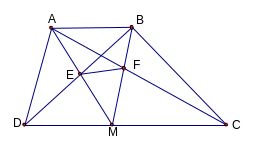 Ví dụ 1:
Cho hình thang ABCD (AB // CD). Gọi M là trung điểm của CD,
E là giao điểm của MA và BD; F là giao điểm của MB và
AC. Chứng minh rằng EF / / AB
Ví dụ 1:
Cho hình thang ABCD (AB // CD). Gọi M là trung điểm của CD,
E là giao điểm của MA và BD; F là giao điểm của MB và
AC. Chứng minh rằng EF / / AB
Định hướng giải:
- Sử dụng trường hợp đồng dạng của tam giác
- Định nghĩa hai tam giác đồng dạng
- Dấu hiệu nhận biết hai đường thẳng song song (định lý Ta lét đảo)
Sơ đồ phân tích:
AB // CD (gt) AB // CD (gt)
AB // DM AB // MC
MED P AEB GT MFC P BFA
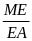 =
=
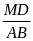 ; MD = MC
; MD = MC
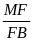 =
=
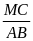
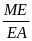 =
=
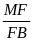
EF // AB (Định lý Ta lét đảo)
+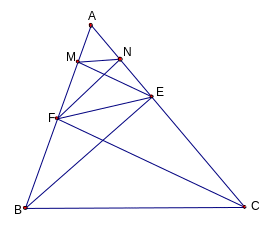 Ví dụ 2:
Cho
ABC có các góc nhọn, kẻ BE, CF là hai đường cao. Kẻ EM,
FN là hai đường cao của AEF.
Chứng minh MN // BC
Ví dụ 2:
Cho
ABC có các góc nhọn, kẻ BE, CF là hai đường cao. Kẻ EM,
FN là hai đường cao của AEF.
Chứng minh MN // BC
Sơ đồ phân tích
AMF P AFC (g.g); AFN P ABE
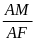 =
=
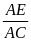
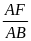 =
=
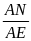
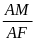 .
.
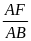 =
=
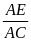 .
.
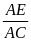
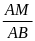 =
=
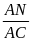
MN // BC (định lý Ta – lét đảo)
+ Ví dụ 3:
Cho ABC,
các điểm D, E, F theo thứ tự chia trong các cạnh AB, BC,
CA theo tỷ số 1 : 3, các điểm I, K theo thứ tự chia trong
các đoạn thẳng ED, FE theo tỉ số 1 : 3. Chứng minh rằng
IK // BC. Gọi M là trung điểm của AF
Ví dụ 3:
Cho ABC,
các điểm D, E, F theo thứ tự chia trong các cạnh AB, BC,
CA theo tỷ số 1 : 3, các điểm I, K theo thứ tự chia trong
các đoạn thẳng ED, FE theo tỉ số 1 : 3. Chứng minh rằng
IK // BC. Gọi M là trung điểm của AF
Giải: Gọi N là giao điểm của DM và EF
Xét ADM và ABC có :
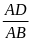 =
=
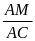 =
=
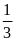 Góc A chung
Góc A chung
ADM P ABC (c.gc)
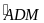 =
=
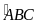 mà 2 góc này ở vị trí đồng vị nên DM // BC
mà 2 góc này ở vị trí đồng vị nên DM // BC
MN // EC mà MF = FC nên EF = FN
Ta
có :
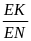 =
=
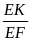 .
.
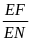 =
=
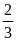 .
.
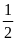 =
=
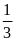 (1)
(1)
mà
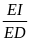 =
=
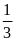 (gt) (2)
(gt) (2)
Từ
(1) và (2)
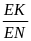 =
=
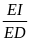 Suy ra IK // DN (định lý Ta – lét đảo)
Suy ra IK // DN (định lý Ta – lét đảo)
Vậy IK // BC.
*Bài tập đề nghị: Cho tứ giác ABCD, đường thẳng đi qua A song song với BC cắt BD. Đường thẳng đi qua B và song song với AD cắt AC ở G. Chứng minh rằng EG // DC
&.DẠNG4: Chứng minh tam giác đồng dạng:
+ Ví dụ 1: Cho ABC; AB = 4,8cn; AC = 6,4cm; BC = 3,6cm .Trên AB lấy điểm D sao cho
AD = 3,2cm, trên AC ,lấy điểm E sao cho AE = 2,4cm, kéo dài ED cắt CB ở F.
CMR : ABC P AED
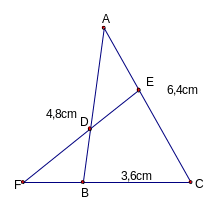 FBD
P
FEC
FBD
P
FECTính ED ; FB?
Bài toán cho gì?
Dạng toán gì?
Để chứng minh 2 đồng dạng có những phương pháp nào?
Bài này sử dụng trường hợp đồng dạng thứ mấy?
Sơ đồ chứng minh:
a) GT
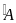 chung
chung
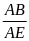 =
=
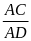 = 2
= 2
ABC P AED (c.g.c)
ABC P AED (câu a)
b)
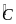 =
=
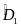 ;
;
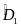 =
=
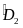
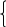
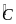 =
=
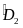
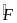 chung
chung
FBD P FEC (g.g)
c) Từ câu a, b hướng dẫn học sinh thay vào tỷ số đồng dạng để tính ED và FB.
+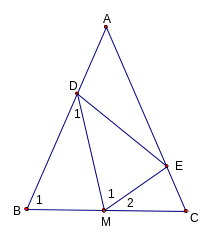 Ví dụ 2:
Cho ABC
cân tại A; BC = 2a; M là trung điểm của BC. Lấy các
điểm D và E trên AB; AC sao cho
Ví dụ 2:
Cho ABC
cân tại A; BC = 2a; M là trung điểm của BC. Lấy các
điểm D và E trên AB; AC sao cho
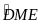 =
=
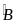 .
a) CMR : BDM
P
CME
.
a) CMR : BDM
P
CME
b) MDE P DBM
c) BD . CE không đổi
? Để chứng minh BDM P CME ta cần chứng minh điều gì.
? Từ gt nghĩ đến 2 có thể P theo trường hợp nào (g.g)
?
Gt đã cho yếu tố nào về góc. (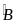 =
=
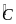 )
)
?
Cần chứng minh thêm yếu tố nào (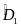 =
=
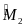 )
)
Hướng dẫn sơ đồ
gt góc ngoài DBM
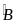 =
=
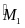 ;
;
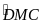 =
=
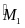 +
+
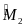 ;
;
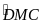 =
=
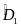 +
+
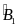
ABC cân
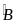 =
=
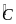 ;
;
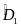 =
=
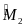
BDM P CME (gg)
Câu a gt
b) 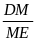 =
=
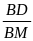 ;
CM = BM
;
CM = BM
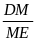 =
=
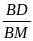
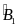 =
=
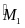 (gt)
;
(gt)
;
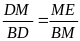
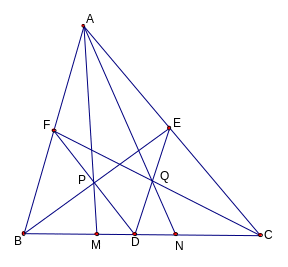
DME P DBM (c.g.c)
c) Từ câu a : BDM P CME (gg)
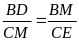 BD
. CE = Cm . BM
BD
. CE = Cm . BM
Mà
CM = BM =
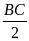 = a
= a
BD
. CE =
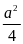 (không đổi)
(không đổi)
Lưu ý: Gắn tích BD . CB bằng độ dài không đổi
Bài đã cho BC = 2a không đổi
Nên phải hướng cho học sinh tính tích BD. CE theo a
+ Ví dụ 3: Cho ABC có các trung điểm của BC, CA, AB
theo thứ tự là D, E, F. Trên cạnh BC lấy điểm M và N sao cho
BM = MN = NC. Gọi P là giao điểm của AM và BE; Q là giao
điểm của CF và AN.
CMR: a) F, P, D thẳng hàng; D, Q, E thẳng hàng.
b) ABC P DQP
* Hướng dẫn
a) Giáo viên hướng dẫn học sinh chứng minh 3 điểm thẳng hàng có nhiều phương pháp. Bài này chọn phương pháp nào?
- Lưu ý cho học sinh bài cho các trung điểm nghĩ tới đường trung bình .
Từ đó nghĩ đến chọn phương pháp: CM cho 2 đường thẳng PD và FP cùng // AC

F, P, D thẳng hàng
PD là đường trung bình BEC PD // AC
FP là đường trng bình ABE FP // AC
Tương tự cho 3 điểm D, Q, E
PD =
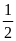 . EC =
. EC =
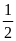 .
.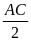 =
=
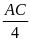

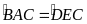 (Đơn
vị EF // AB)
(Đơn
vị EF // AB)
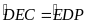 (so
le trong PD // AC)
(so
le trong PD // AC)
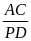 =
4
=
4
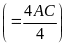
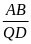 =
4
=
4
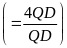
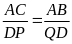 ;
;
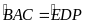
ABC P DQP (c.g.c)
*
Bài tập đề nghị: 1)
Cho ABC,
AD là phân giác
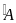 ;
AB < AC. Trên tia đối của DA lấy điểm I sao cho
;
AB < AC. Trên tia đối của DA lấy điểm I sao cho
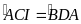 .
Chứng minh rằng.
.
Chứng minh rằng.
ADB P ACI; ADB P CDI
AD2 = AB. AC - BD . DC
2) Cho ABC; H, G, O lần lượt là trực tâm, trọng tâm, giao điểm 3 đường trung trực của . Gọi E, D theo thứ tự là trung điểm của AB và AC.
Chứng minh :
OED P HCB
GOD P GBH
Ba điểm O, G, H thẳng hàng và GH = 2OG
3) Cho ABC có Ab = 18cm, AC = 24cm, BC = 30cm. Gọi M là trung điểm BC. Qua M kẻ đường vuông góc với BC cắt AC, AB lần lượt ở D, E.
CMR : ABC P MDC
Tính các cạnh MDC
Tính độ dài BE, EC
4)
Cho ABC;
O là trung điểm cạnh BC. Góc
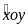 = 600;
cạnh ox cắt AB ở M; oy cắt AC ở N.
= 600;
cạnh ox cắt AB ở M; oy cắt AC ở N.
Chứng minh: OBM P NCO
Chứng minh : OBM P NOM
Chứng minh : MO và NO là phân giác của
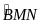 và
và
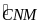
Chứng minh : BM. CN = OB2
&.DẠNG5:Chứng minh đoạn thẳng bằng nhau, góc bằng nhau:
_Ví dụ 1: Cho hình thang ABCD (AB// CD). Hai đường chéo AC và BD cắt nhau tại O. Đường thẳng a qua O và song song với đáy của hình thang cắt các cạnh bên AD, BC theo thứ tự tại E và F.
 C
C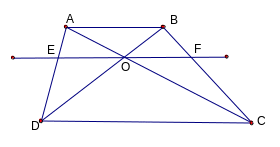 hứng
minh rằng : OE = OF
hứng
minh rằng : OE = OF
Định hướng H:Bài cho đường thẳng EF // AB (và CD) TL: Các tam giác đồng dạng và các đoạn thẳng tỷ lệ H: EO và đoạn nào trên hình vẽ sẽ thường lập được tỷ số? TL:
H: Vậy OF trên đoạn nào? (gợi ý) TL:
|
Sơ đồ giải OE = OF
AEC BOF AOB P P P ADC BDC COD EF // DC AB // CD gt |
H: Vậy để chứng minh đoạn thẳng bằng nhau (OE = OF) ta sẽ đưa về chứng minh điều gì?
TL
:
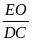 =
=
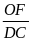 (1)
(1)
H: OE; DC là cạnh của những tam giác nào? (AEO; ADC, các tam giác này đã đồng dạng chưa? Vì dao?
H: Đặt câu hỏi tương tự cho OF , DC.
H:
lập tỷ số bằng
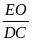 =
=
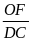
TL:
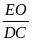 =
=
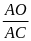 ;
;
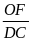 =
=
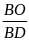
H: Vậy để chứng minh (1) ta cần chứng minh điều gì?
TL:
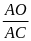 =
=
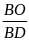
H: Đây là tỷ số có được từ cặp tam giác đồng dạng nào?
TL: AOB; COD
H: Hãy chứng minh điều đó.
Ví
dụ 2:
Trên một cạnh của góc xoy (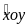
1800),
đặt các đoạn thẳng OA = 5cm, OB = 16cm. Trên cạnh thứ
nhất của góc đó, đặt các đoạn thẳng OC = 8cm, OD =
10cm.
1800),
đặt các đoạn thẳng OA = 5cm, OB = 16cm. Trên cạnh thứ
nhất của góc đó, đặt các đoạn thẳng OC = 8cm, OD =
10cm.
a) Chứng minh hai tam giác OCB và OAD đồng dạng.
 b
b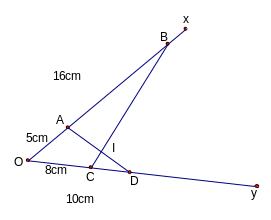 )
Gäi giao ®iÓm c¸c c¹nh AD vµ BC lµ I, CMR: Hai tam gi¸c IAB
vµ ICD cã c¸c gãc b»ng nhau tõng ®«i mét.
)
Gäi giao ®iÓm c¸c c¹nh AD vµ BC lµ I, CMR: Hai tam gi¸c IAB
vµ ICD cã c¸c gãc b»ng nhau tõng ®«i mét.
Giải:a)Ta
có: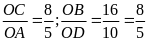
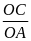 =
=
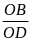
OBC
P
ODA
OBC
P
ODA
Góc O chung
b) Xét IAB và ICD ta dễ nhìn thấy không bằng nhau.
Do đó để chứng minh chúng có các góc bằng nhau
từng đôi một ta đi chứng minh đồng dạng.
Vì
OBC
P
ODA
nên
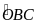 =
=
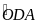 (1)
(1)
Mặt
khác ta có
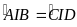 (đối đỉnh)
(đối đỉnh)
BAI P DCI (g.g)
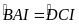
Ví dụ 3: Hình thang ABCD (AB // CD) có AB = 4cm, CD = 16cm và BD = 8cm
C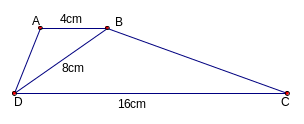 hứng
minh :
hứng
minh :
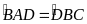
Giải :Xét BAD và DBC có AB // CD do đó :
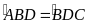 (so
le trong )
(so
le trong )

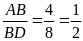
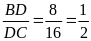
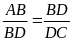 (
cùng bằng
(
cùng bằng
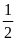 )
)
BAD P DBC (c.g.c)
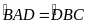
 Ví
dụ 4:
Tam
giác ABC có hai trung tuyến AK và CL cắt nhau tại O. Từ
một điểm P bất kỳ trên cạnh AC, vẽ các đường thẳng
PE song song với AK, PF song song với CL ( E thuộc BC, F thuộc
AB) các trung tuyến AK, CL cắt đoạn thẳng EF theo thứ tự
tại M,
N . Chứng minh rằng các đoạn thẳng FM, MN, NE bằng nhau.
Ví
dụ 4:
Tam
giác ABC có hai trung tuyến AK và CL cắt nhau tại O. Từ
một điểm P bất kỳ trên cạnh AC, vẽ các đường thẳng
PE song song với AK, PF song song với CL ( E thuộc BC, F thuộc
AB) các trung tuyến AK, CL cắt đoạn thẳng EF theo thứ tự
tại M,
N . Chứng minh rằng các đoạn thẳng FM, MN, NE bằng nhau.
Định hướng giải:
Từ giả thiết cho song song ta suy ra
các tỷ lệ thức và tam giác đồng dạng
Ta có :
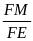
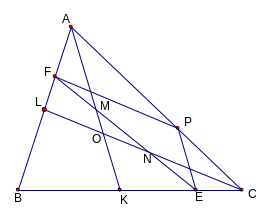 =
=
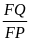 (1)
(1)
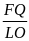 =
=
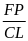 (cùng
(cùng
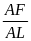 )
)
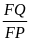 =
=
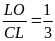 (2) ( ta có trung tuyến
(2) ( ta có trung tuyến
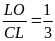 )
)
Từ
(1) và (2) suy ra :
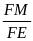 =
=
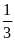
FM =
FM =
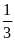 FE
FE
Tương
tự ta cũng có EN =
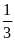 EF
và do đó suy ra MN =
EF
và do đó suy ra MN =
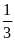 EF
EF
Vậy FM = MN = NE
* Bài tập đề nghị :Cho hình thang ABCD (AB // CD) đường thẳng song song với đáy Ab cắt các cạnh bên và các đường chéo AD, BD, AC và BC theo thứ tự tại các điểm M, N, P, Q. CMR: MN = PQ
&.DẠNG 6: Toán ứng dụng thực tế:
+ Ví dụ 1: Để đo khoảng cách giữa 2 điểm A và M, trong đó M không tới được, người ta tiến hành đo và tính khoảng cách (như hình vẽ) AB BM; BH AM. Biết AH = 15m; AB = 35m.
G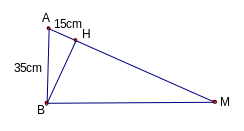 iải
: Xét
AMB và
ABH có ;
iải
: Xét
AMB và
ABH có ;
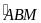 =
=
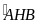 = 900
(gt) ;
= 900
(gt) ;
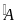 chung
chung
AMB P ABH (gg)
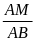 =
=
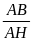
AM =
AM =
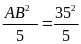 = 81,7(m)
= 81,7(m)
Vậy khoảng cách giữa 2 điểm A và M gần bằng 81,7 m
+ Ví dụ 2: Một ngọn đèn đặt trên cao ở vị trí A, hình chiếu vuông góc của nó trên mặt đất là H. Người ta đặt một chiếc cọc dài 1,6m, thẳng đứng ở 2 vị trí B và C thẳng hàng với H (hình vẽ) Khi đó bóng cọc dài 0,4m và 0,6m . Biết BC = 1,4m. Hãy tính độ cao AH.
Giải
G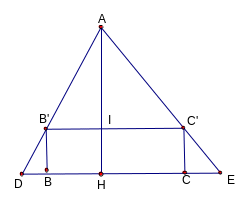 ọi
BD, CE là bóng của cọc và B’ ; C’ là tương ứng của
đỉnh cao. Đặt BB’ = CC’ = a ; BD = b ; CE = c ; BC = d ;
AH = x. Gọi I là giao điểm của AH và B’C’.
ọi
BD, CE là bóng của cọc và B’ ; C’ là tương ứng của
đỉnh cao. Đặt BB’ = CC’ = a ; BD = b ; CE = c ; BC = d ;
AH = x. Gọi I là giao điểm của AH và B’C’.
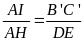
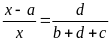
(x – a) (b + d + c) = x.d
x
=
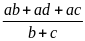 = a(1+
= a(1+
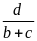 )
)
Thay
số ta được AH = 1,6 (1 +
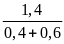 )
= 3,84(m)
)
= 3,84(m)
Vậy độ cao AH bằng 3,84 mét
*Bài tập đề nghị:
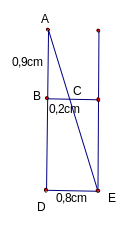
Một giếng nước có đường kính DE = 0,8m (hình vẽ).
Để xác định độ sâu BD của giếng, người ta đặtmột chiếc gậy ở vị trí AC, A chạm miệng giếng,
AC nhìn thẳng tới vị trí E ở góc của đáy giếng. Biết AB = 0,9m; BC = 0,2m. Tính độ sâu BD của giếng.
III/KẾT LUẬN: Tam giác đồng dạng có nhiều ứng dụng trong giải toán. Đây là một khái niệm khó đối với học sinh , do đó giáo viên cần hướng dẫn, phân tích tỉ mỉ để học sinh tìm ra các bước chứng minh . Khi ứng dụng để chứng minh đoạn thẳng bằng nhau, góc bằng nhau thì các phương pháp thường dùng ở đây là :
* Đưa 2 đoạn thẳng cần quy bằng nhau về là tử của 2 tỷ số có cùng mẫu.
* Chứng minh các đoạn thẳng cùng bằng một độ dài nào đó.
* Đưa 2 góc cần chứng minh bằng nhau về là 2 góc tương ứng của 2 tam giác đồng dạng.
* Chứng minh 2 tỷ số bằng nhau sau đó chứng minh tử bằng nhau suy ra 2 đoạn thẳng ở mẫu bằng nhau
*Nói chung tuỳ bài toán cụ thể cần sử dụng kiến thức tam giác đồng dạng để giải, ta phải biết cách chọn cặp tam giác đồng dạng phù hợp để chứng minh. Có thể vẽ thêm để xuất hiện cặp tam giác đồng dạng. Chúc các em thành công trong học tập.
Quy Nhơn ,
NGUYỄN - KIM - CHÁNH
Ngoài SKKN Các Bài Toán Về Tam Giác Đồng Dạng thì các tài liệu học tập trong chương trình 8 sẽ được cập nhật liên tục và nhanh nhất có thể sau khi kỳ thi diễn ra trên Danh mục Tài Liệu Học Tập nhằm giúp các bạn đọc thuận tiện trong việc nghiên cứu tài liệu. Quý thày cô và các bạn đọc có thể chia sẻ thêm những tài liệu học tập hữu ích đến địa chỉ email của chúng tôi, nhằm xây dựng nên kho đề thi phong phú, đa dạng cho các em học sinh tham khảo và rèn luyện.
Xem thêm
| Chuyên Đề Văn Tự Sự Lớp 8 |