Giao tuyến là gì, Bài tập môn Toán liên quan đến giao tuyến
Giao tuyến là gì? Giao tuyến là một khái niệm khá quan trọng trong bộ môn toán hình. Hy vọng những khái niệm, phương pháp giải, bài tập minh họa và các kiến thức liên quan mà Trang Tài Liệu cung cấp sẽ giúp các bạn hiểu rõ hơn về giao tuyến. Từ đó, có thể linh hoạt ứng dụng vào giải bài tập hay giải quyết các vấn đề trong cuộc sống.
Giao tuyến là gì?
Giao tuyến là một thuật ngữ được sử dụng trong hệ thống giao thông đường bộ để chỉ định vị trí giao nhau giữa hai hoặc nhiều tuyến đường khác nhau. Điểm giao tuyến là điểm mà các tuyến đường gặp nhau và tạo thành một điểm giao thông.
Giao tuyến có thể là các dạng khác nhau, bao gồm:
- Ngã tư: Giao tuyến giữa ba tuyến đường.
- Ngã ba: Giao tuyến giữa hai tuyến đường.
- Ngã năm, ngã sáu, và các loại ngã lớn hơn: Giao tuyến giữa nhiều hơn hai tuyến đường.
Giao tuyến đóng vai trò quan trọng trong việc điều phối và điều tiết luồng giao thông giữa các tuyến đường, giúp tăng cường an toàn và hiệu quả giao thông đường bộ. Các biển báo, đèn tín hiệu và các biện pháp điều phối được sử dụng tại giao tuyến để hướng dẫn và điều chỉnh các phương tiện di chuyển một cách an toàn và trơn tru trên các tuyến đường khác nhau.
Thế nào là giao tuyến của hai mặt phẳng
Giao tuyến của hai mặt phẳng là đường thẳng chứa tất cả điểm chung của hai mặt phẳng đó.
Phương pháp xác định giao tuyến của hai mặt phẳng
- Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thi ba giao tuyến áy hoặc đồng quy hoặc đôi một song song.
⇒ Hệ quả: Nếu hai mặt căt nhau lần lượt đi qua hai đường thẳng song song thì giao tuyến của hai mặt phẳng đó song song với hai đường thẳng hoặc trùng với một trong hai đường thẳng.
- Nếu đường thẳng a song song với mặt phẳng (P) thì mọi mặt phẳng (Q) chứa a mà cắt (P) thì cắt theo giao tuyến song song với a.
⇒ Hệ quả: Nếu hai mặt phẳng cắt nhau cùng song song với một đường thẳng thì giao tuyến của chúng cũng song song với mặt phẳng đó.
Nhớ rằng: Một đường thẳng được xác định khi biết hai điểm phân biệt thuộc đường thẳng đó hoặc biết một điểm thuộc đường thẳng đó và phương của đường thẳng. Do vậy, dựa vào định nghĩa của đường giao tuyến, ta có thể xác định đường giao tuyên bằng các phương pháp sau:
- Phương pháp 1. Tìm hai điểm chung phân biệt của hai mặt phẳng. Đường thẳng nối hai điểm chung đó chính là giao tuyến của hai mặt phẳng.
Cách tìm giao tuyến của 2 mặt phẳng
+ Tìm ra hai điểm chung của mặt phẳng thứ nhất và mặt phẳng thứ hai
+ Nối hai điểm chung vừa tìm được ở trên ta được một đường thẳng. Đường thẳng này chính là giao tuyến của 2 mặt phẳng
* Chú ý: Nếu 2 mặt phẳng (P) và (Q) lần lượt chứa 2 đường thẳng a và b, trong đó: a // b và M là điểm chung của 2 mặt phẳng (P) và (Q). Khi đó, giao tuyến của 2 mặt phẳng (P) và (Q) là đường thẳng Mx, trong đó: Mx // a // b
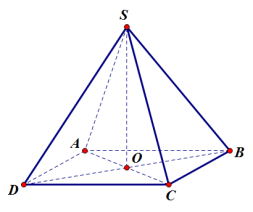
Ví dụ 1. Cho S là một điểm không thuộc mặt phẳng chứa hình bình bình hành ABCD. Tìm giao tuyến của hai mặt phẳng (SAC) và (SBD).
Giải
Dễ dàng thấy rằng, điểm S là một điểm chung của hai mặt phẳng (SAC) và (SBD).
Như vậy, để xác định giao tuyến của hai mặt phẳng này, ta chỉ cần tìm thêm một điểm chung nữa.
Trong mặt phẳng chứa hình bình hành ABCD, lấy điểm O sao cho: O = AC ∩ BD.
Khi đó,
- O ∈ AC mà AC ⊂ (SAC) ⇒ O ∈ (SAC)
- O ∈ BD mà BD ⊂ (SBD) ⇒ O ∈ (SBD).Do vậy O là 1 điểm chung của hai mặt phẳng (SAC) và (SBD).
Vậy, SO là giao tuyến của hai mặt phẳng (SAC) và(SBD).
Ví dụ 2. Cho điểm S không thuộc mặt phẳng chứa hình thang ABCD (AB // CD và AB > CD). Tìm giao tuyến hai mặt phẳng (SAD) và (SBC).
Giải
Dễ dàng thấy rằng, điểm S là một điểm chung của hai mặt phẳng (SAC) và (SBD).
Như vậy, để xác định giao tuyến của hai mặt phẳng này, ta chỉ cần tìm thêm một điểm chung nữa.
Ta thấy, AB > CD. Kẻ đường thẳng AD cắt đường thẳng BC tại I.
Khi đó,
- I ∈ AD mà AD ⊂ (SAD) ⇒ I ∈ (SAD)
- I ∈ BC mà BC ⊂ (SBC) ⇒ I ∈ (SBC)
Do đó, I là một điểm chung của hai mặt phẳng (SAD) và (SBC).
Vậy, SI là giao tuyến của hai mặt phẳng (SAD) và (SBC).
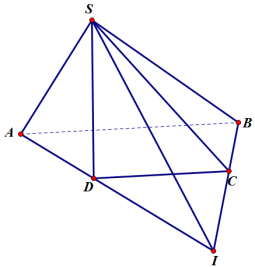
Ví dụ 3. Cho bốn điểm A, B, C, D không thuộc cùng một mặt phẳng. Trên các đoạn thẳng AB, AC, BD lấy lần lượt các điểm M, N, P sao cho MN không song song với BC. Tìm giao tuyến của (BCD) và (MNP).
Giải
Vì P ∈ BD mà BD ⊂ (SBD) ⇒ P là một điểm chung của hai mặt phẳng (MNP) và (SBD).
Bây giờ, chúng ta cần tìm thêm một điểm chung nữa. Vì MN không song song với BC nên kẻ đường thẳng MN cắt đường thẳng BC tại I.
Khi đó,
- I ∈ MN mà MN ⊂ (MNP) ⇒ I ∈ (MNP)
- I ∈ BC mà BC ⊂ (SBC) ⇒ I ∈ (SBC)
Do vậy, I là một điểm chung của hai mặt phẳng (SBC) và (MNP).
Vậy, PI là giao tuyến của hai mặt phẳng (SBC) và (MNP).
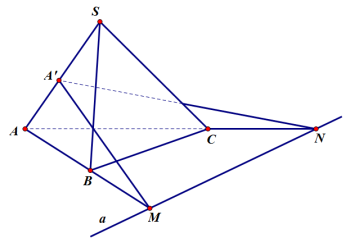
Ví dụ 4. Cho Δ ABC nằm trong mặt phẳng (P) và đường thẳng a nằm trong mặt phẳng (P) không song song với AB, AC. S là một điểm nằm ngoài mặt phẳng (P) và A’ là một điểm thuộc SA. Xác định giao tuyến của hai mặt phẳng (A’; a) và (ABC).
Giải
Kẻ đường thẳng AB cắt đường thẳng a tại M. Nối A’M. Khi đó,
- A’M ⊂ (A’; a) và M ∈ (A’; a).
- M ∈ AB mà AB ⊂ (ABC) ⇒ M ∈ (ABC)
Vậy M là một điểm chung của hai mặt phẳng (A’;a) và (ABC).
Kẻ đường thẳng AC cắt đường thẳng a tại N. Nối A’N. Khi đó,
- A’N ⊂ (A’; a) và N’ ∈ (A’; a).
- N ∈ AC mà AC ⊂ (ABC) ⇒ N ∈ (ABC)
Vậy N là một điểm chung của hạ mặt phẳng (Á’; a) và (ABC).
Do đó, MN là giao tuyến của hai mặt phẳng (A’; a) và (ABC).
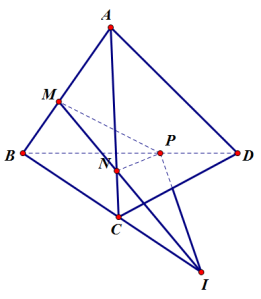
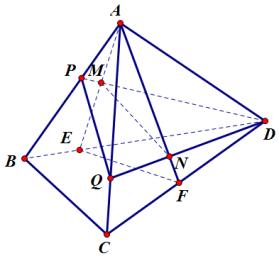
Ví dụ 5. Cho tứ diện A.BCD, M là một điểm bên trong tam giác ABD, N là một điểm bên trong tam giác ACD. Tìm giao tuyến của các cặp mặt phẳng sau:
a) (AMN) và (BCD)
b) (DMN) và (ABC)
Giải
a) Kẻ AM cắt BD tại E.
Khi đó,
- E ∈ AM mà AM ⊂ (AMN) ⇒ E ∈ (AMN)
- E ∈ BD mà BD ⊂ (BCD) ⇒ E ∈ (BCD)
Do đó, E là một điểm chung của hai mặt phẳng (AMN) và (BCD).
Kẻ AN cắt CD tại F.
Khi đó,
- F ∈ AN mà AN ⊂ (AMN) ⇒ F ∈ (AMN)
- F ∈ CD mà CD ⊂ (BCD) ⇒ F ∈ (BCD)
Do đó, F là một điểm chung của hai mặt phẳng (AMN) và (BCD).
Vậy, EF là giao tuyến của hi mặt phẳng (AMN) và (BCD).
b) Kẻ DM cắt AB tại P.
Khi đó,
- P ∈ AB mà AB ⊂ (ABC) ⇒ F ∈ (ABC)
- P ∈ DM mà DN ⊂ (DMN) ⇒ P ∈ (DMN)
Do đó, P là một điểm chung của hai mặt phẳng (ABC) và (DMN).
Kẻ DN cắt AC tại Q.
Khi đó,
- Q ∈ AC mà AC ⊂ (ABC) ⇒ Q ∈ (ABC)
- Q ∈ DN mà DN ⊂ (DMN) ⇒ Q ∈ (DMN)
Do đó, Q là một điểm chung của hai mặt phẳng (ABC) và (DMN).
Vậy, PQ là giao tuyến của hai mặt phẳng (ABC) và (DMN).
Trên đây là phần tóm tắt cách xác định giao tuyến của 2 mặt phẳng và một số bài tập liên quan. Mong rằng thông qua bài viết, các em có thể giải quyết nhiều bài tập liên quan hơn nữa. Đồng thời ôn tập, củng cố kiến thức để chuẩn bị thật tốt cho các kì thi sắp tới.